Computational design of an amidase by combining the best electrostatic features of two promiscuous hydrolases

Abstract

While there has been emerging interest in designing new enzymes to solve practical challenges, computer-based options to redesign catalytically active proteins are rather limited. Here, a rational QM/MM molecular dynamics strategy based on combining the best electrostatic properties of enzymes with activity in a common reaction is presented. The computational protocol has been applied to the re-design of the protein scaffold of an existing promiscuous esterase from Bacillus subtilis Bs2 to enhance its secondary amidase activity. After the alignment of Bs2 with a non-homologous amidase Candida antarctica lipase B (CALB) within rotation quaternions, a relevant spatial aspartate residue of the latter was transferred to the former as a means to favor the electrostatics of transition state formation, where a clear separation of charges takes place. Deep computational insights, however, revealed a significant conformational change caused by the amino acid replacement, provoking a shift in the pK_a of the inserted aspartate and counteracting the anticipated catalytic effect. This prediction was experimentally confirmed with a 1.3-fold increase in activity. The good agreement between theoretical and experimental results, as well as the linear correlation between the electrostatic properties and the activation energy barriers, suggest that the presented computational-based investigation can transform in an enzyme engineering approach.

---

The application of enzymes for desired chemical transformations has been demonstrated by the report of novel and functional designed structures.^1–5 Recent advances in molecular biology and screening technologies have enabled the creation of enzymes via directed evolution. By mimicking the process of natural evolution, iterative cycles of (semi-)random mutations facilitate the improvement of proteins in the laboratory through screening and selection, and hence the identification of active variants.^6–12 Minimal structural information is needed for this strategy and distal sites critical for enzyme catalysis can also be identified. Nevertheless, directed evolution is limited by the fact that, even with the most efficient high-throughput system, only a fraction of all the possible mutants of a given enzyme can be sampled within a set timeframe.¹³ Furthermore, the development of an efficient screening system for a tailored reaction remains challenging. Recently machine-learning (ML) methods have been proposed to expedite evolution and expand the number of properties that can be optimized.^14,15 However, in order to create enzymes with novel reactivities by means of ML methods, protein engineers will have to use proteins with sequences not assigned to the designated reaction or with properties other than those of specific interest, which currently is a technical challenge. Sequence–function data from engineering experiments must be collected to catalogue the natural diversity of proteins in order to convert ML into a useful tool.¹⁵

An alternative approach is a rational design, a technique that modifies selected residues at specific positions of an already existing protein scaffold through the analysis of existing mechanistic and structural data.¹⁶ To reveal the structures of the protein in the full catalytic process under physiological conditions, including metastable transition state (TS) structures, computer simulations are essential. Among all the computer-assisted design strategies, two philosophies can be identified: the redesign of the active site of an existing substrate-promiscuous enzyme and the de novo design that constructs an enzyme “from scratch”. The use of promiscuous enzymes is found to be a very promising starting point for the design of new and highly efficient biocatalysts.^17,18 However, the knowledge about the particular molecular mechanisms that allow enzymes to catalyze more than one chemical reaction is still under debate.^19–22

Because both the enzyme redesign and the de novo design approach require knowledge of the TS of the reaction to be catalyzed, quantum mechanical (QM) calculations offer crucial complementary information that accelerates the development of novel designed reactions. Moreover, multiscale methods are the only tool that can offer a detailed atomistic picture of the reactions in the active site of the enzyme, which can be dramatically different from that in the gas phase or solution. In multiscale methods, electrons of the reacting fragments are explicitly described by QM methods and the large and complex interacting environment (the fully solvated protein) is described by molecular mechanics (MM) force fields. The mechanism of a reaction in the active site of an enzyme can be determined within these hybrid QM/MM methods through the extensive exploration of the Free Energy Surface (FES). This allows the determination of the rate-limiting step in a multi-step process and, within the framework of Transition State Theory (TST),²³ the prediction of rate constants directly comparable with experiments. Previous studies combining computer simulations with experimental kinetic measurements have demonstrated the good agreement that can be achieved,^24,25 which obviously depends on the quality of both simulations and experiments. In this regard, the error in the determination of activation free energies associated with the use of computational methods such as the umbrella sampling method,^26,27 employed in the present study, is usually accepted to be within 1 kcal mol⁻¹.²⁸

Optimizing the secondary activity of promiscuous enzymes is a non-trivial challenge as can be illustrated by analysing the Bacillus subtilis esterase Bs2. While Bs2 is recognized as a serine hydrolase whose primary reaction is the hydrolysis of esters, it can also catalyze the hydrolysis of the amide bond of N-(4-nitrophenyl)-butyramide as a secondary reaction (Fig. 1).^22,29 Previously directed evolution experiments by Arnold and co-workers resulted in a 7-mutation variant with a 100-fold enhancement of the esterase activity (using para-nitrobenzyl butyrate as the substrate).³⁰ Bornscheuer and co-workers used a combination of directed evolution and rational design based on docking and classical energy minimization to get a 3-fold increase of the amidase activity of Bs2 after two single mutations.²² In a larger context, despite the successes of different computer-assisted designs of new enzymes, it has been argued that the high activities of the best artificial enzymes have been largely due to directed evolution and the contribution of computation was comparatively modest.³¹

Fig. 1 Schematic representation of the reaction mechanism of the hydrolysis of N-(4-nitrophenyl)-butyramide catalyzed by Bs2. (a) Acylation step: the nucleophilic addition of Ser189 to the carbonyl followed by the breaking of the C–N bond is triggered by His399-assisted proton shuffling, and the leaving group, in this case, is 4-nitroaniline. (b) Hydrolysis step: the nucleophilic addition of a water molecule followed by the resolution of the acyl–enzyme complex is triggered by His399-assisted protein shuffling, yielding butyric acid as a product.

We envisaged that creating mutations to optimize the preorganization of the protein environment will result in a variant that exhibits improved activity for the desired reaction.³² Based on our recent QM/MM studies of different enzymatic reactions, we have quantified and shown how the reactivity of different proteins can be rationalized from their electrostatic properties,^{24,25,33–36} as the pioneering studies reported by Warshel and co-workers.^37–39 The computed changes of the electrostatic potential or the electric field exerted by the studied proteins on the key atoms of the substrates reflect that there is a small reorganization of these entities when evolving from the reactant state (RS) to the TS at the lowest energy cost.^24,33–36 The electrostatic effects within the active site of the enzyme, therefore, appear to be critical for the electronic reorganization of the reactants during chemical transformations. These studies support the idea that the electrostatic properties of enzymes are the origin of their catalytic features;⁴⁰ consequently, we view that a detailed understanding of the molecular mechanism, including the evolution of electrostatic potential generated in the active site of the enzyme, could be useful in future computer-assisted protein design methods.

To engineer enzymes with optimal electrostatic preorganization, comparative analysis between unrelated natural enzymes that catalyze the same chemical reactions can be a reliable strategy. In previous studies, we have shown that Candida antarctica lipase B (CALB) also displays amidase activity similar to that of Bs2, though being non-homologous with each other.^24,25 QM/MM studies of the amidase reaction catalyzed by wild-type Bs2 and CALB enzymes were previously conducted.^24,25 We expect that the favorable features of each enzyme could be isolated and combined to create a redesigned enzyme with improved catalytic activity for the secondary amidase reaction. In the present paper, based on our knowledge derived from previous comparative studies, and by applying the concept of electrostatic pre-organization,^{24,33–36,40–43} a variant with improved activity for the designated amidase reaction was generated. After overlapping the structures of both proteins in one of the located TSs, through the use of a rotation quaternion around selected atoms of the substrate, a catalytically improved Bs2 variant was delineated. In particular, residues of Bs2 with an unfavorable electrostatic effect on catalysis were substituted by those placed in an equivalent spatial position in CALB with a favorable effect, as explained in detail below. The QM/MM FES of the full catalytic reaction in the proposed variant, combined with the experimental characterization, will be used to propose a general computer-based strategy that can be potentially used to design new enzymes.

Materials and methods

Computational methods

The primary sequence of the wild-type p-nitrobenzyl (PNB) esterase sequence from Bacillus subtilis (with ID P37967) was taken from UniProt.⁴⁴ Due to the lack of a crystallized structure for this specific variant, the framework for the required model, a natural variant of the protein (strain 168) was prepared based on a PNB esterase from a different organism (Bs2; PDB ID: 1QE3).³⁰ Details can be found in previous publications²⁵ and the ESI.† Based on the analysis of the previously computed FES of the amidase reaction catalyzed by wild-type CALB²⁴ and Bs2 (ref. 25) with N-(4-nitrophenyl)-butyramide as the substrate, the structural alignment of the two proteins was subsequently done within the TS1 structures localized at the QM/MM level in both systems. The QM sub-set of atoms was described with the M06-2X hybrid functional⁴⁵ and the solvent water molecules and the protein treated with the TIP3P⁴⁶ and the OPLS-AA⁴⁷ force field, respectively, as implemented in the fDynamo library.⁴⁸ Then, a short 20 ps QM/MM MD simulation was done freezing the geometries of the quantum partition. The alignment of the structures from the trajectory was done using a rotation quaternion⁴⁹ around the positions of atoms of the amide bond and the two neighboring carbon atoms of the substrate (ESI Fig. S1†). When both proteins were aligned, structures were compared based on the averaged position of the centers of mass of every residue of the protein. The residues of Bs2 and CALB were paired based on the proximity of their centers of mass, i.e., the pair of a residue from Bs2 is the residue from CALB whose center of mass lies nearest to the tested residue (ESI Fig. S2†). Finally, the electrostatic potential generated on the Nε of the catalytic histidine residues of Bs2 and CALB by the residues whose center of mass lies within 15 Å of the center of mass of the substrate was computed.

The proposed variants, F398D with aspartate in its standard protonation state at pH 7, F398D with its protonated variant (F398D-H⁺ from now on), and D66I/L335K were prepared from the structure of wild-type Bs2. Then, counterions were placed in the most electrostatically favorable positions in order to neutralize the three systems. Subsequently, the systems containing the protein, counterions, and the substrate were solvated by placing them in a 100 × 80 × 80 ų pre-equilibrated box of TIP3P⁴⁶ water molecules. After initial energy minimization, the systems were heated to 303 K with 0.1 K temperature increments and equilibrated during short (100 ps) NPT MD simulations, followed by non-accelerated classical NVT MD simulations with a time step of 1 fs. The substrate was described with the same force field parameters as determined in our previous studies.^24,25 During 100 ns MD simulations, all atoms were free to move with periodic boundary conditions and cut-offs for nonbonding interactions were applied using a smooth switching function between 14.5 and 16 Å. The time-dependent evolution of the root mean square deviations (RMSDs) and B-factors for all three variants of Bs2 confirm that they were equilibrated and did not suffer dramatic structural modifications (ESI Fig. S3†).

After setting up the model for F398D, F398D-H⁺ and D66I/L335K, the reaction was studied using a QM/MM approach from the equilibrated structures. The semiempirical AM1 (ref. 50) method and the M06-2X⁴⁵ density functional were used to describe the QM sub-set of atoms, corresponding to the active site (ESI Fig. S4†). The OPLS-AA and TIP3P classical force fields were used to treat the protein and the solvent water molecules, respectively, as implemented in the fDynamo library. After PESs were computed, exploring the appropriate distinguished reaction coordinates, FESs for each of the chemical steps were calculated in terms of PMFs using the umbrella sampling (US) technique^26,27 (ESI Fig. S5–S7†). Structures corresponding to the stationary points were finally optimized at the M06-2X/MM level and IRC paths were traced down to the precedent and posterior energy minima structures.

Experimental methods

A short summary of the experimental procedures is provided while a more detailed description of the experimental procedures is reported in the ESI.† The synthesis of N-(4-nitrophenyl)-butyramide was performed according to a known procedure.²⁴ The production of wild-type Bs2 and Bs2 F398D was based on a previously reported procedure.²²

For the 96 well-plate kinetic assays, stock solutions of the respective Bs2 variant (in 50 mM NaP_i, pH 7.0) and N-(4-nitrophenyl)-butyramide (in DMSO) were prepared. The protein stock solution was kept on ice until use and was freshly prepared before each usage. DMSO and substrate stock solution were added to wells of a 96 transparent well-plate to a total of 15 μL. Buffer (50 mM NaP_i, pH 7.0) was added to a total volume of 135 μL (150 μL in the case of controls to monitor substrate stability). The plate was transferred into a plate reader and double orbitally shaken for 5 s and the absorption at λ_Ex = 405 nm was measured to check the correct substrate distribution. Then 15 μL of protein stock solution were added to each well except the enzyme free controls within 5 min. The final assay conditions were 150 μL volume, 10% DMSO, N-(4-nitrophenyl)-butyramide (10, 50, 100, 250 500, 1000, 2000, and 3000 μM), and 20 μg mL⁻¹ protein. The plate was sealed with an airtight and UV-Vis transparent self-adhesive plastic cover sheet. After sealing, the plate was placed into the plate reader and the assay was performed for 14 h.

Results and discussion

Structural and electrostatic comparison of Bs2 vs. CALB

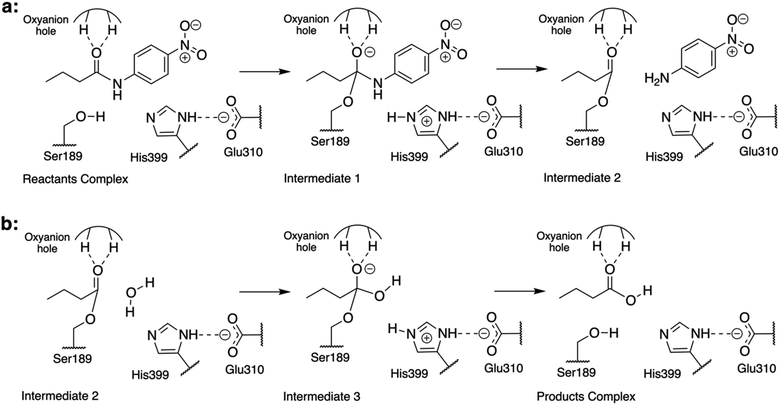
Previous studies of the amidase mechanism catalyzed by CALB²⁴ and Bs2 (ref. 25) (Fig. 1) showed a clear separation of charges in its first step, where a negative charge is accumulated in the carbonyl oxygen atom of the substrate and a positive charge is generated in the Nε atom of His399 (Fig. 1). The stabilization of the negative charge is achieved through interactions with the oxyanion hole that is present in both enzymes through the generation of a microenvironment with positive electrostatic potential.^24,33 As demonstrated before, additional attempts to increase the positive electrostatic potential on this group should not result in a significant catalytic effect.²⁴ Consequently, in the present study we focused on identifying residues in Bs2 and CALB contributing to generate a negative electrostatic potential on the Nε atom of the catalytic histidine residue (His399 or His224 in Bs2 and CALB, respectively), which assists in the positive charge transfer from Ser189/Ser105 that takes place in the first step.

In order to compare the TS1 of two separate protein environments that have significantly low sequence identity, residues located in equivalent spatial positions in both proteins need to be identified (ESI Fig. S1†). The structural alignment of the proteins was done by using a rotation quaternion⁴⁹ around the positions of the atoms of the amide bond of the substrate, and the two adjacent carbon atoms. In particular, the matching was done by pairing the residues of Bs2 and CALB whose averaged centers of mass overlap (or are in close proximity) to each other. The first conclusion derived from the results was good overlapping between the active site triad Ser–His–Glu in Bs2 and the Ser–His–Asp counterpart in CALB (ESI Fig. S2†), implying that both enzymes are preorganized for breaking the C–N bond of the substrate.

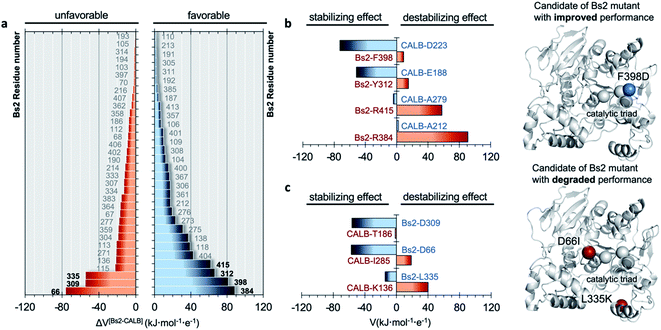
The electrostatic potential on the Nε atom of the active site histidine was computed per residue in Bs2 and CALB. We aimed to seek residues that stabilize the formation of TS1 in CALB which are not found in Bs2 (Fig. 2 and ESI Fig. S8†). The residues that generate a negative potential on Nε can be considered favorable for catalysis whilst those adding a positive potential detrimental to the enzyme activity. The difference between Bs2 and CALB revealed “hot spot” candidates with a positive value for mutagenesis for enhancing the amidase activity in Bs2, whereas residues with negative values proposed to decrease the activity.

Fig. 2 Comparison of electrostatic potential generated by Bs2 and CALB. (a) Difference in the electrostatic potential (ΔV) generated on the Nε atom of the catalytic histidine in the TS1 structure by each residue of Bs2 and CALB, calculated as V_i(Bs2) − V_j(CALB), where i and j are the corresponding paired residues of each enzyme. Only residue numbers of Bs2 are labelled indicating the possible candidates for mutations. The residues are ordered by their estimated role in improving or degrading enzymatic activity: positions with ΔV > 0 have a favorable effect on activity upon mutation (right panel), while those with ΔV < 0 provide an unfavorable effect (left panel). (b) Electrostatic potential generated by selected residues with destabilizing effects in Bs2 (in red) and the corresponding residues from CALB in the same position that have a stabilizing effect (in blue). The proposed mutations to improve Bs2 catalytic activity are shown on the right side of the panel as blue balls. (c) Selected residues with stabilizing effects in Bs2 (blue labels) and the corresponding residues from CALB in the same position that have a destabilizing effect (red labels). The proposed mutations to degrade Bs2 catalytic activity are shown on the right side of the panel as red balls.

Bs2 redesign

As summarized in Fig. 2b, four residues that generate an unfavorable potential on the catalytic His399 in Bs2 were identified (F398, Y312, R415, and R384) by comparison with those located in an equivalent spatial position in CALB with a stabilizing or neutral effect (D223, E188, A279, and A212). Subsequently, the corresponding amino acid replacements in Bs2, F398D, Y312E, R415A, and R384A, were investigated. After the analysis of the surroundings of R384 and R415 in Bs2, these positions were excluded because they form a complex hydrogen-bonding network with the close residues of the amino acids, and the mutation to Ala could be reflected in a large impact in the local structure due to the change in the size and polarity losing all the key hydrogen bond interactions (ESI Fig. S9†). As determined by the calculations with the empirical program PropKa v.3.0.3,^51,52 the substitution of Y312 with glutamate causes a pK_a shift, suggesting that the carboxylic group is protonated in the variant, and hence the predicted increase in the negative electrostatic potential becomes diluted. By elimination, we propose to create just the F398D Bs2 variant. Nevertheless, although calculations with PropKa predict a pK_a value that indicates a deprotonated Asp when inserted in position 398 of Bs2, the possibility of a protonated F398D-H⁺ variant was also investigated by a deep structural analysis of long MD simulations on this variant (ESI Fig. S10†). Indeed, the estimation of the pK_a of the aspartate introduced in position 398 of Bs2 using the equilibrated structure of the protonated F398D-H⁺ variant confirms a shift in its pK_a (from 5.1, in the F398D structure to 7.9 when using the F398D-H⁺ equilibrated structure). This result confirms the requirement of exhaustive structural analysis, in combination with programs such as PropKa, to set up a robust molecular model. Alternatively, constant-pH MD simulation methods^53,54 could be used, where the protonation states of some pre-selected residues can vary during the simulation, in this case for example D398 in the Bs2 variant. The titratable curves derived from these simulations would provide a robust estimation of the protonation state for selected residues.

In silico amidase activity test of the F398D and F398D-H⁺ Bs2 variants

Molecular dynamics (MD) simulations of the Bs2 F398D and F398D-H⁺ variants indicated that the overall protein architecture remains largely unchanged but the protonation of Asp398 appears as a plausible possibility (ESI Fig. S10†). Its catalysis was examined by generating the free energy landscape of the acylation step of the amidase reaction (ESI Fig. S5 and S6†). The barrier of the first step of the reaction decreased 6.2 kcal mol⁻¹ in the F398D variant when compared to the same step catalyzed by wild-type Bs2 (Fig. 3). As anticipated, F398D exerts a stabilization effect for the formation of the first intermediate INT1, decreasing the energy of TS2 relative to the reactants by 3.2 kcal mol⁻¹. In other words, we predicted a significant reduction in the energy barrier of the rate determining step for the acylation step, from 19.2 kcal mol⁻¹ (TS1 in wild-type) to 14.3 kcal mol⁻¹ (TS2 in F398D), which would correspond to an increase of the reaction rate by >3000 fold by applying TST at 303 K. Nevertheless, in the case of the protonated F398D-H⁺ variant this impact is less dramatic generating a lower negative potential on catalytic His399. In this case, the overall barrier of the first step of the reaction is similar to that of wild-type Bs2, with just a small decrease from 19.2 kcal mol⁻¹ in wild-type Bs2 to 18.8 kcal mol⁻¹ in the F398D-H⁺ variant. This difference in the energy barrier indicates a negligible effect.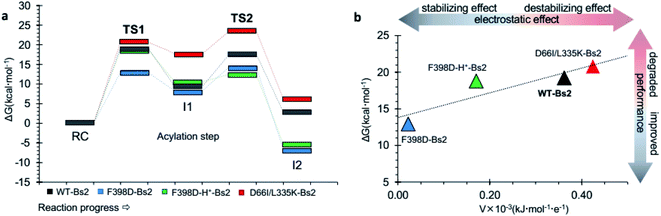

Fig. 3 (a) QM/MM free energy profiles of the acylation step catalyzed by wild-type Bs2 (in grey), by the improved F398D Bs2 variant (in blue), the protonated F398D-H⁺ Bs2 variant (in green), and the degraded D66I/L335K Bs2 variant (in red). Data from wild-type Bs2 was taken from ref. 33. (b) Correlation between the activation free energy of the acylation step and the electrostatic potential in the Nε atom of His.

In order to verify the reliability of our computational strategy, an additional in silico proof test was carried out by designing a Bs2 variant with decreased activity. Based on the comparative analysis of the electrostatic properties of Bs2 and CALB, two possible mutations were identified to decrease the activity of the enzyme including D66I and L335K (see Fig. 2c). The replacement of D309 with threonine was discarded due to the loss of hydrogen bond interactions. For the D66I/L335K mutation, there is a meaningful increase in the free energy barrier for the C–N bond cleavage, up to 23.5 kcal mol⁻¹ (Fig. 3a and ESI Fig. S7†), which aligns with our predictions based on the importance of protein electrostatic. Depending on the Bs2 variant, different turnover frequency determining transition states (TDTSs) in the acylation step of the reaction can be identified.⁵⁵ In accordance with the changes in free energy barriers, TS1 forms the TDTS for wild-type Bs2 and Bs2 F398D, while TS2 constitutes the TDTS in the case of Bs2 F398D-H⁺ and Bs2 D66I/L335K.

In sum, a clear correlation between the free energy barriers and the electrostatic potential generated on catalytic His399 was observed. The lower electrostatic potential on Nε results in a lower energy barrier (Fig. 3b). Although the number of values in Fig. 3b does not allow the confirmation of a statistical correlation, the trend that has been previously observed in our laboratory when exploring the correlation between the electrostatic properties of enzymes and their catalytic activity^34–36 appears to be evident.

Kinetic measurements of the amidase activity of the F398D Bs2 variant

The predictions derived from the QM/MM computational protocol were assessed by experimentally comparing the catalytic activities of the wild-type Bs2 (ref. 25) and F398D variants. The experimental turnover constants (k_cat) measured via UV-Vis spectrophotometric assay are higher than those previously reported by two orders of magnitude (Fig. 4a).^22,29 This could be caused by an alternative arrangement of the hexahistidine tag which includes a C-terminal linker or by the discrepancy of the assay setup. Attempts to use the original assays were found to generate non-reproducible kinetic profiles, possibly due to the low amount of protein used (66 ng mL⁻¹) and long reaction times leading to protein degradation.²⁹ Hence, the present 96-well plate assay methodology, which was proven to be successful in our previous work on CALB²⁴ and showed good agreement between experimental and theoretical k_cat constants for wild-type Bs2,²⁵ was applied. Assays were performed in triplicate. The k_cat and K_M constants for wild-type Bs2 and Bs2 F398D were obtained from the V_max values (Fig. 4c) and the Michaelis–Menten plots (Fig. 4d). The kinetic parameters were obtained using graph fitting software (see Fig. S17–S25†) with excellent Michaelis–Menten kinetics fits (R² ≈ 0.97–0.99). The mean values and population standard deviations show p-values of <0.05. The k_cat constant for the F398D variant is 1.3-fold higher than that for the wild-type. The free energy barrier derived from this experimentally measured rate constant agrees with the computationally assessed enzyme activity for the protonated F398D-H⁺ Bs2 variant (ΔG^‡_exp = 19.4 kcal mol⁻¹ and ΔG^‡_theo = 18.8 kcal mol⁻¹, respectively). On the other hand, the K_M constant for the mutant was noticeably higher resulting in a decrease in the overall catalytic efficiency k_cat/K_M. As the binding step was not explored in the simulation studies, this effect was not predicted. The increase of the K_M in the mutant variant could be explained by the loss of key hydrogen bonds that R415 and Y118 establish with the nitro group of the substrate (ESI Fig. S10a and b†). The mutation of F398 to Asp causes a conformational change in the vicinity of the active site forcing R415 and Y118 to lose the contact with the substrate (ESI Fig. S11a and b†). This observation is supported by the analysis of electrostatic interactions during the MD simulation. The interactions of the substrate with mainly G105, Y118, and R415 could have a role in the stabilization of the Michaelis complex, and those interactions are more favorable in the wild-type than in the F398D-H⁺ Bs2 variant (ESI Fig. S12†).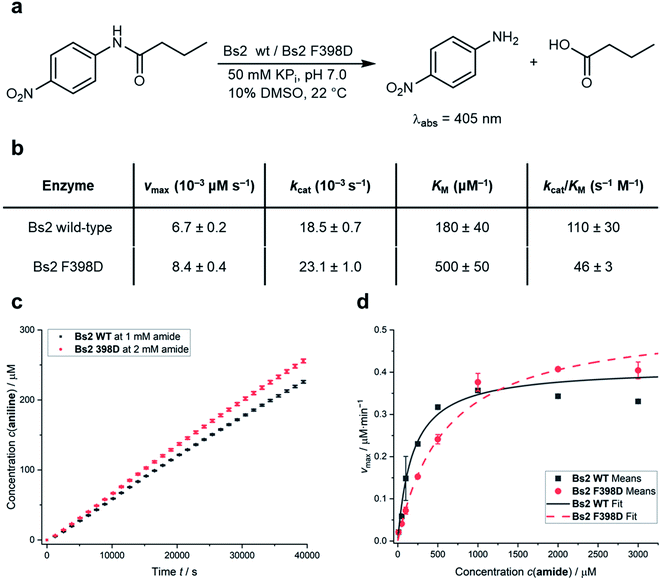

Fig. 4 (a) Model assay reaction and conditions to spectrophotometrically determine the catalytic activities. (b) Table summarizing the kinetic parameters of wild-type Bs2 and F398D Bs2 variants for the reaction shown in (a). Rounded values for simpler visualization are given and exact values are shown in Table S11.† (c) Comparison of 4-nitroaniline formation over time between wild-type Bs2 and F398D Bs2 variants; see the Experimental methods in the ESI† for details on v_max determination. (d) Comparison of Michaelis–Menten plots of wild-type Bs2 and F398D Bs2 variants. All values shown are mean values obtained from triplicate measurements with error bars representing the population standard deviations. Fitting data and errors can be found in Fig. S17–S25.†

Conclusions

We have illustrated a computational strategy to redesign enzymes to enhance their catalytic activity. An in-depth analysis on the electrostatic properties of the chemical transformations under the effect of the protein along the reaction, explored by QM/MM MD simulations, illustrated that the rate-limiting transition states can be stabilized by modifying the electrostatic field on the key fragments of the chemical system through site-directed mutagenesis. In particular, comparative analysis between Bs2 and CALB has facilitated the identification of key residues with a different impact for the amidase reaction; the residues of the former with an unfavorable effect on catalysis are substituted by those at equivalent spatial positions in CALB that exert a favorable effect. In addition, the same strategy was employed to prepare variants of Bs2 with lower catalytic activities, as a control test of the method. The resulting FESs for the acylation step of the amidase reaction catalyzed by the different variants show a linear correlation between the activation free energy of the acylation step and the electrostatic potential in the Nε atom of active site His399.

Our in silico method predicts an, a priori, significant increase of the rate constant after a single mutation of Phe398 to aspartate, which is ∼10 Å away from the active site. Nevertheless, although the estimation of the pK_a of Asp398 in Bs2 indicates that it is deprotonated, in-depth structural analysis of the F398D Bs2 variant during long-term MD simulations suggests that the newly added aspartate residue is most likely protonated, providing a different but stable protein conformational structure. In this regard, the future applications of the proposed computational-based method can include the use of constant-pH MD simulations,^53,54 as a means to obtain titratable curves for selected residues that provide a robust estimation of their protonation states, independent of the starting protein structure.

QM/MM FESs with the F398D-H⁺ variant predict a lower electrostatic effect on the Nε atom of His399, which results in a less dramatic decrease of the energy barrier of the reaction, as confirmed by the experimental kinetic measurement of the variant where Phe398 was converted to aspartate.

While a mild enhancement in the k_cat value of the mutant F398D (23.1 s⁻¹) was obtained, compared with wild type Bs2 (18.5 s⁻¹) in the present study, an excellent agreement between the experimentally determined rate constants and the predicted activation free energies has been achieved, when including a large conformational sampling of the designed enzymes in the protocol. This allowed providing valuable insights such as the role of the electrostatic potential generated by the protein in the active site, which supports the fundamentals of the proposed computational protocol. For future work, several non-titratable residues including artificial amino acids can be introduced together, instead of only converting Phe398 to aspartate, which resulted in an unwanted shift in pK_a. According to our analysis (see Fig. 2a), although their individual contribution is less considerable, when combined together these non-titratable residues can act concertedly to modify the protein electrostatics. Alternatively, this F398D first-generation variant can be subjected to additional engineering work, including QM/MM and structural analyses as well as laboratory evolution, to provide guidance on how additional modifications can favour the new aspartate residue to remain deprotonated. Improvement on the K_M values should also be made as a means to improve the catalytic efficiency of the redesigned enzyme. Supported by the good agreement between theoretical and experimental results achieved in the present and previous studies of the amidase reaction catalyzed by wild-type CALB and Bs2,^24,25 as well as the linear correlation between the electrostatic properties and the activation energy barriers, we hope that upon optimization the presented computer-guided rational design will become a valuable component in the toolkit of enzyme redesign and engineering.

Data availability

The datasets supporting this article have been uploaded as part of the ESI.†

Author contributions

M. A. G. carried out all the calculations. K. Ś. and V. M. supervised the computational work and designed the project. L. Y. P. L. and A. R. N. designed the kinetic measurements. K. H. performed cloning, mutagenesis and initial synthesis of the wild-type under the supervision of A. R. N. A. R. N. performed the synthesis of the mutants and all the kinetic experiments. All authors contributed to analyzing the results and writing the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work was supported by the Spanish Ministerio de Ciencia, Innovación y Universidades (ref. PGC2018-094852-B-C21 and PID2019-107098RJ-I00), the Generalitat Valenciana (ref. AICO/2019/195 and SEJI/2020/007), Universitat Jaume I (UJI-A2019-04 and UJI-B2020-03), and Cardiff University through the start-up fund provided by the Cardiff School of Chemistry. LYPL thanks the BBSRC (BB/T015799/1), the Leverhulme Trust (RPG-2017-195) and the Royal Society (RG170187). K. Ś. thanks the Ministerio de Ciencia, Innovación y Universidades for a Ramón y Cajal contract (REF: RYC2020-030596-I). MAG thanks Universitat Jaume I for the FPI-UJI grant (PREDOC/2017/23). The authors acknowledge computational resources from the Servei d'Informàtica of Universitat Jaume I.

References

1. K. Chen and F. H. Arnold, Tuning the Activity of an Enzyme for Unusual Environments: Sequential Random Mutagenesis of Subtilisin E for Catalysis in Dimethylformamide, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 5618–5622.
2. F. H. Arnold, Combinatorial and Computational Challenges for Biocatalyst Design, Nature, 2001, 409, 253–257.
3. R. Blomberg, H. Kries, D. M. Pinkas, P. R. E. Mittl, M. G. Grütter, H. K. Privett, S. L. Mayo and D. Hilvert, Precision Is Essential for Efficient Catalysis in an Evolved Kemp Eliminase, Nature, 2013, 503, 418–421.
4. P.-S. Huang, S. E. Boyken and D. Baker, The Coming of Age of de Novo Protein Design, Nature, 2016, 537, 320–327.
5. C. Zeymer and D. Hilvert, Directed Evolution of Protein Catalysts, Annu. Rev. Biochem., 2018, 87, 131–157.
6. W. P. C. Stemmer, Searching Sequence Space, Bio/Technology, 1995, 13, 549–553.
7. O. Kuchner and F. H. Arnold, Directed Evolution of Enzyme Catalysts, Trends Biotechnol., 1997, 15, 523–530.
8. U. T. Bornscheuer, Directed Evolution of Enzymes, Angew. Chem., Int. Ed., 1998, 37, 3105–3108.
9. G. MacBeath, P. Kast and D. Hilvert, Redesigning Enzyme Topology by Directed Evolution, Science, 1998, 279, 1958–1961.
10. Y. Yoshikuni, T. E. Ferrin and J. D. Keasling, Designed Divergent Evolution of Enzyme Function, Nature, 2006, 440, 1078–1082.
11. F. H. Arnold, Directed Evolution: Bringing New Chemistry to Life, Angew. Chem., Int. Ed., 2018, 57, 4143–4148.
12. R. Otten, R. A. P. Pádua, H. A. Bunzel, V. Nguyen, W. Pitsawong, M. Patterson, S. Sui, S. L. Perry, A. E. Cohen, D. Hilvert and D. Kern, How Directed Evolution Reshapes the Energy Landscape in an Enzyme to Boost Catalysis, Science, 2020, 370, 1442–1446.
13. H. A. Bunzel, X. Garrabou, M. Pott and D. Hilvert, Speeding up Enzyme Discovery and Engineering with Ultrahigh-Throughput Methods, Curr. Opin. Struct. Biol., 2018, 48, 149–156.
14. R. J. Fox, S. C. Davis, E. C. Mundorff, L. M. Newman, V. Gavrilovic, S. K. Ma, L. M. Chung, C. Ching, S. Tam, S. Muley, J. Grate, J. Gruber, J. C. Whitman, R. A. Sheldon and G. W. Huisman, Improving Catalytic Function by ProSAR-Driven Enzyme Evolution, Nat. Biotechnol., 2007, 25, 338–344.
15. K. K. Yang, Z. Wu and F. H. Arnold, Machine-Learning-Guided Directed Evolution for Protein Engineering, Nat. Methods, 2019, 16, 687–694.
16. K. Świderek, I. Tuñón and V. Moliner, Predicting Enzymatic Reactivity: From Theory to Design, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 407–421.
17. I. Nobeli, A. D. Favia and J. M. Thornton, Protein Promiscuity and Its Implications for Biotechnology, Nat. Biotechnol., 2009, 27, 157–167.
18. R. B. Leveson-Gower, C. Mayer and G. Roelfes, The Importance of Catalytic Promiscuity for Enzyme Design and Evolution, Nat. Rev. Chem., 2019, 3, 687–705.
19. P. Deslongchamps, Stereoelectronic Control in the Cleavage of Tetrahedral Intermediates in the Hydrolysis of Esters and Amides, Tetrahedron, 1975, 31, 2463–2490.
20. E. Busto, V. Gotor-Fernández and V. Gotor, Hydrolases: Catalytically Promiscuous Enzymes for Non-Conventional Reactions in Organic Synthesis, Chem. Soc. Rev., 2010, 39, 4504–4523.
21. P. O. Syrén, P. Hendil-Forssell, L. Aumailley, W. Besenmatter, F. Gounine, A. Svendsen, M. Martinelle and K. Hult, Esterases with an Introduced Amidase-Like Hydrogen Bond in the Transition State Have Increased Amidase Specificity, ChemBioChem, 2012, 13, 645–648.
22. S. Hackenschmidt, E. J. Moldenhauer, G. A. Behrens, M. Gand, I. V. Pavlidis and U. T. Bornscheuer, Enhancement of Promiscuous Amidase Activity of a Bacillus Subtilis Esterase by Formation of a π-π Network, ChemCatChem, 2014, 6, 1015–1020.
23. D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, Current Status of Transition-State Theory, J. Phys. Chem., 1996, 100, 12771–12800.
24. M. Galmés, E. García-Junceda, K. Świderek and V. Moliner, Exploring the Origin of Amidase Substrate Promiscuity in CALB by a Computational Approach, ACS Catal., 2020, 10, 1938–1946.
25. M. Galmés, A. R. Nödling, L. Luk, K. Świderek and V. Moliner, Combined Theoretical and Experimental Study to Unravel the Differences in Promiscuous Amidase Activity of Two Nonhomologous Enzymes, ACS Catal., 2021, 11, 8635–8644.
26. B. Roux, The Calculation of the Potential of Mean Force Using Computer-Simulation, Comput. Phys. Commun., 1995, 91, 275–282.
27. G. M. Torrie and J. P. Valleau, Non-Physical Sampling Distributions in Monte-Carlo Free-Energy Estimation - Umbrella Sampling, J. Comput. Phys., 1977, 23, 187–199.
28. M. J. Field, A Practical Introduction to the Simulation of Molecular Systems, 2nd edn, 2007, vol. 9780521852.
29. R. Kourist, S. Bartsch, L. Fransson, K. Hult and U. T. Bornscheuer, Understanding Promiscuous Amidase Activity of an Esterase from Bacillus Subtilis, ChemBioChem, 2008, 9, 67–69.
30. B. Spiller, A. Gershenson, F. H. Arnold and R. C. Stevens, A Structural View of Evolutionary Divergence, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 12305–12310.
31. G. Jindal, K. Slanska, V. Kolev, J. Damborsky, Z. Prokop and A. Warshel, Exploring the Challenges of Computational Enzyme Design by Rebuilding the Active Site of a Dehalogenase, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 389–394.
32. M. P. Frushicheva, J. Cao and A. Warshel, Challenges and Advances in Validating Enzyme Design Proposals: The Case of Kemp Eliminase Catalysis, Biochemistry, 2011, 50, 3849–3858.
33. K. Świderek, S. Martí and V. Moliner, Theoretical Study of Primary Reaction of Pseudozyma Antarctica Lipase B as the Starting Point to Understand Its Promiscuity, ACS Catal., 2014, 4, 426–434.
34. K. Świderek, I. Tuñón, V. Moliner and J. Bertran, Protein Flexibility and Preorganization in the Design of Enzymes. The Kemp Elimination Catalyzed by HG3.17, ACS Catal., 2015, 5, 2587–2595.
35. A. Krzemińska, V. Moliner and K. Świderek, Dynamic and Electrostatic Effects on the Reaction Catalyzed by HIV-1 Protease, J. Am. Chem. Soc., 2016, 138, 16283–16298.
36. K. Świderek, I. Tuñón, I. H. Williams and V. Moliner, Insights on the Origin of Catalysis on Glycine N-Methyltransferase from Computational Modeling, J. Am. Chem. Soc., 2018, 140, 4327–4334.
37. A. Warshel, Energetics of Enzyme Catalysis, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 5250–5254.
38. A. Warshel, Electrostatic Origin of the Catalytic Power of Enzymes and the Role of Preorganized Active Sites, J. Biol. Chem., 1998, 273, 27035–27038.
39. M. H. M. Olsson, W. W. Parson and A. Warshel, Dynamical Contributions to Enzyme Catalysis: Critical Tests of a Popular Hypothesis, Chem. Rev., 2006, 106, 1737–1756.
40. A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Electrostatic Basis for Enzyme Catalysis, Chem. Rev., 2006, 106, 3210–3235.
41. R. García-Meseguer, S. Martí, J. J. Ruiz-Pernía, V. Moliner and I. Tuñón, Studying the Role of Protein Dynamics in an SN2 Enzyme Reaction Using Free-Energy Surfaces and Solvent Coordinates, Nat. Chem., 2013, 5, 566–571.
42. S. A. Kholodar, A. K. Ghosh, K. Swiderek, V. Moliner, A. Kohen, K. Świderek, V. Moliner and A. Kohen, Parallel Reaction Pathways and Noncovalent Intermediates in Thymidylate Synthase Revealed by Experimental and Computational Tools, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10311–10314.
43. D. De Raffele, S. Martí and V. Moliner, QM/MM Theoretical Studies of a de Novo Retro-Aldolase Design, ACS Catal., 2019, 9, 2482–2492.
44. T. U. Consortium, UniProt: A Worldwide Hub of Protein Knowledge, Nucleic Acids Res., 2018, 47, D506–D515.
45. Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function, Theor. Chem. Acc., 2008, 120, 215–241.
46. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of Simple Potential Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 79, 926–935.
47. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236.
48. M. J. Field, M. Albe, C. Bret, F. Proust-De Martin and A. Thomas, The Dynamo Library for Molecular Simulations Using Hybrid Quantum Mechanical and Molecular Mechanical Potentials, J. Comput. Chem., 2000, 21, 1088–1100.
49. G. R. Kneller, Superposition of Molecular Structures Using Quaternions, Mol. Simul., 1991, 7, 113–119.
50. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, Development and Use of Quantum Mechanical Molecular Models. 76. AM1: A New General Purpose Quantum Mechanical Molecular Model, J. Am. Chem. Soc., 1985, 107, 3902–3909.
51. M. H. M. Olsson, C. R. SØndergaard, M. Rostkowski and J. H. Jensen, PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa predictions, J. Chem. Theory Comput., 2011, 7, 525–537.
52. C. R. Søndergaard, M. H. M. Olsson, M. Rostkowski and J. H. Jensen, Improved Treatment of Ligands and Coupling Effects in Empirical Calculation and Rationalization of pKa Values, J. Chem. Theory Comput., 2011, 7, 2284–2295.
53. J. Mongan, D. A. Case and J. A. McCammon, Constant pH Molecular Dynamics in Generalized Born Implicit Solvent, J. Comput. Chem., 2004, 25, 2038–2048.
54. B. K. Radak, C. Chipot, D. Suh, S. Jo, W. Jiang, J. C. Phillips, K. Schulten and B. Roux, Constant-pH Molecular Dynamics Simulations for Large Biomolecular Systems, J. Chem. Theory Comput., 2017, 13, 5933–5944.
55. S. Kozuch and S. Shaik, How to Conceptualize Catalytic Cycles? The Energetic Span Model, Acc. Chem. Res., 2011, 44, 101–110.

---

Footnote

† Electronic supplementary information (ESI) available: Overlapped centers of mass of paired residues from Bs2 and CALB; structural alignment of Bs2 and CALB; analysis of MD simulations; schematic representation of the QM region; M06-2X:AM1/OPLS-AA free energy surfaces; electrostatic potential generated by Bs2 and CALB per residue; structural analysis of wild-type Bs2 and mutants of Bs2; key interatomic distances and charges; computational and experimental details; cartesian coordinates of M06-2X/MM TS optimized structures and imaginary frequencies; LC chromatograms and mass spectrum; Michaelis–Menten plots. See DOI: 10.1039/d2sc00778a

---