Open Access Article
Open Access ArticleAngle-dependent strength of a single chemical bond by stereographic force spectroscopy†
Wanhao
Cai
 a,
Jakob T.
Bullerjahn
a,
Jakob T.
Bullerjahn
 b,
Max
Lallemang
b,
Max
Lallemang
 ac,
Klaus
Kroy
ac,
Klaus
Kroy
 d,
Bizan N.
Balzer
d,
Bizan N.
Balzer
 *ace and
Thorsten
Hugel
*ace and
Thorsten
Hugel
 *ac
*ac
aInstitute of Physical Chemistry, University of Freiburg, Albertstr. 21, 79104, Freiburg, Germany. E-mail: bizan.balzer@pc.uni-freiburg.de; thorsten.hugel@pc.uni-freiburg.de
bDepartment of Theoretical Biophysics, Max Planck Institute of Biophysics, Max-von-Laue-Straße 3, 60438, Frankfurt am Main, Germany
cCluster of Excellence livMatS@FIT – Freiburg Center for Interactive Materials and Bioinspired Technologies, University of Freiburg, Georges-Köhler-Allee 105, 79110, Freiburg, Germany
dInstitute for Theoretical Physics, Leipzig University, Brüderstraße 16, 04103, Leipzig, Germany
eFreiburg Materials Research Center (FMF), University of Freiburg, Stefan-Meier-Str. 21, 79104, Freiburg, Germany
First published on 26th April 2022
Abstract
A wealth of chemical bonds and polymers have been studied with single-molecule force spectroscopy, usually by applying a force perpendicular to the anchoring surface. However, the direction-dependence of the bond strength lacks fundamental understanding. Here we establish stereographic force spectroscopy to study the single-bond strength for various pulling angles. Surprisingly, we find that the apparent bond strength increases with increasing pulling angle relative to the anchoring surface normal, indicating a sturdy mechanical anisotropy of a chemical bond. This finding can be rationalized by a fixed pathway for the rupture of the bond, resulting in an effective projection of the applied pulling force onto a nearly fixed rupture direction. Our study is fundamental for the molecular understanding of the role of the direction of force application in molecular adhesion and friction. It is also a prerequisite for the nanoscale tailoring of the anisotropic strength of bottom-up designed materials.
Introduction
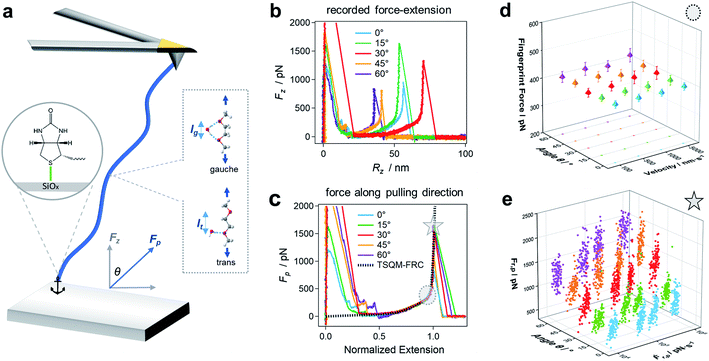
The reaction of a system to an external force and its direction is one of the most fundamental topics in chemistry and physics. A direction-dependent response to applied forces matters for a wide variety of systems across all scales (Fig. 1). For a bottom-up comprehensive understanding and control of this effect, the mechanics of the smallest load-bearing elements, i.e., single molecular bonds, needs to be characterized. Throughout the last three decades, individual bonds have been extensively studied by atomic force microscopy (AFM)-based single-molecule force spectroscopy (SMFS) using vertical pulling (θ = 0°, Fig. 2).1–10 However, the direction-dependence of the rupture force of a bond has hardly been systematically studied. For mechanophores the role of topology and force-transduction by polymer chains has already been noted a decade ago,11,12 but the effect of force vectors on single molecular bonds has remained largely unclear. In addition, coarse-grained theoretical approaches like molecular dynamics (MD) simulations rely on spherical symmetric force fields, and therefore lack abilities to provide molecular details for direction-dependent bond rupture.In this study, we develop AFM-based stereographic force spectroscopy to investigate the strength of single surface bonds along various pulling directions. Forces are applied at defined, preset pulling angles by simultaneously driving the z- and x-piezos with nanometer accuracy (Fig. S1†).13–15
Note that several potential confounding effects, such as vertical or lateral deflections and torsions of the cantilever, as well as the accuracy of the piezo system, may induce errors in stereographic pulling. We have largely eliminated these effects in our experiments and shown that the remaining uncertainties are negligible. The details of the analysis can be found in the Analysis of various effects in stereographic pulling in the ESI and Fig. S2 and S3.†
Results and discussion
First, we study the chemical bond strength between biotin and a glass surface, with a single polyethylene glycol (PEG) chain acting as a linker. This can result in a sulfur-glass bond as an anchor to the surface in H2O (Fig. 2a),16–18 whose strength will be tested in the following experiments under different pulling angles. The formation of such an anchor bond is further validated by three different systems (PEG-thiol, PEG-methoxy, PEG-NHS on glass, respectively, see Fig. S4†): rupture events at high forces (>400 pN) are only observed for PEG-thiol, confirming that these rupture events originate from the sulfur-glass bond and not from any non-specific interactions between the PEG chain and the substrate. Starting from vertical pulling (θ = 0°), we collect several hundred (n >500) force–extension curves, where high stretching forces (Fp >500 pN) can be observed. Such high forces allow us to see the well-defined force–extension fingerprint (kink) of PEG at around 400 pN for vertical pulling (Fig. 2b), which has previously been ascribed to the force-induced gauche–trans transition of PEG monomers in H2O (Fig. 2a).19 This well-understood kink is a crucial control for the following stereographic pulling experiments.Then, we show that the force can be transmitted to the anchor bond along the pulling direction via the PEG chain. This is evident from the constant single-chain elasticity of PEG during stereographic pulling at different angles as detailed in the following. The recorded PEG force–extension curves are shown in Fig. 2b. Here, the recorded force Fz is the vertical (θ = 0°) component of the force along the pulling direction Fp (see Fig. 2a), because the AFM cantilever deflects and records the force in the vertical direction. To recover the force–extension curve along the pulling direction, we convert the force Fz to Fp with the corresponding pulling angle θ (θ = 0° for vertical pulling):
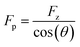 | (1) |
Similarly, we obtain Rp = Rz cos(θ)−1 for the chain extension along the pulling direction (see Reconstruction of the curves along pulling direction in ESI and Fig. S4 for details†). Then, we normalize the traces under different angles as shown in Fig. 2c (see Fig. S5–S7 for details†). These force–extension curves can be well superposed, confirming that the elastic response of a polymer chain does not depend on the pulling direction.
In addition, we can fit the PEG force–extension curves in the whole force region and for different pulling angles with a two-state (gauche, trans) coupled freely rotating chain model, where the elastic stretching modulus γ of PEG at high forces is obtained from quantum mechanical calculations (TSQM-FRC model, see Single-chain elasticity model in ESI†):20
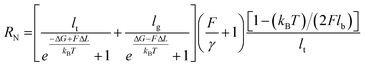 | (2) |
Here, RN is the normalized extension, lg, lt, lb, ΔL are all fixed structural parameters of PEG, thus leaving the free energy difference (ΔG) between the two states as the only unknown parameter.19 As shown in Fig. 2c and S5,† the PEG force–extension curves in H2O can be well fitted with ΔG = 3.6 kBT, in good agreement with previous reports in H2O (3 to 4 kBT).19,21
Fig. 2d shows that the mean fingerprint (kink) position is also independent on the pulling velocity (along the pulling direction) in the range accessible by AFM, indicating that the chain is in a quasi-equilibrium in our study.22 This is reasonable because of the very fast relaxation of conformational changes on the picosecond timescale:19,23 the PEG chain reacts faster than the timescale of the experiment to the applied pulling force, and thus always gets rearranged along the pulling direction. This conclusion is also supported by the results of several previous studies on single-chain elasticity using similar or different technical methods.24–27
Now we assess the rupture force of the bond at the surface in an angle-dependent way, which has not been done before. Therefore, we determine the rupture force Fr,p and loading rate Ḟr,p along the pulling direction and construct angle-dependent dynamic force spectra. Fig. 2e shows that Fr,p increases with Ḟr,p as expected, since the bond rupture is a non-equilibrium process.28 Surprisingly, Fr,p also increases with increasing pulling angle θ: this means that the anchor bond strength seemingly changes with the pulling direction. For a pulling velocity of 5000 nm s−1, the mean Fr,p is 949 (±173) pN for θ = 0° and almost doubles for θ = 60°, giving 1832 (±228) pN. Note that a force of approx. 2000 pN is usually associated with the rupture of a covalent bond.1,29,30 As this force acts on all bonds within the PEG chain, one could expect bond ruptures anywhere between the anchoring points. We have observed hundreds of rupture events at rupture forces higher than 1500 pN (n = 257) and find that these high rupture forces and the respective rupture positions remain constant throughout the experiment (Fig. S8†). As the force–extension curves can be repeated obtaining the same signature for hundreds of consecutive curves with the same PEG-biotin functionalized AFM cantilever tip on the same glass substrate, these results validate that the rupture almost always happens at the anchor bond, which is consistent with recent studies on pathogen adhesin.31 This means that the bonds within the polymer chain are still stronger than the anchor bond even under the imposed conditions of oblique pulling, as required for stereographic force spectroscopy.
To determine the underlying mechanism of the angle-dependence of the bond strength, we construct the free-energy landscape of the bond for different pulling angles and obtain the rupture pathway. This is commonly done by analyzing the rupture forces via the Bell–Evans model,32 which is based on the heuristic Bell rate33 that is accurate on the force scale of a few pN. At higher forces, the Bell rate only offers a crude approximation, as seen by the fact that the Bell–Evans variance of the rupture force (and all higher moments) deviate strongly from Brownian dynamics simulation data.28 Instead, we rely on the microscopically exact Dudko–Hummer–Szabo (DHS) model,28,34 which predicts the following functional form for the force-dependent dissociation rate (see Rupture force data analysis in ESI†):
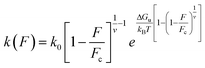 | (3) |
This expression holds for rupture forces F below the critical force Fc = ΔGu(vxu)−1, where ΔGu denotes the height of the free-energy barrier, xu is the distance from the bound state to the barrier, and v is a dimensionless parameter that can take the values v = 1/2, v = 2/3, and v = 1. The former two values correspond to cusp and linear-cubic free-energy profiles respectively, while the latter value reduces eqn (3) to the Bell rate.28 The Bell rate is also retrieved for arbitrary v-values in the low-force limit F ≪ Fc. Note that k(F = 0) coincides with the spontaneous escape rate k0. In order to precisely extract the parameters, we build a systematic protocol to remove the outliers and fit the DHS model with v = 2/3 to our data via the maximum likelihood method (Fig. S9†). Our choice of v is based on the assumption that the corresponding free energy profile has a smooth barrier, but consistent results are also obtained for v = 1/2. We provide a fast open-source implementation of our data fitting protocol for the analysis of rupture force spectra.35
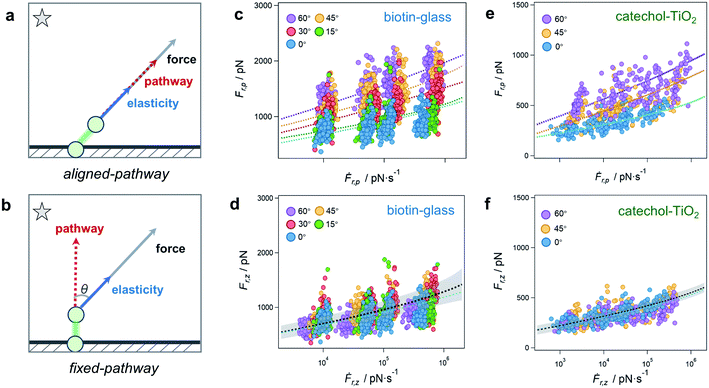
The rupture of a bond is tentatively ascribed to either of two idealized rupture scenarios, which we call the aligned-pathway and fixed-pathway scenario, respectively (Fig. 3a and b). In the aligned-pathway scenario, the bond is assumed to rupture along the direction of the pulling force.36,37 This describes a flexible bond angle as it implies that the system can easily be bent and rotated by force, such that the rupture direction follows the pulling direction. This would correspond to Fig. 1c that describes no preferred rupture direction of a bond. As shown in Fig. 3c, the force spectra can be fitted with this model for each angle separately. However, for this aligned-pathway scenario, different parameters are obtained for different pulling angles. As the bond is the same, these parameters should actually be similar for each pulling angle.
Therefore we now test the fixed-pathway scenario, where the bond direction is strongly confined by its geometry, i.e., where the bond angle is largely fixed and stays nearly constant upon pulling.38,39 That is, rather than adjusting to the bond direction, the bond ruptures along the same single pathway for all pulling angles. This would correspond to Fig. 1a that describes a highly preferred rupture direction of a bond. In this fixed-pathway scenario, in which the force and bond directions are generally misaligned, only the force projection along the pathway contributes to bond rupture.40 Taking θ = 0° as the ideal pathway direction of the surface bond, as commonly assumed in vertical pulling assays, a global fit is applied to the vertical component of rupture force and loading rate (Ḟr,zvs. Ḟr,z) for all angles. Surprisingly, the results for the θ = 0° fit and the global fit are in very good agreement (Fig. 3d), validating that the bond ruptures along the same pathway for all angles. As only the vertical force component affects the bond rupture under angle-dependent pulling, higher apparent rupture forces Fr,p along the pulling direction are required for steeper angles to provide enough force in vertical direction.
To further validate the direction-dependence of chemical bonds, the catechol–TiO2 bond is studied as a second system (n = 200 for each angle, Fig. 3e and f).41,42 We note that catechol can be easily oxidized to quinone under high pH and hence leads to different bond types and rupture forces with TiO2.43 To ensure the formation of the catechol–TiO2 bond, the experiments are carried out under pH 3, where catechol remains unoxidized. Similar to the biotin-glass experiments, the force is transmitted to the catechol–TiO2 bond along the pulling direction via a PEG chain (Fig. S10†). We again observe an increase of Fr,p for larger angles, while Fr,z stays nearly constant. This indicates that the force direction plays a universally important role for the perceived strength of single chemical bonds at surfaces, which are much less flexible than one might have thought.
The fit results indicate a barrier height ΔGu of 14 to 17 kBT for both the biotin-glass bond and the catechol–TiO2 bond (see Tables S1–S4 for fit parameters†), comparable to a coordination/covalent bond.30,44 Such an anchor strength prevents the target molecule from slipping on the surface,14 which is essential to obtain a well-defined angle when driving the piezo positioning system in vertical and lateral directions, respectively.
Conclusions and outlook
We use stereographic force spectroscopy to study how the direction of an applied force affects the strength of single chemical bonds at a surface. We find that the apparent bond strength increases with increasing pulling angle. Dynamic stereographic force spectroscopy then allows us to determine the bond rupture pathway. Surprisingly, we find that an anchor bond ruptures along a fixed pathway, resulting in an effective projection of the applied pulling force onto a nearly fixed rupture direction.The direction-dependence of the surface bond strength constitutes a sturdy mechanical anisotropy, in particular when the distinction between adhesion (θ = 0°) and friction (θ = 90°) properties matters (as in the extreme scenarios of Fig. 1a and b). As an example, it could be exploited to adjust the adhesion strength of cells or other objects on surfaces. Stiff directional bonds would allow cells to withstand higher shear forces (e.g., due to blood flow), while flexible bonds would facilitate their sliding. Such principles could also guide the bottom-up design of chemical materials, coatings and lubricants. Low friction could be designed by engineering interfacial bonds or interactions that can quickly adapt to the direction of force application (scenario of Fig. 1c) or that show a high in-plane mobility (scenario of Fig. 1b), which has been observed in graphene systems with interfacial π–π stacking.45 High friction is expected for directional bonds (scenario of Fig. 1a), as shown here for a stiff chemical bond. Even friction-switchable interfaces can be thought of, where the stiffness and therefore the direction-dependence of bonds can be switched by an external stimulus, such as for azobenzene. Finally, we anticipate that the inclusion of direction-dependence will contribute to advanced force fields for MD simulations, which currently only have a spherical symmetry (scenario of Fig. 1c). Altogether, our results quantify and highlight the importance of directionality of force application for the anchoring of polymers to surfaces and potentially for any interface.
Materials and methods
Materials and sample preparation
All the chemicals are analytically pure and used without further treatment, if not mentioned otherwise. Triethoxysilane-PEG-biotin and triethoxysilane-PEG-methoxy are purchased from Rapp Polymere (Tübingen, Germany, Mw = 5 kDa), triethoxysilane-PEG-thiol (Mw = 5 kDa) and triethoxysilane-PEG-NHS (Mw = 5 kDa) are purchased from NANOCS (Boston, MA, USA). Dopamine hydrochloride is purchased from Sigma-Aldrich (St. Louis, MO, USA). Glass substrate (Borosilicate glass from hydrolytic class I) is purchased from Carl Roth (Germany). TiO2 substrate is prepared as reported in the literature.46The glass substrates are cleaned as follows: firstly, they are cleaned ultrasonically for 10 min with H2O and methanol and respectively. Secondly, they are immersed in RCA solution at 60 °C for 1 hour. RCA comprises a volume ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of H2O (Purelab Chorus 1, Elga LabWater, Celle, Germany, 18.2 MΩ cm), NH3 solution (Roth, Karlsruhe, Germany, 28.0–30.0%), H2O2 (Sigma-Aldrich, St. Louis, MO, USA, ≥30%). Then, they are rinsed with extensive H2O to remove the residual RCA solution. The TiO2 substrates are cleaned ultrasonically for 10 min with H2O and methanol respectively, then activated with oxygen plasma (40% power, 0.1 mbar, 2 min, Diener Electronics, Germany). The tweezers and glassware are cleaned as follows: firstly, they are immersed in RCA solution at 60 °C for 1 hour, followed by rinsing with extensive H2O; then, they are dried and stored at 120 °C.
1 of H2O (Purelab Chorus 1, Elga LabWater, Celle, Germany, 18.2 MΩ cm), NH3 solution (Roth, Karlsruhe, Germany, 28.0–30.0%), H2O2 (Sigma-Aldrich, St. Louis, MO, USA, ≥30%). Then, they are rinsed with extensive H2O to remove the residual RCA solution. The TiO2 substrates are cleaned ultrasonically for 10 min with H2O and methanol respectively, then activated with oxygen plasma (40% power, 0.1 mbar, 2 min, Diener Electronics, Germany). The tweezers and glassware are cleaned as follows: firstly, they are immersed in RCA solution at 60 °C for 1 hour, followed by rinsing with extensive H2O; then, they are dried and stored at 120 °C.
AFM cantilever tip functionalization
Si3N4 AFM cantilevers (MLCT-BIO-DC, Bruker AFM probes, Camarillo, CA, USA) are used in the force measurements. The cantilevers are activated with oxygen plasma (40% power, 0.1 mbar, 2 min, Diener Electronics, Germany) to generate hydroxyl groups on the cantilever surface.Then, for the functionalization with biotin, the cantilevers are incubated in a solution of triethoxysilane-PEG-biotin in toluene (1.25 mg mL−1, 2 h, 22 °C), then rinsed with toluene, ethanol and H2O respectively to get rid of the loosely adsorbed molecules. For the functionalization with catechol, the cantilevers are incubated in a solution of triethoxysilane-PEG-NHS in toluene (1.25 mg mL−1, 2 h, 22 °C), then rinsed with toluene, ethanol and H2O respectively. After that, these cantilevers are further incubated in a solution of dopamine in PBS buffer (pH = 7.2, 1 h, 22 °C), rinsed 3 times with PBS buffer. For the functionalization with thiol, NHS and methoxy groups, the AFM cantilevers are incubated in a solution of triethoxysilane-PEG-thiol, triethoxysilane-PEG-NHS and triethoxysilane-PEG-methoxy in toluene (1.25 mg mL−1, 2 h, 22 °C), then rinsed with toluene, ethanol and H2O, respectively. Finally, all cantilevers are stored in H2O and used in experiments within 3 days.
AFM-based single-molecule force spectroscopy
All vertical pulling (θ = 0°) SMFS experiments are performed with a MFP3D-Bio (Asylum Research, an Oxford Instruments company, CA, USA) using a fluid cell at room temperature (22 °C). The biotin-glass and thiol-glass experiments are carried out in H2O, while the catechol–TiO2 experiments are carried out in ROTI Calipure buffer solution (pH 3.0, Roth, Karlsruhe, Germany).43 Before the experiment, the inverse optical lever sensitivity (InvOLS) is determined by a linear function to the repulsive regime of a force–extension curve and using an average of at least five InvOLS values. The spring constant of the cantilever is determined by the thermal noise method. The details of the AFM instrumentation can be found elsewhere.47,48AFM-based stereographic force spectroscopy
All stereographic force spectroscopy experiments are performed with the same MFP3D-Bio. A self-written program based on the functions of Asylum Research and Igor Pro, is used to control the movement of the cantilever tip and the scanner (surface). The pulling angle and velocity are realized by driving the z- and x-piezos simultaneously with respective defined velocities, hence applying a stereographic force on the bond. Herein, the x-piezo is defined as the piezo that drives the surface perpendicular to the cantilever axis. The stereographic pulling can be divided into 4 stages: (1) a cantilever tip functionalized with the target molecule is approached to the surface vertically. (2) The cantilever tip contacts the surface with a certain force trigger (approx. 2–10 nN, contact time approx. 0.01–2 s), leading to a contact between cantilever tip and the surface underneath. During the respective contact, the target molecule binds to the surface, i.e., the molecule is anchored. (3) The cantilever tip is retracted with a distance corresponding to the indentation depth. (4) The cantilever tip is further retracted vertically while the piezo system moves the cantilever laterally, which allows the pulling of the target molecule with different angles and velocities. There, the PEG-substrate interaction and solvent related (hydrodynamic) friction of PEG in solution is below the detection limit of our experiment.49During the measurement, the vertical deflection of the cantilever and the ZLVDT (z-piezo movement) are recorded for generating the vertical force–extension curves. The YLVDT, XLVDT, and lateral deflections of the cantilever, are also recorded for further evaluation.
Analytical protocol of dynamic force spectra
The Dudko–Hummer–Szabo (DHS) model is used to analyze the measured rupture forces and the associated loading rates using the maximum likelihood method, and hence to extract the kinetics of the anchor bond under different pulling angles. To perform a reliable analysis, we have built a systematic protocol to optimize the fit quality, which considers the evolution of the fit parameters while trimming rupture force data. A detailed description can be found in the Rupture force data analysis in ESI.†Data availability
The data supporting the findings of this study are available within the article and in the ESI.† The raw data are available from the authors upon reasonable request.Author contributions
W. C., B. N. B. and T. H. designed the study, W. C. and M. L. performed experiments, J. T. B. and W. C. performed the fitting process of bond rupture and elasticity models, W. C. and J. T. B. analyzed data after consultation with K. K., B. N. B. and T. H., W. C., B. N. B. and T. H. wrote the manuscript, J. T. B and K. K. revised the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy − EXC-2193/1 − 390951807 (ML, TH and BNB) and the grant HU 997/13-1 (WC and TH). The authors thank Roland Netz (FU Berlin) and Steffen Wolf (University of Freiburg) for helpful discussions, Gerhard Hummer (MPI of Biophysics, Frankfurt) for helpful feedback on the manuscript and Klaus Rischka (Fraunhofer IFAM) for providing samples, JTB acknowledges support by the Max Planck Society.Notes and references
- M. Grandbois, M. Beyer, M. Rief, H. Clausen-Schaumann and H. E. Gaub, Science, 1999, 283, 1727–1730 CrossRef CAS PubMed.
- M. Rief, F. Oesterhelt, B. Heymann and H. E. Gaub, Science, 1997, 275, 1295–1297 CrossRef CAS PubMed.
- H. Li, W. A. Linke, A. F. Oberhauser, M. Carrion-Vazquez, J. G. Kerkviliet, H. Lu, P. E. Marszalek and J. M. Fernandez, Nature, 2002, 418, 998–1002 CrossRef CAS PubMed.
- D. T. Edwards, J. K. Faulk, A. W. Sanders, M. S. Bull, R. Walder, M.-A. LeBlanc, M. C. Sousa and T. T. Perkins, Nano Lett., 2015, 15, 7091–7098 CrossRef CAS PubMed.
- H. Wang and H. Li, Chem. Sci., 2020, 11, 12512–12521 RSC.
- A. Kolberg, C. Wenzel, K. Hackenstrass, R. Schwarzl, C. Rüttiger, T. Hugel, M. Gallei, R. R. Netz and B. N. Balzer, J. Am. Chem. Soc., 2019, 141, 11603–11613 CrossRef CAS PubMed.
- W. Cai, D. Xu, L. Qian, J. Wei, C. Xiao, L. Qian, Z.-Y. Lu and S. Cui, J. Am. Chem. Soc., 2019, 141, 9500–9503 CrossRef CAS PubMed.
- M. J. Jacobs and K. Blank, Chem. Sci., 2014, 5, 1680–1697 RSC.
- Y. Xue, X. Li, H. Li and W. Zhang, Nat. Commun., 2014, 5, 4348 CrossRef CAS PubMed.
- C. L. Brown and S. L. Craig, Chem. Sci., 2015, 6, 2158–2165 RSC.
- H. M. Klukovich, T. B. Kouznetsova, Z. S. Kean, J. M. Lenhardt and S. L. Craig, Nat. Chem., 2013, 5, 110–114 CrossRef CAS PubMed.
- J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487 CrossRef CAS PubMed.
- F. Kühner, M. Erdmann, L. Sonnenberg, A. Serr, J. Morfill and H. E. Gaub, Langmuir, 2006, 22, 11180–11186 CrossRef PubMed.
- B. N. Balzer, M. Gallei, M. V. Hauf, M. Stallhofer, L. Wiegleb, A. Holleitner, M. Rehahn and T. Hugel, Angew. Chem., Int. Ed., 2013, 52, 6541–6544 CrossRef CAS PubMed.
- L. Grebíková, S. G. Whittington and J. G. Vancso, J. Am. Chem. Soc., 2018, 140, 6408–6415 CrossRef PubMed.
- C. R. Peiris, S. Ciampi, E. M. Dief, J. Zhang, P. J. Canfield, A. P. Le Brun, D. S. Kosov, J. R. Reimers and N. Darwish, Chem. Sci., 2020, 11, 5246–5256 RSC.
- M. Hu, F. Liu and J. M. Buriak, ACS Appl. Mater. Interfaces, 2016, 8, 11091–11099 CrossRef CAS PubMed.
- J. L. Lou, H. W. Shiu, L. Y. Chang, C. P. Wu, Y.-L. Soo and C.-H. Chen, Langmuir, 2011, 27, 3436–3441 CrossRef CAS PubMed.
- S. Liese, M. Gensler, S. Krysiak, R. Schwarzl, A. Achazi, B. Paulus, T. Hugel, J. r. P. Rabe and R. R. Netz, ACS Nano, 2017, 11, 702–712 CrossRef CAS PubMed.
- W. Cai, S. Lu, J. Wei and S. Cui, Macromolecules, 2019, 52, 7324–7330 CrossRef CAS.
- F. Oesterhelt, M. Rief and H. E. Gaub, New J. Phys., 1999, 1, 6.1–6.11 CrossRef.
- D. B. Staple, M. Geisler, T. Hugel, L. Kreplak and H. J. Kreuzer, New J. Phys., 2011, 13, 013025 CrossRef.
- B. Heymann and H. Grubmüller, Chem. Phys. Lett., 1999, 307, 425–432 CrossRef CAS.
- C. Ke, Y. Jiang, M. Rivera, R. L. Clark and P. E. Marszalek, Biophys. J., 2007, 92, L76–L78 CrossRef CAS PubMed.
- M. Dendzik, A. Kulik, F. Benedetti, P. E. Marszalek and G. Dietler, Nanotechnology, 2013, 24, 365703 CrossRef PubMed.
- F. Kühner, M. Erdmann and H. E. Gaub, Phys. Rev. Lett., 2006, 97, 218301 CrossRef PubMed.
- R. Walder, W. J. Van Patten, A. Adhikari and T. T. Perkins, ACS Nano, 2018, 12, 198–207 CrossRef CAS PubMed.
- O. K. Dudko, G. Hummer and A. Szabo, Phys. Rev. Lett., 2006, 96, 108101 CrossRef PubMed.
- S. W. Schmidt, M. K. Beyer and H. Clausen-Schaumann, J. Am. Chem. Soc., 2008, 130, 3664–3668 CrossRef CAS PubMed.
- P. Schwaderer, E. Funk, F. Achenbach, J. Weis, C. Bräuchle and J. Michaelis, Langmuir, 2008, 24, 1343–1349 CrossRef CAS PubMed.
- L. F. Milles, K. Schulten, H. E. Gaub and R. C. Bernardi, Science, 2018, 359, 1527–1533 CrossRef CAS PubMed.
- E. Evans and K. Ritchie, Biophys. J., 1997, 72, 1541–1555 CrossRef CAS PubMed.
- G. I. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- S. Getfert and P. Reimann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 052901 CrossRef PubMed.
- See https://github.com/bio-phys/ForceSpectroscopyMLE for a Julia implementation of our results.
- M. Bertz, A. Kunfermann and M. Rief, Angew. Chem., Int. Ed., 2008, 47, 8192–8195 CrossRef CAS PubMed.
- R. B. Best, E. Paci, G. Hummer and O. K. Dudko, J. Phys. Chem. B, 2008, 112, 5968–5976 CrossRef CAS PubMed.
- T. Hugel, M. Rief, M. Seitz, H. E. Gaub and R. R. Netz, Phys. Rev. Lett., 2005, 94, 048301 CrossRef PubMed.
- C. Schoeler, R. C. Bernardi, K. H. Malinowska, E. Durner, W. Ott, E. A. Bayer, K. Schulten, M. A. Nash and H. E. Gaub, Nano Lett., 2015, 15, 7370–7376 CrossRef CAS PubMed.
- E. Evans, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 CrossRef CAS PubMed.
- Y. Li and Y. Cao, Nanoscale Adv., 2019, 1, 4246–4257 RSC.
- H. Lee, N. F. Scherer and P. B. Messersmith, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12999–13003 CrossRef CAS PubMed.
- S. Krysiak, Q. Wei, K. Rischka, A. Hartwig, R. Haag and T. Hugel, Beilstein J. Org. Chem., 2015, 11, 828–836 CrossRef CAS PubMed.
- P. Das and M. Reches, Nanoscale, 2016, 8, 15309–15316 RSC.
- O. Hod, E. Meyer, Q. Zheng and M. Urbakh, Nature, 2018, 563, 485–492 CrossRef CAS PubMed.
- M. Lallemang, L. Yu, W. Cai, K. Rischka, A. Hartwig, R. Haag, T. Hugel and B. N. Balzer, Nanoscale, 2022, 14, 3768–3776 RSC.
- A. Kolberg, C. Wenzel, T. Hugel, M. Gallei and B. N. Balzer, J. Visualized Exp., 2020, e60934 Search PubMed.
- Y. Bao, Z. Luo and S. Cui, Chem. Soc. Rev., 2020, 49, 2799–2827 RSC.
- F. Rico, L. Gonzalez, I. Casuso, M. Puig-Vidal and S. Scheuring, Science, 2013, 342, 741–743 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01077a |
| This journal is © The Royal Society of Chemistry 2022 |