Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Deep neural network based quantum simulations and quasichemical theory for accurate modeling of molten salt thermodynamics
Yu
Shi
 a,
Stephen T.
Lam
a,
Stephen T.
Lam
 b and
Thomas L.
Beck
b and
Thomas L.
Beck
 *c
*c
aDepartment of Chemistry, University of Cincinnati, Cincinnati, OH 45221, USA
bDepartment of Chemical Engineering, University of Massachusetts Lowell, MA 01854, USA
cNational Center for Computational Sciences, Oak Ridge National Laboratory, Oak Ridge, TN 37830, USA. E-mail: becktl@ornl.gov
First published on 15th June 2022
Abstract
With dual goals of efficient and accurate modeling of solvation thermodynamics in molten salt liquids, we employ ab initio molecular dynamics (AIMD) simulations, deep neural network interatomic potentials (NNIP), and quasichemical theory (QCT) to calculate the excess chemical potentials for the solute ions Na+ and Cl− in the molten NaCl liquid. NNIP-based molecular dynamics simulations accelerate the calculations by 3 orders of magnitude and reduce the uncertainty to 1 kcal mol−1. Using the Density Functional Theory (DFT) level of theory, the predicted excess chemical potential for the solute ion pair is −178.5 ± 1.1 kcal mol−1. A quantum correction of 13.7 ± 1.9 kcal mol−1 is estimated via higher-level quantum chemistry calculations, leading to a final predicted ion pair excess chemical potential of −164.8 ± 2.2 kcal mol−1. The result is in good agreement with a value of −163.5 kcal mol−1 obtained from thermo-chemical tables. This study validates the application of QCT and NNIP simulations to the molten salt liquids, allowing for significant insights into the solvation thermodynamics crucial for numerous molten salt applications.
1 Introduction
The study of molten salt properties has seen a major resurgence in recent decades due to promising applications in clean energy technologies such as molten salt reactors1–3 and concentrated solar power storage.4,5 The diverse application of molten salts is primarily due to their usage in high-temperature heat-transfer media. Molten salts are excellent candidates in these systems due to their favorable physicochemical properties (e.g., thermal conductivity, heat capacity, viscosity, etc.) and relatively low cost of production.6 When designing and optimizing salt mixture compositions for various applications, however, exploration of a high-dimensional material space is required to select for candidates with optimal properties. In addition, it is important to understand corrosion at alloy/molten-salt interfaces and property-evolution during reactor operation. This makes the experiments (such as X-ray and neutron diffraction and electrochemical measurements7–11) expensive and challenging under extreme conditions.Therefore molecular dynamics (MD) simulations have been exploited to calculate molten salt properties. Classical simulations are efficient for modelling systems over timescales on the order of nanoseconds in order to make viable predictions. Empirical force-field molecular dynamics (FFMD) simulations with classical potentials such as the Born–Mayer–Huggins–Tosi–Fumi (BMHTF) rigid-ion potential12–15 have been demonstrated to lack full predictive capabilities due to the lack of many-body interactions that influence local structure. Polarizable ion models (PIM) developed in conjunction with quantum mechanical calculations have led to significant improvements in modeling structure, thermodynamics, and dynamic properties.16,17
Ab initio molecular dynamics (AIMD) simulations have been shown to be capable of accurately capturing local structure and solute chemistry in comparison with experiments.18–26 AIMD is computationally expensive, however, and therefore it is difficult to access long time and large length scales to predict the dynamic and thermal properties. Recently, state-of-the-art artificial neural network-based interatomic potential molecular dynamics simulations (NNIP-MD) have been demonstrated as a promising computational tool to explore the underlying physics of the high-dimensional molten salt compositions by simulating 104 atoms on the timescale of nanoseconds with an accuracy at the level of density functional theory (DFT). It has been demonstrated that the NNIP-MD studies27–30 are capable of accurately predicting molten salt structure, heat capacity, self-diffusion coefficients, thermal conductivity, electrical conductivity, viscosity and the melting/freezing point in comparison with experimental measurements.
Understanding phase behavior remains a great challenge at the forefront of molten salt research. In addition, during reactor operation, there is continuous evolution due to processes such as transmutations, fission/corrosion product generation, gas bubble formation, precipitation of insoluble species and other reactions.31,32 A challenge facing the molten salt research community is to directly model these properties starting from phase diagrams, but many of the phase diagrams have never been constructed.
The CALPHAD method is a principal method for phase diagram and molten salt database development.32–37 Experimental thermodynamic data (from phase equilibria measurements and activities of solution species) and/or AIMD simulations are used to empirically fit models and then predict stable phases at different temperatures or compositions. As mentioned above it would be difficult, expensive, and time-consuming to obtain data for high-dimensional salt systems through either experiments or AIMD simulations.19,38
The chemical potential is central for understanding molten salt thermodynamic properties and predicting phase behavior. Studies of the chemical potential are limited due to the above-mentioned difficulties, however. The classical PIM potential force field has been used to calculate the activity coefficient ratios for lanthanide cations (e.g. U3+ to Y3+ in the LiCl/KCl eutectic mixture39) and the free energy change for the reaction of the Eu3+/Eu2+ redox couple in molten KCl.40,41 The Widom particle insertion method has been employed with AIMD simulations to calculate the chemical potential and the solubility of the sodium atom in molten NaCl.42
The cutting-edge NNIP-MD methods hold significant promise to play a vital role in exploring the thermodynamic properties since they provide quantum-level accuracy with efficiency similar to classical simulations. In the present work, molten NaCl is chosen as a prototype system to demonstrate the validity of the NNIP-based quasichemical theory (QCT) calculations, which is shown to be an efficient approach for directly calculating the solute ion solvation free energy via molecular dynamics simulations.43–45 To our knowledge, this is the first application of deep learning methods to the calculation of excess thermodynamic properties of molten salts.
2 Methods
2.1 Theoretical methods
The chemical potential of the solute X (Na+ or Cl− ion) solvated in the molten salt liquid phase can be expressed as| μX = μidX + μexX | (1) |
The solute(X)-solvent interaction energy is defined as εX = Usolution − Usolvent − Usolute, where U is the system total potential energy. Then the excess chemical potential is given by
μexX = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈e−εX/kT〉0 ln〈e−εX/kT〉0 | (2) |
μexX = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈e−Mλ/kT〉0+kT ln〈e−Mλ/kT〉0+kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈e−Mλ/kT〉εX−kT ln〈e−Mλ/kT〉εX−kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈e−εX/kT〉Mλ ln〈e−εX/kT〉Mλ | (3) |
The LR contribution can also be written as43,44
μexLR = kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈eεX/kT〉Mλ+εX ln〈eεX/kT〉Mλ+εX | (4) |
| fλ(γ)=γ3Mλ, | (5) |
The repulsive potential Mλ(r) is a half-harmonic potential
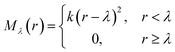 | (6) |
The PK contribution is then expressed as
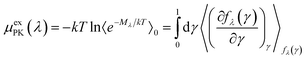 | (7) |
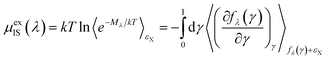 | (8) |
For the long-ranged contribution, a cumulant expansion to second order yields the (uncoupled) expression
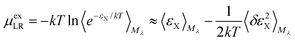 | (9) |
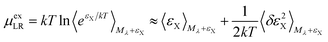 | (10) |
The regularization47 due to the repulsive potential Mλ (that pushes the solvent molecules/ions away from the solute) produces near-Gaussian statistics for εX, and thus the two fluctuation terms of the uncoupled (eqn (9)) and the coupled (eqn (10)) samplings44 are of close magnitude. Consequently, the average of the two mean terms gives a relatively accurate approximation for the LR contribution.
Alternatively, at a value for which the two interaction energy distribution functions are equal,43
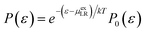 | (11) |
2.2 Computational methods
In the following section, we discuss the implementation of the AIMD simulations with CP2K 2.6.1,50 the training process for the NNIP model with DeePMD-Kit,51,52 and the protocol for the NNIP-MD simulations with LAMMPS.53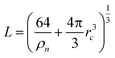 , where the ion number density is ρn = 15.61 (nm)−3,42 and rc = 4.0 γ Å. The coupling parameter γ is varied from 0 to 1 during the thermodynamic integration for the PK and IS contributions.
, where the ion number density is ρn = 15.61 (nm)−3,42 and rc = 4.0 γ Å. The coupling parameter γ is varied from 0 to 1 during the thermodynamic integration for the PK and IS contributions.
The initial configurations were generated during classical molecular dynamics simulations using the GROMACS 4.5.5 package,54 and the ions were modeled with the OPLS-AA force-field.55 With 1 fs as the time step, all classical force-field based simulations were run for 1.5 ns in the NVT ensemble after 1 ns of equilibration in the NPT ensemble. The temperature was set at 1150 K for the classical simulations. For the AIMD simulations, parameters were chosen based on previous studies that accurately predicted local structure, standard reduction potential and sodium solubility in molten NaCl.42 This includes the dual basis sets of Gaussian-type orbitals (double zeta bases, DZVP-GTH) and plane waves with a 600 Ry cutoff.56 Atomic cores were modeled with the Goedecker-Teter-Hutter pseudopotentials (GTH).57 The Perdew–Burke–Ernzerhof (PBE)58 functionals were used for all atoms in the system, and the D2 dispersion corrections59,60 were utilized. D2 dispersion corrections were also employed in a recent NNIP study on molten NaCl liquid.28 While more advanced dispersion methods such as D3 could be used,61 systematic improvement in predictions across different properties is difficult to achieve, due to the semi-empirical nature of most computationally efficient DFT-based dispersion methods. In any case, from density predictions in molten NaCl,42 we find that additional corrections based on higher-level theory are likely necessary to achieve chemical accuracy.
The Ewald potential45,62,63 was applied for the electrostatic interactions under periodic boundary conditions (PBC), and a Nosé-Hoover thermostat chain64 of length 3 was coupled to each ion to maintain a temperature of 1150 K for all the NVT ensemble simulations. Due to the requirement of many simulations along the thermodynamic integration paths to grow the nano-scale cavities, we were not able to employ the path integral formalism for incorporating quantum effects.65 These corrections are expected to be small at such a high temperature, however.
The time step was taken as 0.5 fs. For the LR contribution, two 25 ps simulations (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations, coupled and uncoupled) were implemented. This is found to be sufficient for calculating ensemble-average energies based on previous AIMD studies with molten salts.26–28,42 We performed 9-step integrations for the PK and IS calculations, and we ran simulations for 10 ps (20
000 configurations, coupled and uncoupled) were implemented. This is found to be sufficient for calculating ensemble-average energies based on previous AIMD studies with molten salts.26–28,42 We performed 9-step integrations for the PK and IS calculations, and we ran simulations for 10 ps (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations) for each step.
000 configurations) for each step.
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k = ∑lwklDinl + bk, followed by the non-linear transformation Doutk = φ(
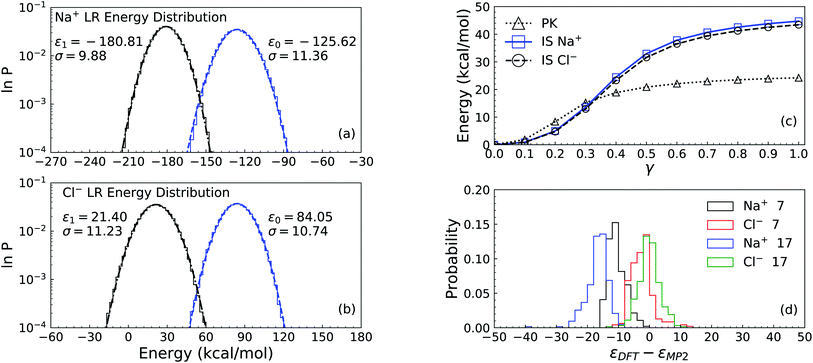
k = ∑lwklDinl + bk, followed by the non-linear transformation Doutk = φ(![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) k), where the hyperbolic tangent function φ is used as the activation function. In the last layer, only the linear transformation is applied to produce atomic energy Ei. The sum of all atomic energies then yields the total energy E. The forces on each atom were computed as negative derivatives with respect to position. The loss function was taken as
k), where the hyperbolic tangent function φ is used as the activation function. In the last layer, only the linear transformation is applied to produce atomic energy Ei. The sum of all atomic energies then yields the total energy E. The forces on each atom were computed as negative derivatives with respect to position. The loss function was taken as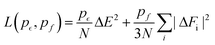 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. The training data consisted of energies and forces from AIMD simulations.
000 steps. The training data consisted of energies and forces from AIMD simulations.
From the AIMD simulations, we generated 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations for each of the first 9 steps of the thermodynamic integration. For the last step, where γ = 1, 50
000 configurations for each of the first 9 steps of the thermodynamic integration. For the last step, where γ = 1, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations were collected from the two coupled simulations (IS of Na+ and Cl−) and one uncoupled simulation (PK), respectively. We trained a model for each step of the TI process (IS and PK, 10 models in total) and another 2 models for the interaction energy calculations over the uncoupled and coupled configurations of the LR simulations, respectively. We also tried to obtain a single NNIP model by using all of the collected AIMD data. This all-in-one model produced an error of magnitude about 3 kcal mol−1 for the solute–solvent interaction energy compared with the AIMD calculation, and a similar error in the free energy. Due to this relatively large error, we did not utilize the all-in-one method further.
000 configurations were collected from the two coupled simulations (IS of Na+ and Cl−) and one uncoupled simulation (PK), respectively. We trained a model for each step of the TI process (IS and PK, 10 models in total) and another 2 models for the interaction energy calculations over the uncoupled and coupled configurations of the LR simulations, respectively. We also tried to obtain a single NNIP model by using all of the collected AIMD data. This all-in-one model produced an error of magnitude about 3 kcal mol−1 for the solute–solvent interaction energy compared with the AIMD calculation, and a similar error in the free energy. Due to this relatively large error, we did not utilize the all-in-one method further.
3 Results and discussion
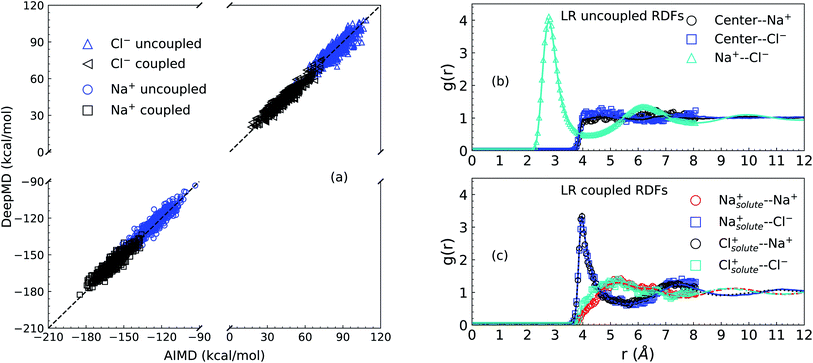
We first present results related to the NNIP model validation. For the LR contributions, the solute–solvent ion interaction energies calculated via AIMD and NNIP-MD simulations are shown in Panel (a) of Fig. 1. Averaging over 11000 configurations drawn from NNIP-MD simulations for the systems of one solute ion and 64 solvent ion pairs, the interaction energy of the solute Na+ calculated via NNIP exhibits a 1.4 kcal mol−1 deviation from AIMD for the uncoupled simulation and 1.3 kcal mol−1 deviation for the coupled case. The deviations for the solute Cl− are −0.4 kcal mol−1 (uncoupled) and 0.4 kcal mol−1 (coupled). These values are close to chemical accuracy (∼1 kcal mol−1) and indicate sufficient accuracy of the NNIP model for the free energy calculations.Next, as shown in Panel (b) and Panel (c) of Fig. 1, the overlapping of radial distribution functions (RDF or g(r)) indicates that NNIP sufficiently reproduces the local structure predicted by the AIMD simulations and uncovers the oscillating structures at larger distances as well. Additionally, the RDF of the Na+–Cl− pair in Panel (b) exhibits a first maximum position at 2.77 Å and a first minimum position at 4.27 Å, which are close to those reported recently27,28 using NNIP training employing a different protocol. This indicates that the presence of a cavity with a radius of 4.0 Å does not significantly affect the average liquid structure in the nearby bulk.
Just outside of the cavity, it is observed that there is a slightly higher density of the Cl− ions than the Na+ cations. Integrating to a distance of 5.5 Å the coordination number of Cl− is 0.7 higher than that of Na+. This leads to a dipole layer in the vicinity of a cavity of 4 Å size. When the solute ion is present at the center of the cavity as shown in Panel (c), however, both solvent ions exhibit charge-symmetrical behavior, as evidenced by the overlaps in the IS RDFs.
The LR contribution is estimated from the two distributions of solute–solvent ion interaction energies, which are calculated over configurations from uncoupled and coupled simulations. As shown in Panel (a) of Fig. 2 for the solute Na+, the mean uncoupled interaction energy is −125.62 kcal mol−1 with a fluctuation contribution (eqn (9)) of 28.2 kcal mol−1, while the mean coupled interaction energy is −180.81 kcal mol−1 with a fluctuation contribution of 21.3 kcal mol−1. The difference between the two fluctuation terms leads to an error of 3.5 kcal mol−1 for the LR free energy contribution, indicating that the Gaussian approximation is inappropriate and a larger cavity is required to observe Gaussian behaviour as was previously seen in the calculation of the hydration free energy of the Na+ ion in water.44,45
 | ||
| Fig. 2 The process of excess chemical potential calculation for the systems of solute Na+ and Cl− ions with 256 solvent ion pairs. Panel (a) and Panel (b) are for the long-ranged (LR) contributions to the solvation free energy of the solute ions Na+ and Cl−, respectively. The logarithms of the distribution of interaction energies from uncoupled (right, blue) and coupled (left, black) configurations are presented with the mean value ε and standard deviation σ. The right dashed curves and the left dash-dotted curves are the Gaussian fit to both distributions. Panel (c) is for the packing (PK) and minus the Inner-Shell (IS) cumulative contributions for both solute ions. Along with the expansion of the cavity with(IS)/without(PK) the solute ions at the center, the coupling parameter γ increases from 0 to 1. The IS and PK contributions are listed in Table 1. Panel (d) is the distributions of interaction energy corrections εDFT − εMP2 for the solute ion with 7 and 17 solvent ion pairs. The sampling is over 400 cluster configurations carved from DFT simulation trajectories. The DFT calculation is under Periodic Boundary Conditions (PBC) in a cell of size 25.4 Å. | ||
As discussed in the theoretical methods section above, however, the long-range contribution is equal to the interaction energy at the intersection point of the two distributions. Thus we estimate the long-ranged contribution for Na+ as −156.0 kcal mol−1. In Panel (b) of Fig. 2, the distributions for the Cl− ion exhibit more closely Gaussian behavior since the fluctuation terms are closer: 25.2 kcal mol−1 for uncoupled simulation with a mean value of 84.05 kcal mol−1 and 27.6 kcal mol−1 for coupled simulation with mean value of 21.40 kcal mol−1.
Based on the estimation of the intersection point of the two energy distributions, we estimate the LR contribution for Cl− ion as 54.0 kcal mol−1. The dramatic increase of the LR contribution (including the sign) for the anion is attributed to the electrostatic potential at the center of the cavity.45 Assuming that the electrostatic interaction dominates the interactions between the center solute ion and solvent ions outside the cavity of 4 Å, the average energies of both Na+ and Cl− ions over the uncoupled configurations gives an estimate of the electrostatic potential at the center of the cavity as −4.55 Volt, relative to the average potential in the bulk region of molten salt liquids.
Multipole electrostatic moment analysis of the cavity-water interfacial potential69 reveals that there is a potential shift of −3.96 Volt from the liquid water bulk phase to the cavity center, which is primarily attributed to the water molecular Bethe potential (quadrupole) contribution. Since the current work focuses on the excess free energy for the solute ion pair (in which case the interfacial potential contributions cancel exactly), the Bethe potential for liquid NaCl is not discussed further here.
The numerical results for the IS and PK contributions are shown in Panel (c) of Fig. 2 by presenting the cumulative work computed during the NNIP-MD simulations. Both Na+ and Cl− ions share the same PK contribution (24.2 kcal mol−1), while the IS contribution to the Na+ solvation free energy is −44.7 kcal mol−1 and that for the Cl− ion is −43.6 kcal mol−1.
The numerical results for both the Na+ and Cl− ions are listed in Table 1. The finite-size correction term is due to the artificial effect of the Ewald potential on the free energy. It is shown to be 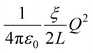 , where Q is the net charge in unit of elementary charge e, L is the box size, ξ = −2.837
, where Q is the net charge in unit of elementary charge e, L is the box size, ξ = −2.837![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 297 for a cubic lattice and
297 for a cubic lattice and  = 332.063301 kcal mol−1 Å−1 × 102.43 The summation of the excess free energy for both solute ions with 256 solvent ion pairs is −178.5 kcal mol−1, which is converged to within the standard error of the mean (SEM) of ±1.1 kcal mol−1 as the system size increases to 512 ion pairs. The SEM in parentheses is calculated using the block-average method (10 blocks) over the production configurations. To the best of our knowledge, this is the first prediction of the absolute solvation free energy for ions in a molten salt using deep learning techniques.
= 332.063301 kcal mol−1 Å−1 × 102.43 The summation of the excess free energy for both solute ions with 256 solvent ion pairs is −178.5 kcal mol−1, which is converged to within the standard error of the mean (SEM) of ±1.1 kcal mol−1 as the system size increases to 512 ion pairs. The SEM in parentheses is calculated using the block-average method (10 blocks) over the production configurations. To the best of our knowledge, this is the first prediction of the absolute solvation free energy for ions in a molten salt using deep learning techniques.
| Solute | μ PKX | μ ISX | μ LRX | FS | μ exX | AIMD | NNIP-MD |
|---|---|---|---|---|---|---|---|
| Na+ | 25.4(0.2) | −44.8(0.2) | −142.8(0.7) | −28.8 | −191.0(0.8) | ||
| Cl− | 25.4(0.2) | −43.8(0.2) | 63.6(0.7) | −28.8 | 16.4(0.7) | ||
| NaCl-64 | −174.6(1.1) | 1.5 × 10−3 | 5.5 × 10−7 | ||||
| Na+ | 24.5(0.3) | −44.6(0.2) | −149.2(0.7) | −23.1 | −192.4(0.8) | ||
| Cl− | 24.5(0.3) | −43.7(0.2) | 58.0(0.7) | −23.1 | 15.7(0.8) | ||
| NaCl-128 | −176.7(1.1) | 3.6 × 10−3 | 2.9 × 10−7 | ||||
| Na+ | 24.2(0.2) | −44.7(0.2) | −156.0(0.7) | −18.4 | −194.9(0.8) | ||
| Cl− | 24.2(0.2) | −43.4(0.2) | 54.0(0.7) | −18.4 | 16.4(0.8) | ||
| NaCl-256 | −178.5(1.1) | 4.0 × 10−3 | 2.7 × 10−7 | ||||
| Na+ | 24.3(0.2) | −44.4(0.2) | −158.8(0.7) | −14.7 | −193.6(0.8) | ||
| Cl− | 24.3(0.2) | −43.6(0.2) | 48.4(0.7) | −14.7 | 14.4(0.8) | ||
| NaCl-512 | −179.1(1.1) | 6.6 × 10−3 | 2.5 × 10−7 |
The computational cost by AIMD and NNIP-MD are shown in the last columns of Table 1, where it is shown that the efficiency of the NNIP-MD simulation is about 3 orders greater than that of AIMD for all the molten salt systems and the SEMs are reduced by about 1 order of magnitude compared to the calculation reported.42 The AIMD cost for 128, 256 and 512 systems are estimated over 100 MD-steps.
The experimental data are analyzed in terms of a Born–Haber cycle as illustrated in Fig. 3. Assuming that all the gas states are well-approximated by the ideal gas, the sum of the solvation free energies of both solute ions is calculated from thermochemical tables67,68 to be −163.5 kcal mol−1. Consequently our QCT calculation at the DFT level over-estimates the excess Gibbs binding free energy by roughly −15 kcal mol−1.
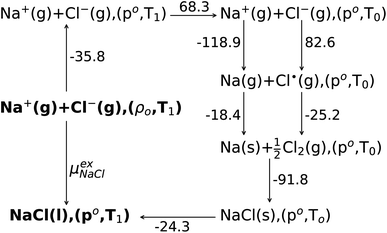 | ||
| Fig. 3 The Born–Haber cycle scheme for Na+ and Cl− ion solvation. The ions are assumed to be solvated from the ideal gas state (g) to liquid state (l) with number density ρo = 15.61(nm)−3 and T1 = 1150 K (NVT ensemble). The ideal gas of ions are changed into the NPT ensemble with pressure ρo = 1 bar and temperature of 1150 K. Then the temperature of the ideal gases is reduced to T0 = 298.15 K isobarically. At room temperature the sodium ion is changed to the sodium atom and chloride ion to the chlorine radical. Both atoms are then changed into elements, respectively. The solid state (s) NaCl is formed from component elements at room temperature and 1 bar pressure. Then the solid salt are heated isobarically into the liquid phase (l) at T1 = 1150 K. The change of free energy from the NVT ensemble (ρo,T1) to the NPT ensemble (po,T1) of the liquid molten NaCl(l) is neglected.43 All of the Gibbs free energy changes are from thermodynamic tables,67,68 and the total change of the solvation free energy is −163.5 kcal mol−1. | ||
In a previous study by Gray-Weale et al.,42 it was noted that the DFT calculation over-estimates the Na atom solvation free energy in liquid Na by −19 kcal mol−1 and the total Gibbs free energy change for the redox reaction Na(l)+ 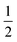 Cl2(g) ⇌ NaCl(l) by −15 kcal mol−1. The molten salt density is over-estimated by up to 10% when using the PBE DFT functional with the D2 dispersion correction, while the system appears to be unstable without the D2 correction. These results indicate both the importance and the subtlety of dispersion forces in the molten salt liquids. It is not surprising that the over-estimation of the density correlates with the over-estimation of the magnitude of the excess free energy. Some over-binding is also observed in ion solvation for the aqueous solution.45
Cl2(g) ⇌ NaCl(l) by −15 kcal mol−1. The molten salt density is over-estimated by up to 10% when using the PBE DFT functional with the D2 dispersion correction, while the system appears to be unstable without the D2 correction. These results indicate both the importance and the subtlety of dispersion forces in the molten salt liquids. It is not surprising that the over-estimation of the density correlates with the over-estimation of the magnitude of the excess free energy. Some over-binding is also observed in ion solvation for the aqueous solution.45
Herein to estimate the correction for the free energy based on the underlying DFT simulations, we implement higher-level density-fitted MP2 theory70 calculations over 400 cluster configurations with the basis set aug-cc-pvdz71,72 in the Psi4 package.73 The cluster configurations with 7 and 17 solvent ion pairs are carved from a trajectory generated by the DFT simulation.
The correction (in the direction DFT → MP2) to the solvation free energy of each ion Δμex is given by
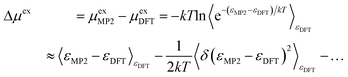 | (13) |
Inclusion of the D2 correction over-estimates the interaction energy by −6.4 kcal mol−1 on average. As mentioned above, the over-binding between ions is also indicated by the 7% over-estimation of the molten NaCl density at 1150 K.42 The PBC interactions (related to the Ewald potential45,62,63) for the simulation cell of size 16.0 Å contributes about 10.0 kcal mol−1 to the interaction energy correction for the solute ion pair, while in the cell of size 25.4 Å it contributes about 2.0 kcal mol−1. The distributions of the interaction energy corrections under PBC in the cell of size 25.4 Å are presented in Panel (d) of Fig. 2.
To estimate the total free energy correction, including contributions from outside the clusters, we extrapolate the cluster interaction energy correction to 256 ion pairs. Considering the cancellation of Ewald potential contributions for the solute ion pair, we assume that it is convergent to 1.6 (1.4) kcal mol−1. Assuming the dispersion interaction energy 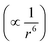 is proportional to the solvent ion density (which is approximately a constant outside the first solvation shell), the spherical integration leads to the expression of dispersion energy correction as a + b/N, where N is the solvent ion pair number. Using the dispersion energy corrections presented in row number 2 of Table 2, we calculate the parameters a and b as (−11.59, 20.23) for Na+ and (−8.88, 16.66) for Cl−, which leads to the extrapolation for the dispersion energy correction as −11.5(1.1) kcal mol−1 for Na+ and −8.8(0.8) kcal mol−1 for Cl− (in the MP2 → DFT direction). The total dispersion energy correction for the solute ion pair is then −20.3(1.4) kcal mol−1 or +20.3 kcal mol−1 in the desired DFT → MP2 direction. The Ewald correction in this direction is −1.6 kcal mol−1.
is proportional to the solvent ion density (which is approximately a constant outside the first solvation shell), the spherical integration leads to the expression of dispersion energy correction as a + b/N, where N is the solvent ion pair number. Using the dispersion energy corrections presented in row number 2 of Table 2, we calculate the parameters a and b as (−11.59, 20.23) for Na+ and (−8.88, 16.66) for Cl−, which leads to the extrapolation for the dispersion energy correction as −11.5(1.1) kcal mol−1 for Na+ and −8.8(0.8) kcal mol−1 for Cl− (in the MP2 → DFT direction). The total dispersion energy correction for the solute ion pair is then −20.3(1.4) kcal mol−1 or +20.3 kcal mol−1 in the desired DFT → MP2 direction. The Ewald correction in this direction is −1.6 kcal mol−1.
| Na+ 07 | Cl− 07 | Na+ 17 | Cl− 17 | |
|---|---|---|---|---|
| 0) MP2 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1) DFT | −1.9(0.5)[2.3] | −0.7(0.4)[3.5] | −3.1(0.4)[4.7] | −1.9(0.4)[3.9] |
| 2) DFT + D2 | −8.7(0.6)[2.8] | −6.5(0.5)[3.5] | −10.4(0.5)[5.3] | −7.9(0.3)[4.8] |
| 3) DFT + D2 PBC 16.0 | −15.9(0.6)[4.2] | 10.8(0.5)[4.4] | −31.3(0.6)[9.6] | 23.6(0.7)[7.0] |
| 4) DFT + D2 PBC 25.4 | −10.5(0.6)[2.8] | −2.5(0.4)[3.5] | −16.7(0.5)[3.4] | 0.0(0.4)[3.4] |
| 5) D2, (2)-(1) | −6.8(0.8) | −5.8(0.6) | −7.3(0.6) | −6.0(0.5) |
| 6) PBC 16.0,(3)-(2) | −7.2(0.8) | 17.3(0.7) | −20.9(0.8) | 31.5(0.8) |
| 7) PBC 25.4,(4)-(2) | −1.8(0.8) | 4.0(0.6) | −6.3(0.7) | 7.9(0.5) |
Summing up the total correction (PBC/Ewald and dispersion) of the solute ions, we see that the correction from the cluster calculations with 17 solvent ion pairs dominates 89.3% of that with 256 solvent ion pairs. As a result, the fluctuation term in eqn (13) is assumed to be primarily captured by the interaction energy correction of 17 solvent ion pair cluster. This leads to a −2.5(0.1) kcal mol−1 correction for each of the Na+ and Cl− solute ions. Inserting these results into eqn (13), we obtain the total correction (in the DFT → MP2 direction) as +13.7(1.9) kcal mol−1 for the solute ions. Compared to the experimental reference value of −163.5 kcal mol−1, the calculated total excess chemical potential of −164.8(2.2) kcal mol−1 provides strong initial validation of the methodology.
4 Conclusions
Through investigation of the solvation thermodynamics of the Na+ and Cl− ions in the molten NaCl liquid, we have presented and validated an efficient and general methodology to calculate the solvation free energy of ionic species in the molten salts. The methodology incorporates ab initio molecular dynamics simulations, interatomic potentials based on deep neural network models, and quasichemical theory. Efficient molecular dynamics simulations with the NNIP model reduces the calculation uncertainty significantly to roughly 1 kcal mol−1. Due to the over-estimation of the magnitude of the attractive interaction energy of the solute ion with the solvent ions at the DFT level (with D2 dispersion corrections), a high-level quantum chemical correction of roughly 15 kcal mol−1 to the free energy is required to make a quantifiable prediction of the excess free energy. These results highlight the importance of dispersion and polarization interactions in the molten salt liquids.The methodology sets the stage for larger-scale simulations of molten salt mixtures at a quantum mechanical level of accuracy, allowing for quantitative investigations of the activities, solubilities, and redox potentials of ionic species (including the corrosion and fission products) in the liquid phase.40–42 The methodology holds the potential to provide essential data for molten salt applications in both concentrated solar energy storage materials and molten salt reactors.
Data availability
Data related to the calculations presented in this paper will be made freely available upon request to the authors.Author contributions
Yu Shi: conceptualization, methodology, software, validation, investigation, data curation, visualization, writing – original draft. Stephen T. Lam: methodology, validation, writing – review&editing. Thomas L. Beck: conceptualization, methodology, supervision, writing – review&editing, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Notes
This manuscript has been authored in part by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The publisher acknowledges the US government license to provide public access under the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan).Acknowledgements
We acknowledge NSF grants CHE-1565632 and CHE-1955161 at the University of Cincinnati for financial support of this research. The computations were performed at the Ohio Supercomputer Center and the Advanced Research Computing Center in University of Cincinnati. Y. Shi acknowledges the support of the College of Arts and Sciences at the University of Cincinnati. S. Lam is supported by the Department of Energy, Office of Nuclear Energy, Nuclear Energy University Program under award no. DE-NE0009204. Research at Oak Ridge National Laboratory is supported under contract DE-AC05-00OR22725 from the U.S. Department of Energy to UT-Battelle, LLC. This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE ASCR Office of Science User Facility supported under Contract DE-AC05-000R22725.References
- C. Le Brun, J. Nucl. Mater., 2007, 360, 1–5 CrossRef CAS.
- D. F. Williams and K. T. Clarno, Nucl. Technol., 2008, 163, 330–343 CrossRef CAS.
- S. Jerome, A. Michel, B. Ondrej, D. Sylvie, F. Olga, G. Veronique, H. Daniel, H. David, I. Victor, K. J. Leen, L. L. andMerle Lucotte Elsa, U. Jan, Y. Ritsuo and Z. Dai, Prog. Nucl. Energy, 2014, 77, 308–319 CrossRef.
- H. Zhang, J. Baeyens, J. Degreve and G. Caceres, Renewable Sustainable Energy Rev., 2013, 22, 466–481 CrossRef.
- U. Pelay, L. Luo, Y. Fan, D. Stitou and M. Rood, Renewable Sustainable Energy Rev., 2017, 79, 82–100 CrossRef.
- M. Mehos, C. Turchi, J. Vidal, M. Wagner, Z. Ma, C. Ho, W. Kolb, C. Andraka and A. Kruizenga, Concentrating Solar Power Gen3 Demonstration Roadmap, National renewable energy laboratory technical report, NREL/TP-5500-67464, 2017 Search PubMed.
- F. G. Edwards, J. E. Enderby, R. A. Howe and D. I. Page, J. Phys. C: Solid State Phys., 1975, 8, 3483–3490 CrossRef CAS.
- S. Biggin and J. E. Enderby, J. Phys. C: Solid State Phys., 1984, 17, 977–985 CrossRef CAS.
- H. Ohno and K. Furukawa, J. Chem. Soc., Faraday Trans. 1, 1981, 77, 1981–1985 RSC.
- G. J. Janz and N. P. Bansal, J. Phys. Chem. Ref. Data, 1982, 11, 505–693 CrossRef CAS.
- A. Di Cicco, M. Minicucci and A. Filipponi, Phys. Rev. Lett., 1997, 78, 460–463 CrossRef CAS.
- J. E. Mayer, J. Chem. Phys., 1933, 1, 270–279 CrossRef CAS.
- M. L. Huggins and J. E. Mayer, J. Chem. Phys., 1933, 1, 643–646 CrossRef CAS.
- F. Fumi and M. Tosi, J. Phys. Chem. Solids, 1964, 25, 31–43 CrossRef CAS.
- M. Tosi and F. Fumi, J. Phys. Chem. Solids, 1964, 25, 45–52 CrossRef CAS.
- M. Sangster and M. Dixon, Adv. Phys., 1976, 25, 247–342 CrossRef CAS.
- M. Wilson and P. A. Madden, J. Phys.: Condens. Matter, 1993, 5, 2687–2706 CrossRef.
- N. Galamba and B. J. Costa Cabral, J. Chem. Phys., 2007, 126, 124502 CrossRef CAS PubMed.
- A. Bengtson, H. O. Nam, S. Saha, R. Sakidja and D. Morgan, Comput. Mater. Sci., 2014, 83, 362–370 CrossRef CAS.
- H. O. Nam and D. Morgan, J. Nucl. Mater., 2015, 465, 224–235 CrossRef CAS.
- X. Li, J. Song, S. Shi, L. Yan, Z. Zhang, T. Jiang and S. Peng, J. Phys. Chem. A, 2017, 121, 571–578 CrossRef CAS PubMed.
- H. Nam, A. Bengtson, K. Vortler, S. Saha, R. Sakidja and D. Morgan, J. Nucl. Mater., 2014, 449, 148–157 CrossRef CAS.
- H. Guo, J. Li, H. Zhang, T. Li, J. Luo, X. Yu, S. Wu and C. Zong, Chem. Phys. Lett., 2019, 730, 587–593 CrossRef CAS.
- F. Wu, S. Roy, A. S. Ivanov, S. K. Gill, M. Topsakal, E. Dooryhee, M. Abeykoon, G. Kwon, L. C. Gallington, P. Halstenberg, B. Layne, Y. Ishii, S. M. Mahurin, S. Dai, V. S. Bryantsev and C. J. Margulis, J. Phys. Chem. Lett., 2019, 10, 7603–7610 CrossRef CAS PubMed.
- S. Roy, F. Wu, H. Wang, A. S. Ivanov, S. Sharma, P. Halstenberg, S. K. Gill, A. M. Abeykoon, G. Kwon and M. Topsakal, et al. , Phys. Chem. Chem. Phys., 2020, 22, 22900–22917 RSC.
- S. T. Lam, Q.-J. Li, J. Mailoa, C. Forsberg, R. Ballinger and J. Li, J. Mater. Chem. A, 2021, 9, 1784–1794 RSC.
- S. Tovey, A. Narayanan Krishnamoorthy, G. Sivaraman, J. Guo, C. Benmore, A. Heuer and C. Holm, J. Phys. Chem. C, 2020, 124, 25760–25768 CrossRef CAS.
- Q. Li, E. Kucukbenli, S. Lam, B. Khaykovich, E. Kaxiras and J. Li, Cell Rep. Phys. Sci., 2021, 2, 100359 CrossRef CAS.
- S. T. Lam, Q.-J. Li, R. Ballinger, C. Forsberg and J. Li, ACS Appl. Mater. Interfaces, 2021, 13, 24582–24592 CrossRef CAS PubMed.
- A. Rodriguez, S. Lam and M. Hu, ACS Appl. Mater. Interfaces, 2021, 13, 55367–55379 CrossRef CAS PubMed.
- J. K. Startt, C. Deo and S. S. Raiman, Modelling Salt-Material Interactions in Molten Salt Reactors: Opportunities and Path., Oak ridge national laboratory technical report, 2019 Search PubMed.
- J. J. McMurray, T. Besmann and S. Utlak, Status of the molten salt thermodynamic database, MSTDB, Oak ridge national laboratory technical report, 2019 Search PubMed.
- J. W. McMurray and T. M. Besmann, in Thermodynamic Modeling of Nuclear Fuel Materials, ed. W. Andreoni and S. Yip, Springer International Publishing, 2020, pp. 2335–2363 Search PubMed.
- T. M. Besmann and J. Schorne-Pinto, Thermo, 2021, 1, 168–178 CrossRef.
- J. Schorne-Pinto, J. A. Yingling, M. S. Christian, A. M. Mofrad, M. A. A. Aslani and T. M. Besmann, ACS Omega, 2022, 7, 362–371 CrossRef CAS PubMed.
- C. Gueneau, N. Dupin, L. Kjellqvist, E. Geiger, M. Kurata, S. Gosse, E. Corcoran, A. Quaini, R. Hania, A. Smith, M. Piro, T. Besmann, P. Turchi, J. Dumas, M. Welland, T. Ogata, B. Lee, J. Kennedy, C. Adkins, M. Bankhead and D. Costa, Calphad, 2021, 72, 102212 CrossRef CAS.
- C. Bale, E. Belisle, P. Chartrand, S. Decterov, G. Eriksson, A. Gheribi, K. Hack, I.-H. Jung, Y.-B. Kang, J. Melancon, A. Pelton, S. Petersen, C. Robelin, J. Sangster, P. Spencer and M.-A. Van Ende, Calphad, 2016, 54, 35–53 CrossRef CAS.
- V. R. Manga, S. Bringuier, J. Paul, S. Jayaraman, P. Lucas, P. Deymier and K. Muralidharan, Calphad, 2014, 46, 176–183 CrossRef CAS.
- M. Salanne, C. Simon, P. Turq and P. A. Madden, J. Phys. Chem. B, 2008, 112, 1177–1183 CrossRef CAS PubMed.
- M. A. Pounds, M. Salanne and P. A. Madden, Mol. Phys., 2015, 113, 2451–2462 CrossRef CAS.
- C. Kwon, S. H. Noh, H. Chun, I. S. Hwang and B. Han, Int. J. Energy Res., 2018, 42, 2757–2765 CrossRef CAS.
- M. Liu, P. Masset and A. Gray-Weale, J. Electrochem. Soc., 2014, 161(8), E3042–E3048 CrossRef CAS.
- T. L. Beck, M. E. Paulaitis and L. R. Pratt, The Potential Distribution Theorem and Models of Molecular Solutions., Cambridge University Press, 2006 Search PubMed.
- Y. Shi and T. L. Beck, J. Chem. Phys., 2013, 139, 044504 CrossRef PubMed.
- Y. Shi and T. L. Beck, Proc. Natl. Acad. Sci., 2020, 117, 30151–30158 CrossRef CAS PubMed.
- L. R. Pratt and D. Asthagiri, in Free Energy Calculations-Theory and Applications in Chemistry and Biology, Springer Berlin HeidelbergNew York, 2006, pp. 323–352 Search PubMed.
- V. Weber, S. Merchant and D. Asthagiri, J. Chem. Phys., 2011, 135, 181101 CrossRef PubMed.
- T. L. Beck, J. Stat. Phys., 2011, 145, 335–354 CrossRef CAS.
- Y. Shi and T. Beck, J. Phys. Chem. B, 2017, 121, 2189–2201 CrossRef CAS PubMed.
- T. D. Kühne, M. Iannuzzi, M. D. Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al., J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ‘t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al., Comp. Phys. Comm., 2022, 271, 10817 Search PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B, 1996, 54, 1703–1710 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. Leung and M. Marsman, J. Chem. Phys., 2007, 127, 154722 CrossRef PubMed.
- S. W. de Leeuw, J. W. Perram, E. R. Smith and J. S. Rowlinson, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1980, 373, 27–56 CAS.
- G. Martyna, M. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- J. A. Morrone and R. Car, Phys. Rev. Lett., 2008, 101, 017801 CrossRef PubMed.
- D. P. Kingma and J. Ba, arXiv preprint arXiv:1412.6980, 2014, 1–15.
- M. W. Chase Jr, J. Phys. Chem. Ref. Data, 1998, Monograph 9, 789–792 Search PubMed.
- I. Barin, in Thermochemical Data of Pure Substances, Third Edition, VCH Verlagsgesellschaft mbH, VCH Publishers, Inc., Weinheim, New York, NY, 3rd Edition, 1995, p. 1118 Search PubMed.
- Y. Shi, C. C. Doyle and T. L. Beck, J. Phys. Chem. Lett., 2021, 12, 10310–10317 CrossRef CAS PubMed.
- U. Bozkaya, J. Chem. Phys., 2014, 141, 124108 CrossRef PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- B. P. Prascher, D. E. Woon, K. A. PeterSon, T. H. Dunning Jr and A. K. Wilson, Theor. Chem. Acc., 2011, 128, 69–82 Search PubMed.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |