Open Access Article
Open Access ArticleManipulating electron transfer – the influence of substituents on novel copper guanidine quinolinyl complexes†‡
Joshua
Heck
 a,
Fabian
Metz
a,
Sören
Buchenau
a,
Fabian
Metz
a,
Sören
Buchenau
 b,
Melissa
Teubner
ab,
Benjamin
Grimm-Lebsanft
b,
Melissa
Teubner
ab,
Benjamin
Grimm-Lebsanft
 b,
Thomas P.
Spaniol
b,
Thomas P.
Spaniol
 a,
Alexander
Hoffmann
a,
Alexander
Hoffmann
 a,
Michael A.
Rübhausen
b and
Sonja
Herres-Pawlis
a,
Michael A.
Rübhausen
b and
Sonja
Herres-Pawlis
 *a
*a
aInstitute of Inorganic Chemistry, RWTH Aachen University, Landoltweg 1a, 52074 Aachen, Germany. E-mail: sonja.herres-pawlis@ac.rwth-aachen.de
bInstitute of Nanostructure and Solid State Physics, University of Hamburg, Luruper Chaussee 149, 22761 Hamburg, Germany
First published on 7th July 2022
Abstract
Copper guanidine quinolinyl complexes act as good entatic state models due to their distorted structures leading to a high similarity between Cu(I) and Cu(II) complexes. For a better understanding of the entatic state principle regarding electron transfer a series of guanidine quinolinyl ligands with different substituents in the 2- and 4-position were synthesized to examine the influence on the electron transfer properties of the corresponding copper complexes. Substituents with different steric or electronic influences were chosen. The effects on the properties of the copper complexes were studied applying different experimental and theoretical methods. The molecular structures of the bis(chelate) copper complexes were examined in the solid state by single-crystal X-ray diffraction and in solution by X-ray absorption spectroscopy and density functional theory (DFT) calculations revealing a significant impact of the substituents on the complex structures. For a better insight natural bond orbital (NBO) calculations of the ligands and copper complexes were performed. The electron transfer was analysed by the determination of the electron self-exchange rates following Marcus theory. The obtained results were correlated with the results of the structural analysis of the complexes and of the NBO calculations. Nelsen's four-point method calculations give a deeper understanding of the thermodynamic properties of the electron transfer. These studies reveal a significant impact of the substituents on the properties of the copper complexes.
Introduction
Copper proteins play an essential role in biological processes of all living organisms since they are responsible for a fast and reversible electron transfer.1 One group is the type 1 or blue copper proteins that have a mononuclear copper center, e.g. plastocyanin. The copper is coordinated by two nitrogen donors of histidine and two sulfur donors of methionine and cysteine.2 Copper proteins exhibit very high electron self-exchange rates k11 which are a scale for the speed of the electron transfer. For these proteins the electron self-exchange rates range from 103 to 108 M−1 s−1.3–6 This is explained by the entatic state concept which is adaptable for different transition metal enzymes.7–11 The exact effectiveness of the entatic state has been discussed intensively in the past and different explanations have been proposed.9,12 In 1968, the term “entatic state” was introduced by Vallee and Williams. In their theory the protein possesses a rigid framework that does not fit the preferred geometry of the bound metal ions or the cofactor. This leads to an energization of the protein's units but not of the rigid framework.11,13 Another explanation for the entatic state was suggested by Malmström with the induced-rack theory.5,6,14 In contrast to the theory of Vallee and Williams the protein framework exhibits some flexibility leading in the ideal case to two different structures. One structure is energetically favored by the protein framework, but the coordination geometry of the metal ion is strained by the protein framework, which is energetically unfavored by the metal ion. In the second structure the coordination geometry is less strained which is energetically favored by the metal ion but energetically unfavored by the protein framework. Rorabacher et al. proposed that the entatic state of type 1 copper proteins is not just based on geometrical constraints but also on electronic effects so that they introduced the term “electronic entatic state”.15 Comba defined entasis as the energization of a complex by an adverse interaction between the metal ion and the ligands.9 In general, the entatic state describes the energization of the reactants and products due to the adverse interaction between the protein or ligands and the metal ion. This results in a lower activation barrier and a faster reaction.10,12 In case of type 1 copper proteins the coordination geometry of the copper center is highly distorted compared to the ideal tetrahedral geometry favored by Cu(I) and the ideal square-planar geometry favored by Cu(II) leading to an easier transition between Cu(I) and Cu(II) and a promoted electron transfer.10,16There are different approaches to apply the concept of the entatic state to transition metal complexes as models for metal proteins and catalysis.7,17 One example is models for electron transfer proteins, especially for type 1 copper proteins. To quantify the electron transfer ability of a model complex redox couple the electron self-exchange rate k11 is necessary. The determined electron self-exchange rates of several copper complex redox couples in the literature span over a wide range. Stanbury et al. analyzed the [Cu(bib)2]+/2+ redox couple with only N donors and the [Cu(bite)]+/2+ redox couple with N and S donors (Fig. 1). For both systems relatively slow electron self-exchange rates compared to type 1 copper proteins were detected. The electron self-exchange rates range from (0.024 ± 0.004) to (0.49 ± 0.06) M−1 s−1 for the [Cu(bib)2]+/2+ redox couple and (1.22 ± 0.29) × 10−3 to (6.90 ± 1.23) × 10−2 M−1 s−1 for the [Cu(bite)]+/2+ redox couple in MeCN at 25 °C depending on the used counter complex (for an explanation of the term counter complex see chapter “Electron transfer studies”).18 The Cu bispidine system reported by Comba et al. features a rigid ligand (Fig. 1).4,9 Due to the rigidity the ligand is preorganized and offers only one possible coordinating conformation, so the ligand is inflexible. However, the coordination sphere is slightly elastic since the metal ion is not completely fixed in the center of the ligand cavity.9 This allows a low-energy rearrangement of the coordination sphere characterized by a low inner-sphere reorganization energy. Nevertheless, this system exhibits a quite low electron self-exchange rate of 15 ± 11 M−1 s−1 in water at 25 °C. The reason for this is that the elastic coordination geometry enables large structural changes which influence the solvation shell significantly resulting in a relatively high outer-sphere reorganization energy. This emphasizes that a low inner-sphere reorganization energy does not lead automatically to a high electron self-exchange rate.4 In contrast, Rorabacher et al. achieved high electron self-exchange rates of ∼105 M−1 s−1 for the [Cu([15]aneS3bpy)]+/2+ redox couple in MeCN at 25 °C (Fig. 1).15 These values are within the range of the electron self-exchange rates of the type 1 copper proteins. Besides the determination via the Marcus cross relation, Rorabacher et al. used the NMR line-broadening method. This method was also applied by Szymczak et al. who measured an electron self-exchange rate of 2.4 × 105 M−1 s−1 in THF at room temperature for the [Cu(H2TpyNMes)Cl]0/+ redox couple.19 In the past, our group has reported the properties of copper guanidine quinolinyl complexes as entatic state models by structural analysis and determination of the electron self-exchange rates via Marcus theory (102–103 M−1 s−1).20–23 The influence of different solvents and substituents was analyzed.22,23 The redox couple [Cu(TMGqu)2]+/2+ exhibits the highest electron self-exchange rate for pure N donor systems in organic solvents.22 In copper guanidine quinolinyl complexes the structures of the Cu(I) and Cu(II) complexes are highly distorted compared to the ideal tetrahedral geometry favored by Cu(I) and the ideal square-planar geometry favored by Cu(II).16,20 This distortion leads to a very high structural similarity between the Cu(I) and Cu(II) complexes.20 In a previous report, substitutions in the 2-, 4- and 6-positions of the quinolinyl backbone were highlighted to have the strongest influence on the donor properties of the ligand. Substituents in the 2- and 4-position mostly affect the quinolinyl donor whereas substituents in the 6-position mostly affect the guanidine donor.24 In another study, substituents with electronic influences were introduced in the 6-position but this did not lead to an enhancement of the entatic state.23 Therefore, substitutions in the 2- and 4-position affecting the quinolinyl donor are of great interest where substituents in the 2-position also have a steric influence on the coordination geometry.
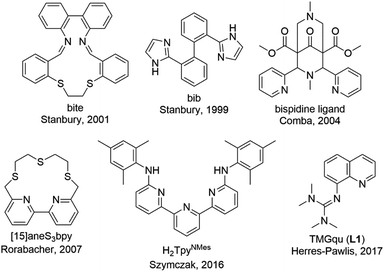 | ||
| Fig. 1 Ligands used in copper complexes that were examined as entatic state models for electron transfer.4,9,15,18–23 | ||
Herein, we examined the influence of substituents in the 2- and 4-position of the guanidine quinolinyl ligand on the properties of the corresponding Cu(I) and Cu(II) complexes. The molecular structures of the complexes were characterized by single-crystal X-ray diffraction (XRD), X-ray absorption spectroscopy (XAS) and density functional theory (DFT) calculations. Moreover, the electron transfer was investigated via Marcus theory and further DFT calculations.
Results and discussion
Strategies to manipulate the electron transfer
In order to manipulate the electron transfer performance of guanidine quinolinyl copper complexes, different substituents were introduced in the quinolinyl backbone of the ligands (Scheme 1). Thus, the steric demand and the donor properties of the ligands were modified compared to the unsubstituted ligand TMGqu (L1). The guanidine donor was not changed for comparability so only ligands with a TMG moiety were synthesized.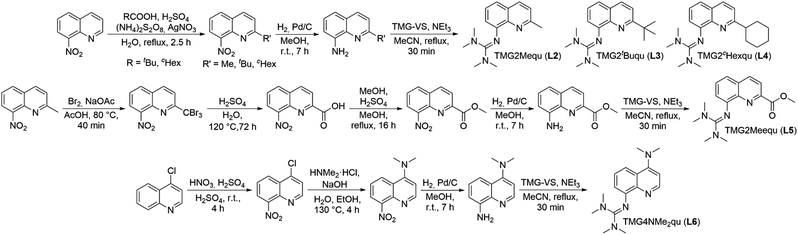 | ||
| Scheme 1 Synthetic routes to a series of substituted guanidine quinolinyl ligands.24–29 * The nitro precursor for L2, 2-methyl-8-nitroquinoline, was commercially available. | ||
First, ligands with alkyl groups in the 2-position with different steric demand (TMG2Mequ (L2), TMG2tBuqu (L3), and TMG2cHexqu (L4)) were synthesized. These substituents only slightly change the electronic properties due to their weak electron density donating feature while the steric requirements in the 2-position should influence the coordination properties.24 Due to the higher steric demand of the ligands, the distortion of the resulting Cu(I) and Cu(II) complexes should be higher compared to that of the Cu(I) and Cu(II) complexes with the unsubstituted ligand (L1). Therefore, this should lead to an improvement of the electron transfer properties. The different alkyl groups should allow the influence of the steric demand to be determined.
Second, a ligand with a methyl ester group in the 2-position (TMG2Meequ (L5)) was synthesized. As the alkyl group in L2−L4 the methyl ester group has an influence on the steric demand. Moreover, the negative mesomeric effect caused by the electron density withdrawing feature increases the delocalization of the π system. This should influence the electron transfer ability of the Cu complexes.
Third, a ligand with a dimethylamine group in the 4-position (TMG4NMe2qu (L6)) was synthesized. Due to its position in the ligand, the dimethylamine group does not influence the coordination by steric demand. However, due to its positive mesomeric effect caused by the electron density donating feature an increase of the delocalization of the π system occurs. Like in L5 but with a more electron-rich aromatic system the influence on the electron transfer properties of the Cu complexes is examined.
Synthetic strategy for the ligands
The nitro precursors for the alkyl substituted ligands L3 and L4 were obtained from 8-nitroquinoline by introducing the alkyl group in a silver catalyzed radical substitution reaction following a modified procedure of Minisci et al.25 According to this, 2-tert-butyl-8-nitroquinoline and 2-cyclohexyl-8-nitroquinoline were synthesized (Scheme 1, first reaction path). The nitro precursor for L2, 2-methyl-8-nitroquinoline, was commercially available. For the precursor synthesis of L5 (Scheme 1, middle reaction path), the first two steps were performed according to a slightly modified procedure of Gadomsky et al.26 In the first step a bromination of the methyl group of 2-methyl-8-nitroquinoline was performed giving 2-tribromomethyl-8-nitro-quinoline. The second step was the hydrolysis to 8-nitroquinoline-2-carboxylic acid. The third step was the esterification of the carboxylic acid with MeOH giving methyl 8-nitroquinoline-2-carboxylate (Scheme 1, middle reaction path). The synthesis of L6 (Scheme 1, lower reaction path) started with the nitration of 4-chloroquinoline in the 8-position yielding 4-chloro-8-nitroquinoline following the procedure of Mosher et al. modified by Yoo et al.27 The next step was the substitution of the chloride by dimethylamine giving 4-dimethylamino-8-nitroquinoline. This reaction was inspired by the procedures of Pozharskii et al. and Matyjaszewski et al. (Scheme 1, lower reaction path).28 The two final steps are the same for all ligands. The nitro precursors were reduced by hydrogen using Pd/C as catalyst yielding the amine precursors.24 The last step is the guanidine synthesis using the Vilsmeier salt N,N,N′,N′tetramethylchloroformamidinium chloride (TMG-VS) performed according to the general procedure of Herres-Pawlis et al. inspired by the procedure of Kantlehner et al. (Scheme 1).29 The molecular structures in the solid state of ligands L2, L3 and L6 have been determined and are depicted in Fig. S36‡ (crystallographic data are shown in Table S11 in the ESI‡).Influence of the substituents on the electronic and donor properties of the ligands
For L1–L6 DFT calculations with the functional TPSSh and the basis set def2-TZVP with the solvent model (PCM) and empirical dispersion correction with Becke–Johnson damping were performed in accordance to previous studies.21–23,30–35 The structural optimizations were followed by natural bond orbital (NBO) calculations to quantify the influence of the different substituents on the guanidine N donor Ngua and quinolinyl N donor Nqu of all ligands and the acyl and alcohol O donors of the methyl ester groups Oacyl and Oalc of L5 (Fig. 2). The charge of the Ngua donor shows no significant deviation after the substitution whereas the charge of the Nqu donor changes. In all ligands, the Ngua donor possesses a more negative NBO charge than the Nqu donor corresponding to a higher basicity of the Ngua donor.21,35,36 Further work pointed out that the higher basicity of the Ngua donor does not implicate a higher donor strength compared to the Nqu donor whereas a higher basicity comparing the same type of donor leads to a higher donor strength in the Cu complexes.21,24,31,35,36 As expected, the alkyl groups have a very weak influence on the charge of the Nqu donor of L2 and L3 so that the basicity and the donor properties are not influenced significantly compared to the unsubstituted ligand L1. The methyl ester group of L5 has the strongest influence on the Nqu donor. Due to its electron density withdrawing effect the charge of the Nqu donor increases significantly whereby the Nqu donor is less basic compared to L1–L4 leading to weaker donor properties. The dimethylamine group of L6 induces a decrease of the charge of the Nqu donor compared to L1 because of its electron density donating effect. Therefore, the basicity and the donor properties of the Nqu donor are increased compared to those of the unsubstituted ligand.Copper complex synthesis and structural characterization
The reaction of the synthesized ligands L2–L6 with various Cu(I) and Cu(II) salts with weakly coordinating anions leads for all ligands except L3 to a bis(chelate) complexation of the corresponding Cu(I) and Cu(II) centers. For L3 only a mono(chelate) complexation of the Cu(I) species is observed in solution due to the high steric encumbrance of the tert-butyl group (further information in ESI Section 4.3‡). Due to the different coordination behavior in the Cu(I) and Cu(II) species, L3 is of no further interest for this study. The targeted bis(chelate) Cu(I) complexes were synthesized by dissolving the ligands L2 and L4–L6 and a Cu(I) salt, [Cu(MeCN)4]PF6, [Cu(MeCN)4]BF4 or [Cu(MeCN)4]OTf, in DCM. By vapor diffusion or layering with pentane the complexes could be crystallized (Scheme 2, left, top). The bis(chelate) Cu(II) complexes were synthesized analogously by dissolving the ligands L2 and L4–L6 and a Cu(II) salt, [Cu(MeCN)4](BF4)2 or [Cu(MeCN)4](OTf)2, in MeOH, MeCN or a mixture of MeCN and DCM. By vapor diffusion or layering with Et2O or pentane the complexes could be crystallized (Scheme 2, left, bottom). The molecular structures of the complex cations [Cu(TMG2Mequ)2]+ (C3), [Cu(TMG2Mequ)2]2+ (C4), [Cu(TMG2cHexqu)2]+ (C5), [Cu(TMG2cHexqu)2]2+ (C6), [Cu(TMG2Meequ)2]+ (C7), [Cu(TMG2Meequ)2]2+ (C8), [Cu(TMG4NMe2qu)2]+ (C9) and [Cu(TMG4NMe2qu)2]2+ (C10) could be structurally characterized by XRD measurements (Fig. 3) of the crystallized compounds C3−X to C10−X (Scheme 2, right; key structural data in Table 1; molecular structures in the solid state and crystallographic data are shown in Fig. S37–S47 and Tables S12–S15 in the ESI‡). For the complex cations C3, C4 and C8 crystals with different anions could be characterized. Due to insignificant differences in the structures of the cationic complexes the results of C3–OTf, C4–OTf and C8–OTf are not discussed in the manuscript (results are shown in Table S1 in the ESI‡).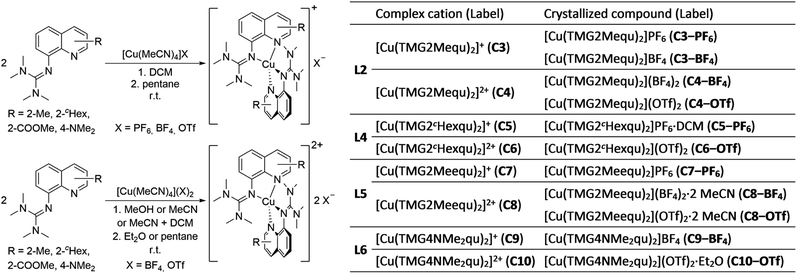 | ||
| Scheme 2 Synthesis of the bis(chelate) Cu(I) (left, top) and Cu(II) (left, bottom) complexes C3−X to C10−X and overview of all complex cations and crystallized compounds ordered by ligand (right). | ||
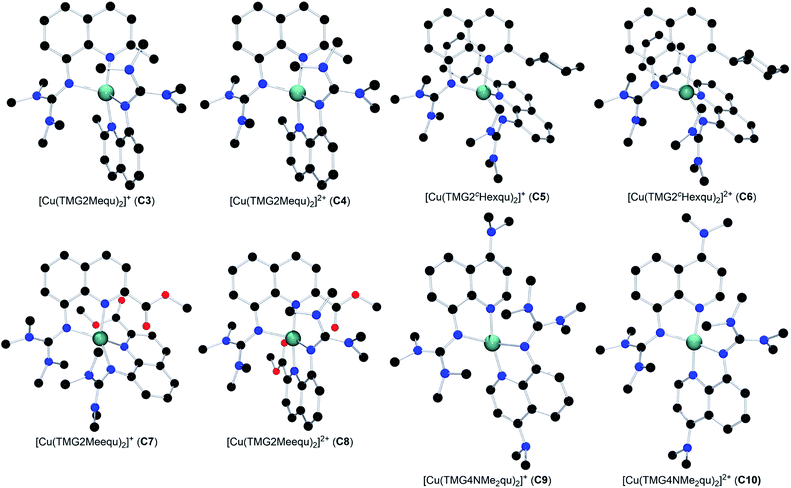 | ||
| Fig. 3 Molecular structures of the Cu(I) and Cu(II) complex cations C3–C10 in crystals of C3−X to C10−X. H atoms, non-coordinating anions and solvent molecules are omitted for clarity. | ||
| [Cu(TMGqu)2]+/2+ (ref. 20) | [Cu(TMG2Mequ)2]+/2+ | [Cu(TMG2cHexqu)2]+/2+ | [Cu(TMG2Meequ)2]+/2+ | [Cu(TMG4NMe2qu)2]+/2+ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C1 (Cu(I)) | C2 (Cu(II)) | C3 (Cu(I)) | C4 (Cu(II)) | C5 (Cu(I)) | C6 (Cu(II)) | C7 (Cu(I)) | C8 (Cu(II)) | C9 (Cu(I)) | C10 (Cu(II)) | |
a
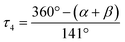 .37
b The τ4 value of the Cu(II) complex may be biased due to the 4 + 2 coordination motif.
c The value may be biased due to the 4 + 2 coordination motif in the Cu(II) complex.
d .37
b The τ4 value of the Cu(II) complex may be biased due to the 4 + 2 coordination motif.
c The value may be biased due to the 4 + 2 coordination motif in the Cu(II) complex.
d
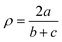 with a = d(Cgua − Ngua), b = d(Cgua − Namine,1) and c = d(Cgua – Namine,2).38 with a = d(Cgua − Ngua), b = d(Cgua − Namine,1) and c = d(Cgua – Namine,2).38
|
||||||||||
| Bond lengths [Å] | ||||||||||
| Cu–Ngua,1/2 | 2.068(3), 2.095(3) | 1.959(2), 1.964(2) | 2.091(3), 2.097(3) | 1.979(4), 1.978(4) | 2.018(3), 2.024(3) | 1.973(2), 1.973(2) | 2.047(4), 2.029(4) | 2.039(2), 2.043(2) | 2.065(4), 2.146(4) | 1.964(2), 1.968(2) |
| Cu–Nqu,1/2 | 1.966(4), 1.999(3) | 1.976(2), 1.975(2) | 1.994(3), 1.994(3) | 1.987(4), 1.972(4) | 2.084(3), 2.081(3) | 1.988(2), 1.988(2) | 2.053(3), 2.083(4) | 1.960(2), 1.959(2) | 1.983(4), 1.947(4) | 1.957(2), 1.952(2) |
| Cu–Oacyl,1/2 | 2.962(4), 4.312(4) | 2.616(2), 2.595(2) | ||||||||
| Cu–Oalc,1/2 | 4.511(4), 3.235(4) | 4.428(2), 4.441(2) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Bond angles [°] | ||||||||||
| Ngua,1/2–Cu–Nqu,1/2 | 82.6(2), 82.1(2) | 83.5(1), 83.7(1) | 81.7(2), 81.6(2) | 83.2(2), 83.6(2) | 81.2(2), 81.3(2) | 82.9(1), 82.9(1) | 81.3(2), 81.3(2) | 82.2(1), 82.2(1) | 82.2(2), 82.4(2) | 82.9(1), 82.9(1) |
| Ngua,1–Cu–Ngua,2 | 129.1(2) | 149.4(1) | 126.0(2) | 135.9(2) | 135.0(2) | 124.7(2) | 124.4(2) | 120.2(1) | 119.6(2) | 150.7(1) |
| Ngua,1/2–Cu–Nqu,2/1 | 108.2(2), 114.1(2) | 102.6(1), 103.5(1) | 111.7(2), 113.2(2) | 105.4(2), 107.2(2) | 128.7(2), 127.9(2) | 135.8(1), 135.8(1) | 133.0(2), 137.8(2) | 105.3(1), 106.9(1) | 123.0(2), 107.1(2) | 102.9(1), 104.2(1) |
| Nqu,1–Cu–Nqu,2 | 149.0(2) | 154.9(1) | 149.9(2) | 154.6(2) | 104.9(2) | 100.7(2) | 105.9(2) | 163.7(1) | 145.1(2) | 154.9(1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Structure parameters | ||||||||||
| τ 4 [ ]a | 0.58 | 0.40 | 0.60 | 0.49 | 0.68 | 0.63 | 0.63 | 0.54b | 0.65 | 0.39 |
| Δτ4 [ ] | 0.18 | 0.10 | 0.06 | 0.09c | 0.27 | |||||
| øτ 4 [ ] | 0.49 | 0.54 | 0.65 | 0.59c | 0.52 | |||||
|
65.1 | 42.5 | 68.2 | 54.7 | 78.1 | 65.5 | 69.0 | 65.6 | 75.6 | 41.8 |
| Δ∡ [°] | 22.6 | 13.5 | 12.6 | 3.5 | 33.8 | |||||
| ρ [ ]d | 0.97, 0.96 | 1.00, 0.99 | 0.97, 0.98 | 1.00, 1.00 | 0.99, 0.99 | 1.01, 1.01 | 0.99, 1.00 | 1.01, 1.00 | 0.97, 0.95 | 1.01, 1.01 |
The Cu–Ngua bond lengths in the Cu(I) complex cations are significantly longer (approx. 0.1 Å) than in the corresponding Cu(II) complex cations expect for C7 and C8. This is related to the stronger coordination of the guanidine moiety to the Cu(II) center compared to the Cu(I) center due to the higher charge. Moreover, in the Cu(I) complex cations the Cu–Ngua bond lengths are significantly longer than the Cu–Nqu bond lengths expect for C5 and C7. To compare the coordination geometry, the structure parameter τ4 (ref. 37) and the plane angle ∡ between the planes stretched by the two N donors of each ligand and the copper center are calculated. The τ4 value describes whether the coordination is ideal square-planar (τ4 = 0) or ideal tetrahedral (τ4 = 1). The results show that for all complexes highly distorted coordination geometries were obtained. In all Cu(I) complex cations the observed τ4 value is higher compared to that of the corresponding Cu(II) complex cations since Cu(I) prefers a tetrahedral and Cu(II) a square-planar coordination geometry.16
In C3–C6 the alkyl substituents of the ligands have due to their position a steric influence on the complex cations but no significant electronic influence due to their weak electron density donation properties (see the discussion of the NBO results of the ligands (Fig. 2) and complex cations (Fig. 4)). The steric demand influences the coordination geometry significantly compared to [Cu(TMGqu)2]+ (C1) and [Cu(TMGqu)2]2+ (C2). An elongation of the Cu–Nqu bond length in the Cu(I) complexes is observed. Furthermore, a stronger steric demand of the substituent (H < Me < cHex) leads to a higher τ4 value for the Cu(I) and Cu(II) complex cations and therefore to a higher average øτ4 value of both complex cations. This causes a stabilization of the Cu(I) complex cation and a destabilization of the Cu(II) complex cation since Cu(I) complex cations prefer higher τ4 values.16 As already mentioned the influence on the Cu(II) complex cations is stronger resulting in a smaller difference between the τ4 value of the corresponding Cu(I) and Cu(II) complex cations represented by the Δτ4 value. This means that the corresponding Cu(I) and Cu(II) complex cations become structurally more similar. This suggests that the introduction of alkyl substituents in the 2-position leads to better entatic state models where C5 and C6 are the best entatic state model couples of all investigated complexes.
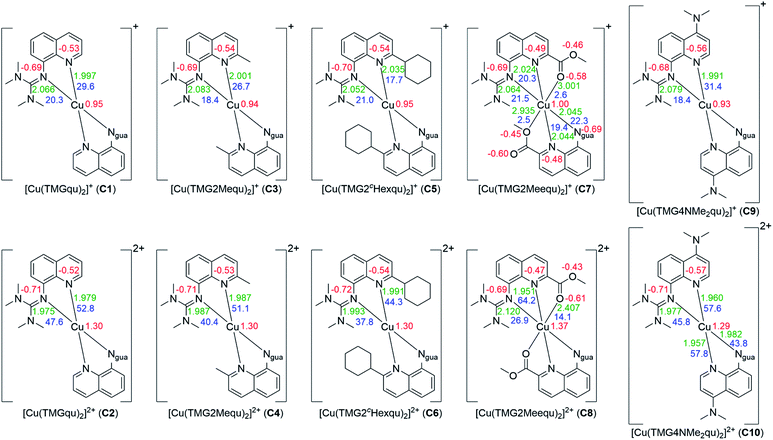 | ||
| Fig. 4 Calculated NBO charges [e units] (red), charge-transfer energies ECT [kcal mol−1] (blue) and selected bond length [Å] (green) for the Cu(I) (top) and Cu(II) (bottom) complex cations C1–C10 (NBO6.0, TPSSh/def2-TZVP and PCM solvent model for MeCN and empirical dispersion correction with Becke–Johnson damping). If neither of the ligands of one complex exhibits significant differences only one value is shown (all values are shown in Table S18 in the ESI‡). | ||
In C7 and C8 the methyl ester substituent influences the coordination geometry in several ways. According to the alkyl substituents in C3–C6 it has a steric demand but furthermore the substituent has an electronic influence due to its electron density withdrawing effect. This weakens the donor properties of the Nqu donor and therefore the Cu–Nqu bond length in the Cu(I) complex cation is comparatively long (see the discussion of the NBO results of the ligands (Fig. 2) and complexes (Fig. 4)). In addition, the methyl ester group itself has donor abilities leading to different effects in both oxidation states. In the Cu(II) complex cation C8 a weak coordination of the Oacyl donor occurs leading to a 4 + 2 coordination motif. This results in an extended Cu–Ngua bond length compared to complex C2 due to the pulling effect of the Oacyl donor on the Cu(II) center. In the Cu(I) complex cation C7 two different coordination behaviors of both the ligands are taking place. One ligand shows a weak interaction between its Oacyl donor and the Cu(I) center and the other ligand between its Oalc donor and the Cu(I) center. C7 is the only complex cation in which both ligands exhibit different coordination behaviors. Due to the different effects of the methyl ester group, the comparison of the τ4 values of the Cu(I) and Cu(II) complex cations is not possible like for C1–C6.
The dimethylamine substituent in C9 and C10 has due to its position no steric demand, hence only its electron density donating effect influences the donor properties of the Nqu donor (see the discussion of the NBO results of the ligands (Fig. 2) and complexes (Fig. 4)). Moreover, the structure parameter ρ was calculated. It describes the degree of delocalization of the electrons in the guanidine moiety.38 For Cu(II) complex cations higher values were found than for the Cu(I) complex cations. This is caused by the stronger coordination of the guanidine moiety to the Cu(II) center compared to the Cu(I) center which is also indicated by the shorter Cu–Ngua bond lengths in the Cu(II) complex cations compared to the Cu(I) complex cations. The stronger coordination comes with a shift of electron density from the Cgua–Ngua bond to the Cu–Ngua bond leading to an elongation of the Cgua–Ngua bond length. Parallelly, a shift of electron density from the amine groups to the Cgua–Namine bonds takes place to compensate for the missing electron density. This induces a shortening of the Cgua–Namine bond lengths. The results reveal that a larger difference in the Cu–Ngua bond length between the corresponding Cu(I) and the Cu(II) complex cations leads to a larger difference in the ρ value between these two complex cations.
XAS and structural DFT calculations of the copper complexes
XAS in solution with MeCN as solvent was performed (see the ESI‡ for details) to characterize the oxidation state and structure of the novel complexes C3–C10 in solution. This was performed to confirm that the structural information found in the solid state accords with the structures present in solution. X-ray absorption near-edge structure (XANES) spectroscopy provides information about the oxidation state of the complexes (spectra are shown in Fig. S1 in the ESI‡). The edge position and the resulting chemical shifts between two associated Cu(I) and Cu(II) complexes identify C3, C5, C7 and C9 as Cu(I) complexes and C4, C6, C8 and C10 as Cu(II) complexes. This is further supported by the pre-edge shapes of the spectra. The Cu(I) complexes show a strong characteristic peak between 8980 and 8985 eV with a normalized absorption of 0.7 to 0.9 that belongs to the 1s → 4p transition.39 In contrast, the Cu(II) complexes show in this area only a weak shoulder but moreover they show a weak peak between 8976 and 8978 eV with a normalized absorption of 40 to 60 × 10−3 belonging to a 1s → 3d transition.40 The results confirm that all complexes are present in the expected oxidation states in solution. Furthermore, the extended X-ray absorption fine structure (EXAFS) spectroscopy provides information about the structure in solution (spectra and determined bond lengths are shown in Fig. S2–S9 and Tables S2–S9 in the ESI‡). The results indicate an accordance of the solid state structures of all complexes with the structures in solution (Tables S21–S24 in the ESI‡). Hence, the anion does not influence the coordination geometry of the complexes and is not responsible for the distortion of the complexes. This is in accordance with previous studies.20DFT calculations were performed for all complexes C1–C10 with the functional TPSSh and the basis set def2-TZVP with the solvent model (PCM) and empirical dispersion correction with Becke–Johnson damping.21–23,30–35 In the first step structure optimization calculations were executed (results are shown in Table S16 in the ESI‡). All complexes exhibit a high agreement between the molecular structure in the solid state, the structure in solution and the calculated structure by DFT (Tables S20–S24 in the ESI‡).
Based on the optimized structures NBO calculations were performed for all complexes to examine the influence of the substituents on the NBO charges of the copper and the N donors and on the charge-transfer energies (ECT) (Fig. 4, see the ESI‡ for details). In general, in all complexes independent of the substituent or the oxidation state of the copper the Ngua donor exhibits a more negative charge compared to the Nqu donor. For this reason, the Ngua donor is a stronger base than the Nqu donor. In all complexes except C5 and C7 the Nqu donor exhibits a higher charge-transfer energy than the Ngua donor. Especially in C2, C4 and C6 the charge-transfer energy of the Nqu donor is significantly higher compared to that of the Ngua donor for similar bond lengths between the Cu(II) center and the N donors. Due to this the Nqu donor is a stronger donor than the Ngua donor. Moreover, the charge-transfer energies from the Ngua and the Nqu donors to the Cu center and the charge of the Cu center are significantly higher in the Cu(II) complexes compared to the corresponding Cu(I) complex. This is in accordance with the results of previous NBO calculations of copper guanidine quinolinyl complexes.21,31
In the Cu(I) complexes the substituents do not influence the charge of the Ngua donor significantly whereas only a weak influence on the charge of the Nqu donor is visible except for C7. In contrast, the influence on the charge-transfer energy and bond length between the Nqu donor and the Cu(I) center in C3, C5 and C7 is evident compared to that in the unsubstituted complex C1. For C3 and C5 the weak electron density donating effect of the alkyl substituents in the 2-position becomes visible. This results in a slightly lower charge of the Nqu donor compared to C1 which suggests better donor properties. Instead, a lower charge-transfer energy and a longer bond length between the Nqu donor and the Cu(I) center compared to C1 occur. This is caused by the steric demand of the alkyl substituents which prevents the shortened bond length between the Nqu donor and the Cu(I) center. The bond length becomes elongated and therefore the charge-transfer energy decreases with the increasing steric demand of the substituent in the 2-position (H < Me < cHex). In C7 the same effect is active but beyond that the electron density withdrawing effect of the methyl ester group leads to an increase of the charge of the Nqu donor. Thus, the charge-transfer energy is lower and the bond length is longer between the Nqu donor and the Cu(I) center compared to C1. The electron density donating effect of the dimethylamine group in C9 induces a small decrease of the charge of the Nqu donor provoking a slightly higher charge-transfer energy and a slightly shorter bond length between the Nqu donor and the Cu(I) center.
In contrast, the influence of the substituents is stronger in the Cu(II) complexes. The charges of the Ngua donor are similar for C2, C4, C6 and C10 but for C8 the charge is significantly higher. In the complexes C2 and C4 to C6 an elongation of the Cu–Ngua bond length occurs due to the steric influence of the alkyl substituents resulting in lower values for the charge-transfer energy. In C8 a 4 + 2 coordination is present and the charge-transfer energy is drastically lower and the bond length much longer compared to those in the other Cu(II) complexes. This is caused by the donor ability of the Oacyl donor of the methyl ester group exhibited by the charge-transfer energy and bond length between the Oacyl donor and the Cu(II) center. Compared to the corresponding Cu(I) complex C7 the charge-transfer energy is significantly higher and the bond length significantly shorter. This is caused by the orientation of the Oacyl donor to the Cu(II) center which does not occur in the Cu(I) complex. The weak coordination between the Oacyl donor and the Cu(II) center in turn weakens the coordination between the Ngua donor and the Cu(II) center by elongation. The influence of the substituents on the Nqu donor in the Cu(II) complexes C2, C4, C6 and C10 is comparable with that in the corresponding Cu(I) complexes C1, C3, C5 and C9, but especially for C10 the influence of the dimethylamine group is stronger than for C9. The higher steric demand of the substituent in the 2-position produces an elongation of the Nqu–Cu bond length and therefore a lower value of the charge-transfer energy. The Cu(II) complex C8 exhibits the opposite effect compared to the corresponding Cu(I) complex C7. In this case the methyl ester substituent leads to an increase of the charge-transfer energy and a shorter bond length between the Nqu donor and the Cu(II) center although the methyl ester substituent still increases the charge of the Nqu donor due to its electron density withdrawing effect. The reason is again as for the Ngua donor the weak coordination between the Oacyl donor and the Cu(II) center. By this, the bond length between the Nqu donor and the Cu(II) center becomes shortened.
Electron transfer studies
The associated Cu(I) and Cu(II) complexes of one ligand form a copper complex redox couple leading to the redox couples [Cu(TMGqu)2]+/2+ (R1), [Cu(TMG2Mequ)2]+/2+ (R2), [Cu(TMG2cHexqu)2]+/2+ (R3), [Cu(TMG2Meequ)2]+/2+ (R4) and [Cu(TMG4NMe2qu)2]+/2+ (R5) (Table 2). To analyze the electron transfer properties of the redox couples the electron self-exchange rates k11 were determined by following the Marcus cross relation (eqn (1)–(4), further information in ESI Section 7‡). The Marcus cross relation emerges from Marcus theory which describes the outer-sphere electron transfer between metal complexes.41 The electron self-exchange rate k11 is the reaction rate of the redox reaction of the reduced form with the oxidized form of the same redox couple. An electron is transferred from the reduced form to the oxidized form. The net result is the same oxidation states of the redox couple as before (Scheme 3, top). The electron self-exchange rate of a redox couple depends on the temperature, the solvent and the activity coefficients of the reactants. Therefore, the direct comparison of redox couples is only reasonable if the electron self-exchange rates are determined under identical conditions. For the Marcus cross relation, a cross reaction with a counter complex with a known electron self-exchange rate has to be analyzed. The function of the counter complex is to oxidize or reduce one oxidation state of the investigated redox couple during the cross reaction (further information in ESI Section 7‡). In theory it makes no difference for the determination of the electron self-exchange rate which counter complex is used and in which direction the cross reaction takes place. However, to enable a direct comparison of the electron self-exchange rates of the investigated redox couples the same counter complex should be used for all cross reactions. The reason is that only small unavoidable inaccuracies in the electron self-exchange rates of different counter complexes can cause an incomparableness of the determined electron self-exchange rates. In this case the complex [Co(bpy)3]3+ of the redox couple [Co(bpy)3]2+/3+ was used as the counter complex for all cross reactions due to its properties (Scheme 3, bottom). The redox potential of the redox couple [Co(bpy)3]2+/3+ enables the oxidation of all Cu(I) complexes without any side reactions, it is soluble in MeCN and it has no significant absorption in the monitored spectral region.22,23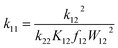 | (1) |
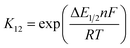 | (2) |
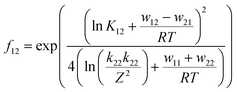 | (3) |
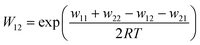 | (4) |
| Complex cation (label) | Complex redox couple (label) | |
|---|---|---|
| L1 | [Cu(TMGqu)2]+ (C1) | [Cu(TMGqu)2]+/2+ (R1) |
| [Cu(TMGqu)2]2+ (C2) | ||
| L2 | [Cu(TMG2Mequ)2]+ (C3) | [Cu(TMG2Mequ)2]+/2+ (R2) |
| [Cu(TMG2Mequ)2]2+ (C4) | ||
| L4 | [Cu(TMG2cHexqu)2]+ (C5) | [Cu(TMG2cHexqu)2]+/2+ (R3) |
| [Cu(TMG2cHexqu)2]2+ (P6) | ||
| L5 | [Cu(TMG2Meequ)2]+ (C7) | [Cu(TMG2Meequ)2]+/2+ (R4) |
| [Cu(TMG2Meequ)2]2+ (C8) | ||
| L6 | [Cu(TMG4NMe2qu)2]+ (C9) | [Cu(TMG4NMe2qu)2]+/2+ (R5) |
| [Cu(TMG4NMe2qu)2]2+ (C10) |
For the calculation of k11 the experimentally determined reaction rate k12 and equilibrium constant K12 (eqn (2)), the correction term f12 (eqn (3)), the work term W12 (eqn (4)) and the electron self-exchange rate k22 of the counter complex redox couple are necessary (eqn (1)). The equilibrium constant K12 depends on the difference between the redox potentials of the counter complex redox couple and the investigated copper complex redox couple ΔE1/2 (eqn (2)). The electron self-exchange rate k22 of the counter complex redox couple [Co(bpy)3]2+/3+ in MeCN at 298 K is used as reported in the literature.42
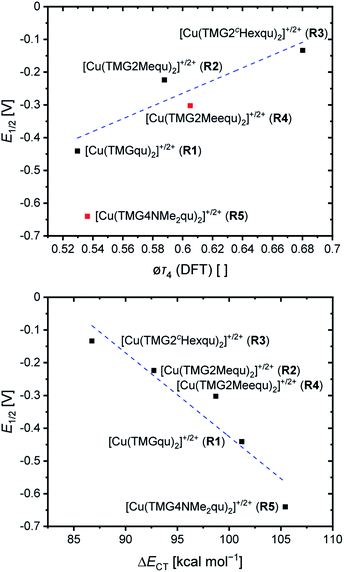
For the determination of the equilibrium constant K12 the redox potentials E1/2 of the copper complex redox couples and of the counter complex redox couple are required. The redox potentials were determined by cyclic voltammetry in MeCN starting from the Cu(I) complexes (example shown for R2 in Fig. 5, for R1–R5 see Fig. S24–S28 in the ESI‡). The measurements indicate that the redox process of all redox couples is reversible which is caused by the small structural changes between the Cu(I) and Cu(II) complexes and by the absence of any side reactions during the cyclic voltammetry measurement. The results show that the substituents have a significant influence on the redox potentials E1/2 of the redox couples and therefore on the equilibrium constants K12 (Table 3). The redox potentials span a range of 0.5 V from −0.640 V to −0.134 V vs. the Fc/Fc+ potential. For R1–R3 the introduction of an alkyl substituent in the 2-position leads to higher redox potentials. In previous work the introduction of alkyl substituents in the 6-position led to lower redox potentials due to the stronger donor properties of the ligand induced by the weak electron density donating feature of the alkyl substituent.24 This emphasizes the effect of the steric demand of the substituent in the 2-position. The redox potentials increase with the steric demand of the substituent (H < Me < cHex). As mentioned before, a higher steric demand of the alkyl substituents results in Cu(I) and Cu(II) structures with higher τ4 values and therefore in a higher average øτ4 value of both. High τ4 values are favored by Cu(I) complexes, so that the distortion caused by the substituents leads to a stabilization of the Cu(I) complexes and hence higher redox potentials. The plot of the redox potential against the calculated øτ4 values emphasizes this trend for R1–R3 (Fig. 6, top; for correlation with experimental øτ4 values see Fig. S29 in the ESI‡). For R4 this trend is also visible but due to the other influences of the methyl ester group the redox potential is not just influenced by the steric demand of the methyl ester group. Therefore, a direct comparison with R1–R3 is not possible. The average øτ4 of R5 is similar to the one of R1, but the redox potential is considerably lower. This underlines that not only is the distortion of the complexes responsible for the redox potentials but also the electronic influence of the substituents of the ligands on the coordination to the Cu center. As mentioned before, the charge-transfer energies from all donors to the Cu center are significantly higher in the Cu(II) complexes compared to the corresponding Cu(I) complexes but the differences vary depending on the substituent. The difference in the calculated charge-transfer energies ΔECT from all N donors to the Cu center of the corresponding Cu(II) and Cu(I) complexes indicates a correlation between the redox potentials and the donor properties of the ligands for all redox couples (Fig. 6, bottom). The redox potential decreases with an increasing difference in the charge-transfer energy because a higher difference induces a stronger stabilization of the electron-poor Cu(II) complex. For R1–R3 the difference in the charge-transfer energies decreases with an increasing steric demand of the substituent in the 2-position because the steric demand causes a longer bond length between the Ngua and Nqu donors and the Cu center and therefore a weaker donation. R4 also fits this correlation if the O donors are not considered. This indicates that only the donor properties of the N donors influence the redox potential. The methyl ester group weakens the stabilization of the Cu(II) complex compared to R1. This results in a higher redox potential. If the O donors are considered the stabilization would be much stronger and a lower redox potential would be expected (for comparison see Fig. S30 in the ESI‡). In the correlation the redox couple R5 exhibits the highest difference in the charge-transfer energies and therefore the lowest redox potential. This is in accordance with previous work that investigated the influence of the dimethylamine group in the 6-position.43 However, the effect of the dimethylamine group in the 4-position is much stronger which is also indicated in previous work. This showed that the influence of substituents in the 4-position is stronger compared to substituents in the 6-position.24 The charge-transfer energies indicate that the electron density donating effect of the dimethylamine group on the donation of the Nqu donor is stronger in the Cu(II) complex than in the Cu(I) complex compared with R1 (Fig. 4). This leads to a better stabilization of the electron-poor Cu(II) complex.
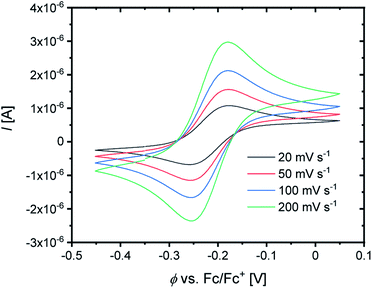 | ||
| Fig. 5 Cyclic voltammogram of R2 starting from C3 (c = 10−3 M) in MeCN with [NBu4][PF6] (c = 0.1 M). | ||
| E 1/2 [V] vs. Fc/Fc+ | ΔE1/2 [V] | K 12 [ ] | k 12 [M−1 s−1] | k 11 [M−1 s−1] | øτ 4 (DFT) | Δτ4 (DFT) | |
|---|---|---|---|---|---|---|---|
| a The value may be influenced by the 4 + 2 coordination motif in the Cu(II) complex. | |||||||
| [Cu(TMGqu)2]+/2+ (R1) | −0.441 | 0.385 | 3.19 × 106 | (2.31 ± 0.07) × 104 | (2.81 ± 0.18) × 102 | 0.53 | 0.20 |
| [Cu(TMG2Mequ)2]+/2+ (R2) | −0.224 | 0.168 | 6.81 × 102 | (1.63 ± 0.16) × 103 | (2.19 ± 0.44) × 103 | 0.59 | 0.13 |
| [Cu(TMG2cHexqu)2]+/2+ (R3) | −0.134 | 0.078 | 2.04 × 101 | (2.25 ± 0.14) × 102 | (1.15 ± 0.15) × 103 | 0.68 | 0.07 |
| [Cu(TMG2Meequ)2]+/2+ (R4) | −0.302 | 0.246 | 1.46 × 104 | (6.67 ± 0.30) × 103 | (2.33 ± 0.22) × 103 | 0.61a | 0.00a |
| [Cu(TMG4NMe2qu)2]+/2+ (R5) | −0.640 | 0.584 | 7.45 × 109 | (4.74 ± 0.27) × 105 | (3.38 ± 0.44) × 102 | 0.54 | 0.20 |
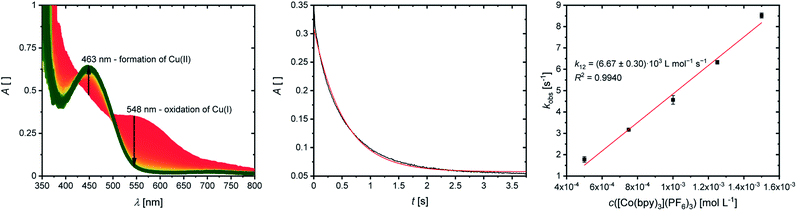
The cross reactions of the Cu(I) complexes C1, C3, C5, C7 and C9 with the counter complex [Co(bpy)3]3+ were monitored by stopped-flow UV/Vis spectroscopy at 298 K in MeCN. An excess of the counter complex was used so that the cross reaction is pseudo-first order and the concentration of the counter complex stays nearly constant throughout the reaction. The influence of the ionic strength on the activity coefficients of the reactants is not considered (further information in ESI Section 6.1‡). During the cross reaction the time-dependent changes in the UV/Vis spectra were examined. The absorption of the characteristic bands of the Cu(I) complexes decreases whereas the absorption of the characteristic bands of the Cu(II) complexes increases because the Cu(I) complex is oxidized to the Cu(II) complex. As an example, this is shown for the reaction of [Cu(TMG2Meequ)2]+ (C7) with [Co(bpy)3]3+ (Fig. 7, left). The reaction rate kobs of the cross reaction was determined by a first-order fit of the decrease of the Cu(I) absorption against the reaction time (Fig. 7, middle). The cross reaction was performed with various concentrations of the counter complex so that the reaction rate k12 was determined by a linear fit of the reaction rate kobs against the concentration of the counter complex (Fig. 7, right; Table 3).
The electron self-exchange rate k11 is calculated with the determined equilibrium constant K12 and the reaction rate k12 following the Marcus cross relation (eqn (1) and Table 3). The results implicate that all substituents have a high impact on the equilibrium constant K12 and the reaction rate k12 of the cross reaction. The differences between the equilibrium constants K12 are a result of the different redox potentials E1/2 of the copper complex redox couples. Due to the influence of the equilibrium constant K12 on the reaction rate k12 of the cross reaction the electron self-exchange rate k11 is needed to compare the electron transfer properties of the copper complex redox couples. For R2 and R3 higher electron self-exchange rates k11 were obtained compared to unsubstituted redox couple R1 which means that the alkyl substituents in the 2-position of the ligands lead to a faster electron transfer. This is caused by the steric demand of the alkyl substituents that leads to more similar structures of the corresponding Cu(I) and Cu(II) complexes and therefore to better entatic state models compared to R1. For this reason, the highest electron self-exchange rate would be expected for R3 because it shows the highest structural accordance, represented by the Δτ4 (DFT) value, between the Cu(I) and Cu(II) complexes. However, the highest electron self-exchange rate is obtained for R2. This implicates that not only the structural accordance is important. Moreover, the “average” of the Cu(I) and the Cu(II) complex, represented by the øτ4 (DFT) value, is relevant. It describes whether the redox couple is in average more like a Cu(I) or a Cu(II) species. For a good entatic state model it is mandatory that the redox couple does not structurally favor one oxidation state. For R2 a higher Δτ4 value is obtained compared to R3 but the øτ4 value shows that the mean structure does not favor one oxidation state like in R3 whose mean structure prefers the Cu(I) oxidation state. For R4 a similar electron self-exchange rate k11 compared to R2 is determined although this is not expected due to the large differences between the structures of the Cu(I) and Cu(II) complexes. Therefore, this redox couple should be a worse entatic state model. The reason for the high electron self-exchange rate could be that the donor ability of the methyl ester influences the entatic state of R4. In the Cu(I) complex weak interactions between the methyl ester group and the Cu center are observable although Cu(I) prefers to be coordinated tetrahedrally by four donor moieties. In the Cu(II) complex the interactions are much stronger leading to a 4 + 2 coordination motif. If Cu(II) is four-coordinate, it prefers to be coordinated in a square-planar geometry and if it is six-coordinate, it prefers to be coordinated octahedrally. The interaction between the Cu center and the methyl ester group could induce a different type of entatic state compared to the other complex redox couples that do not exhibit any further interactions between the ligand and the Cu besides the coordination of the guanidine and quinolinyl moieties. R5 exhibits a similar electron self-exchange rate k11 compared to R1. Both redox couples have similar øτ4 and Δτ4 values. This suggests that no oxidation state is structurally favored by the introduction of the dimethylamine group. Characteristic of this redox couple is the extremely low redox potential which stabilizes the Cu(II) complex but this does not have a significant influence on the electron self-exchange rate. Therefore, the dimethylamine group only has a thermodynamic effect but not a kinetic effect on the electronic properties of the redox couple. Hence, the electronic influence of the dimethylamine group on the ligand does not affect the entatic state of the redox couple. For a deeper understanding between the electron transfer and the structural change during the electron transfer, the calculation of the reorganization energy is necessary.
Calculation of the reorganization energy
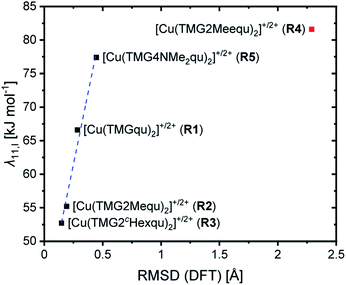
During the electron self-exchange reaction (characterized kinetically by k11), the ligand spheres of the complexes and the solvent spheres around the complexes have to reorganize. The necessary energy for the reorganization of the ligand sphere is described by the internal reorganization energy λ11,I and the energy for the reorganization of the solvent sphere by the solvent reorganization energy λ11,S. Together they result in the total reorganization energy λ11,T which describes the whole process. The reorganization energies were determined via DFT calculations using Nelsen's four-point method (Table 4, further information in ESI Section 9.4‡).22,23,44| λ 11,I [kJ mol−1] | λ 11,S [kJ mol−1] | λ 11,T [kJ mol−1] | Δτ4 (DFT) [ ] | Δ∡ (DFT) [°] | RMSD (DFT) [Å] | |
|---|---|---|---|---|---|---|
| a The value may be influenced by the 4 + 2 coordination motif in the Cu(II) complex. | ||||||
| [Cu(TMGqu)2]+/2+ (R1) | 66.6 | 135.2 | 201.8 | 0.20 | 23.8 | 0.283 |
| [Cu(TMG2Mequ)2]+/2+ (R2) | 55.2 | 128.6 | 183.8 | 0.13 | 17.06 | 0.191 |
| [Cu(TMG2cHexqu)2]+/2+ (R3) | 52.7 | 110.7 | 163.3 | 0.07 | 13.3 | 0.147 |
| [Cu(TMG2Meequ)2]+/2+ (R4) | 81.6 | 123.5 | 205.1 | 0.00a | −7.5 | 2.289 |
| [Cu(TMG4NMe2qu)2]+/2+ (R5) | 77.4 | 128.2 | 205.6 | 0.20 | 24.5 | 0.446 |
For R2 and R3 with ligands with alkyl substituents in the 2-position significantly lower internal reorganization energies λ11,I were calculated compared to R1 with the unsubstituted ligand L1. In contrast, for R4 and R5 with ligands with substituents that have an electronic influence, significantly higher internal reorganization energies were calculated. The results indicate that for R1–R3 the internal reorganization energy shrinks with the increasing steric demand of the substituent (H < Me < cHex). This is in accordance with the expectations because the higher steric demand leads to more similar structures of the Cu(I) and Cu(II) complexes and therefore to small Δτ4 or Δ∡ values between the complexes. Similar structures reduce the internal reorganization energy necessary for the electron self-exchange. The results for R4 and R5 do not correlate with the Δτ4 or Δ∡ values like for R1–R3. The reason is that the τ4 value and the plane angle ∡ do not represent all structural features of a complex because they only depend on the Cu center and the four N donors. The other atoms are not considered and therefore changes in the bond lengths and angles between the Cu(I) and Cu(II) complexes are not recognized. Hence, the root-mean-square deviation (RMSD) values of the atomic positions between the corresponding Cu(I) and Cu(II) complexes were calculated. The internal reorganization energies and the RMSD values correlate much better (Fig. 8). A lower RMSD value indicates a higher structural accordance which leads to a lower internal reorganization energy. For R1–R3 and R5 a linear correlation was found. The unusual coordination behavior of the ligand in R4 could be the reason why this complex does not follow this linear correlation.
The solvent reorganization energy λ11,S decreases for R2–R5 by the introduction of a substituent compared to the unsubstituted R1. For R1–R3 the solvent reorganization energy decreases with the steric demand of the substituent (H < Me < cHex). Due to the greater resemblance between the structures of the Cu(I) and Cu(II) complexes of R2 and R3 the solvent sphere is not as affected by the structural change of the complex during the electron transfer as for R1. Moreover, a substituent in the 2-position insulates the solvent sphere from the copper center. Hence, the influence of the change of the oxidation state during the electron transfer does not affect the solvent sphere of R2 and R3 as much as of R1. This effect is stronger in R3 than in R2 because the substituent is larger and therefore the shielding of the copper center stronger. A similar effect occurs in R4 but the methyl ester group in the 2-position not only insulates the solvent sphere from the copper center structurally but also electronically and by its weak coordination ability especially in the Cu(II) species. This leads to the second lowest solvent reorganization energy of the analyzed redox couples. However, also the isolated electronic influence of the dimethylamine group in R5 leads to a decrease of the solvent reorganization energy compared to R1. Due to the stronger donor properties of the Nqu donor caused by the electron density donating feature of the dimethylamine group the positive charge of the copper center is better stabilized especially in the Cu(II) species. This results in a weaker electronic influence on the solvent sphere and therefore a lower solvent reorganization energy.
In sum, the total reorganization energy λ11,T decreases significantly for R2 and R3 with the introduction of alkyl substituents in the 2-position compared to R1 whereas for R4 and R5 a small increase occurs.
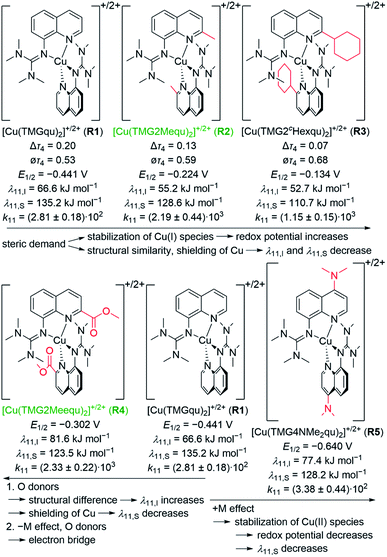
Discussion and correlation of the results
All complexes exhibit a strongly distorted geometry between the ideal tetrahedral and the ideal square-planar geometry. The alkyl substituents in the 2-position of R2 and R3 have a steric influence on the coordination where an increasing steric demand of the ligand leads to a greater similarity between the structures of the Cu(I) and Cu(II) complexes compared to the unsubstituted R1 (Fig. 9). Further, the geometries of the Cu(I) and Cu(II) complexes approach the tetrahedral geometry with the steric demand of the substituents (H < Me < cHex). In contrast, the methyl ester substituent in the 2-position of R4 has in addition to the steric demand an electronic influence and weak coordination ability especially in the Cu(II) complex. This weak coordination ability leads to the least similar Cu(I) and Cu(II) complex structures. The influence of the dimethylamine group in the 4-position of R5 is limited to an electron density donating effect which does not induce a significant change in the coordination geometry. From the structural point of view R3 should be the best entatic state model.The redox couples' potentials possess a strong dependency on the structural and electronic properties of the complexes. In case of R1, R2 and R3 the redox potential increases with a tendency towards a tetrahedral geometry leading to a stabilization of the Cu(I) species (Fig. 9). Moreover, the redox potential decreases with an increasing difference between the charge-transfer energies of the corresponding Cu(II) and Cu(I) complexes because the Cu(II) complex becomes better stabilized. Especially in R5, the electron density donating feature of the dimethylamine leads to a strong stabilization of the Cu(II) complex. Furthermore, the substituents have a significant impact on the electron self-exchange rates. The introduction of an alkyl substituent leads to higher electron self-exchange rates of R2 and R3 compared to R1. This correlates with the smaller internal and solvent reorganization energies of R2 and R3 compared to R1. However, R3 exhibits the lowest reorganization energy but not the highest electron self-exchange rate. This result emphasizes that besides a structural similarity between the Cu(I) and Cu(II) complexes a mean structure that does not favor one oxidation state of the redox couple is important for a fast electron transfer. Therefore, R2 is a better functional entatic state model than R3. R4 possesses the highest internal and the second lowest solvent reorganization energy, in sum the second highest total reorganization energy. Nevertheless, it exhibits the highest electron self-exchange rate. A correlation between the electron self-exchange rate and the reorganization energy is not possible. This underlines that a high electron self-exchange rate cannot only be achieved by a high structural accordance between the Cu(I) and Cu(II) complexes and a low total reorganization energy. A possible explanation for the high electron self-exchange rate of R4 is that the ester group has a significant influence on the process of the outer-sphere electron transfer itself. Due to its negative mesomeric effect (−M effect) it is part of the aromatic system of the ligand in which the electrons can move freely. Moreover, the donor properties of the ester group may lead to a reinforcement of the interactions between two individual complexes. Especially in the Cu(I) species the ester groups do not exhibit any strong interactions with the Cu(I) center and could therefore interact with a different complex. In sum, the ester group could act as a bridge for the outer-sphere electron transfer and by this reduce the length of the jump of the electron through space between the two complexes. This effect is not considered in the calculated reorganization energies. An analogous but less intense effect could occur in R5 and explain the similar electron self-exchange rate compared to R1 although the total reorganization energy is higher. Overall, R2 and R4 are the best functional entatic state models but for different reasons, namely the interplay between steric and mesomeric effects. Therefore, different approaches to reach higher electron self-exchange rates and to enhance the entatic state model with the same ligand framework are possible. The steric manipulation facilitates the transition between the two oxidation states whereas the electronic manipulation by a mesomeric effect facilitates the transfer of the electron from one complex to another complex.
Conclusions
In this study, novel guanidine quinolinyl copper complexes were synthesized and their electron transfer properties analyzed to gain a deeper understanding of the entatic state for electron transfer. Ligands with substituents in the 2- or 4-position of the quinolinyl backbone that exert steric and electronic influences on the donor properties of the ligands were synthesized to design complexes with specific features. The complexes were characterized by XRD, XAS, and DFT revealing significant impacts of the substituents on the structural and electronic properties of the complexes. To examine the influence on the electron transfer, the electron self-exchange rates were determined and the reorganization energies calculated. In R2 and R3 the steric demand of the alkyl substituents in the 2-position leads to lower total reorganization energies and higher electron-self exchange rates compared to R1. Therefore, the entatic state of the electron transfer is manipulated sterically in R2 and R3. The methyl ester group in the 2-position of R4 leads to a higher steric demand and enhanced donor properties; furthermore, it has an electron density withdrawing effect. Although R4 exhibits a high total reorganization energy, it possesses the highest electron self-exchange rate. The ester group possibly enables a different type of manipulation of the entatic state by serving as an electron bridge in the electron transfer. The pure electron density donating feature of the dimethylamine group in the 4-position of R5 exhibits the smallest influence on the electron transfer.In general, the ability of the copper complex redox couples to act as functional entatic state models could be tuned and significantly improved which is due to the varied substituents in the aromatic system. This opens up new avenues in the design of entatic state complexes and, in general, electron transfer systems where the thermodynamics and kinetics can be tuned.
Data availability
All synthetic details are described in the ESI.‡ Additional information on the synthesis of the target compounds and original analysis data files are available in the Chemotion repository (for corresponding links see the ESI‡). The optimized calculated structures were deposited in the repository RADAR4Chem by FIZ Karlsruhe – Leibniz-Institut für Informationsinfrastruktur and are published under an Open Access model (CC BY-NC-SA 4.0 Attribution-NonCommercial-ShareAlike; https://doi.org/10.22000/613).Author contributions
J. H. synthesized the ligands, complexes and the XAS samples. J. H. performed and evaluated the CV, NMR, IR, UV/Vis and stopped-flow spectroscopic measurements, evaluated additionally the MS data, determined the equilibrium constants and the electron self-exchange rates and performed Nelsen's four-point method calculations. Furthermore, J. H. executed the DFT and NBO calculations and the analysis under supervision of A. H. F. M. synthesized two ligands and helped to characterize the complexes with these ligands with CV and stopped-flow spectroscopy. A. H. and T. P. S. checked and finalized the crystallographic data. S. B., M. T. and B. G.-L. measured and analyzed the XAS data. J. H., A. H., M. R. and S. H.-P. wrote the manuscript. M. R. and S. H.-P. supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. H.-P. and M. R. acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG, 413524714). Further, M. R. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG) via RU 773/8-1 and the Bundesministerium für Bildung und Forschung (BMBF) via 05K19GU5. We thank the Paderborn Center for Parallel Computing, PC2, for providing computing time on the High-Performance Computing (HPC) system OCuLUS as well as support. Moreover, we thank the Regional Computing Center of the University of Cologne (RRZK) for providing computing time on the DFG-funded High Performance Computing (HPC) system CHEOPS as well as support. We thank NFDI4Chem for support and funding of the repository RADAR4Chem. Finally, we thank Edmund Welter and Wolfgang Caliebe for their support at PETRA III.Notes and references
- (a) J. Liu, S. Chakraborty, P. Hosseinzadeh, Y. Yu, S. Tian, I. Petrik, A. Bhagi and Y. Lu, Chem. Rev., 2014, 114, 4366 CrossRef CAS PubMed; (b) E. I. Solomon and R. G. Hadt, Coord. Chem. Rev., 2011, 255, 774 CrossRef CAS; (c) E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659 CrossRef CAS PubMed.
- (a) J. Mitchell Guss and H. C. Freeman, J. Mol. Biol., 1983, 169, 521 CrossRef; (b) P. M. Colman, H. C. Freeman, J. M. Guss, M. Murata, V. A. Norris, J. A. M. Ramshaw and M. P. Venkatappa, Nature, 1978, 272, 319 CrossRef CAS.
- (a) S. Dahlin, B. Reinhammar and M. T. Wilson, Biochem. J., 1984, 218, 609 CrossRef CAS PubMed; (b) C. Buning, G. W. Canters, P. Comba, C. Dennison, L. Jeuken, M. Melter and J. Sanders-Loehr, J. Am. Chem. Soc., 2000, 122, 204 CrossRef CAS; (c) F. A. Armstrong, P. C. Driscoll, H. Allen and O. Hill, FEBS Lett., 1985, 190, 242 CrossRef CAS; (d) K. Kataoka, A. Kondo, K. Yamaguchi and S. Suzuki, J. Inorg. Biochem., 2000, 82, 79 CrossRef CAS; (e) K. Kataoka, K. Yamaguchi, M. Kobayashi, T. Mori, N. Bokui and S. Suzuki, J. Biol. Chem., 2004, 279, 53374 CrossRef CAS PubMed; (f) K. Kataoka, K. Yamaguchi, S. Sakai, K. Takagi and S. Suzuki, Biochem. Biophys. Res. Commun., 2003, 303, 519 CrossRef CAS; (g) T. Kohzuma, S. Takase, S. Shidara and S. Suzuki, Chem. Lett., 1993, 22, 149 CrossRef; (h) A. Lommen and G. W. Canters, J. Biol. Chem., 1990, 265, 2768 CrossRef CAS PubMed; (i) K. Sato, P. B. Crowley and C. Dennison, J. Biol. Chem., 2005, 280, 19281 CrossRef CAS PubMed; (j) K. Sato, T. Kohzuma and C. Dennison, J. Am. Chem. Soc., 2003, 125, 2101 CrossRef CAS PubMed; (k) S. Suzuki, K. Kataoka, K. Yamaguchi, T. Inoue and Y. Kai, Coord. Chem. Rev., 1999, 190–192, 245 CrossRef CAS.
- P. Comba, M. Kerscher and A. Roodt, Eur. J. Inorg. Chem., 2004, 2004, 4640 CrossRef.
- B. G. Karlsson, R. Aasa, B. G. Malmström and L. G. Lundberg, FEBS Lett., 1989, 253, 99 CrossRef CAS.
- B. G. Malmström, Eur. J. Biochem., 1994, 223, 711 CrossRef PubMed.
- J. Stanek, A. Hoffmann and S. Herres-Pawlis, Coord. Chem. Rev., 2018, 365, 103 CrossRef CAS.
- (a) D. B. Rorabacher, Chem. Rev., 2004, 104, 651 CrossRef CAS PubMed; (b) R. J. P. Williams, Inorg. Chim. Acta, Rev., 1971, 5, 137 CrossRef CAS; (c) W. R. Hagen, Metallomics, 2019, 11, 1768 CrossRef CAS PubMed.
- P. Comba and W. Schiek, Coord. Chem. Rev., 2003, 238–239, 21 CrossRef CAS.
- P. Comba, Coord. Chem. Rev., 2000, 200–202, 217 CrossRef CAS.
- B. L. Vallee and R. J. Williams, Proc. Natl. Acad. Sci. U. S. A., 1968, 59, 498 CrossRef CAS PubMed.
- P. Comba, Coord. Chem. Rev., 1999, 182, 343 CrossRef.
- R. J. Williams, Eur. J. Biochem., 1995, 234, 363 CrossRef CAS PubMed.
- B. G. Malmström, Biol. Met., 1990, 3, 64 CrossRef.
- G. Chaka, J. L. Sonnenberg, H. B. Schlegel, M. J. Heeg, G. Jaeger, T. J. Nelson, L. A. Ochrymowycz and D. B. Rorabacher, J. Am. Chem. Soc., 2007, 129, 5217 CrossRef CAS PubMed.
- P. R. Raithby, G. P. Shields, F. H. Allen and W. D. S. Motherwell, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 444 CrossRef PubMed.
- (a) P. Comba, S. Fukuzumi, C. Koke, B. Martin, A.-M. Löhr and J. Straub, Angew. Chem., Int. Ed., 2016, 55, 11129 ( Angew. Chem. , 2016 , 128 , 11295 ) CrossRef CAS PubMed; (b) Y. Ren, J. Forté, K. Cheaib, N. Vanthuyne, L. Fensterbank, H. Vezin, M. Orio, S. Blanchard and M. Desage-El Murr, iScience, 2020, 23, 100955 CrossRef CAS PubMed; (c) B. Dicke, A. Hoffmann, J. Stanek, M. S. Rampp, B. Grimm-Lebsanft, F. Biebl, D. Rukser, B. Maerz, D. Göries, M. Naumova, M. Biednov, G. Neuber, A. Wetzel, S. M. Hofmann, P. Roedig, A. Meents, J. Bielecki, J. Andreasson, K. R. Beyerlein, H. N. Chapman, C. Bressler, W. Zinth, M. Rübhausen and S. Herres-Pawlis, Nat. Chem., 2018, 10, 355 CrossRef CAS PubMed; (d) G. D. Stroscio, R. D. Ribson and R. G. Hadt, Inorg. Chem., 2019, 58, 16800 CrossRef CAS PubMed; (e) L. Garcia, F. Cisnetti, N. Gillet, R. Guillot, M. Aumont-Nicaise, J.-P. Piquemal, M. Desmadril, F. Lambert and C. Policar, J. Am. Chem. Soc., 2015, 137, 1141 CrossRef CAS PubMed; (f) D. F. Schrempp, S. Leingang, M. Schnurr, E. Kaifer, H. Wadepohl and H.-J. Himmel, Chem.–Eur. J., 2017, 23, 13607 CrossRef CAS PubMed; (g) D. F. Schrempp, E. Kaifer and H.-J. Himmel, Eur. J. Inorg. Chem., 2018, 2018, 3660 CrossRef CAS.
- (a) B. Xie, L. J. Wilson and D. M. Stanbury, Inorg. Chem., 2001, 40, 3606 CrossRef CAS PubMed; (b) B. Xie, T. Elder, L. J. Wilson and D. M. Stanbury, Inorg. Chem., 1999, 38, 12 CrossRef CAS.
- E. W. Dahl and N. K. Szymczak, Angew. Chem., Int. Ed., 2016, 55, 3101 CrossRef CAS PubMed.
- A. Hoffmann, S. Binder, A. Jesser, R. Haase, U. Flörke, M. Gnida, M. Salomone Stagni, W. Meyer-Klaucke, B. Lebsanft, L. E. Grünig, S. Schneider, M. Hashemi, A. Goos, A. Wetzel, M. Rübhausen and S. Herres-Pawlis, Angew. Chem., Int. Ed., 2014, 53, 299 ( Angew. Chem. , 2014 , 126 , 305–310 ) CrossRef CAS PubMed.
- A. Hoffmann, J. Stanek, B. Dicke, L. Peters, B. Grimm-Lebsanft, A. Wetzel, A. Jesser, M. Bauer, M. Gnida, W. Meyer-Klaucke, M. Rübhausen and S. Herres-Pawlis, Eur. J. Inorg. Chem., 2016, 2016, 4731 CrossRef CAS.
- J. Stanek, N. Sackers, F. Fink, M. Paul, L. Peters, R. Grunzke, A. Hoffmann and S. Herres-Pawlis, Chem.–Eur. J., 2017, 23, 15738 CrossRef CAS PubMed.
- J. Stanek, M. Konrad, J. Mannsperger, A. Hoffmann and S. Herres-Pawlis, Eur. J. Inorg. Chem., 2018, 2018, 4997 CrossRef CAS.
- T. Rösener, A. Hoffmann and S. Herres-Pawlis, Eur. J. Inorg. Chem., 2018, 2018, 3164 CrossRef.
- F. Fontana, F. Minisci, M. C. Nogueira Barbosa and E. Vismara, Tetrahedron, 1990, 46, 2525 CrossRef CAS.
- S. Y. Gadomsky and I. K. Yakuschenko, Russ. Chem. Bull., 2016, 65, 816 CrossRef CAS.
- (a) H. J. Cho, M. I. El-Gamal, C.-H. Oh, S. H. Lee, T. Sim, G. Kim, H. S. Choi, J. H. Choi and K. H. Yoo, Chem. Pharm. Bull., 2013, 61, 747 CrossRef CAS PubMed; (b) R. W. Gouley, G. W. Moersch and H. S. Mosher, J. Am. Chem. Soc., 1947, 69, 303 CrossRef CAS.
- (a) O. V. Dyablo, E. A. Shmoilova, A. F. Pozharskii, V. A. Ozeryanskii, O. N. Burov and Z. A. Starikova, Org. Lett., 2012, 14, 4134 CrossRef CAS PubMed; (b) T. G. Ribelli, M. Fantin, J.-C. Daran, K. F. Augustine, R. Poli and K. Matyjaszewski, J. Am. Chem. Soc., 2018, 140, 1525 CrossRef CAS PubMed.
- (a) W. Kantlehner, E. Haug, W. W. Mergen, P. Speh, T. Maier, J. J. Kapassakalidis, H.-J. Bräuner and H. Hagen, Liebigs Ann. Chem., 1984, 1984, 108 CrossRef; (b) S. Herres-Pawlis, A. Neuba, O. Seewald, T. Seshadri, H. Egold, U. Flörke and G. Henkel, Eur. J. Org. Chem., 2005, 2005, 4879 CrossRef.
- A. Hoffmann, R. Grunzke and S. Herres-Pawlis, J. Comput. Chem., 2014, 35, 1943 CrossRef CAS PubMed.
- A. Hoffmann, M. Rohrmüller, A. Jesser, I. dos Santos Vieira, W. G. Schmidt and S. Herres-Pawlis, J. Comput. Chem., 2014, 35, 2146 CrossRef CAS PubMed.
- A. Jesser, M. Rohrmüller, W. G. Schmidt and S. Herres-Pawlis, J. Comput. Chem., 2014, 35, 1 CrossRef CAS PubMed.
- M. Rohrmüller, S. Herres-Pawlis, M. Witte and W. G. Schmidt, J. Comput. Chem., 2013, 34, 1035 CrossRef PubMed.
- M. Rohrmüller, A. Hoffmann, C. Thierfelder, S. Herres-Pawlis and W. G. Schmidt, J. Comput. Chem., 2015, 36, 1672 CrossRef PubMed.
- T. Rösener, O. Bienemann, K. Sigl, N. Schopp, F. Schnitter, U. Flörke, A. Hoffmann, A. Döring, D. Kuckling and S. Herres-Pawlis, Chem.–Eur. J., 2016, 22, 13550 CrossRef PubMed.
- P. Liebhäuser, K. Keisers, A. Hoffmann, T. Schnappinger, I. Sommer, A. Thoma, C. Wilfer, R. Schoch, K. Stührenberg, M. Bauer, M. Dürr, I. Ivanović-Burmazović and S. Herres-Pawlis, Chem.–Eur. J., 2017, 23, 12171 CrossRef PubMed.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955 RSC.
- V. Raab, K. Harms, J. Sundermeyer, B. Kovacević and Z. B. Maksić, J. Org. Chem., 2003, 68, 8790 CrossRef CAS PubMed.
- L. S. Kau, D. J. Spira-Solomon, J. E. Penner-Hahn, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1987, 109, 6433 CrossRef CAS.
- J. E. Hahn, R. A. Scott, K. O. Hodgson, S. Doniach, S. R. Desjardins and E. I. Solomon, Chem. Phys. Lett., 1982, 88, 595 CrossRef CAS.
- (a) R. A. Marcus, Pure Appl. Chem., 1997, 69, 13 CrossRef CAS; (b) R. A. Marcus, Angew. Chem., Int. Ed., 1993, 32, 1111 ( Angew. Chem. , 1993 , 105 , 1161–1172 ) CrossRef; (c) R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265 CrossRef CAS.
- B. C. Dunn, L. A. Ochrymowycz and D. B. Rorabacher, Inorg. Chem., 1995, 34, 1954 CrossRef CAS.
- K. W. Kröckert, J. S. Mannsperger, T. Rösener, A. Hoffmann and S. Herres-Pawlis, Z. Anorg. Allg. Chem., 2021, 647, 832 CrossRef.
- (a) S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677 CrossRef CAS; (b) S. F. Nelsen and M. J. R. Yunta, J. Phys. Org. Chem., 1994, 7, 55 CrossRef CAS.
Footnotes |
| † Dedicated to Professor Jun Okuda on the occasion of his 65th birthday. |
| ‡ Electronic supplementary information (ESI) available: Experimental data of the methods and details of the synthesis with characterization (IR, NMR, and MS), crystallographic information, XAS data, UV/Vis-, CV- and stopped-flow-spectra, DFT details, pictures of all NMR spectra and additional plots and further discussions. CCDC 2132917–2132931. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2sc02910c |
| This journal is © The Royal Society of Chemistry 2022 |