Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Origin of low melting point of ionic liquids: dominant role of entropy†
Takatsugu
Endo
 *a,
Kouki
Sunada
b,
Hiroki
Sumida
b and
Yoshifumi
Kimura
*a,
Kouki
Sunada
b,
Hiroki
Sumida
b and
Yoshifumi
Kimura
 ab
ab
aDepartment of Molecular Chemistry and Biochemistry, Faculty of Science and Engineering, Doshisha University, 1-3 Tatara Miyakodani, Kyotanabe, Kyoto 610-0394, Japan. E-mail: taendo@mail.doshisha.ac.jp
bDepartment of Applied Chemistry, Graduate School of Science and Engineering, Doshisha University, 1-3 Tatara Miyakodani, Kyotanabe, Kyoto 610-0394, Japan
First published on 8th June 2022
Abstract
Ionic liquids (ILs) are salts with an extremely low melting point. Substantial efforts have been made to address their low melting point from the enthalpic standpoint (i.e. interionic interactions). However, this question is still open. In this study, we report our findings that entropic (large fusion entropy), rather than enthalpic, contributions are primarily responsible for lowering the melting point in many cases, based on a large thermodynamic dataset. We have established a computational protocol using molecular dynamics simulations to decompose fusion entropy into kinetic (translational, rotational, and intramolecular vibrational) and structural (conformational and configurational) terms and successfully applied this approach for two representatives of ILs and NaCl. It is revealed that large structural contribution, particularly configurational entropy in the liquid state, plays a deterministic role in the large fusion entropy and consequently the low melting point of the ILs.
Introduction
Salts are defined as materials composed solely of ions. Since interactions between cations and anions are governed by strong coulombic interactions, with the order of magnitudes of several hundred kJ mol−1, melting points of salts tend to be extremely high. The typical example is table salt (NaCl), whose melting point is 1073 K. However, in the late 1990s, scientists started to recognize salts with extremely low melting points corresponding to room temperature or even below. Nowadays, these salts are called room temperature ionic liquids or simply ionic liquids (ILs). ILs have attracted considerable attention because they have several substantial properties, such as negligible vapor pressure and flammability, high thermal/chemical/electrochemical stabilities, high ionic/electric conductivity, and unique solubilities.1–3 These properties mark ILs as promising candidates in a wide range of applications, for example, green solvents, electrolytes, CO2 absorbents, and cellulose solvents.1–3The melting point is considered the most important physical property of ILs since it distinguishes them from other salts. Many investigations have been intensively conducted to answer why ILs have such a low melting point; moreover, various solutions have been proposed.1,4–9 Thermodynamically, contributions to the melting point are divided into two terms, i.e., enthalpic and entropic terms. Although the importance of the entropic contributions (e.g., conformational entropy stemming from flexible side groups) were pointed out,1,4,6,8,9 the mainstream discussion thus far has been made on enthalpic contributions.1,4–9 Namely, coulombic interaction among ions and lattice energy are weakened in ILs due to bulky, asymmetric, and sometimes charge-delocalized ions. In this work, we demonstrate that this is not the right approach and that the low melting point is caused due to entropic contribution in the majority of ILs.
Results and discussion
Alkali halides versus ionic liquids
From a thermodynamical standpoint, melting point (Tm) of material is the ratio of fusion enthalpy (ΔfusH) and fusion entropy (ΔfusS):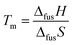 | (1) |
This rigorous expression shows that the melting point is low when ΔfusH is small and/or ΔfusS is large. Stating that the melting point of ILs is “low” requires a reference material for comparison. NaCl with a melting point of 1073 K is frequently selected. For statistical comparison purposes, 20 alkali halides were selected in this study, and their thermodynamic quantities10 were compared with those of 257 ILs.11,12 As the name suggests, the average Tm of ILs is ∼3 times lower than that of alkali halides (Fig. 1A). An average value of ΔfusH for ILs, associated with interionic interactions in the liquid and crystal states, is only 0.85 times the ΔfusH value of alkali halides (Fig. 1B). Meanwhile, the average ΔfusS of ILs is 2.67 times larger than that of alkali halides (Fig. 1C), which indicates that, in general, the large ΔfusS plays a more critical role than the small ΔfusH for lowering Tm of ILs.
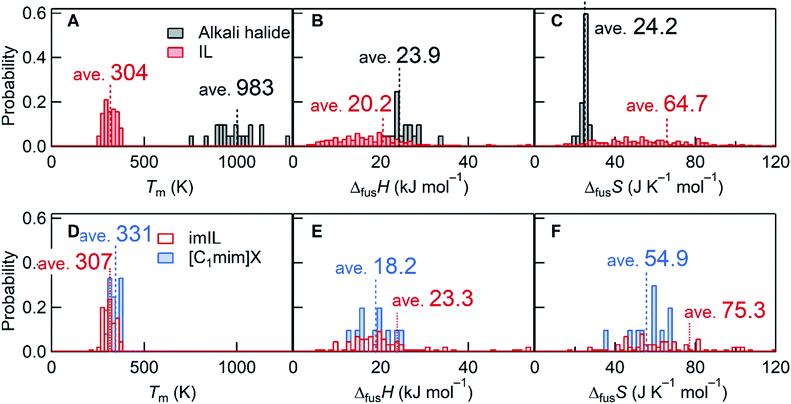 | ||
| Fig. 1 Histogram comparisons of Tm, ΔfusH, and ΔfusS. (A–C) 20 alkali halides10versus 257 ILs11,12 and (D–F) 84 imILs versus 12 [C1mim]X. For [C1mim]X, this work reported 10 data and the two additional data were taken from the ref. 41 and 42 (Table S3†). Bin widths for the Tm, ΔfusH, and ΔfusS histograms were 20 K, 1 kJ mol−1, and 2 J K−1 mol−1, respectively. For ILs and imILs, several data of ΔfusH and ΔfusS are out of range of the figures. | ||
Since the discussion would depend on the ions constituting the IL, we focus on imidazolium-based ILs (imILs) as the most representative IL series. Analyzing the available data on 84 imILs,11,12 the importance of the large ΔfusS is emphasized as seen in Fig. 1D–F. While ΔfusH values are comparable, their ΔfusS values are 3.11 times larger than those corresponding to alkali halides. Considering the origin of the large ΔfusS of ILs (or imILs), a prominent contribution may come from conformational entropy as described above.1,4,6,8,9 For example, most IL cations contain flexible alkyl chains that produce multiple conformations in the liquid state. This increases the entropy of the liquid state and consequently ΔfusS. An approach to thermodynamically elucidate the role of conformational entropy is to compare ΔfusS of imILs with flexible side chains to those without flexible groups. However, such data is rare. Therefore, we synthesized ten 1,3-dialkylimidazolium salts ([C1mim]X) with no conformational entropy in the cation and the anion and measured Tm, ΔfusH, and ΔfusS. The difference in Tm between [C1mim]X and imILs is rather low, whereas both ΔfusH and ΔfusS of [C1mim]X are smaller than those of imILs (Fig. 1D–F). The small ΔfusH and ΔfusS values would be primarily due to the losses of inter-chain interactions1,6–9 and (as expected) conformational entropy, respectively. However, even without conformational entropy, not the small ΔfusH (18.2 kJ mol−1) but the large ΔfusS (54.9 J K−1 mol−1) seems to prevail in lowering Tm of ILs, compared to alkali halides (ΔfusH = 23.9 kJ mol−1 and ΔfusS = 24.2 J K−1 mol−1).
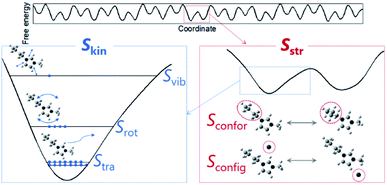
Fusion entropy decomposition
To quantitatively unravel ambiguous entropic contributions, entropy needs to be decomposed into individual components associated with molecular-level properties. The decompositions were conducted based on the free energy landscape model13,14 (Fig. 2). Absolute entropy (S) can be expressed as the sum of kinetic (Skin) and structural (Sstr) entropies. The former is further divided into translational (Stra), rotational (Srot), and intramolecular vibrational (Svib) terms and the latter is composed of conformational/intramolecular (Sconfor) and configurational/intermolecular (Sconfig) entropies. Since we focus on the difference in entropy between liquids and crystals at the melting point, by assuming individual terms are independent, appropriate equations are as follows:| ΔfusS = ΔkinS + ΔstrS | (2) |
| ΔkinS = ΔtraS + ΔrotS + ΔvibS | (3) |
| ΔstrS = ΔconforS + ΔconfigS | (4) |
To perform the ΔfusS decomposition, we have developed a computational protocol using classical molecular dynamics (MD) simulations (see the ESI† for details). ΔfusS and ΔconforS were estimated from the thermodynamic integration15,16 and conformational analyses, respectively. We employed the two-phase thermodynamic (2PT) approach, initially developed by Lin et al., for the kinetic entropy estimations.17–19 Conventionally, the entropy of vibrational motions for molecules in a solid state has been estimated through the density of states functions g(v) by assuming that all vibrational motions are harmonic oscillators. However, this technique cannot treat diffusive motions existing in a liquid state. The 2PT approach enables the estimation of entropy in a liquid state by dividing g(v) in the liquid state into solid-like (for harmonic oscillators) and gas-like (for diffusive motions) components. The remaining ΔconfigS was obtained based on eqn (2)–(4) by the deduction of the other terms. For reliable discussion on results obtained from classical MD simulations, a selection of force fields is critical. We selected the force fields developed by Maginn et al. for two prototype imILs as 1-ethyl-3-methylimidazolium hexafluorophosphate ([C2mim]PF6) and 1-butyl-3-methylimidazolium hexafluorophosphate ([C4mim]PF6).20 Partial charges in these force fields were determined by ab initio MD in the crystal state with periodic boundary conditions so that the charge transfer and polarization in the condensed state are implicitly included. Furthermore, MD simulations on NaCl with the Tosi–Fumi potential21 were conducted for comparison. Simulated Tm, ΔfusH, and ΔfusS were in good agreement with the experimental values (Table S7†). It is noted that the absolute entropies also satisfactorily reproduced experimental data (Table S10†).
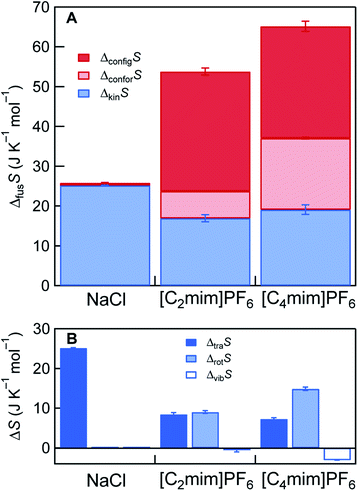
The results of the ΔfusS decompositions for NaCl and the two ILs are presented in Fig. 3. In NaCl that is composed of monoatomic ions, the following stands: ΔfusS ≈ ΔkinS = ΔtraS. For the ILs, ΔkinS is smaller than that of NaCl, even though the ILs have larger absolute entropy than NaCl in any state of matter, mainly due to the presence of Srot and Svib (Fig. S14†). There are three reasons for this counter-intuitive behavior. First, ΔvibS of the ILs does not contribute to ΔkinS, or they are even slightly negative. This would result from the fact that intramolecular vibrations are mostly unchanged by melting, as suggested by previous reports.22,23 The second reason is related to the difference in melting point. Since the melting points of the ILs are intrinsically lower than that of NaCl, diffusive motions (translational + rotational) represented by g(0) (density of states at zero frequency) are not activated by melting in the ILs, compared to NaCl (Fig. S11–S13 and Table S12†). The slow diffusive motions are also expected for other ILs since their viscosity is generally as high as several tens or more mPa s at the melting point. Third, the spherical PF6− anions already gain rotational diffusivity in the crystal state (Fig. S12C and S13C†), consistent with previous NMR observations,24 resulting in lowering ΔrotS.
Despite the small ΔkinS of the ILs, the presence of large ΔstrS (=ΔconforS + ΔconfigS) is the cause for the large ΔfusS. The presence of ΔconforS has been previously pointed out by several groups.1,4,6,8,9 The calculated ΔconforS values were 6.8 J K−1 mol−1 for [C2mim]PF6 and 18.0 J K−1 mol−1 for [C4mim]PF6. These values are slightly smaller than the previously reported Sconfor in the gas state (8.3 J K−1 mol−1 for [C2mim]PF6 and 22.8 J K−1 mol−1 for [C4mim]PF6).25 This would result from the fact that Sconfor in the crystalline state was calculated to be non-zero due to the slight disordering of the alkyl group in the cation (Tables S8 and S9†). A significant feature in Fig. 3A is that ΔconfigS plays a more prominent role in lowering Tm than ΔconforS. The ΔconfigS (=here Sconfig in the liquid state) values of [C2mim]PF6 and [C4mim]PF6 were estimated to be 30.0 J K−1 mol−1 and 28.1 J K−1 mol−1, respectively. Assuming Sconfig = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W, where W is the number of distinguishable microscopic states, at least 30–40 potential energy basins exist for these ILs in the liquid state. Although multiple configurations in ILs were already pointed out, and they were associated with the low melting point in a few papers,8,26 we quantitatively demonstrate the dominant role of ΔconfigS in the low melting point of ILs. The origin of multiple configurations is considered to come from the delocalized charges in the ion and the asymmetric ion structure.26 It is worth noting that these characteristics of ILs have been previously considered to contribute to lowering the melting point enthalpically by reducing coulombic interactions and packing efficiency.1,6,8,9 Our findings indicate that the delocalized charge and the asymmetric ion structure can be entropically, rather than enthalpically, important for the low melting point. Since large ΔkinS cannot be expected for general ILs, because of close-to-zero ΔvibS and high viscosity (small ΔtraS + ΔrotS), large ΔstrS (particularly large ΔconfigS) is the key for the large ΔfusS and the consequent low melting point of ILs.
W, where W is the number of distinguishable microscopic states, at least 30–40 potential energy basins exist for these ILs in the liquid state. Although multiple configurations in ILs were already pointed out, and they were associated with the low melting point in a few papers,8,26 we quantitatively demonstrate the dominant role of ΔconfigS in the low melting point of ILs. The origin of multiple configurations is considered to come from the delocalized charges in the ion and the asymmetric ion structure.26 It is worth noting that these characteristics of ILs have been previously considered to contribute to lowering the melting point enthalpically by reducing coulombic interactions and packing efficiency.1,6,8,9 Our findings indicate that the delocalized charge and the asymmetric ion structure can be entropically, rather than enthalpically, important for the low melting point. Since large ΔkinS cannot be expected for general ILs, because of close-to-zero ΔvibS and high viscosity (small ΔtraS + ΔrotS), large ΔstrS (particularly large ΔconfigS) is the key for the large ΔfusS and the consequent low melting point of ILs.
Conclusions
In this work, we have discovered that the low melting point of ILs is mainly driven entropically, i.e., the large ΔfusS dominantly decreases the melting point of ILs. To unravel the origin of the large ΔfusS, imILs as the most representative IL series were focused. With the developed protocol based on MD simulations, ΔfusS of the two imILs as well as NaCl were successfully decomposed into individual components with a clear physical origin. The simulations indicated that, somewhat counterintuitively, not the kinetic but the structural part, particularly ΔconfigS, was the main contributor to the low melting point of the ILs. Breaking the mainstream of the previous “enthalpic” discussion, our findings based on the “entropic” contributions can change the bottom concept for designing ILs and could consequently accelerate the production of a number of novel functional ILs.Experimental
Selection of thermodynamic data of ILs
The thermodynamic data, Tm, ΔfusH, ΔfusS for ILs were taken from the ILThermo database as summarized in Table S1.†11,12 (It is noted that Tm, ΔfusH, ΔfusS for alkali halide are also summarized in Table S2†).10 The ILThermo database seems to contain some inappropriate data for discussion, i.e., Tm is too high to be ILs, or ΔfusH or ΔfusS is too low to be considered as enthalpy/entropy difference on melting. In this work, we excluded the data with Tm > 373.2 K, ΔfusH < 3 kJ mol−1, or ΔfusS < 10 J K−1 mol−1 from the discussion. In some cases, several different data were reported in one IL because of, e.g., differences in experimental conditions, experimental error, and purities as well as the existence of polymorphism. Considering the purity and thermodynamic stability of polymorphs, we selected the one with the highest melting point.IL syntheses and characterizations
The ILs [C1mim]X were synthesized following standard procedures.1 The detailed procedures were described in the ESI.† The ILs were vacuum-dried with heating for several days (typically 353 K for 2 days) before use. The synthesized ILs were characterized with NMR spectroscopy (JEOL, JNM-ECA300W). No recognizable impurities were observed via NMR spectra except for water. The water content of the ILs was determined by Karl Fischer titration (MKC-501, Kyoto Electronics). When an IL was in the crystal state at room temperature, the water content measurement was conducted by dissolving it in anhydrous acetonitrile. Several ILs potentially contain a slight amount of alkali halides as a byproduct, the content of which was determined by Na+ meter (LAQUAtwin Na-11, Horiba) or the Mohr's method.DSC measurements
Differential scanning calorimetry (DSC) measurements were performed with a DSC7020 (Hitachi High-Tech Science). A dried IL was sealed in an Al pan in an Ar-atmosphere glovebox. In the measurements, the sample was first melted by heating, and data was subsequently collected by cooling down to 175 K and re-heating above the melting point at a scanning rate of 5 K min−1. The obtained DSC traces are shown in Fig. S1,† and the numerical values are listed in Tables S3 and S4.†Quantum chemical calculations
Quantum chemical calculations were performed to estimate absolute entropies of NaCl, [C2mim]PF6, and [C4mim]PF6 in the gas phase with Gaussian0927 program package. B3LYP28–30 combined with GD3 (ref. 31) correction at 6-311++G(d,p) level were employed for the calculations. Full geometry optimization and subsequent vibrational frequency analyses were performed. The initial structure of the IL ion pairs for the geometry optimization was referred to the ones reported previously32 (Fig. S2†). It is noted that no imaginary frequency was obtained for the optimized structures, which confirms that they are local minima. The absolute entropies and the decomposed kinetic entropies (Stra, Srot, and Svib) for NaCl, [C2mim]PF6, and [C4mim]PF6 are summarized in Table S5.†Molecular dynamics simulations
Classical MD simulations were performed with Gromacs 2018.4 Software package33,34 (single precision) with the periodic boundary condition. Newton's equation of motion was solved in 1 fs time step with the leap-frog algorithm unless otherwise stated. Cut-off radii for both coulombic and LJ potentials were set to be 1.2 nm. Long-range dispersion corrections were applied. Long-range coulombic interactions were treated with the particle mesh Ewald summation method.35,36 Temperature and pressure were controlled with Nose–Hoover thermostat and Parrinello–Rahman barostat, respectively. No constraint was applied for intramolecular bonds and angles.Ion pairs of 2048 (NaCl), 400 ([C2mim]PF6), and 250 ([C4mim]PF6) were used in MD simulations. The force field of NaCl was based on the Tosi–Fumi potential.21 The ones developed by Maginn et al.20 with the aid of the general AMBER force field37,38 were used for the two ILs. A crystal structure with fcc lattice was employed for the NaCl crystal. Crystal structures of [C2mim]PF6 (ref. 39) and [C4mim]PF6 (ref. 40) were taken from the references. For liquid state simulations, ions were randomly placed into a cubic cell. After energy minimizations with the steepest descent algorithm, an initial simulation box was first equilibrated in the NPT ensemble until system energy became constant, at least for 2 ns. If necessary, a subsequent NVT ensemble simulation was conducted with the equilibrated cell size. For statistical error estimation, a production run after the equilibration was equally divided into 4 blocks. The standard deviation based on 4 simulations was taken as the statistical error. It is noted that in the figures displayed in the main text and the ESI,† the average data of the 4 blocks are shown. Detailed procedures of estimations of Tm, ΔfusH, ΔfusS, and the entropies were described in the ESI.†
Data availability
All available data are included in the ESI.†Author contributions
T. Endo conceived and designed this study. K. Sunada synthesized the compounds. T. Endo performed the molecular dynamics simulations. H. Sumida performed the quantum chemical calculations. T. Endo analyzed the data. T. Endo produced the manuscript. K. Sunada, H. Sumida and K. Kimura checked and modified the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Miguel Caro (Aalto University, Finland) for his helpful advice on the 2PT analyses. The work was supported by JSPS KAKENHI Grant Number JP19K05393.Notes and references
- D. R. MacFarlane, M. Kar and J. M. Pringle, Fundamentals of Ionic Liquids: From Chemistry to Applications, Wiley-VCH, 2017 Search PubMed.
- D. Rogers Robin and R. Seddon Kenneth, Science, 2003, 302, 792–793 CrossRef CAS PubMed.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150 RSC.
- I. Krossing, J. M. Slattery, C. Daguenet, P. J. Dyson, A. Oleinikova and H. Weingärtner, J. Am. Chem. Soc., 2006, 128, 13427–13434 CrossRef CAS PubMed.
- S. Zahn, F. Uhlig, J. Thar, C. Spickermann and B. Kirchner, Angew. Chem., Int. Ed., 2008, 47, 3639–3641 CrossRef CAS PubMed.
- P. M. Dean, J. M. Pringle and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2010, 12, 9144–9153 RSC.
- Y. V. Nelyubina, A. S. Shaplov, E. I. Lozinskaya, M. I. Buzin and Y. S. Vygodskii, J. Am. Chem. Soc., 2016, 138, 10076–10079 CrossRef CAS.
- E. I. Izgorodina, Z. L. Seeger, D. L. A. Scarborough and S. Y. S. Tan, Chem. Rev., 2017, 117, 6696–6754 CrossRef CAS PubMed.
- F. Philippi and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 6993–7021 RSC.
- G. J. Janz, Molten Salts Handbook, Academic, 1967 Search PubMed.
- Q. Dong, C. D. Muzny, A. Kazakov, V. Diky, J. W. Magee, J. A. Widegren, R. D. Chirico, K. N. Marsh and M. Frenkel, J. Chem. Eng. Data, 2007, 52, 1151–1159 CrossRef CAS.
- A. Kazakov, J. W. Magee, R. D. Chirico, E. Paulechka, V. Diky, C. D. Muzny, K. Kroenlein and M. Frenkel, NIST Standard Reference Database 147: NIST Ionic Liquids Database – (ILThermo), Version 2.0, National Institute of Standards and Technology, Gaithersburg MD, 2021, p. 20899, http://ilthermo.boulder.nist.gov Search PubMed.
- L. Berthier, M. Ozawa and C. Scalliet, J. Chem. Phys., 2019, 150, 160902 CrossRef PubMed.
- F. H. Stillinger, Science, 1995, 267, 1935–1939 CrossRef CAS.
- D. M. Eike, J. F. Brennecke and E. J. Maginn, J. Chem. Phys., 2005, 122, 014115 CrossRef PubMed.
- K. Bernardino, Y. Zhang, M. C. C. Ribeiro and E. J. Maginn, J. Chem. Phys., 2020, 153, 044504 CrossRef CAS PubMed.
- S. T. Lin, M. Blanco and W. A. Goddard III, J. Chem. Phys., 2003, 119, 11792–11805 CrossRef CAS.
- M. A. Caro, T. Laurila and O. Lopez-Acevedo, J. Chem. Phys., 2016, 145, 244504 CrossRef PubMed.
- S. T. Lin, P. K. Maiti and W. A. Goddard III, J. Phys. Chem. B, 2010, 114, 8191–8198 CrossRef CAS PubMed.
- Y. Zhang and E. J. Maginn, Phys. Chem. Chem. Phys., 2012, 14, 12157–12164 RSC.
- J. L. Aragones, E. Sanz, C. Valeriani and C. Vega, J. Chem. Phys., 2012, 137, 104507 CrossRef CAS PubMed.
- J. Dupont, J. Braz. Chem. Soc., 2004, 15, 341–350 CrossRef CAS.
- V. H. Paschoal, L. F. O. Faria and M. C. C. Ribeiro, Chem. Rev., 2017, 117, 7053–7112 CrossRef CAS PubMed.
- T. Endo, H. Murata, M. Imanari, N. Mizushima, H. Seki, S. Sen and K. Nishikawa, J. Phys. Chem. B, 2013, 117, 326–332 CrossRef CAS PubMed.
- T. Endo, T. Higuchi and Y. Kimura, Bull. Chem. Soc. Jpn., 2020, 93, 720–729 CrossRef CAS.
- P. A. Hunt, J. Phys. Chem. B, 2007, 111, 4844–4853 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- B. A. Marekha, O. N. Kalugin and A. Idrissi, Phys. Chem. Chem. Phys., 2015, 17, 16846–16857 RSC.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- C. Kutzner, S. Páll, M. Fechner, A. Esztermann, B. L. de Groot and H. Grubmüller, J. Comput. Chem., 2019, 40, 2418–2431 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- H. Chen, T. Yan and G. A. Voth, J. Phys. Chem. A, 2009, 113, 4507–4517 CrossRef CAS PubMed.
- W. M. Reichert, J. D. Holbrey, R. P. Swatloski, K. E. Gutowski, A. E. Visser, M. Nieuwenhuyzen, K. R. Seddon and R. D. Rogers, Cryst. Growth Des., 2007, 7, 1106–1114 CrossRef CAS.
- A. R. Choudhury, N. Winterton, A. Steiner, A. I. Cooper and K. A. Johnson, J. Am. Chem. Soc., 2005, 127, 16792–16793 CrossRef CAS PubMed.
- T. Endo, T. Morita and K. Nishikawa, Chem. Phys. Lett., 2011, 517, 162–165 CrossRef CAS.
- U. Domańska, A. Pobudkowska and F. Eckert, Green Chem., 2006, 8, 268–276 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02342c |
| This journal is © The Royal Society of Chemistry 2022 |