Open Access Article
Open Access ArticleCoherent ring-current migration of Mg-phthalocyanine probed by time-resolved X-ray circular dichroism†
Shichao
Sun
 *,
Haiwang
Yong
*,
Haiwang
Yong
 ,
Feng
Chen
and
Shaul
Mukamel
,
Feng
Chen
and
Shaul
Mukamel
 *
*
Department of Chemistry and Department of Physics & Astronomy, University of California, Irvine, USA. E-mail: shichas2@uci.edu; smukamel@uci.edu
First published on 11th August 2022
Abstract
The coherent ring current of Mg-phthalocyanine created by a broad band UV-visible pump pulse shows variation with time, where the ring currents at the corner benzene rings, around the Mg cation and on the outer ring oscillate with different time periods and the current density migrates among these regions. The 7 pairs of Eu degenerate excited states populated upon photoexcitation, generate 21 distinct coherent ring currents. We further calculate the time-resolved X-ray circular dichroism (TRXCD) spectrum of the coherences contributing to the ring current obtained by an attosecond X-ray probe pulse resonant with the nitrogen K-edge. A frequency domain TRXCD signal obtained by a Fourier transform of the signal with respect to the pump-probe delay time clearly separates the currents induced by different state pairs.
Controlling and measuring attosecond movements of electrons in molecules are of fundamental importance for photoinduced chemical reactions. Ring current, a circular electron motion, can be induced in cyclic conjugated molecules by applying a static magnetic field,1–10 by using circularly polarized light (CPL)11 or by coupling the molecule to an optical chiral cavity.12 Magnetic-field-induced ring currents are widely applied in nuclear magnetic resonance,8,13–15 where a static field non-resonant with electronic excited states perturbs the ground state and creates a ground state ring current. The direction of the magnetic field induced current is determined by the direction of the applied magnetic field and the aromaticity of the molecule, where aromatic (antiaromatic) molecules produce diamagnetic (paramagnetic) ring currents.1,2,16–19
In this theoretical study, we focus on the CPL induced ring currents, which are receiving considerable attention.11,20–34 The sense of the resulting ring current is determined by the circular polarization of the pulse. Furthermore, CPL can create ring currents in selected states by tuning the pulse frequency to specific electronic states. This offers an additional control over the ring current generation.
We consider a molecule with two excited states with perpendicular transition dipoles to the ground state. We denote the excited states |Ex〉 and |Ey〉, whose transition dipole 〈g|μ|Ex,y〉 are along the x and y direction respectively. If the bandwidth of the circularly polarized pulse with polarization 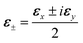 covers both states, the pulse will excite them with a phase difference of
covers both states, the pulse will excite them with a phase difference of 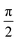 , giving the electron oscillation in x and y direction a
, giving the electron oscillation in x and y direction a 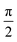 phase difference, thus driving the electrons to move in a circle.11
phase difference, thus driving the electrons to move in a circle.11
If this pair of excited states is degenerate, by a linear combination, we can create a pair of degenerate current-carrying eigenstates 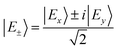 .11,30 A circularly polarized ε± light pulse increases the population of state |E±〉 respectively. Thus, the ring current created by the pulse can be viewed as population ring current which remains time-independent after the pump pulse is over. If the excited state pair is non-degenerate, the ring current is proportional to their coherence and is denoted coherent ring current.24,25,35 After the pulse is over, the population is stationary while the coherent ring current oscillates with a period inversely proportional to the energy difference between the coherent states.
.11,30 A circularly polarized ε± light pulse increases the population of state |E±〉 respectively. Thus, the ring current created by the pulse can be viewed as population ring current which remains time-independent after the pump pulse is over. If the excited state pair is non-degenerate, the ring current is proportional to their coherence and is denoted coherent ring current.24,25,35 After the pulse is over, the population is stationary while the coherent ring current oscillates with a period inversely proportional to the energy difference between the coherent states.
Previous research on coherent ring currents had focused on a single pair of coherence, where the current of the entire molecule evolves with the same pace.11,20–26,28–30 Here, we study the ring-current dynamics resulting from the superposition of multiple ring-current pairs created by a broad band circularly pump pulse. Due to the interplay of multiple coherences, we find that the evolution of ring current at different locations in the molecule show distinct feature. As the coherent current density evolves with time, we see the redistribution of current density between different regions of the molecule, which can be viewed as current migration. This behavior is analogous to the light-induced charge migration and the following evolution of electrons.36,37,54 Localized ring currents created at different regions within the molecule, create new possibilities for designing molecular device.38
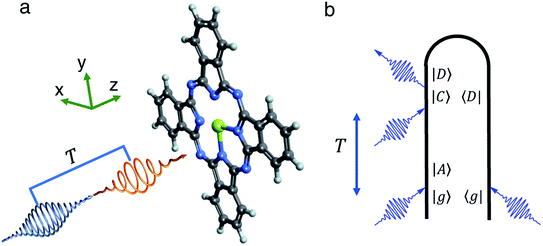
We focus on phthalocyanine which has broad applications in e.g. dye-sensitized solar cells39,40 and photosensitizers for cancer photodynamic therapy.41 Its derivative Mg-phthalocyanine (MgPc) has a rigid structure (see Fig. 1), which remains stable during the electronic dynamics.42,43 MgPc has a high density of states belonging to the Eu irreducible representation (Table S1†), which facilitates the coherent excitation of many excited states. The molecule has multiple rings, including a central ring and the four benzene rings in the corners, which makes it possible to observe the dynamics of both local and global ring currents. We use a broadband UV pump pulse with 2 eV bandwidth made possible by recently developed attosecond UV-visible pulses.44 Upon excitation, 7 pairs of degenerate excited states are populated within the pulse bandwidth to create 21 coherence pairs. These coherent ring currents have different profiles, giving rise to distinct evolution of local and the global ring currents. We further show that these coherences can be observed in time-resolved X-ray circular dichroism (TRXCD) spectrum resonant to the nitrogen K-edge. Contributions from each ring-current pair can be clearly identified in the Fourier-transformed CD spectrum.
As illustrated in Fig. 1, a circularly polarized pump pulse 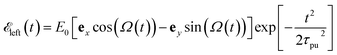 propagating along z perpendicular to the molecular x–y plane with an amplitude of 6.9934 × 109 V m−1, central frequency Ω = 4.0 eV and duration of τpu = 4.64 fs is applied at 0 fs to generate a ring current. The pulse duration and amplitude are chosen to excite 91.5% of the ground state population to excited states (Fig. S2†), thus create a high excited state population in this multi-level system. The mechanism is similar to Rabi-flop of two-level system. The electronic wave function is obtained by numerically solving the time-dependent Schrödinger equation
propagating along z perpendicular to the molecular x–y plane with an amplitude of 6.9934 × 109 V m−1, central frequency Ω = 4.0 eV and duration of τpu = 4.64 fs is applied at 0 fs to generate a ring current. The pulse duration and amplitude are chosen to excite 91.5% of the ground state population to excited states (Fig. S2†), thus create a high excited state population in this multi-level system. The mechanism is similar to Rabi-flop of two-level system. The electronic wave function is obtained by numerically solving the time-dependent Schrödinger equation 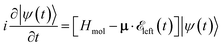 , where Hmol is the molecular Hamiltonian and the wave function is expanded in the molecular ground and valence excited states basis
, where Hmol is the molecular Hamiltonian and the wave function is expanded in the molecular ground and valence excited states basis 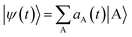 . Atomic units are used throughout. MgPc belongs to the D4h point group. Its excited states are obtained by a TDDFT calculation. The molecular geometry is optimized using DFT with the B3LYP functional45–48 and the 6-31g(d) basis set and Gaussian 16.49 Both valence and core excited states are computed with TDDFT in the Tamm–Dancoff approximation (TDA) using the Chronus Quantum software package.50 The TDA calculations employ the same density functional and basis set used in the geometry optimization. The valence excited states are listed in Table S1.† For CPL with circularly polarization in x–y plane, the excited states of Eu irreducible representation with two-fold degeneracy are dipole allowed, and denoted mEux and mEuy, where x, y denote the transition dipole direction, and m, n = 1, 2, …, 7 is the index of pair of degenerate states. The state with A2u irreducible representation has transition dipole 〈g|μ|e〉 along z and is thus not excited by the pump pulse. The current density is given by51
. Atomic units are used throughout. MgPc belongs to the D4h point group. Its excited states are obtained by a TDDFT calculation. The molecular geometry is optimized using DFT with the B3LYP functional45–48 and the 6-31g(d) basis set and Gaussian 16.49 Both valence and core excited states are computed with TDDFT in the Tamm–Dancoff approximation (TDA) using the Chronus Quantum software package.50 The TDA calculations employ the same density functional and basis set used in the geometry optimization. The valence excited states are listed in Table S1.† For CPL with circularly polarization in x–y plane, the excited states of Eu irreducible representation with two-fold degeneracy are dipole allowed, and denoted mEux and mEuy, where x, y denote the transition dipole direction, and m, n = 1, 2, …, 7 is the index of pair of degenerate states. The state with A2u irreducible representation has transition dipole 〈g|μ|e〉 along z and is thus not excited by the pump pulse. The current density is given by51
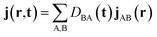 | (1) |
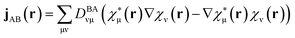 | (2) |
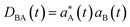 is the density matrix at time t, aB(t) is the coefficient of electronic states. DBAνμ is the transition one-electron density matrix (1PDM) between electronic state B and A in the atomic orbital basis and νμ denote atomic orbital. χμ(r) and ∇χμ(r) are the atomic orbital basis and its gradient respectively.
is the density matrix at time t, aB(t) is the coefficient of electronic states. DBAνμ is the transition one-electron density matrix (1PDM) between electronic state B and A in the atomic orbital basis and νμ denote atomic orbital. χμ(r) and ∇χμ(r) are the atomic orbital basis and its gradient respectively.
The induced ring current is further probed by the TRXCD signal at the nitrogen K-edge. The Gaussian X-ray probe pulse has central frequency ωc = 383.172 eV, σ = 0.7 fs and time delay T scanned from 0 to 25 fs. The TRXCD signal is derived in ESI S1† using time dependent perturbation theory in the probe pulse–molecule interaction
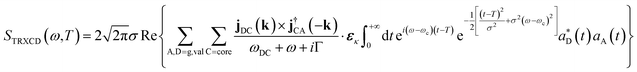 | (3) |
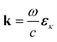 .
. 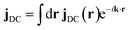 is the momentum space transition current density. ωDC is the transition energy from state C to D. ω is the angular frequency. Γ = 0.093 eV is core line width for nitrogen.53 Here we focus on the nitrogen K-edge since the Mg line width (Γ = 0.45 eV)53 is too broad to resolve different excited states as shown in Fig. S2.†
is the momentum space transition current density. ωDC is the transition energy from state C to D. ω is the angular frequency. Γ = 0.093 eV is core line width for nitrogen.53 Here we focus on the nitrogen K-edge since the Mg line width (Γ = 0.45 eV)53 is too broad to resolve different excited states as shown in Fig. S2.†
Ring current migration and the corresponding excited state coherences
The ring-currents formed by a pair of degenerate states populations, for example the mEu reach a stationary value after the pulse is over. Ring-currents can also be formed by the coherence between states which belong to different degenerate pairs, for example, the coherence mEux–nEuy, where m ≠ n. This coherence oscillates in time with the period .
.
During the pulse, the ground/excited state (g–ex) coherence makes a large contribution to the current. When the pulse is switched off, the coefficient of ground state is small, thus the fast oscillatory component of induced ring current becomes weaker as shown in Fig. S4.† Since the oscillation is faster than the probe pulse duration, the g–ex coherence is not resolved by the TRXCD signal. We thus focus on the excited state-excited state (ex–ex) coherences, which contribute to slower components of the ring current.
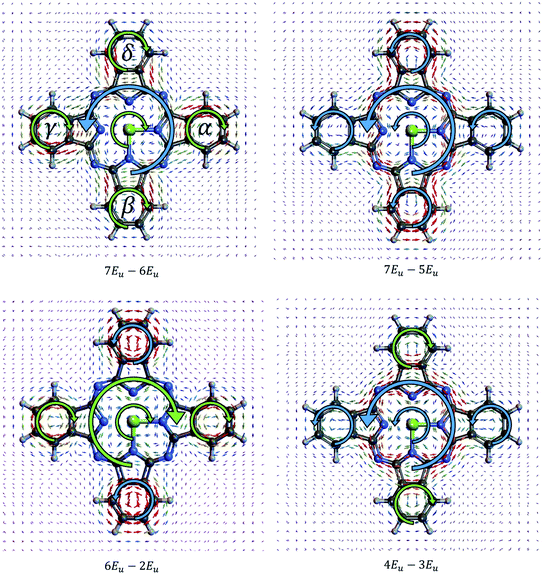
The ring currents associated with different ex–ex coherence pairs jAB have distinct spatial profiles. Ring currents can arise in four zones in the MgPc molecule. First is in the center around Mg cation denoted “CT”, second is the current on the outer ring denoted “OT”, third is the current on the right and left benzene rings denoted “α” and “γ” respectively, fourth is the lower and upper benzene rings labelled “β” and “δ” respectively, as shown in Fig. 2. Currents associated with several pairs of states are shown in Fig. 2. For the same coherence, the ring current at different locations can have a different direction. For example, the 7Eu–5Eu coherent ring current has the same direction around the Mg (CT) and on the outer loop (OT), while for the 7Eu–6Eu current, the direction of CT and OT are opposite. The direction of the α, γ and β, δ ring currents are the same in 7Eu–5Eu and 7Eu–6Eu, while in 6Eu–2Eu and 4Eu–3Eu, the α, γ and β, δ have opposite direction.
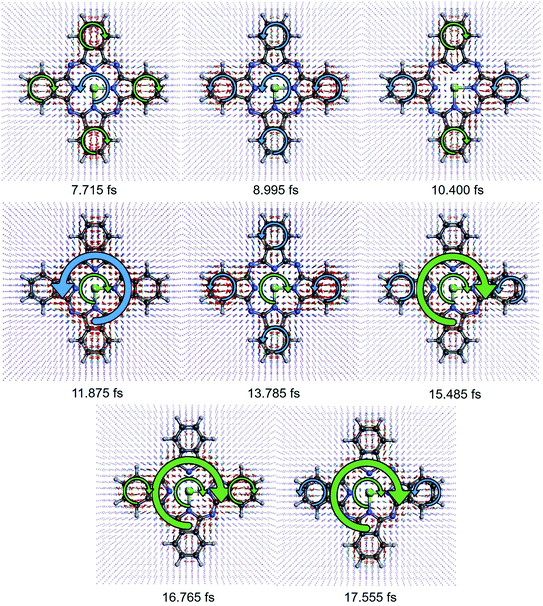
As each component of the coherent ring current jmEu,nEu oscillates with its own period of  , the total induced ring current varies with time, where the current evolutions at different locations is unsynchronized. This behavior is different from the ring current induced by narrow band pump,35 where the ring current in the entire molecule oscillates uniformly. This unsynchronized evolution of currents at different zones causes the redistribution of current density, resulting in the current migration in the whole molecule. The total ex–ex coherent ring current profile at various time delays T after CPL are depicted in Fig. 3. We show the local ring current profiles at the four corner benzene rings (α, γ and β, δ), the center zone around Mg (CT), and the outer loop of the total molecule (OT) reverse direction at different times. For example, at 7.715 fs, α, γ and β, δ are clockwise whereas CT is counter-clockwise. At 8.995 fs, all currents are counter-clockwise. Between 7.715 fs and 8.995 fs, α, γ and β, δ change from clockwise to counter-clockwise while CT is unchanged. From 8.995 fs to 10.400 fs, the β, δ change to clockwise, while CT vanishes. Moving to 11.875 fs, the ring current around α, γ and β, δ disappear, while a counter-clockwise OT ring current and clockwise ring current CT appear. Then at 13.785 fs, counter-clockwise currents α, γ and β, δ rings appear, the OT ring current disappears, and the clockwise ring current CT remains intact. At 15.485 fs, the clockwise current OT is formed while the counter-clockwise current in the β, δ current vanishes. At 16.765 fs, the current α, γ changes from counter-clockwise to clockwise, and then changes back to counter-clockwise at 17.555 fs.
, the total induced ring current varies with time, where the current evolutions at different locations is unsynchronized. This behavior is different from the ring current induced by narrow band pump,35 where the ring current in the entire molecule oscillates uniformly. This unsynchronized evolution of currents at different zones causes the redistribution of current density, resulting in the current migration in the whole molecule. The total ex–ex coherent ring current profile at various time delays T after CPL are depicted in Fig. 3. We show the local ring current profiles at the four corner benzene rings (α, γ and β, δ), the center zone around Mg (CT), and the outer loop of the total molecule (OT) reverse direction at different times. For example, at 7.715 fs, α, γ and β, δ are clockwise whereas CT is counter-clockwise. At 8.995 fs, all currents are counter-clockwise. Between 7.715 fs and 8.995 fs, α, γ and β, δ change from clockwise to counter-clockwise while CT is unchanged. From 8.995 fs to 10.400 fs, the β, δ change to clockwise, while CT vanishes. Moving to 11.875 fs, the ring current around α, γ and β, δ disappear, while a counter-clockwise OT ring current and clockwise ring current CT appear. Then at 13.785 fs, counter-clockwise currents α, γ and β, δ rings appear, the OT ring current disappears, and the clockwise ring current CT remains intact. At 15.485 fs, the clockwise current OT is formed while the counter-clockwise current in the β, δ current vanishes. At 16.765 fs, the current α, γ changes from counter-clockwise to clockwise, and then changes back to counter-clockwise at 17.555 fs.
The time evolution of the local ring currents is plotted in Fig. 4. The currents in ampere are calculated by integrating the current density on a plane. Details of the integration are explained in ESI S9.† After the pump pulse, the corner rings at opposite position (like α, γ and β, δ) have the same ring current rotation direction, while neighboring rings have no such relationship. This is due to the fact that these coherent ring currents are generated by excited states with Eu irreducible representation whose jmEu,nEu are invariant under C2 rotation with respect to the principle axis. We can clearly see the transfer of ring currents among the four corner rings, between {α, γ} and {β, δ}. Overall, Fig. 4 depicts the unsynchronized evolution of the current at four different zones (CT, OT, α, γ and β, δ). The redistribution of ring currents among these zones results in ring current migration dynamics.
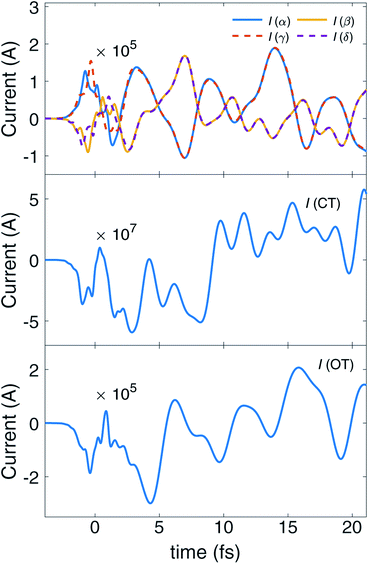 | ||
| Fig. 4 Time evolution of local ring current induced by excited state-excited state coherence. From top to bottom, the plots are ring currents of the four corner benzene rings (α, β, γ and δ ring), around the Mg atom at center (CT) and the outer ring (OT). Currents in Ampere are calculated by numerically integrating the current density at a plane, as illustrated in Fig. S8.† Positive values of currents indicate clockwise ring current. After the pump pulse, the currents of γ/δ are identical to α/β. We can clearly see the currents migrate between ring αγ and βδ. | ||
In summary, the coherent ring current induced by a broad band pump pulse for a multi-ring molecule can change its direction and magnitude locally, in contrast to changing the total ring current direction globally when a narrow band pulse is applied. The ring current migration among different zones in the molecule is caused by the interplay of multiple pairs of coherent ring currents. The directions and strengths of induced ring current result in an induced magnetic field, computed with Biot–Savart law, as displayed in Fig. S4 and S5.† The induced magnetic field is further decomposed into the contributions of different coherences.
The time-resolved circular dichroism signal at the K-edge
For the time domain TRXCD signal S(ω,T) in the upper panel of Fig. 5, peaks are located where ω coincides with valence to a core excitation energy ωCD. The peak intensity is proportional to the numerator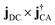 of eqn (3) and the coherence
of eqn (3) and the coherence 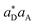 . To assign each peak to a valence-core excitation, we take a vertical slice of the spectrum at time 10.40 fs from the TRXCD and identify important valence to core state transitions as described in ESI.†
. To assign each peak to a valence-core excitation, we take a vertical slice of the spectrum at time 10.40 fs from the TRXCD and identify important valence to core state transitions as described in ESI.†
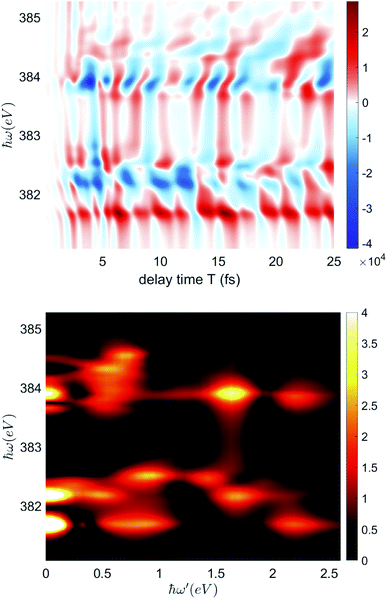 | ||
| Fig. 5 Upper panel: Simulated nitrogen K-edge X-ray TRXCD signal eqn (3). The delay time T is scanned from 0 fs to 25 fs. The intensity of the signal is in arbitrary units. Lower panel: Fourier transformed circular dichroism spectrum of nitrogen K-edge. ℏω is detection frequency and ℏω′ is the conjugate variable of delay time T. For each bright peak, the ℏω is the excitation energy and the ℏω′ values indicate the frequency of oscillation corresponding to the coherence contributing to the peak. | ||
The time dependence of the TRXCD signal arises from the coherence between Eu states. To separate the signals with different oscillation period, we perform a Fourier transform of the time domain TRXCD signal S(ω,T) with respect to the delay time T which results in the frequency domain signal ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (ω,ω′). Since the pump pulse is centered at 0 fs, the pump pulse driven part of the TRXCD spectrum is eliminated by taking the Fourier transform for the TRXCD in the 3.72 fs to 21.10 fs interval. The Fourier transformed CD spectra as a function of the oscillation frequency ω′ and excitation energy ℏω is depicted in the lower panel of Fig. 5. The ℏω′ value of the bright colored peaks indicates the energy difference of the coherent states, which coincides with oscillation angular frequency of the coherence. Table 1 lists the coherences as well as their oscillation frequencies.
(ω,ω′). Since the pump pulse is centered at 0 fs, the pump pulse driven part of the TRXCD spectrum is eliminated by taking the Fourier transform for the TRXCD in the 3.72 fs to 21.10 fs interval. The Fourier transformed CD spectra as a function of the oscillation frequency ω′ and excitation energy ℏω is depicted in the lower panel of Fig. 5. The ℏω′ value of the bright colored peaks indicates the energy difference of the coherent states, which coincides with oscillation angular frequency of the coherence. Table 1 lists the coherences as well as their oscillation frequencies.
| Coherence | Period (fs) | Energy difference (eV) | Coherence frequency ℏω′ (eV) | Excitation energy ℏω (eV) | Transition valence to core |
|---|---|---|---|---|---|
| 4Eu–3Eu | 40.427 | 0.1023 | 0.2377 | 382.4157 | 4Eu to core states 6 |
| 7Eu–6Eu | 8.545 | 0.4840 | 0.4666 | 382.1627 | 6Eu to core state 7, 8 |
| 7Eu–5Eu | 7.726 | 0.5353 | 0.5354 | 384.2041 | 5Eu to core state 22 |
| 384.3369 | 5Eu to core state 25 | ||||
| 383.6690 | 7Eu to core state 22 | ||||
| 383.8017 | 7Eu to core state 25 | ||||
| 7Eu–3Eu | 4.929 | 0.8391 | 0.8798 | 381.6788 | 7Eu to core state 7, 8 |
| 382.5179 | 3Eu to core state 6 | ||||
| 4Eu–1Eu | 2.776 | 1.4896 | 1.4308 | 382.4157 | 4Eu to core states 6 |
| 5Eu–1Eu | 2.446 | 1.6911 | 1.6374 | 383.9051 | 1Eu to core state 7 |
| 6Eu–1Eu | 2.374 | 1.7424 | 1.7063 | 381.6788 | 7Eu to core state 7, 8 |
| 382.1627 | 6Eu to core state 7, 8 | ||||
| 7Eu–1Eu | 1.858 | 2.2264 | 2.1884 | 383.9051 | 1Eu to core state 7 |
The CD signal at peak energies and the corresponding coherence frequencies
We first consider the peaks for ℏω′ = 0 in the lower panel of Fig. 5, which originate from the time independent population ring current. The peaks at ℏω = 381.6788, 383.669, 383.8017 eV represent the population ring current of 7Eu, with excitation to core states 7, 23, 25 respectively (see ESI S2† for the labels of core excited states).The remaining peaks correspond to coherent ring currents. ℏω′ indicates the energy gap between the coherent states, resolved in Fig. 5, with both energy gaps of the coherent states and the coherence frequency obtained from the peaks listed in Table 1. The coherence pairs with a similar energy gap can be separated by different core state excitation energy ℏω, for example, 4Eu–1Eu and 5Eu–1Eu. Such separation can be achieved for the nitrogen K-edge but not in the Mg K-edge due to its large line width.53 With the aid of ω and ω′, each peak in Fig. 5 assigned to a coherence with its valence to core transitions is listed in Table 1.
The coherence with longest period is 4Eu–3Eu with an energy difference of 0.1023 eV. It contributes to the peak at ℏω = 382.4157 eV with coherence frequency ℏω′ = 0.2377 eV. Since the total simulation time is kept short to avoid decoherence, the 4Eu–3Eu coherence did not complete a single period, which causes the deviation of ω′ from the energy difference.
The brightest peak at ℏω′ = 1.6374 eV and ℏω = 383.9051 eV corresponds to the excitation from 1Eu to core state 7, contributed by 5Eu–1Eu coherence.
At ℏω′ = 0.5354 eV, the peaks with excitation energy between 383.6 and 384.5 eV correspond to the transition from 7Eu and 5Eu to different core excited states, contributed by the 7Eu–5Eu coherence. The peaks at ℏω = 384.2041, 384.3369 eV represent the excitation from 5Eu to core state 22 and 25 respectively; peak at 383.669 eV and 383.8017 are excitation from 7Eu to core state 22 and state 25 respectively.
Decoherence effects
The ring current is expected to decay due to the interaction of electronic system with a nuclear bath. Such dephasing effects are not included in the Schrödinger equation, but can be described phenomenologically. Pure dephasing can be included by (1) multiplying the signal expression eqn (3) by a dephasing factor e−Γ1,DAτ, where Γ1,DA is the valence–valence coherence dephasing rate and (2) add a term iΓ2,DC to the denominator of eqn (3) as given in the ESI.† In Section S8,† the TRXCD spectra and the Fourier transformation are shown for different values of dephasing rates, i.e., from 1/100 fs−1 to 1/10 fs−1 (Fig. S7†). The valence states-core states dephasing broadens the peak in energy domain ℏω. Since the dephasing rate contribution is less than the lifetime broadening of core excited states, this effect is not significant. The valence excited state-valence excited state dephasing causes a decay of the TRXCD signal with the delay time T. Higher dephasing rates result in earlier decay of TRXCD signal in time domain, as well as lower resolution in frequency domain ℏω′. Nevertheless, distinct coherence components can still be assigned in the Fourier transformed spectrum even with a high dephasing rate of 1/10 fs−1. The dephasing of ground state–valence excited state does not affect the TRXCD signal, since such coherence has shorter oscillation period than the probe pulse duration, thus not observed in the signal. In summary, although dephasing of coherence results in lower resolution of the spectra, it does not change peak assignments.Apart from dephasing, the coherence of excited states can cause magnetic dipole radiation, since the transition magnetic dipoles between excited state of Eu irreducible representation are nonzero while their transition electric dipoles vanish. This radiation causes damping of excited states. However, since the magnetic dipole radiation is weak, this effect is ignored in our simulation.
In conclusion, a broad band (2 eV) UV-visible circularly polarized pump pulse is used in this study to create a superposition of 7 degenerate pairs of excited states. The coherent ring currents at different locations in the molecule show distinct features, where the coherent ring current on the corner rings, outer ring and inner ring around the Mg evolve unsynchronizedly due to the interplay of many coherence pairs of Mg-Pc excited states. This coherence may be probed by time-resolved X-ray circular dichroism spectrum at the nitrogen K-edge. By Fourier transforming the CD signal with respect to the probe delay time T, we obtain the CD spectrum as a function of excitation energy and oscillation frequency. Bright peaks are assigned to pairs of excited state coherence by the coherence frequency and its excitation energy in the two dimensional spectrum Fig. 5. This suggests a way to probe the evolution of ring current in time domain and separate individual excited state coherence contributing to the coherent ring current in the frequency domain. The redistribution of current density within the molecule pave the way for controlling the local electron movement within the molecule, enabling light control of electron at sub-molecular scale and femtosecond time scale.
Data availability
All study data are included in the article and/or ESI.†Author contributions
S. M. supervised and conceived the project. S. S. and F. C. derived the equations for the signal. S. S. performed the electronic structure calculations. S. S., F. C. and H. Y. performed spectroscopy simulations. All authors contributed to the analysis and interpretation of the results, and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of the National Science Foundation through Grant No. CHE-1953045 is gratefully acknowledged. S. M. was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award DE-FG02-04ER15571. S. M. is a fellow of the Hagler Institute for Advanced Study at Texas A&M University.References
- F. London, Théorie quantique des courants interatomiques dans les combinaisons aromatiques, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- R. Breslow, Antiaromaticity, Acc. Chem. Res., 1973, 6, 393–398 CrossRef CAS.
- P. Lazzeretti, Ring Currents, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88 CrossRef CAS.
- J. Jusélius and D. Sundholm, The Aromatic Character of Magnesium Porphyrins, J. Org. Chem., 2000, 65, 5233–5237 CrossRef PubMed.
- E. Steiner and P. W. Fowler, Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions, J. Phys. Chem. A, 2001, 105, 9553–9562 CrossRef CAS.
- G. Merino, T. Heine and G. Seifert, The Induced Magnetic Field in Cyclic Molecules, Chem.–Eur. J., 2004, 10, 4367–4371 CrossRef CAS PubMed.
- E. Steiner, A. Soncini and P. W. Fowler, Ring Currents in the Porphyrins: π Shielding, Delocalisation Pathways and the Central Cation, Org. Biomol. Chem., 2005, 3, 4053–4059 RSC.
- T. Heine, C. Corminboeuf and G. Seifert, The Magnetic Shielding Function of Molecules and Pi-Electron Delocalization, Chem. Rev., 2005, 105, 3889–3910 CrossRef CAS PubMed.
- B. Kudisch, M. Maiuri, L. Moretti, M. B. Oviedo, L. Wang, D. G. Oblinsky, R. K. Prud'homme, B. M. Wong, S. A. McGill and G. D. Scholes, Ring Currents Modulate Optoelectronic Properties of Aromatic Chromophores at 25 T, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11289–11298 CrossRef CAS PubMed.
- M. D. Peeks, T. D. Claridge and H. L. Anderson, Aromatic and Antiaromatic Ring Currents in a Molecular Nanoring, Nature, 2017, 541, 200–203 CrossRef CAS PubMed.
- I. Barth, J. Manz, Y. Shigeta and K. Yagi, Unidirectional Electronic Ring Current Driven by a Few Cycle Circularly Polarized Laser Pulse: Quantum Model Simulations for Mg- porphyrin, J. Am. Chem. Soc., 2006, 128, 7043–7049 CrossRef CAS PubMed , PMID: 16719485..
- S. Sun, B. Gu and S. Mukamel, Polariton Ring Currents and Circular Dichroism of Mg-porphyrin in a Chiral Cavity, Chem. Sci., 2022, 13, 1037–1048 RSC.
- L. Jackman, F. Sondheimer, Y. Amiel, D. Ben-Efraim, Y. Gaoni, R. Wolovsky and A. Bothner-By, The Nuclear Magnetic Resonance Spectroscopy of a Series of Annulenes and Dehydro-Annulenes, J. Am. Chem. Soc., 1962, 84, 4307–4312 CrossRef CAS.
- R. H. Mitchell, Measuring Aromaticity by NMR, Chem. Rev., 2001, 101, 1301–1316 CrossRef CAS PubMed , PMID: 11710222..
- A. D. Allen and T. T. Tidwell, Antiaromaticity in Open-Shell Cyclopropenyl to Cycloheptatrienyl Cations, Anions, Free Radicals, and Radical Ions, Chem. Rev., 2001, 101, 1333–1348 CrossRef CAS PubMed.
- L. Pauling, The Diamagnetic Anisotropy of Aromatic Molecules, J. Chem. Phys., 1936, 4, 673–677 CrossRef CAS.
- J. Pople, Proton Magnetic Resonance of Hydrocarbons, J. Chem. Phys., 1956, 24, 1111 CrossRef CAS.
- J. Pople and K. Untch, Induced Paramagnetic Ring Currents, J. Am. Chem. Soc., 1966, 88, 4811–4815 CrossRef CAS.
- J. Gomes and R. Mallion, Aromaticity and Ring Currents, Chem. Rev., 2001, 101, 1349–1384 CrossRef CAS PubMed.
- I. Barth and J. Manz, Periodic Electron Circulation Induced by Circularly Polarized Laser Pulses: Quantum Model Simulations for Mg Porphyrin, Angew. Chem., Int. Ed., 2006, 45, 2962–2965 CrossRef CAS PubMed.
- I. Barth and J. Manz, Electric Ring Currents in Atomic Orbitals and Magnetic Fields Induced by Short Intense Circularly Polarized π Laser Pulses, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 012510 CrossRef.
- I. Barth, J. Manz and L. Serrano-Andrés, Quantum Simulations of Toroidal Electric Ring Currents and Magnetic Fields in Linear Molecules Induced by Circularly Polarized Laser Pulses, Chem. Phys., 2008, 347, 263–271 CrossRef CAS , Ultrafast Photoinduced Processes in Polyatomic Molecules..
- M. Kanno, H. Kono, Y. Fujimura and S. H. Lin, Nonadiabatic Response Model of Laser-Induced Ultrafast π-Electron Rotations in Chiral Aromatic Molecules, Phys. Rev. Lett., 2010, 104, 108302 CrossRef PubMed.
- H. Mineo, M. Yamaki, Y. Teranishi, M. Hayashi, S. H. Lin and Y. Fujimura, Quantum Switching of π-Electron Rotations in a Nonplanar Chiral Molecule by Using Linearly Polarized UV Laser Pulses, J. Am. Chem. Soc., 2012, 134, 14279–14282 CrossRef CAS PubMed.
- M. Kanno, Y. Ono, H. Kono and Y. Fujimura, Laser-Polarization Effects on Coherent Vibronic Excitation of Molecules with Quasi-Degenerate Electronic States, J. Phys. Chem. A, 2012, 116, 11260–11272 CrossRef CAS PubMed , PMID: 22834970..
- H. Mineo, S. Lin and Y. Fujimura, Coherent π-Electron Dynamics of (P)-2,2′-biphenol Induced by Ultrashort Linearly Polarized UV Pulses: Angular Momentum and Ring Current, J. Chem. Phys., 2013, 138, 074304 CrossRef CAS PubMed.
- H. Mineo, S. Lin and Y. Fujimura, Vibrational Effects on UV/Vis Laser-Driven π-Electron Ring Currents in Aromatic Ring Molecules, Chem. Phys., 2014, 442, 103–110 CrossRef CAS.
- J. J. Rodriguez and S. Mukamel, Probing Ring Currents in Mg-Porphyrins by Pump–Probe Spectroscopy, J. Phys. Chem. A, 2012, 116, 11095–11100 CrossRef CAS PubMed , PMID: 22881200..
- K.-J. Yuan, C.-C. Shu, D. Dong and A. D. Bandrauk, Attosecond Dynamics of Molecular Electronic Ring Currents, J. Phys. Chem. Lett., 2017, 8, 2229–2235 CrossRef CAS PubMed , PMID: 28468499..
- M. Kanno, H. Kono and Y. Fujimura, Laser-Control of Ultrafast π-Electron Ring Currents in Aromatic Molecules: Roles of Molecular Symmetry and Light Polarization, Appl. Sci., 2018, 8, 2347 CrossRef CAS.
- K. R. Nandipati and O. Vendrell, On the Generation of Electronic Ring Currents under Vibronic Coupling Effects, J. Chem. Phys., 2020, 153, 224308 CrossRef CAS PubMed.
- K. R. Nandipati and O. Vendrell, Dynamical Jahn-Teller effects on the generation of electronic ring currents by circularly polarized light, Phys. Rev. Res., 2021, 3, L042003 CrossRef CAS.
- S. Eckart, et al., Ultrafast Preparation and Detection of Ring Currents in Single Atoms, Nat. Phys., 2018, 14, 701–704 Search PubMed.
- O. Neufeld and O. Cohen, Background-Free Measurement of Ring Currents by Symmetry-Breaking High-Harmonic Spectroscopy, Phys. Rev. Lett., 2019, 123, 103202 CrossRef CAS PubMed.
- Y. Nam, J. R. Rouxel, J. Y. Lee and S. Mukamel, Monitoring Aromatic Ring-Currents in Mg-Porphyrin by Time-Resolved Circular Dichroism, Phys. Chem. Chem. Phys., 2020, 22, 26605–26613 RSC.
- H. J. Wörner, C. A. Arrell, N. Banerji, A. Cannizzo, M. Chergui, A. K. Das, P. Hamm, U. Keller, P. M. Kraus and E. Liberatore, et al., Charge migration and charge transfer in molecular systems, Struct. Dyn., 2017, 4, 061508 CrossRef PubMed.
- L. S. Cederbaum and J. Zobeley, Ultrafast charge migration by electron correlation, Chem. Phys. Lett., 1999, 307, 205–210 CrossRef CAS.
- M. Di Ventra, S. Pantelides and N. Lang, First-principles calculation of transport properties of a molecular device, Phys. Rev. Lett., 2000, 84, 979 CrossRef CAS PubMed.
- M. G. Walter, A. B. Rudine and C. C. Wamser, Porphyrins and Phthalocyanines in Solar Photovoltaic Cells, J. Porphyrins Phthalocyanines, 2010, 14, 759–792 CrossRef CAS.
- M. Urbani, M.-E. Ragoussi, M. K. Nazeeruddin and T. Torres, Phthalocyanines for Dye-Sensitized Solar Cells, Coord. Chem. Rev., 2019, 381, 1–64 CrossRef CAS.
- Z. Jiang, J. Shao, T. Yang, J. Wang and L. Jia, Pharmaceutical development, composition and quantitative analysis of phthalocyanine as the photosensitizer for cancer photodynamic therapy, J. Pharm. Biomed. Anal., 2014, 87, 98–104 CrossRef CAS PubMed.
- J. Mi, L. Guo, Y. Liu, W. Liu, G. You and S. Qian, Excited-State Dynamics of Magnesium Phthalocyanine Thin Film, Phys. Lett. A, 2003, 310, 486–492 CrossRef CAS.
- D. Potamianos, M. Nuber, A. Schletter, M. Schnitzenbaumer, M. Haimerl, P. Scigalla, M. Wörle, L. I. Wagner, R. Kienberger and H. Iglev, Full Dynamics Description of Mg Phthalocyanine Crystalline and Amorphous Semiconductor Systems, J. Phys. Chem. C, 2021, 125, 18279–18286 CrossRef CAS.
- M. T. Hassan, T. T. Luu, A. Moulet, O. Raskazovskaya, P. Zhokhov, M. Garg, N. Karpowicz, A. Zheltikov, V. Pervak, F. Krausz and E. Goulielmakis, Optical Attosecond Pulses and Tracking the Nonlinear Response of Bound Electrons, Nature, 2016, 530, 66–70 CrossRef CAS PubMed.
- A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- D. B. Williams-Young, A. Petrone, S. Sun, T. F. Stetina, P. Lestrange, C. E. Hoyer, D. R. Nascimento, L. Koulias, A. Wildman, J. Kasper, J. J. Goings, F. Ding, A. E. DePrince III, E. F. Valeev and X. Li, The Chronus Quantum Software Package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, e1436 Search PubMed.
- J. R. Rouxel, M. Kowalewski and S. Mukamel, Current vs. Charge Density Contributions to Nonlinear X-ray Spectroscopy, J. Chem. Theory Comput., 2016, 12, 3959–3968 CrossRef CAS PubMed.
- J. R. Rouxel, V. Y. Chernyak and S. Mukamel, Non-local real-space analysis of chiral optical signals, Chem. Sci., 2016, 7, 6824–6831 RSC.
- J. Campbell and T. Papp, Widths of the Atomic K–N7 Levels, At. Data Nucl. Data Tables, 2001, 77, 1–56 CrossRef CAS.
- G Hermann, V Pohl, G Dixit and JC Tremblay, Probing Electronic Fluxes via Time-Resolved X-Ray Scattering, Phys. Rev. Lett., 2020, 124(1), 013002 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Coherent ring-current dynamics of Mg-phthalocyanine probed by time-resolved circular dichroism. See https://doi.org/10.1039/d2sc02768b |
| This journal is © The Royal Society of Chemistry 2022 |