Impact of anion polarizability on ion pairing in microhydrated salt clusters

Abstract

Despite longstanding interest in the mechanism of salt dissolution in aqueous media, a molecular level understanding remains incomplete. Here, cryogenic ion trap vibrational action spectroscopy is combined with electronic structure calculations to track salt hydration in a gas phase model system one water molecule at a time. The infrared photodissociation spectra of microhydrated lithium dihalide anions [LiXX′(H₂O)_n]⁻ (XX′ = I₂, ClI and Cl₂; n = 1–3) in the OH stretching region (3800–2800 cm⁻¹) provide a detailed picture of how anion polarizability influences the competition among ion–ion, ion–water and water–water interactions. While exclusively contact ion pairs are observed for n = 1, the formation of solvent-shared ion pairs, identified by markedly red-shifted OH stretching bands (<3200 cm⁻¹), originating from the bridging water molecules, is favored already for n = 2. For n = 3, Li⁺ reaches its maximum coordination number of four only in [LiI₂(H₂O)₃]⁻, in accordance with the hard and soft Lewis acid and base principle. Water–water hydrogen bond formation leads to a different solvent-shared ion pair motif in [LiI₂(H₂O)₃]⁻ and network formation even restabilizes the contact ion pair motif in [LiCl₂(H₂O)₃]⁻. Structural assignments are exclusively possible after the consideration of anharmonic effects. Molecular dynamics simulations confirm that the significance of large amplitude motion (of the water molecules) increases with increasing anion polarizability and that needs to be considered already at cryogenic temperatures.

---

1. Introduction

Salt ions strongly disrupt hydrogen-bond networks in water impacting a multitude of biochemical, industrial, and atmospheric processes such as the stability of proteins, homogeneous catalysis or aerosol formation.^1–3 Thus, it is instructive to study the underlying mechanisms of the salt–water interaction on a molecular level. The course of salt dissolution, i.e. the weakening and ultimately the breaking of ionic bonds by interposing water molecules, is typically discussed considering transformations from contact (CIP) over solvent-shared (SIP) to solvent-separated ion pairs (2SIP).^4,5 Recent studies with dielectric relaxation,^4,6 infrared,⁷ neutron diffraction and X-ray absorption spectroscopy^8,9 have provided evidence for CIP, SIP and 2SIP motifs in salt solution,³ but the mechanistic details of the process are still elusive from experiment and currently only available from computational studies. A step forward in this context is the characterization of salt pairs according to the cooperative or anticooperative effects¹⁰ of the respective counterion on specific ion–water interactions.¹¹ But studies in the aqueous phase – due to the highly fluxional nature of hydrogen-bond networks and the heterogeneity of the local hydration shells in water – notoriously fail to capture the specificity and the spatial extent of ion–water interactions as is evident from X-ray and neutron diffraction investigations on dilute LiCl and NaCl solutions.⁹ On the computational side, it has become evident over the last two decades that the reliable description of salt dissolution, in general, and ion pairing, in particular, requires considering solvent polarization effects.^12–17

Archetypical models of the first hydration shell, i.e. salt ions with a well-defined number of water molecules, can be isolated in the form of microhydrated gas-phase clusters and then selectively probed using spectroscopic tools. This reduction of complexity allows us to monitor different types of interactions at the molecular level. As theory and experiment advance in parallel, experimental outcomes can be used to test available theories on salt hydration.¹⁸ The experimental investigation on neutral alkali halide salt–water complexes, which was started in the condensed phase by matrix isolation infrared spectroscopy (MI-IR) in the 1970s,¹⁹ has now been extended to the gas-phase with Fourier-transform microwave,²⁰ femto-second pump–probe,²¹ and helium droplet IR spectroscopy techniques.^22,23

However, mass selection of neutral clusters remains challenging and therefore obtaining size-specific interaction details is currently only viable with ionic species. Anion photoelectron spectroscopy (APES) was employed to characterize systems like LiI⁻(H₂O)_0–6, NaCl⁻(H₂O)_0–6, CsI⁻(H₂O)_0–6, NaSO₄⁻(H₂O)_0–4, and NaBO₂⁻(H₂O)_0–4.^24–27 LiI was found prone to solvent induced charge separation as can be expected from Pearson’s hard and soft acid base (HSAB) theory.²⁸ ‘Hard’ ions feature a high ionic potential (charge/ionic radii) and are weakly polarizable. ‘Soft’ refers to ions with large ionic radii and small charges, which are highly polarizable. However, unambiguous structural assignments are more difficult to obtain solely from APES studies.

In this regard, infrared photodissociation (IRPD) spectroscopy is a more versatile tool for structure characterization. Reports on microhydrated (NaSO₄⁻)₂, Mg₂SO₄²⁺, Ni₂(SO₄)₃²⁺, CaOH⁻, MgOH⁻ or MgNO₃⁺ yield insight into the effect of stepwise hydration on ion–ion, ion–water and water–water interactions.^29–33 The formation of ionic hydrogen bonds (IHBs) is accompanied by characteristic shifts of the corresponding O–H stretching frequencies.³⁴ In our recent study on [LiCl₂(H₂O)_n]⁻ (n = 1–3), we established that SIP vs. CIP formation can be distinguished based on the extent of the observed frequency shifts of the hydrogen-bonded O–H stretching oscillators.³⁵

In the present work, we extend our study to include iodide anions and focus on the microhydration of archetypical salt–water anions of the type [LiXX′(H₂O)_n]⁻ with XX′ = I₂, ClI and Cl₂ and n = 1–3. We investigate these systems in the gas-phase at cryogenic temperatures, which enables us to dissect the interaction between salt ions and a few water molecules as a function of anion polarizability. Note that the iodide anion is roughly twice as polarizable as the chloride anion.³⁶ We focus on characterizing ion-pairing in light of Collin’s “law of matching water affinity” which states that hard–soft (vs. hard–hard and soft–soft) ion combinations, like Li⁺/I⁻, are more prone to solvent-induced charge separation.^28,37 Methodologically, we utilize vibrational action spectroscopy of D₂-tagged [LiXX′(H₂O)_1–3]⁻ anions complemented by ab initio simulations. The inclusion of anharmonic effects is crucial for a reliable interpretation of the experimental vibrational spectra of these systems,³⁵ and we perform this here both in a static and in a dynamic fashion.

2. Results and analysis

2.1 IRPD spectroscopy

Fig. 1 shows the vibrational action spectra of [LiI₂(H₂O)_1–3]⁻ (a–c), [LiClI(H₂O)_1–3]⁻ (d–f) and [LiCl₂(H₂O)_1–3]⁻ (g–i) in the O–H stretching region (3800–2800 cm⁻¹). The data for [LiCl₂(H₂O)_n]⁻ are from ref. 35. All IRPD spectra were recorded using D₂-tagging (D₂-loss) to ensure probing (a) in the linear absorption region and (b) colder ions. An exception is the spectrum of [LiClI(H₂O)]⁻ (trace d), for which the D₂-tagged ion-signal levels were too low and therefore the H₂O-loss channel from the untagged anion was monitored. Spectra obtained with monitoring D₂ and H₂O-loss are very similar (except the band due to D₂ stretching) for these monohydrates as shown for [LiI₂(H₂O)]⁻ and [LiCl₂(H₂O)]⁻ in Fig. S1 in the ESI.† The position and assignments of the observed IRPD bands are summarized in Table S1 (ESI†). In order to evaluate the influence of the nature of the two halide anions on the course of microhydration of these ion pairs, we first focus on the lithium diiodide anion (LiI₂)⁻, and then discuss the mixed halide system (LiClI)⁻, after which we compare the present results to those obtained for microhydrated lithium dichloride anions [LiCl₂(H₂O)_1–3]⁻ that have been discussed in detail previously.³⁵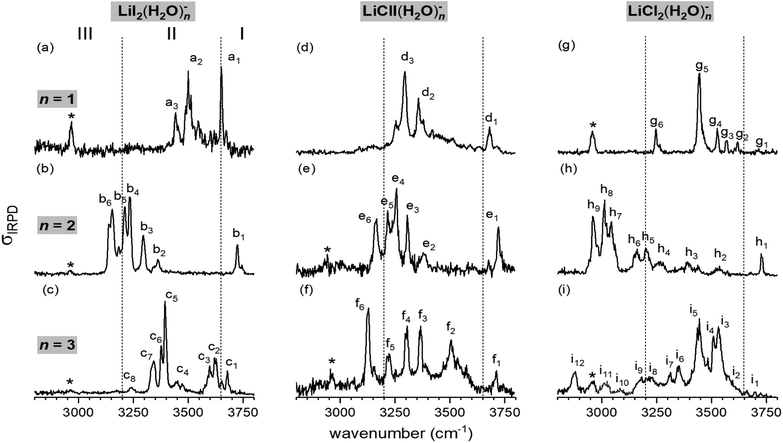

Fig. 1 Vibrational action spectra of the [LiXX′(H₂O)_n]⁻ anions with XX′= I₂, ClI, and Cl₂ from left to right and n = 1–3 (top to bottom) in the spectral region of O–H stretching modes measured at an ion trap temperature of 13 K. All IRPD spectra were recorded using D₂-tagging (D₂-loss) to ensure probing in the linear absorption region, except for [LiClI(H₂O)]⁻ (trace d), for which ion signal levels were too low and therefore the H₂O-loss channel from the untagged anion was monitored. Bands attributed to the excitation of the messenger molecule (D₂-stretching vibration) are denoted by asterisks. The spectra for [LiCl₂(H₂O)_n]⁻ are from ref. 35.

The characteristic H₂O binding motifs are encoded in the IRPD band pattern, in particular, in the relative red-shifts of the fundamental O–H stretching excitations with respect to those in the free water molecule.^30,35 The three previously defined spectral regions for [LiCl₂(H₂O)_1–3]⁻ anions prove useful for a qualitative discussion of the measured spectra and therefore we make use of these also for the present systems.³⁵ The excitation of free O–H oscillators is typically found in region I (>3650 cm⁻¹). Region II (3650–3200 cm⁻¹) covers O–H oscillators involved in water–water as well as weaker halide–water hydrogen bonds. Region III (<3200 cm⁻¹) is characteristic of strong halide–water interactions. Note that the excitation of the nominally IR-inactive D₂ stretching mode, which gains IR-activity upon polarization, is observed around 2960 cm⁻¹ in many of the IRPD spectra (denoted by an asterisk), blue-shifted by roughly 25–35 cm⁻¹ from the value for free D₂.³⁸

2.1.1 [LiI₂(H₂O)_1–3]⁻. The IRPD spectra of D₂-tagged [LiI₂(H₂O)_n]⁻ anions with one to three water molecules (Fig. 1a–c) appear substantially more complex than expected, when considering the small number of O–H oscillators in each of the systems. Hence, similar to the [LiCl₂(H₂O)_1–3]⁻ anions, anharmonic effects, possibly combined with the contribution from multiple isomers, need to be considered.³⁵ All three spectra (see Fig. 1a–c) exhibit absorption in region I, indicating the presence of free O–H stretching oscillators. However, band a₁ (n = 1, 3652 cm⁻¹) is close to the typical cut-off value for a free O–H stretching frequency, indicating the onset of weak H-bonding. Moreover, band a₁ is also relatively intense. This favors an assignment to a slightly red-shifted antisymmetric stretching fundamental of two coupled O–H oscillators, like in [Li(H₂O)]⁺, rather than a single uncoupled O–H oscillator. Band c₁ (n = 3, 3679 cm⁻¹) is also found red-shifted with respect to the average absorption frequency of a free water molecule (3707 cm⁻¹), while band b₁ (n = 2, 3724 cm⁻¹) is indeed blue-shifted, suggesting different local environments of the free O–H oscillators in these three anions.

In the hydrogen-bonded O–H stretching region (<3650 cm⁻¹), a clear dependence of the extent of the O–H stretching frequency red-shift on the degree of microhydration is observed. For n = 1, the red-shift is modest and bands are only observed above 3450 cm⁻¹, indicating weaker iodide–water hydrogen bonds. The most pronounced red-shift is observed for n = 2. This is the only spectrum that exhibits absorption in region III, which is indicative of strong iodide–water hydrogen-bonding and therefore implies the presence of a solvent-shared ion pair.³⁵ For n = 3, the red-shift is intermediate, with the most intense IR signal found at 3400 cm⁻¹. The comparison of this spectrum to the reported spectra of Li⁺(H₂O)₃ and I⁻(H₂O)₃ (see Fig. S2 in the ESI†) reveals no clear similarities.^34,39,40 Hence, a characteristic structure motif like a water trimer ring, characterized by a sharp doublet feature at ∼3550 cm⁻¹, is probably not present in [LiI₂(H₂O)₃]⁻.

2.1.2 [LiClI(H₂O)_1–3]⁻. The IRPD spectra of [LiClI(H₂O)_n]⁻ anions with n = 1 to 3 are shown in the middle column of Fig. 1 (spectra d–f). The spectra show similar trends to those discussed previously for the lithium diiodide anions in the free O–H stretching region (region I). Moreover, the n = 2 spectra appear nearly identical for both systems, suggesting similar structures for these systems. On the other hand, the n = 1 and n = 3 spectra differ significantly. They exhibit more pronounced red-shifts, which are indicative of stronger hydrogen bonding. Hence, the water molecules probably prefer to interact with the chloride rather than the iodide anion in the mixed-halide systems. Both spectra also exhibit substantial, quasi-continuous IR activity over a broad spectral region, roughly from 3600 cm⁻¹ down to 3100 cm⁻¹, different from the other spectra discussed up to now, which we interpreted as an indication for less rigid but still strong hydrogen-bonded networks characterized by larger amplitude motion.

2.1.3 Comparison to [LiCl₂(H₂O)_1–3]⁻. Additional information can be gained by comparing the present data for the [LiXX′(H₂O)_1–3]⁻ series to previously reported IRPD spectra for X = X′ = Cl.³⁵ For n = 1, the spectra of the three halide systems are substantially different suggesting characteristically different structures. For example, the iodide-containing systems show significant IR activity in the free O–H stretching region, which is not observed in the [LiCl₂(H₂O)]⁻ spectrum. Moreover, the [LiClI(H₂O)]⁻ spectrum reveals the most red-shifted features, hinting at a particular strong Cl⁻⋯H–OH IHB. Finally, even though the IRPD spectra of all three n = 1 systems appear similarly complex, IR²MS² measurements provide no evidence for multiple isomers, in contrast to the two isomers reported for [LiCl₂(H₂O)]⁻.³⁵

The n = 2 spectra, on the other hand, show greater similarity, suggesting similar structures, i.e. the solvent-shared structure containing two bridging water molecules previously identified for [LiCl₂(H₂O)₂]⁻. The markedly red-shifted bands in region III in combination with a rather intense free O–H stretching band around or even above 3700 cm⁻¹ can be attributed to two decoupled O–H oscillators for each water molecule, one bridging the Li⁺/X⁻ ion pair and the other dangling freely. The position of the most red-shifted band in the spectrum of [LiClI(H₂O)₂]⁻ (e₆) coincides with the corresponding band in the [LiI₂(H₂O)₂]⁻ spectrum (b₆), while band h₉ in the [LiCl₂(H₂O)₂]⁻ spectrum is found to be red-shifted roughly 200 cm⁻¹ more. Hence, the water molecules bridge the Li⁺/I⁻ rather than the Li⁺/Cl⁻ ion pair in [LiClI(H₂O)₂]⁻. Note that the present IRPD spectra of the LiI₂ and LiClI species show no absorption in the upper part of region II, indicating that water–water hydrogen bonds are not present and that, in contrast to [LiCl₂(H₂O)₂]⁻, again only a single isomer (i.e. containing two bridging water molecules) is present in the iodide-containing systems.

The n = 3 spectra are markedly different from each other. [LiI₂(H₂O)₃]⁻ seems to yield the simplest spectrum, hinting at a structure of higher symmetry. The spectrum of [LiClI(H₂O)₃]⁻ extends over a broader spectral range with the most intense IRPD band (f₆) located in region III, indicating that also for n = 3 a solvent-shared motif, in which the Li⁺/I⁻ ion pair is bridged, is preferred. IR²MS² experiments for [LiI₂(H₂O)₃]⁻ and [LiClI(H₂O)₃]⁻ (see Fig. S3†) demonstrate that only a single stable isomer is present. This is in contrast to the [LiCl₂(H₂O)₃]⁻ spectrum, which was assigned to three isomers, two solvent-shared ones that predominantly absorb below 3200 cm⁻¹, characteristic for a bridged Li⁺/Cl⁻ ion pair, and one intact core structure contributing mainly in the 3400–3600 cm⁻¹ region.³⁵ The role of isomers is discussed together with the results of the AIMD simulations in the following sections.

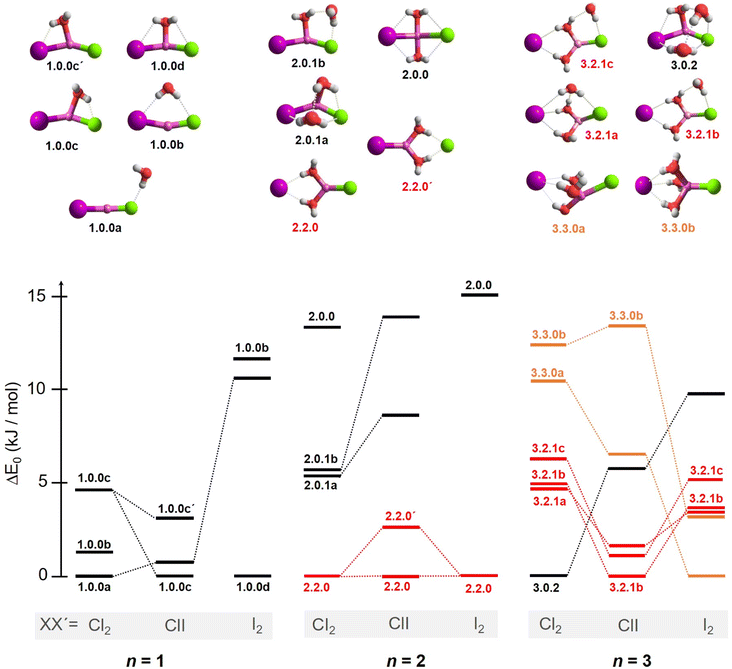
2.2 Microhydration motifs and energetics

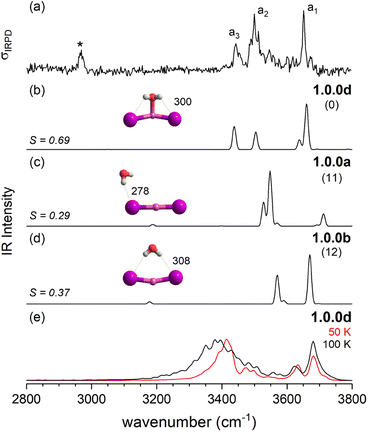
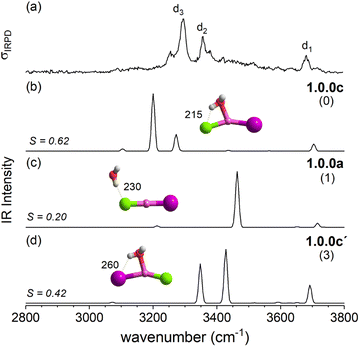
In order to assign the spectra, we performed a minimum-energy structure search using the MP2 method in combination with the def2TZVP basis set. All structures and energies are shown in Fig. S4–S6 in the ESI.† Bare lithium dihalide anions are found to adopt a linear (X–Li–X′) structure of either D_∞h (X = X′) or C_∞v (X ≠ X′) symmetry (see Table S2a and S2b† for MP2 bond distances). Characteristic microhydration motifs (top), relevant for the assignment of the IRPD spectra, and their relative zero-point energy corrected energies ΔE₀ (bottom) are plotted in Fig. 2. We make use of the same m.bw.i nomenclature scheme for the isomers as introduced in our previous publication on [LiCl₂(H₂O)_1–3]⁻.³⁵ Here, m refers to the number of water molecules, bw to the number of interion bridging water molecules and i to the number of water–water hydrogen bonds. Additionally, the letters a–z were employed in the ascending order to differentiate between multiple (m.bw.i) isomers according to ΔE₀ for the LiCl₂ species. In order to facilitate the comparison of microhydration motifs over all systems studied here, we use the same letter/motif combinations for the LiClI and LiI₂ species, even though these then do not necessarily reflect the order (with respect to energy) for these particular systems anymore. In addition, water molecules are labeled according to their hydrogen bond donating (D) and accepting (A) capacities in the hydrogen-bonded network.⁴¹

Fig. 2 Top panel: relevant structural motifs for [LiClI(H₂O)_n]⁻ anions in the size range n = 1–3, representative for all [LiXX′(H₂O)_n]⁻ systems studied here. Bottom panel: zero-point energy corrected relative energies ΔE₀ (see the Computational methods section) for [LiXX′(H₂O)_1–3]⁻ with XX′= Cl₂, ClI, I₂. Similar structural motifs for a certain cluster size are connected with lines and distinctive motifs for n > 1 are colour-coded to guide the eye. A prime symbol (e.g. 1.0.0c vs. 1.0.0c′ or 2.2.0 vs. 2.2.0′) is used for the mixed-halide anions XX′ = ClI to denote related motifs, in which exclusively the position of two halide anions is switched.

For n = 1, we find only intact core structures (CIP/CIP), in which the Li–X distances are elongated by less than 4% compared to the bare structures. The water either interacts exclusive with a single halide (1.0.0a), with two halides (1.0.0b), with Li and one halide (1.0.0c and 1.0.0c′) or substantially with all three ions (1.0.0d). The energetic ordering of these motifs depends intimately on the nature of the halides (see the bottom part of Fig. 2) and each system indeed exhibits a different global minimum structure, i.e., 1.0.0a, 1.0.0c and 1.0.0d for XX′ = Cl₂, ClI and I₂, respectively.

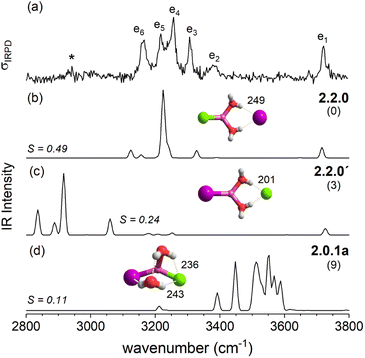
In contrast, the lowest energy motif for n = 2, the SIP/CIP configuration 2.2.0 in which one of the halides interacts with two bridging water molecules, is the same for all three systems. In the SIP moiety, the interion distance is roughly 1.7 times longer than in the bare ion core. For the mixed halide system, the hydration of the more polarizable halide (2.2.0 vs. 2.2.0′) is energetically favored. Intact-core CIP/CIP structures with (2.0.1a/b) and without (2.0.0) inter-water hydrogen bonds are higher in energy and this energy gap increases with increasing polarizability of the halides.

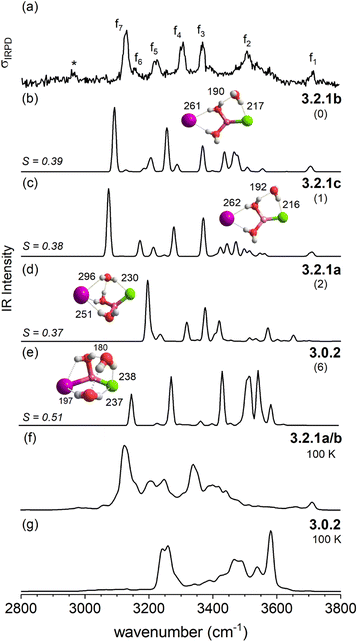
For n = 3, halide-dependent differences in the lowest-energy microhydration motif are most obtrusive. The dichloride system prefers an intact-core CIP/CIP configuration (3.0.2) that is stabilized by extended water–water and strong anion–water hydrogen bonds. In contrast, the highest degree of Li-solvation involving three bridging D-H₂Os is apparent for the diiodide system (3.3.0). The mixed halide system prefers a slightly different SIP/CIP configuration (3.2.1) containing only two bridging water molecules between the Li⁺/I⁻ ion pair as well as a third water molecule (AD-H₂O) strongly interacting with the chloride. This 3.2.1 motif is found to be the next most stable structure for dichloride and diiodide systems.

2.3 Assignment of the IRPD spectra

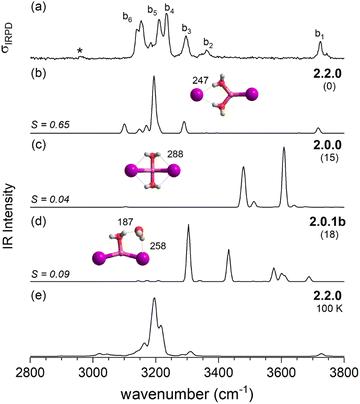
After this more general discussion of the predicted microhydration motifs, we now proceed with the structural assignment based on a detailed comparison of the experimental and computed vibrational spectra. An unambiguous spectral assignment requires the consideration of anharmonic effects for these systems.³⁵ These can be included either in a static (VPT2/MP2 method) or in a dynamic fashion (AIMD simulations). In this section, we focus on the VPT2/MP2 results (see Section 2.4 for the analysis of the AIMD results). For each system, we first discuss the relative energies of low-energy isomers. Subsequently, we compare the VPT2/MP2 vibrational spectra with the experimental ones. A cosine similarity score (S) analysis^42,43 is employed to evaluate the agreement in order to consolidate the structure assignments.

2.3.1 [LiI₂(H₂O)]⁻. In Fig. 3, the IRPD spectrum of D₂-tagged [LiI₂(H₂O)]⁻ (trace a) is compared to the anharmonic spectra (VPT2) of 1.0.0d, 1.0.0a and 1.0.0b (traces b–d). The highest cosine similarity score (S = 0.69) is found for the lowest energy isomer 1.0.0d and we therefore assign the structure accordingly. Indeed, this spectrum reproduces the relative red-shifts of each of the three bands a₁ to a₃ the best, while there are differences regarding the relative intensities, in particular for a₂. Bands a₁ and a₃ then correspond to the excitation of the antisymmetric and symmetric H₂O stretching modes, respectively, and a₂ is a combination band involving the symmetric H₂O stretching with the H₂O rocking mode (Table S1†). The similarity score associated with the spectra of the other two isomers is substantially smaller; however, a small contribution to the IRPD spectrum cannot be ruled out.

Fig. 3 Comparison of the IRPD spectrum of the D₂-tagged [LiI₂(H₂O)]⁻ (trace a) to VPT2/MP2 static anharmonic (traces b–d) and dynamic anharmonic spectra (e). The IRPD band due to D₂-stretching mode is denoted by an asterisk. VPT2 spectra along with corresponding cosine similarity scores (S) of three most stable isomers 1.0.0d (trace b), 1.0.0a (c) and 1.0.0b (d), their structures, ΔE₀ (in kJ mol⁻¹) and characteristic bond lengths (in pm) are shown. The AIMD spectra at 50 and 100 K were obtained with 1.0.0d as the starting structure.

2.3.2 [LiI₂(H₂O)₂]⁻. The most stable structure obtained for n = 2 is the solvent-shared structure 2.2.0 (see Fig. 4 and Table S2a†) shared (SIP) motif, which contains two symmetrically arranged D-H₂Os, each donating a single hydrogen bond to the same iodide anion. These IHBs are considerably shorter and hence stronger compared to all n = 1 systems. The strong interaction with water leads to an SIP interion distance that is 1.6 times larger than the CIP one, but with a similar interion angle (α_I–Li–I = 158°). The lowest lying intact-core structures are predicted considerably higher in energy. These are 2.0.0 (+15 kJ mol⁻¹, C_2v) with two equivalent DD-H₂Os and 2.0.1b (+17.5 kJ mol⁻¹, C₁) with a DD-H₂O donating a hydrogen bond to an AD-H₂O.

Fig. 4 Comparison of the IRPD spectrum of the D₂-tagged [LiI₂(H₂O)₂]⁻ (trace a) to VPT2/MP2 static anharmonic (traces b–d) and dynamic anharmonic spectra (e). VPT2 spectra along with the corresponding cosine similarity score (S) of three most stable isomers 2.2.0 (trace b), 2.0.0 (c) and 2.0.1b (d), ΔE₀ (in kJ mol⁻¹) and characteristic bond lengths (in pm) are shown. The AIMD spectrum was obtained exploring structure 2.2.0 at 100 K. The IRPD band due to D₂-stretching mode is denoted by an asterisk.

Fig. 4 compares the IRPD spectrum of D₂-tagged [LiI₂(H₂O)₂]⁻ (a) to the VPT2/MP2 spectra of the three most stable isomers (b–d). The corresponding IR spectra show key differences and the most reasonable agreement with the experimental spectrum in terms of absorption regions and most dominant peak positions is obtained for the global-minimum energy structure 2.2.0 (S = 0.65). The similarity score for 2.2.0 is much higher than those for other low-energy isomers like 2.0.0 (S = 0.04) and 2.0.1b (S = 0.09).

2.3.3 [LiI₂(H₂O)₃]⁻. Five SIP/CIP structures (see Fig. S4 and Table S2b†) are predicted to be the most stable for [LiI₂(H₂O)₃]⁻ lying within 5 kJ mol⁻¹. Two 3.3.0 motifs (see Fig. 5), which contain three bridging D-H₂Os, each with a free dangling OH bond, are found lowest in energy. 3.3.0a and 3.3.0b (+3.2 kJ mol⁻¹) have almost the same connectivity, but differ in the interion angle α_I–Li–I. The lower energy structure corresponds to a bent ion core geometry (α_I–Li–I = 134°) of C₁ symmetry, while the higher energy one exhibits a linear ion core and adopts a C_3v symmetry. Next in the energy are 3.2.1a (3.4 kJ mol⁻¹), 3.2.1b (3.6 kJ mol⁻¹) and 3.2.1c (5.0 kJ mol⁻¹). They contain two water molecules in the first coordination sphere of Li⁺, one DD-H₂O and one D-H₂O, as well as a third water molecule that either forms one short IHB with the halide anion comprising the CIP (AD-H₂O in 3.2.1b, c) or two longer hydrogen bonds bridging the two halide anions (ADD-H₂O in 3.2.1a). The lowest intact-core (CIP/CIP) structure is 3.0.2 (+9.8 kJ mol⁻¹). The IRPD spectrum of D₂-tagged [LiI₂(H₂O)₃]⁻ is compared to the VPT2/MP2 IR spectra of three lowest-energy isomers in Fig. 5. The best agreement in terms of band positions and relative intensives is not found for the spectrum of the lowest energy isomer 3.3.0a (S = 0.54), but for the spectrum of the related isomer 3.3.0b (S = 0.81). Note that the 3.3.0a spectrum does reproduce the spectral region above 3500 cm⁻¹, i.e. bands c₁ to c₃, significantly better, but the lower relative intensities give this region a lower weight in calculating S with respect to the lower energy region comprising bands c₄–c₈. The 3.2.1a spectra (S = 0.18) show much poorer agreement. This raises the following question: do multiple isomers contribute to the IRPD spectrum? The IR²MS² spectra (see Fig. S3†) obtained by probing at peak c₅ and c₈ show no evidence for long-lived isomers. However, there could be the possibility of fast interconversion, i.e. faster than the delay time of 10–20 μs between the IR²MS² pump and probe laser pulses.

Fig. 5 Comparison of the IRPD spectrum of D₂-tagged [LiI₂(H₂O)₃]⁻ (trace a) to VPT2/MP2 static (traces b–d) and dynamic anharmonic spectra (traces e and f). VPT2 spectra along with the corresponding cosine similarity score (S) of the three most stable isomers 3.3.0a (trace b), 3.3.0b (c) and 3.2.1b (d), structures, ΔE₀ (in kJ mol⁻¹) and characteristic bond lengths (in pm) are shown. The AIMD spectrum obtained at 100 K exploring structures 3.3.0a/b and 3.2.1a is presented in traces e and f, respectively.

2.3.4 [LiClI(H₂O)₁]⁻. We now proceed with the discussion of the spectra of the mixed halide system. Microhydration of [LiClI]⁻ with one water molecule leads to three intact-core structures 1.0.0c (0.0 kJ mol⁻¹), 1.0.0a (0.9 kJ mol⁻¹) and 1.0.0c′ (3.2 kJ mol⁻¹), all with C₁ symmetry (Fig. 6). The lowest energy isomer 1.0.0c contains a D-H₂O directly coordinated to Li⁺ forming a hydrogen bond with the chloride terminus (r_Cl⋯H = 215 pm). The more symmetric DD-H₂O structures 1.0.0b and 1.0.0d, identified for [LiI₂(H₂O)]⁻, do not lead to energy minima for [LiClI(H₂O)]⁻.

Fig. 6 Comparison of the IRPD spectrum (trace a) of [LiClI(H₂O)]⁻ to the VPT2/MP2 anharmonic spectra of the three lowest energy isomers 1.0.0c, 1.0.0a and 1.0.0c′ as presented in traces b–d, respectively. Cosine similarity score (S), structures, ZPE-corrected relative energies ΔE₀ (kJ mol⁻¹) and characteristic bond lengths (pm) are also shown. For D₂-tagged [LiClI(H₂O)]⁻ insufficient photoinduced D₂-loss was observed and therefore the H₂O-loss channel was monitored.

The IRPD spectrum of [LiClI(H₂O)]⁻ is compared to the VPT2/MP2 anharmonic spectra of 1.0.0c (S = 0.62), 1.0.0a (S = 0.20) and 1.0.0c′(S = 0.42) in Fig. 6. The best agreement is observed for the lowest energy isomer 1.0.0c. While the similarity score is significantly larger than for the other two isomers, it remains rather small, mainly since the red-shifts of the band pair d₂/d₃ are significantly overestimated. Interestingly, the relative band intensities agree better. Hence, bands d₁ and d₃ correspond to the excitation of the free and the hydrogen-bonded O–H stretching fundamentals, respectively. d₂ is due to the combination of d₁ and the lowest energy rocking motion involving Li and O units (60 cm⁻¹).

2.3.5 [LiClI(H₂O)₂]⁻. The lowest energy isomer predicted for n = 2 is the SIP/CIP structure 2.2.0 (see Fig. 7), which exhibits two bridging D-H₂Os, each donating a single hydrogen bond to the iodide anion. 2.2.0′, in which the D-H₂Os form hydrogen bonds with the chloride instead of the iodide anion, is predicted to be +2.7 kJ mol⁻¹ higher in energy. The lowest energy intact core structure is 2.0.1a (+8.5 kJ mol⁻¹).

Fig. 7 Comparison of the IRPD spectrum (trace a) of D₂-tagged [LiClI(H₂O)₂]⁻ to the VPT2/MP2 anharmonic spectra of the two lowest energy solvent-shared core structures 2.2.0 and 2.2.0′ and intact-core structure 2.0.1a presented in traces b–d, respectively. Cosine similarity score (S), structures, ZPE-corrected relative energies ΔE₀ (kJ mol⁻¹) and characteristic bond lengths (pm) are also shown.

The IRPD spectrum of D₂-tagged [LiClI(H₂O)₂]⁻ is compared to the VPT2/MP2 anharmonic spectra of 2.2.0, 2.2.0′ and 2.0.1a in Fig. 7. The three computed spectra are quite different from each other and reasonable agreement with experiment is only found for the spectrum of the minimum energy structure 2.2.0 (S = 0.49). Similar to n = 1, the simulated spectrum appears simpler than the experimental one. Indeed, VPT2 calculations predict a number of combination bands that could account for the additional features in the experimental spectrum; however their intensities are predicted too small. Note that similar discrepancies between experimental and the predicted spectra were observed for the corresponding structure 2.2.0 of [LiI₂(H₂O)₂]⁻ (see Fig. 4a and b). In both cases, the increase in experimental IR intensities is attributed to structural dynamics (see Section 2.4).

2.3.6 [LiClI(H₂O)₃]⁻. The three lowest energy structures for n = 3 are the solvent-bridged structures 3.2.1b (0.0 kJ mol⁻¹), 3.2.1c (1.1 kJ mol⁻¹) and 3.2.1a (1.7 kJ mol⁻¹) in which the iodide anion is separated from the LiCl core by two bridging water molecules (Fig. 8). The lowest intact-core structure 3.0.2 is predicted to be 5.8 kJ mol⁻¹ higher than 3.2.1b. The structure corresponding to the global minimum-energy structure of [LiI₂(H₂O)₃]⁻, 3.3.0a (6.5 kJ mol⁻¹), is even higher in energy for [LiClI(H₂O)₃]⁻ (see Table S2b†).

Fig. 8 Comparison of the IRPD spectrum of D₂-tagged [LiClI(H₂O)₃]⁻ (trace a) to VPT2/MP2 static anharmonic (traces b–e) and dynamic anharmonic spectra (f and g). VPT2 spectra of three most stable solvent-shared structures 3.2.1b (trace b), 3.2.1c (c), and 3.2.1a (d) and the intact core structure 3.0.2 (e), corresponding ΔE₀ (in kJ mol⁻¹) and characteristic bond lengths (in pm) are shown. The AIMD spectra were obtained from MD simulations at 100 K. The band for the polarized D₂ tag in trace a is marked with an asterisk.

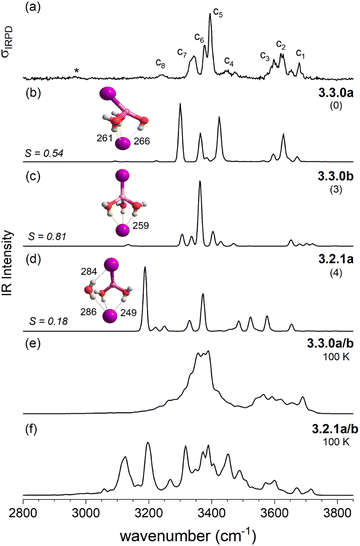
The IRPD spectrum of D₂-tagged [LiClI(H₂O)₃]⁻ is compared to the VPT2/MP2 anharmonic spectra of the three lowest energy isomers 3.2.1a, 3.2.1b and 3.2.1c in Fig. 8. Since the three structures are rather similar, it is not surprising that the three simulated IR spectra and their associated S values are rather similar (and relatively small) too. Indeed, none of the three spectra reproduces all experimentally observed features satisfactorily. Notably, the IR²MS² and one-color IRPD spectra are similar and show no evidence for the presence of multiple isomers. However, fast interconversion between these three isomers is again possible, since this would only involve the reorientation of the H₂O molecule hydrogen-bonded to chloride.

2.4 Analysis of structural dynamics

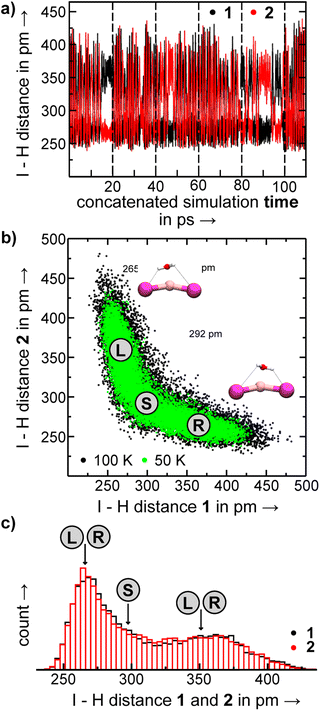
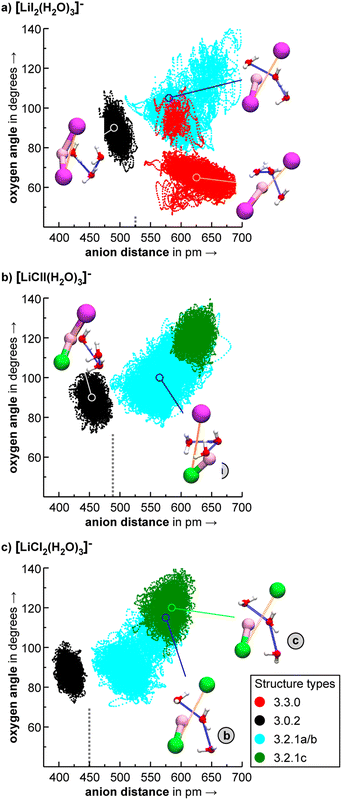
With AIMD simulations, we investigated the dynamics of selected [LiXX′(H₂O)_n]⁻ anions in order to study the stability and dynamic interconversion of different structure motifs and also to derive vibrational spectra, which are compared to the spectra of the static structures in order to elucidate the impact of anharmonicities and structural rigidity/diversity on the spectral assignment.

2.4.1 [LiI₂(H₂O)]⁻. We first tested the effect of temperature of the equilibration step in the AIMD simulations. Fig. 3e shows the anharmonic spectra obtained for the structural motif 1.0.0d of [LiI₂(H₂O)]⁻ at 50 K (red) and 100 K (black). The 100 K AIMD spectrum agrees reasonably well with the experimental IRPD spectrum consolidating the previous assignment. The MD simulations indicate that the lowest energy isomer, the C_s symmetric structure 1.0.0d, is not a stable minimum at finite T (see Fig. 9a). Instead, we observe a constant fluctuation between two C₁ structures connected by a rocking motion of the water molecule (see Fig. 9c and d). This rocking water dipole results in an increase of the relative IR intensity (with respect to the VPT2 intensity) of the signal corresponding to the IRPD band a₂, a combination band involving the symmetric O–H stretching and the H₂O rocking modes. The AIMD spectrum at 100 K has rather broad features. Decreasing the simulation temperature to 50 K has two effects. First, it leads to narrower bands as a result of a smaller amplitude of the rocking motion that is visualized in Fig. 9b, in particular for the intense feature around 3400 cm⁻¹ that corresponds to the combination band a₂. Second, the maximum of this feature as well as of the feature slightly below 3650 cm⁻¹ exhibits a shift to higher wavenumbers. Both effects improve the agreement with the experimental IRPD spectrum.

Fig. 9 In the MD simulations of [LiI₂(H₂O)]⁻ we observe oscillator between structures where the water molecule leans toward one of the iodine anions, while the symmetric structure 1.0.0d is not stable. (a) I–H distances versus time for the concatenated constant energy MD simulations of [LiI₂(H₂O)]⁻. (b) Comparison of MD frames plotted according to their I–H distances from trajectories at 50 K and at 100 K and representative structures with the water molecule leaning to either side (L and R) and the symmetric structure (S). (c and d) Histograms of the two Li–H distances.

2.4.2 [LiI₂(H₂O)₂]⁻. Also the spectra for structural motif 2.2.0 of [LiI₂(H₂O)₂]⁻ shown in Fig. 4e suggest that apparent discrepancies with respect to the VPT2 IR intensities are again due to structural dynamics, even though the 100 K AIMD spectrum still underestimates some of the relative IR intensities, e.g. those of b₂, b₃ and b₆.

2.4.3 [LiXX′(H₂O)₃]⁻. For each of the three types of anions containing three water molecules, i.e., [LiI₂(H₂O)₃]⁻, [LiClI(H₂O)₃]⁻, and [LiCl₂(H₂O)₃]⁻, DFT-based MD simulations covering more than 500 ps were performed. Despite the outcome of the comparison of simulation temperatures for [LiI₂(H₂O)]⁻, we decided to simulate at T = 100 K for equilibration, as this leads to a faster sampling than cooler trajectories. Subsequently, frames were selected to start constant energy MD simulations from which the AIMD spectra above were derived. This results in a good overview of the dynamics in the free energy basins around the low energy minima that is mainly descriptive for the vibrational spectra.

We visualize the structural dynamics in the constant energy trajectories of [LiI₂(H₂O)₃]⁻, [LiClI(H₂O)₃]⁻, and [LiI₂(H₂O)₃]⁻ as well as representative structure snapshots in Fig. 10. In order to represent “a map of the structure space”, we choose to representative coordinates, namely the distance between the anions and the largest angle formed by the three water oxygens, and these are highlighted in the structures depicted in Fig. 10 by orange and blue lines, respectively. These coordinates allow us to distinguish the different isomers from each other. For [LiI₂(H₂O)₃]⁻, for example, we see that solvent-separated structures are clearly distinguished from structures with an intact ion core (3.0.2) by an anion distance above 525 pm. Since all three plots in Fig. 10 share the same axis scaling, we can now directly see the effect of exchanging anions. By reducing ionic radii going from the diiodide to chloride–iodide to dichloride systems, we see a general shift to the left, i.e., to lower anion distances. The indicated border between water separated structures and intact ion core structures shifts from 525 pm (Fig. 10a) to below 500 pm (Fig. 10b) to 450 pm (Fig. 10c). Fig. 10 also exemplifies which anion has the dominant role in these salt–water complexes: the presence of the “harder” chloride anion is the reason why the mixed system [LiClI(H₂O)₃]⁻ shares more features with the dichloride than with diiodide system. In the intact-core motif 3.0.2, the three water molecules form a hydrogen-bonded network and only slightly dislocate the cation out of the straight line between the two anions. Interestingly, this motif is the one experimentally assigned to the [LiCl₂(H₂O)₃]⁻ system with the hard–hard Li–Cl interactions. In the following, we will take a closer look at the individual structural motifs.

Fig. 10 Visualization of representative constant energy trajectories for (a) [LiI₂(H₂O)₃]⁻, (b) [LiClI(H₂O)₃]⁻, and (c) [LiCl₂(H₂O)₃]⁻. The dots represent frames (every 10 fs) from different NVE trajectories that are colored based on their starting structure. The axes of the plots allow for a good overview of the overall available structure space. In the displayed structure snapshots, the x-axis dimension (the anion distance) is illustrated by an orange dotted line and the y-axis dimension (the largest angle between the three water oxygens) is highlighted by a blue dotted line. A bond is drawn between lithium and the anions, if they are close enough. We also draw a vertical dashed line to separate the portion of structure space where water does not break the cation–anion interaction (left of the dashed line) from the region where water breaks this interaction (right of the dashed line). Isomer 3.0.2 (black dots) does not leave the local minimum at 100 K and during the simulation time, while in contrast, alternative structures like different types of 3.2.1 interconvert. In the case of [LiI₂(H₂O)₃]⁻, isomer 3.3.0 is not stable at 100 K and transforms into 3.2.1a eventually (see panel a).

As discussed above in Section 2.3, the VPT2/MP2 anharmonic spectra for the structural motifs 3.3.0 and 3.2.1 show the best agreement for [LiI₂(H₂O)₃]⁻ and [LiClI(H₂O)₃]⁻, respectively and this holds also for the AIMD spectra as shown in Fig. 5 and 8. In the case of the diiodide, 3.3.0b converts to the lower-symmetry isomer 3.3.0a (cf., Fig. 2). In a concerted movement, one water rotates and aligns its dipole with a second water molecule, and the iodide closest to the Li⁺ moves in the same direction, thus aligning the corresponding dipole antiparallel. In the MD simulations at 100 K, we observe the transformation of 3.3.0a to 3.2.1a eventually. In the constant energy trajectories that are being partly visualized in Fig. 10, we observe multiple crossings only from the 3.3.0 to the 3.2.1 basin and never back.

An interesting effect can be seen for the 3.2.1 motifs. 3.2.1a and b differ only slightly in energy (cf.Fig. 2 and Table S2b†) and interconvert frequently in the constant energy and constant temperature MD simulations; in Fig. 10, this can be seen by the cyan coloured clouds of dots extending widely diagonal in the upper right corner of the individual plots. For the mixed halide salt system, since none of the structures 3.2.1a/b/c reproduces all experimentally observed features satisfactorily (cf.Fig. 8), this fast interconversion seems probable even in the experiments. Also, for the dichloride system the best agreement between experiment and AIMD can be found for the spectra including both the 3.2.1a/b motifs (cf. Fig. S15†). However, the barrier from 3.2.1c to 3.2.1a/b is apparently high. Motif 3.2.1c is plotted (green dots) for [LiClI(H₂O)₃]⁻ and [LiCl₂(H₂O)₃]⁻. The respective green clouds overlap with the cyan clouds and the “heavy” atom structures look almost identical. A detailed view on the structures reveals the difference in the orientation of one of the water molecules. A transition between the 3.2.1c and 3.2.1a/b basins never occurs in our AIMD simulations since the dipole rearrangement due to the needed 180° rotation of one water molecule (cf.Fig. 8) costs too much energy. For the mixed chloride/iodide system, the 3.2.1b motif is slightly lower in energy changing its position with 3.2.1a compared to [LiI₂(H₂O)₃]⁻.

In the 3.0.2 motif, the interactions between the Li cation and the two anions are essentially unperturbed by the water molecules. In the plots in Fig. 10, the respective black dot clouds remain isolated and appear rather well defined in comparison to alternative structural motifs that spread wider in structure space and that also interconvert. The dot clouds also appear to shrink from Fig. 10a–c. To take a clearer look we compute root mean square fluctuations over AIMD trajectories and plot the respective distributions in Fig. 11. The overlay illustrates that the green distribution representing [LiCl₂(H₂O)₃]⁻ is more narrow than the others; in particular [LiI₂(H₂O)₃]⁻ (blue) is characterized by a comparably long tail. We interpret this as a result of the stronger anion–water interaction due to the harder chloride anions in [LiCl₂(H₂O)₃]⁻.

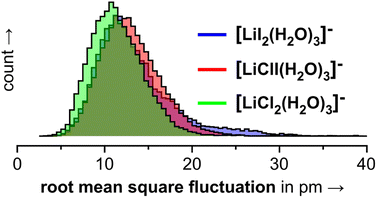Fig. 11 Root mean square fluctuations (RMSFs) for the individual frames of the 3.0.2 simulations shown in Fig. 10.

3. Discussion

We now focus on the bigger picture that emerges from our microhydration study, namely the changes in the stability of CIP vs. SIP structures as the number of water molecules is increased, how this depends on the nature of the halide anions involved and in what way this may manifest itself in the corresponding vibrational spectra of the solution phase species.

In the microhydrated lithium dihalide anions studied here, we observed a competition of several driving forces (i) interion interactions can be viewed based on the hard and soft acid and base (HSAB) concept. The interaction of the hard Li cation is stronger with the harder chloride anion than with the softer iodide anion, and hence the Li–I bond is severed more readily than the Li–Cl bond. (ii) The Li cation strives to fill its first coordination sphere with up to four ligands.^44,45 (iii) Anionic binding sites have a tendency to form IHBs, the strength of which correlates with the proton affinity (PA) of the halide.³⁴ Since the PA of chloride (1396 kJ mol⁻¹) is more than 80 kJ mol⁻¹ higher than that of iodide (1315 kJ mol⁻¹), chloride also forms significantly stronger IHBs than iodide does. Note that the IHB strength also manifests itself directly in its IR signature in the form of a characteristic red-shift of the corresponding O–H stretching frequencies (see also Fig. 1). (iv) Besides interacting with the anions and cations, water molecules also form hydrogen-bonded networks. Such networks contribute substantially to the stability of the cluster, in particular, when the ionic core structure can accomodate the hydrogen bonds without significantly interfering with their directional nature. (v) Finally, the alignment of the water dipoles along the direction of cation–anion ion pairs leads to further stabilization. Summarizing, the interactions at play in salt–water complexes, in the order of decreasing bond strengths, are:^37,46 hard ion–hard ion > hard ion–water > water–water > soft ion–water > soft ion–soft ion.

Fig. 12 summarizes the structures that were assigned in the present and our previous study³⁵ on lithium dihalide anions microhydrated with up to three water molecules. For n = 1, we mainly observe the competition between two driving forces that determine the relative isomer stabilities, in particular the stability of isomers 1.0.0a/b vs. 1.0.0c/d. In 1.0.0a, the ionic core remains quasi-linear as in the bare anion and is further stabilized by the formation of a single, almost linear IHB. In 1.0.0b, two weaker IHBs are formed. Such isomers are preferred, when only hard ions are involved and both are observed for [LiCl₂(H₂O)]⁻. Conversely, in isomers 1.0.0c/d the water O-atom binds to the Li cation, increasing its coordination number to three. In addition, a weaker hydrogen bond is formed with a more electronegative anion. Interestingly, the mixed halide system also prefers the latter structure, because the weaker Li–I interaction (reflected in the relatively larger Li–I distance, Table S2a†) allows a shorter Li⋯OH₂ distance and hence stronger cation–water interaction, which can also be viewed as an initiation of solvent induced charge separation. In principle, this observation accords with Collins “law of matching affinities”,³⁷ which states that salt pairs of widely different ionic radii are prone to dissolve. Rationally, hard anions tend to form more compact, rigid structures with Li⁺, while the structures involving two soft anions are more flexible and indeed their spectra show evidence for large amplitude motion as indicated by the arrow in the case of the [LiI₂(H₂O)]⁻ structure, 1.0.0d, in Fig. 12.

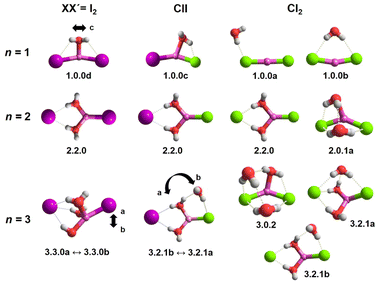Fig. 12 Assigned MP2/def2TZVP minimum-energy structures of [LiXX′(H₂O)_n]⁻ anions. Large amplitude motion indicated by AIMD analysis is represented by an arrow.

With the addition of a second water molecule, water–water hydrogen bond interactions, in principle, become possible. However, as seen in Fig. 12, the dominant isomer in all three systems is 2.2.0, demonstrating that at least two water molecules are necessary to form a SIP in the gas phase and this motif's stability is independent of anion polarizability. Note that in the case of the dichloride also a CIP isomer, 2.0.1a, is observed experimentally, but with lower abundance. This CIP isomer contains a strained water–water hydrogen bond. Once the constraints are relaxed, e.g., by addition of a third water molecule, the corresponding CIP motif returns to its position as the most stable isomer in the dichloride system.

In contrast, the SIP motif persists as the most stable one in the iodide-containing systems for n = 3. These systems are characterized by a Li cation with a complete first coordination sphere, composed of one halide anion and three D-H₂Os (3.3.0). Similar to [Li(H₂O)₃]⁺, water–water hydrogen bond formation is not observed in [LiI₂(H₂O)₃]⁻.⁴⁰ In the mixed halide system, [LiClI(H₂O)₃]⁻, however, an AD-H₂O is present that does not directly interact with the Li cation (3.2.1), driven by the formation of a strong IHB involving the chloride anion. On similar grounds, the CIP motif 3.0.2 in [LiCl₂(H₂O)₃]⁻ is restabilized. Here, the extended hydrogen-bonded network involves three water molecules along with two moderately strong chloride IHBs from an ADD-H₂O, resulting in a compact cluster with no available H-bond donors. Hence, while already two water molecules are sufficient to create a stable SIP, we see that three water molecules are needed for dynamic interconversion between (sub)-motifs already at low temperatures (Fig. 12).

4. Summary and conclusions

In this work, we studied microsolvation of lithium dihalide anions with one to three water molecules by means of a combination of gas phase spectroscopy and computational studies. In the process of structural assignments, we observe an interplay of different interaction types that is at first glance surprisingly complex. We observe that the SIP formation starts already with two water molecules, but that in particular for the hard Li⁺/Cl⁻ ion pair, the cation–anion interaction is competitive to the water-ion interactions. Iodide systems with large, more polarizable anions allow for richer dynamics of water in the clusters even at cryogenic temperature. While we explored solvent-shared motifs here, we would expect the earliest onset of solvent-separated ion pairs for the lithium diiodide system. Besides ion-pair and hydrogen-bond interactions, we find that dipole arrangements play a crucial structure defining role.

Regarding the computation of vibrational spectra, we can confirm that anharmonicity needs to be considered when treating microhydrated salt systems. The VPT2 method produces useful IR spectra. However, when larger amplitude motions come into play, spectra derived from the AIMD simulations provide better matches.

Our present study focuses on the early onset of solvation of electrolytes. Kirby and Jungwirth¹⁶ described in their “charge scaling manifesto” approaches to model such systems in molecular simulations: the macroscopic view assumes a continuum of a given polarizability modeled by a dielectric constant, while the microscopic view is based on the explicit interaction of – in a force field approach – atoms with partial charges. Electronic polarization is modelled in the macroscopic view only as a mean field while it is completely neglected in standard force fields. There are various approaches to include polarizability into classical force-field simulations besides the charge-scaling approach advocated for in the Kirby–Jungwirth paper.⁴⁷

For the charge scaling approach, the “right” scaling factor has to be defined, which is challenging, as it is unclear how much of the charge shielding due to an environment is already parametrized into the partial charges. Alternative approaches to explicitly include polarization (and even charge transfer) into force fields require extensive reference data to (re)parametrize the extended force field, e.g., by using ab initio data sets.^48,49

The surgical control over the cluster composition, the IR spectra containing structural information, and the possibility to assign these structures by combination with first principles theory, suggest such studies also as a basis to help improve molecular simulations: on the one hand, the scaling behavior from the micro- to the macroscopic view can be investigated by studying clusters with continuously increasing numbers of solvent molecules, i.e., up to more than several hundred water molecules.⁵⁰ The parameters of new polarizable force fields may be tuned to reproduce the vibrational spectra of well-designed charged clusters that represent challenging molecular and interaction motifs of relevance in molecular simulations of, for example, peptides and proteins.

5. Methods

5.1 Experimental methods

IRPD experiments were performed on the Leipzig 6 K ring-electrode trap triple mass spectrometer described previously.⁵¹ Microhydrated lithium dihalide anions, [LiXX′(H₂O)_n]⁻ with XX′ = I₂, ClI, Cl₂ were generated by a nanospray ion source from the corresponding 10 mM lithium halide solutions in a 1 : 1 water/acetonitrile mixture. The beam of anions is skimmed, thermalized to room temperature in a helium-filled radio-frequency (RF) ion-guide, and then mass-selected using a quadrupole mass filter. The mass-selected [LiXX′(H₂O)_n]⁻ ions are trapped in a RF ring-electrode ion trap held at a temperature in-between 6 and 300 K using a closed-cycle helium cryostat where they are thermalized to the ambient temperature of the trap and messenger tagged with D₂ (He used for bare ions). These microhydrated salt anions are found to be tagged efficiently to D₂via three-body collisions⁵² at an ion trap temperature of 13 K. The quadrupole mass spectra exhibiting the generation of these hydrated clusters can be found in Fig. S7–S9 in the ESI.†

IRPD spectra are recorded using the IR¹MS² technique, which allows for a background-free photofragment detection.^53,54 To this end, all ions (bare and messenger-tagged) are extracted from the ion trap every 100 ms and focused both temporally and spatially into the center of the extraction region of an orthogonally mounted double-focusing reflection time-of-flight (TOF) tandem photofragmentation mass spectrometer. Using a first set of 30 μs long high voltage (HV) pulses, the ions are accelerated into the reflectron stage, spread out in space according to their mass-to-charge ratio (m/z) and are refocused in the initial extraction region. Prior to reacceleration towards the MCP detector, ions with a particular m/z value are irradiated with a properly timed, widely wavelength tunable (750–7000 cm⁻¹) IR laser pulse (bandwidth: ∼3.5 cm⁻¹), supplied by an optical parametric oscillator/amplifier (LaserVision: OPO/OPA/AgGaSe₂) laser system.⁵⁵ IRPD spectra are recorded by continuously scanning the laser wavelength monitored online using a HighFinesse WS6-600 wavelength meter with a scan speed such that an averaged TOF mass spectrum (over 100 laser shots) is obtained every 2 cm⁻¹. Typically, at least such five scans are measured and averaged and the photodissociation cross section σ_IRPD is determined as described previously.^51,56

Double-resonance IR²MS² spectra using the ion-dip technique are obtained by employing two tunable IR lasers in a pump–probe approach and tandem mass selection stages. Briefly, the method is sensitive to laser-induced population changes of isomers that are maintained longer than the delay between the pump and probe laser pulses (∼10–20 μs). The IR spectra of isomers interconverting faster than this timescale cannot be isolated using this method. Details regarding the IR²MS² technique can be found elsewhere.^43,53

5.2 Computational methods

5.2.1 Structure search and vibrational spectra. Structure search was performed by chemical intuition and confirmed later on by a random structure search that yielded no additional low-energy conformers. MP2 minimum-energy structures⁵⁷ and their relative energies ΔE were determined using the def2TZVP basis set.⁵⁸ Sequential water binding energies were also calculated and are shown in Fig. S10.† Energy minima were validated by a subsequent harmonic frequency analysis. For a number of lowest energy isomers, we performed anharmonic frequency calculations using the second-order vibrational perturbation theory (VPT2) method as implemented by Bloino and Barone⁵⁹ and using the same basis sets as above. IR spectra are determined from the computed stick spectra, which are convoluted with a Gaussian line shape function (FWHM = 12 cm⁻¹) for better comparability. Zero-point energies (ZPE) are determined from the anharmonic vibrational frequencies and yield ZPE-corrected relative energies ΔE₀ = ΔE + ZPE. These calculations were performed with the Gaussian 16 package.⁶⁰

5.2.2 Molecular dynamics simulations. We used DFT-based molecular dynamics simulations in order to study the dynamic behavior of representative structure types of lithium dihalide water clusters. In these systems, the consideration of van der Waals interactions is crucial. Prior to the molecular dynamics simulations, we had to decide which combination of density functional approximation and van der Waals correction to use. For a set of approximately 100 different water clusters, we compared the basis-set extrapolated DLPNO-CCSD(T) energies^61,62 of MP2-relaxed structures to the exchange–correlation functionals BLYP, B3LYP, PBE, and PBE0 in combination with dispersion corrections based either on the pairwise Tkatchenko–Scheffler scheme (vdW-TS)⁶³ or a many-body dispersion correction (MBD).^64,65 The wavefunction calculations were performed with ORCA software.^66,67 Details can be found in the ESI.† In summary, the best combination giving overall good agreement in all different clusters is PBE0-TS. The MBD correction is slightly better but had convergence problems in some of the AIMD simulations.

The DFT ab initio molecular dynamics (AIMD) simulations were performed using the FHI-aims code⁶⁸ together with iPI.⁶⁹ For multiple low-energy conformers, constant temperature MD simulations at T = 100 K, and for testing also at T = 50 K, were run for 20 ps with a 0.5 fs time step. The velocity rescaling thermostat presented by Bussi, Donadio, and Parrinello was used.⁷⁰ After an equilibration period of approximately 10 ps, 11 individual structures were extracted every 1 ps. These 11 frames per structure served as starting structures for 10 ps long constant energy MD simulations with a step size of 0.5 fs. The electric dipole moment of the cluster was calculated every 1 fs step and used to compute IR spectra based on the dipole–dipole autocorrelation function.⁷¹ The best agreement with the experimental spectra has been found after redshifting the computed spectra by 210 cm⁻¹.

Data availability

Gaussian files on geometry optimization and anharmonic spectra can be found with the DOI: 10.17172/NOMAD/2022.03.18-1. Trajectories for all NVT and NVE calculations can be found with the DOI: 10.17172/NOMAD/2022.05.23-1

Author contributions

KRA and CB designed the study, coordinated the project and supervised the research. AC and SS recorded experimental data. AC has performed static computer simulations such as geometry optimization, harmonic and anharmonic spectra calculation. The analysis and interpretation of these data were performed by AC and KRA. AIMD simulations and their interpretation were made by TB and CB. HW, TB and CB performed and analyzed the benchmark calculations for the selection of the exchange–correlation functional and the dispersion correction used in AIMD simulations. All authors were involved in the preparation of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the German Research Foundation (DFG) as part of the individual research Grant No. 321027174 (AS133/3-1 “Spectroscopic Characterization of Salt Dissolution in Microhydrated Cluster Ions and at the Water/Vapor Interface”). The authors are thankful to Alexandra Giermann (Leipzig University) for her assistance in preparing and handling solutions. KRA acknowledges instrumental support from the Fritz Haber Institute of the Max Planck Society. TB and CB gratefully acknowledge computational resources provided by the Max Planck Computing and Data Facility.

Notes and references

1. Y. Marcus, Chem. Rev., 2009, 109, 1346.
2. D. J. Tobias and J. C. Hemminger, Science, 2008, 319, 1197.
3. B. J. Finlayson-Pitts, Chem. Rev., 2003, 103, 4801.
4. R. Buchner, S. G. Capewell, G. Hefter and P. M. May, J. Phys. Chem. B, 1999, 103, 1185.
5. N. F. A. van der Vegt, K. Haldrup, S. Roke, J. Zheng, M. Lund and H. J. Bakker, Chem. Rev., 2016, 116, 7626.
6. E. Levy, A. Puzenko, U. Kaatze, P. Ben Ishai and Y. Feldman, J. Chem. Phys., 2012, 136, 114503.
7. H. Bian, X. Wen, J. Li, H. Chen, S. Han, X. Sun, J. Song, W. Zhuang and J. Zheng, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4737.
8. I. Juurinen, T. Pylkkänen, K. O. Ruotsalainen, C. J. Sahle, G. Monaco, K. Hämäläinen, S. Huotari and M. Hakala, J. Phys. Chem. B, 2013, 117, 16506.
9. I. Harsányi, L. Temleitner, B. Beuneu and L. Pusztai, J. Mol. Liq., 2012, 165, 94.
10. A. La Sauza-de Vega, T. Rocha-Rinza and J. M. Guevara-Vela, ChemPhysChem, 2021, 22, 1269.
11. S. T. van der Post and H. J. Bakker, Phys. Chem. Chem. Phys., 2012, 14, 6280.
12. S. Yoo, Y. A. Lei and X. C. Zeng, J. Chem. Phys., 2003, 119, 6083.
13. C. J. Fennell, A. Bizjak, V. Vlachy and K. A. Dill, J. Phys. Chem. B, 2009, 113, 6782.
14. E. Pluhařová, P. E. Mason and P. Jungwirth, J. Phys. Chem. A, 2013, 117, 11766.
15. A. Vargas-Caamal, J. L. Cabellos, F. Ortiz-Chi, H. S. Rzepa, A. Restrepo and G. Merino, Chem. – Eur. J., 2016, 22, 2812.
16. B. J. Kirby and P. Jungwirth, J. Phys. Chem. Lett., 2019, 10, 7531.
17. P. Jungwirth and D. J. Tobias, Chem. Rev., 2006, 106, 1259.
18. D. Laage, T. Elsaesser and J. T. Hynes, Chem. Rev., 2017, 117, 10694.
19. B. S. Ault, J. Am. Chem. Soc., 1978, 100, 2426.
20. A. Mizoguchi, Y. Ohshima and Y. Endo, J. Chem. Phys., 2011, 135, 64307.
21. G. Grégoire, M. Mons, I. Dimicoli, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard and D. Solgadi, J. Chem. Phys., 2000, 112, 8794.
22. J. A. Davies, M. Mugglestone, S. Yang and A. M. Ellis, J. Phys. Chem. A, 2020, 124, 6528.
23. J. Tandy, C. Feng, A. Boatwright, G. Sarma, A. M. Sadoon, A. Shirley, N. D. N. Rodrigues, E. M. Cunningham, S. Yang and A. M. Ellis, J. Chem. Phys., 2016, 144, 121103.
24. R.-Z. Li, C.-W. Liu, Y. Q. Gao, H. Jiang, H.-G. Xu and W.-J. Zheng, J. Am. Chem. Soc., 2013, 135, 5190.
25. G.-L. Hou, C.-W. Liu, R.-Z. Li, H.-G. Xu, Y. Q. Gao and W.-J. Zheng, J. Phys. Chem. Lett., 2017, 8, 13.
26. X.-B. Wang, H.-K. Woo, B. Jagoda-Cwiklik, P. Jungwirth and L.-S. Wang, Phys. Chem. Chem. Phys., 2006, 8, 4294.
27. Y. Feng, M. Cheng, X.-Y. Kong, H.-G. Xu and W.-J. Zheng, Phys. Chem. Chem. Phys., 2011, 13, 15865.
28. R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533.
29. T. Wende, N. Heine, T. I. Yacovitch, K. R. Asmis, D. M. Neumark and L. Jiang, Phys. Chem. Chem. Phys., 2016, 18, 267.
30. J. W. DePalma, P. J. Kelleher, C. J. Johnson, J. A. Fournier and M. A. Johnson, J. Phys. Chem. A, 2015, 119, 8294.
31. D. Schröder, L. Duchácková, J. Tarábek, M. Karwowska, K. J. Fijalkowski, M. Oncák and P. Slavícek, J. Am. Chem. Soc., 2011, 133, 2444.
32. C. J. Johnson, L. C. Dzugan, A. B. Wolk, C. M. Leavitt, J. A. Fournier, A. B. McCoy and M. A. Johnson, J. Phys. Chem. A, 2014, 118, 7590.
33. L. Jiang, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Am. Chem. Soc., 2010, 132, 7398.
34. W. H. Robertson and M. A. Johnson, Annu. Rev. Phys. Chem., 2003, 54, 173.
35. A. Chakraborty, S. Schmahl and K. R. Asmis, ChemPhysChem, 2021, 22, 1036.
36. V. G. Solomonik, J. Struct. Chem., 1979, 19, 860.
37. K. D. Collins, Q. Rev. Biophys., 2019, 52, e11.
38. G. D. Dickenson, M. L. Niu, E. J. Salumbides, J. Komasa, K. S. E. Eikema, K. Pachucki and W. Ubachs, Phys. Chem. Chem. Phys., 2013, 110, 193601.
39. P. Ayotte, G. H. Weddle and M. A. Johnson, J. Chem. Phys., 1999, 110, 7129.
40. O. Rodriguez and J. M. Lisy, J. Phys. Chem. Lett., 2011, 2, 1444.
41. J.-C. Jiang, Y.-S. Wang, H.-C. Chang, S. H. Lin, Y. T. Lee, G. Niedner-Schatteburg and H.-C. Chang, J. Am. Chem. Soc., 2000, 122, 1398.
42. L. J. M. Kempkes, J. Martens, G. Berden, K. J. Houthuijs and J. Oomens, Faraday Discuss., 2019, 217, 434.
43. M. Mayer and K. R. Asmis, J. Phys. Chem. A, 2021, 125, 2801.
44. H. H. Loeffler and B. M. Rode, J. Chem. Phys., 2002, 117, 110.
45. C. Baldauf, K. Pagel, S. Warnke, G. von Helden, B. Koksch, V. Blum and M. Scheffler, Chem. – Eur. J., 2013, 19, 11224.
46. K. D. Collins, Biophys. J., 1997, 72, 65.
47. Z. Jing, C. Liu, S. Y. Cheng, R. Qi, B. D. Walker, J.-P. Piquemal and P. Ren, Annu. Rev. Biophys., 2019, 48, 371.
48. K. S. Amin, X. Hu, D. R. Salahub, C. Baldauf, C. Lim and S. Noskov, J. Chem. Phys., 2020, 153, 144102.
49. M. Ropo, M. Schneider, C. Baldauf and V. Blum, Sci. Data, 2016, 3, 160009.
50. J. T. O’Brien and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 10228.
51. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34, 1.
52. M. Brümmer, C. Kaposta, G. Santambrogio and K. R. Asmis, J. Chem. Phys., 2003, 119, 12700.
53. N. Heine, M. R. Fagiani, M. Rossi, T. Wende, G. Berden, V. Blum and K. R. Asmis, J. Am. Chem. Soc., 2013, 135, 8266.
54. B. M. Elliott, R. A. Relph, J. R. Roscioli, J. C. Bopp, G. H. Gardenier, T. L. Guasco and M. A. Johnson, J. Chem. Phys., 2008, 129, 94303.
55. W. R. Bosenberg and D. R. Guyer, J. Opt. Soc. Am. B, 1993, 10, 1716.
56. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2016, 35, 507.
57. M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275.
58. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753.
59. J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108.
60. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao and N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian Inc., Wallingford CT, 2016.
61. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 34106.
62. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
63. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 73005.
64. A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402.
65. A. Tkatchenko, A. Ambrosetti and R. A. DiStasio, J. Chem. Phys., 2013, 138, 74106.
66. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(8), e1327.
67. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73.
68. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175.
69. V. Kapil, M. Rossi, O. Marsalek, R. Petraglia, Y. Litman, T. Spura, B. Cheng, A. Cuzzocrea, R. H. Meißner, D. M. Wilkins, B. A. Helfrecht, P. Juda, S. P. Bienvenue, W. Fang, J. Kessler, I. Poltavsky, S. Vandenbrande, J. Wieme, C. Corminboeuf, T. D. Kühne, D. E. Manolopoulos, T. E. Markland, J. O. Richardson, A. Tkatchenko, G. A. Tribello, V. van Speybroeck and M. Ceriotti, Comput. Phys. Commun., 2019, 236, 214.
70. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 14101.
71. C. Baldauf and M. Rossi, J. Phys.: Condens. Matter, 2015, 27, 493002.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc03431j

---