Open Access Article
Open Access ArticleIsomer recognition by dynamic guest-adaptive ligand rotation in a metal–organic framework with local flexibility†
Ying-Jie
Zhao‡
a,
Wen-Qi
Tang
b,
Xiao-Wei
Wang
a,
Hui-Fang
Zhao
a,
Zhi-Yuan
Gu
 b,
Qingyuan
Yang
b,
Qingyuan
Yang
 a and
Dahuan
Liu
a and
Dahuan
Liu
 *ac
*ac
aState Key Laboratory of Organic-Inorganic Composites, College of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, PR China. E-mail: liudh@mail.buct.edu.cn
bJiangsu Key Laboratory of Biofunctional Materials, College of Chemistry and Materials Science, Nanjing Normal University, Nanjing 210023, PR China
cCollege of Chemical Engineering, Qinghai University, Xining 810016, China
First published on 27th September 2022
Abstract
Local flexibility in a metal–organic framework is intriguing for reconstructing a microenvironment to distinguish different guest molecules by emphasizing their differences. Herein, guest-adaptive flexibility is observed in a metal–organic framework for efficiently discriminating aromatic isomers. Microcrystal electron diffraction directly reveals that the anthracene rings can rotate around the single bond with the adsorption of guest molecules. Disorder transformation of the ligand enables the preferential adsorption of ethylbenzene over other xylene isomers. Especially, a coated capillary column combining single/multi-component adsorption confirms a unique separation order of ethylbenzene > p-xylene > m-xylene > o-xylene with excellent selectivities, which has not been reported in other materials. Density functional theory calculations and the calculated Hirshfeld surface of guest molecules in the framework demonstrate that a guest-induced splint-like confinement structure makes the main contribution to such separation performance. This finding will provide a rational strategy for molecular recognition utilizing the local flexibility of metal–organic frameworks.
Introduction
As novel porous functional materials, metal–organic frameworks (MOFs) attract increasing interest because of their highly designable and adjustable structures as well as chemical features.1,2 Flexibility is an appealing property, which can lead to the switch of the structure between different states in response to external stimuli, such as the guest molecule, pressure, light irradiation, and temperature.3,4 Especially, the motion of sub-molecular components in the framework can be utilized to construct intriguing molecular machine systems that can be used to perform complex tasks.5–8 By taking advantage of this feature, flexible MOFs have exhibited excellent performances in storage, separation, sensing, catalysis and energy transfer.9,10 For example, the breathing effect can open their pores to improve the adsorption capacity of target molecules.11,12 The flexible framework may enhance the ability of detecting various guest species of MOFs as chemosensors.13,14 However, co-adsorption of guest molecules in a mixture after the structural transformation may diminish the detection performance and selectivity of the desired molecule, especially for those with a slight difference like isomers.1 Towards this point, creating a dynamic motion area in a rigid framework may be an efficient way to achieve machine-like function for molecular recognition, while maintaining the framework integrity.15,16 Unfortunately, it is still a challenge for controlling such guest-adaptive local flexibility, which is of great potential in practical applications like separation.As important chemical raw materials in the petrochemical industry, C8 aromatic isomers (p-xylene (PX), m-xylene (MX), o-xylene (OX), and ethylbenzene (EB)) have high commercial value.17 For instance, PX is widely used to produce terephthalic acid and further be transformed into poly(ethylene terephthalate).18 MX can be converted to isophthalic acid and isophthalic nitrite.18 OX is a precursor of phthalic anhydride.18 EB is an indispensable monomer for the manufacture of styrene.19 It also has utility in the pharmaceutical industry, for example, as a starting material for drugs.18,20 However, owing to their very similar chemical and physical properties, the separation of C8 aromatics is complex and high energy consuming in industry, and complete isolation using a single process has not yet been realized.21–23 Currently, the promising method is adsorptive separation based on advanced functional materials. However, most of the reports are focused on the separation of PX, OX and MX, while the selective adsorption of EB is rarely studied. Considering the relatively small amount, the preferential separation of EB can not only reduce the energy consumption of the subsequent xylene isomerization process, but also make full use of EB resources and improve the economic benefits of aromatics separation. In addition, the general separation sequence accords with that of the boiling point, that is, the isomer with a high boiling point is the preferentially adsorbed one or has a longer retention time in the dynamic separation process.24,25 For example, MIL-53(Al) preferentially adsorbs OX, with the elution order of OX > MX = PX > EB.26 ZU-61 exhibited high MX/PX separation selectivity with the separation order of OX > MX > EB ≈ PX.27 Zn(o-phen)(2,6-NDC)·DMF exhibited the selective adsorption of MX through π–π and C–H⋯π interactions.28 The azobenzene cage can only separate PX with high selectivity.29 Moreover, efficient separation performance can be achieved by directly adjusting the pore size/shape/functionality, like zeolites, but this strategy often only achieves the separation of a single component. Considering the physical and chemical nature of C8 aromatic isomers, developing a dynamic and adaptable porous material may effectively separate the individual components of the adsorption mixture.
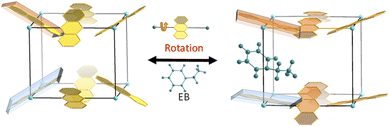
Herein, a kind of Ni-MOF with reversible structural changes, Ni(ADC)(TED)0.5, is proposed to discriminate C8 aromatics through controlling the guest-adaptive flexibility of the framework. It is interesting to observe that the anthracene linkers can rotate around bonds between the metal ion and the ligand when the skeleton traps guest molecules (Fig. 1), revealed by powder X-ray diffraction (PXRD) and microcrystal electron diffraction (MicroED) of the sample combining theoretical calculations. Besides, the framework exhibits unusual dynamic behaviors: the skeleton shrinks upon guest trapping and expands once releasing. Due to such guest-induced behaviors with the host–guest noncovalent interactions, the sample can recognize C8 aromatics by adjusting its structure to amplify the difference between guest molecules. As a result, preferential adsorption of EB over other xylene isomers is displayed and confirmed by the coated capillary column for gas chromatographic separation, single/multi-component adsorption experiments and breakthrough experiments. The adsorption and elution sequence follows the order of EB > PX > MX > OX, which is unique and has not been reported in other materials, to the best of our knowledge. These results not only prove the excellent C8 aromatics separation performance of this material, but also provide a new idea for the design of functional materials for efficient recognition and separation utilizing the guest-driven rotation of the ligand in MOFs.
Results and discussion
Characterization of MOFs
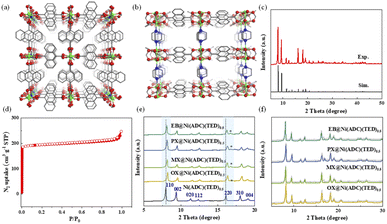
Ni(ADC)(TED)0.5 was obtained by the solvothermal reaction of NiCl2·6H2O, H2ADC and TED in DMF, and isolated as a yellow powder. The paddle-wheel units and ADC are bonded to form undulated 2D layers, which are connected with TED to generate 3D frameworks (Fig. 2a and b). The anthracene groups that form part of the framework can provide abundant π planes to interact with guests. The PXRD patterns of the activated sample are shown in Fig. 2c, which is in well agreement with the simulated ones. Calculated from the N2 adsorption and desorption isotherm at 77 K, the BET surface area of the activated sample is 754 m2 g−1, close to the theoretical and reported values in the literature29 (Fig. 2d). After being exposed to air for one year, the PXRD and BET surface area are still consistent with those of the original one (Fig. S1†), indicating good stability and potential for industrial application in combination with high thermal stability confirmed by the TGA curve (Fig. S2†).Similar to the single-crystal structure of Ni(NDC)(TED)0.5 (CCDC code: 1953742), the dicarboxylate ligand in Ni(ADC)(TED)0.5 is orientationally disordered.30 Thus, it is reasonable to speculate that these rings may reconstruct to match the different molecules in the adsorption process.16,31 The disorder switchability may be navigated by guest sorption. To confirm this, the sample was immersed into a commercial single component C8 aromatic solution for 24 h in the first step, and then PXRD was performed. From Fig. 2e and S3,† all the peaks shift to higher diffraction degrees and a new peak appears at about 16.7°, except for (00l) reflections. Since the (00l) reflections are determined by the distance between the 2D layers, the TED pillars remain unchanged. Thus, the change of PXRD may have stemmed from the flexibility of ADC with the effective inclusion of C8.32,33
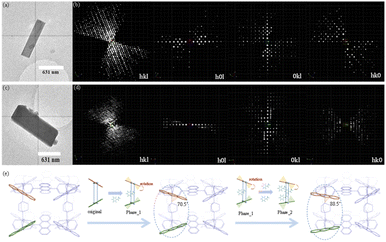
To directly investigate the structural transformation, MicroED was applied for a guest-included samples, which is an efficient technique for structure determination of nano- or submicron-sized crystals, including MOFs, COFs and zeolites.34 By taking an EB-included sample as an example, 3D electron diffraction data were collected on a JEM-2100 Plus TEM, and then processed by using XDS software (Fig. 3a–d).35 After extracting the intensities, a direct method, SHELXT,36 was used to obtain the atomic coordinate information, and the detailed data can be found in the ESI (Tables S1–S4†). As shown in Fig. S4,† the preferential adsorption sites of EB are between the adjacent ADC ligands along the TED pillars. It is interesting to observe that the anthracene ring of ADC may rotate around the axis (single bonds between the metal ion and the ligand) with the inclusion of EB. With the variation of the number of EB molecules adsorbed in the framework, the rotation degree changes accordingly. For example, the resolved structures contain Phase_1 with a few guest molecules and Phase_2 with more guest molecules, as shown in Fig. S4.† The unit cell parameters were determined to be orthorhombic with a = 13.77, b = 16.22, and c = 18.22 for Phase_1, and a = 21.22, b = 10.73, and c = 18.19 for Phase_2. From Fig. 3e, under the condition of few EB molecules in the pores, the angles between the anthracene plane and the axis of TED pillars are 56.4° or 70.5°, and the entire volume of the framework is 4069.4 Å3 (Phase_1, Fig. 3e). With increasing the number of EB, such a twist angle further increases to be 80.5°, and the corresponding volume of the framework is 4141.7 Å3 (Phase_2, Fig. 3e). Thus, the guest-induced rotation behavior of the anthracene ligand endows the framework with unique flexibility for reconstructing its structure to match and recognize the guest molecules (Fig. 3e).
 | ||
| Fig. 3 TEM images and 3D reciprocal lattices of Phase_1 (a) and (b) and Phase_2 (c) and (d); schematic illustration of the ligand transformation (e). | ||
Attempting to further explain this behavior, the PXRD patterns of Ni(ADC)(TED)0.5 were simulated by exquisitely adjusting the configuration of anthracene rings with different rotating degrees (Fig. S5†). A new peak appears at about 16°, under the condition that the adjacent anthracene configuration tends to be parallel. On the basis of this structure, Pawley refinements were performed using the pseudo-Voigt profile function and Finger–Cox–Jephcoat method.37 From Fig. 2f and S6,† the obtained PXRD patterns are in good agreement with the experimental ones. The pore size may be decreased, as illustrated by the calculated largest cavity diameter (LCD) shown in Table S5,† providing an opportunity for enhancing the host–guest interactions. In fact, the parallel configuration of the ADC ligand exhibits the lowest calculated energy during the optimization of the framework.38 More importantly, this transformation is reversible and the structure can be restored by immersing the samples into methanol to remove the adsorbed guest molecules (Fig. S7†).
Separation performance for aromatic isomers
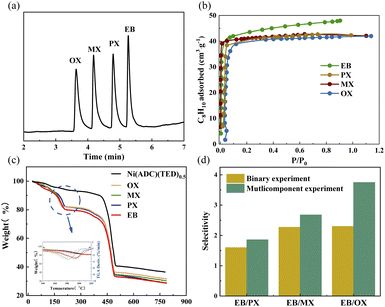
Such guest-responsive flexibility encouraged us to investigate the separation performance, due to the subtle regulation of the structure and the possible discrimination of C8 aromatic isomers. The powder of Ni(ADC)(TED)0.5 was firstly packed into a capillary column through a simple dynamic method. As shown in Fig. S8,† the sample was successfully coated on the inner wall of the capillary column. The thicknesses at two different positions are 2.5 μm and 1.6 μm, respectively. After optimizing the temperature process, the mixture of C8 aromatics can achieve a baseline separation from each other within 6 min on the column (Fig. 4a). The order of elution is OX < MX < PX < EB, which is quite different from the commercial column HP-5MS and the column packed with other materials, like co-pillar[4 + 1]arene, MOF-5, untwisted Zr-BTB-FA, Zr-BTB and UiO-66.39–42 The column exhibits good separation factors (αMX/OX = 1.22, αPX/MX = 1.21, and αEB/PX = 1.13, Table S6†) and signal resolutions (RMX/OX = 1.56, RPX/MX = 1.90, and REB/PX = 1.53). The resolution of PX and MX can be completely differentiated (R = 1.90), which is obviously better than commercial columns, like VF-WAXMS (R = 0.47).42 Especially, EB molecules are the last component out of isomers eluted from the column, indicating the ability to adopt specific identification and shape-selective affinity to the guest molecules. Furthermore, to evaluate the separation performance intuitively, the adsorption enthalpy was calculated by using van't Hoff formula. As shown in Fig. S9 and Table S7,† the EB has higher adsorption enthalpy than other isomers, reflecting that EB molecules exhibit stronger interaction with the framework than other isomers. The sequence of adsorption enthalpy is OX < MX < PX < EB, which is in agreement with the separation order observed in the experiment.To explain the separation performance of the column, a single component adsorption experiment was firstly performed. From Fig. 4b, it can be seen that the saturation capacity (48.01 cm3 g−1) of EB is higher than those of other isomers, such as 42.31, 42.07 and 41.99 cm3 g−1 for PX, MX, and OX, respectively. This indicates the EB-selective adsorption performance. Notably, this sample also displays higher adsorption capacity of four components than zeolites used in industry.27,43 To further evaluate the separation performance of the sample, adsorption kinetic experiments were carried out. As shown in Fig. S10,† the adsorption of EB is faster than for other isomers, indicating that the sample has a distinct adsorption preference for EB. In general, the weight loss temperature of the guest molecules will increase with the enhancement of host–guest interaction.44 To confirm this peculiar adsorption performance, TGA analysis was conducted. As shown in Fig. 4c, S11 and Table S8,† the adsorbed guest molecules are released at different temperatures (the maximum position of weight loss derivative). The order of weight loss temperature is EB > PX > MX > OX, revealing the difference of host–guest interaction to determine the selectivity. As shown in FT-IR (Fig. S12†), the characteristic peak assigned to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching frequency of aromatic rings45 is shifted from 1452 to 1444, 1442, 1441, and 1440 cm−1 after the adsorption of EB, PX, MX, and OX, respectively. This also demonstrates that the anthracene rings are the primary interaction sites with these isomers and play an important role in adsorption, as revealed by MicroED results.
C stretching frequency of aromatic rings45 is shifted from 1452 to 1444, 1442, 1441, and 1440 cm−1 after the adsorption of EB, PX, MX, and OX, respectively. This also demonstrates that the anthracene rings are the primary interaction sites with these isomers and play an important role in adsorption, as revealed by MicroED results.
Liquid phase binary experiments were then conducted to further investigate the C8 aromatics separation ability of Ni(ADC)(TED)0.5. As shown in Fig. 4d, the selectivities of EB toward PX, MX, and OX are 1.61, 2.27, and 2.31, respectively. Besides, from the adsorption experiments for a four-component equimolar mixture shown in Fig. 4d, the EB/PX, EB/MX, and EB/OX selectivities are 1.86, 2.68, and 3.75, outperforming all of the reported materials, including Co2(dobdc),23 Zn2(aip)2(bpy),44 and sql-1-Co-NCS.22 Such preferential adsorption toward EB can be confirmed by a multicomponent adsorption experiment in the vapor phase (Fig. S13†). Moreover, the sample still maintains its original separation performance after three adsorption recycles (Fig. S14†). The BET of the regenerated sample was almost the same as that of the original material (Fig. S15†), indicating good stability. Besides, in the liquid phase breakthrough experiment, an n-heptane solution containing equimolar (0.005 mM) components of EB, PX, MX, and OX was pumped through the column with a flow rate of 0.2 mL min−1. All of the solutions are adsorbed by Ni(ADC)(TED)0.5 in the first 9 min. A roll-up effect is observed (Fig. S16†), where the EB molecule replaces other adsorbed molecules in the framework and competes for the same site within the pores, resulting in the eluted concentration of PX, MX, and OX temporarily exceeding those of the feed. Although the four isomers occur simultaneously, the eluted concentration also follows the order of EB > PX > MX > OX. Combining the above results, it can be concluded that Ni(ADC)(TED)0.5 has a distinct adsorption preference for EB and the ability to separate C8 isomers with a unique sequence.
Adsorption mechanism
To gain molecular insight into the adsorption mechanism, the binding energy of C8 aromatics was calculated by the DFT method. On the basis of the above discussions, the anthracene rings can rotate in the adsorption process. Thus, the parallel configuration of the ADC ligand was used with the lowest calculated energy. The possible adsorption configurations between the guest molecule and the framework were optimized as well as the orientation of the methyl/ethyl group in the guest molecule, namely the edge-to-face and face-to-face configurations (Fig. S17†). As shown in Table S9,† the binding energy of the edge-to-face configuration is lower than that of the face-to-face one, and the sequence of the binding energy is consistent with the adsorption results. Thus, the xylene isomers stack on the framework preferentially in an edge-to-face configuration. From Fig. S18,† EB can not only interact with the parallel anthracene rings, but also with other adjacent ligands due to the large molecular size (EB: 9.6 Å, PX: 9.2 Å, MX: 8.9 Å, and OX: 7.6 Å, Fig. S19 and Table S10†). The calculated binding energy increases along with the increase of the guest molecular length, that is, OX (71.80 kJ mol−1) < MX (81.14 kJ mol−1) < PX (85.32 kJ mol−1) < EB (90.70 kJ mol−1). This is because the C–Hxylene⋯π and CH3/C2H5⋯π interactions as well as van der Waals interactions exhibit the main contribution to the total binding energy. The longer guest molecule of EB has more interaction sites with the anthracene rings to induce a stronger interaction than those of other isomers.The Hirshfeld surface of a target molecule in the framework was calculated by using CrystalExplorer to investigate the host–guest interaction at the molecular level. It is constructed on the basis of the electron distribution calculated as the sum of spherical atom electron densities, and can provide a three-dimensional picture of intermolecular contacts in the framework based on the distance between the surface and the nearest atom interior or exterior to the surface (di and de). From the calculated Hirshfeld surface (dnorm) of EB in Fig. 5a(I) and (II), the red region represents H⋯H (HEB⋯Hframework) and C⋯H (CEB⋯Hframework and HEB⋯Cframework) contact distances between the host and guest, which are within the range of the vdW interaction distance.46 The blue region indicates a contact distance larger than the vdW interaction distance. To describe the intermolecular interactions more intuitively, decomposed fingerprint plots were generated to depict the contact for particular kinds of interactions and their relative contributions. Fig. S20† illustrates that most components of the intermolecular contacts are H⋯H (68.52%) and C⋯H (22.98%) contacts, that is, the van der Waals interactions and C–H⋯π interactions are prominent in the adsorption process. The shortest internal distances of H⋯H and C⋯H contacts (the minimum value of de + di) are about 2.00 Å and 2.67 Å as shown in Fig. 5a(III) and (IV), respectively, corresponding to the red region of the Hirshfeld surface. C⋯C contacts (Fig. 5a(V)) with an estimated minimum distance of 3.60 Å indicate that the π⋯π interaction is not the main contribution to the C8 aromatic isomer selectivity. In addition, the presence of “wings” at the top left and bottom right of the fingerprint plot (Fig. 5a(IV)) corresponds to the CEB⋯Hframework/HEB⋯Cframework contacts. The wing at the top left (di < de) corresponds to points on the Hirshfeld surface around the C–H donor, while the bottom right (di > de) corresponds to points on the Hirshfeld surface around the π acceptor. A similar behavior can be also found in the Hirshfeld surface (dnorm) and 2D fingerprint plots of other xylene isomer molecules (Fig. 5b–d), except for the slight difference in the distances between the guest and host. As shown in Table S11,† the distance between EB and the framework is the shortest among the isomers, further demonstrating the presence of strong host–guest interactions enhancing the EB selectivity. The distances for other isomers follow the trend of PX > MX > OX, which is in agreement with the adsorption experiments. Therefore, the mechanism that the sample preferentially adsorbs EB with a unique elution sequence is mainly attributed to the unique geometry of EB and the dynamic motion of the ligand in the framework. These structures allow the ethyl groups/H atoms of C8 to have a strong interaction with anthracene linkers, whose rotation provides optimal host–guest interactions to discriminate C8 aromatic isomers by amplifying the guest molecule differences.
To confirm the findings mentioned above, a series of control experiments were performed by replacing the ADC ligand and using C9 isomers as guest molecules. Using Ni(BDC)(TED)0.5, OX-selective separation behavior is observed, and efficient separation and discrimination of EB and MX are unsuccessful (Fig. S21†). This confirms the vital role of the presence of anthracene rings and its unique pore shape in the separation process. Furthermore, for the C9 mixture, Ni(ADC)(TED)0.5 can also efficiently separate ethyltoluene isomers and n-propylbenzene (Fig. S22 and Tables S12, S13†), and exhibits an unique separation sequence (N-PB > P-ET > M-ET > O-ET), which is consistent with the order of molecular lengths and has not been reported, to the best of our knowledge. This is similar to C8 aromatic isomer selectivities, again stressing the fact that Ni(ADC)(TED)0.5 can differentiate longer isomers through its adaptable and dynamic structural transformation.
Conclusions
Efficient recognition and separation of C8 aromatic isomers can be achieved through the guest-adaptive flexibility in Ni(ADC)(TED)0.5. The result of a coated capillary column exhibits that the separation hierarchy follows the order EB > PX > MX > OX. Single and multi-component adsorptions also confirm the preferential adsorption of EB over other xylene isomers, which is a rare MOF with such a unique adsorption sequence so far. In addition, the adsorption capacity of C8 aromatic isomers is higher than those of the state-of-the-art zeolites. The separation mechanism for the recognition of C8 isomers has been demonstrated by experimental and theoretical methods, indicating that the guest-responsive splint-like confinement structure of the ADC ligand plays an important role in the separation process. These findings not only provide an efficient adsorbent for separating aromatic isomers, but also give guidance for the application of ligand rotation in MOFs, for example, as molecular motors.Experimental
Synthesis of MOFs
Ni(ADC)(TED)0.5 was prepared based on a previously reported method.29 A mixture of NiCl2·6H2O (119 mg, 0.5 mmol), H2ADC (133 mg, 0.5 mmol), and TED (28 mg, 0.25 mmol) was dissolved in DMF (15 mL) and then heated at 393 K for 48 h in a Teflon lined autoclave. After cooling to room temperature, a yellow product was isolated by filtration and washed with DMF and methanol at least three times. Finally, the sample was dried at 373 K under vacuum overnight.Ni(BDC)(TED)0.5 was prepared by a hydrothermal method.47 Typically, 214 mg NiCl2·6H2O, 120 mg H2BDC and 66 mg TED were dissolved in 30 mL of DMF, and then heated at 393 K for 48 h in a Teflon lined autoclave. After natural cooling, a green product was isolated by filtration and washed with DMF and methanol at least three times. Finally, the sample was dried at 373 K under vacuum overnight.
Preparation of MOF-coated capillary columns
The pretreatment of the capillary column (15 m long × 0.25 cm i.d., Yong Optic Fiber Plant, Hebei, China) was the same as a previously reported method.48 The sample was packed into a capillary column through a simple dynamic coating method. Ethanol suspension containing MOFs (1 mL, 2.5 mg mL−1) was pumped into the capillary column. The residual suspension was flushed out of the column at a velocity of 30 cm min−1. Then the packed column was conditioned with a temperature program: 303 K for 30 min, 1 K min−1 to 523 K, and 523 K for 240 min.Characterization
Powder X-ray diffraction patterns of the samples were obtained with Cu Kα radiation (λ = 1.54178 Å) at a scan rate of 4° min−1. Fourier-transform infrared spectroscopy (FT-IR) was conducted on a Nicolet 6700 FT-IR spectrophotometer. Single-component vapor-phase adsorption experiments were performed using a Micromeritics ASAP 2460 equipped with a vapor dosing tube. 1H NMR spectra were recorded using a Bruker Advance 400 NMR spectrometer. The N2 adsorption–desorption isotherm was obtained on 3H-2000PS1/2A series automatic surface and aperture analyzers (BeiShiDe Instruments). Thermogravimetric analysis (TGA) was carried out using a NETZSCH STA 449F3 analyzer in a N2 atmosphere with a flow rate of 10 mL min−1. The samples were heated at a rate of 10 K min−1. MicroED data were collected by transmission electron microscopy (JEM-2100 Plus) and operated at 200 kV with a MerlinEM fast pixelated detector (512 × 512 pixels, pixel size 55 μm). A 3D reciprocal lattice was constructed from the ED frames using XDS, from which the unit cell parameters can be obtained with the indexed reflection and extracted intensities. The adsorption kinetic experiments were conducted on a dynamic vapor sorption analyzer (BSD-DVS).Adsorption experiments
For single component vapor-phase adsorption, each C8 aromatic adsorption isotherm was collected using a Micromeritics ASAP 2460 at 333 K. Before measurement, the samples were loaded into the sample tube and then degassed under vacuum at 423 K for 12 h. To avoid adsorption errors, a parallel experiment was performed by using at least two batches of samples.For competitive adsorption experiments, about 20 mg of the sample was loaded into a 4 mL vial containing 2 mL of an equal volume of binary (EB/PX, EB/MX, and EB/OX) or multicomponent (EB/PX/MX/OX) mixed solution, which was placed in a thermostatic vibration shaker at 303 K for 24 h. For binary or multi-component experiments, the adsorbed sample was isolated by filtration and then soaked in 2 mL of CDCl3 for at least two days. The supernatant was collected and used for NMR analysis.
For vapor phase experiments, approximate 20 mg of the sample was put into a 4 mL open bottle, which was placed in a 20 mL vial containing 2 mL of an equal volume of binary (EB/PX, EB/MX, and EB/OX) or multicomponent (EB/PX/MX/OX) mixed solution. Then the 20 mL vial was sealed and transferred into an oven at 303 K for 24 h. After adsorption, the sample in a 4 mL open bottle was immersed in 2 mL CDCl3 for at least two days. Finally, the CDCl3 solution was collected for NMR analysis to calculate the selectivity of isomers.
The multicomponent liquid phase breakthrough experiment was carried out using a stainless-steel column (about 4.6 mm inner diameter × 100 mm). An n-heptane solution containing a multicomponent mixture of equimolar (0.005 mM) components was pumped through the column with a flow rate of 0.2 mL min−1. The concentration of the sample was detected by gas chromatography-mass spectrometry (GC-MS).
Computational methods
Density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP).49 The exchange–correlation interaction was calculated within the Perdew–Burke–Ernzerhof functional (PBE) with the projector augmented wave (PAW) method50,51 and empirical correction in D3 Grimme's method was used.52 The cutoff energy for the plane-wave basis sets was 520 V. The convergence criterion of the self-consistent field (SCF) was set as 10−5 eV. An ordered structure was adopted to simplify the DFT calculations. The Brillouin zone of the structure was sampled with a k-point mesh of 2 × 2 × 2 (generated using the Monkhorst–Pack scheme). The binding energy was calculated by using the following eqn (1):| Ebinding energy = Eframework+guest − Eframework − Eguest | (1) |
The Hirshfeld surface was calculated through the program CrystalExplorer,46,53 and it was constructed on the basis of the calculated electron distribution as the sum of spherical atom electron densities.54 The normalized contact distance (dnorm) is defined by eqn (2), which can identify the regions that are particularly important for intermolecular interactions. The 2D fingerprint consisting of the distances di and de of the Hirshfeld surface can provide the interaction between the guest and host, which is a novel visual representation of all the intermolecular interactions.
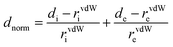 | (2) |
Data availability
All data supporting this study are available in the manuscript and ESI.†Author contributions
D. L. and Y. Z. designed the work and wrote the paper; Y. Z., W. T., W. W. and H. Z. conducted the experiments and analyzed the data; Y. Z. and Q. Y. conducted the calculations; D. L. and Z. G. discussed the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key R&D Program of China (No. 2021YFB3802200) and the Natural Science Foundation of China (No. 21978005).Notes and references
- W. Cui, T. Hu and X. Bu, Adv. Mater., 2020, 32, 1806445 CrossRef CAS PubMed.
- F. Saraci, V. Quezada-Novoa, P. R. Donnarumma and A. J. Howarth, Chem. Soc. Rev., 2020, 49, 7949–7977 RSC.
- X. Yang, H. Zhou, C. He, Z. Mo, J. Ye, X. Chen and J. Zhang, Research, 2019, 2019, 9463719 CrossRef CAS PubMed.
- J. Zhang, H. Zhou, D. Zhou, P. Liao and X. Chen, Natl. Sci. Rev., 2018, 5, 907–919 CrossRef CAS.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- W. Danowski, T. van Leeuwen, S. Abbolahzadeh, D. Roke, W. R. Browne, S. J. Wezenberg and B. L. Feringa, Nat. Nanotechnol., 2019, 14, 488–494 CrossRef CAS PubMed.
- J. Perego, S. Bracco, M. Negroni, C. X. Bezuidenhout, G. Prando, P. Carretta, A. Comotti and P. Sozzani, Nat. Chem., 2020, 12, 845–851 CrossRef CAS PubMed.
- V. García-López, D. Liu and J. M. Tour, Chem. Rev., 2019, 120, 79–124 CrossRef PubMed.
- X. Zhang, D. Zhou and J. Zhang, Chem, 2021, 7, 1006–1019 CAS.
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096 RSC.
- C. Gu, N. Hosono, J. Zhang, Y. Sato, S. Kusaka, S. Sakaki and S. Kitagawa, Science, 2019, 363, 387–391 CrossRef CAS PubMed.
- S. Hiraide, Y. Sakanaka, H. Kajiro, S. Kawaguchi, M. T. Miyahara and H. Tanaka, Nat. Commun., 2020, 11, 3867 CrossRef CAS PubMed.
- S. Seth and S. Jhulki, Mater. Horiz., 2021, 8, 700–727 RSC.
- Z. Chang, D. Yang, J. Xu, T. Hu and X. Bu, Adv. Mater., 2015, 27, 5432–5441 CrossRef CAS PubMed.
- R. Matsuda, Nature, 2014, 509, 434–435 CrossRef CAS PubMed.
- S. Horike, R. Matsuda, D. Tanaka, S. Matsubara, M. Mizuno, K. Endo and S. Kitagawa, Angew. Chem., Int. Ed., 2006, 118, 7384–7388 CrossRef.
- H. Wang, Y. Liu and J. Li, Adv. Mater., 2020, 32, 2002603 CrossRef CAS PubMed.
- N. Kumar, S. Q. Wang, S. Mukherjee, A. A. Bezrukov, E. Patyk-Kazmierczak, D. O'Nolan, A. Kumar, M. H. Yu, Z. Chang, X. H. Bu and M. J. Zaworotko, Chem. Sci., 2020, 11, 6889–6895 RSC.
- M. A. Moreira, J. C. Santos, A. F. P. Ferreira, J. M. Loureiro and A. E. Rodrigues, Ind. Eng. Chem. Res., 2011, 50, 7688–7695 CrossRef CAS.
- Y. Jeon, S. Park, S. Choi, Y. J. Seo, Y. H. Chu and Y. G. Shul, J. Porous Mater., 2014, 21, 177–187 CrossRef CAS.
- D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437 CrossRef PubMed.
- S. Wang, S. Mukherjee, E. Patyk-Kazmierczak, S. Darwish, A. Bajpai, Q. Yang and M. J. Zaworotko, Angew. Chem., Int. Ed., 2019, 58, 6630–6634 CrossRef CAS PubMed.
- M. I. Gonzalez, M. T. Kapelewski, E. D. Bloch, P. J. Milner, D. A. Reed, M. R. Hudson, J. A. Mason, G. Barin, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2018, 140, 3412–3422 CrossRef CAS PubMed.
- Z. R. Herm, E. D. Bloch and J. R. Long, Chem. Mater., 2014, 26, 323–338 CrossRef CAS.
- Y. Wu and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2021, 60, 18930–18949 CrossRef CAS PubMed.
- L. Alaerts, M. Maes, L. Giebeler, P. A. Jacobs, J. A. Martens, J. F. M. Denayer, C. E. A. Kirschhock and D. E. De Vos, J. Am. Chem. Soc., 2008, 130, 14170–14178 CrossRef CAS PubMed.
- X. Cui, Z. Niu, C. Shan, L. Yang, J. Hu, Q. Wang, P. C. Lan, Y. Li, L. Wojtas, S. Ma and H. Xing, Nat. Commun., 2020, 11, 5456 CrossRef CAS PubMed.
- S. Laha, R. Haldar, N. Dwarkanath, S. Bonakala, A. Sharma, A. Hazra, S. Balasubramanian and T. K. Maji, Angew. Chem., Int. Ed., 2021, 60, 19921–19927 CrossRef CAS PubMed.
- B. Moosa, L. O. Alimi, A. Shkurenko, A. Fakim, P. M. Bhatt, G. Zhang, M. Eddaoudi and N. M. Khashab, Angew. Chem., Int. Ed., 2020, 59, 21367–21371 CrossRef CAS PubMed.
- J. Pei, J. Wang, K. Shao, Y. Yang, Y. Cui, H. Wu, W. Zhou, B. Li and G. Qian, J. Mater. Chem. A, 2020, 8, 3613–3620 RSC.
- S. Ehrling, E. M. Reynolds, V. Bon, I. Senkovska, T. E. Gorelik, J. D. Evans, M. Rauche, M. Mendt, M. S. Weiss, A. Poppl, E. Brunner, U. Kaiser, A. L. Goodwin and S. Kaskel, Nat. Chem., 2021, 13, 568–574 CrossRef CAS PubMed.
- D. N. Dybtsev, H. Chun and K. Kim, Angew. Chem., Int. Ed., 2004, 116, 5143–5146 CrossRef.
- D. Tanaka, S. Horike, S. Kitagawa, M. Ohba, M. Hasegawa, Y. Ozawa and K. Toriumi, Chem. Commun., 2007, 30, 3142–3144 RSC.
- Z. Huang, T. Willhammar and X. Zou, Chem. Sci., 2021, 12, 1206–1219 RSC.
- W. Kabsch, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 125–132 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- F. Auras, L. Ascherl, A. H. Hakimioun, J. T. Margraf, F. C. Hanusch, S. Reuter, D. Bessinger, M. Doblinger, C. Hettstedt, K. Karaghiosoff, S. Herbert, P. Knochel, T. Clark and T. Bein, J. Am. Chem. Soc., 2016, 138, 16703–16710 CrossRef CAS PubMed.
- M. Chang, J. Ren, Y. Wei, J. Wang, Q. Yang, D. Liu and J. Chen, Sep. Purif. Technol., 2021, 279, 119656 CrossRef CAS.
- S. Mekapothula, M. A. Addicoat, D. J. Boocock, J. D. Wallis, P. J. Cragg and G. W. V. Cave, Chem. Commun., 2020, 56, 1792–1794 RSC.
- W. Tang, J. Xu and Z. Gu, Chem.–Asian J., 2019, 14, 3462–3473 CrossRef CAS PubMed.
- Q. Lv, S. Feng, L. Jing, Q. Zhang, M. Qi, J. Wang, H. Bai and R. Fu, J. Chromatogr. A, 2016, 1454, 114–119 CrossRef CAS PubMed.
- Z. Tao, J. Wu, Y. Zhao, M. Xu, W. Tang, Q. Zhang, L. Gu, D. Liu and Z. Gu, Nat. Commun., 2019, 10, 2911 CrossRef PubMed.
- M. Minceva and A. E. Rodrigues, AIChE J., 2007, 53, 138–149 CrossRef CAS.
- J. Lee, Y. Kim, Y. Son, H. Kim, Y. Nam Choi, D. D'Alessandro, P. Chandra Rao and M. Yoon, Chem.–Eur. J., 2021, 27, 14851–14857 CrossRef CAS PubMed.
- A. Karmakar and I. Goldberg, CrystEngComm, 2011, 13, 339–349 RSC.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed.
- W. Liang, F. Xu, X. Zhou, J. Xiao, Q. Xia, Y. Li and Z. Li, Chem. Eng. Sci., 2016, 148, 275–281 CrossRef CAS.
- W. Tang, Y. Zhao, M. Xu, J. Xu, S. Meng, Y. Yin, Q. Zhang, L. Gu, D. Liu and Z. Gu, Angew. Chem., Int. Ed., 2021, 133, 6996–7001 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. K. Wolff, D. J. Grimwood, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Crystal Explorer 17.5, University of Western Australia, Perth, 2007, hirshfeldsurface.net Search PubMed.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc03923k |
| ‡ Present address: China Fire and Rescue Institute, Beijing 102202, PR China. |
| This journal is © The Royal Society of Chemistry 2022 |