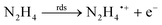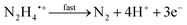Electroanalytical overview: the electroanalytical sensing of hydrazine

Abstract

In this overview, we explore the electroanalytical sensing of the important chemical reagent hydrazine, highlighting the plethora of electrochemical sensing strategies utilised from the first reports in 1951 to the present day. It is observed that a large proportion of the work developing electrochemical sensors for hydrazine focus on the use of metallic nanoparticles and some other surface modifications, although we note that the advantages of such strategies are often not reported. The use of nanoparticle-modified electrodes to this end is explored thoroughly, indicating that they allow the same electrochemical response as that of a macroelectrode made of the same material, with clear cost advantages. It is recommended that significant studies exploring the surface coverage/number of nanoparticles are performed to optimise electroanalytical devices and ensure that thin-layer effects are not producing false observations through electrocatalysis. Development of these sensor platforms has begun to transition away from classical macroelectrodes, toward more mass producible supporting electrodes such as screen-printed and inkjet-printed electrodes. We suggest significant advances in this area are still to be found. The vast majority of developed electroanalytical sensors for hydrazine are tested in aqueous based environments, such as tap, river and industrial effluent waters. There is significant scope for development of hydrazine sensors for gaseous environments and biologically relevant samples such as blood, serum and urine, aiming to produce sensors for accurate occupational exposure monitoring. Finally, we suggest that the levels of publications with independent validation of hydrazine concentrations with other well-established laboratory-based measurements is lacking. We believe that improving in these areas will lead to the development of significant commercial products for the electroanalytical detection of hydrazine.

---

Robert D. Crapnell

Robert D. Crapnell achieved both his MChem and Ph.D. from the University of Hull, UK respectively, in 2014 and 2018. Immediately after, Robert undertook a PDRA position for 18 months and is currently a technical specialist at Manchester Metropolitan University, UK. Robert's research is focussed on fundamental electrochemistry, electrochemical, and thermal biosensor development, molecularly imprinted polymers and additive manufacturing.

Craig E. Banks

Craig E. Banks holds a personal chair in nano- and electrochemical technology and has published over 500 papers and works on next generation additive manufacturing and screen-printed electrochemical sensing platforms as well as water splitting, sensor design, supercapacitors and battery development.

---

Introduction: hydrazine

Hydrazine is an important chemical reagent, with the chemical formula N₂H₄, widely used in agricultural chemicals, air bags, pharmaceutical intermediates, photography chemicals, textile dyes, fuel for rockets, spacecraft and fuel cells and in boiler feed water systems where it acts a scavenger to remove traces of oxygen and reduces corrosion of metal pipes and fittings.^1,2 The US National Institute for Occupational Safety and Health (NIOSH) reports that the recommended exposure limit (REL) in air is 0.03 ppm (2 h) and the permissible exposure limit 8 h total weight average (TWA) is 1 ppm, while the “Immediately Dangerous to Life or Health” (IDLH) is 50 ppm.³ The U.S. Environmental Protection Agency has classified hydrazine as an irritant and group B2, probable human carcinogen.⁴ The threshold limit value is reported to be no higher than 10 ppb.^5,6 Due to hydrazine's industrial significance and toxicological effects, its sensing is widely explored. Methods for the detection of hydrazine sensing include: solid-phase spectrophotometry,² gas chromatography-mass spectrometry,⁷ high-performance liquid chromatography-tandem mass spectrometry,⁸ and matrix-assisted laser desorption/ionization time-of-flight mass spectrometry.⁹ Many sensors have been reported for the sensing of hydrazine, such as fluorescence,^10,11 surface-enhanced Raman spectroscopy,¹² chemiluminescence¹³ and electrochemistry to name just a few. In this overview we focus specifically on providing a thorough overview of the endeavours dedicated to the electroanalytical sensing of hydrazine.

The electrochemical oxidation of hydrazine was studied as early as 1951 via polarography and oxide-coated platinum rotating disc electrodes.^14,15 These works reported that the reaction in aqueous media yields nitrogen as a principal component and that the reaction proceeded more rapidly on an oxide-coated surface over that of a bare (clean) platinum surface. Bard explored the effect of electrode pre-treatment on the chronopotentiometric oxidation of hydrazine at a platinum electrode in aqueous solutions agreeing with Karp and Meites¹⁵ that a freshly prepared layer of platinum oxide plays an active role.¹⁶ Michlmayr and Sawyer explored the electrochemical oxidation of hydrazine, 1,1-dimethylhydrazine and 1,2-dimethylhydrazine in DMSO with chronopotentiometry, controlled-potential coulometry, and cyclic voltammetry at platinum electrodes, reporting that the overall reaction is a one-electron oxidation.¹⁷ Wang and Cao¹⁸ reported the first use of glassy carbon for the electrochemical oxidation of hydrazine, exploring the mechanism in both aqueous and non-aqueous media. Carbon based materials have the advantages of being economical, stable, having chemical inertness, give rise to relatively wide potential windows and low background current making them suitable for different types of electroanalysis, in-particular the sensing of hydrazine.

Compton et al. have recently provided a thorough overview of the electrochemical oxidation of hydrazine demonstrating that the phenomenological Butler–Volmer theory is not appropriate for interpreting the electrochemical process of hydrazine but rather reveals a strong potential dependence on the anodic transfer coefficient, consistent with the symmetric Marcus–Hush theory.^19,20 Hydrazine in aqueous media has pK_a1 and pK_a2 values of 8.0 and −1.0 at 298 K respectively, which corresponds to the following chemical equilibria:^19,20

N₂H₅⁺ ⇆ N₂H₄ + H⁺

N₂H₆²⁺ ⇆ N₂H₅⁺ + H⁺

Fig. 1A helpfully shows the speciation of hydrazine in aqueous media as a function of pH, which is useful for electroanalysts to know the species they are measuring within different pH aqueous media.

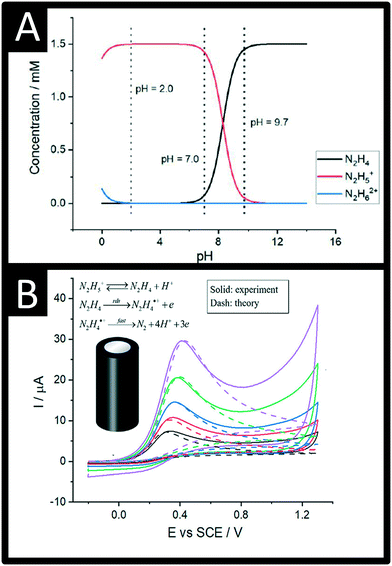Fig. 1 A: The speciation of hydrazine as a function of pH in pure water; B: Comparison between the experimental and DIGISIM-simulated voltammetry at a glassy carbon macroelectrode of 1.5 mM hydrazine supported by 0.1 M KNO₃ at pH 9.7 (solid for experiment, dash for simulation). Simulation parameters: initial concentrations of N₂H₄, N₂H₅⁺, and H⁺ are 1.44 mM, 0.06 mM, and 2 × 10⁻¹⁰ M, respectively; formal potential of N₂H₄/N₂H₄˙⁺ is 0.14 V; reorganization energy is 0.35 eV; equilibrium constant of N₂H₄/N₂H₅⁺ is 5.0 × 10⁻⁹ M; diffusion coefficients of N₂H₄ and N₂H₅⁺ are 7.1 × 10⁻⁶ cm² s⁻¹ and 2.8 × 10⁻⁶ cm² s⁻¹, respectively; standard rate constant of the rds step is 4.5 × 10⁻⁵ cm s⁻¹; second-order rate constant for the protonation of hydrazine is 1.1 × 10⁵ M⁻¹ s⁻¹; figures reproduced with permission from ref. 19. Copyright 2021 American Chemical Society.

The electrochemical oxidation of hydrazine at a glassy carbon electrode in aqueous media is shown in Fig. 1B along with fitting of the voltammetric profiles with DIGISIM, a commercial electrochemical simulation software. An excellent fit between theory and experiment is evident (Fig. 1B) and the electrochemical mechanism is described as:^19,20

N₂H₅⁺ ⇆ N₂H₄ + H⁺

A rigorous study by Compton et al.^19,20 has elegantly shown that hydrazine is only electroactive in its unprotonated form, N₂H₄ whereas the protonated species N₂H₅⁺ is electro-inactive. Overall, the electrochemical oxidation of hydrazine occurs via a 4-electron process with the second step (see mechanism above) rate-determining step (rds). The standard rate constant of the rds step is 4.5 × 10⁻⁵ cm s⁻¹; the second-order rate constant for the protonation of hydrazine is 1.1 × 10⁵ M⁻¹ s⁻¹. The approximate estimation of the associated standard heterogeneous rate constant, k⁰, for the rate-determining step has been reported to be 4.5 (±1.0) × 10⁻⁵ cm s⁻¹.^19,20

Electroanalytical approaches

Table 1 provides an extensive overview of the current literature reported for the electroanalytical sensing of hydrazine, which shows the wide and diverse approaches utilised to measure this important analyte. From inspection of Table 1 we can observe that a plethora of electroanalytical approaches have been developed to provide electrochemical platforms for sensing hydrazine. Table 1 is in chronological order, showing one of the first studies utilised liquid chromatography with electrochemical detection in conjunction with cobalt phthalocyanine bulk modified carbon paste electrodes for the sensing of hydrazine over the range 10⁻³–10⁻⁸ M, with 6.4 pg (200 fmol) able to be routinely measured.²¹ Based on early electrochemical work, it is well known that the electrochemical oxidation of hydrazine is possible on palladium electrodes. Consequently, Liu et al.²² developed palladium nanoparticle modified carbon fiber microdisk array electrodes, which were employed in capillary electrophoresis for the simultaneous detection of hydrazine, methylhydrazine, and isoniazid. A wide linear range from 1 μM–5 mM was shown to be possible with a limit of detection (LOD) found to correspond to 1.2 pg. The authors successfully applied their sensor for the determination of hydrazine in spiked human urine, one of only a handful to determine hydrazine in this sample matrix.²² Wang et al. utilised capillary electrophoresis in conjunction with screen-printed carbon electrodes (SPEs) modified with palladium via electrodeposition, with low micromolar concentrations over the range 0.2–200 μM able to be readily detected.²³ Capillary electrophoresis has not been widely used for hydrazine determination with electrochemistry and there is scope to explore this method further.

Table 1 An overview of various electrochemical approaches reported towards the detection of hydrazine, highlighting the electrode material, electrode modifications used, electroanalytical method of detection, linear range, limit of detection and the real sample medium the sensor platform was applied to

Electrode	Method of detection	Linear range	Limit of detection	Sample medium of real samples	Ref.
Key: Pd: palladium; CFMDE: carbon fibre microdisk electrode; ZnO: zinc oxide; NRs: nanorods; GCE: glassy carbon electrode NPs: nanoparticles; PEDOT–PSS: poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate); NR: not reported; MnO2: manganese oxide; MWCNTs: multi-walled carbon nanotubes; FePC: iron phthalocyanine; CoHCF: cobalt hexacyanoferrate; PoPD: poly(o-phenylenediamine); SPEs: screen-printed electrodes; CNTs: carbon nanotubes; ErGO: electrochemical reduced graphene oxide; BDD: boron-doped diamond; PDTYB: poly(4,5-dihydro-1,3-thiazol-2-ylsulfanyl-3-methyl-1,2-benzenediol); ITO: indium tin oxide; PANI: polyaniline; PAYR: poly(alizarin yellow R) Ag@C: Ag core–shell nanoparticles; PDDA: poly(diallyldimethylammonium chloride); CuHCF: copper(II) hexacyanoferrate nanocubes; CoPC: cobalt phthalocyanine; CPE: carbon paste electrode; LC-EC: liquid chromatography with electrochemical detection; EGN-IL: electrodeposited graphene ionic liquid composite film; PEDOT:PSS: poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate); CB: carbon black; CuS-OMC: copper sulfide-ordered mesoporous carbon; ZIF-8: zeolitic imidazolate framework-8 nanocrystals; PDI-GABA: perylene diimide derivative; PxDA: para benzylamine; CFCME: carbon fiber cylinder microelectrode; CoCuHCF: cobalt and copper hexacyanoferrate; ANSA: 1-amino-2-naphtol-4-sulfonic acid; PB: Prussian blue; CNP: nitrogen-doped carbon nanopolyhedra; PPy: polypyrrole; CNF: carbon nanofibre; VC@Ag: Vulcan carbon modified with silver nanoparticles; EDAC: ethylenediamine cellulose; PVP: poly(vinylpyrrolidone); AgNCs: silver nanocubes; 2-CDMA: 2-chloro-N′-[1-(2,5-dihydroxyphenyl) methylidene]aniline; polyCoTAPc: cobalt tetraamino phthalocyanine; EGNS: electroactivated graphite nanosheets; AG: activated graphite; GG-g-PAM: Guar gum grafted with poly(acrylamide); AuBPE: gold barrel plating electrode; PAMSA: poly(2-acryalamido-2-methyl-propane-sulfonic acid)-doped polyaniline layers; [hmim][PF6]: n-hexyl-3-methylimidazolium hexafluorophosphate; EFTA: ferrocene-derivative (ethyl2-(4-ferrocenyl[1,2,3]triazol-1-yl)acetate); NG: nitrogen-doped graphene; ZIF-67: cobalt-based zeolitic imidazolate framework; CTS; chitosan; poly(BCP): poly bromocresol purple; CCLP: calcium ions cross linked pectin film; FTO: fluorinated tin oxide glass; MBCPE: magnetic bar carbon paste electrode; DPB: 2-(3,4-dihydroxyphenyl) benzothiazole; FcD: 2,7-bis(ferrocenyl ethynyl)fluoren-9-one (2,7-BFE; 2PHC: 2-(4-oxo-3-phenyl-3,4-dihydroquinazolinyl)-N′-phenyl-hydrazinecarbothioamide; DHBPD: N,N′(2,3-dihydroxybenzylidene)-1,4-phenylene diamine; NPZ: nano P zeolite; ZSM-5: zeolite; CTAB: cetyltrimethyl ammonium bromide; NPC: N-doped porous carbon; OMC: ordered mesoporous carbon; BHD: bimetallic heterodimer; BCS: bimetallic core–shell; poly(CoOBImPc): cobalt(II) octabenzimidazolephthalocyanine; HRGO: honey reduced graphene oxide; TPP: platinum(II) tetraphenylporphyrin nanocomposite; NB: nile-blue; P-MWCNTs: polydopamine-modified multiwalled carbon nanotubes; MOF: zinc-metal organic frameworks; SSG: silicate sol–gel matrix; CH: choline film; CC: carbon cloth; APS: aminopropyl)triethoxysilane; AuTPP: gold tetra phenyl porphyrin; HM: redox mediator hematein; SPGEs: screen-printed graphene electrodes; BPPG: basal plane pyrolytic graphite electrode.
CoPC/CPE	Cyclic voltammetry, LC-EC	10^−3–10^−8 M	6.4 pg (200 fmol)	NR	21
Pd NPs/CFMDE	Cyclic voltammetry, electrophoresis	1 μM–5 mM	1.2 pg	Spiked human urine	22
Chlorogenic acid/GCE	Amperometry	0.05–3 mM	NR	NR	52
CoCuHCF/CFCME	Potentiometric	1 μM–1 mM	0.5 μM	NR	53
Pd/SPEs	Capillary electrophoresis	0.2–200 μM	1.5 μM	NR	23
FePc/Au	Square-wave voltammetry	13–92 μM	5 μM	NR	54
Pyrogallol red/GCE	Linear sweep	5–600 μM	1.7 μM	NR	55
CuCo – HCF/CPE	Amperometry	0.1–12 mM	NR	NR	56
Pd-NPs/BDD	Linear sweep	6.8–102 μM	1.8 μM	NR	31
Pd-NPs – GC spheres/BPPG	Cyclic voltammetry	100–600 μM	2 μM	NR	57
ZnO – MWCNTs/GCE	Amperometry	0.6 to 250 μM	0.18 μM	Distilled water	58
Pd NPs – CNF/GCE	Differential pulse voltammetry	10–4000 μM	2.9 μM	NR	59
Curcumin – MWCNTs/GCE	Amperometry	2–44 μM	1.44 μM	NR	60
Au NPs/Ti	Cyclic voltammetry	5–40 mM	NR	NR	61
Au-NPs – ZnO-MWCNTS/GCE	Amperometry	0.5–1800 μM	0.15 μM	Drinking water	62
TiO2 NPs – DHBPD/CPE	Differential pulse voltammetry	0.01–4 μM	9.15 nM	Drinking and river water	63
C@ZnO nanorod array	Cyclic voltammetry	0.5–4 μM	0.1 μM	NR	62
ZnO nanorod array	Cyclic voltammetry	0.5–3 μM	0.2 μM	NR	62
Pd/SPEs	Linear sweep voltammetry	8–72 μM	3.7 μM	NR	38
Pd NPs – PANI/GCE	Amperometry	10–300 μM	0.06 μM	NR	64
Pd micro-domains/SPEs	Linear sweep voltammetry	12.5–175 μM	8.9 μM	NR	65
Pd NPs/TiO2	Cyclic voltammetry	5–30 mM	23 μM	NR	66
Ni(II) complex/GCE	Cyclic voltammetry	1.0–100 mM	0.4 μM	Drinking water	67
TiO2–Pt nanofibers/GCE	Amperometry	2–1030 μM	0.14 μM	Lake water	68
TiC – CNF arrays	Amperometry	0.1–1635 μM	0.026 μM	NR	69
Pd-NPs/MWCNTs/GCE	Differential pulse voltammetry	2.5–700 μM	1 μM	NR	70
CuO NPs/GCE	Amperometry	0.1–600 μM	0.03 μM	Drinking water and industrial wastewater	71
Pd/plaster-trodes	Cyclic voltammetry	50–500 μM	31 μM	NR	72
TiO2 NPs – quinizarine/CPE	Differential pulse voltammetry	0.5–1900.0 μM	77 nM	Drinking, river and wastewater	73
PANI-Ag-NPs/GCE	Amperometry	20–90 μM	NR	NR	74
Pd-NPs-carbon/GCE	Cyclic voltammetry	NR	NR	NR	75
Au NPs – CH/GCE	Cyclic voltammetry	0.5 μM–0.5 mM	0.1 μM	Distilled water	76
Pd NPs – PAMSA/GCE	Amperometry	40 μM–1 mM	0.42 μM	NR	77
Mn2O3 nanofibres/GCE	Amperometry	Up to 644 μM	0.3 μM	Lake water	78
ZnO nanorods/PET	Amperometry	0.5–50 μM	0.17 μM	NR	79
Pd NPs-CB/GCE	Cyclic voltammetry	5–500 μM, 0.5–10 mM	8.8 μM	NR	80
Nickel ferrite NPs – MWCNTs/GCE	Amperometry	5–2500 μM	1.5 μM	Drinking water	81
CoHCF – MWCNTs/graphite paste	Amperometry	2.0–1200 μM	0.91 μM	River water sample and pharmaceutical tablets	82
AuCu NPs-EGN-IL/GCE	Amperometry	0.2–110 μM	0.1 μM	Wastewater	83
Pd-NPs-decorated PoPD	Amperometry	1 μM–1 mM	96 nM	NR	84
Pt–SPEs	Amperometry	50–500 μM	0.12 μM	NR	46
TiO2 NPs/CPE	Cyclic voltammetry	0.03–7 μM	27.3 nM	Drinking water	85
MnO2–GO/GCE	Amperometry	3 μM–1 mM	0.16 μM	Lake water	86
PANI – ERGO/FTO	Linear sweep voltammetry	0.01 μM–0.1 mM	15 mM	NR	87
Vertically aligned ZnO nanorod/ITO	Cyclic voltammetry	0.3 μM-0.3 mM	515.7 μM	NR	88
Au nonporous/ITO	Amperometry	5.00 nM–2.05 mM,	4.37 nM	Drinking water	89
Ni(OH)2–MnO2-NPs/GCE	Linear sweep voltammetry	5–18 mM	0.12 μM	NR	90
PVP-AgNCs/GCE	Amperometry	0.005–0.46 mM	1.1 μM	NR	91
Pd NPs – EDAC/GCE	Differential pulse voltammetry	5–150 μM	1.5 μM	NR	92
Pd NPs – PEDOT/GCE	Amperometry	0.5–30, 200–5000 μM	0.8 μM	NR	93
SWCNT–SPEs	Cyclic voltammetry	100–1000 μM	54 μM	NR	40
Pd–SPEs	Cyclic voltammetry	200–600 μM, 600–1000 μM	4 μM	NR	45
Ag – CB NPs/GCE	Amperometry	50–800 μM	3.47 μM	NR	94
Au NPs/graphite pencil electrode	Amperometry	0.05–250 μM	42 mM	Drinking water	95
AuCu3/AuBPE	Amperometry	0.1–1000 μM	0.04 μM	Lake and ground water	96
Pt NPs/BDD	Differential pulse voltammetry	10–500 μM	3.3 μM	NR	97
WO3-NPs/Au	Amperometry	100–1000 μM	144.73 μM	NR	98
Pd-NPs – rGO/GCE	Amperometry	0.04–200 μM	7 nM	Wastewater	32
ERGO – CCLP-Au NPs/GCE	Amperometry	10–600 nM, 0.6–197.4 μM	1.6 nM	Drinking and rain water, urine	99
FcD – GO/CPE	Square wave voltammetry	0.22 μM–0.3 mM	98 nM	Drinking and river water	100
Pd NPs–GG-g-PAM	Cyclic voltammetry	50 μM–0.6 mM, 0.6 mM–180 mM	4.1 μM	NR	101
Ag NPs-PPy/GCE	Cyclic voltammetry	0.5–1000 and 1000–10 000 μM	0.2 μM	Drinking and river water, industrial wastewater	102
Poly(BCP)–CNT/GCE	Amperometry	0.5 μM–1 mM	0.1 μM	NR	103
CoPC–SPEs	Cyclic voltammetry	10–100 μM	6.21 μM	NR	47
CoPC SPEs	Cyclic voltammetry	10–100 μM	9 μM	NR	104
Au NPs – AG/SPEs	Amperometry	2 nM–936 μM	0.57 nM	NR	105
Pd–Au NPs/GCE	Amperometry	0.1–500 μM	0.07 μM	Drinking water	106
Pd NPs – CoTAPc/GCE	Amperometry	0.2–1 mM	1.3 μM	NR	107
Au-NPs – PDTYB – MWCNTs/GCE	Cyclic voltammetry	2–130 and 130–350 μM	0.6 μM	NR	108
PdPt NPs – CNTS/GCE	Amperometry	0.55–1200 μM	0.28 μM	Drinking water	109
TiO2 NPs – Mn(III) salen/CPE	Square wave voltammetry	0.03 μM–0.4 mM	10 nM	Drinking and river water	110
Co3O4–MWCNTs/GCE	Amperometry	20 μM–1.1 mM	0.8 μM	Drinking water	111
Back-to-back CoPC SPEs	Cyclic voltammetry	7.9–104 μM	2.9 μM	NR	48
TiO2 nanowires	Amperometry (photoelectrochemistry)	0–1000 μM	1.9 μM	NR	112
Ag/ITO	Amperometry	100–1700 μM	0.5 μM	Drinking water	113
ANSA/CPE	Cyclic voltammetry	50 μM–25 mM	43 μM	NR	114
Ag-ZIF-8/CPE	Amperometry	6–5000 μM	1.6 μM	Drinking and river water	115
Au@Pd core–shell NPs-rGO/GCE	Amperometry	2–40 μM	0.08 μM	Drinking, pond and river water	116
PEDOT:PSS – Pd NPs/GCE	Amperometry	0.4 to 100 μM	0.12 μM	NR	117
Pd NPs – PxDA-rGO/GCE	Amperometry	1 μM–7.4 mM	0.17 μM	NR	118
Au-NPs – CNTs-ErGO/GCE	Amperometry	0.3–319 μM	65 nM	Drinking water	119
Fe3O4@SiO2−MWCNT – 2PHC-IL/CPE	Square wave voltammetry	0.07 μM–0.5 mM	40 nM	Drinking and river water	120
pDA/ITO	Cyclic voltammetry	100 μM–10 mM	1 μM	Drinking water	121
DPB – Fe3O4 NPs/MBCPE	Differential pulse voltammetry	0.1–0.4 μM, 0.7–12.0 μM	18 nM	Drinking and river water	122
GO – CTS – Pt NPs/GCE	Amperometry	20 μM–10 mM	3.6 μM	Wastewater	123
CoHCF-SSG/ITO	Cyclic voltammetry	100–600 μM	NR	NR	124
Mesoporous Au–ZnO/GCE	Amperometry	0.2–14.2 μM	0.24 μM	NR	125
ZnO nanorods/glass	Amperometry	0.8–101 μM	0.08 μM	NR	126
NG-PVP – Au NPs/SPEs	Square wave voltammetry	2–300 μM	0.07 μM	High sugar fruit and vegetable samples	41
Au-NPs – poly(taurine)/GCE	Amperometry	1000 μM	0.05 μM	River water	24
Au–Pd NPs/GCE	Amperometry	0.02–166.6 μM	5 nM	NR	127
Cu nanoclusters/GCE	Amperometry	1.04–425 μM	1.04 μM	NR	128
CoS2-CNTs	Amperometry	0.1 nM–1.0 mM	0.1 nM	Industrial effluent and sea water	129
PEDOT-CuO/GCE	Amperometry	0.5 μM–53 mM	0.2 μM	Drinking and lake water	130
Pd NPs – EGNS/SPEs	Amperometry	0.05–1415 μM	4 nM	Wastewater	39
AuTPP-rGO/GCE	Amperometry	20 nM to 198 nM	3 nM	Ground, rain and river water	34
Cu NPs – MWCNTs/pencil graphite electrode	Amperometry	0.1 to 800 μM	70 nM	River, well and wastewater	131
Co3O4 nanosheets-rGO/CC	Amperometry	5–470 μM	0.14 μM	NR	130
Cu-NPs-PANI zeolites/GCE	Differential pulse voltammetry	4 nM–800 μM	1 nM	Drinking and river water	132
Pd NPs – MWCNTs/GCE	Cyclic voltammetry	2–28 mM	NR	NR	133
MnO2 – VC@Ag NPs/GCE	Amperometry	0.1–350 μM	0.1 μM	Drinking water	134
Pd-NPs – rGO – MWCNTs/GCE	Amperometry	1–1100 μM	0.15 μM	Drinking water	135
ZrO2 NPs/Au electrode	Cyclic voltammetry	20–90 μM	1.05 μM	Well water, hand pump water and canal water	136
APS – Au NPs/GCE	Amperometry	10 nM–12 μM	10 mM	NR	25
TiO2 NPs/GCE	Cyclic voltammetry	1 nM to 10 mM	28.8 pM	Drinking and sea water, industrial effluent, PC bottle, PVC packaging bag	137
Pt-TPP – RGO/GCE	Amperometry	13 nM to 232 μM	5 nM	River, sea and rain water	138
RuO2 NPs – CTAB – GO/GCE	Cyclic voltammetry	10 μM–1 mM	2.3 μM	Drinking and river water	139
CuO – ZSM-5 NPs/CPE	Amperometry	25 μM to 0.9 mM, 0.9–4.5 mM	3.6 μM	Drinking and river water	140
PB-CNP-PPy/GCE	Amperometry	0.75 μM–1.7 mM	0.29 μM	Drinking water	141
Co–CeO2 nanoflake/steel electrode	Amperometry	0.005–0.1, 0.13–0.37 μM	0.006, 0.0012 μM	Drinking and river water	142
Ag-Zeolite NPs/CPE	Amperometry	10 μM–0.4 mM, 0.4–4 mM	1.5 μM	Drinking and river water	143
PDDA – CuHCF/SPEs	Amperometry	0.03–536.6 μM	0.01 μM	Drinking and lake water	44
Au@Pt-nanoflowers – GO/GCE	Amperometry	0.8 μM–0.429 mM	0.43 μM	Drinking water	144
Au NPs – ERGO/Au	Differential pulse voltammetry	4–1000, 2000–8000 μM	74 nM	Drinking water	145
CuO NPs – IL/CPE	Differential pulse voltammetry	0.05–150 μM	0.03 μM	Drinking, river and wastewater	146
CuO NPs – IL/CPE	Differential pulse voltammetry	0.05–150 μM	0.03 μM	Drinking, river and wastewater	146
PAYR – Ag@C/GCE	Amperometry	0.3–3.6, 3.9–7.2 μM	0.09 μM	Drinking and lake water	147
rGO-Co3O4@Au NPs/GCE	Amperometry	10–620 μM	0.44 μM	River, sea and lake water123	33
Au NPs – MWCNTs – CTAB-GO/GCE	Differential pulse voltammetry	1.0–1000 μM	0.38 μM	Drinking and lake water	148
MnO2–N-doped RGO/GCE	Rotating disc	20–100 μM	0.09 μM	Drinking and lake water	149
CMDA/CPE	Square-wave voltammetry	0.08–400 μM	0.03 μM	Drinking, river and wastewater	150
Pd NPs – graphene/ITO	Amperometry	0.1 μM to 2.5 mM	0.02 μM	NR	151
Au–Cu NPs – NPZ/CPE	Amperometry	0.01–150 mM	0.04 μM	Drinking, rain and river water	152
CuO – CNTS/SPEs	Amperometry	5 to 50 μM	5 μM	NR	43
Polythiophene-mesoporous ZnO/GCE	Amperometry	0.5–48 μM	0.207 μM	NR	153
Cu3P@NH2-MIL-125(Ti)/GCE	Amperometry	5 μM to 7.5 mM	79 nM	Drinking and river water	154
Au@CeO2 NPs – RGO/GCE	Amperometry	0 nM to 3 mM	3 nM	Drinking, river and lake water	155
Au@Ni-BHD NPs-rGO/GCE	Amperometry	0.2 μM to 1 mM, 1 mM to 9 mM	0.06 μM	Drinking water	156
Au@Ni-BCS NPs-rGO/GCE	Amperometry	3 μM to 1 mM, 1 mM to 20 mM	0.9 μM	Drinking water	156
NiFeCo nanoalloy/GCE	Amperometry	0.020–3080 μM	6.4 nM	Drinking, lake, river, sewage water	27
CuO – OMC/GCE	Amperometry	1 μM to 2.11 mM, 2.11 mM to 21.1 mM	0.89 μM	NR	155
Pt–Pd NPS – ErGO/GCE	Amperometry	0.007–5.5 mM	1.7 μM	Drinking water	157
Curcumin-AgNPs – rGO-FeCo2O4 nanosheets/SPCE	Differential pulse voltammetry	2.5–1200 μM	23.7 nM	River and wastewater	42
FeCo oxide carbon spheres/GCE	Amperometry	0.1–516.6 μM	0.1 μM	River water	158
Sb2S3 – PDI-GABA/GCE	Amperometry	10–250, 250–1300 μM	0.05 nM	Drinking, river, sea water and industrial effluent	159
AuNPs@NPC-RGO/GCE	Amperometry	0.05 to 1.00 μM	9.6 nM	Drinking, river and lake water. Hydrazine sensing in an air environment	35
Ag NPs – ZIF-67/CPE	Amperometry	4 to 326 μM, 326 to 4700 μM	1.45 μM	Drinking and rainwater	160
β-Ni(OH)2/CPE	Amperometry	1–1300 μM	0.28 μM	Drinking water	161
P-MWCNTs – RGO/GCE	Amperometry	1 μM–3 mM, 3–55 mM	0.31 μM	Drinking and river water	162
ZnO-NRs/GCE	Cyclic voltammetry	NR	NR	NR	163
Au NPs-NiO nanosheets/GCE	Cyclic voltammetry	0.0001–0.110 μM	0.05 nM	NR	164
CdO NPs – MWCNTs/GCE	Amperometry	0.01 nM–0.1 mM	4 pM	Seawater, industrial effluent, PVC-food packaging bag	165
Co@SnO2 – HRGO/GCE	Cyclic voltammetry	NR	NR	NR	166
Poly(CoOBImPc) – rGO/GCE	Amperometry	100–900 nM	33 nM	Drinking and river water	167
Au NPs/graphite pencil electrode	Amperometry	0.01 to 100 μM	0.002 μM	Drinking and sea water	168
NiCo2S4 nanospheres/GCE	Amperometry	1.7 μM to 7.8 mM	0.6 μM	Drinking water	169
ZnO-NPs/PEDOT–PSS	Amperometry	10–500 μM	5 μM	Drinking and sea water	50
MnO2/GCE	Amperometry	0.007–10 mM	129 nM	Drinking water	170
CuS-OMC/GCE	Amperometry	0.25–40 μM	0.1 μM	Drinking and reverse osmosis water	171
AuNPs-rGO/Ni foam	Amperometry	0.2–200 μM	0.056 μM	Drinking water	170
Au–Pd NPs – rGO/GCE	Amperometry	0.1–200 μM	16 nM	River and lake water	172
Ru–Co NPs/GCE	Cyclic voltammetry	0.0025–9.55 mM	0.00025 mM	Drinking water	173
CeO2 NPs – NB/GC	Differential pulse voltammetry	0.001–3.22 mM	57 nM	Drinking water and industrial effluent	174
Rhodium acetamidate/CPE	Cyclic voltammetry	0.1 μM–0.1 mM	5 μM	NR	175
Zn-MOF – rGO/Au electrode	Amperometry	0.001–100 μM	8.75 nM	Drinking water	176
Au/Nd–Gd-titania nanotubes-Pd/Au electrode	Cyclic voltammetry	0.01–10 μM	0.15 μM	Irrigation water	177
Pt NPs/nanoporous gold electrode	Amperometry	5–6105 μM	1.03 μM	River and lake water	178
Ti3C2Tx – ZIF-8/GCE	Amperometry	10–7700 μM	5.1 μM	NR	179
SrTiO3 NPs – PANI/GCE	Amperometry	16–58 μM	0.95 μM	Drinking water	180
EFTA – [hmim][PF6] – CoS2-CNT/CPE	Differential pulse voltammetry	0.03 to 500 μM	0.015 μM	Drinking and river water	181
Ag@SO-gCN/FTO	Cyclic voltammetry	8–110 μM	0.143 μM	NR	182
HM-Al^3+-(2D-MoS2)/SPGEs	Amperometry	3.81–400 μM	1.05 μM	Drinking and river water	51

---

As can be seen from Table 1, a diverse range of metal and metal oxide in the form of nanoparticles, spheres, rods, cubes and more, are used for the electroanalytical sensing of hydrazine. The most common is the use of nanoparticles to modify an underlying supporting electrode, such as carbon electrodes, which allows electrical “wiring” of the nanoparticles. From an electroanalytical point of view, the electrochemical response of hydrazine at a bare glassy carbon electrode is reported to exhibit slow electrode kinetics with a voltammetric signal that occurs at high overpotentials with a relatively small electroanalytical signal. When the electrode is modified with the chosen nanoparticles, the electrochemical oxidation of hydrazine signal occurs at lower overpotentials compared to that seen at the bare electrode and with a larger electroanalytical signal.^24,25 The reason for the improvements is based around arguments on the nanoparticles increased surface area, improved electrode kinetics, changed electronic structure and adsorption behaviour.²⁶ Using such an approach provides advantages over that, of say, carbon based materials but economics need to be considered; generally, such a response is routinely reported to be “electrocatalytic”.

Annalakshmi et al.²⁷ reported the sensing of hydrazine using trimetallic NiFeCo nanospheres supported upon a glassy carbon electrode, where the nanospheres were synthesized through a one-pot, facile hydrothermal methodology; see Fig. 2. The nanosphere modified electrode was reported to be an excellent electrocatalyst, where the bare glassy carbon electrode was reported to exhibit a high oxidation overpotential (+0.83 V), and no noticeable peak was observed compared to the nanosphere decorated glassy carbon electrode which exhibited a voltammetric signal at +0.56 V. The authors state that the modified electrode gives rise to an improved response, which might arise from its low impedance behaviour, nanospheres-like architecture and synergic effect among the metallic nanoparticles.²⁷ The electroanalytical sensor was able to detect hydrazine over a large concentration range (0.020–3080 μM) with a very low LOD of 6.4 nM. The practical applicability of the sensor was successfully validated in spiked river, lake, tap, and sewage water with satisfactory recoveries.²⁷ Generally, researchers overlook exploring a coverage study, that is, the effect of increasing the number of nanoparticles on the electrode surface against the electrochemical/electroanalytical response. One must not forget false electrocatalysis can result for thick porous layers of nanoparticles where the electrochemical response changes from that, at low monolayer coverage, of semi-infinite diffusion to that of thin layer diffusion for large coverages/porous layers.²⁸

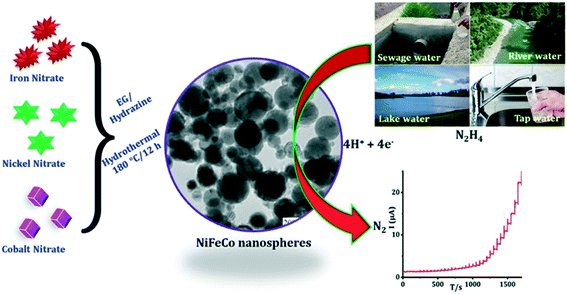Fig. 2 Schematic representation of trimetallic NiFeCo nanospheres synthesized through a one-pot, facile hydrothermal method. The practical applicability of the proposed novel HY sensor was successfully evaluated in real water samples with satisfactory recoveries. Figure reproduced with permission from ref. 27. Copyright 2019 Elsevier.

If we consider that the case of nanoparticle modified electrodes have been extensively developed to sense hydrazine, let's again ask why would you adopt this strategy? The answer lies in not only the physical and chemical properties of nanoparticles differing greatly from that of the bulk material, but also the geometric configuration of the constructed electrochemical platform. If we consider an isolated hemispherical nanoparticle for a simple electrode reaction (e.g.: A + ne⁻ ⇆ B), a diffusion-limited current (at suitably slow scan rates) is given by: I_lim = 2πnFDr[A]_bulk, where n is the number of electrons transferred, r is the radius of the nanoparticle, [A]_bulk is the bulk concentration of A, D is the diffusion coefficient of molecule A, and F is the Faraday constant. It is interesting to compare the limiting current for a spherical nanoparticle on an electrode surface which is described as: I_lim = 8.71nFDr[A]_bulk. Note that that the difference between these equations is due to a ‘shielding effect’, produced as a result of the underling supporting electrode that reduces the limiting current.²⁹ The above cases are for diffusion-limited cases, in essence when the voltammetric experiment is conducted at suitably slow scan-rates. When the scan rate of the voltammetric experiment is increased, the voltammetry deviates from that of the expected steady-state to that of a peak-shaped response.³⁰ However, in reality it is very rare for electroanalysts to conduct electroanalytical measurements on a single nanoparticle. In most, if not all cases, electroanalysts will decorate a chosen electrode surface with nanoparticles; for example, see Table 1 for the various endeavours using a diverse range of nanoparticle compositions.

The voltammetry at nanoparticle-modified electrodes has been elegantly reported by Compton et al.,³⁰ where the mass transport is different compared to that of a bulk electrode. In electroanalytical experiments, the modification of an electrode surface with nanoparticles results in a random array, that is, an assembly of nanoparticles randomly distributed over the supporting electrode surface. Fig. 3 shows simulations for a single reversible electron transfer process at a spherical nanoparticle array on an inert surface. Fig. 3 shows that four distinct categories arise, dependent upon the applied experimental voltage scan rates, which is represented in a dimensionless form: 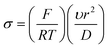, where T is the temperature and R is the universal gas constant. As the voltammetric scan rate changes, so does the diffusion layer.^28,30

Fig. 3 A: Simulated concentration profiles at a diffusion domain containing a spherical particle. Category 1: σ = 1000. Category 2: σ = 10. Category 3: σ = 1. Category 4: σ = 0.01. For all categories R₀ = 2. Concentration profiles were taken at the linear sweep's peak potential. B: Simulated linear sweep voltammetry of a reversible electron transfer at a spherical particle modified electrode. Scan rate σ = 0.01, θ varies from 10⁻⁴ to 0.1. Figures reproduced with permission from ref. 30. Copyright 2007 American Chemical Society.

In the case of category 1, the diffusion layers are small, corresponding to fast voltammetric scan rates, and the nanoparticles are diffusionally independent. Mass transport in this regime is linear and the cyclic voltammetric profile is the classic peak shape and the peak current (I_p) is governed by the Randles–Ševčík equation, i.e.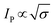, while the chronoamperometric response is governed by the Cottrell equation, i.e.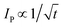. In the case of category 2 (see Fig. 3), the voltammetric scan rate is slowed and the diffusion layers become larger where diffusional independence is still observed. In this category, diffusion is hemispherical (or convergent) and the resultant cyclic voltammetric responses are steady-state shaped (rather than peak shaped). In category 3, the scan rate is further slowed, and we see that the diffusional layers are no longer independent, but rather overlap. In this case, the cyclic voltammetric response is peak shaped but the absolute current is smaller than theoretically expected. Last, category 4, the diffusion layers heavily overlap, and mass transport is linear over the entire nanoparticle array. The observed voltammetric response is the same as that observed in category 1. Note that the reason for the nanoparticle size dependence of the peak potential is that this reflects a switch over between rate-determining electrode kinetics, which control the current before the peak potential, to rate determining mass transport (diffusion) after the peak potential.

Next, if the voltammetric scan rate is fixed, what is the effect of changing the surface coverage? As shown in Fig. 3B, linear sweep voltammograms are shown for a fixed scan rate where the y axis is presented in terms of the dimensionless current per particle: j = i/NDrF[A], where N is the number of spherical particles present on the surface. The x-axis is presented in terms of a dimensionless potential, θ = F/RT(E − E⁰_f). In Fig. 3B, the effect of the surface coverage, Θ upon the voltammetric response is shown from 0.1–10⁻⁴, where Θ = Nr²/A and A is the area of the supporting electrode. Fig. 3B elegantly shows that at low nanoparticle coverage (Θ = 10⁻⁴), the diffusion zones at each nanoparticle are diffusionally independent and a steady-state response is observed, falling within category 1 or 2. As the nanoparticle coverage is increased, the distance between each nanoparticle decreases and passes through category 3 finally arriving at category 4; the change in the voltammetric wave shape is easily visualised (Fig. 3). An important observation is the dimensionless current decreases since the region of the solution available to each nanoparticle is reduced.³⁰ The above demonstrates that the voltammetric shape of a nanoparticle array will depend upon the scan rate and surface coverage of the nanoparticles.³⁰

One interesting aspect most pertinent to electroanalysts is that when in category 4, where heavy diffusional overlap occurs at a nanoparticle random array, the current response (the electroanalytical response) is similar to that obtained if one had used a complete electrode (e.g. a film or a solid electrode) of the same material. This unique property is extremely useful in electroanalysis as in the category 4 region, a nanoparticle array yields a similar amount of electrolytic depletion to a macroelectrode of the same total area. Consequently, minimal amounts of expensive catalyst, such as platinum or gold, can be used to offer a maximal electrochemical response over that of a solid electrode comprised of platinum or gold with significant cost savings. This critical issue is generally overlooked/not reported when nanoparticle modified electrodes are utilised, particularly to the sensing of hydrazine.

To this end, Batchelor-McAuley and co-workers³¹ have explored the random distribution of palladium nanoparticles supported on a boron-doped diamond (BDD) electrode with that of a palladium plated BDD microelectrode array comprising 362 palladium 25 μm diameter microdisks. In comparison of the two electrodes, the palladium nanoparticle decorated BDD electrode exhibits low micro-molar detection and a highly linear response toward hydrazine (see Table 1). The authors suggest that it is likely that the palladium nanoparticles are also acting as an array of microelectrodes with AFM images of the modified electrode revealing nanoparticles that are close together which effectively makes them act as single, larger particles.³¹ One important aspect, is that both the array and the nanoparticle assemble provide lower detection limits and highly linear responses compared to that of palladium macroelectrodes. The beneficial cost implications of using palladium nano- or micro-particles in sensors compared to a palladium macroelectrode are evident and gives a substantial reason to pursue nanoparticle-decorated electrodes.

Rather than directly modify an electrode surface, as new 2D nanomaterials have appeared with reported beneficial properties, such as large surface areas and improved conductivity, these have been utilised to support various nanoparticle compositions.²⁶ For example, palladium nanoparticles have been synthesized upon reduced graphene oxide (PdNPs – rGO) using an in situ polyol method; see Fig. 4.³² Palladium(II) ions and graphene oxide are reduced together with the reducing agent ethylene glycol and the size of the PdNPs can be readily controlled by varying the concentration of metal salt precursor from 3.7 nm up to 10.8 nm (diameter). Using rotating disk voltammetry, the PdNPs – rGO were modified upon a glassy carbon electrode and studied toward the detection of hydrazine where the smallest Pd nanoparticle size (3.7 nm) gave rise to the highest electroanalytical sensitivity and lowest limit of detection.³² This is attributed by the authors to be due to a higher electrochemical active surface area-to-volume ratio as well as to quantum confinement, for which the valence band centre of the PdNPs was shifted ca. +0.2 eV vs. Pd bulk leading to faster charge transfer.³² Using the 3.7 nm diameter PdNPs – rGO, a very low limit of detection of about 7 nM (at a rotation speed of 6000 rpm) was shown to be possible with a wide linear range of 0.04–200 μM. The sensor was shown to be highly selective to hydrazine without interference from uric acid, glucose, ammonia, caffeine, methylamine, ethylenediamine, hydroxylamine, n-butylamine, adenosine, cytosine, guanine, thymine, and L-arginine. The PdNPs – rGO based hydrazine sensor was shown to successfully determine hydrazine in spiked wastewater samples. Another approach has utilised reduced graphene oxide which is modified with cobalt oxide nanocubes@gold (rGO-Co₃O₄@Au) nanocomposites,³³ fabricated using a one-pot hydrothermal synthesis (Fig. 5A). Using amperometry, the detection of hydrazine was shown to be viable over the range of 10–620 μM with a LOD of 0.44 μM. The effect of interferents were explored (NO₃⁻, SO₄²⁻, Cl⁻, Ag⁺, Na⁺, K⁺, ethanol, 4-nitrophenol, ascorbic acid and glucose) which showed no detrimental effect upon the sensor. The sensing of hydrazine in spiked sea, lake and river water was shown to be viable. Following a similar approach, a gold tetra phenyl porphyrin (AuTPP) modified reduced graphene oxide nanocomposite film modified glassy carbon electrode (GCE) was fabricated and explored towards hydrazine sensing (see Fig. 5B). Initially graphene oxide (GO) was prepared from graphite by a modified Hummer's method, which was then mixed with the Au-TPP and drop cast upon a GCE surface and electrochemically reduced to prepare the final AuTPP – rGO/GCE sensor. Using amperometry, a linear 20 nM to 198 μM was shown to be possible with a very low LOD of 3 nM. The sensor was found to selectively detect hydrazine in the presence of 500 fold excess concentrations of a range of interfering ions and was shown to be viable for hydrazine sensing in spiked ground, rain and river water samples.³⁴

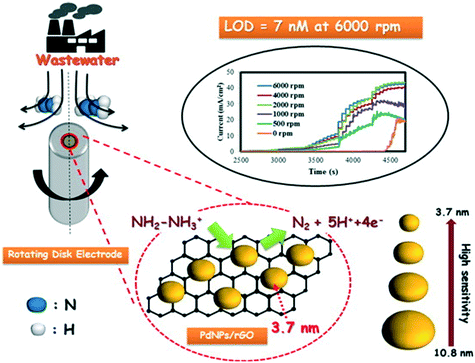Fig. 4 Palladium nanoparticles upon reduced graphene oxide (PdNPs/rGO) composites, synthesized using an in situ polyol method. Palladium(II) ions and graphene oxide are reduced together with a reducing agent, ethylene glycol. The size of the PdNPs can be controlled, which gives rise to improvements in the sensing of hydrazine via rotating disc electrochemistry. The approach is shown to be successful for determining hydrazine in wastewater samples. Figure reproduced with permission from ref. 32. Copyright 2014 American Chemical Society.

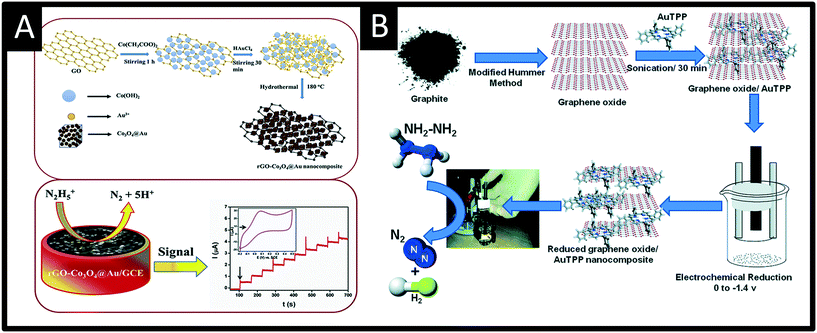Fig. 5 A: Summary of the synthesis of reduced graphene oxide-cobalt oxide nanocube@gold (rGO-Co₃O₄@Au) nanocomposite prepared using a one-pot hydrothermal synthesis. The nanocomposite is drop casted upon a glassy carbon electrode and successfully used to measure hydrazine via amperometry. B: Schematic representation for the preparation of reduced graphene oxide – gold tetra phenyl porphyrin nanocomposite glassy carbon modified electrode for hydrazine sensing. Figures reproduced from ref. 33 and 34. Copyright 2018 Elsevier and 2016 Royal Society of Chemistry.

Zhang et al. utilised Au nanoparticles N-doped porous carbon anchored upon reduced graphene oxide nanosheets, supported upon a GCE which was fabricated via a confinement synthetic process in the frame structure of zeolitic imidazolate framework-67 (ZIF-67).³⁵ The authors explored the role of the N-doped porous carbon and found that its incorporation provided a framework to immobilize Au nanoparticles. This prevents shifting and agglomeration, improving the wettability of rGO and therefore, avoiding irreversible restacking due to π–π interactions of rGO layers, which can reduce the performances of rGO-based support.³⁵Fig. 6 shows a schematic illustration of the sensing mechanism (note the GCE is absent) which was explored toward sensing hydrazine in both aqueous and gaseous environments. In the aqueous solutions a linear detection from 0.05 to 1.00 μM was shown to be viable with an LOD of 9.6 nM, with the authors validating the sensor towards the sensing of hydrazine in spiked drinking, river and lake water. Notably, the authors explored the electrochemical platforms as the basis of a practical electrochemical gas sensor, which exhibited a LOD of 1.8 ppm with fast response/recovery. Those advantages of the electrochemical sensors based on AuNPs@NPC–rGO can be attributed to the key design element of sensing material with structural and compositional advantages leading to the synergy of AuNPs, NPC and rGO.³⁵

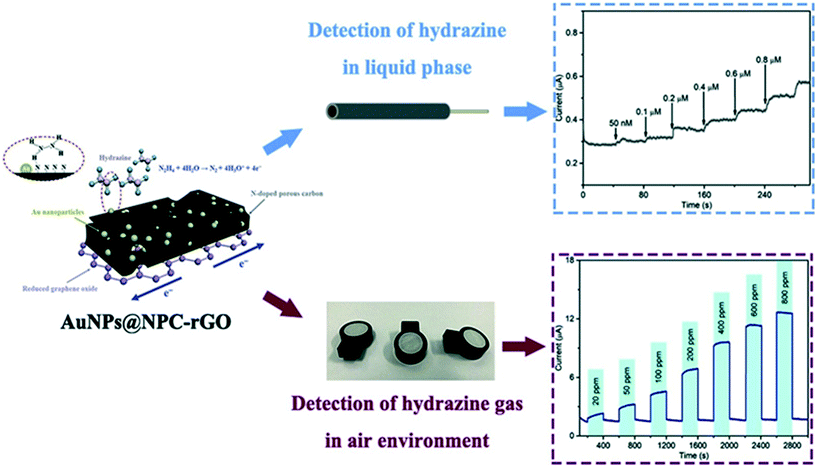Fig. 6 Schematic illustration of the sensing mechanism for Au nanoparticles-embedded N-doped porous carbon anchored on reduced graphene oxide (AuNPs@NPC-rGO) nanosheets, constructed by a confinement preparation process in the frame structure of zeolitic imidazolate framework-67 (ZIF-67). The sensor has been successfully demonstrated to sense hydrazine in both aqueous and gaseous environments. Figure reproduced with permission from ref. 35. Copyright 2019 Elsevier.

In the majority of cases where modifiers are utilised, they generally use a solid electrode with the electrode of choice seemingly being a GCE. Another tacit is to utilise screen-printed graphite/carbon electrodes (SPEs), which offer numerous advantages such as low cost, flexibility of their design, high reproducibility and the ability to manufacture them with different designs and materials, while performing as a low cost electrode.^36,37 For example, as we noted above, one of the first electroanalytical studies for the sensing of hydrazine utilised palladium nanoparticle modified SPEs, where the palladium was formed via electrodeposition.²³ This has been extended to where palladium microdomain have been formed on SPEs, and via linear sweep voltammetry a linear detection range of 8–72 μM is possible with an LOD of 3.7 μM.³⁸ Other variations include palladium nanoparticles on electroactivated graphite nanosheet modified SPEs,³⁹ single-walled carbon nanotube (SWCNT) bulk modified SPEs,⁴⁰ nitrogen-doped graphene-polyvinylpyrrolidone gold nanoparticle modified SPEs,⁴¹ curcumin-stabilized silver nanoparticle-coated reduced graphene oxide magnetic spinel (FeCo₂O₄) nanosheets supported upon SPEs,⁴² copper oxide nanoparticles/carbon nanotube modified SPEs⁴³ and polydimethyldiallylamine stabilized copper(II) hexacyanoferrate nanocube modified SPEs.⁴⁴ Metters et al. reported the first complete palladium screen-printed macroelectrodes⁴⁵ which exhibited linear ranges from 200–600 μM and 600–1000 μM with a LOD of 4 μM possible in model aqueous solutions. This approach for hydrazine sensing has been extended to platinum SPEs, where a linear range and LOD was reported to be 50–500 μM and 0.12 μM respectively.⁴⁶ In these instances, they are different from that of solid/bulk electrodes, as the metal on the surface of the SPEs is only microns thick (∼10 μm) and have obvious cost savings, but also allow mass-produced and highly reproducible electrodes to be fabricated, providing an avenue to bridge the gap between the laboratory and the field. The use of SPEs have been extended to cobalt(II) phthalocyanine – SPEs, (CoPc–SPEs), with the CoPc in the bulk of the SPEs demonstrating ultra-flexible sensors, which successfully measured hydrazine after extensive contortion giving rise to a LOD of 6.2 μM.⁴⁷ Another approach utilising CoPc–SPEs⁴⁸ is the concept of back-to-back electroanalytical sensors,^47–49 where both sides of a plastic substrate are screen-printed upon. This utilises the usually redundant back of the screen-printed sensor, converting this “dead-space” into a further electrochemical sensor which results in improvements in the analytical performance.

Other recent advances following a similar theme are reported by Beduk and co-workers⁵⁰ who have developed a fully inkjet-printed hydrazine sensor (Fig. 7A) which is comprised of a poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS) electrode functionalized with zinc oxide nanoparticles and encapsulated in a Nafion matrix. Using amperometry, the authors were able to show the inkjet-printed sensor was able to measure hydrazine over the range of 10 to 500 μM with a LOD of 5 μM and was successfully applied to measure hydrazine in spiked drinking and sea water samples. The ability to use inkjet printed electrochemical architectures provides another useful avenue to allow the mass production of cheap yet reproducible electroanalytical sensors. Other exciting work is by Villa-Manso et al.⁵¹ who have developed screen-printed graphene electrodes (Fig. 7B), which are modified with 2D-MoS₂ and a AI³⁺ hematein (HM) complex which facilitates the electrocatalytic determination of hydrazine. The electrochemical mechanism is shown in Fig. 7B, which proceeds via an EC_cat mechanism with a catalytic rate constant (k_cat) found to be 8.1 (±0.1) × 10⁴ M⁻¹ s⁻¹, confirming the AI³⁺ hematein complex has a high electrocatalytic activity. The sensor was shown to successfully determine hydrazine in spiked drinking and river water with good recoveries (96 and 90% respectively). Screen-printing and inkjet printing appear to be useful fabrication approaches for producing next generation disposable sensors that have scales of economy, allowing low-cost hydrazine sensors to be realised; future work should be directed to this endeavour.

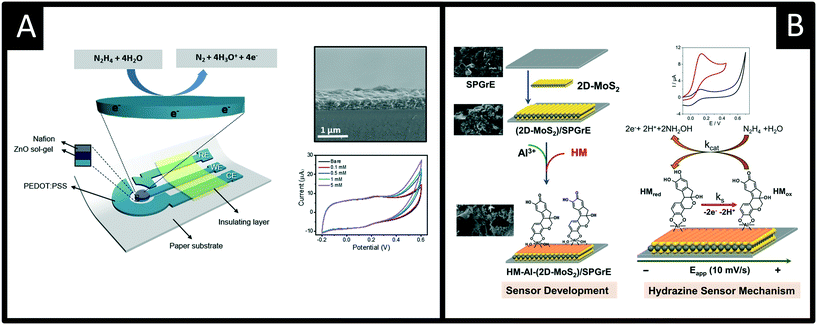Fig. 7 A: Schematic of the sensor comprising the working, reference and counter electrodes consisting of printed PEDOT:PSS, insulator, ZnO sol–gel and Nafion layers. Also shown is an SEM cross-section of the electrode surface and cyclic voltammetric responses using the ZnO-NPs/PEDOT–PSS in the presence of 0 (bare), 0,1, 0.5, 1, 5 mM of hydrazine in 0.1 M PBS (pH 7.4). B: A screen-printed graphene electrode modified with 2D-MoS₂ and a AI³⁺ hematein (HM) complex, which provides an electrocatalytic determination of hydrazine. Figures reproduced with permission from ref. 50 and 51. Copyright 2020 Elsevier and 2021 Elsevier.

Conclusions and outlook

We have overviewed the electroanalytical sensors that have been reported for the sensing of hydrazine. A large majority of electroanalytical sensors utilise metallic nanoparticles and other surface modifications, where the advantage of such is generally not explicitly stated. The use of nanoparticle modified electrodes allow the same electrochemical response as that of macroelectrode comprised of the same macro bulk electrode to be realised and have clear cost advantages. It is observed that coverage studies, exploring the amount/number of nanoparticles (coverage), are not routinely studied to optimise the electroanalytical sensor but also ensure that thin-layer effects are not giving rise to false observations of electrocatalysis. There is also scope to further explore the underlying supporting electrode, with screen-printed and inkjet-printed based sensors having clear advantages that can be further utilised. While there are a substantial number of academic papers reporting the determination of hydrazine sensing for aqueous based measurements, the majority, if not all, are still within the laboratory and there is not currently an electrochemical based hydrazine sensor commercially available; this is where screen-printed and inkjet-printed based sensor are the most suitable for hydrazine sensing, most likely with metallic modifications utilising the benefits of the nanoscale. We note that the majority, if not all electrochemical based hydrazine sensors are explored to aqueous samples, such as drinking, river and industrial effluent waters. Only a very limited number of papers explore gaseous environments and even fewer biological samples, such as its quantitative detection in blood/serum/urine for accurate occupational exposure monitoring; this is clearly another area for future development. Last, while electroanalytical hydrazine sensors are explored to a range of potential interferents and spiked water samples, independent validation with other well-established measurement techniques is lacking, which is likely hindering the uptake into a commercial product.

Conflicts of interest

The authors confirm there are no conflicts to declare.

References

1. U. EPA, https://www.epa.gov/sites/default/files/2016-09/documents/hydrazine.pdf.
2. P. Ortega-Barrales, A. Molina-Díaz, M. I. Pascual-Reguera and L. F. Capitán-Vallvey, Anal. Chim. Acta, 1997, 353, 115–122.
3. N. P. G. t. C. Hazards, DEPARTMENT OF HEALTH AND HUMAN SERVICES Centers for Disease Control and Prevention National Institute for Occupational Safety and Health, September, 2007.
4. U. S. E. P. Agency, Integrated Risk Information System (IRIS) on Hydrazine/Hydrazine Sulfate, National Center for Environmental Assessment, Office of Research and Development, Washington, DC, 1999.
5. S. Zelnick, D. Mattie and P. Stepaniak, Aviat., Space Environ. Med., 2003, 74, 1285.
6. D. o. H. a. H. S. National Toxicology Program, https://ntp.niehs.nih.gov/ntp/roc/content/profiles/hydrazine.pdf.
7. J.-A. Oh, J.-H. Park and H.-S. Shin, Anal. Chim. Acta, 2013, 769, 79–83.
8. J.-A. Oh and H.-S. Shin, J. Chromatogr. A, 2015, 1395, 73–78.
9. G.-C. Gil, Y.-G. Kim and B.-G. Kim, Anal. Biochem., 2008, 379, 45–59.
10. K. Wang, X. He, X. Yang and H. Shi, Acc. Chem. Res., 2013, 46, 1367–1376.
11. X.-Y. Zhang, Y.-S. Yang, W. Wang, Q.-C. Jiao and H.-L. Zhu, Coord. Chem. Rev., 2020, 417, 213367.
12. X. Gu and J. P. Camden, Anal. Chem., 2015, 87, 6460–6464.
13. G. E. Collins, S. Latturner and S. L. Rose-Pehrsson, Talanta, 1995, 42, 543–551.
14. S. Vivarelli, Ann. Chim., 1951, 41, 415.
15. S. Karp and L. Meites, J. Am. Chem. Soc., 1962, 84, 906–912.
16. A. J. Bard, Anal. Chem., 1963, 35, 1602–1607.
17. M. Michlmayr and D. T. Sawyer, J. Electroanal. Chem. Interfacial Electrochem., 1969, 23, 375–385.
18. B. Wang and X. Cao, Electroanalysis, 1992, 4, 719–724.
19. R. Miao and R. G. Compton, J. Phys. Chem. Lett., 2021, 12, 1601–1605.
20. R. Miao, L. Chen and R. G. Compton, Sci. China: Chem., 2021, 64, 322–329.
21. K. M. Korfhage, K. Ravichandran and R. P. Baldwin, Anal. Chem., 1984, 56, 1514–1517.
22. J. Liu, W. Zhou, T. You, F. Li, E. Wang and S. Dong, Anal. Chem., 1996, 68, 3350–3353.
23. J. Wang, M. P. Chatrathi, B. Tian and R. Polsky, Electroanalysis, 2000, 12, 691–694.
24. Ç. C. Koçak, A. Altın, B. Aslışen and S. Koçak, Int. J. Electrochem. Sci., 2016, 11, 233–249.
25. G. Maduraiveeran and R. Ramaraj, J. Anal. Sci. Technol., 2017, 8, 14.
26. R. D. Crapnell and C. E. Banks, Microchim. Acta, 2021, 188, 1–23.
27. M. Annalakshmi, P. Balasubramanian, S.-M. Chen and T.-W. Chen, Sens. Actuators, B, 2019, 296, 126620.
28. R. G. Compton and C. E. Banks, Understanding Voltammetry, World Scientific, 3rd edn, 2018.
29. S. R. Belding, F. W. Campbell, E. J. F. Dickinson and R. G. Compton, Phys. Chem. Chem. Phys., 2010, 12, 11208–11221.
30. I. Streeter, R. Baron and R. G. Compton, J. Phys. Chem. C, 2007, 111, 17008–17014.
31. C. Batchelor-McAuley, C. E. Banks, A. O. Simm, T. G. J. Jones and R. G. Compton, Analyst, 2006, 131, 106–110.
32. A. Krittayavathananon, P. Srimuk, S. Luanwuthi and M. Sawangphruk, Anal. Chem., 2014, 86, 12272–12278.
33. M. M. Shahid, P. Rameshkumar, W. J. Basirunc, U. Wijayantha, W. S. Chiu, P. S. Khiew and N. M. Huang, Electrochim. Acta, 2018, 259, 606–616.
34. S. Sakthinathan, S. Kubendhiran, S.-M. Chen and P. Tamizhdurai, RSC Adv., 2016, 6, 56375–56383.
35. Y. Zhang, Y. Zhang, D. Zhang, S. Li, C. Jiang and Y. Su, Sens. Actuators, B, 2019, 285, 607–616.
36. C. E. Banks, C. W. Foster and R. O. Kadara, Screen-Printing Electrochemical Architectures, Springer, 2016.
37. A. G.-M. Ferrari, S. J. Rowley-Neale and C. E. Banks, Talanta Open, 2021, 100032.
38. N. A. Choudhry, M. Khairy, R. O. Kadara, N. Jenkinson and C. E. Banks, Electroanalysis, 2010, 22, 1831–1836.
39. C. Karuppiah, M. Velmurugan, S.-M. Chen, R. Devasenathipathy, R. Karthik and S.-F. Wang, Electroanalysis, 2016, 28, 808–816.
40. J. P. Metters, M. Gomez-Mingot, J. Iniesta, R. O. Kadara and C. E. Banks, Sens. Actuators, B, 2013, 177, 1043–1052.
41. C. Saengsookwaow, R. Rangkupan, O. Chailapakul and N. Rodthongkum, Sens. Actuators, B, 2016, 227, 524–532.
42. A. Mejri, A. Mars, H. Elfil and A. H. Hamzaoui, Microchim. Acta, 2019, 186, 561.
43. Neelam, G. Rani and M. Kumar, Sens. Transducers J., 2018, 223, 22–25.
44. S. Ramaraj, R. Sakthivel, S.-M. Chen, S. Palanisamy, V. Velusamy, T.-W. Chen, S. Ramaraj and K. Pandian, Int. J. Electrochem. Sci., 2017, 12, 5567–5582.
45. J. P. Metters, F. Tan and C. E. Banks, J. Solid State Electrochem., 2013, 17, 1553–1562.
46. J. P. Metters, F. Tan, R. O. Kadara and C. E. Banks, Anal. Methods, 2012, 4, 1272–1277.
47. C. W. Foster, J. P. Metters, D. K. Kampouris and C. E. Banks, Electroanalysis, 2014, 26, 262–274.
48. A. P. Ruas de Souza, M. Bertotti, C. W. Foster and C. E. Banks, Electroanalysis, 2015, 27, 2295–2301.
49. A. P. Ruas de Souza, C. W. Foster, A. V. Kolliopoulos, M. Bertotti and C. E. Banks, Analyst, 2015, 140, 4130–4136.
50. T. Beduk, E. Bihar, S. G. Surya, A. N. Castillo, S. Inal and K. N. Salama, Sens. Actuators, B, 2020, 306, 127539.
51. A. M. Villa-Manso, M. Revenga-Parra, M. Vera-Hidalgo, M. Vázquez Sulleiro, E. M. Pérez, E. Lorenzo and F. Pariente, Sens. Actuators, B, 2021, 345, 130385.
52. S. M. Golabi and H. R. Zare, J. Electroanal. Chem., 1999, 465, 168–176.
53. J.-W. Mo, B. Ogorevc, X. Zhang and B. Pihlar, Electroanalysis, 2000, 12, 48–54.
54. K. I. Ozoemena and T. Nyokong, Talanta, 2005, 67, 162–168.
55. A. A. Ensafi and E. Mirmomtaz, J. Electroanal. Chem., 2005, 583, 176–183.
56. A. Abbaspour and M. A. Kamyabi, J. Electroanal. Chem., 2005, 576, 73–83.
57. R. Baron, B. Šljukić, C. Salter, A. Crossley and R. G. Compton, Electroanalysis, 2007, 19, 1062–1068.
58. B. Fang, C. Zhang, W. Zhang and G. Wang, Electrochim. Acta, 2009, 55, 178–182.
59. H. Zhang, J. Huang, H. Hou and T. You, Electroanalysis, 2009, 21, 1869–1874.
60. L. Zheng and J.-F. Song, Sens. Actuators, B, 2009, 135, 650–655.
61. Q. Yi and W. Yu, J. Electroanal. Chem., 2009, 633, 159–164.
62. C. Zhang, G. Wang, Y. Ji, M. Liu, Y. Feng, Z. Zhang and B. Fang, Sens. Actuators, B, 2010, 150, 247–253.
63. M. Mazloum-Ardakani, H. Rajabi, B. B. F. Mirjalili, H. Beitollahi and A. Akbari, J. Solid State Electrochem., 2010, 14, 2285–2292.
64. S. Ivanov, U. Lange, V. Tsakova and V. M. Mirsky, Sens. Actuators, B, 2010, 150, 271–278.
65. N. A. Choudhry, R. O. Kadara, N. Jenkinson and C. E. Banks, Electrochem. Commun., 2010, 12, 406–409.
66. Q. Yi, F. Niu and W. Yu, Thin Solid Films, 2011, 519, 3155–3161.
67. U. P. Azad and V. Ganesan, Electrochim. Acta, 2011, 56, 5766–5770.
68. Y. Ding, Y. Wang, L. Zhang, H. Zhang, C. M. Li and Y. Lei, Nanoscale, 2011, 3, 1149–1157.
69. W. Zhang, K. Huo, Y. Jiang, L. Hu, R. Chen and P. K. Chu, Microchim. Acta, 2011, 175, 137.
70. J. Zhao, M. Zhu, M. Zheng, Y. Tang, Y. Chen and T. Lu, Electrochim. Acta, 2011, 56, 4930–4936.
71. Z. Yin, L. Liu and Z. Yang, J. Solid State Electrochem., 2011, 15, 821–827.
72. N. A. Choudhry and C. E. Banks, Analyst, 2011, 136, 1153–1156.
73. M. Mazloum-Ardakani, Z. Taleat, H. Beitollahi and H. Naeimi, Nanoscale, 2011, 3, 1683–1689.
74. P. Paulraj, N. Janaki, S. Sandhya and K. Pandian, Colloids Surf., A, 2011, 377, 28–34.
75. Y. Liang, Y. Zhou, J. Ma, J. Zhao, Y. Chen, Y. Tang and T. Lu, Appl. Catal., B, 2011, 103, 388–396.
76. J. Li, H. Xie and L. Chen, Sens. Actuators, B, 2011, 153, 239–245.
77. V. Lyutov and V. Tsakova, J. Electroanal. Chem., 2011, 661, 186–191.
78. Y. Ding, C. Hou, B. Li and Y. Lei, Electroanalysis, 2011, 23, 1245–1251.
79. K. N. Han, C. A. Li, M.-P. N. Bui, X.-H. Pham and G. H. Seong, Chem. Commun., 2011, 47, 938–940.
80. J. Panchompoo, L. Aldous, C. Downing, A. Crossley and R. G. Compton, Electroanalysis, 2011, 23, 1568–1578.
81. B. Fang, Y. Feng, M. Liu, G. Wang, X. Zhang and M. Wang, Microchim. Acta, 2011, 175, 145.
82. X. Li, Z. Chen, Y. Zhong, F. Yang, J. Pan and Y. Liang, Anal. Chim. Acta, 2012, 710, 118–124.
83. L. Shang, F. Zhao and B. Zeng, Electroanalysis, 2012, 24, 2380–2386.
84. F. Liao, Z. Wang, T. Guo, T. Zhang and Z. Wu, J. Electroanal. Chem., 2012, 673, 38–42.
85. M. Mazloum-Ardakani, H. Rajabi and H. Beitollahi, Chin. Chem. Lett., 2012, 23, 213–216.
86. J. Lei, X. Lu, W. Wang, X. Bian, Y. Xue, C. Wang and L. Li, RSC Adv., 2012, 2, 2541–2544.
87. S. Ameen, M. S. Akhtar and H. S. Shin, Sens. Actuators, B, 2012, 173, 177–183.
88. S. Ameen, M. Shaheer Akhtar and H. S. Shin, Talanta, 2012, 100, 377–383.
89. Y.-Y. Tang, C.-L. Kao and P.-Y. Chen, Anal. Chim. Acta, 2012, 711, 32–39.
90. M. U. Anu Prathap, V. Anuraj, B. Satpati and R. Srivastava, J. Hazard. Mater., 2013, 262, 766–774.
91. Y. Wang, X. Yang, J. Bai, X. Jiang and G. Fan, Biosens. Bioelectron., 2013, 43, 180–185.
92. H. Ahmar, S. Keshipour, H. Hosseini, A. R. Fakhari, A. Shaabani and A. Bagheri, J. Electroanal. Chem., 2013, 690, 96–103.
93. V. V. Kondratiev, T. A. Babkova and E. G. Tolstopjatova, J. Solid State Electrochem., 2013, 17, 1621–1630.
94. C. Tan, X. Xu, F. Wang, Z. Li, J. Liu and J. Ji, Sci. China: Chem., 2013, 56, 911–916.
95. M. Abdul Aziz and A.-N. Kawde, Talanta, 2013, 115, 214–221.
96. Y.-C. Chou, C.-Y. Tai, J.-F. Lee, T.-S. Chan and J.-M. Zen, Electrochim. Acta, 2013, 104, 104–109.
97. R. B. Channon, J. C. Newland, A. W. T. Bristow, A. D. Ray and J. V. Macpherson, Electroanalysis, 2013, 25, 2613–2619.
98. S. Shukla, S. Chaudhary, A. Umar, G. R. Chaudhary and S. K. Mehta, Sens. Actuators, B, 2014, 196, 231–237.
99. R. Devasenathipathy, V. Mani, S.-M. Chen, D. Arulraj and V. S. Vasantha, Electrochim. Acta, 2014, 135, 260–269.
100. S. E. Baghbamidi, H. Beitollahi and S. Tajik, Anal. Bioanal. Electrochem., 2014, 6, 91–105.
101. P. K. Rastogi, V. Ganesan and S. Krishnamoorthi, Electrochim. Acta, 2014, 125, 593–600.
102. K. Ghanbari, Synth. Met., 2014, 195, 234–240.
103. S. Koçak and B. Aslışen, Sens. Actuators, B, 2014, 196, 610–618.
104. C. W. Foster, J. Pillay, J. P. Metters and C. E. Banks, Sens. Actuators, B, 2014, 14, 21905–21922.
105. C. Karuppiah, S. Palanisamy, S.-M. Chen, S. K. Ramaraj and P. Periakaruppan, Electrochim. Acta, 2014, 139, 157–164.
106. M. Shamsipur, Z. Karimi, M. A. Tabrizi and A. Shamsipur, Electroanalysis, 2014, 26, 1994–2001.
107. A. Maringa and T. Nyokong, Electroanalysis, 2014, 26, 1068–1077.
108. A. R. Fakhari, H. Ahmar, H. Hosseini and S. Kazemi Movahed, Sens. Actuators, B, 2015, 213, 82–91.
109. S. P. Kim, S. G. Lee, M. Y. Choi and H. C. Choi, J. Nanomater., 2015, 2015, 120485.
110. H. Mahmoudi Moghaddam, H. Beitollahi, S. Tajik, I. Sheikhshoaie and P. Biparva, Environ. Monit. Assess., 2015, 187, 407.
111. J. Zhang, H. Liu, M. Dou, F. Wang, J. Liu, Z. Li and J. Ji, Electroanalysis, 2015, 27, 1188–1194.
112. M. Ongaro, M. Signoretto, V. Trevisan, A. M. Stortini and P. Ugo, Chemosensors, 2015, 3, 146–156.
113. R. Sivasubramanian and M. V. Sangaranarayanan, Sens. Actuators, B, 2015, 213, 92–101.
114. R. Ojani, V. Rahemi and J.-B. Raoof, J. Chin. Chem. Soc., 2015, 62, 90–96.
115. A. Samadi-Maybodi, S. Ghasemi and H. Ghaffari-Rad, Sens. Actuators, B, 2015, 220, 627–633.
116. S. Dutta, C. Ray, S. Mallick, S. Sarkar, A. Roy and T. Pal, RSC Adv., 2015, 5, 51690–51700.
117. E. G. Tolstopjatova, V. V. Kondratiev and S. N. Eliseeva, J. Solid State Electrochem., 2015, 19, 2951–2959.
118. A. Ejaz, M. S. Ahmed and S. Jeon, Sens. Actuators, B, 2015, 221, 1256–1263.
119. Z. Zhao, Y. Sun, P. Li, W. Zhang, K. Lian, J. Hu and Y. Chen, Talanta, 2016, 158, 283–291.
120. H. Beitollahi, S. Tajik and S. Jahani, Electroanalysis, 2016, 28, 1093–1099.
121. J. Y. Lee, T. L. Nguyen, J. H. Park and B.-K. Kim, Sensors, 2016, 16, 647–657.
122. A. Benvidi, S. Jahanbani, B.-F. Mirjalili and R. Zare, Chin. J. Catal., 2016, 37, 549–560.
123. D. Rao, Q. Sheng and J. Zheng, Sens. Actuators, B, 2016, 236, 192–200.
124. I. Kang, W.-S. Shin, S. Manivannan, Y. Seo and K. Kim, J. Electrochem. Sci. Technol., 2016, 7, 277–285.
125. A. A. Ismail, F. A. Harraz, M. Faisal, A. M. El-Toni, A. Al-Hajry and M. S. Al-Assiri, Mater. Des., 2016, 109, 530–538.
126. J. Hu, Z. Zhao, Y. Sun, Y. Wang, P. Li, W. Zhang and K. Lian, Appl. Surf. Sci., 2016, 364, 434–441.
127. Y. Liu, Z. Qiu, Q. Wan, Z. Wang, K. Wu and N. Yang, Electroanalysis, 2016, 28, 126–132.
128. X. Gao, C. Du, C. Zhang and W. Chen, ChemElectroChem, 2016, 3, 1266–1272.
129. M. M. Rahman, J. Ahmed, A. M. Asiri, I. A. Siddiquey and M. A. Hasnat, RSC Adv., 2016, 6, 90470–90479.
130. F. Xu, Y. Liu, S. Xie and L. Wang, Anal. Methods, 2016, 8, 316–325.
131. H. Heydari, M. B. Gholivand and A. Abdolmaleki, Mater. Sci. Eng., C, 2016, 66, 16–24.
132. B. Kaur, R. Srivastava and B. Satpati, Catal. Sci. Technol., 2016, 6, 1134–1145.
133. F. Giroud, A. J. Gross, D. F. Junior, M. Holzinger, C. E. M. de Campos, J. J. S. Acuña, J. B. Domingos and S. Cosnier, J. Electrochem. Soc., 2016, 164, H3052–H3057.
134. K. J. Babu, A. Zahoor, K. S. Nahm, M. A. Aziz, P. Vengadesh and G. G. Kumar, New J. Chem., 2016, 40, 7711–7720.
135. J. Hu, Z. Zhao, J. Zhang, G. Li, P. Li, W. Zhang and K. Lian, Appl. Surf. Sci., 2017, 396, 523–529.
136. P. Bansal, G. Bhanjana, N. Prabhakar, J. S. Dhau and G. R. Chaudhary, J. Mol. Liq., 2017, 248, 651–657.
137. M. M. Rahman, V. G. Alfonso, F. Fabregat-Santiago, J. Bisquert, A. M. Asiri, A. A. Alshehri and H. A. Albar, Microchim. Acta, 2017, 184, 2123–2129.
138. S. Sakthinathan, S. Kubendhiran, S.-M. Chen, M. Govindasamy, F. M. A. Al-Hemaid, M. Ajmal Ali, P. Tamizhdurai and S. Sivasanker, Appl. Organomet. Chem., 2017, 31, e3703.
139. Y. J. Yang, X. Hu and Z. Xu, Fullerenes, Nanotubes, Carbon Nanostruct., 2017, 25, 435–441.
140. S. Rostami, S. Naser Azizi and S. Ghasemi, New J. Chem., 2017, 41, 13712–13723.
141. J. Zhao, P. Yue, S. Tricard, T. Pang, Y. Yang and J. Fang, Sens. Actuators, B, 2017, 251, 706–712.
142. S. Premlatha, P. Sivasakthi and G. N. K. Ramesh Bapu, J. Electroanal. Chem., 2017, 788, 107–117.
143. N. Salek Gilani, S. Naser AzizI and S. Ghasemi, Bull. Mater. Sci., 2017, 40, 177–185.
144. Z. Yang, X. Zheng and J. Zheng, Chem. Eng. J., 2017, 327, 431–440.
145. H. M. A. Amin, M. F. El-Kady, N. F. Atta and A. Galal, Electroanalysis, 2018, 30, 1757–1766.
146. N. Teymoori, J. B. Raoof, M. A. Khalilzadeh and R. Ojani, J. Iran. Chem. Soc., 2018, 15, 2271–2279.
147. A. Maleki, R. Rezaee, H. Daraei, B. Shahmoradi and N. Amini, J. Alloys Compd., 2018, 763, 997–1004.
148. Y. J. Yang and W. Li, Fullerenes, Nanotubes, Carbon Nanostruct., 2018, 26, 837–845.
149. P. Wuamprakhon, A. Krittayavathananon, N. Ma, N. Phattharasupakun, T. Maihom, J. Limtrakul and M. Sawangphruk, J. Electroanal. Chem., 2018, 808, 124–132.
150. F. Tahernejad-Javazmi, M. Shabani-Nooshabadi, H. Karimi-Maleh and H. Naeimi, Res. Chem. Intermed., 2018, 44, 5389–5401.
151. Y. He, X. Yang, Y. Huo, Q. Han and J. Zheng, Open Access Journal of Chemistry, 2018, 2, 15–22.
152. F. Amiripour, S. N. Azizi and S. Ghasemi, Biosens. Bioelectron., 2018, 107, 111–117.
153. M. Faisal, F. A. Harraz, A. E. Al-Salami, S. A. Al-Sayari, A. Al-Hajry and M. S. Al-Assiri, Mater. Chem. Phys., 2018, 214, 126–134.
154. M. Wang, L. Yang, B. Hu, Y. Liu, Y. Song, L. He, Z. Zhang and S. Fang, Appl. Surf. Sci., 2018, 445, 123–132.
155. H. Huang, T. Li, Y. Sun, L. Yu, C. Wang, R. Shen, W. Ye, D. Wang and Y. Li, Microchim. Acta, 2019, 186, 46–56.
156. X. Zhang and J. Zheng, Appl. Surf. Sci., 2019, 493, 1159–1166.
157. S. Ghasemi, S. R. Hosseini, F. Hasanpoor and S. Nabipour, Microchim. Acta, 2019, 186, 601.
158. D. M. Nguyen, L. G. Bach and Q. B. Bui, J. Pharm. Biomed. Anal., 2019, 172, 243–252.
159. Y. Gao, S. Zhang, W. Hou, H. Guo, Q. Li, D. Dong, S. Wu, S. Zhao and H. Zhang, Appl. Surf. Sci., 2019, 491, 267–275.
160. F. Asadi, S. N. Azizi and S. Ghasemi, J. Mater. Sci.: Mater. Electron., 2019, 30, 5410–5420.
161. A. Avanes, M. Hasanzadeh-Karamjavan and G. Shokri-Jarcheloo, Microchim. Acta, 2019, 186, 441.
162. X. Zhang and J. Zheng, Microchim. Acta, 2020, 187, 89.
163. R. Wahab, N. Ahmad, M. Alam and J. Ahmad, Vacuum, 2019, 165, 290–296.
164. R. Ahmad, T. Bedük, S. M. Majhi and K. N. Salama, Sens. Actuators, B, 2019, 286, 139–147.
165. M. M. Rahman, M. M. Alam and K. A. Alamry, J. Ind. Eng. Chem., 2019, 77, 309–316.
166. S. Ramanathan, E. Elanthamilan, A. Obadiah, A. Durairaj, P. SanthoshKumar, J. Princy Merlin, S. Ramasundaram and S. Vasanthkumar, J. Electron. Mater., 2019, 48, 542–550.
167. M. Nemakal, S. Aralekallu, I. Mohammed, S. Swamy and L. K. Sannegowda, J. Electroanal. Chem., 2019, 839, 238–246.
168. İ. Teoman, S. Karakaya and Y. Dilgin, Anal. Lett., 2019, 52, 2041–2056.
169. C. Duan, Y. Dong, Q. Sheng and J. Zheng, Talanta, 2019, 198, 23–29.
170. P. Wuamprakhon, A. Krittayavathananon, S. Kosasang, N. Ma, T. Maihom, J. Limtrakul, N. Chanlec, P. Kidkhunthod and M. Sawangphruk, Inorg. Chem., 2020, 59, 15595–15605.
171. G. Srinidhi, S. Sudalaimani, K. Giribabu, S. J. S. Basha and C. Suresh, Microchim. Acta, 2020, 187, 359.
172. H. Zhou, L. Chen, S. Li, S. Huang, Y. Sun, Y. Chen, Z. Wang, W. Liu and X. Li, J. Colloid Interface Sci., 2020, 566, 473–484.
173. A. L. Lavanya, K. G. Bala Kumari, K. R. S. Prasad and P. K. Brahman, Int. J. Environ. Anal. Chem., 2020, 1–16,  DOI:10.1080/03067319.2020.1726333.
174. N. S. K. Gowthaman, H. Ngee Lim, V. Balakumar and S. Shankar, Ultrason. Sonochem., 2020, 61, 104828–110438.
175. E. S. Gil and L. T. Kubota, J. Braz. Chem. Soc., 2000, 11, 304–310.
176. S. Rani, S. Kapoor, B. Sharma, S. Kumar, R. Malhotra and N. Dilbaghi, J. Alloys Compd., 2020, 816, 152509–152519.
177. K. M. Emran, S. M. Ali and H. E. Alanazi, J. Electroanal. Chem., 2020, 856, 113661–113669.
178. Y. Pei, M. Hu, Y. Xia, W. Huang, Z. Li and S. Chen, Sens. Actuators, B, 2020, 304, 127416–127424.
179. Y. Yao, X. Han, X. Yang, J. Zhao and C. Chai, Chin. J. Chem., 2021, 39, 330–336.
180. M. Faisal, M. A. Rashed, M. M. Abdullah, F. A. Harraz, M. Jalalah and M. S. Al-Assiri, J. Electroanal. Chem., 2020, 879, 114805–114818.
181. S. Tajik, H. Beitollahi, R. Hosseinzadeh, A. Aghaei Afshar, R. S. Varma, H. W. Jang and M. Shokouhimehr, ACS Omega, 2021, 6, 4641–4648.
182. A. Mohammad, M. E. Khan, M. R. Karim, M. H. Cho and T. Yoon, Ceram. Int., 2021, 47, 23578–23589.

---