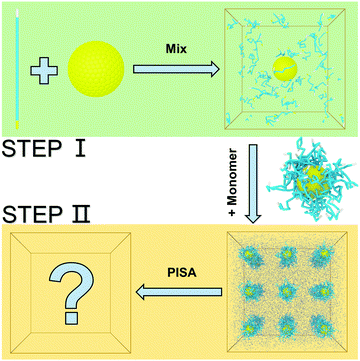
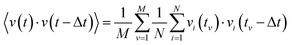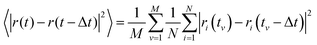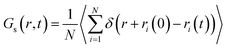Polymer pattern-induced self-assembly of inorganic nanoparticles†
Junfeng
Wang
 ,
Bojin
Zhu
,
Yining
Wang
,
Yujian
Hao
,
Jun
Zhang
and
Zhen
Li
,
Bojin
Zhu
,
Yining
Wang
,
Yujian
Hao
,
Jun
Zhang
and
Zhen
Li
 *
*
School of Materials Science and Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China
First published on 15th November 2021
Abstract
Functional assemblies of inorganic nanoparticles (NPs) are widely studied owing to their collective electromagnetic properties and various application from nanodrugs and bioimaging. In most cases, the superstructures of NPs are prepared with the assistance of templates or external fields. Therefore, how to prepare the functional assemblies of NPs more simply remains a challenge. Here, a free-template assembly strategy for preparing the superstructures of NPs is proposed in our work. In our strategy, we design poly(glycerol monomethacrylate)-b-poly(2-hydroxypropyl methacrylate) (PGMA-b-PHPMA) coated NPs. Then, using the polymerization-induced self-assembly (PISA), hydrophobic PHPMA blocks resulted in the phase separation to form the orderly patterns, which is expected to induced NPs to self-assemble into the orderly superstructures. By DPD simulations, we find that the disk, ring, composite superstructures can be obtained by regulating the graft density, verifying that our assembly strategy of NPs is feasible. Even more interesting is that NPs are also distributed in an orderly way on the surface of aggregations to form the orderly NP patterns. Besides that, the thermodynamics, dynamics, and structure details in the self-assembly process of HINPs are shown in our work, providing a new idea and elaborate physical picture for the following preparation of the superstructure of NPs.
1 Introduction
Functional assemblies of inorganic nanoparticles (NPs) have attracted a surge of attention for their collective electronic, optical, and magnetic characteristics, which are significantly different from those of the individual nanoparticles and bulk samples.1 These excellent properties mainly arise from the electromagnetic coupling of nanoparticles when the interparticle distances are smaller than five times their individual radius.2 In addition, assemblies of NPs can solve the contradiction of the required particle size to the strong absorption in near-infrared (NIR) and the desirable medical context of the human body.3 Through protracted and unremitting efforts, assemblies of NPs have been applied in energy capture, data storage, construction materials, bioimaging, and cancer therapy.4–9Many assembly strategies are developed to prepare the superstructures of NPs. In most strategies, the superstructures can always be obtained using templates. For example, the NPs ring structure can be obtained under the assistance of various templates, such as lithographic patterns,10 microspheres,11 droplets,12,13 and bubbles,14,15 during the solvent evaporation or liquid flow processes. Moreover, Reiko Oda et al. synthesized the nanometric helices by the Gemini surfactant, and then the silica helices were obtained by sol–gel condensation of the organic helices. Finally, the silica helices were loaded with gold nanoparticles.16 To the ferromagnetic nanoparticles, the induction of the magnetic field is also a viable option.17 In addition, surface modification of NPs with organic coatings (e.g., small molecules, biomolecules, or polymers) is another optional strategy,18–20 and the polymer coatings seemed to have more potential among these coatings because NPs grafted with polymers, called “hairy” inorganic nanoparticles (HINPs), can naturally combine the unique features of NPs and polymers.21–23 To HINPs, using the template-based strategy, HINPs can aggregate into the confined region of templates prepared by amphiphilic copolymers or inorganic materials.24 However, the template-based method always needs a more complex preparation process, which increases the difficulty of preparation. In order to further simplify the preparation process, the amphiphilic copolymers are grafted as organic coatings, and NPs directly self-assemble into superstructures by the induction of the phase separation of copolymers without templates. Besides that, the superstructures of NPs always determine the performance of the whole nanomaterials. For example, Chen et al. reported on the carbon nanotube ring (CNTR) coated with gold nanoparticles using polymer-grafted CNTR as the template, and the Raman and optical signals can be improved substantially compared to the straight carbon nanotube coated with gold nanoparticles.25 Nevertheless, to the direct self-assembly strategy of NPs, the aggregation mode of NPs is still not rich, and the linear structure and dispersion structure are reported in most experimental or theoretical work.26–29 Therefore, the non-template assembly of NPs into superstructures with desired complexity and functionality remains a challenge.
The work from the Kumacheva group gives us helpful inspiration. They reported that different polymer surface patterns were obtained by regulating the graft density of the polymer with the reduction in solvent quality,30 and they further induced Ag nanoparticles to self-assemble into patchy composite nanoparticles by using polymer surface patterns.31 According to the work from the Kumacheva group, our goal may be achieved by regulating the polymer surface patterns to induce NPs to assemble in an orderly way. There has been theoretical work to explore the microscopic mechanism of the evolution of the polymer surface patterns and try to design different patterns. For example, Lu et al. explored the evolution rules of the homopolymer and diblock copolymers surface patterns with different particle sizes and polymer lengths.32,33 Wang et al. studied the influence of the polymer chain length and graft density on the surface patterns.34 Vasilevskaya designed a polymer with an amphiphilic monomer and found a new flower-like pattern.35 However, it is still unclear whether the polymer surface patterns can be further used for the controlled self-assembly of NPs.
In order to verify the feasibility of our assumption, we designed an amphiphilic diblock copolymers-coated NP and explored the microscopic mechanism of self-assembly of NPs by the dissipative particle dynamics simulation (DPD). We chose the poly(glycerol monomethacrylate)-b-poly(2-hydroxypropyl methacrylate) (PGMA-b-PHPMA) as the polymer coatings of NPs. There are two reasons to choose this copolymer. Firstly, PGMA-b-PHPMA can self-assemble into various nanostructures in the aqueous solution, suitable for in vivo environments.36 Secondly, we developed a set of precise DPD parameters for the phase separation of PGMA-b-PHPMA in the aqueous solution.37 Moreover, we replaced the traditional copolymer self-assembly strategy, which is by the reduction in solvent quality, with the polymerization-induced self-assembly strategy (PISA). PISA is a recently developed copolymer self-assembly strategy, which is more efficient than the traditional strategy.38 Kumacheva et al. also demonstrated the feasibility of using the PISA strategy to prepare the copolymer-grafted NPs by the experimental study.31
In this work, we found that under the appropriate block ratio, disk, ring, and composite superstructures of NPs can be obtained just by regulating the graft density of copolymers. At the same time, NPs also distribute in an orderly way on the surface of NPs to form NPs patterns. Moreover, the microscopic details of the thermodynamics, kinetics, and structures shown in our work will provide an overall physical picture for the patterned self-assembly of NPs, including the assembly process, driving force, and diffusion. This article is organized as follows. The following section contains our assembly strategy and simulation results. The detailed analysis then reports the formation of polymer patterns and the patterned self-assembly of NPs. Finally, the theory and the simulation parameters are explained in the Methods section.
2 Results and discussion
2.1 Assembly strategy and simulation results
We constructed our HINPs by two steps in our simulation. As shown in Fig. 1, firstly, we put hydrophilic PGMA blocks and one NP in aqueous solution, and the cube simulation box size is 20rc (∼38.074 nm). PGMA chains were evenly distributed, and the nanoparticle was confined to the centre of the box. Then, PGMA chains freely diffused in the aqueous environment, and the end will be bonded with the nanoparticle's surface when the end of the PGMA chains is close to the nanoparticle at a certain distance. Secondly, the PGMA-grafted HINPs and HPMA monomers were evenly placed into a larger system, and the cube simulation box size is 60rc (∼114.222 nm). For the actual situation, the concentration of NPs should not be too high to prevent NPs agglomeration, and the concentration of NPs in our system was about 0.03 mM (27 NPs). Then, the PGMA chains initiate the polymerization of HPMA monomers by the reaction model method, as shown in S1.2 (ESI†), and the hydrophobicity of the PHPMA chains is gradually enhanced with the growth of PHPMA chains. Finally, the PHPMA blocks result in the phase separation to induce the self-assembly of NPs. In addition, the repulsive interaction parameters are used to reflect the solubility of PGMA, PHPMA and monomers, which are described in S2 (ESI†) in detail.In our work, we mainly explore the influences of the length of PGMA chains and the graft density on the self-assembly behaviour of HINPs. The NP size is kept at 4rc (∼7.6148 nm). The degree of polymerization is used to reflect the polymer length. We kept the final average length of the PHPMA chains at 16 in our simulation, and one polymer unit in our simulation is equal to 10 polymer units in the actual situation. We change the PGMA chain length from 4 to 16, and the graft density is increased from 0.5/rc2 (∼0.137/nm2) to 2/rc2 (∼0.549/nm2). The structures of the PGMA-grafted NPs with different graft densities and PGMA chain lengths are shown in Fig. 2(a). All of the systems are simulated for 2.2 × 105τ (∼10 μs). From Fig. 2(b), the orderly self-assembly morphologies can be obtained when the PGMA chain length is 4, and the morphology changes from linear to ellipsoid to sphere with increasing graft density. More interestingly, the NPs not only self-assemble into the orderly superstructure, but are also evenly distributed on the surface of the whole aggregation to form the NP pattern, as shown In Fig. 2(c). With increasing PGMA chain length, the long soft PGMA chain will disturb the orderly distribution of NPs. At the same time, the chaotic distribution of NPs makes the morphology of the whole aggregation disordered. According to our simulation results, the morphology of the whole aggregation and the superstructure of NPs can be regulated just by changing the graft density under the appropriate PGMA chain length, showing that our assumption is feasible.
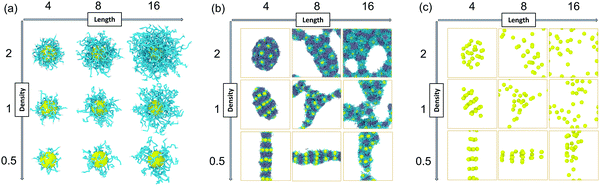 | ||
| Fig. 2 (a) The PGMA-grafted NPs, (b) The final self-assembly morphologies, (c) and the superstructures of NPs with different graft densities and pgma chain lengths. | ||
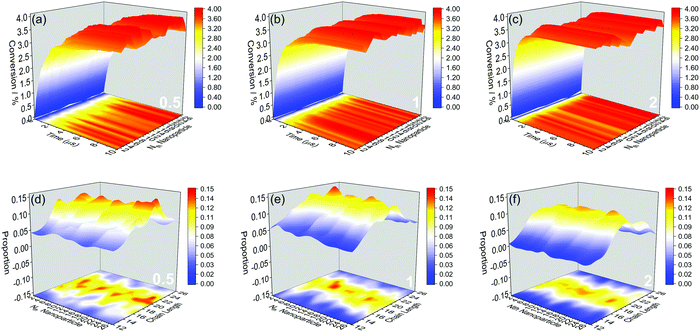
We further show more details of the three systems that HINPs can self-assemble into the orderly morphology. Firstly, the total polymerization kinetics and distribution of the polymer chain length are shown in Fig. 3(a). The conversion of the HPMA monomers is used to reflect the polymerization rate, and the polymerization rate decreases gradually versus time because of the decreasing concentration of monomers. At the same time, there are more active ends (see Information) of PGMA chains under the same contact area with increasing graft density. The possibility that the HPMA monomers get close to the active end of the PGMA chains is increased, and the possibility of the polymerization of the monomers increases accordingly. Therefore, the polymerization rate increases with increasing grafted density. Moreover, the graft density does not influence the distribution of the polymer chain length, as shown in Fig. 3(b).
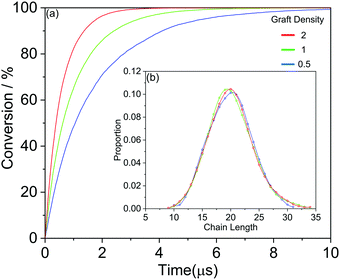 | ||
| Fig. 3 (a) The whole HPMA polymerization kinetics for the targeted PGMA4-b-PHPMA16 diblock copolymer. (b) The whole distribution of the polymer chain length. | ||
Then, the polymerization rate of every NP and the distribution of the polymer chain length on every NP were further studied. In Fig. 4(a–c), the change rule of the polymerization rate to every NP has the same trend, and the polymerization rate increases with increasing graft density, which is also with the whole change rule. According to the polymer chain length distribution shown in Fig. 4(d–f), the average chain length to every NP is similar, and it is also consistent with the whole average length. However, because the grafted polymers have more free volume under the low graft density, the spatial distribution of the active ends of PGMA chains has a more significant variance among NPs. Moreover, more free volume means less interference between the active ends. At the same time, the longer polymers have more contact area with monomers, which will lead to the further accumulation of length differences. These large distribution differences will also lead to the significant variance of the final consumption of monomers, as shown from the projection of Fig. 4(a–c). In turn, when the graft density increases, the competition among polymers will hinder the accumulation of length differences. Therefore, the polymer chain length distribution is more even, and there is also a minor variance among NPs with increasing graft density.
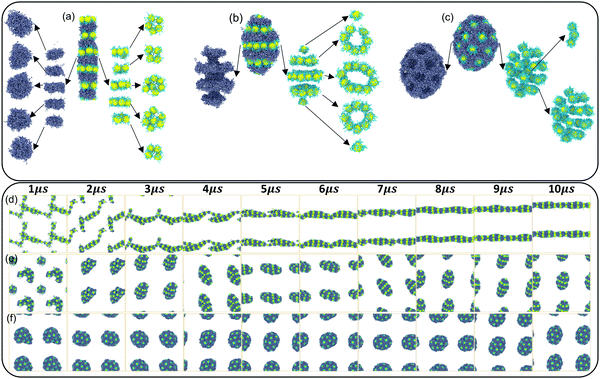
Finally, the details of the three orderly self-assembly morphologies and the whole self-assembly process of HINPs are described in detail. In Fig. 5(a), when the graft density is 0.5, HINPs can self-assemble into the linear morphology, and PHPMA blocks aggregate into the disk-like morphology. NPs also self-assembled into the disk superstructure, and they are nearly close-packed in their plane when the number of NPs to construct the disk superstructure is equal to 7. When the number is less than 7, the NPs will prioritize the disk superstructure. In addition, the PHPMA disk and the NPs disk are alternately distributed to form the multi-layer pattern. When the graft density increases to 1, HINPs can self-assemble into the ellipsoid morphology, and the PHPMA blocks aggregate with the ring grooves. The NPs are inlaid into these grooves and form the ring superstructure. These ring superstructures are symmetrically distributed, and the middle ring is larger than either side of the ring. There is one NP on each end of the aggregation, and all NPs form the pupa-like pattern. When the graft density is 2, HINPs can self-assemble into the sphere morphology, and PHPMA blocks aggregate into the porous aggregation. The NPs are inlaid into these cavities and evenly distributed on the surface to form the spots pattern. At the same time, a few NPs enter the aggregation to form the short rod superstructures. Fig. 5(d–f) shows the self-assembly process of HINPs with the graft density from 0.5 to 2, and all the morphologies remain stable after 8 μs, which shows that the simulation time is enough for the balance of self-assembly of HINPs.
Furthermore, the self-assembly processes with different grafted densities are explored. When the graft density is 0.5, HINPs firstly assemble into the short rod from the fusion of some small clusters, and the longer cross-linked morphology can be observed by the further fusion of the short rods. After the fusion, NPs continue to restructure further. Finally, the linear aggregation with the multi-layer NP pattern is formed. Self-assembly processes of HINPs when the graft density is 1 and 2 are similar to the self-assembly process of HINPs when the graft density is 0.5. Firstly, irregular aggregations are formed by the fusion of small clusters, and then whether aggregations or NPs transform into the orderly structures by the following restructuring. According to the above simulation results, the fusion and the restructuring are the main stages in the whole self-assembly of HINPs. The fusion stage is mainly responsible for the growth of NP aggregations, and the restructuring stage is mainly responsible for the formation of orderly superstructures of NPs. In addition, the whole balance time decreases with increasing graft density. Next, more details in the self-assembly process are explored from the surface patterning of polymers and the patterned self-assembly of NPs.
2.2 Surface patterning of PHPMA blocks
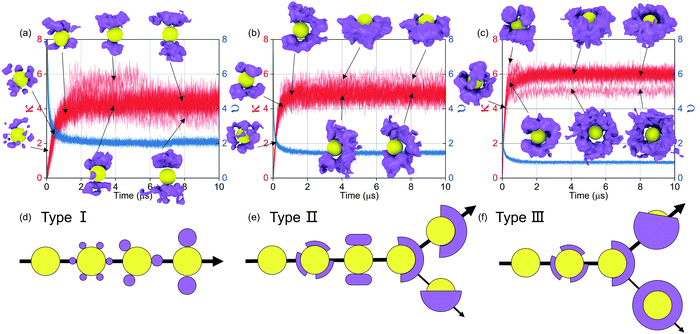
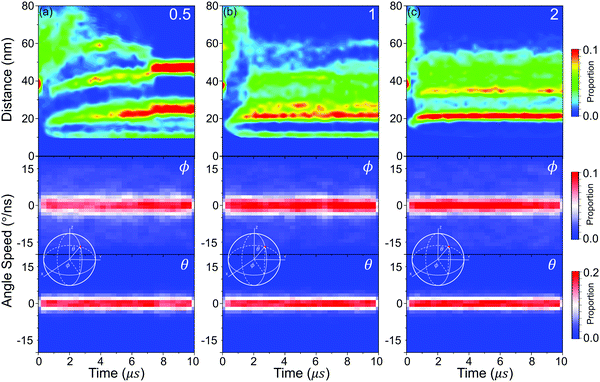
In order to confirm the surface patterning of PHPMA blocks, we define two indexes, which are κ and υ (see Method) to quantitatively describe the patterning of PHPMA blocks to every NP. κ is used for reflecting the evolution of PHPMA patterns. As shown in Fig. 6(a–c), the PHPMA patterns are constantly readjusted in the fusion time and become stable before the restructuring of NPs, showing that different PHPMA patterns will influence the distribution of NPs in the restructuring stage, and finally regulate the orderly superstructure of NPs. In addition, the formation time of the PHPMA patterns increases with the graft density, and the evolution way of the PHPMA pattern is different under different graft densities. When the graft density is 0.5, the PHPMA blocks firstly aggregate into some small clusters that are not evenly distributed around the NP. During the polymerization, the number of clusters gradually decreases with the fusion of small clusters, and the patchy pattern is finally formed. Moreover, the κ of a few NPs is larger than the average value at 2 μs–4 μs. These NPs are at the end of the linear aggregations, and their PHPMA clusters are tighter because more hydrophobic PHPMA blocks are exposed in the aqueous evironment. By the further fusion, the periodic linear aggregation is formed and the NP ends disappeared. At the same time, the large κ also disappeared. Moreover, the κ of a few NPs is slightly smaller than the average value after the balance. These NPs are inside the assembly, and their PHPMA clusters are looser because the PHPMA chains are away from the aqueous solutions. When the graft density is 1, the PHPMA blocks firstly form the patchy pattern from the random pattern, and the patchy pattern finally transforms into the semicircular pattern. Besides that, the κ of some NPs is also slightly larger than the average value. These NPs are at the end of the ellipsoid assembly, and their PHPMA blocks form the hemispheric pattern. When the graft density is 2, the PHPMA blocks firstly form the semicircular pattern from the random patterns, and then the pattern transforms into the hemispheric pattern. At the same time, the κ of a few NPs is slightly larger than the average value at around 1 μs. The PHPMA pattern of these NPs is a mixture between the semicircular pattern and the hemispheric pattern, and it will rapidly transform into the hemispheric pattern. In addition, the κ of a few NPs is significantly smaller than the average value. These NPs are inside the aggregation, and their PHPMA blocks form the circular pattern. υ is used for reflecting the uniformity of distribution of PHPMA blocks around the NP. The smaller υ is, the more even the distribution of PHPMA blocks will be. From Fig. 6(a–c), υ and its fluctuation decrease with increasing the graft density, showing that the pattern transforms from anisotropy to isotropy, which also induces the NPs from the directed distribution to the even distribution.2.3 Patterned self-assembly of NPs
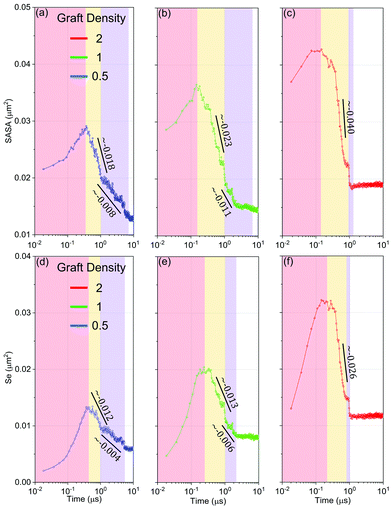
Firstly, we understand the whole evolution of self-assembly of HINPs from the driving force. On the one hand, the solvent accessible surface area (SASA) reflects the entropy driving force. Because the small molecular solvent is the majority of the whole system, they are the major contributor to entropy. The larger free space of the solvent molecules will increase the entropy and decrease the free energy of the whole system.39 SASA is the surface area of aggregations that is accessible to a solvent bead. Decreasing SASA can increase the free space of solvent to increase the whole entropy of the system, and then decrease the whole free energy. On the other hand, the exposed area of hydrophobic PHPMA blocks (Se) reflects the enthalpy driving force. Too much contact between PHPMA blocks and the aqueous solution will increase the whole hydrophobic interaction energy, and increase the system's internal energy accordingly.As shown in Fig. 7, the whole self-assembly process is subdivided into four stages. The first stage is the accumulation stage (red region). The PHPMA blocks do not immediately result in the phase separation until the SASA and Se accumulate to a certain degree. When the driving force is enough, the self-assembly process enters the second stage (yellow region), the fusion stage. In the fusion stage, the SASA and Se begin to linearly decrease as log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t, and at the same time, HINPs begin to spontaneously fuse. Although the accumulation time slightly decreases with increasing graft density, the initial value and the polymerization rate observably increase with the graft density. Therefore, the peak value of the SASA and Se increases with the graft density, leading to a larger driving force so that the descent speed of the SASA and Se increases with the graft density. Moreover, the reduction of the SASA is earlier than the reduction of the Se regardless of the graft density, showing that NPs getting close to each other in the early fusion stage is driven by entropy. After around 1 μs, the primary fusion is finished, as shown in Fig. 5(e). At the same time, the descent speed of the SASA and Se is also decreased, and the self-assembly process enters the third stage (blue region), the restructuring stage. The pattern of PHPMA blocks needs time to form, and the formation time of the pattern is similar to the fusion time when the graft density is 0.5 and 1. Therefore, there is the independent fusion and restructuring stage. However, when the graft density is increased to 2, the strong driving force improves the restructuring speed of HINPs so that the restructuring will be finished after the fusion stage, as shown in Fig. S4 (ESI†). Therefore, there is almost no additional restructuring stage in the self-assembly process. In addition, the Se converges faster than the SASA in the restructuring stage or has a few distinct plateaus in the restructuring stage, showing that entropy is the main driving force to the restructuring of NPs.
t, and at the same time, HINPs begin to spontaneously fuse. Although the accumulation time slightly decreases with increasing graft density, the initial value and the polymerization rate observably increase with the graft density. Therefore, the peak value of the SASA and Se increases with the graft density, leading to a larger driving force so that the descent speed of the SASA and Se increases with the graft density. Moreover, the reduction of the SASA is earlier than the reduction of the Se regardless of the graft density, showing that NPs getting close to each other in the early fusion stage is driven by entropy. After around 1 μs, the primary fusion is finished, as shown in Fig. 5(e). At the same time, the descent speed of the SASA and Se is also decreased, and the self-assembly process enters the third stage (blue region), the restructuring stage. The pattern of PHPMA blocks needs time to form, and the formation time of the pattern is similar to the fusion time when the graft density is 0.5 and 1. Therefore, there is the independent fusion and restructuring stage. However, when the graft density is increased to 2, the strong driving force improves the restructuring speed of HINPs so that the restructuring will be finished after the fusion stage, as shown in Fig. S4 (ESI†). Therefore, there is almost no additional restructuring stage in the self-assembly process. In addition, the Se converges faster than the SASA in the restructuring stage or has a few distinct plateaus in the restructuring stage, showing that entropy is the main driving force to the restructuring of NPs.
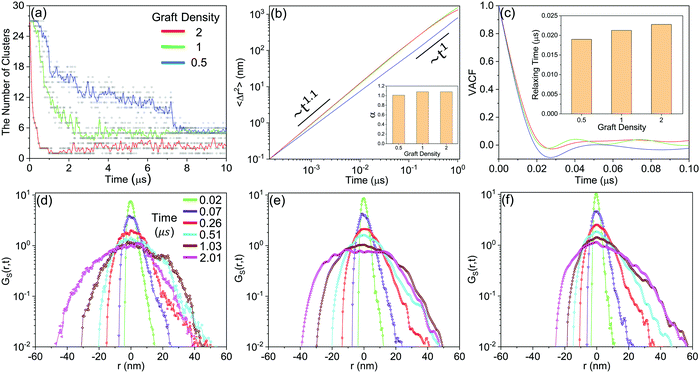
As shown in Fig. 8(a–c), the details of the patterned self-assembly process of NPs are further discussed. On the one hand, the early stage of the self-assembly process is the same regardless of the graft density. The dimer and trimer are formed in sequence, and the following NP clusters are constructed by fusing these basic units. On the other hand, the NP clusters tend to grow by leaps and bounds with the larger graft density. Moreover, all the NPs clusters, regardless of the graft density, need further restructuring after the fusion, showing that the restructuring of NPs is the key to induce the orderly superstructure of NPs. More details of the restructuring of NPs are shown in Fig. S4 (ESI†).
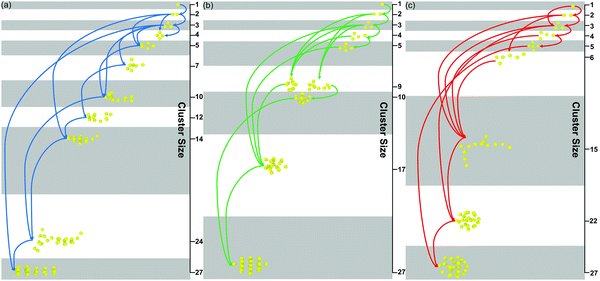 | ||
| Fig. 8 The self-assembly process of the nanoparticles with different graft densities (a) 0.5, (b) 1, (c) 2. | ||
Then, the details of the dynamics of NPs in the self-assembly process are quantitatively analysed. Fig. 9 shows the relative displacements between NPs and the rotation of NPs. To the relative motion of NPs, NPs tend to move far away from each other in the early stage because of the diffusion of NPs, and then NPs begin to get close when the driving force is accumulated to a certain degree, as shown in Fig. 7. Because the driving force increases with increasing graft density according to the above analysis, the cases that NPs are far away disappeared more rapidly with increasing graft density. Moreover, the distribution of the centre distances between the NPs reaches a balance before the restructuring stage. It is also shown that the restructuring of NPs is collectively motion related to all the NPs, rather than the local structural fine-tuning. To the rotation of NPs, we define two azimuthal angles: the angle ϕ with the X-axis (−180°–180°) and the angle θ with the Z-axis (0°–180°). From Fig. 9, almost all NPs rotate between the equilibrium positions with the angle speed of ±5°. There are also a few larger rotations with the largest angle speed of ±15°. Thus, the rotation of NPs is not influenced by aggregation during self-assembly. Moreover, when the graft density is 0.5, there is a larger fluctuation to the rotation of NPs. This is because there is less resistance from the PHPMA blocks.
Fig. 10(a) shows that the aggregation rate of NPs increases with increasing graft density, even in the accumulation stage of the self-assembly process. By the velocity autocorrelation functions (VACF) (see Method), we explore the first collision relaxing time of NPs,40 which is the intercept when the VACF line intersects the X-axis for the first time. More graft polymers provide more resistance during the collision of NPs. Therefore, the relaxing time increases with increasing graft density, as shown in Fig. 10(c), which is favourable for the aggregation of NPs. At the same time, we further explored the details of the diffusion dynamics of NPs. As shown in Fig. 10(b), we fit the mean-square displacement (MSD) (see Method) to the time tα, obtaining the diffusion parameter, α. The diffusion of NPs when the graft density is 0.5 enters the Fickian regime with α = 1. However, the diffusion of NPs shows the superdiffusive behaviour when the graft density is 1 and 2, where the diffusion exponent α > 1.41,42 The typical characteristic of the superdiffusive behaviour is an anomalous long–range drift of particles,43 which is also confirmed from the van Hove correlation function (Gs(r, t)) (see Method). In Fig. 10(d–f), a more obvious bias in moving probability can be observed by increasing the graft density. On the one hand, from Fig. 7, a stronger driving force provides the larger impulse to improve the large displacement of NPs in the fusion stage. On the other hand, the larger SASA and Se after the fusion stage increases the strength and the possibility of collisions between the PHPMA blocks and the water molecules.
3 Method
3.1 DPD simulations
The dissipative particle dynamic (DPD) is a coarse-grained simulation method to study the complex hydrodynamic behaviour in the larger system, which was proposed by Hoogerbrugge and Koelman in 1992.44 All of the DPD coarse-grained beads are restricted by Newton's equation of motion: mi·dνi/dt = fi, where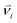 and mi are the velocity and the mass of the bead ith, respectively. The non-bonded interaction between each pair of particles includes the conservative force FC, the random force FR, and the dissipative force FD. So, the pairwise non-bonded interaction force, Fi, between the ith bead and the jth bead, is the summation of three forces:
and mi are the velocity and the mass of the bead ith, respectively. The non-bonded interaction between each pair of particles includes the conservative force FC, the random force FR, and the dissipative force FD. So, the pairwise non-bonded interaction force, Fi, between the ith bead and the jth bead, is the summation of three forces: 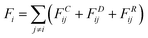 . Three non-bonded interaction forces FC, FR, and FD are FCij = αijω(rij)rij, FDij = −γω2(rij)(rij·νij)rij and FRij = σω(rij)θijrij, where αij is the repulsion interaction parameter between each two beads, and can be estimated by the Flory-Huggins parameter χij with such equation: αij = αii + 3.5χij, where χij represents the solubility between two kinds of DPD beads. The interaction parameters are shown in ESI.†γ is the friction coefficient, and σ is the noise amplitude. γ and σ can be unified by one formula: σ2 = 2γkBT. ω(rij) is the weight function, which is given by Groot and Warren.45θij is a randomly fluctuating variable with zero mean and unit variance. The bonded interaction force between each pair of bonded beads is regarded as a harmonic spring force: FBij = KB(1 − rij/rs)rij, where KB is set to be 50 to prevent the copolymer model elongating excessively. The unified time τ can be formulated by
. Three non-bonded interaction forces FC, FR, and FD are FCij = αijω(rij)rij, FDij = −γω2(rij)(rij·νij)rij and FRij = σω(rij)θijrij, where αij is the repulsion interaction parameter between each two beads, and can be estimated by the Flory-Huggins parameter χij with such equation: αij = αii + 3.5χij, where χij represents the solubility between two kinds of DPD beads. The interaction parameters are shown in ESI.†γ is the friction coefficient, and σ is the noise amplitude. γ and σ can be unified by one formula: σ2 = 2γkBT. ω(rij) is the weight function, which is given by Groot and Warren.45θij is a randomly fluctuating variable with zero mean and unit variance. The bonded interaction force between each pair of bonded beads is regarded as a harmonic spring force: FBij = KB(1 − rij/rs)rij, where KB is set to be 50 to prevent the copolymer model elongating excessively. The unified time τ can be formulated by 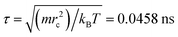 . The friction coefficient γ is set to be 4.5, and the noise amplitude σ is set to be 3. The numerical density of beads is 3, and the time step is 0.04τ. The growth of the PHPMA chain is achieved by the reaction model (ESI†). The simulations were performed by a coarse-grained molecular dynamics program based on LAMMPS, and the morphologies was observed by VMD and OVITO.46–48
. The friction coefficient γ is set to be 4.5, and the noise amplitude σ is set to be 3. The numerical density of beads is 3, and the time step is 0.04τ. The growth of the PHPMA chain is achieved by the reaction model (ESI†). The simulations were performed by a coarse-grained molecular dynamics program based on LAMMPS, and the morphologies was observed by VMD and OVITO.46–48
3.2 Index κ & υ
We use the index κ as a dynamically evolving graph of the PHPMA blocks, in which all the PHPMA blocks compose the vertices V = {ν1, ν2⋯νn} and the edges E = {e1,2, e1,3⋯en−1,n} are assigned between pairs of vertices ν1 and ν2, if dE < rcut = 1.0. The index κ(t) is equal to κ(t) = 2*|E(t)|/|V(t)|. ν is used to reflect the uniform distribution of the PHPMA blocks. We divided the space around the particles into 360 regions on average, and the number of the PHPMA beads in every region Ni(t)is calculated. The index ν(t) is equal to ν(t) = (Ni(t) − Ni(t))2/Ni(t).3.3 Velocity autocorrelation function (VACF)
The VACF for a given time difference Δt is obtained by averaging the product of the velocity of each particle at time t and the velocity of the same particle at the time t − Δt:3.4 Mean-square displacement (MSD)
The MSD for a given time difference Δt is obtained by averaging the square of the distance between each particle at time t and the same particle at the time t − Δt:3.5 Van Hove correlation function
The Van Hove function is the probability density of finding a particle i in the vicinity of r at time t, knowing that a particle j is in the vicinity of the origin at time t = 0.4 Conclusions
In this article, a free-template strategy is proposed to prepare the superstructures of NPs and further prove the feasibility by the DPD simulation, thereby providing a new idea for the subsequent experimental preparation. First, we design diblock copolymer-coated (PGMA-b-PHPMA) NPs, called “hairy” inorganic nanoparticles (HINPs). Hydrophobic PHPMA blocks can then result in the phase separation and form the orderly patterns by PISA strategy. Then, we demonstrate that under an appreciated length of PGMA blocks, different PHPMA patterns can be regulated by the graft density and induce NPs to self-assemble into the disk, ring, and composite superstructures. What is more interesting is that the distribution of superstructures of NPs is also orderly to form various NP patterns. Finally, the microscopic mechanism of self-assembly of HINPs is further explored, which is outlined below.Firstly, according to the whole self-assembly process, we find that the fusion and restructuring stages are the main stages in the self-assembly process. Generally speaking, the growth of aggregations occurs mainly in the fusion stage, and the formation of superstructures of NPs occurs mainly in the fusion stage.
Then, with increasing graft density, the PHPMA pattern is transformed from the patchy pattern to a semicircular pattern to the hemispheric pattern, and the balance time of the PHPMA patterns decreases with increasing graft density. In addition, PHPMA blocks readjust the configuration in the fusion stage, keep the stable pattern in the restructuring stage, and then influence the distribution of NPs to regulate the superstructures of NPs.
Finally, the thermodynamics, dynamics, and structure details in the self-assembly process of HINPs are further shown. We first understand the self-assembly of HINPs from the driving force, and the solvent accessible surface area (SASA) and exposed area of hydrophobic PHPMA blocks (Se) are used to reflect the entropy and enthalpy driving force. According to the SASA and Se evolution, the self-assembly process is subdivided into four stages: the accumulation stage, the fusion stage, the restructuring stage, and the balance stage. The enthalpy and entropy driving forces are increased in the accumulation stage, and the entropy driving force is the main driving force to induce NPs to get close in the early fusion stage. In addition, the peak value and the descent speed of the SASA and Se increase with the graft density. In the restructuring stage, the entropy driving force is the key driving force to the restructuring of NPs. When the graft density is 2, the strong driving force results in the fusion and restructuring being finished simultaneously. Therefore, there is almost no additional restructuring stage. Next, the structural evolution of the NPs aggregations is shown. The initial stage of self-assembly of NPs is all the same to all three graft densities. The dimer and trimer are firstly formed in order, and the following aggregations are all formed by the fusion of these assembly units. Moreover, the restructuring of NPs is an overall movement to all the NPs rather than the local structural rearrangement. The details of the dynamics of NPs are finally explored. The stronger driving force and the longer collision relaxing time improve the faster aggregation with increasing graft density during the whole self-assembly process. At the same time, the strong driving force makes NPs have superdiffusive behaviour when the graft density is 1 or 2 compared with the Fickian diffusion when the graft density is 0.5.
Author contributions
Junfeng Wang: Software, methodology, investigation, writing – original draft. Bojin Zhu: validation, writing – review & editing. Yining Wang: visualization, data curation. Yujian Hao: formal analysis. Jun Zhang: conceptualization, funding acquisition, supervision. Zhen Li: resources, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
National Key R&D Program of China (2018YFA0702400); National Natural Science Foundation of China (12004438); Shandong Provincial Natural Science Foundation, China (ZR2019MB023); the Fundamental Research Funds for the Central Universities (YCX2019071, 19CX05001A).Notes and references
- Z. Nie, A. Petukhova and E. Kumacheva, Nat. Nanotechnol., 2010, 5, 15–25 CrossRef CAS PubMed.
- H. E. Toma, V. M. Zamarion, S. H. Toma and K. Araki, J. Braz. Chem. Soc., 2010, 21, 1158–1176 CrossRef CAS.
- K. J. Bishop, Angew. Chem., Int. Ed., 2016, 55, 1598–1600 CrossRef CAS PubMed.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS PubMed.
- P. Huang, J. Lin, W. Li, P. Rong, Z. Wang, S. Wang, X. Wang, X. Sun, M. Aronova and G. Niu, Angew. Chem., 2013, 125, 14208–14214 CrossRef.
- J. Lin, S. Wang, P. Huang, Z. Wang, S. Chen, G. Niu, W. Li, J. He, D. Cui and G. Lu, ACS Nano, 2013, 7, 5320–5329 CrossRef CAS PubMed.
- C. Yi, S. Zhang, K. T. Webb and Z. Nie, Acc. Chem. Res., 2017, 50, 12–21 CrossRef CAS PubMed.
- D. Hou, W. Zhang, M. Sun, P. Wang, M. Wang, J. Zhang and Z. Li, Cem. Concr. Res., 2020, 136, 106166 CrossRef CAS.
- M. Wang, K. Zhang, X. Ji, P. Wang, H. Ma, J. Zhang and D. Hou, Constr. Build. Mater., 2021, 316, 125800–125812 CrossRef.
- Y. Yin, Y. Lu, B. Gates and Y. Xia, J. Am. Chem. Soc., 2001, 123, 8718–8729 CrossRef CAS PubMed.
- J. Chen, W.-S. Liao, X. Chen, T. Yang, S. E. Wark, D. H. Son, J. D. Batteas and P. S. Cremer, ACS Nano, 2009, 3, 173–180 CrossRef CAS PubMed.
- W.-S. Chang, L. S. Slaughter, B. P. Khanal, P. Manna, E. R. Zubarev and S. Link, Nano Lett., 2009, 9, 1152–1157 CrossRef CAS PubMed.
- L. Zhang, H.-Y. Si and H.-L. Zhang, J. Mater. Chem., 2008, 18, 2660–2665 RSC.
- S. Darwich, K. Mougin, L. Vidal, E. Gnecco and H. Haidara, Nanoscale, 2011, 3, 1211–1217 RSC.
- S. Fujii, K. Kanaizuka, S. Toyabe, K. Kobayashi, E. Muneyuki and M.-A. Haga, Langmuir, 2011, 27, 8605–8610 CrossRef CAS PubMed.
- J. Cheng, G. Le Saux, J. Gao, T. Buffeteau, Y. Battie, P. Barois, V. Ponsinet, M.-H. Delville, O. Ersen and E. Pouget, ACS Nano, 2017, 11, 3806–3818 CrossRef CAS PubMed.
- S. L. Tripp, S. V. Pusztay, A. E. Ribbe and A. Wei, J. Am. Chem. Soc., 2002, 124, 7914–7915 CrossRef CAS PubMed.
- A. M. Kalsin, M. Fialkowski, M. Paszewski, S. K. Smoukov, K. J. Bishop and B. A. Grzybowski, Science, 2006, 312, 420–424 CrossRef CAS PubMed.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347 Search PubMed.
- M. G. Moffitt, J. Phys. Chem. Lett., 2013, 4, 3654–3666 CrossRef CAS.
- N. J. Fernandes, H. Koerner, E. P. Giannelis and R. A. Vaia, MRS Commun., 2013, 3, 13–29 CrossRef CAS.
- C. Yi, Y. Yang, B. Liu, J. He and Z. Nie, Chem. Soc. Rev., 2020, 49, 465–508 RSC.
- M. Wang, K. Zhang, D. Hou and P. Wang, Nanoscale, 2020, 12, 24107–24118 RSC.
- N. Yan, Y. Zhang, Y. He, Y. Zhu and W. Jiang, Macromolecules, 2017, 50, 6771–6778 CrossRef CAS.
- J. Song, F. Wang, X. Yang, B. Ning, M. G. Harp, S. H. Culp, S. Hu, P. Huang, L. Nie and J. Chen, J. Am. Chem. Soc., 2016, 138, 7005–7015 CrossRef CAS PubMed.
- Y. Huang, Y. Zheng, A. Sarkar, Y. Xu, M. Stefik and B. C. Benicewicz, Macromolecules, 2017, 50, 4742–4753 CrossRef CAS.
- Y. Liu, J. He, K. Yang, C. Yi, Y. Liu, L. Nie, N. M. Khashab, X. Chen and Z. Nie, Angew. Chem., Int. Ed., 2015, 54, 15809–15812 CrossRef CAS PubMed.
- J. P. Koski and A. L. Frischknecht, Macromolecules, 2021, 54, 5144–5154 CrossRef CAS.
- Y. Zhou, X. Ma, L. Zhang and J. Lin, Phys. Chem. Chem. Phys., 2017, 19, 18757–18766 RSC.
- R. M. Choueiri, E. Galati, H. Thérien-Aubin, A. Klinkova, E. M. Larin, A. Querejeta-Fernández, L. Han, H. L. Xin, O. Gang and E. B. Zhulina, Nature, 2016, 538, 79–83 CrossRef CAS PubMed.
- C. Rossner, E. B. Zhulina and E. Kumacheva, Angew. Chem., Int. Ed., 2019, 58, 9269–9274 CrossRef CAS PubMed.
- L. Yu, N. Zhang, N.-N. Zhang, Q. Gu, Y. Xue, Y.-X. Wang, C.-L. Han, K. Liu, Z.-Y. Sun and H.-J. Qian, J. Phys. Chem. Lett., 2021, 12, 7100–7105 CrossRef CAS PubMed.
- L. Yu, R. Shi, H.-J. Qian and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2019, 21, 1417–1427 RSC.
- M. Gong, Q. Yu, C. Wang and R. Wang, Langmuir, 2019, 35, 5534–5540 CrossRef CAS PubMed.
- A. S. Ushakova, A. A. Lazutin and V. V. Vasilevskaya, Macromolecules, 2021, 54, 6285–6295 CrossRef CAS.
- A. Blanazs, J. Madsen, G. Battaglia, A. J. Ryan and S. P. Armes, J. Am. Chem. Soc., 2011, 133, 16581–16587 CrossRef CAS PubMed.
- J. Wang, T. Fang, J. Li, Y. Yan, Z. Li and J. Zhang, Langmuir, 2020, 36, 8009–8016 CrossRef CAS PubMed.
- S. L. Canning, G. N. Smith and S. P. Armes, Macromolecules, 2016, 49, 1985–2001 CrossRef CAS PubMed.
- T. Shinbrot and F. J. Muzzio, Nature, 2001, 410, 251–258 CrossRef CAS PubMed.
- P. Ray, R. Elfgen and B. Kirchner, Phys. Chem. Chem. Phys., 2019, 21, 4472–4486 RSC.
- B. Liu and J. Goree, Phys. Rev. Lett., 2008, 100, 055003 CrossRef PubMed.
- A. Baskaran and M. C. Marchetti, Phys. Rev. Lett., 2008, 101, 268101 CrossRef PubMed.
- P. Chen, Z. Huang, J. Liang, T. Cui, X. Zhang, B. Miao and L.-T. Yan, ACS Nano, 2016, 10, 11541–11547 CrossRef CAS PubMed.
- P. Hoogerbrugge and J. Koelman, EPL, 1992, 19, 155 CrossRef.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- S. Plimpton, P. Crozier and A. Thompson, Sandia National Laboratories, 2007, 18, 43.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01388b |
| This journal is © The Royal Society of Chemistry 2022 |