Dense shearing flows of soft, frictional cylinders
Diego
Berzi
 *a,
Kevin E.
Buettner
bc and
Jennifer S.
Curtis
d
*a,
Kevin E.
Buettner
bc and
Jennifer S.
Curtis
d
aPolitecnico di Milano, 20133 Milano, Italy. E-mail: diego.berzi@polimi.it
bUniversity of Florida, 32611 Gainesville, FL, USA
cExxonMobil Research and Engineering, 77389 Spring, TX, USA
dUniversity of California, 95616 Davis, CA, USA
First published on 17th November 2021
Abstract
We perform discrete numerical simulations at a constant volume of dense, steady, homogeneous flows of true cylinders interacting via Hertzian contacts, with and without friction, in the absence of preferential alignment. We determine the critical values of the solid volume fraction and the average number of contacts per particle above which rate-independent components of the stresses develop, along with a sharp increase in the fluctuations of angular velocity. We show that kinetic theory, extended to account for a velocity correlation at solid volume fractions larger than 0.49, can quantitatively predict the measured fluctuations of translational velocity, at least for sufficiently rigid cylinders, for any value of the cylinder aspect ratio and friction investigated here. The measured pressure above and below the critical solid volume fraction is in agreement with a recent theory originally intended for spheres that conjugates extended kinetic theory, the finite duration of collisions between soft particles and the development of an elastic network of long-lasting contacts responsible for the rate-independency of the flows in the supercritical regime. Finally, we find that, for sufficiently rigid cylinders, the ratio of shear stress to pressure in the subcritical regime is a linear function of the ratio of the shear rate to a suitable measure of the fluctuations of translational velocity, in qualitative accordance with kinetic theory, with an intercept that increases with friction. A decrease in the particle stiffness gives rise to nonlinear effects that greatly diminishes the stress ratio.
1 Introduction
Granular flows composed of non-spherical particles are encountered in a number of applications, ranging from industry to geophysics. Reliable mathematical models of flows of particles with complicated shapes would permit, e.g., to increase the efficiency and decrease the energy required for handling and transporting granular materials in industrial apparatus.Discrete modelling of granular flows composed of spheres has been around for a long time1 and is now able to deal with a number of complicated effects such as aggregation, breakage, cohesion and poly-dispersity.2–5 Continuum models that extend the seminal studies in the literature on kinetic theory of granular gases6,7 to account for strong inelasticity,8 friction,9–11 velocity correlation,12,13 finite stiffness and the presence of rate-independent components of the stresses14 can now satisfactorily reproduce the flows of rigid and soft spheres in a number of geometrical configurations.
In the last decade, discrete element simulations of shearing flows of true cylinders15–18 and spherocylinders19–22 have also been carried out. These simulations confirmed the experimental observation23,24 that non-spherical particles, in which the ratio of major-to-minor axis is sufficiently far from one, develop a preferential alignment. This has a number of consequences on the constitutive relations to be adopted in continuum models.19,21,25–28 In particular, it means that at least the mean orientation angle should be treated as an additional state variable, while phrasing the associated evolution equation.29
The kinetic theory of granular gases is capable of predicting stresses and velocity fluctuations in homogeneous shearing flows of frictionless cylinders in a wide range of length-to-diameter (aspect) ratio and solid volume fraction.30,31 To do that, one has to introduce a number of phenomenological, although physically sound, modifications: the critical solid volume fraction at which the functions of kinetic theory diverge, because the particles are on average in close contact, depends on the cylinder aspect ratio;30 the shape of the particles induces rotation in collisions even in the absence of friction, so that the effective coefficient of restitution (the negative ratio of post- to pre-collisional normal relative velocity between two impending cylinders) in the rate of collisional dissipation of fluctuation kinetic energy is less than the actual value set in the numerical simulations;31 and finally a measure of the cylinder alignment, relevant when the aspect ratio is less than 0.5 or greater than 2, must be taken into account in the expressions of the shear stress30 and was shown to increase the correlation in the particle velocity fluctuations at solid volume fractions larger than 0.49.31
Here, we extend our previous studies in the literature to include the roles of friction and stiffness on the steady, homogeneous, shearing flows of cylinders. We perform discrete numerical simulations of true cylinders, interacting through inelastic, Hertzian contacts, in the absence of preferential alignment, at solid volume fractions as large as 0.68 and measure the stresses, average number of contacts per particle, and translational and rotational velocity fluctuations. This permits us to first identify the dependence of the critical volume fraction, at which the cylinders are on average in close contact, on the particle friction and aspect ratio. We then highlight similarities and differences compared to what is observed in the case of soft, frictional spheres in terms of velocity fluctuations and stresses. We also show that the stresses can be qualitatively, and sometimes even quantitatively, predicted by constitutive relations that merge contributions associated with collisional exchange of momentum, modelled using extended kinetic theory, and elastic deformations of the contact network, once the critical volume fraction is exceeded.
2 Simulations
True identical cylinders of mass density ρp, diameter d and length l are placed in a cell of constant volume and subjected to steady, homogeneous shearing in the absence of gravity. The flow, gradient and vorticity directions are x, y and z, respectively (Fig. 1).Periodic, in the x- and z-directions, and Lees–Edwards,32 in the y-direction, boundary conditions ensure that, once the simulation reaches a steady state, the x-component of the mean velocity, u, the only one present, is a linear function of y (that is, the shear rate u′ is constant) and the flow is uniform. The number of cylinders in the cell is chosen to attain the desired solid volume fraction ν, in the range between 0.5 and 0.68.
Cylinders interact via Hertzian contact model in the normal direction, with a Young's modulus E and a fixed Poisson's ratio ψ equal to 0.3; and Coulomb sliding in the tangential direction, with a coefficient of sliding friction μ. The normal contact is damped to mimic the energy dissipation due to the propagation of elastic waves inside the material; this results in a coefficient of normal restitution en that we kept constant and equal to 0.95. More details about the numerical implementation of the discrete simulations are reported elsewhere.15–17
We vary the aspect ratio l/d, from 0.5 to 2, the surface friction μ, from 0 to 1, and the dimensionless Young's modulus 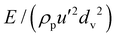 (where dv is the equivalent diameter of a sphere having the same volume of the cylinder), from 2.6 × 104 to 2.6 × 108, and report measurement of coordination number Z (average number of contacts per particle), average rotational and translational velocity fluctuations, particle pressure p and shear stress s in the following section. In all simulations, the order parameter, that is the largest eigenvalue of a symmetric traceless tensor measuring the average orientation of the cylinders,23 is always less than 0.35, well below the value 0.6 above which a phase transition between a disordered, gaseous and a liquid crystal state takes place in the frictionless case.30,31
(where dv is the equivalent diameter of a sphere having the same volume of the cylinder), from 2.6 × 104 to 2.6 × 108, and report measurement of coordination number Z (average number of contacts per particle), average rotational and translational velocity fluctuations, particle pressure p and shear stress s in the following section. In all simulations, the order parameter, that is the largest eigenvalue of a symmetric traceless tensor measuring the average orientation of the cylinders,23 is always less than 0.35, well below the value 0.6 above which a phase transition between a disordered, gaseous and a liquid crystal state takes place in the frictionless case.30,31
3 Results and modelling
3.1 Critical point
Discrete element simulations of steady, homogeneous shearing flows of soft, identical spheres at constant volume33,34 show that, above a critical value νc of the solid volume fraction that is only a function of the sliding friction μ, the stresses are characterized by rate-independent components proportional to the particle stiffness. In the proximity of νc, average stresses and translational velocity fluctuations dramatically increase11 while fluctuations in pressure and coordination number peak.34Peaks in the fluctuations of Z have also permitted identification of νc in the case of steady, inhomogeneous shearing flows35,36 and confirm the presence of rate-independent components of the stresses above the critical solid volume fraction. Rate-independence has instead been observed at values of the coordination number larger than a critical Zc in the case of unsteady, homogeneous shearing flows37 at constant volume fractions less than νc. Depending on the flow configuration, then, either νc or Zc can determine the phase transition from a purely rate-dependent to a combination of rate-dependent and rate-independent stresses.
Actually, in steady, homogeneous shearing, there is a one-to-one relation between solid volume fraction and coordination number, so that when ν = νc, Z = Zc. It has been suggested14 that at solid volume fractions larger than νc the spheres in the discrete simulations are on average overlapped, thus creating a continuously rearranging network of slightly compressed springs. This would explain why the rate-independent components of the stresses are proportional to the particle stiffness. It also implies that, at the critical solid volume fraction, the average overlap between the spheres as well as the average interparticle distance, at least along the principal axis of compression, are exactly zero. Instead, the average interparticle distance measured along the principal axis of extension might be nonzero. This anisotropy, associated also with differences in the normal stresses,38,39 increases with friction,33 hence providing a physical explanation for the monotonic decrease of νc (and Zc) with μ.
If the average overlap is zero at νc, then the particle stiffness should play little to no role there. In the plane ν–Z, curves obtained on steady, homogeneous shearing flows of spheres of different dimensionless particle stiffness are expected to intersect at the critical point νc–Zc. This was indeed firstly observed many years ago40 and exploited to determine the critical values of solid volume fraction and coordination number for frictionless41 and frictional42 spheres.
Our discrete numerical simulations reveal that curves of the coordination number against solid volume fraction, measured for values of the dimensionless Young's modulus that differ in orders of magnitude, also intersect at a critical point in the case of steady, homogeneous shearing flows of true cylinders (an example is reported in Fig. 2a). This permits us to obtain the dependence of νc and Zc on the friction coefficient μ for different cylinder aspect ratios and make comparisons with previous results on spheres (Fig. 2b and c). Both νc and Zc monotonically decrease with μ irrespective of the particle geometry, hinting at the crucial role that friction plays on the spatial anisotropy in the particle arrangement also in the case of cylinders. The critical coordination number is always less for spheres than for cylinders (Fig. 2c). On the other hand, the critical solid volume fraction is less for frictionless spheres than for frictionless cylinders, whereas the opposite is true when friction exceeds 0.3 (Fig. 2b).
 | ||
Fig. 2 (a) Measured coordination number against solid volume fraction for cylinders with the aspect ratio l/d = 0.8, sliding friction μ = 0.1, and Young's modulus 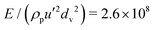 (hollow diamonds) and (hollow diamonds) and 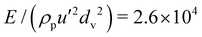 (solid diamonds). Critical (b) solid volume fraction and (c) coordination number as functions of sliding friction for spheres (solid circles, after33) and cylinders with aspect ratio l/d equal to: 0.5 (squares); 0.8 (diamonds); 1 (hollow circles); 1.25 (lower triangles); 2 (upper triangles). (solid diamonds). Critical (b) solid volume fraction and (c) coordination number as functions of sliding friction for spheres (solid circles, after33) and cylinders with aspect ratio l/d equal to: 0.5 (squares); 0.8 (diamonds); 1 (hollow circles); 1.25 (lower triangles); 2 (upper triangles). | ||
3.2 Velocity fluctuations
If we define as C and Ω the fluctuation in translational and angular velocity, respectively, with respect to their average values, we can measure the intensities of such fluctuations in the simulations via the translational temperature, T = 〈C2〉/3, and the rotational temperature, Θ = I〈Ω2〉/Nrotm,43 where the angular brackets denote ensemble averaging and Nrot is the number of rotational degrees of freedom (2 or 3 for frictionless or frictional cylinders, respectively). In the expression of Θ, I is the moment of inertia and m is the mass of the particle. In steady, homogeneous granular flows, the ratio Θ/T is a measure of how much translational fluctuation energy is transformed into rotational fluctuation energy.44 As such, it is an indicator of the geometry of the collisions at the microscopic level.45
Fig. 3a depicts the behaviour of the measured ratio Θ/T as a function of ν–νc – with the critical volume fraction given in Fig. 2b – in our simulations on cylinders with 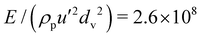 for all the investigated values of friction and aspect ratio. Also shown are the theoretical predictions in the case of spheres.10
for all the investigated values of friction and aspect ratio. Also shown are the theoretical predictions in the case of spheres.10
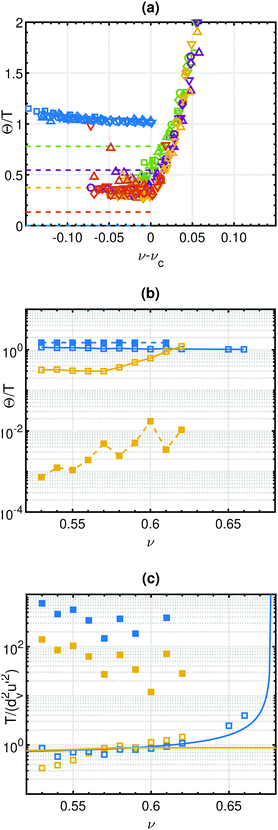 | ||
Fig. 3 (a) Measured ratio of rotational to translational temperature against the deviation from the critical solid volume fraction for cylinders with different aspect ratios (same symbols as in Fig. 2) and 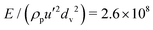 when: μ = 0 (blue symbols); μ = 0.1 (orange symbols); μ = 0.3 (yellow symbols); μ = 0.5 (purple symbols); μ = 1 (green symbols). The dashed lines represent the theoretical predictions in the case of spheres. Measured (b) ratio of rotational to translational temperature and (c) dimensionless translational temperature against the solid volume fraction for cylinders with l/d = 0.5, μ = 0 (blue squares) and μ = 0.3 (yellow squares), and when: μ = 0 (blue symbols); μ = 0.1 (orange symbols); μ = 0.3 (yellow symbols); μ = 0.5 (purple symbols); μ = 1 (green symbols). The dashed lines represent the theoretical predictions in the case of spheres. Measured (b) ratio of rotational to translational temperature and (c) dimensionless translational temperature against the solid volume fraction for cylinders with l/d = 0.5, μ = 0 (blue squares) and μ = 0.3 (yellow squares), and  (hollow squares) and (hollow squares) and 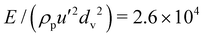 (solid squares). The solid lines in (c) are the predictions of the extended kinetic theory (eqn (1) and (2)). (solid squares). The solid lines in (c) are the predictions of the extended kinetic theory (eqn (1) and (2)). | ||
Spheres and cylinders behave very differently. Frictionless spheres interact through central forces, i.e., directed along the line joining the centers of the particles, so that rotation cannot be induced in contacts, and therefore the rotational temperature is zero. Collisions between frictionless cylinders can instead generate rotation, and indeed the fluctuations in the angular velocity are about the same as the fluctuations in the translational velocity, irrespective of the cylinder aspect ratio and the solid volume fraction (Fig. 3a).
When μ increases, more and more spheres interact through rolling contacts and the ratio Θ/T increases. Unexpectedly, this is not the case for frictional cylinders. Apart from a few points, we observe a nice collapse, irrespective of the aspect ratio and the friction coefficient, as long as the latter is nonzero: Θ/T is roughly constant and about 0.4 at solid volume fractions less than critical and dramatically increases for ν > νc (Fig. 3a). The increasing fluctuations in angular velocity with the distance from the critical point are further evidence that a phase transition takes place there.
Decreasing the particle stiffness by 4 orders of magnitude slightly increases the ratio Θ/T in the case of frictionless cylinders. In the case of frictional cylinders, instead, Θ/T decreases by 2 to 3 orders of magnitude (see an example in Fig. 3b for l/d = 0.5; we obtained similar results, not shown here for brevity, for all aspect ratios).
Decreasing the cylinder stiffness greatly increases the fluctuations in the translational velocity for both frictionless and frictional cylinders (Fig. 3c). However, Fig. 3b reveals that softer frictionless cylinders also experience larger fluctuations in rotational velocity, that are instead suppressed when friction is present. It has been shown, on the other hand, that stiffness plays a little role on the fluctuations in translational velocity in the case of frictional spheres.14
Extended kinetic theory,13,46 that is kinetic theory which takes into account the decrease in the collisional rate of dissipation of translational fluctuation energy due to correlation in velocities that develops once the freezing point, ν = 0.49,47 is exceeded, predicts the dependence of the dimensionless translational temperature on the solid volume fraction in dense, homogeneous shearing flows of spheres as14
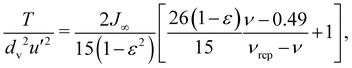 | (1) |
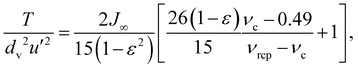 | (2) |
In eqn (1) and (2), ε is an effective coefficient of restitution that is used in the expression for the collisional dissipation rate of kinetic theory to incorporate the exchange between rotational and translational kinetic energy in the translational fluctuation energy balance and avoid the necessity of introducing an additional balance equation for the rotational fluctuation energy. For cylinders, ε should be a function of both the aspect ratio and the friction coefficient. Here, we have determined ε from the translational temperature measured in our simulations via linear regression by approximating eqn (1) and (2) as the first-order Taylor series around ε = e, where e is the effective coefficient of restitution in the case of frictionless cylinders.31 The obtained deviation ε − e as a function of the friction coefficient is reported in Fig. 4. Also shown are the results in the case of spheres (for which e = en) and a previously suggested analytical expression.48
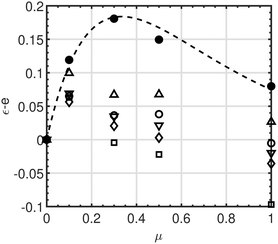 | ||
Fig. 4 Dependence of the deviation of the effective coefficient of restitution from its value at μ = 0 on the friction coefficient for cylinders with different aspect ratios (same symbols as in Fig. 2a). Also shown are the results for spheres (solid circles) and the corresponding interpolating expression 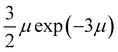 (dashed line).48 (dashed line).48 | ||
Fig. 4 indicates that the influence of the particle geometry on the effective coefficient of restitution in the presence of friction cannot be simply captured through its value e in the absence of friction. We also notice that ε for cylinders seems to peak for μ about 0.1 (in the case of spheres the peak is closer to μ = 0.3) and that the complicated interaction between friction and shape can even lead, counter-intuitively, to an effective coefficient of restitution that is higher for frictional than for frictionless cylinders. Finally, the collapse of Θ/T in the case of frictional cylinders (Fig. 3a) also points out that the effective coefficient of restitution is not simply a function of the temperature ratio, as in the case of spheres.9,10
When we employ the effective coefficient of restitution of Fig. 4 in eqn (1) and (2), we can satisfactorily reproduce the translational temperature measured in the simulations (see two examples in Fig. 3c; similar agreement is obtained for all values of friction and aspect ratio), at least for the stiffest particles. The translational temperature is, on the other hand, poorly predicted once the particle stiffness is reduced. A reduction of 4 orders of magnitude of the stiffness implies an increase in T of about 2 orders of magnitude, for both frictional and frictionless cylinders (Fig. 3c). The latter observation, and the difference between frictional and frictionless cylinders in terms of the relation between Θ/T and their stiffness (Fig. 3b), suggests that the increase in translational velocity fluctuations for softer cylinders has nothing to do with the role of fluctuations in the angular velocity. We instead suspect that the particle stiffness plays a role in determining the velocity correlation thus requiring larger fluctuations to dissipate the same amount of kinetic energy. We postpone this investigation to a future study.
3.3 Stresses
The kinetic theory of granular gases predicts that, for rigid spheres and, thus, instantaneous collisions, the pressure, p, is proportional to the translational temperature through a function of coefficient of normal restitution and volume fraction. In the case of soft spheres, at volume fraction less than the critical (subcritical regime), accounting for the finite duration of contact, induced by the finite particle stiffness, by taking the dense limit of the expression of kinetic theory8,46 and multiplying it by the ratio of the free flight time, tf, to the sum of free flight time and contact duration, tc, was suggested:11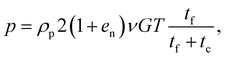 | (3) |
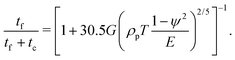 | (4) |
When the solid volume fraction of the spheres exceeds νc (supercritical regime), an elastic component of the pressure, proportional to the particle stiffness, is superimposed onto a component still associated with collisional exchange of momentum, that is assumed to be expressed through eqn (3), with, however, the denominator tf + tc replaced by tc only (the time of free flight is taken to be zero when the interparticle distance is zero on average). In the case of Hertzian contacts, the supercritical pressure reads therefore as follows:11
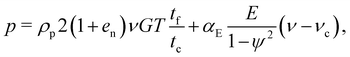 | (5) |
Using the definition of G and eqn (4), we can recast the expression for the subcritical pressure (eqn (3)) as follows:
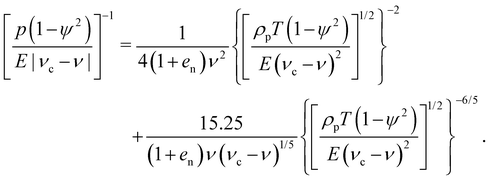 | (6) |
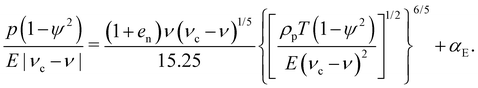 | (7) |
If the analysis performed for spheres held also in the case of cylinders, eqn (6) and (7) would imply a collapse of the measured scaled pressure p(1 − ψ2)/E/|νc − ν| as a function of the square root of the scaled translational temperature ρpT(1 − ψ2)/E/(ν − νc)2, given the low variability of ν. Fig. 5 indeed shows such a collapse, independent of the cylinder aspect ratio, friction and stiffness.
 | ||
| Fig. 5 Dependence of the scaled pressure on the square root of the scaled translational temperature in the case of true cylinders for all values of aspect ratio, friction and stiffness (same legend as in Fig. 3a). Also shown are the predictions of eqn (6) (solid line) and 7 (dashed line) when ν = 0.6, |ν − νc| = 0.05 and αE = 0.0005. | ||
Similar collapses, with the scaled shear rate instead of the square root of T on the x-axis, have been previously obtained in the case of steady, homogeneous34 and steady, inhomogeneous35 flows of soft spheres. For unsteady, homogeneous flows of spheres, instead, the collapse can be obtained using the coordination number rather than the volume fraction in the scaling of p and T.42
For the scaled T that tends to 0 (that is, for rigid particles or very low agitated soft particles), the plot of Fig. 5 shows two limiting behaviours. At volume fractions less than the critical, collisions are essentially binary and instantaneous, and the soft contribution to the subcritical pressure of eqn (6) (the second term on the right hand side) is negligible. The scaled pressure is, therefore, proportional to the second power of the scaled square root of the temperature (rigid collisional limit35 or inertial regime34).
For volume fractions larger than critical, the elastic component of the supercritical pressure dominates in eqn (7) and p is independent of T. The momentum exchange in collisions is negligible and an anisotropic contact network spans the entire domain, corresponding to a shear jammed condition,35 also called the quasistatic regime.34
When the scaled T tends to infinity, eqn (6) and (7) coincide, and the pressure mainly arises because of momentum exchange in collisions, with the frequency of interaction set by the inverse of tc. This has been termed the soft collisional limit35 or the intermediate regime.34
Eqn (6) and (7) can reproduce the results of the numerical simulations (Fig. 5). There, for simplicity, we have taken ν = 0.6 and |ν −νc| = 0.05, but the results are only mildly dependent on the solid volume fraction and the distance from its critical value, at least in the range investigated in the present work.
Part of the scattering of the data in Fig. 5 might be due to the residual dependence of the scaled pressure on the solid volume fraction, and on some role played by the aspect ratio. Also, we could have certainly improved the agreement between the measurements and the theory in the shear jammed limit, if we had taken different values of αE as a function of friction (as done in ref. 34 for spheres); and in the rigid collisional limit, if we had modified the numerical constant in the expression for G (a value larger than 2 for the case of frictionless cylinders and less than 2 for frictional cylinders). We claim, however, that these are simply details, while eqn (6) and (7) seem to capture the essential physics.
In the case of steady, homogeneous flows of soft spheres,14 the dense limit expression of kinetic theory for the shear stress, s, reads46
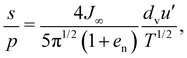 | (8) |
Fig. 6 indicates that eqn (8) can indeed reproduce with sufficient accuracy the stress ratio measured in previous discrete simulations of steady, homogeneous shearing of spheres interacting via Hookean contacts,41,48 for different values of friction and coefficient of normal restitution, at ν < νc. These simulations were performed with dimensionless Young's moduli ranging from 103 to 107, and we notice that the lowest values of the stress ratio, corresponding to the largest values of the dimensionless T, are obtained for the stiffest particles.
 | ||
| Fig. 6 Dependence of the subcritical stress ratio on the square root of the inverse dimensionless translational temperature in the case of spheres interacting via Hookean contacts, with en = 0.95 (hollow circles48) and en = 0.7 (solid circles41) and: μ = 0 (blue symbols); μ = 0.1 (orange symbols); μ = 0.5 (purple symbols). Also shown are the predictions of eqn (8) when en = 0.95 (solid line) and en = 0.7 (dashed line). | ||
Fig. 7 depicts the measured dependence of the stress ratio on the square root of the inverse dimensionless T in the case of true cylinders, when ν ≤ νc (subcritical regime). For 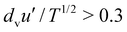 (which roughly corresponds to the stiffest cylinders, with
(which roughly corresponds to the stiffest cylinders, with 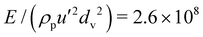 ), the data indeed confirm that s/p is proportional to
), the data indeed confirm that s/p is proportional to 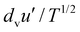 , with a coefficient of proportionality equal to 0.1, lower than the value 0.28 valid for spheres, independent of friction. However, unlike what is predicted by kinetic theory, the linear interpolation gives a nonzero intercept μs for
, with a coefficient of proportionality equal to 0.1, lower than the value 0.28 valid for spheres, independent of friction. However, unlike what is predicted by kinetic theory, the linear interpolation gives a nonzero intercept μs for 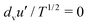 , which increases with friction (see the caption of Fig. 7). The estimated values of μs, that can be interpreted as the stress ratio at yielding, are similar to what was observed in the case of frictional, elongated sphero-cylinders.21 At the lowest values of
, which increases with friction (see the caption of Fig. 7). The estimated values of μs, that can be interpreted as the stress ratio at yielding, are similar to what was observed in the case of frictional, elongated sphero-cylinders.21 At the lowest values of 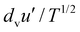 , which, unlike for spheres, correspond to the softest cylinders, the measured stress ratio exhibits a nonlinear behaviour and can be extremely low (even less than 0.01). We believe that this behaviour can be captured only by nonlinear kinetic theories.38,39 Without any theoretical justification, the data of Fig. 7 can be tentatively fitted by modified logistic functions of the form
, which, unlike for spheres, correspond to the softest cylinders, the measured stress ratio exhibits a nonlinear behaviour and can be extremely low (even less than 0.01). We believe that this behaviour can be captured only by nonlinear kinetic theories.38,39 Without any theoretical justification, the data of Fig. 7 can be tentatively fitted by modified logistic functions of the form
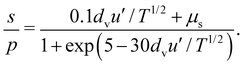 | (9) |
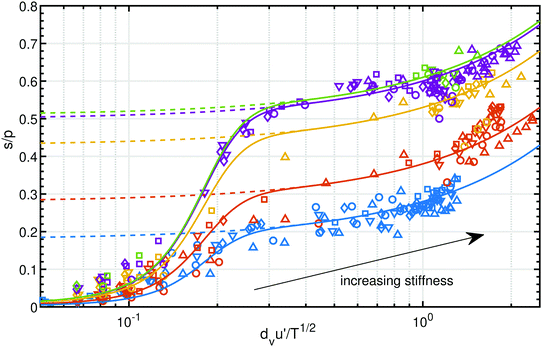 | ||
| Fig. 7 Dependence of the subcritical stress ratio on the square root of the inverse dimensionless translational temperature in the case of true cylinders for all values of aspect ratio, friction and stiffness (same legend as in Fig. 3a). Also shown are the predictions of eqn (9) (solid lines) and the associated linear asymptotes (dashed lines), with μs = 0.18, 0.28, 0.43, 0.5, and 0.51 when μ = 0, 0.1, 0.3, 0.5, and 1, respectively. | ||
When ν is larger than the critical, eqn (9) still agrees with the measurements when 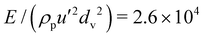 . However, there is a larger scattering when the stiffness increases, an indication that the stress ratio must depend on some parameters other than simply the inverse square root of the dimensionless T. In the case of spheres, for instance, the stress ratio at ν > νc strongly depends on the anisotropy of the fabric tensor.33
. However, there is a larger scattering when the stiffness increases, an indication that the stress ratio must depend on some parameters other than simply the inverse square root of the dimensionless T. In the case of spheres, for instance, the stress ratio at ν > νc strongly depends on the anisotropy of the fabric tensor.33
4 Conclusions
We have performed discrete numerical simulations of dense, steady, homogeneous shearing flows of frictionless and frictional cylinders interacting via Hertzian contacts at different values of solid volume fraction and particle stiffness. The cylinder aspect ratio ranged from 0.5 to 2, sufficiently close to unity to avoid ordering in the alignment of the cylinder axis.As for spheres, we have identified a critical point in the solid volume fraction–coordination number plane that marks the transition from a purely rate-dependent to a mixed regime, in which rate-dependent and rate-independent components of the stresses coexist. This critical point depends on the particle aspect ratio and surface friction but is independent of the particle stiffness.
We have measured fluctuations in angular and translational velocity and confirmed that, due to the nonspherical shape, fluctuations in angular velocity are present even in the case of frictionless particles. Also, in contrast to spheres, the ratio of the rotational to the translational temperature seems to be a unique function of the distance from the critical point for frictional cylinders, with a strong increase in the supercritical regime. The rotational temperature is only slightly affected by the particle stiffness, while the translational temperature increases by 2 orders of magnitude if the stiffness is reduced of 4 orders of magnitude. This effect has no parallel in the case of spheres, and it might point to an enhanced velocity correlation that decreases the rate at which translational, fluctuation kinetic energy is dissipated in collisions. For the stiffest cylinders, however, the dependence of the translational temperature on the solid volume fraction is well predicted using extended kinetic theory, once an appropriated effective coefficient of restitution depending on the particle aspect ratio and friction is adopted.
As in the case of spheres, the granular pressure exhibits three limits, corresponding to three physical regimes: (i) a rigid, collisional limit, at solid volume fractions less than the critical and large particle stiffness, in which particles exchange momentum in binary, instantaneous collisions; (ii) a shear jammed limit, at solid volume fractions larger than the critical and large particle stiffness, where a network of long lasting contacts spans the entire domain and stresses originate from the compression of the springs in the Hertzian contact model; and (iii) a soft, collisional limit, in which particles exchange momentum in collisions at a frequency set by the inverse time scale associated with the spring compression. We have shown that a recent theory, developed for spheres, that incorporates the role of the particle stiffness in a kinetic theory and adds a component of the pressure proportional to the Young's modulus of the particle, can also describe the pressure in flows of true cylinders.
Finally, at solid volume fractions less than critical, the ratio of shear stress to pressure is a linear increasing function of the inverse square root of the dimensionless translational temperature when the cylinders are sufficiently rigid. As in the case of elongated spherocylinders, measurements suggest the existence of a nonzero stress ratio in the limit of vanishing shear rate (yield) that increases with friction. Nonlinearity arises as the particle stiffness decreases, an effect that was never observed in the case of spheres. This nonlinear behaviour is particularly interesting because it is associated with extremely low values of the stress ratio, sometimes termed as macroscopic friction, with possible practical applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. B. wishes to thank Prof. James T. Jenkins for many stimulating discussions and invaluable suggestions. The authors also acknowledge the University of Florida Research Computing organization for providing computational resources and technical support.Notes and references
- P. A. Cundall and O. D. L. Strack, Geotechnique, 1979, 29, 47–65 CrossRef.
- S. Luding, Granular Matter, 2008, 10, 235–246 CrossRef.
- V. Ogarko and S. Luding, Soft Matter, 2013, 9, 9530–9534 RSC.
- N. Kumar, O. I. Imole, V. Magnanimo and S. Luding, Particuology, 2014, 12, 64–79 CrossRef.
- Y. Guo and J. S. Curtis, Annu. Rev. Fluid Mech., 2015, 47, 21–46 CrossRef.
- J. Jenkins and S. Savage, J. Fluid Mech., 1983, 130, 187–202 CrossRef.
- S. Savage and M. Sayed, J. Fluid Mech., 1984, 142, 391–430 CrossRef.
- V. Garzó and J. W. Dufty, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5895–5911 CrossRef PubMed.
- J. T. Jenkins and C. Zhang, Phys. Fluids, 2002, 14, 1228–1235 CrossRef CAS.
- M. Larcher and J. T. Jenkins, Phys. Fluids, 2013, 25, 113301 CrossRef.
- D. Berzi and D. Vescovi, Phys. Fluids, 2015, 27, 013302 CrossRef.
- J. T. Jenkins, Phys. Fluids, 2006, 18, 103307 CrossRef.
- J. T. Jenkins, Granular Matter, 2007, 10, 47–52 CrossRef.
- D. Berzi and J. T. Jenkins, Soft Matter, 2015, 11, 4799–4808 RSC.
- M. Kodam, R. Bharadwaj, J. Curtis, B. Hancock and C. Wassgren, Chem. Eng. Sci., 2010, 65, 5852–5862 CrossRef CAS.
- Y. Guo, C. Wassgren, W. Ketterhagen, B. Hancock, B. James and J. Curtis, J. Fluid Mech., 2012, 713, 1–26 CrossRef.
- Y. Guo, C. Wassgren, W. Ketterhagen, B. Hancock and J. Curtis, Powder Technol., 2012, 228, 193–198 CrossRef CAS.
- Y. Guo, C. Wassgren, B. Hancock, W. Ketterhagen and J. Curtis, Phys. Fluids, 2013, 25, 063304 CrossRef.
- D. B. Nagy, P. Claudin, T. Börzsönyi and E. Somfai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2017, 96, 2–6 CrossRef PubMed.
- T. Marschall, Y. E. Keta, P. Olsson and S. Teitel, Phys. Rev. Lett., 2019, 122, 188002 CrossRef CAS PubMed.
- D. B. Nagy, P. Claudin, T. Börzsönyi and E. Somfai, New J. Phys., 2020, 22, 073008 CrossRef.
- T. A. Marschall and S. Teitel, Phys. Rev. E, 2020, 101, 32907 CrossRef CAS PubMed.
- T. Börzsönyi, B. Szabó, G. Törös, S. Wegner, J. Török, E. Somfai, T. Bien and R. Stannarius, Phys. Rev. Lett., 2012, 108, 228302 CrossRef PubMed.
- T. Börzsönyi, B. Szabó, S. Wegner, K. Harth, J. Török, E. Somfai, T. Bien and R. Stannarius, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 1–8 CrossRef PubMed.
- X. Hong, M. Kohne, M. Morrell, H. Wang and E. R. Weeks, Phys. Rev. E, 2017, 96, 1–9 Search PubMed.
- A. Ashour, T. Trittel, T. Börzsönyi and R. Stannarius, Phys. Rev. Fluids, 2017, 2, 1–9 Search PubMed.
- R. Stannarius, D. Sancho Martinez, T. Finger, E. Somfai and T. Börzsönyi, Granular Matter, 2019, 21, 1–10 CrossRef.
- K. Harth, J. Wang, T. Börzsönyi and R. Stannarius, Soft Matter, 2020, 16, 8013–8023 RSC.
- B. Nadler, F. Guillard and I. Einav, Phys. Rev. Lett., 2018, 120, 198003 CrossRef CAS PubMed.
- D. Berzi, N. Thai-Quang, Y. Guo and J. Curtis, Phys. Rev. E, 2016, 93, 040901 CrossRef PubMed.
- D. Berzi, N. Thai-Quang, Y. Guo and J. Curtis, Phys. Rev. E, 2017, 95, 050901 CrossRef PubMed.
- W. Lee, R. Bennett and K. Meagher, A method of estimating magnitude of local earthquakes from signal duration, U.S. geological survey technical report, 1972.
- J. Sun and S. Sundaresan, J. Fluid Mech., 2011, 682, 590–616 CrossRef.
- S. Chialvo, J. Sun and S. Sundaresan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021305 CrossRef PubMed.
- D. Berzi, J. T. Jenkins and P. Richard, Soft Matter, 2019, 15, 7173–7178 RSC.
- D. Berzi, J. T. Jenkins and P. Richard, J. Fluid Mech., 2020, 885, A27 CrossRef.
- D. Berzi and J. T. Jenkins, Phys. Rev. Fluids, 2018, 3, 094303 CrossRef.
- S. Saha and M. Alam, J. Fluid Mech., 2016, 795, 549–580 CrossRef CAS.
- J. T. Jenkins, M. Alam and D. Berzi, Phys. Rev. Fluids, 2020, 5, 072301(R) CrossRef.
- S. Ji and H. H. Shen, J. Rheol., 2008, 52, 87–103 CrossRef CAS.
- D. Vescovi and S. Luding, Soft Matter, 2016, 12, 8616–8628 RSC.
- D. Vescovi, D. Berzi and C. di Prisco, Granular Matter, 2018, 20, 27 CrossRef.
- K. E. Buettner, Y. Guo and J. S. Curtis, Powder Technol., 2020, 365, 83–91 CrossRef CAS.
- C. Lun, J. Fluid Mech., 1991, 233, 539–559 CrossRef CAS.
- O. Herbst, M. Huthmann and A. Zippelius, Granular Matter, 2000, 2, 211–219 CrossRef CAS.
- J. T. Jenkins and D. Berzi, Granular Matter, 2010, 12, 151–158 CrossRef CAS.
- S. Torquato, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 3170–3182 CrossRef CAS.
- S. Chialvo and S. Sundaresan, Phys. Fluids, 2013, 25, 070603 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |