Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Clustering of self-thermophilic asymmetric dimers: the relevance of hydrodynamics†
Sergi
Roca-Bonet
 ,
Martin
Wagner
and
Marisol
Ripoll
,
Martin
Wagner
and
Marisol
Ripoll
 *
*
Theoretical Physics of Living Matter, Institute of Biological Information Processing, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: m.ripoll@fz-juelich.de
First published on 20th July 2022
Abstract
Self-thermophilic dimers are characterized by a net phoretic attraction which, in combination with hydrodynamic interactions, results in the formation of crystalline-like aggregates. To distinguish the effect of the different contributions is frequently an important challenge. We present a simulation investigation done in parallel in the presence and the absence of hydrodynamic interactions for the case of asymmetric self-thermophoretic dimers. In the absence of hydrodynamics, the clusters have the standard heads-in configurations. In contrast, in the presence of hydrodynamics, clusters with heads-in conformation are being formed, in which dimers with their propulsion velocity pointing out of the cluster are assembled and stabilized by strong hydrodynamic osmotic flows. Significant variation in the material properties is to be expected from such differences in the collective behavior, whose understanding and control is of great relevance for the development of new synthetic active materials.
1 Introduction
Active matter treats systems with at least one component able to draw energy from its environment and transform it into locomotion, replication or growth.1–6 A subset of active matter systems are synthetic microswimmers, which have in the recent years attracted large attention due to their potential in mimicking biological microorganisms,7 in practical applications in fields such as microfluidics or microsurgery,4,8 or in the development of new bio-mimetic materials.6 Artificial microswimmers with a locomotion based on phoretic effects behave as passive colloids unless activated via thermal,9–13 electric,14–18 chemical,19,20 or magnetic21–23 gradients. Thermally activated phoretic microswimmers, or thermophoretic swimmers, are colloids whose surfaces are composed of or simply coated by materials with different absorption coefficients, such that local temperature gradients are created around the colloid by environmental heating. Furthermore, given that the heating sources, mainly lasers or magnets, are very precisely controlled in time and space, a large versatility is expected from systems based on thermophoresis.24,25 Another advantage of thermophoresis is its bio-compatibility, given that thermophoretic microswimmers can be powered without any modification of the solvent, and even very small temperature gradients will lead to a noticeable colloidal drift.The collective behaviour of phoretic artificial microswimmers shares many properties with other active matter and biological systems. Schooling behaviour has been observed in both the macroscopic as well as the microscopic world, with examples ranging from birds and fishes26 to bacteria colonies.27 In the field of phoretic artificial swimmers, chemically propelled Janus particles showed aggregation behaviour,19,28,29 and light-powered micro-robots were observed to form living crystals.30–32 The appearance of clustering and comet-like swarming structures was predicted by Brownian thermophilic active colloids.33,34 The system dimensionality35,36 and the presence and form of hydrodynamic interactions have shown to play a relevant role for the collective behaviour of such thermophilic swimmers.37,38
Numerical investigations of systems with Janus-like phoretic particles have already employed various simulation approaches, which we divide in two groups. The first group includes those methods with no explicit consideration of the presence of a solvent, such that the self-phoretic propulsion is accounted for simply by a constant impulse,33,39,40 or even a constant acceleration in systems that are supposed to increase their temperature as a function of time.34 In the absence of an explicit solvent, phoretic interactions between particles are considered with an additional term, which might, or not, be coupled to the self-propulsion term. Thermal fluctuations are also mostly considered, and in a few cases also hydrodynamic interactions which are non-specific and typically only a far field approximation.41 The second type of approaches considers the presence of an explicit solvent, such that phoretic effects arise in the presence of temperature or concentration gradients.10,42,43 In these approaches the details of self-propulsion, inter-colloidal phoretic interactions, and hydrodynamic interactions are not directly imposed or tuned, but a consequence of the solvent–colloid interaction, colloid shape, and solvent-intrinsic inhomogeneities. Furthermore, in studies of collective properties of these phoretic active systems, it is typically not possible to properly identify the ultimate effect of each contribution, which might lead to inappropriate interpretations and later assumptions. In this work, we aim at identifying the effect of hydrodynamic interactions in the aggregation mechanism of thermophilic self-phoretic dimeric colloids. For this purpose, we investigate the same system with two different simulation methods. One is the already well-established multiparticle collision dynamics (MPC) where both phoresis and hydrodynamic interactions have been proved to be properly incorporated.38,44,47,48 The second method is a recently proposed modification of the standard Brownian simulation method, designed to include friction, propulsion and phoresis in a similar manner as the MPC method, but without hydrodynamics.45,46
The manuscript is structured as follows: we first introduce some details of the hydrodynamic model, and of the matching phoretic Brownian model. Following, a detailed discussion of the solvent flow fields around a single freely moving self-thermophilic asymmetric dimer is included, as well as around a fixed one. Both are necessary to understand their behavior in the concentrated regime. Then simulations with a large number of dimers in a quasi-2 dimensional confinement at different densities with both simulation approaches are presented and discussed first phenomenologically and then analyzed more deeply through quantitative measurements, these are mainly the bounding time, the clusters size evolution, and the pair correlation function, from which a precise evaluation of the effect of hydrodynamics can be performed.
2 Single hydrodynamic self-phoretic dimer
Multiparticle collision dynamics is here used to simulate the explicit solvent particles and their interactions,49,50 while molecular dynamics (MD) is employed for colloid–colloid and colloid–solvent interactions, as shown in Fig. 1a for the single dimer case. This hybrid MPC-MD approach has already extensively proved to include both hydrodynamics and phoretic effects.51–532.1 Hydrodynamic simulation model
The MPC method considers a solvent composed of N point particles of mass m performing alternate streaming and collision steps, with an average kinetic temperature![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) . During the streaming step, fluid particles translate ballistically for a certain time, h, the collision time, this is
. During the streaming step, fluid particles translate ballistically for a certain time, h, the collision time, this is ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k(t + h) =
k(t + h) = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k(t) + h
k(t) + h![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) k(t). In the collision step, particles are binned into cubic cells of side a, with a grid shift applied to the binning in order to restore Galilean invariance.54 Interparticle interactions are treated within each of these cells, in which particles interchange linear momentum with other particles within the same cell. Here we employ the stochastic rotational dynamics collision rule, in which the momentum interchange is made by rotating by an angle α the relative velocities to the centre of mass around a random axis on the cell,
k(t). In the collision step, particles are binned into cubic cells of side a, with a grid shift applied to the binning in order to restore Galilean invariance.54 Interparticle interactions are treated within each of these cells, in which particles interchange linear momentum with other particles within the same cell. Here we employ the stochastic rotational dynamics collision rule, in which the momentum interchange is made by rotating by an angle α the relative velocities to the centre of mass around a random axis on the cell,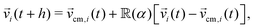 | (1) |
 (α) the rotation matrix, i = 1,…, N the particle index, and
(α) the rotation matrix, i = 1,…, N the particle index, and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) cm,i the centre of mass velocity of the cell where particle i was sorted into. It can be shown that the choice of eqn (1) ensures the local conservation of both linear momentum and kinetic energy in each collision cell. Simulation units are defined by the choice of a = 1 = m = kB
cm,i the centre of mass velocity of the cell where particle i was sorted into. It can be shown that the choice of eqn (1) ensures the local conservation of both linear momentum and kinetic energy in each collision cell. Simulation units are defined by the choice of a = 1 = m = kB![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) , with which we rescale all quantities in this work, and where kB is the Boltzmann factor. The time is for example scaled with
, with which we rescale all quantities in this work, and where kB is the Boltzmann factor. The time is for example scaled with  and the velocities with
and the velocities with 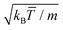 . In the simulations here performed, the fluid properties are determined by the values of the collision angle α = 120°, the average fluid particles per cell ρ = 10, and the collision time, h = 0.1. With these choices, the solvent diffusion coefficient is D = 0.06, the kinematic viscosity ν = 0.79, and the thermal diffusivity κT = 0.15.55–58 The resulting Schmidt number, Sc = ν/D = 13, is smaller than the one of water, but still large enough to ensure that momentum transfer is faster than that of mass, which already provides a very efficient way to include hydrodynamic interactions.53,58 The related Prandtl number, Pr = ν/κT = 5.3, is close to that of water and also enables the stability of local temperature gradients under adequate boundary conditions.
. In the simulations here performed, the fluid properties are determined by the values of the collision angle α = 120°, the average fluid particles per cell ρ = 10, and the collision time, h = 0.1. With these choices, the solvent diffusion coefficient is D = 0.06, the kinematic viscosity ν = 0.79, and the thermal diffusivity κT = 0.15.55–58 The resulting Schmidt number, Sc = ν/D = 13, is smaller than the one of water, but still large enough to ensure that momentum transfer is faster than that of mass, which already provides a very efficient way to include hydrodynamic interactions.53,58 The related Prandtl number, Pr = ν/κT = 5.3, is close to that of water and also enables the stability of local temperature gradients under adequate boundary conditions.
Colloid–colloid and colloid–fluid interactions have been modelled using molecular dynamics, with the equations of motion being integrated using the velocity Verlet algorithm.59,60 The thermophoretic nature of the colloids is determined by the choice of the fluid–colloid interactions, for which we used here a repulsive displaced Mie-like potential,61,62
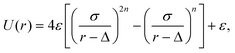 | (2) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) relates to the strength of the potential. The parameter Δ can be understood as a the size of a core with hard-sphere interactions, and σ the size of an additional layer with potential interactions, construction that minimizes the solvent-induced depletion interactions,63 and also affects the potential stiffness. In this work, repulsive interactions are ensured with the cutoff radius of the interactions is rc = 21/nσ + Δ, and n = 24 is chosen for the hot bead. The non-heated bead interacts then with the solvent via a soft repulsive potential (n = 3) which is proved to result into a significant thermophilic behavior.47,64 When applied to the colloid–solvent interaction, the bead radius is determined by s ≡ σ + Δ. The hot bead radius is denoted as sh, while the non-heated bead (phoretic) radius as sp. In this work we use σ = Δ, and sp = 6. The two beads of the dimer are linked together with a strong harmonic potential, which fixes the beads equilibrium distance b as the sum of the beads' radii, b = sp + sh. The geometry of the dimer is defined by the beads radii aspect ratio, γ = sp/sh. In order to mimic the heating produced by laser illumination of partially gold-coated colloids,66 we rescale the temperature of the fluid within a small shell (of thickness 0.08sh) around the hot bead to Th = 1.5, while cooling the average temperature of the whole system to
relates to the strength of the potential. The parameter Δ can be understood as a the size of a core with hard-sphere interactions, and σ the size of an additional layer with potential interactions, construction that minimizes the solvent-induced depletion interactions,63 and also affects the potential stiffness. In this work, repulsive interactions are ensured with the cutoff radius of the interactions is rc = 21/nσ + Δ, and n = 24 is chosen for the hot bead. The non-heated bead interacts then with the solvent via a soft repulsive potential (n = 3) which is proved to result into a significant thermophilic behavior.47,64 When applied to the colloid–solvent interaction, the bead radius is determined by s ≡ σ + Δ. The hot bead radius is denoted as sh, while the non-heated bead (phoretic) radius as sp. In this work we use σ = Δ, and sp = 6. The two beads of the dimer are linked together with a strong harmonic potential, which fixes the beads equilibrium distance b as the sum of the beads' radii, b = sp + sh. The geometry of the dimer is defined by the beads radii aspect ratio, γ = sp/sh. In order to mimic the heating produced by laser illumination of partially gold-coated colloids,66 we rescale the temperature of the fluid within a small shell (of thickness 0.08sh) around the hot bead to Th = 1.5, while cooling the average temperature of the whole system to ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1, by means of a simple velocity re-scale.57,66 All colloid–colloid interactions have been implemented viaeqn (2), with n = 24, Δ = 0, σ = (si + sj)δ, where si and sj refers to the two interacting beads, and δ = 1.1 provides a small additional separation which avoids both depletion and lubrication effects.63,65 Finally, the interactions have a finite range given by rc = 21/24σ.
= 1, by means of a simple velocity re-scale.57,66 All colloid–colloid interactions have been implemented viaeqn (2), with n = 24, Δ = 0, σ = (si + sj)δ, where si and sj refers to the two interacting beads, and δ = 1.1 provides a small additional separation which avoids both depletion and lubrication effects.63,65 Finally, the interactions have a finite range given by rc = 21/24σ.
This method has been implemented on LAMMPS,67 where we have modified the “srd” package routine68 to include the colloid solvent potential interactions. The MD timestep has been chosen as Δt = 0.01h, and the mass M of the colloidal beads are chosen to make the colloids neutrally buoyant.
2.2 Phoretic Brownian dynamics (Ph-BD)
In order to perform a fair comparison of the systems with and without hydrodynamic interactions, we use a recently introduced method named phoretic Brownian dynamics (Ph-BD)45,46 which very precisely includes propulsion, steric, and inter-particle phoretic effects in a similar fashion as the previously discussed MPC-MD simulations, but excluding all hydrodynamic interactions. The idea is to consider the overdamped Langevin equation for each bead i valid at low Reynolds numbers,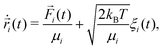 | (3) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i(
i(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the total sum of forces acting on each bead particle i, and ξi(t) is a random delta-correlated Gaussian force with Ns the number of simulated dimeric swimmers. The coefficient, μi, is considered to have the form of the Stokes friction coefficient μi = Cfπηsi, with si the radius of the particle i, η the fluid viscosity, and the numerical factor Cf, which depends on the boundary conditions. The algorithm to integrate the equations of motion used here is stochastic Euler. Although not very efficient in general, the obtained precision is sufficient in our study, since we fix the same integration time step dt for the Ph-BD and the MPC-MD simulations. If necessary, more efficient algorithms could be straightforwardly implemented.The details of the interactions are then provided by the forces. The two beads forming each dimer are linked by a strong harmonic force, and all non-linked beads interact with excluded volume interactions taken into account with the force. These two forces are exactly the same as those considered for the MPC-MD simulations. The hot beads are considered to be at a higher but constant temperature, such that they do not feel any additional interaction. Meanwhile, the non-heated or phoretic bead is the one where the temperature gradient has a drift effect, which in this Ph-BD approach is considered in an effective manner by including the effect of a thermophoretic force
) is the total sum of forces acting on each bead particle i, and ξi(t) is a random delta-correlated Gaussian force with Ns the number of simulated dimeric swimmers. The coefficient, μi, is considered to have the form of the Stokes friction coefficient μi = Cfπηsi, with si the radius of the particle i, η the fluid viscosity, and the numerical factor Cf, which depends on the boundary conditions. The algorithm to integrate the equations of motion used here is stochastic Euler. Although not very efficient in general, the obtained precision is sufficient in our study, since we fix the same integration time step dt for the Ph-BD and the MPC-MD simulations. If necessary, more efficient algorithms could be straightforwardly implemented.The details of the interactions are then provided by the forces. The two beads forming each dimer are linked by a strong harmonic force, and all non-linked beads interact with excluded volume interactions taken into account with the force. These two forces are exactly the same as those considered for the MPC-MD simulations. The hot beads are considered to be at a higher but constant temperature, such that they do not feel any additional interaction. Meanwhile, the non-heated or phoretic bead is the one where the temperature gradient has a drift effect, which in this Ph-BD approach is considered in an effective manner by including the effect of a thermophoretic force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) T calculated as,
T calculated as,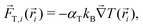 | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) iT the gradient of temperature at the bead location.
iT the gradient of temperature at the bead location.
The corresponding Laplace equations need to be solved to obtain a good estimation of the temperature gradient, for which we consider,
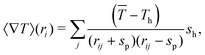 | (5) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) , and then also the temperature field is integrated along the phoretic bead's diameter.45 Note that for an isolated swimmer the gradient is determined just by the linked hot bead, such that rij = sp + sh is the only contributing term. For denser systems, the gradient takes into account all neighboring hot heads, such that in the center of highly compact configurations the gradients eventually vanish and therefore also the thermophoretic force.
, and then also the temperature field is integrated along the phoretic bead's diameter.45 Note that for an isolated swimmer the gradient is determined just by the linked hot bead, such that rij = sp + sh is the only contributing term. For denser systems, the gradient takes into account all neighboring hot heads, such that in the center of highly compact configurations the gradients eventually vanish and therefore also the thermophoretic force.
The dimer velocity vs and the rotational diffusion Dr are therefore not direct inputs of the model, but indirectly determined from other input values, mainly αT, ∇T, sp, and γ. The value of the module of vs is given by
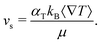 | (6) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) )/(sh + 2sp) depend on the hot and phoretic bead sizes.
)/(sh + 2sp) depend on the hot and phoretic bead sizes.
2.3 Parameters for the comparison MPC vs. Ph-BD
In order to perform a fair comparison of the methods with and without HI we are interested in having systems as similar as possible. Some values are input parameters in the Brownian dynamics simulations, and therefore very easy to match such as the average temperature kB![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1, or the fluid viscosity η = νρ = 7.9. The numerical factor Cf for the friction coefficient, is fixed as Cf = 3 in order to match the employed MPC-SRD algorithm without angular momentum conservation and slip boundary conditions.71,72 Other parameters are not direct input and need to be more carefully considered. For a proper comparison, it is of importance that parameters chosen for the two simulations models result in matching self-propulsion velocity and the Péclet number of diluted swimmer dimers systems, which are indirectly determined via the input parameters αT, Th, and sbdp.
= 1, or the fluid viscosity η = νρ = 7.9. The numerical factor Cf for the friction coefficient, is fixed as Cf = 3 in order to match the employed MPC-SRD algorithm without angular momentum conservation and slip boundary conditions.71,72 Other parameters are not direct input and need to be more carefully considered. For a proper comparison, it is of importance that parameters chosen for the two simulations models result in matching self-propulsion velocity and the Péclet number of diluted swimmer dimers systems, which are indirectly determined via the input parameters αT, Th, and sbdp.
The self-propulsion velocity is first measured in MPC-MD simulations with a single dimer considering vs = ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) ·
·![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) , with
, with ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) the axis direction of the swimmer. By averaging 20 repetitions of 50 MPC time units, we get that a thermophilic dimer with γ = 3 and sp = 6 propels with vs = 0.0127. This velocity value first allows the determination of the ballistic time τB = sp/vs, this is the time in MPC units that a dimer takes to propel its own radius. This time can then be mapped to the Ph-BD time and to one second for a real system in which colloids of 1 μm radius propagate at a velocity of 1 μm s−1. With this value of vs and using eqn (6) the value of the thermodiffusion coefficient can also be determined, which in this case is αT = −213. The rotational diffusion coefficient Dr has been obtained via the fit of Δ
the axis direction of the swimmer. By averaging 20 repetitions of 50 MPC time units, we get that a thermophilic dimer with γ = 3 and sp = 6 propels with vs = 0.0127. This velocity value first allows the determination of the ballistic time τB = sp/vs, this is the time in MPC units that a dimer takes to propel its own radius. This time can then be mapped to the Ph-BD time and to one second for a real system in which colloids of 1 μm radius propagate at a velocity of 1 μm s−1. With this value of vs and using eqn (6) the value of the thermodiffusion coefficient can also be determined, which in this case is αT = −213. The rotational diffusion coefficient Dr has been obtained via the fit of Δ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) 2 = 〈(
2 = 〈(![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) (t) −
(t) − ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) (t′))2〉, resulting in Dr = 2.6 × 10−4. With these values, and sp = 6, the Péclet number results in Pe = vsp/(Drsp) = 8 in +HI case. For the Ph-BD simulations to achieve the same value of vs and Pe, it has been shown that sbdp = 8 and Th = 1.28 are the optimal parameters (for details see ref. 45).
(t′))2〉, resulting in Dr = 2.6 × 10−4. With these values, and sp = 6, the Péclet number results in Pe = vsp/(Drsp) = 8 in +HI case. For the Ph-BD simulations to achieve the same value of vs and Pe, it has been shown that sbdp = 8 and Th = 1.28 are the optimal parameters (for details see ref. 45).
3 Results
3.1 Dynamics of a single dimer
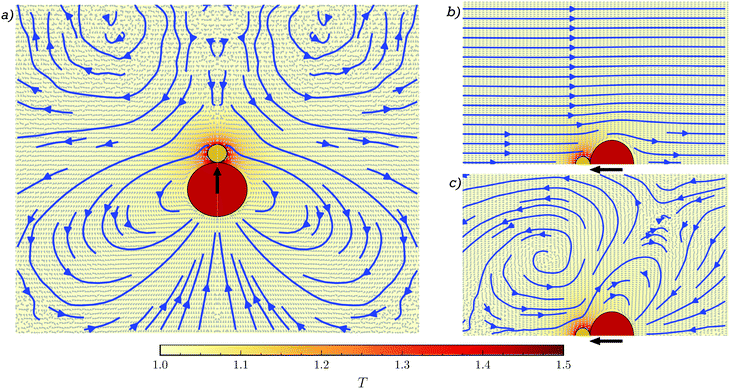
The motion of the dimer in the MPC-MD case is highly influenced by the presence of the motion induced in the fluid, which we characterize first for the case of a single swimming dimer.38 The stream lines of the fluid flow are calculated in the co-moving frame of the dimer freely moving in a cubic box of size 5ls with periodic boundary conditions and swimmer length ls = 2(sp + sh), as shown in Fig. 1a. The fluid velocities have been obtained from 20 repetitions of time length 100τB, and a cylindrical average of all the simulations and Fig. 1a has been obtained by mirroring the flow fields obtained in order to show the symmetric field. The flow shows front fluid vortexes and axial fluid coming towards the dimer, which translates into a hydrodynamic weak attraction in the long-range, but becomes repulsive at short-range distances. The lateral flow shows a radial repulsion due to fluid departing from the dimer, followed by a rear attraction. The combination of these interactions lead to a hydrodynamic-induced torque on neighbouring colloids and an overall attraction towards the rear back of the philic dimer. Note first that, this induced flow is significantly different from those exhibited by spherically symmetric Janus particles36,43,69,70 calculated by simulation, analytical, and experimental approaches. Note also that although the flow field of these dimeric asymmetric swimmers resembles some aspects of hydrodynamic pullers,4 the torque and side-back attraction makes that these dimers can not be classified as standard pullers.Since in some situations the dimer gets into a stuck configuration, we also analyze the flow field of a fixed dimer. Phoresis induces a non-vanishing fluid field also in the fixed case as shown in Fig. 1b, where the dimer acts as a pump. The fluid moves opposite to the eventual propulsion, approaching the swimmer from the head and departing from the back, leading to hydrodynamic attraction at the front and repulsion on the back. This flow field can be understood as the superposition of a constant flow with another one that strongly resembles the co-moving flow field seen in Fig. 1a. This is seen from Fig. 1c, where we have subtracted a constant fraction of the self-propulsion velocity of the dimer to the fluid velocity in Fig. 1b. The precise subtracted value, 0.87vsp, is obtained from the fluid flow at the limit of the simulation box for the fixed dimer Fig. 1b, which is in contrast to the vanishing one in the case of the swimming dimer in Fig. 1a. Note that these fluid flows are valid in the single case here discussed, and when two or more dimers interact, actual flow fields are a modification of these ones.
3.2 Early nucleation
Ensembles of Ns = 200 asymmetric thermophilic dimers have been studied in a quasi-2d system (see scheme in Fig. 2), where the dimers are only allowed to move in the xy plane. In the −HI case this corresponds to a two-dimensional system, whereas in the +HI case a full three dimensional set up with fluid particles are free to move in the bulk contained between two walls. These walls are placed at z = 0 and z = Lz, with the upper limit Lz = ceil(1.67ls). Simulations are started from an homogeneous configuration in which particles are distributed on the nodes of a squared lattice with a random orientation of the dimer axes. This is done for convenience and in order to ensure an initial state without any aggregation. The temperature gradient is considered from the very beginning of the simulation, and the initial order is almost immediately lost due to the dimers activity. To quantify the density we use the area fraction ϕa = Nsπ(sp2 + sh2)/L2. Periodic boundary conditions are considered and the box dimensions Lx = Ly = L are modified with the considered density.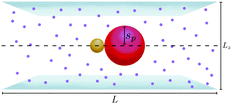 | ||
| Fig. 2 Sketch of a quasi-2d confinement of thermophilic dimers in a slide, with purple small dots representing the MPC fluid particles. | ||
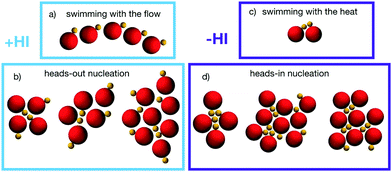
Simulation results show that ensembles of asymmetric thermophilic dimers tend to form aggregates regardless of the presence/absence of hydrodynamics simulations. The aggregation mechanisms are however qualitatively different in both cases as can be observed already at early nucleation stages as those shown in Fig. 3. At very early stages and for a small number of dimers encounters, events in which these dimer pairs or small groups propel together are frequent. In the presence of hydrodynamics, dimers have a tendency to swim behind other dimers as shown in Fig. 3a. This is due to the strong rear attractive flow field of the swimming dimers shown in Fig. 1a. We refer to this state as swimming with the flow. Nevertheless, the swimming behaviour in the presence of hydrodynamics is not really stable. The rear flow induces eventually a torque on dimers placed laterally, leading to small dimer groups which are united by both phoretic and flow induced attraction, as seen in Fig. 3b. When dimers get a frontal encounter, they first get attracted by their front flow field, although when getting closer, the front field becomes softly repulsive, which together with the lateral hydrodynamic torque of the other dimer leads to rear attraction. These processes lead to small aggregates with heads-out configurations, where the dimers of the surface of an aggregate have their hot beads, and therefore their propulsion direction, pointing outwards the cluster, as shown in Fig. 3b. Once that small clusters are formed, they might have still swarming states depending on the particular dimer arrangement. The states with larger velocities quickly destabilize, and those with almost vanishing velocities have dimers with a flow field with a strongly attractive front component, as that shown in Fig. 1b, which favors the aggregation of other closely swimming dimers, as shown in that later snapshots of Fig. 3b. In the absence of hydrodynamics, the only attraction is phoretic. Configurations with the phoretic bead of one dimer getting very close to the hot bead of a neighbouring dimer while keeping certain degree of alignment are then favored, which brings both dimer heads together and leads to a propelling component. We refer to this as swimming with the heat, and show it in Fig. 3c. When more of these Brownian dimers collide frontwards they get stuck in a configuration with vanishing resulting phoretic thrust, constituting an early nucleation of an aggregate with a heads-in configuration, as seen in Fig. 3d.
3.3 Collective long time dynamics
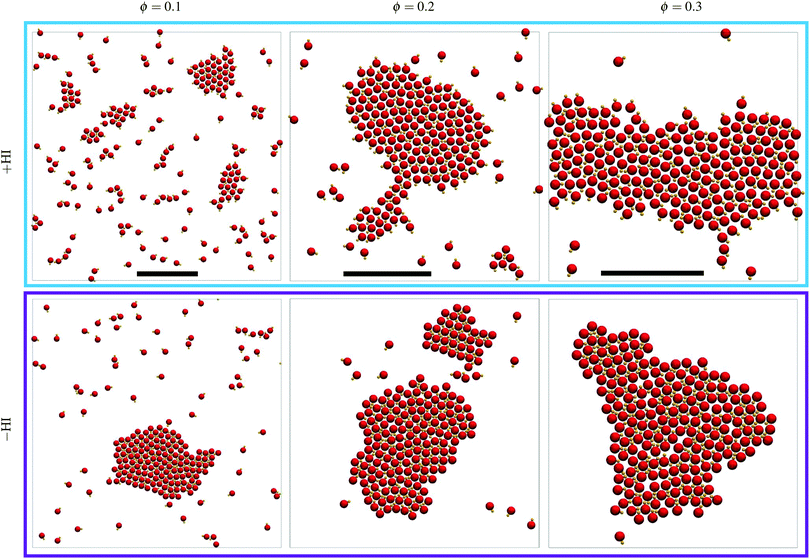
Simulations at three density values have been performed for a total time of ∼300τB in all cases, and final representative snapshots are shown in Fig. 4. Note that this time would be equivalent to 5 minutes when considering colloids of 1 μm radius moving with a speed of 1 μm s−1. Increasing the density increases the probability of encounters, such that clusters are larger the larger the density, given that the total time is the same in all cases. It can be seen that small clusters are frequently unstable and dissolve, but a few larger cluster remain stable and grow over all the simulation time (see also Movie S1, ESI†). Clusters tend to minimize their surface and have the trend to become circular, and when relatively large cluster come close to each other they coalesce. For the largest density value studied in the hydrodynamic simulations, the cluster has even reached the boundary system and displays a percolated state.However, the most notorious difference between the simulations with and without HI is that the cluster conformation follows the trend explained for the early nucleation, clearly showing that large clusters also display heads-out aggregation for the +HI case, and heads-in for −HI. In the presence of hydrodynamic interactions, a dimer approaching the cluster feels a slightly repulsive hydrodynamic interaction due to the front vortex of the moving dimer (see Fig. 1a), which also exerts a torque on the dimer. This torque makes the dimer turn and join the cluster due to the hydrodynamic attraction both the moving dimer in its rear direction, and of the unmoving dimers at the cluster surface in their front direction. The motion of these dimers propelling first towards the cluster, rotating in its proximity, and getting finally pulled towards the cluster is a peculiar hydrodynamic mechanism which resembles a car performing a backwards parking. This hydrodynamic mechanism underlines the importance of the near-field hydrodynamic interactions in the system. In the absence of hydrodynamic interactions, dimers collide simply due to propulsion and get stuck in a cluster due the phoretic attraction and the geometry of the dimer. This leads to the already discussed heads-in structures, which are also typically observed in various other systems of active Brownian particles (ABP).73,74 For increasingly larger aggregates, the temperature field is nearly homogeneous around each dimer in the center of the aggregate. This means that these central dimers do not have any propulsion thrust, and that the forces around each dimer produces certain rearrangements which result into more regular structures, eventually also clusters with faceted boundaries. In any case, the axis of the dimers do not significantly rotate in the absence of flow, and the clusters clearly remain heads-in over time.
The aggregates of dimers with hydrodynamic interactions are characterized by rough surfaces, in contrast to the Brownian aggregates, which have straighter surfaces. In the presence of hydrodynamics, the structures are less compact due to the dimers lateral and rear repulsion, the hot beads are pointing out due to the hydrodynamic torque, and this configuration makes that dimers orientations are more affected by thermal fluctuations. This all together results in structures with rough interfaces. In the absence of hydrodynamic interactions, hot heads at the perimeter of the cluster tend to point towards the center of the aggregate, there is not short range repulsion. This leads to more compact structures and therefore straighter surfaces, which can become even faceted clusters.
3.4 Bounding time evolution
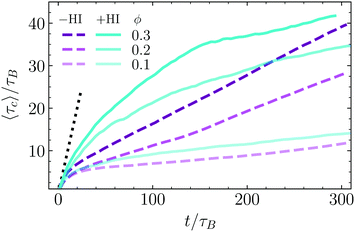
In order to quantitatively analyze the aggregation procedure, we analyze the evolution of some relevant quantities as a function of time. Results are obtained as an average of five independent simulation in the −HI case and for a single one in the +HI case. First we discus the bounding time τc, which is calculated as a time average in Fig. 5 for the three considered values of the density and for the ±HI cases. The bounding time is here introduced as the average time that two dimers remain close to each other after an eventual encounter. The maximum distance from colloid surface to colloid surface considered as “close” is chosen to be 0.75sp. With this definition, particles forming unstable clusters reach after some time a well-defined constant average bounding time. Meanwhile particles inside a stable cluster display a bounding time growing with the simulation averaging time, since they have an asymptotically infinite bounding time. All the results in Fig. 5 clearly show the formation of stable clusters. The characteristics of this growth provide further information about the stability of the clusters and the aggregation speed. In the limiting case of infinitely large attraction, each two particles that get closer to each other would never separate anymore, then the bounding time would be by construction exactly the time used for the average, this is τc = t. And this is independent on density and of how many pairs have actually aggregated. Following this logic, any growth slower than this indicates that from the pairs that have an encounter some of them remain together, while some of them separate after some time. For very short times the growth follows indeed the τc = t behavior, but after a few τB it changes into a lower increase, which is in fact slower the smaller is the area fraction ϕ. Encounters of two particles swimming together typically dissolve after some time (see related movies in ESI†). If collision of these pairs with other dimers or pairs of dimers occur, we have a case of early nucleation as previously discussed, but clusters of small number of particles are not as stable as larger clusters. The faster increase of τc for larger values of ϕ is then related to the higher frequency of encounters for higher densities, which, given the 2D geometry, is expected to increase with ϕ2. With only three density values this trend cannot be confirmed, but the fact the distance from ϕ = 0.1 to ϕ = 0.2 is larger than from ϕ = 0.2 to ϕ = 0.3 is consistent with it. Interestingly, the time dependence in the Brownian case can be very well identified to be linear with a slope lower than that at short times, but larger the larger the density. Following the same reasoning as before, this might indicate that Brownian phoretic dimers aggregated into a large enough cluster do not have anymore the possibility of leaving the cluster, while pairs, triplets or small clusters remain being unstable. Medium-short times are characterized by clusters still growing in size and the presence of many non-bonded swimmers. In the presence of hydrodynamics, small clusters are more stable since both phoresis and the hydrodynamic flow are attractive, than in the absence of hydrodynamics where only phoresis is holding the clusters together. In the limit of very long times, one or very few large clusters contain almost all swimmers, and only very few dimers are still freely swimming, or in very small aggregates. In the absence of hydrodynamics, dimers are linked to the others by phoresis, without any destabilising factor, resulting in very stable bonding. In the presence of hydrodynamics, all dimers of the non-moving cluster have certain rear and lateral hydrodynamic repulsion, as previously discussed, which makes the structures less compact and also a bit less stable. This together with the heads-out configuration implies that the escape probability of dimers at the surface of a large cluster, albeit small, is clearly larger in the presence of hydrodynamics.3.5 Time evolution of the cluster size
The bounding time has provided very useful information about the stability of formed aggregates, but not about how large they are, how fast they are formed, or how many aggregates are formed. We explicitly calculate now the relative size of the largest cluster nmax = Nmax/Nd, with Nmax the number of dimers in the largest cluster, and Nd the total number of clusters as shown in Fig. 6a. The cluster growth is faster the larger the density since the probability of encounters and therefore of nucleation increases with density. For the smallest density here shown, ϕ = 0.1, the largest cluster grows faster in the absence of HI than in their presence, which is related to the larger instability of the very small clusters, for which the lateral hydrodynamic repulsion has a destabilizing effect. For larger densities, the presence or absence of hydrodynamics does almost not affect the formation of the largest cluster, besides that the hydrodynamic case is noisier, which indicates that the stability of the clusters with medium or larger sizes is similarly stable with and without hydrodynamics. The relative number of single dimers, nsing, is also calculated and displayed in Fig. 6b. Initially we impose that all dimers swim independently such that this number is large but, in a time of about 10τB, it very quickly drops to a value from which the decrease is much slower. The number of single swimmers that remain after the fast drop is smaller the larger is the dimer density. After much longer times, nsing, decays to almost vanishing for the two largest density here considered in the absence of HI, while with HI it seems that a small number of single dimers remain freely swimming. This agrees with the idea that in the presence of HI, the dimers aggregated in the cluster surface have a non-vanishing probability of escape. Finally the average number of dimers per cluster, nav, is calculated as shown Fig. 6c. This quantity combines information about the total number of clusters and of their size. For the smallest density nav is very small due to the large number of very small clusters, such as pairs or triplets (see snapshots in Fig. 4). Increasing density makes nav clearly increase. Curiously, for medium-short times, there is no difference for simulations with and without hydrodynamics, but from a time around 100–120τB the average number of particles in a cluster grows much faster in the absence of HI, although the largest cluster are almost identical. This indicates that there is a larger number of small clusters in the presence of HI, which is mainly related to the larger stability of small hydrodynamic clusters, and eventually also to the non-vanishing probability of surface dimers to escape for the cluster and form pairs or triples, processes which are also responsible for the large fluctuations of nav in the presence of HI.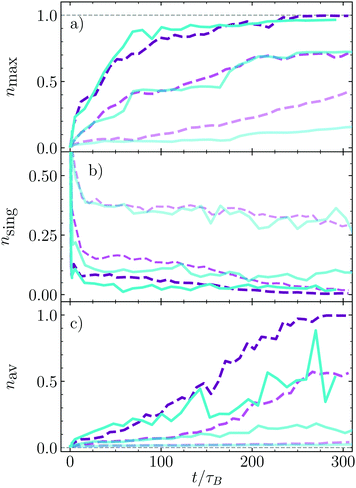 | ||
| Fig. 6 Time evolution of the normalized cluster sizes nk = Nk/Ns with Ns that total number of dimers. (a) Bigger cluster present in the system, nmax; (b) number of single swimmers, nsing; (c) average cluster size, nav. Colors and lines code correspond to the labels in Fig. 5. | ||
3.6 Clusters structure
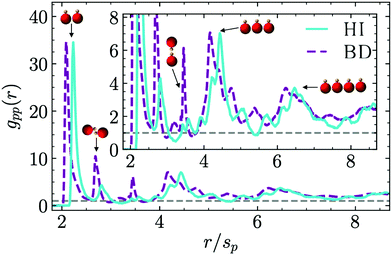
In Section 3.3 we already discussed the qualitative behavior of the aggregate states formed by thermophilic asymmetric dimers, and the differences induced by the presence or absence of hydrodynamics. Additional quantitative information can be obtained by the explicit calculation of the pair correlation function g(r). We use a standard definition of g(r),75 given by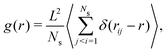 | (7) |
An inherent ordering within the clusters can be clearly distinguished due to the presence of peaks at well defined distances. The first peak corresponds to pairs of phoretic beads at close contact (for 2 ≲ r/sp ≲ 2.3) which are the most probable and thus higher and narrower. The peak for Ph-BD simulations occurs at smaller distances than for MPC-MD simulations, which can also be seen in the more compact structures in the snapshots in Fig. 4. This difference originates in the short distance lateral repulsion occurring both for moving and fixed dimers, as can be seen in the flow fields of Fig. 1a and c. The second and third peaks for r/sp ≃ 2.7 and r/sp ≃ 3.5 correspond to configurations in which the phoretic beads are separated by one or two hot beads, as can be seen in the sketched configurations in Fig. 7. These configuration occur both in the presence and absence of hydrodynamics, but they are clearly much more frequent without hydrodynamics, due to the overall heads-in cluster configuration, where many more hot beads inside the cluster are separating phoretic beads. Fourth and fifth peaks for 4.2 ≲ r/sp ≲ 4.5 and for 6.1 ≲ r/sp ≲ 6.6, correspond to phoretic beads separated by one or two other phoretic beads, which are configurations with at least three and four consecutive beads. For these peaks, the shift towards larger separations in the hydrodynamic case are related again to the short-range lateral hydrodynamic repulsion. The structure factor can also be calculated (see ESI,† Fig. S3) and similar conclusions can be drawn from it, although in this case the outcome is less clear than the discussion here with the pair correlation function.
3.7 Comparison with other self-phoretic dimers
The equations governing the phoretic mechanism are inherently similar for the different types of phoresis,76 and for thermophoresis and diffusiophoresis in particular, with some differences considering the different gradients. Chemically-propelled dimeric microswimmers have been investigated in the presence of hydrodynamics with a MPC simulation model strongly related to the one employed here.42,77–80 However, in their work with chemophilic asymmetric dimers the formation of aggregates is reported to have heads-in configurations,80,81 which is in contrast to the hydrodynamic results we report here, and more similar to the collective behavior of phoretic Brownian dimers. Both methods consider the same type of MPC solvent–solvent interactions and similar solvent−dimer interactions through repulsive Mie-like potentials in eqn (2). In both cases the gradients are imposed by changing the solvent properties at the surface of the smaller beads, this is by imposing a higher solvent temperature or by changing the solvent composition. We understand the main difference between both approaches is that in thermophoresis the thrust arises from the temperature dependence of the solvent-dimer potential interaction in the phoretic bead, while in diffusiophoresis the thrust arises by distinguishing two types of solvent particles with different interaction with the phoretic or non-catalytic bead. In principle, both strategies create a force imbalance between front and back of the dimer which produces the phoretic thrust, and also the related flow fields around the dimeric swimmers, which result to be different in both cases. Fig. 4 in ref. 79 shows a qualitatively different flow than the one Fig. 1. The larger symmetry of the flow lateral to the diffusiophoretic swimmer makes that there is a non-existing or much smaller lateral torque for two approaching particles, and the long range front attraction of the diffusiophoretic dimer enhances also the heads-in configuration. Another difference between both simulations is the beads separation. Beads are in contact in our thermophoretic case, and separated by a short distance in the diffusiophoretic case. To test the effect of such separation we have performed one set of hydrodynamic simulations for thermophilic dimers, but the resulting flow profiles and collective behavior is qualitatively similar to the other thermophoretic swimmers here discussed (see results in ESI,† Fig. S4). Other implementations of the solvent dimer interactions might eventually change the effect of the hydrodynamically induced flow field, and therefore their collective behavior. This remains however task of future investigations.4 Conclusions
The collective behaviour of thermophilic asymmetric dimers shows here to be strongly dependent both on phoretic and hydrodynamic interactions. Although systems with and without hydrodynamic interactions lead to overall aggregation, the clustering mechanism and cluster structure is inherently different in both systems. Phoretic Brownian dimers aggregate due to propulsion after an eventual encounter and remain aggregated due to phoresis. The phoretic Brownian dimers keep essentially their original orientations, only slightly rearranging in order to balance phoretic interactions of various surrounding particles, forming clusters with heads-in conformations. Hydrodynamic dimers are under the effect not only of propulsion and phoresis, but also importantly influenced by the induced solvent flow field around each dimer. After an eventual encounter, dimers frequently feel a torque which makes them turn into a heads-out orientation. This is an unusual configuration in active matter systems in which the swimmers have their propulsion direction pointing outwards the cluster. The stability of the aggregated configurations is due to both phoretic and more crucially due to hydrodynamic attraction at the dimer rear. The relevant flow fields are not only related with actually swimming dimers, but also to dimers which are trapped in the surfaces of the aggregates. The collective dynamics of self-thermophilic dimers is affected by hydrodynamics with other consequences like the larger stability of small clusters, the less compact structures, and the larger probability of escape of dimers at the cluster surface, which can be quantified for example in the measurements of the bounding time, the average size of a cluster, or location of the peaks in the pair correlation function. This means that the functionality of these materials is importantly influenced by hydrodynamics conditioning for example their rheological or conductivity properties which can be understood to be different in case of heads-in or heads-out configurations, especially when the heads are typically metallic and the bodies non-metallic. Furthermore, this work shows that the effect of hydrodynamic interactions can be both subtle and strong, such that assumptions like neglecting hydrodynamics or considering them only in far field approximation can result into misleading results. In this regard, the present discussion encourages the use of combined approaches with and without hydrodynamics that allow to disentangle the importance of both contributions, as well as other possible contributions such as induced alignment or of the damping of the phoretic force in the proximity of neighbouring sources.45 We expect the results here presented foster further investigations on related phoretic structures, and are also useful for the development of practical applications of synthetic active phoretic materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank fruitful discussions with R. Kapral about the comparison of collective behaviour of different phoretic dimeric systems. We would also like to acknowledge Judit Clopés for her help with the cover art work. This work was supported by the DFG priority program SPP 1726 on “Microswimmers – from Single Particle Motion to Collective Behaviour”. The authors gratefully acknowledge the computing time granted by the JARA Vergabegremium and provided on the JARA Partition part of the supercomputer JURECA at Forschungszentrum Jülich.82References
- G. Gompper, R. G. Winkler, T. Speck, A. Solon, C. Nardini, F. Peruani, H. Löwen, R. Golestanian, U. B. Kaupp and L. Alvarez, et al., The 2020 motile active matter roadmap, J. Phys.: Condens. Matter, 2020, 32(19), 193001 CrossRef CAS PubMed.
- S. Ramaswamy, The mechanics and statistics of active matter, Annu. Rev. Condens. Matter Phys., 2010, 1, 323 CrossRef.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and A. S. Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- J. Elgeti, R. G. Winkler and G. Gompper, Physics of microswimmers--single particle motion and collective behavior: a review, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- G. De Magistris and D. Marenduzzo, An introduction to the physics of active matter, Phys. A, 2015, 418, 2065 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt and G. Volpe, Active particles in complex and crowded environments, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Microscopic artificial swimmers, Nature, 2005, 437, 862 CrossRef CAS PubMed.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. St. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, Catalytic nanomotors: autonomous movement of striped nanorods, J. Am. Chem. Soc., 2004, 126, 13424 CrossRef CAS PubMed.
- H. R. Jiang, N. Yoshinaga and M. Sano, Active motion of a Janus particle by self-thermophoresis in a defocused laser beam, Phys. Rev. Lett., 2010, 105, 268302 CrossRef PubMed.
- M. Yang and M. Ripoll, Simulations of thermophoretic nanoswimmers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061401 CrossRef PubMed.
- J. Burelbach, M. Zupkauskas, R. Lamboll, Y. Lan and E. Eiser, Colloidal motion under the action of a thermophoretic force, J. Chem. Phys., 2017, 147(9), 094906 CrossRef PubMed.
- R. Piazza and A. Parola, Thermophoresis in colloidal suspensions, J. Phys.: Condens. Matter, 2008, 20(15), 153102 CrossRef.
- A. Würger, Thermal non-equilibrium transport in colloids, Rep. Prog. Phys., 2010, 73, 126601 CrossRef.
- F. A. Morrison, Electrophoresis of a particle of arbitrary shape, J. Colloid Interface Sci., 1970, 34(2), 210–214 CrossRef CAS.
- K. Makino and H. Ohshima, Electrophoretic mobility of a colloidal particle with constant surface charge density, Langmuir, 2010, 26(23), 18016–18019 CrossRef CAS PubMed.
- M. M. Hatlo, D. Panja and R. van Roij, Translocation of dna molecules through nanopores with salt gradients: The role of osmotic flow, Phys. Rev. Lett., 2011, 107, 068101 CrossRef PubMed.
- B. Sabass and U. Seifert, Dynamics and efficiency of a self-propelled, diffusiophoretic swimmer, J. Chem. Phys., 2012, 136(6), 064508 CrossRef PubMed.
- S. Samin and R. van Roij, Solvo-osmotic flow in electrolytic mixtures, J. Fluid Mech., 2017, 819, R1 CrossRef CAS.
- R. Kapral, Perspective: nanomotors without moving parts that propel themselves in solution, J. Chem. Phys., 2013, 138, 020901 CrossRef PubMed.
- S. Saha, R. Golestanian and S. Ramaswamy, Clusters, asters, and collective oscillations in chemotactic colloids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89(6), 062316 CrossRef PubMed.
- M. Suwa and H. Watarai, Magnetoanalysis of micro/nanoparticles: a review, Anal. Chim. Acta, 2011, 690(2), 137–147 CrossRef CAS PubMed.
- M. Benelmekki, L. M. Martinez, J. S. Andreu, J. Camacho and J. Faraudo, Magnetophoresis of colloidal particles in a dispersion of superparamagnetic nanoparticles: theory and experiments, Soft Matter, 2012, 8(22), 6039–6047 RSC.
- Z. M. Sherman, J. L. Pallone, R. M. Erb and J. W. Swan, Enhanced diffusion and magnetophoresis of paramagnetic colloidal particles in rotating magnetic fields, Soft Matter, 2019, 15(33), 6677–6689 RSC.
- R. S. M. Rikken, R. J. M. Nolte, J. C. Maan, J. C. M. van Hest, D. A. Wilson and P. C. M. Christianen, Manipulation of micro- and nanostructure motion with magnetic fields, Soft Matter, 2014, 10, 1295–1308 RSC.
- U. Khadka, V. Holubec, H. Yang and F. Cichos, Active particles bound by information flows, Nat. Commun., 2018, 9, 3864 CrossRef PubMed.
- T. Vicsek and A. Zafeiris, Collective motion, Phys. Rep., 2012, 517(3), 71–140 CrossRef . Collective motion.
- C. J. Ingham and E. Ben Jacob, Swarming and complex pattern formation in paenibacillus vortex studied by imaging and tracking cells, BMC Microbiol., 2008, 8, 36 CrossRef PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Dynamic clustering in active colloidal suspensions with chemical signaling, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- B. Liebchen, D. Marenduzzo, I. Pagonabarraga and M. E. Cates, Clustering and pattern formation in chemorepulsive active colloids, Phys. Rev. Lett., 2015, 115, 258301 CrossRef PubMed.
- M. Ibele, T. Mallouk and A. Sen, Schooling behavior of light-powered autonomous micromotors in water, Angew. Chem., Int. Ed., 2009, 48(18), 3308–3312 CrossRef CAS PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Living crystals of light-activated colloidal surfers, Science, 2013, 339(6122), 936–940 CrossRef CAS PubMed.
- S. A. Mallory, C. Valeriani and A. Cacciuto, An active approach to colloidal self-assembly, Annu. Rev. Phys. Chem., 2018, 69(1), 59–79 CrossRef CAS PubMed , PMID: 29106809.
- R. Golestanian, Collective behavior of thermally active colloids, Phys. Rev. Lett., 2012, 108, 038303 CrossRef PubMed.
- J. A. Cohen and R. Golestanian, Emergent cometlike swarming of optically driven thermally active colloids, Phys. Rev. Lett., 2014, 112, 068302 CrossRef PubMed.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Phase behaviour of active brownian particles: the role of dimensionality, Soft Matter, 2014, 10, 1489–1499 RSC.
- A. Wysocki, R. G. Winkler and G. Gompper, Cooperative motion of active Brownian spheres in three-dimensional dense suspensions, EPL, 2014, 105(4), 48004 CrossRef.
- J.-B. Delfau, J. Molina and M. Sano, Collective behavior of strongly confined suspensions of squirmers, EPL, 2016, 114(2), 24001 CrossRef.
- M. Wagner, S. Roca-Bonet and M. Ripoll, Collective behavior of thermophoretic dimeric active colloids in three-dimensional bulk, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44(3), 43 CrossRef CAS PubMed.
- O. Pohl and H. Stark, Dynamic clustering and chemotactic collapse of self-phoretic active particles, Phys. Rev. Lett., 2014, 112, 238303 CrossRef PubMed.
- O. Pohl and H. Stark, Self-phoretic active particles interacting by diffusiophoresis: A numerical study of the collapsed state and dynamic clustering, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 93 CrossRef PubMed.
- S. Saha, S. Ramaswamy and R. Golestanian, Pairing, waltzing and scattering of chemotactic active colloids, New J. Phys., 2019, 21, 063006 CrossRef CAS.
- G. Rückner and R. Kapral, Chemically powered nanodimers, Phys. Rev. Lett., 2007, 98, 150603 CrossRef PubMed.
- K. Kroy, D. Chakraborty and F. Cichos, Hot microswimmers, Eur. Phys. J.: Spec. Top., 2016, 225, 2207 Search PubMed.
- M. Yang, A. Wysocki and M. Ripoll, Hydrodynamic simulations of self-phoretic microswimmers, Soft Matter, 2014, 10, 6208–6218 RSC.
- S. Roca-Bonet and M. Ripoll, Self-phoretic brownian dynamics simulations, Eur. Phys. J. E: Soft Matter Biol. Phys., 2022, 45, 25 CrossRef CAS PubMed.
- S. Roca-Bonet, Thermophoretic microswimmers: interplay of phoresis, geometry and hydrodynamics, PhD Thesis, Cologne University, Germany, 2021.
- M. Wagner and M. Ripoll, Hydrodynamic front-like swarming of phoretically active dimeric colloids, EPL, 2017, 119, 66007 CrossRef.
- M. Wagner, Colloidal microswimmers driven by thermophoresis, PhD Thesis, Cologne University, Germany, 2017.
- A. Malevanets and R. Kapral, Mesoscopic model for solvent dynamics, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- A. Malevanets and R. Kapral, Solute molecular dynamics in a mesoscale solvent, J. Chem. Phys., 2000, 112, 7260 CrossRef CAS.
- G. Gompper, T. Ihle, D. Kroll and R. Winkler, Advanced Computer Simulation Approaches for Soft Matter Sciences III, Advances in Polymer Science, 221 of Advanced Computer Simulation Approaches for Soft Matter Sciences III, Springer Berlin Heidelberg, 2009, pp. 1–87 Search PubMed.
- K. Mussawisade, M. Ripoll, R. G. Winkler and G. Gompper, Polymer dynamics in a mesoscopic solvent, J. Chem. Phys., 2005, 123, 144905 CrossRef CAS PubMed.
- M. Yang and M. Ripoll, Thermophoretically induced flow field around a colloidal particle, Soft Matter, 2013, 9, 4661–4671 RSC.
- T. Ihle and D. M. Kroll, Stochastic rotation dynamics: A Galilean-invariant mesoscopic model for fluid flow, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201 CrossRef CAS PubMed.
- E. Tüzel, M. Strauss, T. Ihle and D. M. Kroll, Transport coefficients for stochastic rotation dynamics in three dimensions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 036701 CrossRef PubMed.
- E. Tüzel, T. Ihle and D. M. Kroll, Dynamic correlations in stochastic rotation dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 056702 CrossRef PubMed.
- D. Lüsebrink and M. Ripoll, Temperature inhomogeneities simulated with multiparticle-collision dynamics, J. Chem. Phys., 2012, 136(8), 084106 CrossRef PubMed.
- M. Ripoll, K. Mussawisade, R. G. Winkler and G. Gompper, Dynamic regimes of fluids simulated by multiparticle-collision dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 016701 CrossRef CAS PubMed.
- L. Verlet, Computer experiments on classical fluids. I. thermodynamical properties of Lennard-Jones molecules, Phys. Rev., 1967, 159, 98 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulations, Academic Press, 1996 Search PubMed.
- G. Mie, Zur kinetischen Theorie der einatomigen Korper, Ann. Phys., 1903, 316, 657 CrossRef.
- T. Kihara, Virial coefficients and models of molecules in gases, Rev. Mod. Phys., 1953, 25, 831 CrossRef CAS.
- M. Wagner and M. Ripoll, Solvent-induced depletion interactions in multiparticle collision dynamic simulations, Int. J. Mod. Phys. C, 2019, 30, 1941008 CrossRef CAS.
- D. Lüsebrink, M. Yang and M. Ripoll, Thermophoresis of colloids by mesoscale simulations, J. Phys.: Condens. Matter, 2012, 24(28), 284132 CrossRef PubMed.
- N. J. Wagner and J. F. Brady, Shear thickening in colloidal dispersions, Phys. Today, 2009, 62(10), 27 CrossRef CAS.
- H. Jiang and T. Kiørboe, Propulsion efficiency and imposed flow fields of a copepod jump, J. Exp. Biol., 2011, 214(3), 476 CrossRef PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- M. K. Petersen, J. B. Lechman, S. J. Plimpton, G. S. Grest, P. J. in't Veld and P. R. Schunk, Mesoscale hydrodynamics via stochastic rotation dynamics: Comparison with Lennard-Jones fluid, J. Chem. Phys., 2010, 132, 174106 CrossRef PubMed.
- F. Rojas-Pérez, B. Delmotte and S. Michelin, Hydrochemical interactions of phoretic particles: a regularized multipole framework, J. Fluid Mech., 2021, 919, A22 CrossRef.
- A. I. Campbell, S. J. Ebbens, P. Illien and R. Golestanian, Experimental observation of flow fields around active Janus spheres, Nat. Commun., 2019, 10, 3952 CrossRef PubMed.
- C. M. Pooley and J. M. Yeomans, Kinetic theory derivation of the transport coefficients of stochastic rotation dynamics, J. Phys. Chem. B, 2005, 109, 6505–6513 CrossRef CAS PubMed.
- M. Yang, M. Theers, J. Hu, G. Gompper, R. G. Winkler and M. Ripoll, Effect of angular momentum conservation on hydrodynamic simulations of colloids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 013301 CrossRef PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- T. Speck, Collective behavior of active Brownian particles: From microscopic clustering to macroscopic phase separation, Eur. Phys. J.: Spec. Top., 2016, 225(11), 2287–2299 CAS.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 4th edn, 2013 Search PubMed.
- J. L. Anderson, Colloidal transport by interfacial forces, Ann. Rev. Fluid Mech., 1989, 21, 61 CrossRef.
- L. F. Valadares, Y.-G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Catalytic nanomotors: Self-propelled sphere dimers, Small, 2010, 6(4), 565–572 CrossRef CAS PubMed.
- S. Thakur and R. Kapral, Collective dynamics of self-propelled sphere-dimer motors, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 026121 CrossRef PubMed.
- S. Y. Reigh and R. Kapral, Catalytic dimer nanomotors: continuum theory and microscopic dynamics, Soft Matter, 2015, 12, 3149–3158 RSC.
- P. H. Colberg and R. Kapral, Many-body dynamics of chemically propelled nanomotors, J. Chem. Phys., 2017, 147(6), 064910 CrossRef PubMed.
- P. H. Colberg, Collective motion of chemically powered nanomotors, PhD Thesis, University of Toronto, Canada, 2018.
- J. S. Centre, JURECA: General-purpose supercomputer at Jülich Sumpercomputing Centre, Journal of large-scale research facilities, 2016, 2, A12 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Movies show the aggregation process of self-thermophilic dimers with and without hydrodynamic interactions. See DOI: https://doi.org/10.1039/d2sm00523a |
| This journal is © The Royal Society of Chemistry 2022 |