Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modulation of lipid vesicle–membrane interactions by cholesterol†
Choon-Peng
Chng
 a,
K. Jimmy
Hsia
*ab and
Changjin
Huang
a,
K. Jimmy
Hsia
*ab and
Changjin
Huang
 *a
*a
aSchool of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore 639798, Republic of Singapore. E-mail: kjhsia@ntu.edu.sg; cjhuang@ntu.edu.sg
bSchool of Chemical and Biomedical Engineering, Nanyang Technological University, Singapore 637459, Republic of Singapore
First published on 26th August 2022
Abstract
Nanoscale lipid vesicles are attractive vehicles for drug delivery. Although often considered as soft nanoparticles in terms of mechanical deformability, the fluidic nature of the lipid membrane makes their interactions with another lipid membrane much more complex. Cholesterol is a key molecule that not only effectively stiffens lipid bilayer membranes but also induces membrane fusion. As such, how cholesterol modulates lipid vesicle–membrane interactions during endocytosis remains elusive. Through systematic molecular dynamics simulations, we find that membrane stiffening upon incorporating cholesterol reduces vesicle wrapping by a planar membrane, hindering endocytosis. Membrane fusion is also accelerated when either the vesicle or the planar membrane is cholesterol-rich, but fusion becomes minimal when both the vesicle and planar membrane are cholesterol-rich. This study provides insights into vesicle–membrane interactions in the presence of cholesterol and enlightens how cholesterol may be used to direct the cellular uptake pathways of nanoliposomes.
1 Introduction
Nanoscale artificial lipid vesicles, also known as nanoliposomes, have attracted extensive attention as promising drug delivery carriers over the past few decades.1,2 Because of their great biocompatibility, non-immunogenicity and minimal toxicity, the majority of nanomedicines approved by the Food and Drug Administration (FDA) are nanoliposome-based.3,4 In biological systems, nanoscale lipid vesicles released by cells, termed small extracellular vesicles (sEVs), serve as carriers of biologically active molecules and play an essential role in cell–cell communications.5–7 Motivated by their high biocompatibility and potentially high targeting specificity due to their natural origin, sEVs have been engineered to deliver therapeutic and imaging molecules.8 In both cell–cell communications and drug delivery applications, lipid vesicles have to be either endocytosed by the host cell or fused with the membrane of the host cell in order for the vesicle cargo to be released into targeted cells.5 Hence, understanding the mechanism of vesicle–membrane interactions is important from both biological and biomedical standpoints.The interaction of rigid nanoparticles (NPs) with a fluid membrane has been extensively studied. Possible endocytic pathways include membrane wrapping and direct penetration. Driven by the adhesion energy between the NP and the membrane, the wrapping of a NP by a planar membrane is resisted by the elastic deformation in the membrane,9 and regulated by the design of the NP, such as particle size10–12 and shape.13–16 The direct penetration of NPs through a fluid membrane tends to occur when the NPs approach the membrane with a high initial velocity and may occur in a cooperative manner mediated by the NP surface chemistry.17,18 For deformable NPs, the NP stiffness further complicates their interaction with the planar membrane. By modelling both elastic vesicles and planar membrane as continuum surfaces with out-of-plane bending rigidities, Yi et al. predicted that the large deformation of soft vesicles during the early stage of wrapping would make full wrapping more difficult to occur than their stiff counterparts.19 The theoretical analysis by Sun et al. showed that a rigid ellipsoidal NP with an aspect ratio of 2 takes 30% more membrane deformation energy to be fully wrapped compared to a rigid spherical NP with the same volume, which explains why a lower cellular uptake efficiency is observed for their softer NPs with a polymeric core and lipid shell.20 The enhanced cellular uptake of stiffer NPs has also been confirmed both experimentally using various other types of deformable NPs (e.g., hydrogels, silica, polymer micelles, and hybrid nanolipogels),21–25 and computationally using molecular dynamics (MD) simulations.26 However, contradictory results have also been reported in some other experiments.27–29
More importantly, changes in NP stiffness in existing experimental and simulation studies are due to the nature of the NP core for lipid-shell NPs,20,21,29 the cross-linking level in hydrogel NPs,22,27 or the use of different silica precursors in silica-based NPs.23 Although lipid vesicles have been represented using elastic NPs in theoretical analyses,19 the fluidic nature of the lipid membrane at the molecular level allows many other endocytic pathways to occur in addition to membrane wrapping. Examples include hemi-fusion or complete fusion of the vesicle with the membrane or even rupture of the vesicle as revealed by previous simulation studies.30–33 Furthermore, lipid membrane stiffness may be regulated by the lipid composition and membrane curvature,34 or lipid peroxidation in a oxidation site-dependent manner.35,36 Considering that both vesicle wrapping and membrane fusion may be modulated by lipid membrane stiffness, how membrane stiffness regulates vesicle–membrane interactions remains unclear.
It is known that the stiffness of lipid bilayer membranes increases with the incorporation of sterol molecules.37,38 Both previous experiments and MD simulations have shown that increasing the cholesterol content of lipid bilayer membranes to 50 mol% increases the relative bending rigidity by about 3–3.5-fold.37–39 This is because cholesterol drives lipids to pack more densely, leading to a reduction in the area per lipid.39 On the other hand, cholesterol plays an important role in membrane fusion by modulating and stabilizing membrane fusion pores.40 Due to its intrinsic negative curvature as a result of its small polar headgroup relative to its apolar tail, cholesterol lowers the energy required for two adjacent membranes to form concave-shaped lipid stalks, which are intermediate states in the vesicle–membrane fusion process.40–42 Stalk formation is also a fusion mechanism for cell membranes under dehydration.43,44 Lee et al. demonstrated that increasing the cholesterol content in planar membranes enhanced their fusion with protein-free liposomes.45 During vesicle–membrane docking mediated by soluble N-ethylmaleimide-sensitive factor attachment protein receptor (SNARE) complex assembly, cholesterol was shown to dramatically stabilize the open state of exocytotic membrane fusion pores formed (via lowering the free energy of fusion-pore formation) and consequently facilitate content release.46 Additionally, the presence of 20 mol% cholesterol in membranes was found to completely abolish the efficacy of a peptide-based membrane fusion inhibitor.47,48 Thus, cholesterol may influence vesicle–membrane interactions via two different aspects: increasing lipid membrane stiffness and enhancing vesicle–membrane fusion. These two effects are not mutually exclusive. It has been suggested that cholesterol stabilizes SNARE-mediated exocytic fusion pores via both its preference of negative membrane curvature and its enhancement of membrane bending rigidity.49 But it remains unclear how these two aspects of cholesterol affect the lipid vesicle–membrane interactions during endocytosis.
In this study, we have performed coarse-grained MD simulations to investigate the role of cholesterol in vesicle–membrane interactions during endocytosis. Coarse-grained MD simulations using the popular Martini force-field have been successfully applied to model phospholipid vesicle–vesicle fusion50,51 and to study the distribution of cholesterol in the mammalian plasma membrane composed of various lipid types.52 The fractions of cholesterol in both vesicle and planar membranes are varied systematically. Our simulations demonstrate that the presence of cholesterol in either the vesicle or planar membrane accelerates membrane fusion and consequently hinders the occurrence of further wrapping. However, minimal membrane fusion is observed when both membranes are incorporated with high levels of cholesterol. In this case, the wrapping of the vesicle by the planar membrane is hindered by the increased membrane stiffness. Our results thus provide new molecular-level insights into nanoliposome–membrane interactions in the presence of cholesterol as a membrane stiffening agent and highlight the potential function of cholesterol as an additive to dictate the endocytic pathways of nanoliposomes.
2 Model
MD simulations of coarse-grained lipid vesicles
MD simulations were carried out for 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid vesicles with different fractions of cholesterol using the coarse-grained Dry Martini force-field version 2.1 implemented in GROMACS version 4.6.7 software.51,53 In the Martini model, about four non-hydrogen atoms are grouped into one particle. Due to coarse-graining, dynamics are sped-up by about 4 times and hence the effective time sampled is about 4 times that of an equivalent atomistic simulation.54 Times reported here are simulation times, not effective times. The dry (i.e., implicit solvent) Martini model was chosen for computational efficiency. It has been demonstrated that standard and dry versions of Martini predict a similar vesicle fusion process.51 As cholesterol is not available in Dry Martini, standard Martini force-field was adopted but with a more attractive interaction between the polar particle of cholesterol (type SP1) and charged lipid head-group particles (type Q0/Qa).51 The initial configurations and simulation set-up files for lipid vesicles (POPC with 0%, 20% or 50% cholesterol) were generated using the Martini Vesicle Maker within the CHARMM-GUI web-based platform.55,56 Lipid vesicles were generated with an initial outer diameter of 20 nm with six symmetrically placed 2 nm-diameter pores for exchange of inner and outer water as well as facilitating lipid flip-flops between the inner and outer leaflets.After energy minimization steps, stochastic dynamics simulations were carried out with progressively reduced restraints on lipid tails to close the pores with the simulation time-step as 20 fs. Unrestrained simulations were subsequently carried out in canonical (NVT) ensemble for 200 ns. Electrostatic interactions were computed using the reaction-field method with a dielectric constant of 15 and cut-off distance of 1.1 nm as suggested by CHARMM-GUI Martini Maker for Dry Martini.57 van der Waals (vdW) interactions were computed using the cut-off method with the same distance of 1.1 nm. The system temperature was maintained at 310 K with the velocity-rescale thermostat with a time constant of 4 ps.
MD simulations of coarse-grained lipid planar membranes
As the lipid planar membrane size we need to generate is larger than the maximum size that can be generated using the CHARMM-GUI server (at 1 million atoms or particles),57 we used the INSert membrane (INSane) tool implemented in Python58 to generate POPC lipid bilayer membranes with a size of about 160 nm × 160 nm (85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 coarse-grained lipids) and various cholesterol levels (0%, 20%, and 50%). Simulation setup files were obtained from CHARMM-GUI webserver under Martini Bilayer Maker using the Dry Martini model.55 Again, the interaction between polar bead of cholesterol and charged lipid head-group particles made more attractive as suggested for use with Dry Martini as mentioned above. Periodic boundary conditions were applied in all directions. After energy minimization steps, stochastic dynamics simulations were carried out with progressively reduced positional restraints on lipid head-groups (with force constants reducing from 200 to 10 kJ mol−1 nm−2 by halving each time) with the simulation time-step as 20 fs (10 fs for membranes containing cholesterol). Unrestrained simulations were subsequently carried out in the isothermal–isobaric (NPT) ensemble for 100 ns. Similar simulation parameters were used for lipid vesicles (see above) except that pressure was maintained at 0 bar for a tensionless membrane via semi-isotropic coupling (membrane plane in the X–Y directions coupled together but separately from the Z direction) using the Berendsen barostat with a time constant of 4 ps and compressibility of 3.4 × 10−5 bar−1.
696 coarse-grained lipids) and various cholesterol levels (0%, 20%, and 50%). Simulation setup files were obtained from CHARMM-GUI webserver under Martini Bilayer Maker using the Dry Martini model.55 Again, the interaction between polar bead of cholesterol and charged lipid head-group particles made more attractive as suggested for use with Dry Martini as mentioned above. Periodic boundary conditions were applied in all directions. After energy minimization steps, stochastic dynamics simulations were carried out with progressively reduced positional restraints on lipid head-groups (with force constants reducing from 200 to 10 kJ mol−1 nm−2 by halving each time) with the simulation time-step as 20 fs (10 fs for membranes containing cholesterol). Unrestrained simulations were subsequently carried out in the isothermal–isobaric (NPT) ensemble for 100 ns. Similar simulation parameters were used for lipid vesicles (see above) except that pressure was maintained at 0 bar for a tensionless membrane via semi-isotropic coupling (membrane plane in the X–Y directions coupled together but separately from the Z direction) using the Berendsen barostat with a time constant of 4 ps and compressibility of 3.4 × 10−5 bar−1.
Estimation of the biophysical properties of lipid membranes
To characterize the biophysical properties of membranes with different fractions of cholesterol, we have generated a smaller membrane with 2048 lipids based on the Dry Martini model using the Martini Bilayer Maker for computational efficiency. Each membrane was equilibrated for 2000 ns and the last 500 ns was used for analyses. Bilayer thickness was calculated as the difference in the mean locations of PO4 particles between the two leaflets. Distributions of PO4 particle positions relative to the centre of mass of the bilayer along its normal direction were extracted from each simulation snapshot. The average thickness over a series of simulation snapshots for each membrane was reported. The area compressibility modulus KA was calculated using the membrane area fluctuation method with KA = KBT〈A〉/〈δA2〉, where 〈A〉 is the average projected membrane area, 〈δA2〉 is the mean square fluctuation, kB is the Boltzmann constant and T is the temperature.59 The membrane bending modulus kC is then estimated as kC = KA(h − 1)2/24 according to the polymer brush model of the lipid bilayer, where h is the bilayer thickness defined above.60 The obtained area compressibility moduli and corresponding bending moduli are presented in Table S1 (ESI†). The order parameter of the bonds along each lipid molecule was calculated according to the following definition: P2 = (3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈θ〉 − 1)/2, where θ is defined as the angle between the bond vector and the bilayer normal for planar bilayers. The angle brackets represent an average over all lipids in the membrane and over simulation time.
〈θ〉 − 1)/2, where θ is defined as the angle between the bond vector and the bilayer normal for planar bilayers. The angle brackets represent an average over all lipids in the membrane and over simulation time.
MD simulations and characterization of vesicle–membrane interactions
Equilibrated lipid vesicles with different fractions of cholesterol were placed atop the centre of equilibrated planar membranes also with different fractions of cholesterol (Fig. S1, ESI†). As both systems had been equilibrated separately, a reduced number of equilibration steps with positional restraints on lipid head-groups were used (with force constants 200, 100 and 10 kJ mol−1 nm−2) before unrestrained simulations were performed. These steps were performed as a pre-caution against possible steric clash in case vesicle head-groups were placed too close to planar membrane head-groups. The simulations were stopped when the vesicle wrapping fraction (fraction of vesicle surface that is wrapped by the planar membrane) reached a steady state, which varied from 300 ns to 1200 ns among the vesicle–membrane pairs simulated. Although the system may have not attained final equilibrium at the end of our simulation as cholesterol redistribution may be still ongoing, the wrapping fraction is no longer changing since further wrapping stops after fusion stalks are formed.The wrapping fraction was computed by determining the number of head-group PO4 particles (representing the phosphate groups) of the inner leaflet of the vesicle that were within 4 nm of the planar membrane lipid head-group PO4 particles. The reason why vesicle inner leaflet lipids were used as a reference is that using outer leaflet lipids could potentially produce an over-estimation of the wrapping fraction in the cases where extensive vesicle lipid leakage due to membrane fusion onto the planar membrane occurred. Lipids from the inner leaflet remained within the inner leaflet of the vesicle as inter-leaflet flip-flop is a thermally activated process and is unlikely to occur on the microsecond time-scale of our simulations.61 To determine the number of vesicle lipids that leaked from the vesicle surface, we first identified the vesicle lipids that were within 10 nm of planar membrane lipids. Next, head-to-tail vectors of these lipids were computed using PO4 particles as the “head” and the last particle of each fatty acid tail as the “tail”. If both head-to-tail vectors of a lipid were oriented at an angle >90° to the radial vector taken from the vesicle centre to the “head” particle, this lipid was then deemed to have “flipped” its orientation and thus leaked from the vesicle surface. This approach, however, may under-estimate the number of cholesterol molecules leaked from vesicle as the molecules could readily undergo flip-flop across the planar membrane leaflets. Hence, a different approach was devised whereby the radius of the vesicle–membrane contact rim was estimated and any cholesterol that drifts further than this radius from the centre of the vesicle is considered as leaked from the vesicle. Similarly, any membrane lipid or cholesterol moving closer than the contact rim radius and higher than the maximum z-location of the contact rim is considered to have migrated onto the vesicle.
The aspect ratio of the vesicle was defined as the ratio of the vesicle height to its width. Due to vesicle lipid leakage mentioned above, the height and width of the vesicle were determined based on the locations of vesicle inner leaflet lipids and the membrane thickness. Using vesicle outer leaflet lipids could lead to over-estimation of the vesicle width as leaked lipids diffuse away on the planar membrane.
3 Results and discussion
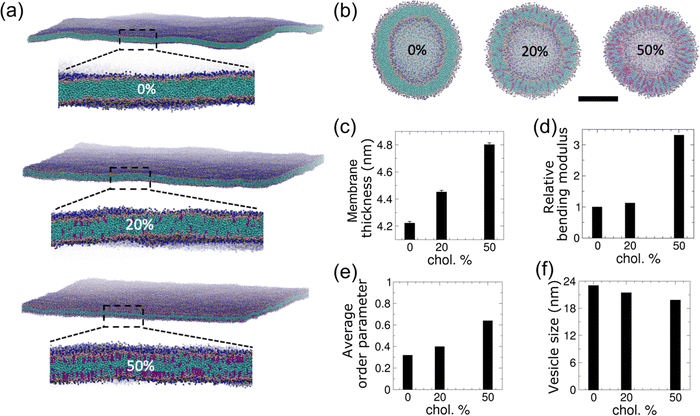
We incorporated cholesterol of various fractions into both the planar and vesicle membranes as shown in Fig. 1(a and b). As expected, the equilibrated planar membranes are found to become thicker as the cholesterol content increases (Fig. 1(c)). The membrane bending modulus increases by 3.3-fold as the membrane cholesterol fraction increases from 0% to 50% (Fig. 1(d)). The increase in membrane thickness and bending modulus with cholesterol agrees with previous experimental observations,39 and is due to an enhancement in the lipid packing induced by cholesterol (Fig. 1(e)). As a result of the enhanced lipid packing, equilibrated vesicles become smaller with increasing cholesterol content (Fig. 1(f)). The vesicle diameter reduces by 7% and 14% when the vesicle membrane is mixed with cholesterol at a fraction of 20% and 50%, respectively. As cholesterol molecules could undergo lipid flip-flop across lipid bilayer leaflets on the time-scale of tens of nanoseconds,62 we monitored the cholesterol distributions within the inner and outer leaflets of vesicle membranes. We found that cholesterol molecules tend to become enriched in the inner leaflet of the vesicle (Fig. S2(a, b) and Table S2, ESI†). In comparison, cholesterol fractions in either leaflet of planar membranes remain unchanged (Fig. S2(c and d), ESI†). Both vesicles with 20% and 50% cholesterol showed a higher ratio of the number of cholesterol molecules in the inner leaflet to that in the outer leaflet as compared to that of PC lipids present in the vesicles, with the 20% cholesterol vesicle showing a more significant increase (Table S2, ESI†). For comparison, the ratio of PC lipids in the inner to the outer leaflet is not significantly different (0.62 vs. 0.66) between the two vesicles with different cholesterol levels. The lower lipid packing order in the 20% cholesterol vesicle might have facilitated the migration of cholesterol molecules from the outer to the inner leaflet. This observation agrees with the expectation that cholesterol molecules’ affinity to negatively curved membrane makes them localize in concave membrane regions.To investigate how cholesterol in the vesicle membrane modulates vesicle–membrane interactions, we have placed vesicles with different cholesterol levels adjacent to a planar POPC membrane (Fig. 2). The electrostatic and vdW interactions between the vesicle and the planar membrane drive the planar membrane to wrap around the vesicle; however, vesicle wrapping is penalized by the membrane bending energy in both membranes. The vesicle with 0% cholesterol undergoes dramatic shape changes as it is gradually wrapped by the planar membrane (Fig. 2(a) and Movie S1, ESI†). During wrapping, the vesicle shape evolution undergoes base widening to maximize the contact area with the planar membrane (Fig. 2(b)), deformation into an oblate shape to facilitate rapid wrapping, and the slowing down of wrapping due to the high membrane curvature around the contact rim (Fig. 2(c)). In order for the planar membrane to continue to wrap the vesicle, the vesicle deforms from the oblate shape into a rod, allowing the system to by-pass the high bending energy needed to continue wrapping an oblate vesicle with high curvatures.14,30 The aspect ratio of the vesicle reaches a value higher than 2.0 (Fig. 2(b)). This shape evolution resembles that reported by Yue and Zhang for their vesicle–membrane endocytosis simulation using a more simplified 3-bead lipid model,30 and is consistent with the rotational pathway of rigid non-spherical NPs reported previously.13,15,30,63
 | ||
| Fig. 2 Effect of cholesterol in lipid vesicles on their interaction with a cholesterol-free planar membrane. (a) Zoomed-in cutaway views of simulation snapshots of vesicle–membrane interaction for POPC vesicles with 0%, 20% and 50% cholesterol on POPC planar membrane. Lipid particles are colored as in Fig. 1. Only PO4 particles are shown for the planar membrane for clarity. (b) The temporal evolution of the vesicle aspect ratios, defined as the ratio of height of the vesicle to its width. (c) The temporal evolution of the wrapping fractions, defined as the fraction of the wrapped vesicle surface. (d) The temporal evolution of the number of leaked vesicle PC lipids. | ||
Membrane fusion between the vesicle and planar membrane is observed during the late stage of wrapping after 0.5 μs and eventually hinders complete wrapping to occur (Fig. 2(c and d)). It is facilitated by the exposure of hydrophobic defects of the membranes within the circular rim at the interface between wrapped and unwrapped regions as a result of the large and positive membrane curvature of both the vesicle membrane and the apposed planar membrane. Due to the lack of solvent in our simulations, lipid flip-flops across the two bilayers are expected to be greatly accelerated as hydrophobic lipid tails do not suffer high energetic penalty for exposure to polar water particles, resulting in the enhancement of vesicle–membrane adhesion and membrane fusion probability.51 Despite this limitation, it has been confirmed that the vesicle fusion process simulated using the solvent-free Martini model is the same as that predicted by the standard Martini model.51 In terms of kinetics, the mobility of coarse-grained phospholipids and cholesterol molecules is expected to be faster in our coarse-grained models due to smoother energy landscapes and lack of friction from atomistic degrees of freedom as pointed out by the Martini model authors.64 As a result, vesicle and planar membrane deformation as well as lipid/cholesterol exchange across the fused regions are expected to be accelerated as compared to atomistic models.
The vesicle–membrane interactions are affected by the presence of cholesterol in the vesicle membrane. The stiffer vesicles with cholesterol deform to much lower extents when wrapped by the planar membrane. A vesicle with 20% cholesterol first changes to an ellipsoidal shape as its base does not flatten as much as the cholesterol-free vesicle (Fig. 2(a and b)). As it gets further wrapped by the membrane, the vesicle becomes elongated but to a smaller degree in comparison to the more deformable cholesterol-free vesicle. The aspect ratio of deformed vesicle only reaches about 1.5 at 1.2 μs as compared to >2.0 for the cholesterol-free vesicle. The slower wrapping rate (relative to the cholesterol-free vesicle) and reduced final wrapping fraction of cholesterol-containing vesicles may be attributed to its slightly lower deformability (Fig. 2(c)). Although the theoretical analysis by Yi et al. showed that a stiff vesicle is more likely to be fully wrapped than its soft counterpart,19 the same group also predicted that wrapping of softer NPs is kinetically faster which is consistent with the relative wrapping rates observed here.65 The leakage of PC lipids and cholesterol from the 20% cholesterol vesicle occurs much later (after 1 μs) and to a much lower extent than the cholesterol-free vesicle (Fig. 2(d) and Fig. S3(a), ESI†). The results suggest that the reduced membrane fusion is due to the reduced local vesicle membrane curvature at the interface between wrapped and unwrapped vesicle surfaces compared to their cholesterol-free counterpart. With 50% cholesterol incorporated into the vesicle membrane, the vesicle remains nearly spherical initially and then becomes ellipsoidal in shape with an aspect ratio below 1.0 (Fig. 2(a, b) and Movies S2, ESI†). Membrane fusion starts much earlier (at ∼0.3 μs) with significant leakage of PC lipids and cholesterol from the vesicle along the rim between unwrapped and wrapped vesicle regions (Fig. 2(d) and Fig. S3(a), ESI†), which hampers the occurrence of further vesicle wrapping as the membranes are torn at the fused region. Despite being the stiffest vesicle considered here, the wrapping fraction achieved is limited by membrane fusion, highlighting the important effect of cholesterol on vesicle–membrane interactions. While lipids and cholesterol migrate from the vesicle to the planar membrane, the lipids in the planar membrane also migrate to the vesicle via the fused membrane regions. The number of PC lipids moving from the planar membrane onto the vesicle (Fig. S3(b), ESI†) shows a similar trend and final value as for the movement of PC lipids from the vesicle onto the membrane in Fig. 2(d), suggesting that a balanced process has been achieved across the fused contact rim. As the outer leaflet of the vesicle membrane is fused with the upper leaflet of the planar membrane, seemingly sharp bends or kinks appear around the contact rim (Fig. 2(a) 50% cholesterol vesicle). Such kinks may be due to the following two effects. First, the adhered vesicle resembles a fluid droplet on a soft hydrophilic surface which shows a kink at the fluid–solid–air triple junction (e.g. capillary action of fluid on a solid surface).66 Because of the finite bending stiffness of the lipid membrane, such kinks are not prevalent in most of our simulations. Second, the vesicle and planar membranes become continuous around the contact rim upon fusion, which enhances kink formation. Fusion and associated kink formation slow down or completely stop further wrapping of the vesicle, making complete internalization of vesicles extremely difficult.
Lipid vesicle–membrane fusion has been studied in great detail by Grafmuller et al. using dissipative particle dynamics (DPD) simulations.32,33 Their studies found that fusion probability is modulated by membrane tension and the time to fusion increases exponentially with decreasing tension.32 For a tensionless membrane, vesicle adhesion with limited fusion is expected,33 which is consistent with our observations for the cases with low cholesterol levels in the vesicle. It has also been found that vesicle–membrane fusion was governed by two successive energy barriers: a first barrier for flips of lipid molecules across the two bilayers, and a second barrier for the nucleation of a hemi-fused bilayer patch.32 The first energy barrier corresponds to the splayed lipid configuration with one chain inserted in each membrane, resulting in the exposure of the hydrophobic tails to the solvent.67 In our solvent-free simulation, this barrier should be significantly lowered, resulting in an acceleration of the vesicle–membrane fusion process. The second energy barrier is also lowered with the help of cholesterol molecules with intrinsic negative curvature.40–42
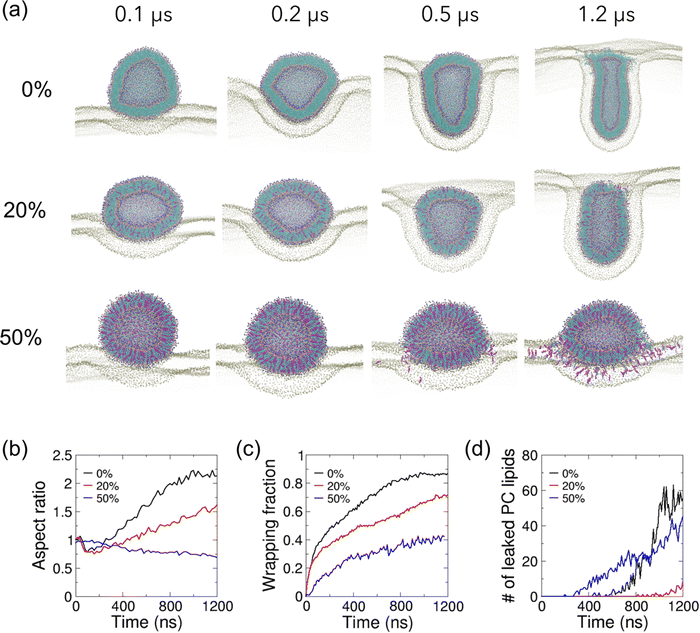
We next investigate how cholesterol in the planar membrane modulates the vesicle–membrane interactions by incorporating cholesterol into the planar membrane at various fractions. The cholesterol-free vesicle follows a similar shape transformation pathway on the planar membrane with 20% cholesterol to that on the cholesterol-free membrane (Fig. 3(a and b)). Although the vesicle on the 20% cholesterol membrane is less elongated compared to that on the cholesterol-free membrane during the late stage of wrapping, the temporal evolution of the wrapping fraction is highly similar on these two membranes (Fig. 3(c)), despite the 20% cholesterol membrane being 1.1 times stiffer (Fig. 1(e)). However, an interestingly different picture emerges when the planar membrane is incorporated with 50% cholesterol. The vesicle undergoes a similar initial spreading on the planar membrane as the other two cases to reach an aspect ratio of 0.75 (Fig. 3(b)). However, the vesicle maintains a spread shape throughout the rest of the simulation (Fig. 3(a) and Movie S3, ESI†). The much stiffer planar membrane shows much reduced deformation and the vesicle is only adhered onto the membrane with a small wrapping fraction of 0.25 (Fig. 3(c)). Membrane fusion occurs in the very early stage of wrapping, resulting in significant exchange of PC lipids from vesicle to membrane (Fig. 3(d)), and exchange of cholesterol and PC lipids from the membrane to the vesicle (Fig. S4, ESI†), consistent with the experimental observation of about 3.5 times higher liposome–membrane fusion rates with 30% higher cholesterol content in the membrane.45 Similar membrane fusion-induced kinks are observed around the contact rim as observed above for the 50% cholesterol vesicle on the cholesterol-free planar membrane (Fig. 2(a)).
 | ||
| Fig. 3 Effect of cholesterol in lipid planar membranes on their interaction with a cholesterol-free lipid vesicle. (a) Zoomed-in cutaway views of simulation snapshots of vesicle–membrane interaction for POPC vesicles on POPC planar membranes with 0%, 20% and 50% cholesterol. Lipid particles are colored as in Fig. 1. Only PO4 particles and cholesterol are shown for the planar membrane for clarity. (b) The temporal evolution of the vesicle aspect ratios, defined as the ratio of height of the vesicle to its width. (c) The temporal evolution of the wrapping fractions, defined as the fraction of wrapped vesicle surface. (d) The temporal evolution of the number of leaked vesicle PC lipids. | ||
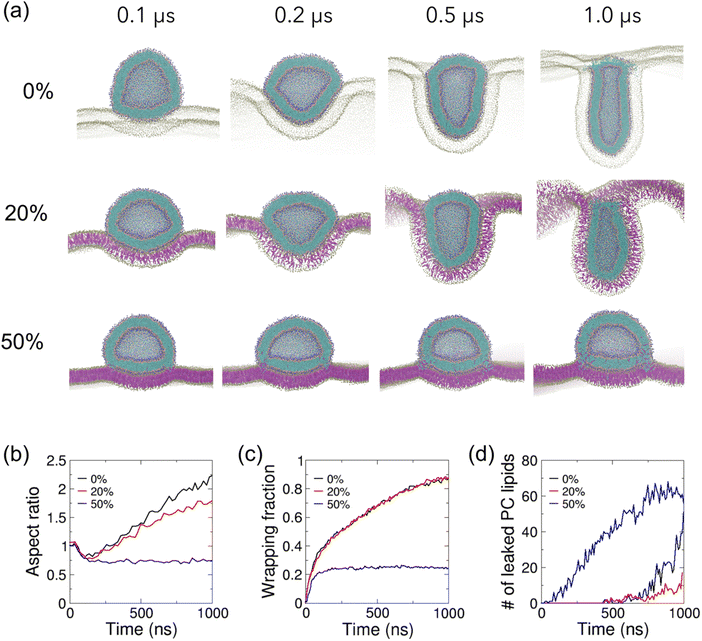
Variations in the steady-state vesicle shape and the degree of membrane wrapping at various cholesterol contents in the vesicle and planar membrane are shown in Fig. S5 (ESI†). Fig. 4 shows phase diagrams depicting the variation in the wrapping of the vesicle as well as the propensity of vesicle–membrane fusion as a function of cholesterol fraction in the vesicle and planar membranes. The wrapping fraction and fusion propensity data used in Fig. 4 are presented in Tables S3 and S4 (ESI†), respectively. The diagrams clearly show that the wrapping of the vesicle by the planar membrane is easy when both membranes have low cholesterol contents (“highly wrapped” region in Fig. 4(a)). Wrapping becomes harder as the cholesterol content in either or both membranes increases, with the wrapping of vesicle being most difficult when both membranes contain 50% cholesterol (“limited wrapping” region in Fig. 4(a) and see also Fig. S6 and Movie S4, ESI†). In contrast, the membrane fusion level is low when both membranes contain either low fraction or high fraction of cholesterol (“limited fusion” region in Fig. 4(b)). The highest membrane fusion propensity occurs when either the vesicle or the planar membrane contains a high fraction of cholesterol (“extensive fusion” regions in Fig. 4(b)). The most severe membrane fusion is observed for high cholesterol content in the planar membrane but low cholesterol content in the vesicle membrane. In this case, the vesicle is highly deformable and therefore exposes lipid packing defects along the contact rim where cholesterol molecules may fit (see Fig. 3(a)). When both vesicle and planar membranes contain high cholesterol content, planar membrane bending and vesicle deformation are both limited (Fig. S6, ESI†), inhibiting the exposure of lipid packing defects and hence membrane fusion.
 | ||
| Fig. 4 Cholesterol content in membranes modulates vesicle wrapping and membrane fusion. Phase diagrams showing variation of (a) wrapping fraction and (b) membrane fusion propensity as a function of cholesterol content in vesicle and planar membranes. Membrane fusion propensity is defined as the ratio of the number of leaked vesicle PC lipids to the number of vesicle PC lipids that are wrapped by the planar membrane at the steady state, normalized by the maximum ratio observed. Solid circles are for values >0.5 and open circles are for values ≤0.5. Dashed lines act as a guide to the eye by partitioning the phase diagrams into regions with values lower or higher than 0.5. Available data points are shown in Tables S3 and S4 (ESI†). | ||
Our coarse-grained lipid vesicle–membrane simulation results suggest that complete internalization of bare lipid vesicles by lipid membranes is difficult to achieve, in contrast to elastic NPs with strong adhesion with the planar membrane as reported in previous MD simulations.68 Simulations by Sun et al. also demonstrated that polymeric core–water–lipid shell NPs deformed in a similar way to lipid vesicles and also remained partially wrapped by the membrane.20 In agreement with the theoretical analysis by Yi et al., their wrapping phase diagram clearly indicates that full wrapping of very soft elastic NPs such as lipid vesicles is difficult to achieve unless the adhesion interaction between vesicle and membrane is sufficiently strong.19 In addition to large membrane deformations involved in the wrapping of lipid vesicles, our work demonstrates that membrane fusion might be an additional complication that hinders the complete internalization of lipid vesicles by lipid membranes. Nevertheless, fusion of vesicles with membranes can also be an efficient endocytic pathway for cellular uptake. Extracellular vesicles may be uptaken by recipient cells either via fusion with the plasma membrane or endocytosed.5 The membrane fusion-enabled cell internalization pathway effectively enhances the uptake of soft nanolipogels.29 Fusogenic liposomes have also been demonstrated to be efficient nanocarriers to deliver intracellular proteins to the cell cytoplasm via fusion of the liposome with the cellular membrane.69 Csiszár et al. have explored this balance between fusion or wrapping of the vesicle by the membrane by modulating the lipid composition of vesicles. It was found that conical-shaped lipids with a small head group such as phosphoethanolamine (PE) favors fusion whereas cylindrical lipids such as phosphatidylcholine (PC) favors wrapping.70 Here, membrane fusion is promoted by conical shaped cholesterol in the presence of large, positive membrane curvatures.
4 Conclusions
In this work, we seek to understand how cholesterol in lipid bilayer membranes of nanoscale vesicles and planar membranes modulates their interactions. By performing systematic coarse-grained MD simulations, we found that cholesterol hinders the wrapping of vesicles by a planar membrane via mediating the membrane stiffness and/or fusion propensity between the membranes. Specifically, vesicle wrapping by the planar membrane is most complete when both membranes are cholesterol-poor, with also low propensity for membrane fusion. When either the planar or vesicle membrane is cholesterol-rich, vesicle wrapping is hindered with an increase in propensity of membrane fusion, likely due to the exposure of lipid packing defects around highly bent membrane regions with positive curvatures. Cholesterol molecules may then promote the formation of membrane fusion pores in those regions.40–42 However, when both membranes are cholesterol-rich, bending of each membrane becomes limited which hinders endocytosis as well as the exposure of lipid packing defects on either membrane. Our results highlight the complex interplay of cholesterol both as a membrane stiffener and as a membrane-fusion enhancer in the uptake of cholesterol-containing liposomes. Our study suggests that cholesterol can be used an effective additive to affect the endocytosis pathways of nanoliposomes.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
K. J. H. would like to acknowledge financial support from Nanyang Technological University (start-up grant M4082428). C. H. would also like to acknowledge financial support from Nanyang Technological University (start-up grant M4082352) and Ministry of Education, Singapore, under its Academic Research Fund Tier 2 (MOE-T2EP50121-0004). The computational work for this article was fully performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).References
- Y. Li, H. Cong, S. Wang, B. Yu and Y. Shen, Biomater. Sci., 2020, 8, 6442–6468 RSC.
- B. Almeida, O. K. Nag, K. E. Rogers and J. B. Delehanty, Molecules, 2020, 25, 5672 CrossRef CAS.
- E. Beltrán-Gracia, A. López-Camacho, I. Higuera-Ciapara, J. B. Velázquez-Fernández and A. A. Vallejo-Cardona, Nanomedicine review: Clinical developments in liposomal applications, Springer, Vienna, 2019, vol. 10 Search PubMed.
- A. C. Anselmo and S. Mitragotri, Bioeng. Transl. Med., 2019, 4, 1–16 CrossRef.
- G. Raposo and W. Stoorvogel, J. Cell Biol., 2013, 200, 373–383 CrossRef CAS PubMed.
- S. L. N. Maas, X. O. Breakefield and A. M. Weaver, Trends Cell Biol., 2017, 27, 172–188 CrossRef CAS PubMed.
- L. Margolis and Y. Sadovsky, PLoS Biol., 2019, 17, 1–12 CrossRef.
- X. Luan, K. Sansanaphongpricha, I. Myers, H. Chen, H. Yuan and D. Sun, Acta Pharmacol. Sin., 2017, 38, 754–763 CrossRef CAS PubMed.
- M. Deserno, Phys. Rev. E: Stat. Nonlinear, Soft Matter Phys., 2004, 69, 1–14 CrossRef PubMed.
- H. Gao, W. Shi and L. B. Freund, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9469–9474 CrossRef CAS.
- H. Yuan, C. Huang and S. Zhang, PLoS One, 2010, 5, e13495 CrossRef.
- S. Zhang, H. Gao and G. Bao, ACS Nano, 2015, 9, 8655–8671 CrossRef CAS PubMed.
- C. Huang, Y. Zhang, H. Yuan, H. Gao and S. Zhang, Nano Lett., 2013, 13, 4546–4550 CrossRef CAS PubMed.
- S. Dasgupta, T. Auth and G. Gompper, Soft Matter, 2013, 9, 5473–5482 RSC.
- S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693 CrossRef CAS PubMed.
- Y. Li, M. Kröger and W. K. Liu, Nanoscale, 2015, 7, 16631–16646 RSC.
- H. Zhang, Q. Ji, C. Huang, S. Zhang, B. Yuan, K. Yang and Y. Q. Ma, Sci. Rep., 2015, 5, 1–10 Search PubMed.
- Y. Zhang, Z. Meng, X. Qin and S. Keten, Nanoscale, 2018, 10, 4761–4770 RSC.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 1–5 CrossRef.
- J. Sun, L. Zhang, J. Wang, Q. Feng, D. Liu, Q. Yin, D. Xu, Y. Wei, B. Ding, X. Shi and X. Jiang, Adv. Mater., 2015, 27, 1402–1407 CrossRef CAS PubMed.
- M. Yu, L. Xu, F. Tian, Q. Su, N. Zheng, Y. Yang, J. Wang, A. Wang, C. Zhu, S. Guo, X. X. Zhang, Y. Gan, X. Shi and H. Gao, Nat. Commun., 2018, 9, 1–11 CrossRef PubMed.
- A. C. Anselmo, M. Zhang, S. Kumar, D. R. Vogus, S. Menegatti, M. E. Helgeson and S. Mitragotri, ACS Nano, 2015, 9, 3169–3177 CrossRef CAS.
- Y. Hui, D. Wibowo, Y. Liu, R. Ran, H. F. Wang, A. Seth, A. P. J. Middelberg and C. X. Zhao, ACS Nano, 2018, 12, 2846–2857 CrossRef CAS PubMed.
- T. Stern, I. Kaner, N. Laser Zer, H. Shoval, D. Dror, Z. Manevitch, L. Chai, Y. Brill-Karniely and O. Benny, J. Controlled Release, 2017, 257, 40–50 CrossRef CAS.
- Y. Hui, X. Yi, D. Wibowo, G. Yang, A. P. J. Middelberg, H. Gao and C. X. Zhao, Sci. Adv., 2020, 6, 1–11 Search PubMed.
- Z. Shen, H. Ye and Y. Li, Phys. Chem. Chem. Phys., 2018, 20, 16372–16385 RSC.
- W. Liu, X. Zhou, Z. Mao, D. Yu, B. Wang and C. Gao, Soft Matter, 2012, 8, 9235–9245 RSC.
- Z. Teng, C. Wang, Y. Tang, W. Li, L. Bao, X. Zhang, X. Su, F. Zhang, J. Zhang, S. Wang, D. Zhao and G. Lu, J. Am. Chem. Soc., 2018, 140, 1385–1393 CrossRef CAS.
- P. Guo, D. Liu, K. Subramanyam, B. Wang, J. Yang, J. Huang, D. T. Auguste and M. A. Moses, Nat. Commun., 2018, 9, 1–9 CrossRef PubMed.
- T. Yue and X. Zhang, Soft Matter, 2013, 9, 559–569 RSC.
- J. C. Shillcock and R. Lipowsky, Nat. Mater., 2005, 4, 225–228 CrossRef CAS.
- A. Grafmüller, J. Shillcock and R. Lipowsky, Phys. Rev. Lett., 2007, 98, 1–4 CrossRef.
- A. Grafmüller, J. Shillcock and R. Lipowsky, Biophys. J., 2009, 96, 2658–2675 CrossRef PubMed.
- C. P. Chng, Y. Sadovsky, K. J. Hsia and C. Huang, Extrem Mech. Lett., 2021, 43, 101174 CrossRef PubMed.
- C. P. Chng, Y. Sadovsky, K. J. Hsia and C. Huang, Extrem Mech. Lett., 2021, 42, 101148 CrossRef.
- K. Kajiwara, O. Beharier, C. P. Chng, J. P. Goff, Y. Ouyang, C. M. St Croix, C. Huang, V. E. Kagan, K. J. Hsia and Y. Sadovsky, J. Cell Sci., 2022, 135, jcs255737 CrossRef CAS PubMed.
- H. P. Duwe and E. Sackmann, Phys. A, 1990, 163, 410–428 CrossRef CAS.
- P. Méléard, C. Gerbeaud, T. Pott, L. Fernandez-Puente, I. Bivas, M. D. Mitov, J. Dufourcq and P. Bothorel, Biophys. J., 1997, 72, 2616–2629 CrossRef.
- S. Chakraborty, M. Doktorova, T. R. Molugu, F. A. Heberle, H. L. Scott, B. Dzikovski, M. Nagao, L. R. Stingaciu, R. F. Standaert, F. N. Barrera, J. Katsaras, G. Khelashvili, M. F. Brown and R. Ashkar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21896–21905 CrossRef CAS.
- S. T. Yang, A. J. B. Kreutzberger, J. Lee, V. Kiessling and L. K. Tamm, Chem. Phys. Lipids, 2016, 199, 136–143 CrossRef CAS PubMed.
- M. A. Churchward, T. Rogasevskaia, D. M. Brandman, H. Khosravani, P. Nava, J. K. Atkinson and J. R. Coorssen, Biophys. J., 2008, 94, 3976–3986 CrossRef CAS PubMed.
- Z. Chen and R. P. Rand, Biophys. J., 1997, 73, 267–276 CrossRef CAS PubMed.
- S. J. Marrink and A. E. Mark, Biophys. J., 2004, 87, 3894–3900 CrossRef CAS PubMed.
- C. P. Chng, K. Wang, W. Ma, K. J. Hsia and C. Huang, Plant Physiol., 2022, 188, 526–539 CrossRef CAS PubMed.
- D. E. Lee, M. G. Lew and D. J. Woodbury, Chem. Phys. Lipids, 2013, 166, 45–54 CrossRef CAS PubMed.
- B. S. Stratton, J. M. Warner, Z. Wu, J. Nikolaus, G. Wei, E. Wagnon, D. Baddeley, E. Karatekin and B. O’Shaughnessy, Biophys. J., 2016, 110, 1538–1550 CrossRef.
- G. P. Pattnaik and H. Chakraborty, Langmuir, 2021, 37, 3477–3489 CrossRef CAS PubMed.
- G. P. Pattnaik and H. Chakraborty, Biochim. Biophys. Acta, Biomembr., 2019, 1861, 183056 CrossRef CAS PubMed.
- L. Wu, K. C. Courtney and E. R. Chapman, Biophys. J., 2021, 120, 1367–1377 CrossRef CAS.
- S. J. Marrink and A. E. Mark, J. Am. Chem. Soc., 2003, 125, 11144–11145 CrossRef CAS PubMed.
- C. Arnarez, J. J. Uusitalo, M. F. Masman, H. I. Ingólfsson, D. H. de Jong, M. N. Melo, X. Periole, A. H. de Vries and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 260–275 CrossRef CAS.
- H. I. Ingólfsson, M. N. Melo, F. J. Van Eerden, C. Arnarez, C. A. Lopez, T. A. Wassenaar, X. Periole, A. H. De Vries, D. P. Tieleman and S. J. Marrink, J. Am. Chem. Soc., 2014, 136, 14554–14559 CrossRef PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- Y. Qi, H. I. Ingólfsson, X. Cheng, J. Lee, S. J. Marrink and W. Im, J. Chem. Theory Comput., 2015, 11, 4486–4494 CrossRef CAS.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- Y. Qi, H. I. Ingo, X. Cheng, J. Lee, S. J. Marrink and W. Im, J. Chem. Theory Comput., 2015, 11, 4486–4494 CrossRef CAS.
- T. A. Wassenaar, H. I. Ingólfsson, R. A. Böckmann, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 2144–2155 CrossRef CAS PubMed.
- R. M. Venable, F. L. H. Brown and R. W. Pastor, Chem. Phys. Lipids, 2015, 192, 60–74 CrossRef CAS PubMed.
- W. Rawicz, K. C. Olbrich, T. Mcintosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- J. Liu and J. C. Conboy, Biophys. J., 2005, 89, 2522–2532 CrossRef CAS.
- W. F. D. Bennett, J. L. MacCallum, M. J. Hinner, S. J. Marrink and D. P. Tieleman, J. Am. Chem. Soc., 2009, 131, 12714–12720 CrossRef CAS PubMed.
- X. Shi, A. Von Dem Bussche, R. H. Hurt, A. B. Kane and H. Gao, Nat. Nanotechnol., 2011, 6, 714–719 CrossRef CAS PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- X. Yi and H. Gao, Nanoscale, 2017, 9, 454–463 RSC.
- R. W. Style, Y. Che, S. J. Park, B. M. Weon, J. H. Je, C. Hyland, G. K. German, M. P. Power, L. A. Wilen, J. S. Wettlaufer and E. R. Dufresne, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12541–12544 CrossRef CAS PubMed.
- Y. G. Smirnova, S. J. Marrink, R. Lipowsky and V. Knecht, J. Am. Chem. Soc., 2010, 132, 6710–6718 CrossRef CAS.
- Z. Shen, H. Ye, M. Kröger and Y. Li, Nanoscale, 2018, 10, 4545–4560 RSC.
- S. Kube, N. Hersch, E. Naumovska, T. Gensch, J. Hendriks, A. Franzen, L. Landvogt, J. P. Siebrasse, U. Kubitscheck, B. Hoffmann, R. Merkel and A. Csiszár, Langmuir, 2017, 33, 1051–1059 CrossRef CAS PubMed.
- R. Kolašinac, S. Jaksch, G. Dreissen, A. Braeutigam, R. Merkel and A. Csiszár, Nanomaterials, 2019, 9, 1–16 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00693f |
| This journal is © The Royal Society of Chemistry 2022 |