Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Facet-engineered TiO2 nanomaterials reveal the role of water–oxide interactions in surface protonic conduction†
Xiaolan
Kang
,
Athanasios
Chatzitakis
 ,
Thomas
Aarholt
,
Xinwei
Sun
,
Chiara
Negri
and
Truls
Norby
,
Thomas
Aarholt
,
Xinwei
Sun
,
Chiara
Negri
and
Truls
Norby
 *
*
Centre for Materials Science and Nanotechnology (SMN), University of Oslo, NO-0318 Oslo, Norway. E-mail: truls.norby@kjemi.uio.no
First published on 9th December 2021
Abstract
Water adsorption and surface protonic conduction have been investigated at 25–400 °C in wet (H2O and D2O) atmospheres on nanocrystalline TiO2 hydrothermally grown to a predominance of different crystal facets. In situ Fourier transform infrared spectrometry shows that a portion of the water molecules in the first chemisorbed layer adsorbs dissociatively on the {001} and {100} surfaces, but molecularly on the {101} surface. The next layer of physisorbed molecular water is solid (ice)-like on the {001} and {100} surfaces, a fact that is attributed to relatively strong bonds to the surface terminating hydroxyls. On the other hand, it is looser, liquid-like on the {101} surface due to the lack of rigid hydroxyl groups to bond to. As relative humidity (RH) increases with decreasing temperature, additional water layers physisorb and eventually become liquid-like also on the {001} and {100} surfaces. The differences can be attributed to the different atomic arrangements and surface energies of the different crystal facets. Surface protonic conduction on {001} and {100} dominated samples exhibits high pre-exponentials, indicating a high concentration of sites for dissociative chemisorption, and high activation energies reflecting difficult proton migration in the rigid water layers on those surfaces. The surface protonic conduction on the {101} dominated sample reflects a lower coverage of dissociable water and lower activation enthalpies for protonic migration in the more loosely bonded water. This suggests that, more generally, surfaces with dissociative chemisorption may exhibit high surface protonic conductivity at the highest and lowest temperatures (corresponding to lowest and highest RH, respectively), while surfaces with molecular chemisorption may exhibit a relatively high conductivity (less deep minimum) at intermediate temperatures. H/D isotope effects show that the protonic conduction mechanism changes from Grotthuss to vehicle as the physisorbed water layers gain thickness and become liquid-like. The protonic conductivity decreased when the surface was terminated by more strongly bonded fluoride ions, believed to reflect that they block the sites for water adsorption.
Introduction
Surface protonic conduction comprises Grotthuss migration of free protons (H+) and vehicular migration mainly of hydronium ions (H3O+) in chemisorbed and physisorbed water layers on oxides or other materials.1 Mesoporous and other nanocrystalline TiO2 materials exhibit high surface protonic conductivity in wet atmospheres, of importance for use as photocatalysts, sensors, and electrodes, and proposedly also as electrolytes in fuel cells.2–4 As an electrolyte material, TiO2 cannot compete with the traditional proton exchange membranes (PEM), such as Nafion® that typically operates at temperatures between 80 and 100 °C with high relative humidity (RH),5 and proton conducting ceramics like Y-substituted BaZrO3 (BZY) employed at higher working temperatures (>400 °C).6 However, over a broad range of temperatures between 400 °C and room temperature, TiO2 nanomaterials exhibit considerable protonic conductivities7,8 that in the case of anatase nanofilms have even been reported to exceed that of Nafion® at low temperatures.3Previous studies on the surface protonic conduction of TiO2-based nanomaterials mainly focused on the effects of the specific surface area, pore networks, and grain size, as well as intrinsic or extrinsic dopants.7,9–11 For example, Maglia et al. found that the surface protonic conductivity of dense anatase samples with grain sizes between 24 and 56 nm increased strongly with decreasing grain size.10 Stub et al. reported that donor and acceptor doped porous TiO2 materials give rise to increased and decreased surface protonic conductivity, respectively, compared to undoped TiO2. Based on this, they suggested the possible effect of heterovalent doping on the acid–base properties of the TiO2 surface.11 The results of the past few years imply that the orientation of different crystal facets of TiO2 significantly affects water adsorption and dissociation,12 however, to the best of our knowledge, their influence on surface protonic conductivity has not been systematically investigated.
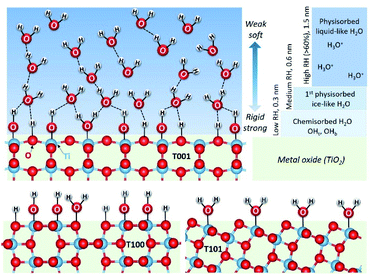
The adsorption of the first layer of water on oxides is generally considered to be the chemisorption of water molecules that bond to terminating cations, followed and stabilized by various degrees of dissociation into adsorbed hydroxyl groups and protons. The latter bonds to terminating surface oxide anions forming another surface hydroxyl group. As RH increases, a second layer of molecular water physisorbs fairly strongly by hydrogen bonds to the chemisorbed layer underneath. The possibility to make double hydrogen bonds to dissociated hydroxyl groups in a dissociated chemisorbed layer makes it rather crystalline and solid (“ice-like”). At high RH, a few layers more of water molecules physisorb by weaker hydrogen bonds that make them randomly oriented (“liquid-like”).
Dissociated protons migrate by Grotthuss-type hopping in the chemisorbed and ice-like physisorbed layers, while at RH > 0.6 (60%) vehicular transport of H3O+ ions in the liquid-like water takes over.11,13
Generally, abundant dangling bonds, such as under-coordinated cations and oxide anions, serve as sites for water adsorption and dissociation,12,14 that can decrease the initial surface energy excess. Anatase TiO2 crystals expose mainly {101}, {001}, and {100} facets. The most stable {101} facet has a saw-tooth-like appearance with half Ti5c (five-fold coordinated Ti4+ cations) and Ti6c atoms as well as half O2c (two-fold coordinated O2− anions) and O3c atoms, featuring alternating rows of Ti5c and O2c along the [010] direction.15 The high surface energy of the {001} facet originates mainly from the under-coordinated nature of surface species (Ti5c and O2c). The {100} facet comprises of Ti5c, O2c, and O3c atoms and is more stable than the {001} facet but less stable than the {101}.16 Different surface energies, atomic arrangements, and steric hindrance lead to different degrees of molecular or dissociative adsorption characteristics, and we here investigate the effects of these variables on surface protonic conduction.
The extent and configuration of molecularly and dissociatively chemisorbed water on the different facets of anatase TiO2 are debated. For example, Vittadini et al.17 found that molecular adsorption on the {101} facet is energetically favored over dissociative adsorption by 0.44 eV at low coverage and by 0.28 eV at monolayer coverage. They report that on the {001} facet, low coverage is dominated by dissociative adsorption, which turns into mixed molecular/dissociative adsorption at a monolayer coverage. Based on synchrotron radiation core level photoelectron spectroscopy, Walle et al.18 proposed mixed molecular and dissociative water adsorption on the {101} facet.
In this work, in situ Fourier transform infrared spectrometry (FTIR) has been utilized to study the adsorption, dissociation, and water layer formation as a function of RH and temperatures on anatase nanocrystallites with predominance of three low-index facets {101}, {001}, and {100}. Surface protonic conductivity on such facet-engineered porous anatase samples was measured with impedance spectroscopy under controlled temperatures and fixed partial pressure of water. Additionally, the effects of H/D isotope exchange and fluoride ion termination were studied to improve our understanding of the processes underpinning the surface protonic conduction. We model the conductivity in terms of pre-exponentials and activation enthalpies of contributions from bulk, Grotthuss protonic conduction in the chemisorbed and ice-like physisorbed layers, vehicular conduction in the liquid-like layer, and correlate them with adsorption, dissociation, and layer rigidity on the differently terminated surfaces, an approach possibly applicable also to surface protonic conduction of other oxides.
Experimental
Synthesis of anatase TiO2 nanoparticles with predominance of different facets
TiO2 nanoparticles with a predominance of the {101} facet (T101) were synthesized with a two-step hydrothermal procedure based on previous reports.19 First, a precursor of potassium titanate powder with nanotubular morphology was prepared by adding 1 g of commercial TiO2 powder (P25, Sigma-Aldrich) to 40 mL freshly made 17 M KOH (aq). The mixture was stirred for 20 min and introduced into a Teflon vessel with an inner volume of 50 mL for the hydrothermal treatment at 110 °C for 20 h. The resulting powder was rinsed with dilute HCl (aq) and deionized water until neutral (pH ≈ 7). In the second step, the as-prepared potassium titanate powder was dispersed in 35 mL deionized water. The pH was adjusted to 3.5 with HCl (aq) during stirring and the mixture was transferred to a 50 mL Teflon-lined autoclave for the hydrothermal reaction at 200 °C for 12 h. The T101 powder was finally collected by centrifugation and washed with deionized water.To synthesize anatase TiO2 with a predominance of the {100} facet (T100), a similar procedure was used. In the first hydrothermal process, instead of using P25, TiO2 nanoparticles were prepared according to a previously reported method20 and used as precursor to synthesize potassium titanate nanotubes. The as-synthesized nanotubes were washed with deionized water, dried at 80 °C. In the second hydrothermal process, pH was kept neutral.
TiO2 nanosheets with exposed {001} crystal surface (T001) were synthesized by a modified HF hydrothermal method according to the previous report.21 In a typical procedure, 1.2 mL HF (aq) (0.6 mL 48% wt HF mixed with 0.6 mL deionized water) were added dropwise into the 10 mL of tetrabutyl titanate solution under stirring for 1 h. Then, the suspension was transferred into a 50 mL Teflon-lined autoclave and kept at 200 °C for 24 h. The precipitate was collected and washed with water and ethanol. After drying, the powder was dispersed in 0.1 M NaOH (aq), stirred for 3 h to remove the adsorbed fluorine ions, and then washed with deionized water until neutral (pH ≈ 7).
Sample characterization
Scanning electron microscopy (SEM, Hitachi SU8230, operated at 1 kV acceleration voltage) and X-ray diffraction (XRD, Bruker D8 Discover, Cu Kα1, Bragg-Brentano) were used to analyze the morphology and phase purity of the as-synthesized TiO2 nanoparticles. Transmission electron microscopy (TEM) and high-resolution TEM (HRTEM) were performed on an FEI Tecnai-G2 F30 transmission electron microscope at 200 kV to determine the lattice parameters of the three samples. The surface adsorbates were detected using in situ FTIR (Bruker Vertex 70) equipped with a high-temperature and high-pressure transmission IR-cell (Harrick Scientific Products Inc, NY, US) and a mercury cadmium telluride (MCT) detector. Specifically, the samples were outgassed under vacuum (p < 3 × 10−3 mbar). In situ measurements under flowing O2 (15 mL min−1) were performed during ramps from 30 to 400 °C at 5 °C min−1. The applied water pressure was fixed with 0.35 RH at 30 °C. BET surface analyses were operated with nitrogen physisorption measurements in the range of pressure of 0.6587 kPa to 101.48 kPa at liquid nitrogen temperature.Conductivity measurements
The as-prepared samples (T101, T001, and T100) were compacted into pellets with a diameter of 13 mm using a uniaxial cold press and then sintered at 400 °C for 4 h in ambient air. The thickness was about 1.5 mm, and the relative density was about 50% calculated from the weight and geometry of the pellet. Ag ink was painted as electrodes on both sides of the pellet that was then dried at 120 °C for 20 min. All the electrical measurements were carried out in a ProboStat™ sample holder cell (NORECS, Norway) with a standard 2-electrode 4-wire set up connected to a Novocontrol alpha-A impedance spectrometer via a ZG4 interface. A steel outer tube was used to electrically shield the cell. The impedance spectra were recorded from 10 MHz to 1 mHz at oscillation voltages of 0.1–0.3 V RMS in dry or wet (PH2O = 0.026 atm or PD2O = 0.023 atm) air as a function of temperature (25–400 °C). The data were analyzed and modelled using the ZView equivalent circuit fitting software (ZView ver. 3.5a; Scribner Associates Inc.). The specific conductivity, σ, of the porous material was calculated from the macroscopic dimensions, i.e., the area of the electrodes and thickness of the pellet.Results and discussion
Structure characterization
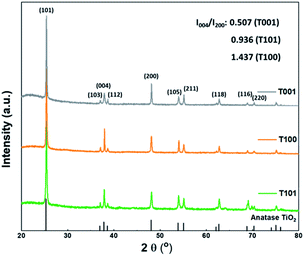
To investigate the morphology and crystal structure of the synthesized TiO2 samples, XRD, SEM, HRTEM, and BET characterizations were performed. Fig. 1 shows the XRD patterns, matching well with the anatase phase (tetragonal, JCPDS 21-1272). Obviously, the (004) diffraction line of the T001 sample weakened and its full width at half maximum (FWHM) broadened. According to the Scherrer equation, the broad peak represents the decreased crystallite size along the [001] axis vertical to (001) plane, corresponding to a smaller thickness in that direction.22 In addition, the (200) peak intensified and its FWHM narrowed, revealing the increased side length of T001 nanosheets in the [100] direction. Therefore, the thickness and side length in the [001] and [100] direction, respectively, can be roughly estimated based these two peaks. The relative peak intensity of (004) and (200) was estimated in the insert. T001 has the lowest value, indicative of dominance of {001} facets.23 For the T100 sample, changes of the (004) and (200) peaks show an opposite trend, suggesting that the crystals grew preferentially in the [001] direction, while the growth in the [100] direction was suppressed.24.
Fig. 2a shows the rectangular sheet-like shape of the T001 sample. The HRTEM image and the corresponding fast Fourier transform (FFT) displayed in the inset of Fig. 2a clearly show the lattice spacing of around 0.189 nm, which corresponds to the (001) plane of anatase. Fig. 2b suggests that most of the T100 particles have a tetragonal faceted nanorod morphology. Three sets of clear lattice fringes with spacing of 0.35 nm, 0.35 nm, and 0.48 nm, respectively, can be attributed to the (101), (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and (002) planes of the anatase phase, which is typical for the {100} facet.25 The images of the T101 sample (Fig. 2c) show the truncated bipyramidal shape with the bottom and top surfaces being composed of the {001} facet and either side surfaces found to be the {101} facet based on previous literature findings. The lattice fringe with a d-spacing of 0.35 nm corresponds to (101) planes of anatase.26 Additional SEM images and indicative particle dimensions of each sample can be found in Fig. S1.† Specific surface areas as calculated from N2 adsorption isotherms at 77 K (Table S1†) are higher for the T001 sample than the other two, attributed to its thin sheet-like morphology.
) and (002) planes of the anatase phase, which is typical for the {100} facet.25 The images of the T101 sample (Fig. 2c) show the truncated bipyramidal shape with the bottom and top surfaces being composed of the {001} facet and either side surfaces found to be the {101} facet based on previous literature findings. The lattice fringe with a d-spacing of 0.35 nm corresponds to (101) planes of anatase.26 Additional SEM images and indicative particle dimensions of each sample can be found in Fig. S1.† Specific surface areas as calculated from N2 adsorption isotherms at 77 K (Table S1†) are higher for the T001 sample than the other two, attributed to its thin sheet-like morphology.
 | ||
| Fig. 2 Typical SEM, TEM, and HRTEM images and the corresponding FFT patterns of (a) T001, (b) T100, and (c) T101 sample. | ||
H2O–TiO2 interactions
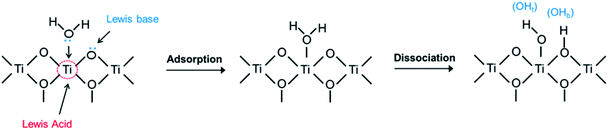
The surface of TiO2 has both Lewis basic (O2c) and acidic (Ti5c) sites. Water adsorbs molecularly, which may be followed by dissociation,12 as illustrated in Fig. 3. Molecular adsorption involves a direct interaction of the oxygen atom of H2O (Ow) with the surface Ti4+ acidic site (Ti5c), or/and the hydrogen atom of H2O (Hw) with the surface O2−. In the later dissociation, a basic site (O2c) can extract a proton from the water molecule that was adsorbed on the adjacent Ti5c, forming two surface hydroxyl groups (the terminal hydroxyl group, OHt, and the bridging hydroxyl group, OHb).27As discussed above, the surface atom coordination and geometric arrangement, as well as the resulting steric hindrance considerably affect the behavior on water adsorption on different anatase facets. However, previous studies investigating water adsorption and desorption were mainly conducted at very low temperatures and ultra-high vacuum (UHV),12 where pH2O is low, but RH is considerable. In practical applications at ambient temperatures, pH2O is higher, and RH is still high. At higher temperatures, RH is often lower, resulting in a lower coverage of adsorbed water. A main effect of increased temperature, even at the same RH, is increased dissociation of adsorbed molecular water. The question is how the thermodynamics of adsorption and dissociation vary with the configuration of surface sites on different facets.
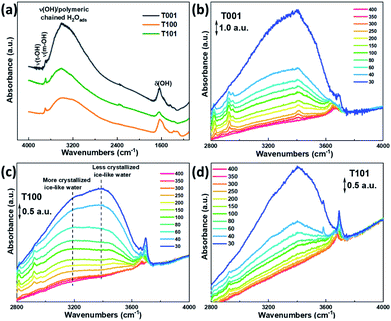
Fig. 4 shows the FTIR spectra of the as-prepared TiO2 samples outgassed at elevated temperatures. From the evolution of –OH absorbance with temperatures, the degree of dehydration and thermal stability of various –OH groups is indicated. We can distinguish three main IR absorption bands. A broad absorption band at around 3600–2800 cm−1 corresponds to the stretching vibration modes of –OH group, ν(OH), and the H2O molecule perturbed by hydrogen bonding (Fig. 4a). The broadness is related to the length and strength of several possible O–H bonds in a dynamic intermolecular interaction. A series of sharp peaks at around 3600–3750 cm−1 correspond to the unperturbed terminal hydroxyls and water molecules.28 Peaks below 1800 cm−1 can be assigned to the bond bending of –OH groups, δ(OH). Clearly, the amount of adsorbed water at the same RH is more significant on the {001} and {100} facets, probably due to their higher surface energy with a large amount of under-coordinated sites compared to that of the {101} facet.
The evolution of the FTIR spectra due to the changed surface hydration species by the progressive outgassing from 30 °C to 400 °C, was monitored. As shown in Fig. 4b–d, the integrated intensity in 3600–2800 cm−1 gradually decreases with increasing temperature, and is completely flattened out at 400 °C for all the three TiO2 samples, reflecting the condensation of –OH groups and desorption of water.28 The change in peak intensities on the T101 and T001 surfaces as the temperature increased from 30 to 40 °C indicates the massive loss of water on these two surfaces.
Previous studies suggested that the formation of the ice-like layer is almost completed at 0.3 RH, and at 0.3–0.6 RH, the second physisorbed water layer forms.29 Here, we propose that the chemisorbed water layer dissociates and mainly consists of –OHt and –OHb groups on the {001} and {100} facets, while it remains mainly undissociated H2O molecules (Ti5c–H2O) on the {101} facet. In the first physisorbed water layer, the incoming H2O forms double or single hydrogen bonds with the hydroxyls underneath on the surface of T001 and T100, making this layer rigid enough to be ice-like. Since the density of –OHb on {001} is the highest (100% O-2c sites) among these three facets, more OHb–H2O hydrogen bonds are expected. On the {101} surface, however, instead of forming hydrogen bonds with Ti5c–H2O, the incoming H2O adsorbs molecularly on surface O2c sites due to the unique zigzag configuration of the {101} facet.30,31 The aforementioned ice-like physisorbed water layer follows after the formation of the O2c–H2O is completed and therefore at higher RH compared to the ice-like layer on {001} and {100} facets.
Above 0.3 RH, the second physisorbed water layer develops by weaker hydrogen bonds, and the outermost layer changes gradually from ice-like to liquid-like.29 During the degassing process, a massive water loss at 40 °C is observed for the {001} (Fig. 4b), reflecting the weak hydrogen bonds in the outmost water layer. Therefore, it appears that the second physisorbed water layer that is thermally unstable forms on the {001} surface at 30 °C with 0.35 RH, while its formation is less favorable on the {101} and {100} under these conditions.
As for the T101 sample, most water molecules desorb at temperatures up to 150 °C, whereas they are still visible on the {001} and {100} facets at around 200–250 °C (Fig. 4b–d), indicating the unstable nature of the less crystallized ice-like layer on {101} surface due to the lack of hydroxyls underneath, as well as the relatively weak interaction of water hydrogen and surface oxygen. Noticeably, a lower-lying absorbance maximum at around 3200 cm−1 is more visible for the T100 than the other two samples (Fig. 4c), which can be ascribed to the more crystalline (ice-like) water. In comparison, the one at around 3400 cm−1 is from the more amorphous and liquid-like water.32 Hence, it is reasonable to infer that a crystallized ice-like water layer is established on the surface of these three samples during the in situ FTIR test, but the ice-like layer is more crystallized on the {100} surface than the other two.
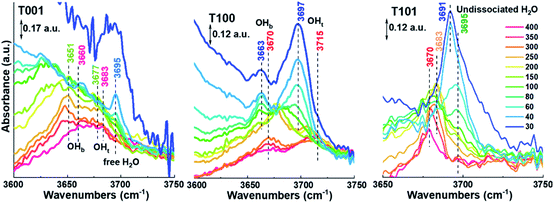
A detailed analysis at the 3600–3750 cm−1 region where peaks are persistent even at 400 °C is displayed in Fig. 5. For the T001 sample, two peaks at around 3651 cm−1 and 3677 cm−1 can be ascribed to OHb and OHt, respectively. When increasing the temperature to 400 °C, they positively shift to 3660 cm−1 and 3683 cm−1, respectively, due to the disappearance of the additional water molecules bonding to these –OH species.33,34 A peak at around 3695 cm−1 is only seen in the low-temperature range (below 100 °C), which can be assigned to the free H2O in the second physisorbed layer where the outermost layer with less H-bonds is involved. A similar change takes place on the T100 sample, in which the two peaks at 3663 cm−1 (OHb) and 3697 cm−1 (OHt) shift to 3670 cm−1 and 3715 cm−1, respectively, as temperatures increase to 400 °C. Noticeably, compared to T001, the OHt signal is more pronounced than OHb on T100 surfaces, which is probably due to its higher density of Ti5c (100%) than O2c (50%).
With regard to the T101 sample (Fig. 5), only one distinctive peak appears, which positively shifts from 3691 cm−1 to 3695 cm−1 with the temperature increasing from 30 to 150 °C, then negatively shifts to 3670 cm−1 at 400 °C. Based on the above discussion, this single peak belongs to H2O molecularly adsorbed on the {101} surface, and the peak-shifting probably originates from the desorption of water from Ti5c–H2O, O2c–H2O, and H2O–H2O species as temperature increases. The above explanation is further supported by a detailed analysis of peak evolution in O–H bending region in conjunction with Fig. S2.† It is worth noting though that calculations by Tilocca and Seloni indicated that molecular adsorption is favored in the case of a defect-free {101} surface, while a defective surface containing oxygen vacancies can induce dissociative adsorption, attributed to H2O–H2O interactions.31 Further investigations are needed to elucidate the degree of dissociative adsorption in relation to the amount of oxygen vacancies in the surface.
Based on the above discussion, water layers adsorbed on different facets of TiO2 are displayed in Fig. 6. As the RH increases, different water layers gradually form on the surface of these three TiO2 samples. Here, we use the {001} facet as an example to show all these water layers. The first chemisorbed water layer forms at temperatures above 275 °C with mainly hydroxyls (OHb and OHt) on {001} and {100} facets and mainly molecularly adsorbed water on {101} facets. These results are in line with several theoretical findings in the literature.35–37
As RH increases, a hierarchical ice-like water layer starts forming on the top of the chemisorbed layer on {001} and {100} facets. On the {101} surface, the incoming water molecules first bond to O2c,30 and then to the surface adsorbed H2O with hydrogen bonds are not as strong as those on the {001} and {100} facets where water molecules form hydrogen bonds with the surface –OH groups. The ice-like water layer is more rigid on the {100} facet than that on the {001} because of its special surface atomic arrangement. Previous theoretical calculations indicated that the coinciding orientations of water adsorbed on the surface active sites of {100} facets (with respect to the TiO2 surface plane) yield hydration layers with an enhanced density, and lead to strongly ordered water layers.16 As the RH further increases, a third water layer physisorbs first on {001} surfaces, and propagates further into liquid-like layers at RH above 0.6.
As discussed in the introduction, the formation of protonic charge carriers originates from the surface water–oxide interactions, while the conduction of these charge carriers takes place in all water layers. Therefore, the proton conduction mechanism and conductivity on different crystal facets are expected to be different.
Conductivity measurements
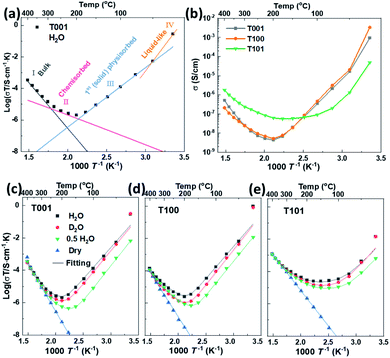
Impedance spectra were measured for all samples as a function of temperature in various atmospheres. Temperatures were kept below 400 °C to avoid sintering and change of crystal facets. A representative Nyquist plot of the impedance at 50 °C of the {101} facet dominated TiO2 sample, and the corresponding simplified equivalent circuit used to model all spectra, are displayed in Fig. S3.† Based on the associated capacitances, the impedance at high frequencies is ascribed to the transport in the bulk and over the surface of the grains. Although the high frequency impedance arc is asymmetrical, our data don't allow a consistent further deconvolution of this impedance, and we here assign only one resistance and conductivity to it. The response at low frequencies is assigned to the electrode impedance. The inset in Fig. S3† shows the impedance in nominally dry air that is orders of magnitude higher at this temperature.Based on impedance spectra and sample geometries, the conductivities of the different samples under both dry and wet conditions were extracted and form basis for Fig. 7. The curves were fitted with TableCurve 2D software. The pre-exponentials (σ0) and activation energies (Ea) of total conductivities corresponding to the bulk transport, the chemisorbed water layer, and the ice-like physisorbed layer were obtained separately, as shown in Fig. 7a, and the numerical results are provided in Table S2.† For the T101 sample, we fitted the σ0 and Ea for four different contributions: bulk transport, and transport in the Ti5c–H2O layer, O2c–H2O layer, and ice-like physisorbed layer.
For nominally dry conditions, the data, shown only at the highest temperatures in Fig. 7c–e (region I), exhibit linear Arrhenius behaviors with activation enthalpies (Ea) calculated from log(σT) vs. 1/T in the range of 0.8–1.2 eV. This can be attributed to the ionic conductivity of nanometric anatase,38,39 and the variation between samples may be understood by their different textures and dominance of different crystallographic directions. Under wet conditions, the conductivity at the highest temperatures is still dominated by bulk transport and does not deviate much from that under dry conditions.
Below approximately 300 °C, the surface protonic contribution becomes significant under wet conditions, giving rise to activation enthalpies in region II (chemisorbed water layer) in the range 0.3–0.4 for T001, 0.4–0.5 eV for T100 and 0.4–0.6 eV for T101. The difference between samples is clear from the direct comparison of the conductivities in wet atmosphere (pH2O = 0.026 atm) in Fig. 7b. The conductivity in range II is attributed to mainly chemisorbed water, with proton migration by the Grotthuss mechanism.3 For T001 and T100 we expect that the chemisorbed layer is at full coverage and fully dissociated, so that the activation energies reflect the enthalpy of proton charge mobility (diffusion). They are in overall agreement with the 58 kJ mol−1 (0.60 eV) found for bulk proton migration in polycrystalline rutile and within the range of proton diffusivities in the different directions of single crystal rutile,40 knowing that surface transport has somewhat lower activation enthalpies than in bulk. The activation energy of T101 should, on the one hand, contain some dissociation enthalpy, but may on the other hand reflect easier jumps between the loosely bonded water molecules on the surface of T101 than the more rigid and dissociated water on T001 and T100.
At temperatures below approximately 200 °C (region III, 1st physisorbed layer), the conductivity increased with decreasing temperature for T001 and T100, as expected, attributed to the protolysis of the dissociated protons from the chemisorbed layer into the increasing coverage of physisorbed water, where the mobility is higher.41,42 The conductivities down to around 50 °C follow remarkably straight lines in the Arrhenius plot corresponding to apparent enthalpies of around −0.8 eV. For T101, we get instead a shallow conductivity minimum in region III, suggested to originate from the continued adsorption of H2O on O2c sites, and the sharper increase due to the more continuous molecular physisorbed layer appears only around 100 °C. Whether this is ice-like on T101 like on T001 and T100 is uncertain, but it still comes with the high mobility.
The observed negative activation energy for the temperature dependency of proton conductivity in the ice-like physisorbed water in range III have several contributions: the enthalpy of adsorption of the first physisorbed layer should correspond to something a bit more negative than that of condensation of water (−0.45 eV at RT). But the enthalpy of mobility goes in the opposite direction. To get to −0.8 eV, we must therefore expect that the increasing coverage of the first physisorbed layer increases the degree of protolysis31 and decreases the activation enthalpy of mobility. What appears as a negative temperature dependence with an enthalpy of −0.8 eV is actually a continuously decreasing (yet positive) activation enthalpy of conduction with increasing coverage, as pointed out by others before.43 One may say that the enthalpy of conduction is positive, but the differential enthalpy is negative.
The contribution from entropy with respect to the formation and conduction of protons should also not be neglected in rationalizing the apparent negative enthalpy. As the first physisorbed water layer gains in coverage, protons can move into it at lower density (concentration), which increases both the vibrational and configurational entropy and drives the water protolysis forward, and, in turn, dissociation to increase the total number of mobile protons.
At temperatures below 50 °C (in ambient humidity, with pH2O = 0.026 atm), region IV, the conductivities of T001 and T100 increase even more sharply with decreasing temperature, reflecting increasingly high vehicular mobility of protons in the thicker and liquid-like physisorbed layers. The mobility is approaching that of bulk water, independent of the characteristics of the oxide surface. Thus, the different conductivities observed on these three facets are now mostly determined by the concentration of protonic species.
Sample T101, which displayed a lower activation energy of proton conductivity in the chemisorbed layer and hence had a higher conductivity than the others at the minima around 150 °C, does not exhibit the behavior attributed to the first physisorbed layer that we saw in T001 and T100. Instead, it appears that it goes more directly from conduction in chemisorbed water to liquid-like physisorbed water layers, in agreement with the conclusions from the FTIR studies. It should be noted that the apparent activation energy of T101 is less negative than that of T001 and T100 at temperatures from 150 to 50 °C, during which the first physisorbed water layer forms. For {001} and {100} facets, water molecules form hydrogen bonds with surface –OH groups, while they are bonded to the molecular water on {101} facets in the chemisorbed water layer, which decreases the magnitude of the enthalpy of the water adsorption/condensation process (makes it less exothermic). The increasing coverage of the first physisorbed layer with decreasing temperature hence lags behind for T101 as compared to T001 and T100, the apparent enthalpy gets less negative, and the conductivity increases less sharply.
T101 ends up at 1–2 orders of magnitude lower conductivity than T001 and T100 at room temperature with a RH of 80%. Assuming that this reflects the concentration of protons, this must, in turn, stem from a lower degree of dissociation and/or protolysis. A lower degree of dissociation is in agreement with what FTIR analyses concluded about molecular water adsorption on the {101} facet. Another possibility lies in lower adsorption energies of water on the {101} facet resulting in lower total thickness and less liquid-like character of water here.
Interestingly, the pre-exponential factors acquired from the fitting of conductivities in the chemisorbed water are higher for T001 and T100 than for T101, see Table S2.† This reflects only differences in entropy, attempt frequencies, and density of sites. We suggest that it reflects that the {101} facet has much fewer active sites for adsorption and dissociation of water.
All in all, we find that surfaces with dissociative chemisorption exhibit high surface protonic conductivity at the highest and lowest temperatures, due to a high concentration of sites for adsorption and dissociation and unrestricted mobilities for two very different reasons. At intermediate temperatures, however, they exhibit deep minima from the high activation energies for mobility in the chemisorbed and the rigid first physisorbed layers. Surfaces with less dissociation and hence molecular chemisorption, on the other hand, appear to offer fewer protons (fewer sites for adsorption and dissociation) but cross the temperature range with a much shallower minimum at intermediate temperatures because the activation energies are smaller.
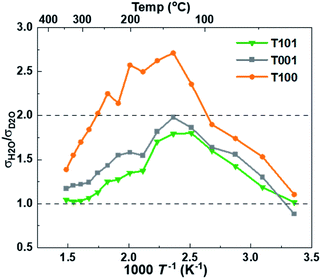
The findings and conclusions above were supported by H/D isotope effects. The classical model predicts that the proton hopping rate in oxides is proportional to the O–H/O–D vibration frequency, but the model has uncertainties related to sticking probability and other mechanistic aspects. Instead, the isotope effect stems mostly from a higher activation energy of jumps from O–D vibrations due to different semiclassical zero-point energies of O–H and O–D compared to their O–H–O and O–D–O jump saddle point energies, accounting for observed H/D isotope effects.44 The significant isotope effect ratio of ∼2 around 150 °C (Fig. 8) shows that Grotthuss free proton jumps is the dominating mechanism. It decreases with increasing temperatures as the effect of the different activation energies diminish44 and native bulk conductivity becomes significant. The isotope effect also gradually diminishes at temperatures below 150 °C (higher RH) and almost disappears as RH surpassed 60%, indicating a change to vehicular transport in liquid-like water layers.
The T001 sample was synthesized using HF as the capping agent. It is well-known that fluoride ions can bond strongly to Ti5c sites and stabilize the surface,45 therefore, fluoride ions would inevitably adsorb on the sample surface during synthesis. When the surface Ti atoms are terminated by fluoride ions, the strong bonding between the Ti-5c and water oxygen (Ow–Ti5c) is no longer possible. Moreover, the hydrogen bond between the water hydrogen and surface O-2c (Hw–O2c) also becomes unfavorable due to the repulsive interactions between surface oxygen and fluoride ions. In this case, water layers cannot be formed on the surface of TiO2 at low temperatures, and as a result, the conductivity remained <10−7 S cm−1 throughout the temperature range of interest (Fig. 9). However, when the surface absorbed fluoride ions were removed by washing with NaOH (aq),46,47 the observed conductivity was greatly improved.
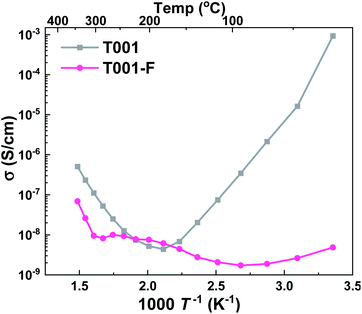 | ||
| Fig. 9 Apparent conductivities in wet air of T001 samples capped with HF (T001-F) and after washing with NaOH solution to remove the surface adsorbed fluorine ions (T001). | ||
Conclusions
We systematically varied the dominance of different crystal facets and thereby surface chemistry of nanocrystalline TiO2 to shed light on their role in water–oxide interactions and proton conduction. In situ FTIR suggests that the coordination of surface atoms on {001} and {100} dominated facets makes water chemisorb strongly and dissociatively, while chemisorption on {101} is weaker and more molecular. In ambient humidity (pH2O = 0.026 atm) and below 300 °C, surface protonic conduction in the chemisorbed layer becomes dominating, with activation enthalpies in the range of 0.4–0.6 eV for {001} and {100} and 0.3–0.4 eV for {101}. Then, the conductivity of all samples crosses a minimum, which is shallower for the {101} surface because of the low activation energy for mobility in the soft molecular water. Below approximately 150 °C, the coverage of the first ice-like physisorbed layer becomes significant, and its higher proton mobility increases the surface protonic conductivity with decreasing temperature. This sets in at higher temperatures and is steeper for {001} and {100} because physisorption is stronger (more exothermic) on the rigid dissociated than the soft molecular chemisorbed water underneath. Further down at 50 °C (RH ≈ 30% for ambient humidity) this layer is considered complete and as we approach room temperature and RH surpasses 60%, liquid-like water layers physisorb, and the proton mobility and conductivity increase further. This is more pronounced on {001} and {100} due to more dissociation and thicker water layers, accommodating higher total concentrations of dissociated protons of higher mobility. This is supported by H/D isotope effect measurements showing a transition from Grotthuss H+ hopping in the chemisorbed and first physisorbed layers to vehicular H3O+ transport in the liquid-like outer layers. The surface chemistry was further studied by terminating {001} facets with fluoride ions, which effectively suppressed surface protonic conduction by blocking H2O–Ti5c interaction and protonation of surface O2c. This study contributes mechanistic insights into surface protonic conduction governed by adsorbed water layers on specific surfaces of polycrystalline oxides.Author contributions
XK synthesized the samples, designed and performed the measurements, analyzed the data and wrote the original draft. TA and CN did the TEM measurements and in situ FTIR tests, respectively. XS contributed interpretation of data and revision of the manuscript. AC and TN conceived and supervised the study. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is enabled by a scholarship for XK by the China Scholarship Council (201806060141). Additional resources from collaboration within projects SUPROX (280868), and PH2ON (288320) financed by the Research Council of Norway are acknowledged.Notes and references
- R. Sato, S. Ohkuma, Y. Shibuta, F. Shimojo and S. Yamaguchi, J. Phys. Chem. C, 2015, 119, 28925–28933 CrossRef CAS.
- K. Xu, A. Chatzitakis and T. Norby, Photochem. Photobiol. Sci., 2017, 16, 10–16 CrossRef CAS PubMed.
- M. T. Colomer, Adv. Mater., 2006, 18, 371–374 CrossRef CAS.
- H. Ekström, B. Wickman, M. Gustavsson, P. Hanarp, L. Eurenius, E. Olsson and G. Lindbergh, Electrochim. Acta, 2007, 52, 4239–4245 CrossRef.
- L. Liu, W. Chen and Y. Li, J. Membr. Sci., 2016, 504, 1–9 CrossRef CAS.
- D. Han and T. Uda, J. Mater. Chem. A, 2018, 6, 18571–18582 RSC.
- M. I. Tejedor-Tejedor, F. M. Vichi and M. A. Anderson, J. Porous Mater., 2005, 12, 201–214 CrossRef CAS.
- E. L. Runnerstrom, G. K. Ong, G. Gregori, J. Maier and D. J. Milliron, J. Phys. Chem. C, 2018, 122, 13624–13635 CrossRef CAS.
- F. M. Vichi, M. I. Tejedor-Tejedor and M. A. Anderson, Chem. Mater., 2000, 12, 1762–1770 CrossRef CAS.
- F. Maglia, I. G. Tredici, G. Spinolo and U. Anselmi-Tamburini, J. Mater. Res., 2012, 27, 1975–1981 CrossRef CAS.
- S. Ø. Stub, K. Thorshaug, P. M. Rorvik, T. Norby and E. Vollestad, Phys. Chem. Chem. Phys., 2018, 20, 15653–15660 RSC.
- R. Mu, Z. J. Zhao, Z. Dohnalek and J. Gong, Chem. Soc. Rev., 2017, 46, 1785–1806 RSC.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Phys. Chem. C, 2017, 121, 12817–12825 CrossRef CAS.
- O. Bikondoa, C. L. Pang, R. Ithnin, C. A. Muryn, H. Onishi and G. Thornton, Nat. Mater., 2006, 5, 189–192 CrossRef CAS.
- Y. He, A. Tilocca, O. Dulub, A. Selloni and U. Diebold, Nat. Mater., 2009, 8, 585–589 CrossRef CAS PubMed.
- L. Agosta, E. G. Brandt and A. P. Lyubartsev, J. Chem. Phys., 2017, 147, 024704 CrossRef PubMed.
- A. Vittadini, A. Selloni, F. P. Rotzinger and M. Grätzel, Phys. Rev. Lett., 1998, 81, 2954–2957 CrossRef CAS.
- L. E. Walle, A. Borg, E. M. J. Johansson, S. Plogmaker, H. Rensmo, P. Uvdal and A. Sandell, J. Phys. Chem. C, 2011, 115, 9545–9550 CrossRef CAS.
- Q. Bai, M. Lavenas, L. Vauriot, Q. Le Trequesser, J. Hao, F. Weill, J. P. Delville and M. H. Delville, Inorg. Chem., 2019, 58, 2588–2598 CrossRef CAS PubMed.
- X. Kang, X.-Z. Song, S. Liu, M. Pei, W. Wen and Z. Tan, Nanoscale Adv., 2019, 1, 1372–1379 RSC.
- N. Liu, Y. Chang, Y. Feng, Y. Cheng, X. Sun, H. Jian, Y. Feng, X. Li and H. Zhang, ACS Appl. Mater. Interfaces, 2017, 9, 5907–5915 CrossRef CAS PubMed.
- J. Wang, P. Zhang, X. Li, J. Zhu and H. Li, Appl. Catal., B, 2013, 134–135, 198–204 CrossRef CAS.
- F. Tian, Y. Zhang, J. Zhang and C. Pan, J. Phys. Chem. C, 2012, 116, 7515–7519 CrossRef CAS.
- Q. Shi, Y. Li, E. Zhan, N. Ta and W. Shen, CrystEngComm, 2015, 17, 3376–3382 RSC.
- L. Jiang, L. Sun, D. Yang, J. Zhang, Y. J. Li, K. Zou and W. Q. Deng, ACS Appl. Mater. Interfaces, 2017, 9, 9576–9583 CrossRef CAS PubMed.
- F. Lin, Y. Chen, L. Zhang, D. Mei, L. Kovarik, B. Sudduth, H. Wang, F. Gao and Y. Wang, ACS Catal., 2020, 10, 4268–4279 CrossRef CAS.
- M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1–308 CrossRef CAS.
- L. Mino, G. Spoto, S. Bordiga and A. Zecchina, J. Phys. Chem. C, 2012, 116, 17008–17018 CrossRef CAS.
- D. B. Asay and S. H. Kim, J. Phys. Chem. B, 2005, 109, 16760–16763 CrossRef CAS PubMed.
- A. Tilocca and A. Selloni, Langmuir, 2004, 20, 8379–8384 CrossRef CAS PubMed.
- A. Tilocca and A. Selloni, J. Phys. Chem. B, 2004, 108, 4743–4751 CrossRef CAS.
- C. C. Pradzynski, R. M. Forck, T. Zeuch, P. Slavíček and U. Buck, Science, 2012, 337, 1529 CrossRef CAS PubMed.
- E. M. Kock, M. Kogler, B. Klotzer, M. F. Noisternig and S. Penner, ACS Appl. Mater. Interfaces, 2016, 8, 16428–16443 CrossRef PubMed.
- C. Deiana, E. Fois, S. Coluccia and G. Martra, J. Phys. Chem. C, 2010, 114, 21531–21538 CrossRef CAS.
- G. Zhou and L. Huang, Mol. Simul., 2021, 47, 925–941 CrossRef CAS.
- R. Wang, M. L. Klein, V. Carnevale and E. Borguet, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1537 CAS.
- X. Lang, Y. Liang, J. Zhang, L. Li, L. Cao and H. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 1371–1380 RSC.
- P. Knauth and H. L. Tuller, J. Appl. Phys., 1999, 85, 897–902 CrossRef CAS.
- I. G. Tredici, F. Maglia, C. Ferrara, P. Mustarelli and U. Anselmi-Tamburini, Adv. Funct. Mater., 2014, 24, 5137–5146 CrossRef CAS.
- S. Erdal, C. Kongshaug, T. S. Bjørheim, N. Jalarvo, R. Haugsrud and T. Norby, J. Phys. Chem. C, 2010, 114, 9139–9145 CrossRef CAS.
- M.-H. Du, A. Kolchin and H.-P. Cheng, J. Chem. Phys., 2003, 119, 6418–6422 CrossRef CAS.
- A. Schaefer, V. Lanzilotto, U. Cappel, P. Uvdal, A. Borg and A. Sandell, Surf. Sci., 2018, 674, 25–31 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Mater. Chem. A, 2018, 6, 8265–8270 RSC.
- A. S. Nowick and A. V. Vaysleyb, Solid State Ionics, 1997, 97, 17–26 CrossRef CAS.
- C. Sun, A. Selloni, A. Du and S. C. Smith, J. Phys. Chem. C, 2011, 115, 17092–17096 CrossRef CAS.
- T. R. Gordon, M. Cargnello, T. Paik, F. Mangolini, R. T. Weber, P. Fornasiero and C. B. Murray, J. Am. Chem. Soc., 2012, 134, 6751–6761 CrossRef CAS PubMed.
- Q. Huang, Y. Hu, G. He, C. Lin and C. Wei, Environ. Sci. Pollut. Res., 2018, 25, 35342–35351 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta06075a |
| This journal is © The Royal Society of Chemistry 2022 |