Phase stability and sodium-vacancy orderings in a NaSICON electrode†
Ziliang
Wang
a,
Sunkyu
Park
bcd,
Zeyu
Deng
 a,
Dany
Carlier
cd,
Jean-Noël
Chotard
*bd,
Laurence
Croguennec
a,
Dany
Carlier
cd,
Jean-Noël
Chotard
*bd,
Laurence
Croguennec
 cd,
Gopalakrishnan Sai
Gautam
cd,
Gopalakrishnan Sai
Gautam
 e,
Anthony K.
Cheetham
e,
Anthony K.
Cheetham
 af,
Christian
Masquelier
af,
Christian
Masquelier
 bd and
Pieremanuele
Canepa
bd and
Pieremanuele
Canepa
 *ag
*ag
aDepartment of Materials Science and Engineering, National University of Singapore, 9 Engineering Drive 1, 117575, Singapore. E-mail: pcanepa@nus.edu.sg
bLaboratoire de Réactivité et de Chimie des Solides (LRCS), CNRS UMR 7314, Université de Picardie Jules Verne, 80039 Amiens Cedex, France. E-mail: jean-noel.chotard@u-picardie.fr
cCNRS, Univ. Bordeaux, Bordeaux INP, ICMCB, UMR CNRS 5026, Pessac, F-33600, France
dRS2E, Réseau Français sur le Stockage Electrochimique de l'Energie, FR CNRS 3459, F-80039 Amiens Cedex 1, France
eDepartment of Materials Engineering, Indian Institute of Science, Bengaluru, Karnataka 560012, India
fMaterials Department and Materials Research Laboratory, University of California, Santa Barbara, California 93106, USA
gDepartment of Chemical and Biomolecular Engineering, National University of Singapore, 4 Engineering Drive 4, 117585 Singapore, Singapore
First published on 2nd December 2021
Abstract
We elucidate the complex thermodynamics of sodium (Na) intercalation into the sodium super-ionic conductor (NaSICON)-type electrode, NaxV2(PO4)3, for promising Na-ion batteries with high-power density. This is the first report of a computational temperature-composition phase diagram of the NaSICON-type electrode NaxV2(PO4)3. Based on our computational data, we identify a thermodynamically stable phase with a composition of Na2V2(PO4)3 and describe its structural features. We also identify another metastable configuration that can occur at room temperature, namely Na3.5V2(PO4)3. We unveil the crystal-structure and the electronic-structure origins of the ground-state compositions associated with specific Na/vacancy arrangements, which are driven by charge orderings on the vanadium sites. These results are significant for the optimization of high-energy and power density electrodes for sustainable Na-ion batteries.
Introduction
The urgent demands for the next-generation of clean energy technologies put increasing pressure on researchers to develop innovative materials and devices. Due to the high energy densities and desirable electrochemical cycling performance, lithium-ion batteries (LIBs) have been extensively investigated for their use in portable devices and vehicular transportation.1 However, the expanding LIB industry may soon be limited by the availability of lithium and specific transition metals (mostly cobalt and nickel) that are only accessible in limited geographic locations, often with socio-political instabilities and/or restrictions by government policies.2,3 Given the widespread abundance of Na-metal resources, sodium (Na)-ion batteries (NIBs) appear to be an ideal alternative of LIBs particularly for stationary applications.4–8The Natrium Super Ionic CONductor (NaSICON),9,10 relying on a robust covalent framework and tunable electrochemical properties,11,12 has been actively investigated as alternative electrode materials to the transition-metal layered oxides for NIBs.13,14 The high-voltages delivered by specific NaSICON compositions require a careful selection of liquid electrolytes15 and an understanding of the solid-electrolyte interphase.16–18 NaSICON-type solid electrolytes have also been applied to NIBs due to their prominent Na ionic conductivity.19
The NaSICON-based vanadium phosphate, in the Na3V2(PO4)3 (N3VP) phase and its electrochemically-derived phases, Na1V2(PO4)3 (N1VP) and Na4V2(PO4)3 (N4VP) have received significant attention as a promising positive electrode material for NIBs.11,12,14,20,21 Throughout this manuscript, we use NxVP to indicate NaxV2(PO4)3 at a Na composition, x. Several investigations have been conducted to improve the electrochemical performance of NxVP (energy density ∼ 370 W h kg−1 theoretically cycling at N3VP-N1VP), for example, by mixing V partially with other transition metals.11,21–23 Specifically, in the composition range 1 ≤ x ≤ 3, NxVP intercalates Na at a relatively high voltage (∼3.4 V vs. Na/Na+)20 and displays a limited volume change upon reversible Na insertion (i.e., ∼234.41 Å3 f.u.−1 in N3VP and ∼219.50 Å3 f.u.−1 in N1VP). In contrast, reversible Na (de)intercalation in layered transition metal oxides typically provides lower voltages than NaSICON electrodes, as well as volume changes that may curb their use in practical NIBs.6,24–26
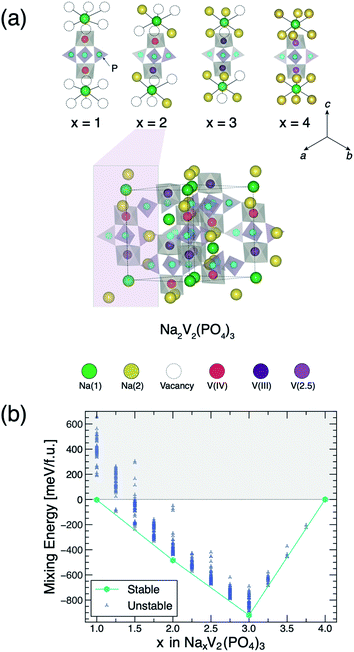
As shown in Fig. 1(a), the framework of NxVP is built around a common structural motif—the “lantern unit”—consisting of two VO6 octahedra sharing corners with three PO4 tetrahedra moieties.9–11,27 In principle, the NaSICON structure can host up to 4 Na ions to form N4VP6,28,29 with a rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) structure.30–32 In practice, the Na+ extraction/insertion is limited to only 3 ions (per two vanadiums) in the range N1VP–N4VP. It is impossible to extract the 4th Na ion from N1VP although the V(IV)/V(V) redox couple is theoretically accessible.21,33,34 In the R
c) structure.30–32 In practice, the Na+ extraction/insertion is limited to only 3 ions (per two vanadiums) in the range N1VP–N4VP. It is impossible to extract the 4th Na ion from N1VP although the V(IV)/V(V) redox couple is theoretically accessible.21,33,34 In the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c NxVP, two distinct Na sites exist: Na(1) and Na(2). The Na(1) site is 6-coordinated and sandwiched between 2 VO6 octahedra, whereas Na(2) (yellow or black-outlined circles in Fig. 1(a)) occupies the “interstitials” formed by PO4 units. In N4VP, both Na(1) and Na(2) sites are fully occupied. A partial occupancy of Na in the Na(2) sites (such as in N3VP, where sodium ordering occurs) can further reduce the R
c NxVP, two distinct Na sites exist: Na(1) and Na(2). The Na(1) site is 6-coordinated and sandwiched between 2 VO6 octahedra, whereas Na(2) (yellow or black-outlined circles in Fig. 1(a)) occupies the “interstitials” formed by PO4 units. In N4VP, both Na(1) and Na(2) sites are fully occupied. A partial occupancy of Na in the Na(2) sites (such as in N3VP, where sodium ordering occurs) can further reduce the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c symmetry, resulting in a monoclinic structure.31
c symmetry, resulting in a monoclinic structure.31
While these studies are certainly important, the community still does not fully understand the sheer complexity of the mechanism of Na extraction from N3VP, itself (during the first charge of the battery), which must be clarified to make NxVP a successful commercial electrode material. Chotard et al. identified specific Na/vacancy orderings in N3VP at different temperatures using synchrotron X-ray diffraction.31 Upon reversible Na (de)intercalation, such orderings may be facilitated by charge ordering on the vanadium sites, though the mechanism is far from being fully understood.20,21,31 These studies suggest that a complex interplay of Na/vacancy orderings, together with the variation in the electronic structure of vanadium, drives the formation of specific NxVP phases during Na (de)intercalation, which is the focus of this work.
Here, we reveal the driving forces behind the phase transitions of the NxVP framework, which occur as temperature and Na composition (1 ≤ x ≤ 4) are varied, using a multiscale model based on density functional theory (DFT) and grand-canonical Monte Carlo (gcMC) simulations. We analyze the relevant Na site occupancies, intercalation voltages, and entropies of Na intercalation as a function of temperature. Importantly, our theoretical study reveals the Na/vacancy ordering in the thermodynamically stable phase, N2VP, whose signature has been previously reported.35 Recent operando measurements have also confirmed the existence and the structural features of this intermediate N2VP phase.36 Notably, this is the first instance where the compositional phase diagram of a NaSICON electrode is derived from first principles. The results of our work shed light on the complexity of Na (de)insertion in NaSICON electrodes for novel NIBs.
Results
To understand the process of sodium extraction/intercalation in the NxVP structure, we use DFT calculations to parameterize a cluster expansion Hamiltonian, which in turn is used for energy evaluations within gcMC simulations, resulting in the estimation of thermodynamic properties as a function of temperature (and composition).37–39 We described the exchange and correlation term in DFT using the strongly constrained and appropriately normed (SCAN) meta-generalized gradient approximation (meta-GGA) functional.40 Additionally, we added a Hubbard U correction of 1.0 eV on all V atoms (i.e., SCAN + U) to appropriately localize the 3d electrons and reduce the spurious self-interaction errors.41,42 Details on these methodologies are provided in the Methodology and ESI.†41,42Fig. 1(b) shows the DFT mixing energies of the NxVP system at 0 K, referenced to the N1VP and N4VP compositions, which elucidate the thermodynamic driving forces for Na (de)intercalation. The mixing energies in Fig. 1(b) do not include entropy contributions. We enumerated all the different Na/vacancy configurations within 2 × 2 × 1 supercells (with 168 atoms) of the primitive rhombohedral cell (2 f.u. with 21 atoms per f.u.) and sampled Na compositions with a step size of x = 0.25 (see details in ESI†). The envelope of points minimizing the mixing energy—the convex hull—comprises the stable Na/vacancy orderings (aqua hexagons in Fig. 1(b)) at 0 K, namely, x = 1, 2, 3, and 4 in NxVP. Other Na/vacancy configurations (blue markers in Fig. 1(b)) are metastable (or unstable) and will decompose or phase separate into nearby stable phases at 0 K. Several metastable configurations are observed to be close to the convex hull, such as N1.5VP, N2.5VP and N3.5VP (with energy ∼4.4 meV f.u.−1, ∼24.5 meV f.u.−1, and ∼8.0 meV f.u.−1 above the convex hull, respectively).
Our calculations indicate that the stable “end-member” compositions, namely N1VP and N4VP adopt the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c rhombohedral space group, in agreement with existing X-ray diffraction experiments.21 We find the monoclinic distortion of N3VP (Cc), which is also a global minima (∼920 meV f.u.−1) in the convex hull of Fig. 1(b), in agreement with experimental observation.31 Remarkably, our DFT calculations discover a previously uncharted, thermodynamically stable Na-vacancy configuration at x = 2, i.e., N2VP (Fig. 1(a)). In the ground state structure of N2VP, the Na ions and vacancies are initialized in a monoclinic setting (C2/c), with geometry optimization by DFT further distorting the structure into a triclinic (P
c rhombohedral space group, in agreement with existing X-ray diffraction experiments.21 We find the monoclinic distortion of N3VP (Cc), which is also a global minima (∼920 meV f.u.−1) in the convex hull of Fig. 1(b), in agreement with experimental observation.31 Remarkably, our DFT calculations discover a previously uncharted, thermodynamically stable Na-vacancy configuration at x = 2, i.e., N2VP (Fig. 1(a)). In the ground state structure of N2VP, the Na ions and vacancies are initialized in a monoclinic setting (C2/c), with geometry optimization by DFT further distorting the structure into a triclinic (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) symmetry (see further discussions below).
) symmetry (see further discussions below).
Fig. 1(a) shows the “lantern units” of the computed ground states of NxVP at x = 1, 2, 3, and 4, emphasizing the Na/vacancy orderings in relation to the charge orderings on the vanadium(V) sites. The integration of the DFT-calculated spin density on each V site provides magnetic moments, which are directly related to the oxidation states of the V atoms (see Table S4 of ESI†). Table S3 of ESI† lists the V–O bond lengths for all the NxVP ground states, which is particularly useful for identifying V(IV) sites, as demonstrated by the existence of shorter (∼1.82 Å) V(IV)–O bonds. In N1VP and N3VP, only one type of V site is observed, i.e., V(IV) and V(III), respectively, which fulfils the charge-neutrality of the corresponding structures. On the other hand, the ground state configuration at N2VP exhibits “lantern units” containing one V(III) and one V(IV).
In N4VP, we could not distinguish the two V sites (light violet circles in Fig. 1(a)), as this composition shows metallic behaviour, which is discussed in the density of states (DOS) and the band structures of Fig. S1 and S3,† respectively. The metallic behaviour of N4VP results in fractional oxidation states of V (∼2.5), as extracted from the calculated magnetic moments (Table S4†), and in agreement with previous theoretical calculations.12 The analysis of the N4VP band structure in Fig. S3† suggests that only four bands contribute actively at the Fermi energy, which indicates that the predicted metallic behaviour may be an artifact of DFT. In fact, prior hybrid DFT calculations predicted N4VP as a semiconductor with a small band gap of ∼0.3 eV.12
The projected DOS in Fig. S1(a) to (d)† exhibit predominant V 3d states at the valence band edges and/or near the Fermi energy. As Na concentration (x) increases in NxVP from 1 to 4, the V 3d states are shifted to higher energies, first reducing and eventually closing the band gap at N4VP. The decreasing band gap with the reduced vanadium oxidation state (and increasing Na content) in NxVP also follows the trends of other compounds containing V,43–45 where compounds with V(IV) show less tendency to undergo a semiconductor-to-metal transition near room temperature than compounds containing V(III). Hence, the qualitative trend of our band gap predictions is robust.
The appreciable increase in band gap at N3VP (∼1.4 eV), with respect to N1VP (∼0.7 eV) or N2VP (∼0.3 eV) is attributed to the monoclinic distortion, which stabilizes the N3VP structure.12 As shown by the spin-polarized DOS projected onto the V 3d orbitals of Fig. S2,† the valence band edge (VBE) of N3VP is mainly dominated by vanadium orbitals with t2g character, whereas the conduction band edge (CBE) consists of both V t2g and eg orbitals. Note that the monoclinic distortion in N3VP is largely driven by electrostatic interactions, which is signified by Na fully occupying the Na(1) sites while selectively occupying a subset of Na(2) sites (see Fig. 1(a)). Thus, the increase in band gap of N3VP can be attributed to the electrostatic interactions within the monoclinic structure, which preferably stabilize the V t2g states of the VBE relative to the t2g and eg states comprising the CBE.
The knowledge of the temperature vs. Na composition (T vs. x) phase diagram is also of immediate importance for understanding the extraction/intercalation of Na+ from/into NxVP and for identifying commonalities in the structure–property relationships of other NaSICON electrodes or electrolytes. The temperature vs. composition phase diagram in Fig. 2 is derived from gcMC simulations, with supercells containing more than 172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032 atoms and ranged over 32
032 atoms and ranged over 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768
768![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–327
000–327![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680
680![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Monte Carlo steps for all T and x samples combined. The cluster expansion Hamiltonian, used for the energy evaluations in gcMC was fitted on DFT-calculated mixing energies of ∼849 Na/vacancy configurations (see ESI† for more details).
000 Monte Carlo steps for all T and x samples combined. The cluster expansion Hamiltonian, used for the energy evaluations in gcMC was fitted on DFT-calculated mixing energies of ∼849 Na/vacancy configurations (see ESI† for more details).
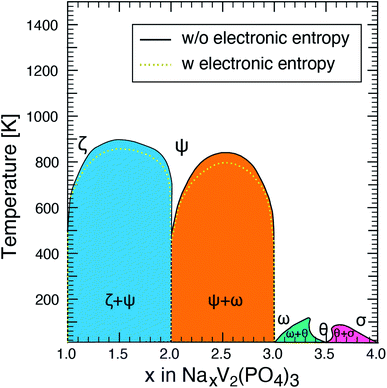
Fig. 2 exhibits five single-phase regions, namely, ζ, ψ, ω, θ and σ, which correspond largely to Na compositions of x = 1, 2, 3, 3.5, and 4, respectively. The two-phase regions in Fig. 2 are indicated by the coloured domes, with solid black and dashed yellow lines indicating their boundaries without and with electronic entropy contributions, respectively (see discussion below). Specifically, the two-phase regions in Fig. 2 are: ζ + ψ below 890 K and at 1 < x < 2 (light-blue dome), ψ + ω (orange dome at 2 < x < 3, T < 840 K), ω + θ (aqua dome at 3 < x < 3.5, T < 120 K), and θ + σ (pink dome at 3.5 < x < 4, T < 100 K). Notably, the ζ + ψ, and ψ + ω two-phase regions are stable over a wide-range of temperatures (0–800 K) compared to the other two-phase regions. The θ phase detected by gcMC appears to be stable only above 10 K (not visible in Fig. 2), and is metastable at 0 K (Fig. 1(b)). Thus, θ decomposes to form a two-phase ω + σ mixture, via an eutectoid reaction at ∼10 K and x = 3.5.
One remarkable finding from this phase diagram is the previously unidentified single-phase (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), ψ, at x = 2, which exists as a line compound up to T < 480 K. The solubility of excess Na in the ψ phase increases significantly at higher temperatures (T > 480 K), eventually leading to the closing of the ψ + ω miscibility gap at ∼850 K. The ψ phase also exhibits Na-vacancy solubility at high temperatures (T > 630 K), resulting in the closing of the ζ + ψ two-phase region at T ∼890 K. In general, we note that the NxVP phase diagram appears qualitatively similar to that of the NaSICON solid electrolyte, Na1+xZr2SixP3−xO12,27 which exhibits three distinct single-phase regions.
), ψ, at x = 2, which exists as a line compound up to T < 480 K. The solubility of excess Na in the ψ phase increases significantly at higher temperatures (T > 480 K), eventually leading to the closing of the ψ + ω miscibility gap at ∼850 K. The ψ phase also exhibits Na-vacancy solubility at high temperatures (T > 630 K), resulting in the closing of the ζ + ψ two-phase region at T ∼890 K. In general, we note that the NxVP phase diagram appears qualitatively similar to that of the NaSICON solid electrolyte, Na1+xZr2SixP3−xO12,27 which exhibits three distinct single-phase regions.
We assign oxidation states of V(III) and V(IV) to the vanadium atoms in N3VP and N1VP, respectively, for our 0 K calculations based on integrated magnetic moments. However, at intermediate Na compositions (1 < x < 3), the charges V(III) and V(IV) may disorder across the available V sites, owing to thermally-activated electronic or polaronic hops,46,47 especially at higher temperatures. Therefore, we introduce the effect of electronic entropy, ΔSelectronic, as induced by possible disordering (or accessing multiple configurations) of V(III)/V(IV) charges via the ideal solution model (eqn (1)):
| ΔSelectronic = −kBN[(mln(m) + (1 − m)ln(1 − m))] | (1) |
The inclusion of electronic entropy modifies the phase boundaries of the ζ + ψ and ψ + ω two-phase regions (see dashed yellow lines in Fig. 2). Specifically, including electronic entropy lowers the critical temperatures of both the two-phase regions (i.e., the highest temperature up to which a two-phase region exists) by ∼50 K. The electronic entropy also increases the Na solubility in ψ phase, characterized by an increase in the stability range of the ψ phase at higher Na contents for a given temperature.
We also analysed the occupancy of Na(1) and Na(2) sites, obtained from the gcMC simulations, across the Na composition range (1 ≤ x ≤ 4) at three specific temperatures: 263 K (Fig. 3(a)), 473 K (Fig. 3(b)) and 920 K (Fig. 3(c)), and compared with available experimental data at 263 K and 473 K,31 respectively. The 920 K is selected to represent the Na occupancy in the solid solution region where all two-phase regions cease to exist (Fig. 2). For all Na compositions in NxVP and at all temperatures considered, the occupation of Na(2) increases monotonically from 0 to 1 upon increasing x (see pink lines and dots in Fig. 3). In contrast, the Na(1) site remains fully occupied at 263 K (green lines and dots) across the whole composition range. Our predictions at 263 K are in excellent agreement with the experimental value from synchrotron X-ray experiments by Chotard et al.31 At higher temperatures (473 K and 920 K), Na(1) is fully occupied only for 1 ≤ x ≤ 3, while its occupancy decreases between N3VP and N3.1VP and subsequently increases again from N3.1VP to N4VP. Remarkably, at 473 K and 920 K and x > 3.05, both Na(1) and Na(2) sites show similar occupancies, indicating significant disorder across both Na sites, in line with the observed single-phase regions (ω/θ/σ) of Fig. 2.
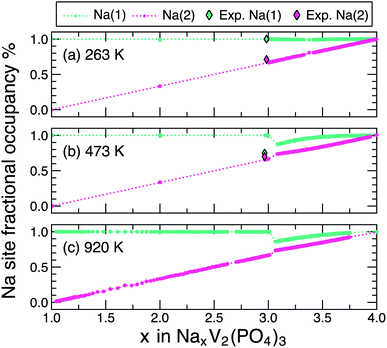 | ||
| Fig. 3 Na occupancies of Na(1) sites (green) and Na(2) sites (pink) in NxVP at 263 K (panel (a)), 473 K (panel (b)), and 920 K (panel (c)) vs. Na composition as extracted from gcMC simulations. Coloured dots represent data in the single-phase regions of the phase diagram of Fig. 2. The dashed lines denote the Na(1)/Na(2) distributions within the two-phase regions and are derived by interpolation between gcMC-simulated fractional occupations of the bounding single-phase regions. The experimental occupancies of Na(1) and Na(2) at 263 K and 473 K (ref. 31) are represented by green and pink diamond, respectively. | ||
Our simulated Na occupancy of the Na(2) site at the N3VP composition at 473 K accurately reproduces the experimental data of ref. 31. Although we overestimate the Na(1) occupancy (∼1) compared to experiment (∼0.75) at N3VP,31 we predict a sharp decrease of the Na(1) occupation at x slightly above 3 (e.g., x = 3.05), which is in better agreement with the experimental occupancy of Na(1).27 This suggests that the experimental samples intended as N3VP may be slightly off-stoichiometric. In any case, the decrease of Na(1) occupancy at x marginally greater than 3, especially at higher temperatures (473 K and 920 K) is likely because of a higher gain in configurational entropy by distributing Na atoms across both the Na(1) and the Na(2) sites as compared to the configurational entropy that can be obtained from only within Na(2) sites (a full occupation of Na in Na(1) sites gives rise to a net zero configurational entropy from the Na(1) sites). Indeed, recent work on oxide perovskites has shown that configurational entropy on two different “sub-lattices” can often lead to higher entropy gain compared to a single sub-lattice.48
The configurational entropy S(x) vs. Na content (1 ≤ x ≤ 3) at different temperatures is shown in Fig. S7 of ESI.†S(x) shows a local minimum at x = 1, 2, and 3, in agreement with the single-phases observed in the phase diagram (Fig. 2). The low Na off-stoichiometry, up to temperatures as high as ∼500 K at x = 1 and x = 2, reflects a trivial gain in configurational entropy with Na off-stoichiometry, available to these systems, as shown in Fig. S7.† Although we observe sizeable values of configurational entropy computed at high temperatures (above ∼800 K) in the single-phase regions (ζ, ψ, and ω), these phases are still preserved and full “compositional” disorder is only achieved above ∼900 K.
It is surprising that the metastable N1.5VP ordering (∼4.4 meV f.u.−1 above convex hull at 0 K, Fig. 1(b)) does not appear as a stable ordering at any temperature in our phase diagram (Fig. 2), while the metastable N3.5VP ordering (∼8.0 meV f.u.−1 above convex hull) becomes stable at ∼10 K. While the energy above the convex hull is usually a good rule of thumb to estimate (meta)stability of phases, the important factor is which other phases are in competition with the (meta)stable phase of interest and their entropies.49–51 In the case of N1.5VP, the primary competing phase is N2VP (the other competing phase is N1VP), which remains a stable, stoichiometric compound up to ∼480 K. Importantly, both N1.5VP and N2VP orderings have their Na(1) sites fully occupied by Na, while 0.5 and 1 Na(2) sites per f.u. are occupied by Na, respectively (Fig. 3). Given that there are a maximum of three Na(2) sites per f.u., the N2VP ordering can exhibit higher configurational entropy (corresponding to a Na occupancy of 0.33 in the Na(2) sites and assuming an ideal-solution-like behaviour), compared to the N1.5VP ordering (0.16 Na occupancy), resulting in N2VP remaining stable relative to N1.5VP with increasing temperature and preventing the N1.5VP phase from appearing on the phase diagram. On the other hand, the primary phase that N3.5VP competes with is N3VP (the other phase is N4VP), which should exhibit lower configurational entropy than N3.5VP, given that N3VP exhibits an electrostatically-driven monoclinic distortion. This allows the stabilization of the N3.5VP ordering at low temperatures, albeit its higher energy above the convex hull.
The computed NxVP voltage – composition curves at 0 K, 10 K, 300 K, and 500 K compared with the experimental voltage – composition data recorded at 298 K (ref. 21) are shown in Fig. 4. The blue (10 K), aqua (300 K) and gold (500 K) voltage profiles are obtained from gcMC simulations, and the crimson profile is obtained directly from DFT calculations (see eqn (S6) of the ESI†) at 0 K. Notably, the 0 K profile shows two voltage steps, corresponding to ψ and ω single phases, and consequently three voltage plateaus, corresponding to ζ + ψ (∼3.29 V vs. Na/Na+), ψ + ω (∼3.24 V), and ω + σ (∼1.89 V) two-phase regions. Generally, the computed voltage profiles at 0 K are in agreement with previous reports.12,34,52,53
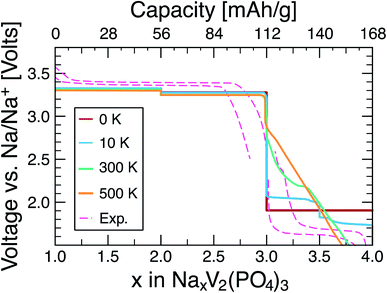 | ||
| Fig. 4 Computed intercalation voltage (volts vs. Na/Na+) curves as a function of Na content (x) in NxVP. The pink dashed lines indicate the experimental voltage response of NxVP at room temperature (digitized from ref. 21 for 3 ≤ x ≤ 4). Notably, the experimental profile for 1 ≤ x ≤ 3 is obtained from the unpublished works of some of the authors. The crimson line shows the computed voltage curve at 0 K derived by the DFT results from Fig. 1(b). The blue, aqua and gold lines display the computed voltage curves at 10 K, 300 K and 500 K, respectively, generated by the gcMC results. The discharge capacities (top x-axis in the unit of mA h g−1) are normalized to N4VP. | ||
Apart from a small (∼50 mV) previously unreported voltage step at x = 2 (N2VP), the voltage profiles for 1 ≤ x ≤ 3 at different temperatures display a similar shape. Although there is good qualitative agreement between theory and experiment for the entire Na composition range, all the predicted voltage curves at the selected temperatures underestimate the average voltage across 1 ≤ x ≤ 3, and overestimate the average voltage in the 3 ≤ x ≤ 4 range compared to experiment.21 Notably, the voltage curve in 3 ≤ x ≤ 4 at 10 K shows a step at x = 3.5, which corresponds to the formation of θ phase via the eutectoid reaction shown in Fig. 2. At higher temperatures (300 K and 500 K), the voltage profile for 3 ≤ x ≤ 4 region exhibits a sloping feature, characteristic of the predicted single phase domain (ω/θ/σ) at such temperatures (Fig. 2).
Discussion and conclusions
In this paper, we have investigated the thermodynamics of Na (de)intercalation in the NaSICON electrode material, Na3V2(PO4)3, for Na-ion batteries. Specifically, we derived the temperature-composition phase diagram of the NxVP system and the temperature dependent voltage curves for the reversible (de)intercalation of Na-ions. Notably, we have identified a previously uncharted, thermodynamically stable phase with composition N2VP, and another metastable ordering at N3.5VP. The existence of the N2VP phase between N1VP and N3VP has been simultaneously confirmed by recent operando measurements.36 In addition, we have studied other important properties, such as, the phase diagram at 0 K, the Na/vacancy and charge-ordered V configurations of the 0 K ground states, and the evolution of Na(1) and Na(2) occupancies with temperature and Na content. The following paragraphs contain additional observations from the data presented in this work as well as suggestions for future work.Unarguably, DFT-based simulations of highly correlated systems, such as NxVP (and other Na metal phosphates), present significant theoretical and computational challenges, which explain the scarce studies of such phase diagrams. Knowledge of compositional phase diagrams is however very important to accurately chart the electrochemical properties of these complex frameworks. Importantly, this is the first instance to report the composition vs. temperature phase diagram and temperature dependent voltage curves for NaSICON electrode NxVP.
Three important observations can be made from the sodium occupancy data of the NxVP system: (i) The Na(1) site does not appear electrochemically active at room temperature (and below), for 1 ≤ x ≤ 3, which indicates that the Na+ (de)intercalation is mostly driven by the Na(2) sites; (ii) at higher temperatures (>470 K) and higher Na contents (x > 3), both Na(1) and Na(2) attain nearly the same fractional occupations, which clearly indicates that the Na(1) site is indeed electrochemically active in these circumstances; and (iii) at x = 1, all Na(2) sites are empty and further Na removal will require the extraction of Na from Na(1) sites. With respect to observations (i) and (ii), we suggest that, at high temperature and x, Na+ will be transferred between Na(1) and Na(2), which might kinetically facilitate the reversible Na (de)intercalation (at least for x > 3). Also, we expect that any electronic entropy arising from charge disordering on the vanadium sites in 1 ≤ x ≤ 3 will promote disordering among the Na(1) and Na(2) sites. For observation (iii), we note that in 1992, Gopalakrishnan claimed chemical extraction of the last Na+ from N1VP,54 but this result has not been yet successfully reproduced. 11–13,39 Our data indicates that, at x = 1, all Na ions only occupy Na(1) sites, and their extraction may affect the structural integrity of N1VP, thus suppressing the chemical or electrochemical extraction of the last Na+. Indeed, Na migration between Na(1) sites at N1VP is hindered by high migration barriers (∼755 meV, computed previously),52 which usually indicate highly stable arrangement of atoms. Furthermore, the thermodynamic instability of the V2(PO4)3 framework with respect decomposition into VPO5 + VP2O7 can also account for the lack of reproduceable extraction of the last Na+ from N1VP.12
Previously, Na ion migration has been investigated in a number of NxVP compositions. Huang et al. and Ishado et al. independently used nudged elastic band calculations to estimate Na migration barriers between Na(1) and Na(2) sites (∼420 meV, and ∼304 meV, respectively) in N3VP, which suggest facile Na mobility in N3VP as opposed to Na migration in N1VP (∼755 meV).52,55
During the construction of the NxVP phase diagram, we isolated two novel low-temperature stable Na/vacancy orderings at the compositions N2VP and N3.5VP. Other low energy structures are visible from an analysis of the convex hull of Fig. 1, for example N1.5VP and N3.25VP, but their structures are not stabilized by configurational entropy at increasing temperatures (see Fig. 2). Notably, the signature of N2VP has been reported through operando X-ray diffraction by Zakharkin et al.,35 but its structural features were never identified and reported. In addition, our gcMC predicts a new stable phase, N3.5VP, that exists as the θ phase from 10 to ∼120 K, after which it merges with the ω and σ phases into a larger monophasic region (Fig. 2).
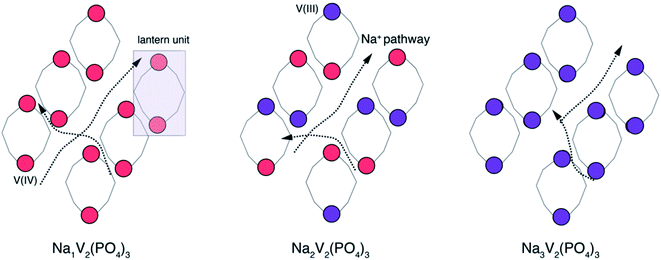
The ground state triclinic structure of N2VP (Fig. 2 and 4), which exists as a line compound from 0 K to ∼480 K, displays a specific Na/vacancy ordering at low temperatures. At the structural level, the N2VP ordering is achieved by the cooperative organization of the highly mobile Na-ions (occupying Na(2) sites) near V(III) sites and away from more positive V(IV) sites. The stability of the stoichiometric N2VP ordering (i.e., the solubility of excess Na or Na-vacancies) also depends upon the adaptability of the vanadium oxidation states by inter-valence electron transfer, which can be quantified by the impact of electronic entropy on the phase boundary of the ψ phase. Notably, we find that the inclusion of electronic entropy in our model only marginally modifies the NxVP phase boundaries (Fig. 2), in contrast to other phosphate electrode materials (e.g., LiFePO4), where electron–hole localization affects the features of the phase diagram significantly.56 Thus, we can conclude that charge ordering on the vanadium sites (as shown in Fig. 5) is more likely to drive specific Na/vacancy arrangements, especially at low temperatures. Since Na ions are expected to be highly mobile in NaSICON structures (as indicated in Fig. 5),10 the disorder in the Na/vacancy sites is the main contributor to the configurational entropy of the ψ phase at higher temperatures and not any charge-disorder on the V sites, thus restricting the extent of Na off-stoichiometry exhibited by the ψ phase up to T ∼ 480 K.
There are several reasons why N2VP might be difficult to be observed in practice. First, we speculate that N2VP might be difficult to isolate upon electrochemical (de)intercalation of Na. For example, the voltage step corresponding to N2VP formation (∼50 mV at x = 2 in Fig. 4) is similar to the magnitude of polarization that is typically observed in experiments. Standard electrochemical measurements may “bypass” the voltage signature of the stable N2VP ordering. Second, N2VP is only marginally stable with respect to disproportionation into N1VP and N3VP, as can be seen from Fig. 1(b) and 4, which may increase the difficulty of a direct solid-state synthesis of N2VP from other precursors. Third, it may be simply too difficult to recognize the monoclinic or triclinic (C2/c or P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) according to our DFT relaxations) distorted N2VP structures in the presence of the dominant rhombohedral N1VP and/or N3VP phases. In this context, specialized synthesis routes and/or “operando” experiments can be carried out to verify the existence of the N2VP ordering, similar to recent efforts that have been undertaken. Previous computational studies, with different exchange-correlation functionals, had indeed assigned N2VP as a slightly metastable phase (∼2 meV per atom above the convex hull), which might give an indication of the error bar in our computed data.12
according to our DFT relaxations) distorted N2VP structures in the presence of the dominant rhombohedral N1VP and/or N3VP phases. In this context, specialized synthesis routes and/or “operando” experiments can be carried out to verify the existence of the N2VP ordering, similar to recent efforts that have been undertaken. Previous computational studies, with different exchange-correlation functionals, had indeed assigned N2VP as a slightly metastable phase (∼2 meV per atom above the convex hull), which might give an indication of the error bar in our computed data.12
The experimental voltage curve of Fig. 4 in the region 3 ≤ x ≤ 3.5 shows an appreciable sloping behaviour followed by a voltage-composition plateau in the 3.5 ≤ x ≤ 4 region, which is partially captured in our calculated voltage profiles at 300 K or 500 K.21 It is not clear whether this sloping region is due to polarization effects (during either charging or discharging) encountered in the experiment, or due to solid solution behaviour, as evidenced by our predictions in Fig. 2 and 4. It also appears that the experiment could not achieve full Na insertion to reach N4VP, which may be facilitated by higher temperature experiments, and requires further theoretical and experimental investigations.
The emergence of the intermediate N2VP phase questions the accepted two-phase reaction between N3VP and N1VP, and calls for deeper investigations of the complex electrochemical behaviour of the NxVP system and potentially other NaSICON electrodes. Our current understanding of the phase behaviour suggests that during charging (and discharging), particles of NxVP will simultaneously contain domains with high (N3VP) and low (N1VP) levels of sodium content. The lattice mismatch between N3VP and N1VP domains can give rise to interfacial regions with significant strain (∼6% volumetric strain, see Table S2†), which may affect the particle integrity, especially when cycled at a high-rate and/or over numerous cycles.57 Our computed phase diagram and recent operando experiments36 have revealed the presence and thermodynamic stability of the N2VP phase. Importantly, N2VP can act as a “bridge” phase between high-Na N3VP and low-Na N1VP phases, reducing the lattice mismatch between the N3VP and N1VP phases, eventually lowering the interfacial strain and enabling high-rate and/or sustained cycle life upon reversible Na intercalation in NxVP.
Note that unearthing the thermodynamically stable phases in an electrode material has had significant impact on battery design and development in the past.56 For example, understanding the phase behaviour of LixFePO4 has enabled the optimization of rate-performance of this cathode material.58 Thermodynamically, LixFePO4 (0 ≤ x ≤ 1) should follow a two-phase reaction during Li (de)intercalation, where each LixFePO4 cathode particle is split into Li-rich and Li-poor domains. However, when nano-sized, LixFePO4 can access several transient phases, as confirmed by experimental studies,59–65 which enable its high-rate performance. Similar sizing-effects may be explored for the optimization of the rate performance and cycle behavior in NxVP, for which our work will act as a guide.
Methodology
To assess the structural, thermodynamic and electronic properties of NxVP, we used the Vienna ab initio simulation package (VASP 6.1.0),66,67 which implements density functional theory (DFT) to solve the Schrödinger equation of many-electron systems. The projector augmented wave (PAW) potentials, specifically Na 08Apr2002 3s1, V_pv 07Sep2000 3p63d44s1, P 06Sep2000 2s23p3, O 08Apr2002 2s22p4, were used for the description of the core electrons.68 The valence electrons were expanded in terms of orthonormal plane-waves up to an energy cutoff of 520 eV.To describe the electronic exchange-correlation, we employed the strongly constrained and appropriately normed (SCAN) meta-generalized gradient approximation (meta-GGA) functional.40 SCAN includes the kinetic energy density contributions, which has been shown to remove the O2 overbinding problem of GGA, while providing statistically-better ground-state electronic structures.42 We also added a Hubbard U correction of 1.0 eV on all vanadium atoms to improve the localization of 3d electrons (i.e., SCAN + U), and thus reduce the spurious electron self-interaction error.42 In contrast to typical GGA + U calculations, a smaller U value is required for SCAN calculations, whose construction limits the self-interaction error.41,42,69 All our DFT calculations were spin-polarized and we initialized all structures in a ferromagnetic arrangement. The total energy of each calculation was converged to within 10−5 eV per cell, atomic forces within 10−2 eV Å−1 and the stress within 0.29 GPa.
To explore a sufficiently large number of Na/vacancy configurations in NxVP, which is required to parameterize a cluster expansion (CE) model (see Section S2 in ESI†), we enumerated all the symmetrically distinct orderings in supercells containing as many as 8 f.u. (168 atoms) and with a resolution on the composition axis of Δx = 0.25. The enumeration process was performed with the pymatgen package.70 At each composition, we chose a maximum of 500 structures with the lowest Ewald energy,71 based on point charges (Na = +1, V = +2.5, P = +5, O = −2), to keep our calculations computationally tractable, followed by selecting only a subset of symmetrically distinct structures. In total, we have performed DFT structure relaxations (i.e., relax the cell volume, cell shape, and ionic positions) for 849 structures, across 1 ≤ x ≤ 4 in NxVP, which formed our training set for the cluster expansion. The DFT total energy of the Na/vacancy orderings was integrated on a 3 × 3 × 3 Γ-centered Monkhorst–Pack72k-point mesh for all primitive structures containing 2 NxVP formula units (f.u.), 42 atoms, a 1 × 3 × 3 k-point mesh applied to all supercells with 4 f.u. (84 atoms), and a 1 × 1 × 3 mesh in 8 f.u. (168 atoms), respectively.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. C., C. M., A. K. C., and J.-N. C. are grateful to the ANR-NRF NRF2019-NRF-ANR073 Na-MASTER. P.C. acknowledges funding from the National Research Foundation under his NRF Fellowship NRFF12-2020-0012. L. C., D. C. and C. M. acknowledge the ANRT and TIAMAT for the funding of S. P.'s PhD thesis as well as the financial support from the Région Nouvelle Aquitaine and from the French National Research Agency (STORE-EX Labex Project ANR-10-LABX-76-01). The computational work was performed using resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).References
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- E. A. Olivetti, G. Ceder, G. G. Gaustad and X. Fu, Joule, 2017, 1, 229–243 CrossRef.
- J.-M. Tarascon, Nature Chem, 2010, 2, 510 CrossRef CAS PubMed.
- S.-W. Kim, D.-H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710–721 CrossRef CAS.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Energy Environ. Sci., 2012, 5, 5884 RSC.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- J. L. Kaufman, J. Vinckevičiūtė, S. Krishna Kolli, J. Gabriel Goiri and A. Van der Ven, Phil. Trans. R. Soc. A., 2019, 377, 20190020 CrossRef CAS PubMed.
- R. Usiskin, Y. Lu, J. Popovic, M. Law, P. Balaya, Y.-S. Hu and J. Maier, Nat. Rev. Mater., 2021, 6, 1020–1035 CrossRef CAS.
- H. Y.-P. Hong, Mater. Res. Bull., 1976, 11, 173–182 CrossRef CAS.
- J. B. Goodenough, H. Y.-P. Hong and J. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS.
- C. Masquelier and L. Croguennec, Chem. Rev., 2013, 113, 6552–6591 CrossRef CAS PubMed.
- B. Singh, Z. Wang, S. Park, G. S. Gautam, J.-N. Chotard, L. Croguennec, D. Carlier, A. K. Cheetham, C. Masquelier and P. Canepa, J. Mater. Chem. A, 2021, 9, 281–292 RSC.
- T. Jin, H. Li, K. Zhu, P.-F. Wang, P. Liu and L. Jiao, Chem. Soc. Rev., 2020, 49, 2342–2377 RSC.
- N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain, Y. Chen, M. Chhowalla, Y.-S. Choi, S. I. R. Costa, M. Crespo Ribadeneyra, S. A. Cussen, E. J. Cussen, W. I. F. David, A. V. Desai, S. A. M. Dickson, E. I. Eweka, J. D. Forero-Saboya, C. P. Grey, J. M. Griffin, P. Gross, X. Hua, J. T. S. Irvine, P. Johansson, M. O. Jones, M. Karlsmo, E. Kendrick, E. Kim, O. V. Kolosov, Z. Li, S. F. L. Mertens, R. Mogensen, L. Monconduit, R. E. Morris, A. J. Naylor, S. Nikman, C. A. O'Keefe, D. M. C. Ould, R. G. Palgrave, P. Poizot, A. Ponrouch, S. Renault, E. M. Reynolds, A. Rudola, R. Sayers, D. O. Scanlon, S. Sen, V. R. Seymour, B. Silván, M. T. Sougrati, L. Stievano, G. S. Stone, C. I. Thomas, M.-M. Titirici, J. Tong, T. J. Wood, D. S. Wright and R. Younesi, J. Phys. Energy, 2021, 3, 031503 CrossRef CAS.
- A. Ponrouch, E. Marchante, M. Courty, J.-M. Tarascon and M. R. Palacín, Energy Environ. Sci., 2012, 5, 8572 RSC.
- P. G. Kitz, M. J. Lacey, P. Novák and E. J. Berg, Anal. Chem., 2019, 91, 2296–2303 CrossRef CAS PubMed.
- Na-ion Batteries, ed. L. Monconduit and L. Croguennec, ISTE Ltd/John Wiley and Sons Inc, Hoboken, 2020 Search PubMed.
- V. Lacivita, Y. Wang, S.-H. Bo and G. Ceder, J. Mater. Chem. A, 2019, 7, 8144–8155 RSC.
- Q. Ma, C.-L. Tsai, X.-K. Wei, M. Heggen, F. Tietz and J. T. S. Irvine, J. Mater. Chem. A, 2019, 7, 7766–7776 RSC.
- K. Saravanan, C. W. Mason, A. Rudola, K. H. Wong and P. Balaya, Adv. Energy Mater., 2013, 3, 444–450 CrossRef CAS.
- F. Lalère, V. Seznec, M. Courty, R. David, J. N. Chotard and C. Masquelier, J. Mater. Chem. A, 2015, 3, 16198–16205 RSC.
- F. Lalère, J. B. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, J. Power Sources, 2014, 247, 975–980 CrossRef.
- T. Lan, Q. Ma, C. Tsai, F. Tietz and O. Guillon, Batteries Supercaps, 2021, 4, 479–484 CrossRef CAS.
- C. Delmas, J. Braconnier, C. Fouassier and P. Hagenmuller, Solid State Ionics, 1981, 3–4, 165–169 CrossRef CAS.
- A. J. Toumar, S. P. Ong, W. D. Richards, S. Dacek and G. Ceder, Phys. Rev. Appl., 2015, 4, 064002 CrossRef.
- I. Hasa, S. Mariyappan, D. Saurel, P. Adelhelm, A. Y. Koposov, C. Masquelier, L. Croguennec and M. Casas-Cabanas, J. Power Sources, 2021, 482, 228872 CrossRef CAS.
- Z. Deng, G. Sai Gautam, S. K. Kolli, J.-N. Chotard, A. K. Cheetham, C. Masquelier and P. Canepa, Chem. Mater., 2020, 32, 7908–7920 CrossRef CAS.
- S. Y. Lim, H. Kim, R. A. Shakoor, Y. Jung and J. W. Choi, J. Electrochem. Soc., 2012, 159, A1393–A1397 CrossRef CAS.
- H. Kabbour, D. Coillot, M. Colmont, C. Masquelier and O. Mentré, J. Am. Chem. Soc., 2011, 133, 11900–11903 CrossRef CAS PubMed.
- X. Yao, Z. Zhu, Q. Li, X. Wang, X. Xu, J. Meng, W. Ren, X. Zhang, Y. Huang and L. Mai, ACS Appl. Mater. Interfaces, 2018, 10, 10022–10028 CrossRef CAS PubMed.
- J.-N. Chotard, G. Rousse, R. David, O. Mentré, M. Courty and C. Masquelier, Chem. Mater., 2015, 27, 5982–5987 CrossRef CAS.
- Z. Jian, C. Yuan, W. Han, X. Lu, L. Gu, X. Xi, Y.-S. Hu, H. Li, W. Chen, D. Chen, Y. Ikuhara and L. Chen, Adv. Funct. Mater., 2014, 24, 4265–4272 CrossRef CAS.
- Y. Ishado, A. Inoishi and S. Okada, Electrochemistry, 2020, 88, 457–462 CrossRef CAS.
- Y. Noguchi, E. Kobayashi, L. S. Plashnitsa, S. Okada and J. Yamaki, Electrochim. Acta, 2013, 101, 59–65 CrossRef CAS.
- M. V. Zakharkin, O. A. Drozhzhin, S. V. Ryazantsev, D. Chernyshov, M. A. Kirsanova, I. V. Mikheev, E. M. Pazhetnov, E. V. Antipov and K. J. Stevenson, J. Power Sources, 2020, 470, 228231 CrossRef CAS.
- S. Park, Z. Wang, Z. Deng, I. Moog, P. Canepa, F. Fauth, D. Carlier, L. Croguennec, C. Masquelier and J.-N. Chotard, Crystal Structure of the Intermediate Na2V2(PO4)3 Phase and Electrochemical Reaction Mechanisms in NaxV2(PO4)3 (1 ≤ x ≤ 4) System, 2021, DOI:10.33774/chemrxiv-2021-q6z1p.
- J. M. Sanchez, F. Ducastelle and D. Gratias, Phys. A, 1984, 128, 334–350 CrossRef.
- A. Van der Ven, J. C. Thomas, Q. Xu and J. Bhattacharya, Math. Comput. Simulat., 2010, 80, 1393–1410 CrossRef.
- J. C. Thomas and A. V. der Ven, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214111 CrossRef.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- G. Sai Gautam and E. A. Carter, Phys. Rev. Mater., 2018, 2, 095401 CrossRef CAS.
- O. Y. Long, G. Sai Gautam and E. A. Carter, Phys. Rev. Mater., 2020, 4, 045401 CrossRef CAS.
- J. Feinleib and W. Paul, Phys. Rev., 1967, 155, 841–850 CrossRef CAS.
- C. Didier, M. Guignard, J. Darriet and C. Delmas, Inorg. Chem., 2012, 51, 11007–11016 CrossRef CAS PubMed.
- M. Guignard, C. Didier, J. Darriet, P. Bordet, E. Elkaïm and C. Delmas, Nat. Mater., 2013, 12, 74–80 CrossRef CAS PubMed.
- T. Holstein, Ann. Phys., 1959, 8, 325–342 CAS.
- M. Reticcioli, U. Diebold, G. Kresse and C. Franchini, in Handbook of Materials Modeling, ed. W. Andreoni and S. Yip, Springer International Publishing, Cham, 2020, pp. 1035–1073 Search PubMed.
- G. Sai Gautam, E. B. Stechel and E. A. Carter, Chem. Mater., 2020, 32, 9964–9982 CrossRef CAS.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed.
- D. C. Hannah, G. Sai Gautam, P. Canepa and G. Ceder, Adv. Energy Mater., 2018, 8, 1800379 CrossRef.
- D. De Fontaine, Principles of Classical Thermodynamics: Applied to Materials Science, World Scientific Publishing Co. Pte. Ltd, Singapore ; Hackensack, NJ, 2019 Search PubMed.
- Y. Ishado, A. Inoishi and S. Okada, Electrochemistry, 2020, 88, 457–462 CrossRef CAS.
- X. Guo, Z. Wang, Z. Deng, B. Wang, X. Chen and S. P. Ong, Chem. Mater., 2020, 32, 6875–6885 CrossRef CAS.
- J. Gopalakrishnan and K. K. Rangan, Chem. Mater., 1992, 4, 745–747 CrossRef CAS.
- Y. Huang, X. Li, J. Wang, L. Miao, C. Li, J. Han and Y. Huang, Energy Storage Materials, 2018, 15, 108–115 CrossRef.
- F. Zhou, T. Maxisch and G. Ceder, Phys. Rev. Lett., 2006, 97, 155704 CrossRef PubMed.
- A. Abdellahi, O. Akyildiz, R. Malik, K. Thornton and G. Ceder, J. Mater. Chem. A, 2014, 2, 15437–15447 RSC.
- R. Malik, A. Abdellahi and G. Ceder, J. Electrochem. Soc., 2013, 160, A3179–A3197 CrossRef CAS.
- C. Delacourt, J. Rodríguez-Carvajal, B. Schmitt, J.-M. Tarascon and C. Masquelier, Solid State Sci., 2005, 7, 1506–1516 CrossRef CAS.
- C. Delacourt, P. Poizot, J.-M. Tarascon and C. Masquelier, Nat. Mater., 2005, 4, 254–260 CrossRef CAS.
- R. G. Iyer, C. Delacourt, C. Masquelier, J.-M. Tarascon and A. Navrotsky, Electrochem. Solid-State Lett., 2006, 9, A46–A48 CrossRef CAS.
- L. Laffont, C. Delacourt, P. Gibot, M. Y. Wu, P. Kooyman, C. Masquelier and J. M. Tarascon, Chem. Mater., 2006, 18, 5520–5529 CrossRef CAS.
- Y. Orikasa, T. Maeda, Y. Koyama, H. Murayama, K. Fukuda, H. Tanida, H. Arai, E. Matsubara, Y. Uchimoto and Z. Ogumi, Chem. Mater., 2013, 25, 1032–1039 CrossRef CAS.
- I. Takahashi, T. Mori, T. Yoshinari, Y. Orikasa, Y. Koyama, H. Murayama, K. Fukuda, M. Hatano, H. Arai, Y. Uchimoto and T. Terai, J. Power Sources, 2016, 309, 122–126 CrossRef CAS.
- T. Yoshinari, T. Mori, K. Otani, T. Munesada, K. Yamamoto, T. Uchiyama, K. Fukuda, Y. Koyama, R. Hagiwara, Y. Orikasa and Y. Uchimoto, Chem. Mater., 2019, 31, 7160–7166 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. A. Kitchaev, H. Peng, Y. Liu, J. Sun, J. P. Perdew and G. Ceder, Phys. Rev. B, 2016, 93, 045132 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748–1749 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta09249a |
| This journal is © The Royal Society of Chemistry 2022 |