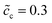Impedance modelling of all-solid-state thin film batteries: influence of the reaction kinetics
Yao
Liu
 a,
Wen-Bei
Yu
*b and
Bai-Xiang
Xu
a,
Wen-Bei
Yu
*b and
Bai-Xiang
Xu
 *a
*a
aMechanics of Functional Materials Division, Department of Materials Science, TU Darmstadt, Otto-Berndt-Straße 3, Darmstadt 64287, Germany. E-mail: xu@mfm.tu-darmstadt.de
bState Key Laboratory of Advanced Technology for Materials Synthesis and Processing, Wuhan University of Technology, Wuhan 430070, China. E-mail: yuwenbei252302@163.com
First published on 12th November 2021
Abstract
Understanding the effect of material properties on the interface impedance is crucial for high energy all-solid-state thin film lithium-ion battery design. Nevertheless, reaction kinetics determined by the free enthalpy difference at the interface and the vacancy effect in solids are always ignored or simplified when simulating battery impedance. In this work, we obtain the numerical impedance results by using an advanced electrochemical model (modified Planck–Nernst–Poisson model coupled with the new Frumkin–Butler–Volmer equation), whereby the mentioned issues are taken into account. More importantly, we derive a comprehensive equivalent circuit model from the electrochemical model, where all circuit elements are quantified from material properties. The results show that the high-frequency semicircle in the impedance spectrum is due to the bulk impedance and is associated with ion migration. Moreover, the plots at low and medium frequencies are assigned to the charge transfer resistance and the space charge layer capacitance. The results show that batteries with a higher free enthalpy difference lead to a significant decrease of the charge transfer resistance, but increase the electrostatic potential drop. Lithium-ion diffusivity has no impact on the interface impedance, but can dominantly reduce the bulk resistance. The simulation results were verified at the end against experimental impedance spectra.
1 Introduction
For over decades, lithium-ion batteries, typically using liquid electrolytes, have become ubiquitous by the powerful revolution in portable electronic devices.1–5 Due to the energy density and the safety issue related to liquid electrolytes, all-solid-state lithium-ion batteries have been researched extensively as promising alternatives for future energy storage devices.6–10 Currently, the electrode/electrolyte interface is a challenging issue for the development of high performance battery systems for electrical vehicles and other applications.11–14 During the charging and discharging process, charges accumulate or deplete at the interface and form the electrical double layer (EDL),15 which is called the space charge layer in solids.16 The space charge layer is determined by the lithium-ion kinetic reaction.17 The understanding of how material properties affect the interface impedance18,19 is very limited. To deepen the understanding, the electrochemical impedance spectroscopy (EIS) method has been extensively applied to investigate the kinetics of the cathode in lithium-ion batteries.20–24 The physical origin and the assignment of EIS features remain controversial. The EIS method determines the total impedance of batteries and is difficult to single out the interface impedance associated with the lithium-ion kinetic reaction. Therefore, research efforts have been focused on utilizing theoretical and numerical tools to clarify the origin of impedance.The current state-of-the-art impedance modelling and simulations can be roughly classified into three categories, i.e., the electrochemical model,25 the equivalent circuit model,26,27 and the density functional theory (DFT) calculations.28 Electrochemical models are derived from basic thermodynamics, e.g., the electrochemical potential, and the numerical results of such models provide spatial and temporal distributions of the concentration and electrostatic potential. They can be used for the battery cell impedance calculation.29–31 However, the present work ignores or simplifies the lithium-ion kinetic reaction at the interface.30 As shown in Ref. 11, the interface impedance decreases from 1710 Ω cm2 to 1 Ω cm2 with the formation of an ultrathin Al2O3 layer, and the reason lies in the lithium-ion binding energy difference of materials (11.4 to 1.6 eV nm−2). Nevertheless, the energy parameters that appear in the Butler–Volmer (BV) equation are never addressed in current electrochemical impedance models. Moreover, the extensively employed Planck–Nernst–Poisson (PNP) model is mostly taken from the case of liquid electrolytes and the specific feature of solid materials is overlooked, e.g., the unoccupied regular lattice sites (or called vacancies). In comparison to the electrochemical model, the equivalent circuit model is more simple and is able to quantify the impedance of each part. However, this model fails to explain the physical origin of the battery impedance and different equivalent circuit models can produce the same results. As shown in ref. 27 and 32, two different equivalent circuit models are proposed to explain the thin film battery impedance but both produce the same spectroscopy results. Therefore, the electrochemical model and the corresponding equivalent circuit model are combined to analyse the battery impedance. The DFT calculations show an obvious advantage when explaining the interface impedance from material properties, i.e., the atomic structure11 and the activation energy. Unfortunately, this method cannot calculate the interface impedance directly and fails to estimate the overall impedance of batteries as well. Therefore, a methodology to include the information of the atomic structure and the energy barrier within the impedance calculation directly is still missing.
To overcome this issue, an advanced electrochemical model and the corresponding equivalent circuit model for all-solid-state thin film battery impedance calculations are proposed in this work. The classical diffusion model can be extended to model ionic diffusion in solids, which describes ionic transport as the hopping of individual ions from one lattice site to the vacancies in the crystal structural framework.33,34 To consider this feature, the effect of vacancies in the framework of solids is concluded in the modified Planck–Nernst–Poisson (MPNP) model. Moreover, the lithium-ion kinetic reaction at the electrode/electrolyte interface is modelled by using the new Frumkin–Butler–Volmer (FBV) equation. Unlike the widely applied BV equation,35,36 in this equation, the standard activation energy of materials and the affordable lattice sites for lithium-ion transfer at the interface are taken into consideration. This work shows the possibility to calculate thin film battery impedance by considering the energy barrier for the specific material. On the other hand, we take a further step and propose a corresponding equivalent circuit model based on the advanced electrochemical model to gain deeper understanding of impedance spectroscopy. All the elements in the equivalent circuit model can be quantified from material properties and the related equilibrium quantities such as the exchange current and the bulk electrostatic potentials. This work is the first theoretical study that considers reaction kinetics in the battery impedance calculation. It provides a novel perspective on the microscopic origin of the interface resistance. The article is organized as follows: In Section 2, lithium-ion reaction kinetics at the solid/solid interface, the MPNP-FBV model, the impedance calculation methodology, and the novel equivalent circuit model are presented. Section 3 shows the calculated exchange current and the impedance spectroscopy results. Here, the impact of the free enthalpy difference, diffusivity, and the electric double layer structure on the impedance is investigated. A summary of this work and an outlook are shown in Section 4.
2 Solid-state battery impedance models
2.1 Interface reaction kinetics
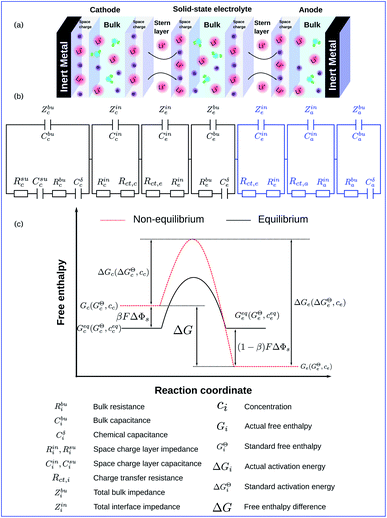
Fig. 1a shows the schematics of characteristic regions in an all-solid-state thin film lithium-ion battery that operates with a perturbation potential. Due to the initial free enthalpy difference of materials, the lithium-ion reaction occurs spontaneously at the electrode/electrolyte interface and forms the space charge layers. The thickness of the cathode is denoted by Lc, the solid-state electrolyte by Le and the anode by La. Based on the electrochemical continuum model, which will be explained in following subsections, we propose the equivalent circuit model illustrated in Fig. 1b. Thereby the circuit elements are closely related to material properties, and physical explanations are shown in the following sections. According to ref. 36 and 37, the Butler–Volmer equation has been applied to study the charge transfer reaction at the anode/electrolyte interface, which is similar to the cathode/electrolyte interface. Therefore, to emphasize the influence of the reaction kinetics on the thin film battery impedance, the anode has been overlooked in this work. It should be noted that the anode can also be included if necessary.To deepen the understanding, the free enthalpy profile of the electrochemical reaction is depicted in Fig. 1c. Unless otherwise stated, the subscripts “c” and “e” in this work indicate the cathode and the electrolyte, respectively. Gc (Ge) denotes the corresponding actual free enthalpy and is determined by both the standard free enthalpy GcΘ (GeΘ) and the concentration cc (ce). In addition, ΔG is the free enthalpy difference of materials and is expressed as ΔG = Gc − Ge.
To take the vacancy effect into consideration, the modified FBV equation is employed to model the lithium-ion reaction at the cathode/electrolyte interface and is given by 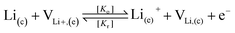 .17 It should be noted that the amount of vacancies, e.g., VLi+,(e) and VLi,(c), constrains the lithium-ion reaction rate at the interface. The partial flux of the reaction is given by the following equation:
.17 It should be noted that the amount of vacancies, e.g., VLi+,(e) and VLi,(c), constrains the lithium-ion reaction rate at the interface. The partial flux of the reaction is given by the following equation:
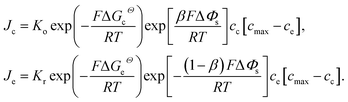 | (1) |
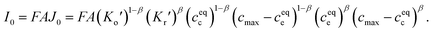 | (2) |
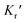 and
and 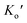 are expressed as
are expressed as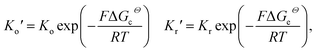 | (3) |
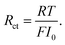 | (4) |
Eqn (2) and (4) indicate that the charge transfer resistance is explicitly determined by the standard activation energy barrier ΔGiΘ (i indicating c or e) and the equilibrium concentrations cc and ce at the interface. The latter is also eventually determined by the other material parameters.
The two electrostatic potentials at the solid/solid interface can be related using the Gouy–Chapman–Stern model (or called the diffuse double layer model).38 Moreover, the experimental results15 also show the similar distribution of the electrostatic potential in solid-state batteries. Within the diffuse double layer model, the electrostatic potential drops both in the space charge layer and the Stern layer. Therefore, the potential distribution in the space charge layer should be numerically identified and the interface condition is defined as
Φc = Φe − ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) λs∇Φc. λs∇Φc. | (5) |
2.2 Electrochemical model and methodology
The electrochemical models of the solid components, i.e., cathode or electrolyte, share a similar structure but are subjected to the corresponding material parameters. The electrochemical potential of the component i (i = c or e) is expressed as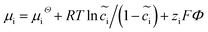 , where μiΘ indicates the standard chemical potential and
, where μiΘ indicates the standard chemical potential and 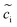 denotes the normalized concentration of the corresponding component ci (more exactly cc or ce).39 Under this circumstance, a material balance leads to the differential conservation law and is given by
denotes the normalized concentration of the corresponding component ci (more exactly cc or ce).39 Under this circumstance, a material balance leads to the differential conservation law and is given by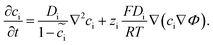 | (6) |
In addition, the relationship between the electric charge density and the electrostatic potential is denoted by the Poisson equation
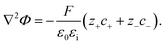 | (7) |
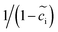 is employed in eqn (6) of the MPNP model to consider the vacancy effect in solids. As shown in Fig. 1a, the thin film battery operates under pulse electric potential conditions, which is formulated as Φ = Φdc + Φac(cos
is employed in eqn (6) of the MPNP model to consider the vacancy effect in solids. As shown in Fig. 1a, the thin film battery operates under pulse electric potential conditions, which is formulated as Φ = Φdc + Φac(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt + j
ωt + j![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt), where Φdc and Φac denote the direct current (dc) and alternating current (ac) potentials, respectively. The imaginary number j is equal to
ωt), where Φdc and Φac denote the direct current (dc) and alternating current (ac) potentials, respectively. The imaginary number j is equal to 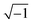 , and ω is the frequency of the ac signal. The resulting current should have the same type of structure and is expressed as I = Idc + Iac[cos(ω − ω0)t + j
, and ω is the frequency of the ac signal. The resulting current should have the same type of structure and is expressed as I = Idc + Iac[cos(ω − ω0)t + j![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ω − ω0)t], where ω0 is the phase angle difference. Therefore, the impedance Z is expressed as30,31
sin(ω − ω0)t], where ω0 is the phase angle difference. Therefore, the impedance Z is expressed as30,31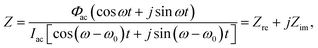 | (8) |
2.3 Equivalent circuit model and element quantification
The MPNP-FBV model and the numerical methodology for the battery impedance calculation are comprehensive and fully based on physical chemistry. Nevertheless, the complete impedance of such an electrochemical model is difficult to distinguish the contribution of each part and consumes the computation resources as well. Thereby, an equivalent circuit model for all-solid-state thin film batteries is derived here based on the electrochemical model. The derived model is depicted in Fig. 1b. It reflects the impedance spectroscopy contribution of individual components and interfaces.In batteries, charges are prone to accumulate or deplete at the interface and form the space charge layer, however, lithium-ion concentrations remain almost homogeneous in the bulk. We first derive the bulk impedance of thin film batteries40
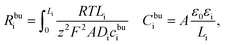 | (9) |
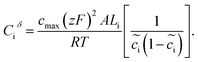 | (10) |
According to our previous investigation,17 the analytical concentration distribution in the MPNP model can be expressed as
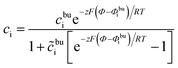 | (11) |
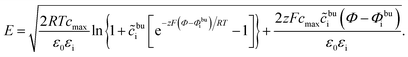 | (12) |
The space charge layer capacitance is related to the charge density43 and the analytical solution is defined as
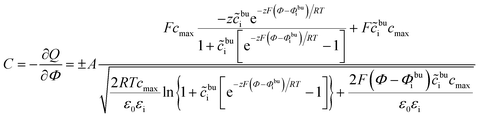 | (13) |
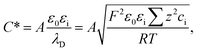 | (14) |
The charge transfer resistance Rct and the space charge layer capacitance can be calculated from eqn (4) and (13) as explained in the previous subsection. The anode has been overlooked in this study, thus, no lithium-ion reaction occurs at the right-hand side of the electrolyte. Consequently, the equivalent circuit model of the solid-state thin film battery is simplified and the blue elements cannot be taken into account. Based on Fig. 1b and the analytical results, the impedance of the proposed equivalent circuit model is given by
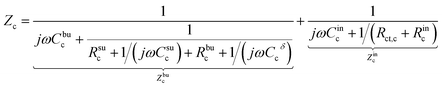 | (15) |
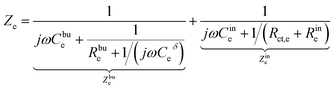 | (16) |
| Z = Zc + Ze. | (17) |
In particular, Cini is the space charge layer capacitance at the interface, and Csuc is the charge accumulation at the cathode surface. Rini and Rsui are the space charge layer resistances, and are associated with the frequency dependent charge density in the space charge layer. In most studies, the Warburg impedance is widely applied to explain the diffusion induced impedance and the analytical results can be expressed as44Z = RTci(ω)/FI(ω)ceqi, where I(ω) and ci(ω) are the frequency dependent current and concentration. Therefore, the finite-length or the finite-space Warburg impedances are the results obtained with specific boundary conditions and electrochemical models. In this work, we followed the method introduced by Maier45,46 to investigate the space charge layer impedance and more details will be given in the following section. The charge transfer resistance in the cathode (or the electrolyte) is proportional to the concentration and is depicted by
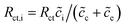 | (18) |
3 Results and discussion
The numerical methodologies of impedance calculation based on the electrochemical model and the derived equivalent circuit model presented in Section 2 are both comparatively applied in this section for specific cases and parameter studies. The calculated impedance evolutions of the main electrochemical parameters are given here and show the applicability of battery impedance models. To make the problem mathematically tractable, several additional assumptions and boundary conditions given in the literature have been adopted in this work. (1) The cathode/solid-state electrolyte half cell, as shown in Fig. 1a, is regarded as a one-dimensional domain and operated with an alternating current (ac) potential perturbation in the frequency range. (2) Only mobile lithium-ions are considered in the half cell, and electrons are assumed to be immobile. Moreover, the lithium-ion kinetic reaction only occurs at the interface. (3) The perturbation potential of all-solid-state thin film batteries is expressed as ΦL = Φdc + Φac(ejωt) and ΦR = 0, respectively. (4) Heat generation is ignored and the temperature is uniform and constant in the half cell. Numerical simulations have been performed with the finite element method in the MOOSE framework with 2000 first-order bulk elements.47 In particular, finite element interface elements between the components are subjected to the FBV model, while in the infinite element bulk elements the MPNP equations are solved for individual components. Moreover, to improve the convergence of numerical calculations, normalization of the model is carried out by using the following dimensionless parameters indicated by the tilde hat.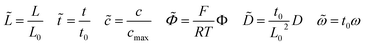 | (19) |
3.1 EIS current
To better understand the impedance calculation by using the MPNP-FBV model, the resulting current as a function of time is plotted here. The total electric current I is composed of the faradaic current If and the maxwell displacement current Id, and is expressed as I = If + Id. The faradaic current is due to the species migration and is given by If = FA∑iziJi. The maxwell displacement current results from the frequency of the electric field strength and is given by Id = − Aε0εi[∂(∇Φ)/∂t]. In this work, the dimensionless alternate-current potential at the left-hand side leads to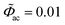 and the direct-current potential is given by
and the direct-current potential is given by 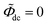 , and other parameters are taken from Table 1.
, and other parameters are taken from Table 1.
| Parameter | Unit | Value | Description |
|---|---|---|---|
| a Designed parameters. b Parameters taken from the literature.30,37,48 | |||
| L e | nm | 50 | Thickness of the electrolytea |
| L c | nm | 50 | Thickness of the cathodea |
| λ s | nm | 0.3 | Thickness of the stern layerb |
| D c | m2 s−1 | 10−14 | Diffusivity of lithium ions in the cathodea |
| D e | m2 s−1 | 10−14 | Diffusivity of lithium ions in the electrolytea |
| ΔGcΘ | eV | 0.5 | Activation energy barrierb |
| ΔGeΘ | eV | 0.8 | Activation energy barrierb |
| ε 0 | F m−1 | 8.85 × 10−12 | Vacuum permittivityb |
| ε e | — | 80 | Relative permittivity of the electrolytea |
| ε c | — | 80 | Relative permittivity of the cathodea |
| c max | mol m−3 | 104 | Maximum lithium ion concentrationa |
| c e | mol m−3 | 5 × 103 | Initial concentration in the electrolytea |
| c c | mol m−3 | 5 × 103 | Initial concentration in the cathodea |
| β | — | 0.5 | Symmetry factorb |
| F | C mol−1 | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 485 |
Faraday constantb |
| T | K | 298.15 | Temperatureb |
| R | J mol−1 K−1 | 8.314 | Gas constantb |
| z + | — | 1 | Lithium-ion valenceb |
| z − | — | −1 | Electron valenceb |
| K o | m4 mol−1 s−1 | 100 | Oxidation reaction ratea |
| K r | m4 mol−1 s−1 | 100 | Reduction reaction ratea |
| A | m2 | 10−4 | Geometrical surfacea |
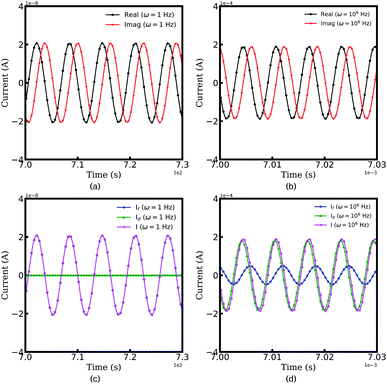
Fig. 2 depicts the resulting currents of the half cell as a function of time at two specific frequencies, i.e., ω = 1 and 106 Hz. The legends “Real” and “Imaginary” indicate the real and the imaginary parts of the total current, respectively. It should be noted that the half cell reaches a quasi-equilibrium state with the perturbation potential, and the amplitude of the resulting current is utilized for the battery impedance calculation, as shown in eqn (8). From Fig. 2a and b, we can conclude that the amplitude of current increases with increasing frequency. Therefore, this conclusion can explain that the impedance magnitude of batteries decreases at high frequencies.49
Moreover, to identify the impedance contribution, the faradaic current If and the maxwell displacement current Id, as well as the total current I are shown in Fig. 2c and d,. At frequency ω = 1 Hz, the displacement current equals zero and the plots of the faradaic current and the displacement current appear to be superimposed. The results show that the impedance associated with the lithium-ion migration plays an important role at low frequencies. However, in the high-frequency region, the maxwell current increases while the faradaic current decreases, which means that the applied potential plays a more important role. The reason is that lithium-ions cannot migrate inside materials because of the rapid frequency change. Therefore, thin film batteries are prone to exhibit dielectric properties at high frequencies.
3.2 Charge transfer resistance with dependency on the free enthalpy difference
In this section, the kinetics of the lithium-ion reaction is discussed from the fundamental point of view. The related thermodynamic properties of the electrode/electrolyte interface are shown in Fig. 1c, and the actual free enthalpy Gi of material is expressed as follows: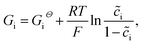 | (20) |
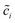 denotes the normalized concentration. Thus, the free enthalpy difference of materials yields
denotes the normalized concentration. Thus, the free enthalpy difference of materials yields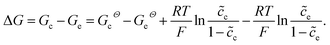 | (21) |
It should be noted that the standard free enthalpy difference GcΘ − GeΘ numerically equals the standard activation energy difference −(ΔGcΘ − ΔGeΘ). To investigate the influence of the free enthalpy difference on the charge transfer resistance, the lithium-ion concentration and the standard activation energy are discussed here, respectively. The diffusion coefficients are De = Dc = 10−14 m2 s−1, and other parameters are shown in Table 1.
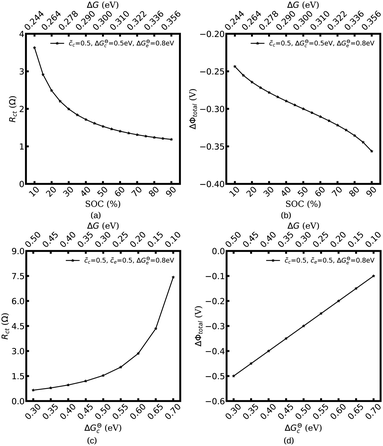
Fig. 3 shows the plot of the charge transfer resistance and the total electrostatic potential drop with respect to the free enthalpy difference, e.g., the state of charge and the standard activation energy. The charge transfer resistance is calculated by using eqn (2) and (4), and the concentrations at the intrinsic equilibrium state are determined numerically by using the MPNP-FBV model. The total electrostatic potential drop equals to the difference of bulk potentials and is expressed by ΔΦtotal = Φbuc − Φbue. As can be seen in Fig. 3a and b, the lithium-ion concentration of the solid-state electrolyte is 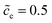 , and the standard activation energies are assumed to be ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV. It should be noted that the activation energies of materials can be identified through the DFT calculations.48 The initial concentrations of the cathode are
, and the standard activation energies are assumed to be ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV. It should be noted that the activation energies of materials can be identified through the DFT calculations.48 The initial concentrations of the cathode are 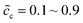 , which represents that the theoretical state of charge (SOC) varies from 10% to 90%.
, which represents that the theoretical state of charge (SOC) varies from 10% to 90%.
Fig. 3c and d show that lithium-ion concentrations are 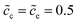 and the electrolyte standard activation energy remains ΔGeΘ = 0.8 eV, while the cathode activation energy varies from ΔGcΘ = 0.3–0.7 eV. Here, the free enthalpy difference ΔG is calculated by using eqn (21), Fig. 3a and c show that the charge transfer resistance decreases with increasing free enthalpy difference. In addition, ref. 50 and 51 show that the charge transfer resistance decreases with increasing concentration and verify the numerical results. Furthermore, Fig. 3b and d show the plot of the total electrostatic potential drop as a function of the free enthalpy difference. The results demonstrate that the potential drop is equal to the free enthalpy difference, i.e., ∣ΔΦtotal∣ = ΔG. It is evident that when the electrolyte free enthalpy remains stable, increasing the free enthalpy difference can significantly reduce the charge transfer resistance. Nevertheless, increasing the large free enthalpy difference also leads to a large electrostatic potential drop at the interface, which is harmful to the working potential. Therefore, the free enthalpy difference between the cathode and the electrolyte is a paradox criterion for high performance battery design and has to be optimized.
and the electrolyte standard activation energy remains ΔGeΘ = 0.8 eV, while the cathode activation energy varies from ΔGcΘ = 0.3–0.7 eV. Here, the free enthalpy difference ΔG is calculated by using eqn (21), Fig. 3a and c show that the charge transfer resistance decreases with increasing free enthalpy difference. In addition, ref. 50 and 51 show that the charge transfer resistance decreases with increasing concentration and verify the numerical results. Furthermore, Fig. 3b and d show the plot of the total electrostatic potential drop as a function of the free enthalpy difference. The results demonstrate that the potential drop is equal to the free enthalpy difference, i.e., ∣ΔΦtotal∣ = ΔG. It is evident that when the electrolyte free enthalpy remains stable, increasing the free enthalpy difference can significantly reduce the charge transfer resistance. Nevertheless, increasing the large free enthalpy difference also leads to a large electrostatic potential drop at the interface, which is harmful to the working potential. Therefore, the free enthalpy difference between the cathode and the electrolyte is a paradox criterion for high performance battery design and has to be optimized.
3.3 Influence of the standard activation energy on the thin film battery impedance
Section 2.3 shows the analytical expressions for the equivalent circuit elements. Note that thereby the bulk electrostatic potential applied in eqn (13) still needs to be determined. As demonstrated in Section 3.2, the total potential drop is associated with the free enthalpy difference. Therefore, the approach to identify the bulk electrostatic potential based on material properties is established in this section. Furthermore, impedance spectroscopy results of the half cell calculated by using the MPNP-FBV model are also plotted to compare the analytical results.The initial normalized concentrations are fixed at 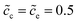 , and lithium-ion diffusion coefficients are Dc = De = 10−14 m2 s−1. The effect of the free enthalpy difference is assessed by performing simulations for the cathode standard activation energies which are given as ΔGcΘ = 0.5 and 0.6 eV, while the electrolyte standard activation energy is given as ΔGeΘ = 0.8 eV. The considered frequency for the perturbation potential is from 1 ≤ ω ≤ 106 Hz, and other parameters are shown in Table 1. It should be noted that 50 samples of the corresponding current are recorded. Therefore each point in the impedance curves denotes a specific frequency.
, and lithium-ion diffusion coefficients are Dc = De = 10−14 m2 s−1. The effect of the free enthalpy difference is assessed by performing simulations for the cathode standard activation energies which are given as ΔGcΘ = 0.5 and 0.6 eV, while the electrolyte standard activation energy is given as ΔGeΘ = 0.8 eV. The considered frequency for the perturbation potential is from 1 ≤ ω ≤ 106 Hz, and other parameters are shown in Table 1. It should be noted that 50 samples of the corresponding current are recorded. Therefore each point in the impedance curves denotes a specific frequency.
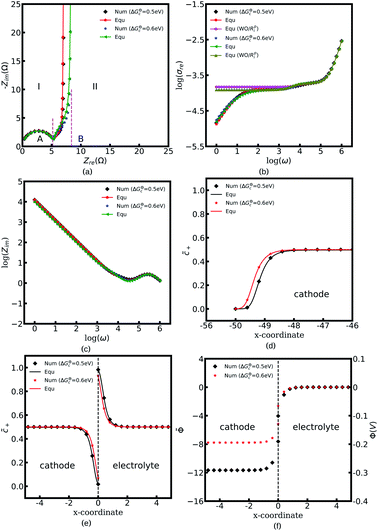
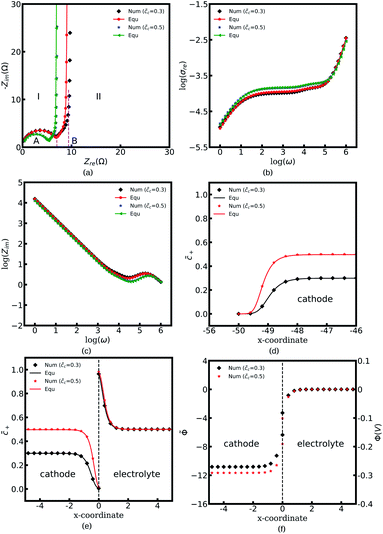
Fig. 4a to c depict all-solid-state thin film battery impedance curves for the two different standard activation energies of the cathode, ΔGcΘ = 0.5 and 0.6 eV. The corresponding equilibrium states are shown in Fig. 4d to f. In the legend, “Num” denotes the impedance results calculated by using the MPNP-FBV model, and “Equ” represents the analytical results estimated by using the equivalent circuit model. Fig. 4a shows that the impedance plots of the half cell can be divided into two regions, “I” and “II”, and the intersection points with the real impedance are denoted by “A” and “B”, respectively. In addition, “I” is the high-frequency region, and the impedance results in the region “II” are calculated at the medium and low frequencies.
In the region “I”, the impedance curve shows an ideal semicircle and is assumed to be a resistor in series with a capacitor.30 It can be observed that the impedance plots are overlapped in the region “I” which means that the activation energy cannot influence the thin film battery impedance in the high-frequency region. According to the numerical calculations, the value of intersection point “A” equals to 5.4 Ω and the capacitance is calculated to be 2.84 × 10−6 F. Based on the analytical solution in eqn (9), the bulk impedances are Rbuc = Rbue = 2.66 Ω and Cbuc = Cbue = 1.42 × 10−6 F. The results indicate that the value of the intersection point “A” equals the total bulk resistance, e.g., Rbuc + Rbue, and the capacitance is associated with the bulk capacitor. From the discussion, it can be concluded that the region “I” shown in Fig. 4a is caused by the thin film battery bulk impedance.
The region “II” contributes to the interface and surface impedance, and is regarded as a capacitor in parallel with a resistor then in series with a capacitor. The shunt-wound resistor and capacitor attribute to the cathode/electrolyte interface impedance, i.e., the charge transfer resistance and the interface space charge layer capacitance. The series-wound capacitor is explained by the space charge layer at the cathode surface, as shown in Fig. 1b. The discrepancy between the impedance curves in the region “II” indicates that the lithium-ion kinetic reaction plays an important role in the charge transfer resistance.
As can be seen from Fig. 4a the charge transfer resistance can be read as Rct = 2.9 Ω for the case of ΔGcΘ = 0.6 eV. The value of the intersection point “B” is 8.3 Ω, and equals the total thin film battery resistance, i.e., Rct + Rbuc + Rbue. A similar conclusion can be drawn when the standard activation energy is ΔGcΘ = 0.5 eV. The space charge layer capacitances at the interface and the surface are calculated by using eqn (13). Thus, the bulk electrostatic potential plays an important role in the capacitance calculation. In this study, the standard activation energies are ΔGcΘ = 0.5 and 0.6 eV, ΔGeΘ = 0.8 eV and the concentrations is equal to 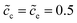 . Based on eqn (21), the free enthalpy differences are calculated to be ΔG = 0.3 and 0.2 eV, respectively. Moreover, the previous section indicates that the total electrostatic potential drop equals to the free enthalpy difference, as shown in Fig. 3b and d. Therefore, the total electrostatic potential drops lead to ΔΦtotal = −0.3 and −0.2 V. With the boundary conditions, e.g., Φbue = 0 and ∇Φbue = 0, the cathode bulk electrostatic potentials are equal to Φbuc = −0.3 and −0.2 V. Referring to eqn (13), the space charge layer capacitances at the interface are calculated to be Cinc = Cine = 1.52 × 10−4 and 1.90 × 10−4 F and the surface capacitances Csuc as 8.03 × 10−5 and 1.02 × 10−4 F, for the two cases ΔGcΘ = 0.5 and 0.6 eV, respectively. By using these results and eqn (17), the analytical impedance spectra are plotted and fit quite well with the numerical curves as predicted.
. Based on eqn (21), the free enthalpy differences are calculated to be ΔG = 0.3 and 0.2 eV, respectively. Moreover, the previous section indicates that the total electrostatic potential drop equals to the free enthalpy difference, as shown in Fig. 3b and d. Therefore, the total electrostatic potential drops lead to ΔΦtotal = −0.3 and −0.2 V. With the boundary conditions, e.g., Φbue = 0 and ∇Φbue = 0, the cathode bulk electrostatic potentials are equal to Φbuc = −0.3 and −0.2 V. Referring to eqn (13), the space charge layer capacitances at the interface are calculated to be Cinc = Cine = 1.52 × 10−4 and 1.90 × 10−4 F and the surface capacitances Csuc as 8.03 × 10−5 and 1.02 × 10−4 F, for the two cases ΔGcΘ = 0.5 and 0.6 eV, respectively. By using these results and eqn (17), the analytical impedance spectra are plotted and fit quite well with the numerical curves as predicted.
However, if we analyse in depth, the space charge layer cannot be simply regarded as an ideal capacitor. As shown in the citations,52–55 the real portion of the interface impedance involves two contributions: the charge transfer resistance and the space charge layer resistance. Therefore, the space charge layer impedance consists of a capacitance and a resistance. In addition, the space charge layer resistance is regarded as a constant ohmic resistance and is independent of the lithium-ion concentration.52 Nevertheless, Maier45,46 pointed out that the space charge layer resistance is caused by the deviation from the bulk contribution and is expressed as
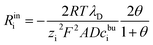 | (22) |
The parameter θ, which is called the degree of influence, expresses this in a straightforward way, where θ refers to the enrichment or depletion effect on the charge carrier number in the space charge layer regions. During the impedance measurement a perturbation potential is applied. Hence, the charge accumulation or depletion θ and the space charge layer resistance should be frequency dependent. The mobility in eqn (22) is taken as independent. However, lithium-ion diffusivity in the space charge layer is strongly dependent on the concentration and differs from the bulk according to the study.19 Therefore, to consider this effect, a frequency-dependent ohmic resistance is employed in the proposed equivalent circuit model, and is expressed as Rpi = Rsuc + Rinc + Rine. Adjusting with numerical results, it can be found that Rpi = Zre/ω, where ω indicates the applied frequency, and Zre is the real impedance of the battery system at ω = 1 Hz. Fig. 4b shows thin film battery conductivity with the proposed frequency-dependent resistance. “Equ (WO/Rpi)” denotes the equivalent circuit model without the space charge layer resistance. It can be concluded that the frequency-dependent ohmic resistance can well explain the tail of material conductivity in the low-frequency region, and this conclusion is also presented in our previous work.40 As expected, the analytical imaginary portion of the complex impedance fits well with the numerical results, as shown in Fig. 4c.
To explain the impedance results more clearly, the equilibrium states with the different standard activation energies are also presented in Fig. 4d to f. It shows that the bulk concentrations remain 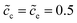 for both the standard activation energies ΔGcΘ = 0.5 and 0.6 eV. Therefore, we can conclude that the bulk resistance and the capacitance are not influenced by the activation energy, and the impedance results are also verified by the overlapped curves in the region “I”. However, the concentration distributions at the interface are different and indicate that the interface impedance in these two cases are different, as depicted in Fig. 4e. Hence, it can explain the diversity in the region “II” shown in Fig. 4a. Moreover, the similar conclusion about the cathode surface capacitance also can be drawn using Fig. 4d.
for both the standard activation energies ΔGcΘ = 0.5 and 0.6 eV. Therefore, we can conclude that the bulk resistance and the capacitance are not influenced by the activation energy, and the impedance results are also verified by the overlapped curves in the region “I”. However, the concentration distributions at the interface are different and indicate that the interface impedance in these two cases are different, as depicted in Fig. 4e. Hence, it can explain the diversity in the region “II” shown in Fig. 4a. Moreover, the similar conclusion about the cathode surface capacitance also can be drawn using Fig. 4d.
3.4 Influence of the concentration on thin film battery impedance
Eqn (21) indicates that the free enthalpy difference is determined by both the standard activation energy and the concentration. While Section 3.3 addresses the influence of the standard activation energy on the half cell impedance, the influence of the concentration is discussed here. The electrolyte concentration remains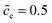 , and the standard activation energy barriers for ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV are assumed. Two cases with different normalized lithium-ion concentrations in the cathode, i.e.,
, and the standard activation energy barriers for ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV are assumed. Two cases with different normalized lithium-ion concentrations in the cathode, i.e., 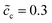 and 0.5 are compared in this subsection.
and 0.5 are compared in this subsection.
The impedance curves and the equilibrium states with different concentrations are compared for the two cases as shown in Fig. 5. Fig. 5a shows that the intersection point “A” of the semi-circle in the region “I” increases with concentration. This phenomenon can be explained by using eqn (9). The analytical results for the total bulk resistances Rbuc + Rbue are 7.1 and 5.4 Ω for 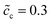 and 0.5, respectively. They are very well verified by the numerical results as shown in Fig. 5a. In addition, the charge transfer resistances can be determined from the figure: Rct = 2 and 1.53 Ω, which can be confirmed from the intersection point “B”. Referring to eqn (21), the free enthalpy differences are obtained as ΔG = 0.278 and 0.3 eV, respectively. Thus, the bulk electrostatic potentials in the cathode at the equilibrium state should be Φbuc = −0.278 and −0.3 V, and the cathode surface space charge capacitances are Csuc = 6.43 × 10−5 and 8.03 × 10−5 F, respectively. The capacitance is calculated from C = − ∂Q/∂Φ, and is determined by the electric field and the charge density. As shown in eqn (13), the space charge layer capacitance is related to the initial concentration. Thus, the analytical interface capacitances are Cinc = 1.08 × 10−4 F and Cine = 1.7 × 10−4 F when the cathode concentration is
and 0.5, respectively. They are very well verified by the numerical results as shown in Fig. 5a. In addition, the charge transfer resistances can be determined from the figure: Rct = 2 and 1.53 Ω, which can be confirmed from the intersection point “B”. Referring to eqn (21), the free enthalpy differences are obtained as ΔG = 0.278 and 0.3 eV, respectively. Thus, the bulk electrostatic potentials in the cathode at the equilibrium state should be Φbuc = −0.278 and −0.3 V, and the cathode surface space charge capacitances are Csuc = 6.43 × 10−5 and 8.03 × 10−5 F, respectively. The capacitance is calculated from C = − ∂Q/∂Φ, and is determined by the electric field and the charge density. As shown in eqn (13), the space charge layer capacitance is related to the initial concentration. Thus, the analytical interface capacitances are Cinc = 1.08 × 10−4 F and Cine = 1.7 × 10−4 F when the cathode concentration is 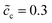 . For the case of
. For the case of 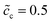 , the charge densities are equal and the capacitances are calculated to be Cinc = Cine = 1.51 × 10−4 F. A comparison between Fig. 4 and 5 shows that the lithium-ion concentration has relatively smaller influence on the interface impedance than the standard activation energy. Nevertheless, the concentration plays a comparatively more important role in the bulk resistance.
, the charge densities are equal and the capacitances are calculated to be Cinc = Cine = 1.51 × 10−4 F. A comparison between Fig. 4 and 5 shows that the lithium-ion concentration has relatively smaller influence on the interface impedance than the standard activation energy. Nevertheless, the concentration plays a comparatively more important role in the bulk resistance.
3.5 Influence of diffusivity on thin film battery impedance
In previous sections, we performed a specific investigation of thin film battery impedance spectroscopy with the free enthalpy difference, e.g., the standard activation energy and the concentration. In practice, increasing lithium-ion diffusivity, especially that of the electrolyte, is mostly the preferred attempt by researchers to develop high performance batteries. Therefore, a particular discussion on the interface impedance at different lithium-ion diffusivity constants is presented here. For the sake of simplicity, only ion diffusion coefficients of the electrolyte are regarded here, and two different cases with De = 10−13 and 10−14 m2 s−1 are compared. The diffusivity of the cathode remains the same, i.e., Dc = 10−14 m2 s−1, and the normalized concentrations are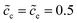 . In addition, the standard activation energies for both cases are assumed to be the same, more exactly, ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV.
. In addition, the standard activation energies for both cases are assumed to be the same, more exactly, ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV.
Fig. 6a to c depict the impedance plots for the two cases with different lithium-ion diffusion coefficients of the solid-state electrolyte. The analytical impedance curves again fit very well with the numerical results and show the applicability of the proposed equivalent circuit model for all-solid-state thin film batteries. Fig. 6a shows that the intersection point “A” decreases if the lithium-ion diffusivity is increased, while the charge transfer resistances in these two cases are numerically equal. By using eqn (9), the electrolyte analytical bulk resistances are calculated to be Rbue = 0.27 and 2.7 Ω, for De = 10−13 and 10−14 m2 s−1, respectively. Thus, the total bulk resistances are 2.97 and 5.4 Ω, and confirm the numerical results. The charge transfer resistance can be clearly explained by using the half cell at the equilibrium state, as depicted in Fig. 6d to f. The results show that the charge density and the electrostatic potential are not influenced by the lithium-ion diffusion coefficient. Therefore, the space charge layer resistance and the space charge layer capacitance remain the same for the two cases under comparison. From these results, it can be concluded that increasing the lithium-ion diffusion coefficients may not help to reduce the interface impedance, but it can play an important role in the bulk resistance.
3.6 Influence of the electrical double layer on thin film battery impedance
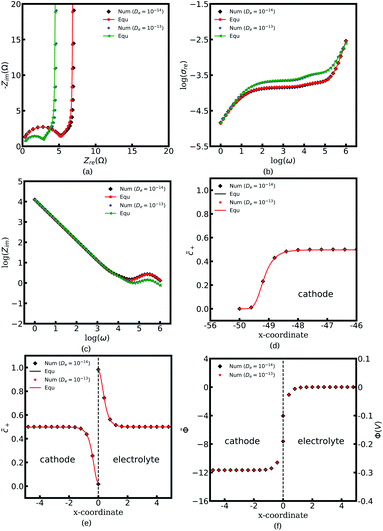
In this work, the electrostatic potential drop at the interface is determined by using the Gouy–Chapman–Stern formulation38 also called the diffuse double layer model, i.e., Φc = Φe −![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) λs∇Φc. Under this circumstance, the electrostatic potential drops both in the diffuse layer and the Stern layer, and is in agreement with the experimental observations.15 Nevertheless, the diffuse double layer model is utilized to analyze the solution/solid interface and is still questionable for researchers to analyze the solid/solid interface. Therefore, to deepen the understanding of the interface impedance, the Helmholtz-layer model, also called the compacted double layer model, is also employed here to calculate the half cell impedance. With this assumption, the electrostatic potential only drops in the Stern layer, and the potential gradient equals zero in the diffuse layer, i.e., ∇Φc = ∇Φe = 0. To focus on the interface structure, lithium-ion concentrations of the cathode and the electrolyte are
λs∇Φc. Under this circumstance, the electrostatic potential drops both in the diffuse layer and the Stern layer, and is in agreement with the experimental observations.15 Nevertheless, the diffuse double layer model is utilized to analyze the solution/solid interface and is still questionable for researchers to analyze the solid/solid interface. Therefore, to deepen the understanding of the interface impedance, the Helmholtz-layer model, also called the compacted double layer model, is also employed here to calculate the half cell impedance. With this assumption, the electrostatic potential only drops in the Stern layer, and the potential gradient equals zero in the diffuse layer, i.e., ∇Φc = ∇Φe = 0. To focus on the interface structure, lithium-ion concentrations of the cathode and the electrolyte are 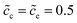 , and the diffusion coefficients are equal to Dc = De = 10−14 m2 s−1. Furthermore, the standard activation energies are given as ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV.
, and the diffusion coefficients are equal to Dc = De = 10−14 m2 s−1. Furthermore, the standard activation energies are given as ΔGcΘ = 0.5 eV and ΔGeΘ = 0.8 eV.
Fig. 7a to c present the half cell impedance spectroscopy results for the above two cases, namely the diffuse double layer model and the compact double layer model. Note that the analytical results fit well with the numerical results based on the electrochemical model, and confirms the applicability of the proposed equivalent circuit model. As shown in Fig. 7a, the Nyquist plots nearly overlap on the same line in the region “I” regardless of the electrical double layer (EDL) structural changes. In other words, the interface structure has no significant effects on the impedance plots at medium and high frequencies. By contrast, it is interesting to note that the semicircle caused by the charge transfer resistance and the interface capacitance in the region “II” vanishes in the compact double layer model. To further explore the reason for this phenomenon, the concentration and the potential distributions at the intrinsic equilibrium state are plotted. Fig. 7e shows that no charge density formation or depletion occurs at the interface in the case of the compact double layer structure. The space charge layer capacitance is associated with the redox reaction and is determined by the charge density, referring to eqn (13). Thus, the interface capacitance Cini can be ignored under this circumstance. The charge transfer resistance of the diffuse double layer structure is equal to Rct = 1.53 Ω and is much larger than that of the compact double layer case, i.e., Rct = 0.10 Ω. The surface concentration distributions with different EDL structures appear to be superimposed as shown in Fig. 7d and indicates that the surface capacitance Csuc is not influenced by the EDL structure when the material thickness is much larger than that of the surface space charge layer, i.e., Ls ≪ L. Based on these results, we can conclude that all-solid-state thin film batteries with a large potential drop in the Stern layer lead to a relatively high charge transfer resistance and the space charge layer capacitance.
3.7 Experimental verification
The electrochemical MPNP-FBV model and the corresponding equivalent circuit model for all-solid-state thin film battery impedance calculations are introduced in the above sections. Here, in this section, the experimental verifications are presented to confirm the proposed equivalent circuit model and the electrochemical continuum model.Fig. 8 shows the charge transfer resistance curves for the experimental and numerical results. As shown in Fig. 8a and b, Rct decreases with increasing battery temperature or increasing SOC. The same tendency is also observed in our numerical results. More specifically, the experimental value of the charge transfer resistance at 318 K is reduced to 1/10 of that at 278 K, and the measured Rct at a SOC of 90% decreases to 1/3 of that at 10%. As can be seen, the calculated charge transfer resistance at SOC = 10% and SOC = 90% reads Rct = 1.53 mΩ and 0.41 mΩ, respectively. In other words, similar conclusions can also be derived from our numerical model. Because of the ideal assumption and the realistic situation, the calculated results show deviations at certain points from the corresponding experimental data, particularly at 278 K. This is attributed to parameter deviations at different temperatures such as permittivity. Nevertheless, it is still sufficient to demonstrate the applicability of the MPNP-FBV model for the charge transfer resistance calculation.
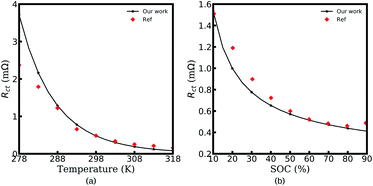 | ||
| Fig. 8 The experimental and calculated charge transfer resistance Rct at different temperatures (a) and states of charge (b). Reproduced with permission from Xueyuan Wang et al.50 Copyright 2019 Elsevier. | ||
Fig. 9 shows the numerical and the experimental impedance spectroscopy results of the LiCoO2/LiPON/Li thin film battery. Even though a slight difference exists, it can be concluded that the equivalent circuit model makes it possible to estimate the impedance of the thin-film battery at the solid-state. Similar to the experimental data, two semicircles appear in the numerical impedance spectra, and the semicircular arcs in the high frequency region are due to lithium-ion conduction in the LiPON bulk. Another semicircle is due to the charge transfer reaction at the LiCoO2/LiPON interface, and the same conclusion is also drawn in Fig. 4. The tail in the low-frequency region originates from the charge accumulation in the space charge layer as expected. Therefore, the charge transfer resistance and the thin film battery impedance verification can still demonstrate the applicability of the proposed equivalent circuit model.
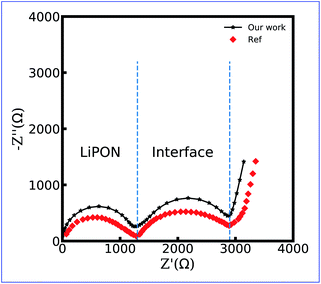 | ||
| Fig. 9 Impedance spectroscopy of the LiCoO2/LiPON/Li all-solid-state thin film battery. Reproduced with permission from Yasutoshi Iriyama et al.61 Copyright 2005 Elsevier. | ||
4 Concluding remarks
In this project, we investigate all-solid-state lithium-ion thin film battery impedance by utilizing an advanced electrochemical model and the corresponding equivalent circuit model. Different from most equivalent circuit models available in the literature, this new equivalent circuit model is based on the electrochemical continuum model, and the constants of the elements in the circuit are characterized by fundamental material parameters and state variables. For the first time, the lithium-ion kinetic reaction at the cathode/electrolyte interface is physically coupled in the proposed MPNP-FBV model to calculate battery impedance. It enables us to estimate the impedance of batteries from the fundamental material properties, e.g., the activation energy, the concentration, and diffusivity. The comparison between the calculated and the measured charge transfer resistance of LiFePO4 at different temperatures and at different SOCs implies that the proposed equivalent circuit model is reliable. In addition, the total impedance spectroscopy results are also verified against all-solid-state thin film batteries.Since in the MPNP-FBV model, the vacancy effect in solids is included, we could obtain reasonable results for the concentration and the electrostatic potential distributions in the space charge layer region. In addition, we derived successfully the analytical results for the MPNP-FBV model. Thereafter, we take a further step and introduce a methodology to identify the bulk electrostatic potential which is critical for the space charge layer capacitance calculation. Thus, all the circuit elements in the proposed model are quantified based on the analytical solutions and stem closely from material properties. To deepen the understanding of battery impedance, the influence of different material parameters on the battery impedance has been investigated. The results show that the thin film battery with a large free enthalpy difference will lead to a large potential drop across the interface, and is unfavorable for battery applications. Nevertheless, it has a low charge transfer resistance. On the other hand, increasing the electrolyte conductivity cannot help to reduce the interface impedance, but reduces the bulk resistance. Since the solid/solid interface model is still unsettled, different EDL structures have also been discussed comparatively in this work. We observe that the impedance associated with the space charge layer capacitance vanishes when the diffuse double layer model is applied. Interestingly, under this circumstance, impedance spectroscopy is unusual in comparison to the experimental results. Therefore, our work provides an easy way to quantify the battery impedance from the fundamental material properties and also shows the perspective to optimize the solid–solid interface. As future work, the MPNP-FBV model can make use of the DFT results in the calculation of the activation energy for specific systems. In this sense a multiscale modeling of impedance can be expected.
Author contributions
Yao Liu carried out the conceptualization, methodology, and writing. All other authors participated in manuscript writing, data analysis, and discussion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the China Scholarship Council (CSC). The calculations for this study have been conducted on the “Lichtenberg” high-performance computer of the TU Darmstadt, which we gratefully acknowledge.References
- L. Zou, Y. He, Z. Liu, H. Jia, J. Zhu, J. Zheng, G. Wang, X. Li, J. Xiao and J. Liu, et al. , Nat. Commun., 2020, 11, 1–8 Search PubMed.
- Z. Gao, H. Sun, L. Fu, F. Ye, Y. Zhang, W. Luo and Y. Huang, Adv. Mater., 2018, 30, 1705702 CrossRef.
- M. F. Lagadec, R. Zahn and V. Wood, Nat. Energy, 2019, 4, 16–25 CrossRef CAS.
- J. Wang, Y. Yamada, K. Sodeyama, C. H. Chiang, Y. Tateyama and A. Yamada, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- M. A. Hannan, M. H. Lipu, A. Hussain and A. Mohamed, Renewable Sustainable Energy Rev., 2017, 78, 834–854 CrossRef.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 1–4 Search PubMed.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 1–16 Search PubMed.
- S. Xia, X. Wu, Z. Zhang, Y. Cui and W. Liu, Chem, 2019, 5, 753–785 CAS.
- C. Sun, J. Liu, Y. Gong, D. P. Wilkinson and J. Zhang, Nano Energy, 2017, 33, 363–386 CrossRef CAS.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213 CrossRef CAS.
- X. Han, Y. Gong, K. K. Fu, X. He, G. T. Hitz, J. Dai, A. Pearse, B. Liu, H. Wang and G. Rubloff, et al. , Nat. Mater., 2017, 16, 572–579 CrossRef CAS.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 1–14 Search PubMed.
- R. Xu, X. Xia, S. Zhang, D. Xie, X. Wang and J. Tu, Electrochim. Acta, 2018, 284, 177–187 CrossRef CAS.
- S. A. Pervez, M. A. Cambaz, V. Thangadurai and M. Fichtner, ACS Appl. Mater. Interfaces, 2019, 11, 22029–22050 CrossRef CAS.
- K. Yamamoto, Y. Iriyama, T. Asaka, T. Hirayama, H. Fujita, C. A. Fisher, K. Nonaka, Y. Sugita and Z. Ogumi, Angew. Chem., Int. Ed., 2010, 49, 4414–4417 CrossRef CAS PubMed.
- N. Sato, Electrochemistry at metal and semiconductor electrodes, Elsevier, 1998 Search PubMed.
- Y. Liu, Y.-B. Ma, W. Jaegermann, R. Hausbrand and B.-X. Xu, J. Power Sources, 2020, 454, 227892 CrossRef CAS.
- A. C. Luntz, J. Voss and K. Reuter, Interfacial challenges in solid-state Li ion batteries, 2015 Search PubMed.
- N. J. de Klerk and M. Wagemaker, ACS Appl. Energy Mater., 2018, 1, 5609–5618 CAS.
- Q. Xia, S. Sun, J. Xu, F. Zan, J. Yue, Q. Zhang, L. Gu and H. Xia, Small, 2018, 14, 1804149 CrossRef.
- M. Thomas, P. Bruce and J. Goodenough, J. Electrochem. Soc., 1985, 132, 1521 CrossRef CAS.
- M. D. Levi, G. Salitra, B. Markovsky, H. Teller, D. Aurbach, U. Heider and L. Heider, J. Electrochem. Soc., 1999, 146, 1279 CrossRef CAS.
- C. Chen, J. Liu and K. Amine, J. Power Sources, 2001, 96, 321–328 CrossRef CAS.
- R. Tatara, P. Karayaylali, Y. Yu, Y. Zhang, L. Giordano, F. Maglia, R. Jung, J. P. Schmidt, I. Lund and Y. Shao-Horn, J. Electrochem. Soc., 2018, 166, A5090 CrossRef.
- S. Braun, C. Yada and A. Latz, J. Phys. Chem. C, 2015, 119, 22281–22288 CrossRef CAS.
- M. Fingerle, R. Buchheit, S. Sicolo, K. Albe and R. Hausbrand, Chem. Mater., 2017, 29, 7675–7685 CrossRef CAS.
- P. Schichtel, M. Geiß, T. Leichtweiß, J. Sann, D. A. Weber and J. Janek, J. Power Sources, 2017, 360, 593–604 CrossRef CAS.
- J. Haruyama, K. Sodeyama, L. Han, K. Takada and Y. Tateyama, Chem. Mater., 2014, 26, 4248–4255 CrossRef CAS.
- J. Jamnik, Solid State Ionics, 2003, 157, 19–28 CrossRef CAS.
- B.-A. Mei, O. Munteshari, J. Lau, B. Dunn and L. Pilon, J. Phys. Chem. C, 2018, 122, 194–206 CrossRef CAS.
- B.-A. Mei, J. Lau, T. Lin, S. H. Tolbert, B. S. Dunn and L. Pilon, J. Phys. Chem. C, 2018, 122, 24499–24511 CrossRef CAS.
- S. Larfaillou, D. Guy-Bouyssou, F. Le Cras and S. Franger, J. Power Sources, 2016, 319, 139–146 CrossRef CAS.
- S. Hull, Rep. Prog. Phys., 2004, 67, 1233 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 1–7 CrossRef.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533 CrossRef CAS.
- D. Danilov, R. Niessen and P. Notten, J. Electrochem. Soc., 2011, 158, A215–A222 CrossRef CAS.
- M. Landstorfer, S. Funken and T. Jacob, Phys. Chem. Chem. Phys., 2011, 13, 12817–12825 RSC.
- C. Hamann, A. Hamnett and W. Vielstich, Electrochemistry, Wiley, 1998 Search PubMed.
- J. Maier, Physical chemistry of ionic materials: ions and electrons in solids, John Wiley & Sons, 2004 Search PubMed.
- Y. Liu, Y. Bai, W. Jaegermann, R. Hausbrand and B.-X. Xu, ACS Appl. Mater. Interfaces, 2021, 13(4), 5895–5906 CrossRef CAS.
- J. Jamnik and J. Maier, Phys. Chem. Chem. Phys., 2001, 3, 1668–1678 RSC.
- J. Maier, Zeitschrift für Naturforschung B, 2020, 75, 15–22 CrossRef CAS.
- J. Newman and K. E. Thomas-Alyea, Electrochemical systems, John Wiley & Sons, 2012 Search PubMed.
- M. Schönleber, C. Uhlmann, P. Braun, A. Weber and E. Ivers-Tiffée, Electrochim. Acta, 2017, 243, 250–259 CrossRef.
- J. Maier, Berichte der Bunsengesellschaft für physikalische Chemie, 1986, 90, 26–33 CrossRef CAS.
- J. Jamnik, J. Maier and S. Pejovnik, Solid State Ionics, 1995, 80, 19–26 CrossRef CAS.
- D. Gaston, C. Newman, G. Hansen and D. Lebrun-Grandie, Nucl. Eng. Des., 2009, 239, 1768–1778 CrossRef CAS.
- M. Okubo, Y. Tanaka, H. Zhou, T. Kudo and I. Honma, J. Phys. Chem. B, 2009, 113, 2840–2847 CrossRef CAS PubMed.
- J. P. Meyers, M. Doyle, R. M. Darling and J. Newman, J. Electrochem. Soc., 2000, 147, 2930–2940 CrossRef CAS.
- X. Wang, X. Wei and H. Dai, Journal of Energy Storage, 2019, 21, 618–631 CrossRef.
- J. Illig, M. Ender, T. Chrobak, J. P. Schmidt, D. Klotz and E. Ivers-Tiffée, J. Electrochem. Soc., 2012, 159, A952 CrossRef CAS.
- M. Schleutker, J. Bahner, C.-L. Tsai, D. Stolten and C. Korte, Phys. Chem. Chem. Phys., 2017, 19, 26596–26605 RSC.
- J. Jamnik, S. Pejovnik and J. Maier, Electrochim. Acta, 1993, 38, 1975–1978 CrossRef CAS.
- J. Jamnik, J. Maier and S. Pejovnik, Solid State Ionics, 1995, 75, 51–58 CrossRef CAS.
- J. Maier, Prog. Solid State Chem., 1995, 23, 171–263 CrossRef CAS.
- D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2003, 7, A30 CrossRef.
- T. Maxisch, F. Zhou and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104301 CrossRef.
- C. Ouyang, S. Shi, Z. Wang, X. Huang and L. Chen, Phys. Rev. B, 2004, 69, 104303 CrossRef.
- J. Li, W. Yao, S. Martin and D. Vaknin, Solid State Ionics, 2008, 179, 2016–2019 CrossRef CAS.
- G. Xu, K. Zhong, J.-M. Zhang and Z. Huang, J. Appl. Phys., 2014, 116, 063703 CrossRef.
- Y. Iriyama, T. Kako, C. Yada, T. Abe and Z. Ogumi, Solid State Ionics, 2005, 176, 2371–2376 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |