Differentiability of cell types enhanced by detrending a non-homogeneous pattern in a line-illumination Raman microscope

Abstract

A line illumination Raman microscope extracts the underlying spatial and spectral information of a sample, typically a few hundred times faster than raster scanning. This makes it possible to measure a wide range of biological samples such as cells and tissues – that only allow modest intensity illumination to prevent potential damage – within feasible time frame. However, a non-uniform intensity distribution of laser line illumination may induce some artifacts in the data and lower the accuracy of machine learning models trained to predict sample class membership. Here, using cancerous and normal human thyroid follicular epithelial cell lines, FTC-133 and Nthy-ori 3-1 lines, whose Raman spectral difference is not so large, we show that the standard pre-processing of spectral analyses widely used for raster scanning microscopes introduced some artifacts. To address this issue, we proposed a detrending scheme based on random forest regression, a nonparametric model-free machine learning algorithm, combined with a position-dependent wavenumber calibration scheme along the illumination line. It was shown that the detrending scheme minimizes the artifactual biases arising from non-uniform laser sources and significantly enhances the differentiability of the sample states, i.e., cancerous or normal epithelial cells, compared to the standard pre-processing scheme.

---

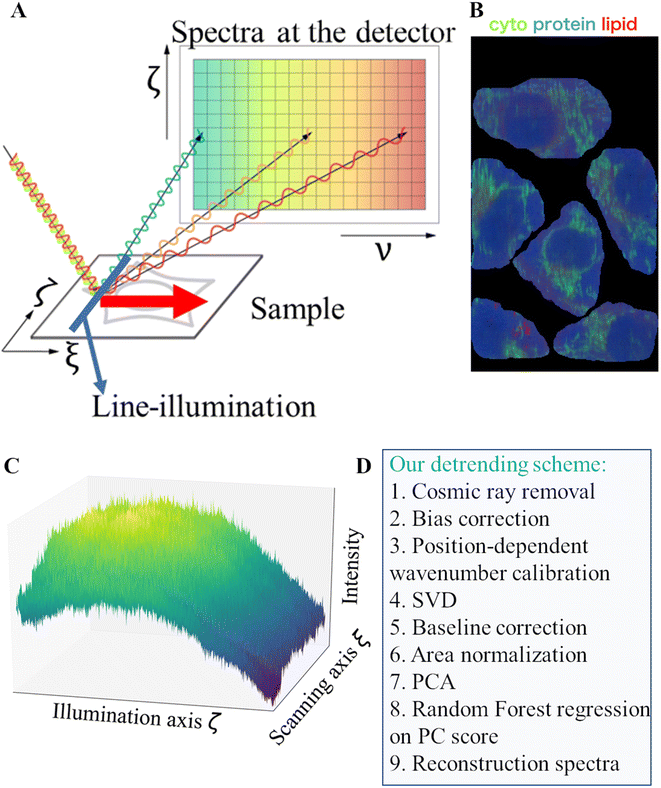
1. Introduction

Raman microscopy is a label-free, vibrational imaging technique that reflects the underlying, unique spectral features of molecules constituting a sample to measure.^1–3 Despite its potential for use in areas such as disease diagnosis,^4,5 treatment monitoring,⁶ drug design,⁷ and cell therapy development,⁸ the practical application of Raman spectroscopy in clinical settings faces challenges with regard to the relatively long acquisition time of Raman images^9–11 and the lack of data standardization¹² protocols between different microscope systems and experiments. The former is the consequence of the weak nature of Raman scattering, which requires a long exposure time to capture enough signal for analysis. The latter is influenced by various instrumental and experimental factors such as optics, sample preparation, laser power fluctuations, spectrometer drifts, autofluorescence, and multiple sources of noise. Multi-step preprocessing workflows have been proposed to remove such artifacts in raw Raman data. The workflows prioritize an objective design that involves optimizing cost functions or quality parameters to assess the effectiveness of preprocessing.^13–15 The traditional preprocessing techniques for Raman tabular data such as cosmic ray removal, spectrometer calibration, denoising, baseline correction, and normalization have been proved to be effective at reducing setup dependencies and improving data comparability.^16–18 However, the standard preprocessing workflows that considered only the spectral dimension in the process may lead to only suboptimal correction and overlooking of important artifacts present in the spatial dimension of Raman images such as non-uniform illumination, focus drift, and stripes. Here, non-uniform illumination refers to spatial variation in the intensity of the laser source that is used to scan a sample. Line-illumination Raman microscopes^19–21 which supply an illumination laser line to scan a sample in question result in significantly shorter acquisition time (typically several hundred times) compared to raster scanning based on point illumination. Here, the illumination line, typically generated through a sequence of cylindrical lens, creates some non-homogeneous illumination sources, which can affect the spatial distribution of photon counts in a Raman image and negatively impact the results of the subsequent chemometric analysis. Despite attempts to remove the consequence of a non-uniform illumination source in Raman data, using scaling techniques such as area normalization under a spectral curve, there exists room to improve further, as demonstrated in a paper. Additionally, non-uniform illumination in Raman microscopy can be caused by various factors such as laser misalignment, poor lens quality, dust, or vignetting effects, and has a negative effect on all types of Raman microscopes. Therefore, techniques that address non-uniform illumination correction are in high demand for the restoration of Raman images. In this paper, an analytical methodology that effectively eliminates non-uniform illumination in Raman images using the Karhunen–Loeve basis is presented.²² The method's performance is evaluated using follicular thyroid cancer cells (FTC-133)²³ and normal thyroid cells (Nthy-ori 3-1) as samples in a Raman measurement analysis. Accurate wavenumber calibration is emphasized to avoid potential inaccuracies, including reference sample Raman peak position shifts caused by uneven illumination, and is performed pixel-by-pixel along the line axis. The standard preprocessing protocol^24,25 recommended in the literature for Raman tabular data is found to be insufficient in correcting intensity variation in Raman data due to non-uniform illumination, as indicated by the existence of a correlation between the spatial coordinates (illumination axis and scanning axis) and the distribution of Raman intensities at different wavenumbers. Therefore, potential misclassification of cells based on their spatial location rather than their actual chemical composition is unavoidable. We propose a solution to mitigate the issue of intensity variations coming from an uneven illumination laser source in Raman images using a random forest regression model²⁶ in the Karhunen–Loeve basis. Following a position-dependent wavenumber calibration scheme along the illumination line (axis), the process involves estimating low-frequency dependencies between the illumination axis and chemical features expressed in the basis and subtracting these estimations from each chemical feature to minimize unwanted intensity variations along the axis. The same procedure is repeated for the vertical axis (scanning direction) to the illumination line to further minimize intensity variations throughout the images. This process, similar to a detrending technique, assumes that each individual chemical feature in the basis should follow a symmetric distribution. The proposed method is applied after standard preprocessing, and its performance is evaluated through a comparison of chemical homogeneity among single cells from the same phenotype. The results show that this method significantly improves chemical homogeneity between single cells of the same phenotype, and enhances chemical separability between two different phenotypes, FTC-133 and Nthy-ori 3-1, by reducing the risk of misclassification caused by undesired intensity variations.

2. Materials and methods

2.1. Cell culture

In this research, two cell lines were used: FTC-133 (human thyroid follicular carcinoma) as a cancer cell line and Nthy-ori 3-1 (human thyroid follicular epithelial) as a non-cancer cell line. The cells were seeded in 2 mL of medium containing DMEM/Ham's F-12 (FUJIFILM Wako Pure Chemical Corporation, 042-30795) for FTC and RPMI1640 (nacalai tesque, 05176-25) for Nthy, along with 10% fetal bovine serum (GE Healthcare, SH30910.03) and 1% penicillin–streptomycin–glutamine (FUJIFILM Wako Pure Chemical Corporation, 161-23201) at a cell number of 2 × 10⁵, on a calcium fluoride substrate (CRYSTRAN Ltd, Raman grade CaF₂ CAFP13-0.2). After seeding, the cells were incubated in a CO₂ incubator (5% CO₂, 37 °C) for 40–48 hours. Before the Raman measurement, the cellular culture medium was replaced with warmed-up Tyrode's buffer solution (145 mM NaCl, 1 mM CaCl₂, 1 mM MgCl₂, 5.4 mM KCl, 10 mM glucose and 10 mM HEPES with deionized distilled water at a final pH of 7.4) after being rinsed twice with it.

2.2. Line illumination Raman microscope

The Raman images were acquired using a home-built line-illumination Raman microscope²⁷ equipped with a continuous wave laser at 532 nm (Verdi V18; COHERENT). The power density was set to 3.3 mW μm⁻² at the sample, and the laser was expanded into a line shape using a cylindrical lens and then focused onto the sample through a ×40 water immersion objective lens (NA 1.25, CFI Apo 40× WI λ S; Nikon). The Raman photons were backscattered through the same objective lens and collected using a spectrophotometer (MK-300; Bunkoukeiki) after passing through a long-pass edge filter (LP03-532RE-25; Semrock) that eliminates excitation line emission and Rayleigh photons. The Raman photons were dispersed using a 600 L mm⁻¹ grating (500 nm blaze) and the dispersed transmission was captured using a cooled (−70 °C) CCD camera (PIXIS 400 eXcelon, Teledyne Princeton Instruments). For each passage, the line allows the collection of 400 Raman spectra simultaneously with an exposure time of 5 s. To form Raman images, a galvano-mirror is used to scan the sample with the line from left to right. A Raman image was 400 × 240 pixels totaling 96 000 spectra, each with a spectral range of 182 cm⁻¹ to 3086 cm⁻¹ and a size of 910 pixels. In the following, we denote a Raman image by a data cube u(m, n, ν), in which (m, n, ν) = (400, 240, 910) in this work. The spectrometer calibration was carried out using ethanol with spectrometer software.

2.3. Wavenumber calibration along the illumination line

In line-illumination microscopy experiments, the wavenumber axis is calibrated based on the reference sample spectrum and for each individual pixel along the line direction. This accounts for potential drifts in Raman peak positions that may occur along the line axis. The calibration protocol assumes a consistency of Raman shift drift errors in the scanning direction and is established with a single Raman line measurement of ethanol, using a 0.5-second exposure time. Consequently, 400 spectra of ethanol are recorded in the CCD detector and organized into a matrix of dimensions (m, ν) = (400, 910), with 910 being the number of pixels along the wavenumber axis. For each of the 400 ethanol spectra, the seven theoretical Raman peaks of ethanol solution (884, 1052, 1096, 1454, 2880, 2930, and 2974 cm⁻¹) were detected at different pixel indices, and a third-order polynomial model was used to estimate the continuous nonlinear relationship between pixel indices and Raman shifts. Each estimated third order polynomial model provides a new wavenumber axis of size 910 pixels resulting in the estimation of 400 new wavenumber axes in total. A cubic spline model denoted by f_kl, with the spatial position along the scanning axis k ∈ [1, 240] and the spatial position along the illumination line axis l ∈ [1, 400], learns the mapping between the new Raman shift axis ν_j to the Raman intensity of an individual spectrum of a Raman image as f_kl(ν_j). These different cubic spline models are then used to interpolate all the individual spectra of a Raman image on a consistent linear grid of spectral resolution 3.8 cm⁻¹ to have a common wavenumber axis between all spectra of a Raman image and between different measurements.

2.4. Data preprocessing

Raman images underwent preprocessing with a standard protocol. The preprocessing workflow consisted of several steps: after the steps (1) cosmic ray removal and (2) bias correction, (3) the position-dependent wavenumber calibration was performed along the illumination axis (section 2.3). Then, (4) noise reduction by singular value decomposition with keeping the first 8 singular value components, and (5) autofluorescence background correction, by using the modified polynomial algorithm of order 8, were performed. Finally, (6) area normalization was performed (see also in the ESI and Fig. S19–S22†).

2.5. Non-homogeneous profile correction

After the standard preprocessing with position-dependent wavenumber calibration, the unfolded (= preprocessed) Raman image of size (nm, ν) is expanded in an orthonormal basis known as the Karhunen–Loève (K–L) basis or principal component (PC) basis²⁸ to translate the Raman image as a set of 2D maps of PC scores of n × m pixels, denoted as Q_i(k, l) with 1 ≤ k ≤ n and 1 ≤ l ≤ m, or simply Q_i unless otherwise noted. These maps reflect a series of spectral variations over the physical space buried in the Raman image, which can reflect the presence of a slowly varying change of intensity related to non-homogeneous illumination effects as illustrated by the example of the 5th PC score Q₅ (Fig. S12B†) with a gradient of intensity. To further visualize these effects, we plot individual Q₅(k, l) as a function of the scanning axis ξ (corresponding to k) and the laser illumination line axis ζ (corresponding to l), respectively (see Fig. S12C and S12E†).

We suppose that, for Raman images without spatial degradation, the individual PC score Q_i should be non-correlated with both illumination and scanning axes, leading to symmetric distributions centered around zero between each PC score and these spatial axes. However, some correlations between the first tens (≪ ν) principal component scores and the spatial axes remain even after the application of position-dependent wavenumber calibration (Fig. S12A†) (note again that, without calibration, artifactual spatial correlations are much more significant, e.g., Fig. S2†). Importantly in the PC orthonormal basis, the PC scores are mutually uncorrelated, as shown by the correlation matrix of the full set of PC scores (Fig. S13B†).

This implies that the application of a nonlinear detrending correction is straightforward, i.e., the detrending operation to Q_i does not affect one another. This is not true if we correct the individual Raman shifts because the spectral features of a Raman image are mutually correlated among them, as can be seen from the correlation matrix of the preprocessed Raman image (Fig. S13A†).

The workflows to detrend the spatial correlation Q_i along each spatial axis are as follows: we first employ a series of random forest regression (RFR) models^26,29 to estimate the slowly varying relationship between each Q_i and the illumination axis ζ. Here, we chose the random forest regression model to estimate the underlying trend because of its nonparametric nature, which is more adaptable in estimating unknown nonlinear relationships compared to parametric models such as polynomial regression. An example of the estimated trend by RFR is given for the 5th PC score Q₅ along ζ (Fig. S12C†). The spatially averaged trend in Q_i along the illumination axis ζ (denoted by Q̂_i(l)) that could not be removed by position-dependent wavenumber calibration is then subtracted from each Q_i, that is, Q′_i(k, l) = Q_i(k, l) − Q̂_i(l) for all pairs of k and l. Afterwards, the same process is repeated to remove the spatial correlation along the scanning axis ξ. That is, a new series of RFR are performed to estimate the correlation with the scanning axis ξ (denoted by Q̄_i(k)) remaining in Q′_i (Fig. S12E†). The final correction of Q_i (denoted by Q̄_i) is then given by Q̄_i(k, l) = Q′_i(k, l) − Q̄_i(k) for all the pairs (k, l).

The detrended 2D PC maps along both the illumination and scanning axes on the top of position-dependent wavenumber calibration are then translated to a detrended 3D Raman image with size (n, m, ν) (see the Detrending scheme in the ESI†). We also performed our scheme on a Raman image of dimethyl sulfoxide (DMSO) (Fig. S14 and S15†). The advantages of using random forest regression (RFR) to estimate the trend in each PC score over just using the average PC score or other parametric models such as polynomial regressions are presented in the ESI (Detrending scheme section) and Fig. S16–S18.†

2.6. Data set characteristics and post-processing

Ten Raman images û_i (i = 1, …, 10) (5 FTC-133 and 5 Nthy-ori 3-1) were considered for the analysis. From these 10 images, 60 single cells (28 cells of FTC-133 and 32 cells of Nthy-ori 3-1) were extracted based on manual image segmentation. We preprocessed each individual spectrum belonging to the cell region where the preprocessing runs over all pixels belonging to the defined cell regions. Overall, the sample size of the preprocessed data is 362 593, with 5 labeled FTC-133 and 5 labeled Nthy-ori 3-1. We performed k-means clustering³⁰ based on the individual spectrum of each Raman image to identify the uniformity of the proportion of the clusters within the individual single cells. For low dimensional projection of all single-cell average spectra, we applied multidimensional scaling (MDS)³¹ and Uniform Manifold Approximation and Projection (UMAP).³²

3. Results and discussion

In this section, we first highlight the significant impact of wavenumber calibration along the line axis to detect subtle differences in Raman spectra between human thyroid carcinoma FTC-133 and Nthy-ori-3-1 cell lines. Our explanatory analysis reveals that the use of a standard wavenumber calibration procedure determined with a reference sample measurement independent of positions along the illumination line can lead to the emergence of artifactual Raman intensity spatial biases. This issue has not been widely acknowledged in the literature. Second, to reduce intensity variations related to uneven illumination in Raman images, we propose a preprocessing workflow that introduces some spatial correction in the principal component basis. This approach effectively reduces non-uniform intensity profiles in Raman images and enhances the accurate differentiation of Raman spectra between FTC-133 and Nthy-ori 3-1 cell lines.

Line illumination Raman microscopy uses laser illumination that is shaped as a straight line and scans the sample from left to right, collecting Raman spectra simultaneously at each spatial position along the line axis (Fig. 1A). Fig. 1B provides a representative example of a Raman image of FTC-133, where the intensity distribution of three Raman shifts (749 cm⁻¹, 1683 cm⁻¹, and 2853 cm⁻¹) in the physical space domain is displayed. The line intensity variation is the primary cause of non-homogeneous illumination. The line intensity profile often deviates from the theoretical Gaussian profile due to some laser alignment inaccuracies or lens quality degradation. Subsequently Raman spatial distribution at a specific Raman shift follows such deviations. An illustration of this deviation is given in Fig. 1C, which shows a non-linear intensity profile at 325 cm⁻¹, a prominent peak of a calcium fluoride (CaF₂) substrate. Fig. 1D displays a schematic diagram of the proposed preprocessing workflow for Raman image analysis. While wavenumber calibration is an important step in the preprocessing of Raman data, it is mentioned separately as we observed a shift in the peak position of spectra obtained from different cells located at different spatial positions when applying wavenumber calibration independent of the position along the illumination axis ζ (referred to here as ‘without wavenumber calibration’ or ‘uncalibrated’) (Fig. S1†). As a consequence, some non-negligible spatial dependence appears in some of the resulting Raman images and PC score images when the standard preprocessing without wavenumber calibration (Fig. S2†) is applied. Then we fixed our standard preprocessing workflow along with the position-dependent wavenumber calibration along the illumination axis ζ to minimize spatial dependencies between the spatial axis and chemical intensity distribution in the following analysis. Furthermore, we present a detrending scheme based on random forest regression to enhance the differentiability of the Raman signals between FTC-133 and Nthy-ori 3-1.

Fig. 1 (A) The concept of a line illumination Raman microscope. (B) A representative overlaid intensity distribution of three Raman shifts of cytochrome (749 cm⁻¹), protein (1683 cm⁻¹), and lipid (2853 cm⁻¹) for a representative Raman image FTC-133(#2). (C) A surface plot of the Raman intensities at 325 cm⁻¹ known as a prominent peak common to calcium fluoride (CaF₂) for a representative Raman image FTC-133(#2). (D) Our preprocessing workflow.

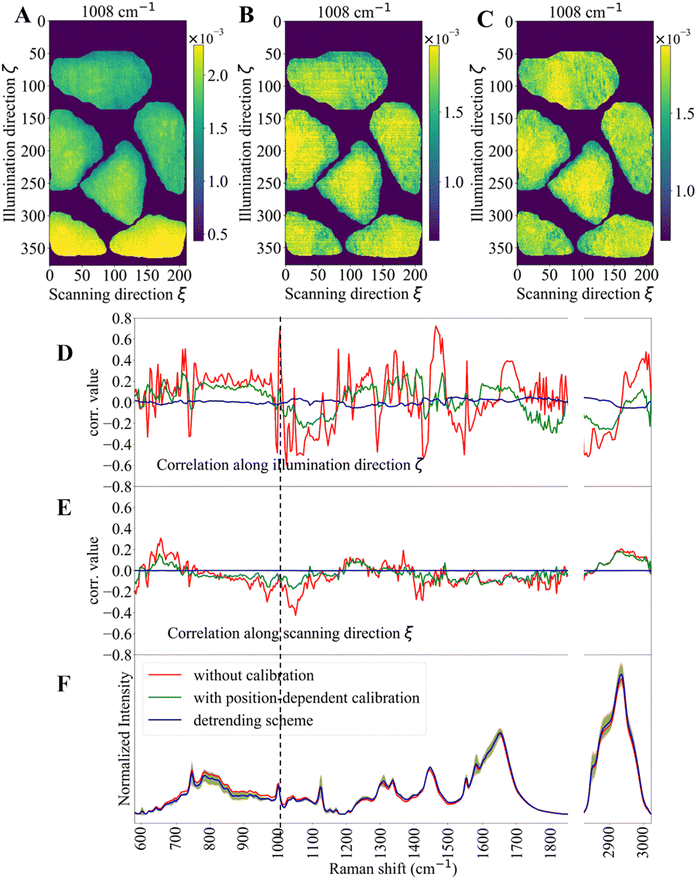
3.1. Applications of the position-dependent wavenumber calibration and the detrending scheme

Fig. 2 presents a series of visualization and descriptive statistics estimated on representative Raman images with and without position-dependent wavenumber calibration and with the detrending scheme on top of the calibration. Panel (A) shows an uncalibrated Raman image, while panel (B) shows the same image with position-dependent wavenumber calibration, which significantly reduces the artifactual spatial correlation of the image. Panel (C) shows the Raman image with the detrending scheme on top of the calibration. Panels (D) and (E) show Pearson correlation coefficients (r) between the Raman image at each individual wavenumber and the illumination axis ζ and the scanning axis ξ, respectively. Panel (F) shows the averaged with one standard deviation Raman spectrum for the cell region with the three preprocessings. Fig. 2D, without wavenumber calibration, shows high positive correlation at certain Raman shifts, high negative correlation at other Raman shifts, and weak correlation for some Raman shifts. The sign of the correlation coefficient is dependent on the definition of the coordinate system. We suppose that a Pearson correlation coefficient is positive about +0.8. It is equally possible that the value is −0.8 if one inverts the axis from positive to negative in the definition of the coordinate system. However, note that the relative relationship, such that some Raman intensities correlate along one direction (e.g., positively) but the others do along the inverse direction (e.g., negatively) to the chosen axis, holds once the coordinate system is fixed. This spatial correlation is significantly reduced by the position-dependent calibration strategy indicating an apparent wavenumber drift along the illumination axis, which could be attributed to chromatic aberration or changes in physical properties resulting from laser light power variation along this axis. Along the scanning axis, some correlation patterns also exist for data without wavenumber calibration as observed in Fig. 2E, but with a lower amplitude than those observed along the illumination axis. It should be noted that, in Panel (F), the averaged cell spectra of this Raman image are almost identical to each other, and the difference between the position-dependent wavenumber calibration and the detrending scheme correction is undetectable by visual inspection. However, the Pearson correlation analysis manifests further reduction of apparent spatial correlation (cf., the green and blue lines in Panels (D) and (E)). The absolute value of the Pearson correlation coefficient along the illumination axis ζ for the detrending scheme remains very small but non-zero (≪0.05) although that along the scanning axis ξ is almost zero (≪0.001). This reflects the fact that the apparent spatial correlation is more pronounced along the illumination axis than along the scanning axis.

Fig. 2 (A)–(C) The Raman intensity distribution at 1008 cm⁻¹ (dashed vertical line) in the space domain of FTC-133(#2): (A) after standard preprocessing without wavenumber calibration, (B) after standard preprocessing with position-dependent wavenumber calibration, and (C) after the detrending scheme applied on top of position-dependent wavenumber calibration. (D) and (E) The Pearson correlation coefficients between the Raman images at each wavenumber obtained by the three preprocessing schemes: (D) the illumination axis coordinate and (E) the scanning axis coordinate. (F) The average with one standard deviation Raman spectrum over all cell regions, with three different preprocessing schemes. Note that the silent region at wavenumbers 1880–2805 cm⁻¹ is omitted and replaced by a small gap.

3.2. Classifications of FTC-133 and Nthy-ori 3-1 based on Raman images

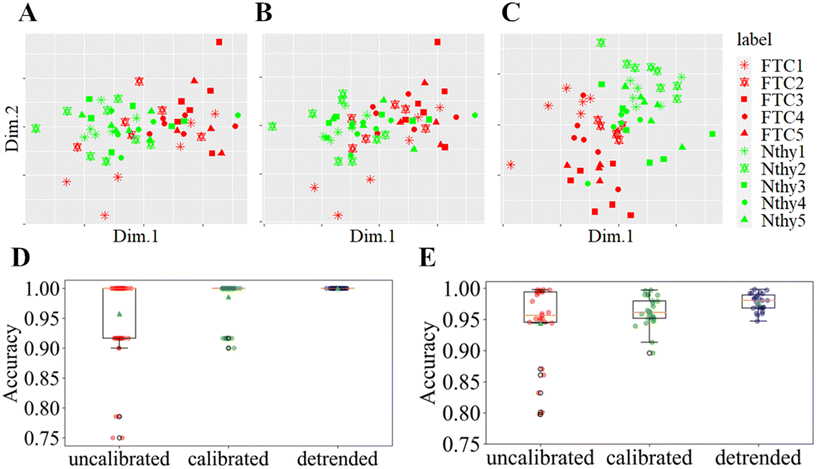
To evaluate the quality of the three different preprocessing schemes including with/without the position-dependent wavenumber calibration and the detrending scheme on top of the position-dependent wavenumber calibration, in the Raman images, a comparative analysis of the classification performance of the two cell lines was conducted. Additionally, to provide a visual representation of the effect of the three preprocessing strategies on the data, the average single cell Raman spectra are projected into a low-dimensional space. Fig. 3A–C visualize the projection of sixty average single-cell spectra in a low-dimensional space by performing multidimensional scaling (MDS) based on the distance matrix (Fig. S9†). This low dimensional representation manifests that the detrending scheme clearly enhances the differentiability between FTC-133 and Nthy-ori 3-1, as shown in Fig. 3C (cf., Fig. 3A and B). (See also Fig. S10† for the nonlinear projection, Uniform Manifold Approximation and Projection (UMAP).) It is revealed that the enhanced differentiability by the detrending scheme on top of the position-dependent wavenumber calibration is statistically ensured, free from the choice of the 2D linear basis of MDS or by using a 2D nonlinear embedding algorithm like UMAP. Fig. 3D and E show the box-and-whisker plot of 25 cross-validated accuracies of random forest classifier (RFC)³³ models in predicting FTC-133/Nthy-ori 3-1 for the three different preprocessing schemes. That is, for each preprocessing, a pair of two images of FTC-133 and Nthy-ori 3-1 were randomly chosen 25 times as test images to estimate the classification accuracy while the remaining 4 FTC-133 and 4 Nthy-ori 3-1 images were used to train the RFC. The RFC creates an ensemble of 100 decision trees on different subsets of the training data on Raman spectra coming from the training set, and predicts the class (FTC-133 or Nthy-ori 3-1) membership of unseen Raman spectra from the test set based on the majority class voting of the 100 decision trees. Fig. 3D shows the RFC accuracy when considering average single-cell Raman spectra, while Fig. 3E is obtained by considering all the spectra belonging to cells. From these figures, it is evident that a proper wavenumber calibration adapted for line-illumination microscopes and/or a detrending scheme is essential to stabilize the performance of the classifiers. Indeed, the average RFC accuracy increases progressively from uncalibrated data to detrended data, while the standard deviation of the accuracy decreases. This trend emphasizes that our preprocessing method improves the stability of the RFC classifier by reducing the number of outliers.

Fig. 3 (A)–(C) The multi-dimensional scaling (MDS) projection of the ten Raman images including sixty single cells in total: (A) standard preprocessing without wavenumber calibration, (B) the position-dependent wavenumber calibration, and (C) the detrending scheme. (D) and (E) The box-and-whisker plot of test accuracy in the prediction of FTC-133/Nthy-ori 3-1 for three different preprocessing schemes of 25-fold cross validation: (D) based on single-cell average spectra and (E) based on pixel-wise spectra. Here, (D) shows 25-fold cross validation test accuracy for three different preprocessing schemes considering only 60 spectra by taking the average of 60 single cells. However, (E) shows 25-fold cross validation test accuracy for three different preprocessing schemes considering all 362 593 spectra at the pixel position of cells.

3.3. Visualization of spectral stability via cluster analysis

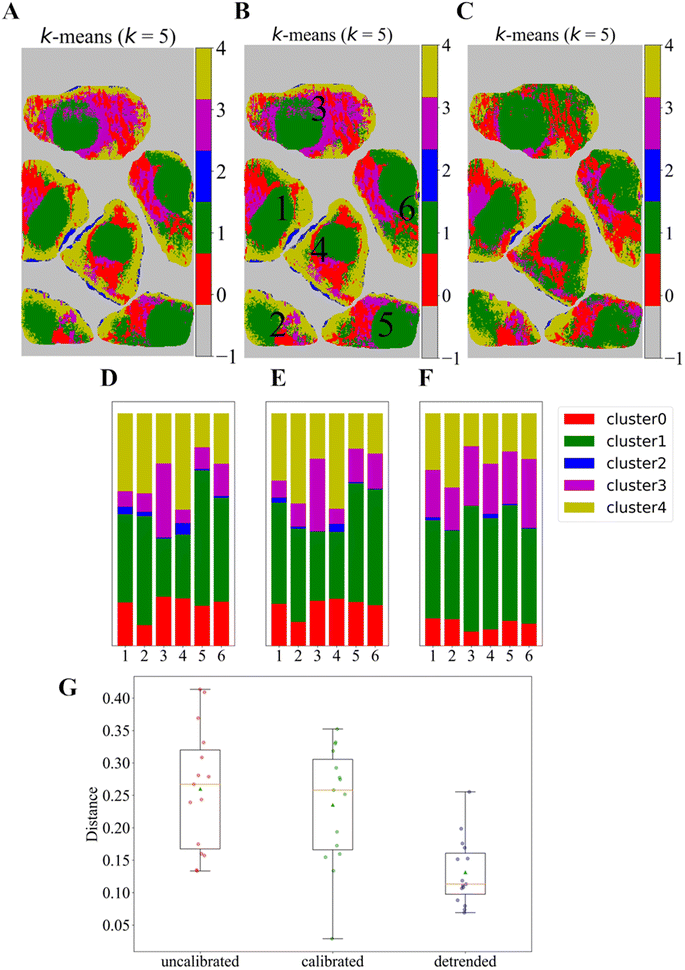
Fig. 4A–C depict the results of k-means clustering maps with 5 clusters for a representative Raman image of the human follicular thyroid carcinoma cell line FTC-133 for the three different preprocessing schemes. Here, the k-means clustering was performed independently for each preprocessing strategy. To compare visually between the three sets of clusters, the cluster indices for each scheme were reordered in each image, so that the Euclidean distance between the centroid (corresponding to the median in the spectral space) of each cluster computed for three different preprocessed Raman images is minimized by rearranging the index of the cluster for each image (see the distance matrix between the rearranged clusters of the three data sets in Fig. S4†). From Fig. S4,† the corresponding clusters between the three preprocessed images could be identified rather straightforwardly. The corresponding cluster population ratios can be seen in Fig. 4D–F. One can see in Fig. 4D–F that the population of the clusters within individual cells tends to be relatively more diverse without using the detrending scheme. For example, the proportion of cluster 3 (magenta) is relatively very high for cell 3 compared to that for other cells, which would suggest the manifestation of a phenotypic difference. In turn, the proportion of cluster 3 for cell 3 as well as those of other clusters are relatively less diverse across different single-cells in the detrending scheme compared to those in the other two preprocessing schemes. (In the ESI,† the results of the same analyses for all ten Raman images are given in Fig. S5–S8.†) We then emphasize that the detrending scheme reduces the variation of the cluster proportion between single cells of a Raman image. This is illustrated in Fig. 4G by showing a comparative single-cell pairwise spectral cluster proportion Euclidean distance distribution for the three preprocessing strategies via a box-and-whisker plot. Fig. 4G manifests that the detrending scheme naturally provides statistically consistent population distributions for each single-cell within the same image. (See also Fig. S11† that shows the suppression of the average Raman spectral variation of individual cells by using our detrending scheme, compared to those from the other two preprocessing strategies.)

Fig. 4 (A)–(C) The k-means clustering maps with k = 5 for individual Raman spectra in the Raman image for representative FTC-133(#2): (A) standard preprocessing without wavenumber calibration and (B) the position-dependent wavenumber calibration. (C) The detrending scheme based on random forest regression. (D)–(F) The relative populations of the clusters within each single cell for FTC-133(#2): (D) standard preprocessing without wavenumber calibration, (E) the position-dependent wavenumber calibration and (F) the detrending scheme. (G) The dependence of the diversity measure of cluster distributions within individual single cells on the kinds of the three preprocessing schemes.

4. Conclusions and outlooks

Preprocessing is a central aspect of a microscopic data science pipeline, as it minimizes unwanted variations in data and enhances differentiability between different phenotypes assuming that the underlying information can support it. To improve the standardization of hyperspectral Raman images obtained with line-scanning set-ups, we incorporated corrections in the spatial domain. In particular, we showed potential wavenumber drifts along the line illumination axis that altered the quality of the preprocessed Raman images. It has been shown that neglecting to consider a wavenumber calibration that varies with the pixel position along the illumination axis results in an artifactual spatial positive, negative, or small gradient in Raman images dependent on wavenumbers. Additionally, we proved that the standard preprocessing methods used in the field are ineffective at removing the influence of the non-homogeneous illumination, including slowly varying intensity fluctuations, in Raman images. Using standard preprocessing methods that do not correct spatial variations usually reduces the accuracy of the analysis and leads to misclassification of cells or questionable spectral composition of cells.

To address this issues, we introduced a novel position-dependent wavenumber calibration to reflect the possible chromatic aberration or changes in physical properties resulting from laser light intensity variation along the illumination line direction, combined with a detrending scheme of spatial correlation along the illumination and scanning directions, based on the Karhunen–Loeve basis and a random forest regression model. By using this proposed preprocessing strategy, enhanced differentiability was observed between phenotypes in the MDS plot and UMAP space, compared to the position-dependent wavenumber calibration. The performance of classification between FTC-133 and Nthy-ori 3-1, based on the accuracy metric, was used to evaluate the effectiveness of the random forest regression (RFR)-based detrending protocol in minimizing the influence of spatial trends in Raman images, compared to the other detrending protocols of average PC scores and polynomial fitting of various orders (3, 7, 8, 9, and 12) (see Fig. S16–S18†). We observed that a random forest classifier demonstrates a better accuracy performance when using RFR and averaged PC scores compared to polynomial fitting of any order. It should also be noted that, in the detrended Raman image by polynomial-regressions, some (but negligibly small) stripe patterns along the illumination axis were present as indicated by orange arrow marks in Fig. S17,† while both RFR and average PC score protocols removed such stripes. A brief explanation of RFR is given in the ESI (Random forest regression section) and Fig. S23 and S24.† Finally, we emphasize the adaptability of random forest regression over averaging PC scores in the detrending scheme. For example, the average PC score scheme inevitably removes any spatial trends irrespective of sample characteristics by definition. There exists a room in tuning the hyperparameter value implemented in the random forest architecture, which can adapt to diverse experimental scenarios. With appropriate parameter tuning, random forest regression can model diverse spatial trend topologies which may be set-up dependent, and can also provide accurate trend estimations in contexts with high signal to noise ratios. In this paper, our working hypothesis (at least) for the sample we analyzed was that, for those Raman images, the individual PC score should not be correlated with the physical space. With such assumption, random forest regression and average PC score detrending schemes provide a similar performance. If the sample distribution would actually have some apparent biases or trends in the physical space in the data set of Raman images, this hypothesis does not necessarily hold. Thus, in actual applications, we must take into account how sufficiently the position-dependent wavenumber calibration eliminates artifactual spatial biases, and how samples are distributed in the physical space over the data-set to be analyzed, with a comparison of the differentiability of phenotypes in their constructed Raman signals.

Author contributions

A. H. B.: data curation, formal analysis, software, visualization, and writing – original draft. J. E. C.: conceptualization, methodology, software, resources, validation, and writing – original draft. Z. F.: data curation, software, writing review & editing. K. M.: investigation, writing review & editing. K. T.: software, writing review & editing. J. N. T.: software, supervision, writing review & editing. Y. M.: investigation, writing review & editing. Y. H.: supervision, resources, writing review & editing. T. B.: supervision, writing review & editing. K. F.: supervision, project administration, resources, writing review & editing. T. K.: conceptualization, supervision, project administration, resources, funding acquisition, and writing – original draft.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

We would like to thank Yuta Mizuno and Atsuyoshi Nakamura for helpful discussions. This research was partially supported by the Japan Science and Technology Agency (JST)/Core Research for Evolutional Science and Technology (CREST), Grant Number JPMJCR1662, Japan (to T. K., K. F., Y. H.), JSPS (no. 25287105 and 25650044 to T. K., and no. JP22K18179 to J. E. C.), Grant-in-Aid for Scientific Research on Innovative Areas (Singularity biology) (No. 18H05408) (to T. K.), and the Research Program of Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials in Network Joint Research Center for Materials and Devices (to K. F. and Y. H.). The Institute for Chemical Reaction Design and Discovery (ICReDD) was established by the World Premier International Research Initiative (WPI), MEXT, Japan. J. E. C. also acknowledges the support of the Carnot foundation, France.

References

1. J. R. Ferraro, Introductory Raman spectroscopy, Elsevier, 2003.
2. R. L. McCreery, Raman Spectroscopy for Chemical Analysis, John Wiley & Sons, 2005.
3. I. I. Patel and F. L. Martin, Analyst, 2010, 135, 3060–3069.
4. T. Yamamoto, T. Minamikawa, Y. Harada, Y. Yamaoka, H. Tanaka, H. Yaku and T. Takamatsu, Sci. Rep., 2018, 8, 14671.
5. K. M. Helal, J. N. Taylor, H. Cahyadi, A. Okajima, K. Tabata, Y. Itoh, H. Tanaka, K. Fujita, Y. Harada and T. Komatsuzaki, FEBS Lett., 2019, 593, 2535–2544.
6. J. L. González-Solís, J. C. Martínez-Espinosa, J. M. Salgado-Román and P. Palomares-Anda, Lasers Med. Sci., 2014, 29, 1241–1249.
7. M. Li, H.-X. Liao, K. Bando, Y. Nawa, S. Fujita and K. Fujita, Anal. Chem., 2022, 94, 10019–10026.
8. S. Rangan, H. G. Schulze, M. Z. Vardaki, M. W. Blades, J. M. Piret and R. F. Turner, Analyst, 2020, 145, 2070–2105.
9. Y. Li, B. Shen, S. Li, Y. Zhao, J. Qu and L. Liu, Adv. Biol., 2021, 5, 2000184.
10. Y. Kumamoto, Y. Harada, T. Takamatsu and H. Tanaka, Acta Histochem. Cytochem., 2018, 51, 101–110.
11. C. Orillac, T. Hollon and D. A. Orringer, Biomed. Eng. Technol., 2022, 1, 225–236.
12. J. D. Rodriguez, B. J. Westenberger, L. F. Buhse and J. F. Kauffman, Analyst, 2011, 136, 4232–4240.
13. T. Bocklitz, A. Walter, K. Hartmann, P. Rösch and J. Popp, Anal. Chim. Acta, 2011, 704, 47–56.
14. J. Engel, J. Gerretzen, E. Szymańska, J. J. Jansen, G. Downey, L. Blanchet and L. M. Buydens, TrAC, Trends Anal. Chem., 2013, 50, 96–106.
15. A. Martyna, A. Menżyk, A. Damin, A. Michalska, G. Martra, E. Alladio and G. Zadora, Chemom. Intell. Lab. Syst., 2020, 202, 104029.
16. N. K. Afseth, V. H. Segtnan and J. P. Wold, Appl. Spectrosc., 2006, 60, 1358–1367.
17. P. Lasch, Chemom. Intell. Lab. Syst., 2012, 117, 100–114.
18. S. Guo, J. Popp and T. Bocklitz, Nat. Protoc., 2021, 16, 5426–5459.
19. K. Hamada, K. Fujita, N. I. Smith, M. Kobayashi, Y. Inouye and S. Kawata, J. Biomed. Opt., 2008, 13, 044027–044027.
20. J. Qi and W.-C. Shih, Appl. Opt., 2014, 53, 2881–2885.
21. H. He, M. Xu, C. Zong, P. Zheng, L. Luo, L. Wang and B. Ren, Anal. Chem., 2019, 91, 7070–7077.
22. M. D. Graham and I. G. Kevrekidis, Comput. Chem. Eng., 1996, 20, 495–506.
23. M. Sobrinho-Simoes, C. Eloy, J. Magalhaes, C. Lobo and T. Amaro, Mod. Pathol., 2011, 24, S10–S18.
24. T. Dörfer, T. Bocklitz, N. Tarcea, M. Schmitt and J. Popp, Z. Phys. Chem., 2011, 225, 753–764.
25. T. Bocklitz, T. Dörfer, R. Heinke, M. Schmitt and J. Popp, Spectrochim. Acta, Part A, 2015, 149, 544–549.
26. V. Rodriguez-Galiano, M. Sanchez-Castillo, M. Chica-Olmo and M. Chica-Rivas, Ore Geol. Rev., 2015, 71, 804–818.
27. A. F. Palonpon, M. Sodeoka and K. Fujita, Curr. Opin. Chem. Biol., 2013, 17, 708–715.
28. H. Abdi and L. J. Williams, Wiley Interdiscip. Rev.: Comput. Stat., 2010, 2, 433–459.
29. H. Ishwaran, Mach. Learn., 2015, 99, 75–118.
30. A. Likas, N. Vlassis and J. J. Verbeek, Pattern Recognit., 2003, 36, 451–461.
31. M. C. Hout, M. H. Papesh and S. D. Goldinger, Wiley Interdiscip. Rev.: Cogn. Sci., 2013, 4, 93–103.
32. L. McInnes, J. Healy and J. Melville, arXiv preprint arXiv:1802.03426, 2018.
33. A. Liaw and M. Wiener, et al. , R News, 2002, 2, 18–22.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3an00516j

‡ These authors contributed equally to this work.

---