A density functional theory study of a water gas shift reaction on Ag(111): potassium effect

Abstract

Density functional theory (DFT) calculations are executed to investigate the effect of a potassium (K) promoter on the activity of the water gas shift reaction (WGSR) over an Ag(111) surface. It is found that the WGSR proceeds mainly through the OH(O)-assisted carboxy pathway in which H₂O dehydrogenation is the rate-controlling step on both Ag(111) and K/Ag(111) surfaces. Energetic span model analysis shows that K addition can enhance the activity of the WGSR by reducing the apparent activation energy of the whole reaction since it can promote H₂O dissociation and stabilize the adsorption of the reactants (CO and H₂O). Importantly, the K adatom can stabilize the binding of all oxygenates by direct K–O bonding and the stabilizing effect of K on OH adsorption of the transition state (TS) plays a leading role in promoting H₂O dissociation. Moreover, the K–O distance and K coverage are two key factors affecting H₂O activation, that is, the shorter the K–O distance (2–3 Å) the more the K coverage (25%) contributes to the stronger promotion effect. For various metals catalyzing the WGSR, K promotes H₂O dissociation on inert metals like Ag, Au and Cu better than those on reactive metals (Pd and Ni) since the more inert metal surfaces would weaken the K and O binding and accordingly strengthen the interaction between them, resulting in a higher promotion effect.

---

1. Introduction

The water–gas-shift reaction (WGSR), that is, CO + H₂O → CO₂ + H₂, is regarded as one of the most vital means to produce hydrogen and to remove CO in industrial production.¹ The generally accepted mechanisms for the WGSR include redox, carboxyl, and formate mechanisms, and which mechanism dominates relies on the kinds of metal catalysts as well as their surface configurations, experimental conditions and so on.^2,3 For example, the previous DFT calculations show that the WGSR proceeds mainly via the carboxyl pathway on Cu(111)^4–8 and Pt(111) surfaces,^9,10 while the redox mechanism is identified to be the most dominant one on the Au(111) surface.^2,3 Catapan et al. reported that the carboxyl pathway plays a pivotal role on both Ni(111) and Ni(211) surfaces, and the formate route is equally significant on Ni(211).¹¹ All these studies achieve consensus that H₂O dehydrogenation is the rate-controlling step in terms of different mechanisms of different metal surfaces.

As is known to all of us introducing small amounts of additives to heterogeneous catalysts is thought to be an efficient method to change the catalytic performance through the promotion or inhibition effect.¹² Alkali additives, such as potassium (K), have drawn great attention since they serve as special electron donors to improve the activity of many reactions including the WGSR and the promotion effect on the WGSR by alkali has been studied widely.^13,14 The study of the WGSR catalyzed by LaNiO₃ doped with K shows that K addition makes stable K–OH species form at the interface between Ni nanoparticles and the La₂O₃ support, and promotes the formation of a formate intermediate and further generation of CO₂ products.¹⁵ The experimental results of Sanz et al. indicate that K/Cu/TiO₂ shows better catalytic performance for the WGSR than the Cu/TiO₂ catalyst because the presence of a K promoter greatly enhances the activity of water dissociation, which is the rate-controlling step for K/Cu/TiO₂. Additionally, this study also shows that the rate of H₂ production gradually increases with the increase of K coverage which reaches the maximum of 0.15 ML and the productivity of H₂ begins to decrease when the coverage is higher.¹⁶ Ma et al. reported that with increasing K loading on the 100Fe/5.1Si/2Cu/xK (x = 1.25 or 3) catalyst, the WGS rate constant is accordingly increased during the Fischer–Tropsch synthesis (FTS).¹⁷ These experimental studies emphasize the significance of alkali addition for the WGSR as well as its coverage. The promotion effect of alkali on the WGSR is also theoretically studied over Cu, Pt and Ni surfaces, in which the interaction between alkali and O in oxygenates contributes to its promotion effect.^18–20 Additionally, the K(Na)–O distance is found to play an important role in determining the K effect since the degree to which K(Na) promotes CO dissociation over the Rh(111) surface depends on the distance between K(Na) and molecular CO and the shorter the distance, the stronger the promotion effect.^21,22 However, the fundamental reason why alkali coverage and closeness between alkali and oxygenate matters has not been disclosed so far. It has been reported that noble metal-based catalysts are good catalysts for the WGSR due to their high activity, selectivity, and stability.^23,24 However, the study of alkali effect on the Ag metal surface at the atomic level is scarce despite the certain catalytic capacity of silver to the WGSR.^25–28

In this work, the pathways of the WGSR are investigated by the DFT method on a clean Ag(111) surface and the corresponding K-promoted surface (K/Ag(111)) to explore the effect of K additive on the mechanism and activity of the WGSR on Ag catalysts. In the light of energetic and electronic effect analysis, the origin of the K effect is revealed and factors like the K–O distance and K coverage affecting the K promotion effect are also clarified.

2. Calculation methods and models

2.1 Methods

The Vienna ab initio simulation package (VASP)^29,30 was used to perform the present DFT calculations. The projector augmented wave (PAW)^31,32 method and the Perdew–Burke–Ernzerhof (PBE)³³ exchange correlation functional were adopted to describe the valence electron and core interactions. A plane wave basis was carried out with the cut-off energy of 400 eV. The transition states (TSs) were searched using the climbing-image nudged elastic band (CI-NEB) method,³⁴ and further confirmed by the existence of a single imaginary vibrational mode along the reaction coordinate. Charge distributions were estimated using the algorithm developed by Henkelman through Bader's atoms in molecules (AIM) theory.^35,36 The binding energy (E_bind) was calculated by the following equation E_bind = E_ads/sub − E_ads − E_sub, in which E_ads/sub, E_ads and E_sub denote the energies of the adsorbate/substrate system, the adsorbate in the gas phase and the substrate, respectively. The activation energies were calculated with E_a = E_TS − E_IS, where E_TS and E_IS represent the energies of the transition and initial states, respectively. The reaction energies were calculated with ΔE = E_FS − E_IS, E_FS was the energy of the final state. The charge density difference was evaluated by Δρ = ρ_ads/sub − ρ_ads − ρ_sub, where ρ_ads/sub represents the total charge density of the adsorbate/substrate system, while ρ_ads and ρ_sub denote the charge density of the adsorbate molecule and the metal substrate, respectively, fixed at the adsorbed geometry.

2.2 Models

To model the Ag(111) surface, a p(3 × 3) supercell with four layers was built, which was separated by 15 Å of a vacuum region. The first two layers as well as the adsorbed molecules were allowed to relax until the forces were less than 0.03 eV Å⁻¹, while the other two layers were fixed. The Brillouin zone sampling was used with the 3 × 3 × 1 Monkhorst–Pack grid.³⁷ Moreover, a p(4 × 4) supercell of the Ag(111) surface with four layers was also constructed for the sake of research and a 2 × 2 × 1 Monkhorst–Pack grid was adopted to sample the Brillouin zone.

3. Results

3.1 Adsorption of pertinent intermediates

The optimum adsorption structures of pertinent intermediates involved in the WGSR on Ag(111) and K/Ag(111) surfaces are displayed in Fig. 1. The preferred binding sites and binding energies of such intermediates on both surfaces are summarized in Table 1. From Fig. 1, it can be found that K addition alters the adsorption structures of most intermediates dramatically. The most stable adsorption site for the K adatom on the Ag(111) surface is the face-centered cubic site with a binding energy of −1.96 eV and K tends to go far away from the surface with the distance of K and the nearest Ni atom being 3.44 Å. Once the reaction species adsorb on the K pre-adsorbed surfaces, K atom tends to depart from its preferred face-centered cubic (fcc) site to get close to the O sites in oxygenates. Simultaneously, the geometrical configuration of most adsorbed oxygenates would make readjustments to ensure that the contained O atoms point toward K and remain at a short distance away from K (2.0–3.0 Å). As analyzed above, all the structural changes in adsorbates caused by K addition indicate that a kind of attractive interaction exists between K and O atoms. This result is further confirmed by Bader charge analysis of the single K atom adsorption on the Ag(111) surface in which K is positively charged with +0.80 e, while the vicinal Ag atoms are negatively charged, signifying that the K adatom tends to transmit its valence electrons to the Ag(111) surface. As a result, the electropositive K is apt to attract the much more electronegative O atoms compared to other less electronegative C and H atoms (electronegativity for O, C and H is 3.4, 2.5 and 2.2, respectively). Such electrostatic attraction proves a direct K–O bonding as discussed later. Table 1 shows that the K adatom can stabilize the adsorption of all oxygenates by increasing their binding energies and it is later found that the direct K–O bonding can strengthen their adsorption. However, K addition has little impact on the binding strength of H and H₂ on the Ag(111) surface due to the negligible attractive interactions between K and H atoms.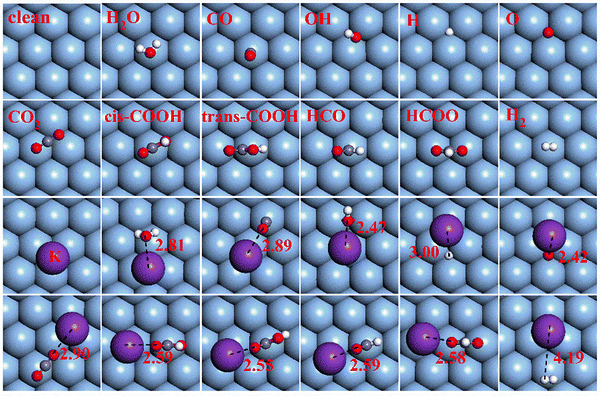

Fig. 1 Optimized structures of all pertinent intermediates on Ag(111) and K/Ag(111) surfaces. The red, gray, white and purple balls represent O, C, H and K atoms, respectively.

Table 1 Preferred adsorption sites (site), binding energies (BE) and key bond lengths for intermediates on Ag(111) and K/Ag(111) surfaces

	Ag(111)			K/Ag(111)
	Site	BE/eV	d O–Ag/C–Ag	Site	BE/eV	d O–Ag/C–Ag
H2O	Top	−0.07	2.68	Pointing to K	−0.57	3.27
CO	Top	−0.16	2.17	Top	−0.22	2.16
OH	fcc	−2.62	2.29	Bridge	−3.21	2.43
H	fcc	−2.07	1.92	fcc	−2.09	1.94
O	fcc	−3.41	2.15	fcc	−4.34	2.22
CO2	Physisorption	−0.01	3.60	Pointing to K	−0.24	3.74
cis-COOH	Top	−1.11	2.17	Top	−1.93	2.22
trans-COOH	Top–top	−1.02	2.19	Top	−1.88	2.21
HCO	fcc	−0.75	2.18	Top	−1.29	2.18
HCOO	Top–top	−2.26	2.28	Top–top	−3.11	2.60
H2	Physisorption	−0.02	3.22	Physisorption	−0.02	3.23

---

3.2 WGSR pathway on Ag(111) and K/Ag(111) surfaces

The previously proposed pathways for the WGSR on Ag(111) and K/Ag(111) surfaces containing redox, carboxyl, and formate pathways are taken into account in the present study. No matter which pathway plays the leading role, the primary reaction step is H₂O dissociation to produce OH, O and H species, which then oxidize CO through these three pathways to generate the final CO₂. The calculated energy barriers, reaction energies and the lengths of forming or breaking bonds at TSs for all elementary steps involved in the three pathways on both surfaces are summarized in Table 2. The TS structures regarding these elementary steps are presented in Fig. 2. The properties of each step involved in H₂O and OH activation as well as the three pathways are elucidated next to search for the optimal pathway for the WGSR on both surfaces.

Table 2 Calculated reaction barriers (E_a), reaction energies (ΔE) and forming or breaking bond lengths of TSs (d) of the elementary steps on Ag(111) and K/Ag(111) surfaces

	Elementary steps	Ag(111)			K/Ag(111)
		E a/eV	ΔE/eV	d/Å	E a/eV	ΔE/eV	d/Å
R1	H2O → OH + H	1.77	1.06	1.65	1.41	0.92	1.77
R2	OH → O + H	2.41	1.82	1.88	2.09	1.50	1.76
R3	OH + OH → H2O + O	0.26	0.14	—	0.34	0.15	—
R4	H + H → H2	1.21	−0.40	1.56	1.03	−0.37	1.48
R5	CO + OH → cis-COOH	0.07	−0.35	2.05	0.06	−0.56	1.91
R6	cis-COOH → trans-COOH	0.50	0.00	—	0.52	−0.04	—
R7	COOH → CO2 + H	1.27	−0.68	1.32	1.14	−0.13	1.53
R8	COOH + O → CO2 + OH	—	—	—	—	—	—
R9	COOH + OH → CO2 + H2O	—	—	—	—	—	—
R10	CO + O → CO2	0.03	−2.72	2.19	0.03	−2.06	2.53
R11	CO + H → CHO	0.63	0.27	1.46	0.53	−0.18	1.84
R12	CHO + O → HCOO	0.02	−3.29	2.75	0.48	−2.72	2.28
R13	HCOO → CO2 + H	1.93	0.16	1.01	2.21	0.78	—

---

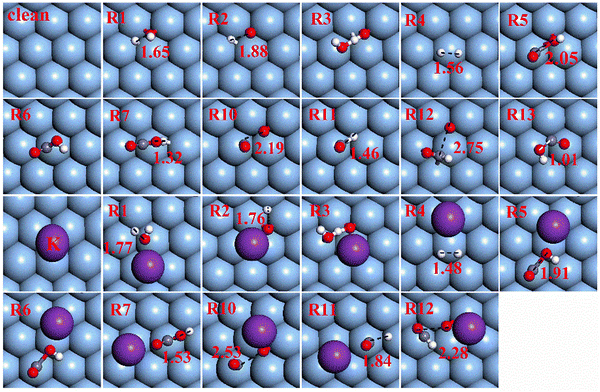Fig. 2 Transition state (TS) structures of elementary steps on Ag(111) and K/Ag(111). The red, gray, white and purple balls represent O, C, H and K atoms, respectively.

3.2.1 H₂O and OH activation. The H₂O molecule is apt to bind on the top site by its O atom connecting to the surface Ag atom with a binding energy of −0.07 eV. With O–H bond cleavage, the OH fragment tends to bind the fcc site and the detached H atom would connect to the adjacent fcc site. Such a dehydrogenation step from H₂O is quite hard, being endothermic by 1.06 eV with a large energy barrier of 1.77 eV, which is in accordance with the theoretically calculated result of 1.66 eV on the Ag(111) surface by Wang et al.^2,3 Besides, the barrier of this reaction step is higher than that on Cu(111) (1.37 eV),¹⁸ Pt(111) (0.98 eV)^2,3 and Ni(111) (0.86 eV)²⁰ due to the lower activity of Ag than these transition metals. The produced OH tends to adsorb at the fcc site and its further dehydrogenation is endothermic by 1.82 eV with an energy barrier of 2.41 eV, which is much higher than that of H₂O activation, meaning completing this step is rather difficult. Another alternative step for generating the O atom is by disproportionation of OH in which two OH groups separately occupy two bridge sites. This step is very facile with an activation barrier of 0.26 eV being endothermic by 0.14 eV. Consequently, OH disproportionation rather than direct OH dissociation is the favorable way to produce O and H.

When K is introduced to the Ag(111) surface, the initial state (IS), transition state (TS) and final state (FS) geometrical structures involved in H₂O and OH activation alter dramatically due to the attractive interaction between K and O. Such an effect of K on O atoms causes the H₂O plane to stay far away from the Ag(111) plane with the O atom orienting toward K and two H atoms pointing to the Ag surface. Additionally, K addition makes the adsorption site of OH at both TS and FS structures change from the fcc site of the clean surface to the top site by its O atom pointing to K. The large stabilizing effect of K on OH or O of TS and FS renders H₂O and OH dehydrogenation kinetically and thermodynamically favored with both energy barriers decreasing by about 0.30 eV and the endothermy reducing by 0.14 and 0.32 eV, respectively. For OH disproportionation, the K adatom prefers to interact with dual O atoms in IS, TS and FS structures and the kinetics of this reaction is slightly suppressed by K with the activation barrier increasing to 0.34 eV from 0.26 eV on a clean surface, while its endothermy (about 0.14 eV) is barely affected by K addition.

3.2.2 H₂ formation. Once H atoms are formed¹ on the Ag(111) surface, the adsorbed H atoms would occupy the fcc sites and combine with each other to form H₂ with an energy barrier of 1.21 eV, being exothermic by −0.40 eV. The K adatom slightly affects the geometrical structures and energetics involved in the combination of H atoms to H₂, since little interaction exists between K and H. The reaction energy is thus almost equal on Ag(111) and K/Ag(111) surfaces (−0.40 vs. −0.37 eV) and the reaction barrier on the K/Ag(111) surface (1.02 eV) is lower than that on the Ag(111) surface (1.21 eV).

3.2.3 CO oxidation through the redox pathway. When CO co-adsorbs with the produced O atom from OH activation, CO tends to shift to the top site from the preferred hollow site and the adsorbed O atom continues to stay in the fcc site. With molecular CO gradually approaching O, the distance between C and O shortens to 2.19 Å to reach the TS structure. The process of CO oxidation is extremely facial with an energy barrier of 0.03 eV and high exothermicity of 2.72 eV. The yielded CO₂ physically adsorbs over the Ag(111) surface in a direction parallel to the plane.

When K is added to this co-adsorption system, K adatom prefers to interact with the adsorbed O atom and the C–O distance would elongate to 2.53 Å at the TS. The oxidation of CO is kinetically as easy as on a clean surface with an energy barrier of 0.03 eV and thermodynamically less favored with an exothermicity of 2.06 eV.

3.2.4 CO oxidation through the carboxyl pathway.
3.2.4.1 CO oxidation by OH to form COOH. In addition to being oxidized by O, CO can also be oxidized by OH to generate surface carboxyl species (COOH). The most stable co-adsorption sites for CO and OH are similar to those for CO and O, that is, CO binds to the top site and OH occupies the fcc site. This C–O bond formation process is also facile with a reaction barrier of 0.07 eV, but is thermodynamically less favored with an exothermicity of 0.35 eV, much less than that of 2.72 eV for CO oxidation by O. We notice that the activation barrier of CO oxidation by OH on the Ag(111) surface is much lower than that on Cu(111) (0.54 eV), Pt(111) (0.31 eV) and Ni(111) (0.96 eV) and CO oxidation by O also needs higher energy barriers of 0.48, 0.91 and 0.97 eV on Cu, Pt and Ni surfaces, respectively.^18–20 The reason can be attributed to that compared to other metals, more inert metals like Ag would weaken CO and OH (O) binding with the surface and accordingly strengthen the ability to combine with each other.

When K is introduced into the co-adsorption system for CO and OH, OH would shift from the preferred fcc site to the bridge one with the O–H axis parallel to the surface so that its O can better interact with K with an O–K distance of 2.45 Å, while CO still binds to the top site with O inclining toward K and the distance between them equals to 2.90 Å. K addition rarely affects the kinetics of this oxidation step with an activation barrier of 0.06 eV, but enhances the thermodynamics by decreasing the reaction energy to −0.56 eV from the original −0.35 eV.

3.2.4.2 Transformation of cis-COOH to trans-COOH. The produced COOH species is featured by its H atom pointing upwards relative to the surface, named cis-COOH, in which the atomic H is unable to fall to the surface. As a result, the cis-COOH would convert to another form with the H atom pointing to the surface (namely, trans-COOH) before further dehydrogenation. The transformation from cis-COOH to trans-COOH is thermoneutral with an energy barrier of 0.50 eV.

The translation from cis-COOH to trans-COOH is also considered on the K/Ag(111) surface, which is thermally neutral (−0.04 eV) with an energy barrier of 0.52 eV, the same reactivity as on the corresponding pure surface.

3.2.4.3 Trans-COOH dehydrogenation. One possible way for CO₂ generation is through trans-COOH direct dehydrogenation with an exothermicity of 0.68 eV, which is thermodynamically advantageous. Nevertheless, this step is still hard to occur due to so large activation barrier (1.27 eV). K addition can enhance the kinetics of trans-COOH dehydrogenation by decreasing the activation barrier to 1.14 eV from the original 1.27 eV, but restrain the thermodynamics with a lower exothermicity of 0.13 eV (compared to 0.68 eV on a clean surface). In this way, trans-COOH direct dehydrogenation is still a tough process under the effect of K.

Besides direct dehydrogenation, COOH dehydrogenation assisted by OH or O species supplies an alternative way to yield CO₂. Whether on the pure or on the K-adsorbed Ag(111) surface, once OH or O species adsorbs in the position near COOH, COOH species would automatically transfer its H atom to adjacent OH or O, leading to CO₂ and H₂O (OH) formation. Hence, assisted by OH and O species, abstraction of H from trans-COOH turns into a spontaneous process which needs no reaction barrier on both surfaces. Consequently, OH(O)-assisted COOH dehydrogenation rather than its direct dehydrogenation dominates the carboxyl pathway.

3.2.5 CO oxidation through the formate pathway. For the formate pathway to generate the CO₂ product, formate (HCOO) is the most crucial intermediate which can be produced by two successive steps involving the combination of CO and H to form CHO, and then oxidation of CHO to HCOO. The former reaction for CHO generation needs an energy barrier of 0.63 eV, being exothermic by 0.27 eV, while the latter one is quite facile with a negligible energy barrier of 0.02 eV and the exothermicity reaches as high as 3.29 eV. Such high reactivity and exothermicity are caused by the strong affinity of HCOO species, which connects to the Ag(111) surface in a bidentate form with its two atomic O binding on two neighboring Ag sites (named bi-HCOO). Despite the facility of HCOO formation, its dehydrogenation to yield CO₂ is virtually impossible, as the dual O–Ag and C–H bonds require a much high activation barrier of 1.93 eV and the exothermicity of 0.16 eV to break.

K addition tends to promote the formation of CHO in kinetics and thermodynamics with the energy barrier decreasing by 0.10 eV and reaction energy decreasing to −0.18 eV from the original 0.53 eV. However, whether CHO oxidation or HCOO dissociation reaction, the effect of the K adatom on them is adverse with activation barriers increasing by 0.46 eV for the C–O bond formation and 0.28 eV for C–H bond breaking, while the exothermicity reduces by 0.57 and 0.62 eV, respectively.

The above analysis shows that the formate pathway is the most undesirable pathway on both Ag(111) and K/Ag(111) surfaces due to the difficulty of C–H bond breaking from HCOO to form CO₂. Both redox and carboxyl pathways are favorable for the WGSR on both surfaces, since C–O bond formation in both pathways is facile and C–H bond cleavage to form CO₂ in OH(O)-assisted carboxyl pathway is also kinetically favored. However, the redox pathway is more sensitive to the availability of O, which derives from OH disproportionation in advance. Thus, the OH-assisted carboxyl pathway rather than the redox pathway is the optimal one for the WGSR on both surfaces. For all elementary reaction steps involved in the OH(O)-assisted carboxyl pathway, H₂O dissociation is the most difficult step with the highest energy barrier and thus would be the rate-controlling step. K addition can lower the energy barrier of such rate-controlling step and consequently enhance the activity of the whole the WGSR.

3.3 Energetic span model analysis

Fig. 3 exhibits the free energy profiles on Ag(111) and K/Ag(111) surfaces for the OH-assisted carboxyl pathway since such pathway dominates the WGSR of both surfaces as expounded above. The typical experimental condition of 500 K and 100 kPa is used to calculate the free energies. The entropy contributions for the adsorption of CO and H₂O reactants and the desorption of CO₂ and H₂ products are drawn into the free energy calculations. The translational, rotational, and vibrational entropy contributions have been considered for these species in their gaseous and adsorption states. For the gas-phase species, the entropies are obtained from the NIST Chemistry WebBook.³⁸ The Campbell Sellers (CS) equation, a semi-empirical relationship between the gas phase and surface entropies (seen in eqn (1)), was proposed to accurately evaluate the entropies of weakly bound molecular adsorbates.³⁹ In the present work, the entropies of reactants and products (CO, H₂O, CO₂ and H₂) are computed using the CS equation on account of their weak adsorption strength and low frequency modes on both Ag(111) and K/Ag(111) surfaces. The CS equation is as follows:

S^ad₀(T) = 0.7S^gas₀(T) − 3.3R (1)

where S^ad₀ and S^gas₀ refer to the entropy of adsorbates and the corresponding gas-phase species, respectively, and R denotes the ideal gas constant.

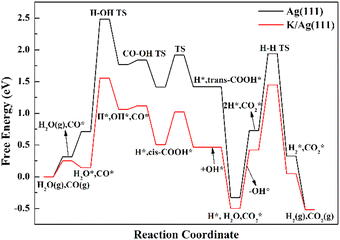Fig. 3 Free energy profiles of the WGSR via OH-assisted carboxyl mechanism over Au(111) and K/Au(111) at 500 K.

The activity of the rate-controlling step has been determined, but it is not enough to determine the whole reaction activity since the steps around it also work. Instead, the apparent activation energy would be a more suitable indicator to evaluate the activity of the entire cycle and it would be analyzed by the energetic span model proposed by Kozuch et al.⁴⁰ with regard to the carboxyl pathway of the whole WGSR on both clean and K-promoted surfaces. In this model, the TOF-determining transition state (TDTS) and TOF-determining intermediate (TDI) play a key role to define the energy span (δE), namely, the apparent activation energy of the entire cycle, which is expressed as follows:

where ΔG_r was the free energy of the WGS reactions.

For both Ag(111) and K/Ag(111) surfaces, the TDTSs are the TSs for H₂O → OH + H with free energies of 2.48 and 1.56 eV, and the TDIs are the coadsorption of CO₂ and H₂ in the gas phase with free energies of −0.52 eV on both surfaces. Since the TDTSs appear before TDI, the energy spans are calculated to be 2.48 and 1.56 eV, respectively, on Ag(111) and K/Ag(111) surfaces. Apparently, K addition can dramatically decrease the apparent activation energy on the clean Ag(111) surface, due to the much lower position of TDTSs on K/Ag(111) than on clean Ag(111), caused by the dual effects of smaller energy barrier of H₂O dissociation and stronger binding strength of reactants with the help of K.

4. Discussion

4.1 Origin of the K affects the activity of the WGSR

As analyzed above, K addition can enhance the activity of the WGSR by reducing the apparent activation energy of the WGSR circle through decreasing the energy barrier of H₂O dissociation (the rate-controlling step) and stabilizing the adsorption of reactants (CO and H₂O). To further explore the origin of the K promoting H₂O dissociation, the energetic effect analysis adopting the energetic decomposition method proposed by Hammer⁴¹ will be indispensable.

4.1.1 Energetic effect analysis. For a certain dissociation reaction XY → X + Y, its energy barrier can be split as follows:

E_a = E_bond(XY) – E^IS_XY + E^TS_X + E^TS_Y + E^TS_int (2)

where E_bond(XY) signifies the bond energy of XY (e.g., H₂O) in the gas phase; E^IS_XY, E^TS_X and E^TS_Y denote the binding energy of XY to the substrate at the IS geometry and that of X (Y) without Y (X) at the TS; and E^TS_int indicates the strength of interaction between X and Y at the TS.

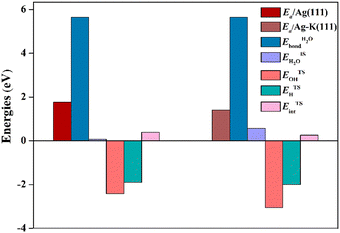
By eqn (2), the decomposition results for the energy barrier of H₂O dissociation have been acquired and illustrated in Fig. 4. It can be found that K additive would alter the magnitude of each term to varying degrees. On the one hand, the K adatom tends to stabilize H₂O binding with the Ag(111) surface, which is not conducive to dissociation of the H₂O molecule, but on the other hand, K prefers to slightly weaken the interaction between OH and H fragments at the TS and meanwhile strengthen their adsorption, especially OH adsorption on the Ag(111) by greatly increasing OH binding energy, contributing to H₂O cleavage. Given the above, the stability effect of K on OH adsorption of TS plays a leading role in promoting H₂O dissociation. Actually, the K adatom would stabilize almost all the oxygenates adsorbed on the Ag(111) surface including the reactants (CO, H₂O) by increasing their binding energies (see Table 1). It is amazingly found that the interaction between the oxygenated adsorbates and Ag atoms become weakened, as evidenced by the elongated O–Ag and C–Ag bonds (see Table 1). Besides interacting with surface Ag atoms, these oxygenates also tend to interact with K since their O atoms and K adatom get close to each other, as shown in Fig. 1 and 2 for the co-adsorbed structures of adsorbates and K. Thus it is supposed that the attractive interaction between oxygenates and the K adatom render their adsorption more stable than their counterparts on pure surfaces. Yet the origin of such interactions between them is vague and remains to be disclosed further through electronic effect analysis.

Fig. 4 The decomposition results for the energy barriers of H₂O dissociation on Ag(111) and K/Ag(111) surfaces.

4.1.2 Electronic effect analysis. The charge transfer between the OH group and K/Ag(111) substrate at the TS is illustrated in Fig. 5, in which the charge depletion occurs at the K site, while it accumulates around O, meaning that electrostatic attraction exists between K and O, that is, forming K^δ+ and O^δ− ions. This result is further verified by the Bader charge analysis in which the K adatom and O atom keep oppositely charged with 0.85 e and −1.25 e, respectively. The partial density of states (PDOS) of the K 3p states and O 2p states for OH adsorption on K/Ag(111) surface at the TS as well as that for bulk K₂O as a comparison are also illustrated (see Fig. 5). As presented in Fig. 5, the occupied K 3p state has contribution to the O 2p state of K₂O at the location of about −0.5 eV, implying formation of a typical ionic bond in bulk K₂O. A similar case occurs on PDOS of K and OH co-adsorption, in which K and O also have resonance at about −6 eV, featured by the direct K–O bonding as found in K₂O, meaning that the electrostatic interaction between K and O in oxygenates have developed into the ionic one. Additionally, the distance between K and O in most oxygenates ranges from 2.47 to 2.90, which can compare with that in the K₂O bulk (2.80 Å), showing the direct ionic bond exists between K and O atoms in most oxygenates. As a consequence, it is the ionic K–O bonding, the predominate interaction between K and O, stabilize the adsorption of oxygenates (including reactants of CO and H₂O) and the stabilization effect on OH adsorption of TS contributes to promoting H₂O dissociation.

Fig. 5 Calculated PDOS of K 3p states and O 2p states for TS of H₂O dissociation and K₂O bulk.

4.2 The factors affecting the K promotion effect

4.2.1 The factor of the K–O distance. As discussed above, the direct K–O bond forms when the distance between K and O ranges from 2 to 3 Å, and in general, the shorter the K–O bond, the stronger the bonding interaction. If the distance between K and O extends by more than 3 Å, will the K–O bond will be so weak that such bonding interaction tends to vanish? To resolve this doubt, the distance between K and O will be restricted in the range of 3.5–4 Å (long-range) in the structures involved in the process of K promoting H₂O dissociation and the homologous optimized IS, TS and FS structures, as well as the K–O short-range counterparts (K–O distance ranging from 2 to 3 Å), are depicted in Fig. S1 (ESI†). The charge density difference for OH adsorption at such a long-range TS geometry is plotted in Fig. S2 (ESI†) in comparison with that of the original short-range TS structure. Fig. S2 (ESI†) shows that no charge depletion occurred at the K site, while charge accumulation is mainly located between OH and surface Ag atoms, which suggests that almost no ionic bond but electrostatic attraction exist between K and O if their distance is long-range. This clue is further demonstrated by the fact that H₂O binding becomes weaker (−0.27 vs. −0.57 eV) and its dissociation barrier turns larger (1.73 vs. 1.41 eV) when compared to those in the short-range case. The above study indicates that the K–O distance is a key factor affecting H₂O activation, and the presence of K–O bond is conducive to the WGSR.

4.2.2 The factors of K coverage. Besides the factor of the K–O distance, another factor of K coverage has a marked influence on its promotion effect. To further shed light on the effect of such factors theoretically, we would probe the other two models with two kinds of K coverages (6.25% and 25% K), that is, one and four K atoms on the p(4 × 4) Ag(111) surface in comparison with the model in this study with a K coverage of 11.1% (one K atom on the p(3 × 3) surface). It is noticed from Fig. 6 that the energy barriers and reaction energies of H₂O dissociation become lower as K coverage becomes larger, especially for the case of K coverage in 25%, in which the energy barrier and reaction energy decreases dramatically and the reason will be explored in geometric and electronic factors. The IS, TS and FS structures of H₂O dissociation on surfaces with three different K coverages are exhibited in Fig. S3 (ESI†). It can be seen that the product OH tends to bind both K and Ag atoms when it interacts with one K atom, that is, one K–O bond exists for the K coverage of 6.25% and 11.1%, while OH prefers to move away from the Ag surface and is strongly stabilized by bridging the two adjacent K atoms forming two K–O bonds when K coverage is 25%. The stabilization energy of OH by Ag(111) surfaces with different coverages of K are calculated and summarized in Table S1 (ESI†), which shows that OH molecules are much more stabilized by two K–O bonds rather than the single K–O bond. Additionally, the dissociated H atom would connect to three surface Ag atoms in all cases, in which Ag atoms all stay away from K at its low coverage of 6.25% and 11.1%, but come close to the K site when the coverage is higher (25%) (see Fig. S3, ESI†). The Ag atom being close to K would bind H more strongly than the distant one since less electronegative K would transfer its valence electrons to the nearby Ag atoms, which become negatively charged (see Fig. S3, ESI†) and thus attract H proton more strongly than Ag atoms away from K. Given all that, the dissociated OH and H are much more stabilized by K in its higher coverage than in lower coverage, resulting in a remarkable decrease of reaction energy and barrier of H₂O dissociation when K coverage is high (25%).

Fig. 6 The energy barriers and reaction energies of H₂O dissociation versus K coverage.

4.3 Comparison of the K promotion effect on Au, Ag, Cu, Ni and Pt surfaces

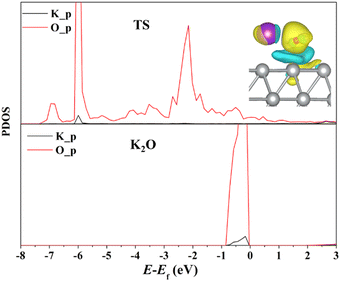
Promotion effects of K on H₂O dissociation over different metal surfaces (such as Au(111), Cu(111), Ni(111) and Pt(111)) have been reported previously.^2,3,18–20 Comparing these results with that over the Ag(111) surface, it is found that K addition reduces energy barriers on inert metal (Au, Ag and Cu) surfaces to a much larger extent (by 0.29–0.31 eV) than those on reactive metals like Ni and Pt (by 0.05–0.07 eV) and thus we deduce that the strength of K promotion effects may be associated with the activities of catalytic metal surfaces. To confirm this, we quantitatively plot the relationship between K-induced barrier reduction on various metal surfaces and the d-band center of the surfaces, as displayed in Fig. 7. The d-band center can be calculated by the formula: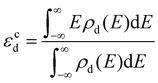 , where ρ_d represents the density of states projected onto metal atom's d-band and E is the energy of the d-band. Fig. 7(a) shows energy barrier differences for different metals linearly relate to the corresponding d-band center and the closer the d-band center to the Femi energy level, the lower the dissociation barrier difference, that is, the weaker the promotion effect of K. According to the rule proposed by Nørskov et al., the higher or more positive the d-band, the more active the metal surface.⁴² Consequently, K has a stronger promotion effect over more inert metals. As discussed in the last section, the direct K–O bonding forming at the TSs is the major cause of the K promotion effect on H₂O dissociation, hence the stronger K–O bonding (i.e., the shorter the K–O bond) results in a stronger promotion effect, which is further confirmed by the fact that the lengths of K–O bonds on different metal surfaces are found well correlated with the K promotion effect (see Fig. 7(b)). The strengths of K–O bonds at the TSs for H₂O dissociation on Ag(111) and Ni(111) surfaces are measured by the projected crystal orbital Hamilton population (pCOHP) method developed by the Dronskowski group⁴³ and the related results are presented in Fig. S4 (ESI†) which shows that the K–O bonds on Ag(111) is much stronger than those on the Ni(111) surface. The length of the K–O bond on the Ag(111) surface is 2.44 Å, shorter than 2.60 Å on the Ni(111) and the result reconfirms that the shorter K–O bond means a stronger K–O bonding. Then why does stronger K–O bonding appear over the more inert metals? The reason may be that the more inert metal surfaces would weaken K and O binding and accordingly strengthen the interaction between them.

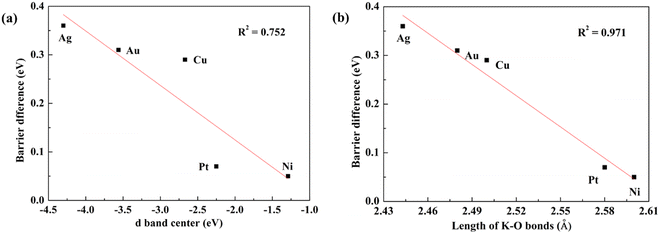Fig. 7 Plot of energy barrier difference for water dissociation on clean and K-doped metal surfaces versus (a) the d-band center and (b) the length of K–O bond.

5. Conclusion

The effect of the K promoter on the activity of the WGSR over the Ag(111) surface has been probed by DFT calculations systematically. The conclusions are summarized as follows:

(1) The K adatom can stabilize the adsorption of all oxygenates by increasing their binding energies and the direct K–O bonding would strengthen their adsorption. However, K addition has little impact on the binding strength of H and H₂ on the Ag(111) surface since negligible attractive interaction exits between K and H atoms.

(2) For both Ag(111) and K/Ag(111) surfaces, the WGSR proceeds mainly through the OH-assisted carboxy pathway and H₂O dehydrogenation is found to be the rate-controlling step on both surfaces. K addition can enhance the activity of the WGSR by reducing the apparent activation energy of the whole reaction since it can promote H₂O dissociation and stabilize adsorption of the reactants (CO and H₂O). It is the ionic K–O bonding, the predominant interaction between K and O, which stabilizes the adsorption of oxygenates (including reactants of CO and H₂O) and the stabilization effect on OH adsorption of TS contributes to promoting H₂O dissociation.

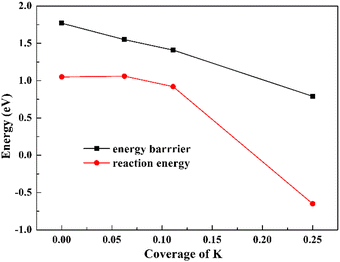
(3) The K–O distance is a key factor to affect H₂O activation, that is, when the K–O distance is long, the electrostatic interaction exists between them and the reduction of the dissociation barrier is small, while if the K–O distance is short, the direct K–O bonding dominates, which results in the barrier reduction to a large extent. Another factor of K coverage also has influence on its promotion effect and the dissociated OH and H are much more stabilized by K in its higher coverage, resulting in a remarkable decrease of the reaction energy and barrier of H₂O dissociation when K coverage is high (25%).

(4) For various metals catalyzing the WGSR, K promotes H₂O dissociation on inert metals like Ag, Au and Cu further than those on reactive metals (Pd and Ni) since the more inert metal surfaces would weaken K and O binding and accordingly strengthen the interaction between them, resulting in a higher promotion effect.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work is financially supported by the Applied Basic Research Project of Shanxi Province (No. 20210302124212) and the 1331 Engineering of Shanxi Province.

References

1. D. C. Grenoble, M. M. Estadt and D. F. Ollis, The chemistry and catalysis of the water gas shift reaction: 1. The kinetics over supported metal catalysts, J. Catal., 1981, 67, 90–102.
2. C. H. Lin, C. L. Chen and J. H. Wang, Mechanistic studies of water-gas-shift reaction on transition metals, J. Phys. Chem. C, 2011, 115, 18582–18588.
3. S. C. Huang, C. H. Lin and J. H. Wang, Trends of water gas shift reaction on close-packed transition metal surfaces, J. Phys. Chem. C, 2010, 114, 9826–9834.
4. A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, On the mechanism of low-temperature water gas shift reaction on copper, J. Am. Chem. Soc., 2008, 130, 1402–1414.
5. Q. L. Tang, Z. X. Chen and X. A. He, Theoretical study of the water gas shift reaction mechanism on Cu (111) model system, Surf. Sci., 2009, 603, 2138–2144.
6. R. J. Madon, D. Braden, S. Kandoi, P. Nagel, M. Mavrikakis and J. A. Dumesic, Microkinetic analysis and mechanism of the water gas shift reaction over copper catalysts, J. Catal., 2011, 281, 1–11.
7. Z. Y. Li, N. Li, N. Wang, B. Zhou, P. Yin, B. Y. Song, J. Yu and Y. S. Yang, Mechanism investigations on water gas shift reaction over Cu (111), Cu (100), and Cu (211) surfaces, ACS Omega, 2022, 7, 3514–3521.
8. H. Prats, L. Álvarez, F. Illas and R. Sayós, Kinetic monte carlo simulations of the water gas shift reaction on Cu (111) from density functional theory based calculations, J. Catal., 2016, 333, 217–226.
9. L. C. Grabow, A. A. Gokhale, S. T. Evans, J. A. Dumesic and M. Mavrikakis, Mechanism of the water gas shift reaction on Pt: First principles, experiments, and microkinetic Modeling, J. Phys. Chem. C, 2008, 112, 4608–4617.
10. J. P. Clay, J. P. Greeley, F. H. Ribeiro, W. N. Delgass and W. F. Schneider, DFT comparison of intrinsic WGS kinetics over Pd and Pt, J. Catal., 2014, 320, 106–117.
11. R. C. Catapan, A. A. M. Oliveira, Y. Chen and D. G. Vlachos, DFT study of the water-gas shift reaction and coke formation on Ni(111) and Ni(211) surfaces, J. Phys. Chem. C, 2012, 116, 20281–20291.
12. G. Ertl, H. Kniizinger, J. Weitkamp, S. Professor and K. S. Suslick, Handbook of heterogeneous catalysis, VCH, Weinheim, 1997, pp. 2449–2479.
13. H. P. Bonzel, Alkali-metal-affected adsorption of molecules on metal surfaces, Surf. Sci. Rep., 1988, 8, 43–125.
14. R. D. Diehl and R. McGrath, Structural studies of alkali metal adsorption and coadsorption on metal surfaces, Surf. Sci. Rep., 1996, 23, 43–171.
15. T. Maneerung, M. K. Hidajat and S. Kawi, K-doped LaNiO₃ perovskite for high-temperature water-gas shift of reformate gas: Role of potassium on suppressing methanation, Int. J. Hydrogen Energy, 2017, 42, 9840–9857.
16. J. A. Rodriguez, E. R. Remesal, P. J. Ramírez, I. Orozco, Z. Liu, J. Graciani, S. D. Senanayake and J. F. Sanz, Water-gas shift reaction on K/Cu(111) and Cu/K/TiO₂(110) surfaces: Alkali promotion of water dissociation and production of H₂, ACS Catal., 2019, 9, 10751–10760.
17. W. Ma, G. Jacobs, U. M. Graham and B. H. Davis, Fischer-tropsch synthesis: Effect of K loading on the water-gas shift reaction and liquid hydrocarbon formation rate over precipitated iron catalysts, Top. Catal., 2014, 57, 561–571.
18. Y. X. Wang and G. C. Wang, A systematic theoretical study of water gas shift reaction on Cu(111) and Cu(110): Potassium effect, ACS Catal., 2019, 9, 2261–2274.
19. Y. X. Wang and G. C. Wang, A systematic theoretical study of the water gas shift reaction on the Pt/ZrO₂ interface and Pt(111) face: Key role of a potassium additive, Catal. Sci. Technol., 2020, 10, 876–892.
20. M. Zhou and B. Liu, DFT investigation on the competition of the water-gas shift reaction versus methanation on clean and potassium-modified nickel (111) surfaces, ChemCatChem, 2015, 7, 3928–3935.
21. Z. P. Liu and P. Hu, An insight into alkali promotion: A density functional theory study of CO dissociation on K/Rh (111), J. Am. Chem. Soc., 2001, 123, 12596–12604.
22. L. Y. Gan, R. Y. Tian, X. B. Yang and Y. J. Zhao, Theoretical study of the influence of Na on CO adsorption and dissociation on Pd(111): Long-range or short-range interactions between co-adsorbates?, Chem. Phys. Lett., 2011, 511, 33–38.
23. M. G. Castano, T. R. Reina, S. Ivanova, M. A. Centeno and J. A. Odriozola, Pt vs. Au in water-gas shift reaction, J. Catal., 2014, 314, 1–9.
24. R. J. Lin, H. L. Chen, S. P. Ju, F. Y. Li and H. T. Chen, Quantum-chemical calculations on the mechanism of the water–gas shift reaction on nanosized gold cluster, J. Phys. Chem. C, 2012, 116, 336–342.
25. M. Bingham and A. Mills, Catalytic and photocatalytic water gas shift reaction (WGSR) using a continuous flow, gas phase reactor, J. Photochem. Photobiol., A, 2021, 409, 113–133.
26. A. Arab, D. Sharafie and M. Fazli, Theoretical study of water-gas shift reaction on the silver nanocluster, J. Phys. Chem. Solids, 2017, 109, 100–108.
27. D. Sharafie, A. Arab and M. Fazli, The formate and redox mechanisms of water-gas shift reaction on the surface of Ag: A nanocluster model based on DFT study, Iran. J. Catal., 2019, 9, 213–221.
28. F. Boccuzzi, A. Chiorino, M. Manzoli, D. Andreeva, T. Tabakova, L. Ilieva and V. Iadakiev, Gold, silver and copper catalysts supported on TiO₂ for pure hydrogen production, Catal. Today, 2002, 75, 169–175.
29. G. Kresse, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11187.
30. G. Kresse and P. Furthmuller Effeciency, of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comp, Mater. Sci., 1996, 6, 15–50.
31. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
32. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
34. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
35. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for bader charge allocation, J. Comput. Chem., 2007,(28), 899–908.
36. G. Henkelman, A. Arnaldsson and H. Jonsson, A fast and robust algorithm for bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
37. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
38. NIST Chemistry WebBook: https://webbook.nist.gov/chemistry/, in NIST Standard Reference Database Number 69, June 2005 Release, ed. W. G. Mallard, National Institute of Standards and Technology, 2005.
39. C. T. Campbell and J. R. V. Sellers, The entropies of adsorbed molecules, J. Am. Chem. Soc., 2012, 134, 18109–18115.
40. S. Kozuch and S. Shaik, How to conceptualize catalytic cycles? The energetic span model, Acc. Chem. Res., 2011, 44, 101–110.
41. B. Hammer, Adsorption, diffusion, and dissociation of NO, N and O on flat and stepped Ru(0001), Surf. Sci., 2000, 459, 323–348.
42. B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343, 211–220.
43. V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets, J. Phys. Chem. A, 2011, 115, 5461–5466.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03757b

---