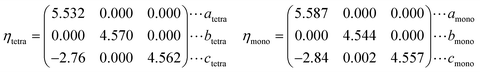A theoretical study on pseudo Mott phase transition of vanadium dioxide

Abstract

The structural phase transition (SPT) and metal–insulator phase transition (MIT) always occur simultaneously upon heating from the low-temperature insulator M₁ phase to the high-temperature metal R phase in vanadium dioxide, and it is still unclear which one of Mott correlation and Peierls distortion plays a decisive role in the thermally induced phase transition (PT) since 1959. Our density functional theory (DFT)-based calculations revealed that the intermediate phase in the PT, the so-called monoclinic metal phase, is a zero indirect band gap semimetal (P2₁/c space group) with a pseudo gap (199 meV). From the M₁ phase to the monoclinic metal phase, the band gap decreases gradually to zero, and the bonding lengths between vanadium–vanadium atoms remain nearly constant. The SPT and MIT from the intermediate structure to the R phase occur simultaneously with a sudden change of bonding lengths between vanadium–vanadium atoms, in which electrons can jump down rather than jump up to the conduction band minimum (CBM) from the valence band maximum (VBM) under thermal fluctuation in order to lower the total energy of the system to push forward the occurrence of PT. The electron jumping does not require additional energy from Coulomb repulsion between electrons even though it is always present. This SPT is a typical Peierls PT or a pseudo Mott PT rather than an actual Mott PT in the each of the two stages. Our conclusions provide a new understanding of SPT and MIT in vanadium dioxide that has been debated for more than 80 years.

---

1 Introduction

Vanadium dioxide (VO₂) has a broad range of applications in the fields of smart windows, memory storage materials, photoelectric conversion devices, and other fields owing to reversible MIT near room temperature.^1–4 These applications require that the electrical resistivity and optical properties should change dramatically and suddenly in an ultra-short time during the MIT. The emergence of its MIT is accompanied by the first-order SPT from the monoclinic semiconductor phase (M₁, space group P2₁/c) to the tetragonal metal phase (R, space group P4₂/mnm) at approximately 340 K. Its slower SPT always has an important influence on the MIT temperature and the MIT velocity. The expansion of its practical application depends heavily on the fundamental understanding of its MIT. Based on the experimental observation, electron-correlation-driven Mott transition^5–9 and structure- distortion-driven Peierls transition^10–16 were proposed to understand the MIT. And now increasing studies^17–23 suggest that both Mott correlation and Peierls distortion cooperatively play an important role in the PT at the same time.

Recently, a strongly correlated nanoscale metallic intermediate phase (the so-called monoclinic metal phase) with a diverging quasiparticle mass and an optical pseudo band gap was observed at approximately 333–342 K on heating.^7,24 These metallic nanopuddles actually can be experimentally stabilized or captured by a surface coordination approach.²⁵ Their Hall measurement further revealed²⁶ that there exists alternation of the dominant carrier type from electrons to holes near 330 K and then from holes to electrons near 332 K. The existence of an intermediate phase allows us to divide the thermally induced PT from low to high temperature into two stages, i.e. the M₁ to an intermediate phase and the intermediate phase to the R phase.²⁷

Gibbs free energy and potential energy are continuous functions existing from the low temperature phase to the high temperature phase on heating, and the Gibbs free energy of the intermediate phase should be a local minimum in the potential energy or free energy surface. An earlier study²⁸ on the potential energy surface in the structural evolution of thermally induced PT was based on the molecular dynamics method with empirical potential, in which the monoclinic metal phase and electron–electron correlation cannot be involved owing to the theoretical method with innate defects. Based on the temperature-dependent in situ X-ray absorption fine structure measurement and DFT calculations, Yao et al.²⁹ revealed that the abrupt change of V–V spacing and twisting angle δ occurs simultaneously with the sudden reduction of the band gap in the structural evolution from the M₁ to the intermediate phase. Whether Peierls distortion or electronic correlation plays the major role in the PT is not mentioned. Later, Chen et al.³⁰ found that the abrupt change of V–V spacing and twisting angle δ of V–V pairs occurs simultaneously with the sudden reduction of the band gap in the structural evolution from the M₁ to the R phase. Unfortunately, the intermediate phase i.e. the so-called monoclinic metal phase in the structural evolution was not observed since the too-large effective on-site Coulomb interaction was chosen. A recent important theoretical study³¹ with dynamical mean-field theory (DMFT) within the adiabatic Born–Oppenheimer approximation predicted that there is a distorted metal phase between the low-temperature distorted insulator and high-temperature undistorted metal. However, whether the V–V spacing and electronic structure have abruptly changed when the intermediate phase appears was not reported. Despite that the previous studies mentioned above have found out the cooperation of Mott correlation and Peierls distortion, all of them were based on the experimental observations with one-stage PT. It is still unclear which of Peierls geometrical distortion and Mott electronic correlation plays a crucial role in the PT from the M₁ to R phase in VO₂, especially in each of the two stages.

In this paper, based on DFT with Dudarev implementation (DFT+U),³² the gradual evolution of the V–V spacing and energy band was studied from the M₁ to R phase in the thermally induced PT. We found that the band gap gradually decreased to zero or even a negative value corresponding to the semimetal intermediate phase without an abrupt change of V–V spacing and MIT on heating in the first stage PT. During the second stage PT, MIT and SPT occur simultaneously with an abrupt change of V–V spacing. The Coulomb repulsion between electrons is always present and does not have an effect in any one of the two stages, that is, the PT from the M₁ to R phase is a pseudo Mott PT.

2 Calculation details

The calculations of our pure system, correlated doping system, excited state with a Δ self-consistent field scheme and ground state were studied at the DFT level with Vienna ab initio simulation package (VASP).^33,34 The projector augmented wave pseudo-potentials (PAW) were chosen in all calculations. Meta-generalized-gradient approximation SCAN³⁵ with spin-unpolarization solutions (non-magnetic states) were used to optimize the geometrical structures and scan the potential energy surface. Dudarev implementation³² was adopted to treat the effective on-site Coulomb interaction U_eff (= U − J) = 2.0 eV for 3d orbitals of vanadium. In experimental observations, M₁ and R phases are the nonmagnetic state and paramagnetic state with a weak local magnetic moment,^30,36 respectively. In addition, both previous theoretical study^30,37,38 and our calculations (Table S1 in the ESI†) showed that the relative stability of the R and M₁ phases will be the wrong order in the spin-polarization calculations. So the spin-unpolarization calculations were finally chosen to simulate various structures. In the last decade, many publications have shown that a description of the dynamical correlations is important such as with DMFT or its cluster extensions. Unfortunately, different calculations by state-of-the-art DFT+DMFT methods do not even agree about a unanimous view of the M₁ monoclinic phase. Specifically, M₁ has been regarded from time to time as a correlation-assisted Peierls insulator,^22,39 or vice versa, as a Peierls-assisted Mott insulator,⁴⁰ or finally as a genuine Mott insulator.^20,41,42 In our calculations, a consistent computational functional (DFT+U with a nonmagnetic solution) is greatly important to yield a smooth potential energy surface and then can observe a rational and continual electronic structure evolution during MIT.

In agreement with the experimental energy band gap (E_g = 0.6 eV),⁴³ SCAN+U (U = 2) is equally good for calculating the energy band and reducing the cost of the calculation.⁴⁴ Our theoretical gap was 0.58 eV as shown in Table 1, which agrees well with the experimental energy gap. Mott et al.⁶ predicted that the theoretical energy gap is U−(B₁ + B₂)/2 in which B₁ and B₂ are bandwidths of the upper and lower Hubbard bands. Their theoretical Mott gap is 1.18 eV for the M₁ phase which is much larger than the experimental band gap (0.6 eV). In order to evaluate whether the U value used in our DFT calculations mentioned above is reasonable, their formula was used to calculate the energy gap, and it was found that our energy gap also should be 1.18 eV (B₁ = 1.11 eV and B₂ = 0.53 eV). Our effective on-site Coulomb interaction (U = 2) should be overestimated in the energy band gap calculations.

Table 1 Lattice parameters (Å) and energy gap (eV) for R and M₁ phases at various U values

U (eV)	0	1	2	3	4	Exp.
a/c (R)	2.77/4.56	2.77/4.57	2.78/4.58	2.79/4.59	2.80/4.59	2.85/4.55
a/b/c (M1)	5.58/4.54/5.37	5.58/4.55/5.38	5.58/4.56/5.39	5.58/4.57/5.39	5.60/4.58/5.40	5.74/4.52/5.37
Gap	0.17	0.24	0.58	0.79	1.06	0.60

---

The relative energies and structural properties calculated within SCAN+U are reliable and are shown in Table 1 for solving temperature-induced phase transitions in VO₂.^45,46 The Brillouin zone⁴⁷ was obtained by using special 5 × 7 × 6 k-grid points of Monkhorst–Pack type with a plane-wave function truncation energy ENCUT of 600 eV to ensure that the total energy converges to 10⁻⁶ eV per atom, performing complete structural relaxation until the Hellmann–Feynman force is less than 0.02 eV Å⁻¹.

There are basically two classes of methods for calculating excitation energies. The first is a calculation based on the Dyson equation and the fact that the self-energy entering this equation is a functional of the density. Here we focus on another class of methods where the ground-state scheme is applied to both the excited state (each of the top valence band and bottom conduction band is occupied by one electron) and the ground state (the top valence band is occupied by two electrons) for various possible intermediate configurations owing to the large saving of machine time, and their energy differences were calculated. This approach is referred to as the Δ self-consistent field scheme (ΔSCF),^48–50 since it is based on the energy difference between two self-consistent-field calculations. In the theoretical simulations of the ΔSCF-excited state, we introduced noninteracting electron–hole pairs by changing the occupation numbers of the Kohn–Sham orbitals.

In order to analyze the phase transition mechanism of VO₂ in detail, the free energy and vibrational entropy of VO₂ with different phase structures were calculated by the density functional perturbation (DPFT)⁵¹ method (VASP package). Separately, density functional perturbation theory (DFPT) has been widely applied to compute the properties of phonons from DFT, including the phonon density of states and vibrational contributions to entropy. This has allowed direct calculation of free energies of different systems. The conductivity and carrier concentration were obtained by post-processing the VASP output results using the Boltzmann transport equation (BTE)⁵² in the VASPKIT package.⁵³ The electronic transport coefficients of both n- and p-type VO₂ are obtained using semiclassical Boltzmann theory within the relaxation-time approximation (RTA) in the VASPKIT package.⁵³

3 Results and discussion

3.1 Potential energy landscape with linear interpolation

During the SPT, the two phases involved in martensitic-type transformation should have a lattice correspondence and orientation relationship, or a strain invariant plane.⁵⁴ There exists a group–subgroup relationship between the symmetry groups of the R tetragonal parent and M₁ monoclinic product phases owing to their same [010] crystal orientation. Their specific crystallographic correspondences are [010]_mono||[010]_tetra and (100)_mono||(100)_tetra. Because the martensitic-type transformation involves the continuous shear of the crystal cell and the shuffle of alternate atoms, the potential energy surface and the minimum energy path are functions of the internal atomic coordinates and lattice constants of the crystal cell. We rebuild a new crystal cell for the R phase as shown in Fig. 1 to simulate its shuffle and shear in martensitic-type transition.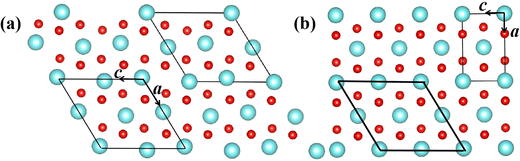

Fig. 1 Crystal cell of (a) M₁ and (b) R phases. Primitive cell (thin) and rebuilt cell (thick line). Red spheres represent oxygen atoms while the others represent vanadium atoms.

Each vanadium atom is coordinated with 6 oxygen atoms to form respective octahedra/distorted octahedral in R/M₁ phases¹⁵ in Fig. 1. The low temperature M_l phase has low symmetry, and the V atoms along the basis vector c_mono direction form zigzag chains and the V atoms on each chain are paired into V–V pairs, in which there are two different bond lengths, 2.48 Å and 3.15 Å. From the R to the M₁ phase, the unit cell volume and beta angle (β) decrease by 0.26% and 0.71°, respectively. The delicate lattice change under monoclinic symmetry cannot be accurately described by the DFT-based first-principles calculations. After cell reselection, the crystal basis vector matrix of the R phase and M₁ phase containing 12 atoms is as follows

where a_tetra/b_tetra/c_tetra and a_mono/b_mono/c_mono represent the lengths of three basis vectors for the R and M₁ phases, respectively. The lattice correspondences of the R and M₁ phases are a_tetra → a_mono, b_tetra → b_mono, and c_tetra → c_mono in the transformation. We assume that the atomic correspondence ensures a minimum displacement of the atoms in consideration of the unchanged coordination number of the vanadium atoms. The fractional coordinates of the R and M₁ phases are written as {V^i,β_tetra} and {V^i,β_mono}, respectively, where i corresponds to the atomic order number and β = x, y, and z. The potential energy surfaces are functions of the atomic coordinates along different directions and crystal angle. The PT process from the M₁ to R phase is independent of the unit cell shearing as shown in Fig. S1 (ESI†) and the shuffling of V atoms along the basis vector b direction. Therefore, the potential energy surface we constructed is that the V atoms shuffle along the basis vector a and c directions, respectively. To simplify the potential energy surface, we adopt the following approximation. Atomic coordinates x and z vary uniformly with phase transformation, respectively. Now we can write the potential energy surface as a function of two parameters.⁵⁵

E(x, z) = E({Vⁱ_x}, {Vⁱ_z})

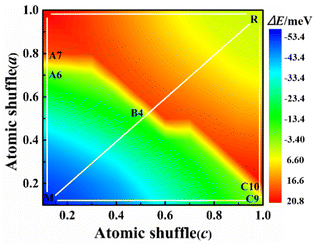
Here x and z are determined by linear interpolation, where Vⁱ_x = xV^ix_tetra + (1 − x)V^ix_mono describes the x-direction atomic coordinates of the system. Vⁱ_z = zV^iz_tetra + (1 − z)V^iz_mono is a set of atomic coordinates describing the z-direction of the system, where x and z vary from 0 to 1, with 0 representing the M₁ phase and 1 representing the R phase. We use x and z as variables to describe the potential energy surface for the transformation from the M₁ to R phase as shown in Fig. 2. In the whole potential energy surface, except the M₁ and R phase, no potential energy minimum is found, that is, no intermediate state is found only from the zero-temperature potential energy landscape.

Fig. 2 Potential energy surface of atomic shuffle from the M₁ to R phase.

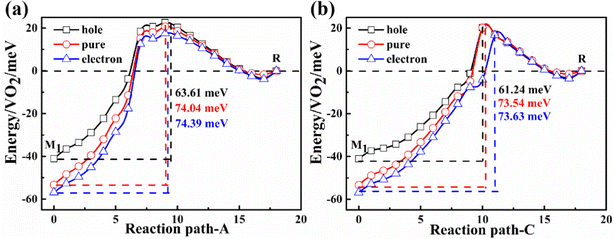
Their energy difference between the M₁ and the R phase is calculated to be 53 meV per VO₂ (experimental latent heat, 44 meV⁵⁶). The PT path can be artificially divided into three paths: A, B, and C. In path A, the alternative V atoms first shuffle along the a_mono-axis and then along the c_mono-axis. For path B, these vanadium atoms shuffle simultaneously along the a_mono-axis and the c_mono-axis. In path C, these V atoms shuffle in the opposite order to path A. After them, the geometrical structure of the M₁ phase gradually transfers to be the R structure. Their potential energy barriers of paths A, B and C are 74.04 (A6 configuration), 67.00 (B4 configuration), and 73.54 (C9 configuration) meV per VO₂, respectively, which are one order of magnitude lower than that of the previous theoretical energy barrier (approximately 600 meV per VO₂).³⁰ The PT from the M₁ to R phase is very easy to occur at 340 K on heating considering the average kinetic energy per VO₂ (103 meV at 340 K) under the ideal gas model.

The Gibbs free energies and vibrational entropies of several structures at 300 and 400 K along the paths A, B and C are shown in Fig. S2 (ESI†). At 300 or 400 K, the A6 configuration has the lowest free energy (−0.95 eV for the A6 configuration, −0.85 eV for the B4 configuration, and −0.77 eV for the C9 configuration at 400 K) and the largest vibrational entropy among various structures along the paths A, B and C, indicating that this structure can be easily stabilized experimentally.

3.2 Evolution of electronic and geometrical structures

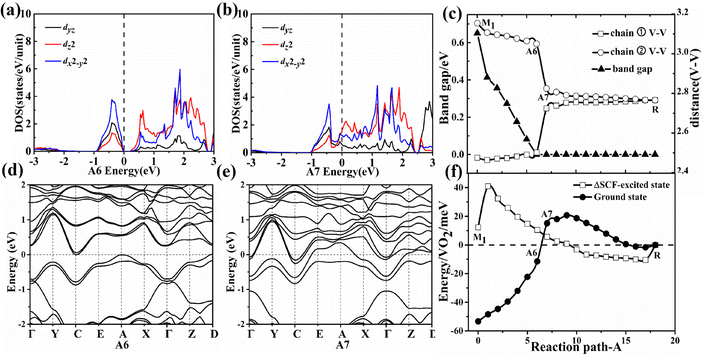
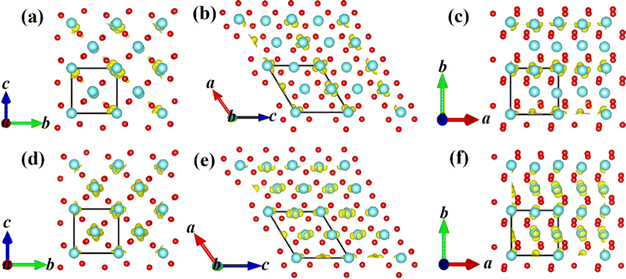
In the first-stage of two-stage PT from the M₁ phase to the A6 configuration along path A, the energy band gap gradually decreases and the V–V distances (chain ① V–V = 2.48 Å and chain ② V–V = 3.15 Å in the M₁ phase as shown in Fig. S3, ESI†) are nearly constant as shown in Fig. 3(c). The A6 configuration becomes an indirect semimetal with a 199 meV pseudo-gap as shown in Fig. 3(d). The pseudo-gap (199 meV) actually comes from the energy difference between the filled bonding orbit and the empty anti-bonding orbit as shown in Fig. 3(a), which is driven by sufficiently large crystal field splitting and the hybridization gap.¹⁵ The larger value of the pseudo-gap is determined by the stronger bonding strength between vanadium–vanadium atoms, so the pseudo-gap with 199 meV corresponds to the weakest V–V chain dimerization. The experimentally measured pseudo-gap (approximately 118 meV¹⁸) for the intermediate phase is on the same order of magnitude as our theoretical value. The energy difference ΔE₁, obtained by subtracting the ground-state energy of intermediate possible configuration from that of its corresponding ΔSCF-excited state, is 22 meV in the A6 configuration as shown in Fig. 3(f). The absolute value of energy difference ΔE₁ increases in the A6 configuration as the U value continues to increase from 2 to 6 eV. Surprisingly, the larger Coulomb repulsion between electrons is unfavorable to the formation of the ΔSCF-excited state for the A6 configuration since a larger U value indicates a stronger effective on-site Coulomb interaction. Further calculations revealed that the larger Coulomb repulsion will make the V–V spacing increase and then the band gap enlarges. So the larger Coulomb repulsion between the electrons increases the V–V spacing and then enlarges the band gap, which prevents the occurrence of Mott PT. The first stage has a typical characteristic of structurally distortion-driven Peierls transformation in which the paired electrons at the VBM does not jump up to the CBM even the Mott correlation is always present during this stage.

Fig. 3 Projected density of states (DOS) and energy bands of characteristic points A6 (a and d) → A7 (b and e) along the path A. (c) Change of the V–V spacing for the path A. (f) Energy evolution of the ground state of various intermediate possible configurations and their corresponding ΔSCF-excited states. Only the three d orbitals with the largest DOS are shown in the figure.

In the second-stage of two-stage PT from the A6 to the A7 configuration along path A, it transforms into a metallic state from a zero gap indirect semimetal. With the atomic shuffle of the middle layer along the [100]_mono crystal direction in the A6 to A7 configuration, the sudden disappearance of V–V chain dimerization and the appearance of metallic states in the A7 configuration shown in Fig. 3(c) occurred simultaneously after the band gap has closed in the A6 configuration. The bonding orbital d_z² and antibonding orbitals d_z² as shown in Fig. 3(a) merge into two orbitals with the same energy during the disappearance of dimerization between the nearest neighbor V–V atoms as shown in Fig. 3(b). Owing to the thermal fluctuation rather than Mott correlation, one of the two electrons can jump down to the d_z²-C k-point at the CBM from d_z²-A and D k-point in the VBM, and then lower the total energy in the A7 configurations as shown in Fig. 3(f). The presence of Coulomb repulsion between the electrons does not have an effect as shown in Fig. 3(a, d and b, e) and Fig. S4 (ESI†), that is, pseudo Mott PT. The energy difference ΔE₁ is −10 meV in the A7 configuration as shown in Fig. 3(f). The absolute value of energy difference ΔE₁ decreases in the A7 configuration as the U value continues to increase from 2 to 6 eV. The larger Coulomb repulsion between electrons is also unfavorable to the formation of the ΔSCF-excited state for the A7 configuration. Further calculations showed that the larger Coulomb repulsion makes both the V–V spacing and the total energy difference between A6 and A7 configuration increase, which means that the larger Coulomb repulsion makes the transformation more difficult from the A6 to the A7 configuration.

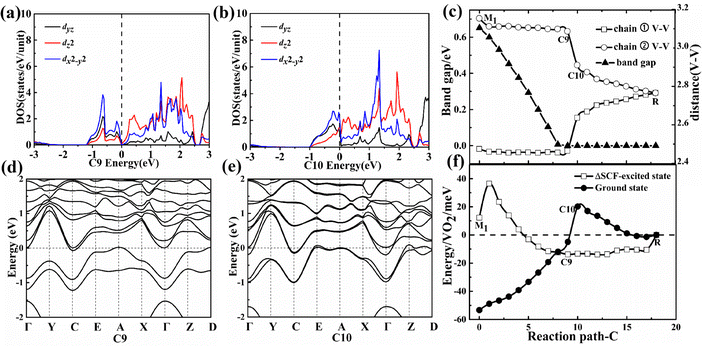
In the first-stage of the two-stage from the M1 to the C9 configuration along path C, the band gap also gradually decreases and the V–V spacing still remains nearly constant as shown in Fig. 4(c) until the metallic C10 configuration while the C8 (80 meV pseudo-gap) and C9 (0 meV pseudo-gap) configurations (P2₁/c space group) have become zero or negative gap indirect semimetal as shown in Fig. 4(a, d and b, e). The smaller pseudo-gap (0–80 meV) is determined by the weaker bonding strength between vanadium–vanadium atoms in comparison with the A6 configuration.

Fig. 4 Projected DOS and energy band of characteristic points C9 (a and d) → C10 (b and e) along the path C. (c) Change of the V–V spacing for the path C. (f) Energy evolution of the ground state of various intermediate possible configurations and their corresponding ΔSCF-excited states. Only the three d orbitals with the largest DOS are shown in the figure.

In the second-stage of the two-stage from the C9 to the C10 configuration along path C, the bonding (with lower energy than the d_yz orbital) and antibonding (with higher energy than the d_yz orbital) energy levels of the d_z² orbital also return to two energy levels with the same energy during the disappearance of dimerization between the nearest neighbor V–V atoms as shown in Fig. 4(a and b). Owing to the thermal fluctuation rather than Mott correlation, one of the two electrons will jump down to the CBM from the VBM and then lower the total energy in the C9 configurations as shown in Fig. 4(f), which shows the characteristic of pseudo Mott PT. The absolute value of energy difference ΔE₁ increases and decreases in the C7 and C10 configurations, respectively, as the U value continues to increase from 2 to 6 eV. The larger Coulomb repulsion between electrons is unfavorable to the formation of the ΔSCF-excited state for the C10 configuration and makes the transformation more difficult from the C8 to the C10 configuration.

The evolution of energy band is also calculated along path B. From the M₁ phase to the B4 configuration along path B, the band gap also gradually decreases and the V–V spacing still remains nearly constant until the metallic B5 configuration. The main difference for path B compared with path C is that those semimetal intermediate phases exist in smaller areas in Fig. 2. Owing to space limitations, the electronic structure evolution along the path B will not be discussed in the following paragraphs.

Obviously, the band gap has changed greatly from the M₁ phase to the intermediate phase, however, the electronic structure of the intermediate phase is still an indirect band gap semiconductor rather than a metal phase. The appearance of metal phase, as expected, comes from the change of distance between V–V atoms. The SPT can also be definitely characterized by both the twisting angle δ and V–V distance. However, the variation of nearest V–V pairs in the intermediate structures is found to play a key role in the evolution of the electronic structures, so, the V–V distance is used as an index to describe the phase transition.²⁹

In the previous experimental observations,⁵⁷ the PT from the M₁ to intermediate phase and then to the R phase is regarded as the MIT and SPT, respectively. According to our calculations, it can be found that it is a semiconductor–semimetal PT rather the semiconductor–metal PT from the M₁ to intermediate phase along any one of the paths A, B, and C in the thermally induced PT. MIT and SPT always occur at the same time from the intermediate phase to R phase along any one of the paths A, B, and C.

In the process of photoinduced PT, lots of electrons are excited by laser to the VBM. When the band gap decreases to be very small around the A6 or C9 configuration, the lots of d-orbital electrons crowded in the narrow space may jump up or down to the CBM under Mott repulsion. However, this process do not negate the conclusion that the Mott electronic correlation does not have an effect in the thermally induced PT.

3.3 From hole to electron carriers

In the calculations of conductivity and carrier concentration, the electronic relaxation time (τ) is extremely time-consuming.⁵⁸ So for complex multi-structure PT systems or high-throughput operations, a constant relaxation time (τ = 10) approximation⁵⁸ is usually used. Our theoretical conductivity and carrier concentration are strongly supported by previous experimental observations²⁶ as shown in Fig. S5, ESI† and Fig. 5(a and b). As the temperature increases (from 273 K to 340 K), the intermediate phase (A6 configuration) theoretically appears at T = 321 K and are very accurate compared with the experimental temperature (333 K) in ref. 24. The zero gap indirect semimetal A6 configuration corresponds to the monoclinic and correlated metal phase²⁴ in which its main carriers are holes rather than electrons.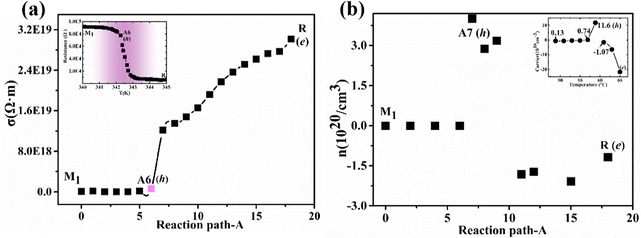

Fig. 5 Theoretical conductivity (a) and carrier concentrations (b) along the path A. The two inset maps are from ref. 24.

The Fermi level of the nanodomain for the intermediate phase enhances with the increase of temperature, and those electrons at the CBM in the nanodomain will migrate to the intermediate regions between nanodomains with a lower Fermi level. The absence of electrons in the nanodomains leads to the conversion of the main carriers from electrons to holes. As the temperature continues to increase, the nanodomains transform into the metal phase and electronic conduction begins to recover.

The square of electronic wavefunction at the VBM of the A6 configuration localized around partial V atoms along [100]_mono as shown in Fig. 6, while the electrons in the CBM uniformly distributes in three crystal directions, which means it is a little difficult for electrons at the conduction band to return to the valence band and then lead to recombination of e–h pairs owing to the existence of their different space region. This is one of the reasons why p-type semiconductors can appear in the PT.

Fig. 6 Square of electronic wavefunction of the VBM (a–c) and CBM (d–f) at Γ reciprocal points for the A6 configuration. Square of electronic wavefunction of the VBM and CBM at other k-reciprocal points is basically the same as those of Γ points.

3.4 Electron and hole injection

Electrons or holes will be injected when experimentally measuring conductivity. These injected carriers will change the PT temperature. The theoretical reduction in the PT temperature was essentially attributable to charge injection as a dopant.⁵⁹ To simulate the effect of carriers on the phase transition temperature, the number of electrons of the simulated system is changed. The changed carriers are compensated by background jellium to maintain the charge neutrality.

According to Fig. 7(a), the energy barrier of phase transition is reduced by approximately 11–12 meV f.u.⁻¹, which is equivalent to the reduction of phase transition temperature by approximately 14–15 K in the hole doping case. The phase transition temperature is almost not changed in the electron doping case. Similar results are found in path-C as shown in Fig. 7(b). The SPT temperature for the sample on the metal substrate (i.e. Au substrate) is also approximately 20 K lower than that on the semiconductor substrate (i.e. Si substrate), which is determined by using metal and semiconductor substrates to study the PT.⁶⁰ One possible reason for such experimental finding is that the electrons transfer to the metal substrate, inducing p-type doping. These electrons in the sample at the CBM in the VO₂ nanodomain easily migrate to the metal substrate, leading to the conversion of the dominant carriers from electrons to holes. On the other hand, electron doping has little effect on the PT temperature.

Fig. 7 Potential energy surface with doped concentrations of 10²¹ cm⁻³.

4 Conclusion

The evolution of the geometric and electronic structures of vanadium dioxide was studied with DFT+U calculations. Our theoretical calculations revealed the electronic structures of the intermediate phase, i.e. the monoclinic metal phase is a zero indirect band gap semimetal with a pseudo gap in the thermally induced phase transition from low to high temperature. The collapse of the energy gap precedes the appearance of the metal phase, which is always accompanied by the change of distance between V–V atoms. The Peierls geometrical distortion rather than the Mott electronic correlation always plays a decisive role in the thermally induced phase transition in which the presence of Coulomb repulsion between electrons does not have an effect. It means that such a PT is a pseudo Mott phase transition. These electrons at the CBM in the nanodomain will migrate to the intermediate regions between nanodomains with the increase of temperature. The absence of electrons in the nanodomains leads to the conversion of the main carriers from electrons to holes. As the temperature continues to increase, the nanodomains transform into the metal phase and electronic conduction begins to recover. The different space distributions of electrons in the CBM and VBM may lead to difficulty in recombination of e–h pairs.

Author contributions

Jinyi Miao and Wenxuan Wang are responsible for drafting the manuscript and theoretical calculations. Zhenyi Jiang, Xiaodong Zhang and Aijun Du contributed to scheme design, provided research ideas and revised the full text. Jiming Zheng revised the partial text and designed the partial scheme. All authors have read and approved the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grants (51872227, 51572219).

References

1. J. D. Valle, N. M. Vargas, R. Rocco, P. Salev, Y. Kalcheim, P. N. Lapa, C. Adda, M. H. Lee, P. Y. Wang, L. Fratino, M. J. Rozenberg and I. K. Schuller, Science, 2021, 373, 907–911.
2. D. Wickramaratne, N. Bernstein and I. I. Mazin, Phys. Rev. B, 2019, 99, 214103.
3. Y. H. Matsuda, D. Nakamura, A. Ikeda, S. Takeyama, Y. Suga, H. Nakahara and Y. Muraoka, Nat. Commun., 2020, 11, 1–7.
4. L. L. Chen, Y. Y. Cui, H. J. Luo and Y. F. Gao, RSC Adv., 2020, 10, 18543–18552.
5. M. M. Qazilbash, M. Brehm, B. G. Chae, P. C. Ho, G. O. Andreev, B. J. Kim, S. J. Yun, A. V. Balatsky, M. B. Maple, F. Keilmann, H. T. Kim and D. N. Basov, Science, 2007, 318, 1750–1753.
6. A. Zylbersztejn and N. F. Mott, Phys. Rev. B: Solid State, 1975, 11, 4383–4395.
7. T. J. Huffman, C. Hendriks, E. J. Walter, J. Yoon, H. Ju, R. Smith, G. L. Carr, H. Krakauer and M. M. Qazilbash, Phys. Rev. B, 2017, 95, 075125.
8. A. Cavalleri, T. Dekorsy, H. H. W. Chong, J. C. Kieffer and R. W. Schoenlein, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 161102.
9. T. M. Rice, H. Launois and J. P. Pouget, Phys. Rev. Lett., 1994, 73, 3042.
10. R. M. Wentzcovitch, W. W. Schulz and P. B. Allen, Phys. Rev. Lett., 1994, 72, 3389–3392.
11. M. M. Qazilbash, A. A. Schafgans, K. S. Burch, S. J. Yun, B. G. Chae, B. J. Kim, H. T. Kim and D. N. Basov, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115121.
12. J. B. Goodenough, Phys. Rev., 1960, 117, 1442–1451.
13. J. M. Booth and P. S. Casey, Phys. Rev. Lett., 2009, 103, 086402.
14. V. Eyert, Ann. Phys., 2002, 11, 650–702.
15. J. B. Goodenough, J. Solid State Chem., 1971, 3, 490–500.
16. D. Adler and H. Brooks, Phys. Rev., 1967, 155, 826–840.
17. O. Najera, M. Civelli, V. Dobrosavljevic and M. J. Rozenberg, Phys. Rev. B, 2017, 95, 035113.
18. V. Jonsson, L. Piazza, M. Månsson, J. Weissenrieder, O. Tjernberg, S. Khartsev, Y. Sassa, D. G. Mazzone, N. Gauthier, M. Muntwiler, C. S. Ong, D. Iuşan, P. Thunström and O. Eriksson, Phys. Rev. Res., 2021, 3, 033286.
19. M. W. Haverkort, Z. Hu, A. Tanaka, W. Reichelt, S. V. Streltsov, M. A. Korotin, V. I. Anisimov, H. H. Hsieh, H. J. Lin, C. T. Chen, D. I. Khomskii and L. H. Tjeng, Phys. Rev. Lett., 2005, 95, 196404.
20. W. H. Brito, M. C. O. Aguiar, K. Haule and G. Kotliar, Phys. Rev. Lett., 2016, 117, 056402.
21. D. Paquet and P. Leroux-Hugon, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 5284–5301.
22. S. Biermann, A. Poteryaev, A. I. Lichtenstein and A. Georges, Phys. Rev. Lett., 2005, 94, 026404.
23. D. Plašienka, R. Martoňák and M. C. Newton, Phys. Rev. B, 2017, 96, 054111.
24. H. T. Kim, Y. W. Lee, B. J. Kim, B. G. Chae, S. J. Yun, K. Y. Kang, K. J. Han, K. J. Yee and Y. S. Lim, Phys. Rev. Lett., 2006, 97, 266401.
25. Z. J. Li, J. J. Wu, Z. P. Hu, Y. Lin, Q. Chen, Y. Q. Guo, Y. H. Liu, Y. C. Zhao, J. Peng, W. W. Chu, C. Z. Wu and Y. Xie, Nat. Commun., 2017, 8, 1–7.
26. J. J. Feng, C. F. Li, C. L. Luo, H. Yang, A. H. Zhang, Q. Li, M. Guo, D. Gao, Z. Fan, D. Y. Chen, M. H. Qin, M. Zeng, X. S. Gao, Y. Lin, X. B. Lu and J. M. Liu, Appl. Phys. Lett., 2020, 116, 082106.
27. N. Kumar, A. Rúa, F. E. Fernández and S. Lysenko, Phys. Rev. B, 2017, 95, 235157.
28. S. M. Woodley, Chem. Phys. Lett., 2008, 453, 167–172.
29. T. Yao, X. D. Zhang, Z. H. Sun, S. J. Liu, Y. Huang, Y. Xie, C. Z. Wu, X. Yuan, W. Q. Zhang, Z. Y. Wu, G. Q. Pan, F. C. Hu, L. W. Wu, Q. H. Liu and S. Q. Wei, Phys. Rev. Lett., 2010, 105, 226405.
30. S. Chen, J. J. Liu, H. J. Luo and Y. F. Gao, J. Phys. Chem. Lett., 2015, 6, 3650–3656.
31. F. Grandi, A. Amaricci and M. Fabrizio, Phys. Rev. Res., 2020, 2, 013298.
32. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
33. Z. J. Fang and L. J. Shi, Phys. Lett. A, 2008, 372, 3759–3762.
34. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
35. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
36. K. Takanashi, H. Yasuoka, Y. Ueda and K. Kosuge, J. Phys. Soc. Jpn., 1983, 52, 3953–3959.
37. R. G. Crespo, H. Wang and U. Schwingenschlogl, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 081101.
38. X. Yuan, Y. B. Zhang, T. A. Abtew, P. H. Zhang and W. Q. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235103.
39. A. S. Belozerov, M. A. Korotin, V. I. Anisimov and A. I. Poteryaev, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045109.
40. C. Weber, D. D. ORegan, N. D. M. Hine, M. C. Payne, G. Kotliar and P. B. Littlewood, Phys. Rev. Lett., 2012, 108, 256402.
41. M. S. Laad, L. Craco and E. M. Hartmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195120.
42. W. H. Brito, M. C. O. Aguiar, K. Haule and G. Kotliar, Phys. Rev. B, 2017, 96, 195102.
43. W. R. Mondal, E. Evlyukhin, S. A. Howard, G. J. Paez, H. Paik, D. G. Schlom, L. F. J. Piper and W. C. Lee, Phys. Rev. B, 2021, 103, 214107.
44. Y. Y. Hinuma, H. Hayashi, Y. Kumagai, I. Tanaka and F. Oba, Phys. Rev. B, 2017, 96, 094102.
45. S. Kim, J. Korean Phys. Soc., 2021, 78, 613–617.
46. O. Y. Long, G. S. Gautam and E. A. Carter, Phys. Rev. Mater., 2020, 4, 045401.
47. R. Resta, Rev. Mod. Phys., 1994, 66, 899–915.
48. R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746.
49. A. Görling, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 3912–3915.
50. A. Hellman, B. Razaznejad and B. I. Lundqvist, J. Chem. Phys., 2004, 120, 4593–4602.
51. S. Baroin, S. Gironcoli, A. Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562.
52. Y. H. Wang, L. M. Yan and Y. Ma, Phys. Rev. E, 2017, 95, 063313.
53. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
54. K. Otsuka and X. Ren, Prog. Mater. Sci., 2005, 50, 511–678.
55. X. H. Luo, W. Zhou, S. V. Ushakov, A. Navrotsky and A. A. Demkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 134119.
56. F. Pintchovski, W. S. Glaunsinger and A. Navrotsky, J. Phys. Chem. Solids, 1978, 39, 941–949.
57. F. J. Morin, Phys. Rev. Lett., 1959, 3, 34–36.
58. J. Yang, H. Li, T. Wu, W. Zhang, L. D. Chen and J. H. Yang, Adv. Funct. Mater., 2008, 18, 2880–2888.
59. J. Zhang, H. Y. He, Y. Xie and B. Pan, Phys. Chem. Chem. Phys., 2013, 15, 4687–4690.
60. Z. Tao, T. R. T. Han, S. D. Mahanti, P. M. Duxbury, F. Yuan and C. Y. Ruan, Phys. Rev. Lett., 2012, 109, 166406.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04763b

---