The mechanical response and microscopic deformation mechanism of graphene foams tuned by long carbon nanotubes and short crosslinkers†
Shuai
Wang
 a,
Tian
Yang
bc,
Chao
Wang
a,
Tian
Yang
bc,
Chao
Wang
 *bc and
Lihong
Liang
*bc and
Lihong
Liang
 *a
*a
aCollege of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing, 100029, China. E-mail: lianglh@mail.buct.edu.cn
bLNM, Institute of Mechanics, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: wangchao@lnm.imech.ac.cn
cSchool of Engineering Science, University of Chinese Academy of Sciences, Beijing, 100049, China
First published on 28th November 2022
Abstract
The mechanical response of graphene foams (GrFs) can be enhanced by both short crosslinkers (e.g. C–C bond) and long carbon nanotubes (CNTs) in experiments; however, the underlying mechanism is still unclear. Here, a coarse-grained molecular dynamics method is used to study the mechanical response and microscopic mechanism of GrF interconnected by both short crosslinkers and long CNTs (named CNT bonded GrF, CbGrF) under tension and compression, and the effect of the properties of graphene and CNTs on the mechanical properties of CbGrF is also investigated. Compared with short bonds, long CNTs play a reinforcing role at a larger tensile strain, leading to larger tensile strength and toughness. Under compression, the sliding and rotation of graphene sheets in CbGrF are prevented by long CNTs, resulting in higher compressive stiffness than that of pure GrFs. Furthermore, the tensile and compressive moduli increase by more than 300% with increasing thickness of graphene sheets from 1 to 9 layers; they increase by no more than 50% as the CNT bending stiffness increases and are almost independent of the stretching stiffness of CNTs. These results should be helpful for understanding the tunability of GrFs using both short and long crosslinkers and guiding the preparation of advanced GrF-based composites.
1. Introduction
Graphene foam (GrF) material is a kind of three-dimensional (3D) nano-porous material composed of a large number of two-dimensional (2D) graphene sheets.2 Thanks to the excellent mechanical and electrical properties of graphene as well as the porous structure of foams, GrF possesses combined properties of extremely low density,3 super-elasticity,4,5 high electrical conductivity,6 thermal conductivity,7 superior energy dissipation,8etc., which enable its widespread application in energy conversion and storage,9,10 flexible electronics,11,12 supercapacitors,13 sensors,14,15 catalysis,16 and so on. However, compared to the exceptional mechanical properties of a graphene sheet with a modulus of ∼1 TPa17 and a strength of ∼130 GPa,18 the mechanical properties of GrFs are much poor due to weak connections between constituent graphene sheets,11,19,20e.g., the tensile strength is only about 5 kPa,21 tensile elongation is less than 10%,22,23 and compressive modulus is less than 100 kPa,24 which seriously limit its practical applications that require relatively high mechanical properties.One strategy for improving the mechanical properties of GrFs is to strengthen the connections of neighbor graphene sheets by short (nano- or sub-nanoscale) crosslinkers, such as carbon bonds,25 functional groups,26 and ions.27 Zhao et al.28 reported a GrF having wide temperature-invariant large-strain super-elastic behavior that persists even at a liquid helium temperature of 4 K by adding highly thermal stable covalent bonds (C–O/C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) between the sheets. Hu et al.26 produced GrF crosslinked by nitrogen functional groups and obtained a stable foam-like structure with ultralight and highly compressible mechanical properties. Wu et al.29 reported GrFs having graphene sheets covalently interconnected by oxygen-containing groups (OH, COOH, and epoxy) located at the edges of graphene sheets and obtained super compressive elasticity and a near-zero Poisson's ratio. Park et al.27 prepared an oxide graphene paper with linked graphene sheets via Mg2+ and Ca2+ ions, and obtained significantly enhanced mechanical stiffness and fracture strength.
C) between the sheets. Hu et al.26 produced GrF crosslinked by nitrogen functional groups and obtained a stable foam-like structure with ultralight and highly compressible mechanical properties. Wu et al.29 reported GrFs having graphene sheets covalently interconnected by oxygen-containing groups (OH, COOH, and epoxy) located at the edges of graphene sheets and obtained super compressive elasticity and a near-zero Poisson's ratio. Park et al.27 prepared an oxide graphene paper with linked graphene sheets via Mg2+ and Ca2+ ions, and obtained significantly enhanced mechanical stiffness and fracture strength.
The other strategy is to introduce long (from nano- to micro-scale) semi-flexible carbon nanotubes (CNTs) into GrFs to strengthen inter-sheet connections. Zhang et al.30 and Zhu et al.31 experimentally prepared GrFs with CNTs perpendicularly connected to graphene sheets by covalent bonds, and obtained a large specific surface area and efficient electrical connections in the resulting GrF/CNT materials. Kuang et al.32 fabricated a graphene/CNT composite foam with a hierarchical honeycomb-like structure, in which CNTs weave graphene sheets into a continuous structure, resulting in the superb properties of combined high specific strength, elasticity and mechanical stability. Sun et al.33 experimentally indicated that a small amount of CNTs is enough to reinforce relatively flexible graphene sheets, and the resulting GrF/CNT composites are endowed with good intrinsic elasticity. Guo et al.1 obtained a highly stretchable GrF/CNT composite with a retractable 200% elongation by bonding CNTs with graphene sheets to prevent crack propagation and brittle breakage. Vinod et al.34 pointed out that the mechanical failure of GrF/CNTs is highly related to vertical CNTs using both experiments and molecular dynamics simulations.
Both strategies can effectively improve the compressive elasticity of GrFs by introducing short or long crosslinkers between graphene sheets; comparatively speaking, the short-crosslinking strategy is more effective in improving the stiffness and strength of the composites while the long-crosslinking strategy is better at improving stretchability and tensile toughness. So, what combined properties can be obtained if both long and short-crosslinker strategies are adopted? In many GrF/CNT composites,30,31 graphene flakes are always intentionally or unintentionally connected by both short crosslinkers and long CNTs. Although the mechanical behaviors and microscopic mechanisms of pure GrFs with or without short crosslinkers have been well understood based on a series of studies by Wang et al.,35,36 Xie et al.,37 Pan et al.,38,39 and our group,40–43 we know much less about the cooperative effect of short crosslinkers and long CNTs on the microscopic mechanism and mechanical response of GrFs, as only a few theoretical/numerical studies have been carried out.
In this paper, we established a mesoscopic model of CNT-bonded graphene foam (CbGrF) and revealed the underlying mechanism by studying the two strategies of adding short bonds and long CNTs. The rest of this paper is organized as follows. First, a coarse-grained numerical model of CbGrF is established and the two typical crosslinking schemes are illustrated. Then, both tensile and compressive loads are applied to investigate the mechanical properties of tensile strength, tensile toughness, and a compressive modulus. Next, the microscopic deformation mechanism of CbGrF under tension and compression is revealed, respectively. Finally, the effect of some key structural parameters of graphene sheets and CNTs is investigated. Conclusions are given at the end of this paper.
2. Coarse-grained molecular dynamics
In coarse-grained (CG) models, groups of physical atoms are clustered into coarse grains that interact through force fields, which enables the simulation of the mesoscale physical processes while cost-effectively retaining microscale details. The two CG models of graphene sheets44,45 and CNTs46,47 are combined to describe the deformation of GrF/CNT composites, whose validity has been verified in our previous work48 on the mechanical properties of CNT-coated GrFs. The harmonic potential Ect = kct (rc − rc0)2/2 and Ecb = kcb (θc − θc0)2/2 are adopted to describe the stretching and bending deformation of CNTs, where the variable parameters rc and θc are the current bond length between two CNT beads and the current angle among three CNT beads; the constant parameters kct, rc0, kcb and θc0 are the tensile stiffness, the equilibrium bond length, the bending stiffness, and the angle of the equilibrium triplet, respectively. To characterize the stretching, bending and shearing deformation of graphene, three harmonic potential functions Egt = kgt (rg − rg0)2/2, Egb = kgb (θg − θg0)2/2, and Egs = kgs (φg − φg0)2/2 are adopted, where the variable parameters rg, θg, and φg are the current bond length, the current out-of-plane bending angle and the current in-plane shearing angle, respectively; the constant parameters kgt, rg0, kgb, θg0, kgs, and φg0 are the tensile stiffness, the equilibrium bond length, the bending stiffness, the equilibrium angle related to bending deformation, the shearing stiffness, and the equilibrium angle related to shearing deformation, respectively. The Lennard-Jones (LJ) potential functions EvdW = 4ε ((σ/r)12 − (σ/r)6) are used to depict the weak van der Waals interaction among CNT chains and graphene sheets, in which ε and σ are the energy well depth and the zero-energy distance, and r is the distance between beads of CNTs and/or graphene sheets. In addition to weak van der Waals forces, some strong chemical bonds are introduced between adjacent CNT chains, neighbor graphene sheets, and between CNT chains and graphene sheets, which are all depicted through a harmonic potential Eb = kb (rb − rb0)2/2, where kb, rb, and rb0 are the corresponding stretching stiffness, the current bond length, and the equilibrium bond length, respectively. All these parameters are taken from full atomistic calculations based on the conservation of potential energy, and the main force-field parameters of the 5-layer GrF are listed in Table 1.| Parameters | Values | Parameters | Values |
|---|---|---|---|
| r c0 (Å) | 10 | k ct (kcal mol−1 Å−2) | 1000 |
| r g0 (Å) | 25 | k gt (kcal mol−1 Å−2) | 2323 |
| θ c0 (rad) | 180 | k cb (kcal mol−1 rad−2) | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
| θ g0 (rad) | 180 | k gb (kcal mol−1 rad−2) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
| φ g0 (rad) | 90 | k gs (kcal mol−1 rad−2) | 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 350 |
| Parameters | Description | Values | Parameters | Description | Values |
|---|---|---|---|---|---|
| ε (kcal mol−1) | Gra–Gra | 473.0 | k b (kcal mol−1 Å−2) | Gra–Gra | 2323 |
| Gra–CNT | 473.0 | Gra–CNT | 2323 | ||
| CNT–CNT | 15.1 | CNT–CNT | 1000 | ||
| σ (Å) | Gra–Gra | 23.84 | r b0 (Å) | Gra–Gra | 25 |
| Gra–CNT | 23.84 | Gra–CNT | 25 | ||
| CNT–CNT | 9.35 | CNT–CNT | 10 |
A piece of CbGrF is composed of a large number of graphene sheets randomly distributed as the main skeleton, and a mass of CNT chains filled in the inter-sheet gaps and weaving graphene sheets into continuous structures. Our previous work shows that the equilibrium density41 and elastic energy density42 of pure GrF decrease with the increasing flake size. However, the influence of graphene and CNT size is complicated, especially for the relative sizes of graphene and CNTs, which will be further discussed in our future work. In this paper, we focus on the role of long CNTs and short crosslinkers in the mechanical response of GrF; therefore, a typical uniform size is used for simplicity.
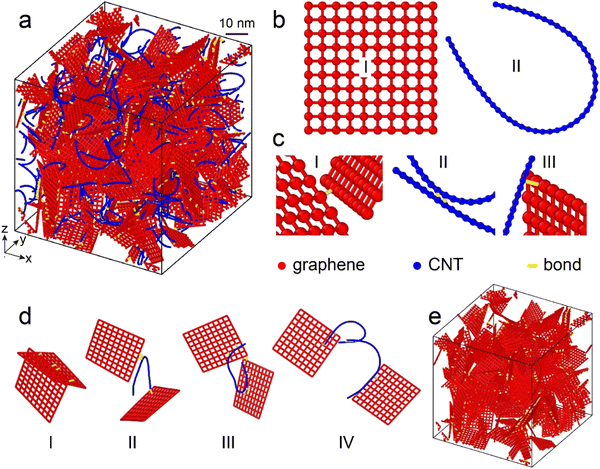
Fig. 1a gives a well-equilibrated numerical model of CbGrF having 100 square CG graphene sheets with an average side length of ∼25 nm and 125 CG CNT chains with an average length of ∼50 nm. Fig. 1b-I shows a representative CG graphene sheet with each coarse grain denoting a 5-layered graphene sheet with a side length of 2.5 nm. Correspondingly, a CNT chain color-coded by blue is shown in Fig. 1b-II, in which every CNT bead denotes a single-walled CNT with a length of 1 nm. Bond junctions may not only exist between adjacent graphene sheets28,29 and neighbor CNTs,49 but also between adjacent graphene sheets and CNT chains,50 which can be represented by the bond illustrated in Fig. 1c-I–III, respectively. Based on these three kinds of bonds, graphene sheets can be crosslinked by different types. The bond junctions between adjacent graphene sheets connect them directly, as illustrated in Fig. 1d-I, which are named short crosslinkers in this paper. The adjacent graphene sheets can be crosslinked by one CNT chain through bond junctions as depicted in Fig. 1d-II, which is named the long CNT crosslinker. Furthermore, there exist more complex crosslinker structures in the CbGrF, such as the adjacent graphene sheets crosslinked by both short bonds and long CNT crosslinkers as illustrated in Fig. 1d-III, and the graphene sheets far away from each other are crosslinked and connected by a CNT network as illustrated in Fig. 1d-IV. To distinguish the effects of short bond and long CNT crosslinkers on the microscopic mechanism and mechanical response, a numerical model of pure GrF crosslinked only by short crosslinkers is established as shown in Fig. 1e. The bonds in CNTs, graphene and crosslinks will break if their fracture strain exceeds a critical value of approximately 12%, which is comparable to the fracture strain of approximately 12–28% given in ref. 17, 44, 46. The density of the relaxed simulation model is about 460 mg cm−3 in accord with the density range of 3–950 mg cm−3 in the experiments.33,51
Periodic boundary conditions are applied in all directions during simulations; the isothermal–isobaric ensemble (NPT) technique is first adopted to relax the system to a stable state at a constant temperature of 300 K and 1 barometric pressure. After relaxation, the potential energy and volume of the system reach constant values, as shown in Fig. S1 of the ESI,† but some residual stress is still present due to the drag and extrusion of adjacent graphene and CNTs. Then, uniaxial tension and compression loads are applied in the x-direction with a strain rate of ∼107 s−1, respectively. In the meantime, the Langevin thermostat 300 K is adopted, while the Berendsen barostat 1 Pa is only adopted in the other two directions. The time step is set as 10 fs in all simulations. An open-source software Large-scale Atomic/Molecular Massively Parallel Simulator52 (LAMMPS) is used to implement all simulations, and the open-source software Ovito53 is used to illustrate the figures and movies.
3. Results and discussion
3.1 Stress–strain relationship
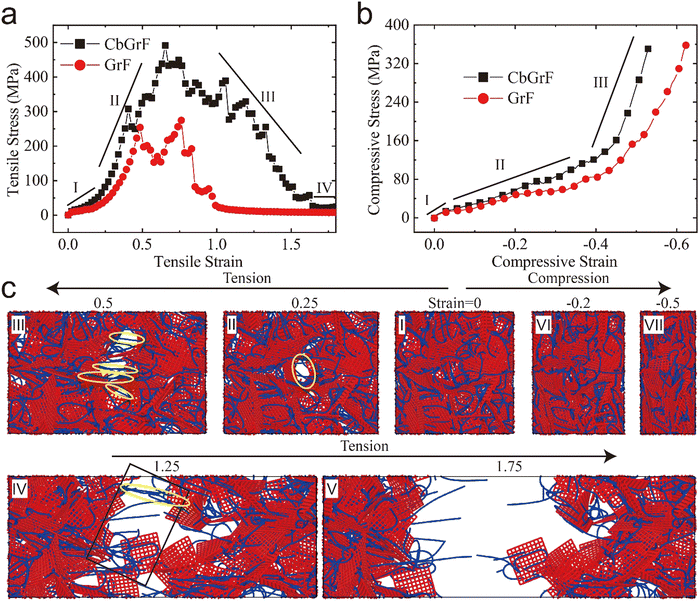
To evaluate the tensile and compressive properties of CbGrF compared to pure bonded GrF, corresponding stress–strain curves and typical snapshots are calculated and depicted in Fig. 2. Fig. 2a shows that the tensile stress–strain response of both CbGrF and GrF can be divided into 4 stages, taking CbGrF as an example, in stage I, i.e., when the tensile strain is lower than 0.25, the tensile stress increases slowly and almost linearly, at the same time, a void gradually forms due to the separation of adjacent graphene sheets and CNTs as depicted in the yellow ellipse in Fig. 2c-II. As the tensile strain increases further to about 0.75, i.e., in stage II, the tensile stress linearly increases at a larger rate, indicating a larger stiffness in this stage; in the meantime, more voids form and grow larger, and the CNTs across the void are straightened as illustrated in a yellow ellipse in Fig. 2c-III. Tensile strength is about 492 MPa, much larger than the strength of 5 kPa measured in experiment.21 This is because the density is much lower, and the defects are widespread in the experiment, while in simulation, the density is relatively larger, and perfect graphene sheets without cracks are used, and they are all woven into one continuous structure through bond and CNT crosslinkers. In the next stage when the tensile strain is larger than 0.75 but lower than 1.7, the tensile stress goes down linearly, and the voids expand to be a crack as labeled by the black rectangle in Fig. 2c-IV, in other words, the graphene skeleton is almost broken, but still connected by a few CNTs. Finally, the tensile stress–strain relationship enters into stage IV when the tensile strain surpasses 1.7, the CbGrF is completely divided into two parts as shown in Fig. 2c-V, and the corresponding stress decreases to zero. Furthermore, compared with pure GrFs, the slope of the constitutive relation of CbGrF in the first two stages is slightly larger, which means the tensile stiffness is slightly improved; comparatively speaking, the tensile strength and toughness are significantly improved as illustrated by the higher maximum tensile stress and the maximum tensile strain of CbGrF.Similarly, the rubber-like compressive stress–strain response could be divided into three stages, which is consistent with a series of ref. 33, 41, 48. To be specific, the CbGrF exhibits linear constitutive relation when the compressive strain is lower than 0.05 (stage I). Subsequently, the compressive stress increases until the corresponding strain reaches approximately 0.35 (stage II) with the slope slightly higher than that in stage I. After that, the compressive stress increases sharply in stage III. In the whole compression process, the shape of CNTs and graphene sheets almost does not change as shown in the snapshots in Fig. 2c-I, -VI, and -VII, except that adjacent graphene sheets and CNTs get closer to each other and the whole material becomes denser. Comparing the CbGrF to pure GrF, the stress of CbGrF is also slightly larger at a given compressive strain, indicating an increased compressive stiffness for the CbGrF.
The gravimetric tensile strength (1.07 GPa g−1 cm3), gravimetric tensile toughness (0.84 kJ g−1) and gravimetric compressive modulus (0.52 GPa g−1 cm3) of the CbGrF are also calculated to compare with other materials. Although it is far less than the high-performance materials54,55 or their theoretical bounds,56 but larger than a series of foam materials including GrF,41 CNT foam,57 and silica foam.58
3.2 The microscopic deformation mechanism of CbGrF under tension
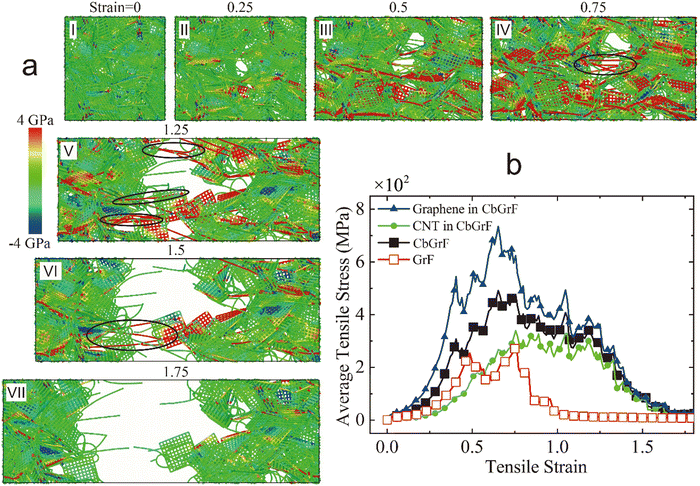
To explore the roles of CNTs and graphene sheets in the tensile properties of foam materials, the distribution of local normal stress of CbGrF is calculated and depicted in Fig. 3. In this paper, the virial stress is used to express the local stress, the detailed calculation is explained in the Methods part. Initially, when the tensile strain is 0, most of the CNT and graphene beads are colored green in Fig. 3a-I, and the red and blue beads are rarely observed, indicating that the local stress in CbGrF is approximately uniform and almost negligible. As the tensile strain gradually increases to about 0.75, there is a significant increase in the number of red beads (as shown in Fig. 3a-II–IV), which means more and more CNT chains and graphene sheets are bearing tensile loads. Moreover, the tensile stress reaches the maximum under a tensile strain of about 0.75 as indicated by the more red area observed in Fig. 3a-IV, which is exactly consistent with the tensile stress–strain curves in Fig. 2a. After that, the tensile stress of the CbGrF decreases with the tensile strain as shown by the decreased number of red beads in Fig. 3a-V and VI. Eventually, as the tensile strain increases to about 1.75, the CbGrF breaks and most of the red areas vanished because the tensile stress is reduced to zero.Further observation shows that the local stress distribution in CNTs and graphene sheets is related to the tensile strain and the formation of voids. Under a relatively small tensile strain of less than 0.75, as shown in Fig. 3a-II–IV, the increasing red areas are mostly located on graphene beads, which indicates that graphene sheets bear the main tensile loading under a small strain. In the meantime, voids form during the separation of adjacent graphene sheets, but the separated graphene sheets are still connected by several straightened CNTs which are colored red as labeled in the black ellipse in Fig. 3a-IV, which clearly shows that the CNTs near the void also bear tensile loads to inhibit the fracture of the CbGrF. As the tensile strain increases further to 1.25 and 1.5 as shown in Fig. 3a-V and VI, although the total number of red beads is significantly decreased, the proportion of red CNT beads bearing tensile loads and locating near the void as labeled in the black ellipse in Fig. 3a-V and VI seems increased. When the tensile strain finally increases to 1.75 as shown in Fig. 3a-VII, the number of red beads on CNT is also decreased, the CbGrF breaks into two parts and the local stress in it gradually dissipates.
To quantitatively characterize the stress distribution, the average stress of all CNT beads and all graphene beads in CbGrF are calculated and depicted in Fig. 3b. The average stress is the statistical average of the local stress, whose calculation method can be found in the Methods part. The overall tensile stress–strain curves of both CbGrF and pure GrF are also given in Fig. 3b for comparison. It shows that both the average stress values of graphene sheets and CNTs in CbGrF increase as the tensile strain increases to 0.75, and the average stress value in graphene sheets is larger than that in CNTs, indicating that graphene sheets act as the skeleton to bear the main tensile load at a lower strain. However, as the strain further increases, the average stress value in graphene sheets decreases sharply, while the average stress value in CNTs increases further and remains at a higher value, which begins to decrease when the strain exceeds 1.2. The reduction of the stress in graphene sheets is consistent with the formation of voids as shown in Fig. 3a-IV and V, and graphene sheets are not loaded anymore as crack forms. Nonetheless, the gradually separated graphene sheets are still connected by CNTs, and their separation would cause the straightening of the CNTs and lead to the increase of the stress in CNTs. Finally, both average stresses reach a close value and decrease gradually with an increasing strain, which indicates that graphene sheets and CNTs bear the whole tensile loads approximately equally.
Moreover, the stress value of pure GrF stops increasing after the strain increases to about 0.5, while the average stress of CNTs and graphene sheets in CbGrF keeps increasing until a larger tensile strain of 0.75, resulting in a higher tensile strength and toughness of CbGrF than that of pure GrF.
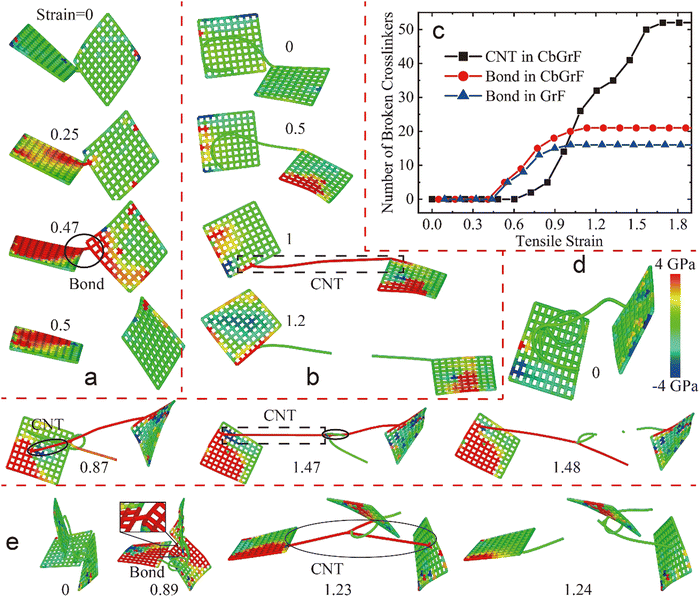
The adjacent graphene sheets in CbGrF can be crosslinked by both short bonds and long CNT crosslinkers. The corresponding breaking processes are illustrated in Fig. 4a and b. As shown in Fig. 4a, short bond crosslinked graphene sheets bear almost no stress initially. However, as the strain increases to about 0.25, the separation of two connected graphene sheets due to the applied tensile load is prevented by the short crosslinker, as a result, the tensile stress on it increases, and reaches its maximum under a strain of about 0.47. Whereafter, the short crosslinker breaks and the corresponding stress decreases. Similarly, the stress on the two adjacent graphene sheets crosslinked by a long CNT crosslinker is also negligible initially as shown in Fig. 4b, and the stress does not increase significantly even when the strain exceeds 0.5. This is because the originally crimped CNTs are gradually straightened until the strain of CbGrF reaches 1 and the stress on the CNTs reaches its maximum. Then, the CNT crosslinker breaks as the tensile strain reaches 1.2, which is much larger than the maximum tensile strain of 0.47 at which a short crosslinker breaks.
The number of both short broken crosslinkers and long CNT crosslinkers as a function of strain is further calculated and illustrated in Fig. 4c. It shows that no crosslinker breaks if the tensile strain of both pure GrF and CbGrF is less than 0.45, then the short crosslinkers in pure GrF and CbGrF start to break first until the strain reaches ∼1.2, which is qualitatively consistent with the results of pure GrF in ref. 40 that short crosslinkers do not break at a small strain but the number of broken bonds begins to increase as the strain increases further. In contrast, the CNT crosslinkers break in a strain range of 0.6 to 1.65, indicating that the CNT crosslinkers work in a larger strain and a wider strain range. This trend is also consistent with the average tensile stress of graphene sheets and CNTs in CbGrF, shown in Fig. 3b, the short crosslinkers break under small strains, causing separation of the graphene sheets and reduction in average tensile stress on graphene sheets when the strain exceeds 0.75. While CNT crosslinkers will break at a larger strain, so that the CNTs can bear loading at a larger strain, thus, the average stress on CNTs in CbGrF begins to decrease when the strain exceeds a larger strain of 1.2. Compared to pure GrF, the CbGrF can be enhanced in the whole tension process by CNT crosslinkers. At a small strain, the CNTs are gradually straightened due to the separation of graphene sheets; in this process, they can slightly prevent the separation of adjacent graphene sheets, which leads to a slight increase in the stiffness of CbGrF compared to pure GrFs. At a larger strain, the fully straightened CNTs strongly restrict the separation of graphene sheets before they completely break, which greatly improves the strength and toughness of CbGrF.
The adjacent graphene sheets in real materials may be crosslinked by several CNTs or by both short and long CNT crosslinkers.32,50 Typical snapshots of adjacent graphene sheets crosslinked by several CNTs are illustrated in Fig. 4d, in which the CNT in the black circle has been straightened at a strain of 0.87. As the tensile strain of CbGrF increases to 1.47, the CNT in the circle breaks, but the graphene sheets are still crosslinked by the newly straightened CNT in the dotted rectangle, which breaks at a much larger strain of 1.48. Another type of combined crosslink of a bond and several CNTs is shown in Fig. 4e. The short crosslinker is completely straightened and is about to break at a strain of 0.89; after it breaks, the graphene sheets are still connected by the gradually straightened CNT crosslinker labeled in the black ellipse at a strain of 1.23. Such multilevel crosslinkers connect adjacent graphene sheets into a continuous structure and limit the separation of graphene sheets in a larger strain range, which further increases the toughness of the composite foam.
3.3 The microscopic deformation mechanism of CbGrF under compression
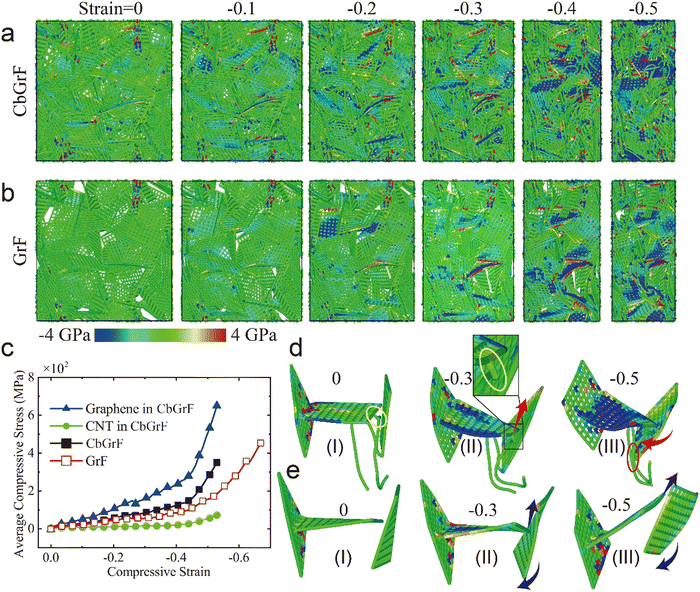
The local normal stress distribution and microscopic deformation mechanism of CbGrF and pure bonded GrF under compression are also investigated. Three characteristics of stress distribution can be identified by comparing Fig. 5a and b. First, the local compressive stress in both CbGrF and pure GrF increases with increasing compressive strain as more compressive beads color-coded by blue emerge in both systems, which is also consistent with the compressive stress–strain curves shown in Fig. 2b. Second, graphene sheets act as the main skeleton to bear the main compressive loads during compression because larger local compressive stress mainly emerges in graphene sheets. Third, comparing the areas of regions with the compressive state (color-coded by blue) in Fig. 5a and b, the compressive stress in CbGrF is slightly larger than that in pure GrF.To further quantitatively compare the value of the compressive stress in CbGrF and pure GrF, the average compressive stress as a function of the compressive strain is calculated and illustrated in Fig. 5c. It shows that the average compressive stress on graphene sheets in CbGrF is much larger than that in CNTs, and both of them increase with increasing compressive strain, which quantitatively illustrates that graphene sheets act as the main skeleton bearing the compressive load. Moreover, although the average compressive stress in CNTs is negligible, the average compressive stress in graphene sheets of CbGrF is much larger than that in pure bonded GrF, which indicates that the introduction of CNTs increases the capacity of graphene sheets to bear compressive loads and leads to increased stiffness of CbGrF. To explore the underlying mechanism, the microscopic deformation of representative local structures in CbGrF and pure GrF is extracted and shown in Fig. 5d and e, respectively. As shown in Fig. 5d-I, a horizontal graphene sheet is initially sandwiched between two vertical ones, and several CNTs are in contact and crosslinked to the bottom of the horizontal graphene sheet (labeled in the yellow ellipse). As the compressive strain increases to −0.3 as shown in Fig. 5d-II, the middle graphene sheet is apt to slide up along the red arrow, but is prevented by the CNT underneath as labeled in the yellow ellipse. As a result, the middle graphene sheet delivers the compressive loads to the two vertical sheets. When the compressive strain increases to −0.5, the graphene sheet on the right tends to rotate along the red arrow, but is still prevented by the CNTs labeled in the red ellipse; as a result, the stress on the middle graphene sheet increases further. However, if there is no restriction from CNTs in pure GrF as shown in Fig. 5e, the graphene in the middle and on the right can slide and rotate freely along the two blue arrows, respectively, and the stress can be released eventually at a strain of −0.5. So, the introduced CNT prevents the graphene sheets from sliding and rotating in CbGrF, which leads to an increased compressive modulus.
3.4 The effect of graphene and CNT properties
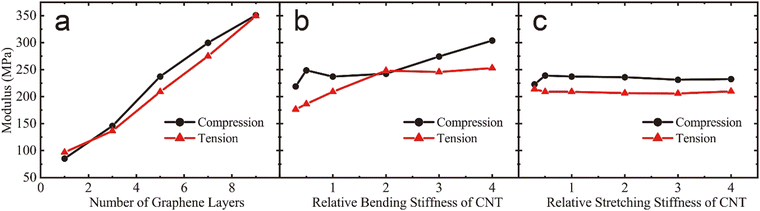
The chirality of CNTs59 and the thickness of graphene60 in practical materials are significantly different, to understand their contributions to the tensile and compressive modulus of CbGrF, the effects of graphene layers’ number, the bending stiffness and stretching stiffness of CNTs are further studied. As described above in Fig. 2, both compressive and tensile stress of CbGrF increase almost linearly in stage I, so, the compressive and tensile moduli can be obtained by calculating the slope of the initial linear part in the corresponding stress–strain curves. As shown in Fig. 6a, both tensile and compressive modulus increase from ∼100 MPa to ∼350 MPa as the number of graphene layers increases from 1 to 9, which is qualitatively consistent with our previous results on pure GrF that the elastic energy density increases with the graphene thickness under both tension and compression.40 In contrast, the effect of CNTs seems limited. As shown in Fig. 6b and c, the tensile and compressive moduli have a slight increase of no more than 50% with an increased bending stiffness of CNTs, but almost remains constant with an increased stretching stiffness of CNTs. These results further show that graphene sheets act as the skeleton of CbGrF, which is consistent with that found in Fig. 3b and 5c. As discussed in Fig. 3–5, the CNTs have not been fully straightened under a relatively small compressive and tensile strain (in stage I), so, the bending stiffness of CNTs slightly affects the modulus of CbGrF, while the stretching stiffness has negligible effect.4. Conclusions
In this paper, a coarse-grained molecular dynamics method is used to investigate the microscopic deformation mechanism of CbGrF under tension and compression. Compared to pure bonded GrFs, CbGrF has higher tensile stiffness, tensile strength, tensile toughness, and compressive stiffness. The graphene sheets in pure bonded GrFs are only crosslinked by short bond crosslinkers, while graphene sheets in CbGrF are connected by both short bond and long CNT crosslinkers. Under a smaller tensile strain, the deformation of long CNT crosslinkers slightly prevents the separation of graphene sheets and thus slightly enhances the stiffness of CbGrF; under a larger tensile strain, the CNT crosslinkers strongly restrict the separation of graphene sheets until they completely break, and thus improve the strength and toughness of CbGrF. When CbGrF is subjected to compressive loading, the CNT crosslinkers prevent the graphene sheets from sliding and rotating, and thus slightly increase its compressive stiffness. The effect of the intrinsic properties of CNTs and graphene sheets is further studied, and it is found that the tensile and compressive moduli of CbGrF increase significantly with the graphene thickness and increase slightly with the CNT bending stiffness, but are almost independent of the stretching stiffness of CNTs. The results in this paper deepen the understanding of the effect of short and long crosslinkers on the mechanical response and microscopic mechanisms of GrFs and provide scientific guidance for the design and application of GrF-based composites.5. Methods
5.1 The local stress
On the micro/mesoscale, the virial stress is viewed as a measure of the local stress; the virial stress on the atom i can be achieved according to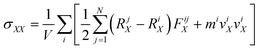 , in which V is the volume of one atom, and RαX and RβX denote the positions of atoms α and β in the x-axis. FαβX is the force acting on atom i induced by atom j in the X direction, mi is the mass of atoms i, viX is the velocity of atom i in the x-axis, and V is the volume of atoms i.
, in which V is the volume of one atom, and RαX and RβX denote the positions of atoms α and β in the x-axis. FαβX is the force acting on atom i induced by atom j in the X direction, mi is the mass of atoms i, viX is the velocity of atom i in the x-axis, and V is the volume of atoms i.
5.2 The average stress
The average stress is the statistical average of the local stress. Suppose the volume that the graphene bead i in CbGrF occupies is a cube with volume VG,i = LG,i3 = LG,i3, where LG,i is the side length of the cube. The axial force on graphene bead i in the loading direction can be calculated as fG,i = σG,iLG,i2, where σG,i is the normal virial stress of the graphene bead i in the loading direction. And the average stress of graphene in CbGrF is calculated as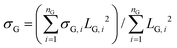 , where nG is the number of graphene beads in CbGrF. When the stress is greater than 0, it is the average tensile stress, otherwise, it is the average compressive stress. Similarly, the average stress of CNT in CbGrF is
, where nG is the number of graphene beads in CbGrF. When the stress is greater than 0, it is the average tensile stress, otherwise, it is the average compressive stress. Similarly, the average stress of CNT in CbGrF is 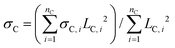 .
.
5.3 The bond junctions
If two graphene beads belong to different graphene sheets, the distance between them is less than 2.8 nm, and neither of them has formed a bond junction with any other beads, the bond junction between these two graphene beads will be created. In this way, plenty of bond junctions are created between adjacent graphene sheets, between neighbor CNTs, and between adjacent graphene sheets and CNT chains.Author contributions
Shuai Wang: investigation, methodology, software, data curation, formal analysis, and writing—original draft. Tian Yang: methodology, data curation, and writing—original draft. Chao Wang: conceptualization, formal analysis, supervision, funding acquisition, and writing—review & editing. Lihong Liang: supervision, funding acquisition, and writing—review & editing.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China through Grants # 12002034, # 11972348, # 12172035, and # 92160203, the Strategic Priority Research Program of the Chinese Academy of Sciences (Grants No. XDB22040503) and the Fundamental Research Funds for the Central Universities of China (buctrc201930).References
- F. Guo, Y. Jiang, Z. Xu, Y. Xiao, B. Fang, Y. Liu, W. Gao, P. Zhao, H. Wang and C. Gao, Highly stretchable carbon aerogels, Nat. Commun., 2018, 9, 881 Search PubMed.
- K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Two-dimensional atomic crystals, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef CAS PubMed.
- L. Qiu, B. Huang, Z. He, Y. Wang, Z. Tian, J. Z. Liu, K. Wang, J. Song, T. R. Gengenbach and D. Li, Extremely Low Density and Super-Compressible Graphene Cellular Materials, Adv. Mater., 2017, 29, 1701553 Search PubMed.
- Y. C. Wang, Y. B. Zhu, F. C. Wang, X. Y. Liu and H. A. Wu, Super-elasticity and deformation mechanism of three-dimensional pillared graphene network structures, Carbon, 2017, 118, 588–596 Search PubMed.
- X. Xu, Q. Zhang, Y. Yu, W. Chen, H. Hu and H. Li, Naturally Dried Graphene Aerogels with Superelasticity and Tunable Poisson's Ratio, Adv. Mater., 2016, 28, 9223–9230 CrossRef CAS PubMed.
- M. a Worsley, P. J. Pauzauskie, T. Y. Olson, J. Biener, J. H. Satcher and T. F. Baumann, Synthesis of Graphene Aerogel with High Electrical Conductivity, J. Am. Chem. Soc., 2010, 132, 14067–14069 CrossRef CAS PubMed.
- C. Zhang, R. Huang, P. Wang, Y. Wang, Z. Zhou, H. Zhang, Z. Wu and L. Li, Highly Compressible, Thermally Conductive, yet Electrically Insulating Fluorinated Graphene Aerogel, ACS Appl. Mater. Interfaces, 2020, 12, 58170–58178 CrossRef CAS PubMed.
- P. Nautiyal, B. Boesl and A. Agarwal, The mechanics of energy dissipation in a three-dimensional graphene foam with macroporous architecture, Carbon, 2018, 132, 59–64 CrossRef CAS.
- Y. Wu, J. Zhu and L. Huang, A review of three-dimensional graphene-based materials: Synthesis and applications to energy conversion/storage and environment, Carbon, 2019, 143, 610–640 CrossRef CAS.
- S. Han, D. Wu, S. Li, F. Zhang and X. Feng, Porous graphene materials for advanced electrochemical energy storage and conversion devices, Adv. Mater., 2014, 26, 849–864 CrossRef CAS PubMed.
- S. P. Patil, V. G. Parale, H.-H. Park and B. Markert, Mechanical modeling and simulation of aerogels: A review, Ceram. Int., 2021, 47, 2981–2998 CrossRef CAS.
- Y. Yuan, W. Yin, M. Yang, F. Xu, X. Zhao, J. Li, Q. Peng, X. He, S. Du and Y. Li, Lightweight, flexible and strong core-shell non-woven fabrics covered by reduced graphene oxide for high-performance electromagnetic interference shielding, Carbon, 2018, 130, 59–68 CrossRef CAS.
- Z. Yang, J. Tian, Z. Yin, C. Cui, W. Qian and F. Wei, Carbon nanotube- and graphene-based nanomaterials and applications in high-voltage supercapacitor: A review, Carbon, 2019, 141, 467–480 CrossRef CAS.
- K. Senthil Kumar, P.-Y. Chen and H. Ren, A Review of Printable Flexible and Stretchable Tactile Sensors, Research, 2019, 2019, 1–32 CrossRef PubMed.
- J. Ma, P. Wang, H. Chen, S. Bao, W. Chen and H. Lu, Highly Sensitive and Large-Range Strain Sensor with a Self-Compensated Two-Order Structure for Human Motion Detection, ACS Appl. Mater. Interfaces, 2019, 11, 8527–8536 Search PubMed.
- B. Qiu, M. Xing and J. Zhang, Recent advances in three-dimensional graphene based materials for catalysis applications, Chem. Soc. Rev., 2018, 47, 2165–2216 RSC.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- R. Grantab, V. B. Shenoy and R. S. Ruoff, Anomalous Strength Characteristics of Tilt Grain Boundaries in Graphene, Science, 2010, 330, 946–948 Search PubMed.
- I. K. Moon, S. Yoon, K.-Y. Chun and J. Oh, Highly Elastic and Conductive N-Doped Monolithic Graphene Aerogels for Multifunctional Applications, Adv. Funct. Mater., 2015, 25, 6976–6984 CrossRef CAS.
- G. Gorgolis and C. Galiotis, Graphene aerogels: a review, 2D Mater., 2017, 4, 032001 CrossRef.
- A. Nieto, B. Boesl and A. Agarwal, Multi-scale intrinsic deformation mechanisms of 3D graphene foam, Carbon, 2015, 85, 299–308 Search PubMed.
- M. Li, X. Zhang, X. Wang, Y. Ru and J. Qiao, Ultrastrong Graphene-Based Fibers with Increased Elongation, Nano Lett., 2016, 16, 6511–6515 Search PubMed.
- H. Wang, X. Yuan, G. Zeng, Y. Wu, Y. Liu, Q. Jiang and S. Gu, Three dimensional graphene based materials: Synthesis and applications from energy storage and conversion to electrochemical sensor and environmental remediation, Adv. Colloid Interface Sci., 2015, 221, 41–59 CrossRef CAS PubMed.
- Y. Lin, F. Liu, G. Casano, R. Bhavsar, I. A. Kinloch and B. Derby, Pristine Graphene Aerogels by Room-Temperature Freeze Gelation, Adv. Mater., 2016, 28, 7993–8000 Search PubMed.
- F. Meng, C. Chen, D. Hu and J. Song, Deformation behaviors of three-dimensional graphene honeycombs under out-of-plane compression: Atomistic simulations and predictive modeling, J. Mech. Phys. Solids, 2017, 109, 241–251 Search PubMed.
- H. Hu, Z. Zhao, W. Wan, Y. Gogotsi and J. Qiu, Ultralight and highly compressible graphene aerogels, Adv. Mater., 2013, 25, 2219–2223 CrossRef CAS PubMed.
- S. Park, K.-S. Lee, G. Bozoklu, W. Cai, S. T. Nguyen and R. S. Ruoff, Graphene Oxide Papers Modified by Divalent Ions—Enhancing Mechanical Properties via Chemical Cross-Linking, ACS Nano, 2008, 2, 572–578 CrossRef CAS PubMed.
- K. Zhao, T. Zhang, H. Chang, Y. Yang, P. Xiao, H. Zhang, C. Li, C. S. Tiwary, P. M. Ajayan and Y. Chen, Super-elasticity of three-dimensionally cross-linked graphene materials all the way to deep cryogenic temperatures, Sci. Adv., 2019, 5, eaav2589 CrossRef CAS PubMed.
- Y. Wu, N. Yi, L. Huang, T. Zhang, S. Fang, H. Chang, N. Li, J. Oh, J. A. Lee, M. Kozlov, A. C. Chipara, H. Terrones, P. Xiao, G. Long, Y. Huang, F. Zhang, L. Zhang, X. Lepró, C. Haines, M. D. Lima, N. P. Lopez, L. P. Rajukumar, A. L. Elias, S. Feng, S. J. Kim, N. T. Narayanan, P. M. Ajayan, M. Terrones, A. Aliev, P. Chu, Z. Zhang, R. H. Baughman and Y. Chen, Three-dimensionally bonded spongy graphene material with super compressive elasticity and near-zero Poisson's ratio, Nat. Commun., 2015, 6, 6141 CrossRef CAS PubMed.
- W. Zhang, H. Xie, R. Zhang, M. Jian, C. Wang, Q. Zheng, F. Wei and Y. Zhang, Synthesis of three-dimensional carbon nanotube/graphene hybrid materials by a two-step chemical vapor deposition process, Carbon, 2015, 86, 358–362 CrossRef CAS.
- Y. Zhu, L. Li, C. Zhang, G. Casillas, Z. Sun, Z. Yan, G. Ruan, Z. Peng, A.-R. O. Raji, C. Kittrell, R. H. Hauge and J. M. Tour, A seamless three-dimensional carbon nanotube graphene hybrid material, Nat. Commun., 2012, 3, 1–7 Search PubMed.
- J. Kuang, Z. Dai, L. Liu, Z. Yang, M. Jin and Z. Zhang, Synergistic effects from graphene and carbon nanotubes endow ordered hierarchical structure foams with a combination of compressibility, super-elasticity and stability and potential application as pressure sensors, Nanoscale, 2015, 7, 9252–9260 RSC.
- H. Sun, Z. Xu and C. Gao, Multifunctional, ultra-flyweight, synergistically assembled carbon aerogels, Adv. Mater., 2013, 25, 2554–2560 Search PubMed.
- S. Vinod, C. S. Tiwary, L. D. Machado, S. Ozden, R. Vajtai, D. S. Galvao and P. M. Ajayan, Synthesis of ultralow density 3D graphene–CNT foams using a two-step method, Nanoscale, 2016, 8, 15857–15863 RSC.
- Y. Wang, Y. Zhu and H. Wu, Porous Characteristics of Three-Dimensional Disordered Graphene Networks, Crystals, 2021, 11, 127 Search PubMed.
- Y. Wang, Y. Zhu and H. Wu, Formation and topological structure of three-dimensional disordered graphene networks, Phys. Chem. Chem. Phys., 2021, 23, 10290–10302 RSC.
- W. Xie and Y. Wei, Roughening for Strengthening and Toughening in Monolayer Carbon Based Composites, Nano Lett., 2021, 21, 4823–4829 CrossRef CAS PubMed.
- D. Pan, C. Wang and X. Wang, Graphene Foam: Hole-Flake Network for Uniaxial Supercompression and Recovery Behavior, ACS Nano, 2018, 12, 11491–11502 CrossRef CAS PubMed.
- D. Pan, C. Wang, T.-C. Wang and Y. Yao, Graphene foam: Uniaxial tension behavior and fracture mode based on a mesoscopic model, ACS Nano, 2017, 11, 8988–8997 Search PubMed.
- C. Wang, C. Zhang and S. Chen, Micro-mechanism and influencing factors of graphene foam elasticity, Carbon, 2019, 148, 267–276 CrossRef CAS.
- C. Wang, C. Zhang and S. Chen, The microscopic deformation mechanism of 3D graphene foam materials under uniaxial compression, Carbon, 2016, 109, 666–672 CrossRef CAS.
- C. Wang, D. Pan and S. Chen, Energy dissipative mechanism of graphene foam materials, Carbon, 2018, 132, 641–650 CrossRef CAS.
- T. Yang, C. Wang and Z. Wu, Strain Hardening in Graphene Foams under Shear, ACS Omega, 2021, 6, 22780–22790 CrossRef CAS PubMed.
- S. Cranford and M. J. Buehler, Twisted and coiled ultralong multilayer graphene ribbons, Modell. Simul. Mater. Sci. Eng., 2011, 19, 054003 CrossRef.
- S. Cranford and M. J. Buehler, Twisted and coiled ultralong multilayer graphene ribbons, Modell. Simul. Mater. Sci. Eng., 2011, 19, 054003 CrossRef.
- M. J. Buehler, Mesoscale modeling of mechanics of carbon nanotubes: self-assembly, self-folding, and fracture, J. Mater. Res., 2006, 21, 2855–2869 CrossRef CAS.
- S. Cranford, H. Yao, C. Ortiz and M. J. Buehler, A single degree of freedom ‘lollipop’ model for carbon nanotube bundle formation, J. Mech. Phys. Solids, 2010, 58, 409–427 CrossRef CAS.
- S. Wang, C. Wang, M. B. Khan and S. Chen, Microscopic deformation mechanism and main influencing factors of carbon nanotube coated graphene foams under uniaxial compression, Nanotechnology, 2021, 32, 345704 CrossRef CAS PubMed.
- Z. Dai, L. Liu, X. Qi, J. Kuang, Y. Wei, H. Zhu and Z. Zhang, Three-dimensional Sponges with Super Mechanical Stability: Harnessing True Elasticity of Individual Carbon Nanotubes in Macroscopic Architectures, Sci. Rep., 2016, 6, 18930 CrossRef CAS PubMed.
- S. Kabiri, D. N. H. Tran, T. Altalhi and D. Losic, Outstanding adsorption performance of graphene–carbon nanotube aerogels for continuous oil removal, Carbon, 2014, 80, 523–533 CrossRef CAS.
- Z. Ma, A. Wei, J. Ma, L. Shao, H. Jiang, D. Dong, Z. Ji, Q. Wang and S. Kang, Lightweight, compressible and electrically conductive polyurethane sponges coated with synergistic multiwalled carbon nanotubes and graphene for piezoresistive sensors, Nanoscale, 2018, 10, 7116–7126 Search PubMed.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1993, 117, 1–19 CrossRef.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 Search PubMed.
- E. Gao, R. Li and R. H. Baughman, Predicted Confinement-Enhanced Stability and Extraordinary Mechanical Properties for Carbon Nanotube Wrapped Chains of Linear Carbon, ACS Nano, 2020, 14, 17071–17079 Search PubMed.
- E. Gao, Y. Guo, Z. Wang, S. O. Nielsen and R. H. Baughman, The strongest and toughest predicted materials: Linear atomic chains without a Peierls instability, Matter, 2022, 5, 1192–1203 CrossRef CAS.
- E. Gao, X. Yuan, S. O. Nielsen and R. H. Baughman, Exploring the Bounds on the Young's Modulus and Gravimetric Young's Modulus, Phys. Rev. Appl., 2022, 18, 014044 Search PubMed.
- C. Wang, L. Wang and Z. Xu, Enhanced mechanical properties of carbon nanotube networks by mobile and discrete binders, Carbon, 2013, 64, 237–244 CrossRef CAS.
- S. P. Patil, A. Rege, Sagardas, M. Itskov and B. Markert, Mechanics of Nanostructured Porous Silica Aerogel Resulting from Molecular Dynamics Simulations, J. Phys. Chem. B, 2017, 121, 5660–5668 Search PubMed.
- J.-J. Shao, W. Lv, Q. Guo, C. Zhang, Q. Xu, Q.-H. Yang and F. Kang, Hybridization of graphene oxide and carbon nanotubes at the liquid/air interface, Chem. Commun., 2012, 48, 3706–3708 RSC.
- K. H. Kim, Y. Oh and M. F. Islam, Graphene coating makes carbon nanotube aerogels superelastic and resistant to fatigue, Nat. Nanotechnol., 2012, 7, 562–566 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04221e |
| This journal is © the Owner Societies 2023 |