Relationship between the electron-transfer coefficients of the oxygen reduction reaction estimated from the Gibbs free energy of activation and the Butler–Volmer equation†
Rajan
Maurya
 ,
Rubul
Das
,
Rubul
Das
 ,
Anand Kumar
Tripathi
,
Anand Kumar
Tripathi
 and
Manoj
Neergat
and
Manoj
Neergat
 *
*
Department of Energy Science and Engineering, Indian Institute of Technology Bombay (IITB), Powai, Mumbai-400076, India. E-mail: nmanoj@iitb.ac.in; Fax: +91 22 2276 4890; Tel: +91 22 2576 7893
First published on 28th November 2022
Abstract
The rate of electron-transfer reactions, irrespective of whether electrochemical or electrocatalytic, is universally explained on the basis of Butler–Volmer (B–V) theory. The charge-transfer coefficient (α) obtained is typically in the range of 0.0–1.0, and is 0.6 ± 0.1 for the oxygen reduction reaction (ORR) on Pt, which is the subject of the present investigation. Alternatively, α can be estimated from the derivative of the change in Gibbs free energy of activation (ΔG#) with respect to the overpotential (η) and has the unreasonably high value of 1.1 ± 0.2. The origin of the difference in the α values obtained from these two methods is investigated. The value of α greater than 1.0 stems from the alternative potential-dependent lower energy barrier path for the formation of the activated complex, offered by the electrified catalyst surface. For the electrocatalytic reaction, the α value derived from the ΔG# is the true kinetic parameter. The theoretical background of such processes is presented to justify our claims.
1. Introduction
The electrocatalysis of redox reactions that are relevant to fuel cells, electrolyzers, metal–air batteries, and flow batteries has been reported widely in the literature.1–10 Recently, the electrochemical reduction of CO2 for the synthesis of fuels and towards reducing global warming has also gained significant research momentum.11,12 The development of cost-effective electrocatalysts with improved catalytic activity and durability has dominated the domain of electrocatalysis in the past few decades. Notable among these are the development of high surface area precious-metal-based catalysts (PMCs)7,13–18 non-precious metal catalysts (NPMCs),4,8,19,20 and metal-free carbon-based catalysts.20–23 Over the years, the descriptor of catalytic activity has evolved from the area-specific activity (mA cm−2) and the mass-specific activity (mA g−1) to the turnover frequency (ToF) at a specific potential.2,24 To estimate the area-specific activity or ToF, an accurate measure of the electrochemical active surface area (ESA) or the active site density is required. For PMCs (Pt and Pd), the hydrogen underpotential deposition (Hupd) and CO/Cu stripping are reported in the literature for estimation of the ESA.25–28 Once the electrode is conditioned/activated, the number of active sites remains unchanged under the usual time scale of characterization. With NPMCs, measurement of the active site density for estimation of the ToF is contentious, and several methods have been proposed although no consensus has yet been reached.21,29,30 With metal-free catalysts, which are primarily based on carbon and doped-carbon, the catalytic activity is reported to improve upon thermal, chemical, and electrochemical treatment.31–33 Such treatments generate hydrophilic functional groups on the catalyst surface, thus enhancing the activity. The overall effect is to increase the wettability of the electrode and expose more active sites to the redox species.34 At times, however, degradation of the electrode material, and precipitation of the adsorbing species can impede the reaction rates.35The electrochemical reaction rate is usually explained using Butler–Volmer (B–V) theory, the Tafel equation at high overpotentials (η), and the Arrhenius equation.36–38 Our understanding of correction of the kinetic current for the surface coverage (θ), interaction parameters, and free energy of adsorption has improved over time.13,39–43 Usually, the catalytic activity is characterized in terms of the exchange current density (i0), the Tafel slope/charge-transfer coefficient (α), and the apparent enthalpy of activation (ΔH#) at a specific potential.44–50 Recently, Choudhury et al. estimated the α from Arrhenius analysis for the hydrogen evolution reaction (HER) on a MoS2 catalyst surface, and the values were within the range of 0.0–1.0, as predicted by B–V theory.51 Tripathi et al. reported an increasing trend in the ΔH# with η, as well as surprisingly high enthalpic charge-transfer coefficient (αH) values (of ∼3) for the V5+/V4+ reaction on a carbon surface. This deviation in the αH value was attributed to blocking of the active sites on the electrode surface by precipitates and/or adsorbates.35
In the present investigation, our primary interest is to test the η dependence of ΔH# for the oxygen reduction reaction (ORR) so that αH can be estimated from ∂ΔH#/∂η. The α values estimated from the Tafel slope are different, and the origin of such difference is investigated and a theoretical background is provided. For an electrochemical reaction, the applied η changes the free energy of the reactant/electrons, and this change in ΔH# is reflected as an increase in the kinetic current (ik) in the B–V equation. For an electrocatalytic reaction, the enthalpy of formation of the activated complex (H#) and ΔH# of the activated complex are also altered with η since the electrode surface offers an alternative lower energy barrier path for the electron-transfer reaction. Thus, α is derived from the change in the apparent Gibbs free energy (ΔG#) of the activated complex, and it captures the true energetics of electrocatalytic reactions on an electrode surface.
2. Experimental details
2.1. Materials
Platinum black powder (HiSPEC® 1000) used for preparation of the catalyst ink was procured from Alfa Aesar. Perchloric acid (70 volume% with stated purity 98%) was purchased from Merck. The supporting electrolyte, 0.1 M HClO4, was prepared using de-ionised (DI) water obtained from Millipore Direct-Q3 (18.2 M Ohm cm, TOC ≈ 56 ppm). High purity (99.9999%) argon (Ar) and oxygen (O2) gases were procured from Medgas N Equipments India Ltd.2.2. Electrochemical characterization
All the electrochemical experiments were conducted using a standard water jacketed three-electrode system with a “Wave driver 200” Bi-potentiostat (from Pine Instrument USA). A Pt-black coated glassy carbon rotating ring disk electrode (RRDE) (disk geometric area: 0.196 cm2, ring area: 0.44 cm2 and collection efficiency: 0.25) was the working electrode. The Pt ink was prepared using the method reported by Neergat et al.52 As per the procedure, 5 mg of Pt black was dispersed in 5 mL of DI water, and the resulting suspension was transferred to a 25 mL bottle and sonicated for 15 min. After that, 10 mL of isopropanol was added and the mixture was sonicated for a further 15 min to ensure the homogeneity of the ink suspension. The required amount of catalyst ink was drop-cast on the RRDE. The Pt loading on the glassy carbon electrode was 51 μg cm−2. To wet the surface and condition the electrode, cyclic voltammograms (CVs) in 0.1 M HClO4 were recorded initially for 50 cycles at a scan rate of 50 mV s−1. The supporting electrolyte was purged with argon for 15 min prior to recording the background CVs. Subsequently, the electrolyte was saturated with oxygen for 20 min before recording the ORR polarization curves. A platinum coil (area 5 cm2) and double junction Ag/AgCl (saturated KCl) were the counter and reference electrodes, respectively. The counter electrode platinum coil was kept in a separate glass tube sealed with a frit to avoid any Pt dissolution and contamination from the coil to the working electrode. The reference electrode was kept in a separate compartment to avoid the effects of temperature on the reference electrode potential and minimise the chloride contamination of the electrolyte, but it was connected to the main cell via a salt-bridge. Although all of the experiments were conducted with a double junction Ag/AgCl reference electrode, the data are presented against a reversible hydrogen electrode (RHE). For the temperature-dependent measurements, the electrolyte temperature (293, 303, 313, 323 and 333 K) was maintained by the circulating water jacket of the electrochemical cell. The voltammograms of Pt black (∼51 μg cm−2) in argon (Fig. S1 in ESI†) and oxygen-saturated (Fig. S2 in ESI†) 0.1 M HClO4 were recorded in the temperature range of 293–333 K. The scan during ORR polarization was limited to 1.05 V vs. RHE. Five independent measurements were conducted to ensure the reproducibility of the results and add the error bar to the required plots. Residual R2 values for all of the linear fits were greater than 95%, unless mentioned otherwise.3. Result and discussion
The kinetic current (ik) obtained after correcting the ORR voltammogram for the background current, solution resistance, and mass-transfer resistance is used for the Tafel analysis. Since the applied η range of interest is sufficiently high (0.3–0.4 V), correction of the back reaction current (anodic current) is neglected. In the temperature range of 293–333 K, the macroscopic changes on the surface structure and composition are negligible; in addition, no prominent effect of temperature is observed on the surface structure from the CVs (Fig. S1, ESI†) recorded before and after conducting all the temperature-dependent experiments. The detailed procedure used to obtain ik from the measured current is explained in Section 1 of the ESI.†As reported by Paulus et al.,37 the η with respect to the O2/H2O equilibrium potential at various temperatures (ηO2) is determined from the potential against the RHE and the reversible H2/O2 cell potential (Ecell(T)) using eqn (1):
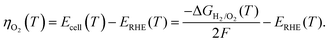 | (1) |
The temperature dependence of the Gibbs free energy of the formation of water (ΔGH2/O2(T)) is given by eqn (2):
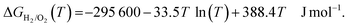 | (2) |
As the equilibrium potential of O2/H2O shifts with temperature, the zero potential for the RHE also shifts to a new value that is different from the 0.0 V, ensuring that the theoretical equilibrium potential for the ORR at all temperatures is constant, i.e., 1.229 V.53
While analysing the Eyring plot at various overpotentials, the effect of temperature on the theoretical equilibrium potential of O2/H2O and the measured zero-current zero-potential of the RHE with temperature were taken into account.
3.1. Tafel analysis and the transfer-coefficient (α)
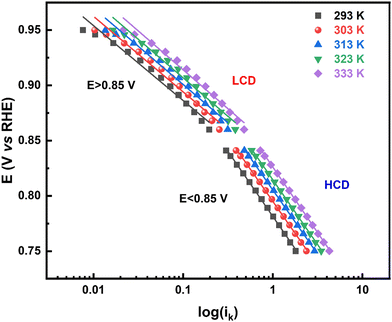
The rate of any electrochemical reaction can be controlled using an external applied η, and the free energy of the reacting species/electrons changes (increases or decreases) by Fη, where F is the Faraday constant. However, only a fraction of the total energy – as indicated by the α – is used to increase the rate of the reaction. For a charge-transfer reaction at the electrode–electrolyte interface, α is an intrinsic kinetic parameter, independent of the η, and it is usually determined from the Tafel equation. It can also be considered to be an adjustable parameter when obtained from curve fitting using the B–V equation. Typically, it is in the range of 0.0–1.0 and it is often taken as ∼0.5 for most electrochemical reactions. The α is also defined as the ratio of the reduction in the energy barrier height to the total energy applied for a given electron-transfer reaction.50As reported in the literature, the Tafel plot (Fig. 1) of the ORR is fitted with two slopes: one from the high current density (HCD) region (0.75–0.85 V), and the other from the low current density (LCD) region (0.85–0.95 V). The α values for the ORR obtained from the Tafel slopes in the HCD and LCD regions (Fig. 2) are 0.4 ± 0.1, and 0.8 ± 0.1, respectively. The Tafel slopes thus obtained are comparable to those reported in the literature.13,14,37,40 The α values estimated from B–V fitting (Fig. S5, ESI†) of the polarization curves are around 0.6 ± 0.1 (Table ST1 in the ESI†). Comparable α values are obtained from fitting the Tafel plot with a single slope. In the temperature range of 293–333 K, the α values are more or less independent of temperature in both the HCD and LCD regions. Moreover, α values estimated from the instantaneous Tafel slopes (0.7 ± 0.1) do not change much with the applied η (Fig. S6, ESI†). For a detailed derivation of the Tafel equation, instantaneous Tafel slope, and B–V fitting, see Section 2 of the ESI.†
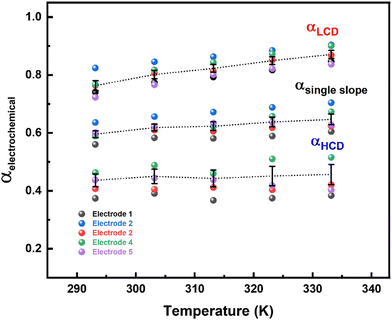 | ||
| Fig. 2 Electrochemical α values obtained from the Tafel slope (LCD, single slope and HCD) in the temperature range of 293–333 K, for five independent electrodes. | ||
Overall, the α values for the ORR obtained from the Tafel analysis (LCD, HCD, and single slope), instantaneous Tafel slope, and B–V fitting are less than 0.9.
3.2. Eyring analysis and electrocatalytic α
Alternatively, α can also be estimated from its definition given below (eqn (3)):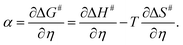 | (3) |
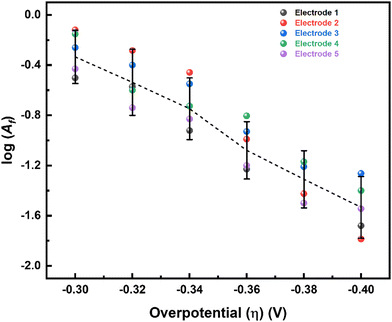
Here, ΔS# is entropy of activation, and ΔG# and ΔH# are already defined. For a negative η, ΔH# and ΔS# are given by eqn (4) and (5), respectively:54,55
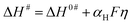 | (4) |
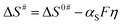 | (5) |
| α = αH + TαS. | (6) |
To estimate α, ΔH# and ΔS# at various overpotentials are obtained from the Eyring plot (log ik/T vs. 1/T) (Fig. 3). Since the effect of surface coverage (θ) is contained in the pre-exponential term (Af) of the Eyring relation (eqn (S18) in the ESI†), the slope (ΔH#) is not affected by θ. The effect of temperature on the equilibrium potential/overpotential of the ORR is accounted for in the Eyring analysis (see the details in Section 3 of the ESI†).
 | ||
| Fig. 3 Eyring plots of the ORR on Pt black (∼51 μg cm−2) at various overpotentials (0.30–0.40 V) on an RRDE in oxygen-saturated 0.1 M HClO4 solution at 1600 rpm in the temperature range of 293–303 K. | ||
The ΔH# value at a given η is widely used in the literature to characterize the catalytic activity of various surfaces towards the ORR, the HER, CO oxidation, etc.17,51,56,57 For the ORR on Pt, the ΔH# values estimated are 28 and 22 kJ mol−1, respectively, at 0.35 and 0.4 V overpotentials. These values are comparable to those reported in the literature at the respective overpotentials (Table 1).
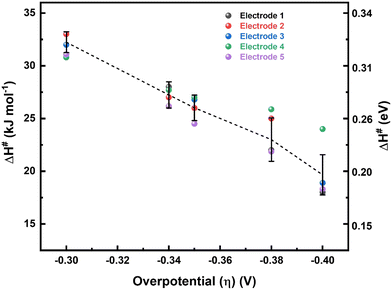
Values of ΔH# for the ORR at different overpotentials obtained from the Eyring slopes (Fig. 3) are plotted as a function of η to estimate the enthalpic α (αH) (Fig. 4). A systematic and consistent reduction in ΔH# with η is observed. The derivative of ΔH# with respect to η, the slope of the curve in Fig. 4, yields αH, the value of which is around 1.4 ± 0.2. To ensure the accuracy of the method applied to estimate αH, the ΔH# values obtained from the Eyring analysis for five independent electrodes were used, and the errors in these measurements were within an acceptable range. Details on the estimation of αH are given in Section 3.2 of the ESI.†
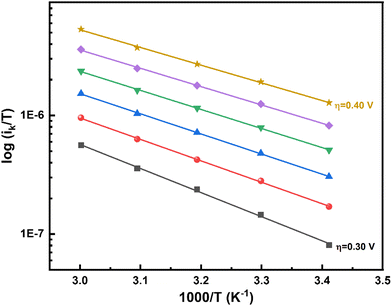
Intercept of the Eyring plot (Af) as a function of η yields ΔS# for the ORR (eqn (S18) in the ESI†). The intercept depends on ΔS# in addition to (1 − θ), concentration of the reacting species, the value of the transmission coefficient (κ), and the other constant terms in Af. The value of κ is in the range of 0–1, but is usually taken as 0.5, and all other quantities except for ΔS# are constant with respect to η. Therefore, the plot of Afvs. η (Fig. 5) yields αS (eqn (S18) in the ESI†). Typically, standard entropy of formation (s0f) values are three orders of magnitude lower than the standard enthalpy of formation (h0f) values.60 In the case of the ORR, it appears that TαS can also contribute significantly to the total α (see Table ST2 and eqn (S23) in the ESI†). Although αS can be estimated from the intercept of the Eyring plot, it is highly sensitive to the surface coverage by oxygenated species (a function of both the potential and the temperature), and, most importantly, errors in the measurements (the slope of the Eyring plot). Since the temperature range of analysis is narrow, extrapolating the Eyring plot to a higher temperature may not give the correct estimate of Af. Therefore, the calculation of αS may be precarious. In any case, we used the plot of log (Af) vs. η (Fig. 5) to estimate αS for all five independent measurements with five different electrodes. The effect of surface coverage on the slope of the log (Af) vs. η plot (with and without surface coverage correction) is shown in the ESI† (Fig. S10 and eqn (S25) in the ESI†). The broad range of contributions of αS to the total α is from −0.2 to −0.5. Thus, the overall range of α including TαS is obtained from eqn (6) and is in the range of 1.0–1.2.
 | ||
| Fig. 5 Plot of log (Af) (as estimated from the intercepts of Eyring plots) vs. η for five independent electrodes. | ||
To the best of our knowledge, ΔH# as function of η, and α derived from ΔH# and ΔS# for the ORR have not been reported in the literature. The origin of the high α (≫1) from Eyring analysis is intriguing, and unexpected, and may seem unreasonable compared with that estimated from the B–V equation, which is limited in the range of 0.0–0.8. The question is, what does α greater than 1 mean? Is this possible, and can we explain the difference in the α values obtained from both methods? For this, we must look closely at what is happening.
In the B–V theory of electrochemical reactions, η influences the free energy/enthalpy of the reactant (ΔGR = Fη), or it provides activation energy to the reactant. The apparent change in ΔH# is reflected as an exponential increase in ik across the electrified interface. Eqn (7) captures the effect of η and the temperature on ik as per the B–V model for electrochemical reactions at high η (obtained by rearranging the Tafel eqn (S7) in the ESI†).61
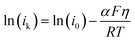 | (7) |
Thus, the slope of the Arrhenius plot does not change and the effect of η is given by the separation of the parallel lines (inset to Fig. S11 of the ESI†). If this is the case, the Arrhenius plots are parallel on the basis of eqn (7). In other words, the enthalpy of formation of the activated complex (H#) does not change. However, if only the energy state of the reactant is affected, the Eyring plots will also be parallel at each overpotential (the slope does not change) and the lines are separated by the current predicted by the B–V equation. This means that there is no electrocatalytic effect, and α cannot be calculated from ∂ΔH#/∂η, since the slope of the Eyring plots does not change.
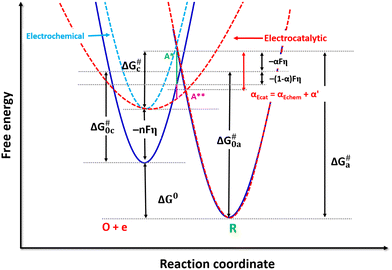
Contrary to electrochemical kinetics, the catalyst surface interacts with the activated complex in electrocatalytic reactions to provide an alternative lower energy barrier path as well for the formation of the activated complex. Thus, ΔH# changes due to an increase in the enthalpy of the reactant and a decrease in the enthalpy of formation of the activated complex (H#) on an electrified surface, and both are functions of η. This interaction of the catalyst with the activated complex is not captured in the B–V analysis, although the Eyring analysis can account for this. As a consequence of this, ΔH# decreases with η, as observed from the Eyring plots (the slope decreases). The α obtained from the ΔG# or ΔH# and ΔS# values of the activated complex are relevant only for electrocatalytic reactions, since the change in ΔH# due to the change in ΔG of the reactant with η is already captured in the B–V equation.
The value of α estimated from Tafel analysis and that from the derivative of the Eyring plot (ΔH#vs. η) can differ. This is because the α of electrocatalytic reactions has contributions from both electrochemical (αEchem) and electrocatalytic effects (αEcat). Here, the αEchem and αEcat contributions originate from the change in the free energy/enthalpy of the reactant and from the change in H# of the activated complex through interaction with the catalyst surface, respectively. The α from ∂ΔG#/∂η is always greater than the α from B–V theory, but it is not always necessary that α is greater than 1.
If it is greater than 1, the enthalpy of formation of the activated complex (H#) is lower in energy than that predicted by B–V theory, Fη + γ > ΔH#, where γ is the reduction in H# by the η on a catalytic surface. Therefore, the new activated complex (A**) position on a catalyst surface is lower (relative to the A* not affected by η) when the Morse's curve of the reactant is broadened (Fig. 6 red dotted line) on applying η. The broadening of the Morse curve originates from the interaction of the reactant with the catalyst surface.
For a reaction that proceeds with a very low η, or for a reaction with fast kinetics, for example, the HER, αEcat is slightly greater than αEchem (from B–V theory).51 By contrast, for reactions that require a very high η, ΔH# can be a strong function of η, and αEcat can be much higher than αEchem. Thus, α can be greater than unity (α ≫ 1). The electrocatalysis of the ORR on a Pt surface is one such reaction.
The α values estimated from B–V theory are in the range of 0–1, where 0.5 is most adopted for electrochemical reactions. The α values estimated from the change in the apparent free energy (ΔG#) are highly relevant to electrocatalytic reactions, since the catalyst surface is expected to offer a lower energy barrier path for the electron-transfer process. Moreover, since the exchange current density is affected by α (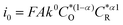 ), this certainly has strong implications for electrocatalyzed reactions.
), this certainly has strong implications for electrocatalyzed reactions.
Therefore, the conclusion based on Eyring analysis at a selected η may not reflect the true electrocatalytic nature of the surface. However, what is more important is the rate of change of the formation enthalpy of the activated complex (∂ΔH#/∂η) because it decides the electrocatalysis at an electrified interface. B–V theory does not differentiate/discriminate the effects of H# reduction and the increase in the free energy of the reactant ΔG#R. The difference in the magnitudes of α is a measure of the catalytic nature of the electrode. Thus, the electrochemical and electrocatalytic parameters are different.
4. Conclusions
In both electrochemical and electrocatalytic processes, the overall effect of η is to increase ik. In an electrochemical process, the activation energy is supplied to the reactants and a corresponding exponential rise in ik is predicted by the B–V theory of electrode kinetics. This effect of applied η for an electrochemical process yields parallel lines in the Eyring plot. However, for an electrocatalytic process that requires a high η, such as the ORR, which is the subject of current investigation, the derivative of ΔH# and ΔS# can be higher (1.1 ± 0.2) and may seem unreasonable or illogical. The difference in the α values derived from the B–V equation/Tafel analysis (0.6 ± 0.1) and the plot of ΔG#vs. η stems from the strong η dependence of the ΔH# and ΔS# values. In an electrocatalytic reaction, the interaction between the catalyst surface and the reacting species offers a potential-dependent, alternative, lower energy barrier path for the formation of the activated complex, and this interaction is a function of the applied η. The η dependence of ΔH# and ΔS# in an electrocatalytic process may bring it to a lower energy than that predicted for an electrochemical process. Therefore, αEcat, which captures the electrocatalytic effect, will be greater than αEchem. The higher α values (>1) for the ORR can be explained by the contribution to α from the electrocatalytic effect from the catalyst surface. Moreover, α derived from ∂ΔG#/∂η is the most important kinetic parameter that unifies all the theories of electrocatalysis. It can qualitatively account for the adsorption strength, binding energy of the reactant on the catalyst surface, and the electronic structure of the catalyst surface, in addition to fulfilling the conventional meaning of α. Thus, the α value obtained from Eyring analysis is the true reflection of the reaction kinetics on an electrocatalyst surface.The α value derived from the B–V equation and ∂ΔG#/∂Δη may be comparable in cases where the reaction rate is inherently fast or in a reaction that requires a very low overpotential and ΔG# is a weak function of η, such as that for the HER on a Pt surface.
Author contributions
Rajan Maurya conducted all the voltammetry and ORR measurements and made the primary draft. Rubul Das made the schematics and diagrams. Anand Kumar Tripathi did the data analysis. The concept, design and interpretation of the work is from Manoj Neergat. All the authors discussed the results and were involved in the writing.Conflicts of interest
Author(s) declares no conflict of interest.Acknowledgements
National Centre for Photovoltaic Research and Education (NCPRE), India, and Joint Indo-UK Collaborative Effort in Clean Energy (JUICE) are acknowledged for the financial support through the grants P16MNRE002 and 16DST050, respectively.References
- T. J. Schmidt, V. Stamenkovic, M. Arenz, N. M. Markovic and P. N. Ross, Oxygen electrocatalysis in alkaline electrolyte: Pt(hkl), Au(hkl) and the effect of Pd-modification, Electrochim. Acta, 2002, 47, 3765–3776 CrossRef CAS.
- H. A. Gasteiger and N. M. Marković, Just a dream—Or future reality?, Science, 2009, 324, 48–49 CrossRef CAS PubMed.
- R. Gómez, J. M. Feliu and H. D. Abruña, Induced adsorption of chloride and bromide by submonolayer amounts of copper underpotentially deposited on Pt(111), J. Phys. Chem., 1994, 98, 5514–5521 CrossRef.
- F. Jaouen, F. Charreteur and J. P. Dodelet, Fe-based catalysts for oxygen reduction in PEMFCs, J. Electrochem. Soc., 2006, 153, A689–A698 CrossRef CAS.
- M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, Progress in flow battery research and development, J. Electrochem. Soc., 2011, 158, R55–R79 CrossRef CAS.
- M. Lefèvre, E. Proietti, F. Jaouen and J. P. Dodelet, Iron-based catalysts with improved oxygen reduction activity in polymer electrolyte fuel cells, Science, 2009, 324, 71–74 CrossRef PubMed.
- O. Savadogo, K. Lee, K. Oishi, S. Mitsushima, N. Kamiya and K. I. Ota, New palladium alloys catalyst for the oxygen reduction reaction in an acid medium, Electrochem. Commun., 2004, 6, 105–109 CrossRef CAS.
- F. Jaouen, E. Proietti, M. Lefèvre, R. Chenitz, J. P. Dodelet, G. Wu, H. T. Chung, C. M. Johnston and P. Zelenay, Recent advances in non-precious metal catalysis for oxygen-reduction reaction in polymer electrolyte fuel cells, Energy Environ. Sci., 2011, 4, 114–130 RSC.
- J. R. C. Salgado, E. Antolini and E. R. Gonzalez, Carbon supported Pt-Co alloys as methanol-resistant oxygen-reduction electrocatalysts for direct methanol fuel cells, Appl. Catal., B, 2005, 57, 283–290 CrossRef CAS.
- U. Babic, M. Suermann, F. N. Büchi, L. Gubler and T. J. Schmidt, Critical review-Identifying critical gaps for polymer electrolyte water electrolysis development, J. Electrochem. Soc., 2017, 164, F387–F399 CrossRef CAS.
- L. D. Chen, M. Urushihara, K. Chan and J. K. Nørskov, Electric field effects in electrochemical CO2 reduction, ACS Catal., 2016, 6, 7133–7139 CrossRef CAS.
- M. Y. Lee, K. T. Park, W. Lee, H. Lim, Y. Kwon and S. Kang, Current achievements and the future direction of electrochemical CO2 reduction: A short review, Crit. Rev. Environ. Sci. Technol., 2020, 50, 769–815 CrossRef CAS.
- V. Stamenković, T. J. Schmidt, P. N. Ross and N. M. Marković, Surface composition effects in electrocatalysis: Kinetics of oxygen reduction on well-defined Pt3Ni and Pt3Co alloy surfaces, J. Phys. Chem. B, 2002, 106, 11970–11979 CrossRef.
- U. A. Paulus, A. Wokaun, G. G. Scherer, T. J. Schmidt, V. Stamenkovic, N. M. Markovic and P. N. Ross, Oxygen reduction on high surface area Pt-based alloy catalysts in comparison to well defined smooth bulk alloy electrodes, Electrochim. Acta, 2002, 47, 3787–3798 CrossRef CAS.
- G. Wu, K. L. More, C. M. Johnston and P. Zelenay, High-performance electrocatalysts for oxygen reduction derived from polyaniline, iron, and cobalt, Science, 2011, 332, 443–447 CrossRef CAS PubMed.
- R. Devivaraprasad, T. Kar, P. Leuaa and M. Neergat, Recovery of active surface sites of shape-controlled platinum nanoparticles contaminated with halide ions and its effect on surface-structure, J. Electrochem. Soc., 2017, 164, H551–H560 CrossRef CAS.
- N. M. Marković, T. J. Schmidt, B. N. Grgur, H. A. Gasteiger, R. J. Behm and P. N. Ross, Effect of temperature on surface processes at the Pt(111) – liquid interface: hydrogen adsorption, oxide formation, and CO oxidation, J. Phys. Chem. B, 1999, 103, 8568–8577 CrossRef.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Alloys of platinum and early transition metals as oxygen reduction electrocatalysts, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed.
- G. Liu, X. Li, P. Ganesan and B. N. Popov, Development of non-precious metal oxygen-reduction catalysts for PEM fuel cells based on N-doped ordered porous carbon, Appl. Catal., B, 2009, 93, 156–165 CrossRef CAS.
- B. Bera, T. Kar, A. Chakraborty and M. Neergat, Influence of nitrogen-doping in carbon on equivalent distributed resistance and capacitance – Implications to electrocatalysis of oxygen reduction reaction, J. Electroanal. Chem., 2017, 805, 184–192 CrossRef CAS.
- A. Chakraborty, B. Bera, D. Priyadarshani, P. Leuaa, D. Choudhury and M. Neergat, Electrochemical estimation of active site density on a metal-free carbon-based catalyst, RSC Adv., 2019, 9, 466–475 RSC.
- J. H. Dumont, U. Martinez, K. Artyushkova, G. M. Purdy, A. M. Dattelbaum, P. Zelenay, A. Mohite, P. Atanassov and G. Gupta, Nitrogen-doped graphene oxide electrocatalysts for the oxygen reduction reaction, ACS Appl. Nano Mater., 2019, 2, 1675–1682 CrossRef CAS.
- J. Weiss, H. Zhang and P. Zelenay, Recent progress in the durability of Fe-N-C oxygen reduction electrocatalysts for polymer electrolyte fuel cells, J. Electroanal. Chem., 2020, 875, 114696 CrossRef CAS.
- H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Activity benchmarks and requirements for Pt, Pt-alloy, and non-Pt oxygen reduction catalysts for PEMFCs, Appl. Catal., B, 2005, 56, 9–35 CrossRef CAS.
- S. Trasatti and O. A. A. Petrii, Real Surface Area Measurements, J. Electroanal. Chem., 1993, 321, 353–376 Search PubMed.
- M. Lukaszewski, M. Soszko and A. Czerwiński, Electrochemical methods of real surface area determination of noble metal electrodes – an overview, Int. J. Electrochem. Sci., 2016, 11, 4442–4469 CrossRef CAS.
- T. C. Franklin and N. F. Franklin, The use of underpotential deposition to measure the surface area of metals, Surf. Technol., 1976, 4, 431–440 CrossRef CAS.
- B. E. Conway, Electrochemical surface science: The study of monolayers of ad-atoms and solvent molecules at charged metal interfaces, Prog. Surf. Sci., 1984, 16, 1–137 CrossRef CAS.
- A. Chakraborty, R. Devivaraprasad, B. Bera and M. Neergat, Electrochemical estimation of the active site density on metal-free nitrogen-doped carbon using catechol as an adsorbate, Phys. Chem. Chem. Phys., 2017, 19, 25414–25422 RSC.
- R. Z. Snitkoff-Sol, A. Friedman, H. C. Hoing, Y. Yurko, A. Kozhushner, M. J. Zachman, P. Zelenay, A. M. Bond and L. Elbaz, Quantifying the electrochemical active site density of precious metal-free catalysts in situ in fuel cells, Nat. Catal., 2022, 5, 163–170 CrossRef CAS.
- L. Eifert, R. Banerjee, Z. Jusys and R. Zeis, Characterization of carbon felt electrodes for vanadium redox flow batteries: Impact of treatment methods, J. Electrochem. Soc., 2018, 165, A2577–A2586 CrossRef CAS.
- I. Derr, M. Bruns, J. Langner, A. Fetyan, J. Melke and C. Roth, Degradation of all-vanadium redox flow batteries (VRFB) investigated by electrochemical impedance and X-ray photoelectron spectroscopy: Part 2 electrochemical degradation, J. Power Sources, 2016, 325, 351–359 CrossRef CAS.
- H. Y. Chen, N. Bucher, S. Hartung, L. Li, J. Friedl, H. P. Liou, C. L. Sun, U. Stimming and M. Srinivasan, A multi-walled carbon nanotube core with graphene oxide nanoribbon shell as anode material for sodium ion batteries, Adv. Mater. Interfaces, 2016, 3, 1–12 Search PubMed.
- U. Stimming, J. Wang and A. Bund, The vanadium redox reactions – Electrocatalysis versus non-electrocatalysis, ChemPhysChem, 2019, 20, 3004–3009 CrossRef CAS PubMed.
- A. K. Tripathi, M. E. Joy, R. Maurya and M. Neergat, The impact of ovepotential on the enthalpy of activation and pre-exponential factor of the electrochemical redox reactions, Phys. Chem. Chem. Phys., 2022, 24, 3886–3895 RSC.
- J. Zhang, M. B. Vukmirovic, Y. Xu, M. Mavrikakis and R. R. Adzic, Controlling the catalytic activity of platinum-monolayer electrocatalysts for oxygen reduction with different substrates, Angew. Chem., Int. Ed., 2005, 44, 2132–2135 CrossRef CAS PubMed.
- U. A. Paulus, T. J. Schmidt, H. A. Gasteiger and R. J. Behm, Oxygen reduction on a high-surface area Pt/Vulcan carbon catalyst: A thin-film rotating ring-disk electrode study, J. Electroanal. Chem., 2001, 495, 134–145 CrossRef CAS.
- J. Huang, J. Zhang and M. Eikerling, Unifying theoretical framework for deciphering the oxygen reduction reaction on platinum, Phys. Chem. Chem. Phys., 2018, 20, 11776–11786 RSC.
- N. M. Marković, B. N. Grgur and P. N. Ross, Temperature-dependent hydrogen electrochemistry on platinum low-index single-crystal surfaces in acid solutions, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
- J. X. Wang, N. M. Markovic and R. R. Adzic, Kinetic analysis of oxygen reduction on Pt(111) in acid solutions: Intrinsic kinetic parameters and anion adsorption effects, J. Phys. Chem. B, 2004, 108, 4127–4133 CrossRef CAS.
- K. Krischer and E. R. Savinova, Special Catalytic Systems: Electrocatalysis. Handbook of Heterogeneous Catalysis, 2008, vol. 3–5 Search PubMed.
- V. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Changing the activity of electrocatalysts for oxygen reduction by tuning the surface electronic structure, Angew. Chem., Int. Ed., 2006, 45, 2897–2901 CrossRef CAS PubMed.
- R. Guidelli, R. G. Compton, J. M. Feliu, E. Gileadi, J. Lipkowski, W. Schmickler and S. Trasatti, Definition of the transfer coefficient in electrochemistry (IUPAC Recommendations 2014), Pure Appl. Chem., 2014, 86, 259–262 CrossRef CAS.
- J. X. Wang, A. F. Uribe, E. T. Springer, J. Zhang and R. R. Adzic, Intrinsic kinetic equation for oxygen reduction reaction in acidic media: the double Tafel slope and fuel cell applications, Faraday Discuss., 2008, 140, 347–362 RSC.
- B. Hammer and J. K. Nørskov, Theoretical surface science and catalysis—calculations and concepts, Adv. Catal., 2000, 45, 71–129 CAS.
- Z. W. She, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining theory and experiment in electrocatalysis: Insights into materials design, Science, 2017, 355, 146–158 Search PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- A. Holewinski and S. Linic, Elementary mechanisms in electrocatalysis: Revisiting the ORR Tafel slope, J. Electrochem. Soc., 2012, 159, H864–H870 CrossRef CAS.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Insight on Tafel slopes from a microkinetic analysis of aqueous electrocatalysis for energy conversion, Sci. Rep., 2015, 5, 1–21 Search PubMed.
- J. O. Bockris and A. K. N. Reddy, Modern Electrochemistry: an introduciton to an interdisiplinary area, Plenum Publishing Corporation, 1970, vol. 2 Search PubMed.
- D. Choudhury, R. Das, A. K. Tripathi, D. Priyadarshani and M. Neergat, Kinetics of hydrogen evolution reactions in acidic media on Pt, Pd, and MoS2, Langmuir, 2022, 38, 4341–4350 CrossRef CAS PubMed.
- M. Neergat, V. Gunasekar and R. Rahul, Carbon-supported Pd–Fe electrocatalysts for oxygen reduction reaction (ORR) and their methanol tolerance, J. Electroanal. Chem., 2011, 658, 25–32 CrossRef CAS.
- G. Jerkiewicz, Standard and reversible hydrogen electrodes: Theory, design, operation, and applications, ACS Catal., 2020, 10, 8409–8417 CrossRef CAS.
- B. E. Conway and D. P. Wilkinsont, Comparison of entropic and enthalpic components of the barrier symmetry factor β for proton discharge at liquid and solid Hg in relation to variation of tafel slopes and β with temperature, J. Chem. Soc., Faraday Trans., 1989, 85, 2355–2367 RSC.
- B. E. Conway, D. F. Tessier and D. P. Wilkinson, Experimental evidence for the potential dependence of entropy of activation in electrochemical reactions in relation to the temperature dependence of tafel slope, J. Electroanal. Chem., 1986, 199, 249–269 CrossRef CAS.
- H. A. Gasteiger, N. Markovic, P. N. Ross and E. J. Cairns, Temperature-dependent methanol electro-oxidation on well characterized Pt-Ru alloys, J. Electrochem. Soc., 1994, 141, 1795–1803 CrossRef CAS.
- N. Wakabayashi, M. Takeichi, H. Uchida and M. Watanabe, Temperature dependence of oxygen reduction activity at Pt-Fe, Pt-Co, and Pt-Ni alloy electrodes, J. Phys. Chem. B, 2005, 109, 5836–5841 CrossRef CAS PubMed.
- A. Damjanovic and D. B. Sepa, An analysis of the pH dependence of enthalpies and Gibbs energies of the activation for O2 reduciton at Pt electrodes in acid solutions, Electrochim. Acta, 1990, 35, 1157–1162 CrossRef CAS.
- A. Parthasarathy, S. Srinivasan, A. J. Appleby and C. R. Martin, Temperature dependence of the electrode kinetics of oxygen reduction at the platinum/Nafion® interface – A microelectrode investigation, J. Electrochem. Soc., 1992, 139, 2530–2537 CrossRef CAS.
- J. G. Speight, Lange's Handbook Of Chemistry, McGraw Hill, New York, 16th edn, 2005 Search PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, Inc., 2015, vol. 8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Background voltammograms and ORR polarization curves; corrections to measured current and potentials; Butler–Volmer fitting and Tafel analysis; Eyring equation and α calculations; surface coverage correction results; schematic of electrochemical and electrocatalytic process; theoretical limiting current and its temperature dependence; schematic of energy surface diagram for the electrocatalytic process. See DOI: https://doi.org/10.1039/d2cp04331a |
| This journal is © the Owner Societies 2023 |