Accurate ab initio based global adiabatic potential energy surfaces for the 13A′′, 13A′ and 21A′ states of SiH2†
Received
14th October 2022
, Accepted 20th November 2022
First published on 22nd November 2022
Abstract
Three accurate global adiabatic potential energy surfaces for the 13A′′, 13A' and 21A' states of SiH2 are constructed by fitting numerous ab initio energies calculated at the aug-cc-pV(Q+d)Z and aug-cc-pV(5+d)Z basis sets based on the multi-reference configuration interaction level with Davidson correction. It is worth noting that the potential energy surface of the 13A′′ state is established for the first time. The topographic features of these novel potential energy surfaces are investigated in detail and are very consistent with those obtained in the available literature. Moreover, the integral cross-sections of the corresponding reaction are calculated for the first time using a quasi-classical trajectory method and time-dependent wave packet method, indicating that the 13A′′ state makes a major contribution to the reaction of Si(3P) + H2(X1Σ+g) (v = 0, j = 0) → H(2S) + SiH(X2Π) at high collision energies. These new potential energy surfaces provide a reliable foundation for investigation of the dynamics and a component for constructing larger silicon-/hydrogen-containing systems.
1. Introduction
The silylene radical, SiH2, is considered as an intermediate in the reaction for the preparation of amorphous silicon by chemical vapor deposition,1–4 which plays an important role in organic silicon chemistry.5–7 Thin silicon films, essential for the industrial production of solar cells and semiconductor devices, are produced by chemical vapor deposition following the decomposition of SiH4.8 In addition, the studies on the SiH2 reaction system are of great significance in astrophysics and spectroscopy.9,10 For instance, SiH radicals have long been observed in the spectra of the sun and other cool stars, and are important for modelling M-dwarf atmospheres.11
In the late 1960s, the spectrum of SiH2 was first observed12,13 and has been extensively studied experimentally since then.2,14–20 In particular, Milligan14 and Fredin15 successively reported the vibration frequency of silica and the former carried out extensive research on the infrared and vacuum photodegradation of silane. Thoman et al.16 reported the fluorescence lifetime of SiH2 free radicals and Escribano2 observed the A1B1–X1A1 absorption spectrum of SiH2 using intracavity laser absorption spectroscopy. High resolution spectra of low vibrational energy levels and precise molecular constants are provided by Hirota and colleagues.17 Ishikawa et al.18 observed high excited vibration levels using laser-induced fluorescence and stimulated emission pumping techniques, and then they carried out a more detailed reanalysis of vibration resonance.19 Several years later, they first observed the spin–orbit interaction between the X1A1 state and a3B1 state.20
Early ab initio calculations concentrated on stationary points on the theoretical side.21–24 As for the potential energy surface (PES), the first global PES of the SiH2 (13A′′) was calculated by Gabriel25 from highly correlated coupled electron pair approach electronic wavefunctions in 1993. Duxbury and co-workers26 reported Renner–Teller between X1A1 and A1B1 states and spin orbital coupling with the lowest triplet a3B1 state during the same year. After that, Tokue et al.27 developed ab initio interpolated PESs for the X1A1, A1B1 and B1A1 states and then studied the photolysis process.28 The conical intersection in the reaction system was systematically studied by means of high level ab initio calculations,29 and the geometric phase effect related to conical intersections (CIs) was proved by Wu et al.30 Recently, Clark et al.31 conducted a comprehensive theoretical study of the rotation–vibration spectrum of ground state electrons using the newly constructed PES and the associated dipole moment which achieved good agreement with the experiment. Most recently, Cao and colleagues32 investigated the deuterated isotope change quantum dynamics and cyclic polymer molecular dynamics of Si (1D) + H2 (X1Σ+g) → H (2S) + SiH (X2Π) reactions on the global PES of SiH2 constructed by the permutation invariant polynomial neural network (PIP-NN) method, while a three-dimensional (3D) PES using many-body expansion (MBE) theory33,34 to study the integral cross-section (ICS) for the Si (1D) + H2 (X1Σ+g) → H (2S) + SiH (X2Π) reaction was investigated in our preceding paper.35 Most of the research on this radical focuses on the X1A1 and A1B1 states, but there has been little research on the three excited states mentioned in the title.
The three accurate global PESs of the SiH2 radical are formed with high level ab initio energies calculated by the aug-cc-pV(Q+d)Z basis set (AV(Q+d)Z) and aug-cc-pV(5+d)Z basis set (AV(5+d)Z).36–38 Based on a multi-reference configuration interaction method with Davidson correction (MRCI(Q)) using the full-valence-complete-active-space wave function as a reference,39,40 a uniform singlet-pair and triplet-pair extrapolation (USTE) scheme is adopted to extrapolate the dynamical correlation energy to the complete basis set (CBS) limit,41 for reducing the associated resource consumption. The MBE theory33,34 is adopted to fit the accurate PESs with good behavior in the short, intermediate and long range of the whole potential. In this paper, the specific characteristics of three excited states are reported based on three full-dimensional PESs. To our knowledge, it is the first time that the 3D PES of the 13A′ state including the geometry and the relative energy is reported in detail. Eventually, quasi-classical trajectory (QCT) theory42,43 and time-dependent wave packet (TDWP) theory are adopted to calculate the ICSs to obtain as much information as possible about the dynamic characteristics of the SiH2 radical.
The article is structured as follows: We describe the theoretical approach in Section 2 including the ab initio calculations and the subsequent fitting of the PESs. In Section 3, the major topographical features of the adiabatic PESs are examined and discussed in detail. Moreover, the dynamical characteristics calculated by the QCT and TDWP theory of these electronic states are analyzed. Finally, a summary is given in Section 4.
2. Theoretical approaches
A.
Ab initio calculations and the extrapolation method
The ab initio calculations presented in this work are performed using the MOLPRO2012 software package.44 In this calculation, the active space consists of six electrons distributed among six orbitals (6e,6o), and the molecular orbitals are determined by the state-averaged complete active space self-consistent field (SA-CASSCF)45,46 with the same weighting on the three states for further MRCI(Q) calculation.47 All the calculations are performed in Cs symmetry including two lower states of A′ symmetry (13A′ and 21A′) and one lower state of A′′ symmetry (13A′′), which correspond to the 3A1 state, B1A1 state and a3B1 state in the C2v symmetry respectively. A total of 7555, 6320 and 6992 ab initio points are obtained at the MRCI+Q/AV(Q+d,5+d)Z level in the 21A′ state, 13A′ state and 13A′′ state respectively. The internal coordinates are used in this calculation, where rHH denotes the distance between two hydrogen atoms, RSi−HH represents the distance between the Si atom and the center of the two hydrogen atoms, and γ is the angle between the two bonds. The data points sampled in the symmetrical configuration Si–H2 is distributed by 1.2 ≤ RSi–HH/a0 ≤ 4.2, 1.0 ≤ rHH/a0 ≤ 15.0, 0 ≤ γ/deg ≤ 90, while asymmetric configuration H–SiH is constrained by 1.7 ≤ RH–SiH/a0 ≤ 4.8, 1.2 ≤ rSiH/a0 ≤ 12.0, 0 ≤ γ′/deg ≤ 180.
Dunning's correlation consistent basis sets are constructed to relate the correlation energy to the cardinal number X in a systematic manner. And the AV(Q+d,5+d)Z ab initio energies can be treated by pointwise extrapolation to the CBS limit:41
where the subscript X indicates the energy has been calculated in the AV(
X+d)Z basis, the superscript CAS stands for the complete active space energies, and dc represents the dynamical correlation energies.
A proposed generalization of the protocol adopted by Karton and Martin to extrapolate CAS energies is utilized, namely48
where
α = 8.74 is an optimal decay index when extrapolating energies calculated at the CAS/AV(
Q+d,5+d)Z level to the CBS limit. The dc energies are extrapolated using a uniform singlet-pair and triplet-pair extrapolation scheme, and a popular protocol is
49| | 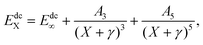 | (3) |
with the auxiliary relationship
where
Edc∞,
A3,
γ,
A5(0) and
c are parameters, where
γ = −3/8,
A5(0) = 0.0037685459,
c = −1.17847713, depending on the
ab initio method, which can be obtained completely by referring to Table 1 of ref.
41. By fixing these parameters,
eqn (3) can be transformed into a two-parameter formula (
Edc∞,
A3). In fact, this method has been successfully applied to various other systems,
41,50,51 providing readers with more details.
B. Analytic function for the PES
As shown in Fig. 1(a), four potential energy curves (PECs) are formed by placing the Si atom at 25 a0 from the center of H–H and changing the distance between two H atoms. While the H atoms are placed at a distance of 25 a0 at the Si–H center, by changing the distance between the H atom and the Si atom, the four PECs in Fig. 1(b) are formed. All curves are calculated at the MRCI(Q)/AV(Q+d)Z level and correspond to the 11A′ state, 13A′′ state, 13A′ state and 21A′ state, respectively. In panel (a) and (b) of Fig. 1, there are two dissociation limits when the SiH2 system is completely dissociated: Si (1D) + H (2S) + H (2S) and Si (3P) + H (2S) + H (2S). The 21A′ state follows the former, while the remaining three states follow the latter. It is worth mentioning that the PEC of the 11A′ state in panel (a) is folded down due to the transition of the Si atom from the 1D state to the 3P state in the process of increasing the H–H distance.35 After a comprehensive analysis of panel (a) and (b), the energy correlation diagram for the four lower-lying electronic states of SiH2 are shown clearly in panel (c). The ground state 11A′ follows the reaction process of Si (1D) + H2 (X1Σ+g) → H (2S) + SiH (X2Π) taken from our recent paper,35 and both the 13A′ state and 13A′′ state follow the reaction process of Si (3P) + H2 (X1Σ+g) → H (2S) + SiH (X2Π), while the 21A′ state follows the reaction process of Si (1D) + H2 (X1Σ+g) → H (2S) + SiH (A2Δ). By analyzing the energy changes of the reactants and products, the reactions are all endothermic.
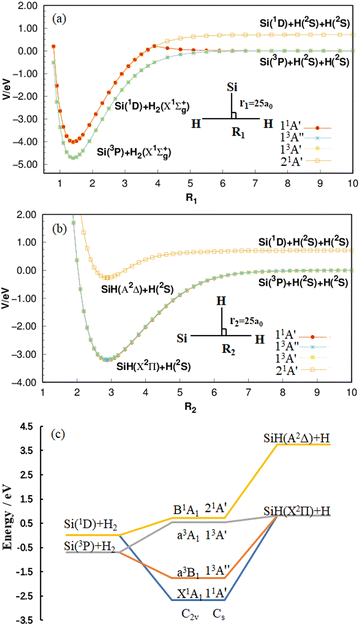 |
| | Fig. 1 (a) Potential energy curves for H–H bond stretching when r1 = 25 a0 at the MRCI(Q)/AV(Q+d)Z level. (b) Potential energy curves for Si–H bond stretching when r2 = 25 a0 at the same level. The energies are relative to the Si(3P) + H(2S) + H(2S) asymptote in (a) and (b). (c) Energy correlation diagram of the 11A′ state, 13A′′ state, 13A′ state and 21A′ state of the SiH2 system with an energy relative to the Si(1D) + H2 asymptote. | |
Considering the dissociation scheme above, the analytic function of the SiH2 PES is expressed as a combination of one-, two-, and three-body terms after using the MBE method, written as:52
| | 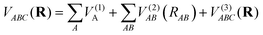 | (5) |
where
R =
RAB,
RAC,
RBC is the vector of the three internuclear coordinates.
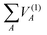
are the energies of the separated atoms in their corresponding electronic state. We assume that all these energy terms approach zero at the dissociation limit in this work.
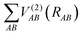
is the two-body energy terms, defined as
| | | V(2)AB = V(2)short + V(2)long | (6) |
The Aguado and Paniagua methods33,34 are adopted to simulate the analytic function of SiH2 for the two-body energy terms, which is indicated as the sum of short-range potential energy V(2)short and long-range potential energy V(2)long as in eqn (6). Specifically, the two terms are written as
| | 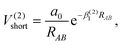 | (7) |
and
| | 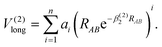 | (8) |
As RAB approaches zero, the short-range potential V(2)short tends toward infinity, while the long-range potential V(2)long tends toward zero when RAB approaches infinity. Eleven parameters, including two nonlinear parameters βi (i = 1, 2) and nine linear parameters ai (i = 0, 1, …, 8), have been obtained by fitting diatomic PECs of SiH(X2Π), SiH(A2Δ) and H2(X1Σ+g).
The modeling of the three-body term adopts a three-body distribution-polynomial form,53 which has been applied to calculate the ground and excited states of a range of systems.51,54,55
| | 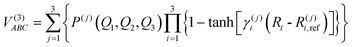 | (9) |
where
V(3)ABC is the corresponding interaction energy minus the two-body energy terms, the polynomial
P(j)(
Q1,Q2,Q3) is written in symmetric coordinates, all of third order, and
R(j)i,ref is a reference geometry.
γ(j)i represents the nonlinear range parameters determined by parameter optimization through a trial and error program to ensure correct asymptotic behavior and minimize root mean square deviation (rmsd) during dissociation. The complete parameter set has a total of 150 linear coefficients, 9 nonlinear ones and 9 reference bond distances which are gathered in the tables of the ESI.
† In this paper, the three-body term rmsd values were 0.224 kcal mol
−1 for the 1
3A′′ state, 0.269 kcal mol
−1 for the 1
3A′ state, and 0.412 kcal mol
−1 for the 2
1A′ state, respectively.
3. Results and discussion
The equilibrium geometries, dissociation energies, vibrational frequencies, and spectroscopic constants of the two-body term potential energy curves (PECs) and comparison with other theoretical and experimental values are displayed in Table 1. The SiH (X2Π), SiH (A2Δ) and H2(X1Σ+g) PECs shown in Fig. 2, accurately simulate the MRCI(Q)/CBS(Q+d,5+d) ab initio energies calculated in the current work. As collected in Table 1, for the SiH (X2Π) state, the Re results obtained by these groups of calculations are of high quality, and compared with the corresponding experimental data,56,57 the two calculated Re results by Shi et al. are slightly worse than the results of this work.58,59 Overall, the present spectroscopic results of the SiH (X2Π) state, especially αe and βe, are in excellent agreement with the measurements.56,57 The dissociation energies calculated are slightly higher than the experimental and theoretical values provided in the table, but within the acceptable range.56–59 The SiH (A2Δ) has an equilibrium geometry of 2.879 a0 and dissociation energy of 0.955 eV, which is in excellent agreement with the experimental value provided by Huber et al.56 The error percentages of the remaining three spectral constants are 2.4% (ωe), 13.9% (ωeχe), and 0.0% (βe), respectively, while the error of αe is relatively large, but it is acceptable considering that its experimental value is only 0.345 cm−1.56 Compared with the experimental values, the H2(X1Σ+g) parameters obtained in the three electronic states are not much different, within a reasonable range.63 In addition, the three PECs ensure the smooth convergence trend of the long-range and short-range regions obviously from Fig. 2.
Table 1 Equilibrium geometries, dissociation energies, vibrational frequencies, and spectroscopic constants of SiH (X2Π), SiH (A2Δ) and H2 (X1Σ+g), with the unit of Re in bohr, De in eV, and ωe, ωeχe, αe and βe in unit cm−1
|
|
R
e
|
D
e
|
ω
e
|
ω
e
χ
e
|
α
e
|
β
e
|
|
Calculated at the 13A′′ state.
Calculated at the 13A′ state.
Calculated at the 21A′ state.
|
| SiH(X2Π) |
| This worka |
2.874 |
3.212 |
2051.512 |
40.616 |
0.218 |
7.494 |
| This workb |
2.873 |
3.210 |
2055.903 |
40.813 |
0.219 |
7.494 |
| Theor.58 |
2.864 |
3.189 |
2043.47 |
30.932 |
0.201 |
7.726 |
| Theor.59 |
2.877 |
3.181 |
2046.91 |
36.771 |
0.184 |
7.478 |
| Exp.56 |
2.873 |
≤3.1855 |
2041.80 |
35.51 |
0.219 |
7.500 |
|
|
| SiH(A2Δ) |
| This workc |
2.879 |
0.995 |
1904.118 |
112.967 |
0.508 |
7.466 |
| Theor.58 |
2.862 |
1.030 |
1857.63 |
83.043 |
0.307 |
7.502 |
| Exp.56 |
2.879 |
≤0.9591 |
1858.90 |
99.175 |
0.345 |
7.466 |
| Exp.60 |
2.872 |
0.8924–0.9406 |
— |
— |
0.215 |
7.503 |
|
|
| H2(X1Σ+g) |
| This worka |
1.401 |
4.756 |
4427.370 |
127.744 |
2.252 |
60.827 |
| This workb |
1.401 |
4.745 |
4410.083 |
127.057 |
2.242 |
60.885 |
| This workc |
1.401 |
4.751 |
4407.621 |
126.739 |
2.234 |
60.865 |
| Theor.61 |
1.401 |
4.749 |
4404.613 |
126.636 |
2.233 |
60.861 |
| Theor.62 |
1.401 |
4.711 |
4389.660 |
121.560 |
3.162 |
60.826 |
| Exp.63 |
1.401 |
4.47864 |
4401.210 |
121.330 |
3.062 |
60.853 |
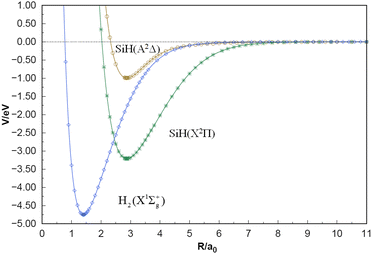 |
| | Fig. 2 Potential energy curves of SiH(X2Π), SiH(A2Δ) and H2(X1Σ+g). | |
Table 2 collects the properties of special stationary points for the 13A′′, 13A′ and 21A′ states PESs of SiH2, including geometries, energies and vibrational frequencies, in which only part of the experimental and theoretical data for the 13A′′ state is obtained, and the remaining states only have theoretical data. R1 represents the H–H distance, R2 represents the Si–H distance, and θHSiH represents the [H–Si–H] angle. ΔE is the energy relative to the 11A′ state and ΔV is the energy relative to the Si (1D) + H2 (X1Σ+g) asymptote. In the 13A′′ state, the H–H and Si–H bond lengths of global minimum (GM) are 4.860 a0 and 2.816 a0, respectively, with θHSiH = 119.3°, which are basically consistent with other theoretical values.24,25,27,65 The energy difference ΔE between the 13A′′ state and the 11A′ state is 0.9145 eV, within the reference range of the experimental value provided by Berkowitz et al.66 Unfortunately, there is no experimental value for the 13A′ state and the 21A′ state to compare, and only the theoretical value can be referred to.24,27,30,65 For the 21A′ state, the GM is located at θHSiH = 165.0°, R1 = 5.466 a0, R2 = 2.757 a0 with a barrier height of 0.5490 eV relative to the Si (1D) + H2 (X1Σ+g) asymptote, showing a D∞h symmetry geometry. While the GM of the 13A′ state is located at R1 = 6.240 a0, R2 = 3.120 a0 with a barrier height of 3.3759 eV relative to the energies of the 11A′ state.35 In addition, the transition state 2 (TS2) of the 21A′ state is also discovered in the D∞h geometry, whose energy is very close to the GM by only 0.0013 eV. Therefore, a denser grid of points is taken near the GM position of the 21A′ state during the calculation and special weights have been attributed to these points in the least-squares fitting procedure, warranting an accurate description of the topographical features of the PES at this region. For the harmonic frequencies, the calculated values of the three GMs are consistent with the existing theoretical results, and only the ω3 = 228 cm−1 of the GM for the 21A′ state is significantly different from the ω3 = 856 cm−1 reported by Yamaguchi et al.65 However, neither experimental data comparisons nor other theoretical results are available for reference. The properties of other stationary points in three PESs are also summarized in Table 2.
Table 2 Stationary points for three PESs of the SiH2 system, with the units of R1 and R2 in a0, θHSiH in deg, ΔE and ΔV in eV, and ω1, ω2 and ω3 in cm−1
|
|
R
1
|
R
2
|
θ
HSiH
|
ΔEa |
ΔVb |
ω
1
|
ω
2
|
ω
3
|
|
Relative to the energies of the respective 11A′ state.
Relative to the Si (1D) + H2 (X1Σ+g) asymptote.
|
| 13A′′ |
| GM(C2v) |
4.860 |
2.816 |
119.3 |
0.9145 |
−1.749 |
2142 |
2057 |
931 |
| Theor.65 |
4.786 |
2.789 |
118.2 |
0.8856 |
|
2292 |
2237 |
910 |
| Theor.27 |
4.799 |
2.802 |
117.8 |
0.9121 |
|
|
|
|
| Theor.24 |
4.792 |
2.791 |
118.3 |
0.8478 |
|
2241 |
2295 |
921 |
| Theor.25 |
4.802 |
2.795 |
118.4 |
0.8626 |
|
2224 |
2285 |
934 |
| Exp.66 |
|
|
|
0.91 ± 0.03 |
|
|
|
|
| LM1(C2v) |
1.411 |
4.211 |
19.7 |
|
−0.817 |
4049 |
640 |
331 |
| LM2(C∞v) |
4.512 |
7.376 |
0.0 |
|
0.7600 |
472 |
2247 |
174 |
| TS1 (D∞h) |
5.528 |
2.764 |
180.0 |
|
−0.706 |
2502 |
4045 |
1950i |
| TS2(C2v) |
2.879 |
2.990 |
57.6 |
|
0.0464 |
1734i |
1831 |
1598 |
|
|
| 13A′ |
| GM(D∞h) |
6.240 |
3.120 |
180.0 |
3.2124 |
0.5490 |
989 |
854 |
1472 |
| Theor.27 |
6.230 |
3.115 |
180.0 |
3.1818 |
|
|
|
|
| Theor.67 |
5.628 |
2.814 |
180.0 |
3.163 |
|
|
|
|
| LM(C∞v) |
4.008 |
2.854 |
0.0 |
|
0.8452 |
2101 |
36 |
219 |
| TS1(C∞v) |
2.887 |
5.838 |
0.0 |
|
0.8812 |
747i |
1468 |
391 |
| TS2(D∞h) |
7.575 |
2.869 |
180.0 |
|
0.8152 |
2048 |
427 |
537i |
| TS3(C2v) |
4.024 |
3.546 |
69.1 |
|
2.3347 |
1213 |
2069 |
789i |
|
|
| 21A′ |
| GM(C2v) |
5.466 |
2.757 |
165.0 |
3.3759 |
0.7125 |
2499 |
2361 |
228 |
| Theor.65 |
5.444 |
2.755 |
162.3 |
3.5556 |
|
2416 |
2294 |
856 |
| Theor.30 |
5.507 |
2.777 |
165.1 |
|
0.7086 |
|
|
|
| Theor.27 |
5.503 |
2.776 |
164.8 |
3.3480 |
|
|
|
|
| TS1(C2v) |
3.261 |
3.168 |
61.9 |
|
4.1005 |
2479i |
1288 |
1006 |
| TS2(D∞h) |
5.515 |
2.757 |
180.0 |
|
0.7138 |
2327 |
4175 |
266i |
Fig. 3 shows contour plots for the C2v insertion of the silicon atom into the hydrogen molecule. All the potential energies involved take the Si (1D) + H2 (X1Σ+g) dissociation energy as the asymptote. Visible from Fig. 3(a) are the stationary points corresponding to local minimum 1 (LM1), TS2, GM and transition state 1 (TS1) successively, among which the highest potential barrier is TS2 with 0.0464 eV. By analyzing the configuration of each stationary point in the reaction process, it presents a regular characteristic that with RSi–H2 decreases, the angle of H–Si–H gradually increases, and the Si–H bond length gradually shortens. As silicon atoms collide with hydrogen molecules from infinity in a C2v symmetry manner, a transition state and a GM appear in panel (b), with the bond angle increasing and the bond length decreasing during the reaction process. Similarly, the 21A′ state tends to increase the bond angle and shorten the bond length in the reaction, and its reaction path in panel (c) is the reactant – TS1 – GM – TS2 – product. The minimum potential energy curves at different angles for the 11A′,35 13A′′, 13A′ and 21A′ states of SiH2 are illustrated in Fig. 4. The structure for the symmetric geometry configuration of minimum energy at each angle is from the H–Si–H bond angle of 10° to 180°. The potential well at 91.5° of the 11A′ state is wide and deep (−2.663 eV), and the energy decreases from 10° to 91.5° and then rises to 180° monotonically. The highest potential barriers for the 13A′′ and 13A′ states correlated with Si (3P) + H2 (X1Σ+g) are TS2 with 0.0464 eV and transition state 3 (TS3) with 2.3347 eV, respectively. The 21A′ state which correlates with Si (1D) + H2 (X1Σ+g) is seen to have a maximum (4.1005 eV) at 61.9° before dropping to its minima. Furthermore, there are no discrepancies between the theoretical predictions21,67 and our work for the minimum potential energy curves from 60° to 180°. Taking the potential barriers of three excited states into account, it can be predicted that the occurrence of the molecular reaction is easiest in the 13A′′ state, followed by the 13A′ state, and is the hardest in the 21A′′ state due to the highest potential barrier, which will be further verified in the following dynamic calculations.
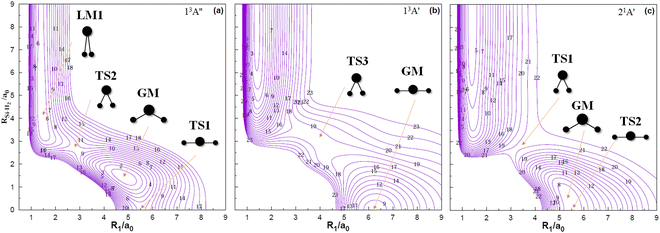 |
| | Fig. 3 Contour plots for bond stretching for the C2v insertion of the Si into H2 which are equally spaced in panel (a) and (b) by 0.190 eV and in panel (c) by 0.245 eV, starting from −5.660 eV, −4.898 eV and −5.578 eV, respectively. | |
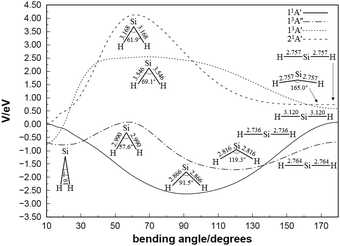 |
| | Fig. 4 Minimum potential energies in eV at different angles for the 11A′, 13A′′, 13A′ and 21A′ states of silylene. | |
The molecular reaction dynamics of Si (1D) + H2 (X1Σ+g) (v = 0, j = 0) → H (2S) + SiH (X2Π) and Si (3P) + H2 (X1Σ+g) (v = 0, j = 0) → H (2S) + SiH (A2Δ) are investigated using the QCT method42,43 to better understand the reaction mechanism and complement the relevant dynamical calculations based on the three novel PESs. The ICS is defined as
| | 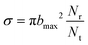 | (10) |
where
bmax is the maximum impact parameter, and
Nr and
Nt represent the number of trajectories participating in the reaction and the total number of trajectories, respectively. 20
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 trajectories were run for each collision energy in the final formal calculations. In addition, the reaction time step is 0.1 fs, and the initial distance from Si to the center of mass of the H
2 molecule is separated by 15 Å to keep the initial interaction energy between Si and H
2 infinitesimal. While in the TDWP method, ICS is obtained by superposition of the reaction probabilities of selected initial states under different quantum numbers of angular momentum
| | 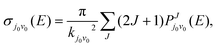 | (11) |
Where
kj0v0 is the initial wave number corresponding to the selected translational energy
E, and
J is the total angular momentum of the reaction system.
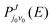
represents the reaction probabilities of the initial state in
eqn (11).
r is the distance between the two H atoms, and
R is the distance between the Si atom and the center of mass of the two H atoms. Specific details about the calculation method of TDWP are described in other works.
68–71 The numerical parameters involved are summarized in
Table 3.
Table 3 Numerical parameters used in the time-dependent wave packet calculation
| Parameter |
13A′′ |
13A′ |
21A′ |
| Scattering coordinate (R) range/bohr |
0.1–17 |
0.1–20 |
0.1–17 |
| Number of translational basis functions |
211 |
199 |
241 |
| Internal coordinate (r) range/bohr |
0.5–16 |
0.5–18 |
0.5–17 |
| Number of vibrational basis functions |
155 |
112 |
189 |
| Number of rotational basis functions |
100 |
110 |
100 |
| Centre of the initial wave packet on scattering coordinate/bohr |
13.1 |
16.1 |
13.1 |
| The energy of the initial wave packet/eV |
2.5 |
1.0 |
4.5 |
| Width parameter of the wave packet/bohr |
0.23 |
0.20 |
0.32 |
| Propagation time/a.u. |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
To investigate the number of component wave convergence required by ICS, Fig. 5 provides the curves of Si + H2 reaction probability as a function of collision energy for different total angular momenta, and the reactant H2 (v = 0, j = 0) molecule is in the ground vibration–rotation state in panels (a)–(c). The range of selected collision energy varies between 1.5–3.5 eV, 1.5–2.3 eV and 3.5–5.5 eV for the 13A′′, 13A′ and 21A′ states, respectively. Overall, with the increase of collision energy, all the reaction probabilities total angular momenta increase corresponding to the 13A′′, 13A′ and 21A′ states, which is consistent with the result given by the MEP in Fig. 1(c), in that all three reactions are endothermic. It is also observed that the threshold increases with the increase of the total angular momentum J, and the total angular momentum J converges at J = 85, 50 and 60 for the 13A′′, 13A′ and 21A′ states. The maximum reaction probability of the 21A′ state doesn’t exceed 0.055, which is due to the existence of the high potential barrier (see Fig. 4) of the minimum potential energy path in the C2v insertion reaction. However, the maximum reaction probabilities of the 13A′′ state and 13A′ state can reach 0.85 and 0.33, respectively, which means that the occurrence of the molecular reaction is easiest in the 13A′′ state, followed by the 13A′ state and the 21A′ state. The contributions of the J partial wave to the total ICS of the 13A′′, 13A′ and 21A′ states are shown in Fig. 6 under the different translational energies respectively. As expected, the contribution of the partial wave under total angular momentum to the ICS increases with the collision energy. At the maximum translational energy of the 13A′′, 13A′ and 21A′ states (3.5 eV, 2.3 eV and 5.5 eV) studied in this work, calculation of the ICS for exact evaluation must include all partial waves with J < 80, J < 50 and J < 60 respectively.
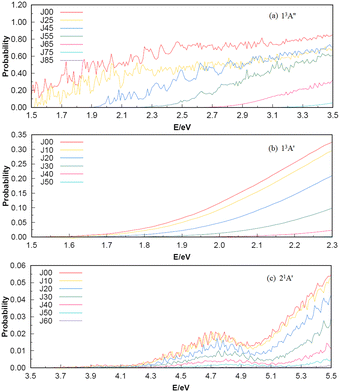 |
| | Fig. 5 The energy dependence reaction probabilities of 13A′′, 13A′ and 21A′ states for several selected total angular momentum J contributions. | |
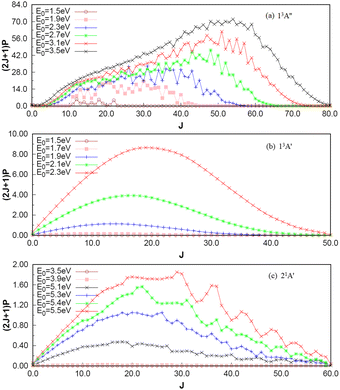 |
| | Fig. 6 Contribution of wave fractions corresponding to J to the total integral cross section under different translational energies for 13A′′, 13A′ and 21A′ states. | |
The ICSs of the 13A′′, 13A′ and 21A′ states for the reaction Si (1D) + H2 (X1Σ+g) (v = 0, j = 0) → H (2S) + SiH (X2Π) and reaction Si (3P) + H2 (X1Σ+g) (v = 0, j = 0) → H (2S) + SiH (A2Δ), as a function of the collision energy, are shown in Fig. 7. In panel (a), the initial scattering energy thresholds of the 13A′′and 21A′ electron states are 1.301 and 4.770 eV, respectively, which are greater than the highest potential barriers of the minimum potential energy paths in the C2v insertion reaction: 0.0464 and 4.1005 eV. However, the initial scattering energy threshold of the 13A′ state is 1.778 eV, which is smaller than the highest barrier of 2.3347 eV for the minimum potential energy path in the C2v insertion reaction, probably due to the quantum tunneling effect. In addition, there are no large oscillations among the three ICSs, and the entire ICS behavior is smooth. As predicted in Fig. 4 and 5, the ICS responds easily in the 13A′′ state, followed by the 13A′ state, and has the most difficulty responding in the 21A′ state. Furthermore, the ICS of the three electronic states increases with the scattering energy and reaches the highest point at scattering energies of 4.336, 6.505 and 7.589 eV, respectively. In addition, ICS is calculated using the TDWP method and compared with the results from QCT in panels (b)–(d). The results show that the two calculations have roughly the same trend, but with the increase of collision energy, the difference between the results of QCT and TDWP increases gradually. Considering that the QCT method is statistical and has an inherent error range, the oscillation characteristics are not obvious. For the quantum mechanical behavior, however, the resonance and quantum tunneling near the threshold energy (low collision energy) will be present. This may be the main reason that the quantum dynamics results are obviously higher than the QCT results. In panel (d), although both results are positively correlated with the collision energy, the QM results show clear oscillations, which are stronger due to the higher barrier of the 21A′ state. Unfortunately, no other experimental or theoretical studies on the dynamics of the three low-lying electronic states were found until the first report of the dynamic calculations of the 13A′′, 13A′ and 21A′ states on global PESs for SiH2 were performed in the present work. Only the ICSs of v = 0 and j = 0 are calculated in this paper, which be valuable to further explore the dynamical information of the vibration–rotation distribution and the isotope effect on the Si + H2 (v = 0, j = 0) → H + SiH molecular reaction.
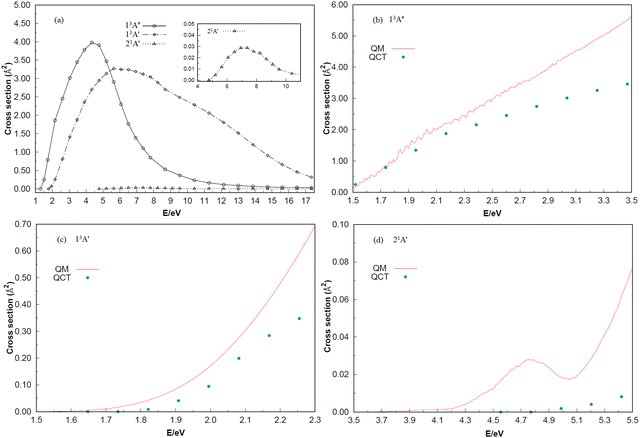 |
| | Fig. 7 (a) The integral cross sections of three electronic states calculated by QCT for the Si + H2 (v = 0, j = 0) → H + SiH reaction. Shown in the inset are the cuts of regions with collision energies from 4 to 12 eV of the 21A′ state. (b–d) The integral cross sections of three electronic states calculated by QCT and QM for the Si + H2 (v = 0, j = 0) → H + SiH reaction. | |
4. Conclusions
Three global adiabatic PESs have been reported for the 13A′′, 13A′ and 21A′ states based on a least-squares fit to high-level MRCI(Q) energies, calculated using AV(Q+d,5+d)Z basis sets. A variety of stationary points including geometries, energies and vibrational frequencies were predicted and the energy correlation diagram of the title states was reported. All topographical features have been carefully examined and compared with previous high-quality reported ones and the available experimental results are in good agreement. Finally, the ICSs of the Si + H2 (v = 0, j = 0) → H + SiH reaction based on novel PESs were calculated using the QCT method and TDWP method, which provides a theoretical reference for other research work in the absence of experimental values. In conclusion, the novel PESs reported in this paper cannot only be adopted for dynamics studies of the Si + H2 (v = 0, j = 0) → H + SiH reaction, but as a component of PESs for the construction of larger Si/H containing systems.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the LiaoNing Revitalization Talents Program (Grant No. XLYC2007094).
References
- S. Koseki and M. S. Gordon, J. Mol. Spectrosc., 1987, 123, 392–404 CrossRef CAS.
- R. Escribano and A. Campargue, J. Chem. Phys., 1998, 108, 6249–6257 CrossRef CAS.
- M. Wang, X. Sun and W. Bian, J. Chem. Phys., 2008, 129, 084309 CrossRef PubMed.
- J. Cao, Z. Zhang, C. Zhang, K. Liu, M. Wang and W. Bian, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13180–13185 CrossRef CAS PubMed.
- J. M. Jasinski and J. O. Chu, J. Chem. Phys., 1988, 88, 1678–1687 CrossRef CAS.
- M. D. Su, J. Am. Chem. Soc., 2002, 124, 12335–12342 CrossRef CAS PubMed.
- M. Denk, J. C. Green, N. Metzler and M. Wagner, J. Chem. Soc., Dalton Trans., 1994, 16, 2405–2410 RSC.
- S. N. Yurchenko,
et al.
, Can. J. Chem., 2004, 82, 694–708 CrossRef CAS.
- B. Wirsam, Chem. Phys. Lett., 1971, 10, 180–182 CrossRef CAS.
- S. N. Yurchenko, F. Sinden, L. Lodi, C. Hill, M. N. Gorman and J. Tennyson, Mon. Not. R. Astron. Soc., 2018, 473, 5324–5333 CrossRef CAS.
- F. Allard and P. Hauschildt, Astrophys. J., 1995, 445, 433 CrossRef CAS.
- I. Dubois, G. Herzberg and R. D. Verma, J. Chem. Phys., 1967, 47, 4262–4263 CrossRef CAS.
- I. Dubois, Can. J. Phys., 1968, 46, 2485–2490 CrossRef CAS.
- E. Milligan and M. Jacox, J. Chem. Phys., 1970, 52, 2594 CrossRef.
- L. Fredin, R. Hauge, Z. Kafafi and J. Margrave, J. Chem. Phys., 1985, 82, 3542–3545 CrossRef CAS.
- J. Thoman and J. Steinfeid, Chem. Phys. Lett., 1986, 124, 35 CrossRef CAS.
- E. Hirota and H. Ishikawa, J. Chem. Phys., 1999, 110, 4254–4257 CrossRef CAS.
- H. Ishikawa and O. Kajimoto, J. Mol. Spectrosc., 1991, 150, 610–619 CrossRef CAS.
- H. Ishikawa and O. Kajimoto, J. Mol. Spectrosc., 1995, 174, 270–273 CrossRef CAS.
- H. Ishikawa, Y. Muramoto and N. Mikami, J. Mol. Spectrosc., 2002, 216, 90–97 CrossRef CAS.
- B. Wirsam, Chem. Phys. Lett., 1972, 14, 214–216 CrossRef CAS.
- J. H. Meadows and H. F. Schaefer, J. Am. Chem. Soc., 1976, 98, 4383–4386 CrossRef CAS.
- M. E. Colvin, R. S. Grev, H. F. Schaefer and J. Bicerano, Chem. Phys. Lett., 1983, 99, 399–405 CrossRef CAS.
- W. Allen and H. F. Schaefer III, Chem. Phys., 1986, 108, 243–274 CrossRef CAS.
- W. Gabriel, P. Rosmus, K. Yamashita, K. Morokuma and P. Palmieri, Chem. Phys., 1993, 174, 45–56 CrossRef CAS.
- G. Duxbury, A. Alijah and R. R. Trieling, J. Chem. Phys., 1993, 98, 811–825 CrossRef CAS.
- I. Tokue, K. Yamasaki and S. Nanbu, J. Chem. Phys., 2005, 122, 144307 CrossRef PubMed.
- I. Tokue, K. Yamasaki and S. Nanbu, J. Chem. Phys., 2006, 124, 114308 CrossRef PubMed.
- X. Liu, W. Bian, X. Zhao and X. Tao, J. Chem. Phys., 2006, 125, 074306 CrossRef PubMed.
- Y. Wu, C. Zhang and H. Ma, RSC Adv., 2017, 7, 12074–12084 RSC.
- V. H. Clark, A. Owens, J. Tennyson and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2020, 246, 106929 CrossRef CAS.
- J. Cao, Y. Wu, H. Ma, Z. Shen and W. Bian, Phys. Chem. Chem. Phys., 2021, 23, 6141–6153 RSC.
- A. Aguado and M. Paniagua, J. Chem. Phys., 1992, 96, 1265–1275 CrossRef CAS.
- A. Aguado, C. Tablero and M. Paniagua, Comput. Phys. Commun., 1998, 108, 259–266 CrossRef CAS.
- H. N. Wang, Y. L. Lü, J. X. Chen, Y. Z. Song, C. Y. Zhang and Y. Q. Li, Phys. Chem. Chem. Phys., 2022, 24, 7759–7767 RSC.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- T. H. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef CAS.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- A. J. C. Varandas, J. Chem. Phys., 2007, 126, 244105 CrossRef CAS PubMed.
- K. L. Han, G. Z. He and N. Q. Lou, J. Chem. Phys., 1996, 105, 8699–8704 CrossRef CAS.
- M. D. Chen, K. L. Han and N. Q. Lou, J. Chem. Phys., 2003, 118, 4463–4470 CrossRef CAS.
-
H. J. Werner, et al., MOLPRO Version 2012.1, 2012, see http://www.molpro.net Search PubMed.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS.
- A. Karton and J. M. L. Martin, Theor. Chim. Acta, 2006, 115, 330–333 CrossRef CAS.
- A. J. C. Varandas, J. Chem. Phys., 2000, 113, 8880 CrossRef CAS.
- A. J. C. Varandas, J. Chem. Phys., 2008, 129, 234103 CrossRef CAS PubMed.
- Y. Q. Li, Y. Z. Song, P. Song, Y. Z. Li, Y. Ding, M. T. Sun and F. C. Ma, J. Chem. Phys., 2012, 136, 194705 CrossRef CAS PubMed.
-
J. N. Murrell, S. Carter, S. C. Farantos, P. Huxley and A. J. C. Varandas, Molecular Potential Energy Functions, Wiley, Chichester, 1984 Search PubMed.
- A. J. C. Varandas, J. Chem. Phys., 1989, 90, 4379–4391 CrossRef CAS.
- Y. Q. Li, Y. Z. Song and A. J. C. Varandas, Eur. Phys. J. D, 2015, 69, 22 CrossRef.
- Y. Q. Li, F. C. Ma and M. T. Sun, J. Chem. Phys., 2013, 139, 154305 CrossRef CAS PubMed.
-
K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. Vol. 4, Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979, and references herein Search PubMed.
- M. Betrencourt, D. Boudjaadar, P. Chollet, G. Guelachvili and M. Morillon-Chapey, J. Chem. Phys., 1986, 84, 4121–4126 CrossRef CAS.
- D. H. Shi, P. L. Li, Z. L. Zhu and J. F. Sun, Spectrochim. Acta, Part A, 2013, 115, 259–268 CrossRef CAS PubMed.
- D. H. Shi, J. P. Zhang, J. F. Sun, Z. L. Zhu, B. H. Yu and Y. F. Liu, J. Mol. Struct., 2008, 851, 30–34 CrossRef CAS.
- R. S. Ram, R. Engleman and P. F. Bernath, J. Mol. Spectrosc., 1998, 190, 341–352 CrossRef CAS PubMed.
- S. J. Chai, H. N. Wang, Y. L. Lü, Q. Guo and Y. Q. Li, Phys. Chem. Chem. Phys., 2020, 22, 26544–26551 RSC.
- C. L. Yang, Y. J. Huang, X. Zhang and K. L. Han, J. Mol. Struct., 2003, 625, 289–293 CrossRef CAS.
-
K. P. G. H. Huber, NIST Chemistry WebBook 69, 2001, see http://webbook.nist.gov/chemistry Search PubMed.
- A. Balakrishnan, V. Smith and B. P. Stoicheff, Phys. Rev. Lett., 1992, 68, 2149–2152 CrossRef CAS PubMed.
- Y. Yamaguchi, T. J. Van Huis, C. D. Sherrill and H. F. Schaefer III, Theor. Chem. Acc., 1997, 97, 341–349 Search PubMed.
- J. Berkowitz, J. P. Greene, H. Cho and B. Ruščić, J. Chem. Phys., 1987, 86, 1235–1248 CrossRef CAS.
- J. E. Rice and N. C. Handy, Chem. Phys. Lett., 1984, 107, 365–374 CrossRef CAS.
-
J. Z. H. Zhang, Theory and Applications of Quantum Molecular Dynamics, World Scientific, Singapore, 1999 Search PubMed.
- T. S. Chu, Y. Zhang and K. L. Han, Int. Rev. Phys. Chem., 2006, 25, 201–235 Search PubMed.
- Z. G. Sun, S. Y. Lee, H. Guo and D. H. Zhang, J. Chem. Phys., 2009, 130, 174102 CrossRef PubMed.
- P. Y. Zhang and K. L. Han, J. Phys. Chem. A, 2013, 117, 8512–8518 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a
*a
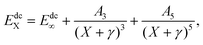
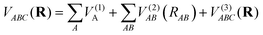
 are the energies of the separated atoms in their corresponding electronic state. We assume that all these energy terms approach zero at the dissociation limit in this work.
are the energies of the separated atoms in their corresponding electronic state. We assume that all these energy terms approach zero at the dissociation limit in this work. 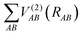 is the two-body energy terms, defined as
is the two-body energy terms, defined as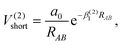
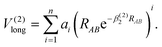
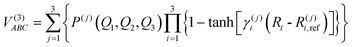

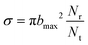
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were run for each collision energy in the final formal calculations. In addition, the reaction time step is 0.1 fs, and the initial distance from Si to the center of mass of the H2 molecule is separated by 15 Å to keep the initial interaction energy between Si and H2 infinitesimal. While in the TDWP method, ICS is obtained by superposition of the reaction probabilities of selected initial states under different quantum numbers of angular momentum
000 trajectories were run for each collision energy in the final formal calculations. In addition, the reaction time step is 0.1 fs, and the initial distance from Si to the center of mass of the H2 molecule is separated by 15 Å to keep the initial interaction energy between Si and H2 infinitesimal. While in the TDWP method, ICS is obtained by superposition of the reaction probabilities of selected initial states under different quantum numbers of angular momentum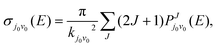
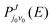 represents the reaction probabilities of the initial state in eqn (11). r is the distance between the two H atoms, and R is the distance between the Si atom and the center of mass of the two H atoms. Specific details about the calculation method of TDWP are described in other works.68–71 The numerical parameters involved are summarized in Table 3.
represents the reaction probabilities of the initial state in eqn (11). r is the distance between the two H atoms, and R is the distance between the Si atom and the center of mass of the two H atoms. Specific details about the calculation method of TDWP are described in other works.68–71 The numerical parameters involved are summarized in Table 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000





