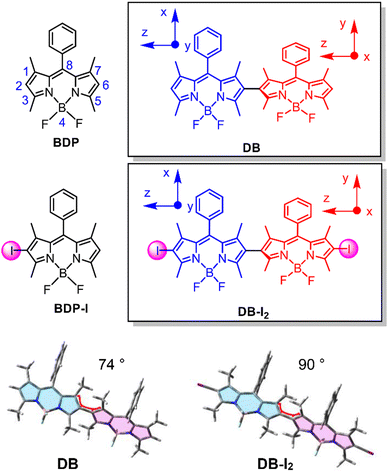
Observation of the triplet energy transfer in orthogonal photoexcited iodinated-BODIPY dimers†
Andrey A.
Sukhanov‡
 a,
Huaiman
Cao‡
a,
Huaiman
Cao‡
 b,
Xue
Zhang
b,
Xue
Zhang
 b,
Jianzhang
Zhao
b,
Jianzhang
Zhao
 *bc and
Yuri E.
Kandrashkin‡
*bc and
Yuri E.
Kandrashkin‡
 *a
*a
aZavoisky Physical-Technical Institute, FRC Kazan Scientific Center of RAS, 420029, Kazan, Russia. E-mail: yuk@kfti.knc.ru
bState Key Laboratory of Fine Chemicals, Frontiers Science Center for Smart Materials, School of Chemical Engineering, Dalian University of Technology, Dalian, 116024, P. R. China. E-mail: zhaojzh@dlut.edu.cn
cState Key Laboratory of Chemistry and Utilization of Carbon Based Energy Resources, College of Chemistry, Xinjiang University, Urumqi, 830017, P. R. China
First published on 6th December 2022
Abstract
Intramolecular charge and energy transfer processes initiated by light absorption can change the photosensitization properties of molecular conjugates. Transient optical and electron paramagnetic resonance (TREPR) spectroscopies are well suited for the study of these processes. In the TREPR spectra of the triplet state of an iodinated BODIPY dimer, we have observed the effect of the averaging of the zero-field (ZFS) parameter E, which becomes more efficient with increasing temperature. This property is associated with triplet energy transfer from one chromophore in the dimer to another, implying the presence of a dynamic equilibrium between the two chromophores of the dimer. From the comparison of the ZFS parameters of the monomer and the dimer, the rates of the reversible hopping are derived within the framework of a two-site model. The obtained data indicate that the triplet states are separated by an energy barrier of ca. 70 K (ca. 0.006 eV) and that below this temperature energy transfer occurs via tunneling.
1. Introduction
Chromophores in which the triplet excited state can be populated following photoexcitation are of essential importance in fundamental photochemical research and numerous applications.1–3 In particular, the development of triplet photosensitizers is desirable for many applications in photocatalysis,4,5 photodynamic therapy,6–8etc. Compact dimers with a fixed orthogonal geometry have a beneficial increase of the sensitization quantum yield,9 which is a result of the photoinduced generation of charge-transfer states and subsequent charge recombination (CR)-induced intersystem crossing (ISC) via metastable states.10–13 Due to the orthogonal planes of the chromophores there are several metastable states with close energies. As a result, these states are often characterized by intramolecular charge and energy transfer that can potentially increase the electronic relaxation to the ground state as well as the energy transfer to the nearby molecules.10,14 Thus, these processes can play an important role in determining the efficiency of the sensitizing. In particular, it has been shown that the energy hopping increases the rate of flip-flop spin transitions between distant species.15During the past several years we have intensively studied rigid molecular conjugates with several chromophores16–18 and studied a number of remarkable phenomena by transient optical and magnetic resonance spectroscopy. Recently, we have developed a model for the description of the evolution of the spin populations in molecular conjugates due to reversible transitions between nearly degenerate triplet states, which we denote as triplet exciton hopping.15,19,20 The model allows the spectral and kinetic properties of the molecule to be related to one another, which gives a better understanding of the processes involved. However, some challenges still exist. For instance, it is difficult to monitor the energy transfer between two identical chromophores, because the initial and final states are optically indistinguishable.21,22 To expand the nature of the fundamental processes initiated by the light absorption we have prepared several Bodipy dimers in which the molecular planes of the two chromophores are orthogonal to one another. The analysis of the optical and time-resolved electron paramagnetic resonance (TREPR) spectra allows the presence of the dynamic equilibrium between several excited states to be demonstrated.16,18 One of the fingerprints of the dynamic equilibrium is the reduction of the zero field splitting (ZFS) parameters of the triplet state, which is a well-known property of molecules with D4h symmetry.15,23,24 The averaging of the spectral parameters in these molecules occurs via vibronic interactions known as the Ham effect and serves as evidence of the dynamic Jahn-Teller effect.23,25 The reduction of the parameter E has been detected in the triplet state of the primary donor P700 of Photosystem I, and has been explained as a result of the energy transfer between chromophores.26–29 However, to the best of our knowledge, no such phenomenon has been observed in the molecular dimers.
Herein we report the observation of reversible exciton hopping between two chromophores in an orthogonal Bodipy dimer. Two identical Bodipy moieties are rigidly linked along the molecular z-axis as shown in Scheme 1. Based on the orthogonal structure, the x and y axes of one chromophore align respectively along the y and x axes of the other chromophore. This property leads to a change of the sign of the ZFS parameter E following the energy transfer. Thus, reversible back and forth triplet energy transfer reduces the E-value observed in the transient EPR (TREPR) experiments. The comparison of the E-values of the monomers and the dimers and their temperature dependence allows us to estimate the rate of the energy exchange processes. The Arrhenius plot of these rates clearly demonstrates the presence of the energy barrier between the two triplet states and yields an estimate of 70 K (ca. 0.006 eV) for the barrier height. The reduction of the E-value is also detected below 70 K. However, it has a much weaker temperature dependence, which indicates the existence of an additional energy transfer mechanism operating in the tunnelling regime.
2. Results and disscusion
2.1 Molecular structure designing rationales
We prepared the dimer (DB) by linking two Bodipy units at the 2-position (Scheme 1). This structure is different from the previously reported Bodipy dimer in which the two units were connected at the 2- and meso-positions, respectively.30–32 This molecular structural difference leads to the two units being distinguishable in the previously reported dimer due to the different substitution positions. However, for DB, the two units are identical because they are both substituted at the same position. Efficient ISC was observed for the previously reported orthogonal Bodipy dimers,17,30,31 which is believed to be due to spin–orbit charge transfer ISC (SOCT-ISC).11,12,33–35 The two Bodipy dimers shown in Scheme 1 were synthesized using previously reported methods, and the synthesis procedures are presented in the ESI† (Scheme S1 and Fig. S1–S4).36For DB, the ISC efficiency was found to be very low, which is different from the previously reported results for the orthogonal dimers.16,30,31 Thus we prepared the iodinated Bodipy dimer, DB-I2, to access the triplet state of the dimer. The corresponding monomer BDP-I was also prepared as a reference compound. In both the dimer and monomer, iodination enhances the ISC substantially as has been observed previously for related compounds.6,37–41
2.2 Steady state spectroscopy: UV-vis absorption spectra and fluorescence emission spectra
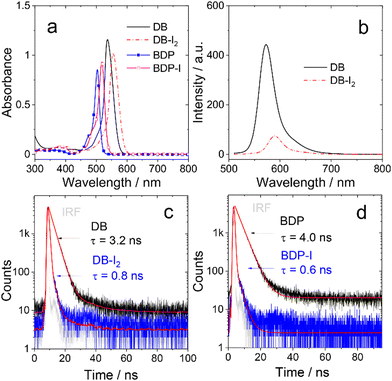
The steady state absorption and fluorescence of the compounds were studied (Fig. 1, Fig. S5 and S6, ESI†). The monomer BDP shows a sharp, strong absorption band centered at 504 nm, which is characteristic for the Bodipy chromophore.42,43 With mono iodination, BDP-I shows a slightly red-shifted absorption band centered at 518 nm. For the dimer DB, an absorption band centered at 537 nm is observed, which is not split. Thus, similar to the previously reported orthogonal Bodipy dimers,30 there is no exciton coupling effect for DB.45,46 A red shift of the main absorbance was also observed for DB-I2 (λabs = 555 nm). The increase of the red-shift is attributed to the substitution effect on the 2,6-position of the BDP chromophore. Dimers show slightly red-shifted absorption bands compared with the corresponding monomers, indicating a weak conjugate interaction between two subunits for dimers. The iodination effect on the relaxation of S1 state of the Bodipy monomer and dimer was studied by monitoring the fluorescence. The quantum yield of fluorescence is high in non-iodized BDP and DB (Table 1). Whereas, for both BDP-I and BD-I2, the fluorescence was substantially quenched as compared to the non-iodinated chromophores. This is in agreement with the expected heavy atom effect on the relaxation of the S1 state due to enhanced ISC caused by the iodine atom.6,37,38| λ abs | ε | λ em | Φ F (%) | Φ Δ (%) | τ F (ns) | k r | k nr | τ T (μs) | |
|---|---|---|---|---|---|---|---|---|---|
| a The maximum absorption wavelength, in nm. b The molar extinction coefficient at the absorption maxima, in 104 M−1 cm−1. c The wavelength of fluorescence emission band, in nm. d Fluorescence quantum yields. The valid values are accurate to 0.1%. e Singlet oxygen quantum yield. The values are derived within 5% accuracy. f The fluorescence average lifetime, in ns. The valid values are accurate to 0.1 ns. g The radiative rate constant (kr = ΦF/τF), in 107 s−1. The values are derived within 10% accuracy. h The nonradiative rate constant (knr = (1 − ΦF)/τF), in 107 s−1. The values are derived within 10% accuracy. Note herein knr = knr (S1 → S0) + kISC (S1 → T1). i The lifetime of the triplet excited state. The valid values are accurate to 1 ns. j Literature data.44 k Intrinsic triplet state lifetime eliminates the self-quenching effect of TTA. The values are derived within 5% accuracy. | |||||||||
| BDP | 504 | 8.5 | 513 | 68.0 | 3.0 | 4.0 | 17.0 | 8.00 | 210j |
| DB | 537 | 11.6 | 573 | 99.1 | 4.2 | 3.2 | 31.0 | 0.281 | 559 |
| BDP-I | 518 | 9.3 | 533 | 6.2 | 67.5 | 0.6 | 10.3 | 156 | 225k |
| DB-I2 | 555 | 10.2 | 591 | 19.9 | 57.6 | 0.8 | 24.9 | 100 | 148k |
The relaxation of the emissive S1 states of the compounds were studied by monitoring the decay traces of the fluorescence (Fig. 1 and Fig. S7, ESI†). For BDP, the fluorescence lifetime was determined as 4.0 ns. DB gives a similar fluorescence lifetime of 3.2 ns. Upon iodination, the fluorescence lifetimes are greatly reduced to 0.6 ns (BDP-I) and 0.8 ns (DB-I2), respectively. It should be noted that under the experimental conditions, only one of the two BDP units in either DB or DB-I2 was excited (Scheme 1), but no information can be derived from the fluorescence data whether or not there is singlet energy migration in the dimers.
The ISC efficiency of the compounds was analysed by measuring the quantum yield (ΦΔ) of singlet oxygen (Table 1). The quantum yield of the non-iodinated compounds is low, <5%. However, it is much higher for the iodinated compounds, 67.5% (BDP-I) and 57.6% (DB-I2). Iodination also has a significantly different effect on the rates of radiative and non-radiative decay, characterized by the rate constants, kr and knr, respectively. The radiative rate constants kr of DB and DB-I2 are similar (3.10 vs. 2.49 × 108 s−1), but the corresponding non-radiative rate constants knr differ dramatically (0.28 vs. 100 × 107 s−1). Similar results were observed for BDP and BDP-I.
2.3 Nanosecond transient absorption spectroscopy: triplet excited-state properties
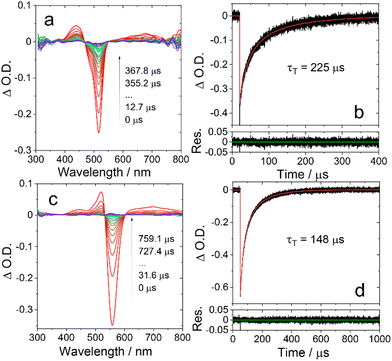
The triplet states of Bodipy compounds are usually non-phosphorescent in fluid solution at room temperature.47 Thus, the triplet states of the compounds were studied with nanosecond transient absorption (ns-TA) spectroscopy (Fig. 2, Fig. S8 and S9, ESI†). Upon ns pulsed laser excitation, an excited state absorption (ESA) band centered at 435 nm was observed for BDP-I, and a weak and broad ESA band was detected in the range of 550–800 nm. A sharp, strong ground state bleaching (GSB) band centered at 517 nm was also observed, these are the typical features of the triplet state transient absorption of Bodipy chromophores.38 It should be noted that an ESA band may be superimposed on the GSB band, i.e. in the range 450–550 nm. The triplet state lifetime is determined as 225 μs. This is the intrinsic triplet state lifetime with the additional triplet–triplet-annihilation (TTA) self-quenching effect considered in the numerical fitting of the decay traces,48,49 and it is much longer than the apparent value (ca. 50 μs, experimental condition-dependent) determined directly from the experimental data.38 We also measured the concentration-dependent triplet state lifetime of BDP-I (Fig. S10, ESI†). The estimated error of the least-square fitting was determined as 5.3% (or ±12 μs), and the intrinsic triplet lifetime of BDP-I is 225 ± 12 μs, which is consistent with the result obtained by fitting the decay curves with the kinetic model (225 s, Fig. 2b).A slightly different ESA feature is observed in the ns-TA spectra of DB-I2 (Fig. 2c), as indicated by the strong absorption at ca.555 nm. The overlap of the ESA and the GSB is more significant for DB-I2. The intrinsic triplet state lifetime is determined as 148 μs (Fig. 2d). The triplet state lifetime of DB is determined as 559 μs (Fig. S8, ESI†).
2.4 Time-resolved electron paramagnetic resonance spectroscopy
The TREPR datasets of BDP-I and DB-I2 in frozen solution (toluene/2MeTHF (3/1, v/v), 80 K) are presented in Fig. 3a and b, which show the overall evolution of the spectra at different delay times. The spectra of the monomer BDP-I show well-resolved ZFS of the triplet state. DB-I2 exhibits broader linewidths of the resonance transitions than BDP-I. Compared to BDP-I, it has the same value of the ZFS parameter D but a smaller value of the parameter E (see below).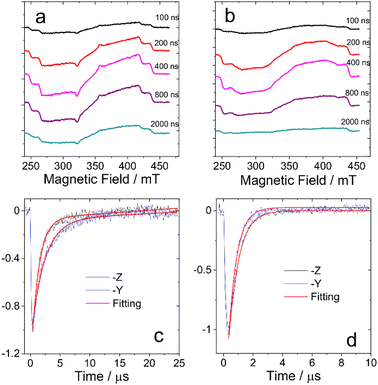 | ||
| Fig. 3 TREPR spectra of (a) BDP-I and (b) DB-I2 in frozen solution of toluene/2MeTHF (3/1, v/v) at 80 K. The spectra are obtained at several delay times after the laser flash as indicated in the right side of the panels (in ns). The time window is 0.1 μs. The normalized decay curves of the TREPR signal of (c) BDP-I and (d) DB-I2 at 80 K. Black curves show the TREPR transients measured at for BDP-I and DB-I2 at B = 254 mT which corresponds to the resonance conditions for molecules with z-axes aligned along the external magnetic field. Blue curves show the TREPR transients measured at B = 320 mT for BDP-I and at B = 315 mT for DB-I2 which correspond to the resonance conditions for molecules with y-axes aligned along the external magnetic field. Red curves represent the monoexponential (DB-I2) and biexponential (BDP-I) fitting of the experimental data. The decay rate constants are listed in Table 2. | ||
The TREPR signal decay curves of the triplet states of BDP-I and DB-I2 also differ. Fig. 3c and d show the decay traces chosen at critical points at which the signal arises from molecules with one of the molecular ZFS axes nearly parallel to the external magnetic field. The comparison of the decay rates (see Fig. 3 and Table 2) demonstrates several differences between the transients of the monomer and the dimer. First, the signal of the dimer decays monoexponentially while the signal of the monomer has biexponential character. Second, the mean lifetimes of the transients of the dimer are significantly shorter than those of the monomer. Third, in the monomers, the signal with the molecular z-axis parallel to the field decays more slowly than the signal with the field along the y-axis, while the opposite situation occurs in dimers. Thus, the time evolution of the TREPR spectra of the dimer is significantly different from that the monomer. The multiexponential character of the dimer decay curves implies the presence of extra processes that modulate the local environment.19,20 Thus, the properties of the dimer spectra cannot be explained within the framework of a triplet state confined to single subunit of the dimer.
Fig. 4 shows the comparison of the experimental and simulated spectra for a delay time of 0.5 μs after the laser flash. As can be seen, the spectra of the BDP-I and DB-I2 are reproduced well by the numerical simulation. The parameters used in simulations are listed in Table 3. The spin sublevel population parameters px, py and pz are practically the same for both molecules (see Table 3). This suggests that the triplet state in the dimer is populated by SOC-induced ISC, as in the monomer. Some properties of the dimer spectrum are modelled with less accuracy. The emissive net polarization of the dimer (see Fig. 4b), which is most noticeable by comparing the signal along the molecular z-axis (250–260 mT and 400–410 mT), indicates the presence of additional processes that influence the spin coherence and the populations of the spin sublevels. The relatively less EPR intensity of the dimer along z-axis might be also due to changes in rates of intersystem crossing populating the triplet state. The spin-Hamiltonian used for the simulations is given by the following expression:
| H/ħ = gβeBħ−1 + D(Sz2 − S2/3) + E(Sx2 − Sy2) | (1) |
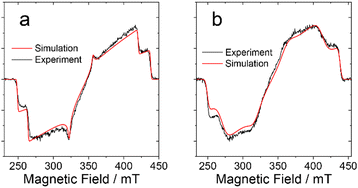 | ||
| Fig. 4 TREPR spectra of (a) BDP-I and (b) DB-I2 in frozen solution of toluene at 80 K. The spectra are recorded within the window 0.1 μs centered at 0.5 μs after the laser flash. Experimental data are in black and the simulation results are in red. The simulations parameters are listed in Table 3. | ||
| Compounds | D, MHz | E, MHz | p x | p y | p z |
|---|---|---|---|---|---|
| a ZFS parameters are derived within 10% accuracy. | |||||
| BDP-I | −2650 | 572 | 0 | 0.17 | 1 |
| DB-I2 | −2650 | 405 | 0 | 0.17 | 1 |
Here, the first term is the Zeeman frequency, determined by the value of the external field B, g-factor of the triplet state, Bohr magneton (βe) and the reduced Planck constant (ħ). The second and third terms represent the ZFS, determined by the parameters D and E.
Overall, the comparison of the spectral and kinetic properties of the EPR spectrum of dimers with those of monomers reveals several differences. These are (1) broadening of the EPR lines and (2) no change in value of the parameter D but a decrease in the value of the parameter E; (3) faster and more uniform signal decay across the spectrum, which is described well by a monoexponential function; and (4) a relative increase in the spin polarization decay along the y axis of the molecule compared to the decay along the z axis. The most natural way to explain these features is to assume intramolecular triplet energy transfer between two chromophores of the dimer. Given that the π-conjugation planes of these chromophores are orthogonal to each other and that the z-axis of the chromophore is directed along the molecular axis (see Scheme 1), one would expect the E-value of the ZFS tensor and spin polarization to decrease during the reversible energy transfer from one chromophore to the other while the D-value would remain unchanged. The formation of dynamic equilibrium between the two chromophores will also increase the rate of equalization of the populations of the spin sublevels caused by modulation of the local environment.19 Thus, it can be postulated that reversible energy transfer also promotes the acceleration of the signal decay in the dimer. Equilibration of the spin sublevels is faster for dimers because they undergo a greater change in the spin wave functions during energy transfer.17,19,20 For a given dimer structure (Scheme 1), the hopping between the two sites is expected to affect more strongly those molecules for which the magnetic field direction is close to the molecular xy-plane. Thus, the decay of spin polarization along the y-axis in the dimer should be faster compared to the decay along the z-axis. Finally, the energy transfer event changes the resonance conditions due to the difference in chromophore orientations, as well as due to the variation in interactions with the magnetic nuclei. This reduces the lifetime of the spin coherence and, as a consequence, increases the linewidth of the EPR transition.
Overall, the data obtained confirm the presence of a dynamic equilibrium between the two triplet states localized on the individual chromophores of the dimer. Similar effects in the TREPR spectra of dimers have been described previously.15–17,24,26–28 Note the transient decay indicates mainly the lifetime of the electron spin polarization of the T1 states of the compounds, not the lifetime of the T1 state itself.50–52
To confirm this hypothesis, we performed measurements at different temperatures. The results of these studies are shown in Fig. 5. All spectra are extracted from the time/field dataset at early times after the laser pulse. This figure clearly shows the change of the E parameter with temperature, while the magnitude of the D parameter remains practically unchanged. At lower temperatures, the value of the parameter E tends to become similar to the value of the monomer, while with increasing temperature there is a significant decrease in the value of E. This observation is supported by numerical simulations, which are also shown in Fig. 5a together with the experimental data.
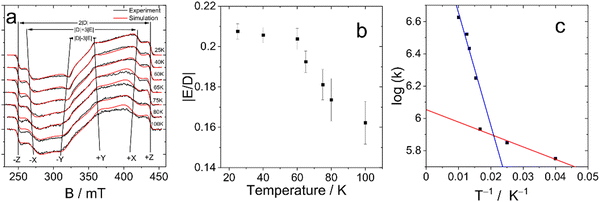 | ||
| Fig. 5 (a) Temperature dependence of TREPR Spectra of DB-I2 (black traces: experiment, red traces: simulation). The delay after the laser flash is 500 ns for spectra at 25–60 K and 200 ns for spectra at 65–100 K, the signal recording window is 0.1 μs. (b) The dependence of the ratio of the ZFS parameters of DB-I2 with the temperature. (c) Arrhenius plot of the exchange rate constant. The k-values are given in μs−1. The ZFS parameters and rate constants are listed in Table S1 (ESI†). | ||
The values of the ZFS parameters and the initial spin polarization obtained from the fitting of the experimental data are shown in Table 3 and Table S1 (ESI†) and are illustrated in Fig. 5b. These data confirm the change in the value of E as a result of the dynamic equilibrium between the two Bodipy units of the dimer as mentioned above.
The temperature dependence of the E parameter infers an additional feature of the photoexcited dimer (see Fig. 5b). It can be seen that changes in this parameter are nonlinear. The most dramatic change occurs in the range 60–70 K. Thus, we assume that there is a significant acceleration of the rate of exciton hopping at this temperature and above, i.e. the energy transfer between the triplet states of the two Bodipy units in the dimer has an energy barrier of the order of 60–70 K (kBT: ca. 6 meV).
Given that the change in the parameter E persists even at very low temperatures (25 K), we can suggest that the forward and reverse energy transfer rates are practically equal. This assumption is consistent with the structure of the dimer. Indeed, the two chromophores are directly connected by a single bond, and their planes are orthogonal (Scheme 1). In addition, the orthogonal structure of the dimer implies that the energy transfer from one chromophore to the other occurs nonadibatically. Under these conditions, the rate constant can be estimated from the two-site model. In the case of equal back and forward rates, k, they can be found from the shift of the resonance frequency caused by the energy transfer event. The expression (2) is a solution of the Bloch-McConnell equations for the shape of the EPR signal:19,20,53
 | (2) |
Here, the resonance offset frequencies ΔωA,B of one of the triplet transitions in the sites A and B are unequal, which is the result of the different orientations of the chromophores in the laboratory frame. The offset frequencies are expressed as ΔωA,B = gβeBħ−1 − ω0 ± Δω0/2. The first term here is the Zeeman frequency (see eqn (1)), the second term represents the microwave frequency, and the third term is the shift between two resonance frequencies at k = 0.
In the general case when k ≠ 0, the resonance fields can be found by solution of the equation dG/dB = 0, which gives the spacing between two resonance lines 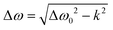 . This expression allows the hopping rates to be estimated from the analysis of the TREPR spectra. Indeed, according to the structure of the dimer (Scheme 1), the x- and y-axes of the chromophore swap during the non-adiabatic transition. As consequence, the resonance frequency also changes. By definition (see eqn (1)), the spacing between the resonances from the canonical x- and y-orientations is determined by the parameter E. Thus, for the given E-value at k = 0, one can easily find the rate constant.
. This expression allows the hopping rates to be estimated from the analysis of the TREPR spectra. Indeed, according to the structure of the dimer (Scheme 1), the x- and y-axes of the chromophore swap during the non-adiabatic transition. As consequence, the resonance frequency also changes. By definition (see eqn (1)), the spacing between the resonances from the canonical x- and y-orientations is determined by the parameter E. Thus, for the given E-value at k = 0, one can easily find the rate constant.
In the absence of fast exciton hopping or differences in the localized triplet state wavefunctions, the principal values of the ZFS tensor in dimers are the same as those of monomers (for example, in the presence of slow energy transfer little or no change in the resonance conditions is observed).16,17 This is also valid for the parameter D found from the analysis of the spectra of the monomer and dimer analyzed here. Indeed, energy transfer does not change the resonance properties of molecules with the z axis directed along the external magnetic field. As a result, the D values of the monomer and dimer are the same (see Table 3 and Fig. 4). Therefore, the E-value of the monomer, E0, should match well the E-value of the dimer at k = 0 which implies Δω0 = 2E0. Therefore, the energy hopping rate can be found as
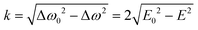 | (3) |
This expression is used to analyze the temperature dependence of the hopping rates. The Arrhenius plot of the obtained data is presented in Fig. 5c. It demonstrates significantly non single-exponential behavior of the exchange rate. On the logarithmic scale used in the Arrhenius plot, single-exponential behavior results in a straight line, while the experimental points form two distinct lines. The experimental data above 60 K can be fitted reasonably well by an exponent with an activation energy of ca. 70 K (red line). Below 60 K, there is a weak temperature dependence corresponding to an energy barrier of ca. 7.7 K (blue line).
The clear difference between the rate dependence below and above 60 K indicates the presence of two different energy transfer mechanisms and suggests that tunnelling occurs at low temperature. Given that the energy transfer is accompanied by a change in the orbital wave function, this mechanism is expected to affect the total wave function of the electron. Thus, it can be assumed that the exchange interaction plays an important role for energy transfer at low temperatures, which supports the Dexter type mechanism of the energy transfer.
The energy barrier derived for the DB-I2 dimer has a value similar to the barrier found for the previously studied Bodipy dimers (ca. 100 K).16,17 However, the energy transfer rate in the DB-I2 is much higher than in the previously studied dimers. This difference might be determined by the difference in the structures of these dimers but also by the presence of the heavy atoms in the DB-I2. The spin–orbit coupling in the latter dimer is much stronger than in the other dimers including the DB dimer studied here. Spin–orbit coupling can enhance not only the intersystem crossing but also promote mixing of the electronic wavefunctions of the confined triplet states of the two orthogonal chromophores. If this mechanism dominates, then the energy transfer in the DB dimer should be less than observed in DB-I2. Unfortunately, as discussed above, the quantum yield of the triplet state in DB is too low to allow the triplet states to be observed by the TREPR, although we can expect that further investigation of the orthogonal dimers with different substituting atoms instead of iodine might help to resolve this problem.
3. Conclusions
In conclusion, we have demonstrated the effect of the averaging of the ZFS parameter E (the Ham effect) in the orthogonal dimers formed by connection of two identical Bodipy moieties at their 2-positions. This phenomenon is associated with the reversible energy transfer from one dimer chromophore to the other. The data obtained from the TREPR spectra confirm the existence of dynamic equilibrium between the excited triplet states of the two Bodipy moieties of the dimer. Further analysis is done within the framework of two-site model which allows to derive the hopping rates of the triplet exciton. The energy barrier between two excited triplet states is estimated ca. 70 K (kBT = 0.006 eV). Below this temperature the tunneling mode of energy transfer is observed. These results address the challenge of observing energy transfer between two highly identical chromophores, which is difficult to study with transient optical spectroscopic methods.The non-adiabatic changes of the electron state during the energy transfer reduce the lifetime of these states and, hence, can stimulate the processes caused weak intermolecular interactions. Thus, one can expect that the intramolecular energy transfer can also promote the sensitizing properties which is a subject of further investigation.
Author contributions
A. A. S., H. C., and Y. E. K. contributed equally to this work. J. Z. and Y. E. K. conceived the study and designed the experiments. H. C. and X. Z. synthesized the target compounds and the references. H. C., A. A. S., Y. E. K. and X. Z. conducted the experiments. J. Z., Y. E. K., A. A. S. and H. C. prepared the manuscript and H. C. wrote the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. A. S. and Y. E. K. acknowledge financial support from the government assignment for FRC Kazan Scientific Center of RAS. J. Z. thanks the NSFC (U2001222), the Fundamental Research Funds for the Central Universities (DUT22LAB610) and the State Key Laboratory of Fine Chemicals for financial support. We thank Prof. Art van der Est, at Brock University, Canada, for fruitful comments and checking of the language of the manuscript.References
- J. Tian, J. Zhou, Z. Shen, L. Ding, J.-S. Yu and H. Ju, Chem. Sci., 2015, 6, 5969–5977 RSC.
- V. N. Nguyen, Y. Yim, S. Kim, B. Ryu, K. Swamy, G. Kim, N. Kwon, C. Y. Kim, S. Park and J. Yoon, Angew. Chem., Int. Ed., 2020, 59, 8957–8962 CrossRef CAS PubMed.
- X. Li, S. Kolemen, J. Yoon and E. U. Akkaya, Adv. Funct. Mater., 2017, 27, 1604053 CrossRef.
- L. Shi and W. Xia, Chem. Soc. Rev., 2012, 41, 7687–7697 RSC.
- X.-Z. Wang, Q.-Y. Meng, J.-J. Zhong, X.-W. Gao, T. Lei, L.-M. Zhao, Z.-J. Li, B. Chen, C.-H. Tung and L.-Z. Wu, Chem. Commun., 2015, 51, 11256–11259 RSC.
- A. Kamkaew, S. H. Lim, H. B. Lee, L. V. Kiew, L. Y. Chung and K. Burgess, Chem. Soc. Rev., 2013, 42, 77–88 RSC.
- O. J. Stacey and S. J. Pope, RSC Adv., 2013, 3, 25550–25564 RSC.
- C. Liu, L. Zhou, F. Wei, L. Li, S. Zhao, P. Gong, L. Cai and K. M.-C. Wong, ACS Appl. Mater. Interfaces, 2019, 11, 8797–8806 CrossRef CAS PubMed.
- M. Lv, X. Lu, Y. Jiang, M. E. Sandoval Salinas, D. Casanova, H. Sun, Z. Sun, J. Xu, Y. Yang and J. Chen, Angew. Chem., Int. Ed., 2022, 61, e202113190 CAS.
- J. W. Verhoeven, J. Photochem. Photobiol., C, 2006, 7, 40–60 CrossRef CAS.
- D. J. Gibbons, A. Farawar, P. Mazzella, S. Leroy-Lhez and R. M. Williams, Photochem. Photobiol. Sci., 2020, 19, 136–158 CrossRef CAS PubMed.
- M. A. Filatov, Org. Biomol. Chem., 2020, 18, 10–27 RSC.
- Y. Hou, X. Zhang, K. Chen, D. Liu, Z. Wang, Q. Liu, J. Zhao and A. Barbon, J. Mater. Chem. C, 2019, 7, 12048–12074 RSC.
- S. Fukuzumi, Org. Biomol. Chem., 2003, 1, 609–620 RSC.
- M. G. Dal Farra, C. Martin, E. Bergantino, Y. E. Kandrashkin, A. van der Est and M. Di Valentin, Phys. Chem. Chem. Phys., 2020, 22, 19982–19991 RSC.
- Y. E. Kandrashkin, Z. Wang, A. A. Sukhanov, Y. Hou, X. Zhang, Y. Liu, V. K. Voronkova and J. Zhao, J. Phys. Chem. Lett., 2019, 10, 4157–4163 CrossRef CAS PubMed.
- Y. E. Kandrashkin, X. Zhang, A. A. Sukhanov, Y. Hou, Z. Wang, Y. Liu, V. K. Voronkova and J. Zhao, J. Phys. Chem. C, 2020, 124, 3939–3951 CrossRef CAS.
- H. Cao, A. A. Sukhanov, M. M. Bakirov, Y. E. Kandrashkin, J. Zhao and V. K. Voronkova, J. Phys. Chem. C, 2022, 126, 5473–5482 CrossRef CAS.
- Y. E. Kandrashkin, M. Di Valentin and A. van der Est, J. Chem. Phys., 2020, 153, 094304 CrossRef CAS PubMed.
- Y. E. Kandrashkin and A. van der Est, J. Chem. Phys., 2022 DOI:10.1063/5.0132157.
- M. T. Whited, P. I. Djurovich, S. T. Roberts, A. C. Durrell, C. W. Schlenker, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2011, 133, 88–96 CrossRef CAS PubMed.
- S. S. Razi, Y. H. Koo, W. Kim, W. Yang, Z. Wang, H. Gobeze, F. D’Souza, J. Zhao and D. Kim, Inorg. Chem., 2018, 57, 4877–4890 CrossRef CAS PubMed.
- J. van der Waals, W. van Dorp and T. Schaafsma, in The Porphyrins, Physical Chemistry, Part B, 1979, vol. 4 Search PubMed.
- A. Regev, T. Galili, C. J. Medforth, K. M. Smith, K. M. Barkigia, J. Fajer and H. Levanon, J. Phys. Chem., 1994, 98, 2520–2526 CrossRef CAS.
- F. S. Ham, Phys. Rev., 1965, 138, A1727 CrossRef.
- I. Sieckmann, K. Brettel, C. Bock, A. van der Est and D. Stehlik, Biochemistry, 1993, 32, 4842–4847 CrossRef CAS PubMed.
- A. Kamlowski, L. Frankemöller, A. van der Est, D. Stehlik and A. Holzwart, Ber. Bunsen-Ges., 1996, 100, 2045–2051 CrossRef CAS.
- J. Niklas, in Investigation of the Electron Donor P700 and the Electron Acceptor A1 in Photosystem I of Oxygenic Photosynthesis Using EPR Spectroscopy, 2007 Search PubMed.
- J. Niklas, A. Agostini, D. Carbonera, M. Di Valentin and W. Lubitz, Photosynth. Res., 2022, 152, 213–234 CrossRef CAS PubMed.
- Y. Cakmak, S. Kolemen, S. Duman, Y. Dede, Y. Dolen, B. Kilic, Z. Kostereli, L. T. Yildirim, A. L. Dogan, D. Guc and E. U. Akkaya, Angew. Chem., Int. Ed., 2011, 50, 11937–11941 CrossRef CAS PubMed.
- W. Wu, X. Cui and J. Zhao, Chem. Commun., 2013, 49, 9009–9011 RSC.
- X.-F. Zhang and X. Yang, J. Phys. Chem. B, 2013, 117, 9050–9055 CrossRef CAS PubMed.
- E. Bassan, A. Gualandi, P. G. Cozzi and P. Ceroni, Chem. Sci., 2021, 12, 6607–6628 RSC.
- X. F. Zhang and N. Feng, Chem. – Asian J., 2017, 12, 2447–2456 CrossRef CAS PubMed.
- W. Hu, M. Liu, X.-F. Zhang, Y. Wang, Y. Wang, H. Lan and H. Zhao, J. Phys. Chem. C, 2019, 123, 15944–15955 CrossRef CAS.
- Z. Li, Y. Chen, X. Lv and W.-F. Fu, New J. Chem., 2013, 37, 3755–3761 RSC.
- T. Yogo, Y. Urano, Y. Ishitsuka, F. Maniwa and T. Nagano, J. Am. Chem. Soc., 2005, 127, 12162–12163 CrossRef CAS PubMed.
- W. Wu, H. Guo, W. Wu, S. Ji and J. Zhao, J. Org. Chem., 2011, 76, 7056–7064 CrossRef CAS PubMed.
- M.-R. Ke, S.-L. Yeung, D. K. Ng, W.-P. Fong and P.-C. Lo, J. Med. Chem., 2013, 56, 8475–8483 CrossRef CAS PubMed.
- D. Chen, Z. Zhong, Q. Ma, J. Shao, W. Huang and X. Dong, ACS Appl. Mater. Interfaces, 2020, 12, 26914–26925 CrossRef CAS PubMed.
- J. Zou, Z. Yin, K. Ding, Q. Tang, J. Li, W. Si, J. Shao, Q. Zhang, W. Huang and X. Dong, ACS Appl. Mater. Interfaces, 2017, 9, 32475–32481 CrossRef CAS PubMed.
- X. Zhang, Y. Xiao and X. Qian, Angew. Chem., Int. Ed., 2008, 47, 8025–8029 CrossRef CAS PubMed.
- D. Zhang, Y. Wang, Y. Xiao, S. Qian and X. Qian, Tetrahedron, 2009, 65, 8099–8103 CrossRef CAS.
- K. Chen, M. Taddei, L. Bussotti, P. Foggi, J. Zhao and M. Di Donato, ChemPhotoChem, 2020, 4, 487–501 CrossRef CAS.
- M. Bröring, R. Krüger, S. Link, C. Kleeberg, S. Köhler, X. Xie, B. Ventura and L. Flamigni, Chem. – Eur. J., 2008, 14, 2976–2983 CrossRef PubMed.
- B. Ventura, G. Marconi, M. Bröring, R. Krüger and L. Flamigni, New J. Chem., 2009, 33, 428–438 RSC.
- T. Zhang, X. Ma and H. Tian, Chem. Sci., 2020, 11, 482–487 RSC.
- Z. Lou, Y. Hou, K. Chen, J. Zhao, S. Ji, F. Zhong, Y. Dede and B. Dick, J. Phys. Chem. C, 2018, 122, 185–193 CrossRef CAS.
- Z. Wang, A. A. Sukhanov, A. Toffoletti, F. Sadiq, J. Zhao, A. Barbon, V. K. Voronkova and B. Dick, J. Phys. Chem. C, 2018, 123, 265–274 CrossRef.
- H. Levanon and J. R. Norris, Chem. Rev., 1978, 78, 185–198 CrossRef CAS.
- S. Richert, C. E. Tait and C. R. Timmel, J. Magn. Reson., 2017, 280, 103–116 CrossRef CAS PubMed.
- S. Weber, in Transient EPR, 2017 Search PubMed.
- A. Regev, H. Levanon, T. Murai and J. L. Sessler, J. Chem. Phys., 1990, 92, 4718–4723 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental section and supplementary figures. See DOI: https://doi.org/10.1039/d2cp04824h |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2023 |