Open Access Article
Open Access ArticleOn the 12C2H2 near-infrared spectrum: absolute transition frequencies and an improved spectroscopic network at the kHz accuracy level†
Antonio
Castrillo
 a,
Eugenio
Fasci
a,
Eugenio
Fasci
 a,
Tibor
Furtenbacher
a,
Tibor
Furtenbacher
 b,
Vittorio
D'Agostino
b,
Vittorio
D'Agostino
 a,
Muhammad A.
Khan
a,
Stefania
Gravina
a,
Muhammad A.
Khan
a,
Stefania
Gravina
 a,
Livio
Gianfrani
a,
Livio
Gianfrani
 *a and
Attila G.
Császár
*a and
Attila G.
Császár
 *b
*b
aDepartment of Mathematics and Physics, Università degli Studi della Campania “Luigi Vanvitelli”, 81100, Caserta, Italy. E-mail: livio.gianfrani@unicampania.it
bLaboratory of Molecular Structure and Dynamics, Institute of Chemistry, ELTE Eötvös Loránd University and MTA-ELTE Complex Chemical Systems Research Group, Pázmány Péter sétány 1/A, H-1117 Budapest, Hungary. E-mail: attila.csaszar@ttk.elte.hu
First published on 25th August 2023
Abstract
Lamb dips of twenty lines in the P, Q, and R branches of the ν1 + ν3 + ν41 vibrational band of 12C2H2, in the spectral window of 7125–7230 cm−1, have been measured using an upgraded comb-calibrated frequency-stabilized cavity ring-down spectrometer, designed for extensive sub-Doppler measurements. Due to the large number of carefully executed Lamb-dip experiments, and to the extrapolation of absolute frequencies to zero pressure in each case, the combined average uncertainty of the measured line-center positions is 15 kHz (5 × 10−7 cm−1) with a 2-σ confidence level. Selection of the twenty lines was based on the theory of spectroscopic networks (SN), ensuring that a large number of transitions, measured previously by precision-spectroscopy investigations, could be connected to the para and ortho principal components of the SN of 12C2H2. The assembled SN contains 331 highly precise transitions, 119 and 121 of which are in the ortho and para principal components, respectively, while the rest remain in floating components. The para- and ortho-12C2H2 energy-level lists, determined during the present study, contain 82 and 80 entries, respectively, with an accuracy similar to that of the lines. Based on the newly assembled lists of para- and ortho-12C2H2 empirical energy levels, a line list, called TenkHz, has been generated. The TenkHz line list contains 282 entries in the spectral range of 5898.97–7258.87 cm−1; thus far, only 149 of them have been measured directly via precision spectroscopy. The TenkHz line list includes 35 intense lines that are missing in the HITRAN2020 database.
1 Introduction
In 2018, Chubb et al.1 published a MARVEL (Measured Active Rotational–Vibrational Energy Levels)2,3 analysis of the experimentally measured and assigned rovibrational transitions of 12C2H2 available at that time: a total of 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 813 experimental transitions from 61 publications were considered. Ref. 1 complemented earlier reviews, of Herman and co-workers4–7 and others,8–10 on the high-resolution spectroscopy of rovibrational states on the ground electronic state of acetylene. From the extended set of measured transitions collated in ref. 1, 5200 para- and 6013 ortho-12C2H2 empirical rovibrational energy levels, with usually dependable associated uncertainties, could be determined.
813 experimental transitions from 61 publications were considered. Ref. 1 complemented earlier reviews, of Herman and co-workers4–7 and others,8–10 on the high-resolution spectroscopy of rovibrational states on the ground electronic state of acetylene. From the extended set of measured transitions collated in ref. 1, 5200 para- and 6013 ortho-12C2H2 empirical rovibrational energy levels, with usually dependable associated uncertainties, could be determined.
There are several line-by-line spectroscopic databanks, like HITRAN,11 GEISA,12 ASD-1000,10 and ExoMol,13 usually containing mixed experimental and empirical rovibrational entries on 12C2H2 (and other isotopologues of acetylene). These datasets contain rovibrational energy-level and transition information about acetylene at very different accuracy levels, ranging from a few kHz (∼10−7 cm−1) to a few hundred MHz (∼0.01 cm−1). The largest one is the ExoMol line list, ACeTY, which has ∼4.3 billion rovibrational transitions among ∼5 million energy levels and it includes wavenumbers up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.13
000 cm−1.13
Nowadays, line-center-position measurements can be performed for polyatomic molecular systems at the 10−11 relative uncertainty level in the near-infrared portion of the electromagnetic spectrum. These precision-spectroscopy measurements are made possible by a combination of optical frequency-comb synthesizers with the most advanced cavity-enhanced spectroscopic methods. In particular, exploiting the resonant enhancement of the intracavity optical power, Lamb-dip observations are possible for weak overtone transitions. These measurements facilitate the determination of highly accurate line-center positions.14,15 Non-linear mixing techniques allow these determinations to be extended to longer wavelengths, throughout the mid-infrared region.16,17
A considerable number of transitions have been measured for acetylene isotopologues with close to kHz accuracy.18–33 In this regard, the comprehensive study of ref. 1 concerning the experimental spectroscopic measurements on the parent isotopologue, 12C2H2, should be considered incomplete: at the time the MARVEL dataset was assembled, results from several important precision-spectroscopy studies were simply not available and a few existing ones were not utilized to their full extent. As of today, the precision-spectroscopy measurements available on 12C2H2 include the ν1 + ν3,21,22,29 2ν3 + ν5,1,32 and ν1+ 3ν330 bands, as well as ν4- and ν5-excited hot bands,27 involving wavenumber regions around 6500, 7200, and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1. Highly-accurate measured transitions are also available for the ν5–ν4 difference band25 (see Table 1 for the meaning of the quantum numbers used to designate the vibrational bands as well as for the vibrational fundamentals of 12C2H21,34,35). For 12C2H2, many of the precision-spectroscopy measurements provided lines which do not connect with each other, hindering the full utilization of these accurate transitions in an improved understanding of acetylene spectroscopy. It should also be mentioned that the accuracy of these precision-spectroscopy measurements21,22,25,27,30,32 have not been checked against each other in a consistent manner (see the related critique of ref. 1 above).
700 cm−1. Highly-accurate measured transitions are also available for the ν5–ν4 difference band25 (see Table 1 for the meaning of the quantum numbers used to designate the vibrational bands as well as for the vibrational fundamentals of 12C2H21,34,35). For 12C2H2, many of the precision-spectroscopy measurements provided lines which do not connect with each other, hindering the full utilization of these accurate transitions in an improved understanding of acetylene spectroscopy. It should also be mentioned that the accuracy of these precision-spectroscopy measurements21,22,25,27,30,32 have not been checked against each other in a consistent manner (see the related critique of ref. 1 above).
| Label | Description (symmetry) | Fundamental |
|---|---|---|
| v 1 | CH symmetric stretch (σg+) | 3372.8491(1)35 |
| v 2 | CC symmetric stretch (σg+) | 1974.317(6)1 |
| v 3 | CH antisymmetric stretch (σu+) | 3294.840(2)1 |
| v 4 | Symmetric (trans) bend (πg) | 612.871(2)34 |
| l 4 | Vibrational angular momentum associated with v4 | |
| v 5 | Antisymmetric (cis) bend (πu) | 730.332(2)34 |
| l 5 | Vibrational angular momentum associated with v5 | |
| L | Total vibrational angular momentum, |l4 + l5| | |
| J | Rotational angular momentum quantum number | |
| e/f | Rotationless parity of the rovibrational state |
There are several reasons why the knowledge of transition frequencies with very high accuracy is important for acetylene.1,4–6,8,36,37 First, there are several rovibrational transitions in coincidence with the International Telecommunication Union's C-band, situated at 1530–1560 nm, that are ideally suited to satisfy the demand of improved frequency standards to be used in telecommunication for the aims of wavelength division multiplexing. Second, the near-infrared spectrum of acetylene is of considerable interest in the field of optical frequency metrology: (a) the P(16) ν1 + ν3 transition of 13C2H2 has been included by the International Committee for Weights and Measures (CIPM) in the list of recommended reference lines for the practical realization of the definition of the meter, and (b) acetylene was used as a molecular target in Doppler-broadening gas thermometry for the optical determination of the Boltzmann constant,36 and subsequently enabled for the implementation of the new SI definition of the unit Kelvin.37 Third, the acetylene spectrum can be extremely useful for studying the atmosphere of young Earth-like exoplanets,38,39 requiring the availability of high-quality spectroscopic parameters.
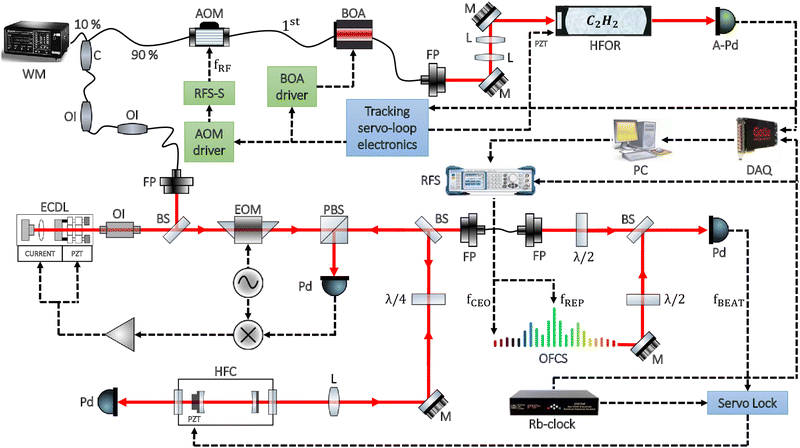
To increase the number of acetylene lines known at the kHz accuracy level and make the best use of the previously determined ones, we decided to undertake a measurement campaign using the modern technique of comb-calibrated frequency-stabilized cavity ring-down spectroscopy (CC-FS-CRDS).40–42 Our experimental study was designed with several goals and achievements in mind. Our first aim was to simplify and upgrade the cavity ring-dwon (CRD) spectrometer in Caserta to facilitate extensive precision-spectroscopy measurements while preserving the same level of accuracy as reported in ref. 32. Part of the apparatus improvement involved building a CRD spectrometer in a more compact way using fiber-coupled and integrated optics devices, thus reducing as much as possible the optical path length in air (see Fig. 1). This helps to avoid laser attenuation due to water absorption in air, which likely occurs during our measurements. Second, after checking the connectivity and the accuracy of existing ultraprecise measurements via tools offered by the theory of spectroscopic networks,43–46 our aim was to assemble the largest possible list of rovibrational energies and transitions, all known at the kHz accuracy level. The SN approach allows the transfer of the high experimental accuracy, in the kHz regime in the present case, to the empirical energy values derived and the line positions predicted. These energy and transition lists should supplement databanks containing entries which are orders of magnitude less accurate. As part of this effort, our aim was to connect at present unconnected components and orphans to the para and ortho principal components of the SN of 12C2H2via a small set of carefully selected newly measured transitions. For example, in ref. 27 there are 135 measured transitions within two hot bands and none could be connected with other kHz-accuracy measurements prior to the present work.
2 Experimental details
2.1 Apparatus
In this study, saturated absorption spectra were acquired using a comb-calibrated frequency-stabilized CRD spectrometer. Schematically shown in Fig. 1, the set-up is an upgraded and simplified version of the apparatus described in ref. 32. The main element of novelty is the use of just one laser referenced to an optical frequency-comb synthesizer. In addition, extensive use was made of fiber optic components and devices to make the spectrometer more compact. The set-up essentially consists of three modules: (i) a 10 kHz-linewidth laser source, referred to as the probe laser (PL); (ii) an absolute frequency calibration unit; and (iii) a high-finesse ring-down optical resonator (HFOR).The probe laser is an external-cavity diode laser (ECDL) with an emission wavelength in the range between 1.38 and 1.41 μm. As already described in ref. 47, in order to reduce its emission linewidth the ECDL was tightly locked to a high-finesse optical cavity (HFC) by means of the Pound–Drever–Hall technique. The absolute frequency calibration unit is based upon a self-referenced optical frequency-comb synthesizer (OFCS, from Menlo Systems, model FC1500-250-WG), stabilized against the 10 MHz time-base signal from a GPS-disciplined Rb clock. The HFC is weakly locked to one of the comb teeth, with an offset frequency, fBEAT, of 20 MHz. This technical expedient has twofold advantage: on the one hand, it allowed us to determine the absolute frequency of the probe laser, on the other hand, we could straightforwardly perform calibrated frequency scan of PL around a selected 12C2H2 transition. In fact, the PL frequency, fPL, which is given by the equation fPL = N × fREP ± fCEO ± fBEAT + fRF, could be finely tuned by a variation of the comb repetition rate (through an external electrical frequency synthesizer referenced to the GPS-disciplined Rb oscillator). In the fPL equation, N represents the comb tooth order, while fREP = 250 MHz, fCEO = 20 MHz, and fRF are the comb repetition rate, the carrier envelope offset frequency, and the RF frequency driving the acousto-optic modulator (AOM), respectively. For each of the investigated transitions, the ± signs were easily determined by slightly varying fCEO and fREP and observing the subsequent variation of fBEAT, whereas the tooth order was obtained by measuring the PL wavelength by means of a 7-digit wavemeter. The relative stability of the entire frequency chain is 2.5 × 10−12, limited by the frequency stability of the Rb clock.37
The HFOR consists of two plano-concave high-reflectivity mirrors, spaced 43 cm apart by a Zerodur block. The mirrors have a radius of curvature of 1 m and a nominal reflectivity greater than 99.99%. One of the mirrors is equipped with a piezo transducer for a fine tuning of the cavity length. The finesse of the cavity was about 230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (corresponding to a ring-down time under vacuum conditions of about 105 μs), while the cavity-mode width was 1.5 kHz. At the output of the cavity, an InGaAs avalanche detector (APd, with an effective bandwidth of 420 kHz and a noise-equivalent power of 0.46 pW Hz−1/2) monitored the light emerging from the resonator. A digital acquisition board (DAQ) was used to record the ring-down events. The DAQ works at a sample rate of 107 samples s−1, its vertical resolution being 16 bit.
000 (corresponding to a ring-down time under vacuum conditions of about 105 μs), while the cavity-mode width was 1.5 kHz. At the output of the cavity, an InGaAs avalanche detector (APd, with an effective bandwidth of 420 kHz and a noise-equivalent power of 0.46 pW Hz−1/2) monitored the light emerging from the resonator. A digital acquisition board (DAQ) was used to record the ring-down events. The DAQ works at a sample rate of 107 samples s−1, its vertical resolution being 16 bit.
A portion of the PL beam was sent into a pair of fiber-coupled optical isolators, followed by a fiber-coupled AOM, whereas the first-order diffracted beam was coupled to the HFOR by means of a mode-matching telescope. The frequency of the laser light emerging from the AOM was up-shifted by a constant amount fRF = 40 MHz (as monitored by a universal counter not shown in Fig. 1). The AOM was also used as an optical switch to initiate ring-down decays. This was accomplished by means of a pair of radio-frequency switches, ensuring an extinction ratio of about 90 dB. Before entering the resonator, the first-order beam was amplified by a fiber-coupled booster optical amplifier (BOA) up to about 20 mW. The signal produced by the APd on the cavity transmission was used as input to a threshold detector in order to monitor whether a resonance condition takes place while scanning the PL frequency. The threshold detector unit was part of the tracking servo-loop circuit that allows for high-resolution spectral acquisitions.48 Moreover, the threshold detector was set so that only the occurrence of a TEM00 excitation could be detected. In this case, a TTL trigger signal was produced and sent to the AOM switches and to the BOA driver in order to suddenly switch off the laser beam. The same TTL pulse simultaneously triggered the DAQ, while its internal clock was locked to the GPS Rb standard. The duration of the TTL signal was 700 μs, namely, about a factor of 7 larger than the ring-down time under vacuum conditions.
The CRD spectrometer is characterized by doing repeated acquisitions of empty cavity ring-down events. The Allan deviation analysis of such datasets led to an estimation of the minimum detectable absorption coefficient, given by 7.8 × 10−12 cm−1, while the noise equivalent absorption (NEA) figure was 8.4 × 10−11 cm−1 Hz−1/2.
Under our experimental conditions, the comb tooth order (N) is around 860![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and a 12.5 Hz wide scan of fREP corresponds to an optical frequency tuning of about 10 MHz. This is sufficiently wide to allow recording the Lamb-dip feature for all the selected rovibrational lines. This is another element of novelty as compared to ref. 32, in which laser scans were more than a factor of 200 larger. In particular, PL scans were performed setting a frequency step of fREP = 0.025 Hz, thus resulting in a Lamb-dip spectrum consisting of 500 spectral points. For each of them, twenty repeated acquisitions of the exponential decay were performed. As a consequence, at the end of each PL scan across the selected transition, 10
000 and a 12.5 Hz wide scan of fREP corresponds to an optical frequency tuning of about 10 MHz. This is sufficiently wide to allow recording the Lamb-dip feature for all the selected rovibrational lines. This is another element of novelty as compared to ref. 32, in which laser scans were more than a factor of 200 larger. In particular, PL scans were performed setting a frequency step of fREP = 0.025 Hz, thus resulting in a Lamb-dip spectrum consisting of 500 spectral points. For each of them, twenty repeated acquisitions of the exponential decay were performed. As a consequence, at the end of each PL scan across the selected transition, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ring-down events were collected. A LabView code, expressly developed to implement this experimental strategy, was used to control the frequency of the repetition rate, to guide the data acquisition board, and to collect ring-down events.
000 ring-down events were collected. A LabView code, expressly developed to implement this experimental strategy, was used to control the frequency of the repetition rate, to guide the data acquisition board, and to collect ring-down events.
2.2 Data analysis and line-center-frequency determinations
The dataset associated with each ring-down event was analyzed by means of a fit to an exponential decay function. The decay time, τ(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), was then converted into total loss per unit length (in cm−1) according to the well-known relation
), was then converted into total loss per unit length (in cm−1) according to the well-known relation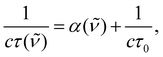 | (1) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the PL wavenumber (in cm−1), c is the speed of light (in cm s−1), α(
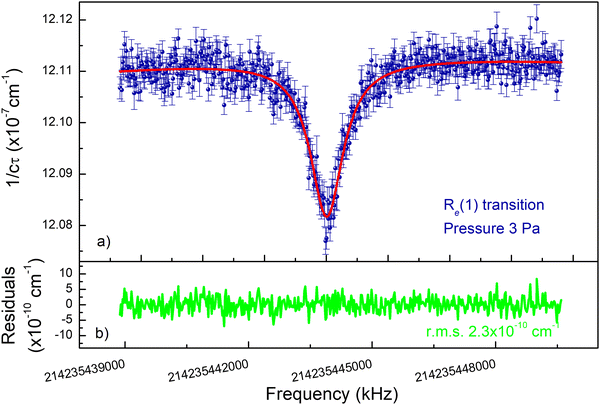
is the PL wavenumber (in cm−1), c is the speed of light (in cm s−1), α(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) (in cm−1) is the absorption coefficient of the gas sample, and τ0 is the ring-down time (in s) under vacuum conditions. An example of a recorded Lamb-dip is shown in panel (a) of Fig. 2.
) (in cm−1) is the absorption coefficient of the gas sample, and τ0 is the ring-down time (in s) under vacuum conditions. An example of a recorded Lamb-dip is shown in panel (a) of Fig. 2.
It is important to note that the ring-down decay curve should deviate from the exponential behavior when the absorption is saturated.49 Nevertheless, since the intracavity power was much smaller than the saturation power of the investigated transitions, we could effectively model the decay curve with a pure exponential function.
In the fitting procedure, the Lamb-dip feature, α(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), was modeled by the following equation:
), was modeled by the following equation:
α(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) = gB( ) = gB(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) − AL × gL( ) − AL × gL(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) − − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) L0), L0), | (2) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) is a quadratic baseline, AL is the amplitude of the Lamb-dip, and gL(
) is a quadratic baseline, AL is the amplitude of the Lamb-dip, and gL(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) −
− ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) L0) is given by an area-normalized Lorentzian lineshape function having its line center frequency at
L0) is given by an area-normalized Lorentzian lineshape function having its line center frequency at ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) L0. Panel (b) of Fig. 2 shows the fit residuals, computed as the difference between the experimental spectrum and that calculated with eqn (2). In the fitting procedure, the Lorentzian width, ΓL, as well as AL,
L0. Panel (b) of Fig. 2 shows the fit residuals, computed as the difference between the experimental spectrum and that calculated with eqn (2). In the fitting procedure, the Lorentzian width, ΓL, as well as AL, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) L0, and the three coefficients of the quadratic term were considered as free parameters. The typical deviation between theory and experiment turned out to be comparable to the noise level. In the case of Fig. 2, the root mean square (rms) of the residuals was 2.3 × 10−10 cm−1. This translates into a signal-to-noise ratio (SNR) of about 20. Similar values were found for all the investigated transitions. The residuals provide no signatures of line asymmetry. It is worth noting that the width of the sub-Doppler features was always smaller than 1 MHz. The various contributions to the width will be discussed later in this Section.
L0, and the three coefficients of the quadratic term were considered as free parameters. The typical deviation between theory and experiment turned out to be comparable to the noise level. In the case of Fig. 2, the root mean square (rms) of the residuals was 2.3 × 10−10 cm−1. This translates into a signal-to-noise ratio (SNR) of about 20. Similar values were found for all the investigated transitions. The residuals provide no signatures of line asymmetry. It is worth noting that the width of the sub-Doppler features was always smaller than 1 MHz. The various contributions to the width will be discussed later in this Section.
For a given gas pressure, four consecutive spectra were acquired and analyzed, so as to have four repeated values of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) L0. Subsequently, the line center frequency was retrieved as the mean value of the dataset. The procedure was repeated for other five pressures, in the range of 0.5–3 Pa. A weighted linear fit of these determinations as a function of the C2H2 pressure allowed us to extrapolate the zero-pressure value of the line center frequency, as it is shown in Fig. 3 for the Re(4) transition. For each of the investigated transitions, this procedure was carried out at least three times, over a period of one week, so as to have repeated determinations of the Lamb-dip zero-pressure center frequency. Once this experimental strategy was completed, the final value of the line-center frequency could be determined as the weighted mean,
L0. Subsequently, the line center frequency was retrieved as the mean value of the dataset. The procedure was repeated for other five pressures, in the range of 0.5–3 Pa. A weighted linear fit of these determinations as a function of the C2H2 pressure allowed us to extrapolate the zero-pressure value of the line center frequency, as it is shown in Fig. 3 for the Re(4) transition. For each of the investigated transitions, this procedure was carried out at least three times, over a period of one week, so as to have repeated determinations of the Lamb-dip zero-pressure center frequency. Once this experimental strategy was completed, the final value of the line-center frequency could be determined as the weighted mean, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) wm, of the whole dataset. As far as the statistical uncertainty is concerned, it was calculated after a consistency test, as provided by the Bureau International des Poids et Mesures (BIPM) and reported in Appendix 1 of ref. 50. In particular, we compared the experimental chi-square, χ2exp, with the degrees of freedom, m, as well as with the 95 percentile of the theoretical chi-square, χ2theor, corresponding to m. In the case of a successful consistency test, namely when χ2exp < χ2theor and χ2exp < m, the uncertainty, u
wm, of the whole dataset. As far as the statistical uncertainty is concerned, it was calculated after a consistency test, as provided by the Bureau International des Poids et Mesures (BIPM) and reported in Appendix 1 of ref. 50. In particular, we compared the experimental chi-square, χ2exp, with the degrees of freedom, m, as well as with the 95 percentile of the theoretical chi-square, χ2theor, corresponding to m. In the case of a successful consistency test, namely when χ2exp < χ2theor and χ2exp < m, the uncertainty, u![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) wm, was calculated as the usual uncertainty of a weighted mean. In the other cases, a correction to u
wm, was calculated as the usual uncertainty of a weighted mean. In the other cases, a correction to u![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) wm was applied according to the equation
wm was applied according to the equation 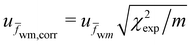 .
.
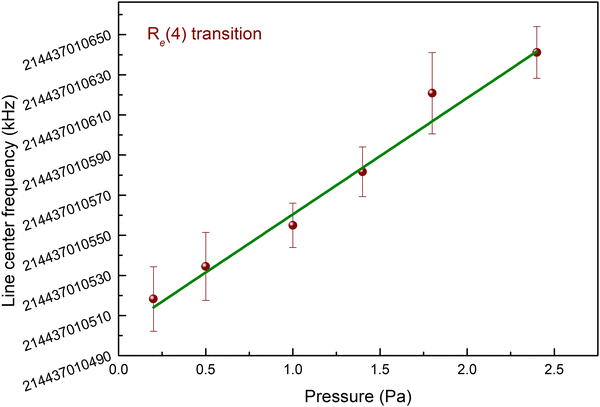 | ||
| Fig. 3 An example showing a set of measurements for the Re(4) transition, from which the zero-pressure absolute frequency can be retrieved. For this dataset, the slope is 58(4) kHz Pa−1. | ||
The entire experimental procedure was applied to a carefully chosen set of para and ortho lines of the P, Q, and R branches of the ν1 + ν3 + ν41 vibrational band of 12C2H2. Line assignments, absolute center frequencies and associated uncertainties at the 2-σ confidence level are reported in Table 2.
| Band | Line | Frequency (kHz) | Expt. uncertainty (kHz) |
|---|---|---|---|
| (1 0 1 11 00)1 | Pe (6) | 213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 661 661![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 027![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 647 |
14 |
| Pe (5) | 213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 751 751![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 551 551 |
17 | |
| Pe (3) | 213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882 882![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 887 |
14 | |
| Qef (16) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 027![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218 218![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
13 | |
| Qef (14) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043 043![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
20 | |
| Qef (13) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282 282![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 791 791 |
14 | |
| Qef (12) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942 942![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 021 021 |
19 | |
| Qef (11) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 063![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087 087![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282 282 |
14 | |
| Re (0) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166 166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 572![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014 014 |
12 | |
| Re (1) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235 235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443 443![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 830 |
15 | |
| Re (2) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 303 303![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931 931 |
12 | |
| Re (3) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 664![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215 215 |
15 | |
| Re (4) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 437![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010 010![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514 514 |
16 | |
| Re (10) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 817 817![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321 321![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921 921 |
14 | |
| Re (11) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 877![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 999 999 |
16 | |
| Re (12) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 937 937![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298 298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310 |
12 | |
| Re (13) | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 996![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 008 008![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 080 |
21 | |
| Re (14) | 215![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864 864![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 720 |
18 | |
| Re (15) | 215![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 867![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741 741 |
14 | |
| Re (16) | 215![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167 167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 019![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970 970 |
20 |
The uncertainty quoted for each transition includes both statistical and systematic contributions. In particular, the statistical uncertainty ranges between 7 to 18 kHz. The systematic contributions were quoted according to the outcomes of ref. 32. The main source of uncertainty could be ascribed to the measurement of the pressure, provided by the absolute pressure gauge that was used (MKS, model 122A), having a full scale and a sensitivity of 1000 Pa and 0.1 Pa, respectively. Since the pressure values enter into each zero-pressure frequency determination, their uncertainty influenced the accuracy of our determinations. To this end, for one of the datasets, we have repeated the weighted linear fit adopting two different pressure scales, in which the pressure readings were decreased and increased by 0.1 Pa, this latter value being the last digit given by the pressure gauge. Doing so, we could include a systematic contribution of 9 kHz in the uncertainty budget. The OFCS contributes with an uncertainty of 1 kHz, which is due to the stability of the GPS-disciplined Rb clock. Moreover, while the recoil shift cancels out in Lamb-dip spectroscopy,51 the second-order Doppler shift has been estimated taking into account the root-mean square velocity of the C2H2 molecules. Under our experimental conditions, it amounts to 0.7 kHz. We did not observe any influence in the retrieved line-center frequencies from the power coupled into the HFOR cavity. However, adopting a very cautious approach, we decided to add a further contribution of 0.8 kHz due to the power shift, according to the outcomes of ref. 52. A further component we considered takes into account the frequency difference between the PL and the cavity resonance.40 Its estimation amounts to 0.4 kHz. The uncertainties associated to the driving frequency of the AOM, to the wave-front curvature, as well as to that coming from possible interfering lines were estimated to be negligible. To summarize, the transition frequencies reported in this work were determined with an overall uncertainty ranging between 12 and 21 kHz in a 2-σ confidence interval.
It is worth noting that the pressure-shifting coefficient, δ, of the twenty lines investigated in this work varies from 3 to ∼70 kHz Pa−1. A few lines exhibit relatively large values of δ compared to those measured for other C2H2 lines in other spectral regions, also in the sub-Doppler regime.30,31 There are examples of anomalies in pressure-shifting coefficients from sub-Doppler experiments. For instance, in 2018, Chen et al.53 measured a self-shifting of +14 kHz Pa−1 for a water line at 790 nm, a value that is quite different from −5 kHz Pa−1 given in HITRAN. Similarly, Cozijn et al.54 measured a pressure-dependent shift of −9 kHz Pa−1 for a sub-Doppler rovibrational line of HD, providing evidence that this collisional-shift coefficient was an order of magnitude larger than the typical coefficients for H2, obtained from Doppler-limited studies. Investigating the reason for these anomalies is out of the scope of the present paper and may be eventually the subject of a future article. Nevertheless, we believe that this issue does not influence the extrapolated zero-pressure value of the line center frequency.
2.3 Measurement conditions
Several 12C2H2 vibrational bands fall within the spectral region covered by the ECDL. For the aims of the present study, 20 lines belonging to the ν1 + ν3 + ν41 band were selected, showing an Einstein coefficient, A, in the interval 0.015–0.050 s−1.11 Combined with the population distribution at room temperature, these A values lead to line intensities which do not exceed 9 × 10−23 cm molecule−1.11 These particular characteristics allowed the detection of Lamb-dip signals under a weak saturation regime. In fact, for the transition showing the highest A value, taking into account that the experimental full width at half-maximum (FWHM) of the observed Lamb-dip never exceeds the 1 MHz value, we calculated a saturation intensity, Isat, of about 1 × 108 W m−2.55 According to the formula given in ref. 56 and considering a 0.05% mode-matching parameter, we estimate that the intracavity intensity, Icav, was much smaller than Isat, the saturation parameter G being ∼0.007.As shown in Fig. 2, the FWHM of the recorded Lamb dip is 850 kHz, as retrieved from the Lorentzian fit. Such a width is in partial agreement with the joint effect of various broadening mechanisms, namely, the transit time broadening (of about 255 kHz for a cavity waist of 430 μm and a gas temperature of 296 K), the intracavity power broadening, which increases the linewidth by a factor of 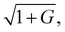 and the 310 kHz collisional broadening that can be calculated using the self-broadening coefficient reported in HITRAN.11 This discrepancy can be ascribed to the fact that the self-broadening coefficient from Lamb-dip experiments can be up to one order of magnitude larger than that retrieved in the Doppler regime.31
and the 310 kHz collisional broadening that can be calculated using the self-broadening coefficient reported in HITRAN.11 This discrepancy can be ascribed to the fact that the self-broadening coefficient from Lamb-dip experiments can be up to one order of magnitude larger than that retrieved in the Doppler regime.31
3 Theoretical details
3.1 Labels
Table 1 explains elements of the label used to denote rovibrational states of 12C2H2. The vibrational states are labelled as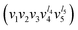 . Note that |l| = v, v − 2,…, 1 for odd v and |l| = v, v − 2,…, 0 for even v. The rotational part of the label includes the traditional J and K quantum numbers, where J is an exact quantum number describing the overall rotation of the molecule and the approximate quantum number K corresponds to the projection of the rotational angular momentum onto the principal axis of acetylene. Overall,
. Note that |l| = v, v − 2,…, 1 for odd v and |l| = v, v − 2,…, 0 for even v. The rotational part of the label includes the traditional J and K quantum numbers, where J is an exact quantum number describing the overall rotation of the molecule and the approximate quantum number K corresponds to the projection of the rotational angular momentum onto the principal axis of acetylene. Overall, 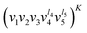 , J, and e/f is used to denote the rovibrational states. e/f is used to denote the rotationless parity of the rovibrational states. For further details about elements of the label and the selection rules the reader may want to consult ref. 1.
, J, and e/f is used to denote the rovibrational states. e/f is used to denote the rotationless parity of the rovibrational states. For further details about elements of the label and the selection rules the reader may want to consult ref. 1.
3.2 Marvel
MARVEL, standing for Measured Active Rotational–Vibrational Energy Levels,2,3 is an inversion technique yielding empirical energies with dependable uncertainties from measured transitions, all equipped with uncertainties and unique labels. MARVEL is based on the theory of spectroscopic networks (SN).43–45 This is basically the same procedure, except for the handling of uncertainties, as used in ref. 1.Since H is a fermion with a nuclear spin of 1/2, 12C2H2 has two nuclear-spin isomers, traditionally called para and ortho. The energy difference between the lowest para and ortho states is colloquially called the ‘magic number’.
One way to derive the absolute energy of the lowest ortho state involves a fit of an effective Hamiltonian model (usually not a global but a local one, considering only the ground vibrational state) to a large number of energy differences. In ref. 7, results of a global fit are reported and the magic number can be taken as 2.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 532
532![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864 cm−1. Considering the experimental accuracy of the lines utilized during the global fit, the accuracy of this magic number is roughly 3 MHz (9 × 10−5 cm−1), which is orders of magnitude larger than the accuracy of the measurements dealt with here.
864 cm−1. Considering the experimental accuracy of the lines utilized during the global fit, the accuracy of this magic number is roughly 3 MHz (9 × 10−5 cm−1), which is orders of magnitude larger than the accuracy of the measurements dealt with here.
Clearly, none of the empirical ortho energy values can have an absolute uncertainty better than that of the magic number upon which they are based, not even those involved in accurate precision-spectroscopy measurements. Therefore, in this study two separate energy-level lists are provided, one for the para and one for the ortho principal components, whereby the energies of the lowest states are both set to zero with zero uncertainty. While this way we cannot provide absolute energies for the ortho-12C2H2 principal component, this issue does not affect the accuracy of the transitions of the linelist to be assembled. It is left to future well-designed precision-spectroscopy measurements to determine the magic number of 12C2H2 with kHz accuracy, similar to how it was done for H216O57 and H218O.58
3.3 Ultraprecise spectroscopic network of 12C2H2
Accuracy has central importance for the present study. Thus, each source was carefully checked about the proper meaning and magnitude of the reported uncertainties of the measured lines. It should also be noted here that there are two important elements of graph/network theory59 which help to ascertain and secure the accuracy of the empirical energy levels and the experimental transitions of SNs: paths and cycles. Paths in a SN secure the formation of energy differences for any pair of the participating states. The redundancy inherent to cycles of the SN provides a powerful self-checking feature; most importantly, cycles can be used to confirm the accuracy of the associated transitions.The measurement uncertainty, 1-σ of the combined type (statistical plus systematic), of the source 96NaLaAwKo19 is larger than 100 kHz. The same can be said about the source 09YuDrPe25. While these are excellent measurements on their own right, we decided not to consider these sources during the present study. Neglecting the transitions reported in 96NaLaAwKo19 has no real effect on our analysis since 06MaAlCzBe22 reported the same lines with significantly lower uncertainties.
The sources we considered during our combined experimental and theoretical study of precision-spectroscopy measurements on 12C2H2 are listed in Table 3. The number of ultraprecise lines available in each source is listed under A (available). The number of lines validated (V) either with (Vafter) or without (Vbefore) the newly measured transitions of this study are indicated in the third column of Table 3. The measurement range and the average and maximum uncertainties of the lines are also given there.
| Source tag | Range/cm−1 | A/Vbefore/Vafter | Avg. unc./cm−1 | Max. unc./cm−1 |
|---|---|---|---|---|
| 05EdBaMaGi21 | 6471.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634–6578.57 634–6578.57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 589 |
41/41/41 | 7.1 × 10−7 | 1.4 × 10−6 |
| 06MaAlCzBe22 | 6471.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634–6617.99 634–6617.99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087 087 |
63/63/63 | 1.6 × 10−7 | 6.1 × 10−7 |
| 09KnWuLiTi24 | 6523.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924–6523.87 924–6523.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
1/1/1 | 6.2 × 10−7 | 6.2 × 10−7 |
| 13WaWhFoGr26 | 6523.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924–6523.87 924–6523.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
1/1/1 | 6.2 × 10−7 | 6.2 × 10−7 |
| 15TwCiSeMc27 | 6448.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318–6564.17 318–6564.17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703 703 |
135/0/48 | 3.6 × 10−7 | 1.5 × 10−6 |
| 16GaGoGaBe29 | 6474.86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134–6487.03 134–6487.03![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
3/3/3 | 1.2 × 10−7 | 1.3 × 10−7 |
| 18TaHuSuWa30 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612.32 612.32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 392–12 392–12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713.38 713.38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 603 603 |
43/43/43 | 2.2 × 10−7 | 2.4 × 10−7 |
| 18TwHaSe31 | 6452.61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818–6471.75 818–6471.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 634 |
7/3/3 | 2.7 × 10−7 | 4.0 × 10−7 |
| 21FaGrPoCa32 | 7167.18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980–7216.97 980–7216.97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 672 |
16/16/16 | 5.3 × 10−7 | 8.7 × 10−7 |
| 22AiSaDeRo33 | 6561.09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411–6561.09 411–6561.09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411 411 |
1/1/1 | 8.0 × 10−8 | 8.0 × 10−8 |
| This work: 23CaFaAgKh | 7126.96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474–7177.19 474–7177.19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923 923 |
20/0/20 | 5.3 × 10−7 | 8.1 × 10−7 |
The source 18TaHuSuWa30 contains two unassigned lines; thus, only 43 transitions out of the 45 given in Table 2 of ref. 30 could be utilized in this study. We could not find reasonable assignments for the two unassigned lines.
A constant pressure of 2.7 ± 0.6 Pa (20 ± 5 mTorr) was maintained inside the chamber throughout the measurements reported in 06MaAlCzBe22 and the pressure shift of each line was not measured. The pressure shift assumed, +1 kHz Pa−1, is likely to be too small and it may even have an incorrect sign, in some cases. Furthermore, the effect of impurities cannot be cancelled out completely at finite pressures. This is the reason why we did measurements as a function of the gas pressure, so we can get rid of any issue related to impurities, which influence the pressure shifting coefficient, and retrieved the zero-pressure value of the line-center frequency. While the reported uncertainties of ref. 22 may be slightly optimistic, our analysis of the cycles these transitions participate in did not suggest that we needed to increase the original uncertainties to the carefully updated BIPM-corrected60 values.
In the source 15TwCiSeMc27 the uncertainty reported is 1-σ of the combined type. Four of the measured transitions form a cycle whereby the discrepancy is too large. Multiplication of the line uncertainties by 1.5 solves the discrepancy problem. Therefore, we decided to multiply all the uncertainties of this source by a factor of 1.5. Note that this is the only source where our checking indicated that the source uncertainties need to be increased.
Without the transitions of the present study, none of the large number of lines of 15TwCiSeMc27 connect to the two principal components of 12C2H2, disallowing their validation and their true utilization when it comes to predicting new transitions accurately. Based on the new measurements of this study, some of the floating components originating in this source are now part of the SN.
The source 18TwHaSe31 reports, with 1-σ uncertainties of the statistical type, seven nearly-kHz-accuracy lines near to 1.5 μm (ν1 + ν3 band). Only three of the seven measured lines connect to the principal components, since the J values of the lower states are high (>31). Within the experimental constraints of the present study no further transitions could be connected to the principal components.
The true accuracy of the measurements can be tested via the even-membered cycles46 they form (see Fig. 4). The original precision-spectroscopy measurements form 66 four-membered cycles. It is comforting to know that the transitions of the sources given in Table 3 achieve self-consistency with the original 2-σ uncertainties, that is an increase of uncertainties, based on these cycles, turned out not to be necessary.
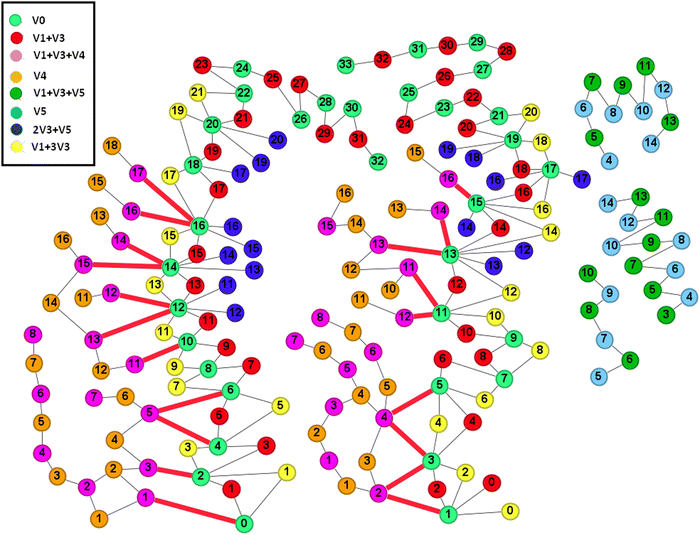 | ||
| Fig. 4 Cartoon, with color-coded bands, depicting the spectroscopic network of 12C2H2, formed by lines measured with ultraprecision spectroscopy, assembled and investigated during this study. The red links correspond to the new measurements (see also Table 2), designed to connect previously measured floating components and orphans to the two principal components of 12C2H2. The para and ortho principal components are in the left and the middle of the figure, respectively, the remaining (large) floating components are in the right. For the sake of clarity, the large number of floating components with less than five transitions are not shown. Numbers within the colored dots (vertices of the spectroscopic network) correspond to the rotational quantum number J. | ||
Careful selection of the lines to be measured followed guidelines of the spectroscopic-network-assisted precision spectroscopy (SNAPS) procedure.57,58,61,62 The panels of Fig. 4 help to visualize how the new measurements connect previous floating SN components to the two principal components. The 20 newly measured lines, 11 para and 9 ortho ones, not only help to connect previously floating components to the roots of the para and ortho principal components by defining ultraprecise paths but some of them are also part of cycles, which can be utilized to confirm the accuracy of the measured lines. As clear from Fig. 4, four para and nine ortho lines are not part of cycles; thus, their measurement accuracy cannot be confirmed this way. Nevertheless, since the majority of the newly measured lines are part of a number of cycles, the results of the uncertainty budget analysis can be accepted for all of the lines.
Table 4 summarizes the most important statistical data about the SN of precision-spectroscopy measurements assembled during this study, both with and without the lines of the present study. The ultraprecise SN of 12C2H2 contains transitions from the following bands: ν4, ν5, ν1 + ν3, ν1 + ν3 + ν4, ν1 + ν3 + ν5, 2ν3 + ν5, and ν1+ 3ν3. The number of validated transitions is lower than the total number of transitions since we cannot validate transitions in floating components and orphans. As seen in Table 4, while originally there were 105 rovibrational energy levels within the two principal components of the SN, the 20 newly-measured lines help to connect a further 57 levels to the principal components. The different measurements nicely complement each other and thus for lower J values one can find a large number of cycles, helping to establish the true accuracy of the measurements.
| Network property | Without this study | With this study |
|---|---|---|
| Number of transitions in the database | 311 | 331 |
| Number of unique transitions in the database | 263 | 283 |
| Number of unique transitions in the two principal components | 127 | 195 |
Number of unique transitions in the two principal components under 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 000 cm−1 |
81 | 149 |
| Number of components in the database | 74 | 63 |
| Number of transitions in the para principal component | 86 | 121 |
| Number of transitions in the ortho principal component | 86 | 119 |
| Number of validated transitions | 172 | 240 |
| Number of energy levels in the database | 314 | 314 |
| Number of energy levels in the para principal component | 53 | 82 |
| Number of energy levels in the ortho principal component | 52 | 80 |
4 The TenkHz line list of 12C2H2
The empirical rovibrational energy levels determined with the help of the MARVEL algorithm can be used to generate a rovibrational line list for 12C2H2. To achieve this, the usual one-photon selection rules1 were employed to identify the transitions. The extensive set of selection rules significantly limits the number and regions of allowed transitions among the rovibrational states of 12C2H2. The intensities were derived from the Einstein-A coefficients of the aCeTY line list13 of the ExoMol project. There are no transitions reported in the Exomol database13 above 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1; thus, the empirical energies above 12
000 cm−1; thus, the empirical energies above 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 cannot be utilized to generate further line-list elements. We employed the value of Q(T = 296 K) = 412.45
000 cm−1 cannot be utilized to generate further line-list elements. We employed the value of Q(T = 296 K) = 412.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 00863 for the total internal partition function, needed to generate the room-temperature line intensities. The complete line list is given in the ESI.†
00863 for the total internal partition function, needed to generate the room-temperature line intensities. The complete line list is given in the ESI.†
Since there are still a relatively large number of transitions and energy levels which are not part of the two principal components (see Table 4) and since the selection rules governing the one-photon transitions are highly restrictive, one cannot expect a very large number of predicted transitions. In fact, the TenkHz line list contains 282 rovibrational transitions, the hot bands starting from ν4 in the ν1 + ν3 and ν1 + ν3 + ν4 regions. 133 predicted lines, in the wavenumber range of 5898.97–7258.87 cm−1, have not been measured before. Since the uncertainties of these predicted lines are about 10 kHz, these lines are perfect candidates even for metrological applications. The list of lines may also act as frequency standards over a wide frequency range, helping future high-resolution experiments.
5 Comparison with HITRAN
It is worth checking whether our new TenkHz database contains lines which are missing from the canonical spectroscopic line-by-line database HITRAN2020.11 It is comforting to observe that 247 of the 282 predicted lines can be found in the HITRAN2020 dataset. The average deviation of these TenkHz and HITRAN2020 lines is only 6.5 × 10−4 cm−1, in perfect agreement within the stated HITRAN2020 uncertainties.11 Of course, the lines in our TenkHz database are orders of magnitude more accurate than this; thus, it is recommended to consider them during the next update of the HITRAN database.Furthermore, the TenkHz line list contains 35 lines that are missing from the HITRAN2020 database. Since the intensity of each of these lines is larger than 4.5 × 10−30 cm molecule−1, all these lines, which are in the 6524.94–6605.48 cm−1 region, should be considered for inclusion. Note that there are 27 lines missing from HITRAN202011 whose intensities, at room temperature, are between 1.5 × 10−22 and 1 × 10−26 cm molecule−1.
6 Summary and conclusions
In this study, the absolute center frequencies of twenty rovibrational lines of 12C2H2, including 11 para and 9 ortho ones, have been measured using Lamb-dip cavity ring-down spectroscopy, assisted by a near-infrared optical frequency comb synthesizer. The spectrometer is an upgraded version of that described in ref. 32 and 48, expressly designed for extensive Lamb-dip investigations. The experimental strategy is based on spectral acquisitions as a function of the gas pressure, so that the zero-pressure center frequency could be retrieved for each of the selected transitions. The combined uncertainty, at the 2-σ confidence level, varies between 12 and 21 kHz, while the average 1-σ uncertainty amounts to about 7 kHz.Selection of the newly measured lines, in the spectral window of 7125–7230 cm−1 supported by our spectrometer, is based on the theory of spectroscopic networks (SN). The few carefully selected and carefully executed new line measurements allow to attach several previously unconnected components and orphans to the two principal components of the SN of 12C2H2. A dataset containing 331 highly precise lines, including 283 unique ones, has been assembled, defining a network composed only of transitions measured with an accuracy better than 10 kHz (1-σ confidence level). 119 and 121 of the lines are in the ortho and para principal components, respectively, while the rest remains in floating components. Based on paths and cycles of the SN, we successfully validated all previous ultraprecise measurements, except one, 15TwCiSeMc,27 where the uncertainties had to be increased by 50%. Then, based on the Measured Active Rotational–Vibrational Energy Levels (MARVEL) procedure, 82 and 80 ultraprecise empirical rovibrational energy levels have been determined in the para- and ortho-12C2H2 principal components, involving the following five vibrational bands: ν4, ν1 + ν3, ν1 + ν3 + ν41, 2ν3 + ν5, and ν1+ 3ν3. The accuracy of the energy levels is similar to that of the lines.
Based on the 162 ultraprecise empirical rovibrational energies, we generated a rovibrational line list, which we call TenkHz, for 12C2H2, containing 282 entries in the spectral range of 5898.97–7258.87 cm−1. Up to now, only 149 of these predicted transitions have been measured directly via precision spectroscopy. Since the accuracy of these predicted lines is better than 10 kHz, these lines are perfect candidates even for metrological applications. The list of TenkHz lines may also act as frequency standards over a wide frequency range, helping future high-resolution and precision-spectroscopy measurements. 247 of the 282 TenkHz lines can be found in the canonical spectroscopic line-by-line database HITRAN2020.11 The average deviation of these 247 lines is only 6.5 × 10−4 cm−1, in perfect agreement within the stated HITRAN2020 uncertainties. Of course, the lines in our TenkHz database are orders of magnitude more accurate than this. The intensity of 27 of the remaining 35 TenkHz lines that are missing from the HITRAN2020 database are between 1.5 × 10−22 and 1 × 10−26 cm molecule−1. Thus, the present ultraprecise Lamb-dip measurements and the TenkHz line list should prove useful during the next upgrade of the HITRAN dataset on 12C2H2.
Despite the large number of rovibrational lines in the TenkHz line list assembled during this study, there are still a number of ways how one can improve our knowledge of the spectroscopy of acetylene at the kHz level. To this aim, future perspectives include new absolute frequency measurements of those transitions that connect the remaining floating components, such as the spectral lines of the ν1 + ν3 + ν5 band or those of the fundamental vibrational mode ν5. In fact, ultra-accurate determinations of molecular transition frequencies can be extended to the mid-infrared spectral region by combining the technology of quantum cascade lasers with the most advanced nonlinear mixing techniques to calibrate the spectroscopic measurements by means of an optical frequency comb in the near infrared.64,65
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The experimental work was partially done within the project PROMETH2O (EMPIR 20IND06), which received funding from the EMPIR programme co-financed by the Participating States and from the European Unions Horizon 2020 research and innovation programme. The work performed in Budapest received support from NKFIH (grant no. K138233). This publication supports research performed within the COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY), funded by the European Cooperation in Science and Technology (COST) and the MSCA Doctoral Network PHYMOL: “Physics, accuracy and machine learning, towards the next generation of molecular potentials”.References
- K. L. Chubb, M. Joseph, J. Franklin, N. Choudhury, T. Furtenbacher, A. G. Császár, G. Gaspard, P. Oguoko, A. Kelly, S. N. Yurchenko, J. Tennyson and C. Sousa-Silva, J. Quant. Spectrosc. Radiat. Transfer, 2018, 204, 42–55 CrossRef CAS.
- T. Furtenbacher, A. G. Császár and J. Tennyson, J. Mol. Spectrosc., 2007, 245, 115–125 CrossRef CAS.
- T. Furtenbacher and A. G. Császár, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 929–935 CrossRef CAS.
- M. Herman, A. Campargue, M. I. El Idrissi and J. Vander Auwera, J. Phys. Chem. Ref. Data, 2003, 32, 921–1361 CrossRef CAS.
- M. Herman, Mol. Phys., 2007, 105, 2217–2241 CrossRef CAS.
- K. Didriche and M. Herman, Chem. Phys. Lett., 2010, 496, 1–7 CrossRef CAS.
- B. Amyay, A. Fayt, M. Herman and J. V. Auwera, J. Phys. Chem. Ref. Data, 2016, 45, 023103 CrossRef.
- B. J. Orr, Int. Rev. Phys. Chem., 2006, 25, 655–718 Search PubMed.
- D. Jacquemart, O. Lyulin and V. I. Perevalov, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 440–453 CrossRef CAS.
- O. M. Lyulin and V. I. Perevalov, J. Quant. Spectrosc. Radiat. Transfer, 2017, 201, 94–103 CrossRef CAS.
- I. E. Gordon, L. S. Rothman, R. J. Hargreaves, R. Hashemi, E. V. Karlovets, F. M. Skinner, E. K. Conway, C. Hill, R. V. Kochanov, Y. Tan, P. Wcisło, A. A. Finenko, K. Nelson, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, A. Coustenis, B. J. Drouin, J. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, E. J. Mlawer, A. V. Nikitin, V. I. Perevalov, M. Rotger, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, E. M. Adkins, A. Baker, A. Barbe, E. Canè, A. G. Császár, A. Dudaryonok, O. Egorov, A. J. Fleisher, H. Fleurbaey, A. Foltynowicz, T. Furtenbacher, J. J. Harrison, J. Hartmann, V. Horneman, X. Huang, T. Karman, J. Karns, S. Kassi, I. Kleiner, V. Kofman, F. Kwabia-Tchana, N. N. Lavrentieva, T. J. Lee, D. A. Long, A. A. Lukashevskaya, O. M. Lyulin, V. Y. Makhnev, W. Matt, S. T. Massie, M. Melosso, S. N. Mikhailenko, D. Mondelain, H. S. P. Müller, O. V. Naumenko, A. Perrin, O. L. Polyansky, E. Raddaoui, P. L. Raston, Z. D. Reed, M. Rey, C. Richard, R. Tóbiás, I. Sadiek, D. W. Schwenke, E. Starikova, K. Sung, F. Tamassia, S. A. Tashkun, J. Vander Auwera, I. A. Vasilenko, A. A. Vigasin, G. L. Villanueva, B. Vispoel, G. Wagner, A. Yachmenev and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2022, 277, 107949 CrossRef CAS.
- T. Delahaye, R. Armante, N. A. Scott, N. Jacquinet-Husson, A. Chédin, L. Crépeau, C. Crevoisier, V. Douet, A. Perrin, A. Barbe, V. Boudon, A. Campargue, L. Coudert, V. Ebert, J.-M. Flaud, R. R. Gamache, D. Jacquemart, A. Jolly, F. K. Tchana, A. Kyuberis, G. Li, O. M. Lyulin, L. Manceron, S. Mikhailenko, N. Moazzen-Ahmadi, H. S. P. Müller, O. V. Naumenko, A. Nikitin, V. I. Perevalov, C. Richard, E. Starikova, S. A. Tashkun, V. G. Tyuterev, J. V. Auwera, B. Vispoel, A. Yachmenev and S. Yurchenko, J. Mol. Spectrosc., 2021, 380, 111510 CrossRef CAS.
- K. L. Chubb, J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2020, 493, 1531–1545 CrossRef CAS.
- J. Ye, L.-S. Ma and J. L. Hall, Opt. Lett., 1996, 21, 1000–1002 CrossRef CAS PubMed.
- R. Aiello, V. Di Sarno, M. G. Delli Santi, M. De Rosa, I. Ricciardi, G. Giusfredi, P. De Natale, L. Santamaria and P. Maddaloni, Photon. Res., 2022, 10, 1803–1809 CrossRef CAS.
- A. Albert Schliesser, N. Picqué and T. W. Haensch, Nat. Photonics, 2012, 6, 440 CrossRef.
- A. Gambetta, E. Vicentini, N. Coluccelli, Y. Wang, T. T. Fernandez, P. Maddaloni, P. De Natale, A. Castrillo, L. Gianfrani, P. Laporta and G. Galzerano, APL Photonics, 2018, 3, 046103 CrossRef.
- W. J. Lafferty, R. D. Suenram and D. R. Johnson, J. Mol. Spectrosc., 1977, 64, 147–156 CrossRef CAS.
- K. Nakagawa, M. de Labachelerie, Y. Awaji and M. Kourogi, J. Opt. Soc. Am. B, 1996, 13, 2708 CrossRef CAS.
- C. S. Edwards, H. S. Margolis, G. P. Barwood, S. N. Lea, P. Gill, G. Huang and W. R. C. Rowley, Opt. Lett., 2004, 29, 566 CrossRef CAS PubMed.
- C. S. Edwards, G. P. Barwood, H. S. Margolis, P. Gill and W. R. C. Rowley, J. Mol. Spectrosc., 2005, 234, 143–148 CrossRef CAS.
- A. A. Madej, A. J. Alcock, A. Czajkowski, J. E. Bernard and S. Chepurov, J. Opt. Soc. Am. B, 2006, 23, 2200–2208 CrossRef CAS.
- A. A. Madej, J. E. Bernard, A. J. Alcock, A. Czajkowski and S. Chepurov, J. Opt. Soc. Am. B, 2006, 23, 741 CrossRef CAS.
- K. Knabe, S. Wu, J. Lim, K. A. Tillman, P. S. Light, F. Couny, N. Wheeler, R. Thapa, A. M. Jones, J. W. Nicholson, B. R. Washburn, F. Benabid and K. L. Corwin, Opt. Expr., 2009, 17, 16017–16026 CrossRef CAS PubMed.
- S. Yu, B. J. Drouin and J. C. Pearson, Astrophys. J., 2009, 705, 786–790 CrossRef CAS.
- C. Wang, N. V. Wheeler, C. Fourcade-Dutin, M. Grogan, T. D. Bradley, B. R. Washburn, F. Benabid and K. L. Corwin, Appl. Opt., 2013, 52, 5430–5439 CrossRef CAS PubMed.
- S. Twagirayezu, M. J. Cich, T. J. Sears, C. P. McRaven and G. E. Hall, J. Mol. Spectrosc., 2015, 316, 64–71 CrossRef CAS.
- E. Fasci, T. A. Odintsova, A. Castrillo, M. D. D. Vizia, A. Merlone, F. Bertiglia, L. Moretti and L. Gianfrani, Phys. Rev. A, 2016, 93, 042513 CrossRef.
- D. Gatti, R. Gotti, A. Gambetta, M. Belmonte, G. Galzerano, P. Laporta and M. Marangoni, Sci. Rep., 2016, 6, 27183 CrossRef CAS PubMed.
- L.-G. Tao, T.-P. Hua, Y. R. Sun, J. Wang, A.-W. Liu and S.-M. Hu, J. Quant. Spectrosc. Radiat. Transfer, 2018, 210, 111–115 CrossRef CAS.
- S. Twagirayezu, G. E. Hall and T. J. Sears, J. Chem. Phys., 2018, 149, 154308 CrossRef PubMed.
- E. Fasci, S. Gravina, G. Porzio, A. Castrillo and L. Gianfrani, New J. Phys., 2021, 23, 123023 CrossRef CAS.
- R. Aiello, V. Di Sarno, M. G. Delli Santi, M. De Rosa, I. Ricciardi, P. De Natale, L. Santamaria, G. Giusfredi and P. Maddaloni, Nat. Commun., 2022, 13, 7016 CrossRef CAS PubMed.
- J. Plíva, J. Mol. Spectrosc., 1972, 44, 165–182 CrossRef.
- A.-M. Tolonen and S. Alanko, Mol. Phys., 1992, 75, 1155–1165 CrossRef CAS.
- R. Hashemi, C. Povey, M. Derksen, H. Naseri, J. Garber and A. Predoi-Cross, J. Chem. Phys., 2014, 141, 214201 CrossRef CAS PubMed.
- A. Castrillo, E. Fasci, H. Dinesan, S. Gravina, L. Moretti and L. Gianfrani, Phys. Rev. Appl., 2019, 11, 064060 CrossRef CAS.
- P. B. Rimmer, M. Ferus, I. P. Waldmann, A. Knížek, D. Kalvaitis, O. Ivanek, P. Kubelík, S. N. Yurchenko, T. Burian, J. Dostál, L. Juha, R. Dudžák, M. Krůs, J. Tennyson, S. Civiš, A. T. Archibald and A. Granville-Willett, Astrophys. J., 2019, 888, 21 CrossRef.
- D. Gasman, M. Min and K. L. Chubb, A&A, 2022, 659, A114 Search PubMed.
- Z. D. Reed, D. A. Long, H. Fleurbaey and J. T. Hodges, Optica, 2020, 7, 1209–1220 CrossRef CAS.
- E. Fasci, A. Castrillo, H. Dinesan, S. Gravina, L. Moretti and L. Gianfrani, Phys. Rev. A, 2018, 98, 022516 CrossRef CAS.
- L.-G. Tao, A.-W. Liu, K. Pachucki, J. Komasa, Y. R. Sun, J. Wang and S.-M. Hu, Phys. Rev. Lett., 2018, 120, 153001 CrossRef CAS PubMed.
- A. G. Császár and T. Furtenbacher, J. Mol. Spectrosc., 2011, 266, 99–103 CrossRef.
- T. Furtenbacher, P. Árendás, G. Mellau and A. G. Császár, Sci. Rep., 2014, 4, 4654 CrossRef PubMed.
- A. G. Császár, T. Furtenbacher and P. Árendás, J. Phys. Chem. A, 2016, 120, 8949–8969 CrossRef PubMed.
- R. Tóbiás, T. Furtenbacher and A. G. Császár, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 557–564 CrossRef.
- H. Dinesan, E. Fasci, A. D'Addio, A. Castrillo and L. Gianfrani, Opt. Expr., 2015, 23, 1757–1766 CrossRef CAS PubMed.
- E. Fasci, H. Dinesan, L. Moretti, A. Merlone, A. Castrillo and L. Gianfrani, Metrologia, 2018, 55, 662–669 CrossRef CAS.
- G. Giusfredi, S. Bartalini, S. Borri, P. Cancio, I. Galli, D. Mazzotti and P. De Natale, Phys. Rev. Lett., 2010, 104, 110801 CrossRef CAS PubMed.
- B. I. des Poids et Mesures (BIPM), CCQM Guidance note: Estimation of a consensus KCRV and associated Degrees of Equivalence, 2013, https://www.bipm.org/documents/20126/28430045/working-document-ID-5794/49d366bc-295f-18ca-c4d3-d68aa54077b5.
- J. L. Hall, C. J. Bordé and K. Uehara, Phys. Rev. Lett., 1976, 37, 1339–1342 CrossRef CAS.
- V. D. Sarno, R. Aiello, M. D. Rosa, I. Ricciardi, S. Mosca, G. Notariale, P. D. Natale, L. Santamaria and P. Maddaloni, Optica, 2019, 6, 436–441 CrossRef.
- J. Chen, T.-P. Hua, L.-G. Tao, Y. Sun, A.-W. Liu and S.-M. Hu, J. Quant. Spectrosc. Radiat. Transfer, 2018, 205, 91–95 CrossRef CAS.
- F. M. J. Cozijn, P. Dupré, E. J. Salumbides, K. S. E. Eikema and W. Ubachs, Phys. Rev. Lett., 2018, 120, 153002 CrossRef CAS PubMed.
- W. Ma, A. Foltynowicz and O. Axner, J. Opt. Soc. Am. B, 2008, 25, 1144–1155 CrossRef CAS.
- L.-S. Ma, J. Ye, P. Dubé and J. L. Hall, J. Opt. Soc. Am. B, 1999, 16, 2255–2268 CrossRef CAS.
- R. Tóbiás, T. Furtenbacher, I. Simkó, A. G. Császár, M. L. Diouf, F. M. J. Cozijn, J. M. A. Staa, E. J. Salumbides and W. Ubachs, Nat. Commun., 2020, 11, 1708 CrossRef PubMed.
- M. L. Diouf, R. Tóbiás, I. Simkó, F. M. J. Cozijn, E. J. Salumbides, W. Ubachs and A. G. Császár, J. Phys. Chem. Ref. Data, 2021, 50, 023106 CrossRef CAS.
- M. E. J. Newman, Networks, Oxford University Press, Oxford, 2010 Search PubMed.
- BIPM report, https://www.bipm.org/en/publications/mises-en-pratique/standard-frequencies-metre.
- M. L. Diouf, R. Tóbiás, T. S. van der Schaaf, F. M. J. Cozijn, E. J. Salumbides, A. G. Császár and W. Ubachs, Mol. Phys., 2022, 120, 1 CrossRef.
- M. L. Diouf, R. Tóbiás, F. M. J. Cozijn, E. J. Salumbides, C. Fábri, C. Puzzarini, A. G. Császár and W. Ubachs, Opt. Expr., 2022, 30, 46040 CrossRef CAS PubMed.
- R. R. Gamache, B. Vispoel, M. Rey, A. Nikitin, V. Tyuterev, O. Egorov, I. E. Gordon and V. Boudon, J. Quant. Spectrosc. Radiat. Transfer, 2021, 271, 107713 CrossRef CAS.
- A. Gambetta, D. Gatti, A. Castrillo, G. Galzerano, P. Laporta, L. Gianfrani and M. Marangoni, Appl. Phys. Lett., 2011, 99, 251107 CrossRef.
- A. Gambetta, N. Coluccelli, M. Cassinerio, T. T. Fernandez, D. Gatti, A. Castrillo, A. Ceausu-Velcescu, E. Fasci, L. Gianfrani, L. Santamaria, V. D. P. Maddaloni, P. De Nataleand, P. Laporta and G. Galzerano, J. Chem. Phys., 2015, 143, 234202 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01835k |
| This journal is © the Owner Societies 2023 |