Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
NMR chemical shift of confined 129Xe: coordination number, paramagnetic channels and molecular dynamics in a cryptophane-A biosensor†
Perttu
Hilla
 * and
Juha
Vaara
* and
Juha
Vaara
 *
*
NMR Research Unit, P.O. Box 3000, FI-90014 University of Oulu, Finland. E-mail: perttu.hilla@oulu.fi; juha.vaara@iki.fi
First published on 7th August 2023
Abstract
Advances in hyperpolarisation and indirect detection have enabled the development of xenon nuclear magnetic resonance (NMR) biosensors (XBSs) for molecule-selective sensing in down to picomolar concentration. Cryptophanes (Crs) are popular cages for hosting the Xe “spy”. Understanding the microscopic host–guest chemistry has remained a challenge in the XBS field. While early NMR computations of XBSs did not consider the important effects of host dynamics and explicit solvent, here we model the motionally averaged, relativistic NMR chemical shift (CS) of free Xe, Xe in a prototypic CrA cage and Xe in a water-soluble CrA derivative, each in an explicit H2O solvent, over system configurations generated at three different levels of molecular dynamics (MD) simulations. We confirm the “contact-type” character of the Xe CS, arising from the increased availability of paramagnetic channels, magnetic couplings between occupied and virtual orbitals through the short-ranged orbital hyperfine operator, when neighbouring atoms are in contact with Xe. Remarkably, the Xe CS in the present, highly dynamic and conformationally flexible situations is found to depend linearly on the coordination number of the Xe atom. We interpret the high- and low-CS situations in terms of the magnetic absorption spectrum and choose our preference among the used MD methods based on comparison with the experimental CS. We check the role of spin–orbit coupling by comparing with fully relativistic CS calculations. The study outlines the computational workflow required to realistically model the CS of Xe confined in dynamic cavity structures under experimental conditions, and contributes to microscopic understanding of XBSs.
1. Introduction
The xenon atom is an excellent nuclear magnetic resonance (NMR) probe1,2 of various microscopic environments such as gases,3–5 liquids,6 liquid crystals,7 porous materials8 and more exotic systems, e.g., self-organising nanocages.9 Its large, polarisable and chemically sensitive electron cloud evokes a broad 129/131Xe NMR chemical shift (CS) range of up to hundreds of ppm in different host materials. The 129Xe isotope has a spin-1/2 nucleus with a natural abundancy of ca. 26%, and is less prone to rapid relaxation than the quadrupolar spin-3/2 isotope, 131Xe (21%). The spin-exchange optical pumping (SEOP) method,10 in which the circular polarisation of laser light is first transferred into the electron-spin polarisation of an effectively single-electron alkali-metal system, and then into the spin polarisation of Xe nuclei, has rendered it easy to hyperpolarise a sample of Xe gas. This means that the Boltzmann-population difference of the nuclear spin levels is increased above that of thermal equilibrium, which enhances the intensity of the NMR signal by orders of magnitude. This significantly reduces the minimal concentration of Xe spins that can be detected. Xe hyperpolarisation methods have inspired growing interest in 129Xe magnetic resonance imaging11 (MRI). From now on, we always refer to the 129Xe isotope.Conventional proton NMR is burdened by its low sensitivity, rendering selective sensing of chemical species at low concentration difficult. The inert Xe does not easily form chemical bonds with other atoms, allowing noninvasive studies of substances with low inherent proton concentration, such as human lungs,12 using hyperpolarised 129Xe MRI. On the other hand, the inertness limits molecular specificity and, hence, the variety of different chemical environments that can be distinguished using Xe alone. In 2001 it was shown13 that Xe could be encapsulated by a cryptophane (Cr) cage to form a supramolecular system that can be applied as a biosensor,11,14,15 an analytical device for the recognition and detection of chemical substances. The Cr cages16–18 are roughly spherical in shape and consist of two bowl-like cyclotribenzylene (CTB) moieties connected by three linker groups that can vary in length and atomic composition. The flexible cavity left between the bowls is capable of undergoing atomic and molecular encapsulation by non-covalent interactions. Also guests other than Xe have been experimentally studied, such as chloroform,19 propylene oxide,20 as well as Cs and Tl cations.21
Water is the natural solvent environment for biomedical applications of Xe biosensors (XBSs). Hence, understanding the host–guest chemistry of especially H2O molecules in connection with the host structures is extremely important. In our recent work22 we performed metadynamics simulations23,24,25 of Xe in the prototypical CrA cage in an explicit H2O solvent. The water molecules were found to play a crucial role in Xe dissociation from within the cage to the bulk solution. Understanding the Xe exchange between solvent and the host cage is crucial for the experimental NMR methods used with XBSs, as discussed below.
In addition to the SEOP method, another important development has been provided by the so-called Hyper-CEST experiments,26,27 where hyperpolarisation is combined with the indirect chemical exchange saturation transfer (CEST) method28,29 to increase the Xe NMR signal intensity by up to 107-fold. In Hyper-CEST, spin polarisation of the SEOP-hyperpolarised bulk Xe is transferred to a scarcely populated site (e.g., Xe in the host cavity) through chemical exchange. The confined Xe is depolarised by continuous frequency-swept irradiation over the CS range of Xe, and exchanged back to the bulk. As a result, the intensity of the bulk Xe NMR signal decreases by an amount that depends on the irradiation frequency, revealing the resonance frequency of the less populated site in the so-called z spectrum.
For the Hyper-CEST experiment, it is required that the host cage (a) has high affinity for Xe, leading to as high a concentration of bound Xe as possible, while (b) still allowing for rapid Xe exchange to and from the solvent. The high affinity ensures that Xe is encapsulated by the host to a sufficient amount, whereas exchange is essential for efficient depolarisation and, hence, a strong signal in the z spectrum. Such energetic and dynamic properties of Xe@Cr biosensors have been studied experimentally27,30–47 and computationally22,48–50. Based on the literature, the free energy of binding and the exchange rate of Xe are ca. 4…6 kcal mol−1 and 102…103 s−1, respectively. For XBS applications, such binding and exchange properties are excellent considering the requirements (a) and (b). It has been shown that Cr cages exhibit an “induced-fit” binding behaviour towards Xe by adjusting the volume of the cavity for high affinity.40 These properties of Xe@Cr XBSs are, however, sensitive to the structure of the host, e.g., the length and atomic composition of the linkers between the CTB caps. On the other hand, this also opens the possibility of tuning the properties of XBSs towards the desired applications. A major drawback of Cr cages is their demanding synthesis procedure, resulting in racemic mixtures.16–18
The exterior of a Cr cage has six “arms” that can be equipped with various functional moieties, such as water solubility-enhancing CH2COOH acetic-acid groups or affinity tags for specific external molecules. Fortunately for biomedical XBS applications, the water-soluble Cr derivatives show a considerably stronger binding affinity of Xe than the organo-soluble ones.35 When an affinity tag binds with an external analyte, the chemistry of the biosensor changes. This affects the NMR shielding properties of the electron cloud of the confined Xe and is, therefore, reported by the Xe CS. A particularly interesting property is the CS difference between different chemical environments of Xe resulting from, e.g., host cage modification, solvent effects, temperature, pH and binding to an analyte. Due to the chemical sensitivity of Xe, remarkably small changes, such as a single-site deuteration of the host structure,31,32 can be seen in the Xe NMR spectrum. Accurate sensing of macroscopic parameters such as temperature51 and the pH value52 has been demonstrated. The combination of high chemical resolution and molecular specificity renders the XBS approach fitting for case-by-case modification and optimisation of properties towards the desired application.
Host–guest systems and their chemistry are of growing general interest due to their use in drug development and delivery, and as molecular storages, contrast agents or chemical sensors.53–56 The microscopic behaviour of these systems can be experimentally challenging to study. Due to the diversification of XBSs designed for different applications, computational modeling is pivotal in providing such microscopic information on XBSs, and on host–guest systems in general. The NMR parameters of XBSs have been studied using experimental30,31,35,37,38,41,45 and computational48,50,52,57,58,59 methods. Using Xe gas as the NMR reference, Xe in bulk water solution resonates experimentally at ca. 190 ppm.6 Confined Xe within a CrA cage in an organic solvent, and within a water-soluble CrA (functionalised with the acetic-acid groups) in aqueous solution resonate at roughly 70 and 60 ppm, respectively30,35,38 (see Section 3 for a more detailed discussion). Computational work on XBSs has shown that relativistic effects should be included in the quantum-chemical (QC) NMR shielding calculations of Xe.52,59 In addition, using dispersion corrections on top of density-functional theory (DFT) calculations is of major importance in the geometry optimisations and MD simulations.50
Concerning a different Xe host–guest system, Straka, Lantto and Vaara60 found in 2008 that relativistic effects, electron correlation and host dynamics all have an important role in the Xe CS of the endohedral Xe@C60 buckminsterfullerene. Straka et al. continued the work in ref. 61 by studying the CS of Xe@C60 dissolved in liquid benzene, thus introducing solvent effects. It was reported that relativistic effects (at the Breit–Pauli perturbation theory level62,63) gave rise to a 9% increase in the Xe CS as compared to a nonrelativistic calculation. The influence of the dynamic cage and solvent increased, in turn, the shift relative to free Xe by 8% and 7%, respectively, compared to a static cage in vacuo. Importantly, the different contributions all had the same, positive sign in this system, so that their effects were cumulative. Hence, it is evident that the sensitivity of the Xe CS requires a realistic model in the C60 fullerene, which is a relatively rigid host structure. Due to the flexible character of the CrA cages, the present Xe@CrA systems are expected to exhibit an even more complex and dynamic behaviour than what is seen for the endohedral Xe@C60. Because XBSs are applied (and, in the present paper, also modelled) in aqueous solution, the aforementioned physical effects can be expected to be significant for the Xe CS in the CrA biosensors. In addition, as individual water molecules have been found22,49 to play an important role in the microscopic dynamics of XBSs, including them in the modeling of Xe CS is also likely to have an important effect.
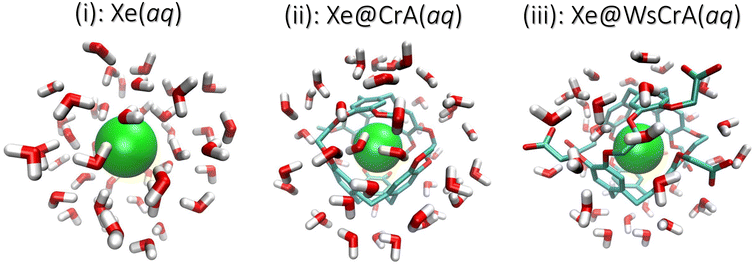
In this study we combine molecular dynamics (MD) simulations with relativistic QC calculations to compute the average NMR CS of Xe in three different environments: (i) free Xe, (ii) Xe in CrA and (iii) Xe in the water-soluble CrA derivative (WsCrA), each at room temperature in explicit water solvent. The three systems are shown in Fig. 1. The Xe CS in these highly dynamic environments is shown to be governed by the coordination number of Xe, Z. We compare the resulting CSs determined from MD trajectories obtained by three different methods, reflecting the quality of the underlying description of Xe dynamics in the chemical environments (i–iii). Besides studying the physical factors influencing the CS of confined Xe and, in particular, of Xe@CrA biosensors, a more general goal of the present work is to realise a computational workflow required to model flexible Xe host–guest systems under experimental conditions with useful accuracy for developing novel XBS systems and applications. This includes electronic-structure features such as relativistic effects, a sufficient basis set and a suitable DFT exchange–correlation functional, as well as physical model features such as system dynamics and solvent effects. The obtained information contributes to the microscopic understanding of Xe NMR, XBSs, and Xe host–guest systems in general, aiding in their design and optimisation, and guiding synthesis towards in vivo applications.
2. Background
Nuclear shielding of noble gases
The experimentally observable NMR CS, δK, of nucleus K is defined as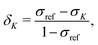 | (1) |
| σ = σd + σp, | (2) |
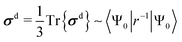 | (3) |
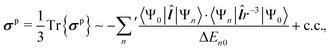 | (4) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) is the orbital angular momentum operator, r is the distance from the NMR nucleus and c.c. means the complex conjugate of the preceding term. The summation is carried over the excited states {Ψn} of the unperturbed system. Instead of the Rayleigh-Schrödinger (sum-over-states) form of eqn (3) and (4), modern QC software use response-theoretical formulations68 where, particularly at the most profound 4-component Dirac level, the division of σ into dia- and paramagnetic contributions appears via the negative and positive-energy branches of the electronic response.69,70 Despite this fact, the nonrelativistic perturbation-theoretical expressions are very useful in gaining qualitative understanding of the relevant physics using familiar textbook concepts (a recent example being ref. 71).
is the orbital angular momentum operator, r is the distance from the NMR nucleus and c.c. means the complex conjugate of the preceding term. The summation is carried over the excited states {Ψn} of the unperturbed system. Instead of the Rayleigh-Schrödinger (sum-over-states) form of eqn (3) and (4), modern QC software use response-theoretical formulations68 where, particularly at the most profound 4-component Dirac level, the division of σ into dia- and paramagnetic contributions appears via the negative and positive-energy branches of the electronic response.69,70 Despite this fact, the nonrelativistic perturbation-theoretical expressions are very useful in gaining qualitative understanding of the relevant physics using familiar textbook concepts (a recent example being ref. 71).
The diamagnetic term, σd, is positive and only depends on the ground state |Ψ0〉 of the system. The expectation value of the only “mildly local” r−1 operator reflects the density of the electron cloud around the nucleus. Therefore, increasing the electron density around the nucleus increases the magnitude of the diamagnetic shielding constant. On the other hand, the paramagnetic term, σp, is negative and arises from orbital couplings via the angular momentum operator between the ground state and the excited-state manifold. Due to the energy denominator in eqn (4), there is an efficient coupling particularly to the low-lying excited states of the system. For a closed-shell atom, the orbital Zeeman operator, essentially ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) , does not couple the spherically symmetric ground state to any excited states. Hence, a free xenon atom in vacuo has σp = 0, when the common gauge is placed at the Xe nucleus. A non-zero orbital paramagnetic contribution requires, therefore, a symmetry lowering of the electron cloud around the nucleus. In the presence of such disturbances, which in our XBS case are caused by the atoms of the host material or solvent molecules, the orbital magnetic couplings, or “paramagnetic channels”, of eqn (4), increase the magnitude of the negative σp. Because of the r−1 and r−3 factors of the corresponding hyperfine operators, density contributions to σd decay relatively slowly when moving away from the nucleus, while σp decays much more rapidly. This spatial “short-sightedness” of σp stems from the paramagnetic nuclear spin-electron orbit (PSO, also known as orbital hyperfine) operator, which is proportional to
, does not couple the spherically symmetric ground state to any excited states. Hence, a free xenon atom in vacuo has σp = 0, when the common gauge is placed at the Xe nucleus. A non-zero orbital paramagnetic contribution requires, therefore, a symmetry lowering of the electron cloud around the nucleus. In the presence of such disturbances, which in our XBS case are caused by the atoms of the host material or solvent molecules, the orbital magnetic couplings, or “paramagnetic channels”, of eqn (4), increase the magnitude of the negative σp. Because of the r−1 and r−3 factors of the corresponding hyperfine operators, density contributions to σd decay relatively slowly when moving away from the nucleus, while σp decays much more rapidly. This spatial “short-sightedness” of σp stems from the paramagnetic nuclear spin-electron orbit (PSO, also known as orbital hyperfine) operator, which is proportional to ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) r−3. Due to this locality of the PSO operator, the symmetry-allowed paramagnetic channels are only efficient when the corresponding excited states are spatially close to the NMR nucleus, explaining the atomic contact-like nature of the shielding interaction.72
r−3. Due to this locality of the PSO operator, the symmetry-allowed paramagnetic channels are only efficient when the corresponding excited states are spatially close to the NMR nucleus, explaining the atomic contact-like nature of the shielding interaction.72
Since σd and σp are positive and negative, respectively, the CS, when referenced to the corresponding free noble-gas atom, tends to become more negative due to the increased electron density (σd) and more positive by the effect of paramagnetic channels (σp), opened by atom-atom contacts. In the XBS context this means that spherically symmetric and/or high electron-density chemical environments of the Xe guest correspond to low or even negative CS, the latter when the shielding constant exceeds the value pertinent to the isolated atom. In contrast, non-symmetric environments with nearby atoms open paramagnetic channels, e.g., upon collisions with other atoms, and correspond to high Xe CS. This way σ connects the electronic environment of Xe, which is governed by the microscopic local molecular structure and dynamics, to the experimentally observable δ. This is exactly what renders Xe such a good probe for different chemical environments.
Coordination number
In the present study, the molecular dynamics of systems (i–iii) in Fig. 1, are analysed in detail and the results for the Xe CS are discussed in the framework of eqn (3) and (4). We re-confirm the atomic contact-type behaviour of the Xe CS, which is governed by the coordination number Z of the xenon atom. Large Z leads to a high number of paramagnetic channels, and therefore to positive values of CS. A point worth noting is that a high symmetry of the environment may prevent the occurrence of a high CS even in the situation of a large Z. An example is the aforementioned endohedral Xe@C60 fullerene, where the Xe CS is modest, around 180 ppm, despite Z = 60, due to the magnetic dipole-allowed excited states being high in energy.71 This implies relative inefficiency of the paramagnetic channels in endohedral noble gas-fullerene systems of high symmetry. Returning to the present XBS case, based on the MD simulations and the Xe CSs computed from the snapshots, we demonstrate here a linear dependence between δ and Z in each system (i–iii). Such a scaling was previously reported for an intermolecular shift in static Xe clusters.72 Similarly, the CS of confined Xe has been found to depend on the size, shape and atomic composition of rigid nanochannels.73 This relationship is presently seen to also hold for a flexible XBS structure undergoing complex dynamics. The dependence of Xe CS on Z in aqueous solution was also investigated in ref. 6.Magnetic absorption spectrum
In addition to the analysis in terms of the structural parameter Z, we relate the occurrence of high and low, even negative Xe CS to features of magnetic-dipole absorption spectra from the corresponding MD snapshots. Such spectra are calculated using the magnetic dipole operator![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) , i.e., essentially the orbital Zeeman operators appearing in eqn (4). The system configurations in which other atoms get very close to Xe, paramagnetic channels open and lead to high-intensity transition moments between the ground state |Ψ0〉 and excited states {|Ψn〉}. Such transitions contribute to the paramagnetic shielding and lead to high CS.
, i.e., essentially the orbital Zeeman operators appearing in eqn (4). The system configurations in which other atoms get very close to Xe, paramagnetic channels open and lead to high-intensity transition moments between the ground state |Ψ0〉 and excited states {|Ψn〉}. Such transitions contribute to the paramagnetic shielding and lead to high CS.
Quality of MD trajectories
The above-discussed facts mean that the NMR shielding of Xe is very sensitive to the details of the structure and dynamics of the surrounding molecules. Hence, Xe CS also serves as a stringent test for the quality of the underlying MD simulations. We compare the chemical shifts obtained from the dynamics driven by the different GFNn-xTB Hamiltonians74–76 to experimental data. Therefore, our data reflect the quality of the different levels of theory within the xTB code77,78 in modeling the free and host-bound Xe in an aqueous environment.Previous computational studies
Early computational work57 on the NMR parameters of Xe@Cr complexes used Monte-Carlo (MC) sampling with potential-energy and shielding surfaces (PES and SS) pre-parameterised using QC calculations. In ref. 57, the PES and SS were calculated as a function of position with respect to a fragment representing one half of the inner surface of the Cr cage. The obtained data were then used to construct a model for the full Cr host comprising both halves. The PES was utilised in the MC averaging of Xe motion inside a rigid cage, from which the average CS could be calculated. A similar approach of pre-parametrisation and MC averaging has found success for Xe also in other organic cavities.9,79–81 Xe@Cr systems have also been modeled using static cages and implicit solvation models.48,50,52,58,59 The two aforementioned studies on Xe@C6060,61 averaged over shielding calculations of MD simulation snapshots to compute the Xe CS, and in ref. 61 even featuring explicit solvent molecules. The xTB code, which is used in the present work, has recently also been used in other MD simulation snapshot-based CS averaging studies.82,83Due to the flexibility of XBS systems and the important role played by the aqueous solution environment in their application, there is clearly demand for studies of NMR properties of Cr-XBS systems where MD of a dynamic cage in an explicit solvent is combined with QC shielding calculations on simulation snapshots. Such studies have been hindered by the large number of atoms involved in these systems and the limited computational resources. However, recent developments of QC methods have rendered it possible to perform direct dynamical averaging of heavy-element NMR chemical shifts based on MD trajectories. This allows computational studies of highly complex and dynamic systems, without the use of “computational shortcuts”, such as pre-parameterised SSs. Hence, an important aim of the present work is to provide a valid computational workflow for modeling free and host-bound Xe in biosensor structures in the experimentally relevant aqueous environment, including relativistic effects, dynamics and explicit solvents.
3. Computational details
Molecular dynamics simulations
Molecular dynamics simulations were performed on the density-functional tight binding-based xTB programme.77,78 The GFNn-xTB family of Hamiltonians include the modern D3–D4 DFT dispersion corrections by Grimme et al.84,85 Xe in all three different chemical environments, systems (i–iii), was simulated at three different levels of theory: the semiempirical GFN274 and GFN075 methods, where the dynamics of the nuclear framework is determined by solving the approximate electronic structure of the system for each MD snapshot on the fly, and the partially polarisable force-field method GFN-FF.76 The MD trajectories of systems (i) and (ii) were adopted from our earlier work,22 while a new trajectory was generated for (iii) in the present study. The simulations were performed at the constant temperature of 300 K, using the Berendsen thermostat,86 a time step of Δt = 1.0 fs and a droplet model with 500 H2O solvent molecules. For each system, the production periods were 2.5–3.0 ns, and snapshots were recorded every 0.1 ps. Further computational details on the MD simulations are provided in ref. 22 and the ESI† therein.NMR shielding calculations
The goal was to efficiently and accurately compute the nuclear magnetic shielding constants of Xe, σi, for each MD snapshot i, which determine the NMR CS as a time average over N snapshots: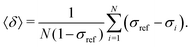 | (5) |
Relativistic effects
Relativistic effects are known to play an important role in heavy-element chemistry,88 and particularly in NMR observables.89 In the context of QC methods, however, using the fully relativistic four-component Dirac level of theory for σ90–92 continues to be extremely demanding for a statistically meaningful number of MD snapshots in a large molecular system. E.g., in the present case, hundreds of snapshots for each of the three roughly 200-atom systems are computed. Several efficient approximate methods exist,93 such as the Douglas–Kroll–Hess method94–98 and zeroth-order regular approximation,99–102 as well as exact decoupling methods, where the small component of the four-spinor describing the positronic states is decoupled from the electronic, chemically relevant states.103Here, we employ the widely used, scalar relativistic exact two-component (X2C) method for heavy-element NMR properties103,104 as implemented in the Turbomole programme,105,106 to account for the relativistic contributions in calculating 〈δ〉 for XBSs in aqueous solvent. Using X2C enables computing σi for hundreds of MD snapshots, thus providing an efficient way of introducing dynamical and solvent effects to mimic experimental conditions. As this method neglects the spin–orbit contributions to Xe CS, we ensured that they are not significant for the conclusions of the present study by also computing for each system (i–iii) three snapshots from the GFN-FF MD simulations by the fully relativistic Dirac–Kohn–Sham (DKS) four-component theory90 in the ReSpect programme.107 By turning the spin–orbit interaction on/off, its contribution to the Xe CS could be calculated, and was found to be on average no more than ca. 2 ppm in the present systems. Computational details and the results of the comparison are presented in the ESI.†
The X2C NMR shielding calculations were performed at the DFT level using the resolution-of-identity (RI) method108–110 for the Coulombic integrals. Based on earlier experience,60,111–113 the hybrid BHandHLYP exchange–correlation (XC) functional114–116 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of DFT and exact Hartree–Fock-based exchange contributions) was chosen for its excellent performance for the NMR properties of Xe. For the atomic orbital basis set of Xe, the completeness-optimised,117 uncontracted [27s25p21d4f] basis by Hanni et al.118 (changed into 4 f-functions in ref. 9 and here denoted as MHA) was used, along with the Karlsruhe def2-QZVPP119–121 quadruple-zeta valence double-polarisation auxiliary basis for the RI method. The “m4a” numerical integration grid of Turbomole was used.
1 mixture of DFT and exact Hartree–Fock-based exchange contributions) was chosen for its excellent performance for the NMR properties of Xe. For the atomic orbital basis set of Xe, the completeness-optimised,117 uncontracted [27s25p21d4f] basis by Hanni et al.118 (changed into 4 f-functions in ref. 9 and here denoted as MHA) was used, along with the Karlsruhe def2-QZVPP119–121 quadruple-zeta valence double-polarisation auxiliary basis for the RI method. The “m4a” numerical integration grid of Turbomole was used.
Cluster extraction and basis set
In QC calculations of σi, the number of atoms of the environment of the nucleus (in our case the CrA cage and the H2O molecules around Xe) to be included, as well as the basis set requirements placed on the atoms of the environment, depend on the studied system. Including each atom present in the MD run also in the QC calculations is computationally far too expensive and often unnecessary. Therefore, a Python122 script was used to extract clusters from the MD snapshots based on the distance from the Xe atom. For the Xe@CrA systems, the entire cage structure, including the solubility groups of the WsCrA system (iii), was always fully included. The aim was to determine the number of water molecules that have to be included in the clusters to remain within an acceptable cut-off error, and the necessary, yet computationally efficient basis set size for the Cr cage and H2O molecules. To this end, we calculated the Xe CS in systems (i) and (iii) as a function of (1) the radius of the cluster, rc, and (2) the quality of the basis set used for the WsCrA and H2O molecules. If an atom belonging to a H2O molecule was inside rc, then the molecule was fully included. These convergence tests were performed for three low-energy snapshots in the GFN-FF MD trajectory. Details are shown in the ESI.†In point (1), the final radii rc for the clusters were chosen when the Xe CS was found to be converged to about 1–2 ppm window. By this criterion we selected rc = 7 Å and 8 Å for Xe(aq) and Xe@WsCrA(aq), respectively. The cut-off rc = 8 Å was used for the prototypic XBS, Xe@CrA(aq). Typical examples of the clusters extracted from the MD snapshots are shown in Fig. 1. In addition to explicit solvent molecules, the implicit COSMO solvation model123 with the dielectric constant of 80 (corresponding to liquid water) was used in the shielding calculations. In particular for the Xe@WsCrA system, it is seen that the inclusion of solvent molecules increases (in line with the observations in ref. 60 and 61) the CS by ca. 10–20 ppm, depending on the snapshot. This would account for 15–30% of the final, motionally averaged CS of Xe@WsCrA(aq) (see Section 4). Therefore, the contribution of the explicit solvent to Xe CS in the present, dynamic and motionally flexible Xe-host systems is, indeed, even higher than that in Xe@C60, in refs. 60 and 61. This further emphasises the importance of accounting for solvent effects also in the QC shielding calculations when modelling XBSs.
Concerning the effects of the basis set [point (2)], improving the cage and H2O basis from x2c-SVPall to x2c-TZVPall124 showed no systematic improvement, as detailed in the ESI,† so the former was chosen for maximal computational efficiency. In dense systems the basis-set requirements are alleviated as compared to the case of individual atoms or molecules due to the beneficial effect of basis-set superposition in providing additional flexibility in describing the intermolecular region. The above-mentioned values were used with all the present trajectories. Computational requirements using the present workflow are reported in the ESI.†
4. Results and discussion
The trajectory-averaged Xe CS, 〈δ〉 for systems (i–iii), corresponding to eqn (5), and computed at the X2C/DFT-BHandHLYP level based on the three different GFNn-level MD simulations, are reported in Table 1 along with previous experimental and computational values.| MD level | Xe(aq) (i) | Xe@CrA(aq) (ii) | Xe@WsCrA(aq) (iii) |
|---|---|---|---|
| a Ref. 6: CS of 190 ppm in H2O solution, and 186 ppm in D2O, both at 300 K. Computational value of 187 ppm obtained by combining shielding-surface calculations with MD simulations using the AMOEBA force field125 parameterised against high-level QC calculations. b Ref. 30 and 38: experiments performed in organic tetrachloroethane (CDCl2)2 solvent. The originally reported value of 62.3 ppm at 278 K scaled to match the present value at 300 K according to ref. 38. c Ref. 35. d Ref. 57: MC motional averaging and shielding-surface calculations in a static cage. e Ref. 50: implicit H2O solvent and a static model for the CrA. | |||
| GFN-2 | 464 (9) | 118 (6) | 278 (8) |
| GFN-0 | 644 (5) | 179 (6) | 187 (7) |
| GFN-FF | 182 (2) | 98 (3) | 67 (2) |
| Experiments | 190a, 186a | 68b | 64c |
| Computations | 187a | 78d, 88e | — |
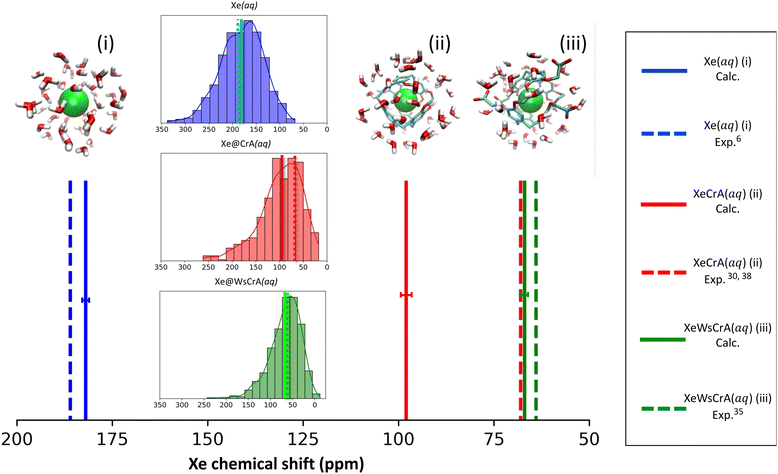
Both semiempirical MD methods, GFN0 and GFN2, are seen to generate trajectories that lead to overestimated Xe CS in each present system. In particular, the CS in H2O, system (i), is hundreds of ppm away from the experimental value of 190 ppm. For the XBSs in H2O, systems (ii) and (iii), the GFN0 and GFN2 dynamics overestimate the Xe CS by 100–200 ppm. In contrast, the agreement of the GFN-FF force-field data with experiment is quite satisfactory. It has been pointed out that the semiempirical (GFN2 and GFN0) Hamiltonians of xTB underestimate the non-covalent repulsive interactions between noble gases and other atoms126. This coincides with our present observation (vide infra) where the nearest cage atoms and water molecules get too close to Xe, leading to a systematic error in σ. In particular, such unrealistically close encounters are expected to lead to an overestimated magnitude of the negative, paramagnetic shielding contributions, which is precisely what we see in the much too positive CSs of Xe in the different media (Table 1) at the semiempirical levels. Overly attractive interactions between Xe and other atoms inside the CrA cage also led to the unrealistically high binding energies at the GFN0 and GFN2 levels, as reported in ref. 22. The obtained Xe CSs in Table 1 suggest that the GFN2 and GFN0 simulations do not produce accurate local environments for either the free or the host-bound Xe in an aqueous environment.
As already mentioned, MD generated by the GFN-FF force-field method is seen to produce, for systems (i) and (iii) for which experiments in aqueous solution6,35 are available, Xe CSs that are in very good agreement with measurements. Indeed, the deviations for systems (i) and (iii) amount only up to 3–4 ppm, and even less if the magnitude of the statistical error margins are taken into account.¶ The prototypic CrA, system (ii), was presently modeled in water solution, whereas the referenced experiments30,38 used an organic solvent. Hence, the deviation of 30 ppm is not surprising. Earlier computational studies of ref. 50 and 57 used static Xe@CrA structures in implicit water solvent and without solvent, respectively. The agreement with the experiment was slightly better than in the present case, although that may have been fortuitous due to the static cage model used.
For systems (i) and (iii), the deviations of the present simulation results from experiments are quite small considering the complexity and highly dynamic nature of the studied systems. Undoubtedly error cancellation also benefits the present GFN-FF MD simulations since, from a purely theoretical point-of-view, it is the simplest of the present GFNn-xTB levels of theory. However, Xe CS is a very sensitive property of the microscopic environment of the Xe atom, and results that agree well with the experimental data taken both in liquid water and the XBS cage environments, are nevertheless a strong indication of fairly accurate molecular dynamics. In ref. 22 and 127, it was also seen that GFN-FF produces good results for the binding energies of both the Xe@CrA XBS and charge-neutral protein–ligand systems, respectively. Motivated on the obtained values in Table 1 and the above remarks, from now on in this work we mainly focus on the analysis of the GFN-FF MD and the resulting Xe CSs for systems (i) and (iii).
Xenon chemical shift distribution
The calculated average Xe CS based on the GFN-FF MD simulations, corresponding experimental values and the distribution of instantaneous shifts along the MD trajectory, are shown in Fig. 2. The correct order of signals is reproduced: the Xe(aq) signal has the highest CS, the prototypical Xe@CrA(aq) XBS the second-highest, and the water-soluble Xe@WsCrA(aq) XBS the lowest. Interestingly, the deviation from the experimental value has a different sign for Xe(aq), where the shift is underestimated by 4 ± 2 ppm, rather than for the Xe@WsCrA XBS, where an overestimation of 3 ± 2 ppm is seen. By comparing the CS values produced by X2C with fully relativistic calculations on a limited set of snapshots, as detailed in Table S1 of the ESI,† both the slight CS underestimation in water and overestimation in WsCrA(aq) can be at least partially related to the approximate scalar relativistic X2C treatment in the main part of the present study. For Xe(aq) and the two XBSs(aq), corrections from fully relativistic treatment would change the Xe CS by about +5 and −2 ppm, respectively, rendering the agreement with experiments even better.Skewed normal CS distributions are found in Fig. 2, with tails towards the high-shift values. The shape of the distribution is more skewed and the average shift is smaller in the two XBS systems than in water. This can be rationalised in the way that there are relatively fewer system configurations with strong paramagnetic channels, which would lead to high Xe CS, than in the case of Xe(aq). In these situations, an atom of the environment would be very close to Xe. Instead, there is a relative preference for fairly spherical local cavity environments of Xe in the XBS cages, implying low Xe CS due to the relative importance of the diamagnetic contribution. In comparison, for Xe in water, the distribution is less skewed and the average CS is considerably higher. This can be understood by the relatively high density and mobility of small H2O molecules of the environment, experiencing frequent collisions with Xe,6 which lead to efficient paramagnetic channels via the PSO operator, and therefore to a high CS.
Connection to the atomic environment of Xe at the GFN-FF level
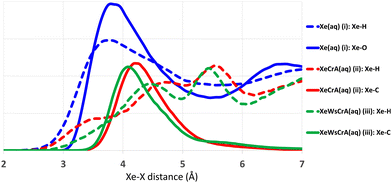
Radial distribution functions (RDFs) between Xe and other atoms based on the GFN-FF MD trajectories are shown in Fig. 3. The average atomic environment of Xe can be used to illustrate the points made above. It can immediately be seen that, on average, there are more atoms close to Xe in the Xe(aq) system than in the XBS systems. Increasing the number of atoms near Xe, as seen from Fig. 3, increases the CS, as in Table 1. The contact-type behaviour of Xe CS arises from the steep decrease (i.e., an increase in δ), on account of the r−3 factor in eqn (4), in the intermolecular shielding function upon diminishing distance.60,72,128–130 Therefore, the most important contributions to the Xe CS arise at short intermolecular separations, corresponding to contacts with other atoms in the environment. Concerning the XBSs, the computed shift is seen to be larger in the prototypic Xe@CrA than in the water-soluble Xe@WsCrA, by more than 30 ppm. The difference in this case is related to the interaction with the “arms” of the host cage, as illustrated by the Xe-H RDFs represented as dashed lines in Fig. 3. The smaller, hydrophobic CH3 arms of the system (ii) prefer to be oriented inwards, away from the H2O solvent, and are thus capable of closer contacts with the confined Xe than the bulkier hydrophilic CH2COOH arms of the water-soluble cage (iii) that prefer to stretch further out into the solvent. In contrast, in organic medium, as was the case in the experiments in ref. 30 and 38, the CH3 arms may be expected to orient more strongly towards the solvent than in aqueous medium. This would lead to fewer close contacts with Xe and, hence, fewer paramagnetic channels, and therefore to lower Xe CS. This is indeed experimentally observed and could explain the deviation of 30 ppm caused by different solvents in the case of system (ii) between the experiments and the present computations. From Fig. 3 it can also be seen that the CS difference between the two XBSs is not strongly related to changes in the interior of the Cr cages, as seen from the nearly identical Xe-C RDFs in the prototypic and water-soluble cages.Different MD methods for Xe(aq)
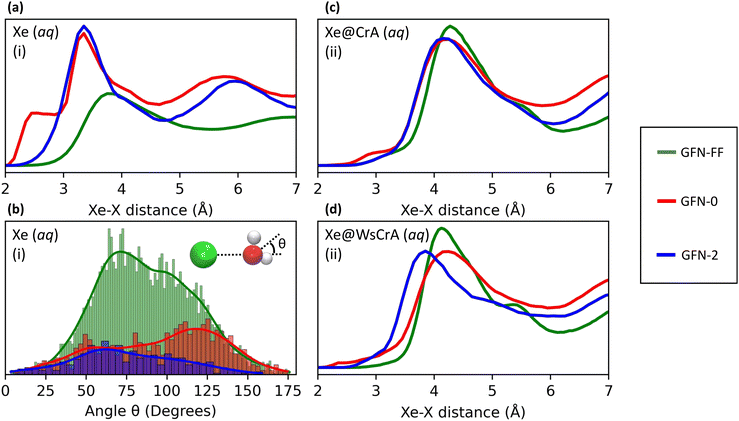
The main differences between the local Xe environments produced by the three distinct GFNn-xTB MD simulations are similarly revealed by the RDFs between Xe and the atoms of the water solvent, in system (i) (Fig. 4(a and b). The orientational distribution of the surrounding water molecules, represented by the distribution of the angle θ between the intermolecular Xe–O vector and the HOH-angle bisector of a neighbouring water molecule, is also important because the H2O molecules have quite anisotropic intermolecular interactions. The RDFs are taken between Xe and any other atom X (we later show that this choice correlates best with the Xe CS), and are calculated over the entire production trajectory of each of the MD simulations. The H2O orientations (Fig. 4(b)) are reported over the snapshots that were used for the Xe CS averaging in the case of system (i).The three MD levels are seen to produce quite different average structures. Especially at the GFN0 level, the neighbouring atoms can get very close to Xe, down to the 2 Å distance (Fig. 4(a)). The angular distribution (Fig. 4(b)) reveals that, on average, the hydrogen atoms of the water molecules prefer to point towards Xe at this level, as evidenced by the maximum of the distribution of θ around 125°. This produces the knee in the GFN0 RDF at ca. 2.5 Å. A high number of mobile atoms close to Xe frequently disturb the spherical symmetry of the environment and cause strong paramagnetic channels to appear, greatly increasing |σp| and, therefore, the Xe CS. This is reflected in the disproportionally overestimated CS result for Xe(aq) at the GFN0 level, in Table 1. Similar reasoning applies for the GFN2 level: although the onset of the Xe–X RDF is now moved to a larger distance than in the case of GFN0, an overestimated CS is nevertheless found with GFN2, underlining the difference to GFN-FF.
To the best of our knowledge, there are no experimental measurements on the Xe-H2O RDFs. However, as already stated, it has been reported that the repulsive interaction between Xe and other atoms is underestimated at the semiempirical GFN2 level.126 The simpler GFN0 method appears to suffer from related (and even worse) issues, as judged from the present simulations. The neighbouring atoms get too close to Xe at both semiempirical levels. In the computational study by Peuravaara et al.,6 high-level QC calculations were used to fit Xe–H2O interactions into the polarisable AMOEBA force field.125 The RDFs and orientational distributions of H2O molecules for Xe in water solution, as produced by the present GFN-FF MD simulations, are in good agreement with the structural properties obtained in ref. 6. In particular, the first minimum of the Xe–O RDF, indicating the radius of the first solvation shell, is found at 5.45 Å at the GFN-FF level (Fig. 3), to be compared to 5.55 Å in ref. 6. The angular distribution (Fig. 4(b)) peaks at ca. 70° in both studies. These findings suggest that the Xe–water interaction is reasonably well described at the GFN-FF level—at least better than at the semiempirical GFN0 and GFN2 levels.
Different MD methods for XBS(aq) systems
Similar trends as in the case of Xe(aq) are seen in the RDFs of Xe@CrA(aq) and Xe@WsCrA(aq) XBSs (Fig. 4(c and d)). However, the differences between the three MD levels are not equally dramatic as for Xe(aq), since the molecular environment of Xe within the CrA cages is less dynamic than in system (i). On average, the cage atoms do not get as close to the Xe guest as the mobile H2O molecules. Xe in the prototypic CrA cage (Fig. 4(c)) shows a knee at the onset region of the first RDF peak, indicating that, at the GFN0 level, the hydrogen atoms of the Cr linkers and the CH3 arms get quite close to Xe. This increases the Xe CS. Another RDF showing relatively close encounters with Xe is obtained at the GFN2 level, for which an overall similar structure of the first RDF peak as for GFN0 is gained after the onset region. Based on Table 1, the distributions of structures generated at the GFN2 and GFN-FF levels are better than those obtained using GFN0, and particularly GFN-FF produces results that are the closest to the experimental values. One should again bear in mind, however, that the experimental Xe CS data of the prototypic CrA cage were obtained in organic solution, as opposed to the presently modelled case of an aqueous solvent.Xe@WsCrA, system (iii) depicted in Fig. 4(d), again shows more pronounced differences between the RDFs produced by the different GFNn MD simulations, than in the case of the prototypic CrA. Apart from occurrences of very close encounters at 2–2.5 Å separation with GFN0, GFN2 interestingly produces structures that lead to a higher Xe CS than at the GFN0 level. This coincides with the first RDF maximum peaking, at the GFN2 level, significantly closer to Xe than in the case of GFN0. However, in the case of system (iii), the GFN0 trajectories also qualitatively differ from the ones obtained at the other two levels. With GFN0, water molecules sometimes briefly enter the Xe-occupied host and coexist there with Xe, a situation that does not occur at the GFN2 and GFN-FF levels. Therefore, directly relating the average structures to the Xe CS is not straightforward in the case of Xe@WsCrA. Nevertheless, the conclusion remains that GFN-FF is the only present method by which a Xe CS in the experimental range is obtained. Particularly for systems (i) and (iii), for which comparison with the experiment is fully justified, the microscopic structures generated at the GFN-FF level, shown in Fig. 3 and 4(a and c), lead to Xe CS values with no more than 4 ppm deviation from their experimental counterparts (Table 1). This, together with the energetic discrepancies with the experiment obtained earlier22,126 and the structural properties produced by the GFN-FF simulations agreeing well with the previous detailed study6 for Xe(aq), suggest that GFN-FF is the method of choice for modelling either free or host-bound Xe in aqueous environment, within the GFNn family.
Coordination number of the Xe guest
We now focus on further structural features and the resulting Xe CSs based on the GFN-FF MD simulations. In ref. 72, a linear dependence between the CS and the Xe coordination number Z with neighbouring, directly contacting atoms was discovered using nonrelativistic Hartree–Fock calculations for static van der Waals Xe cluster structures. The interatomic distance in such a contact situation falls into the relevant range for obtaining significant intermolecular CS effects. Hence, the correlation of CS with Z is understandable. As discussed below, a similar simple, linear relationship between Xe CS and Z is presently found also in the case of highly dynamic Xe(aq) and XBS(aq) environments, by combining explicit-solvent MD simulations with relativistic QC theory.As noted earlier, the steep increase in the intermolecular shielding function σ(RXe–X) characteristically occurs at distances below the first maximum of Xe–X RDF, where X is any other atom. Therefore, unlike in the conventional definition of Z via the integral of the RDF up to its first minimum (corresponding to the number of neighbouring atoms within the entire first solvation shell), Z is here defined as the integral to a shorter distance relevant to σ(RXe–X). We selected the separations rZ = 3.6, 3.5 and 3.7 Å for systems (i–iii), respectively, based on the maximum calculated correlation coefficient (CC) of Xe CS with Z in the range rZ = 3.3–4.3 Å, probed in steps of 0.05 Å. For Xe(aq), nearly identical, negative values of the CC of ca. −0.8 were obtained in the range rZ = 3.45–3.70 Å. Similarly for Xe@CrA(aq) and Xe@WsCrA(aq), CCs of ca. −0.6 for rZ = 3.45–3.60 Å, and −0.6 for rZ = 3.60–3.70 Å, respectively, were obtained. A precisely chosen value of rZ does not therefore play a significant role in the present discussion. Comparing to the RDFs presented in Fig. 4, these values of rZ are, indeed, located before the first maxima in each RDF. A negative value of the CC indicates that, as Z increases, σ decreases and δ increases.
The distributions of different Xe CSs in the systems (i–iii) as a function of Z, and the average CS over the set of snapshots with the same Z, using the definitions stated above, are shown in Fig. 5. There is, indeed, a linear correlation between σ and Z along the MD trajectories. A broad distribution of Xe CSs across the simulation snapshots corresponding to each Z value is nevertheless observed, which shows that the molecular environments of Xe with the same Z can still be quite different. Hence, such fits cannot be used to predict the Xe CS in individual structures, whereas the average shift of a set of configurations with the same value of Z can be reproduced. The Xe CS grows as Z, the number of atom-atom contacts, increases, which can again be understood on the basis of eqn (4) as discussed in Section 2. Therefore, the resulting CS distribution can be interpreted in a straightforward manner. In regions where other atoms or molecules, e.g., the solvent, collide with the noble-gas guest, a high value of CS is expected. The situation is dynamic and pronouncedly non-spherically symmetric during such a collision. In less dynamic and more symmetric instantaneous environments, the Xe nucleus has a low, in some cases even negative CS. Further analysis on the dependence between Z and Xe CS by, e.g., looking at the atomic contributions to the shielding constant from the environment of Xe with the gauge including the magnetically induced current (GIMIC) method131,132,133, could provide additional insight.
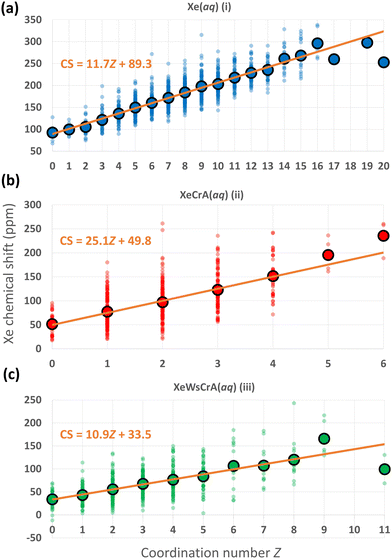 | ||
| Fig. 5 Distributions of instantaneous Xe CSs along the GFN-FF MD trajectories of the three systems (i–iii) with different coordination numbers Z (as defined in the main text), using the same colouring as in Fig. 2. The average CS over the snapshots with the given Z, and a linear fit to the values are also shown. | ||
The linear fits of the Xe CS to Z in Fig. 5 suggest themselves for use in predicting Xe CS without performing a large set of computationally demanding QC calculations. As discussed earlier, a standard route for this has been to use predetermined potential energy and shielding surfaces in MC or MD motional averaging. With the present linear fits to Z, one could, instead, extract the average Z from MD and compute the average CS, saving a lot of computational resources. Applied to the present data, using the average Z equal to 8.9, 2.0 and 3.4 for systems (i–iii), respectively, produces with the fits in Fig. 5 the values of ca. 193, 100 and 71 ppm, respectively, for the Xe CS. These results reproduce reasonably well the shifts of 182 ± 2, 98 ± 3 and 67 ± 2 ppm for Xe(aq), Xe@CrA(aq) and Xe@WsCrA(aq), respectively, from the full simulations at the GFN-FF level, in Table 1. However, the present fits are, of course, obtained via QC calculations on hundreds of snapshots and the fit parameters for each of the three systems are quite different, indicating non-portability to, e.g., different cages. To see whether this procedure can in reality be generalised to Xe in other chemical circumstances, e.g., the same cage within a range of temperatures, or if the GIMIC method could provide additional insight, remain questions for further work.
Differences in prototypic and water-soluble cages
Differences in prototypic and water-soluble cages are found in the average Xe CS, reporting the distinct structural features of the two environments. One interesting aspect is the occurrence of negative CS in the Xe@WsCrA(aq) system, as seen in Fig. 5(c). This means that the 129Xe shielding constant σ is sometimes higher than for Xe in vacuo. Such occurrences correspond to a chemical environment of Xe where there are relatively many electrons distributed in a roughly spherical manner around the guest atom, leading to a strong diamagnetic shielding, as if the Xe atom would have gained additional electronic shells in a “superatom” situation.The question of why only the Xe@WsCrA XBS (and not the prorotypic cage structure) exhibits such negative CS values can, once again, be answered using eqn (3) and (4). When Xe is surrounded by water in system (i), it undergoes frequent collisions with a large number of H2O molecules, resulting in a large paramagnetic shielding component. Inside the prototypic CrA, system (ii), the CH3 arms of the cage tend to rotate in towards Xe, leading to an amount of positive paramagnetic contribution to the CS. In contrast, the WsCrA cage, system (iii), is equipped with bulky CH2COOH moieties that do not easily come into contact with the confined Xe, because the hydrophilic heads prefer to orient towards the bulk water. Therefore, as discussed earlier in relation with Fig. 3, despite the similarity of the CrA and WsCrA cage interior, the different dynamics of their functionalised groups means that there are, on average, less paramagnetic channels in the water-soluble cage, resulting in overall smaller CS for Xe@WsCrA than for Xe@CrA (Table 1). The shape of the WsCrA cage leads to configurations where the CTB bowls and linker groups form a nearly spherically symmetric, yet electron-rich environment, which leads to high diamagnetic shielding.
Magnetic absorption spectrum
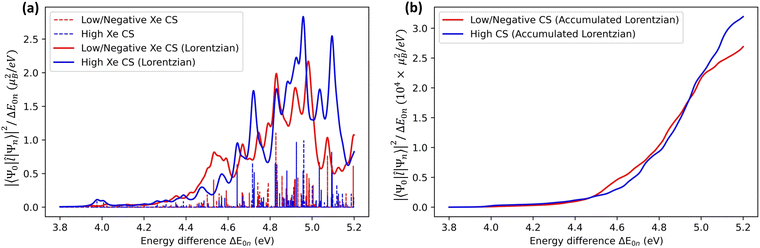
An alternative way of analysing the differences between structures that lead to high or low Xe CS, is to look at the excited-state electronic structure of the system. In particular, the transition moments 〈Ψ0|![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) |Ψn〉 to the low-lying, magnetically allowed excited states are expected to contribute strongly to the paramagnetic shielding, according to eqn (4). To illustrate this, we calculated the magnitudes of the magnetic dipole matrix element between the ground state and the first 20 excited states of the Xe@WsCrA(aq) XBS system. Seven simulation snapshots from the opposite ends of the distribution of instantaneous Xe CSs were chosen, corresponding to either very high (positive) or low, even negative Xe CS. The values |〈Ψ0|
|Ψn〉 to the low-lying, magnetically allowed excited states are expected to contribute strongly to the paramagnetic shielding, according to eqn (4). To illustrate this, we calculated the magnitudes of the magnetic dipole matrix element between the ground state and the first 20 excited states of the Xe@WsCrA(aq) XBS system. Seven simulation snapshots from the opposite ends of the distribution of instantaneous Xe CSs were chosen, corresponding to either very high (positive) or low, even negative Xe CS. The values |〈Ψ0|![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) |Ψn〉|2/ΔE0n, essentially the magnetic dipole matrix elements squared divided by the corresponding energy difference ΔE0n, are shown in Fig. 6(a). Scaling by the energy denominator is done to take into account the inverse dependence of second-order properties on the appropriate excitation energies66. Particularly based on the integral plot in Fig. 6(b), it can be seen that there is on average a higher accumulated intensity of magnetic-dipole transitions in the system configurations corresponding to snapshots that produce a high Xe CS, than in those that produce either a low or a negative shift. This coincides with the expectation that low-lying, magnetically allowed excited states contribute efficiently to the paramagnetic shielding through eqn (4).
|Ψn〉|2/ΔE0n, essentially the magnetic dipole matrix elements squared divided by the corresponding energy difference ΔE0n, are shown in Fig. 6(a). Scaling by the energy denominator is done to take into account the inverse dependence of second-order properties on the appropriate excitation energies66. Particularly based on the integral plot in Fig. 6(b), it can be seen that there is on average a higher accumulated intensity of magnetic-dipole transitions in the system configurations corresponding to snapshots that produce a high Xe CS, than in those that produce either a low or a negative shift. This coincides with the expectation that low-lying, magnetically allowed excited states contribute efficiently to the paramagnetic shielding through eqn (4).
For interpreting chemical-shift trends, one may also choose to look at the electron-density difference maps134,135 between the ground and the magnetically allowed excited states in the vicinity of the NMR nucleus. This would in principle make it possible to take into account the r−3-dependence on the electron-nucleus distance of the PSO operator, in eqn (4). In a study of differently hybridised graphenic nanoflakes,134 the localisation of the magnetically induced density changes made it possible to understand the occurrence of high and low carbon-13 CSs in either the perimeter or the core of the flakes, depending on the hybridisation of the carbon center. Similar reasoning was also used to gain insight into CS trends in differently hybridised graphyne structures.135 However, in our present case involving dynamic and flexible, H2O-dissolved cage structures, no similarly easily analysable trends of the electron-density differences between system configurations corresponding to high or low/negative Xe CS could be observed, which renders the analysis by density differences less appealing than in the referenced cases of rigid molecular structures.
5. Conclusions
The isotropic NMR chemical shift of the guest 129Xe atom was computed in three different chemical environments relevant for the design and application of Xe NMR biosensors: free Xe, Xe in a prototypic cryptophane-A cage and Xe in a water-soluble cryptophane-A derivative, each in aqueous solution. Recent advances in efficient relativistic nuclear shielding calculations enable direct averaging of the xenon chemical shift over a large set of system configurations produced in molecular dynamics simulations. This is in contrast to previous computational studies, where Xe biosensors were modeled in static cages and/or without explicit solvation. Instead, the present work targeted experimentally relevant conditions by combining molecular dynamics simulations in an explicit water solvent with relativistic shift calculations at the density-functional theory level using the X2C method. In practice, finite clusters were extracted from the instantaneous system configurations in the molecular dynamics trajectories, based on the distance from the Xe atom, after which the Xe shifts were averaged over the resulting clusters. A sufficient distance from Xe, determination of the size of the clusters, and basis set for the environment, were reported.Three different methods of molecular dynamics simulations within the xTB code were compared. The partially polarisable GFN-FF force-field method is seen to produce dynamics that lead to chemical shifts of Xe that are in good agreement with the experiment. This is in line with earlier findings on the interaction energy of noble gases with other atoms. Based on the GFN-FF simulations, the computed chemical shifts of Xe(aq), Xe@CrA(aq) and Xe@WsCrA(aq) are 182 (2), 98 (3) and 67 (2) ppm. Neglecting Xe@CrA(aq), as the cage is experimentally not water soluble, the presently computed shifts fall within 4 ppm of their experimental counterparts.
By qualitative reasoning based on a simplified, nonrelativistic common gauge-origin expressions for the dia- and para-magnetic components of nuclear shielding, we showed that the average atomic environment of Xe, represented by radial distribution functions and orientation of surrounding water molecules, correlates strongly with the NMR chemical shift of the free and host-bound Xe in aqueous media. In particular, the “contact-type” character of the chemical shift of Xe, arising from the locality of the orbital hyperfine interaction and which was seen previously in model calculations of static structures, is manifested in the present work as a linear dependence of the Xe chemical shift on the coordination number Z with its neighbouring solvent and/or cage atoms. Remarkably, this simple behaviour holds for the present, highly flexible and dynamic systems.
The present results provide microscopic insight on the 129Xe NMR chemical shift trends in different chemical environments. The computational workflow that has been outlined can also be used to study other systems of Xe NMR relevance, such as different host–guest complexes. Understanding the effects of solvent molecules, structural modifications of the host, and its dynamics on the NMR parameters of the Xe guest, are essential for the further development of Xe NMR biosensors. This work contributes to an understanding of these effects at the microscopic level.
Author contributions
P. Hilla was responsible for data curation, general investigation, software coding, visualisation of methods and results, and writing of the original draft; J. Vaara supervised the entire work. Both authors contributed together to conceptualisation of the project and reviewing/editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Drs P. Lantto and P. Štěpánek, and Mr P. Mayorga Delgado (Oulu) are thanked for many useful discussions. We acknowledge funding from the Academy of Finland (Grant 331008) and U. Oulu (Kvantum Institute). Computations were carried out at CSC – the Finnish IT Centre for Science and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533).Notes and references
- B. Goodson, J. Magn. Reson., 2002, 155, 157–216 CrossRef CAS PubMed.
- D. Raftery, Annu. Rep. NMR Spectrosc., 2006, 57, 206–261 CrossRef.
- A. K. Jameson, C. J. Jameson and H. S. Gutowsky, J. Chem. Phys., 1970, 53, 2310–2321 CrossRef CAS.
- C. J. Jameson, A. K. Jameson and S. M. Cohen, J. Chem. Phys., 1973, 59, 4540–4546 CrossRef CAS.
- C. J. Jameson, A. K. Jameson and S. M. Cohen, J. Chem. Phys., 1975, 62, 4224–4226 CrossRef CAS.
- P. Peuravaara, J. Karjalainen, J. Zhu, J. Mareš, P. Lantto and J. Vaara, Sci. Rep., 2018, 8, 7023 CrossRef PubMed.
- J. Jokisaari, Prog. Nucl. Magn. Reson. Spectrosc., 1993, 26, 1–26 CrossRef.
- E. Weiland, M.-A. Springuel-Huet, A. Nossov and A. Gédéon, Microporous Mesoporous Mater., 2016, 225, 41–65 CrossRef CAS.
- J. Roukala, J. Zhu, C. Giri, K. Rissanen, P. Lantto and V.-V. Telkki, J. Am. Chem. Soc., 2015, 137, 2464–2467 CrossRef CAS PubMed.
- T. Walker and W. Happer, Rev. Mod. Phys., 1997, 69, 629–642 CrossRef CAS.
- S. Zemerov and I. Dmochowski, RSC Adv., 2021, 11, 7693–7703 RSC.
- J. Mugler and T. Altes, J. Magn. Reson. Imaging, 2013, 37, 313–331 CrossRef PubMed.
- M. M. Spence, S. M. Rubin, I. E. Dimitrov, E. J. Ruiz, D. E. Wemmer, A. Pines, S. Qin Yao, F. Tian and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10654–10657 CrossRef CAS PubMed.
- P. Berthault, G. Huber and H. Desvaux, Progr. NMR Spectrosc., 2009, 55, 35–60 CrossRef CAS.
- L. Schröder, Phys. Med., 2013, 29, 3–16 CrossRef PubMed.
- T. Brotin and J.-P. Dutasta, Chem. Rev., 2009, 109, 88–130 CrossRef CAS PubMed.
- T. Brotin, A. Martinez and J.-P. Dutasta, in Calixarenes and Beyond, ed. P. Neri, J. Sessler and M.-X. Wang, Springer, 2016, pp. 525–557 Search PubMed.
- G. El-Ayle and K. Travis, in Comprehensive Supramolecular Chemistry II, ed. J. Atwood, Elsevier, 2017, pp. 199–249 Search PubMed.
- A. Bouchet, T. Brotin, M. Linares, H. Ågren, D. Cavagnat and T. Buffeteau, J. Org. Chem., 2011, 76, 1372–1383 CrossRef CAS PubMed.
- A. Bouchet, T. Brotin, M. Linares, H. Ågren, D. Cavagnat and T. Buffeteau, J. Org. Chem., 2011, 76, 4178–4181 CrossRef CAS PubMed.
- L.-L. Chapellet, J.-P. Dognon, M. Jean, N. Vanthuyne, P. Berthault, T. Buffeteau and T. Brotin, ChemistrySelect, 2017, 2, 5292–5300 CrossRef CAS.
- P. Hilla and J. Vaara, Phys. Chem. Chem. Phys., 2022, 24, 17946–17950 RSC.
- A. Laio and F. Gervasio, Rep. Progr. Phys., 2008, 71, 1–22 Search PubMed.
- A. Barducci, M. Bonomi and M. Parrinello, WIREs Comput. Mol. Sci., 2011, 1, 826–843 CrossRef CAS.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- L. Schröder, T. Lowery, C. Hilty, D. Wemmer and A. Pines, Science, 2006, 314, 446–449 CrossRef PubMed.
- M. Kunth, C. Witte and L. Schröder, J. Chem. Phys., 2014, 141, 1–9 CrossRef PubMed.
- K. Ward, A. Aletras and R. Balaban, J. Magn. Reson., 2000, 143, 79–87 CrossRef CAS PubMed.
- E. Harel, L. Schröder and S. Xu, Annu. Rev. Anal. Chem., 2008, 1, 133–163 CrossRef CAS PubMed.
- K. Bartik, M. Luhmer, J.-P. Dutasta, A. Collet and J. Reisse, J. Am. Chem. Soc., 1998, 120, 784–791 CrossRef CAS.
- T. Brotin, A. Lesage, L. Emsley and A. Collet, J. Am. Chem. Soc., 2000, 122, 1171–1174 CrossRef CAS.
- T. Brotin, T. Devic, A. Lesage, L. Emsley and A. Collet, Chem. – Eur. J., 2001, 7, 1561–1573 CrossRef CAS PubMed.
- T. Brotin and J.-P. Dutasta, Eur. J. Org. Chem., 2003, 973–984 CrossRef CAS.
- M. Spence, J. Ruiz, S. Rubin, T. Lowery, N. Winssinger, P. Schultz, D. Wemmer and A. Pines, J. Am. Chem. Soc., 2004, 126, 15287–15294 CrossRef CAS PubMed.
- G. Huber, T. Brotin, L. Dubois, H. Desvaux, J.-P. Dutasta and P. Berthault, J. Am. Chem. Soc., 2006, 128, 6239–6246 CrossRef CAS PubMed.
- A. Hill, Q. Wei, R. Eckenhoff and I. Dmochowski, J. Am. Chem. Soc., 2007, 129, 9262–9263 CrossRef PubMed.
- H. Fogarty, P. Berthault, T. Brotin, G. Huber, H. Desvaux and J.-P. Dutasta, J. Am. Chem. Soc., 2007, 129, 10332–10333 CrossRef CAS PubMed.
- G. Huber, L. Beguin, H. Desvaux, T. Brotin, H. Fogarty, J.-P. Dutasta and P. Berthault, J. Phys. Chem., 2008, A 112, 11363–11372 CrossRef PubMed.
- A. Hill, Q. Wei, T. Troxler and I. Dmochowski, J. Am. Chem. Soc., 2009, 131, 3069–3077 CrossRef PubMed.
- O. Taratula, A. Hill, N. Khan, P. Carroll and I. Dmochowski, Nat. Commun., 2010, 1, 148 CrossRef PubMed.
- R. Fairchild, A. Joseph, T. Holman, H. Fogarty, T. Brotin, J.-P. Dutasta, C. Boutin, G. Huber and P. Berthault, J. Am. Chem. Soc., 2010, 132, 15505–15507 CrossRef CAS PubMed.
- Y. Bai, A. Hill and I. Dmochowski, Anal. Chem., 2012, 84, 9935–9941 CrossRef CAS PubMed.
- S. Korchak, W. Kilian and L. Mitschang, Chem. Commun., 2015, 51, 1721–1724 RSC.
- S. Korchak, W. Kilian, L. Schröder and L. Mitschang, J. Magn. Reson., 2016, 265, 139–145 CrossRef CAS PubMed.
- P. Berthault, C. Boutin, E. Léonce, E. Jeanneau and T. Brotin, Chem. Phys. Chem., 2017, 18, 1561–1568 CrossRef CAS PubMed.
- M. Kunth and L. Schröder, Chem. Sci., 2021, 12, 158–169 RSC.
- E. Léonce, T. Brotin and P. Berthault, Phys. Chem. Chem. Phys., 2022, 24, 24793–24799 RSC.
- E. Dubost, J.-P. Dognon, B. Rousseau, G. Milanole, C. Dugave, Y. Boulard, E. Léonce, C. Boutin and P. Berthault, Angew. Chem., Int. Ed., 2014, 53, 9837–9840 CrossRef CAS PubMed.
- L. Gao, W. Liu, O.-S. Lee, I. Dmochowski and J. Saven, Chem. Sci., 2015, 6, 7238–7248 RSC.
- T. Demissie, K. Ruud and J. Hansen, J. Phys. Chem., 2017, A 121, 9669–9677 CrossRef PubMed.
- F. Schilling, L. Schröder, K. Palaniappan, S. Zapf, D. Wemmer and A. Pines, Chem. Phys. Chem., 2010, 11, 3529–3533 CrossRef CAS PubMed.
- E. Léonce, J.-P. Dognon, D. Pitrat, J.-C. Mulatier, T. Brotin and P. Berthault, Chem. Eur. J., 2018, 24, 6534–6537 CrossRef PubMed.
- J. Rebek, Angew. Chem., Int. Ed., 2005, 44, 2068–2078 CrossRef CAS PubMed.
- M. Liu, L. Zhang and T. Wang, Chem. Rev., 2015, 115, 7304–7397 CrossRef CAS PubMed.
- S. Barrow, S. Kasera, M. Rowland, J. del Barrio and O. Scherman, Chem. Rev., 2015, 115, 12320–12406 CrossRef CAS PubMed.
- L. Yang, X. Tan, Z. Wang and X. Zhang, Chem. Rev., 2015, 115, 7196–7239 CrossRef CAS PubMed.
- D. N. Sears and C. J. Jameson, J. Chem. Phys., 2003, 119, 12231–12244 CrossRef CAS.
- J. Ruiz, D. N. Sears, A. Pines and C. J. Jameson, J. Am. Chem. Soc., 2006, 128, 16980–16988 CrossRef PubMed.
- A. Bagno and G. Saielli, Chem. – Eur. J., 2012, 18, 7341–7345 CrossRef CAS PubMed.
- M. Straka, P. Lantto and J. Vaara, J. Phys. Chem. A, 2008, 112, 2658–2668 CrossRef CAS PubMed.
- S. Standara, P. Kulhánek, R. Marek and M. Straka, J. Comput. Chem., 2013, 34, 1890–1898 CrossRef CAS PubMed.
- P. Manninen, K. Ruud, P. Lantto and J. Vaara, J. Chem. Phys., 2005, 122, 114107 CrossRef PubMed.
- J. Vaara, P. Manninen and P. Lantto, in Calculations of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH, 2004, pp. 209–226 Search PubMed.
- N. Ramsey, Phys. Rev., 1950, 78, 303–307 CrossRef.
- N. Ramsey, Phys. Rev., 1953, 91, 699–703 CrossRef.
- P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, 5th edn, 2011 Search PubMed.
- W. Lamb, Phys. Rev., 1941, 60, 817–819 CrossRef CAS.
- P. Norman, K. Ruud and T. Saue, Principles and Practices of Molecular Properties: Theory, Modeling, and Simulations, John Wiley & Sons Ltd, 2018 Search PubMed.
- G. A. Aucar, T. Saue, L. Visscher and H. J. Aa. Jensen, J. Chem. Phys., 1999, 110, 6208–6218 CrossRef CAS.
- J. Vaara and P. Pyykkö, J. Chem. Phys., 2003, 118, 2973–2976 CrossRef CAS.
- J. Vícha, J. Vaara and M. Straka, Phys. Chem. Chem. Phys., 2023, 25, 10620–10627 RSC.
- M. Hanni, P. Lantto and J. Vaara, Phys. Chem. Chem. Phys., 2009, 11, 2485–2496 RSC.
- C. J. Jameson and A. C. de Dios, J. Chem. Phys., 2002, 116, 3805 CrossRef CAS.
- S. Grimme, S. Ehlert and C. Bannwarth, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef PubMed.
- P. Pracht, E. Caldeweyher, S. Ehlert and S. Grimme, ChemRxiv: A Robust Non-Self-Consistent Tight-Binding Quantum Chemistry Method for large Molecules, 2019.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- GitHub: xTB, https://github.com/grimme-lab/xtb.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, WIREs Comput. Mol. Sci., 2020, 11, e01493 Search PubMed.
- S. Komulainen, J. Roukala, V. Zhivonitko, M. A. Javed, L. Chen, D. Holden, T. Hasell, A. Cooper, P. Lantto and V.-V. Telkki, Chem. Sci., 2017, 8, 5721–5727 RSC.
- P. Håkansson, M. A. Javed, S. Komulainen, L. Chen, D. Holden, T. Hasell, A. Cooper, P. Lantto and V.-V. Telkki, Phys. Chem. Chem. Phys., 2019, 21, 24373–24382 RSC.
- J. Jayapaul, S. Komulainen, V. Zhivonitko, J. Mareš, C. Giri, K. Rissanen, P. Lantto, V.-V. Telkki and L. Schröder, Nat. Commun., 2022, 13, 1708 CrossRef CAS PubMed.
- S. Komulainen, P. U. A. I. Fernando, J. Mareš, A. Selent, R. Khalili, P. T. Cesana, A. Ebeling, A. M. Kantola, N. K. Beyeh, K. Rissanen, B. DeBoef, P. Lantto and V.-V. Telkki, Cell Rep. Phys. Sci., 2023, 4, 101281 CrossRef CAS.
- S. E. Mailhiot, P. Peuravaara, R. J. Kearsey, B. D. Egleston, J. Mareš, S. Komulainen, R. L. Greenaway, A. I. Cooper, J. Vaara, P. Lantto and V.-V. Telkki, Cage Occupancy and Exchange Dynamics in Porous Liquids Elucidated by 129Xe NMR, 2023, submitted for publication.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- H. Berendsen, J. Postma, W. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- H. Flyvbjerg and H. Petersen, J. Chem. Phys., 1989, 91, 461–466 CrossRef CAS.
- P. Pyykkö, Chem. Rev., 1988, 88, 563–594 CrossRef.
- J. Autschbach, Phil. Trans. R. Soc. A, 2014, 372, 20120489 CrossRef PubMed.
- S. Komorovský, M. Repiský, O. L. Malkina, V. G. Malkin, I. Malkin Ondík and M. Kaupp, J. Chem. Phys., 2008, 128, 104101 CrossRef PubMed.
- M. Iliaš, T. Saue, T. Enevoldsen and H. J. Aa. Jensen, J. Chem. Phys., 2009, 131, 124119 CrossRef PubMed.
- L. Cheng, Y. Xiao and W. Liu, J. Chem. Phys., 2009, 131, 244113 CrossRef PubMed.
- M. Reiher and A. Wolf, Relativistic Quantum Chemistry: The Fundamental Theory of Molecular Science, Wiley-VCH, 2nd edn, 2014 Search PubMed.
- C. Ballard, M. Hada, H. Kaneko and H. Nakatsuji, Chem. Phys. Lett., 1996, 254, 170 CrossRef CAS.
- H. Fukui and T. Baba, J. Chem. Phys., 1998, 108, 3854 CrossRef CAS.
- T. Baba and H. Fukui, J. Chem. Phys., 1999, 110, 131 CrossRef CAS.
- R. Fukuda, M. Hada and H. Nakatsuji, J. Chem. Phys., 2003, 118, 1015 CrossRef CAS.
- R. Fukuda, M. Hada and H. Nakatsuji, J. Chem. Phys., 2003, 118, 1027 CrossRef CAS.
- S. K. Wolff, T. Ziegler, E. van Lenthe and E. J. Baerends, J. Chem. Phys., 1999, 110, 7689 CrossRef CAS.
- J. Autschbach and T. Ziegler, J. Chem. Phys., 2000, 113, 936 CrossRef CAS.
- J. Autschbach and T. Ziegler, J. Chem. Phys., 2000, 113, 9410 CrossRef CAS.
- H. Fukui and T. Baba, J. Chem. Phys., 2002, 117, 7836 CrossRef CAS.
- D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys., 2013, 138, 184105 CrossRef PubMed.
- Y. Franzke and F. Weigend, J. Chem. Theory Comput., 2019, 15, 1028–1043 CrossRef CAS PubMed.
- TURBOMOLE V7.5.1, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, 2020, https://www.turbomole.com.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. M. Khah, S. K. Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- M. Repisky, S. Komorovsky, M. Kadek, L. Konecny, U. Ekström, M. Kaupp, K. Ruud, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2020, 152, 184101 CrossRef CAS PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136–9148 CrossRef CAS.
- M. Straka, P. Lantto, M. Räsänen and J. Vaara, J. Chem. Phys., 2007, 127, 234314 CrossRef PubMed.
- M. Hanni, P. Lantto, M. Iliaš, H. J. Aa. Jensen and J. Vaara, J. Chem. Phys., 2007, 127, 164313 CrossRef PubMed.
- P. Lantto, S. Standara, S. Riedel, J. Vaara and M. Straka, Phys. Chem. Chem. Phys., 2012, 14, 10944–10952 RSC.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- P. Manninen and J. Vaara, J. Comput. Chem., 2006, 27, 434–445 CrossRef CAS PubMed.
- M. Hanni, P. Lantto, M. Repiský, J. Mareš, B. Saam and J. Vaara, Phys. Rev. A, 2017, 95, 032509 CrossRef.
- F. Weigend and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. Ahlrichs and K. May, Phys. Chem. Chem. Phys., 2000, 2, 943–945 RSC.
- G. Van Rossum and F. L. Drake Jr, Python reference manual, Centrum voor Wiskunde en Informatica Amsterdam, 1995 Search PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc. Perkin Trans. 2, 1993, 5, 799–805 RSC.
- P. Pollak and F. Weigend, J. Chem. Theory Comput., 2017, 13, 3696–3705 CrossRef CAS PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- K. Kříž, M. Nováček and J. Řezáč, J. Chem. Theory Comput., 2021, 17, 1548–1561 CrossRef PubMed.
- Y. Chen, Y. Sheng, Y. Ma and H. Ding, Phys. Chem. Chem. Phys., 2022, 24, 14339–14347 RSC.
- C. J. Jameson and A. C. de Dios, J. Chem. Phys., 1992, 97, 417–434 CrossRef CAS.
- C. J. Jameson, A. K. Jameson, B. Baello and H.-M. Lim, J. Chem. Phys., 1994, 100, 5965–5976 CrossRef CAS.
- A. C. de Dios and C. J. Jameson, Annu. Rep. NMR Spectrosc., 1994, 29, 1–69 CrossRef CAS.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- R. K. Jinger, H. Fliegl, R. Bast, M. Dimitrova, S. Lehtola and D. Sundholm, J. Phys. Chem. A, 2021, 125, 1778–1786 CrossRef CAS PubMed.
- H. Fliegl, M. Dimitrova, R. Berger and D. Sundholm, Chemistry, 2021, 3, 1005–1021 CrossRef CAS.
- N. Özcan, J. Mareš, D. Sundholm and J. Vaara, Phys. Chem. Chem. Phys., 2014, 16, 22309–22320 RSC.
- P. Štěpánek and P. Lantto, Phys. Chem. Chem. Phys., 2022, 24, 25513–25521 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Comparison of fully relativistic (including spin–orbit interaction) and scalar relativistic X2C calculations, results of convergence tests for the number of water molecules and the quality of the basis set for the environment of Xe, and computational resources used. See DOI: https://doi.org/10.1039/d3cp02695g |
| ‡ In the XBS field, experimental work typically uses the shielding constant of Xe(aq), our present system (i), as the reference, whereas in computations it is more conventional to use Xe in vacuo, corresponding to low-pressure Xe gas. |
| § At the currently used level of theory (vide infra), the 129Xe shielding constant in the common reference compound, XeOF4, equals 5830.9 ppm. |
| ¶ Comparisons of classical force-field simulations are usually done with experiments in D2O solution, since classical MD does not capture the quantum-mechanical nuclear dynamic features that are important for the hydrogen atoms in H2O. |
| This journal is © the Owner Societies 2023 |