Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Infrared spectrum of the 1-cyanoadamantane cation: evidence of hydrogen transfer and cage-opening upon ionization†
Peter Theodore
Rubli
 and
Otto
Dopfer
and
Otto
Dopfer
 *
*
Institut für Optik und Atomare Physik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany. E-mail: dopfer@physik.tu-berlin.de
First published on 9th August 2023
Abstract
The radical cations of diamondoids are important intermediates in their functionalization reactions and are also candidates as carriers for astronomical absorption and emission features. Although neutral diamondoids have been studied extensively, information regarding their radical cations is largely lacking, particularly for functionalized diamondoid derivatives. Herein, we characterize the structure of the 1-cyanoadamantane radical cation (C10H15CN+, AdCN+) using infrared photodissociation (IRPD) spectroscopy of mass selected AdCN+N2 clusters in the XH stretch range (2400–3500 cm−1) and dispersion-corrected density functional theory calculations (B3LYP-D3BJ/cc-pVTZ). A group of three distinct CH stretch bands are observed in the 2800–3000 cm−1 range, in addition to a highly redshifted absorption at 2580 cm−1 attributed to the acidic CH proton predicted by calculations. An unexpected broad absorption peaking at 3320 cm−1 is also detected and assigned to an NH stretch mode based on its width and frequency. Calculations indicate that hydrogen atom transfer (HAT) from the adamantyl cage (C10H15, Ady) to the N atom of the CN group yields lower energy structures, with an open-cage isomer exhibiting such hydrogen transfer being the global minimum on the potential energy surface. The energy barriers involved in the formation of this open-cage isomer are also lower than those calculated for generation of the analogous open-cage 1-amantadine cation isomer which has previously been identified by IRPD. The combined consideration of IRPD spectra and calculations indicates a major population of the nascent canonical closed-cage isomer and a smaller population of the global minimum isomer featuring both cage-opening and hydrogen transfer.
1. Introduction
1-Cyanoadamantane (C10H15CN, AdCN) is the simplest cyano-functionalized derivative of the smallest diamondoid, adamantane (C10H16, Ada). Diamondoids are a class of nanometer-sized aliphatic hydrocarbon compounds named after their atomic arrangement resembling that of the diamond crystal lattice.1 They are rigid and strain-free cycloalkanes containing sp3-hybridised C atoms arranged into cage-like structures terminated by H atoms.1,2 These molecules were first discovered in crude oil extracts and are accumulating interest in multiple disciplines including molecular electronics,3–5 nanotechnology,6–8 medicinal chemistry,9 chemical synthesis,10,11 and astrochemistry due to their thermodynamic and chemical stability.12–16 Lower diamondoids (those possessing only one structural isomer) are able to be synthesised in the laboratory and can be functionalized to obtain derivatives with properties that are tailored to specific applications.3–5,17–22 One such example is amantadine (C10H15NH2, Ama) which is used to treat Parkinson's disease as well as being an antiviral agent.9,23,24 Previous investigations of Ar-tagged Ama+ ions using infrared photodissociation (IRPD) spectroscopy reveal the formation of two open-cage bicyclic distonic iminium isomers upon electron ionization (EI) of Ama, in addition to the canonical nascent closed-cage tricyclic isomer produced by vertical ionization.25,26 The energy barriers for the formation of the open-cage isomers of Ama+ are computed to be significantly lower than for Ada+ and this result has been attributed to the electron-donating character of the NH2 group.25,26 While solvation of Ama+ with Ar and N2 has little impact on the closed-cage to open-cage isomer population ratio, solvation with H2O molecules results in a drastic reduction in the generation of the open-cage isomer.25 Various studies of bare Ada using synchrotron VUV radiation and XUV femtosecond pulses reveal dissociative channels beginning with opening of the cage structure.27–29 However, IRPD and electronic photodissociation (EPD) spectra of Ada+ and its clusters generated in the same EI source as Ama+ show no evidence of open-cage isomers, similar to the diamantane radical cation (C14H20+, Dia+),12,13,30–32 indicating that reaction barriers are high for bare diamondoid cations. To test this hypothesis further, similar experiments with AdCN have been proposed to understand how electron-withdrawing functional groups influence the stability of diamondoid cage structures.25,26In addition to biochemistry and pharmaceutical applications, diamondoids and their functionalized derivatives are being actively researched in the field of astrochemistry.12–14,16,33–35 It has been hypothesized that diamondoids may account for over 5% of cosmic and 40% of tertiary carbon in interstellar environments.15,16 Evidence suggesting their presence in the interstellar medium (ISM) first came from nanodiamond material discovered in extrasolar meteorites at concentrations up to 400 ppm.34 However, no astronomical observations have confirmed the existence of diamondoids in these regions. Because of the low ionisation energies of diamondoids (∼7–9 eV) and the high flux of UV radiation in certain interstellar regions, their radical cations are also expected to be present in the ISM.33,36 Since the discovery that the fullerene C60+ is responsible for five of the diffuse interstellar band (DIB) features,37,38 other large aliphatic hydrocarbons including diamondoid radical cations have been investigated as candidates for DIB carriers.12,13 Their open-shell electronic structures allow for HOMO ← HOMO−n transitions in the visible and near-IR ranges, where the majority of the DIBs are measured (400–800 nm).33,39–41 However, EPD spectroscopy performed for Ada+ and Dia+ reveal broad and unresolved spectral bands spanning the whole visible frequency range, even when cooled to cryogenic temperatures below 20 K.12,13,42 This spectral broadness is attributed to a combination of short excited state lifetimes (∼20 fs) and Franck–Condon congestion of closely lying vibrational modes resulting in rapid relaxation of the excited state.12–14 Thus, these experiments exclude small bare diamondoid cations as possible carriers of the DIBs.
Functionalized derivatives such as cationic diamondoid nitriles were proposed as more promising candidates because substituents modify the electronic structure and allow for new transitions to occur.13,14 Organic and inorganic molecules possessing nitrile groups are also commonly observed in the interstellar environment by radio astronomy due to intense rotational transitions brought about by their large electric dipole moments.43–46
For these reasons, laboratory spectra of the smallest cyano-functionalized diamondoid, AdCN, were recently recorded to determine its geometric and vibrational structure from microwave and IR spectroscopy,47,48 while its electronic structure was characterized by density functional theory (DFT).49 Previous studies of the AdCN+ radical cation are scarce. An EI mass spectrum reveals the major fragment ions of AdCN+.50 Its electronic EPD spectrum features similar spectral broadness to the bare diamondoid cations which, combined with the relative ease by which it fragments, thus discounts it as a viable DIB carrier.14 This spectral broadness, in addition to the cage-opening mechanism observed for Ama+, motivates the investigation of the geometric structure of AdCN+via IR spectroscopy. Moreover, the most intense fragment peak observed at m/z 134 in the AdCN mass spectrum is attributed to the loss of neutral HCN.14,50 This is an exception among the carbon-linked 1-substituted adamantanes (AdCX), where the loss of the functional CX group is usually observed, producing the rather stable closed-shell adamantyl cation (C10H15+, Ady+) as the main fragment (m/z 135). With the primary goal of characterizing the geometric structure of AdCN+, we report herein the IR spectrum of AdCN+ measured by photodissociation of N2-tagged ions and use DFT calculations to aid the vibrational and isomer assignments of the transitions observed. Comparison with our previous studies of Ada+ and Ama+ will allow one to determine the effects of substitution of the electron-withdrawing CN group on the structure and reactivity of small diamondiod radical cations.
2. Experimental and computational techniques
IRPD spectra of AdCN+Ln clusters are obtained in a quadrupole–octupole–quadrupole (QOQ) tandem mass spectrometer coupled to an EI cluster source described elsewhere.51,52 Cold AdCN+Ln clusters with L = Ar or N2 are produced in a pulsed supersonic plasma expansion by electron (and/or chemical) ionization of AdCN (Sigma Aldrich, >97%, T ∼ 135°) seeded in Ar or N2 carrier gas (10–15 bar) close to the nozzle orifice and subsequent three-body clustering reactions. The filaments of the EI source are powered by an offset voltage of up to 200 V, which sets an upper limit for the kinetic energy of the electrons impacting the molecular beam to 200 eV. A typical mass spectrum using the ion source in the mass range m/z 10–210 is presented in Fig. S1 in ESI.† To confirm the composition of the mass-selected AdCN+Ln clusters, collision-induced dissociation (CID) spectra are recorded (Fig. S2, ESI†). For this purpose, the octupole is filled with N2 gas (10−5 mbar) resulting in collisions at 10 eV energy in the laboratory frame. The desired AdCN+Ln parent clusters are mass selected by the first quadrupole, deflected by 90° into the adjacent octupole ion guide, and irradiated by a tunable IR laser pulse emitted from an optical parametric oscillator pumped by a Q-switched nanosecond Nd:YAG laser (2–5 mJ pulse energy, 10 Hz repetition rate, <4 cm−1 bandwidth). A wavemeter is used to calibrate the IR laser frequency to an accuracy of <1 cm−1. At resonant vibrational frequencies, the IR radiation induces predissociation of the parent cluster into the neutral ligands and AdCN+ daughter ions. The latter are then selected by the second quadrupole and monitored by a Daly detector as a function of laser frequency to obtain IRPD spectra of AdCN+Ln. A pyroelectric detector is used to normalize the IRPD spectra for frequency-dependent variations in the photon flux.DFT calculations are performed at the dispersion-corrected (u)B3LYP-D3BJ/cc-pVTZ level to obtain geometries, energies, and IR spectra of various AdCN+ isomers and their clusters.53 This computational level has been shown to provide reliable results for related diamondoid cations and their clusters,25,26,31,32,54 with the addition of Becke–Johnson damping to yield more accurate results for non-covalent bond distances and intramolecular dispersion interactions. Relative energies and binding energies (Ee, De) are corrected for harmonic zero-point vibrational energies to yield E0 and D0 values. To compare calculated harmonic vibrational frequencies with experimental values, scaling factors are employed to account for vibrational anharmonicity and errors of the harmonic force field estimated by DFT. Appropriate scaling factors are obtained by fitting the calculated frequencies of neutral AdCN to their experimental values.48,55 To this end, frequencies in the mid-IR XH stretch range (>2000 cm−1) are scaled by 0.953, while those in the far-IR fingerprint range (<2000 cm−1) are scaled by 0.978. Calculated IR stick spectra are convoluted with Gaussian line profiles (FWHM = 10 cm−1) to facilitate convenient comparison with the experimental spectra. Natural bond orbital (NBO) analysis is used to evaluate the charge and spin density distributions. Spin contamination for any of the AdCN+ isomers is found to be negligible with the largest value of 〈S2 − 0.75〉 = 0.0131 and 0.0001 before and after annihilation, respectively. To optimize transition state geometries, the synchronous transit-guided quasi-Newton method is employed.56 A complete set of all relevant structures of the AdCN+ isomers (Fig. S3), their AdCN+N2 isomers and respective E0 and D0 energies (Fig. S4–S7), transition state structures and their E0 energies (Fig. S8 and Table S1), NBO charge and spin data (Fig. S9 and S10), computed IR spectra (Fig. S11–S13), HOMO orbitals (Fig. S14), Cartesian coordinates and energies (Tables S2–S20), and vibrational frequencies and IR intensities (Tables S21–S26) is given in ESI.†
3. Results and discussion
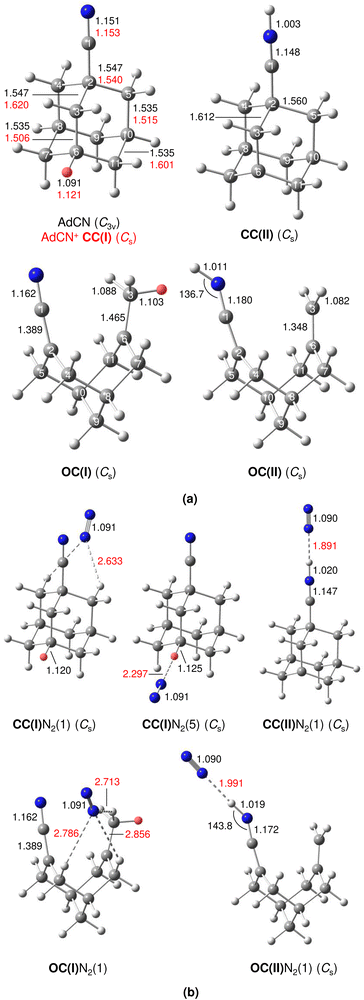
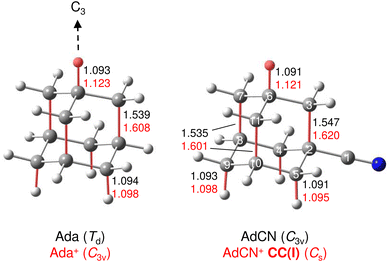
A typical mass spectrum using the EI source is shown in Fig. S1 in ESI.† The major fragments of the parent AdCN+ ion (m/z 161) are observed at m/z 146, 134, 119, 104, 93, 79, 69, 53, 39, and 27. These are consistent with the standard EI mass spectrum of AdCN reported by NIST and confirm AdCN+ as the parent ion.55 AdCN+Ln clusters (L = Ar, N2) are also formed in addition to other undesired cluster ions such as pure Arn+ clusters. CID spectra of mass-selected AdCN+Ln clusters (Fig. S2, ESI†) reveal only loss of the neutral ligands, thus confirming the composition of the parent clusters and excluding isobaric mass contamination.The IRPD spectrum of the AdCN+N2 cluster recorded in the XH stretch range (2400–3500 cm−1) in the N2 loss channel is shown in Fig. 1. Positions and widths of the transitions observed, along with suggested assignments to vibrations of various AdCN+ isomers are listed in Table 1. The structure of neutral AdCN is obtained via substitution of the apical H atom of neutral Ada for a CN group, which lowers the molecular symmetry from Td to C3v. Upon ionization, AdCN (1A1) undergoes geometry changes which lower its symmetry further resulting in the 2A′ cation ground state with Cs symmetry (Fig. 2(a)). This canonical closed-cage AdCN+ isomer obtained by vertical EI of neutral AdCN will henceforth be referred to as closed-cage isomer CC(I). The C2–C3, C7–C8, and C10–C11 bonds elongate substantially upon ionization (by 4.72, 4.30, 4.30%), while all other C–C bonds contract slightly (<1.90%). Most C–H bonds remain largely unaffected (0.30–0.45% change) apart from the C6–H bond which experiences a comparatively large elongation of 2.75%. Similar structural behavior has been observed for Ada+ and Dia+ due to the activity of the (pseudo-)Jahn–Teller (JT) effect.12,13,30,57 For the latter cations, the large elongations occur for their apical C–H bonds and the C–C bonds parallel with their principal axis of rotation which results in characteristically low-frequency CH stretch modes of these acidic C–H bonds.13,30 The analogous bond distortion in AdCN+ does not occur parallel to its C3 axis of rotation (i.e. the axis of H → CN substitution) but instead along one of its three remaining tertiary C–H bonds. A clearer comparison of AdCN(+) with Ada(+) can be made by aligning the C6–H bond of AdCN+ with the C3 axis of Ada+ so that the acidic C–H bonds of both species are in the apical position (Fig. 3). In this orientation, AdCN distorts in a similar way to Ada upon ionization. Inspection of the HOMO of AdCN (Fig. S14, ESI†) shows that it is spread over the entire molecule with significant localization on the C2–C3, C7–C8, C10–C11, and C6–H bonds. Removal of an electron from this bonding orbital explains the resulting elongation of these bonds upon ionization. NBO analysis of AdCN and AdCN+ reveals that the positive partial charges of the CN group, the C atoms of the Ady cage, and the H atoms increase by 102, 162, and 729 me, respectively (Fig. S9, ESI†). This analysis indicates that the positive charge is mostly located on the Ady cage with the CN group being largely unaffected, which is in contrast to Ama+ where the electron is removed from the nonbonding N lone pair of the NH2 group.25,26,54,58
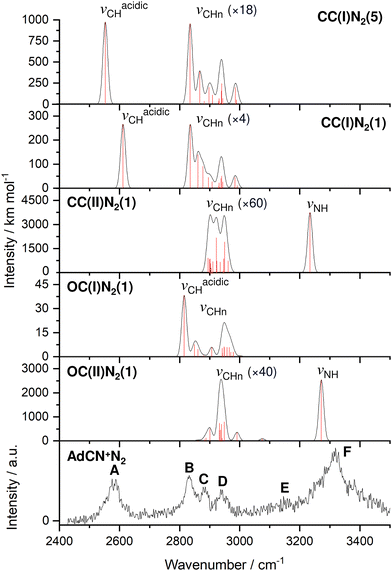 | ||
| Fig. 1 IRPD spectrum of AdCN+N2 recorded in the N2 loss channel compared to linear IR absorption spectra calculated for various isomers (B3LYP-D3BJ/cc-pVTZ, Table 1). Computed scaled harmonic stick spectra are convoluted with Gaussian line profiles (FWHM = 10 cm−1). The weak νCHn stretch bands are vertically expanded by factors given in parentheses. | ||
| Peak | Mode | AdCN+N2 exp | CC(I)N2(5) | CC(I)N2(1) | CC(II)N2(1) | OC(I)N2(1) | OC(II)N2(1) |
|---|---|---|---|---|---|---|---|
| a Computed harmonic frequencies are scaled by 0.953. IR intensities in km mol−1 are listed in parentheses. For overlapping fundamentals in the computed IR spectra, the maxima of convoluted bands are given. b Scaled by 0.978. Scaled harmonic overtone is computed as 3206 cm−1. | |||||||
| A | ν acidicCH | 2580 (53) | 2552a (974) | 2611a (267) | — | — | — |
| B | ν CHn | 2830 (41) | 2835a (53) | 2835a (66) | — | 2815a (38) | — |
| C | ν CHn | 2884 (28) | 2868a (22) | 2861a (38) | 2922a (57) | — | 2899a (13) |
| D | ν CHn | 2939 (60) | 2940a (30) | 2939a (33) | 2949a (59) | 2948a (21) | 2928a (64) |
| E |
ν
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/βCH2 C/βCH2 |
3155 | — | — | — | — | 1603b (266) |
| F | ν NH | 3320 (105) | — | — | 3234a (3740) | — | 3272a (2541) |
The discussed structural changes upon ionization are directly evident in the experimental IRPD spectrum (Fig. 1). Peaks B, C, and D observed at 2830, 2884, and 2939 cm−1, respectively, are assigned as a closely spaced group of CHn stretch modes by comparing their frequency range with computed transitions. A detailed assignment of bands B–D to individual modes is not possible due to substantial overlap of calculated peak positions (after convolution) between different AdCN+N2 cluster isomers in this frequency range. A significantly redshifted C–H stretch band (peak A) is observed at 2580 cm−1 and assigned to the acidic C6–H bond of a N2-tagged isomer of the CC(I) ion (νacidicCH) as no intense absorptions are predicted in this frequency range for any other AdCN+N2 isomer. Which of the possible CC(I)N2 isomers, which arise from various N2 binding sites, is responsible for peak A cannot be determined from our data alone. CC(I) offers several possible N2 binding sites which each lead to slightly different redshifts of νacidicCH. Binding of N2 to the acidic C6–H proton as in isomer CC(I)N2(5) shown in Fig. 2(b) is predicted to occur in a linear fashion which is favoured over a T-shaped approach due to the anisotropy of the polarizability and negative quadrupole moment of N2.25,30,59–61 The relatively high binding energy of N2 in this linear CH⋯N2 hydrogen bond (H-bond, D0 = 9.8 kJ mol−1) compared to other ligands such as He (D0 < 1 kJ mol−1)30 results in significant impact on the structural and spectral properties of the core ion. Most notably, N2 binding to the acidic proton elongates the C6–H bond by 4 mÅ which results in a redshift of νacidicCH from 2601 to 2552 cm−1 and a fourfold increase in its IR intensity compared to the calculated spectrum of untagged CC(I) (Fig. S11, ESI†). The ligand may bind elsewhere to the Ady cage, e.g., as in isomer CC(I)N2(1), the lowest-energy N2 cluster isomer (Fig. 2(b)). N2 attachment elsewhere has little impact on νacidicCH, with isomer CC(I)N2(1) experiencing a slight blueshift of 10 cm−1 relative to the calculated IR spectrum of the bare ion. For Ada+, ligand binding occurs at the acidic proton (for L = He, N2, H2O) because it has the highest positive partial charge of all protons (354 me).30,32 This binding motif is confirmed by the measured redshift of 25 cm−1 for νacidicCH (from 2600 to 2575 cm−1) when switching the ligand from He to N2 and its disappearance from this spectral range upon microhydration.30–32 NBO analysis of CC(I) indicates that the acidic C6H proton has the highest positive partial charge of 353 me. Given that this behaviour is very similar to that of Ada+, it is likely that N2 binding also occurs to the acidic proton for CC(I) of AdCN+. The very similar νacidicCH frequencies of Ada+N2 and CC(I)N2 (2575 vs. 2580 cm−1) provide experimental proof that H → CN substitution has little impact on the acidity of the C6H proton and allows one to estimate νacidicCH of bare CC(I) as 2605 ± 5 cm−1, in excellent agreement with the computational predictions for bare CC(I) and CC(I)N2(1) (2601 and 2611 cm−1). While CC(I)N2(1) is calculated to be slightly more stable than CC(I)N2(5) at T = 0 K (ΔE0 = 2.3 kJ mol−1), free energy calculations at room temperature predict the reverse order (ΔG0 = −2.3 kJ mol−1), because of the higher flexibility of CC(I)N2(5), supporting the given structural assignment to this N2 binding site.
An unexpected intense and broad absorption F centred at 3320 cm−1 (FWHM 105 cm−1) is observed in the IRPD spectrum of AdCN+N2 which is not accounted for by any of the spectra calculated of the tagged or untagged ions of the canonical CC(I) isomer of AdCN+. Considering the N atom present in AdCN+, and that IR spectra of similar N2-tagged ions possessing NH groups reveal broad absorptions in this frequency range, it is likely that peak F arises from an NH stretch mode (νNH).25,59–70 Following this scenario, a range of structures exhibiting intramolecular hydrogen atom transfer (HAT) from the Ady cage of CC(I) to the N atom of the CN group are calculated. Due to the Cs symmetry of CC(I), migration of different hydrogens leads to the same final isomer structure, and thus it is appropriate to categorize the H atoms into groups (Fig. S15, ESI†) which form the same isomer following HAT. Migration of H atoms from group 1 form isomer CC(II) (Fig. 2(a)), and those from groups 2 and 3 form isomers CC(III) and CC(IV) (Fig. S15, ESI†), respectively. The energies of these closed-cage CC(II–IV) isomers resulting from HAT are E0 = −26.9, −21.4, and −17.9 kJ mol−1 relative to CC(I), i.e. they are all significantly more stable than the canonical isomer CC(I), with CC(II) being the most stable one (Table 2). Its highest stability arises upon HAT of the acidic C6H proton, which has the weakest C–H bond and thus is the preferred H donor group. At this point, we note that one cannot easily distinguish whether a neutral hydrogen atom or a proton is moving in this roaming-type process. Nonetheless, we presume herein H atom transfer (HAT), as usually bond breaking resulting in a neutral fragment is lower in energy than removing a proton. For a more detailed discussion about the general processes classified as proton-coupled electron transfer (PCET), the reader is referred to literature reviews.71–73
| AdCN+ isomer | E 0/kJ mol−1 |
|---|---|
| CC(I) | 0 |
| CC(IV) | −17.88 |
| CC(III) | −21.41 |
| CC(II) | −26.90 |
| OC(I) | −41.80 |
| OC(II) | −58.84 |
The IR spectra calculated for CC(II–IV) presented in Fig. S12 (ESI†) are very similar, with the largest differences of 39 cm−1 for the CN stretch (νCN = 2176–2215 cm−1) and 10 cm−1 for the NH stretch (νNH = 3545–3555 cm−1). As the spectral resolution of the IRPD spectrum is insufficient to distinguish between these three isomers, only the most stable isomer CC(II) is considered further for comparison to the experiment in Fig. 1. After HAT, the acidic C–H bond of CC(I) is broken and no longer present in CC(II). NBO analysis reveals that the H atom which migrates to N has a very large positive partial charge of 486 me in CC(II), while the H atoms located on the Ady cage have partial charges in the range 209–230 me. This result explains why geometry optimisation for CC(II)N2 clusters predict the protonated CN group to be by far the most stable N2 binding site, denoted isomer CC(II)N2(1) in Fig. 2(b). N2 binding at the CNH group occurs via a strong and nearly linear ionic NH⋯N2 H-bond (1.891 Å, 179°) with D0 = 23.0 kJ mol−1. This isomer is 12.7–16.4 kJ mol−1 more stable than any other of the CC(II)N2(2–6) isomers, which are stabilized by much weaker CH⋯N2 contacts (D0 = 6.6–10.3 kJ mol−1, Fig. S5 in ESI†). The strong H-bond to N2 causes a large νNH redshift of 321 cm−1 from 3555 cm−1 for bare CC(II) to 3234 cm−1 for CC(II)N2(1) and a strong enhancement in its IR activity by nearly a factor 3 (from 1333 to 3740 km mol−1). As can be seen in Fig. 1, νNH predicted for CC(II)N2(1) deviates only by 86 cm−1 from the maximum of the rather broad band F at 3320, making such an assignment quite reasonable. The structural rearrangement involved with forming CC(II) by HAT also leads to a separation of charge and spin. The spin density of this distonic ion is mostly located on the C6 atom from which the H atom migrated away toward the N atom (sC6 = 0.806, Fig. S10, ESI†), while the majority of the positive charge is localized at the CNH site (qCNH = 719 me).
One of the major motivations of this work has been the impact of the CN group on the cage-opening process upon EI. The largest bond length change calculated for AdCN upon vertical ionization to CC(I) is experienced by the C2–C3 bond adjacent to the CN functional group (Δr = +73 mÅ), indicating a strong activation of this bond. To obtain the open-cage isomer OC(I) shown in Fig. 2(a), this bond ruptures in a similar fashion as for Ama+ where the most activated C–C bond adjacent to the NH2 functional group also breaks upon EI.25,26 A simultaneous 1,2 H-shift of the acidic H atom from C6 to C3 leads to the formation of a methyl group. The OC(I) structure is bicyclic and analogous to the reported open-cage Ama+(III) isomer.25,26 However, for AdCN+ no intermediate isomer analogous to Ama+(II) is obtained, which simply results from cage-opening (without 1,2 H-shift) and is only a shallow minimum with a low barrier of 13 kJ mol−1 toward the canonical Ama+(I) cage isomer. The 1,2 H-shift strongly reduces the acidity of the former C6H proton (rCH decreases from 1.121 to 1.103 Å). However, it remains the most acidic of all protons of OC(I) and is thus responsible for the lowest-frequency and most intense CH stretch band in its calculated IR spectrum (νacidicCH, Fig. S13, ESI†). The boat configuration of OC(I) can be rationalized by inspection of the HOMO (Fig. S14, ESI†) which reveals significant bonding character between C2 and C6 preventing flattening of the structure. To account for the NH stretch band F observed in the IRPD spectrum, the bicyclic open-cage isomer OC(II) in Fig. 2(a) is obtained from OC(I) by HAT of a H atom from the methyl group to the N atom of the CN group. Interestingly, the C–N–H bond angle of the protonated CN group strongly deviates from linearity (136.7°), due to the approximate sp2 hybridization of N (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH) and the repulsive interaction between the N lone pair and the N–H bond (Fig. S14, ESI†). The relative energies of these two open-cage isomers OC(I) and OC(II), E0 = −41.8 and −58.8 kJ mol−1, indicate that they are around 40–60 kJ mol−1 more stable than the canonical closed-cage isomer CC(I) and around 15–30 kJ mol−1 more stable than the most stable closed-cage isomer CC(II) exhibiting HAT (Table 2). Hence, from the energy perspective, one may expect the production of these open-cage isomers in the EI plasma expansion, although barriers of cage-opening and HAT must be considered as well (vide infra).
NH) and the repulsive interaction between the N lone pair and the N–H bond (Fig. S14, ESI†). The relative energies of these two open-cage isomers OC(I) and OC(II), E0 = −41.8 and −58.8 kJ mol−1, indicate that they are around 40–60 kJ mol−1 more stable than the canonical closed-cage isomer CC(I) and around 15–30 kJ mol−1 more stable than the most stable closed-cage isomer CC(II) exhibiting HAT (Table 2). Hence, from the energy perspective, one may expect the production of these open-cage isomers in the EI plasma expansion, although barriers of cage-opening and HAT must be considered as well (vide infra).
The structures and E0 and D0 energies of all seven computed OC(I)N2(1–7) cluster isomers are available in Fig. S6 (ESI†). In isomer OC(I), the positive charge is distributed over the entire structure (Fig. S9, ESI†). As a result, the N2 binding energies to OC(I) are rather low and within a narrow energy range (D0 = 9.1–11.5 kJ mol−1). As a further consequence, the IR spectra predicted for all OC(I)N2 isomers are quite similar and thus we consider only the spectrum of the most stable OC(I)N2(1) isomer shown in Fig. 2(b) for comparison to the experimental spectrum in Fig. 1. The structures and E0 and D0 energies of the eight computed OC(II)N2(1–8) cluster isomers are available in Fig. S7 (ESI†). NBO analysis reveals that the proton at the CN group of OC(II) has a relatively large positive partial charge of 445 me, while those of the aliphatic H atoms are much lower and range from 203 to 248 me (Fig. S9, ESI†). Hence, in the most stable OC(II)N2(1) isomer shown in Fig. 2(b), the N2 ligand forms a strong and nearly linear NH⋯N2 ionic H-bond (1.991 Å, 177°) with D0 = 17.2 kJ mol−1. All other N2 binding sites feature only weaker CH⋯N2 contacts and thus are far less stable (D0 = 7.5–9.4 kJ mol−1) and not considered further. The NH⋯N2 H-bond in OC(II)N2(1) causes a large νNH redshift of 149 cm−1 from 3421 cm−1 of bare OC(II) (Fig. S13, ESI†) down to 3272 cm−1 in the cluster (Fig. 1) and a nearly fivefold enhancement in its IR activity (from 545 to 2541 km mol−1). A significant amount of the positive charge is located on the CNH group (478 me) while the spin density (Fig. S10, ESI†) is largely located on the C2 atom connected to the CNH group (sC2 = 0.366) and the C3 atom from which the H atom migrates (sC3 = 0.232). Inspection of Fig. 1 reveals that contributions of both OC(I/II)N2(1) to the measured IRPD spectrum cannot be ruled out. The IRPD spectrum reveals a weak additional feature E centred at 3155 cm−1, which cannot be assigned to any fundamental of any of the considered AdCN+N2 isomers. It is possible to attribute this band to an overtone of a νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/βCH2 mode at 1603 cm−1 unique to the OC(II) isomer, in which a stretch of a C
C/βCH2 mode at 1603 cm−1 unique to the OC(II) isomer, in which a stretch of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond and CH2 scissoring mode are strongly coupled (Fig. S13, ESI†). Unfortunately, anharmonic vibrational calculations to confirm this assignment have failed so far. Similarly, direct measurements of the fundamental νC
C double bond and CH2 scissoring mode are strongly coupled (Fig. S13, ESI†). Unfortunately, anharmonic vibrational calculations to confirm this assignment have failed so far. Similarly, direct measurements of the fundamental νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/βCH2 mode in the fingerprint range have been unsuccessful, possibly due to the high N2 binding energy of 17 kJ mol−1 (being close to the fundamental frequency) and/or the low photon flux of the OPO laser in this frequency range.
C/βCH2 mode in the fingerprint range have been unsuccessful, possibly due to the high N2 binding energy of 17 kJ mol−1 (being close to the fundamental frequency) and/or the low photon flux of the OPO laser in this frequency range.
In an effort to characterize the energy profile for the HAT and cage-opening reactions, transition states (TS) are located for two different pathways 1 and 2, both starting from the nascent canonical CC(I) structure toward the most stable OC(II) global minimum via either OC(I) or CC(II), respectively (Fig. 4 and Table S1, ESI†). The barrier TS(III) for cage-opening by breaking the activated C2–C3 bond of CC(I) with a simultaneous 1,2 H-shift of the acidic hydrogen from C6 to C3 to form OC(I) is computed as Vb = 83.4 kJ mol−1 (pathway 1). This energy barrier is 39.7 and 102.0 kJ mol−1 lower than the barriers for the formation of the equivalent open-cage isomers of Ama+ and Ada+ (Vb = 123.1 and 185.4 kJ mol−1),25 indicating the substantial impact of substitution of functional groups on these cage-opening reaction barriers. It is also lower than the barriers involved in the formation of closed-cage isomers exhibiting HAT (Vb = 148.0 kJ mol−1) via pathway 2. After cage-opening, a lower barrier of 47.3 kJ mol−1 must be overcome for HAT from the methyl group to the CN group to form isomer OC(II) from OC(I). Isomer CC(II) is the most likely closed-cage isomer exhibiting HAT to form as it has the lowest E0 energy of the closed-cage isomers and the lowest barrier for formation. However, a very low barrier of Vb = 7.0 kJ mol−1 at TS(I) is computed for the formation of OC(II) from CC(II). Therefore, we conclude that even if isomer CC(II) were formed it is likely that it cannot be trapped in the shallow potential well and continues to react to form OC(II) along pathway 2. These TS calculations suggest that the energetically most favorable route for formation of an isomer exhibiting HAT to the CN group is cage-opening of CC(I) to form OC(I) followed by HAT, thereby generating OC(II) (pathway 1). The intense fragment peak observed at m/z 134 in the AdCN mass spectrum (Fig. S1, ESI†) was attributed to the loss of neutral HCN (AdCN+ → C10H14+ + HCN).50 This was an exception among the C-linked 1-substituted AdCX, where the loss of the CX functional group (AdCX+ → Ady+ + CX) was observed as the main fragment with m/z 135 (Ady+). The low energy barriers for HAT to the CN group prior to fragmentation via loss of the CNH group provide an explanation for this observation, as this would lead to the generation of C10H14+ fragments (m/z 134) rather than Ady+ (m/z 135).
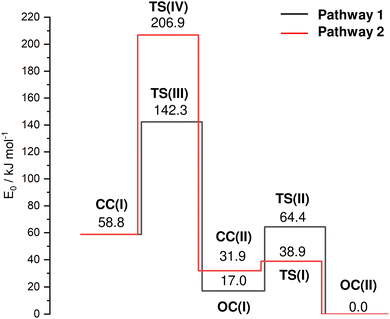 | ||
| Fig. 4 Potential energy surface (E0) of the cage-opening and HAT reactions of AdCN+ upon ionization for the two considered pathways from the nascent CC(I) isomer to the OC(II) global minimum (B3LYP-D3BJ/cc-pVTZ) with minima and transition states (TS). Relevant structures, energies and barriers are provided in the ESI† (Fig. S8 and Table S1). | ||
After considering the energetics of the various AdCN+ isomers, their N2 binding energies, and the potential barriers for cage-opening and HAT reactions, we come to the final assessment of the IRPD spectrum in Fig. 1. From the reaction potential calculations, we may exclude a significant population of CC(II) because of its shallow minimum well. Hence, only the three isomers CC(I), OC(I), and OC(II) remain. Out of these, only OC(II) has an NH group and can explain band F. Thus, this transition is mostly assigned to OC(II)N2(1). Band A can only be attributed to N2 complexes of CC(I), which all have quite similar intermolecular binding energies. While bands F and A are uniquely assigned to OC(II) and CC(I), respectively, there is no clearcut signature for OC(I) in the recorded IRPD spectrum because its CH stretch bands overlap with those of the other isomers. In the following, we crudely estimate the relative population of isomers CC(I) and OC(II) using the relative integrated band intensities of A and F (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) and the computed IR cross sections for νacidicCH of CC(I)N2 (266–974 km mol−1) and νNH of OC(II)N2(1) (2541 km mol−1), yielding population ratios for CC(I)
4) and the computed IR cross sections for νacidicCH of CC(I)N2 (266–974 km mol−1) and νNH of OC(II)N2(1) (2541 km mol−1), yielding population ratios for CC(I)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OC(II) in the range of 1
OC(II) in the range of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 to 2.5
1.5 to 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. However, as the N2 binding energy to OC(II) is substantially larger than to CC(I), D0 = 17 vs. 9–12 kJ mol−1, this ratio probably still increases in favour of CC(I). We cannot make any definitive conclusion about the abundance of OC(I) as the potential well of this minimum also has a relatively low isomerization barrier toward OC(II) when compared to the barrier for its generation. The entrance barrier at TS(III) at 142.3 kJ mol−1 is much higher than the exit channel barrier at TS(II) at 64.4 kJ mol−1, so that it may be challenging to trap a large population in the well of OC(I). In conclusion, the IRPD spectrum of AdCN+N2 indicates a dominant population of the nascent closed-cage isomer CC(I) obtained by vertical EI of neutral AdCN, along with a smaller but detectable population of the most stable OC(II) isomer obtained by cage-opening and HAT.
1. However, as the N2 binding energy to OC(II) is substantially larger than to CC(I), D0 = 17 vs. 9–12 kJ mol−1, this ratio probably still increases in favour of CC(I). We cannot make any definitive conclusion about the abundance of OC(I) as the potential well of this minimum also has a relatively low isomerization barrier toward OC(II) when compared to the barrier for its generation. The entrance barrier at TS(III) at 142.3 kJ mol−1 is much higher than the exit channel barrier at TS(II) at 64.4 kJ mol−1, so that it may be challenging to trap a large population in the well of OC(I). In conclusion, the IRPD spectrum of AdCN+N2 indicates a dominant population of the nascent closed-cage isomer CC(I) obtained by vertical EI of neutral AdCN, along with a smaller but detectable population of the most stable OC(II) isomer obtained by cage-opening and HAT.
4. Concluding remarks
We present the IR spectrum of AdCN+ cations produced by electron ionization of neutral AdCN using N2 tagging photodissociation of mass-selected cluster ions in a tandem mass spectrometer. The IRPD spectrum recorded in the CH/NH stretch range reveals the unique spectral signatures of several isomers indicative of cage-opening and intramolecular hydrogen/proton transfer (HAT) reactions. The potential energy surface for these reactions is analysed with B3LYP-D3BJ/cc-pVTZ calculations to determine minima and transition states with corresponding barriers. The nascent and canonical closed-cage isomer CC(I) contributes a major population of the detected AdCN+ ions and can be safely identified by its acidic CH stretch band (νacidicCH) near 2600 cm−1. The geometry distortion upon vertical ionization and removal of one electron from the HOMO is rather similar to that observed for Ada+, indicating that the H → CN substitution at the 1-position has little impact upon the electronic structure of the HOMO and ground electronic state, apart from symmetry reduction (from C3v to Cs) and the fact that the Jahn–Teller distortion is in both cases along the axis containing a tertiary CH atom, which in Ada+ is along the rotational symmetry axis but in AdCN+ not. The unexpected appearance of an intense NH stretch band near 3300 cm−1 cannot be explained by CC(I) but must result from intramolecular HAT from the Ady cage to the CN group. The energetically most favourable process is transfer of the acidic hydrogen to produce the closed-cage isomer CC(II). Although CC(II) has a spectrum compatible with the IRPD spectrum, it has a rather low barrier toward cage-opening to reach the global minimum on the potential energy surface, OC(II), suggesting that its population is rather low. On the other hand, OC(II) is concluded to have a substantial population and is mostly responsible for the NH stretch band. Under this assumption, its population is significantly lower than that of the nascent CC(I) ion. In addition to the pathway 2, along which cage-opening follows HAT (i.e., CC(I) → CC(II) → OC(II)), there is a second pathway 1 with the same start and end structure but the reversed order of the two processes, i.e., HAT follows cage-opening (CC(I) → OC(I) → OC(II)). The OC(I) intermediate in this reaction profile has a deep well and may be trapped by collisional stabilisation in the employed high-pressure EI plasma expansion. However, all bands predicted for OC(I) overlap with bands of the IRPD spectrum assigned to CC(I) and OC(II), so that we cannot quantify its population. In any case, the combined consideration of the measured IRPD spectrum and B3LYP-D3BJ calculations suggests a dominant population of the nascent cage isomer CC(I), along with a smaller but detectable population of the most stable OC(II) isomer obtained by cage-opening and HAT.The effect of N2 tagging on the structures, energetics, and IR spectra of the various AdCN+ ions is generally minor, with N2 binding energies ranging from D0 = 7 to 23 kJ mol−1 arising from electrostatic, induction, and dispersion forces. In all cases, the anisotropy of these long-range forces prefers a linear approach of N2 to AdCN+ leading to multiple CH⋯N2 contacts with D0 = 7–12 kJ mol−1. Exceptions are the somewhat stronger linear intermolecular NH⋯N2 ionic H-bonds of N2 to isomers with a protonated CN group, D0 = 17–23 kJ mol−1. These isomers experience a substantial redshift in their NH stretch frequencies. All efforts to reduce the tagging effects by replacing N2 with Ar to achieve lower effective ion temperatures and higher-resolved IRPD spectra have failed so far because of insufficient ion production. Similarly, recording spectra in the fingerprint range to better distinguish various AdCN+ isomers have been unsuccessful so far and are future targets.
Recently, the EPD spectrum of AdCN+ ions produced by low-pressure EI has been measured in a cryogenic ion trap and assigned solely to the canonical nascent CC(I) isomer by comparison to time-dependent DFT calculations.14 Whether isomers resulting from HAT or cage-opening also contribute to the measured EPD spectrum is difficult to judge because of the very broad bands observed. In any case, the EPD spectrum can fully be assigned to the electronic spectrum computed for CC(I) and it is also consistent with our unpublished photoelectron spectrum, which cannot contain contributions from OC(I/II). There is no need to assume reacted AdCN+ isomers to explain its EPD spectrum. Moreover, as the AdCN+ ions are produced in that experiment in a low-pressure ion source without the possibility of collisional stabilization and kinetic ion trapping, those ions overcoming the first reaction barrier lying at least 142 kJ mol−1 above the global minimum may readily dissociate upon loss of HCN (requiring only 47 kJ mol−1) on their way from the ion source to the ion trap and thus cannot contribute to the EPD spectrum.
Future efforts will focus on the effects of other monosubstituents (e.g., R = OH/SH, halogen, CH3), other substitution positions, and multiple substituents of the same and different type with various electron-withdrawing and electron-donating character on the cage-opening and HAT reaction profile. Comparison between Ada+, Ama+, and AdCN+ (R = H, NH2, CN) reveals drastic differences in the general topology and energetics of these reaction profiles. Furthermore, microhydration of these cations are highly interesting from the organic chemistry point of view. For example, recent IRPD spectra of [Ada(H2O)n]+ revealed intracluster proton transfer (ICPT) of the acidic CH proton of Ada+ to the (H2O)n solvent cluster at cluster sizes n ≥ 3.31 As the CC(I) isomer of AdCN+ has a similar CH acidity as Ada+, also only a few H2O ligands may be required to drive such an ICPT.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by Deutsche Forschungsgemeinschaft (DFG, project DO 729/8-2). P. T. R. acknowledges financial support from the Erasmus+ programme of the European Union (KA103). The authors thank Martin George and Dashjargal Arildii for their support in the experimental data acquisition and Peter R. Schreiner (Giessen) for valuable discussions on the substitution effects of diamondoids.References
- R. C. Fort and P. V. Schleyer, Chem. Rev., 1964, 64, 277–300 CrossRef CAS.
- J. E. P. Dahl, S. G. Liu and R. M. K. Carlson, Science, 2003, 299, 96–99 CrossRef CAS PubMed.
- W. L. Yang, J. D. Fabbri, T. M. Willey, J. R. I. Lee, J. E. P. Dahl, R. M. K. Carlson, P. R. Schreiner, A. A. Fokin, B. A. Tkachenko, N. A. Fokina, W. Meevasana, N. Mannella, K. Tanaka, X. J. Zhou, T. V. Buuren, M. A. Kelly, Z. Hussain, N. A. Melosh and Z.-X. Shen, Science, 2007, 316, 1460–1462 CrossRef CAS PubMed.
- A. A. Fokin and P. R. Schreiner, Mol. Phys., 2009, 107, 823–830 CrossRef CAS.
- J. L. Teunissen, F. D. Proft and F. D. Vleeschouwer, J. Chem. Theory Comput., 2017, 13, 1351–1365 CrossRef CAS PubMed.
- J. Y. Raty and G. Galli, Nat. Mater., 2003, 2, 792–795 CrossRef CAS PubMed.
- K.-W. Yeung, Y. Dong, L. Chen, C.-Y. Tang, W.-C. Law and G. C.-P. Tsui, Nanotechnol. Rev., 2020, 9, 650–669 CrossRef CAS.
- P. R. Schreiner, N. A. Fokina, B. A. Tkachenko, H. Hausmann, M. Serafin, J. E. P. Dahl, S. Liu, R. M. K. Carlson and A. A. Fokin, J. Org. Chem., 2006, 71, 6709–6720 CrossRef CAS PubMed.
- L. Wanka, K. Iqbal and P. R. Schreiner, Chem. Rev., 2013, 113, 3516–3604 CrossRef CAS PubMed.
- A. A. Fokin and P. R. Schreiner, Chem. Rev., 2002, 102, 1551–1594 CrossRef CAS PubMed.
- A. Fokin, P. Schreiner, P. Gunchenko, S. Peleshanko, T. Shubina, S. Isaev, P. Tarasenko, N. Kulik, H.-M. Schiebel and A. Yurchenko, J. Am. Chem. Soc., 2000, 122, 7317–7326 CrossRef CAS.
- P. B. Crandall, D. Müller, J. Leroux, M. Förstel and O. Dopfer, Astrophys. J., Lett., 2020, 900, L20 CrossRef CAS.
- P. B. Crandall, R. Radloff, M. Förstel and O. Dopfer, Astrophys. J., 2022, 940, 104 CrossRef.
- P. B. Crandall, V. D. Lovasz, R. Radloff, S. Stahl, M. Förstel and O. Dopfer, Mol. Phys., 2023, 121, e2231566 CrossRef.
- T. Henning and F. Salama, Science, 1998, 282, 2204–2210 CrossRef CAS PubMed.
- O. Pirali, M. Vervloet, J. E. P. Dahl, R. M. K. Carlson, A. G. G. M. Tielens and J. Oomens, Astrophys. J., 2007, 661, 919–925 CrossRef CAS.
- H. Schwertfeger and P. R. Schreiner, Chem. Unserer Zeit, 2010, 44, 248–253 CrossRef CAS.
- T. Rander, M. Staiger, R. Richter, T. Zimmermann, L. Landt, D. Wolter, J. E. Dahl, R. M. K. Carlson, B. A. Tkachenko, N. A. Fokina, P. R. Schreiner, T. Möller and C. Bostedt, J. Chem. Phys., 2013, 138, 024310 CrossRef PubMed.
- C. S. Sarap, B. Adhikari, S. Meng, F. Uhlig and M. Fyta, J. Phys. Chem. A, 2018, 122, 3583–3593 CrossRef CAS PubMed.
- W. A. Clay, Z. Liu, W. Yang, J. D. Fabbri, J. E. Dahl, R. M. K. Carlson, Y. Sun, P. R. Schreiner, A. A. Fokin, B. A. Tkachenko, N. A. Fokina, P. A. Pianetta, N. Melosh and Z.-X. Shen, Nano Lett., 2009, 9, 57 CrossRef CAS PubMed.
- L. Landt, M. Staiger, D. Wolter, K. Klünder, P. Zimmermann, T. M. Willey, T. V. Buuren, D. Brehmer, P. R. Schreiner, B. A. Tkachenko, A. A. Fokin, T. Möller and C. Bostedt, J. Chem. Phys., 2010, 132, 024710 CrossRef PubMed.
- M. A. Gunawan, J.-C. Hierso, D. Poinsot, A. A. Fokin, N. A. Fokina, B. A. Tkachenko and P. R. Schreiner, New J. Chem., 2014, 38, 28–41 RSC.
- A. A. Spasov, T. V. Khamidova, L. I. Bugaeva and I. S. Morozov, Pharm. Chem. J., 2000, 34, 1–7 CrossRef CAS.
- R. S. Schwab, A. C. England, D. C. Poskanzer and R. R. Young, JAMA, 1969, 208, 1168–1170 CrossRef CAS PubMed.
- M. A. R. George and O. Dopfer, Chem. – Eur. J., 2022, 28, e202200577 CrossRef CAS PubMed.
- M. A. R. George and O. Dopfer, J. Phys. Chem. Lett., 2022, 13, 449–454 CrossRef PubMed.
- A. Candian, J. Bouwman, P. Hemberger, A. Bodi and A. G. G. M. Tielens, Phys. Chem. Chem. Phys., 2018, 20, 5399–5406 RSC.
- S. Maclot, J. Lahl, J. Peschel, H. Wikmark, P. Rudawski, F. Brunner, H. Coudert-Alteirac, S. Indrajith, B. A. Huber, S. Díaz-Tendero, N. F. Aguirre, P. Rousseau and P. Johnsson, Sci. Rep., 2020, 10, 1–12 CrossRef PubMed.
- A. Boyer, M. Hervé, A. Scognamiglio, V. Loriot and F. Lépine, Phys. Chem. Chem. Phys., 2021, 23, 27477–27483 RSC.
- A. Patzer, M. Schütz, T. Möller and O. Dopfer, Angew. Chem., Int. Ed., 2012, 51, 4925–4929 CrossRef CAS PubMed.
- M. A. R. George and O. Dopfer, Phys. Chem. Chem. Phys., 2023, 25, 13593–13610 RSC.
- M. A. R. George, M. Förstel and O. Dopfer, Angew. Chem., Int. Ed., 2020, 59, 12098–12104 CrossRef CAS PubMed.
- C. W. B. Jr., Y. Liu, A. Rica, A. L. Mattioda and L. J. Allamandola, Astrophys. J., 2007, 671, 458–469 CrossRef.
- R. S. Lewis, T. Ming, J. F. Wacker, E. Anders and E. Steel, Nature, 1987, 326, 160–162 CrossRef CAS.
- O. Guillois, G. Ledoux and C. Reynaud, Astrophys. J., 1999, 521, L133–L136 CrossRef CAS.
- M. Steglich, F. Huisken, J. E. Dahl, R. M. K. Carlson and T. Henning, Astrophys. J., 2011, 729, 91–100 CrossRef.
- G. A. H. Walker, D. A. Bohlender, J. P. Maier and E. K. Campbell, Astrophys. J., Lett., 2015, 812, L8 CrossRef.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed.
- H. Fan, L. M. Hobbs, J. A. Dahlstrom, D. E. Welty, D. G. York, B. Rachford, T. P. Snow, P. Sonnentrucker, N. Baskes and G. Zhao, Astrophys. J., 2019, 878, 151 CrossRef CAS.
- L. M. Hobbs, D. G. York, J. A. Thorburn, T. P. Snow, M. Bishof, S. D. Friedman, B. J. McCall, T. Oka, B. Rachford, P. Sonnentrucker and D. E. Welty, Astrophys. J., 2009, 705, 32–45 CrossRef CAS.
- P. Jenniskens and F.-X. Désert, Astron. Astrophys., Suppl. Ser., 1994, 106, 39–78 CAS.
- M. Kappe, A. Schiller, S. A. Krasnokutski, M. Ončák, P. Scheier and E. M. Cunningham, Phys. Chem. Chem. Phys., 2022, 24, 23142–23151 RSC.
- M. P. Bernstein, S. F. M. Ashbourn, S. A. Sandford and L. J. Allamandola, Astrophys. J., 2004, 601, 365–370 CrossRef CAS.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30 CrossRef.
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef CAS PubMed.
- B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii, M. A. Siebert, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Science, 2021, 371, 1265–1269 CrossRef CAS PubMed.
- Y. D. Chadwick, A. C. Legon and D. J. Millen, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 2064–2069 RSC.
- O. Chitarra, M.-A. Martin-Drummel, Z. Buchanan and O. Pirali, J. Mol. Spectrosc., 2021, 378, 111468 CrossRef CAS.
- K. K. M. Jeneesh and R. Padmanaban, J. Chem. Sci., 2018, 130, 113 CrossRef.
- K. K. Khullar, C. L. Bell and L. Bauer, J. Org. Chem., 1973, 38, 1042–1044 CrossRef CAS.
- O. Dopfer, Z. Phys. Chem., 2005, 219, 125–168 CrossRef CAS.
- O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437–495 Search PubMed.
- M. J. Frisch, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT., 2016 Search PubMed.
- M. A. R. George, F. Buttenberg, M. Förstel and O. Dopfer, Phys. Chem. Chem. Phys., 2020, 22, 28123–28139 RSC.
- P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, NIST Standards and Technology, Gaithersburg, MD, 20889, http://webbook.nist.gov, (accessed 2023-02-28) Search PubMed.
- C. Peng and H. B. Schlegel, Isr. J. Chem., 1993, 33, 449–454 CrossRef CAS.
- A. Gali, T. Demján, M. Vörös, G. Thiering, E. Cannuccia and A. Marini, Nat. Commun., 2016, 7, 11327 CrossRef CAS PubMed.
- I. V. Litvinyuk, Y. Zheng and C. E. Brion, Chem. Phys., 2000, 261, 289–300 CrossRef CAS.
- F. M. Pasker, N. Solcà and O. Dopfer, J. Phys. Chem. A, 2006, 110, 12793–12804 CrossRef CAS PubMed.
- M. Schmies, A. Patzer, S. Kruppe, M. Miyazaki, S. Ishiuchi, M. Fujii and O. Dopfer, ChemPhysChem, 2013, 14, 728–740 CrossRef CAS PubMed.
- N. Solcà and O. Dopfer, J. Phys. Chem. A, 2002, 106, 7261–7270 CrossRef.
- J. Klyne, M. Schmies and O. Dopfer, J. Phys. Chem. B, 2014, 118, 3005–3017 CrossRef CAS PubMed.
- J. Klyne, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3092–3108 RSC.
- J. Klyne and O. Dopfer, Phys. Chem. Chem. Phys., 2019, 21, 2706–2718 RSC.
- N. Solcà and O. Dopfer, Phys. Chem. Chem. Phys., 2004, 6, 2732–2741 RSC.
- M. Schütz, Y. Matsumoto, A. Bouchet, M. Öztürk and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 3970–3986 RSC.
- K. Sakota, M. Schütz, M. Schmies, R. Moritz, A. Bouchet, T. Ikeda, Y. Kouno, H. Sekiya and O. Dopfer, Phys. Chem. Chem. Phys., 2014, 16, 3798–3806 RSC.
- K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2020, 22, 13092–13107 RSC.
- K. Chatterjee and O. Dopfer, ApJ, 2018, 865, 114 CrossRef.
- M. Schmies, A. Patzer, M. Schütz, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2014, 16, 7980–7995 RSC.
- J. M. Mayer, Annu. Rev. Phys. Chem., 2004, 44, 363–390 CrossRef PubMed.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Chem. Rev., 2012, 112, 4016–4093 CrossRef CAS PubMed.
- S. Hammes-Schiffer, J. Am. Chem. Soc., 2015, 137, 8860–8871 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03417h |
| This journal is © the Owner Societies 2023 |