Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From a one-mode to a multi-mode understanding of conical intersection mediated ultrafast organic photochemical reactions
Yorrick
Boeije†‡
 *a and
Massimo
Olivucci
*a and
Massimo
Olivucci
 *bc
*bc
aVan 't Hoff Institute for Molecular Sciences (HIMS), University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
bChemistry Department, University of Siena, Via Aldo Moro n. 2, 53100 Siena, Italy
cChemistry Department, Bowling Green State University, Overman Hall, Bowling Green, Ohio 43403, USA
First published on 27th March 2023
Abstract
Over the last few decades, conical intersections (CoIns) have grown from theoretical curiosities into common mechanistic features of photochemical reactions, whose function is to funnel electronically excited molecules back to their ground state in regions where the potential energy surfaces (PESs) of two electronic states become degenerate. Analogous to transition states in thermal chemistry, CoIns appear as transient structures providing a kinetic bottleneck along a reaction coordinate. However, such a bottleneck is not associated with the probability of crossing an energy barrier but rather with an excited state decay probability along a full “line” of transient structures connected by non-reactive modes, the intersection space (IS). This article will review our understanding of the factors controlling CoIn mediated ultrafast photochemical reactions, taking a physical organic chemist approach by discussing a number of case studies for small organic molecules and photoactive proteins. Such discussion will be carried out by first introducing the “standard” one-mode model based on Landau–Zener (LZ) theory to describe a reactive excited state decay event intercepting, locally, a single CoIn along a single direction, and then by providing a modern perspective based on the effects of the phase matching of multiple modes on the same local event, thus redefining and expanding the description of the excited state reaction coordinate. The direct proportionality between the slope (or velocity) along one mode and decay probability at a single CoIn is a widely applied fundamental principle that follows from the LZ model, yet it fails to provide a complete understanding of photochemical reactions whose local reaction coordinate changes along the IS. We show that in these situations, in particular by focussing on rhodopsin double bond photoisomerization, it is mandatory to consider additional molecular modes and their phase relationship approaching the IS, hence providing a key mechanistic principle of ultrafast photochemistry based on the phase matching of those modes. We anticipate that this qualitative mechanistic principle should be considered in the rational design of any ultrafast excited state process, impacting various fields of research ranging from photobiology to light-driven molecular devices.
1. Conical intersections in ultrafast photochemistry
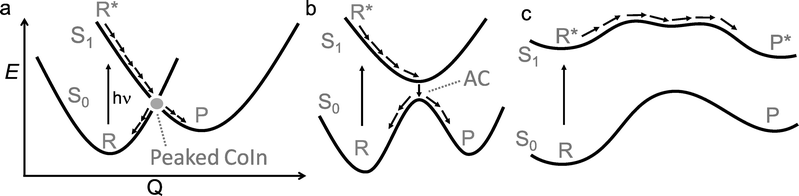
Photochemistry is about the world of electronically excited states that lies, in terms of energy, above the ground state world in which thermal chemistry takes place. The interaction of a molecule with light opens up this higher world, which is not long-lived. In extreme cases, there are regions where these two worlds meet in the form of a conical intersection (CoIn),§ that is capable of funnelling the molecule from the excited state (ES) back into the ground state (GS). The GS relaxation process would then either result in regeneration of the starting molecule (a phenomenon called internal conversion, IC) or formation of a new molecule (a photochemical reaction).1 In the latter case, we speak of a nonadiabatic¶ photochemical reaction (Fig. 1a) involving a real surface crossing between, for instance, a singlet ES PES (S1) and the GS PES (S0). Alternatively, a nonadiabatic photochemical reaction can proceed through an avoided crossing (AC), in which the ES and GS PESs nearly touch (Fig. 1b). In contrast, the situation c in Fig. 1 shows an adiabatic photochemical reaction that takes place entirely on the ES PES, forming an excited product that can relax to the GS through fluorescence emission or IC at an AC or nearby CoIn. Whereas in b and c we indicate reactions involving, in principle, a vibrationally relaxed (i.e. thermalized) intermediate on the ES PES, situation a involves a photochemical reaction in which passage through the CoIn is achieved within a single vibrational period and, therefore, without generating ES intermediates. Below we will see that even the mechanistic case of Fig. 1a is far more complex than this one-dimensional picture suggests.For a long time, it had been argued that situation b was substantially ubiquitous based on the non-crossing rule which states that electronic states with the same symmetry do not cross.2 However, this rule is only strictly valid for diatomic molecules and it quickly became clear that CoIns are, indeed, the most common mechanistic features of photochemistry and not mere curiousities.3–5 In the early 90s this was demonstrated via systematic quantum chemical investigations.6–14 This paradigm shift in mechanistic photochemistry was supported both by advances in computational chemistry enabling the computation of ES PES gradients and therefore mapping of ES PESs as well as advances in laser spectroscopy enabling measurements of ES lifetimes in alkenes, polyenes and aromatic compounds on the femtosecond timescale, which are faster decay times than mechanisms b and c in Fig. 1 could account for.15–18
The nonradiative decay rate in these mechanisms can be calculated with Fermi's Golden Rule, which is a perturbation theory approach in which the overlap of vibrational wavefunctions between two electronic states in the (micro)canonical statistical limit—i.e., after intramolecular vibrational redistribution (∼1 ps) and thermal equilibration in the condensed phase (∼10 ps)—determines the efficiency of nonradiative decay.19,20 Because this overlap is usually between the lowest vibrational state of the ES and a highly excited vibrational state of the GS that contains a significant nodal structure, its magnitude is small, resulting in nonradiative decay rates in the order of several picoseconds, but may extend to nanoseconds for rigid molecules in which the ES is only weakly distorted.21,22 It is currently recognized, therefore, that ultrafast (<10 ps) photochemical and photophysical processes must involve CoIns. Whether it is favorable or unfavorable to have a prompt access to a CoIn and decay, then depends on the selected ES molecular systems. When both efficient photochemistry and high photostability are desired, having a promptly accessible CoIn is favorable, whereas it is unfavorable when a long-lived ES is the goal. Examples of these three groups of ES processes are provided in Fig. 2.
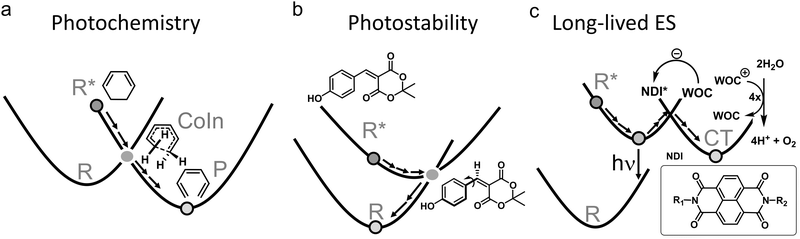 | ||
| Fig. 2 Three groups of photophysical processes. (a) Photochemistry. Efficient decay through a CoIn is desired. The example provided is the electrocyclic ring-opening of 1,3-cyclohexadiene to hexatriene through a S1/S0 CoIn. The S2/S1 CoIn of this reaction is not shown.23 (b) Photostability. Efficient decay through a CoIn is desired. The example provided is the IC process of coumaryl meldrum, which is a molecule being explored for several photoprotection applications.24 (c) Long-lived ES. Efficient decay through a CoIn is not desired to promote longer timescale ES processes, such as fluorescence (hν) and photocatalysis through photoinduced charge transfer (CT). The latter is illustrated for a widely applied dye, naphthalene diimide (NDI), which after photoexcitation extracts an electron from a water oxidation catalyst (WOC) to form the radical anion of NDI. The WOC is then reactive enough to oxidize water producing oxygen in a subsequent step, which combined with the proton reduction half reaction yields hydrogen.25 | ||
Nature provides examples of favorable ultrafast photochemical processes. One is the primary event in vision characterized by the ES of the chromophore of the visual pigment rhodopsin. Herein, the chromophore, corresponding to the protonated Schiff base of 11-cis retinal (rPSB11), undergoes an efficient ultrafast photoisomerization with high quantum yield (QY, defined as the number of molecules product produced divided by the number of photons absorbed), ultimately triggering the transduction pathway carrying over the visual information to the brain.26–28 Other examples of favorable processes are found in the expanding fields of light-driven molecular devices (e.g. molecular motors that make often use of photoisomerization reactions as well)29,30 and synthetic organic photochemistry (e.g. synthesis methods that make use of pericyclic reactions, Fig. 2a).23 In other situations, reactivity of ES molecules is not desired, and CoIns can help to depopulate ESs without causing photoreactions. Nature has figured out methods to dissipate the photon energy efficiently through CoIns in thymine or cytosine DNA base pairs to compete with photochemical [2π+2π] cycloaddition, which is linked to skin cancer through disruption of the DNA strands.31,32 Sunscreen researchers strive to achieve the same goal by designing molecules that absorb the UV light from the sun, but get rid of the excess energy rapidly through IC (Fig. 2b).24,33 Similarly, CoIn mediated IC should be maximized in “molecular heaters”, which are molecular light-to-heat converters with potential applications in agriculture, where their function is to improve crop yields by locally heating the plant surface after UV light absorption.34
Whenever a long-lived ES is required to promote either charge transfer, energy transfer (such as in optoelectronics35–37 or photocatalysis38) or fluorescence (such as in luminescent organic molecular crystals39 or super-resolution microscopy and optogenetics where fluorescent proteins are required to map cellular activity40–42), nonradiative decay through a CoIn should be blocked. This means that the corresponding molecule or material should be designed in such a way to avoid accessing a CoIn as much as possible, thus “resisting” IC. Photocatalysis is a type of photochemistry which requires the simultaneous use of a catalyst and light to promote a synthetic reaction pathway.43 Several scenarios are possible depending on the role of the absorbing species. In one scenario, the photoexcited catalyst transfers an atom or electron to a substrate that is transformed in a reactive intermediate (e.g., a radical) that then triggers a chemical reaction, after which the catalyst is regenerated in a subsequent step (Fig. 2c).25 Alternatively, the photoexcited catalyst may sensitize a substrate through photoinduced energy transfer, changing its reactivity and ultimately triggering a chemical reaction. It has been shown in several ultrafast photoinduced electron and energy transfer processes that CoIns also mediate these processes (Section 3.3).
1.1 Theoretical description of conical intersections
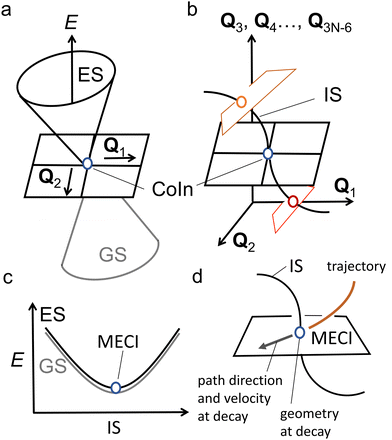
In any of the above cases, it is important to understand CoIns and how they can be tuned to optimize the wanted ES process. As such understanding represents the main objective of the present review, it is convenient to revise few basic theoretical concepts that will be frequently used in the following sections. CoIns are real crossings between two adiabatic electronic states of the same spin multiplicity. Their existence can be demonstrated by considering a pair of electronic states |ϕ1〉 and |ϕ2〉, which might be S0 and S1 respectively. The goal is then to find the nuclear position vectors Qx where the potential energies of the two adiabatic states E1 (Qx) and E2 (Qx) are equal. Notice that Q is a vector whose coordinates Q1, Q2,…, Q3N−6 are expressed on the bases of normal modes where N is the total number of atoms in the reacting system. Hence,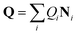 in which Qi are the coordinates and Ni are the normal mode vectors (Ni can be expressed as linear combinations of Cartesian unit vectors).
in which Qi are the coordinates and Ni are the normal mode vectors (Ni can be expressed as linear combinations of Cartesian unit vectors).
If we assume that the other states are far in energy, we can neglect their coupling to |ϕ1〉 and |ϕ2〉 and just consider the subspace formed by the latter two which may be written in terms of an orthogonal basis of diabatic states |η1〉 and |η2〉.44 In the present context diabatic states are associated to specific electronic configurations in a Molecular Orbital language or resonance formulas in a Valence Bond language, the latter being more popular when discussing structures and reactions in organic chemistry. The energies may then be computed as follows:
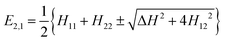 | (1) |
| ΔH (Qx) = 0 and H12 (Qx) = 0 | (2) |
Because diatomic molecules only have one nuclear coordinate, we have two independent equations that need to be solved and one unknown, implying that E1 and E2 cannot be equal. This is exactly what was referred to above as the non-crossing rule and it leads to an AC where H11 and H22 are degenerate but the coupling matrix element H12 is non-zero. However, this rule does not hold when the two states have different (space or spin) symmetries as in this case H12(Q1) is identically zero and only one equation needs to be solved. On the other hand, polyatomic molecules possess at least two coordinates Q1 and Q2 (e.g. three for triatomic molecules), allowing eqn (2) to be solved. In fact, the E1 = E2 condition is satisfied for a set of points with dimension 3N − 8, which is called the intersection space (IS) or crossing seam.
Any CoIn is a point of the IS characterized by two branching plane (BP) vectors, Q1 and Q2, that may be defined by performing a Taylor expansion of ΔH and H12 at Qx.44,45
| Q1 = ∇ΔH(Qx) Q2 = 2∇H12(Qx) | (3) |
| g12 = 〈ϕ1|∇ϕ〉 | (4) |
In spite of the many MECIs and BPs reported and discussed in the literature together with their local reaction coordinate, there is no theorem supporting the decay at the MECI. In fact, it is not trivial to establish which of the IS points truly represents the dominating decay channel and, therefore, the kinetic “bottleneck” or “funnel” most relevant for the control of a photochemical reaction.48 Below we argue that, in general, it is necessary to identify such a bottleneck with an entire IS segment thus effectively passing from a one-mode to a multi-mode description of the ES decay event.
In the following we will often differentiate between one-mode and multi-mode reactive processes. Therefore, it is useful to clarify these terms. As also discussed above, to define a set of modes, one must choose a reference basis. Such basis could correspond to the vibrational modes of the GS reactant at its equilibrium geometry. In this context, “one-mode” may refer to a reaction coordinate dominated by one specific vibrational mode. As we will also explain below, this is not the “one-mode” we are mainly discussing in the present paper. In fact, a linear combination of vibrational modes forming a “curved” reaction coordinate (i.e., where the coefficients of such combination change during the progression from R* to a CoIn) may still be interpreted as a “local” one-mode process when the same trajectory enters the BP along a specific direction. In contrast, the multi-mode process of interest here refers to a motion that has a sizeable component orthogonally to the BP of a single CoIn point, which may be the MECI. In other words, we will discuss situations where the reaction coordinate is, in general, not parallel to the BP because it also projects along the IS. In this context a more convenient reference basis could be the one formally defined by the BP vectors at the MECI point plus a suitable set of modes spanning the IS. We will see that this has consequences for both the dynamics and quantum efficiency of the reaction because multiple CoIns and BPs become implicated in the reaction due to a variation in the weight of the IS spanning modes at the time of the ES decay. Therefore, below we will mostly consider a local coordinate system defined by orthogonalized BP vectors and one of the 3N − 8 remaining modes orthogonal to the BP.
1.2 Conical intersections vs. transition states
As a prerequisite for understanding multi-mode ES decay processes, we start by assuming that single CoIn points (e.g. a MECI) can be used to discuss the dynamics and kinetics of a light-induced ultrafast process (by dynamics we mean the detailed motion of the atoms as a function of time, while kinetics refers to a collective property describing, for instance, the decay time and photoproduct appearance time). This assumption will be considered valid for the rest of this section as well as for the most of Section 2, but will be released in Section 3.Analogously to the transition state (TS) in an elementary GS reaction path (thermal chemistry), the CoIn represents a critical structure on an elementary “interstate” ES/GS reaction path (photochemistry). It can also be stated that, in both cases, the closer in energy such critical structures are to the corresponding products, the closer they would resemble the products, consistent with the Hammond postulate.49 Despite these similarities, there are qualitative differences between a TS and CoIn even for elementary reactions (i.e., a reaction where reactant and products are connected by a single critical structure). These differences are found in the local PES topography and topology (here we use these terms loosely with their meaning specified below), reaction coordinate, reaction energy profile and reaction dynamics (Fig. 4). Usually, the TS of an elementary thermal reaction is, topographically, a one-dimensional “saddle point” (i.e. where Qx is the only nuclear coordinate associated with an energy maximum) with a smooth topology (i.e. with continuous first derivatives) which connects the reactant (R) and the product (P) on the GS PES. On the other hand, a CoIn has a GS PES featuring the topography of a two-dimensional spike (i.e. a singularity defined by discontinuous first derivatives along Q1 and Q2). A matching but opposite spike (a funnel) resides on the ES PES. Thus, such singularities connect the ES reactant (R*) to one, two or more GS products (R, P and P′) via a reaction coordinate that bifurcates along the BP.19 Such a bifurcation determines the number and type of reaction paths and, thus, the photoproducts that might be generated. Of course, one of the GS branches invariably connects R* to R and therefore leads to reactant reconstitution and must correspond to an ultrafast IC event. Such a branching process shall not be confused with the topographically distinct bifurcation described in certain thermal reactions and due to a peculiar GS PES shape where a bifurcation takes place after the passage through the critical TS structure on a PES with continuous derivatives, giving rise to multiple products (for instance different conformers).50
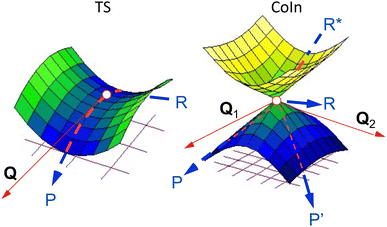 | ||
| Fig. 4 Left: PES of a thermal reaction showing the reactant (R), transition state (TS) and product (P). The red arrow indicates the transition vector, Q. Right: PESs of a diabatic photochemical reaction showing the excited reactant (R*), CoIn, GS reactant (R) and two photoproducts (P and P′). The red arrows indicate the branching plane vectors Q1 and Q2.19 | ||
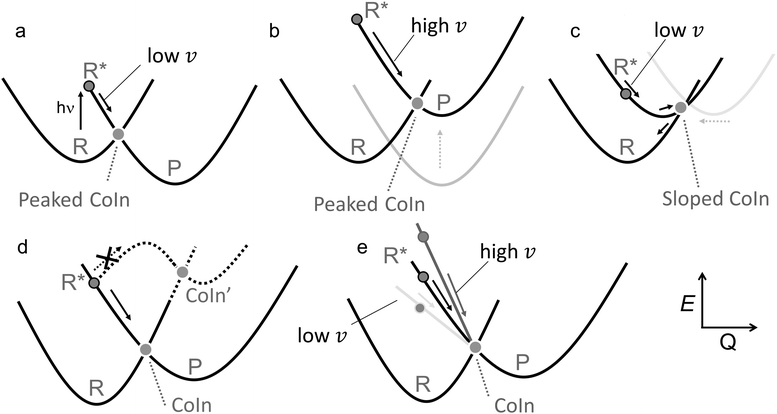
Another fundamental difference between a TS and CoIn concerns the energy profile connecting the reactant to these critical structures. In thermal reactions, TSs are always approached along energetically uphill reaction coordinates. As a result, the reaction efficiency is determined by the number of trajectories overcoming the energy barrier associated with the TS (see Fig. 5a). In contrast, the path towards the CoIn may be either energetically uphill or downhill (in Fig. 5b the CoIn is entered downhill). There is also the case where an activation barrier (i.e. an ES TS) separates a locally stable R* intermediate and the CoIn (Fig. 5c).20 In this case a downhill path exists connecting the ES TS and the CoIn.
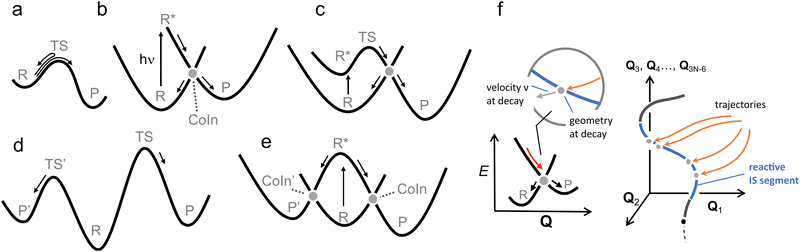 | ||
| Fig. 5 Control in thermal and photochemical reactions. (a) An elementary thermal reaction. (b) Barrierless photochemical reaction leading to photoproduct formation and reactant reconstitution. The P:R* branching ration determines the QY of the reaction. Notice that this diagram corresponds to one branch of the reaction coordinates (R* to P) seen in Fig. 4. An analogue diagram could be written for the other (R* to P′) branch. (c) Photochemical reaction in which the access to the CoIn is controlled by and ES energy barrier located in correspondence of an ES TS.51 (d) R, P and P' are the reactant and competing products respectively. P′ is the kinetically favoured product as TS' is lower in energy than TS. (e) Photochemical reaction in which the accessibility of two CoIns is controlled by the slopes of the ES PES, in this case biasing the reaction towards CoIn indicated by the larger (velocity) arow. A potential example of this situation is reported in Fig. 18. (f) A more realistic representation where a set of trajectories belonging to the same ES reacting population hit diverse CoIns belonging to the same reacting IS segment leading to a single product P. For simplicity we assume that each CoIn is entered along a single dominating direction (see circled inset) where a R:P branching occurs. | ||
Another analogy can be made when comparing elementary schemes for selective thermal (Fig. 5d) and photochemical (Fig. 5e) reactions. It is clear from the illustration that the calculation of the different TSs accessible from R allows the prediction of the selectivity which is determined by the lower TS. The photochemical analogue will rely on different downhill slopes departing from R*. As we discuss in Section 2, a steep downhill path on the ES PES has important implications for the dynamical factors that controls the photochemistry through so called “peaked” CoIns. For “sloped” CoIns, however, the reaction path is uphill. Notice that this type of selectivity precedes, along the reaction path, the potential branching and production of different photoproducts via decay at a single peaked CoIn (see Fig. 4 right).
Steep downhill paths generate a further element of complexity. A R* moving towards the decay region of a peaked CoIn with finite velocity (Fig. 5b) will not decay to the GS at the MECI reached by the reaction path. In general, it will instead hit one specific point along a “line” or “segment” of the 3N − 8 dimensional IS spanning an infinite number of CoIn structures that may include the MECI (Fig. 5f). This dimensionality issue needs to be considered when discussing the fate of the entire population of R* molecules as the one generated by a laser pulse experiment or even by the incoherent light employed in regular photochemical experiments. Thus the decay along an IS segment is a qualitatively distinctive feature of barrierless photochemical reactions not found in the nuclear motion occurring during a thermal reaction where the reactant molecule R moving towards the TS region will usually pass in the vicinity of a single isolated TS point.48 We will now discuss how such features impact the observed reaction kinetics.
1.3 Kinetic control in ultrafast photochemistry
It appears that although there are qualitative differences between TSs and CoIns in the elementary reaction schemes discussed above, the latter can still be regarded as the ES analogue of TSs.20 The aim of this section is to draw parallels between kinetic control in both types of reactions. As mentioned above, in a thermal reaction occurring under kinetic control the yield of product P with respect to competing product (P′) may be increased by lowering the activation barrier at the TS connecting R to P (Fig. 5d). In other words, the TS should be lowered in energy with respect to the TSs controlling other competing reaction paths ultimately leading to a high reaction selectivity.52 Such a rational design relies heavily on the understanding of the geometrical structure and energetics of the corresponding TSs.53 Indeed, chemists have learned to take control of kinetics through the electronic and steric tuning of TSs. Once the wanted TS structure is established and its energy relative to R is estimated, transition state theory (i.e. the TS is regarded as a species in equilibrium with R), amongst other basic principles, allow chemists to predict reaction rates and design thermal chemical reactivity and selectivity.54,55Since there is no activation barrier in the photochemical reaction path of Fig. 5b featuring a peaked CoIn (see Fig. 4 right), the selectivity of the products must be determined by different rules as the decay point is entered in a far-from-equilibrium regime where both the geometry and the velocity at the decay point contribute to determine the reaction outcome. Such geometry and velocity must impact the quantum yields (QYs) of the different products with respect to the number of generated ES reactant molecules R* (i.e. the number of absorbed photons).
A practical complication that has to be considered for kinetic control in photochemical reactions is that the photoproduct might absorb at the irradiation wavelength as well, resulting in a photostationary state.56 In many cases, however, the absorption bands of the photoproduct and reactant are well separated in energy, such as in certain molecular switches or photochromic compounds. In such a kinetically controlled regime it is, exclusively, the photochemical QY of a single transformation that determines the observed photoproduct and, therefore, reaction selectivity.
Whenever a photochemical reaction proceeds via a barrierless ES path through a single CoIn point (Fig. 5b), the QY is determined by the branching ratio to the possible products, which should then be controlled to obtain higher yields and selectivities.57 In the elementary case of Fig. 5b (or Fig. 4 right), this is determined in a far-from-equilibrium regime by the corresponding ES nuclear dynamics that impact the geometry and velocity at the decay point responsible for branching.58 The complexity of the dynamics may be further increased by the presence of multiple chemically distinct (i.e. leading to different photoproducts) energetically accessible CoIns (Fig. 5e) each one featuring different branching ratios.59
Finally, and most relevant for the present contribution, the dynamics of an elementary photoreaction is made dramatically more complex by the possibility (see Fig. 5f for a related description) that the branching itself must be a function of the position of the CoIn along the IS space. In fact, when the molecular population of R* decays not at a single CoIn point, but along an IS segment, each decay point will be associated with a different CoIn geometry, BP orientation and velocities along the BPs. Thus, the final observed selectivity will be the result of an entire range of different branching contributions. We will see how the discussion of this situation requires the anticipated expansion of the basis used to discuss the decay event from (usually) one reactive mode to a set (two or more) of modes.
1.4 Mechanistic principles for ultrafast photochemistry
This review focuses on the possibility to establish mechanistic principles useful to explain, classify and predict the outcome of ultrafast photochemical reactions. Ideally, such principles should inform the chemist on how changes in the chromophore structure and environment affect reaction selectivity and quantum efficiency. In Section 2 we start by discussing the mechanistic principles implied by Landau–Zener (LZ) theory which describes decay at an AC or CoIn considering a one-mode reaction coordinate with constant velocity at the crossing.60 This theory will be applied to a one-mode ultrafast elementary photochemical reaction of Fig. 5b. In this “standard” model a single CoIn is entered along a single direction Qx of the BP (Fig. 3d), which is bifurcating and therefore involves only competitive R and P formation (no competing product P′ will be considered).In many cases predicting photochemical trends with LZ-based guidelines fails owing to the one-mode nature of the model (Section 2.3). Therefore, more sophisticated principles that incorporate the multi-mode nature of photochemical reactions are highly desired. In Section 3 we discuss how the synchronization of vibrational modes with a selected multi-mode basis controls the kinetics and QY (i.e. the P/R* ratio) of an ultrafast photochemical event, hence proposing a key mechanistic principle based on the “'phase matching” of those modes.
As detailed below, this qualitative principle relies on the assumption that the light-triggered nuclear motion maintains a certain level of nuclear coherence. The phase matching between different molecular modes will be regarded as a mechanistic principle of far-from-equilibrium reactivity where the statistical distribution of velocities along the direction of bond formation plays the same role as the transition vector for a barrier controlled chemical reaction starting from a thermally equilibrated reactant.
Notice that, while the presented mechanistic principles form part of a qualitative theory of ultrafast reactivity, such theory shall not be confused with the quantitative theory used to numerically simulate photochemical reactions: nonadiabatic dynamics. In fact, as apparent from the reading of the present work, it is the analysis of nonadiabatic dynamics simulations carried out using suitable computer implementations of nonadiabatic dynamics and atomistic models that often drives the formulation of mechanistic principles.
2. The standard Landau–Zener model: focus on single CoIn structures
The development of Landau–Zener (LZ) theory goes back to the 1930s, where Landau and Zener were independently aiming to understand and calculate atomic collisions.61,62 In their semi-classical one-mode approach, they treated the nuclei classically, introducing externally controlled parameters to deal with nonadiabatic effects occurring during such events. Even though LZ theory is already 90 years old, it is still being applied widely to provide first estimates of nonadiabatic transition probabilities in both complex and simple systems.60,63LZ theory considers a two-state model involving one nuclear coordinate Q to calculate the probability P to change adiabatic state (eqn (5)), i.e., decay to the lower state. For a complete derivation, the reader is referred to ref. 60. We only present here the result and the most important assumptions. In the following discussion, we make frequent use of definitions already set out in Section 1.
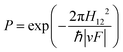 | (5) |
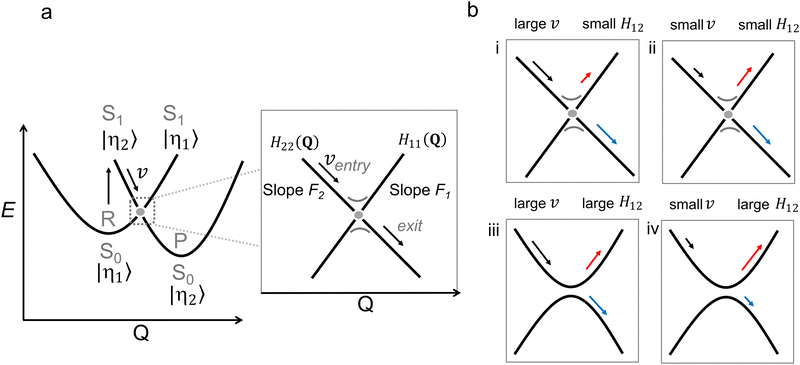 | ||
| Fig. 6 (a) Diabatic representation of a photochemical reaction according to the Landau Zener model. The diabatic parabola are approximated by straight lines close to the crossing region, as shown in the inset. In this inset, the relevant parameters for the Landau Zener formula (eqn (5)) are shown as well. (b) Four situations (labelled i–iv) of a photochemical reaction illustrating its dependence on the velocity and the coupling between the diabatic states H12. The blue and red arrows indicate the probability to switch adiabatic PES (large P) and to stay on the adiabatic PES (small P), respectively. | ||
A key result from the LZ formula is that it relates v to the nonadiabatic decay probability. As demonstrated in panels i and ii in Fig. 6b, P increases when the velocity at the point of (near) degeneracy is larger, i.e., the population continues moving on the same diabatic state after passing the crossing with an exit direction identical to the entry direction.64 This greater velocity could be due to a steeper slope on the ES PES (F is a topographical factor), which implies faster molecular motion (v is a dynamical factor).
The qualitative interpretation of LZ theory, namely the direct proportionality between the nuclear velocity or slope along a diabatic PES and the probability of decaying maintaining the nuclear velocity direction (i.e. assuming one entry and exit direction of motion), can be seen as a fundamental principle valid along the nuclear mode Q intercepting a specific CoIn. This is considered the “standard” LZ model applied to MECI points. Such interpretation is not concerned with the complete nuclear trajectory Q(t) of a molecule, which is dependent on both topographical aspects,65–67 as well as dynamical aspects inherent to the far-from-equilibrium nature of ultrafast photochemical reactions,20,48,68 (e.g. how the photoexcited reactant reaches the CoIn region, which of the infinite number of CoIn is actually reached or whether the population is split before reaching the CoIn). As this trajectory consists of a set of molecular modes, application of the LZ formula may be non-trivial as the choice of Q may be ambiguous for curved reaction coordinates (e.g. when obtained by interpolating reactant and MECI geometries) and a full reaction mapping is rarely carried out due to its relatively high computational cost.
P may be statistically reinterpreted as the fraction of trajectories switching to another adiabatic state (e.g. the fraction hopping from the S1 to S0 PES). Alternatively, we will make frequent use of the term vibrational wavepacket or, simply, wavepacket to describe the temporal evolution of a compact ES population of molecules featuring phased nuclear motion. The reader is referred to Section 3.1 for a more detailed description of vibrational wavepackets and their implied in-phase nuclear motion (vibrational coherence).69 The (center of the) wavepacket moves along a PES with a particular direction and magnitude of velocity, which correlates, similar to the trajectory description, to the efficiency of nonadiabatic decay according to eqn (5).
For barrierless photochemical reactions (such as those in Fig. 6b) v inversely correlates to the experimentally observable ES lifetime τ. For this reason, the relation between v and P has been used to explain a correlation between τ and QY.70,71 This is because, in a one-mode interpretation, if the evolution of the ES wavepacket is such that it points to the CoIn and then, without changing direction, to the photoproduct, a velocity increase leads to a QY enhancement.72 Hence, a larger velocity of the ES wavepacket towards the CoIn, or a shorter experimental τ, correlates with a higher photochemical QY. Many researchers have proposed the validity of such an inverse relation between lifetime and photochemical QY, such as for the reduced QY in isorhodopsin (QY = 0.22, τ = 600 fs) compared to rhodopsin (QY = 0.67, τ = 200 fs),73 or the smaller QY for reverse photoisomerization in overcrowded alkene molecular motors (QY = 0.40, τ = 1770 fs) compared to the forward reaction (QY = 0.92, τ = 1400 fs).74 Below we will see how such a relationship may fail in a number of cases.
2.1 Excited state and CoIn topographies
In this section, we focus on how ES PES and CoIn topographies affect photochemistry within the framework of the standard LZ model by consideration of the entry–exit direction and the magnitude of nuclear velocity v. However, as also mentioned above, it will become clear that applying the LZ formula is often not trivial due to the topographical complexity of the ES PES and CoIn and, therefore, the difficulty in obtaining information on the velocity magnitude and direction at the decay point. The LZ-related models that tackle the relations between ES PES and CoIn topographies and nonadiabatic decay rates can be found in the literature.68,75–80 However, here we summarize their main results by considering six topographical factors (Table 1).| Topographical factor | LZ factor | Illustration | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a If a CoIn becomes energetically inaccessible, the entry direction might be changed to another CoIn. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I ES reaction path with vs. without barrier | Entry direction | Fig. 5c and 9d | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| II Number of independent GS relaxation paths departing near CoIn | Exit direction | Fig. 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| III Local CoIn topographies | Velocity and entry direction | Fig. 7–9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| IV Location and energy of CoIn along the reaction path | Velocitya | Fig. 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V ES Slope on the reaction path to CoIn | Velocity | Fig. 5e and 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| VI Electronic mixing with higher states | Entry direction and velocity | Fig. 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sx = s·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) | (6) |
| sy = s·ŷ | (7) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and ŷ vectors are the orthogonalized and normalized analogues of the Q1 and Q2 vectors we introduced in eqn (3).85 The seam coordinate s is the average gradient of the two states (here labelled as A and B)
and ŷ vectors are the orthogonalized and normalized analogues of the Q1 and Q2 vectors we introduced in eqn (3).85 The seam coordinate s is the average gradient of the two states (here labelled as A and B)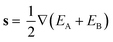 | (8) |
 | (9) |
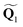 and
and 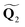 :
: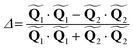 | (10) |
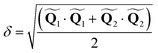 | (11) |
Switching to polar coordinates the energies of the two states, where the energy of the CoIn EX is placed at the origin, are
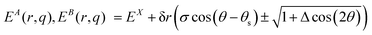 | (12) |
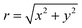 and
and 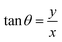 are the polar coordinates in the BP and Δ and δ are now defined as
are the polar coordinates in the BP and Δ and δ are now defined as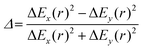 | (13) |
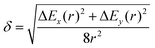 | (14) |
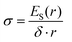 | (15) |
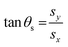 | (16) |
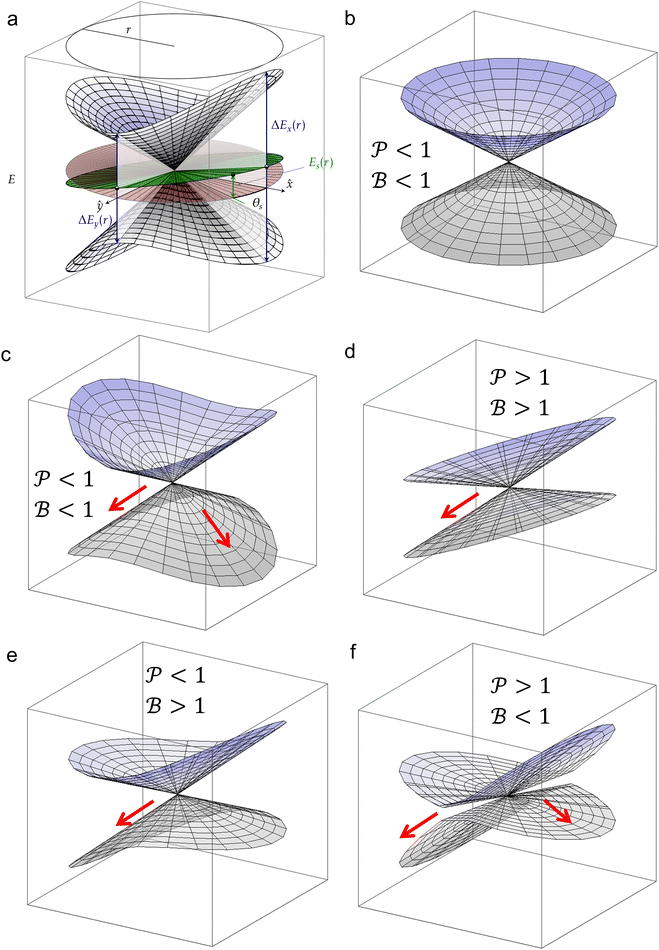 | ||
Fig. 7 (a) Graphical representation of PESs around a CoIn in the branching plane, defined by ˆ}{\mathbf{y}}$--> vectors, which are the orthogonalized and normalized analogues of the Q1 and Q2 vectors, respectively. The topographical CoIn classification (see text, and Table 1) is based on the characteristic parameters and variables shown in this figure. At a distance r from the intersection, the energy differences between the two states along the x and y coordinates are ΔEx(r) and ΔEy(r), respectively. The pitch δ and ellipticity parameter Δ are related to their sum and difference, respectively. The green plane is the average energy, which is tilted with respect to the xy (red) plane. The maximum average energy at a given r, ES(r), is defined at the angle θS, the direction of tilt. The relative tilt σ is defined by both ES(r) and δ. Figure (b)–(f) show different CoIn topographies as defined by the  descriptors, which are dependent on the parameters Δ, σ and θS. For all graphics θS was set to 6 rad and δ to 1. The latter is a scaling factor and does not affect the values of descriptors, which are dependent on the parameters Δ, σ and θS. For all graphics θS was set to 6 rad and δ to 1. The latter is a scaling factor and does not affect the values of  . Adapted from ref. 81, licensed under a Creative Commons Attribution 4.0 International License. (b) peaked/bifurcating (Δ = 0.01, σ = 0). (c) peaked/bifurcating (Δ = 0.5, σ = 0.01). (d) sloped/single-path (Δ = 0.01, σ = 1.5). (e) peaked/single-path (Δ = 0.5, σ = 0.7). (f) sloped/bifurcating (Δ = 0.99, σ = 1). . Adapted from ref. 81, licensed under a Creative Commons Attribution 4.0 International License. (b) peaked/bifurcating (Δ = 0.01, σ = 0). (c) peaked/bifurcating (Δ = 0.5, σ = 0.01). (d) sloped/single-path (Δ = 0.01, σ = 1.5). (e) peaked/single-path (Δ = 0.5, σ = 0.7). (f) sloped/bifurcating (Δ = 0.99, σ = 1). | ||
The motivation for introducing the parameters Δ, σ and θs is that they can be rearranged into two parameters,  , which allow for a complete CoIn characterization (provided that Δ ≥ 0) by distinguishing between peaked or sloped, as well as between bifurcating or single-path,80,81,87 respectively:
, which allow for a complete CoIn characterization (provided that Δ ≥ 0) by distinguishing between peaked or sloped, as well as between bifurcating or single-path,80,81,87 respectively:
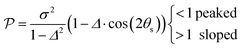 | (17) |
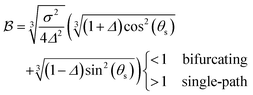 | (18) |
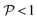 and
and 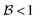 , this situation represents a peaked bifurcating CoIn. The bifurcation is more obvious in the elliptical (peaked) CoIn from Fig. 7c, having two distinct preferential relaxation paths from the CoIn as determined by the larger slopes along those paths. The CoIns of Fig. 7b and c are peaked as they are a local minimum (but not a stationary point as the gradient is discontinuous and nonvanishing at the CoIn) of the energetically higher PES in the BP.
, this situation represents a peaked bifurcating CoIn. The bifurcation is more obvious in the elliptical (peaked) CoIn from Fig. 7c, having two distinct preferential relaxation paths from the CoIn as determined by the larger slopes along those paths. The CoIns of Fig. 7b and c are peaked as they are a local minimum (but not a stationary point as the gradient is discontinuous and nonvanishing at the CoIn) of the energetically higher PES in the BP.
When σ is increased to 1.5 while setting Δ again to 0.01, we obtain a sloped single-path CoIn (both 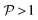 and
and 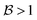 ), as shown in Fig. 7d. In this case there is a true local minimum (i.e. a point where the gradient of the energetically higher PES with respect to the nuclear coordinates is zero) that is lower than the CoIn but located in its vicinity (Fig. 2b).45,88 Atchity et al. further define an intermediate situation, in which the energetically higher PES has a zero slope on one side of the CoIn and the energetically lower PES has a zero slope on the other side (for simplicity purposes, this situation is not further illustrated).45 The relevance of the distinction between peaked and sloped CoIns for photochemical reactions will be discussed below.
), as shown in Fig. 7d. In this case there is a true local minimum (i.e. a point where the gradient of the energetically higher PES with respect to the nuclear coordinates is zero) that is lower than the CoIn but located in its vicinity (Fig. 2b).45,88 Atchity et al. further define an intermediate situation, in which the energetically higher PES has a zero slope on one side of the CoIn and the energetically lower PES has a zero slope on the other side (for simplicity purposes, this situation is not further illustrated).45 The relevance of the distinction between peaked and sloped CoIns for photochemical reactions will be discussed below.
From the conditions set out in (17) and (18) it can be established that a CoIn is sloped for σ > √2 and peaked for σ < √2. Secondly, a CoIn is bifurcating when σ < Δ. If now instead both σ is increased to 0.7 and Δ is increased to 0.5, i.e. both the tilt and ellipticity are increased with respect to Fig. 7b, a peaked single-path CoIn is obtained (Fig. 7e). Finally, a sloped CoIn that is also bifurcating is only possible for Δ > 1/3, which is demonstrated in Fig. 7f. As this is not a common situation, sloped CoIns are often associated with a single-path on the GS (an example is shown in (Fig. 8b)), implying IC and therefore regeneration of the reactant.89 Therefore, based on this topographical difference, peaked CoIns are usually more photoreactive (i.e. higher photochemical QY) than sloped CoIns, which is why they are often referred to as photochemical funnels.69,90
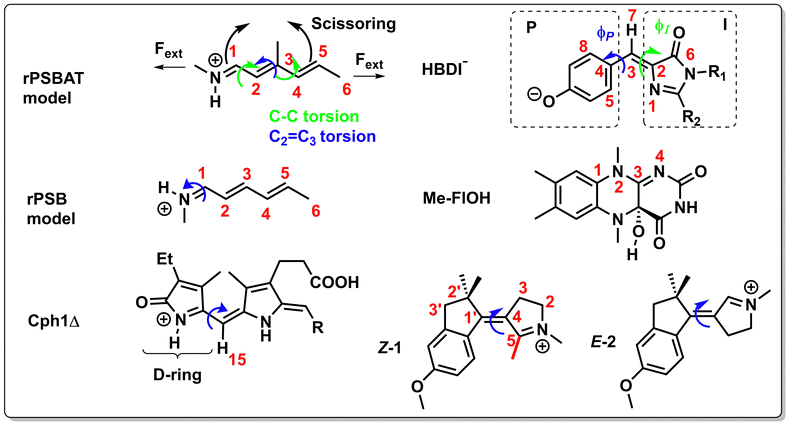
For instance, through ab initio calculations it has been proposed that the distinction in peaked/sloped topography could explain the selective photoisomerization at the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 bond of an abridged model of the protonated Schiff base of all-trans retinal, rPSBAT, (Section 3.1). The local CoIn dynamics, far from the FC-point, at both type of CoIns is illustrated in Fig. 8. Isomerization around the C11
C12 bond of an abridged model of the protonated Schiff base of all-trans retinal, rPSBAT, (Section 3.1). The local CoIn dynamics, far from the FC-point, at both type of CoIns is illustrated in Fig. 8. Isomerization around the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 bond is associated with a peaked CoIn, whereas isomerization around the C13
C12 bond is associated with a peaked CoIn, whereas isomerization around the C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14 bond corresponds to a sloped CoIn, which is associated with a lower nonadiabatic efficiency and is therefore outcompeted by the ultrafast C11
C14 bond corresponds to a sloped CoIn, which is associated with a lower nonadiabatic efficiency and is therefore outcompeted by the ultrafast C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 isomerization.91 The photochemical reaction path of the latter in fact proceeds, with higher probability, through an AC as shown by the one-dimensional slice along the torsional reaction coordinate. The same distinction has been used to explain the faster photoisomerization of a rPSB11 model in aqueous solution (peaked) compared to gas-phase (sloped).51
C12 isomerization.91 The photochemical reaction path of the latter in fact proceeds, with higher probability, through an AC as shown by the one-dimensional slice along the torsional reaction coordinate. The same distinction has been used to explain the faster photoisomerization of a rPSB11 model in aqueous solution (peaked) compared to gas-phase (sloped).51
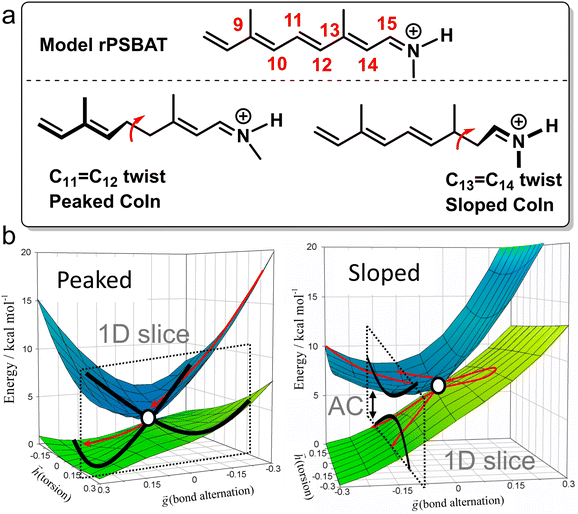 | ||
Fig. 8 Photoisomerization of model rPSBAT through two different routes. (a) Chemical structures of model rPSBAT and the MECIs corresponding to isomerization at the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 bond and the C13 C12 bond and the C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14 bond. The labelling of the carbon framework is chosen to be consistent with the photoisomerization of the complete chromophore, rPSB11, discussed in Section 3. (b) Adiabatic PESs involved for both reactions. Left: Isomerization at the C11 C14 bond. The labelling of the carbon framework is chosen to be consistent with the photoisomerization of the complete chromophore, rPSB11, discussed in Section 3. (b) Adiabatic PESs involved for both reactions. Left: Isomerization at the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 bond, corresponding to a bifurcating/peaked CoIn. Right: Isomerization at the C13 C12 bond, corresponding to a bifurcating/peaked CoIn. Right: Isomerization at the C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14 bond, corresponding to a bifurcating/sloped CoIn. Adiabatic PESs are computed at the CASSCF level, showing the energy as a function of the g and h vectors, which are the analogues of Q1 and Q2, respectively. The red arrows indicate the path of the ES wavepacket. Note the up-funneling process around the sloped CoIn.91 When slicing these two-dimensional plots along one reaction coordinate, the curve representation analogues of Fig. 1 are retrieved. Adapted with permission from ref. 91. Copyright (2002) National Academy of Sciences, USA. C14 bond, corresponding to a bifurcating/sloped CoIn. Adiabatic PESs are computed at the CASSCF level, showing the energy as a function of the g and h vectors, which are the analogues of Q1 and Q2, respectively. The red arrows indicate the path of the ES wavepacket. Note the up-funneling process around the sloped CoIn.91 When slicing these two-dimensional plots along one reaction coordinate, the curve representation analogues of Fig. 1 are retrieved. Adapted with permission from ref. 91. Copyright (2002) National Academy of Sciences, USA. | ||
In general, peaked CoIns are associated with larger nonadiabatic transfer efficiencies compared to sloped CoIns, which Malhado et al. have proposed is not a result of their inherent topographical differences but due to dynamical factors.68 Because a peaked CoIn represents a local minimum on the ES PES, the wavepacket approaches the CoIn with high nuclear velocity (eqn (5)) as the ES PES steers the wavepacket in the right downhill direction (Fig. 9a and b). In contrast, as there are uphill ES paths towards a sloped CoIn, the wavepacket might miss the CoIn as the ES PES steers the wavepacket away from it. Additionally, in peaked CoIns nonadiabatic transfer is likely to occur without any wavepacket fragmentation as the transition takes place in the first passage, which further enhances the nonadiabatic transfer efficiency due to the conservation of coherence of the ES population as we will more precisely describe in Section 3.1.68
 | ||
| Fig. 9 Different CoIn and ES topographies, as classified in Table 1. Graphs a–d illustrate cases where the location and energy of the CoIn is modulated (factor IV), targeting mainly the nuclear velocity for graphs a–c and the entry direction for graph d. Graph e illustrates a case where the ES slope towards the CoIn is modulated (factor V), targeting the nuclear velocity. (a) peaked reactant-like CoIn. (b) Shifting the product parabola with respect to the reactant parabola up results in a peaked product-like CoIn. The relative position of the CoIn with respect to the FC-region (R*) results in different initial nuclear velocities and therefore product QY, as explained by the Hammond postulate. (c) Shifting the product parabola with respect to the reactant parabola to the left results in a sloped CoIn, demonstrating the intimate connection between factors IV and III. Note that sloped CoIns typically only result in regeneration of reactant. (d) the energetic position of CoIn with respect to CoIn’ controls the direction of the photochemical path and therefore the type of CoIn (seam) that is approached. The energetic accessibility of the two CoIns may be controlled by an ES activation barrier (Fig. 5c), demonstrating the intimate connection between factors IV and I. This represents an important design rule for topographical substituent effects (Section 2.2) (e) an increasing ES slope results in higher nuclear velocity towards the CoIn, which may be caused by a protein environment (Section 3.1). The increasing ES slope may favor the entry direction towards one CoIn compared to another (Fig. 5e). | ||
Due to the smaller nuclear velocity that is generally associated with a ES wavepacket reaching a sloped CoIn (Fig. 9c), irreversible passage to the GS PES is not guaranteed as such a wavepacket can travel back along the ES PES (a process called “up-funneling”, which reduces coherence), which manifests itself as oscillations between the ES and GS PESs near the sloped CoIn (see Fig. 8b).48,91–94 Nevertheless, even if the sloped CoIn is reached with sufficient energy, this process may cause wavepacket fragmentation (i.e. partial loss of coherence), which itself decreases nuclear velocity.92,95
As a result of the slower nuclear dynamics and more significant loss of coherence, nonadiabatic transfer at sloped CoIns might occur under near-equilibrium conditions, where (partial) intramolecular vibrational energy redistribution has taken place.96 In contrast, far-from-equilibrium conditions (fast nuclear velocity and coherence) are often maintained for peaked CoIns due to the steep gradient of the ES PES and therefore dominate the photochemistry.69 In other words, photochemical reactions approaching a peaked CoIn are more prone to memory of the initial conditions imposed by the photoexcitation on other regions of the ES PES. One should therefore keep in mind that differences in photochemical reactivity between peaked and sloped CoIns are not only controlled by their local structure but also by these far-from-equilibrium conditions, as well as other topographical factors (Table 1).
QM/MM based nonadiabatic nuclear trajectories demonstrated a key role for the protein environment in shaping the ES PES of rPSB11 (Fig. 10). In methanol solution the ES PES is relatively flat due to significant S2/S1 mixing, resulting in slow reaction dynamics via an energetically high CoIn.99 Additionally, the flat ES PES reduces the coherence (both at the population and single-molecule level, Section 3.1.1), thus changing the entry direction. However, when rPSB11 is embedded in a protein environment, as in rhodopsin, the state mixing is reduced resulting in faster downhill progression through a lower-lying CoIn and eventually an ultrafast photoreaction. Additionally, the coherence on such a steep surface is preserved to a greater degree, increasing the velocity as well.68 Interestingly, the state mixing in microbial rhodopsin is intermediate between these two situations, resulting in an intermediate ES lifetime. Even in the reference bovine rhodopsin and despite the diminished S2/S1 mixing due to the protein environment, there is still some degree of decoherence in the first few tens of femtoseconds as a result of the non-zero probability for wavepackets generated on the S1 PES to be transferred to the S2 PES (Section 3.1).100
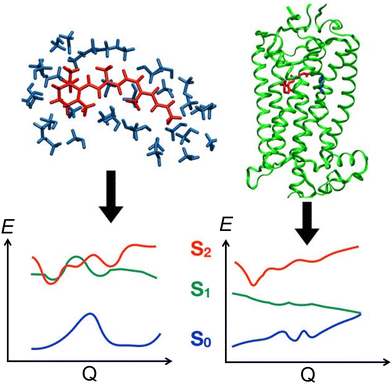 | ||
| Fig. 10 Schematic S2, S1 and S0 PESs for rPSB11 photoisomerization in methanol (left) and in an opsin environment (right).99 In methanol solution the strong S2/S1 mixing results in flat ES PESs, which reduces the coherence and nuclear velocity. The opsin environment reduces this mixing significantly, resulting in steep ES slopes and therefore a high degree of coherence and a large nuclear velocity. Adapted with permission from ref. 99. Copyright 2017 American Chemical Society. | ||
2.2 Effects of chemical substitution
Above we have seen that according to the LZ picture, ultrafast photochemistry is controlled by the direction and velocity with which the reacting system enters the BP of the CoIn that mediates decay to the GS. We have also seen that such direction/velocity can be affected by different topographies (factors I–VI, defined in Table 1) of the PES along the BP making the reactive event complex.We now discuss the effect of chemical substitution on photochemical reactions by considering these topographical factors, still within the framework of decay at a single reference CoIn (e.g. a MECI). As the standard LZ model applies to regions only in the vicinity of the CoIn, we focus on chemical substituents that leave the spectroscopic properties of the chromophore largely unperturbed (i.e., they will not alter the FC-state), but primarily alter the PES along the BP. While chemists often use chemical substitution as a strategy for controlling GS reactivity through modulation of an activation barrier (Fig. 5a), it is less obvious how to apply the same strategy to control reactivity in a (nonstatistical) photochemical process.101 Topographical effects of CoIns caused by strong light-matter coupling in optical cavities are not discussed in this review paper, but have been demonstrated to significantly impact nonradiative decay rates102 and singlet fission rates.103
Schuurman and Stolow distinguished between potential (meaning potential energy. However, in this text this is referred to as topographical for consistency purposes) and inertial substituent effects, where the first primarily controls branching of different ES reaction paths by tuning topographical factors (I–VI), and the second selectively alters the nuclear velocity of a relevant normal mode without modifying the PES topographies in the CoIn region.20 The latter is achieved through addition of bulky substituents, such as methyl or t-Bu, which by first approximation leaves the electronic structure of the molecule, and therefore the force constant in the harmonic oscillator model, unperturbed. As we have discussed above, within the framework of the standard LZ model, an enhancement of nuclear velocity of the mode describing the reaction coordinate results in an enhanced decay probability and photoproduct formation. We will now see how certain substituent effects reveal a non-applicability of the one-mode mechanistic picture of ultrafast photochemical reactions defined above and, therefore, of the LZ treatment.
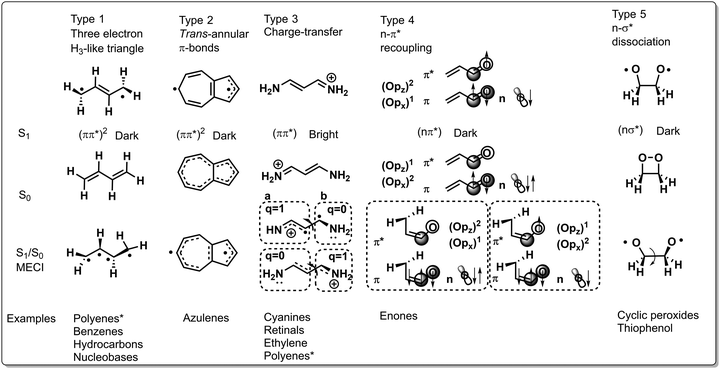
Many of the CoIns discovered in organic photochemistry and characterized via the calculation of the MECI, BP vectors and local PES topographies may be assigned to these five types, yet some situations have been documented that reveal the limitations of such a classification. However, most reported CoIns are of type 1 and 3 and these types are therefore discussed in depth in the following. Fig. 11 displays, schematically, the S1/S0 MECI structures of all types, along with their equilibrium S1 and S0 geometries, as well as the type of photochemical reactions that they may control. The relevant geometrical rearrangements found in these MECI structures typically involve twisting, stretching and pyramidalization. The corresponding BP vectors are instead not discussed systematically here.
2.2.1.1 Type 1 CoIn. In this type the electronic structure is such that there are three weakly coupled unpaired electrons like in the well-known CoIn of H3; an elementary CoIn that has the geometry of an equilateral triangle.10,11,106 Therefore, in a molecule with an even number of “reacting” electrons, type 1 CoIn features a spectator unpaired electron that may be located in a fragment π-orbital. In butadiene the spectroscopically bright ππ* state (single HOMO → LUMO excitation of 1Bu symmetry in MO language) is dominated by CT (closed-shell) character and is energetically slightly higher than the dark (ππ*)2 state (multiconfigurational state of 1Ag symmetry involving double HOMO → LUMO excitation, as well as HOMO−1 → LUMO and HOMO → LUMO+1 excitation) that is dominated by a covalent (diradical) character.107–111 Therefore, after photoexcitation to the ππ* state, populating the (ππ*)2 state through a S2(ππ*)/S1(ππ*)2 CoIn is facile. As will be shown below, both S1(ππ*)2/S0 and S1(ππ*)/S0 CoIns contribute to the ES decay dynamics of butadiene due to their energetic proximity. Focussing on the first for the moment, distinct spin pairing in the (ππ*)2 state with respect to the GS facilitates a photochemical reaction. The S1(ππ*)2/S0 CoIn then directs via the Q1 and Q2 vectors of the BP the repairing of the electron spins in a specific fashion that, in turn, determines which photoproducts will be formed. For example, BP vectors bringing two weakly interacting electrons located on different unbound carbon atoms of type 1 CoIn closer, could lead to spin pairing between these atoms, resulting in the formation of a cyclopropyl radical as a primary reactive photoproduct.10 The S1(ππ*)2/S0 type CoIn may lead to the simultaneous formation of two products (see Fig. 4 right) as it happens, for instance, in the case of hexatriene ring closure.112 Type 1 CoIns control (electrocyclic) ring opening and closure reactions in polyene systems (Schemes 2 and 3) and nucleobases (Fig. 18, Section 3.3), as well as double bond photoisomerization reactions via a hula-twist mechanism, discovered in phytochromes and the green fluorescent protein (Section 3.2).
2.2.1.2 Type 2 CoIn. Due to the rigidity of azulenes in type 2 CoIns, the S1/S0 MECI is primarily characterized by stretching coordinates.14 This CoIn may be rationalized by considering that S1 is a biradical structure with a trans-annular π-bond, whereas S0 only has a trans-annular σ-bond. Hence, compressing the S0 equilibrium geometry along that bond lifts the S0 PES, yet decreases the S1 PES, reaching the S1/S0 MECI.
2.2.1.3 Type 3 CoIn. The photoisomerization of rPSB11,113 related retinal chromophores114 and cyanine dyes115 are controlled by a type 3 CoIn, in which the lowest ES is a bright ππ* state (single HOMO → LUMO excitation) of CT character. The S1(ππ*)/S0 MECI of the latter will be discussed in detail. It appears around half-way through the isomerization coordinate, in which the two halves of the twisted molecule (indicated with fragment a and b in Fig. 11) differ by a charge of one electron. Hence, such a CoIn is similar to a twisted intramolecular charge transfer (TICT) state.116 The degeneracy of the S0 and S1 states at this twisted geometry, and hence the occurrence of the CoIn, can be rationalized by their heterosymmetric biradicaloid nature.90 The frontier π-orbitals at fragments a and b are weakly interacting and degenerate, which is why regardless of the location of the positive charge, the bottom and top resonance structures are energetically degenerate. Other than the extensively discussed double bond photoisomerization of rhodopsin (Fig. 10 and Section 3.1.2) and rhodopsin models (Fig. 8 and Section 3.1.4), type 3 CoIns control double bond photoisomerization of ethylene (Scheme 1), polyenes (Scheme 3) together with type 1 CoIns, the isolated chromophore of the green fluorescent protein (Fig. 17, Section 3.2), as well as the photochemistry of the ring-locked Me-FlOH, N-alkylated indanylidene–pyrroline biomimetic switch (Scheme 7, Section 3.2) and nucleobases (Fig. 18, Section 3.3).
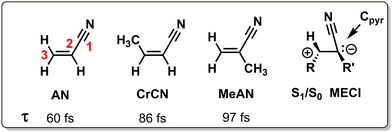 | ||
| Scheme 1 Chemical structures of acrylonitrile (AN), cis-3-metharylonitrile (CrCN), cis-2-metharylonitrile (MeAN) and a schematic geometrical structure of the S1/S0 MECI. Also indicated are their ES lifetimes τ as measured with TRPES.117 | ||
2.2.1.4 Type 4 CoIn. The type 4 CoIn involves a S1(nπ*)/S0 CoIn, which is rationalized by the orbital occupation of n, π and π* and the associated atomic orbitals.118 The in-plane Opx (out-of-plane Opz) orbital is doubly (singly) occupied in S0, but becomes singly (doubly) occupied in S1(nπ*), which is a diradical state not due to a double excitation (as in Type 1 and 2) but due to the single occupation of two orthogonal atomic orbitals Opx and Cpz. These (Opz)2(Opx)1 and (Opz)1(Opx)2 configurations become degenerate when the carbonyl Cpz is weakly interacting with Opz, but strong with an adjacent carbon atom. The twisting of the terminal methylene group facilitates this stronger coupling between the two central carbon atoms, resulting in double-bond character. At the same time, this motion reduces the coupling with the carbonyl oxygen, resulting in a single bond. Type 4 CoIns control the photochemistry of α,β-enones (Fig. 12), involving double bond isomerization and electrocyclic ring-closure.
2.2.1.5 Type 5 CoIn. Lastly, a type 5 CoIn occurs in molecules with low-lying nσ* states. Population of the antibonding σ* orbital results in a large degree of bond stretching, which is why photodissociation reactions are common for type 5 CoIns (see Scheme 5 and related discussion). Furthermore, type 5 CoIns have been identified in chemiluminescent reactions, where thermal decomposition of a strained ring results in an excited state species that luminesces.119–122 For instance, the ring strain in 1,2-dioxetane causes significant O–O bond stretching, resulting in an energetically low-lying σ* orbital which may be populated by transferring an electron from an oxygen located n-orbital. Next to the O–O stretching motion creating a biradical, 1,2-dioxetane decomposition involves an asynchronous C–C stretch and O–C–C–O torsional motion as characterized by the S1(nσ*)/S0 MECI.
Since the methyl group appears to be at the same carbon atom where the CN group is bound in MeAN, the pyramidalization motion is strongly hindered due to the destabilization of the forming lone pair (anionic centre) on that carbon, explaining the longer lifetime. This is a topographical effect and not an inertial effect as the relative energetic position of one CoIn is modulated, biasing the wavepacket towards one specific CoIn along the corresponding BP direction. In fact, one can assume that an inertial effect, due to the difference between the H and CH3 masses, would not have a large effect on the pyramidalization at C3 when comparing the AN and MeAN cases, thus resulting in similar lifetimes. Finally, the same topographical (substituent) effect is consistent with the standard LZ model as a decrease in nuclear velocity in the BP correlates to a less efficient decay.
A similar joint spectroscopy-theory study on methyl substituted ethylene derivatives showed how increasing substitution stabilized the Rydberg π3s state, resulting in an enhanced ES barrier to reach the π3s/ππ* CoIn, which is intrinsically not photoreactive, but populates the reactive ππ* state which dominates the photochemistry of short π-systems.98 This would again be a topographical effect with a reaction scheme more similar to the one in the left diagram of Fig. 10.
Although the two examples above focus on how chemical substitution affects the nonradiative decay rate by topographical effects, chemical substitutions may also completely alter the photochemistry by enforcing nonradiative decay through alternative CoIns (see Fig. 5e and Scheme 2), as demonstrated by quantum chemical calculations on s-cis-butadiene derivatives. After photoexcitation to the spectroscopically bright S2(ππ*) state, both s-cis-butadiene and “tBu-1” follow similar decay dynamics through a S2(ππ*)/S1(ππ*)2 CoIn but follow different paths approaching the type 1 CoIn. Whereas the decay of S1(ππ*)2 in s-cis-butadiene is dominated by a fully asymmetric out-of-plane motion,123 the bulky tBu groups force (possibly also via an inertial effect, see below) a concerted synchronous conrotatory motion of the two terminal CH2 groups that results in cyclopropane formation, followed by an additional ring closure yielding the extremely strained tBu-2.124 In another study, the photoisomerization dynamics and selectivity of s-cis-butadiene was investigated upon CF3 substitution.125
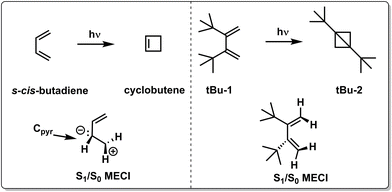 | ||
| Scheme 2 Chemical structures and schematic geometrical structures of S1/S0 MECIs of reactants and photoproducts observed for the photochemistry of s-cis-butadiene and its di-tBu substituted counterpart “tBu-1”.123 | ||
Levine and Martinéz demonstrated the relevance of both type 1 (C2Tr) and type 3 (H1Br) CoIns in the ES dynamics of s-trans-butadiene using Ab initio Multiple Spawning (AIMS) simulations (Scheme 3).126 Following advances in simulations of time-resolved X-ray absorption spectra capturing the evolving electronic wavefunction surrounding the IS,127 Schuurman and co-workers showed a preference for decaying via the transoid C2Tr channel relative to the CT H1Br channel.128 The branching between these two channels may be tuned by electronic tuning with the CN group (Fig. 5e).129 Although it leaves the energy of the C2Tr MECI relatively unaltered, the energies of the CT type MECIs are significantly dependent on the position of the CN group, as determined by single-excitation multireference configuration interaction (MR-CIS) calculations. Similar to the acrylonitrile derivatives of Scheme 1, CN substitution favors pyramidalization at the substituted site in the corresponding MECI due to its stabilizing π-accepting character and presumably faster motion along the corresponding BP vectors. Simultaneously, the ES activation barrier for pyramidalization at C1 (C2) is significantly enhanced for 2-CNBD (1-CNBD). The position of the CN substituent therefore controls the entry direction of the CoIn. It is apparent that, in all examples above, the change in reactivity has been intrinsically interpreted in terms of a variation of the velocity (due to dominating topographic effects) along a single BP direction of a critical MECI and consistently with a LZ scheme.
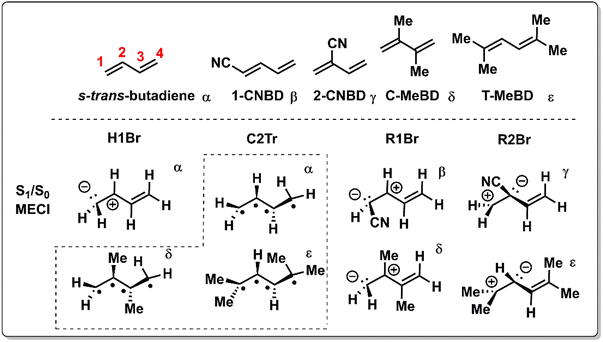 | ||
| Scheme 3 Chemical structures and schematic geometrical structures of the S1/S0 MECIs for trans-butadiene, 1-cyano-1,3-butadiene (1-CNBD), 2-cyano-1,3-butadiene (2-CNBD), 2,3-dimethyl-1,3-butadiene (C-MeBD) and 2,5-dimethyl-2,4-hexadiene (T-MeBD). The H1Br, R1Br and R2Br names refer to the bridging of the H-1, R-1 and R-2 groups, respectively. These CoIns are of type 3 in Scheme 1. C2Tr refers to the transoid structure of the central C2 carbon and is a type 1 CoIn (Scheme 1). The Greek symbols are used to indicate which MECI geometries correspond to which molecule. All MECIs were calculated at the MR-CIS level of theory.130 | ||
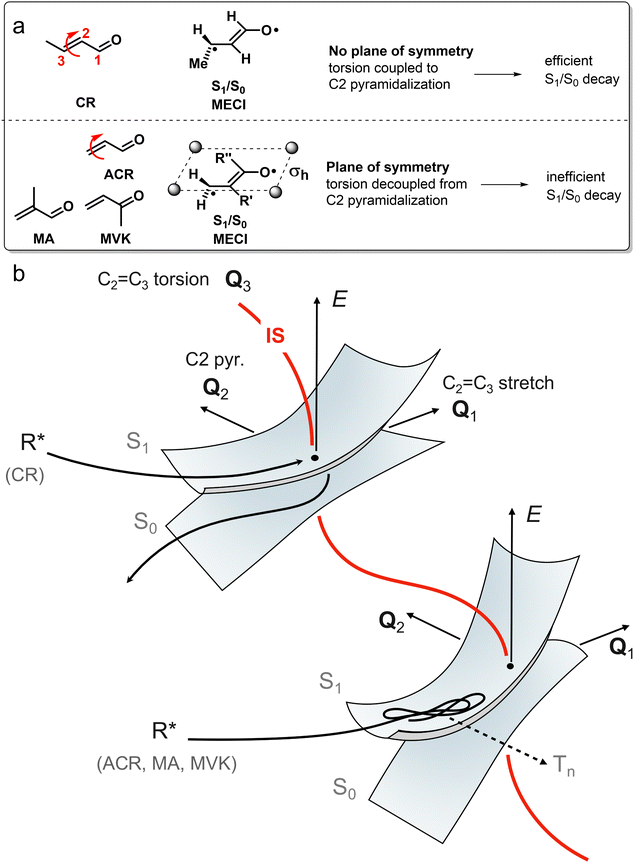
The inertial effect of methyl groups has been applied to the photochemistry of α,β-enones as well, in which the position of a methyl substituent controls the velocity of the wavepacket through a sloped S1(nπ*)/S0 CoIn (Fig. 12) in acrolein derivatives.85 The chemical structures of acrolein (ACR), as well as its substituted derivatives, crotonaldehyde (CR), methylvinylketone (MVK) and methacrolein (MA) are shown in Fig. 12a. The corresponding geometrical MECI structure is characterized by a double bond twist and pyramidalization and is of type 4 (Fig. 11). When the methyl group is positioned at the terminal carbon (C3), as in crotonaldehyde (CR), nonadiabatic decay is favored, resulting in either IC or singlet photochemistry. In contrast, having a methyl-free terminal methylene carbon (ACR, MA and MVK) results in less efficient decay to the GS PES, which extends the S1 lifetime making these molecules more prone to undergo ISC to the Tn manifold, eventually yielding typical α,β-enone triplet state reactivity such as the Norrish type 1 reaction. The original rationalization for these differences in S1(nπ*)/S0 decay efficiencies was based on an inertial substituent effect of the terminal methyl group in CR, which induced (i) low C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 torsional velocity (ii) high velocities along the BP (i.e. along Q1 and Q2). ACR, MA and MVK, on the other hand, have (i) high C2
C3 torsional velocity (ii) high velocities along the BP (i.e. along Q1 and Q2). ACR, MA and MVK, on the other hand, have (i) high C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 torsional velocity (ii) low Q1 and Q2 velocities. As the calculated Q1 and Q2 BP vectors correspond to C2
C3 torsional velocity (ii) low Q1 and Q2 velocities. As the calculated Q1 and Q2 BP vectors correspond to C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 stretching and C2 pyramidalization, according to this interpretation the torsional mode drives the wavepacket to a particular region along the IS that is, therefore, indirectly implied in the dynamics at the CoIn.85 This provides a first example where, clearly the MECI and the motion along the corresponding BP are not sufficient to explain the experimental observations and an extra mode (locally an “IS mode”) needs to be involved in the explanation (Fig. 12b). We reinterpret the distinct nonadiabatic decay behaviour of CR by noting that the large kinetic energy in the torsional motion picked up after S2(ππ*) excitation needs to be (partially) transferred to the C2 pyramidalization mode to facilitate the nonadiabatic transition from S1(nπ*) to S0. This energy transfer should be facile in CR where the coupling between torsion and C2 pyramidalization is large due to the lack of symmetry at the S1/S0 MECI geometry. However, the S1/S0 MECI geometries for ACR, MA and MVK contain a plane of symmetry, which decouples the torsion from C2 pyramidalization, resulting in inefficient nonadiabatic decay to the S0 PES as the Q2 mode is inactive. In conclusion, the coordinated interplay between torsional and pyramidalization normal modes is a manifestation of the multi-mode (e.g. one BP and one IS mode) nature of ultrafast photochemical reactions, which will be the topic of Section 3.
C3 stretching and C2 pyramidalization, according to this interpretation the torsional mode drives the wavepacket to a particular region along the IS that is, therefore, indirectly implied in the dynamics at the CoIn.85 This provides a first example where, clearly the MECI and the motion along the corresponding BP are not sufficient to explain the experimental observations and an extra mode (locally an “IS mode”) needs to be involved in the explanation (Fig. 12b). We reinterpret the distinct nonadiabatic decay behaviour of CR by noting that the large kinetic energy in the torsional motion picked up after S2(ππ*) excitation needs to be (partially) transferred to the C2 pyramidalization mode to facilitate the nonadiabatic transition from S1(nπ*) to S0. This energy transfer should be facile in CR where the coupling between torsion and C2 pyramidalization is large due to the lack of symmetry at the S1/S0 MECI geometry. However, the S1/S0 MECI geometries for ACR, MA and MVK contain a plane of symmetry, which decouples the torsion from C2 pyramidalization, resulting in inefficient nonadiabatic decay to the S0 PES as the Q2 mode is inactive. In conclusion, the coordinated interplay between torsional and pyramidalization normal modes is a manifestation of the multi-mode (e.g. one BP and one IS mode) nature of ultrafast photochemical reactions, which will be the topic of Section 3.
Because the torsional mode in the retinal chromophore of rhodopsin (rPSB11, Section 3.1) is a BP vector for its photoisomerization reaction through a type 3 CoIn and therefore directly involved in the efficiency of this nonadiabatic process, methyl substitution at the torsional skeleton should significantly slow down the reaction. Indeed, QM/MM simulations of a model all-trans retinal (rPSBAT) demonstrated how methyl substitution increased the ES lifetime, both in gas phase and non-polar solvents.51 However, Kukura and co-workers experimentally found that photoisomerization of 10-methyl-rPSBAT (methylation at C10 in rPSBAT) in methanol is much faster than rPSBAT,134 which has been verified using QM/MM simulations in both methanol135,136 and in a protein environment99 and was rationalized by a reduction in S2/S1 mixing resulting in steeper ES slopes (similar to the discussion related to Fig. 10), illustrating again that the methyl group is not a pure inertial substituent. Despite the faster ES decay (higher nuclear velocity), the isomerization QY is drastically smaller in 10-methyl-rPSBAT compared to rPSBAT, being inconsistent with the standard LZ model.134 This result suggests that the actual reaction coordinate (presumably lying along the BP of the rPSBAT MECI), does not represent the real velocity direction at decay. In other words, a multi-mode mechanism also implicating motion with components along the IS must be considered. In Section 3 we will see that this is indeed the case.
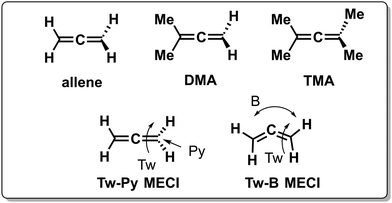
Inertial tuning studies by methyl substitution have also been carried out on allene, where an increasing degree of methyl substitution correlated to longer TRPES measured ES lifetimes after S1(ππ*) excitation.137 The distinct decay dynamics of these molecules has been rationalized with, again, a branching of two channels involving distinct S1(ππ*)/S0 MECIs, calculated at MR-FOCI level of theory (Scheme 4). Whereas decay through the Tw-Py MECI requires twisting and pyramidalization of one CH2 unit (type 3 CoIn), the Tw-B requires twisting and bending of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C framework. AIMS simulations show that in all cases decay through the Tw-Py MECI is dominating. However, upon increasing methyl substitution the twisting motion is retarded, resulting in a greater propensity for C
C framework. AIMS simulations show that in all cases decay through the Tw-Py MECI is dominating. However, upon increasing methyl substitution the twisting motion is retarded, resulting in a greater propensity for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bending as mixing of the two π-bonds is weak in a weakly twisted geometry, which decreases the probability to reach the low-lying Tw-Py MECI. As decay through the Tw-B MECI is not efficient, the lifetime is extended significantly upon methyl substitution. This case appears to be consistent with the standard LZ model as the nonadiabatic decay efficiency decreases with a slower twisting motion approaching the MECI. Finally, increasing the bulkiness of substituents at the 5-position in cyclopentadiene rings leads to longer lifetimes as the vibrational dynamics relevant for ultrafast nonadiabatic decay were inhibited.138
C bending as mixing of the two π-bonds is weak in a weakly twisted geometry, which decreases the probability to reach the low-lying Tw-Py MECI. As decay through the Tw-B MECI is not efficient, the lifetime is extended significantly upon methyl substitution. This case appears to be consistent with the standard LZ model as the nonadiabatic decay efficiency decreases with a slower twisting motion approaching the MECI. Finally, increasing the bulkiness of substituents at the 5-position in cyclopentadiene rings leads to longer lifetimes as the vibrational dynamics relevant for ultrafast nonadiabatic decay were inhibited.138
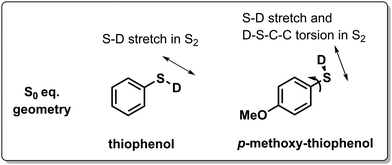
Another strategy to tune the photochemical dynamics was carried out by Lim et al. who exploited the differences in GS conformational preferences between thiophenol and methoxy-substituted thiophenol (Scheme 5) to alter the ES wavepacket trajectories and consequently the S–D photodissociation rate by exciting the S2 (nσ*) state with short laser pulses.139 In thiophenol, the equilibrium geometry is such that the S–D bond is coplanar with the phenyl ring, which results only in a S–D stretching motion upon photoexcitation. The wavepacket dynamics upon S2 excitation is different when a methoxy group is added at the para position, since the S0 equilibrium geometry becomes perpendicular, whereas the S2 equilibrium geometry remains planar. This activates C–C–S–D torsional motion on the ES PES, next to the S–D stretch, which broadens the distribution of velocities (i.e. less coherence) on the ES PES, increasing the chance for the wavepacket to miss the (planar) S2(nσ*)/S0 type 5 CoIn and consequently results in a less efficient nonadiabatic decay. Here a single MECI and BP picture is valid as the efficiency of photodissociation through the S2(nσ*)/S0 CoIn decreases with a decrease in the nuclear velocity along the BP direction of a MECI.
In the nonadiabatic nanoreactor method developed by Martínez and co-workers, vast regions of the IS are explored and the BP vectors for many relevant CoIns are sampled.58 From this study it has become clear that even for a simple molecule such as benzene, a complete characterization of its photochemistry involves the computation of different IS segments, each having distinct CoIn topographies and photoproduct distributions that are intimately linked to its topography as well as the position of the CoIn along the IS. We anticipate that such a method will be crucial for the discovery of multi-mode photochemical reaction mechanisms where, in general, it is insufficient to assume a single CoIn and BP to explain the photochemical QY. However, we acknowledge that currently the computational cost associated with a nanoreactor hampers its application to larger molecules than benzene. Furthermore, although the nanoreactor characterizes the IS completely with CoIn-specific photoproduct distributions, it does not provide the total photochemical QY for a given set of initial conditions. The latter may, however, be computed using a swarm of nonadiabatic nuclear trajectories without the need for a complete IS characterization.148–151
2.3 Limitations of the standard LZ model
In the context of the “standard” model discussed above where decay at a single CoIn channel dominates, a key prediction is that a larger velocity towards the CoIn correlates with a higher QY, which is often reinterpreted in terms of the existence of an inverse relation between ES lifetime and QY. Such relationship has been investigated multiple times with both computational and spectroscopic approaches70,71,73,74,152 and it has been an inspiration for almost all the rational design approaches to photochemical reactivity discussed in the present section. Although those approaches have often succeeded in changing the ES lifetime (related to the reaction or relaxation velocity), a discussion of their effect on QYs has often been omitted. Here a remarkable feature is that an opposite correlation has been found in a number of both computational and experimental studies, i.e., longer ES lifetimes correlate with higher QYs.153–156 One paper in particular, reporting on quantum-classical dynamics simulations for a series of rhodopsin proteins, found that the longest ES lifetime (visual rhodopsin) displayed the largest photoisomerization QY as well (Fig. 13).156 In an experimental pump-probe study, Cheminal et al. measured an isomerization rate of 100 fs for a rPSB isomer present in Anabaena Sensory Rhodopsin, yet with a relatively low QY below 0.25.154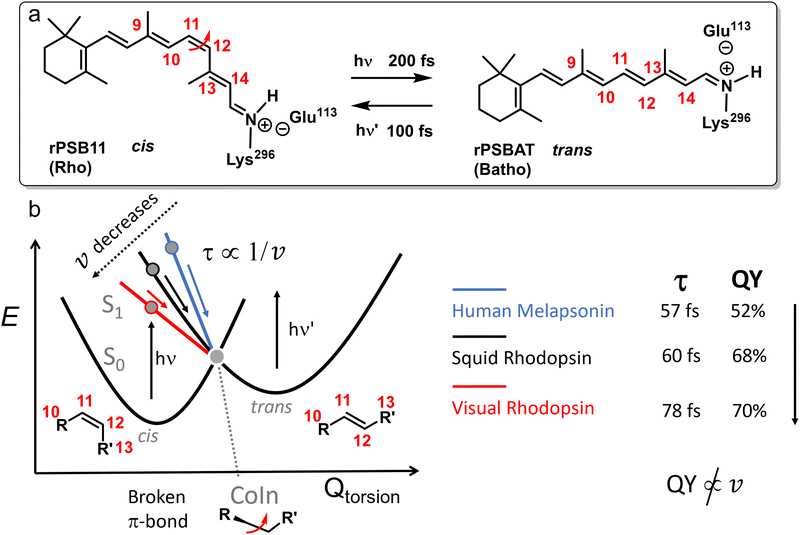 | ||
Fig. 13 (a) Photoisomerization of 11-cis retinal protonated Schiff Base (rPSB11) at the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 bond to its corresponding all-trans form (rPSBAT). (b) A schematic one-mode representation of this reaction along the torsional coordinate, passing through a CoIn where the π-bond is broken. The ES lifetimes τ (inversely proportional to the reaction speed, ν) of various rPSB11 isomerization reactions in different protein environments are proportional to the isomerization QY, which is in contrast with the LZ model (Section 2). As experimental τ and QYs are not available for all systems, the computationally acquired values are shown.156 Note that the ES lifetime is not equal to the total reaction time, which includes relaxation on the GS PES. The trend in v is caused by different protein environments, corresponding to different ES forces exerted on the torsional mode. C12 bond to its corresponding all-trans form (rPSBAT). (b) A schematic one-mode representation of this reaction along the torsional coordinate, passing through a CoIn where the π-bond is broken. The ES lifetimes τ (inversely proportional to the reaction speed, ν) of various rPSB11 isomerization reactions in different protein environments are proportional to the isomerization QY, which is in contrast with the LZ model (Section 2). As experimental τ and QYs are not available for all systems, the computationally acquired values are shown.156 Note that the ES lifetime is not equal to the total reaction time, which includes relaxation on the GS PES. The trend in v is caused by different protein environments, corresponding to different ES forces exerted on the torsional mode. | ||
These failures of the standard LZ model imply that consideration of a single reactive mode, usually a torsional mode for double bond photoisomerization, is not sufficient. In all the above cases, the mechanistic principle generating such critical mode, and the nuclear velocity along such mode, has not been discussed. Most specifically, no attention has been paid to the fact that qualitatively different velocities (e.g. velocities with opposite sign) or spectrum of velocities could be generated during a coherent ES progression and due to established phase relationships between modes initially orthogonal to the putative nuclear reaction coordinate. This makes the qualitative interpretation of the LZ theory effectively depending on the interplay between different modes prior to decay. However, notice that, in principle, this interplay is automatically accounted for in numerical simulations based on the propagation of classical trajectories with surface hopping,157,158 such as the Landau–Zener surface hopping method,159 or other methods based on nonadiabatic dynamics theory.160 Despite this, the mechanistic principle resulting from LZ theory applied to a decay event intercepting a single CoIn along one direction with a specific velocity (i.e. the standard LZ model and the corresponding direct proportionality between the velocity of that mode and the decay efficiency) is still often applied without recognition of the interplay between multiple modes. The impact of such an interplay between modes is that not a single CoIn channel drives nonadiabatic decay, but multiple CoIn points from the reactive IS segment (Fig. 5f), each with a distinct direction and phase relationship between the relevant BP and IS modes.
Indeed, the experimental and computational observations on the acrolein derivatives discussed in Section 2.2 already suggest that the coupling between BP modes and IS modes is important for controlling nonadiabatic decay. This coupling may be readily reinterpreted as a need to consider decay at multiple CoIn points along the IS. The demand for a multi-mode understanding of photochemical reactions is further reinforced by experimental evidence from two-dimensional spectroscopy161 and coherent control laser spectroscopy.162 In the latter, shaped laser pulses were used to control the isomerization QY of rPSB11 through constructive and destructive interference of vibrational modes that are relevant for the reaction on the timescale of coherent chemistry, i.e., before vibrational relaxation.
It should be noted that there are additional limitations to LZ theory and the standard model. One assumption of the standard LZ model that might fail in realistic circumstances is the conservation of vibrational coherence (i.e., in the sense that all molecules of the same population would move along the same reaction coordinate on similar timescales). It is likely that there will always be some vibrational redistribution, which can alter the dynamics.71 Other simplifications inherent to LZ theory that more advanced methods should deal with are the constant slope difference (F) and constant velocity (v) near the CoIn. Additionally, whereas passage of a wavepacket exactly through a CoIn would lead to a 100% efficient nonadiabatic decay according to the LZ formula, wider regions around the CoIn may be implicated in the decay.163 This is because nonadiabatic transfer of wavepackets may be achieved even though the wavepacket does not travel exactly through the CoIn, as shown by Farfan and Turner with quantum dynamics simulations164 and also stressed above when discussing the AC surrounding a real crossing point. Lastly, LZ theory does not consider the potential importance of Berry's phase effects which include modifications of the nuclear forces driving the nonadiabatic dynamics.165
3. Beyond the standard Landau–Zener model: vibrational motion in concert and the role of the intersection space
This section discusses the need of a different approach towards understanding what factors control the quantum yield (QY) in certain ultrafast photochemical processes. As anticipated in previous sections, in these cases a mechanism centred on a single MECI and BP has to be abandoned, as considering the decay along an entire IS segment becomes critical, leading to difficulties in correlating measured velocities (e.g. estimated via ES lifetimes) and QYs as indicated by the one-mode Landau–Zener (LZ) model.60,62 Indeed, both spectroscopic and computational results acquired in the last 10 years indicate that for a proper description of ultrafast photochemistry, it is crucial to incorporate in the ES progression towards the IS: (i) modes that do not belong to (or have a limited projection on) the BP of a single critical CoIn and (ii) the phase relationship between these modes. Below we discuss several case studies illustrating these concepts.3.1 Ultrafast double bond photoisomerization of rhodopsin
Double bond photoisomerization of rhodopsin, the first step in dim-light vision, has been the guinea pig to demonstrate the importance of the relative phase of vibrational modes in controlling the branching ratio at the CoIn. This discovery is based on three pillars, being the spectroscopic observation of vibrational coherence (VC) throughout the complete reaction pathway (I), computational insights into the coordinated interplay of the vibrational modes describing the progression towards the IS (II) and confirmation of such a multi-mode mechanism through the vibrational phase isotope effect (III).Before we discuss these pillars, we summarize some relevant characteristics of the photochemistry of rPSB11 and rPSBAT, which are the chromophores of the rhodopsin (Rho) and bathorhodopsin (Batho), respectively (Fig. 13). The discovery that photoisomerization of rPSB11 takes place through a CoIn instead of an AC is connected to the wide variety of CoIns detected in common organic photochemical reactions.10,19,105,114,166 Furthermore, a barrierless reaction path connects the FC-point to a CoIn whose local topography is peaked and is therefore a great example of the elementary photochemical reaction we set out in Fig. 5b.114 Since this reaction completes in 200 fs, it is considered to be ultrafast.167 The gradient of the S1 PES drives the breaking of the π-bond between the C11 and C12 atoms, leading to an about 90° twisted type 3-like (Section 2.2) CoIn structure. However, it will become clear in this section that this reaction coordinate is not solely composed of a torsional deformation of the reacting double bond but includes other molecular modes as well.
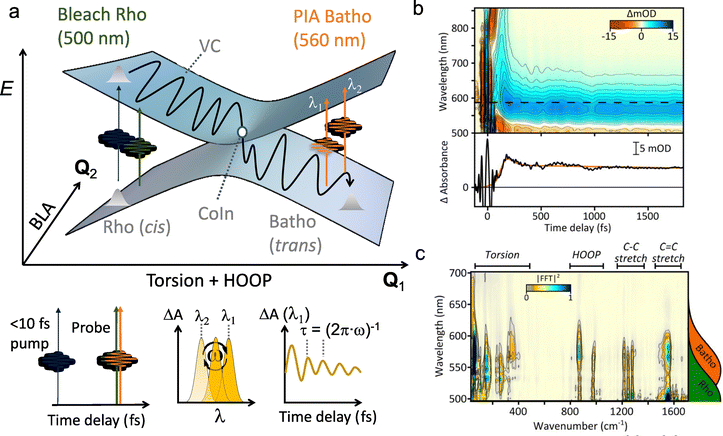 | ||
Fig. 14 Elucidating the mechanism of ultrafast multi-mode rPSB11 (Rhodopsin) photoisomerization to rPSBAT (Bathorhodopsin) with impulsive vibrational spectroscopy (IVS). (a) An ultrashort (<10 fs) laser pump pulse (blue arrow) generates VC on the ES PES, which is probed over time. The green arrow indicates the probe wavelength with which the GS bleach, i.e., reduction in absorbance, of rPSB11 is detected. The photoinduced absorption (PIA) of the photoproduct Batho is indicated with the orange arrow. The differential absorption ΔA (or ΔOD) spectrum is modulated by a frequency ω that is determined by the relevant normal modes. This is illustrated for the PIA of Batho in the bottom schemes, where the intensity at the probe wavelengths λ1 and λ2 changes over time. The vibrational oscillations superimposed on the electronic kinetics become clear when the ΔA is probed at one wavelength λ1 (see bottom right). Notice that in this schematic the wavepacket passes through only one point in the IS, which is not necessarily the MECI. (b) Differential absorption ΔA map of photoexcited rhodopsin with a 8 fs pump pulse at 500 nm. The dashed line at 560 nm indicates the maximum absorbance peak of the PIA, forming on a sub-200 fs timescale. The inset below shows the slice of the ΔA at this probe wavelength, which exhibits vibrational oscillations on top of the electronic kinetics. Reproduced from ref. 170 with permission. Copyright 2015 American Chemical Society. (c) Wavelength resolved Fourier power map obtained after subtraction of the electronic kinetics by global analysis, followed by fast Fourier transformation. The vibrational coherence (VC) observed in the ΔA map is composed of torsional (<400 cm−1), HOOP (800–1000 cm−1), C–C stretch (1200–1300 cm−1) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch (1500–1600 cm−1) modes. The latter two are also collectively referred to as bond length alternation (BLA). These modes are included in the mechanistic drawing in (a) and visualised in Fig. 15. Although the IVS study suggested the HOOP mode to be the coupling mode (the equivalent of the Q2 mode),170 CASPT2 calculations show that the BLA mode corresponds to Q2.152,171 Reproduced from ref. 170 with permission. Copyright 2015 American Chemical Society. C stretch (1500–1600 cm−1) modes. The latter two are also collectively referred to as bond length alternation (BLA). These modes are included in the mechanistic drawing in (a) and visualised in Fig. 15. Although the IVS study suggested the HOOP mode to be the coupling mode (the equivalent of the Q2 mode),170 CASPT2 calculations show that the BLA mode corresponds to Q2.152,171 Reproduced from ref. 170 with permission. Copyright 2015 American Chemical Society. | ||
A key component of these experiments is the use of temporally compressed laser pulses, which can excite multiple vibrational eigenstates in the ES due to its large bandwidth. An ultrashort light pulse excitation projects the GS vibrational eigenfunctions onto the ES PES to generate a wavepacket with the same shape, provided that this pulse is temporally shorter than the vibrational periods of interest (pulses <10 fs are required to observe most vibrations of interest up to ∼3000 cm−1).172 This FC excitation is the vibrational equivalent of an equilibrium structure vertical excitation and the region where the wavepacket is localized in configuration-space is called the FC-region. Because the wavepacket created on the ES PES is not a vibrational eigenstate anymore (in fact, the pump prepares a superposition of vibrational eigenstates), it will evolve in time according to the shape of the ES PES. From a classical point of view, this may be understood by considering that at the FC-point specific modes in the ES are displaced with respect to the GS and therefore experience a force by the ES PES, resulting in a time evolution described by Newton-like equations.173 One important experimental consideration is that through the ISRS mechanism, VC is also created on the GS surface. Whenever it is not possible to spectrally resolve the contributions from excited and ground state, more sophisticated pulse schemes might be employed as described in ref. 168 and 174.
The initially created ES population or wavepacket is vibrationally coherent (i.e., it displays the VC property) in two forms. One is the synchronized motion of molecules at the population level caused by the specific shape of the ES PES (i.e., by the ES force field), or intermolecular VC. Thus, this coherence corresponds to a dynamical behaviour purely in a classical sense.175 One consequence of such state is that, at the single molecule level, VC implies a specific phase relationships between two or multiple normal modes and can be called intramolecular VC. Conservation of VC throughout any photoinduced process implies the conservation of this phase relationship. Decoherence, on the other hand, implies partial randomization of vibrational energy amongst all normal modes, as well as dephasing of the initially vibrationally phased motion. As demonstrated in Fig. 14, VC manifests itself as a time-dependent modulation of a (photoinduced) transient transmission (recorded by a broadband probe pulse) with a frequency determined by the energy differences between the excited vibrational eigenstates, hence providing a spectroscopic marker to study structural dynamics in the ES.169
Based on the torsional intramolecular VC experimentally observed in the photoproduct, the extremely high reaction speed (200 fs) and the lack of fluorescence, Wang et al. concluded that rPSB11 photoisomerization in rhodopsin involves a CoIn (type a photochemical reaction in Fig. 1), which has been verified by subsequent studies.28 When using the vibronic picture given by Fermi's Golden Rule, the CoIn strongly couples the ES vibrational eigenfunctions to those of the GS, which (i) provides an efficient funnel back to the GS, explaining the ultrafast (200 fs) reaction speed (which Fermi's Golden Rule can’t quantitatively account for, being limited to small perturbations only) and (ii) rationalizes the survival of ES PES induced VC created at the FC-point throughout the complete reaction path.73,176 Indeed, neither the adiabatic photoreaction (type c) nor the nonadiabatic photoreaction via a AC (type b) complement these observations, as these would involve a (partially) equilibrated ES intermediate.
Kukura and co-workers revealed many other mode-specific VCs in the photoproduct (Fig. 14c), including the FC-active (i.e., displaced on the ES PES with respect to the GS PES) bond-length alternation (BLA) and hydrogen out-of-plane (HOOP) modes (see below).170,177 In fact, the torsional mode VC is indirectly activated through energy transfer from FC-active modes and is therefore reaction-induced (see below). Further support for a vibrationally coherent CoIn driven mechanism was provided by the transient grating experiments from Miller and colleagues.178
The above results suggest a coherent picture not only at the population level, but also at the single molecule level in which the temporally vibrationally phased motion of multiple modes directs the molecule to the IS with the correct trajectory in phase-space, facilitating an efficient nonadiabatic transition directed towards the product.152 Accordingly, because the initial phase-space trajectory involves the cooperative motion of multiple modes, and because such motion is determined by the slopes of the ES at the FC-point, rational design of CoIns to control the velocity and QY of a photoreaction should take into account the phase relationship of the relevant normal mode basis.179,180 During these studies the researchers were thinking of a rather compact propagating ES population maintaining such compactness while heading to a single favoured CoIn region (notice the single CoIn point in Fig. 14a). Below we will see that a partial decoherence of the population may cause decay at geometrically different CoIns of an IS segment, each CoIn point being associated with different phase relationships between critical modes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cis ratio.
cis ratio.
The initial vibrational dynamics of excited rPSB11 is dominated by the bond length alternation (BLA) mode which is quantified by the difference between the average double-bond lengths and the average of the single-bond lengths of the conjugated chain. This initial relaxing motion can be rationalized by considering the CT nature of the S1 wavefunction, which shows a positive charge build-up at the β-ionone fragment (Fig. 15a), resulting in a driving force to unlock the double bonds and lock single bonds.113 As a result of this bond length inversion, a torsional mode about the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 bond becomes facile, which is accompanied by a torsional motion along the adjacent C9
C12 bond becomes facile, which is accompanied by a torsional motion along the adjacent C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10 bond.114,181 This volume-conserving mechanism was referred to as the bicycle-pedal mechanism by Warshel and is able to explain how an isomerization can take place within a tight protein cavity.182 However, this motion is aborted after decay to the GS, ensuring that only isomerization at the C11
C10 bond.114,181 This volume-conserving mechanism was referred to as the bicycle-pedal mechanism by Warshel and is able to explain how an isomerization can take place within a tight protein cavity.182 However, this motion is aborted after decay to the GS, ensuring that only isomerization at the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 double bond takes place, as was confirmed by CASSCF-based QM/MM calculations.181,183
C12 double bond takes place, as was confirmed by CASSCF-based QM/MM calculations.181,183
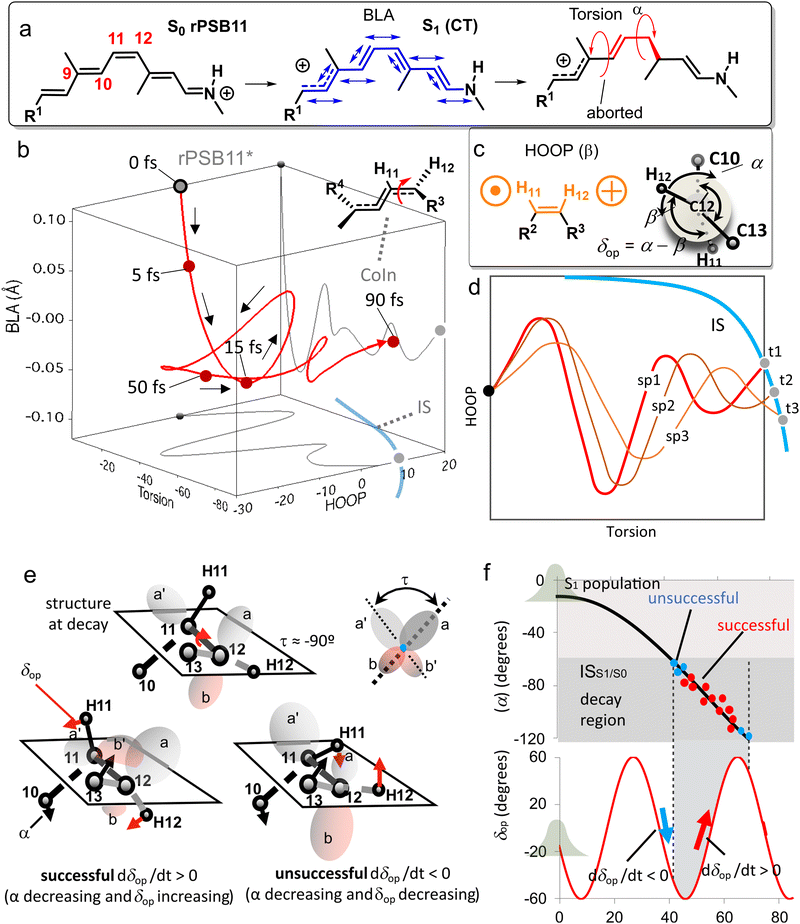 | ||
| Fig. 15 Mechanism of rPSB11 to rPSBAT photoisomerization. (a) Two-state two-mode model. Initial charge redistribution upon photoexcitation is accompanied by bond-length alternation (BLA) and followed by the torsional bicycle pedal motion. (b) QM/MM ES trajectory displaying the center of a coherent wavepacket (red line) is described by three relevant normal modes: BLA, torsion and HOOP. The geometrical CoIn structure is shown at the top right. The grey curves are the projection of the red trajectory on two normal mode coordinates. The dashed curve is the projection of the IS on the torsion-HOOP subspace. Adapted with permission from ref. 113. Copyright 2017 American Chemical Society. (c) Definition of HOOP mode (β) and δop. Relative motion of HOOP with respect to the torsion (α) is indicated with δop. (d) Schematic illustration of the effect of partial decoherence on the phase relationship between HOOP and Torsion. As also detailed in ref. 100, this process can be described as the splitting of the initial populations (e.g. sp1 to sp3) each reaching the IS at different times (e.g. t1 to t3). As a result, different populations decay with different phase relationships between HOOP and torsion. (e) Relation between relative phase HOOP and torsion modes and orbital overlap required for π-bond reconstitution at decay point, represented by the CoIn structure on the top right where τ indicates the dihedral angle between the bisectors a and a′ (∼−90° at CoIn). a + b and a′+ b′ indicate the phases of the p-orbitals at the two central carbon atoms, C12 and C11, respectively. Successful isomerization is achieved with out-of-phase motion of δop and α through overlap of the a and b′ lobes to form the trans π-bond, whereas in-phase-motion prompts unsuccessful isomerization through orbital overlap between the a and a′ lobes which forms the cis π-bond. (f) S1 wavepacket trajectory, represented by a Boltzmann population, evolving coherently along α and δop coordinates. Most successful decay events (i.e. the largest isomerization QY) are achieved when dδop/dt > 0, whereas unsuccessful decay events occur when dδop/dt < 0.100,113 | ||
Up until the early 2000s, this two-state two-mode mechanism involving the torsion that follows the BLA was considered to be the mechanism for the photoisomerization of rPSB11.184 In fact, this was found to correspond to motion along the BP of a single MECI point. Only when quantum-classical trajectories computed using a complete QM/MM model of rhodopsin and an ab initio multiconfigurational wavefunction (Fig. 15b), became computationally feasible, the relevance of the HOOP mode (Fig. 15c) in the coherent photochemical reaction was recognized.113,185 The HOOP motion that appears to be primarily one of the IS coordinates at the MECI, provides a measure of the pyramidalization at the C11 and C12 atoms, reflecting their sp3 character. Both the BLA and HOOP modes facilitate the breaking of the π-bond, even before the torsional mode is activated. Consistent with previous calculations, the first 5 fs of the quantum-classical trajectories are dominated by BLA motion (Fig. 15b). The HOOP motion becomes active after 15 fs when the BLA mode has almost finished a quarter of an oscillation and shows a periodic oscillation in the HOOP-torsion subspace throughout the complete trajectory approaching the CoIn (grey line), which implies the presence of a phase relationship between these two modes. Albeit less perfect, such a periodic oscillation mixes with motion along the BLA-torsion subspace as well, clearly hinting towards a two-state three-mode mechanism (i.e. implicating both the BP and the IS). Although there appears to be a sequential activation of these normal modes, which is due to the shape of the ES PES, the periodicity of these two bimodal subspaces during the trajectory is striking. Apparently, the FC-active BLA mode transfers its energy to the torsional and HOOP modes, presumably through anharmonic coupling. Such an anharmonic coupling-driven activation of FC-inactive modes was also observed as a reaction-induced VC in the ES dynamics of bacteriorhodopsin by comparison of IVS and resonant Raman spectroscopy, in which the first probes any ES active mode, whereas the latter only probes FC-active modes.186 What these quantum-classical trajectories thus show is that not only the ES PES force field may generate VC (since the initial conditions are according to Boltzmann statistics the role of femtosecond pulses is ruled out), but also conserve it, as the wavepacket moves through the (3N − 8)-dimensional IS. The geometrical structure of the CoIn reached in ∼90 fs187 (i.e. different from the MECI) is schematically shown at the top right in Fig. 15b and shows pyramidalization at C12, along with torsional and stretching deformations with respect to the FC-point, showing clear type 3 CoIn characteristics (Section 2.2). It should be pointed out here that the red trajectory represents the center of a wavepacket, hence assuming VC at the population level. However, multiple trajectories leading to the photoproduct are possible. Furthermore, the CoIn structure shown in Fig. 15b only corresponds to a CoIn point, which is part of an IS. Indeed, multiconfigurational quantum chemical calculations show that multiple CoIn points associated with the same IS may be approached.113 Hence, the ES decay does not follow a single pathway, but rather follows a variety of trajectories that may proceed through different CoIn points belonging to the same wide, in terms of C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 torsion (∼60° variation),100 IS segment.188 This explains the HOOP deformation featured by the CoIn point of Fig. 15b and it shows that the trajectories lead to CoIn points where the HOOP mode is now mixed with the torsional mode yielding a local BP oriented differently from the BP at the MECI (see Fig. 3b for a schematic illustration).
C12 torsion (∼60° variation),100 IS segment.188 This explains the HOOP deformation featured by the CoIn point of Fig. 15b and it shows that the trajectories lead to CoIn points where the HOOP mode is now mixed with the torsional mode yielding a local BP oriented differently from the BP at the MECI (see Fig. 3b for a schematic illustration).
The above process may be interpreted in terms of the widening of an initially narrow wavepacket during the ES propagation, caused by partial vibrational decoherence. This process would then lead to different population fractions (or subpopulations) decaying at different times at different CoIns along the IS (see Fig. 15d). Each subpopulation will then decay with a different phase relationship between the HOOP mode and the torsion.
Now that it has been established that three modes are involved in the ES decay of rPSB11, the next goal is to understand how they control the QY and the stereochemical outcome. According to the standard LZ model, a higher velocity of a single reaction coordinate on the S1 PES towards the CoIn would correlate with a higher QY.61 However, the results described above, along with the discussion in Section 2.3, strongly hint towards a multi-mode explanation that can also be interpreted, as mentioned above, in terms of variations in the Q1 and Q2 BP vectors at the “'reactive” IS segment.154,189 Different combinations of the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 torsion and HOOP motion correspond to the Q1 vector (the opposite combination will instead move the molecule along the IS),1 whereas a BLA mode remains the Q2 vector.171
C12 torsion and HOOP motion correspond to the Q1 vector (the opposite combination will instead move the molecule along the IS),1 whereas a BLA mode remains the Q2 vector.171
To understand how these modes work cooperatively to control the branching between the trans-photoproduct (rPSBAT) and the cis-reactant (rPSB11) and therefore the QY, it is important to understand the mechanism of π-bond reconstitution. In Fig. 15e, it is shown how the relative motion of the HOOP (β) compared to the torsional mode (α) controls the cis/trans isomer ratio starting from a structure similar to the CoIn which can originate from both the forward as well as the reverse photoisomerization direction.113 An out-of-phase motion (dδop/dt > 0, in which δop is equal to α–β) leads to a–b′ and b–a′ orbital overlap, resulting in successful isomerization (i.e. the trans-product), whereas an in-phase motion (dδop/dt < 0) leads to a–a′ and b–b′ orbital overlap and therefore an unsuccessful isomerization (i.e. the cis-reactant). These two contrasting situations are also illustrated in Fig. 15f, where photoexcitation to the S1 state generates a wavepacket that coherently evolves with a decreasing α and approaches the ISS1/S0 with a distribution of δop values and an α value of roughly −90°. Successful isomerizations (indicated with red dots) require a HOOP motion with positive velocity while α is becoming more negative. In contrast, unsuccessful isomerizations occur when the HOOP motion is also becoming more negative, i.e., in-phase with the torsional motion. Computational support for this HOOP-phase control was acquired by artificially delaying the HOOP mode by decreasing either its frequency or phase, which indeed resulted in smaller QYs.113 Furthermore, other nonadiabatic molecular dynamics studies of rhodopsin have confirmed that the phase of the HOOP motion is crucial in determining the reaction outcome.181,188,190,191 Again, this dependency on the phase of the HOOP component of the motion leading to decay can also be interpreted in terms of subpopulations decaying at different locations along the IS, each location reached at different times as illustrated in Fig. 15d. A recent computational study demonstrated this concept, showing the effect of the degree of decoherence acquired by the population during ES propagation on the decay dynamics and QY.100
Although it has been mentioned already that the BLA mode initially drives the wavepacket out of the FC-region, we now clarify its role in driving the photoreaction in the CoIn region. Immediately after decay at the CoIn, the BLA mode determines whether the GS wavefunction will be of diradical/covalent (diabatic) character and therefore suitable for double bond reconstitution, or of unbound CT character.113 In the forward direction (rPSB11 to rPSBAT), the wavefunction switches to a bonding diradical character only 20 fs after decay to S0, allowing the HOOP motion to perform half an extra oscillation. At this point, the HOOP motion is out-of-phase with the torsional motion, yielding predominantly rPSBAT. In the reverse direction (rPSBAT to rPSB11) the wavefunction switches to bonding character near the CoIn and therefore the HOOP-phase control is already exerted much closer to where nonadiabatic decay occurs. The critical role of the relative HOOP phase could potentially enable a HOOP-phase driven approach to improve QYs by either tuning the HOOP frequency or phase through protein environment engineering, either retarding or speeding up the HOOP motion relative to the torsional motion, provided that the change of the HOOP amplitude is fast compared to the change in torsion.152 Another way to change the relative phase of the HOOP and torsional modes and thereby the QY is to fix the HOOP frequency, but vary the torsional frequency. In fact, it is likely that in nature the relative nuclear velocity of the torsional mode is varied in different rhodopsins, resulting in a variety of QYs amongst these proteins.152 While this appears a viable modulation effect implemented by the natural selection, in the next subsection we will see that in the lab it has been possible to modulate QY by changing the HOOP frequency. A major takeaway is that QYs can be improved by tuning the relative phase and/or frequency of normal modes. Therefore, any rational design method that aims to optimize QYs in ultrafast photochemical processes, should consider the engineering of VC effects. It should be mentioned that the degree of VC itself also influences the QY, as was already mentioned in Section 2.192,193
In the current analysis the contribution of the S2 state has been disregarded, whereas recent mixed quantum-classical simulations of rhodopsin indicate that S2/S1 mixing, governed by opsin electrostatic interactions, in fact results in population splitting on a 10–30 fs timescale.100 Such an event can be viewed as a partial vibrational decoherence resulting in a widening of the relaxing ES population in terms of temporal width. As a result, the isomerization QY is the sum of the fractional contributions from different subpopulations that pass the ISS1/S0 at different times (see Fig. 15d and f), due to the different dynamics at the ISS2/S1. Even though the S2 state is involved in the initial relaxation dynamics and the decoherence that results from the population splitting, the S1 PES topography and the associated vibrational phase matching rules that follow on a 30–150 fs timescale still determine the cis:trans branching at the ISS1/S0 as illustrated in Fig. 15e. Nevertheless, the impact of the S2 state on the isomerization QY once more illustrates the general complexity of ultrafast photochemical reactions, as the inclusion of another electronic state opens a variety of additional reaction pathways of which their vibrational dynamics should also be considered.
By synthetizing several deuterium-substituted rPSB11 analogues (Scheme 6) and regenerating these chromophores in the opsin protein, followed by spectroscopic measurements to track the QY and isomerization kinetics, they were able to study the effect of isotopic substitution on the photochemistry of retinal. Whereas the effects on the QY were great, the effects on the isomerization kinetics were relatively minor. Both the QYs of 11-D and 12-D decreased significantly (0.45 and 0.48 respectively), whereas the QY of 11,12-D2 was even slightly improved (0.69) compared to native rhodopsin (0.63). Traditional secondary kinetic isotope effects cannot explain this trend, as deuterium substitution would then lead to a decrease in reaction rate. Additionally, from a simple LZ model, for instance considering a reaction coordinate dominated by a single torsional (or mixed torsional/HOOP) mode, it would be expected that the HOOP motion would be retarded significantly upon deuterium substitution, decreasing the nonadiabatic transition probability and QY.
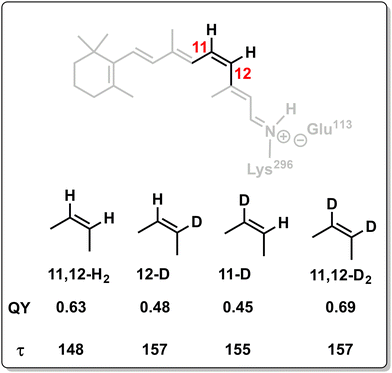 | ||
| Scheme 6 QY and τ (lag time, time to reach the CoIn from the FC-point) values for different isotopomers of rPSB11.194 | ||
Supported by nonadiabatic trajectory calculations, these substitution trends were explained by an intramolecular vibrationally coherent mechanism that involves a correctly phased motion of α (C10–C11–C12–C13 torsion) and δop (H–C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12–H HOOP) at the CoIn. As was explained by Schapiro et al., it is the timing of the two motions at the point where the wavefunction switches from antibonding to the bonding status that controls the stereochemical outcome.113 Whereas the substitution has a minor effect on the torsional mode, since the torsion is predominantly localized on the carbon skeletal framework, it exhibits a greater effect on the HOOP motion.190,195 As it is mainly the torsional mode that drives the wavepacket through the CoIn, modest changes in the reaction rate are observed. Although changes in the HOOP motion do not affect the reaction rate significantly, they do affect the branching ratio at the CoIn (Fig. 15e). This is because in 11,12-H2 and 11,12-D2, the C11-H/D and C12-H/D out-of-plane motions are coupled, resulting in symmetric and anti-symmetric HOOP vibrations, which maintain a certain phase relationship with the torsional motion. Interestingly, it appears that the double deuterium substitution results in an even improved phase matching as demonstrated by its higher QY. In contrast, partial deuteration reduces the vibrational coupling, leading to more isolated C–H and C–D out-of-plane motions and consequently less symmetric and anti-symmetric HOOP motion, which has been measured using resonance Raman spectroscopy.196 This in turn leads to a poorer phase matching with the torsional mode, inhibiting photoproduct formation. Furthermore, nonadiabatic trajectory calculations revealed that the partially deuterated 11-D and 12-D chromophores were more sensitive to the initial velocities than their symmetrically substituted counterparts, as was shown by their more de-phased HOOP motion and hence smaller VC.194 In contrast, the 11,12-H2 and 11,12-D2 chromophores displayed nonadiabatic trajectory dynamics that were relatively independent of the initial conditions, demonstrating that the ES topography rather than initial velocities dominate their ES evolution.
C12–H HOOP) at the CoIn. As was explained by Schapiro et al., it is the timing of the two motions at the point where the wavefunction switches from antibonding to the bonding status that controls the stereochemical outcome.113 Whereas the substitution has a minor effect on the torsional mode, since the torsion is predominantly localized on the carbon skeletal framework, it exhibits a greater effect on the HOOP motion.190,195 As it is mainly the torsional mode that drives the wavepacket through the CoIn, modest changes in the reaction rate are observed. Although changes in the HOOP motion do not affect the reaction rate significantly, they do affect the branching ratio at the CoIn (Fig. 15e). This is because in 11,12-H2 and 11,12-D2, the C11-H/D and C12-H/D out-of-plane motions are coupled, resulting in symmetric and anti-symmetric HOOP vibrations, which maintain a certain phase relationship with the torsional motion. Interestingly, it appears that the double deuterium substitution results in an even improved phase matching as demonstrated by its higher QY. In contrast, partial deuteration reduces the vibrational coupling, leading to more isolated C–H and C–D out-of-plane motions and consequently less symmetric and anti-symmetric HOOP motion, which has been measured using resonance Raman spectroscopy.196 This in turn leads to a poorer phase matching with the torsional mode, inhibiting photoproduct formation. Furthermore, nonadiabatic trajectory calculations revealed that the partially deuterated 11-D and 12-D chromophores were more sensitive to the initial velocities than their symmetrically substituted counterparts, as was shown by their more de-phased HOOP motion and hence smaller VC.194 In contrast, the 11,12-H2 and 11,12-D2 chromophores displayed nonadiabatic trajectory dynamics that were relatively independent of the initial conditions, demonstrating that the ES topography rather than initial velocities dominate their ES evolution.
As these QY measurements were performed with incoherent light sources, the impact of VCs at the single-molecule level and its application in real-life systems irrespective of light conditions is confirmed. Furthermore, the nonadiabatic trajectory calculations with several initial Boltzmann conditions reproduce the QY trend in isotopic substitution, even though in the femtosecond laser experiments a specific vibrational wavepacket is prepared. Both the spectroscopic and quantum chemical results discussed in the current section therefore point towards a fully vibrationally coherent mechanism of rhodopsin photoisomerization, which strongly relies on a coordinated interplay of HOOP and torsion modes at the CoIn (Fig. 16).197
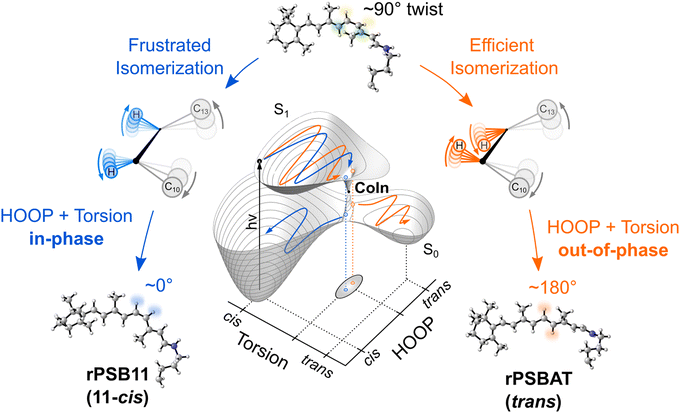 | ||
| Fig. 16 Vibrationally coherent and ultrafast rhodopsin photoisomerization. Compared with the one-mode representation of Fig. 14, this multi-mode model includes both the torsional and HOOP modes (Fig. 15). After photoexcitation of rPSB11 (11-cis) to the FC-point on the S1 PES, the coordinated motion of these modes with conserved relative phases guides the wavepacket to the CoIn, where the torsional angle is approximately 90°. The dynamical phase relationship of these modes controls the branching at the CoIn. Efficient isomerization to the all-trans product (rPSBAT) relies on an out-of-phase mode relationship (orange path). An in-phase relationship, however, results in frustrated isomerization, yielding the reactant 11-cis. Adapted with permission from ref. 197.197 | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 isomerization was enhanced, which is counterintuitive since the product is a more compressed molecule. The explanation provided involved the relative phase of the torsional motions of the C1–C2–C3–C4 and H–C2–C3–Me dihedral angles that was modulated by this mechanical force. Specifically, the force can be tuned such that motion of these torsional coordinates at the nonadiabatic decay point is in-phase, favoring the branching at the MECI towards the product.
C3 isomerization was enhanced, which is counterintuitive since the product is a more compressed molecule. The explanation provided involved the relative phase of the torsional motions of the C1–C2–C3–C4 and H–C2–C3–Me dihedral angles that was modulated by this mechanical force. Specifically, the force can be tuned such that motion of these torsional coordinates at the nonadiabatic decay point is in-phase, favoring the branching at the MECI towards the product.
Another clear manifestation of the phase matching rule was discovered in the 13-cis (rPSB13) to all-trans photoisomerization of Channelrhodopsin 2, which is a protein widely applied in optogenetics (this is a microbial rhodopsin with an ion-gating function, but here we discuss it as a rhodopsin analogue).199 Based on nonadiabatic molecular dynamics simulations, a positive (negative) HOOP velocity at the nonadiabatic decay event correlated to the trans (cis) isomer. A similar QY was found for a mutant protein that changes the electrostatic environment of the rPSB13 chromophore significantly. In contrast with the standard LZ model, a longer lifetime was found in the mutant, which was explained by the introduction of an ES barrier prior to the CoIn (see Fig. 5c).
Filatov et al. studied a rPSBAT model using direct nonadiabatic dynamics, confirming the role of relative phase in controlling the QY.200 In short, they pointed out that the QY for the photoisomerization at the central C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond is not only controlled by the HOOP motion, but also by its synchronization with two lower frequency modes, being a C–C torsional mode and a scissoring (bending) mode of the allyl and vinylamine moieties around the C2
C3 bond is not only controlled by the HOOP motion, but also by its synchronization with two lower frequency modes, being a C–C torsional mode and a scissoring (bending) mode of the allyl and vinylamine moieties around the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond. More specifically, anti-synchronization between the scissoring mode and the Q2 vector, which is a combination of the C–C torsion and HOOP, results in a higher isomerization QY at the C2
C3 bond. More specifically, anti-synchronization between the scissoring mode and the Q2 vector, which is a combination of the C–C torsion and HOOP, results in a higher isomerization QY at the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond. In contrast, when the trajectories are less synchronized, a greater propensity for the backward direction (IC) was observed. CASSCF nonadiabatic molecular dynamics calculations on a similar model compound show consistency with these results, highlighting the synchronization of HOOP and torsion for controlling the QY.201,202
C3 bond. In contrast, when the trajectories are less synchronized, a greater propensity for the backward direction (IC) was observed. CASSCF nonadiabatic molecular dynamics calculations on a similar model compound show consistency with these results, highlighting the synchronization of HOOP and torsion for controlling the QY.201,202
In a different and more simplified rPSB model (Scheme 7), Vukovic et al. showed with nonadiabatic dynamics how the photochemistry of double bond isomerization could be controlled by predistorting certain dihedral angles.203 The cooperative motion of the corresponding torsional modes was shown to be a prerequisite for forcing a double bond isomerization at a N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1 bond instead of a C2
C1 bond instead of a C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond. The protein environment controls the isomerization QY by imposing different predistortions, resulting in different torsional velocities due to the modified ES slopes. As the torsional modes are distorted to different extents their phase relationships are altered.69,204
C3 bond. The protein environment controls the isomerization QY by imposing different predistortions, resulting in different torsional velocities due to the modified ES slopes. As the torsional modes are distorted to different extents their phase relationships are altered.69,204
The importance of the coupling between the HOOP mode and the torsional mode was highlighted by Bovee-Geurts et al. in their Fourier-Transform Infrared study on several analogues of rhodopsin and isorhodopsin, which incorporates the cis-double bond at the 9-position instead of the 11-position.205 The smaller QY of isorhodopsin (0.26) compared to rhodopsin (0.67) was explained by the distortion of the HOOP mode and consequently poorer coupling to the torsional mode. Interestingly, this coupling was improved again by introduction of a cyclopropyl group at the 9-position in isorhodopsin, resulting in a higher QY (0.39).
3.2 Other ultrafast double bond photoisomerizations
Ultrafast double bond photoisomerizations appear in a wide variety of both biological and artificial molecular systems. This section demonstrates how mechanistic details acquired for rhodopsin photoisomerization, which we outlined in the previous section, apply to other systems as well.The ES VCs that were spectroscopically observed throughout the ultrafast (175 fs) E to Z photoisomerization of the truncated Cph1Δ form of phytochrome Cph1 (Scheme 7, E is shown) suggest that a phase relationship between modes that facilitate the nonadiabatic transition is conserved.206 Furthermore, one of these oscillations was assigned to a retinal-like HOOP (H15) motion, whereas another has been inconclusively assigned to a D-ring torsional rotation.207 In addition, these modes were assigned to Q2 and Q1, respectively. Despite these observations, it is not clear yet how the isomerization QY (0.10) is controlled by the relative phase of these modes. This will need to be addressed in the future.
The hula-twist mechanism for double bond photoisomerization provides another example where the cooperative motion of multiple modes (concerted single-bond and double bond rotation) drives photochemical reactions and has been observed in vitamin D, polyenes and stilbene, all involving a type 1 CoIn.107,208–210 Given the type of molecular skeleton of the chromophore and the protein constraints a hula-twist mechanism (aborted or not aborted) may also operate in phytochromes. Additionally, such a mechanism has been discussed in the family of green fluorescent proteins (GFPs),211 which act as a live-cell fluorescent imaging tool to monitor cellular processes,40 although involving an electronically distinct S1(ππ*)/S0 CoIn due to the CT nature of the ES (i.e. a type 3 CoIn). The high fluorescence QY in wild-type GFP is explained by a restricted ϕP torsional motion in the p-hydroxybenzylidene-2,3-dimethylimidazolinone (HBDI−) chromophore due to strong electrostatic interactions, which are diminished in the isolated chromophore,212 leading to enhanced torsional motion and consequently a fluorescence quantum yield of practically zero.213 Due to the variety of protein environments and chemical modification of its chromophore, GFPs may display a variety of functionalities, including photoisomerization.214 As an example, Zhang et al. performed QM/MM based trajectories on a mutant-GFP which, after generation of the anionic fluorophore through ultrafast proton transfer, undergoes photoisomerization through a concerted hula-twist mechanism involving asynchronous P-bond rotation (ϕP, C5–C4–C3–C2 dihedral angle) and I-bond rotation (ϕI, C4–C3–C2–C6 dihedral angle) (Scheme 7).215 Although these two modes are asynchronous, i.e. they do not start simultaneously, they maintain a certain phase relationship upon reaching the CoIn. Furthermore, the synchronized motion of the H15 HOOP mode with the ϕI mode was deemed important to lower the ES barrier to reach the CoIn.
A recent combined spectroscopic and computational study on the ES dynamics of isolated HBDI− investigated the relevance of the relative phase between the HOOP mode and the ϕI mode in controlling the QY of the isomerization of the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 bond (see Scheme 7) through the corresponding energetically uphill IS (Fig. 17).96 The distribution of nonadiabatic events (spawns) along the HOOP and I-torsion coordinates shown in Fig. 17a has maxima centred around out-of-phase configurations (Fig. 17c), where the direction of pyramidalization of the methine carbon (C3 in Scheme 7) is opposite to the torsional direction relative to 90°. The localized orbitals in Fig. 17d demonstrate how the out-of-phase direction of the HOOP mode relative to the torsion maintains the electronic degeneracy, forming the MECI-I (type 3, Section 2.2). Depending on the sign of the I-torsion, either the MECI-I+ (positive) or MECI-I2+ (negative) is reached, which are connected on the IS through a certain linear combination of HOOP and I-torsion (see black lines in Fig. 17a). Because the latter CoIn is closer to the FC-point (Fig. 17b), the majority of nonadiabatic events occur in this region. However, whereas nonadiabatic decay through MECI-I+ predominantly yields the E isomer (photoproduct) due to the negative HOOP phase, passage through MECI-I2+ results in formation of predominantly the Z isomer (reactant) due to the positive HOOP phase. Therefore, a HOOP-phase control similar to the one described in the rhodopsin photoisomerization (Section 3.1) appears to operate in the HBDI− chromophore and potentially in GFP variants.
C3 bond (see Scheme 7) through the corresponding energetically uphill IS (Fig. 17).96 The distribution of nonadiabatic events (spawns) along the HOOP and I-torsion coordinates shown in Fig. 17a has maxima centred around out-of-phase configurations (Fig. 17c), where the direction of pyramidalization of the methine carbon (C3 in Scheme 7) is opposite to the torsional direction relative to 90°. The localized orbitals in Fig. 17d demonstrate how the out-of-phase direction of the HOOP mode relative to the torsion maintains the electronic degeneracy, forming the MECI-I (type 3, Section 2.2). Depending on the sign of the I-torsion, either the MECI-I+ (positive) or MECI-I2+ (negative) is reached, which are connected on the IS through a certain linear combination of HOOP and I-torsion (see black lines in Fig. 17a). Because the latter CoIn is closer to the FC-point (Fig. 17b), the majority of nonadiabatic events occur in this region. However, whereas nonadiabatic decay through MECI-I+ predominantly yields the E isomer (photoproduct) due to the negative HOOP phase, passage through MECI-I2+ results in formation of predominantly the Z isomer (reactant) due to the positive HOOP phase. Therefore, a HOOP-phase control similar to the one described in the rhodopsin photoisomerization (Section 3.1) appears to operate in the HBDI− chromophore and potentially in GFP variants.
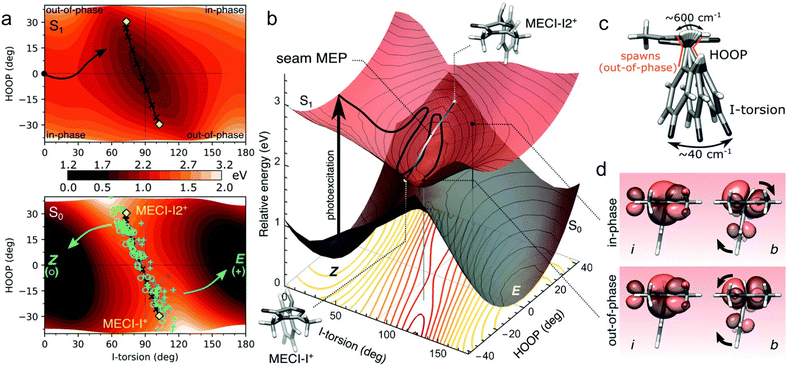 | ||
| Fig. 17 Phase relation between HOOP and I-torsion in HBDI− chromophore in the vicinity of the I-torsional IS.96 (a) S1 and S0 PES contour plots as a function of HOOP and I-torsion coordinates. The black arrow in the top panel indicates the minimum energy reaction path after photoexcitation to the FC-point. The yellow diamonds display the locations of two relevant MECIs (type 3, Section 2.2) along the I-torsion IS (black line connecting the two diamonds), MECI-I+ and MECI-I2+ (their geometrical structures are also shown in (c)), where the + sign indicates the enantiomeric direction (the other direction is not considered here). Nonadiabatic S1 to S0 transfer events (spawns) were computed with the AIMS method. The open green circles represent events resulting in the Z isomer, whereas the blue plus signs indicate events resulting in the E isomer. (b) Three-dimensional representation of the contour plots in (a). The black line again indicates the minimum energy reaction path from the FC-point to the I-torsional IS. The yellow points indicate the MECI structures that are connected by the grey line (the IS). The two black dots on the S1 PES correspond to in-phase and out-of-phase configurations at the same I-torsional angle (see (d)). The red lines demonstrate the coordinates where the S1 and S0 PESs become degenerate, i.e., form the IS. (c) Schematic representation of HOOP and I-torsion modes (ϕI in Scheme 7), indicated with their frequencies as estimated from the dynamics. (d) Localized orbitals on the I-ring (i) and methine bridge (b) for the in-phase and out-of-phase configurations indicated in (b). At this large I-torsional angle (∼90°), these two orbitals are orthogonal, which results in an electronic degeneracy between S1 and S0. This degeneracy is lifted with I-torsional motion but is counteracted by the out-of-phase HOOP motion, which conserves the orthogonality between i and b. Reproduced with permission from ref. 96. Copyright 2022 Royal Society of Chemistry. | ||
The C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N4 double bond in Me-FlOH, a model compound of the fluorophore in bacterial luciferase (Scheme 7), is ring-locked, allowing only IC as a relaxation pathway that involves a highly twisted S1(ππ*)/S0 CoIn (type 3, Section 2.2) through large dihedral angle distortion of C1–N2–C2–N4. The barrierless pathway towards this CoIn involves a sequential BLA stretch and out-of-plane deformation of the pyrimidine ring, that is similar to the relaxation pathway in cytosine and other pyrimidine bases.216–218 Despite the clear requirement of cooperative motion of two modes for nonradiative decay in these systems, it has yet to be investigated how the relative phase of these modes drives IC.
N4 double bond in Me-FlOH, a model compound of the fluorophore in bacterial luciferase (Scheme 7), is ring-locked, allowing only IC as a relaxation pathway that involves a highly twisted S1(ππ*)/S0 CoIn (type 3, Section 2.2) through large dihedral angle distortion of C1–N2–C2–N4. The barrierless pathway towards this CoIn involves a sequential BLA stretch and out-of-plane deformation of the pyrimidine ring, that is similar to the relaxation pathway in cytosine and other pyrimidine bases.216–218 Despite the clear requirement of cooperative motion of two modes for nonradiative decay in these systems, it has yet to be investigated how the relative phase of these modes drives IC.
The photoinduced double bond isomerizations present in biological systems have inspired chemists to design biomimetic switches that can perform the same function, in particular the optomechanical energy transduction found in rhodopsin.73,167 One major asset that these switches should demonstrate is VC throughout the complete reaction path, since a phase relationship between relevant modes should be conserved to achieve high QYs (Section 3.1). Since wavepacket decoherence is more significant on flat PESs, a prerequisite for conservation of VC is a steep gradient towards the CoIn. Chemical modification can be used to engineer VCs as demonstrated in a N-alkylated indanylidene–pyrroline (NAIP) biomimetic switch (Scheme 7).155 Whereas in Z-1 VC of a normal mode created on the S1 PES was conserved in the photoproduct, the VC generated on the ES PES for the demethylated E-2 was not observed. The corresponding QM/MM energy profiles and nonadiabatic trajectories rationalized this by an initial twist present in Z-1 that shapes the S1 and S2 PESs such that they are separated in energy so that the FC-region on the S1 PES displays a steep gradient towards the S1(ππ*)/S0 CoIn (type 3, Section 2.2).155 This twist is not present in E-2, resulting in a flatter ES PES and therefore reduced VC, presumably due to enhanced S2/S1 character mixing similar to rPSB11 isomerization in methanol compared to the opsin environment (Fig. 10).99
Although only the torsional mode VC was spectroscopically detected for Z-1, the nonadiabatic trajectories showed a coordinated interplay of modes similar to rhodopsin.173,219 An initial BLA stretching relaxation (10 fs) is followed by large out-of-plane pyrrolinium ring deformations and double bond torsion. It has been hypothesized that C3 (see Scheme 7), and less likely C2′ (due to the bulkier substituent), out-of-plane motions (COOP) mimic the HOOP motion in rhodopsin by restoring the p-orbital overlap through pyramidalization of C4 (and C1′).220 However, since the COOP motion is lower frequency than HOOP, the phase of the COOP mode might not change significantly upon reaching the CoIn. A poorly phase-matched COOP motion with respect to the torsional motion around the C1′![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 double bond could then be the reason that the QY in these compounds remain as low as 0.20. Alternatively, the phase matching rule may not be valid if the COOP velocity is too low, even though the relative phase is correct. On top of this, as the substituents at the reactive double bond are almost identical, the torsion and COOP modes are more strongly coupled than the torsion and HOOP in rPSB11, which could result in a slower torsional motion. The slower propagation along the reaction coordinate could lead to a broader population decaying on a longer time scale and, possibly, to a full range of phase relationships rather than a single favorable one.
C4 double bond could then be the reason that the QY in these compounds remain as low as 0.20. Alternatively, the phase matching rule may not be valid if the COOP velocity is too low, even though the relative phase is correct. On top of this, as the substituents at the reactive double bond are almost identical, the torsion and COOP modes are more strongly coupled than the torsion and HOOP in rPSB11, which could result in a slower torsional motion. The slower propagation along the reaction coordinate could lead to a broader population decaying on a longer time scale and, possibly, to a full range of phase relationships rather than a single favorable one.
The reasoning above suggests that turning on VCs by chemical substitution, along with optimization of the phase relationship between relevant normal modes, is a promising tool to control QYs.221,222 For double bond isomerization, these relevant normal modes typically involve torsional modes that are coupled to a pyramidalization mode, as has been observed for molecular motors as well.74,223 For instance, a recent quantum dynamics study on a chiral N-alkyl imine motor showed how the interplay of carbon pyramidalization, nitrogen out-of-plane, and torsional modes may control the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N photoisomerization QY and therefore the bias for unidirectional rotation.224
N photoisomerization QY and therefore the bias for unidirectional rotation.224
3.3 Other photochemical and photophysical processes
The current section aims to investigate the applicability of the phase matching rule for rhodopsin photoisomerization (Section 3.1) to any ultrafast vibrationally coherent ES process. The first reaction-induced VCs, i.e. generated by the ES PES far from the FC-region, have been measured by femtosecond laser pulse experiments on photodissociation reactions in the late 80s and 90s.225–229 As these reactions frequently involve a single stretching coordinate, one can, in principle, apply the standard LZ model (Scheme 5). On the other hand, since photochemical pericyclic reactions often involve multiple PESs and CoIns, analysis of the vibrational dynamics in these reactions may be challenging.9–11,105,230 Nevertheless, the concerted nature of these ultrafast reactions has been demonstrated and VCs have been detected for relevant reaction coordinates, such as in the electrocyclic ring-opening of 1,3-cyclohexadiene to Z-hexatriene (more specifically to its cis-Z-cis conformer).23,231,232 However, the direct assignment of the detected VCs to the Z-hexatriene product motion remains speculative for this particular reaction, which occurs within 68 fs upon S1(ππ*) excitation, as was recently observed with TRPES.23 The retro-Diels–Alder reactions of several cationic cyclic alkenes exhibited VCs, which could be identified as product VCs by mass-resolved detection, indicating a concerted mechanism.233Haiser et al. performed a joint time-resolved spectroscopic-quantum chemical study on the photochemically allowed disrotatory 4π-electrocyclization in lesion dinucleotides (simplified structures are shown in Fig. 18a) to understand UV-induced processes in DNA, clearly demonstrating the cooperative motion of multiple modes (red path in Fig. 18b).234 This reaction presumably proceeds through a type 1 CoIn involving an in-phase and out-of-plane (disrotatory) motion of N3 and C6 (the carbon atom making the new σ bond) after formation of an ES minimum in the (ππ*) state. Despite the activation barrier on this path, which is associated with a long ES lifetime (130 ps), the reaction QY is not negligible (0.082).235 Note that in this case the inverse correlation between ES lifetime and reaction QY predicted by the standard LZ model does not apply as it assumes a barrierless reaction path (Fig. 5b). Cleaving the phosphodiester backbone results in the formation of an energetically more accessible CoIn that forms an efficient funnel back to the reactant (green path in Fig. 18b) through out-of-plane motion of N3 accompanied by C4 pyramidalization,236 similar to the aborted double bond isomerization for the CoIn (type 3) found in 5-methylpyrimidinone (5M2P, see structure in Fig. 18a).217,237 The latter motion cannot occur in the intact backbone lesion structure, due to the ring strain from the rigid macrocycle, forcing the ES wavepacket to change its direction to CoInDewar (red path). Although this mechanism implies competition between population of similar molecular modes, it represents a case distinct from the one discussed above for rhodopsin where the HOOP and isomerization mode of rPSB11 contribute to propagation towards a single reactive IS segment. Instead, this case is more reminiscent of a situation like the one depicted in Fig. 5e where the intact backbone modifies the topography of the ES PES to favour one type of CoIn (type 1) rather than the other (type 3).
 | ||
| Fig. 18 (a) Reaction schemes for photochemical dynamics of dinucleotides T(6-4)CT with an intact and cleaved DNA backbone. Note that only the photochemically active core of T(6-4)CT is shown, indicating the remaining part of the DNA backbone with a black line. Photoexcitation of T(6-4)CT with an intact DNA backbone results in formation of the Dewar valence isomer, whereas T(6-4)CT with a cleaved DNA backbone results in IC, having a similar CoIn mediated decay mechanism as 5-methyl-pyrimidone (5M2P). (b) Photochemical and photophysical pathways on the ES PES illustrated for these structures. After photoexcitation to the ππ* state, an initial relaxation on the S1 PES leads to an ES minimum for both the intact and cleaved (without the phosphodiester group) backbone structures. From there, the cleaved structure follows the green pathway to reach CoIn5M2P, which is an efficient funnel for IC. In contrast, for the intact structure this CoIn is not accessible and hence follows the red pathway to a type 1 CoInDewar that leads to either formation of the Dewar valence isomer or the reactant (IC).234 Adapted with permission from ref. 234. Copyright 2011 John Wiley and Sons. | ||
Singlet fission is a photophysical process that converts a singlet ES (S1) molecule into two triplet ES (T1) moieties via a correlated triplet pair intermediate (1TT) (Fig. 19a), which has the potential to increase the theoretical power conversion efficiency in organic photovoltaics (OPVs).238 Multiple studies on thin film singlet fission materials have shown that not only both intramolecular and intermolecular nuclear motions are relevant for driving the singlet fission, but also that the ultrafast S1 to 1TT conversion is vibrationally coherent,239–242 which might be switched off by solvent effects.243 For a complete overview of the vibronic coupling mechanisms in ultrafast coherent 1TT formation, the reader is referred to the recent review by Kim and Musser.244 As an illustration, we focus here on one study where the nature and coordinated interplay of the critical normal modes in a pentacene dimer have been elucidated using a combination of IVS and fully quantum mechanical tree-tensor network state simulations (TTNS).245 By tracking the impulsively generated VCs after photoexciting the S1(ππ*) state, Schnedermann et al. concluded that the wavepacket survives the nonadiabatic transition, hypothetically through a CoIn.103 Combining the spectroscopic data with the TTNS method,246 a detailed molecular movie of the first 200 fs of this singlet fission trajectory could be produced, showing a periodicity in the tuning-coupling mode (practically the Q1 and Q2 vectors of the BP, respectively) subspace that indicates the conservation of a phase relationship between these modes (Fig. 19c). The initial 75 fs are dominated by the tuning mode (vertical orange displacement) that relaxes the wavepacket out of the FC-region by in-plane ring deformations, stretching the central pentacene–pentacene bond length effectively. In the next 125 fs, the activity is shifted towards the coupling mode (horizontal green displacement) that twists this central bond, enforcing a deviation from orthogonality between the pentacene moieties which causes transient overlap between their orbitals, eventually forcing the nonadiabatic S1 to 1TT transition.247 Even though the reaction appears as a subsequently coordinated process in which the photon energy is initially funneled into the tuning mode (A1) after which via energy transfer the B1 mode becomes active, similar to the BLA and HOOP-torsion sequence in rhodopsin (Section 3.1), at every stage there is a cooperative motion of these modes that implies an intramolecular vibrationally coherent process. However, from these simulations it is not evident yet how the relative phase of the tuning and coupling modes controls the near ideal efficiency of 192% for the singlet fission process, which has been quantified by the triplet QY in toluene.248 The phase relationship described in this case appears to focus on the change in the reaction coordinate along the ES PES of the system. Nevertheless, it is likely that the understanding of the QY also requires the comprehension of the decay at an IS segment and, therefore, the participation of one or more extra vibrational modes in the decay process.
 | ||
| Fig. 19 Multi-mode mechanism for ultrafast singlet fission. (a) PES visualization for a general singlet fission reaction. After photoexcitation to the S1 state, the correlated triplet-pair 1TT is populated on an ultrafast timescale through a CoIn, which on a slower timescale decoheres into two triplet states T1.241 Adapted with permission from ref. 241. Copyright 2015 Springer Nature. (b) Vector visualization of the relevant tuning (A1) and coupling (B1) modes for the S1 to 1TT conversion in the pentacene dimer DP-Mes, shown as truncated molecular structures for clarity purposes. (c) Correlation plot for the amplitudes of the A1 and B1 modes during the first 200 fs of the singlet fission trajectory. Indicated in orange is the tuning-mode dominated regime and indicated in green is the coupling-mode dominated regime. The arrows indicate the direction of the trajectory. The quantum dynamics calculations made use of a tree-tensor network state simulation (TTNS).245 Adapted from ref. 245, licensed under a Creative Commons Attribution 4.0 International License. | ||
Several recent studies focus on the interpretation of the VC spectral evidence in terms of wavepacket evolution along different vibrational modes. The importance of VCs and their link with CoIns has been recognized in OPVs, where energy transfer and electron transfer should be controlled.249–252 For instance, it has been suggested that VC enhances the efficiency of energy transfer in a photosynthetic dimer model system253 and charge separation at a donor-acceptor interface.254 Moreover, the intimate coupling between vibrational modes and energy transfer in photosynthetic functions is gaining more attention over the years, driven both by (two-dimensional electronic) spectroscopic achievements255–258 as well as mixed quantum-classical simulations, which clearly show a cooperative effect of multiple modes.259,260 Despite this, often a single mode is assumed to be relevant in the description of vibronic coupling.261–263 However, as has been illustrated multiple times now in this review, there may be coupling of electronic states to multiple vibrational modes, strongly affecting the dynamics and involvement of CoIns.264 Tracking reaction-induced VCs in photoexcited donor–acceptor–donor (D–A–D) dyes has been used to distinguish between the formation of excimer and charge transfer (CT) states,265 and to elucidate the (bimodal) reaction path of ultrafast intermolecular electron transfer in an electron-donating solvent266 and at dye-semiconductor interfaces.267,268 Increasing the electron-donating character by chemical substitution resulted in faster electron transfer reactions in naphthalenediimide (NDI) dyes (Fig. 20a), which was rationalized by the conservation of VC throughout the reaction.269 Crucially, the dye with the fastest electron transfer (shown in Fig. 20a) displayed two relevant VCs in the product involving NDI ring distortion and stretching coordinates, modulating the coupling between D and A. However, the detailed structure of the CoIn and mechanism of cooperation between these two modes, possibly involving an IS segment, could not be determined with just these one-dimensional spectroscopic techniques. Experimental methods that may elucidate the role of multi-mode vibronic couplings in ultrafast ES processes are two-dimensional techniques, such as 2D electronic,161,270 2D vibrational271,272 and 2D vibrational–electronic spectroscopy.273–275 However, even these techniques reach their full potential when combined with nonadiabatic molecular dynamics simulations to elucidate the IS structure,276 as was demonstrated by the recent 2DES study from De Sio et al., who discovered the first intermolecular CoIn and the relevant coupling and tuning modes in an organic A–D–A oligomer.277 The reader is referred to the excellent review by Scholes and co-workers for an overview of 2DES techniques as well as their application to a number of case studies.278
 | ||
| Fig. 20 (a) Vectorial representation of a vibrational mode from a D–A dye involving C–N stretching and NDI ring distortion, which was observed as a VC in the product of an ultrafast electron transfer reaction. Not shown is the antisymmetric analogue of these two reaction coordinates which was detected as a product VC in this D–A dye as well.269 Adapted with permission from the ESI of ref. 269. Copyright 2021 American Chemical Society (b) Fe(II) complex with polypyridyl ligand (left structure) shows large-amplitude motion which facilitates fast nonradiative decay when excited to the MLCT state. Blocking these modes through addition of copper (right structure) results in a significantly longer MLCT lifetime.279 Grey: carbon. Blue: nitrogen. Orange: iron. Green: copper. White: hydrogen. Red: oxygen. Reproduced with permission from ref. 279. Copyright 2020 Springer Nature. | ||
Despite this finding, CoIns in OPVs and other optoelectronic materials have generally been regarded as funnels for IC, leading to charge losses. Theoretical investigations on the structure of CoIns and the relevant vibrational dynamics are again key to avoid these unfavorable decay channels, as tentatively demonstrated for fluorescent molecular crystals,39 D–A dyes36 and (nano)materials, in which defect-induced CoIns (DICIs) are associated with fast nonradiative decay.37,280–284 The relatively low IC rates in lead-halide perovskites,285 which are organic–inorganic hybrid materials considered for next-generation PV applications, have been computationally explained by the energetic inaccessibility of CoIns in molecular and nanomaterial sized models.286
Molecular inorganic systems often find applications in photocatalysis, in which photoinduced electron transfer might be in competition with IC. Retarding specific vibrational modes by rigidifying the chemical structure to facilitate photoredox chemistry is a strategy that was recently applied by McCusker and co-workers with the aim of extending the MLCT lifetime in a Fe(II) complex.287 IVS was used to identify the modes involved in IC, as these appeared as vibronic coherences. The term vibronic is used here instead of vibrational to emphasize that the coherence is maintained across two electronic states. These vibronically coherent modes were synthetically modified to decouple them from the IC reaction coordinate (Fig. 20b),279 resulting in a 20-fold lifetime increase. Targeting vibronic coherences has great potential to understand and control other ultrafast ES processes, such as ISC,288,289 proton-coupled electron transfer290 and singlet fission.291
Although ISC is often regarded as a much slower process than IC due to the spin-forbidden character of this nonadiabatic transition, in some cases it may be ultrafast even in the absence of heavy-atom induced strong spin–orbit coupling.292–294 In a nonrelativistic description ultrafast ISC involves a singlet–triplet crossing, which is topologically not a CoIn (in a fully relativistic description this can be seen as a CoIn)295 but rather a linear—i.e. not conical—crossing part of a 3N − 7 IS as the off-diagonal elements are zero for different spin multiplicities (eqn (2), Section 1). Nevertheless, the coupling of multiple vibrational modes could be relevant to the ISC dynamics in transition–metal complexes leading to mechanistic pictures similar to the ones discussed above. Spectroscopically observed vibrational and vibronic coherences are again relevant markers to track and control ISC and IC pathways.288,296 Khalil and co-workers studied the photochemical dynamics of a Ru(II) complex with 3D EV spectroscopy, which is a technique capable of following vibronic couplings involving multiple normal modes.297 Clear evidence of the cooperation between two normal modes to reach the 3MLCT state through a singlet–triplet crossing was provided in this study.
Recent ground-breaking work of Ihee and co-workers demonstrated how femtosecond time-resolved X-ray liquidography (TRXL) could reveal real-time wavepacket trajectories in the photoinduced asynchronous bond formation of a trimer gold complex, [Au(CN)2−]3, from its monomers in an aqueous solution.298 The multidimensional wavepacket trajectory in Fig. 21 shows how after excitation to the FC-region in the S1 state, its evolution on the T1′ PES in the first 60 fs is dominated by formation of one covalent bond (RAB) and within 360 fs the next one (RBC), which along with increasing bond angle (θ) eventually yields the 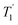 equilibrated linear trimer complex. From the RAB–RBC subspace it is clear how the temporal changes in both coordinates are correlated, implying a vibrationally coherent ultrafast photochemical reaction. The atomistic motions associated of RAB and RBC could also be fitted to the sum of two symmetric stretching modes.299
equilibrated linear trimer complex. From the RAB–RBC subspace it is clear how the temporal changes in both coordinates are correlated, implying a vibrationally coherent ultrafast photochemical reaction. The atomistic motions associated of RAB and RBC could also be fitted to the sum of two symmetric stretching modes.299
 | ||
| Fig. 21 Photoinduced asynchronous bond formation of the gold trimer complex [Au(CN)2−]3. Excitation with a pump pulse generates an ES wavepacket in the S1 state, which undergoes ISC to populate T1′ in 20 fs. (a) Evolution of ES wavepacket in T1′ as a function of multiple nuclear coordinates, RAB, RBC and θ, which show significant changes in the early timescale (<360 fs). Some representative points during this period are indicated with red dots. The trajectory in the RAB − RBC subspace is shown at the bottom. At later time (>360 fs), oscillations around the equilibrium structure of T1′ occur, of which the equilibrium coordinates RAB and RBC are indicated with red dashed lines. (b) Geometrical transient structures at representative points in time, showing with red and blue arrows the changes in bond lengths and angle respectively. Whereas the yellow dots represent the geometrical evolution of Au atoms, the grey dots represent the Au atoms in the FC-region. Covalent bond formation is visualized with the thick black lines. The CN ligands are omitted for clarity.298 Reproduced with permission from ref. 298. Copyright 2020 Springer Nature. | ||
4. Conclusion and outlook
Above we have seen how, in general, the control of “elementary” ultrafast photochemical processes requires information on the precise dynamics leading to the IS. This is provided by state-of-the-art time-resolved spectroscopic and computational studies that, in recent years, have produced results leading to a significantly refined and extended mechanistic spectrum of these processes. This conclusion is schematically illustrated in Fig. 22 that displays the limiting mechanisms affecting the product/reactant branching ratio of a barrierless photochemical reaction of the type shown in Fig. 5b and 6. In Fig. 22a we display what is, essentially, a one-mode mechanism implying decay at a single critical CoIn usually assumed to correspond to the MECI. In such a situation, the population propagates along a single ES path ultimately entering the BP along a specific direction, which is described by a combination of Q1 and Q2. If this direction is known one can apply the standard LZ model that predicts that an increase in nuclear velocity at the point of decay (this may as well arise from a steeper slope of the ES PES) leads to an enhanced QY. As discussed above, this simple conclusion has opened the route to the rationalization of many trends observed by chemical substitution in this review.61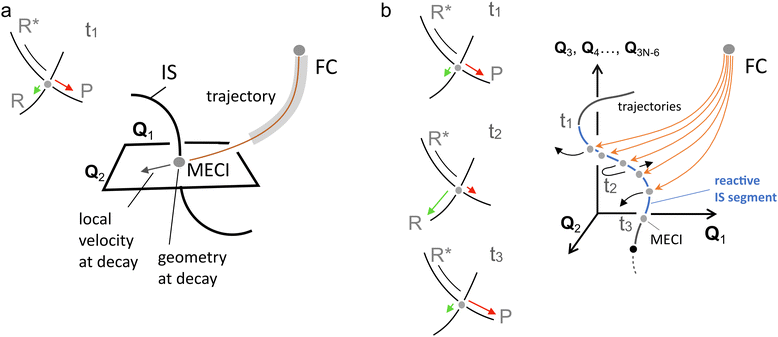 | ||
| Fig. 22 Limiting mechanisms for an “elementary” ultrafast photochemical reaction. (a) One-mode mechanistic picture. The MECI is accessed along a single specific mode (reaction coordinate) describing the trajectory along the BP of a compact (vibrationally coherent) population. The QY is proportional to the corresponding velocity at the decay point (see inset on the top-left). Such mode does not necessarily correspond to the mode driving the system out of the FC region. In fact (see trajectory region highlighted in grey), the ES trajectory may be described by a “curved” coordinate featuring sequential progression along different modes. (b) Multi-mode mechanism. In this case the populations are less compact or partially fragmented thus generating a set of subpopulations reaching the IS at different times (e.g. t1, t2 and t3) and along different BP modes (see also Fig. 3b). Along each trajectory the phase relationship between different modes belonging to BP and/or IS (e.g.Q1 and Q3) changes resulting in different velocity patterns at decay. The QY now becomes a much more complex quantity featuring the contributions of each subpopulation (see insets on the left). | ||
Despite its successes, the one-dimensionality of the reaction coordinate that the above model assumes fails when the photochemical reaction mechanism is of multi-mode character, and it becomes important to consider decay at multiple CoIn points along the IS. Such a mechanism is shown in Fig. 22b and is consistent with the studies of the photoisomerization of the rPSB11 chromophore in rhodopsin where the “reaction coordinate” is described by a number of parallel trajectories each displaying distinct dynamic changes in the weights of the HOOP and torsional modes.134,153 The final QY is, therefore, given by the sum of different QY contributions determined by the evolution of the phase relationship of each trajectory and, in turn, the velocities at decay that may also have opposite orientation for different subpopulations. It is apparent that the multi-mode mechanism can lead to the failure of the standard LZ model. For instance, such event would explain an “anti-LZ” correlation, i.e. slower nuclear velocity leading to enhanced isomerization QY.205 In addition, and irrespective of the operating mechanism, the observation of VCs in complex molecular systems throughout the complete photoisomerization path strongly hints towards a higher-dimensional reaction coordinate that incorporates multiple normal modes and their coordinated interplay.73 This results in vibrationally “curved” reaction coordinates.
Strong computational evidence supported by isotopic substitution experiments has been provided for the photoisomerization of rPSB11 and rPSBAT that demonstrates a multi-mode model, demonstrating the relevance of the relative phase of normal modes in controlling the photochemical QY.113,194 Specifically, it is the branching at different IS points that is controlled by the relative phase of the HOOP mode with respect to the torsional mode. This phase matching is dependent on the ES PES, as this provides the forces on the reactive normal modes and therefore the dynamical progression towards the CoIn. However, again in contrast with the standard LZ model, it is not only the velocity along one relevant normal mode (e.g., the torsional mode) that controls the branching ratio at decay and therefore the QY, but the coordinated motion of multiple modes up until the BP of each CoIn point along the IS segment that is entered (more correctly the point where the wavefunction switches from antibonding to bonding). A prerequisite for this phase-controlled regime is that the nuclear velocities are above a certain threshold, as reactive modes with near zero velocities would not have a favored direction towards either the product or reactant, possibly making the phase rule less effective.
Although it is fascinating that rhodopsin photoisomerization displays multi-mode VC throughout the complete reaction, there is no reason to suspect that it is unique in this regard. Indeed, it is likely that such a mechanism applies to other vibrationally coherent ultrafast ES processes as well, including pericyclic reactions, electron transfer and energy transfer. Although in many of these processes it has been highlighted how the coordinated motion of multiple normal modes drives ES dynamics and in some cases VCs of those modes have even been spectroscopically observed throughout the reaction,215,225,234,245,300 detailed investigations of the decay process at a level similar to what has been done for rhodopsin photoisomerization are required to confirm a multi-mode mechanism for these systems. We anticipate that an increased understanding of the role that the coordinated motion of normal modes play near the CoIn will greatly benefit from advances in both the simulation and spectroscopy fields.152 Computational photochemists in particular will benefit from rapid progress in sampling techniques and machine learning algorithms for the accurate prediction of ES properties and automated discovery of ultrafast photochemical reactions and mechanisms.58,141,142
Owing to major advances in the generation of stable and short laser pulses, ultrafast spectroscopic techniques are capable of studying temporally resolved ES processes with unprecedented high accuracy,301 including ultrafast fluorescence upconversion techniques specifically applied to photochemical reactions in confined media.302 In particular, time-domain Raman spectroscopy has benefited from the availability of <10 fs pulses, allowing the observation of fundamental modes up to ∼3000 cm−1.168 However, the observation of VCs associated with coupling the two ES PESs involved in the nonadiabatic transition remains a challenge, due to the near-zero Huang–Rhys factor.244 Technological progress in higher dimensional ultrafast techniques enables the observation of vibrational and vibronic couplings in the ES, which is critical to develop a multi-mode understanding of photochemical reactions next to the mere detection of the relevant modes.297,303–308 However, the assignment of normal modes is often solely based on a numerical comparison between the frequencies obtained from Fourier-transformation with computationally acquired frequencies. More detailed mechanistic insights of ES dynamics may be obtained through analysis of time-dependent amplitude and phase, providing a more direct comparison to nonadiabatic calculations as well. In particular, addition of an extra “actinic” pulse in IVS experiments allows the time-resolved tracking of ES modes.169,309,310 Although it has already been demonstrated how tracking the time-dependent amplitude provides crucial insights in the ES proton transfer in the photoactive yellow protein311 and GFP,304 we believe that tracking the relative phase of ES modes could elucidate the multi-mode character of photochemical reaction paths and its impact on the QY.
Tracking the time-dependent phase and amplitude of the ES nuclear dynamics might be achieved with alternative spectroscopic techniques that achieve atomistic detail, such as femtosecond electron diffraction.312,313 Alternatively, the recent development of X-ray free electron laser beam sources has enabled techniques which are, in principle, capable of probing photochemical dynamics with such high structural sensitivity and temporal resolution,314 as has been demonstrated experimentally through direct observation of CoIn dynamics with transient X-ray absorption spectroscopy.315–319 To extract information about the underlying nonadiabatic dynamics from their spectral signatures it is key to construct theoretical frameworks,320 with important contributions for transient X-ray absorption spectroscopy,321 but also X-ray based techniques that have only been demonstrated theoretically, such as time-resolved X-ray diffraction,322,323 time-resolved X-ray spontaneous emission spectroscopy324 and TRUECARS. The latter was developed by Mukamel and colleagues to analyse vibronic coherences that are generated by stimulated ultrafast X-ray Raman pulses.325 The TRUECARS probing setup is designed to measure these generally weaker vibronic coherence signals, which are otherwise hidden underneath the much stronger electronic population contributions, allowing the detection of multiple CoIn passages as well as the assignment of the relevant vibronic normal modes of a photoexcited bichromophoric molecule.326 Finally, amplifying vibronic coherences with a correctly timed resonant IR pulse holds further promise to detect these otherwise weak signals in X-ray diffractive imaging.327 The use of IR pulses could also elucidate vibrational energy transfer mechanisms as recently demonstrated in a GS isomerization reaction.328
We propose that the three pillars that have elucidated the mechanism of ultrafast rhodopsin photoisomerization, should function as a template to discover and rationalize similar multi-mode mechanisms in other systems. Although VCs that are preserved after passage through a CoIn could potentially demonstrate the significance of phase matching at different IS points (I), nonadiabatic dynamics calculations are required for a detailed understanding of how this coherence connects to the QY (II). The vibrational phase isotope effect is then the perfect experimental confirmation for such a mechanism, as isotopic substitution only changes the vibrational dynamics, but not the spectroscopic properties or the shape of the ES PES (III). Alternatively, application of an electric field or external forces (Section 3.1.4) will prove fruitful in future research, as subtle tuning of the phases of specific normal modes may be achieved.198,329,330 It is also expected that synergy between coherent control laser experiments and the tuning of the relative phases in controlling photochemistry will increase, as shaped laser pulses are potentially capable of selectively preparing wavepackets on the ES PES with certain mode phase relationships. Although the optimization of the isomerization QY in rhodopsin162,331 and molecular switches,332 or the selective hydrogen abstraction in acetylenes, allenes and toluene333–335 has already been achieved with coherent control, these approaches rely on learning algorithms rather than chemically intuitive tuning or rational design.
Any rational design approach to control the ultrafast ES dynamics and reactivity should start by characterizing the normal modes which drive the nonadiabatic decay through their coherent motion and disentangling them from irrelevant VCs,336,337 which may be derived from mode-specific dephasing times.338 Although the methods described above could achieve this, synthetic modification has proven to be a successful method as well to assess whether a vibronic relevant mode has been targeted through measurement of the reaction rate or QY.205,287 Optimization of the phase matching may, in principle, then be accomplished through a similar chemical modification, shaping the ES PES in such a way that the targeted normal mode either differs in relative phase or frequency. This chemical modification may be an electronically or sterically distinct substituent, a protein environment or solvent.152,339 Finally, with the advent of attosecond laser pulses an initial ES population can be prepared in a mixed electronic state, which may result in “unnatural” populations of coupled vibrational modes, thus having the potential of further improving our understanding of multi-mode photochemistry.340 We predict that such a rational design approach, at the molecular or supramolecular levels, will impact a wide variety of research fields that rely on light induced processes, including molecular motors, artificial sunscreens and solar energy conversion, where photochemistry, photostability and a long-lived ES are the goals respectively.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Christoph Schnedermann and Prof. Fred Brouwer for useful discussions. We also wish to thank Prof. Michael A. Robb for his useful comments on the first version of the manuscript. M. O. acknowledges support from NSF CSDM-A Grant No. 2102619 and European-Union, Next Generation EU, MIUR Italia Domani Progetto mRNA Spoke 6 del “National Center for Gene Therapy and Drugs based on RNA Technology”. – CUP B63C22000610006.References
- D. R. Yarkony, J. Phys. Chem. A, 2001, 105, 6277–6293 CrossRef CAS.
- K. R. Naqvi and W. B. Brown, Int. J. Quantum Chem., 1972, 6, 271–279 CrossRef CAS.
- E. Teller, J. Phys. Chem., 1937, 41, 109–116 CrossRef CAS.
- G. Herzberg and H. C. Longuet-Higgins, Discuss. Faraday Soc., 1963, 35, 77–82 RSC.
- X. Zhu and D. R. Yarkony, Mol. Phys., 2016, 114, 1983–2013 CrossRef CAS.
- F. Bernardi, S. De, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 1990, 112, 592–634 CrossRef.
- M. A. Bernardi, F. De Sushovan, S. Olivucci and M. Robb, J. Am. Chem. Soc., 1990, 112, 1737 CrossRef.
- I. N. Ragazos, M. A. Robb, F. Bernardi and M. Olivucci, Chem. Phys. Lett., 1992, 197, 217–223 CrossRef CAS.
- F. Bernardi, M. Olivucci, M. A. Robb and G. Tonachini, J. Am. Chem. Soc., 1992, 114, 5805–5812 CrossRef CAS.
- M. Olivucci, I. N. Ragazos, F. Bernardi and M. A. Robb, J. Am. Chem. Soc., 1993, 115, 3710–3721 CrossRef CAS.
- I. J. Palmer, I. N. Ragazos, M. A. Robb, F. Bernardi and M. Olivucci, J. Am. Chem. Soc., 1993, 115, 673–682 CrossRef CAS.
- P. Celani, M. Garavelli, S. Ottani, F. Bernardi, M. A. Robb and M. Olivucci, J. Am. Chem. Soc., 1995, 117, 11584–11585 CrossRef CAS.
- I. J. Palmer, I. N. Ragazos, F. Bemardi, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 1994, 116, 2121–2132 CrossRef CAS.
- M. J. Bearpark, F. Bernardi, S. Clifford, M. Olivucci, M. A. Robb, B. R. Smith and T. Vreven, J. Am. Chem. Soc., 1996, 118, 169–175 CrossRef CAS.
- P. J. Reid, S. J. Doig, S. D. Wickham and R. A. Mathies, J. Am. Chem. Soc., 1993, 115, 4754–4763 CrossRef CAS.
- D. R. Cyr and C. C. Hayden, J. Chem. Phys., 1996, 104, 771–774 CrossRef CAS.
- M. O. Trulson and R. A. Mat, J. Phys. Chem., 1990, 94, 5741–5747 CrossRef CAS.
- K. O. Hiller, K. D. Asmus, F. P. Lossing, Y. T. Lam, A. Maccoll and C. E. Klots, J. Am. Chem. Soc., 1993, 115, 682–686 CrossRef.
- F. Bernardi, M. Olivucci and M. A. Robb, Chem. Soc. Rev., 1996, 25, 321–328 RSC.
- M. S. Schuurman and A. Stolow, Annu. Rev. Phys. Chem., 2018, 69, 427–447 CrossRef CAS PubMed.
- P. Avouris, W. M. Gelbart and M. A. El-Sayed, Chem. Rev., 1977, 77, 793–833 CrossRef CAS.
- A. P. Penner, W. Siebrand and M. Z. Zgierski, J. Chem. Phys., 1978, 69, 5496–5508 CrossRef CAS.
- S. Karashima, A. Humeniuk, R. Uenishi, T. Horio, M. Kanno, T. Ohta, J. Nishitani, R. Mitrić and T. Suzuki, J. Am. Chem. Soc., 2021, 143, 8034–8045 CrossRef CAS PubMed.
- J. M. Toldo, M. T. do Casal and M. Barbatti, J. Phys. Chem. A, 2021, 125, 5499–5508 CrossRef CAS PubMed.
- Y. Shao, J. M. De Ruiter, H. J. M. De Groot and F. Buda, J. Phys. Chem. C, 2019, 123, 21403–21414 CrossRef CAS.
- R. R. Birge, Biochim. Biophys. Acta, Bioenerg., 1990, 1016, 293–327 CrossRef CAS PubMed.
- M. Wanko, M. Hoffmann, T. Frauenheim and M. Elstner, J. Comput.-Aided Mol. Des., 2006, 20, 511–518 CrossRef CAS PubMed.
- D. Polli, P. Altoè, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura, R. A. Mathies, M. Garavelli and G. Cerullo, Nature, 2010, 467, 440–443 CrossRef CAS PubMed.
- B. G. Levine and T. J. Martínez, Annu. Rev. Phys. Chem., 2007, 58, 613–634 CrossRef CAS PubMed.
- S. Takeuchi, S. Ruhman, T. Tsuneda, M. Chiba, T. Taketsugu and T. Tahara, Science, 2008, 322, 1073–1077 CrossRef CAS PubMed.
- C. E. Crespo-Hernández, B. Cohen, M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019 CrossRef PubMed.
- W. J. Schreier, T. E. Schrader, F. O. Koller, P. Gilch, C. E. Crespo-Hernández, V. N. Swaminathan, T. Carell, W. Zinth and B. Kohler, Science, 2007, 315, 625–629 CrossRef CAS PubMed.
- J. Fan, L. Finazzi and W. J. Buma, Phys. Chem. Chem. Phys., 2022, 24, 3984–3993 RSC.
- T. T. Abiola, B. Rioux, J. M. Toldo, J. Alarcan, J. M. Woolley, M. A. P. Turner, D. J. L. Coxon, M. Telles Do Casal, C. Peyrot, M. M. Mention, W. J. Buma, M. N. R. Ashfold, A. Braeuning, M. Barbatti, V. G. Stavros and F. Allais, Chem. Sci., 2021, 12, 15239–15252 RSC.
- D. P. Hoffman, S. R. Ellis and R. A. Mathies, J. Phys. Chem. A, 2014, 118, 4955–4965 CrossRef CAS PubMed.
- A. M. El-Zohry, D. Roca-Sanjua and B. Zietz, J. Phys. Chem. C, 2015, 119, 2249–2259 CrossRef CAS.
- B. G. Levine, W. T. Peng and M. P. Esch, Phys. Chem. Chem. Phys., 2019, 21, 10870–10878 RSC.
- J. K. McCusker, Science, 2019, 363, 484–488 CrossRef CAS PubMed.
- M. Rivera, L. Stojanović and R. Crespo-Otero, J. Phys. Chem. A, 2021, 125, 1012–1024 CrossRef CAS PubMed.
- G. U. Nienhaus, Angew. Chem., Int. Ed., 2008, 47, 8992–8994 CrossRef CAS PubMed.
- H. Kandori, Biophys. Rev., 2020, 12, 355–361 CrossRef CAS PubMed.
- B. O. Leung and K. C. Chou, Appl. Spectrosc., 2011, 65, 967–980 CrossRef CAS PubMed.
- P. Vogel and K. N. Houk, Organic Chemistry: Theory, Reactivity and Mechanisms in Modern Synthesis, Wiley-VCH, Weinheim, 2019, pp. 710–726 Search PubMed.
- M. Persico and G. Granucci, Photochemistry: A Modern Theoretical Perspective, Springer, Cham, 2018, pp. 141–175 Search PubMed.
- G. J. Atchity, S. S. Xantheas and K. Ruedenberg, J. Chem. Phys., 1991, 95, 1862–1876 CrossRef.
- H. Koppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 Search PubMed.
- D. R. Yarkony, J. Phys. Chem., 1996, 100, 18612–18628 CrossRef CAS.
- A. M. Virshup, J. Chen and T. J. Martínez, J. Chem. Phys., 2012, 137, 22–519 CrossRef PubMed.
- N. Agmon, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 388–404 RSC.
- Y. J. Hong and D. J. Tantillo, Nat. Chem., 2009, 1, 384–389 CrossRef CAS PubMed.
- M. Ruckenbauer, M. Barbatti, T. Müller and H. Lischka, J. Phys. Chem. A, 2013, 117, 2790–2799 CrossRef CAS PubMed.
- J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, Second edn, 2001, pp. 240–267 Search PubMed.
- I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967 RSC.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- J. M. Anglada, J. M. Bofill and R. Crehuet, J. Comput. Chem., 1999, 20, 1112–1129 CrossRef CAS.
- V. Balzani, P. Ceroni and A. Juris, Photochemistry and Photophysics. Concepts, Research, Applications., Wiley-VCH, Weinheim, 2014, pp. 55–74 Search PubMed.
- H. An, H. Choi, Y. S. Lee and K. K. Baeck, ChemPhysChem, 2015, 16, 1529–1534 CrossRef CAS PubMed.
- E. Pieri, D. Lahana, A. M. Chang, C. R. Aldaz, K. C. Thompson and T. J. Martínez, Chem. Sci., 2021, 12, 7294–7307 RSC.
- L. M. Frutos, U. Sancho, M. Garavelli, M. Olivucci and O. Castaño, J. Phys. Chem. A, 2007, 111, 2830–2838 CrossRef CAS PubMed.
- C. Wittig, J. Phys. Chem. B, 2005, 109, 8428–8430 CrossRef CAS PubMed.
- L. D. Landau, Phys. Z. Sowjetunion, 1932, 1, 88–98 CAS.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 Search PubMed.
- X. R. Ma, J. Zhang, Y. C. Xiong and W. Zhou, Mol. Phys., 2022, 120, e2051761 CrossRef.
- T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-Alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Chem. Rev., 2020, 120, 2215–2287 CrossRef CAS PubMed.
- A. Kühl and W. Domcke, J. Chem. Phys., 2002, 116, 2761 CrossRef.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS PubMed.
- J. Briand, O. Bräm, J. Réhault, J. Léonard, A. Cannizzo, M. Chergui, V. Zanirato, M. Olivucci, J. Helbing and S. Haacke, Phys. Chem. Chem. Phys., 2010, 12, 3178–3187 RSC.
- J. P. Malhado and J. T. Hynes, J. Chem. Phys., 2016, 145, 194104 CrossRef PubMed.
- W. Fuß, S. Lochbrunner, A. M. Muller, T. Schikarski, W. E. Schmid and S. A. Trushin, Chem. Phys., 1998, 232, 161–174 CrossRef.
- R. M. Weiss and A. Warshel, J. Am. Chem. Soc., 1979, 101, 6131–6133 CrossRef CAS.
- J. E. Kim, M. J. Tauber and R. A. Mathies, Biophys. J., 2003, 84, 2492–2501 CrossRef CAS PubMed.
- M. A. Robb and M. Olivucci, J. Photochem. Photobiol., A, 2001, 144, 237–243 CrossRef CAS.
- Q. Wang, R. W. Schoenlein, L. A. Peteanu, R. A. Mathies and C. V. Shank, Science, 1994, 266, 422–424 CrossRef CAS PubMed.
- A. Kazaryan, J. C. M. Kistemaker, L. V. Schäfer, W. R. Browne, B. L. Feringa and M. Filatov, J. Phys. Chem. A, 2010, 114, 5058–5067 CrossRef CAS PubMed.
- E. E. Nikitin, J. Chem. Phys., 1996, 104, 7059–7067 CrossRef.
- E. E. Nikitin, J. Chem. Phys., 1997, 107, 6748–6755 CrossRef CAS.
- A. Alijah and E. E. Nikitin, Mol. Phys., 1999, 96, 1399–1410 CrossRef CAS.
- M. Desouter-Lecomte, C. Sannen and J. C. Lorquet, J. Chem. Phys., 1983, 79, 894–904 CrossRef CAS.
- M. Desouter-Lecomte, D. Dehareng, B. Leyh-Nihant, M. Th Praet, A. J. Lorquet and J. C. Lorquet, J. Phys. Chem., 1985, 89, 214–222 CrossRef CAS.
- C. A. Farfan and D. B. Turner, Phys. Chem. Chem. Phys., 2020, 22, 20265–20283 RSC.
- I. Galván Fernández, M. G. Delcey, T. B. Pedersen, F. Aquilante and R. Lindh, J. Chem. Theory Comput., 2016, 12, 3636–3653 CrossRef PubMed.
- M. Olivucci, F. Bernardi, S. Ottani and M. A. Robb, J. Am. Chem. Soc., 1994, 116, 2034–2048 CrossRef CAS.
- J. J. Serrano-Pérez, F. De Vleeschouwer, F. De Proft, D. Mendive-Tapia, M. J. Bearpark and M. A. Robb, J. Org. Chem., 2013, 78, 1874–1886 CrossRef PubMed.
- A. Nenov, W. J. Schreier, F. O. Koller, M. Braun, R. De Vivie-Riedle, W. Zinth and I. Pugliesi, J. Phys. Chem. A, 2012, 116, 10518–10528 CrossRef CAS PubMed.
- A. M. D. Lee, J. D. Coe, S. Ullrich, M. L. Ho, S. J. Lee, B. M. Cheng, M. Z. Zgierski, I. C. Chen, T. J. Martinez and A. Stolow, J. Phys. Chem. A, 2007, 111, 11948–11960 CrossRef CAS PubMed.
- D. R. Yarkony, J. Chem. Phys., 2000, 112, 2111 CrossRef CAS.
- I. Fernández. Galván, A. Brakestad and M. Vacher, Phys. Chem. Chem. Phys., 2022, 24, 1638–1653 RSC.
- S. Matsika, Chem. Rev., 2021, 121, 9407–9449 CrossRef CAS PubMed.
- I. Fernández Galván, M. G. Delcey, T. B. Pedersen, F. Aquilante and R. Lindh, J. Chem. Theory Comput., 2016, 12, 3636–3653 CrossRef PubMed.
- V. Bonačić-Koutecký, J. Koutecký and J. Michl, Angew. Chem., Int. Ed., 1987, 26, 170–189 CrossRef.
- M. Ben-Nun, F. Molnar, K. Schulten and T. J. Martínez, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 1769–1773 CrossRef CAS PubMed.
- D. R. Yarkony, J. Chem. Phys., 2001, 114, 2601–2613 CrossRef CAS.
- J. P. Malhado and J. T. Hynes, J. Chem. Phys., 2012, 137, 22A543 CrossRef PubMed.
- G. J. Atchity, S. S. Xantheas and K. Ruedenberg, J. Chem. Phys., 1991, 95, 2601 CrossRef.
- T. J. Martínez, Chem. Phys. Lett., 1997, 272, 139–147 CrossRef.
- N. H. List, C. M. Jones and T. J. Martínez, Chem. Sci., 2022, 13, 373–385 RSC.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Mill Valley, California, 2006, pp. 355–421 Search PubMed.
- G. Wu, A. E. Boguslavskiy, O. Schalk, M. S. Schuurman and A. Stolow, J. Chem. Phys., 2011, 135, 164309 CrossRef PubMed.
- M. Manathunga, X. Yang, Y. Orozco-Gonzalez and M. Olivucci, J. Phys. Chem. Lett., 2017, 8, 5222–5227 CrossRef CAS PubMed.
- X. Yang, M. Manathunga, S. Gozem, J. Léonard, T. Andruniów and M. Olivucci, Nat. Chem., 2022, 2022, 1–9 Search PubMed.
- S. Oesterling, O. Schalk, T. Geng, R. D. Thomas, T. Hansson and R. De Vivie-Riedle, Phys. Chem. Chem. Phys., 2017, 19, 2025 RSC.
- R. C. Couto and M. Kowalewski, Phys. Chem. Chem. Phys., 2022, 24, 19199–19208 RSC.
- B. Gu and S. Mukamel, J. Phys. Chem. Lett., 2021, 12, 2052–2056 CrossRef CAS PubMed.
- F. Bernardi, M. Olivucci, J. J. W. McDouall and M. A. Robb, J. Chem. Phys., 1998, 89, 6365 CrossRef.
- F. Bernardi, M. Olivucci and M. A. Robb, Acc. Chem. Res., 1990, 23, 405–412 CrossRef CAS.
- P. Celani, M. OIivucci, F. Bernard, S. Ottani and M. A. Robb, J. Am. Chem. Soc., 1994, 116, 10141–10151 CrossRef CAS.
- D. Sampedro Ruiz, A. Cembran, M. Garavelli, M. Olivucci and W. Fuß, Photochem. Photobiol., 2002, 76, 622–633 CrossRef.
- L. Blancafort, P. Celani, M. J. Bearpark and M. A. Robb, Theor. Chem. Acc., 2003, 110, 92–99 Search PubMed.
- W. J. Glover, T. Mori, M. S. Schuurman, A. E. Boguslavskiy, O. Schalk, A. Stolow and T. J. Martínez, J. Chem. Phys., 2018, 148, 164303 CrossRef PubMed.
- R. L. Christensen, M. G. I. Galinato, E. F. Chu, J. N. Howard, R. D. Broene and H. A. Frank, J. Phys. Chem. A, 2008, 112, 12629–12636 CrossRef CAS PubMed.
- J. Michl and V. Bonačić-Koutecký, Electronic Aspects of Organic Photochemistry, Wiley-Interscience, New York, 1990 Search PubMed.
- M. Garavelli, P. Celani, M. Fato, M. J. Bearpark, B. R. Smith, M. Olivucci and M. A. Robb, J. Phys. Chem. A, 1997, 101, 2023–2032 CrossRef CAS.
- I. Schapiro, M. N. Ryazantsev, L. M. Frutos, N. Ferré, R. Lindh and M. Olivucci, J. Am. Chem. Soc., 2011, 133, 3354–3364 CrossRef CAS PubMed.
- M. Garavelli, P. Celani, F. Bernardi, M. A. Robb and M. Olivucci, J. Am. Chem. Soc., 1997, 119, 6891–6901 CrossRef CAS.
- A. Sanchez-Galvez, P. Hunt, M. A. Robb, M. Olivucci, T. Vreven and H. B. Schlegel, J. Am. Chem. Soc., 2000, 122, 2911–2924 CrossRef CAS.
- Z. R. Grabowski and J. Dobkowski, Pure Appl. Chem., 1983, 55, 245–252 CrossRef CAS.
- R. J. MacDonell, O. Schalk, T. Geng, R. D. Thomas, R. Feifel, T. Hansson and M. S. Schuurman, J. Chem. Phys., 2016, 145, 114306 CrossRef.
- M. Reguero, M. Olivucci, F. Bernardi and M. A. Robb, J. Am. Chem. Soc., 1994, 116, 2103–2114 CrossRef CAS.
- M. Reguero, I. B. Fernando Bernardi, A. Bottoni and M. A. Robb, J. Am. Chem. Soc., 1991, 113, 1566–1572 CrossRef CAS.
- L. Greenman and D. A. Mazziotti, J. Chem. Phys., 2010, 133, 164110 CrossRef PubMed.
- M. Vacher, A. Brakestad, H. O. Karlsson, I. Fernández Galván and R. Lindh, J. Chem. Theory Comput., 2017, 13, 2448–2457 CrossRef CAS PubMed.
- L. Yue and Y. J. Liu, J. Phys. Chem. Lett., 2022, 13, 10671–10687 CrossRef CAS PubMed.
- M. Garavelli, B. Frabboni, M. Fato, P. Celani, F. Bernardi, M. A. Robb and M. Olivucci, J. Am. Chem. Soc., 1999, 121, 1537–1545 CrossRef CAS.
- P. Celani, F. Bernardi, M. Olivucci and M. A. Robb, J. Chem. Phys., 1995, 102, 5733–5742 CrossRef CAS.
- H. Ichikawa and K. Takatsuka, J. Phys. Chem. A, 2017, 121, 315–325 CrossRef CAS PubMed.
- B. G. Levine and T. J. Martínez, J. Phys. Chem. A, 2009, 113, 12815–12824 CrossRef CAS PubMed.
- S. P. Neville, M. Chergui, A. Stolow and M. S. Schuurman, Phys. Rev. Lett., 2018, 120, 243001 CrossRef PubMed.
- I. Seidu, S. P. Neville, R. J. Macdonell and M. S. Schuurman, Phys. Chem. Chem. Phys., 2022, 24, 1345–1354 RSC.
- R. J. MacDonell and M. S. Schuurman, J. Phys. Chem. A, 2019, 123, 4693–4701 CrossRef CAS PubMed.
- R. J. MacDonell, M. E. Corrales, A. E. Boguslavskiy, L. Bañares, A. Stolow and M. S. Schuurman, J. Chem. Phys., 2020, 152, 084308 CrossRef CAS PubMed.
- A. E. Boguslavskiy, O. Schalk, N. Gador, W. J. Glover, T. Mori, T. Schultz, M. S. Schuurman, T. J. Martínez and A. Stolow, J. Chem. Phys., 2018, 148, 164302 CrossRef PubMed.
- R. Srinivasan, J. Am. Chem. Soc., 1962, 84, 4141–4145 CrossRef CAS.
- D. H. Aue and R. N. Reynolds, J. Am. Chem. Soc., 1973, 95, 2027–2028 CrossRef CAS.
- T. Sovdat, G. Bassolino, M. Liebel, C. Schnedermann, S. P. Fletcher and P. Kukura, J. Am. Chem. Soc., 2012, 134, 8318–8320 CrossRef CAS PubMed.
- B. Demoulin, S. F. Altavilla, I. Rivalta and M. Garavelli, J. Phys. Chem. Lett., 2017, 8, 4407–4412 CrossRef CAS PubMed.
- R. Barata-Morgado, M. L. Sánchez, A. Muñoz-Losa, M. E. Martín, F. J. Olivares, D. Valle and M. A. Aguilar, J. Phys. Chem. A, 2018, 122, 3096–3106 CrossRef CAS PubMed.
- S. P. Neville, Y. Wang, A. E. Boguslavskiy, A. Stolow and M. S. Schuurman, J. Chem. Phys., 2016, 144, 14305 CrossRef PubMed.
- O. Schalk, A. E. Boguslavskiy and A. Stolow, J. Phys. Chem. A, 2010, 114, 4058–4064 CrossRef CAS PubMed.
- J. S. Lim, Y. S. Lee and S. K. Kim, Angew. Chem., Int. Ed., 2008, 47, 1853–1856 CrossRef CAS PubMed.
- L. Pedraza-González, L. De Vico, M. D. C. Marĺn, F. Fanelli and M. Olivucci, J. Chem. Theory Comput., 2019, 15, 3134–3152 CrossRef PubMed.
- P. O. Dral and M. Barbatti, Nat. Rev. Chem., 2021, 5, 388–405 CrossRef CAS.
- G. W. Richings and S. Habershon, Acc. Chem. Res., 2022, 55, 209–220 CrossRef CAS PubMed.
- J. Westermayr and P. Marquetand, Chem. Rev., 2021, 121, 9873–9926 CrossRef CAS PubMed.
- D. Hu, Y. Xie, X. Li, L. Li and Z. Lan, J. Phys. Chem. Lett., 2018, 9, 2725–2732 CrossRef CAS PubMed.
- G. W. Richings, C. Robertson and S. Habershon, J. Chem. Theory Comput., 2019, 15, 857–870 CrossRef CAS PubMed.
- J. Westermayr, P. Marquetand and P. Marquetand, J. Chem. Phys., 2020, 153, 154112 CrossRef CAS PubMed.
- T. Husch, J. Sun, L. Cheng, S. J. R. Lee and T. F. Miller, J. Chem. Phys., 2021, 154, 064108 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370 Search PubMed.
- C. Ciminelli, G. Granucci and M. Persico, Chem. – Eur. J., 2004, 10, 2327–2341 CrossRef CAS PubMed.
- D. Tuna, L. Spörkel, M. Barbatti and W. Thiel, Chem. Phys., 2018, 515, 521–534 CrossRef CAS.
- J. K. Yu, C. Bannwarth, R. Liang, E. G. Hohenstein and T. J. Martínez, J. Am. Chem. Soc., 2020, 142, 20680–20690 CrossRef CAS PubMed.
- S. Gozem, H. L. Luk, I. Schapiro and M. Olivucci, Chem. Rev., 2017, 117, 13502–13565 CrossRef CAS PubMed.
- G. Bassolino, T. Sovdat, M. Liebel, C. Schnedermann, B. Odell, T. D. W. Claridge, P. Kukura and S. P. Fletcher, J. Am. Chem. Soc., 2014, 136, 2650–2658 CrossRef CAS PubMed.
- A. Cheminal, J. Léonard, S. Y. Kim, K. H. Jung, H. Kandori and S. Haacke, Phys. Chem. Chem. Phys., 2015, 17, 25429–25439 RSC.
- M. Gueye, M. Manathunga, D. Agathangelou, Y. Orozco, M. Paolino, S. Fusi, S. Haacke, M. Olivucci and J. Leónard, Nat. Commun., 2018, 9, 1–8 CrossRef CAS PubMed.
- M. M. T. El-Tahawy, A. Nenov, O. Weingart, M. Olivucci and M. Garavelli, J. Phys. Chem. Lett., 2018, 9, 3315–3322 CrossRef CAS PubMed.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- A. K. Belyaev, C. Lasser and G. Trigila, J. Chem. Phys., 2014, 140, 224108 CrossRef PubMed.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- M. Sala and D. Egorova, Chem. Phys., 2016, 481, 206–217 CrossRef CAS.
- V. I. Prokhorenko, A. M. Nagy, S. A. Waschuk, L. S. Brown, R. R. Birge and R. J. D. Miller, Science, 2006, 313, 1257–1261 CrossRef CAS PubMed.
- A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2005, 122, 044101 CrossRef PubMed.
- C. A. Farfan and D. B. Turner, J. Phys. Chem. A, 2019, 123, 7768–7776 CrossRef CAS PubMed.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1984, 392, 45–57 Search PubMed.
- V. Bonačić-Koutecký, K. Schöffel and J. Michl, Theor. Chim. Acta, 1987, 72, 459–474 CrossRef.
- R. W. Schoenlein, L. A. Peteanu, R. A. Mathies and C. V. Shank, Science, 1991, 254, 412–415 CrossRef CAS PubMed.
- H. Kuramochi and T. Tahara, J. Am. Chem. Soc., 2021, 143, 9699–9717 CrossRef CAS PubMed.
- M. Liebel, C. Schnedermann, T. Wende and P. Kukura, J. Phys. Chem. A, 2015, 119, 9506–9517 CrossRef CAS PubMed.
- C. Schnedermann, M. Liebel and P. Kukura, J. Am. Chem. Soc., 2015, 137, 2886–2891 CrossRef CAS PubMed.
- P. B. Coto, A. Sinicropi, L. De Vico, N. Ferré and M. Olivucci, Mol. Phys., 2006, 104, 983–991 CrossRef CAS.
- L. Dhar, J. A. Rogers and K. A. Nelson, Chem. Rev., 1994, 94, 157–193 CrossRef CAS.
- J. Léonard, I. Schapiro, J. Briand, S. Fusi, R. R. Paccani, M. Olivucci and S. Haacke, Chem. – Eur. J., 2012, 18, 15296–15304 CrossRef PubMed.
- T. Wende, M. Liebel, C. Schnedermann, R. J. Pethick and P. Kukura, J. Phys. Chem. A, 2014, 118, 9976–9984 CrossRef CAS PubMed.
- W. H. Miller, J. Chem. Phys., 2012, 136, 210901 CrossRef PubMed.
- T. Rosenfeld, B. Honig, M. Ottolenghi, J. Hurley and T. G. Ebrey, Pure Appl. Chem., 1977, 49, 341–351 CAS.
- P. Kukura, D. W. McCamant, S. Yoon, D. B. Wandschneider and R. A. Mathies, Science, 2005, 310, 1006–1009 CrossRef CAS PubMed.
- P. J. M. Johnson, A. Halpin, T. Morizumi, V. I. Prokhorenko, O. P. Ernst and R. J. D. Miller, Nat. Chem., 2015, 7, 980–986 CrossRef CAS PubMed.
- R. A. Mathies, Nat. Chem., 2015, 7, 945–947 CrossRef CAS PubMed.
- G. R. Loppnow and R. A. Mathies, Biophys. J., 1988, 54, 35–43 CrossRef CAS PubMed.
- L. M. Frutos, T. Andruniów, F. Santoro, N. Ferré and M. Olivucci, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7764–7769 CrossRef CAS PubMed.
- A. Warshel, Nature, 1976, 260, 679–683 CrossRef CAS PubMed.
- I. Schapiro, O. Weingart and V. Buss, J. Am. Chem. Soc., 2009, 131, 16–17 CrossRef CAS PubMed.
- R. González-Luque, M. Garavelli, F. Bernardi, M. Merchán, M. A. Robb and M. Olivucci, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 9379–9384 CrossRef PubMed.
- O. Weingart, J. Am. Chem. Soc., 2007, 129, 10618–10619 CrossRef CAS PubMed.
- M. Liebel, C. Schnedermann, G. Bassolino, G. Taylor, A. Watts and P. Kukura, Phys. Rev. Lett., 2014, 112, 238301 CrossRef CAS PubMed.
- W. H. Miller, J. Phys. Chem. A, 2009, 113, 1405–1415 CrossRef CAS PubMed.
- S. Gozem, F. Melaccio, R. Lindh, A. I. Krylov, A. A. Granovsky, C. Angeli and M. Olivucci, J. Chem. Theory Comput., 2013, 9, 4495–4506 CrossRef CAS PubMed.
- G. Zgrablić, A. M. Novello and F. Parmigiani, J. Am. Chem. Soc., 2012, 134, 955–961 CrossRef PubMed.
- O. Weingart and M. Garavelli, J. Chem. Phys., 2012, 137, 22A523 CrossRef CAS PubMed.
- O. Weingart, P. Altoè, M. Stenta, A. Bottoni, G. Orlandi and M. Garavelli, Phys. Chem. Chem. Phys., 2011, 13, 3645–3648 RSC.
- H. G. Duan, R. J. D. Miller and M. Thorwart, J. Phys. Chem. Lett., 2016, 7, 3491–3496 CrossRef CAS PubMed.
- D. L. Qi, H. G. Duan, Z. R. Sun, R. J. D. Miller and M. Thorwart, J. Chem. Phys., 2017, 147, 074101 CrossRef PubMed.
- C. Schnedermann, X. Yang, M. Liebel, K. M. Spillane, J. Lugtenburg and I. Fernández, Nat. Chem., 2018, 10, 449–455 CrossRef CAS PubMed.
- A. Ockenfels, I. Schapiro and W. Gärtner, Photochem. Photobiol. Sci., 2016, 15, 297–308 CrossRef CAS PubMed.
- G. Eyring, B. Curry, A. Broek, J. Lugtenburg and R. Mathies, Biochemistry, 1982, 21, 384–393 CrossRef CAS PubMed.
- C. Schnedermann and R. A. Mathies, On the Critical Role of Vibrational Phase in the Photochemistry of Vision, https://chemistrycommunity.nature.com/amp/posts/31527-on-the-critical-role-of-vibrational-phase-in-the-photochemistry-of-vision, accessed 20 November 2022.
- A. Valentini, D. Rivero, F. Zapata, C. García-Iriepa, M. Marazzi, R. Palmeiro, I. Fernández. Galván, D. Sampedro, M. Olivucci and L. M. Frutos, Angew. Chem., Int. Ed., 2017, 56, 3842–3846 CrossRef CAS PubMed.
- R. Liang, J. K. Yu, J. Meisner, F. Liu and T. J. Martinez, J. Am. Chem. Soc., 2021, 143, 5425–5437 CrossRef CAS PubMed.
- M. Filatov, S. Kyu Min and K. S. Kim, J. Chem. Theory Comput., 2018, 14, 4499–4512 CrossRef CAS PubMed.
- O. Weingart, I. Schapiro and V. Buss, J. Mol. Model., 2006, 12, 713–721 CrossRef CAS PubMed.
- O. Weingart, V. Buss and M. A. Robb, Phase Trans., 2005, 78, 17–24 CrossRef CAS.
- L. Vuković, C. F. Burmeister, P. Král and G. Groenhof, J. Phys. Chem. Lett., 2013, 4, 1005–1011 CrossRef PubMed.
- H. Kandori, H. Sasabe, K. Nakanishi, T. Yoshizawa, T. Mizukami and Y. Shichida, J. Am. Chem. Soc., 1996, 118, 1002–1005 CrossRef CAS.
- P. H. M. Bovee-Geurts, J. Lugtenburg and W. J. DeGrip, Biochim. Biophys. Acta, Bioenerg., 2017, 1858, 118–125 CrossRef CAS PubMed.
- L. A. Bizimana, C. A. Farfan, J. Brazard and D. B. Turner, J. Phys. Chem. Lett., 2019, 10, 3550–3556 CrossRef CAS PubMed.
- J. Dasgupta, R. R. Frontiera, K. C. Taylor, J. C. Lagarias and R. A. Mathies, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1784–1789 CrossRef CAS PubMed.
- W. Fuß, Phys. Chem. Chem. Phys., 2019, 21, 6776–6789 RSC.
- R. S. H. Liu and G. S. Hammond, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 11153–11158 CrossRef CAS PubMed.
- W. Fuß, C. Kosmidis, W. E. Schmid and S. A. Trushin, Angew. Chem., Int. Ed., 2004, 43, 4178–4182 CrossRef PubMed.
- D. Morozov and G. Groenhof, Angew. Chem., 2016, 128, 586–588 CrossRef.
- J. W. Park and Y. M. Rhee, J. Am. Chem. Soc., 2016, 138, 13619–13629 CrossRef CAS PubMed.
- H. Niwa, S. Inouye, T. Hirano, T. Matsuno, S. Kojima, M. Kubota, M. Ohashi and F. I. Tsuji, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13617–13622 CrossRef CAS PubMed.
- T. Grotjohann, I. Testa, M. Leutenegger, H. Bock, N. T. Urban, F. Lavoie-Cardinal, K. I. Willig, C. Eggeling, S. Jakobs and S. W. Hell, Nature, 2011, 478, 204–208 CrossRef CAS PubMed.
- Q. Zhang, X. Chen, G. Cui, W.-H. Fang and W. Thiel, Angew. Chem., 2014, 126, 8793–8797 CrossRef.
- V. B. Delchev, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2010, 12, 5007–5015 RSC.
- M. A. Ismail, N. Blancafort, L. Olivucci, M. Kohler and B. Robb, J. Am. Chem. Soc., 2002, 124, 6818–6819 CrossRef PubMed.
- M. Merchán, R. González-Luque, T. Climent, L. Serrano-Andrés, E. Rodríguez, M. Reguero and D. Peláez, J. Phys. Chem. B, 2006, 110, 26471–26476 CrossRef PubMed.
- M. Gueye, M. Paolino, E. Gindensperger, S. Haacke, M. Olivucci and J. Léonard, Faraday Discuss., 2019, 221, 299–321 RSC.
- I. Schapiro, S. Fusi, M. Olivucci, T. Andruniów, S. Sasidharanpillai and G. R. Loppnow, J. Phys. Chem. B, 2014, 118, 12243–12250 CrossRef CAS PubMed.
- F. Lumento, V. Zanirato, S. Fusi, E. Busi, L. Latterini, F. Elisei, A. Sinicropi, T. Andruniów, N. Ferré, R. Basosi and M. Olivucci, Angew. Chem., 2007, 119, 418–424 CrossRef.
- A. Sinicropi, E. Martin, M. Ryazantsev, J. Helbing, J. Briand, D. Sharma, J. Léonard, S. Haacke, A. Cannizzo, M. Chergui, V. Zanirato, S. Fusi, F. Santoro, R. Basosi, N. Ferré and M. Olivucci, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17642–17647 CrossRef CAS PubMed.
- A. Kazaryan, Z. Lan, L. V. Schäfer, W. Thiel and M. Filatov, J. Chem. Theory Comput., 2011, 7, 2189–2199 CrossRef CAS PubMed.
- L. Liu, W.-H. Fang and T. J. Martinez, J. Am. Chem. Soc., 2023 DOI:10.1021/jacs.3c00275.
- U. Banin and S. Ruhman, J. Chem. Phys., 1993, 98, 4391–4403 CrossRef CAS.
- M. J. Rosker, M. Dantus and A. H. Zewail, J. Chem. Phys., 1988, 89, 6113–6127 CrossRef CAS.
- M. Dantus, R. M. Bowman, M. Gruebele and A. H. Zewail, J. Chem. Phys., 1989, 91, 7437–7450 CrossRef CAS.
- S. A. Trushin, W. Fuss, K. L. Kompa and W. E. Schmid, J. Phys. Chem. A, 2000, 104, 1997–2006 CrossRef CAS.
- S. A. Trushin, W. Fuss, W. E. Schmid and K. L. Kompa, J. Phys. Chem. A, 1998, 102, 4129–4137 CrossRef CAS.
- F. Bernardi, M. Olivucci and M. A. Robb, J. Photochem. Photobiol., A, 1997, 105, 365–371 CrossRef CAS.
- W. Fuß, W. E. Schmid and S. A. Trushin, J. Chem. Phys., 2000, 112, 8347–8362 CrossRef.
- K. Kosma, S. A. Trushin, W. Fuß and W. E. Schmid, Phys. Chem. Chem. Phys., 2009, 11, 172–181 RSC.
- S. Li, B. Jochim, J. E. Jackson and M. Dantus, J. Chem. Phys., 2021, 155, 044303 CrossRef CAS PubMed.
- K. Haiser, B. P. Fingerhut, K. Heil, A. Glas, T. T. Herzog, B. M. Pilles, W. J. Schreier, W. Zinth, R. de Vivie-Riedle and T. Carell, Angew. Chem., Int. Ed., 2012, 51, 408–411 CrossRef CAS PubMed.
- D. E. Lemaire and B. P. Ruzsicska, Photochem. Photobiol., 1993, 57, 755–757 CrossRef CAS PubMed.
- Y. J. Ai, R. Z. Liao, S. F. Chen, Y. Luo and W. H. Fang, J. Phys. Chem. B, 2010, 114, 14096–14102 CrossRef CAS PubMed.
- K. A. Kistler and S. Matsika, J. Chem. Phys., 2008, 128, 215102 CrossRef PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- H. L. Stern, A. Cheminal, S. R. Yost, K. Broch, S. L. Bayliss, K. Chen, M. Tabachnyk, K. Thorley, N. Greenham, J. M. Hodgkiss, J. Anthony, M. Head-Gordon, A. J. Musser, A. Rao and R. H. Friend, Nat. Chem., 2017, 9, 1205–1212 CrossRef CAS PubMed.
- N. R. Monahan, D. Sun, H. Tamura, K. W. Williams, B. Xu, Y. Zhong, B. Kumar, C. Nuckolls, A. R. Harutyunyan, G. Chen, H.-L. Dai, D. Beljonne, Y. Rao and X.-Y. Zhu, Nat. Chem., 2017, 9, 341–346 CrossRef CAS PubMed.
- A. J. Musser, M. Liebel, C. Schnedermann, T. Wende, T. B. Kehoe, A. Rao and P. Kukura, Nat. Phys., 2015, 11, 352–357 Search PubMed.
- H.-G. Duan, A. Jha, X. Li, V. Tiwari, H. Ye, P. K. Nayak, X.-L. Zhu, L. Zheng, T. J. Martinez, M. Thorwart and R. J. D. Miller, Sci. Adv., 2020, 6, eabb0052 Search PubMed.
- A. M. Alvertis, S. Lukman, T. J. H. Hele, E. G. Fuemmeler, J. Feng, J. Wu, N. C. Greenham, A. W. Chin and A. J. Musser, J. Am. Chem. Soc., 2019, 141, 17558–17570 CrossRef CAS PubMed.
- W. Kim and A. J. Musser, Adv. Phys. X, 2021, 6, 1918022 Search PubMed.
- C. Schnedermann, A. M. Alvertis, T. Wende, S. Lukman, J. Feng, F. A. Y. N. Schröder, D. H. P. Turban, J. Wu, N. D. M. Hine, N. C. Greenham, A. W. Chin, A. Rao, P. Kukura and A. J. Musser, Nat. Commun., 2019, 10, 1–11 CrossRef CAS PubMed.
- F. A. Y. N. Schröder, D. H. P. Turban, A. J. Musser, N. D. M. Hine and A. W. Chin, Nat. Commun., 2019, 10, 1062 CrossRef PubMed.
- S. Lukman, K. Chen, J. M. Hodgkiss, D. H. P. Turban, N. D. M. Hine, S. Dong, J. Wu, N. C. Greenham and A. J. Musser, Nat. Commun., 2016, 7, 1–13 Search PubMed.
- S. Lukman, A. J. Musser, K. Chen, S. Athanasopoulos, C. K. Yong, Z. Zeng, Q. Ye, C. Chi, J. M. Hodgkiss, J. Wu, R. H. Friend and N. C. Greenham, Adv. Funct. Mater., 2015, 25, 5452–5461 CrossRef CAS.
- T. Nelson, S. Fernandez-Alberti, V. Chernyak, A. E. Roitberg and S. Tretiak, J. Phys. Chem. B, 2011, 115, 5402–5414 CrossRef CAS PubMed.
- T. R. Nelson, D. Ondarse-Alvarez, N. Oldani, B. Rodriguez-Hernandez, L. Alfonso-Hernandez, J. F. Galindo, V. D. Kleiman, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- S. M. Falke, C. A. Rozzi, D. Brida, M. Maiuri, M. Amato, E. Sommer, A. De Sio, A. Rubio, G. Cerullo, E. Molinari and C. Lienau, Science, 2014, 344, 1001–1005 CrossRef CAS PubMed.
- A. De Sio, F. V. D. A. Camargo, K. Winte, E. Sommer, F. Branchi, G. Cerullo and C. Lienau, Eur. Phys. J. B, 2018, 91, 236 CrossRef CAS.
- A. G. Dijkstra, C. Wang, J. Cao and G. R. Fleming, J. Phys. Chem. Lett., 2015, 6, 627–632 CrossRef CAS PubMed.
- F. R. Díaz, H. G. Duan, R. J. D. Miller and M. Thorwart, J. Phys. Chem. B, 2021, 125, 8869–8875 CrossRef PubMed.
- T. Pullerits, D. Zigmantas and V. Sundström, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1148–1149 CrossRef CAS PubMed.
- E. Thyrhaug, R. Tempelaar, M. J. P. Alcocer, K. Žídek, D. Bína, J. Knoester, T. L. C. Jansen and D. Zigmantas, Nat. Chem., 2018, 10, 780–786 CrossRef CAS PubMed.
- E. Bukartė, A. Haufe, D. Paleček, C. Büchel and D. Zigmantas, Chem. Phys., 2020, 530, 110643 CrossRef.
- S. Sil, R. W. Tilluck, N. Mohan T. M, C. H. Leslie, J. B. Rose, M. A. Domínguez-Martín, W. Lou, C. A. Kerfeld and W. F. Beck, Nat. Chem. 2022, 2022, 1–9 Search PubMed.
- K. H. Cho and Y. M. Rhee, J. Phys. Chem. B, 2021, 125, 5601–5610 CrossRef CAS PubMed.
- K. H. Cho and Y. M. Rhee, Phys. Chem. Chem. Phys., 2021, 23, 26623–26639 RSC.
- J. Clark, C. Silva, R. H. Friend and F. C. Spano, Phys. Rev. Lett., 2007, 98, 206406 CrossRef PubMed.
- S. Tretiak, A. Saxena, R. L. Martin and A. R. Bishop, Phys. Rev. Lett., 2002, 89, 097402 CrossRef CAS PubMed.
- F. C. Spano, Annu. Rev. Phys. Chem., 2006, 57, 217–243 CrossRef CAS PubMed.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- S. Kang, T. Kim, Y. Hong, F. Würthner and D. Kim, J. Am. Chem. Soc., 2021, 143, 9825–9833 CrossRef CAS PubMed.
- S. Rafiq, B. Fu, B. Kudisch and G. D. Scholes, Nat. Chem., 2020, 13, 70–76 CrossRef PubMed.
- R. Huber, L. Dworak, J. E. Moser, M. Grätzel and J. Wachtveitl, J. Phys. Chem. C, 2016, 120, 8534–8539 CrossRef CAS.
- C. Zimmermann, F. Willig, S. Ramakrishna, B. Burfeindt, B. Pettinger, R. Eichberger and W. Storck, J. Phys. Chem. B, 2001, 105, 9245–9253 CrossRef CAS.
- A. Aster, A.-B. Bornhof, N. Sakai, S. Matile and E. Vauthey, J. Phys. Chem. Lett., 2021, 12, 1052–1057 CrossRef CAS PubMed.
- J. Krčmář, M. F. Gelin, D. Egorova and W. Domcke, J. Phys. B, 2014, 47, 124019 CrossRef.
- M. Khalil, N. Demirdöven and A. Tokmakoff, J. Chem. Phys., 2004, 121, 362 CrossRef CAS PubMed.
- M. J. Nee, C. R. Baiz, J. M. Anna, R. McCanne and K. J. Kubarych, J. Chem. Phys., 2008, 129, 084503 CrossRef PubMed.
- T. L. Courtney, Z. W. Fox, L. Estergreen and M. Khalil, J. Phys. Chem. Lett., 2015, 6, 1286–1292 CrossRef CAS PubMed.
- J. D. Gaynor, A. Petrone, X. Li and M. Khalil, J. Phys. Chem. Lett., 2018, 9, 6289–6295 CrossRef CAS PubMed.
- Z. W. Fox, T. J. Blair and M. Khalil, J. Phys. Chem. Lett., 2020, 11, 1558–1563 CrossRef CAS PubMed.
- L. Blancafort, F. Jolibois, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 2001, 123, 722–732 CrossRef CAS PubMed.
- A. De Sio, E. Sommer, X. T. Nguyen, L. Groß, D. Popović, B. T. Nebgen, S. Fernandez-Alberti, S. Pittalis, C. A. Rozzi, E. Molinari, E. Mena-Osteritz, P. Bäuerle, T. Frauenheim, S. Tretiak and C. Lienau, Nat. Nanotechnol., 2020, 16, 63–68 CrossRef PubMed.
- S. Biswas, J. W. Kim, X. Zhang and G. D. Scholes, Chem. Rev., 2022, 122, 4257–4321 CrossRef CAS PubMed.
- J. A. Weinstein, Nat. Chem., 2020, 12, 789–790 CrossRef CAS PubMed.
- Y. Shu and B. G. Levine, J. Chem. Phys., 2013, 139, 81102 CrossRef PubMed.
- W. T. Peng, B. S. Fales, Y. Shu and B. G. Levine, Chem. Sci., 2018, 9, 681–687 RSC.
- Y. Shu, B. S. Fales and B. G. Levine, Nano Lett., 2015, 15, 6247–6253 CrossRef CAS PubMed.
- B. G. Levine, M. P. Esch, B. S. Fales, D. T. Hardwick, W.-T. Peng and Y. Shu, Annu. Rev. Phys. Chem., 2019, 70, 21–43 CrossRef PubMed.
- Y. Shu, B. S. Fales, W. T. Peng and B. G. Levine, J. Phys. Chem. Lett., 2017, 8, 4091–4099 CrossRef CAS PubMed.
- D. W. Dequilettes, K. Frohna, D. Emin, T. Kirchartz, V. Bulovic, D. S. Ginger and S. D. Stranks, Chem. Rev., 2019, 119, 11007–11019 CrossRef CAS PubMed.
- M. P. Esch, Y. Shu and B. G. Levine, J. Phys. Chem. A, 2019, 123, 2661–2673 CrossRef CAS PubMed.
- B. C. Paulus, S. L. Adelman, L. L. Jamula and J. K. McCusker, Nature, 2020, 582, 214–219 CrossRef CAS PubMed.
- P. Kim, A. J. S. Valentine, S. Roy, A. W. Mills, A. Chakraborty, F. N. Castellano, X. Li and L. X. Chen, J. Phys. Chem. Lett., 2021, 12, 6794–6803 CrossRef CAS PubMed.
- T. W. Kim, P. Kim, A. W. Mills, A. Chakraborty, S. Kromer, A. J. S. Valentine, F. N. Castellano, X. Li and L. X. Chen, J. Phys. Chem. C, 2022, 126, 11487–11497 CrossRef CAS.
- Y. Shao, H. J. M. de Groot and B. Francesco, ChemSusChem, 2020, 13, 1–9 CrossRef.
- E. G. Fuemmeler, S. N. Sanders, A. B. Pun, E. Kumarasamy, T. Zeng, K. Miyata, M. L. Steigerwald, X.-Y. Zhu, M. Y. Sfeir, L. M. Campos and N. Ananth, ACS Cent. Sci., 2016, 2, 316–324 CrossRef CAS PubMed.
- S. Mai, M. Pollum, L. Martínez-Fernández, N. Dunn, P. Marquetand, I. Corral, C. E. Crespo-Hernández and L. González, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- J. P. Zobel, J. J. Nogueira and L. González, Chem. – Eur. J., 2018, 24, 5379–5387 CrossRef CAS PubMed.
- D. Valverde, S. Mai, A. V. Sanches de Araújo, S. Canuto, L. González and A. C. Borin, Phys. Chem. Chem. Phys., 2021, 23, 5447–5454 RSC.
- Y. Wang and D. R. Yarkony, J. Chem. Phys., 2021, 155, 174115 CrossRef CAS PubMed.
- J. N. Schrauben, K. L. Dillman, W. F. Beck and J. K. McCusker, Chem. Sci., 2010, 1, 405–410 RSC.
- J. D. Gaynor, J. Sandwisch and M. Khalil, Nat. Commun., 2019, 10, 1–9 Search PubMed.
- J. G. Kim, S. Nozawa, H. Kim, E. H. Choi, T. Sato, T. W. Kim, K. H. Kim, H. Ki, J. Kim, M. Choi, Y. Lee, J. Heo, K. Y. Oang, K. Ichiyanagi, R. Fukaya, J. H. Lee, J. Park, I. Eom, S. H. Chun, S. Kim, M. Kim, T. Katayama, T. Togashi, S. Owada, M. Yabashi, S. J. Lee, S. Lee, C. W. Ahn, D. S. Ahn, J. Moon, S. Choi, J. Kim, T. Joo, J. Kim, S. Ichi Adachi and H. Ihee, Nature, 2020, 582, 520–524 CrossRef CAS PubMed.
- J. G. Kim, E. H. Choi, Y. Lee and H. Ihee, Acc. Chem. Res., 2021, 54, 27 CrossRef PubMed.
- M. Park, A. J. Neukirch, S. E. Reyes-Lillo, M. Lai, S. R. Ellis, D. Dietze, J. B. Neaton, P. Yang, S. Tretiak and R. A. Mathies, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- M. Maiuri, M. Garavelli and G. Cerullo, J. Am. Chem. Soc., 2019, 142, 3–15 CrossRef PubMed.
- I. A. Heisler and S. R. Meech, Chem. Soc. Rev., 2021, 50, 11486–11502 RSC.
- T. Brixner, J. Stenger, H. M. Vaswani, M. Cho, R. E. Blankenship and G. R. Fleming, Nature, 2005, 434, 625–628 CrossRef CAS PubMed.
- G. Fumero, C. Schnedermann, G. Batignani, T. Wende, M. Liebel, G. Bassolino, C. Ferrante, S. Mukamel, P. Kukura and T. Scopigno, Phys. Rev. X, 2020, 10, 011051 CAS.
- J. D. Gaynor, R. B. Weakly and M. Khalil, J. Chem. Phys., 2021, 154, 184201 CrossRef CAS PubMed.
- R. B. Weakly, J. D. Gaynor and M. Khalil, J. Chem. Phys., 2021, 154, 184202 CrossRef CAS PubMed.
- D. R. Austin, A. S. Johnson, F. McGrath, D. Wood, L. Miseikis, T. Siegel, P. Hawkins, A. Harvey, Z. Mašín, S. Patchkovskii, M. Vacher, J. P. Malhado, M. Y. Ivanov, O. Smirnova and J. P. Marangos, Sci. Rep., 2021, 11, 1–8 CrossRef PubMed.
- H. Kuramochi, S. Takeuchi, H. Kamikubo, M. Kataoka and T. Tahara, Sci. Adv., 2019, 5, eaau4490 CrossRef PubMed.
- J. P. Kraack, A. Wand, T. Buckup, M. Motzkus and S. Ruhman, Phys. Chem. Chem. Phys., 2013, 15, 14487–14501 RSC.
- T. Buckup and M. Motzkus, Annu. Rev. Phys. Chem., 2014, 65, 39–57 CrossRef CAS PubMed.
- H. Kuramochi, S. Takeuchi, K. Yonezawa, H. Kamikubo, M. Kataoka and T. Tahara, Nat. Chem., 2017, 9, 660–666 CrossRef CAS PubMed.
- H. Seiler, M. Krynski, D. Zahn, S. Hammer, Y. W. Windsor, T. Vasileiadis, J. Pflaum, R. Ernstorfer, M. Rossi and H. Schwoerer, Sci. Adv., 2021, 7, eabg0869 CrossRef CAS PubMed.
- J. Yang, X. Zhu, J. P. F. Nunes, J. K. Yu, R. M. Parrish, T. J. A. Wolf, M. Centurion, M. Gühr, R. Li, Y. Liu, B. Moore, M. Niebuhr, S. Park, X. Shen, S. Weathersby, T. Weinacht, T. J. Martinez and X. Wang, Science, 2020, 368, 885–889 CrossRef CAS PubMed.
- C. Pellegrini, A. Marinelli and S. Reiche, Rev. Mod. Phys., 2016, 88, 015006 CrossRef.
- A. R. Attar, A. Bhattacherjee, C. D. Pemmaraju, K. Schnorr, K. D. Closser, D. Prendergast and S. R. Leone, Science, 2017, 356, 54–59 CrossRef CAS PubMed.
- A. Bhattacherjee and S. R. Leone, Acc. Chem. Res., 2018, 51, 3203–3211 CrossRef CAS PubMed.
- H. Timmers, X. Zhu, Z. Li, Y. Kobayashi, M. Sabbar, M. Hollstein, M. Reduzzi, T. J. Martínez, D. M. Neumark and S. R. Leone, Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- K. S. Zinchenko, F. Ardana-Lamas, I. Seidu, S. P. Neville, J. van der Veen, V. U. Lanfaloni, M. S. Schuurman and H. J. Wörner, Science, 2021, 371, 489–494 CrossRef CAS PubMed.
- D. T. Matselyukh, V. Despré, N. V. Golubev, A. I. Kuleff and H. J. Wörner, Nat. Phys., 2022, 18, 1206–1213 Search PubMed.
- T. Schnappinger, D. Jadoun, M. Gudem and M. Kowalewski, Chem. Commun., 2022, 58, 12763–12781 RSC.
- M. Kowalewski, B. P. Fingerhut, K. E. Dorfman, K. Bennett and S. Mukamel, Chem. Rev., 2017, 117, 12165–12226 CrossRef CAS PubMed.
- K. Bennett, M. Kowalewski, J. R. Rouxel and S. Mukamel, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6538–6547 CrossRef CAS PubMed.
- H. Yong, D. Keefer and S. Mukamel, J. Am. Chem. Soc., 2022, 144, 7796–7804 CrossRef CAS PubMed.
- D. Jadoun, M. Gudem and M. Kowalewski, Struct. Dyn., 2021, 8, 034101 CrossRef CAS PubMed.
- D. Keefer, T. Schnappinger, R. de Vivie-Riedle and S. Mukamel, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 24069–24075 CrossRef CAS PubMed.
- D. Keefer, V. M. Freixas Lemus, H. Song, S. Tretiak, S. Fernandez-Alberti and S. Mukamel, Chem. Sci., 2021, 12, 5286–5294 RSC.
- D. Keefer, J. R. Rouxel, F. Aleotti, F. Segatta, M. Garavelli and S. Mukamel, J. Am. Chem. Soc., 2021, 143, 13806–13815 CrossRef CAS PubMed.
- G. Chatterjee, A. Jha, A. Blanco-Gonzalez, V. Tiwari, M. Manathunga, H. G. Duan, F. Tellkamp, I. V. Prokhorenko, N. Ferré, J. Dasgupta, M. Olivucci and R. J. D. Miller, Chem. Sci., 2022, 13, 9392–9400 RSC.
- X. F. Xu, A. Kahan, S. Zilberg and Y. Haas, J. Phys. Chem. A, 2009, 113, 9779–9791 CrossRef CAS PubMed.
- E. M. Kempfer-Robertson and L. M. Thompson, J. Phys. Chem. A, 2020, 124, 3520–3529 CrossRef CAS PubMed.
- M. Liebel and P. Kukura, Nat. Chem., 2016, 9, 45–49 CrossRef PubMed.
- D. Geppert, L. Seyfarth and R. De Vivie-Riedle, Applied Physics B: Lasers and Optics, Springer, 2004, vol. 79, pp. 987–992 Search PubMed.
- M. Kübel, R. Siemering, C. Burger, N. G. Kling, H. Li, A. S. Alnaser, B. Bergues, S. Zherebtsov, A. M. Azzeer, I. Ben-Itzhak, R. Moshammer, R. De Vivie-Riedle and M. F. Kling, Phys. Rev. Lett., 2016, 116, 193001 CrossRef PubMed.
- A. S. Alnaser, M. Kübel, R. Siemering, B. Bergues, N. G. Kling, K. J. Betsch, Y. Deng, J. Schmidt, Z. A. Alahmed, A. M. Azzeer, J. Ullrich, I. Ben-Itzhak, R. Moshammer, U. Kleineberg, F. Krausz, R. De Vivie-Riedle and M. F. Kling, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- H. Li, N. G. Kling, B. Förg, J. Stierle, A. Kessel, S. A. Trushin, M. F. Kling and S. Kaziannis, Struct. Dyn., 2016, 3, 043206 CrossRef PubMed.
- S. Rafiq and G. D. Scholes, J. Am. Chem. Soc., 2019, 141, 708–722 CrossRef CAS PubMed.
- R. R. Frontiera, J. Phys. Chem. B, 2022, 126, 5727–5729 CrossRef CAS PubMed.
- Y. Yoneda, B. Kudisch, S. Rafiq, M. Maiuri, Y. Nagasawa, G. D. Scholes and H. Miyasaka, J. Am. Chem. Soc., 2021, 143, 14511–14522 CrossRef CAS PubMed.
- A. Kahan, A. Wand, S. Ruhman, S. Zilberg and Y. Haas, J. Phys. Chem. A, 2011, 115, 10854–10861 CrossRef CAS PubMed.
- M. Olivucci, T. Tran, G. A. Worth and M. A. Robb, J. Phys. Chem. Lett., 2021, 12, 5639–5643 CrossRef CAS PubMed.
Footnotes |
| † Current address: Department of Physics, Cavendish Laboratory, University of Cambridge, JJ Thomson Ave, Cambridge, CB3 0HE, UK, E-mail: yb289@cam.ac.uk |
| ‡ Current address: Department of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge, CB3 0AS, UK. |
| § The often applied acronym “CI” will not be used to avoid confusion with the popular configuration interaction method of electronic structure theory. |
| ¶ Sometimes also called diabatic. Here we use the term nonadiabatic to avoid confusion with the diabatic states composing the adiabatic electronic wavefunction. |
| This journal is © The Royal Society of Chemistry 2023 |