Insights into the ruthenium-catalysed selective reduction of cardanol derivatives via transfer hydrogenation: a density functional theory study

Abstract

The detailed mechanism for ruthenium-catalysed selective reduction of cardanol derivatives by transfer hydrogenation has been fully characterised at the B3PW91-D3/ECP2/PCM//B3PW91/ECP1 level of density functional theory. The explored catalytic cycle involved the hydrogenation of the triene cardanol giving the diene product through a highly stable η³-allylic intermediate via a kinetic barrier of 29.1 kcal mol⁻¹, which followed further hydrogenation leading to a more stable η³-allylic intermediate. The further reduction to the cardanol monoene product required an overall barrier of 29.2 kcal mol⁻¹, which offers a rationale for the requirement of elevated temperatures (refluxing isopropanol). The computed overall barrier of 46.6 kcal mol⁻¹ to accommodate a fully saturated product is unsurmountable—in good agreement with the experiment, where no such full hydrogenation is observed, and rationalising the 100% selectivity towards the monoene product.

---

Introduction

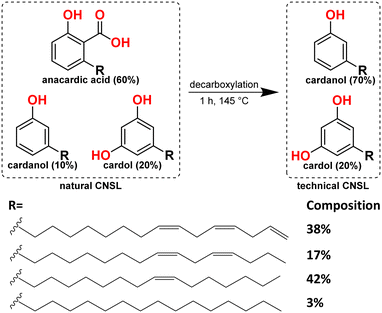
The colossal use of non-renewable fossil fuels as the primary source to meet the global energy demand is not only depleting these resources, but also causing problems on a massive scale.^1,2 Therefore, the search for sustainable sources is at the heart of current energy targets.³ Oleochemicals are attractive renewable sources for easy conversion to biodiesel and producing bulk and fine chemicals.⁴ For example, alcoholysis of monounsaturated fatty esters gives rise to alkenes; in contrast, alkoxycarbonylation of the same substrate leads to the diesters (precursors to the diols).⁵ The current mechanistic study looks at the cashew nut shell liquid (CNSL), a member of the oleochemical family. CNSL, as a sustainable feedstock,^6,7 has many applications, e.g., additive to commercial surfactants, brake linings, cement, laminating resins, paints, surface coatings, varnishes,^8–12 and in the field of nanotechnology,^13–17 in the synthesis of pharmaceutical drugs,¹⁸ and organic solar cells,¹⁹ making it of broad interest within the context of a sustainable chemical economy.

CNSL is a mixture of three phenolic compounds: anacardic acid, cardanol, and cardol,^20–22 where phenol in is each of these compounds is substituted by a 15-carbon chain, with one, two, or three double bonds separated by a methylene group. A few percent of these compounds also contain the fully saturated side chain.²³ Heating of CNSL mixture results in the decarboxylation of anacardic acid to afford cardanol and cardol in roughly a 4 : 1 ratio,^22,24 known as technical CNSL.^22,25 Vacuum distillation of technical CNSL gives cardanol;^25,26 however, it is still a mixture of cardanols with unsaturated side chains containing one, two, or three double bonds or a fully saturated side chain (Scheme 1).

Scheme 1 Components of natural²¹ and technical CNSL.²⁵

de Vries and co-workers devised a method for reducing the mixture of cardanol polyunsaturates to pure monounsaturated cardanol²⁵ to overcome the challenge of adapting CNSL at the industrial scale. They achieved high selectivity towards the cardanol monoene using the RuCl₃/iPrOH system, where iPrOH acted as the reducing agent, arguably via transfer hydrogenation^27–36 with acetone as the by-product. de Vries and co-workers proposed a homogeneous hydrogen transfer from the solvent and the involvement of the aromatic ring of the substrate in the catalytic activity. There are a number of theoretical mechanistic studies on transition metal-catalysed isomerisation, including ruthenium-catalysed isomerisation of alkenes which exhibit great regio- and stereoselectivity.^37–46 However, to our knowledge, mechanistic studies have yet to be performed on ruthenium-catalysed isomerisation followed by the reduction of polyenes via transfer hydrogenation. Such mechanistic insights would furnish atomistic understanding, enabling the development of new reactions to utilise this biomass resource towards more sustainable chemistry.

Electrospray Ionisation Mass Spectrometry (ESI-MS) indicated an intermediate with a mass of 401 amu, consistent with a chemical formula of [RuC₂₁H₃₁O]⁺. With iPrOH acting as an H₂ source, forming a Ru(II) complex from the Ru(III) precursor is highly likely under these reducing conditions; therefore, de Vries and co-workers suggested the intermediate with a mass of 401 amu as a cationic ruthenium allyl complex.²⁵ The location of the allyl moiety on the carbon side chain is ambiguous; however, the isomerisation between the double bonds as a result of hydrogen transfer should lead to an intermediate shown in Scheme 2a and b with the same chemical formula as stated above.

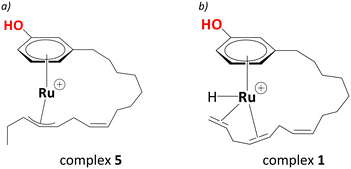Scheme 2 a) Proposed η³-allyl intermediate as evidenced from the ESI-MS (complex 5, see below), b) proposed entry (complex 1) into the catalytic cycle.

Assuming a cationic Ru(II) hydride species to be the active catalyst, and drawing on well-known structures with [Ru(η⁶-arene)(H)] motifs within Ru-mediated catalytic transformations,^29,47–51 a [Ru(C₂₁H₂₉OH)(H)]⁺ complex, where Ru is bonded to the aromatic ring of cardanol, was chosen as a plausible entry point into the catalytic cycle. To saturate the coordination sphere around the metal and activate the double bonds for subsequent reductions, it was assumed that Ru forms an intramolecular chelate complex with η⁴-coordination of the polyene tail to the metal, affording complex 1 in Scheme 2b. Starting from this intermediate and using a DFT protocol that has been applied fruitfully to several reaction catalysed by metals from the second transition row,^52–57 we have now traced complete catalytic cycles leading to the main products. The cycle is divided into several steps, focusing first on the isomerisation of the double bonds, then the reduction to the diene cardanol, followed by reduction to the monoene cardanol. We will eventually discuss the overall barriers associated with the formation of different products and selectivity towards the major product, i.e., the monoene cardanol.

Results and discussion

In complex 1, the metal is bonded in a η⁴ fashion to the π system of the diene with sp² carbons at positions 14,15, and 11,12 of the alkenyl chain (see Scheme 3 for numbering). Starting from such a cationic η⁴ Ru complex makes the current study consistent with the experiment, as the ESI-MS data correspond to cationic ruthenium allyl complexes. Thus, we start our studies with cationic complex, 1, which eventually leads to the η³-allyl complex on the reaction profile compatible with experiment.²⁵ The issue of the conformational flexibility of the alkenyl side chain was addressed at the stage of this allyl complex (5, see below), and the lowest conformation found there was maintained for all other complexes, including 1. In the following, the steps leading to the eventual products are discussed in detail.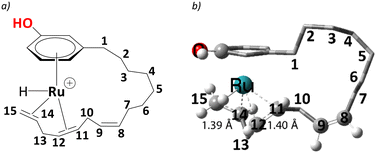

Scheme 3 a) Numbering scheme of unsaturated carbon chain in selected cardanol, b) the computed C_(sp²) – C_(sp²) distances at their η⁴ coordination to the metal are shown along with numbering.

Isomerisation

To reach allyl complexes from coordinated 1,3-dienes, a series of isomerisation steps is required. Starting from 1, a β-agostic intermediate, 2, is obtained as a result of facile hydrogen transfer from the Ru centre to the terminal carbon (ΔG_1→2 = 6.4 kcal mol⁻¹ and ΔG^‡_1→2 = 6.8 kcal mol⁻¹) followed by the loss of η²- coordination of alkene (C_(sp²)#11–C_(sp²)#12) via a higher kinetic barrier (ΔG_2→3 = 12.5 kcal mol⁻¹ and ΔG^‡_2→3 = 16.4 kcal mol⁻¹). In intermediate 3, the metal atom forms a β-agostic interaction with the hydrogen of the sp³ carbon atom (carbon#13 as per Scheme 3). Intermediate 4′ appears as a result of hydrogen transfer to the metal atom by breaking the β-agostic interaction from the central carbon viaTS3–4′ (ΔG_3→4 = −6.0 kcal mol⁻¹ and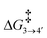 = 1.1 kcal mol⁻¹), which follows a high kinetic barrier viaTS4′–4 giving intermediate 4 (ΔG_4^′→4 = 4.3 kcal mol⁻¹ and 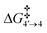= 12.7 kcal mol⁻¹, Scheme 4).

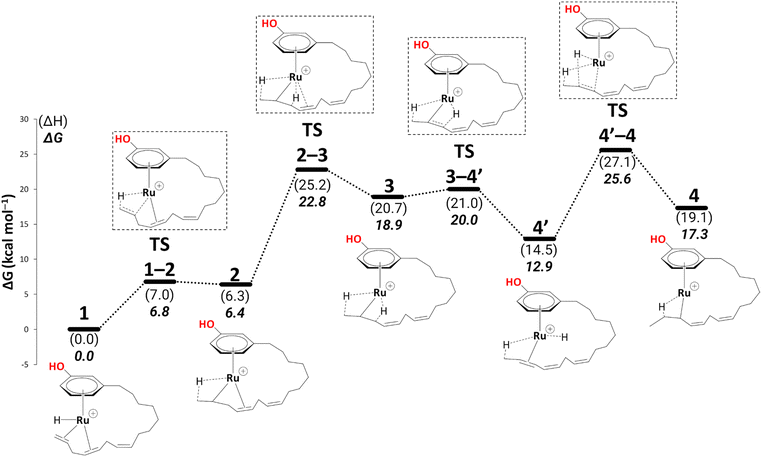Scheme 4 Isomerisation (B3PW91-D3BJ/ECP2/PCM level, iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K). Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. Table S1† shows the reaction energies of individual steps.

Reduction to the cardanol diene

Intermediate 4 rearranges to a η³-allyl complex, 5 (Scheme 5, ΔG_4→5 = −33.4 kcal mol⁻¹) initiating reduction to the cardanol diene. ESI-MS data also suggests a cationic η³-allyl complex as an intermediate;²⁵ therefore, complex 5 was used for a partial conformational analysis (see Fig. S1 in the ESI†). The most stable conformation of the alkenyl chain from the most stable structure was chosen to model all the other intermediates on the energy profiles (excluding those where the alkenyl chain detaches from the metal).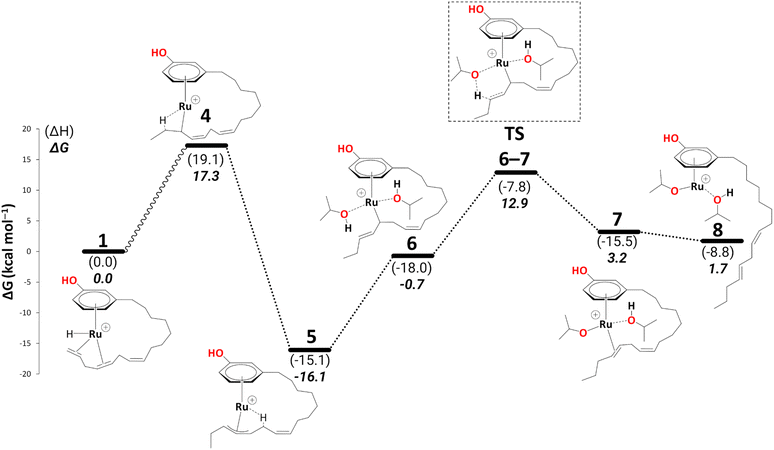

Scheme 5 Reduction to the diene: formation of intermediate 8 (B3PW91-D3BJ/ECP2/PCM level, iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K). Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. The wavy line represents multiple steps. Table S2† shows the reaction energies of individual steps.

The η³-allyl complexes tend to be stable thermodynamic sinks on the PES and thus require significant activation for further reaction.^53–55 Here, we used two equivalents of explicit iPrOH to reduce the two double bonds. Slippage from the η³-allyl bonding mode to a η¹-allyl bonding mode with a Ru–C sigma bond (with carbon#11) helps create room for the incoming solvent molecules forming 6 (ΔG_5→6 = 15.4 kcal mol⁻¹). The first protonation occurs from coordinated isopropanol to the unsaturated system, where one of the coordinated iPrOH donates its proton to carbon#13, allowing the formation of an isopropoxide intermediate 7, where the η¹-allyl complex is transformed into an olefin complex with η²-coordination mode with π back bonding (ΔG_6→7 = 3.9 kcal mol⁻¹ and ΔG^‡_6→7 = 13.7 kcal mol⁻¹). β-Hydrogen transfer from the isopropoxide to the metal restores the Ru–hydride moiety enabling the next olefin reduction. A vacant coordination site (for the acetone produced from the β-H transfer) should facilitate this process. This could either be formed through loss of the intact iPrOH ligand or de-coordination of the olefin. The latter process, affording 8, turns out to be slightly exergonic (ΔG_7→8 = −1.5 kcal mol⁻¹). The iPrO–Ru bond length decreases from 1.96 Å to 1.87 Å upon olefin dissociation (Scheme 5, and Fig. 1).

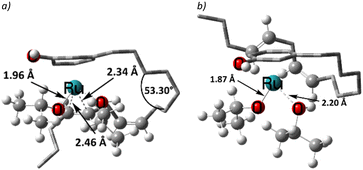Fig. 1 The iPrO–Ru bond lengths and other important structural descriptors: a) intermediate 7, b) intermediate 8.

β-H transfer from isopropoxide to the metal atom viaTS8–9 is facile, albeit somewhat endergonic (ΔG_8→9 = 6.8 kcal mol⁻¹ and ΔG^‡_8→9 = 7.1 kcal mol⁻¹). In context with that dangling olefin, where competing pathways are close, and the energy difference between intermediates and transition states is small, the reliability of the predictions may be limited by the errors in the computed entropies (which may become more critical for more flexible parts of the molecules). The entropic cost is only partially recovered in the computational model because entropy changes in the solvent shell are not included. Extensive calculations with explicit solvent molecules would have to be performed to fully address this problem, presumably involving large-scale molecular dynamics simulations with enhanced sampling techniques to extract free energy profiles. Such simulations, however, are beyond the scope of the present paper.

In 9, the acetone product is side-on bonded to Ru. We ran a PES scan to model its dissociation, where acetone moves from η²-coordination to η¹-coordination before it fully dissociates, and we were able to locate a transition state for this process (TS9–10, see section S1 in the ESI† for a detailed discussion). 10 is thus indicated to have a very fleeting nature (if it exists at all), and the side-on, π-coordinated acetone is expected to rearrange spontaneously to the end-on η¹-coordination mode (10). This is in stark contrast to other alcohol dehydrogenation catalysts based on Ru (with bulky phosphine ligands), where this very step can even be rate-limiting.⁵⁸10 can form an even more stable intermediate 11 after acetone fully dissociates (ΔG_10→11 = −7.1 kcal mol⁻¹). Once the acetone is dissociated, the dangling olefin in 10 can re-coordinate to the metal. This process could occur in a variety of ways (via a dissociative, associative, or interchange mechanism). On the PES, associative and interchange mechanisms are likely to be complicated processes that may involve many additional intermediates. We have not explored any of these scenarios. Given that substitution of the coordinated acetone with the olefin from the side chain does not involve making or breaking of bonds other than simple donor-acceptor interactions, and that this substitution has a significant thermodynamic driving force, we do not expect serious kinetic hindrance for this step—the stability of 11 stems from the η²-coordination of alkene (C_(sp²)#11–C_(sp²)#12) with the vacant coordination site of the Ru metal. We have also modelled an off-cycle intermediate, 11a, by removing iPrOH, which is less stable by 4.9 kcal mol⁻¹ than 11 (Scheme 6).

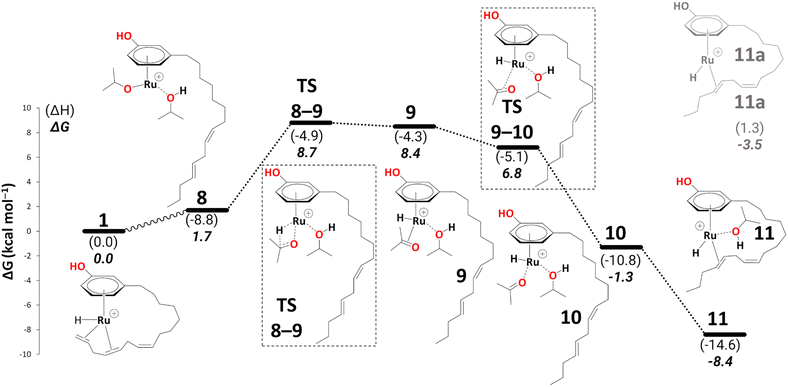Scheme 6 Reduction to the diene: from intermediate 8 to 11 (B3PW91-D3BJ/ECP2/PCM level, iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K). Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. The wavy line represents multiple steps. Table S3† shows the reaction energies of individual steps.

The sequence from 7 to 11 appears rather complicated for a seemingly simple β-H transfer from the isopropoxide to the metal. Because direct transfer via a four-membered transition state (which would avoid intermediate ligand dissociation) is expected to have a higher barrier (cf.TS3–4 in ref. 58), we have traced this multi-step variant, which turns out to be very facile kinetically. Note that even if other, more direct transformations from 7 to 11 were possible with even lower barriers, this would not affect our conclusions as this part is not rate-limiting at all.

Reduction to the cardanol monoene

We did not discuss the overall barriers for the diene reduction in the previous section, nor did we include the diene product formation step. To keep the consistency in the readability of the entire cycle, we shall discuss the most abundant reaction intermediate (MARI) and highest energy transition state with respect to MARI (HETS) along with the overall barriers based on Kozuch's and Shaik's energetic span model^59,60 in a new section. We now explicitly discuss reduction to the monoene.

Reduction to the monoene follows essentially the same steps as reduction to the diene. We traced a continuous pathway via a key to η³-allyl complex, 15 (see Schemes 7 and 8). Starting from complex 11, the highest point enroute to 15 is TS12–13 (a change from one β-agostic interaction to another, 15.9 kcal mol⁻¹ above 11, Schemes 7 and 8, and see section S2 in the ESI† for a detailed description of this part).

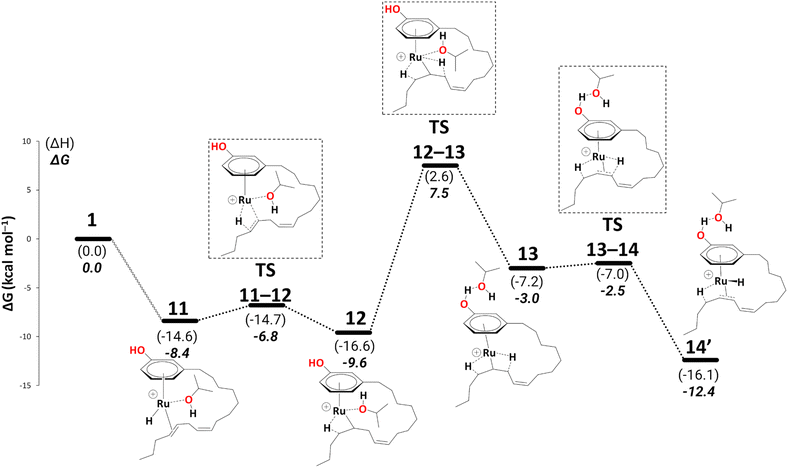Scheme 7 Reduction to the monoene: from intermediate 11 to 14′ (B3PW91-D3BJ/ECP2/PCM level, iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K). Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. The wavy line represents multiple steps. Table S3† shows the reaction energies of individual steps.

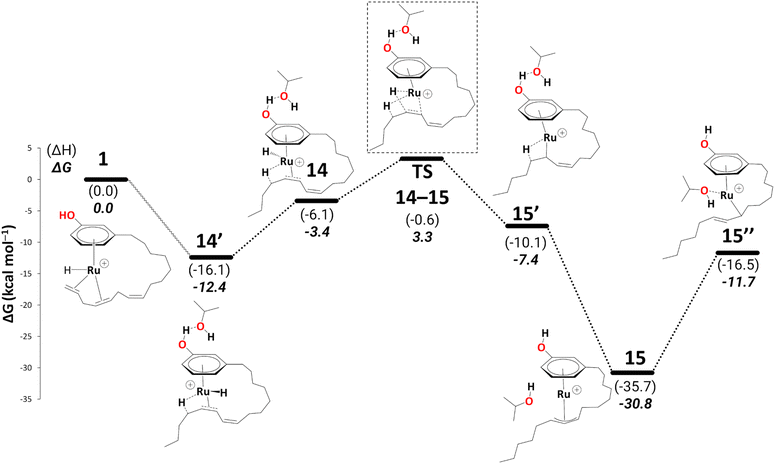Scheme 8 Reduction to the monoene: from intermediate 14′ to 15′′ (B3PW91-D3BJ/ECP2/PCM level, iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K). Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. The wavy line represents multiple steps. Table S3† shows the reaction energies of individual steps.

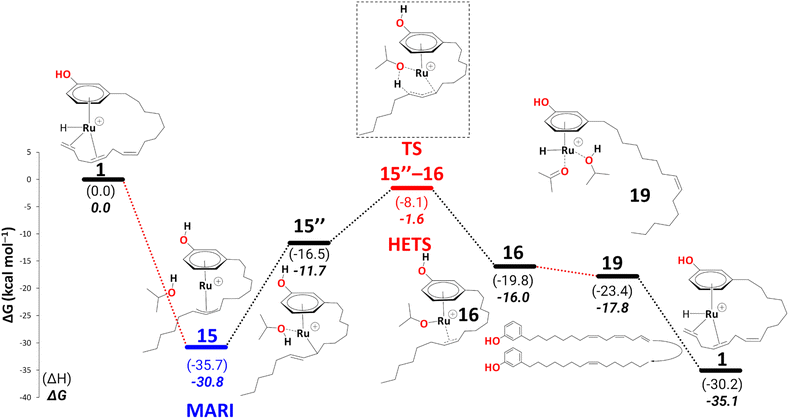
Like 5, 15 is a highly stable intermediate (ΔG_11→15 = −22.1 kcal mol⁻¹). To complete the reduction to the monoene, a proton transfer from the iPrOH to the allyl ligand is required. As in the first reduction path discussed above, we assume this step to proceed through an intermediate with η¹-allyl coordination mode and the iPrOH coordinated to the metal. The intermediate we located after moving the iPrOH from the phenol OH to the metal, isomer 15′′, is significantly less stable than 15 (ΔG_15′→15 = 19.1 kcal mol⁻¹).

In 15, the 1,3 substituents at the η³-allyl ligand are in an exo–syn–anti position. This stereochemistry arises from the cis-configuration of the alkene moiety in 15′. In principle, it could be possible for 15 to rearrange to the exo–syn–syn isomer (with both C7–C8–C9–C10 and C8–C9–C10–C11 moieties in anti-orientation. If that isomer would be more stable and interconversion between both would be rapid (as it had been found, for instance, in Pd(η³-1,3-dimethylallyl) complexes),⁶¹ the olefin in the final monoene would be expected to adopt a trans configuration (which would also be thermodynamically more stable than cis). Because the monoene product in the experimental study is formulated as the cis isomer²⁵ (although it is not clear if the stereochemistry of that product has been verified), we continue to explore the pathways leading to that isomer.

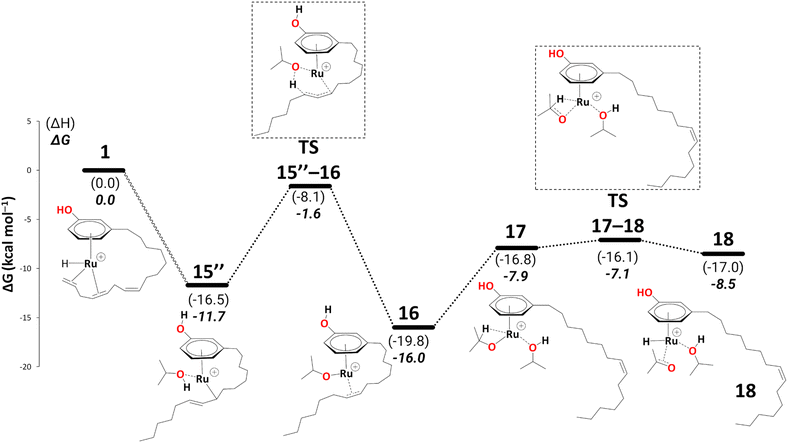
There is a kinetic barrier of 10.1 kcal mol⁻¹ to facilitate the protonation from coordinated iPrOH, affording the alkenyl complex 16 (Scheme 9). So far, after the appearance of the highly stable η³-allyl intermediate, 15, TS15–16 appears to be the highest energy transition state. The hydrogen transfer to C#10 results in an isopropoxide intermediate 16 accompanying η²-coordination with the resulting alkene (ΔG_{15′′→16} = −4.4 kcal mol⁻¹ and 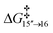= 10.1 kcal mol⁻¹). Similar to 8, where decoordination of the alkenyl chain was found to be favourable (with an additional solvent molecule bound to the metal), we modelled 17 to facilitate hydride transfer from the isopropoxide to the metal, where Ru loses its η²- coordination with the alkene. Another iPrOH is likely to occupy the vacant Ru coordination site; however, 17 is still uphill by 8.2 kcal mol⁻¹ (ΔG_16→17 = 8.2 kcal mol⁻¹). The formation of 17 is endergonic despite its potential stabilisation by a β-agostic interaction with the hydrogen of the isopropoxide. This interaction; however, makes 17 poised for hydride transfer to the metal, affording 18, with a low kinetic barrier of 0.8 kcal mol⁻¹ (ΔG_17→18 = −0.6 kcal mol⁻¹ and ΔG^‡_17→18 = 0.8 kcal mol⁻¹). The following intermediate is now a Ru–H complex, with acetone product weakly bonded with Ru via η²-coordination (Scheme 9).

Scheme 9 Reduction to the monoene: from intermediate 15′′ to 18 (B3PW91-D3BJ/ECP2/PCM level, iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K). Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. The wavy line represents multiple steps. Table S3 shows the reaction energies of individual steps.

Again, for intermediate 18, we ran a relaxed scan of the PES to locate TS and intermediate involved in acetone dissociation. As in the case of 9/10, the acetone moves from η²-coordination to η¹-coordination before it fully dissociates. The first step of acetone dissociation forms an intermediate 19 (ΔG_18→19 = −9.3 kcal mol⁻¹ and ΔG^‡_19→20 = −0.1 kcal mol⁻¹) and follows the complete dissociation by giving rise to intermediate 20 (ΔG_19→20 = 7.7 kcal mol⁻¹). Unlike 11, the formation of 20 is uphill by 7.1 kcal mol⁻¹ (Scheme 10). Although the η²-coordination of alkene should contribute to the system's stability, it is now less flexible causing the steric hindrance from a somewhat strained alkyl chain, making it less stable. Fig. 2 shows such a steric hindrance affecting the stability of both complexes, i.e., 11a and 20.

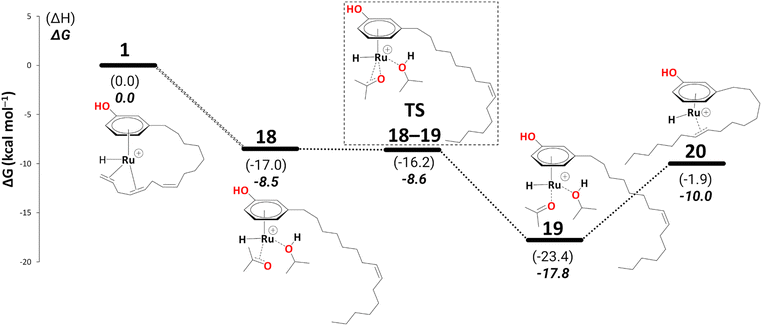Scheme 10 Reduction to the monoene: from intermediate 18 to 20 (B3PW91-D3BJ/ECP2/PCM level, iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K). Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. The wavy line represents multiple steps. Table S3† shows the reaction energies of individual step.

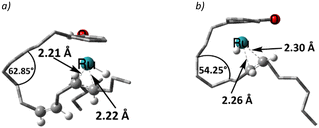Fig. 2 Optimised structures of a) 11a and b) 20 (alkyl and aryl hydrogen atoms omitted for clarity).

Catalytic activity and reduction to the saturated product

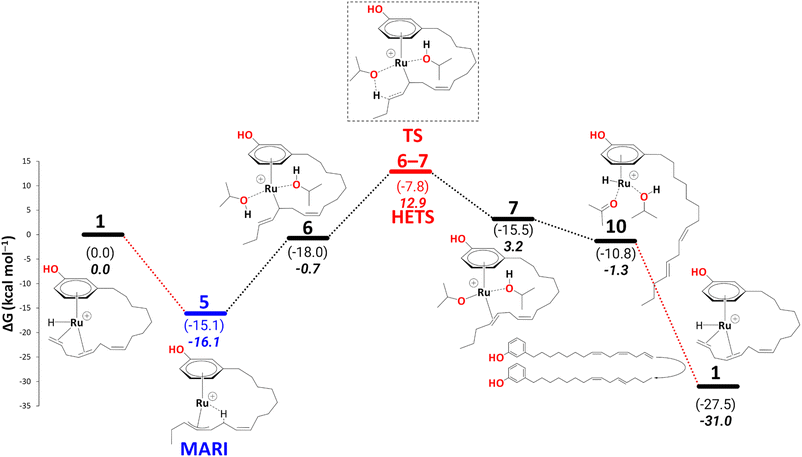
Before turning to complete reduction to the saturated product, we discuss the kinetic barriers leading to the diene and the monoene products. During reduction to the cardanol diene, an intermediate 10 was observed, where the alkenyl chain dissociates from the metal atom to allow hydrogen transfer from isopropoxide to the metal. It is conceivable that the dangling diene in 10 is liberated and replaced with fresh triene, affording intermediate 1. A possible scenario, assuming an associative (or associative interchange) mechanism, could involve intermediates that contain two cardanol moieties bound (see section S3, and Schemes S1 and S2 in the ESI†), possibly with reduced hapticity. Such substitution is expected to be a complicated multistep process and tracing the complete pathway for this would be a formidable task beyond the scope of the present study.

We note, however, that no covalent bonds need to be broken during such a substitution. Therefore, we do not expect prohibitive kinetic barriers for this step (prohibitive in the sense that they would be insurmountable under the reaction conditions). The overall thermodynamic driving force for this substitution, via

10 + triene → 1 + diene + acetone + iPrOH (1)

is computed to be exergonic by ΔG = −29.7 kcal mol⁻¹ (see last step on the profile coloured in black in Scheme 11). If only such a cycle was operating, the energetic span model would identify 5 as the MARI and TS6–7 as the HETS. The free energy difference between both leads to an energy span of 29.1 kcal mol⁻¹ for formation of the diene, which is attainable at the turnover conditions (Scheme 11).

Scheme 11 Reduction to the cardanol diene: key intermediates and transition state are shown, with 5 as MARI and TS6–7 as HETS. Energies (ΔH and ΔG) are calculated at B3PW91-D3BJ/ECP2/PCM level with iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K relative to 1. The red dotted lines represent multiple steps.

10 is thus a potential branching point that can either close the cycle to 1 and form the diene or continue on the path shown in Schemes 6–10, affording further reduction of the cardanol. This further reduction eventually gives rise to a thermodynamic sink in the form of another η³-allyl complex, 15. Once this allyl complex is formed, this further reduction is irreversible because in order to revert on the path back to 10 (in order to enter the branch for diene formation) would require an overall barrier (viaTS12–13, Scheme 7) of 38.3 kcal mol⁻¹. This barrier would be unsurmountable, even under the elevated temperatures of the experiment. The branching ratio between the formation of diene and further reduction is thus determined by the difference in the highest transition states leading from 10 to 1 or from 10 to 15. For the latter step, this highest barrier (again viaTS12–13, Scheme 7) is only 8.8 kcal mol⁻¹. We do not know the highest barrier for the former step (liberation of diene from 10) but seeing that this will be a complicated sequence involving coordination and dissociation of ligands (as, e.g., shown in Scheme 11 above), it is reasonable to assume that this branch will have a much higher barrier. Under this premise, the current catalytic system converts 100% of the produced cardanol diene into the η³-allyl complex, 15, which then gives the cardanol monoene product. This product can be formed at the stage of intermediate 19 on the reaction profile, via a ligand exchange of bound monoene against fresh triene, analogous to the diene-triene exchange discussed above. The thermodynamic driving force for this step that closes the cycle, i.e., via

19 + triene → 1 + monoene + acetone + iPrOH (2)

is computed to be ΔG = −17.3 kcal mol⁻¹ (see last step in Scheme 12). Starting from complex 1 until the production of the cardanol monoene product, we have identified 15 as the MARI and TS15–16 (the transition state associated with the second transfer hydrogenation) as the HETS (see Scheme 12). The resulting overall barrier is computed to be 29.2 kcal mol⁻¹. While this barrier would be too high to be overcome at room temperature, it is compatible with the reaction proceeding at elevated temperature. From the energy span analysis, such an overall barrier would correspond to a TOF of 0.03 h⁻¹. While this value would suggest a rather slow reaction, it should be recalled that absolute rate constants (or TOFs in this case) are notoriously difficult to calculate quantitatively.

Scheme 12 Reduction to the cardanol monoene: key intermediates and transition state are shown, with 15 as MARI and TS15–16 as HETS. Energies (ΔH and ΔG) are calculated at B3PW91-D3BJ/ECP2/PCM level with iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K relative to 1. The red dotted lines represent multiple steps.

Up to this point, the results are consistent with the full conversion of either cardanol triene or diene to the monoene product. The question now is, why is the monoene not reduced further to the fully saturated product? After reduction, all the fully saturated cardanol present in the mixture stems from the raw substrate mixture²⁵ (see Scheme 1 in the Introduction). To model a pathway to full reduction we considered the hydride transfer in intermediate 20 to C_(sp²)#9, giving rise to the intermediate 21 (Scheme 13). We could not locate a transition state for this hydride transfer from Ru to C_(sp²)#9. Still, we think this process should be facile, as the stability of the following intermediate, i.e., 21, is comparable to 20 (ΔG_20→21 = −0.2 kcal mol⁻¹) and the related transformation of, e.g., 14 to 15′ has a low activation barrier of ΔG = 6.7 kcal mol⁻¹ (see Scheme 7). Another solvent molecule coordinates to the Ru to allow the subsequent transfer hydrogenation (ΔG_21→22 = 0.9 kcal mol⁻¹), leading to a cardanol derivative with a fully saturated carbon chain (23, not shown in Scheme 13). The transition state to this product affords a barrier of ΔG^‡_22→23 = 25.2 kcal mol⁻¹. Irrespective of the overall thermodynamic driving force for full reduction, however, such a kinetic barrier associated with the final transfer hydrogenation leading to a fully saturated cardanol gives an overall barrier of 46.6 kcal mol⁻¹ (difference of free energy between MARI, i.e., η³-allyl complex, 15, and TS22–23). This barrier is insurmountable under the turnover conditions, therefore, even if 22 is formed, it should easily revert to 20 (eventually releasing the monoene) rather than proceed toward full reduction. This finding nicely explains why no fully saturated product is formed during the reaction.

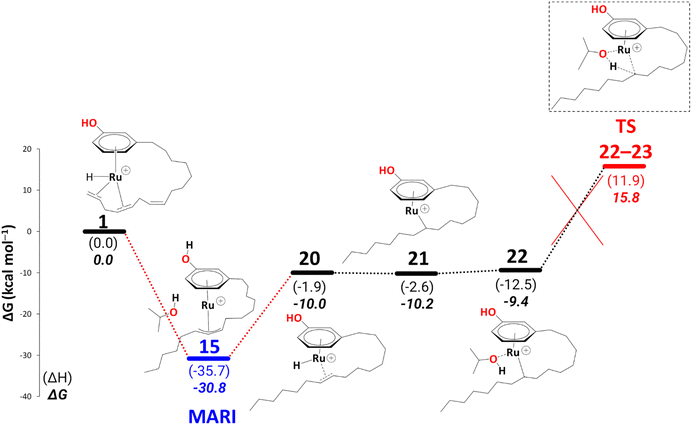Scheme 13 Reduction to the fully saturated cardanol derivative at the B3PW91-D3BJ/ECP2/PCM level with iPrOH as the model solvent with enthalpic and entropic corrections at 355.65 K. Energies (ΔH and ΔG) are in kcal mol⁻¹ relative to 1. The red dotted lines represent multiple steps. Table S4† shows the reaction energies of individual steps.

Conclusions

In the current work we have successfully traced catalytic cycles for the reduction of cardanol triene to the diene and monoene at a cationic Ru(II) centre and iPrOH as the H₂ source. Our results support the presence of cationic η³-allylic complexes as key intermediates and confirm the tentative assignment of the species detected by ESI-MS to one of these. Such cationic η³-allylic complexes are accessible via a [Ru(H)]⁺ centre coordinated to the phenol ring and two double bonds of the cardanol triene substrate. Starting from a cationic Ru hydride complex (1), the first highly stable η³-allylic intermediate (5) can be formed. Once the free energy profile reaches TS6–7, the further free energy barriers, leading to the diene product and another η³-allylic intermediate, are low. The second η³-allylic intermediate (15) is even more stable than the first and is involved in reducing the diene substrate to the monoene product. Considering the entire reaction profile, starting from the second η³-allylic intermediate until the formation of the diene product, the overall barrier, 29.2 kcal mol⁻¹, is associated with the transfer hydrogenation. Barriers of that magnitude should be surmountable under the elevated temperatures of the experiments (refluxing isopropanol). After the first double bond reduction, entry into the path leading to the second η³-allylic intermediate (and eventually, reduction of the second double bond) is so facile that no release of a diene is to be expected, in full accord with the experiment, where selective hydrogenation to the monoene is observed.

The reduction of the monoene to the fully saturated product was also considered. As the double bond moves closer to the phenol moiety of the cardanol, the flexibility of the carbon chain decreases, increasing the steric strain of the carbon chain to the Ru metal. Such a high steric hindrance prevents solvent coordination with the metal atom. There is a high kinetic barrier of 46.6 kcal mol⁻¹ for the final transfer hydrogenation, making the reduction of the monoene to the fully saturated product implausible.

The three kinetic barriers of 29.1 kcal mol⁻¹ (for reduction to the diene), 29.2 kcal mol⁻¹ (for reduction to the monoene), and 46.6 kcal mol⁻¹ (for reduction to the fully saturated product) show the formation of the fully saturated product is unlikely, which agrees with experiment. The formation of the MARI η³-allylic intermediate 5) of the entire reaction profile requires a barrier height of 25.6 kcal mol⁻¹, which further reduces the diene substrate to the monoene product, again in good agreement with the experiment. The current studies, therefore, provide new mechanistic insights into the exquisite selectivity of the Ru–catalysed reduction of cardanol, transforming a complex mixture into essentially a single unsaturated product.

Experimental section

Our computational methodology is based on the B3PW91 (ref. 62–64) hybrid functional, which has been used successfully to study Ru-catalysed transfer hydrogenation of ketones.^34,65–68 Moreover, several other studies involving Ru-catalysed transformations validate the success of this hybrid function.^69–73 For large systems, where DFT does not account very well for dispersive forces, B3PW91 hybrid functional coupled with Grimme's DFT-D3,^74–76 including Becke–Johnson damping,^77,78 benchmarks well against explicitly correlated CCSD(T).⁷⁹

Geometries of all intermediates and transition state were fully optimised at the B3PW91/ECP1 level. ECP1 corresponds to the 6-31G** basis set on all non-metal atoms. The metal atom (Ru) was treated with the SDD basis, denoting the small-core Stuttgart–Dresden relativistic effective core potential (ECP)^80–83 together with its valence basis set. The frequency calculations within the harmonic approximation were used to verify the nature of all intermediates (the possible minima) and transition states. Free energy and enthalpic corrections were determined by computing harmonic frequencies analytically at 355.65 K. The entropic contributions were evaluated at a pressure of 381 atm, corresponding to the pressure at which an ideal gas of isopropanol would have the same density as the real liquid (pressure correction according to Martin, Hay, and Pratt, see section 4 in the ESI†).^84,85 For each step on the reaction profile, thermochemical correction terms δE_G were carried out as a difference of the reaction energy (ΔE_B3PW91/ECP1) and the corresponding free energy (ΔG_B3PW91/ECP1):

δE_G = ΔG_B3PW91/ECP1 − ΔE_B3PW91/ECP1 (3)

Potential energy profile calculations were performed to obtain the starting structures of the transition states, connecting the reactants and the products at the same level, i.e., B3PW91/ECP1. These potential energy profile calculations were performed by increasing or decreasing the distance of the atom of a coordinated moiety, which was dissociating from or associating to the system or moving from one ligand to the other ligand by 0.1 Å and by optimising the remaining geometric parameters with loose convergence criteria. Transition states were confirmed by visual inspection of the imaginary frequency modes and intrinsic reaction coordinate (IRC) calculations.^86,87

Coordinates of the optimised intermediates and transition states were taken to get refined energies using the same hybrid functional at ECP2 level. Ru was treated with the same pseudopotential and valence basis as in ECP1 (SDD), whereas all the non-metal atoms were treated with 6-311+G** basis set. Isopropanol was taken as a solvent in polarisable continuum (PCM)^88–90 model to include the solvent effects. To accurately account for the missing dispersion by DFT, DFT-D3(BJ) corrections were added posteriori. The final free energies (ΔG) and enthalpies (ΔH) were calculated as:

ΔG = ΔE + δE_Solv + δE_DFTD3BJ + δE_G (4)

ΔH = ΔE + δE_Solv + δE_DFTD3BJ + δE_H (5)

where ΔE, and δE_Solv are computed at the B3PW91-D3/ECP2 level, δE_G and δE_H are computed at the B3PW91/ECP1 level. All calculations were performed using Gaussian 09.⁹¹ This level has performed very well in a number of studies from our group.^52–57

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank EaStCHEM and the School of Chemistry for their support. Computations were carried out on a local Opteron PC cluster maintained by Dr H. Früchtl. The research data supporting this publication can be accessed at https://doi.org/10.17630/3b865cea-6293-4f90-9e57-1c030b8e3963.

Notes and references

1. E. Stephens, I. L. Ross, Z. King, J. H. Mussgnug, O. Kruse, C. Posten, M. A. Borowitzka and B. Hankamer, Nat. Biotechnol., 2010, 28, 126–128.
2. Energy scenario development analysis: WEC policy to 2050, 2007.
3. B. Knopf, P. Nahmmacher and E. Schmid, Energy Policy, 2015, 85, 50–60.
4. U. Biermann, U. Bornscheuer, M. A. R. Meier, J. O. Metzger and H. J. Schäfer, Angew. Chem., Int. Ed., 2011, 50, 3854–3871.
5. C. Thurier, C. Fischmeister, C. Bruneau, H. Olivier-Bourbigou and P. H. Dixneuf, ChemSusChem, 2008, 1, 118–122.
6. S. Caillol, Curr. Opin. Green Sustainable Chem., 2018, 14, 26–32.
7. J. Deutsch and A. Köckritz, Food Sci. Nutr., 2020, 8, 3081–3088.
8. A. Fontana, S. Guernelli, N. Zaccheroni, R. Zappacosta, D. Genovese, L. De Crescentini and S. Riela, Org. Biomol. Chem., 2015, 13, 9214–9222.
9. M. C. Lubi and E. T. Thachil, Des. Monomers Polym., 2000, 3, 123–153.
10. D. Balgude and A. S. Sabnis, J. Coat. Technol. Res., 2014, 11, 169–183.
11. T. C. Phatak, S. K. Agarwal and I. Masood, Mater. Struct., 1992, 25, 355–357.
12. T. Otsuka, S. Fujikawa, H. Yamane and S. Kobayashi, Polym. J., 2017, 49, 335–343.
13. S. Sahila and L. S. Jayakumari, Polym. Compos., 2015, 36, 1–7.
14. K. Sethuraman and M. Alagar, RSC Adv., 2015, 5, 9607–9617.
15. D. Chu, J. Wang, Y. Han, Q. Ma and Z. Wang, RSC Adv., 2015, 5, 11378–11384.
16. V. S. Balachandran, S. R. Jadhav, P. K. Vemula and G. John, Chem. Soc. Rev., 2013, 42, 427–438.
17. S. Mahesh, D. Raju, A. S. Arathi and K. Joseph, RSC Adv., 2014, 4, 42747–42750.
18. Y. Shi, P. C. J. Kamer and D. J. Cole-Hamilton, Green Chem., 2019, 21, 1043–1053.
19. B. Rajkumar, L. Khanam, E. N. Koukaras, G. D. Sharma, S. P. Singh and B. Lochab, ACS Sustainable Chem. Eng., 2020, 8, 5891–5902.
20. J. H. Tyman and L. S. Kiong, Lipids, 1978, 13, 525–532.
21. P. Phani Kumar, R. Paramashivappa, P. J. Vithayathil, P. V. Subba Rao and A. Srinivasa Rao, J. Agric. Food Chem., 2002, 50, 4705–4708.
22. J. H. P. Tyman, R. A. Johnson, M. Muir and R. Rokhgar, J. Am. Oil Chem. Soc., 1989, 66, 553–557.
23. J. H. P. Tyman, V. Tychopoulos and P. Chan, J. Chromatogr. A, 1984, 303, 137–150.
24. J. Y. N. Philip, J. Da Cruz Francisco, E. S. Dey, J. Buchweishaija, L. L. Mkayula and L. Ye, J. Agric. Food Chem., 2008, 56, 9350–9354.
25. S. Perdriau, S. Harder, H. J. Heeres and J. G. de Vries, ChemSusChem, 2012, 5, 2427–2434.
26. R. K. Jain and S. Kumar, J. Food Eng., 1997, 32, 339–345.
27. G. Brieger and T. J. Nestrick, Chem. Rev., 1974, 74, 567–580.
28. S. Chowdhury, F. Himo, N. Russo and E. Sicilia, J. Am. Chem. Soc., 2010, 132, 4178–4190.
29. C. P. Casey and J. B. Johnson, J. Org. Chem., 2003, 68, 1998–2001.
30. R. Wu, M. G. Beauchamps, J. M. Laquidara and J. R. Sowa Jr., Angew. Chem., Int. Ed., 2012, 51, 2106–2110.
31. S. Bi, Q. Xie, X. Zhao, Y. Zhao and X. Kong, J. Organomet. Chem., 2008, 693, 633–638.
32. P. Hauwert, R. Boerleider, S. Warsink, J. J. Weigand and C. J. Elsevier, J. Am. Chem. Soc., 2010, 132, 16900–16910.
33. A. Pavlova and E. J. Meijer, ChemPhysChem, 2012, 13, 3492–3496.
34. D. A. Alonso, P. Brandt, S. J. M. Nordin and P. G. Andersson, J. Am. Chem. Soc., 1999, 121, 9580–9588.
35. Y. Wang, Z. Huang, X. Leng, H. Zhu, G. Liu and Z. Huang, J. Am. Chem. Soc., 2018, 140, 4417–4429.
36. F. Perez, S. Oda, L. M. Geary and M. J. Krische, Top. Curr. Chem., 2016, 374, 35.
37. Y. Chen, M. Wang, S. Fang, T. Wang and J. Liu, Organometallics, 2015, 34, 4864–4870.
38. X. Liu, W. Zhang, Y. Wang, Z.-X. Zhang, L. Jiao and Q. Liu, J. Am. Chem. Soc., 2018, 140, 6873–6882.
39. X. Liu, L. Bin and Q. Liu, Synthesis, 2019, 51, 1293–1310.
40. B. J. Spinello, J. Wu, Y. Cho and M. J. Krische, J. Am. Chem. Soc., 2021, 143, 13507–13512.
41. S. Scaringi and C. Mazet, ACS Catal., 2021, 11, 7970–7977.
42. A. M. Camp, M. R. Kita, P. T. Blackburn, H. M. Dodge, C.-H. Chen and A. J. M. Miller, J. Am. Chem. Soc., 2021, 143, 2792–2800.
43. X. Liu, X. Rong, S. Liu, Y. Lan and Q. Liu, J. Am. Chem. Soc., 2021, 143, 20633–20639.
44. C.-F. Liu, H. Wang, R. T. Martin, H. Zhao, O. Gutierrez and M. J. Koh, Nat. Catal., 2021, 4, 674–683.
45. J. Zhao, G. Xu, X. Wang, J. Liu, X. Ren, X. Hong and Z. Lu, Org. Lett., 2022, 24, 4592–4597.
46. S. N. Sluijter and C. J. Elsevier, Organometallics, 2014, 33, 6389–6397.
47. P. Västilä, A. B. Zaitsev, J. Wettergren, T. Privalov and H. Adolfsson, Chem. – Eur. J., 2006, 12, 3218–3225.
48. C. Hedberg, K. Källström, P. I. Arvidsson, P. Brandt and P. G. Andersson, J. Am. Chem. Soc., 2005, 127, 15083–15090.
49. J. Zhang and T.-P. Loh, Chem. Commun., 2012, 48, 11232–11234.
50. M. Mori, Y. Kozawa, M. Nishida, M. Kanamaru, K. Onozuka and M. Takimoto, Org. Lett., 2000, 2, 3245–3247.
51. P. Pertici, V. Ballantini, P. Salvadori and M. A. Bennett, Organometallics, 1995, 14, 2565–2569.
52. S. Ahmad, L. E. Crawford and M. Bühl, Phys. Chem. Chem. Phys., 2020, 22, 24330–24336.
53. S. Ahmad and M. Bühl, Chem. – Eur. J., 2019, 25, 11625–11629.
54. S. Ahmad, A. Lockett, T. A. Shuttleworth, A. M. Miles-Hobbs, P. G. Pringle and M. Bühl, Phys. Chem. Chem. Phys., 2019, 21, 8543–8552.
55. S. Ahmad and M. Bühl, Phys. Chem. Chem. Phys., 2021, 23, 15869–15880.
56. L. Crawford, D. J. Cole-Hamilton, E. Drent and M. Bühl, Chem. – Eur. J., 2014, 20, 13923–13926.
57. L. Crawford, D. J. Cole-Hamilton and M. Bühl, Organometallics, 2015, 34, 438–449.
58. N. Sieffert and M. Bühl, J. Am. Chem. Soc., 2010, 132, 8056–8070.
59. S. Kozuch, S. E. Lee and S. Shaik, Organometallics, 2009, 28, 1303–1308.
60. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
61. J. Vázquez, B. Goldfuss and G. Helmchen, J. Organomet. Chem., 2002, 641, 67–70.
62. A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046.
63. J. P. Perdew and K. Burke, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
64. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
65. S. J. M. Nordin, P. Roth, T. Tarnai, D. A. Alonso, P. Brandt and P. G. Andersson, Chem. – Eur. J., 2001, 7, 1431–1436.
66. R. A. Farrar-Tobar, Z. Wei, H. Jiao, S. Hinze and J. G. de Vries, Chem. – Eur. J., 2018, 24, 2725–2734.
67. D. G. I. Petra, J. N. H. Reek, J.-W. Handgraaf, E. J. Meijer, P. Dierkes, P. C. J. Kamer, J. Brussee, H. E. Schoemaker and P. W. N. M. van Leeuwen, Chem. – Eur. J., 2000, 6, 2818–2829.
68. T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586.
69. R.-L. Zhong and S. Sakaki, J. Am. Chem. Soc., 2020, 142, 16732–16747.
70. J. Neumann, C. Bornschein, H. Jiao, K. Junge and M. Beller, Eur. J. Org. Chem., 2015, 2015, 5944–5948.
71. M. Gulías, A. Collado, B. Trillo, F. López, E. Oñate, M. A. Esteruelas and J. L. Mascareñas, J. Am. Chem. Soc., 2011, 133, 7660–7663.
72. J. M. Lee, D. Y. Bae, J. Y. Park, H. Y. Jo, E. Lee, Y. H. Rhee and J. Park, Org. Lett., 2020, 22, 4608–4613.
73. N. J. Stewart, H. Nakano, S. Sugai, M. Tomohiro, Y. Kase, Y. Uchio, T. Yamaguchi, Y. Matsuo, T. Naganuma, N. Takeda, I. Nishimura, H. Hirata, T. Hashimoto and S. Matsumoto, ChemPhysChem, 2021, 22, 915–923.
74. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
75. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
76. T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591.
77. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108.
78. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104.
79. M. K. Kesharwani and J. M. L. Martin, Theor. Chem. Acc., 2014, 133, 1–14.
80. G. Frenking, I. Antes, M. Böhme, S. Dapprich, A. W. Ehlers, V. Jonas, A. Neuhaus, M. Otto, R. Stegmann, A. Veldkamp and S. F. Vyboishchikov, Rev. Comput. Chem., 2007, 63–144.
81. M. Dolg and X. Cao, Chem. Rev., 2012, 112, 403–480.
82. P. O. Löwdin, Phys. Rev., 1955, 97, 1509–1520.
83. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101.
84. R. L. Martin, P. J. Hay and L. R. Pratt, J. Phys. Chem. A, 1998, 102, 3565–3573.
85. For the use of Martin, Hay, and Pratt's scheme in modelling homogeneous catalysis, see, e.g., S. Gallarati, P. Dingwall, J. A. Fuentes, M. Bühl and M. L. Clarke, Organometallics, 2020, 39, 4544–4556.
86. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
87. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
88. J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226.
89. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
90. A. Klamt, B. Mennucci, J. Tomasi, V. Barone, C. Curutchet, M. Orozco and F. J. Luque, Acc. Chem. Res., 2009, 42, 489–492.
91. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009. The full reference is given in the ESI.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy00135k

---