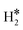Open Access Article
Open Access ArticleHydrogen complexes on single atom alloys: classical chemisorption versus coordination chemistry†
Ilaria
Barlocco
 ,
Giovanni
Di Liberto
,
Giovanni
Di Liberto
 * and
Gianfranco
Pacchioni
* and
Gianfranco
Pacchioni

Dipartimento di Scienza dei Materiali, Università di Milano – Bicocca, via R. Cozzi 55, 20125 Milano, Italy. E-mail: giovanni.diliberto@unimib.it
First published on 3rd August 2023
Abstract
Single Atom Alloys (SAAs) represent one of the most promising classes of heterogeneous catalysts. They are based on isolated transition metal (TM) atoms stabilized in a host metal matrix. Among others, SAAs are widely studied for processes involving hydrogen, such as water splitting or hydrogenation reactions. On a metal surface the H2 molecule forms either weakly physisorbed species (H2phys) or dissociates with formation of chemisorbed H atoms (H*). In electrochemical processes, the adsorption free energy of the H* intermediate is normally used as a descriptor of the catalyst reactivity. Recently, it has been shown that on Single Atom Catalysts (SAC) embedded in carbon-based, sulfide, or oxide supports other species can form, where two H atoms are stably bound to the SAC, forming dihydrogen 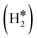 or dihydride (H*H*) surface species reminiscent of the classical Kubas's transition metal complexes in coordination chemistry. In this work we show, based on density functional theory calculations, that dihydrogen and dihydride complexes can also form on SAAs and, depending on the nature of the host metal, can be even more stable than two separated chemisorbed H* species (2H*). These new stable intermediates have not been considered so far in the analysis of the mechanism and kinetics of the reaction. The work shows that the possible formation of dihydrogen and dihydride complexes is not limited to SACs but is also valid for SAAs and needs to be considered in the study of hydrogen-based reactions on these systems.
or dihydride (H*H*) surface species reminiscent of the classical Kubas's transition metal complexes in coordination chemistry. In this work we show, based on density functional theory calculations, that dihydrogen and dihydride complexes can also form on SAAs and, depending on the nature of the host metal, can be even more stable than two separated chemisorbed H* species (2H*). These new stable intermediates have not been considered so far in the analysis of the mechanism and kinetics of the reaction. The work shows that the possible formation of dihydrogen and dihydride complexes is not limited to SACs but is also valid for SAAs and needs to be considered in the study of hydrogen-based reactions on these systems.
1. Introduction
Catalysis is a mature technology that will play a fundamental role in the energy transition. Catalytic materials are adopted in 95% of the chemical processes of industrial interests representing a sizeable fraction of the domestic product of many countries.1 State-of-the-art heterogeneous catalysts are based on supported metal catalysts, such as nanoparticles and nanoclusters. They have been widely studied and applied in different chemical reactions due to their high activity.2,3 The best catalysts are often based on noble metals, raising fundamental problems of overall cost of the processes and availability of raw materials. Indeed, the urgency to reduce the metal loading, tailor the catalytic activity and reduce the use of critical elements is driving the research of the last few years.4–9An effective strategy to increase the active phase is to downscale the size of the metal component to the limit of atomically well-defined and isolated metal centers anchored on a given support.10,11 Such species, called Single Atom Catalysts (SACs), have each a single atom available for the reaction, maximizing the number of active sites.12–20 SACs are attracting a lot of attention also because they bridge heterogeneous and homogeneous catalysis, opening a chance to tune the catalytic properties by playing with the local environment.21–24 In fact, the local coordination of the single metal atom is of paramount importance in determining the actual activity of the material, underlying the similarities with organometallic complexes.25–27
A very promising family of SACs is that of Single-Atom Alloys (SAAs), i.e. catalysts having as a support a metal surface.28–30 The concept of SAA was formulated nearly ten years ago by Sykes and co-workers.31 These species combine a metallic character with the special properties of SACs. Because of these two hallmarks, SAAs have been proven very promising for several reactions.32–35 This has stimulated the development of new and advanced methodologies for the synthesis of novel SAAs. At the same time, quantum chemical studies have been used to shed light on the atomistic nature of such systems, allowing to access the structure, properties, and reactivity of SAAs at the atomic scale.36–38
The apparent simple structure of SACs, including SAAs, has also stimulated the rational design of novel systems based on the screening of large numbers of models and on the search for universal descriptors.39,40 A timely and seminal review on the main achievements made by computational chemistry in the field of SAAs was recently presented by Réocreux and Stamatakis.41
An important aspect when dealing with SACs is their analogy with coordination chemistry compounds. This can manifest itself in reaction intermediates that are not usually formed on conventional catalysts made of supported metal particles. This can have important implications for the overall reactivity by opening up reaction channels that would otherwise be impeded. In the last four decades an intense experimental and theoretical research was devoted to the study of dihydrogen complexes on cations and transition metal complexes.42–50 This kind of complexes can form on SACs.51 similar examples exist for superoxo, peroxo, and other oxygenates species.52–54 However, there is a substantial difference between a TM atom stabilized in graphene or in carbon nitride thanks to localized chemical bonds and the same atom embedded in a metal surface. The first case is clearly reminiscent of coordination chemistry compounds, while with the second one is dealing with a metal impurity in a metallic support with delocalized electronic charge.
Extended metal catalysts are widely applied for hydrogen related reactions, such as the Hydrogen Evolution Reaction (HER) and hydrogenation processes.55–58 On extended metals hydrogen can interact strongly, with dissociative adsorption that results in chemisorbed H atoms, H*, or weakly, forming only physisorbed H2 molecules (H2phys).58–60 When two H* atoms migrating on the surface meet each other they can form H2phys that then evolves into a gas-phase H2 molecule. To the best of our knowledge this is the first report showing the formation of stable complexes where two H atoms are chemically bound to the same surface metal atom impurity forming dihydrogen or dihydride complexes, and discussing the important implications in catalysis and modelling studies. The study of SAAs in hydrogen related reactions reached remarkable achievements,61–66 but the atomistic descriptions of the reaction always assumes the formation of H* intermediates only.
In this work, we demonstrate by means of density functional theory (DFT) calculations that dihydrogen/dihydride complexes can form on SAAs exactly as they form on other SACs. The work is motivated by previous findings of metal single atoms supported on carbon-based materials,51 by recent reports showing that selected SAA catalysts can bind on the same site more than one molecular fragment,67 and by the findings of Greiner et al. showing that to some extent some SAAs retain the atomic nature due to the localized d orbitals.68
Our computational results provide support to the possible formation of the unconventional hydrogen intermediates. In this respect, even SAAs are reminiscent of coordination chemistry complexes. In some cases, these complexes are metastable, i.e. the 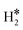 or H*H* species formed on the SAA are less stable than two chemisorbed H atoms, 2H*; in other cases, the dihydrogen or dihydride complexes are thermodynamically more stable than two chemisorbed H atoms. In this case, a new stable intermediate is formed on the surface, with direct consequences on the mechanisms and kinetics of the reaction. Of course, the possible formation of unconventional intermediates opens intriguing new routes for hydrogen related reactions and should be considered in computational studies on the subject.
or H*H* species formed on the SAA are less stable than two chemisorbed H atoms, 2H*; in other cases, the dihydrogen or dihydride complexes are thermodynamically more stable than two chemisorbed H atoms. In this case, a new stable intermediate is formed on the surface, with direct consequences on the mechanisms and kinetics of the reaction. Of course, the possible formation of unconventional intermediates opens intriguing new routes for hydrogen related reactions and should be considered in computational studies on the subject.
Our conclusions are based on a set of model systems consisting of eight hosting metals with very different reactivity towards hydrogen, from highly reactive, Nb and Mo, to quite unreactive, Ag and Au, including some metals with intermediate reactivity such as Rh, Pd, Ni, and Ru. On these supports, six different metal atoms have been considered to form the SAAs. Some of these atoms, Ti, Fe, Co, belong to the first transition metal row, others, W, Ir, and Pt to the third transition metal row. This provides a sufficiently wide spectrum of behaviors to demonstrate that on SAAs dihydrogen and dihydride complexes can form. To summarize, the goal of this study is not to provide a comprehensive H2 dissociation dynamics, but rather to show that non-conventional dihydrogen and dihydride intermediates can form also on single atom alloys, which is of primary importance for modelling studies aiming at performing screenings of new materials, searching for descriptors and eventually predicting new catalysts. It is important to mention that our aim is not to provide predictions of promising catalytic candidates, since to achieve this purpose one should include many other ingredients such as reaction barriers, microkinetic analysis and solvation effects.
2. Computational details
Spin polarized DFT calculations were performed with the VASP code69–71 using the Perdew–Burke–Ernzerhof (PBE) parametrization of the exchange–correlation functional.72 Dispersion forces have been included according to the Grimme's D3 parameterization.73 The valence electrons were expanded on a set of plane waves with a kinetic energy cutoff of 400 eV, whereas the core electrons were treated with the projector augmented wave approach (PAW).74,75 The threshold criteria for electronic and ionic loops were set to 10−6 eV and 10−2 eV Å−1, respectively. The sampling of the reciprocal space was done by adopting a Monkhorst–Pack grid76 according to the size of the simulation cell.The bulk crystal structures were fully optimized starting from the experimental ones.77 The optimized cell parameters are reported in Table S1.† Five layers thick slab models were cut from the optimized bulk structures by adding a sufficiently thick vacuum layer along the non-periodic direction, to avoid interaction between periodic replicas. The atomic coordinates were fully optimized.
Eight different metal surfaces were considered, Mo, Nb, Ni, Rh, Pd, Ru, Ag and Au. All metals with the exception of Mo, Nb and Ru crystallize in the cubic face-centred lattice, and the most stable surface is the (111) one.78 Mo and Nb crystallize in the cubic body-centred lattice and expose the (110) surface.79 Ru is described by an hexagonal crystal lattice and the surface is often by modelled by a (0001) cut.80 The a, b, and γ lattice parameters of each surface model are summarized in Table S2.†
The metals were classified according to their hydrogen chemisorption free energy, ΔGH, see Fig. 1, where ΔGH is plotted against the calculated exchange current, log(i0), a measure of the catalyst activity.58,81 Nb and Mo bind hydrogen very strongly and can be considered as “very reactive” metals towards H2 (ΔGH < −0.5 eV). Rh, Pd, Ni and Ru are close to the apex of the volcano plot, indicating an almost ideal binding free energy, and have an “intermediate” behaviour (−0.5 eV < ΔGH < 0 eV). Pt is also shown on Fig. 1 for comparison, as it is obtained with the present computational setup to show its performance. Ag and Au, on the contrary, display an endergonic free energy for hydrogen adsorption and can be classified as “unreactive” (ΔGH > 0 eV).
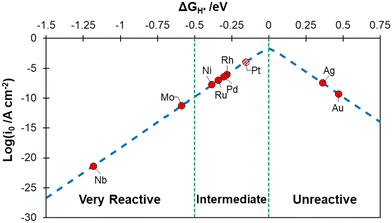 | ||
| Fig. 1 Calculated exchange current, log(i0), for hydrogen evolution reaction over the different metal surfaces plotted as a function of the calculated hydrogen chemisorption free energy (ΔGH). The log(i0) was obtained according to ref. 58. The value calculated for Pt(111) is reported for reference. | ||
The hydrogen adsorption free energies were obtained from the calculated adsorption energies including thermodynamic corrections.58,60,82 Section S2† reports in detail the working equations and key-quantities. Vibrational frequencies were calculated within the harmonic approximation, in which the hydrogen atoms and the metal ones directly bound to H were allowed to move.
3. Results and discussion
On each of the eight metal surfaces (host) reported in Table S2† we substituted one surface atom by a TM atom forming a SAA. We chose three representative elements from the first TM row, Ti, an early 3d TM atom, Fe and Co, two magnetic atoms widely studied as SACs, and three representative elements from the third TM row, W, Ir and Pt, where Pt in particular is chosen due to its excellent catalytic activity. In this way we generated a set of 48 different SAA catalysts, Tables 1–3. In all cases the TM dopant takes the place of the removed metal atom without any relevant protrusion from the surface layer. Since the purpose of the work is not to the provide absolute predictions about the catalytic activity of SAAs under reaction conditions, we did not consider the possible migration of the dopant in the inner part of the host material (sub-surface or bulk).| H | H2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sitea | ΔG/eV | d A–H/Å | d B–H/Å | α/° | Structure | ΔG/eV | d A–H/Å | d H–H/Å | |
| a H = hollow, B = bridge, T = top. | |||||||||
| Ag(111) | H | 0.36 | — | 1.90 | 62.3 | 2H* | 0.64 | 1.88 | 2.88 |
| Ti@Ag(111) | H | −0.06 | 1.85 | 2.03 | 52.3 | H*H* | −0.27 | 1.87 | 2.57 |
| Fe@Ag(111) | H | −0.06 | 1.70 | 1.99 | 56.8 | H*H* | −0.17 | 1.70 | 2.42 |
| Co@Ag(111) | H | −0.03 | 1.58 | 2.1 | 47.1 |
|
−0.14 | 1.51 | 1.04 |
| W@Ag(111) | H | −0.33 | 1.77 | 2.24 | 43.4 | H*H* | −0.84 | 1.75 | 2.00 |
| Ir@Ag(111) | T | −0.51 | 1.59 | — | 0.00 | H*H* | −0.89 | 1.62 | 1.95 |
| Pt@Ag(111) | H | −0.03 | 1.64 | 2.22 | 44.7 | H*H* | −0.02 | 1.67 | 2.35 |
| Au(111) | H | 0.47 | — | 1.88 | 64.1 | 2H* | 0.86 | 1.87 | 2.90 |
| 1.86 | 1.91 | ||||||||
| 1.96 | |||||||||
| Ti@Au(111) | H | 0.08 | 1.88 | 2.01 | 55.2 |
|
0.09 | 2.07 | 0.78 |
| Fe@Au(111) | H | 0.30 | 1.77 | 1.96 | 56.7 | 2H* | 0.27 | 1.90 | 2.76 |
| Co@Au(111) | H | 0.07 | 1.67 | 1.99 | 57.4 |
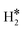
|
0.01 | 1.62 | 0.87 |
| W@Au(111) | T | −0.41 | 1.72 | — | 0.00 | H*H* | −0.70 | 1.73 | 1.85 |
| Ir@Au(111) | T | −0.64 | 1.58 | — | 0.00 | H*H* | −0.90 | 1.60 | 1.75 |
| Pt@Au(111) | T | −0.11 | 1.56 | — | 0.00 | H*H* | 0.26 | 1.69 | 2.32 |
| H | H2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sitea | ΔG/eV | d A–H/Å | d B–H/Å | α/° | Structure | ΔG/eV | d A–H/Å | d H–H/Å | |
| a H = hollow, B = bridge, T = top. | |||||||||
| Rh(111) | H | −0.28 | — | 1.57 | 90.0 | 2H* | −0.70 | 1.86 | 3.09 |
| 1.55 | 1.85 | ||||||||
| 1.52 | |||||||||
| Ti@Rh(111) | H | −0.54 | 2.17 | 1.82 | 56.9 | 2H* | −1.07 | 2.19 | 3.68 |
| 2.21 | |||||||||
| Fe@Rh(111) | H | −0.36 | 1.93 | 1.83 | 56.8 | 2H* | −0.76 | 2.02 | 3.33 |
| 1.94 | |||||||||
| Co@Rh(111) | H | −0.36 | 1.77 | 1.84 | 56.4 | 2H* | −0.78 | 1.77 | 2.93 |
| 1.78 | |||||||||
| W@Rh(111) | H | −0.39 | 2.07 | 1.84 | 55.2 |
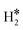
|
−0.16 | 1.93 | 0.85 |
| Ir@Rh(111) | T | −0.40 | 1.62 | — | 0.00 | H*H* | −0.74 | 1.69 | 2.36 |
| Pt@Rh(111) | H | −0.22 | 1.91 | 1.81 | 55.8 | 2H* | −0.54 | 1.85 | 3.13 |
| 1.88 | |||||||||
| Pd(111) | H | −0.30 | — | 1.84 | 60.2 | 2H* | −0.64 | 1.83 | 2.75 |
| Ti@Pd(111) | H | −0.36 | 2.27 | 1.78 | 52.4 | 2H* | −0.64 | 2.21 | 3.04 |
| Fe@Pd(111) | H | −0.43 | 1.72 | 1.87 | 54.9 | 2H* | −1.99 | 2.01 | 2.90 |
| 2.00 | |||||||||
| Co@Pd(111) | H | −0.27 | 1.96 | 1.79 | 58.5 | 2H* | −0.53 | 1.82 | 2.67 |
| W@Pd(111) | H | −0.28 | 2.08 | 1.82 | 54.4 | 2H* | −0.47 | 1.98 | 2.67 |
| Ir@Pd(111) | T | −0.50 | 1.59 | — | 1.49 | H*H* | −1.00 | 1.62 | 1.96 |
| Pt@Pd(111) | T | −0.36 | 1.56 | — | 0.22 | 2H* | −0.62 | 1.74 | 2.48 |
| Ru(0001) | H | −0.34 | — | 1.89 | 54.6 | 2H* | −0.62 | 1.89 | 3.14 |
| 1.90 | |||||||||
| Ti@Ru(0001) | H | −0.52 | 2.10 | 1.86 | 60.5 | 2H* | −1.01 | 2.10 | 3.72 |
| 2.13 | |||||||||
| Fe@Ru(0001) | H | −0.31 | 1.92 | 1.86 | 57.2 | 2H* | −0.68 | 1.86 | 3.15 |
| 1.93 | |||||||||
| Co@Ru(0001) | H | −0.37 | 1.74 | 1.90 | 54.3 | H*H* | −0.77 | 1.73 | 2.87 |
| 1.74 | |||||||||
| W@Ru(0001) | H | −0.37 | 2.03 | 1.89 | 55.3 | 2H* | −0.71 | 2.05 | 3.38 |
| Ir@Ru(0001) | T | −0.21 | 1.63 | — | 0.9 | H*H* | −0.49 | 1.83 | 2.97 |
| 1.82 | |||||||||
| Pt@Ru(0001) | T | −0.05 | 1.60 | — | 1.3 | 2H* | −0.71 | 3.27 | 3.12 |
| 3.28 | |||||||||
| Ni(111) | H | −0.38 | — | 1.71 | 56.4 | 2H* | −0.82 | 1.69 | 2.84 |
| Ti@Ni(111) | H | −0.58 | 2.15 | 1.66 | 62.6 | 2H* | −1.11 | 2.12 | 3.73 |
| 2.13 | |||||||||
| Fe@Ni(111) | H | −0.31 | 1.87 | 1.67 | 57.4 | 2H* | −0.67 | 1.83 | 3.06 |
| Co@Ni(111) | H | −0.36 | 1.76 | 1.7 | 56.0 | 2H* | −0.79 | 1.72 | 2.82 |
| 1.71 | |||||||||
| W@Ni(111) | H | −0.36 | 2.08 | 1.67 | 57.2 | 2H* | −0.64 | 2.03 | 3.27 |
| 2.00 | |||||||||
| Ir@Ni(111) | H | −0.31 | 1.76 | 1.76 | 51.9 | 2H* | −0.64 | 1.77 | 2.78 |
| 1.75 | |||||||||
| Pt@Ni(111) | H | −0.19 | 1.81 | 1.74 | 57.6 | 2H* | −0.39 | 1.82 | 3.10 |
| H | H2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sitea | ΔG/eV | d A–H/Å | d B–H/Å | α/° | Structure | ΔG/eV | d A–H/Å | d H–H/Å | |
| a H = hollow, B = bridge, T = top. | |||||||||
| Mo(110) | H | −0.59 | — | 2.00 | 60.8 | 2H* | −1.153 | 2.01 | 3.12 |
| 2.02 | |||||||||
| Ti@Mo(110) | H | −0.75 | 2.03 | 1.92 | 68.0 |
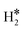
|
0.35 | 2.00 | 0.81 |
| Fe@Mo(110) | H | −0.37 | 1.77 | 2.00 | 59.9 | 2H* | −0.99 | 1.70 | 2.80 |
| Co@Mo(110) | H | −0.62 | 1.74 | 1.95 | 52.3 | H*H* | −1.02 | 1.66 | 2.58 |
| W@Mo(110) | H | −0.65 | 1.91 | 1.99 | 53.4 |
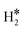
|
0.46 | 1.89 | 0.89 |
| Ir@Mo(110) | H | −0.42 | 1.83 | 2.03 | 60.9 | H*H* | −0.72 | 1.74 | 2.70 |
| Pt@Mo(110) | H | −0.77 | 2.91 | 2.01 | 69.8 | H*H* | −0.53 | 1.75 | 2.79 |
| 1.93 | |||||||||
| Nb(110) | H | −1.182 | — | 2.03 | 58.4 | 2H* | −1.99 | 2.03 | 3.45 |
| 2.05 | 2.05 | ||||||||
| Ti@Nb(110) | H | −1.010 | 1.96 | 2.05 | 60.5 | 2H* | −1.92 | 1.97 | 3.41 |
| 1.98 | |||||||||
| Fe@Nb(110) | H | −0.694 | 1.74 | 2.07 | 53.4 | H*H* | −1.36 | 1.72 | 2.68 |
| 1.74 | |||||||||
| Co@Nb(110) | H | −0.648 | 1.74 | 2.07 | 49.2 | H*H* | −1.20 | 1.69 | 2.69 |
| 2.09 | 1.72 | ||||||||
| W@Nb(110) | H | −0.866 | 1.93 | 2.08 | 53.2 | H*H* | −1.65 | 1.92 | 3.05 |
| Ir@Nb(110) | H | −0.551 | 1.79 | 2.12 | 54.7 | H*H* | −0.91 | 1.76 | 2.78 |
| 1.80 | |||||||||
| Pt@Nb(110) | H | −0.473 | 1.86 | 2.06 | 56.9 | 2H* | −1.74 | 3.23 | 5.88 |
| 3.20 | |||||||||
An important aspect of the electronic structure of SAAs is the more or less localized nature of the d states of the TM. In fact, it has been shown that this can lead to specific features in the chemical reactivity of the SAA.68 This is particularly important for 3d TM atoms towards the end of the series, such as the Fe and Co. In fact, when Fe or Co atoms are incorporated on the Ag(111) and Au(111) metal surfaces they maintain a magnetic structure related to the localized nature of the 3d states. More specifically, Fe has about 3 and Co about 2 unpaired electrons, despite the fact that they are embedded in metallic supports. Similar spin distributions have been found for Fe and Co on the other metal surfaces, see Table S3.† This result has been obtained using a PBE functional, not corrected for self-interaction, which tends to provide delocalized solutions. Therefore, the use of self-interaction corrected hybrid or DFT + U functionals will reinforce the tendency of the impurity atoms to assume magnetic states. This opens the question what is the best DFT functional to describe SAAs based on late 3d TM atoms. Recently, we have shown that the energetics of hydrogen-related reactions can be significantly affected by the choice of the functional.83 Therefore, we have performed test calculations at the level of DFT + U to benchmark our results. We selected a subset of structures, i.e. Ag- and Au-based SAAs. The results and the adopted U parameters are reported in Table S4.† In most cases, the inclusion of the U correction induces minor changes to the stability of the intermediates, and virtually no change on the structures. Nevertheless, in a few cases, Co@Ag(111) and Co@Au(111), the use of DFT + U changes both the stability and the structure of the surface complexes, see Table S4.† These calculations indicate that for the general message of this paper, which shows the possible formation of other intermediates beside chemisorbed H* atoms, this is not essential. However, for predictive studies on the thermodynamic of the reactions, this aspect should be carefully considered.
We started by adsorbing one hydrogen atom on the SAA catalysts or on the pure, undoped, metal surface and we determined both the adsorption energy, ΔEH, and the adsorption free energy, ΔGH, see Tables 1–3. The H atom can adsorb either on top (T), bridge (B), or three-hollow (H) sites, or in intermediate positions, with slightly different energies. To discriminate the various adsorption sites, we use the distances of H from the TM atom and a simple descriptor consisting in the angle (α) formed by the H atom with the normal to the surface passing from the SAA, Fig. S1.† The nature of the guest atom strongly affects the energetics of the process.21,84,85
On the bare metal surface H2 adsorption results in two independent H* atoms, referred to as 2H* in the following, see Scheme 1.
In general, ΔE is a function of the coverage and of the distance between the H atoms; here we considered vicinal adsorption sites, which can be considered the first step when the H2 molecule dissociates into H atoms, or vice versa the last step of the diffusion process before two H atoms recombine, form a physisorbed H2phys species that then desorbs to the gas-phase. In this case the two H atoms occupy two equivalent positions, and their distance coincides with the lattice constant. The mutual repulsion of the two H atoms is relatively small and in general close to zero, as shown by the fact that ΔE(2H*) ≈ 2ΔE(H*), see Tables 1–3.
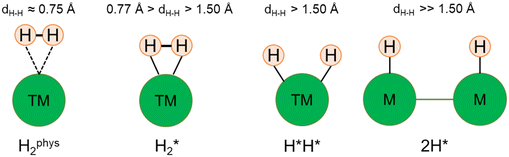
The picture becomes more complex and, to some extent, surprising when we consider the role of the SAAs. In some cases, the most stable arrangement of two H atoms is not the classical one denoted as 2H*, but rather that corresponding to the formation of a dihydrogen, 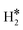 , or a dihydride, H*H*, complex with the two H atoms directly bound to the TM impurity (Scheme 1). A dihydrogen complex is characterized by a significantly bound H2 molecule (ΔEH is typically around −0.4/−0.6 eV, Tables 1 and 2) with a partial elongation of the H–H bond compared to that of the H2 molecule (0.75 Å) but without complete H–H bond breaking; we conventionally set to 1.5 Å.86 the H–H distance that discriminates between
, or a dihydride, H*H*, complex with the two H atoms directly bound to the TM impurity (Scheme 1). A dihydrogen complex is characterized by a significantly bound H2 molecule (ΔEH is typically around −0.4/−0.6 eV, Tables 1 and 2) with a partial elongation of the H–H bond compared to that of the H2 molecule (0.75 Å) but without complete H–H bond breaking; we conventionally set to 1.5 Å.86 the H–H distance that discriminates between 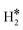 and H*H* complexes.42,43,87,88 Notice that the dihydrogen complex is clearly different from a physisorbed H2 molecule in three aspects: (1) in the dihydrogen complex the bond to the surface is stronger (ΔE
and H*H* complexes.42,43,87,88 Notice that the dihydrogen complex is clearly different from a physisorbed H2 molecule in three aspects: (1) in the dihydrogen complex the bond to the surface is stronger (ΔE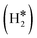 ≈ −0.5 eV while a typical ΔE value for H2phys is −0.06 eV, e.g. on Au(111)); (2) the H–H bond is partly activated, at variance with H2phys; (3) the metal–H2 distance is considerably longer in H2phys (above 3 Å) than in
≈ −0.5 eV while a typical ΔE value for H2phys is −0.06 eV, e.g. on Au(111)); (2) the H–H bond is partly activated, at variance with H2phys; (3) the metal–H2 distance is considerably longer in H2phys (above 3 Å) than in 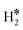 (1.5–2.0 Å).
(1.5–2.0 Å).
In a dihydride complex the charge transfer from the TM d orbitals to the H2 ligand is sufficiently strong to result in a complete dissociation of the H–H bond, as shown by the wide H–H distance which is larger than the conventional value of 1.5 Å, Scheme 1. Notice that the formation of the H*H* species formally corresponds to have two hydride ions bound to the TM which thus increases its oxidation state from 0 to +II. In organometallic chemistry this is known as oxidative addition.89
Thus, the results show that the presence of isolated TM impurities diluted in a metal surface, or SAAs, can lead to new hydrogen complexes that are reminiscent of coordination chemistry compounds. Most important, sometimes the stability of the novel 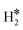 and H*H* complexes is comparable or higher than that of two chemisorbed H atoms on the metal surface, 2H*. Below we discuss three situations that may arise when a SAA is embedded in metal supports with low, medium and high reactivity towards hydrogen, as shown in Fig. 1.
and H*H* complexes is comparable or higher than that of two chemisorbed H atoms on the metal surface, 2H*. Below we discuss three situations that may arise when a SAA is embedded in metal supports with low, medium and high reactivity towards hydrogen, as shown in Fig. 1.
3.1 H adsorption on unreactive Ag and Au metal surfaces
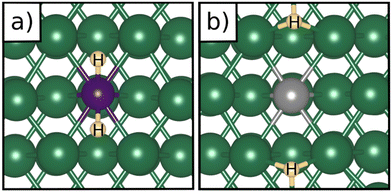
Table 1 reports the case of SAAs on Ag and Au metals. On these surfaces the dissociation of H2 and formation of 2H* species is endergonic, Fig. 1. The presence of diluted TM impurities changes the scenario. On both Ag(111) and Au(111) surfaces the adsorption of a single H atom on the SAA results in a negative ΔGH (W and Ir) or in nearly thermoneutral processes (Ti, Co, Pt). Fe@Au(111) shows a positive ΔGH for the adsorption of a single H atom. In all cases the H atom adsorption is clearly more favourable on the TM impurity than on the Ag(111) and Au(111) surfaces.On Ag(111), no matter which TM is incorporated, the adsorption of two hydrogen atoms on the SAA is exergonic, and the formation of 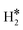 or H*H* complexes is always more stable than having 2H* species adsorbed on the Ag(111) surface. Co@Ag(111) gives raise to the formation of a dihydrogen complex (dH–H = 1.04 Å), Fig. 2a. In the remaining systems a dihydride complex forms, Fig. 2b and Table 1, as shown by the large H–H distance. The TM–H distances range from 1.5 Å to 1.9 Å, typical of other dihydride complexes.44,51
or H*H* complexes is always more stable than having 2H* species adsorbed on the Ag(111) surface. Co@Ag(111) gives raise to the formation of a dihydrogen complex (dH–H = 1.04 Å), Fig. 2a. In the remaining systems a dihydride complex forms, Fig. 2b and Table 1, as shown by the large H–H distance. The TM–H distances range from 1.5 Å to 1.9 Å, typical of other dihydride complexes.44,51
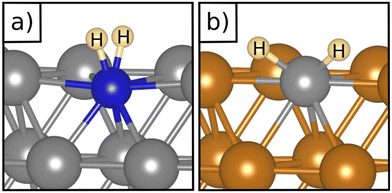 | ||
Fig. 2 Examples of a) a dihydrogen complex (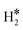 on Co@Ag(111)) and b) a dihydride complex (H*H* on Pt@Au(111)). on Co@Ag(111)) and b) a dihydride complex (H*H* on Pt@Au(111)). | ||
The case of Au resembles that of Ag, since dihydride complexes are generally preferred, while on Co@Au(111) and Ti@Au(111) we observe the formation of a dihydrogen species. The complexes formed on the SAA are more stable than 2H* species on the Au(111) bare surface. In various cases the difference is large: for Ir@Au(111) ΔG(H*H*) is −0.90 eV, while on the Au(111) surface ΔG(2H*) is +0.86 eV, with a gain of about 1.8 eV going from the pure metal to the alloy. Similar is the situation for W@Au(111) where ΔG(H*H*) is −0.70 eV. On the other SAAs the formation of the dihydride complexes is nearly thermoneutral, ΔG ∼ 0.0 ± 0.2 eV, Table 1.
A peculiar situation is that of Pt@Au(111) since here a H*H* complex forms with ΔGH(H*H*) = 0.26 eV, while the adsorption of two separated H* atoms on two Pt@Au(111) sites will result in a negative ΔG(H*) = 2 × (−0.11) eV = −0.22 eV, Table 1. In this case, the Pt impurity prefers to bind a single H* atom and the formation of dihydride complexes will only occur at high hydrogen coverages, when all the Pt sites are saturated by one adsorbed H atom.
Another special case is represented by Fe@Au(111). Here in fact the most stable structure corresponds to two H atoms bound in intermediate positions between the Fe impurity and the Au neighbours. We classified this structure as 2H*, and not as H*H*, since the two H atoms have long Fe–H distances of 1.90 Å. However, this is a borderline case, intermediate between a H*H* complex and a 2H* situation. Notice however that ΔGH for this structures is 0.27 eV, while on the regular Au(111) surface the 2H* complex forms with ΔG = 0.86 eV, Table 1. This further shows that the presence of a Fe impurity on the Au(111) surface the adsorption properties.
3.2 H adsorption on partly reactive Rh, Pd, Ni, and Ru metal surfaces
Table 2 reports the case of SAAs having as a hosting metal the Rh(111), Pd(111), Ni(111), and Ru(0001) surfaces, three metals that exhibit a free energy for hydrogen adsorption close to that of Pt, the state-of-the-art catalyst for hydrogen-related reactions, Fig. 1. On Rh(111), Pd(111), Ni(111) and Ru(0001) the adsorption of a single H atom has similar values of ΔG = −0.28 eV (Rh), −0.30 eV (Pd), −0.34 eV (Ru), and −0.38 eV (Ni). When a SAA is present, the adsorption of a single H atom on the SAA results in similar values of ΔG which changes at most by ±0.2 eV compared to the bare surface, Table 2.More interesting is the case of two H atoms adsorption. Starting from Rh(111), we see that W@Rh(111) and Ir@Rh(111) form respectively a dihydrogen and a dihydride complex, see Fig. 3a and b. The dihydride complex on Ir@Rh(111) is slightly more stable than 2H* on the metal surface (ΔG(H*H*) = −0.74 eV, ΔG(2H*) = −0.70 eV, Table 2). The dihydrogen complex in W@Ir(111), on the contrary, is a local minimum on the potential energy surface being 2H* on the Rh(111) surface more stable (ΔG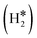 = −0.16 eV, ΔG(2H*) = −0.70 eV).
= −0.16 eV, ΔG(2H*) = −0.70 eV).
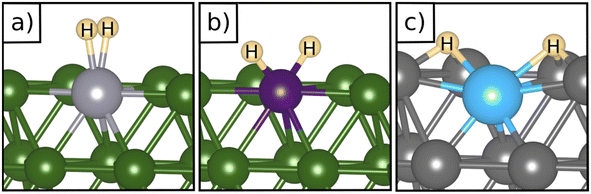 | ||
Fig. 3 Examples of a) a dihydrogen complex ( on W@Rh(111), b) a dihydride complex (H*H* on Ir@Rh(111)), and c) an intermediate situation (2H* Ti@Pd(111)). on W@Rh(111), b) a dihydride complex (H*H* on Ir@Rh(111)), and c) an intermediate situation (2H* Ti@Pd(111)). | ||
In the other cases examined, we did not detect the formation of dihydrogen or dihydride complexes, and the most stable structure is that represented by two separated H* atoms anchored on the SAA site, see e.g. Ti@Rh(111) in Table 2. As we discussed above for the case of Fe@Au(111), the two H atoms are bound in between the SAA and the surrounding Rh atoms, resulting in 2H* complexes that have similar or higher stabilities than two H atoms adsorbed on Rh(111), see Table 2. This is a consequence of the local changes in electronic structure induced by the presence of the TM atom.
Moving to Pd, only Ir@Pd(111) forms a stable dihydride, H*H*, complex (ΔG(H*H*) = −1.00 eV) which is about 0.4 eV more stable than 2H* on Pd(111). This is the only case where a local coordination complex forms, since all the remaining cases show the preference for the formation of 2H* adducts near the SAA, see Fig. 3c where the structure of Ti@Pd(111) is shown.
Also on Pd(111) the presence of a Fe atom results in the formation of an extremely stable complex that we classify as 2H* due to the long Fe–H distance, 2.0 Å, and the very large H–H distance, 2.90 Å. Here the two H atoms are bound in between Fe and Pd atoms, with a ΔG = −1.99 eV which is three times that of a standard 2H* complex on Pd(111), ΔG = −0.64 eV, Table 2. Of course, the formation of extremely stable complexes will have negative implications on the catalytic process, since it implies a sort of poisoning the catalyst and its deactivation. Indeed, in these cases it becomes crucial to include all hydrogen complexes in the theoretical treatment. Overlooking the formation of very stable species will affect the reliability of the computed energy profile hence of the predictions of catalytic activity.
When the Ni(111) surface is the hosting metal, in no case the Gibbs free energy of the  or H*H* complexes on the SAA is preferred compared to the classical case of two adsorbed H atoms on Ni(111), 2H*. In some cases, e.g. Co@Ni(111), binding two H atoms at the SAA, ΔG = −0.79 eV, has virtually the same energy gain that is associated to the chemisorption of two separated H atoms on pure Ni(111), ΔG = −0.82 eV, Table 2. This shows that replacing Ni with Co does not induce large changes in the electronic structure. On the contrary, for Ti@Ni(111) the preferred situation is that where the two H atoms are bound between to the Ti SAA and the other Ni atoms of Ni(111), resulting in an overall more stable binding than on the pure Ni(111) surface, ΔG = −1.11 eV, Table 2. In this case, the perturbation of Ti on the Ni surface is quite pronounced, Table 2. Last, when metal single atoms are hosted by Ru(0001) we found a situation very similar to that of Ni(111). We detected the formation of dihydride complexes on Co@Ru(0001) and Ir@Ru(0001). The first is predicted to be more stable than having two adsorbed hydrogen atoms on the Ru(0001) surface. In the other cases we did not detect the formation of dihydrogen complexes, but only 2H* species.
or H*H* complexes on the SAA is preferred compared to the classical case of two adsorbed H atoms on Ni(111), 2H*. In some cases, e.g. Co@Ni(111), binding two H atoms at the SAA, ΔG = −0.79 eV, has virtually the same energy gain that is associated to the chemisorption of two separated H atoms on pure Ni(111), ΔG = −0.82 eV, Table 2. This shows that replacing Ni with Co does not induce large changes in the electronic structure. On the contrary, for Ti@Ni(111) the preferred situation is that where the two H atoms are bound between to the Ti SAA and the other Ni atoms of Ni(111), resulting in an overall more stable binding than on the pure Ni(111) surface, ΔG = −1.11 eV, Table 2. In this case, the perturbation of Ti on the Ni surface is quite pronounced, Table 2. Last, when metal single atoms are hosted by Ru(0001) we found a situation very similar to that of Ni(111). We detected the formation of dihydride complexes on Co@Ru(0001) and Ir@Ru(0001). The first is predicted to be more stable than having two adsorbed hydrogen atoms on the Ru(0001) surface. In the other cases we did not detect the formation of dihydrogen complexes, but only 2H* species.
3.3 H adsorption on very reactive Mo and Nb metal surfaces
Table 3 shows results arising from SAAs based on Mo(110) and Nb(110), two metals that exhibit strong reactivity with hydrogen, Fig. 1. This is shown by ΔG(H*) = −0.59 eV (Mo) and in particular ΔG(H*) = −1.18 eV (Nb). Compared to the clean Mo(110) surface the adsorption on the SAA results in modest changes in ΔG(H*) that goes from −0.37 eV (Fe) to −0.75 eV (Ti); for Nb(110) there is a general decrease in absolute value of ΔG(H*) on the SAA, indicating a negative effect of the TM impurity on hydrogen dissociation, Table 3.When we considered two H atoms adsorption, in none of the case examined we found hydrogen complexes with the SAA with higher stabilities than two chemisorbed H atoms on the clean surface, see Table 3. Nevertheless, on the Mo(110) surface for most of the cases examined we observe the formation of metastable dihydrogen, e.g. W@Mo(110) and Ti@Mo(110), and dihydride, Ir@Mo(110), Co@Mo(110), Pt@Mo(110), complexes, Table 3. On the dihydrogen complexes on W@Mo(110) and Ti@Mo(110) the H2 molecule is very weakly bound but nevertheless the H–H distances are elongated, 0.8–0.9 Å, Table 3.
On Nb(110) the situation is similar, with formation of metastable H*H* dihydride species for the case of W@Nb(110), Ir@Nb(110), Co@Nb(110), and Fe@Nb(110), Table 3 and Fig. 4a. On Pt@Nb(110) we observe the formation of a 2H* complex where the two H atoms are very far apart, 5.9 Å, Fig. 4b. The corresponding ΔG, −1.74 eV, is less negative than that for 2H* on Nb(110), ΔG = −2.47 eV, Table 3. This is a case where the TM impurity results in a weakening of the bonding with hydrogen. In general, the absence of stable dihydrogen or dihydride complexes on the Mo and Nb surfaces reflects the strong interaction of these metals with hydrogen, which favours the classical picture of chemisorbed isolated H atoms, 2H*. All the calculated TM–H distances in 2H*, H*H*, and 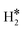 species and the relative Gibbs free energies are reported in Fig. 5, where it is possible to appreciate that the rationalization in terms of the nature of host metal is quite complex. Ti, Co, W are the only TM atoms that form dihydrogen complexes. When the remaining metals form a complex, this assumes a dihydride character. Most of the complexes have a formation Gibbs free energy lower than the reference energy corresponding to the SAA and molecular hydrogen. Interestingly, Ir-based SAAs form complexes with a Gibbs free energy around −1 eV, while Co, and Pt form complexes with −1.0 eV < ΔG < −0.5 eV except for Ag(111) and Au(111) hosting metals, where the complexes are much less stable.
species and the relative Gibbs free energies are reported in Fig. 5, where it is possible to appreciate that the rationalization in terms of the nature of host metal is quite complex. Ti, Co, W are the only TM atoms that form dihydrogen complexes. When the remaining metals form a complex, this assumes a dihydride character. Most of the complexes have a formation Gibbs free energy lower than the reference energy corresponding to the SAA and molecular hydrogen. Interestingly, Ir-based SAAs form complexes with a Gibbs free energy around −1 eV, while Co, and Pt form complexes with −1.0 eV < ΔG < −0.5 eV except for Ag(111) and Au(111) hosting metals, where the complexes are much less stable.
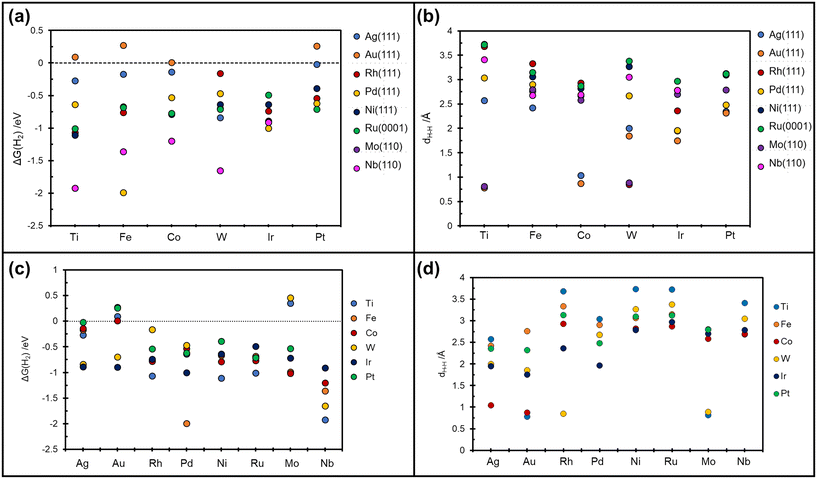 | ||
| Fig. 5 Calculated Gibbs free energy and relative TMs–H distances. (a and b) on the x-axis are reported the guest TMs. (c and d) on the x-axis are reported the host TMs. | ||
4. Proofs and consequences of the existence of hydrogen complexes
Temperature Programmed Desorption (TPD) is a technique that could provide some information about the nature of the species present on the surface. If we use a Redhead equation for first-order desorption processes,90 ΔEdes = RTdes [ln(νTdes) − 3.64], and assuming a pre-factor ν = 1013 s−1, one can estimate the desorption temperature of gas-phase H2 from the SAA. The calculated values are reported in Tables S8–S10.† One obvious observation is that on some surfaces, e.g. Ag(111) and Au(111), hydrogen does not bind at variance with TM@Ag(111) and TM@Au(111) alloys, thus no adsorption/desorption is expected on the clean surfaces, while a specific feature will be present on the SAAs.More subtle is the distinction of cases where isolated H* atoms are present from cases where 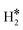 or H*H* complexes form. In most cases, in fact, ΔG for the
or H*H* complexes form. In most cases, in fact, ΔG for the 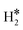 or H*H* species is about twice that of a single H* species, Tables 1–3, so that similar desorption temperatures are expected.
or H*H* species is about twice that of a single H* species, Tables 1–3, so that similar desorption temperatures are expected.
However, some relevant cases exist. On Fe@Pd(111), the ΔE for H* is −0.66 eV, which corresponds to a cost of 1.32 eV for the desorption of an H2 molecule, resulting in desorption temperature of 470 K. The formation of a dihydride complex on Fe@Pd(111), H*H*, has a ΔE of −2.47 eV, corresponding to a desorption temperature of 865 K. In other words, if the dihydride complex forms on Fe@Pd(111), this should be clearly visible in a TPD spectrum.
On Pt@Nb(110) the desorption of two H* atoms bound near the Pt impurity (ΔE = −2.22 eV, Table 3) would result in a desorption T = 785 K. This case is only hypothetical since on Nb the preferred adsorption sites are on the clean metal (ΔE = −2.47 eV, Table 3) where the desorption temperature is expected to be of 870 K. This discussion shows that the formation energy of the complexes where two H atoms are involved can be significantly different from that of isolated H atoms and can result in major changes in the TPD spectra. On the other hand, TPD cannot provide direct information about the structure of the complex.
Methods that can provide structural information are, at least in principle, neutron diffraction, H-NMR and vibrational spectroscopy.91 In particular vibrational spectra obtained via infrared absorption spectroscopy (IRAS) or electron energy loss (EELS) could be able to disentangle between isolated H atoms, dihydrogen, or dihydride species from the M–H and H–H stretching and bending frequencies.51 However, on metal surfaces a selection rule is active, so only vibrations with a dipole moment perpendicular to the surface will be seen for IRAS and EELS in specular mode, while off-specular measurements in EELS could provide additional information. Another problem is that of the sensitivity of the measurement, as hydrogen coverages of at least 5% are probably needed in order to obtain measurable intensities.
Despite these problems, we have computed the vibrational excitations within the harmonic approximation of three representative situations in order to see how different hydrogen complexes could be identified, Table 4. The 2H* species on the Rh(111) surface is characterized by two Rh–H stretches at 1134 cm−1 and 1163 cm−1, Table 4, and low frequency bending modes around 600–700 cm−1. A dihydrogen complex, as 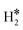 on W@Rh(111), has a typical H–H high frequency stretching mode at 2821 cm−1, and two other modes that can be labelled as stretching and bending, respectively, at 1494 cm−1 and 895 cm−1. Finally, a dihydride complex, see H*H* on Ir@Rh(111), does not display the H–H stretching frequency as expected, while two frequencies at 1699 cm−1 and 1642 cm−1 are M–H stretchings mixed with bending modes. Pure bending modes are found around 550 cm−1, Table 4. From this analysis it is clear that vibrational spectroscopy could provide very useful information to disentangle the nature of the surface hydrogen complexes.
on W@Rh(111), has a typical H–H high frequency stretching mode at 2821 cm−1, and two other modes that can be labelled as stretching and bending, respectively, at 1494 cm−1 and 895 cm−1. Finally, a dihydride complex, see H*H* on Ir@Rh(111), does not display the H–H stretching frequency as expected, while two frequencies at 1699 cm−1 and 1642 cm−1 are M–H stretchings mixed with bending modes. Pure bending modes are found around 550 cm−1, Table 4. From this analysis it is clear that vibrational spectroscopy could provide very useful information to disentangle the nature of the surface hydrogen complexes.
Having discussed how to detect the hydrogen complexes, we briefly comment on the mechanistic and catalytic implications of our results. Clearly, if new stable complexes form they must be taken into account in the construction of the reaction profile in order to provide reliable predictions or to perform screenings based on key descriptors of the catalytic activity. The stability of dihydrogen and dihydride complexes on SAAs is system dependent and must be verified case by case. For instance, for W@Ag(111) if one assumes the classical model where only isolated H* atoms are bound to the SAA, one should expect a catalyst with good catalytic activity for HER (ΔG = −0.33 eV is quite close to the top of the volcano plot corresponding to ΔG = 0 eV, Fig. 1). However, our results show the formation of a very stable dihydrogen complex with ΔG = −0.84 eV which corresponds to a poor catalyst do to the too strong W–H bonds, Table 1. In short, the predicted activity is completely different in the two cases.
Of course, this is not always the case. For Co@Ag(111) the inclusion of the dihydrogen complex does not affect severely the expected catalyst performances: if one considers H* formation only, the free energy is ideal (ΔG = −0.03 eV), but the formation of the dihydrogen complex, ΔG = −0.14 eV, Table 1, remains very close to zero and the catalytic activity is predicted to be high. In this case the formation of a second stable intermediate has implications on the mechanism since the reaction should proceed via two intermediates rather than just one.
As we discussed above, there are cases of SAAs where dihydrogen or dihydride complexes do not form, and the choice of taking the H* adsorption free energy as a unique descriptor of the HER activity is justified (this holds true also for the opposite reaction based on molecular hydrogen oxidation). This is the case of metal surfaces that bind hydrogen strongly, such as Mo and Nb. However, in general it is not possible to decide a priori if this is the case, and unfortunately a careful study of the potential energy surface is necessary in order to verify the possible occurrence of species where more than one H atom is bound.
Finally, it is important to mention that the prediction of the best or worst catalysts goes beyond the purpose of this study. Indeed, several many other effects are important. In order to be reliable, these predictions based on electronic structure calculations should check the role of the method used (e.g. the exchange correlation functional),83,92 they should include important contributions such as solvation and dynamical effects,93–95 the reaction barriers should be evaluated beyond the thermodynamic approximations and the computational data should be complemented by a microkinetic analysis.96
Conclusions
We performed a density functional theory study of Single Atom Alloys catalysts and their role in interaction with hydrogen. We showed that dihydrogen or dihydride complexes can form, in analogy with what has been found for Single Atom Catalysts embedded in carbon matrices.51 In some cases the novel intermediates can be more stable than isolated chemisorbed H atoms on the pure metal surface. When this occurs, the formation of the dihydrogen or dihydride complex needs to be considered in the construction of the reaction profile, as it can result in different thermodynamic barriers for the reaction. Therefore, the common assumption of a single H* intermediate as descriptor of the catalytic activity of a metal electrode or catalyst in hydrogen-related reactions is not always longer valid for SAAs.These results further demonstrate the complex chemistry of single site catalysts where a transition metal atom is embedded in a surrounding matrix. These systems can exhibit very different chemical properties compared to classical metal particles or extended metal surfaces. The reason lies in the rather localized nature of the d orbitals and the atomic-like nature of these impurities embedded in a metallic matrix.68 The possible formation and stability of such unconventional adducts is system-dependent. In principle the formation of these species is essential to be considered in order to provide predictions or to identify descriptors of the catalytic activity.
Author contributions
The manuscript was written through contributions of all authors.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank Livia Giordano for useful discussions. We acknowledge the financial support from Cariplo foundation. Access to the CINECA supercomputing resources was granted via ISCRAB. We also thank the COST Action 18234 supported by COST (European Cooperation in Science and Technology).References
- G. Centi and J. Čejka, ChemSusChem, 2019, 12, 621–632 CrossRef CAS PubMed.
- S. Schauermann, N. Nilius, S. Shaikhutdinov and H.-J. Freund, Acc. Chem. Res., 2013, 46, 1673–1681 CrossRef CAS PubMed.
- P. Kluson and L. Cerveny, Appl. Catal., A, 1995, 128, 13–31 CrossRef CAS.
- L. Zhang, M. Zhou, A. Wang and T. Zhang, Chem. Rev., 2020, 120, 683–733 CrossRef CAS PubMed.
- N. Lopez, J. Catal., 2004, 223, 232–235 CrossRef CAS.
- M. Crespo-Quesada, A. Yarulin, M. Jin, Y. Xia and L. Kiwi-Minsker, J. Am. Chem. Soc., 2011, 133, 12787–12794 CrossRef CAS.
- G. A. Somorjai and J. Y. Park, Chem. Soc. Rev., 2008, 37, 2155 RSC.
- A. Sápi, T. Rajkumar, J. Kiss, Á. Kukovecz, Z. Kónya and G. A. Somorjai, Catal. Lett., 2021, 151, 2153–2175 CrossRef.
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed.
- S. Mitchell and J. Pérez-Ramírez, Nat. Rev. Mater., 2021, 6, 969–985 CrossRef.
- N. Daelman, M. Capdevila-Cortada and N. López, Nat. Mater., 2019, 18, 1215–1221 CrossRef CAS PubMed.
- B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641 CrossRef CAS PubMed.
- D. Liu, X. Li, S. Chen, H. Yan, C. Wang, C. Wu, Y. A. Haleem, S. Duan, J. Lu, B. Ge, P. M. Ajayan, Y. Luo, J. Jiang and L. Song, Nat. Energy, 2019, 4, 512–518 CrossRef CAS.
- L. DeRita, J. Resasco, S. Dai, A. Boubnov, H. V. Thang, A. S. Hoffman, I. Ro, G. W. Graham, S. R. Bare, G. Pacchioni, X. Pan and P. Christopher, Nat. Mater., 2019, 18, 746–751 CrossRef CAS PubMed.
- M. A. Bajada, J. Sanjosé-Orduna, G. Di Liberto, S. Tosoni, G. Pacchioni, T. Noël and G. Vilé, Chem. Soc. Rev., 2022, 51, 3898–3925 RSC.
- G. Vilé, G. Di Liberto, S. Tosoni, A. Sivo, V. Ruta, M. Nachtegaal, A. H. Clark, S. Agnoli, Y. Zou, A. Savateev, M. Antonietti and G. Pacchioni, ACS Catal., 2022, 12, 2947–2958 CrossRef.
- Y. Tang, C. Asokan, M. Xu, G. W. Graham, X. Pan, P. Christopher, J. Li and P. Sautet, Nat. Commun., 2019, 10, 4488 CrossRef PubMed.
- G. Vilé, D. Albani, M. Nachtegaal, Z. Chen, D. Dontsova, M. Antonietti, N. López and J. Pérez-Ramírez, Angew. Chem., Int. Ed., 2015, 54, 11265–11269 CrossRef PubMed.
- E. Vorobyeva, E. Fako, Z. Chen, S. M. Collins, D. Johnstone, P. A. Midgley, R. Hauert, O. V. Safonova, G. Vilé, N. López, S. Mitchell and J. Pérez-Ramírez, Am. Ethnol., 2019, 131, 8816–8821 CrossRef.
- S. Cao, M. Yang, A. O. Elnabawy, A. Trimpalis, S. Li, C. Wang, F. Göltl, Z. Chen, J. Liu, J. Shan, M. Li, T. Haas, K. W. Chapman, S. Lee, L. F. Allard, M. Mavrikakis and M. Flytzani-Stephanopoulos, Nat. Chem., 2019, 11, 1098–1105 CrossRef CAS PubMed.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, ChemCatChem, 2022, 14, e202200611 CrossRef CAS.
- C. Copéret, M. Chabanas, R. Petroff Saint-Arroman and J.-M. Basset, Angew. Chem., Int. Ed., 2003, 42, 156–181 CrossRef PubMed.
- M. K. Samantaray, V. D'Elia, E. Pump, L. Falivene, M. Harb, S. Ould Chikh, L. Cavallo and J.-M. Basset, Chem. Rev., 2020, 120, 734–813 CrossRef CAS.
- G. S. Parkinson, Catal. Lett., 2019, 149, 1137–1146 CrossRef CAS.
- C. Copéret, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Núñez-Zarur and P. A. Zhizhko, Chem. Rev., 2016, 116, 323–421 CrossRef PubMed.
- P. Sautet and F. Delbecq, Chem. Rev., 2010, 110, 1788–1806 CrossRef CAS PubMed.
- C. Copéret, M. Chabanas, R. Petroff Saint-Arroman and J.-M. Basset, Angew. Chem., Int. Ed., 2003, 42, 156–181 CrossRef PubMed.
- E. C. H. Sykes and P. Christopher, Curr. Opin. Chem. Eng., 2020, 29, 67–73 CrossRef.
- R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088 CrossRef CAS PubMed.
- G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Acc. Chem. Res., 2019, 52, 237–247 CrossRef CAS PubMed.
- G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1212 CrossRef CAS PubMed.
- M. B. Boucher, B. Zugic, G. Cladaras, J. Kammert, M. D. Marcinkowski, T. J. Lawton, E. C. H. Sykes and M. Flytzani-Stephanopoulos, Phys. Chem. Chem. Phys., 2013, 15, 12187 RSC.
- G. X. Pei, X. Y. Liu, X. Yang, L. Zhang, A. Wang, L. Li, H. Wang, X. Wang and T. Zhang, ACS Catal., 2017, 7, 1491–1500 CrossRef CAS.
- C. M. Kruppe, J. D. Krooswyk and M. Trenary, ACS Catal., 2017, 7, 8042–8049 CrossRef CAS.
- G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1212 CrossRef CAS PubMed.
- Z.-T. Wang, M. T. Darby, A. J. Therrien, M. El-Soda, A. Michaelides, M. Stamatakis and E. C. H. Sykes, J. Phys. Chem. C, 2016, 120, 13574–13580 CrossRef CAS.
- M. D. Marcinkowski, M. T. Darby, J. Liu, J. M. Wimble, F. R. Lucci, S. Lee, A. Michaelides, M. Flytzani-Stephanopoulos, M. Stamatakis and E. C. H. Sykes, Nat. Chem., 2018, 10, 325–332 CrossRef CAS PubMed.
- M. T. Darby, R. Réocreux, E. Charles, H. Sykes, A. Michaelides and M. Stamatakis, ACS Catal., 2018, 8, 5038–5050 CrossRef CAS.
- R. A. Hoyt, M. M. Montemore, I. Fampiou, W. Chen, G. Tritsaris and E. Kaxiras, J. Chem. Inf. Model., 2019, 59, 1357–1365 CrossRef CAS PubMed.
- C. Zhou, J. Y. Zhao, P. F. Liu, J. Chen, S. Dai, H. G. Yang, P. Hu and H. Wang, Chem. Sci., 2021, 12, 10634–10642 RSC.
- R. Réocreux and M. Stamatakis, Acc. Chem. Res., 2022, 55, 87–97 CrossRef PubMed.
- G. J. Kubas, Acc. Chem. Res., 1988, 21, 120–128 CrossRef.
- R. H. Crabtree, Acc. Chem. Res., 1990, 23, 95–101 CrossRef CAS.
- L. Andrews, Chem. Soc. Rev., 2004, 33, 123 RSC.
- F. Maseras, A. Lledós, E. Clot and O. Eisenstein, Chem. Rev., 2000, 100, 601–636 CrossRef CAS PubMed.
- D. Gavaskar, A. R. Suresh Babu, R. Raghunathan, M. Dharani and S. Balasubramanian, J. Organomet. Chem., 2014, 768, 128–135 CrossRef CAS.
- P. R. Kemper, P. Weis, M. T. Bowers and P. Maître, J. Am. Chem. Soc., 1998, 120, 13494–13502 CrossRef CAS.
- C. W. Bauschlicher and P. Maitre, J. Phys. Chem., 1995, 99, 3444–3447 CrossRef CAS.
- P. Weis, P. R. Kemper and M. T. Bowers, J. Phys. Chem. A, 1997, 101, 2809–2816 CrossRef CAS.
- P. R. Kemper, J. Bushnell, G. Von Helden and M. T. Bowers, J. Phys. Chem., 1993, 97, 52–58 CrossRef CAS.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, J. Am. Chem. Soc., 2021, 143, 20431–20441 CrossRef CAS PubMed.
- L. A. Cipriano, G. Di Liberto and G. Pacchioni, ACS Catal., 2022, 12, 11682–11691 CrossRef CAS.
- L. Zhong and S. Li, ACS Catal., 2020, 10, 4313–4318 CrossRef CAS.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, J. Catal., 2023, 417, 351–359 CrossRef CAS.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184 CrossRef CAS.
- S. Trasatti, Electrochim. Acta, 1984, 29, 1503–1512 CrossRef CAS.
- D. M. Heard and A. J. J. Lennox, Angew. Chem., Int. Ed., 2020, 59, 18866–18884 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- K. Christmann, Surf. Sci. Rep., 1988, 9, 1–163 CrossRef.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- H. L. Tierney, A. E. Baber, J. R. Kitchin and E. C. H. Sykes, Phys. Rev. Lett., 2009, 103, 246102 CrossRef PubMed.
- J. Liu, M. B. Uhlman, M. M. Montemore, A. Trimpalis, G. Giannakakis, J. Shan, S. Cao, R. T. Hannagan, E. C. H. Sykes and M. Flytzani-Stephanopoulos, ACS Catal., 2019, 9, 8757–8765 CrossRef CAS.
- P. Aich, H. Wei, B. Basan, A. J. Kropf, N. M. Schweitzer, C. L. Marshall, J. T. Miller and R. Meyer, J. Phys. Chem. C, 2015, 119, 18140–18148 CrossRef CAS.
- Y. Cao, B. Chen, J. Guerrero-Sánchez, I. Lee, X. Zhou, N. Takeuchi and F. Zaera, ACS Catal., 2019, 9, 9150–9157 CrossRef CAS.
- G. X. Pei, X. Y. Liu, X. Yang, L. Zhang, A. Wang, L. Li, H. Wang, X. Wang and T. Zhang, ACS Catal., 2017, 7, 1491–1500 CrossRef CAS.
- C. M. Kruppe, J. D. Krooswyk and M. Trenary, ACS Catal., 2017, 7, 8042–8049 CrossRef CAS.
- M. T. Darby, R. Réocreux, E. Charles, H. Sykes, A. Michaelides and M. Stamatakis, ACS Catal., 2018, 8, 5038–5050 CrossRef CAS.
- M. T. Greiner, T. E. Jones, S. Beeg, L. Zwiener, M. Scherzer, F. Girgsdies, S. Piccinin, M. Armbrüster, A. Knop-Gericke and R. Schlögl, Nat. Chem., 2018, 10, 1008–1015 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. W. G. Wyckoff, Crystal Structures, Wiley, 1963 Search PubMed.
- J. L. F. Da Silva, C. Stampfl and M. Scheffler, Phys. Rev. Lett., 2003, 90, 066104 CrossRef PubMed.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed.
- P. J. Feibelman, Science, 2002, 295, 99–102 CrossRef CAS PubMed.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, Adv. Theory Simul., 2022, 2200513 CrossRef.
- M. T. Darby, M. Stamatakis, A. Michaelides, E. Charles and H. Sykes, J. Phys. Chem. Lett., 2018, 9, 5636–5646 CrossRef CAS PubMed.
- G. Di Liberto, S. Tosoni, L. A. Cipriano and G. Pacchioni, Acc. Mater. Res., 2022, 3, 986–995 CrossRef CAS.
- D. M. Heinekey, A. Lledós and J. M. Lluch, Chem. Soc. Rev., 2004, 33, 175–182 RSC.
- G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205 CrossRef CAS PubMed.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769 CrossRef CAS PubMed.
- J. Halpern, Acc. Chem. Res., 1970, 3, 386–392 CrossRef CAS.
- P. A. Redhead, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769 CrossRef CAS PubMed.
- A. M. Patel, S. Ringe, S. Siahrostami, M. Bajdich, J. K. Nørskov and A. R. Kulkarni, J. Phys. Chem. C, 2018, 122, 29307–29318 CrossRef CAS.
- F. Calle-Vallejo, R. F. de Morais, F. Illas, D. Loffreda and P. Sautet, J. Phys. Chem. C, 2019, 123, 5578–5582 CrossRef CAS.
- Z.-D. He, S. Hanselman, Y.-X. Chen, M. T. M. Koper and F. Calle-Vallejo, J. Phys. Chem. Lett., 2017, 8, 2243–2246 CrossRef CAS PubMed.
- A. Bouzid, P. Gono and A. Pasquarello, J. Catal., 2019, 375, 135–139 CrossRef CAS.
- M. Rebarchik, S. Bhandari, T. Kropp and M. Mavrikakis, ACS Catal., 2023, 13, 5225–5235 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy00609c |
| This journal is © The Royal Society of Chemistry 2023 |