 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A structure-sensitive descriptor for the design of active sites on MoS2 catalysts†
Hai-Yan
Su
 a,
Federico
Calle-Vallejo
a,
Federico
Calle-Vallejo
 *bc and
Keju
Sun
*d
*bc and
Keju
Sun
*d
aGuangdong Provincial Key Laboratory of Distributed Energy Systems, School of Chemical Engineering and Energy Technology, Dongguan University of Technology, 1 Daxue Road, Dongguan 523808, China
bNano-Bio Spectroscopy Group and European Theoretical Spectroscopy Facility (ETSF), Department of Advanced Materials and Polymers: Physics, Chemistry and Technology, University of the Basque Country UPV/EHU, Av. Tolosa 72, 20018 San Sebastián, Spain. E-mail: federico.calle@ehu.es
cIKERBASQUE, Basque Foundation for Science, Plaza de Euskadi 5, 48009 Bilbao, Spain
dHebei Key Laboratory of Applied Chemistry, School of Environmental and Chemical Engineering, Yanshan University, 438 Hebei Avenue, Qinhuangdao 066004, China. E-mail: kjsun@ysu.edu.cn
First published on 3rd August 2023
Abstract
MoS2 catalysts hold great promise for numerous reactions of industrial and technological interest. However, general guidelines for the design of their active sites remain elusive. We hypothesize that this is because the link between their geometric structure and reactivity is yet to be established at the atomic scale. Here we show that cn, a metric based on the number of sulfur atoms coordinated to Mo atoms, captures the trends in reactivity of MoS2 catalysts with various sulfur vacancy contents. This is illustrated for the adsorption energies of numerous monatomic and polyatomic species. More importantly, cn can be used to predict the reaction and activation energies of common formation and dissociation reactions in catalysis. Finally, cn is used to outline the optimal configuration of MoS2 active sites for the electrocatalytic hydrogen evolution reaction: the highest exchange current density corresponds to terrace sites with adjacent S vacancies with cn in the range of 4.33 to 4.67.
1. Introduction
The computational description of catalytic reactions on transition metals has achieved great advances in the past three decades.1–3 The atomic-scale surface chemistry that determines the observable macroscopic kinetics has been established in numerous cases, and key descriptors such as adsorption energies of intermediates,1,2,4,5 band centers,1 and coordination numbers,6,7 among others,8–10 have been shown to correlate with catalytic activities. These correlations are the groundwork for the rational design of metal catalysts. However, catalysts based on transition metal compounds wherein the metal atoms have nonzero oxidation states are still insufficiently understood in view of their inherent complexity.Indeed, the surface reactivity of oxidized transition metal compounds depends on the interplay between the geometric and electronic structures, the local stoichiometry of the surface, and the oxidation states of the components.11,12 This has traditionally limited the generality of analyses for those catalysts and motivated the appearance of various ad hoc descriptors. For example, the number of outer electrons and the occupancy of eg orbitals correlate with adsorption energies and the oxygen evolution activity on monoxides, perovskites and spinels.13–15 The average oxygen 2p-state energy, oxygen p-band center and vacancy formation energies capture the activity trends for the oxygen reduction reaction (ORR) of solid oxide fuel cell cathodes on rutiles and perovskites.16,17 In addition, the oxygen vacancy formation energy is a descriptor for the trends in C–O and N–O bond scission of rutile oxides.18 The oxygen vacancies of TiO2 electroreduce formic acid to methanol and the activities depend linearly on the formation energies of such vacancies.19 The “adjusted coordination number”, can be used to predict the *H adsorption energy and C–H activation energies at the oxygen sites on V2O3, Cr2O3, Co3O4, and NiO.20 Finally, the activity of Ni3S2 catalysts is determined by the Ni–S coordination number: Ni surface sites with three S nearest neighbors provide nearly optimal energetic conditions for ORR electrocatalysis.21
Molybdenum disulfide (MoS2) is widely studied as a catalyst in various processes including hydrodesulfurization,22 hydrogen evolution reaction (HER),23,24 and catalytic hydrogenation.25–27 While MoS2 edges are generally accepted as the catalytic active sites,22,23,25 recent studies show that the MoS2(001) basal plane modified by doping transition metals or creating S vacancies displays enhanced catalytic performance for the HER,28–30 CO2 hydrogenation,31,32 and hydrodeoxygenation reactions.33 In particular, a Co-doped MoS2(001) basal plane shows long-term durability with >5000 cycles and an overpotential of 156 mV at a current density of 10 mA cm−2 for the HER, comparable to the most active MoS2-based electrocatalysts in acidic media.30 These findings open up new avenues for improved MoS2 catalyst design, as the (001) basal plane has a great density of sites compared to edges. However, the nanoscale factors that enhance the activity remain elusive. Shedding light into this exciting subject requires a direct link between the catalytic activity and the atomic-scale properties of the material. In fact, the design and implementation of MoS2 catalysts could be greatly streamlined by linking the geometric structure of their active sites to the catalytic activity.
To quantitatively outline the active sites of MoS2 catalysts, here we study the adsorption of various monatomic (H, B, C, N, O, and F) and polyatomic species (CO, NO, CH, OH, SH, CH2, CH3, NH2, CNH2, and CCH3) at undercoordinated Mo atoms (namely, S vacancies) on the MoS2(001) basal plane for a wide range of sulfur vacancy coverages (θ = 1/15–7/15 ML). We find that the total number of S atoms coordinated to Mo atoms at sulfur vacancies (denoted by cn) smoothly captures the trends in adsorption energies. In addition, cn is well correlated with the enthalpy and activation energy of elementary reactions such as OH, H2O, CH4 and CH3OH formation and NO dissociation.
For completeness, we benchmark cn against common descriptors such as the formation energies of sulfur vacancies (ΔEVac), cohesive energy (ECoh), work function (ϕ), d-band center of the Mo atoms (εd), charge transferred to the adsorbates, integrated crystal orbital overlap population (coop) and crystal orbital Hamilton population (cohp). We find that cn matches or even surpasses some of those descriptors, while being more easily assessed. Finally, we use cn to outline the optimal coordination environment of MoS2 terrace sites for the HER.
2. Results
We created S vacancies in the range of θ = 1/15–7/15 ML, by sequentially removing one to seven surface S atoms in a clockwise manner, as shown in Fig. 1. The total number of S atoms coordinated to Mo atoms (cn) at a S vacancy (dashed circle, Fig. 1) is defined as cn = NS/NMo, where NS is the number of S atoms coordinated to the three Mo atoms at the vacancy, and NMo is the number of Mo atoms which the S atoms in NS are coordinated to. Ample details, equations and numerical examples are provided in section S1.† In the following, we will illustrate the relationships between common descriptors used to capture adsorption-energy trends on MoS2(001). Although the descriptor-based analyses aim to predict catalytic activities using the properties of clean surfaces only, previous works have pointed out that adsorbate features often need to be incorporated into the descriptors to capture covalent adsorbate–surface interactions.8 Thus, in addition to cn, work function (ϕ), ΔEVac and εd, which are calculated on clean surfaces, we consider as descriptors the excess charge on the adsorbates, and the integrated coop and cohp, which are calculated on the surfaces with adsorbates.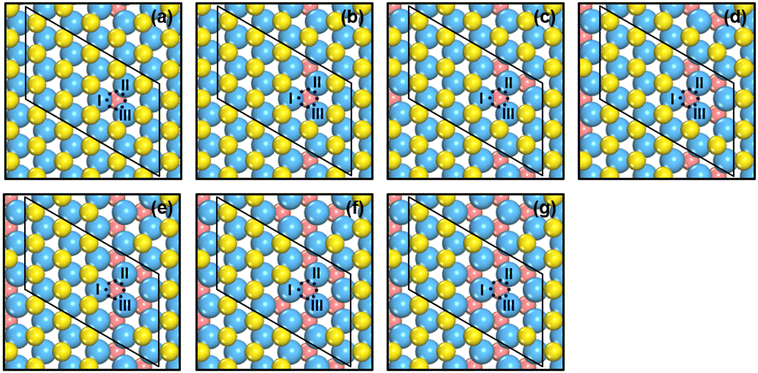 | ||
| Fig. 1 Top view of single-layer MoS2(001) at (a) 1/15 ML (cn = 5.00, ΔEVac = 5.98 eV); (b) 2/15 ML (cn = 4.67, ΔEVac = 6.00 eV); (c) 1/5 ML (cn = 4.33, ΔEVac = 6.25 eV); (d) 4/15 ML (cn = 4.00, ΔEVac = 6.52 eV); (e) 1/3 ML (cn = 3.67, ΔEVac = 6.54 eV); (f) 2/5 ML (cn = 3.33, ΔEVac = 6.67 eV); (g) 7/15 ML (cn = 3.00, ΔEVac = 7.02 eV) S vacancy coverages (θ). Blue, yellow and vermilion balls represent Mo, upper S and lower S atoms, respectively. The x and y coordinates of upper and lower S atoms coincide. If vermilion balls are visible in the top view, S atoms of the upper layer were removed. The blue dashed circle marks the adsorption site under study. I, II, III denote the Mo atoms at the adsorption sites. More details on the calculation of cn are in section S1 in the ESI.† | ||
As shown in Fig. 1 and 2 and Table S1,† cn progressively decreases as the S vacancy coverage goes from 1/15 to 7/15 ML, whereas the reverse trend is observed for S vacancy formation energy (ΔEVac). This is because with decreasing cn, more electrons are available on Mo atoms, which lifts up the Fermi level, leading to smaller ϕ. In turn, a smaller ϕ implies more facile electron donation to S atoms (stronger S adsorption) at the vacancy. Besides, creating a S vacancy is the reverse process of S adsorption at such a vacancy, so: ΔEAds(S) = −ΔEVac (see eqn (2) and (3) in the Methods section). Therefore, the linear relations between cn, ϕ and ΔEVac are expected to have a negative slope, as shown in Fig. 2a and Table S2.† We note that Rahman et al.34 used an (8 × 8) MoS2 supercell to show that the first ΔEVac is 5.85 eV, which is comparable to our first ΔEVac (5.98 eV). The slight discrepancy probably stems from the different plane-wave cutoffs (500 vs. 400 eV) and vacancy coverages (1/64 vs. 1/15 ML). In addition, we found a good correlation between εd and ΔEVac (Fig. S1 and Table S2†).
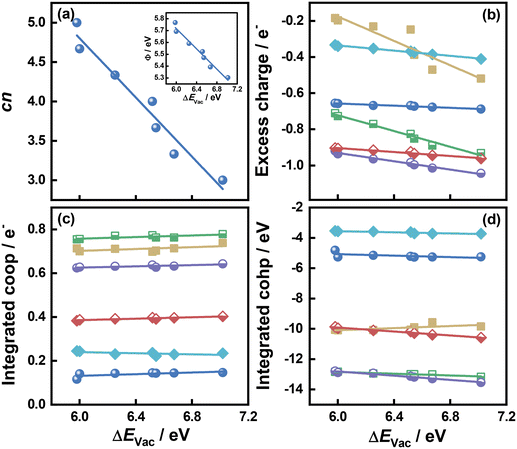 | ||
| Fig. 2 Relationships between the formation energy of S vacancies (ΔEVac) on MoS2(001) and: (a) the number of S atoms coordinated to Mo atoms (cn). Inset: Correlation between ΔEVac and work function (ϕ). (b) The excess charge on the adsorbates. (c) Integrated crystal orbital overlap population (coop). (d) Integrated crystal orbital Hamilton population (cohp) upon atom adsorption. The data in this figure are in Tables S1 and S2† (section S9). | ||
Upon atomic adsorption (see structures in Fig. 3), the charge transferred to the adsorbates gradually increases with increasing ΔEVac (Fig. 2b), which is a result of the smaller ϕ of the MoS2(001) surface at higher vacancy content. The slope becomes more negative as a function of the adsorbate valency, in agreement with bond order conservation theory.35 Indeed, the slopes get increasingly steeper as species with single (F, H), double (O) and triple or higher (B, N and C) valency are considered. Compared to the cn vs. ΔEVac and ϕ vs. ΔEVac relations, the one between excess charge and ΔEVac has less negative slopes (see Table S2†). This can be attributed to the smaller range spanned by the charge transferred (0.86 e−) on MoS2(001) compared to the corresponding value (2.24 e−) on the close-packed surfaces of 4d and 5d transition metals in previous works.8 These results reflect a more modest variation in electronic structure of MoS2(001) as vacancies are introduced, such that the materials properties (i.e., descriptors) need larger variations to reach a given effect compared to pure transition metal surfaces. This is confirmed by the trends in integrated coop for atomic adsorption, which hardly change as a function of ΔEVac in Fig. 2c. Similarly, the trends in integrated cohp are nearly flat as a function of ΔEVac in Fig. 2d. In addition, ΔEVac and cn are linearly related to the cohesive energy of the materials (ECoh), as shown in Fig. S2.† The anticorrelation between ΔEVac and ECoh is physically meaningful, as it reflects the fact that as MoS2 slabs contain less bonds, breaking Mo–S bonds is increasingly difficult. In turn, the correlation between cn and ECoh reflects the fact that as Mo atoms have more S neighbors, there is more energy stored in the solid.
So far, the relationships between a variety of descriptors and ΔEVac on MoS2(001) were presented. Because ΔEVac is in this case equivalent to the additive inverse of ΔEAds(S), it is reasonable to expect that ΔEVac should be able to describe the trends in ΔEAds of other adsorbates.5,8,36 We probed the adsorption of H, B, C, N, O and F on MoS2(001) at various S vacancy contents, and the calculated ΔEAds was correlated with ΔEVac in Fig. 4a (see Tables S3–S9†). We note that scaling relations also exist between ΔEAds of these atoms, as seen from the correlation between ΔEN and ΔEAds of other atomic species in Fig. S3.†
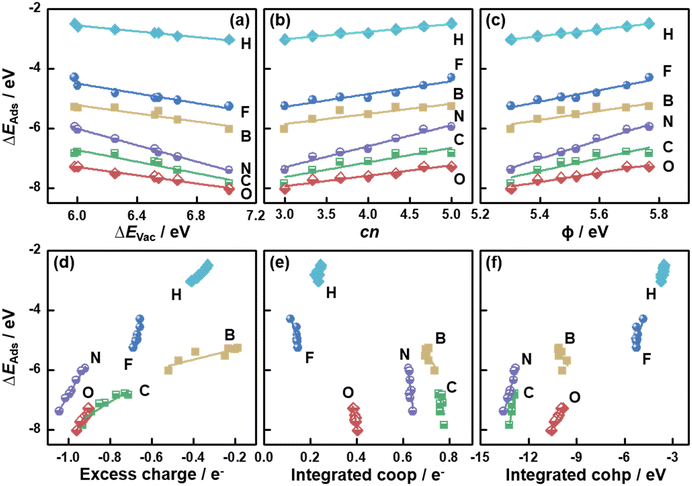 | ||
| Fig. 4 Adsorption energies (ΔEAds) of atomic species on MoS2(001) as a function of (a) the formation energies of S vacancies (ΔEVac); (b) the number of S atoms coordinated to Mo atoms (cn); (c) work function (ϕ); (d) the excess charge on the adsorbates; (e) integrated crystal orbital overlap population (coop); and (f) crystal orbital Hamilton population (cohp). The data in this figure can be found in Tables S3–S9.† | ||
In Fig. 4a, we observe that all atomic species bind more strongly as ΔEVac is increased, which indicates that they all bind to MoS2 similarly, despite their different chemical natures. Since ΔEVac scales with cn, ϕ, εd and excess charge (Fig. 2 and S1†), these descriptors capture the adsorption-energy trends similarly, as confirmed in Fig. 4b–d and S1.† However, the integrated coop and cohp, which are almost independent on ΔEVac, scale with ΔEAds of the atoms with steep slopes, see Fig. 4e and f. Hence, in this case a high accuracy of these two descriptors would be required in order to suitably predict ΔEAds. Averaging the mean absolute errors (MAEs) for the correlations between ΔEAds and ΔEVac, cn, ϕ, εd, excess charge, integrated coop and cohp we obtain 0.06, 0.07, 0.07, 0.07, 0.07, 0.16 and 0.10 eV, respectively (see Table S10†). Hence, cn is as predictive as ΔEVac, ϕ, εd and excess charge. However, cn is arithmetically calculated, unlike the other parameters. This simple fact helps save computational time, as the assessment of ΔEVac, ϕ, εd and excess charge requires electronic-structure calculations.
To understand the nature of the bonds between the atomic species and MoS2(001), we performed the differential charge density analysis in Fig. S4.† The maps show considerable charge withdrawal from the MoS2(001) surfaces by F and O, indicating the creation of mostly ionic bonds. In contrast, considerable charge builds up between the MoS2(001) surfaces and B and C, implying that their bonds are largely covalent. With increasing S vacancy content, less charge withdrawal from B and C is found, which corresponds to the larger excess charge seen in the Bader analysis (Fig. 4d). For N, both ionic and covalent bonding contribute significantly. Despite the different bonding nature, the good correlation between ΔEAds and the charge transferred to the atoms (Fig. 4d) indicates that the ionicity of the bonds is key for the activity trends on MoS2(001) with vacancies.
We also studied the adsorption of diatomic (CO, NO, CH, OH, SH) and multiatomic species (CH2, CH3, NH2, CNH2, CCH3) on MoS2(001). The structural and energetic data appear in Fig. 3 and Table S3.† As shown in Fig. 5a, ΔEAds of diatomic species becomes more negative with increasing ΔEVac (see Table S11†), in line with the monatomic adsorption in Fig. 4. Averaging the MAEs for the diatomic adsorption we obtain 0.11 eV (see Table S11†), which is only slightly larger than the value for monatomic adsorption.
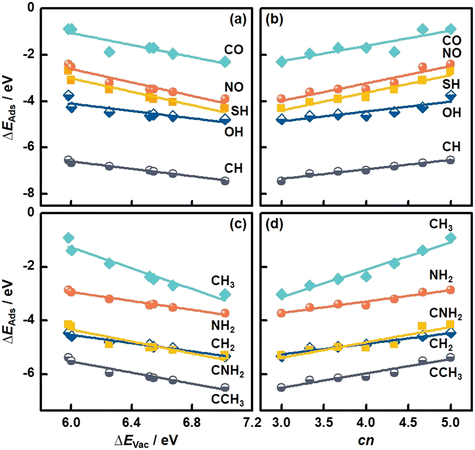 | ||
| Fig. 5 Adsorption energies (ΔEAds) of molecules on MoS2(001) as a function of (a and c) the formation energies of S vacancies (ΔEVac), and (b and d) the number of S atoms coordinated to Mo atoms (cn). See the data in this figure in Tables S11–S14.† | ||
In turn, cn provides trends with positive slopes in Fig. 5b. This means that ΔEAds of diatomic species becomes less negative as cn is increased. This trend is also found for monatomic adsorption and stems from the tendency of less coordinated surface sites to bind more strongly as a means of compensating their undercoordination. It is worth noting that cn is correlated with ΔEAds of the diatomic species with an average MAE of 0.11 eV (see Table S12†), which is as low as that of the correlations based on ΔEVac. In addition, good correlations between ΔEAds of multiatomic adsorbates and ΔEVac and cn are observed, see Fig. 5c and d. Averaging the MAEs for the two descriptors we obtain 0.09 eV in both cases, which are slightly smaller than the corresponding values for diatomic adsorption. Further details can be found in Tables S13 and S14.† We note that various S vacancy arrangements with cn in the range of 3.67 to 4.67 and their relation to the adsorption of species were studied before.37 The results suggest that the correlation between cn and ΔEAds also holds for other S vacancy arrangements, such that cn might be a general adsorption-energy descriptor on MoS2(001).
Moreover, we investigated the ability of cn to describe trends in elementary reactions. As shown in a previous work, ΔEAds of atomic species is closely related to the reaction energy (ΔH) of an elementary reaction step.37 Indeed, for a surface recombination reaction *A + *B → C + 2*, ΔH is given by eqn (1):
| ΔH = ΔHg − ΔEAds(A) − ΔEAds(B) | (1) |
Fig. 6a and Tables S15 and S16† confirm that ΔH of elementary reactions is linearly related to cn. In addition, although the adsorption of reactants and products depends on cn in a similar way, ΔH is well described by cn for *O + *H → *OH + *, and *NO + * → *N + *O. We note that *NO dissociation has a positive slope, unlike the recombination reactions in which the slopes are negative. This positive slope appears because ΔH for dissociations is mostly determined by the products instead of reactants, as opposed to recombination reactions.
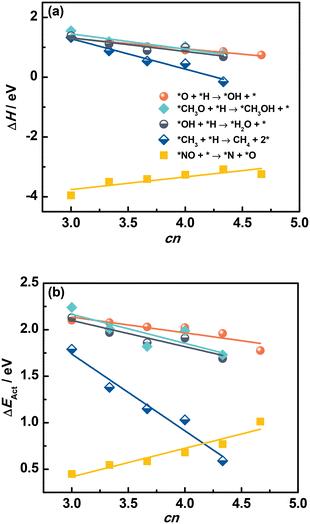 | ||
| Fig. 6 Reaction energies ΔH (a) and activation energies ΔEAct (b) of various elementary reactions as a function of the number of S atoms coordinated to Mo atoms (cn) on MoS2(001). The slopes for *NO dissociation are positive because ΔH and ΔEAct are mostly determined by the products instead of reactants, as opposed to the recombination reactions. The data in this figure appear in Tables S15 and S16.† | ||
Since saddle points are often hard to find, assessing activation energies is an arduous task. Brønsted–Evans–Polanyi (BEP) relations are extremely useful in catalysis, as they linearly connect the activation energy ΔEAct of an elementary reaction to its reaction energy ΔH.38–41 With this in mind, we examined the trends in ΔEAct of elementary reactions as a function of cn in Fig. 6b (see also Fig. S5†). Since the formation of OH, H2O and CH4 has been shown to largely determine the rate of CO and CO2 hydrogenation reactions on MoS2 catalysts,37,42,43 the correlation between ΔEAct and cn is encouraging, as it indicates that cn captures not just the trends in reaction thermodynamics but also the reaction kinetics. Similar to ΔH, the trend of ΔEAct of dissociation reactions is different from that of recombination reactions.
We also tested the applicability of cn on MoS2 edges, as they display high catalytic activity for various reactions. We employed Mo edges with S vacancies to study *O and *OH adsorption, see Table S17 and Fig. S6.† As the S vacancy concentration varies from 100% to 62.5%, cn increases from 2.67 to 3.67 and so do ΔEAds of *O and *OH. Hence, cn seems able to describe adsorption-energy trends on edge sites. However, MoS2 edges, particularly the S edge, are prone to reconstruction. Indeed, recent works found that Mo atoms on the S edge with 50% S vacancies have S–Mo–S angles of ∼100° and 130°, unlike those on the Mo edge with 62.5% S vacancies, which keep a trigonal prismatic coordination similar to MoS2(001) with S–Mo–S angles of ∼80° and 130°.42 Furthermore, Mo edges display S–Mo bond lengths of 2.44, 2.37 and 2.24 Å, while the S–Mo bond lengths on S edges are ∼2.30 Å. The large variations in the structure of Mo atoms on S edges lead to a dissimilar hybridization compared to Mo edges. In such case, cn fails to describe the trends in ΔEAds: Mo atoms at the S vacancy of the S edge with 50% S vacancies have cn = 3.33, which is smaller than the value of 3.67 on the Mo edge with 62.5% S vacancies. However, the species at the S vacancy on the S edge tend to bind more weakly than those on the Mo edge (see Table S18†).42 In sum, cn holds promise as a descriptor for adsorption-energy trends including edges with Mo atoms in similar geometric configurations compared to terrace sites, but if the edge sites undergo important geometric reconstructions, cn is likely to fail.
3. Discussion
Coordination numbers are well-known descriptors for adsorption-energy trends on metals and some oxides. For instance, conventional and “generalized” coordination numbers capture the trends in adsorption energy on extended surfaces and nanoparticles of Pt, Au, Cu and Zn.6,44–50 In fact, there is an analytic relationship between coordination numbers and εd,6 and a linear proportionality between εd and ΔEAds by virtue of the d-band model.1The free energy difference between *O and *OH (ΔGO − ΔGOH) is probably the most widely used computational descriptor for the oxygen evolution reaction (OER) activity.51–53 Previous works found that the number of oxygen atoms coordinated to surface Mn ions on various sites of Mn2O3(110) and MnO2(110) surfaces are linearly related to ΔGO − ΔGOH, such that the OER activities of Mn oxides are sensitive to oxygen coordination at the surface.54 In addition, Jiang et al. reported that “adjusted” coordination numbers exhibit a linear correlation with the *H adsorption energy and C–H activation barrier over various facets and defects on V2O3, Cr2O3, Co3O4, and NiO.20 Viswanathan et al. found that ΔGOH and the ORR activities of surface reconstructed Ni3S2 catalysts are determined by the Ni–S coordination numbers, such that counting S neighbors around Ni surface sites can be used to anticipate the ORR activity.21
Finally, in the following we will illustrate the use of cn to design active sites at MoS2(001) for electrocatalytic hydrogen evolution in two ways. First, as shown in the inset of Fig. 7, a thermodynamic analysis based on the computational hydrogen electrode55 predicts the most active terrace sites to be found for cn between 4.33 and 4.67, as ΔGH goes from negative to positive in that range and it should ideally be zero, as predicted by the Sabatier principle.56,57 In the main panel of Fig. 7, we use the microkinetic model of Nørskov et al.57 to calculate the exchange current density of various MoS2 electrodes. An implicit assumption of this model is that all sites are equivalent, such that each datapoint in Fig. 7 represents an electrode with all active sites of that specific cn (see full details in section S10†). Fig. 7 shows that cn = 4.51 provides the highest HER activity in terms of exchange current density in the range of coordination inspected. Hence, in addition to increasing the coverage of vacancies and straining them,28 an alternative to enhance the HER activity of MoS2 is to maximize the number of terrace sites with neighboring S vacancies having cn in the range of 4.33–4.67. This is a simple quantitative guideline to obtain highly active sites for the HER at sites other than MoS2 edges.
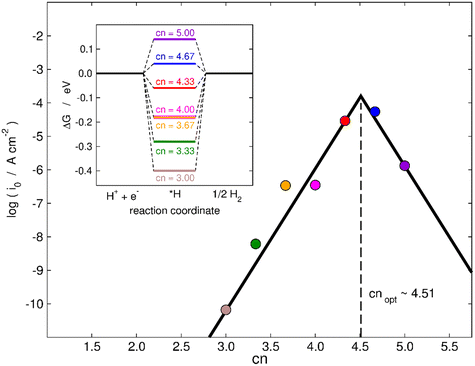 | ||
| Fig. 7 Trends in exchange current density (i0) for hydrogen evolution for various sites on MoS2(001) with S vacancies as a function of cn. The values of i0 were calculated using a microkinetic model,57 see full details in section S10.† The largest HER activity is found for cn = 4.51. Inset: Thermodynamic modelling of the HER on MoS2. The thermodynamically ideal active sites with ΔGH = 0 at 0 V vs. RHE correspond to cn in the range of 4.33–4.67. | ||
4. Conclusions
The number of sulfur atoms coordinated to Mo atoms (cn) is an intuitive, simple and accurate descriptor for the trends in adsorption energies, the thermodynamics and kinetics of several elementary reactions on MoS2. Interestingly, cn is arithmetically assessed, which helps lower the considerable computational cost typically invested in calculating electronic-structure descriptors. Numerous examples in the literature and the present work highlight the potential of coordination-based descriptors in catalysis. Devising similar descriptors for other oxides, sulfides, nitrides, etc. should be possible and may bring a sense of generality to the catalysis theory of oxidized transition metal compounds.Furthermore, taking electrocatalytic hydrogen evolution as a case study, cn was able to outline the geometric configuration of enhanced active sites on MoS2(001). Specifically, MoS2 terrace sites with cn = 4.51, which correspond to moderately undercoordinated sites with neighboring vacancies, should display maximal HER activities.
5. Methods
Spin-unrestricted density functional theory (DFT) calculations were performed with the Vienna ab initio simulation package (VASP).58 The interaction between ionic cores and valence electrons was described by the projector-augmented wave (PAW) method,59 and the Kohn–Sham valence electronic wavefunction was expanded using a plane-wave basis set with a kinetic energy cutoff of 400 eV. Exchange and correlation effects on the total energies were calculated within the generalized gradient approximation using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.60 All slab atoms and adsorbates were fully relaxed, and the total energies were converged below 10−4 eV, while the forces on the atoms were converged below 0.03 eV Å−1.Bulk 2H-MoS2 is a layered material, and the lattice constants are calculated to be a = b = 3.19 Å, c = 12.43 Å, which are close to the experimental values (a = b = 3.16 Å, c =12.29 Å).61 Single-layer MoS2 (denoted MoS2 hereafter) consists of an S–Mo–S sandwich, where the Mo atoms are arranged in a hexagonal lattice with a trigonal prismatic coordination with respect to the two S layers. The pristine MoS2(001) basal plane, with each Mo atom coordinated to six S atoms, was modeled by an S–Mo–S trilayer with (5 × 3) periodicity. To simulate S vacancies in the range of θ = 1/15–7/15 ML, one to seven surface S atoms were removed in a clockwise manner, as shown in Fig. 1. Some S vacancy arrangements in Fig. 1 may not be the most stable configuration for a given coverage. However, the main purpose of this work is to elucidate how adsorption energies at a given S vacancy (dashed circle, Fig. 1) respond to the coordination environment. For completeness, we compared the relative stability of adjacent and far S vacancies at 2/15 ML vacancy coverage and found that the former (Fig. S7a†) is slightly more stable than the latter (Fig. S7b†) by 0.06 eV. The higher stability of adjacent S vacancy compared to far S vacancy was also observed in a previous DFT study.34 The surface Brillouin zone was sampled with a (2 × 3 × 1) Monkhorst–Pack k-point grid for the MoS2(001) surface.62 A vacuum region of at least 15 Å sufficed to avoid interactions between periodically repeated slabs along the z-direction for all systems. More details about the models can be found in previous works.37,42,43
The adsorption energy (ΔEAds) was calculated using the adsorption configurations (EMoSx+ad) relative to the clean surfaces (EMoSx) and the isolated adsorbates (Ead):
| ΔEAds = EMoSx+ad − EMoSx − Ead | (2) |
| ΔEVac = EMoSx−1 + ES − EMoSx | (3) |
All transition states (TSs) were located by the force reversed method.63 The relaxation proceeds until the residual forces in each atom are smaller than 0.03 eV Å−1. The reaction energy (ΔH) of elementary reactions is calculated as:
| ΔH = EFS − EIS | (4) |
| ΔEAct = ETS − EIS | (5) |
Bader charge analyses were performed using a grid-based weight method in which the expression for the fraction of space neighboring each grid point that flows to its neighbors is used as a weight for the discrete integration of functions over the Bader volume.64 A positive or negative charge implies charge depletion or charge accumulation, respectively. The coop and cohp were analyzed using the LOBSTER program.65 The coop is an overlap-population-weighted density of states that provides information about electron distribution. In turn, the cohp is described as an “energy weighted” density of states. When integrated up to the Fermi level, the coop and cohp hint toward the strength of chemical bonds.8 The HER modelling is described in detail in section S10.†
Author contributions
HYS performed the DFT calculations and wrote the first draft of the paper. FCV carried out the electrocatalysis modelling. FCV and KS supervised the project. All authors analyzed the data, discussed the results and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China [22172026, 21872136], Natural Science Foundation of Hebei Province (B2021203016), Guangdong Provincial Key Laboratory of Distributed Energy Systems (2020B1212060075) and Highlevel Talents Project of Dongguan University of Technology (KCYKYQD2017017). FCV received financial support from grants PID2021-127957NB-I00 and TED2021-132550B-C21, which are funded by MCIN/AEI/10.13039/501100011033 and by the European Union.References
- B. Hammer and J. K. Nørskov, Theoretical Surface Science and Catalysis—Calculations and Concepts, Adv. Catal., 2000, 45, 71–129 CAS.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier Principle to a Predictive Theory of Transition-Metal Heterogeneous Catalysis, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- R. A. Van Santen, Complementary Structure Sensitive and Insensitive Catalytic Relationships, Acc. Chem. Res., 2009, 42, 57–66 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the Computational Design of Solid Catalysts, Nat. Chem., 2009, 1, 37–46 CrossRef.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Scaling Properties of Adsorption Energies for Hydrogen-Containing Molecules on Transition-Metal Surfaces, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Fast Prediction of Adsorption Properties for Platinum Nanocatalysts with Generalized Coordination Numbers, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- X. Ma and H. Xin, Orbitalwise Coordination Number for Predicting Adsorption Properties of Metal Nanocatalysts, Phys. Rev. Lett., 2017, 118, 036101 CrossRef PubMed.
- H.-Y. Su, K. J. Sun, W.-Q. Wang, Z. H. Zeng, F. Calle-Vallejo and W.-X. Li, Establishing and Understanding Adsorption−Energy Scaling Relations with Negative Slopes, J. Phys. Chem. Lett., 2016, 7, 5302–5306 CrossRef CAS PubMed.
- B. Huang, L. Xiao, J. Lu and L. Zhuang, Spatially Resolved Quantification of the Surface Reactivity of Solid Catalysts, Angew. Chem., Int. Ed., 2016, 55, 6239–6243 CrossRef CAS PubMed.
- W. Gao, Y. Chen, B. Li, S. P. Liu, X. Liu and Q. Jiang, Determining the Adsorption Energies of Small Molecules with the Intrinsic Properties of Adsorbates and Substrates, Nat. Commun., 2020, 11, 1196 CrossRef CAS.
- C. D. Gelatt, A. R. Williams and V. L. Moruzzi, Theory of Bonding of Transition Metals to Nontransition Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 2005–2013 CrossRef CAS.
- R. A. van Santen, I. Tranca and E. J. M. Hensen, Theory of Surface Chemistry and Reactivity of Reducible Oxides, Catal. Today, 2015, 244, 63–84 CrossRef CAS.
- F. Calle-Vallejo, N. G. Inoglu, H.-Y. Su, J. I. Martinez, I. C. Man, M. T. M. Koper, J. R. Kitchin and J. Rossmeisl, Number of Outer Electrons as Descriptor for Adsorption Processes on Transition Metals and Their Oxides, Chem. Sci., 2013, 4, 1245–1249 RSC.
- C. Wei, Z. Feng, G. G. Scherer, J. Barber, Y. Shao-Horn and Z. J. Xu, Cations in Octahedral Sites: A Descriptor for Oxygen Electrocatalysis on Transition−Metal Spinels, Adv. Mater., 2017, 29, 1606800 CrossRef.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, A Perovskite Oxide Optimized for Oxygen Evolution Catalysis from Molecular Orbital Principles, Science, 2011, 334, 1383–1385 CrossRef CAS.
- C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, An Electronic Structure Descriptor for Oxygen Reactivity at Metal and Metal-Oxide Surfaces, Surf. Sci., 2019, 681, 122–129 CrossRef CAS.
- Y. L. Lee, J. Kleis, J. Rossmeisl, Y. Shao-Horn and D. J. E. Morgan, Prediction of Solid Oxide Fuel Cell Cathode Activity with First-Principles Descriptors, Energy Environ. Sci., 2011, 4, 3966–3970 RSC.
- H. Y. Su, X. F. Ma, K. J. Sun, C. H. Sun, Y. J. Xu and F. Calle-Vallejo, Trends in C–O and N–O Bond Scission on Rutile Oxides Described Using Oxygen Vacancy Formation Energies, Chem. Sci., 2020, 11, 4119–4124 RSC.
- W. J. Teh, O. Piqué, Q. H. Low, W. Zhu, F. Calle-Vallejo and B. S. Yeo, Toward Efficient Tandem Electroreduction of CO2 to Methanol Using Anodized Titanium, ACS Catal., 2021, 11, 8467–8475 CrossRef CAS.
- V. Fung, F. F. Tao and D.-e. Jiang, General Structure–Reactivity Relationship for Oxygen on Transition-Metal Oxides, J. Phys. Chem. Lett., 2017, 8, 2206–2211 CrossRef CAS PubMed.
- B. Yan, D. Krishnamurthy, C. H. Hendon, S. Deshpande, Y. Surendranath and V. Viswanathan, Surface Restructuring of Nickel Sulfide Generates Optimally Coordinated Active Sites for Oxygen Reduction Catalysis, Joule, 2017, 1, 600–612 CrossRef CAS.
- P. G. Moses, B. Hinnemann, H. Topsøe and J. K. Nørskov, The Effect of Co-Promotion on MoS2 Catalysts for Hydrodesulfurization of Thiophene: A Density Functional Study, J. Catal., 2009, 268, 201–208 CrossRef CAS.
- T. F. Jaramillo, K. P. Jorgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Identification of Active Edge Sites for Electrochemical H2 Evolution from MoS2 Nanocatalysts, Science, 2007, 317, 100–102 CrossRef CAS PubMed.
- Y. G. Li, H. L. Wang, L. M. Xie, Y. Y. Liang, G. S. Hong and H. J. Dai, MoS2 Nanoparticles Grown on Graphene: An Advanced Catalyst for the Hydrogen Evolution Reaction, J. Am. Chem. Soc., 2011, 133, 7296–7299 CrossRef CAS PubMed.
- S. Zaman and K. Smith, A Review of Molybdenum Catalysts for Synthesis Gas Conversion to Alcohols: Catalysts, Mechanisms and Kinetics, Catal. Rev.: Sci. Eng., 2012, 54, 41–132 CrossRef CAS.
- L. Sharma, R. Upadhyay, S. Rangarajan and J. Baltrusaitis, Inhibitor, Co-Catalyst, or Co-reactant? Probing the Different Roles of H2S During CO2 Hydrogenation on MoS2 Catalyst, ACS Catal., 2019, 9, 10044–10059 CrossRef CAS.
- A. Wambeke, L. Jalowiecki, S. Kasztelan, J. Grimblot and J. P. Bonnelle, The Active Site for Isoprene Hydrogenation on MoS2γ-Al2O3 Catalysts, J. Catal., 1988, 109, 320–328 CrossRef CAS.
- H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Norskov and X. Zheng, Activating and Optimizing MoS2 Basal Planes for Hydrogen Evolution through the Formation of Strained Sulphur Vacancies, Nat. Mater., 2016, 15, 48–53 CrossRef CAS PubMed.
- C. Tsai, H. Li, S. Park, J. Park, H. S. Han, J. K. Nørskov, X. L. Zheng and F. Abild-Pedersen, Electrochemical Generation of Sulfur Vacancies in the Basal Plane of MoS2 for Hydrogen Evolution, Nat. Commun., 2017, 8, 15113 CrossRef PubMed.
- J. Deng, H. B. Li, S. H. Wang, D. Ding, M. S. Chen, C. Liu, Z. Q. Tian, K. S. Novoselov, C. Ma, D. H. Deng and X. H. Bao, Multiscale Structural and Electronic Control of Molybdenum Disulfide Foam for Highly Efficient Hydrogen Production, Nat. Commun., 2017, 8, 14430 CrossRef CAS PubMed.
- J. T. Hu, L. Yu, J. Deng, Y. Wang, K. Cheng, C. Ma, Q. H. Zhang, W. Wen, S. S. Yu, Y. Pan, J. Z. Yang, H. Ma, F. Qi, Y. K. Wang, Y. P. Zheng, M. S. Chen, R. Huang, S. H. Zhang, Z. C. Zhao, J. Mao, X. Y. Meng, Q. Q. Ji, G. J. Hou, X. W. Han, X. H. Bao, Y. Wang and D. H. Deng, Sulfur Vacancy-Rich MoS2 As a Catalyst for the Hydrogenation of CO2 to Methanol, Nat. Catal., 2021, 4, 242–250 CrossRef CAS.
- H. L. Li, L. B. Wang, Y. Z. Dai, Z. T. Pu, Z. H. Lao, Y. W. Chen, M. L. Wang, X. S. Zheng, J. F. Zhu, W. H. Zhang, R. Si, C. Ma and J. Zeng, Synergetic Interaction between Neighbouring Platinum Monomers in CO2 Hydrogenation, Nat. Nanotechnol., 2018, 13, 411 CrossRef CAS PubMed.
- G. L. Liu, A. W. Robertson, M.-M.-J. Li, W. C. H. Kuo, M. T. Darby, M. H. Muhieddine, Y.-C. Lin, K. Suenaga, M. Stamatakis, J. H. Warner and S. C. E. Tsang, MoS2 Monolayer Catalyst Doped with Isolated Co Atoms for the Hydrodeoxygenation Reaction, Nat. Chem., 2017, 9, 810–816 CrossRef CAS PubMed.
- D. Le, T. B. Rawal and T. S. Rahman, Single-Layer MoS2 with Sulfur Vacancies: Structure and Catalytic Application, J. Phys. Chem. C, 2014, 118, 5346–5351 CrossRef CAS.
- E. Shustorovich and A. T. Bell, Analysis of CO Hydrogenation Pathways Using the Bond-Order-Conservation Method, J. Catal., 1988, 113, 341–352 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Physical and Chemical Nature of the Scaling Relations between Adsorption Energies of Atoms on Metal Surfaces, Phys. Rev. Lett., 2012, 108, 116103 CrossRef CAS.
- H.-Y. Su, K. J. Sun, J.-X. Liu, X. F. Ma, M. Z. Jian, C. H. Sun, Y. J. Xu, H. B. Yin and W.-X. Li, Bridge Sulfur Vacancies in MoS2 Catalyst for Reverse Water Gas Shift: A First-Principles Study, Appl. Surf. Sci., 2021, 561, 149925 CrossRef CAS.
- M. G. Evans and M. Polanyi, Inertia and Driving Force of Chemical Reactions, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, The Bronsted-Evans-Polanyi Relation and the Volcano Curve in Heterogeneous Catalysis, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- S. Wang, V. Petzold, V. Tripkovic, J. Kleis, J. G. Howalt, E. Skúlason, E. M. Fernández, B. Hvolbæk, G. Jones, A. Toftelund, H. Falsig, M. Björketun, F. Studt, F. Abild-Pedersen, J. Rossmeisl, J. K. Nørskov and T. Bligaard, Universal Transition State Scaling Relations for (De)Hydrogenation over Transition Metals, Phys. Chem. Chem. Phys., 2011, 13, 20760–20765 RSC.
- S. Wang, B. Temel, J. Shen, G. Jones, L. C. Grabow, F. Studt, T. Bligaard, F. Abild-Pedersen, C. H. Christensen and J. K. Nørskov, Universal Brønsted-Evans-Polanyi Relations for C–C, C–O, C–N, N–O, N–N, and O–O Dissociation Reactions, Catal. Lett., 2011, 141, 370–373 CrossRef CAS.
- H.-Y. Su, W. B. Liao and K. J. Sun, First-Principles and Microkinetic Simulation Studies of CO2 Hydrogenation Mechanism and Active Site on MoS2 Catalyst, Appl. Surf. Sci., 2023, 635, 157721 CrossRef CAS.
- H.-Y. Su, X. F. Ma, C. H. Sun and K. J. Sun, A Synergetic Effect between a Single Cu Site and S Vacancy on an MoS2 Basal Plane for Methanol Synthesis from Syngas, Catal. Sci. Technol., 2021, 11, 3261–3269 RSC.
- F. Calle-Vallejo, The ABC of Generalized Coordination Numbers and Their Use as a Descriptor in Electrocatalysis, Adv. Sci., 2023, 2207644 CrossRef CAS PubMed.
- H. J. Li, Y. D. Li, M. T. M. Koper and F. Calle-Vallejo, Bond-Making and Breaking between Carbon, Nitrogen, and Oxygen in Electrocatalysis, J. Am. Chem. Soc., 2014, 136, 15694–15701 CrossRef CAS PubMed.
- L. Wang, A. Roudgar and M. Eikerling, Ab Initio Study of Stability and Site-Specific Oxygen Adsorption Energies of Pt Nanoparticles, J. Phys. Chem. C, 2009, 113, 17989–17996 CrossRef CAS.
- L. G. Verga, P. C. D. Mendes, V. K. Ocampo-Restrepo and J. L. F. Da Silva, Exploring the Adsorption Site Coordination as a Strategy to Tune Copper Catalysts for CO2 Electro-Reduction, Catal. Sci. Technol., 2022, 12, 869–879 RSC.
- F. Calle-Vallejo, M. D. Pohl and A. S. Bandarenka, Quantitative Coordination-Activity Relations for the Design of Enhanced Pt catalysts for CO Electro-Oxidation, ACS Catal., 2017, 7, 4355–4359 CrossRef CAS.
- M. D. Pohl, S. Watzele, F. Calle-Vallejo and A. S. Bandarenka, Nature of Highly Active Electrocatalytic Sites for the Hydrogen Evolution Reaction at Pt Electrodes in Acidic Media, ACS Omega, 2017, 2, 8141–8147 CrossRef CAS.
- M. P. L. Kang, M. J. Kolb, F. Calle-Vallejo and B. S. Yeo, The Role of Undercoordinated Sites on Zinc Electrodes for CO2 Reduction to CO, Adv. Funct. Mater., 2022, 32, 2111597 CrossRef CAS.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining Theory and Experiment in Electrocatalysis: Insights into Materials Design, Science, 2017, 355, eaad4998 CrossRef PubMed.
- J. M. Zhang, H. B. Yang, D. J. Zhou and B. Liu, Adsorption Energy in Oxygen Electrocatalysis, Chem. Rev., 2022, 122, 17028–17072 CrossRef CAS PubMed.
- H.-Y. Su, Y. Gorlin, I. C. Man, F. Calle-Vallejo, J. K. Nørskov, T. F. Jaramillo and J. Rossmeisl, Identifying Active Surface Phases for Metal Oxide Electrocatalysts: A Study of Manganese Oxide Bi-Functional Catalysts for Oxygen Reduction and Water Oxidation Catalysis, Phys. Chem. Chem. Phys., 2012, 14, 14010–14022 RSC.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- M. T. M. Koper, Thermodynamic Theory of Multi-Electron Transfer Reactions: Implications for Electrocatalysis, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, Trends in the Exchange Current for Hydrogen Evolution, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Jellinek, G. Brauer and H. Müller, Molybdenum and Niobium Sulphides, Nature, 1960, 185, 376–377 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- K. J. Sun, Y. H. Zhao, H.-Y. Su and W.-X. Li, Force Reversed Method for Locating Transition States, Theor. Chem. Acc., 2012, 131, 1118 Search PubMed.
- M. Yu and D. R. Trinkle, Accurate and Efficient Algorithm for Bader Charge Integration, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- R. Nelson, C. Ertural, J. George, V. Deringer, G. Hautier and R. Dronskowski, LOBSTER: Local Orbital Projections, Atomic Charges, and Chemical-Bonding Analysis from Projector-Augmented-Wave-Based Density-Functional Theory, J. Comput. Chem., 2020, 41, 1931–1940 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Examples for cn calculations, correlations between d-band center and S vacancy formation energies and adsorption energies, correlations between cohesive energies and vacancy formation energies and number of S atoms coordinated to Mo atoms, adsorption-energy scaling relations, differential charge density maps for atomic adsorption, transition-state configurations, adsorption configurations on Mo edges, adjacent and far S vacancy configurations, tabulated data, and details of the electrocatalytic modelling are provided in the ESI. See DOI: https://doi.org/10.1039/d3cy00575e |
| This journal is © The Royal Society of Chemistry 2023 |

