Open Access Article
Open Access ArticleCapturing molecular interactions in graph neural networks: a case study in multi-component phase equilibrium†
Shiyi
Qin
a,
Shengli
Jiang
a,
Jianping
Li
a,
Prasanna
Balaprakash
bc,
Reid C.
Van Lehn
 a and
Victor M.
Zavala
a and
Victor M.
Zavala
 *ab
*ab
aDepartment of Chemical and Biological Engineering, University of Wisconsin–Madison, 1415 Engineering Dr, Madison, WI 53706, USA. E-mail: victor.zavala@wisc.edu
bMathematics and Computer Science Division, Argonne National Laboratory, 9700 S Cass Ave, Lemont, IL 60439, USA
cLeadership Computing Facility, Argonne National Laboratory, 9700 S Cass Ave, Lemont, IL 60439, USA
First published on 30th November 2022
Abstract
Graph neural networks (GNNs) have been widely used for predicting molecular properties, especially for single molecules. However, when treating multi-component systems, GNNs have mostly used simple data representations (concatenation, averaging, or self-attention on features of individual components) that might fail to capture molecular interactions and potentially limit prediction accuracy. In this work, we propose a GNN architecture that captures molecular interactions in an explicit manner by combining atomic-level (local) graph convolution and molecular-level (global) message passing through a molecular interaction network. We tested the architecture (which we call SolvGNN) on a comprehensive phase equilibrium case study that aims to predict activity coefficients for a wide range of binary and ternary mixtures; we built this large dataset using the COnductor-like Screening MOdel for Real Solvation (COSMO-RS). We show that SolvGNN can predict composition-dependent activity coefficients with high accuracy and show that it outperforms a previously-developed GNN used for predicting only infinite-dilution activity coefficients. We performed counterfactual analysis on the SolvGNN model that allowed us to explore the impact of functional groups and composition on equilibrium behavior. We also used the SolvGNN model for the development of a computational framework that automatically creates phase diagrams for a diverse set of complex mixtures. All scripts needed to reproduce the results are shared as open-source code.
1 Introduction
Predicting the physicochemical properties of molecules is crucial for applications such as product and process design. In the past decade, machine learning (ML) techniques have been used as data-driven approaches that help accelerate molecule screening and to reduce experimentation cost, especially when a large chemical space is involved. These models have also shown to be versatile and to predict diverse molecular properties such as water solubility,1–3 toxicity,4–6 and lipophilicity.7,8 A fundamental step in the use of ML models is the pre-definition or pre-calculation of molecular descriptors;9–12 such descriptors are used as input data to develop quantitative structure–property relationship models.13 Recently, there has been growing interest in applying ML models to study more complex chemical systems that might contain multiple components such as chemical reactions,14,15 alloys,16,17 copolymers,18–20 and gas/liquid mixtures.21–33 Among the ML techniques explored, graph neural networks (GNNs)34,35 have gained special popularity because they can directly incorporate molecular representations (in the form of graphs), which enable the capturing of key structural information while potentially avoiding the need to pre-calculate/pre-define descriptors using more advanced but computationally-intensive tools such density functional theory (DFT) or molecular dynamics (MD) models.In a typical GNN architecture for prediction of molecular properties,36 the characteristics of the atoms and of the bonds are propagated based on the chemical structure of a single input molecule, followed by featuring embedding via nonlinear transformation. The embedded features are then fed to fully-connected layers to construct predictive models. GNNs have achieved better performance than conventional descriptor-based approaches in various benchmark datasets.37,38 When dealing with multiple components, several approaches have been devised; a typical way to encode multi-molecule information is to simply average or concatenate the features of individual molecules and to use these as system-level features for property inference with fully connected or attentive layers.14,15,19 Previous studies have also incorporated weighted sums or concatenation to take into account composition information when needed.19 However, these approaches do not capture molecular interactions in an explicit manner, which may limit the predictive power of GNNs for systems in which intermolecular interactions play an important role.
In this work, we present a GNN architecture that explicitly incorporates molecular interactions via the combination of atomic-level (local) graph convolution and molecular-level (global) message passing for property prediction of multi-component chemical systems. To connect local features with global features, we construct a molecular interaction network as an intermediate step. The molecular interaction network is a complete graph in which each node represents a molecule and each edge represents a hypothetical intermolecular interaction (e.g., hydrogen bonding). This representation serves as a physics-informed topological prior that aids feature extraction from multi-component systems. The composition information is also encoded in the architecture as additional node feature for the molecular interaction network. We hypothesize that, with this type of data representation and feature propagation guided by physical intuition, the proposed architecture may better model mixture properties while taking composition information into consideration.
We evaluate the proposed GNN architecture through a comprehensive case study on miscibility calculations for multi-component systems. We choose activity coefficients as the target thermodynamic property of interest, which measures the deviation of a liquid mixture from ideal solution behavior. Activity coefficients are one of the fundamental properties of a mixture and therefore can lead to the derivation of equilibrium conditions (e.g., phase diagrams), which are important in physical chemistry and engineering for understanding and optimizing chemical separations.39 Previous studies have developed ML-based methods to predict infinite-dilution activity coefficients for binary mixtures, including matrix completion on the activity coefficient matrix28,40 and multilayer perceptrons on the system descriptors.41 However, these methods did not account for molecular structural information directly, and the latter is limited to systems of water in ionic liquids. A more recent study by Medina et al.29 used GNN models to tackle this problem; this approach, however, used a data representation that involves a simple concatenation of individual graph features after local embedding (i.e., the GNN architecture does not explicitly captures intermolecular interactions). Furthermore, all these previous studies have focused on predicting infinite-dilution coefficients, which do not take into consideration composition information (this limits their use in more sophisticated thermodynamic predictions such as phase diagrams). To the best of our knowledge, GNNs have not been explored as a method to predict composition-dependent activity coefficients nor have they been extended to predict activity coefficients for systems with more than two components. The proposed GNN architecture is generalizable to multiple component systems and captures composition.
Through our case study, we demonstrate that the proposed GNN (which we call SolvGNN) outperforms prior architectures (that lack an explicit graph representation of molecular interactions) in terms of prediction accuracy. Our study leverages a large dataset that was developed using the COnductor-like Screening MOdel for Real Solvation (COSMO-RS). SolvGNN also enables better modeling of mixture compositions due to the incorporation of global message passing on the molecular interaction network with hydrogen bonding information. We also show that SolvGNN can be applied to both binary and ternary liquid-phase mixtures to predict composition-dependent activity coefficients. To interpret our SolvGNN predictions, we perform counterfactual analysis42 to identify the impact of functional groups on activity coefficients. To demonstrate the applicability of SolvGNN, we developed a framework that can automatically predict phase behavior for complex binary and ternary mixtures. Example outcomes of the framework, such as binary P–x–y diagrams, can be used to study solvent miscibility and to help identify azeotrope compositions to guide the design of targeted mixtures and chemical separations. We share scripts and datasets as open-source code to enable the reproduction of the results and to conduct benchmarks.
2 Materials and methods
2.1 Data set summary
We assembled a list of 700 common solvents,43 covering a wide spectrum of small molecules such as water, alcohols, esters, and ethers. We then used random sampling over the solvent space to generate 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 binary mixtures and 40
000 binary mixtures and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ternary mixtures. For each binary mixture, we explored five molar composition ratios – 10%/90%, 30%/70%, 50%/50%, 70%/30%, 90%/10%; for each ternary mixture, we explored four molar composition ratios – 15%/15%/70%, 15%/70%/15%, 70%/15%/15%, and 33.3%/33.3%/33.4%. Overall, we assembled a large database with 200
000 ternary mixtures. For each binary mixture, we explored five molar composition ratios – 10%/90%, 30%/70%, 50%/50%, 70%/30%, 90%/10%; for each ternary mixture, we explored four molar composition ratios – 15%/15%/70%, 15%/70%/15%, 70%/15%/15%, and 33.3%/33.3%/33.4%. Overall, we assembled a large database with 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 entries for binary mixtures and 160
000 entries for binary mixtures and 160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 entries for ternary mixtures. We further augmented the binary mixture data set with 80
000 entries for ternary mixtures. We further augmented the binary mixture data set with 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 infinite dilution activity coefficients (corresponding to molar composition ratios of 0% or 100%) to determine how these points influence prediction accuracy at extreme compositions. These data are later combined with the previous binary mixture data set to enable a more powerful SolvGNN that can accurately predict activity coefficients across all concentrations, including the infinite dilution case.
000 infinite dilution activity coefficients (corresponding to molar composition ratios of 0% or 100%) to determine how these points influence prediction accuracy at extreme compositions. These data are later combined with the previous binary mixture data set to enable a more powerful SolvGNN that can accurately predict activity coefficients across all concentrations, including the infinite dilution case.
To visualize the coverage of the chemical space, the solvents were grouped into 22 categories based on a predefined list of functional groups (details are provided in the ESI Section 1†). The visualization is provided in Fig. 1a. The sampled binary mixtures are represented by connections between nodes. The number of solvents in each category and the number of sampled pairs are reflected by node size and edge thickness; this illustrates that our random mixture sampling covers a wide range of solvent pairs in different categories. We also visualized the chemical space of the solvents by performing a t-distributed stochastic neighbor embedding (t-SNE)44 dimensionality reduction technique on the Morgan fingerprints,9 also known as extended connectivity fingerprints10 in Fig. 1b. The 2D map from t-SNE shows separation between some solvent categories, such as nitriles and aromatics. However, because some solvents contain more than one identifiable functional group, they may potentially be grouped into another category. As a result, the clustering in a few other categories is less clear, but in general the scattered distribution here suggests the inclusion of diverse and complex chemical structures.
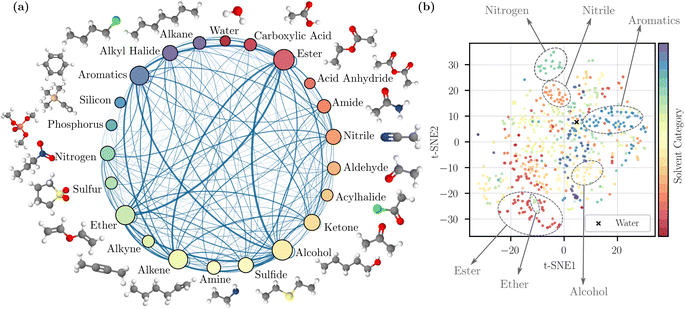 | ||
| Fig. 1 Dataset visualization. (a) Solvent categories based on the primary functional group of individual solvents with examples. The categorization method is detailed in ESI.† The size of a node reflects the number of solvents in that category, and the thickness of an edge reflects the number of sampled pairs between two categories. (b) 2D map obtained by t-SNE dimensionality reduction44 applied to molecular fingerprints. | ||
We categorized the sampled binary and ternary mixtures based on whether each component in the mixture is polar or nonpolar (obtained from RDKit45), as summarized in Table 1. We computed the percentage of each mixture type; this information was used for stratified sampling, which creates training/validation folds by preserving the percentage of samples for each mixture type (this ensure that the model learns different types of molecular interactions). Overall, most mixtures contain at least one polar component, indicating the presence of strong intermolecular interactions (e.g., dipole–dipole forces).
| Mixture type | Count | Percentage | |
|---|---|---|---|
Binary (280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
Polar–polar (p–p) | 162![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547 547 |
58% |
| Polar–nonpolar (p–n) | 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913 913 |
36% | |
| Nonpolar–nonpolar (n–n) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540 540 |
6% | |
Ternary (160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
Polar-polar–polar (p–p–p) | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136 136 |
45% |
| Polar–polar–nonpolar (p–p–n) | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
41% | |
| Polar–nonpolar–nonpolar (p–n–n) | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 848 |
13% | |
| Nonpolar–nonpolar–nonpolar (n–n–n) | 1976 | 1% |
2.2 Activity coefficient calculations
To overcome the challenge of limited experimental data availability, we used the COnductor-like Screening MOdel for Real Solvation (COSMO-RS) to generate ground-truth labels for supervised ML. COSMO-RS calculations are based on surface charge densities (σ-profiles) of mixture components, which are obtained from DFT calculations coupled with the COSMO continuum solvation model,46 and it can be used to calculate the activity coefficients for any mixture as long as the chemical structures are provided and optimized. For each solvent mixture, we obtained activity coefficients γi for individual components i from COSMO-RS and constructed large and structured data sets for model training and evaluation.COSMOtherm47 (version 2019), a software that implements COSMO-RS, was used to obtain composition-dependent activity coefficients for the individual components of each sampled mixture. Prior to COSMO-RS calculations, chemical structures were generated from CirPy (version 1.0.2), a Python library that serves as the interface for the Chemical Identifier Resolver (CIR);48 this searches the National Institutes of Health (NIH) database for the chemical structures and provides the optimized coordinates for the atoms. We next conducted DFT calculations using TURBOMOLE49 (version 7.5) at the BP-TZVP theory level with the Becke–Perdew (BP) functional and the resolution of identity approximation under ideal screening condition (ϵ∞, COSMO continuum solvation model). A single-point calculation was then conducted with the def2-TZVPD basis set and fine cavity parameter to create the σ-profiles. Activity coefficients were then calculated given the σ-profiles of individual components, the mixture compositions in the liquid phase, and temperature (298 K).
2.3 GNN model architecture
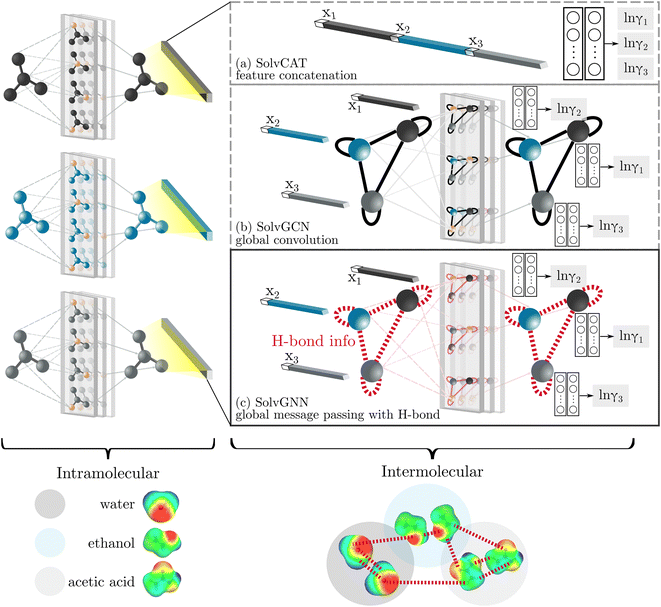
GNNs are a class of neural networks that take graphs as inputs and perform convolutions based on the graph topology by aggregating the features of a node and its connected neighbors. The node features are embedded into a fixed-dimension space where similar nodes are close to each other. Compared with conventional convolution neural networks that operate on grid data (e.g., images), GNNs have the advantage of extracting features from data with more flexible topology and different sizes while keeping locality information, and therefore are applied widely to chemical data.As shown in Fig. 2, each input mixture is represented as molecular graphs 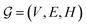 of individual components with nodes v ∈ V, edges e ∈ E, and node feature matrix that encodes atom and bond information such as atom types and degrees.50 A local graph convolution51 was applied to each of the input molecular graphs, and the node features were updated through
of individual components with nodes v ∈ V, edges e ∈ E, and node feature matrix that encodes atom and bond information such as atom types and degrees.50 A local graph convolution51 was applied to each of the input molecular graphs, and the node features were updated through
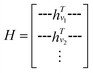 | (1) |
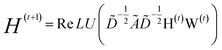 | (2) |
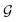 with self-loops,
with self-loops, 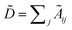 is the degree matrix and W(t) is the learnable weight matrix at time step t.
is the degree matrix and W(t) is the learnable weight matrix at time step t. 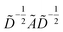 is derived from normalized graph Laplacian that accounts for graph topology and implicitly imitates molecular interactions. The W(t) values are kept the same for each component in the mixture. After local graph convolution, node-level features are averaged to generate the graph-level feature
is derived from normalized graph Laplacian that accounts for graph topology and implicitly imitates molecular interactions. The W(t) values are kept the same for each component in the mixture. After local graph convolution, node-level features are averaged to generate the graph-level feature 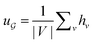 .
.
We compared several approaches to capture molecular interactions. The first approach is illustrated in Fig. 2a and referred to as SolvCAT. In this approach, 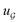 ’s undergo a feature concatenation with composition x to form a fixed-length latent feature vector. For a ternary system, for example,
’s undergo a feature concatenation with composition x to form a fixed-length latent feature vector. For a ternary system, for example, 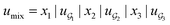 . The system-level feature vector is then sent to fully connected neural network layers for activity coefficient predictions. The second approach is illustrated in Fig. 2b and referred to as SolvGCN. In this approach, a molecular interaction network was constructed to explicitly simulate molecular interactions between the components in a system. The molecular interaction network
. The system-level feature vector is then sent to fully connected neural network layers for activity coefficient predictions. The second approach is illustrated in Fig. 2b and referred to as SolvGCN. In this approach, a molecular interaction network was constructed to explicitly simulate molecular interactions between the components in a system. The molecular interaction network 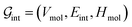 is a complete graph where each node vmol ∈ Vmol denotes a molecule, each edge eint ∈ Eint denotes the existence of certain intermolecular interaction, and molecular-level node feature matrix:
is a complete graph where each node vmol ∈ Vmol denotes a molecule, each edge eint ∈ Eint denotes the existence of certain intermolecular interaction, and molecular-level node feature matrix:
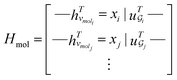 | (3) |
A global graph convolution is applied using the same updating rules as eqn (2); in this case, umix is obtained by concatenating the latent node features hmol's after global graph convolution.
The third approach is illustrated in Fig. 2c and referred to as SolvGNN. Building on SolvGCN, for this approach we developed a more informative representation of the molecular interaction network; we encoded hydrogen-bond (H-bond) information, one of the strongest form of dipole–dipole interactions, as the edge feature. For a ternary system, this feature is formulated as:
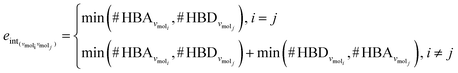 | (4) |
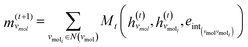 | (5) |
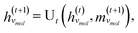 | (6) |
In all three cases mentioned above, the embedded features after “intermolecular interactions” are sent to the fully connected readout layers for the final activity coefficient (γi) prediction.
2.4 GNN training and hyperparameter tuning
SMILES strings were used as molecule identifiers and processed by RDKit (version 2019.03.2)45 to generate molecular graphs. The GNN models were constructed using PyTorch (version 1.2.0)53 and Deep Graph Library (version 0.4.3).54 The major hyperparameters we varied include the number of graph convolution layers (1,2), the number of fully connected readout layers (1,2,3), the number of hidden neurons (128,256), and the learning rate (0.0005,0.001). The model was trained with the average mean-squared-error (MSE) loss for the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi values, the Adam optimizer, a learning rate of 0.001, and a batch size of 100 for 100 epochs. Unlike SolvGCN and SolvGNN where graph convolutions are conducted at the node-level and where model predictions are unaffected by the order of the components, SolvCAT does not naturally preserve permutation invariance. To address this issue, we performed data augmentation during training by randomly flipping the order of the components. For model evaluation, we performed 5-fold cross-validation (CV) with stratified random sampling to split data for hyperparameter tuning and model evaluation. Stratification is based on the type of mixture (e.g., polar–polar, polar–nonpolar, or nonpolar–nonpolar) to ensure that both the training and validation sets contain all types of mixtures. Other than stratification on the type of mixture, we did not enforce any constraints on the components or the compositions, and therefore the validation sets contain completely unseen systems and compositions. To further study the more stringent cases of SolvGNN to generalize to unseen mixtures (and their interactions) or components, we explored three alternative data splitting methods; the results and comparison are discussed in the ESI.† All evaluation metrics are computed using the compilation of the validation data in each fold to obtain a realistic estimation of the model performance. More implementation details about training and validation can also be found in the ESI.†
γi values, the Adam optimizer, a learning rate of 0.001, and a batch size of 100 for 100 epochs. Unlike SolvGCN and SolvGNN where graph convolutions are conducted at the node-level and where model predictions are unaffected by the order of the components, SolvCAT does not naturally preserve permutation invariance. To address this issue, we performed data augmentation during training by randomly flipping the order of the components. For model evaluation, we performed 5-fold cross-validation (CV) with stratified random sampling to split data for hyperparameter tuning and model evaluation. Stratification is based on the type of mixture (e.g., polar–polar, polar–nonpolar, or nonpolar–nonpolar) to ensure that both the training and validation sets contain all types of mixtures. Other than stratification on the type of mixture, we did not enforce any constraints on the components or the compositions, and therefore the validation sets contain completely unseen systems and compositions. To further study the more stringent cases of SolvGNN to generalize to unseen mixtures (and their interactions) or components, we explored three alternative data splitting methods; the results and comparison are discussed in the ESI.† All evaluation metrics are computed using the compilation of the validation data in each fold to obtain a realistic estimation of the model performance. More implementation details about training and validation can also be found in the ESI.†
Because the data sets contain a large number of binary or ternary mixtures at different compositions, it is computationally expensive to generate the corresponding molecular graphs for every training/validation instance. As a result, we designed our data loading and model training algorithm to lower the training time. Upon data set initiation, we generated and stored all 700 molecular graphs at once in a dictionary format. When a training/validation instance was passed to the algorithm, the molecular graphs were obtained from the dictionary using the index and only require simple manipulation (e.g., calculation for intermolecular H-bond) to form the desired mixture data. Doing so largely reduced redundant calculations and saved time (from days to a couple of hours).
We trained separate models for binary and ternary mixtures for simplicity and for a fair comparison between different GNN architectures. In the cases of SolvGNN and SolvGCN, the model architectures are the same (with the same number of learnable parameters) for binary and ternary mixtures given the permutation invariance nature of graph convolutions that perform node-level computation. However, in the case of SolvCAT, the model architectures vary for binary and ternary mixtures as molecule-level embeddings are concatenated together for the final inference, which results in a larger number of learnable parameters for ternary mixtures. Applying the same read-out layers to each molecule-level embedding can guarantee permutation invariance and interchangeability of binary/ternary inputs but worsens the model performance drastically, so we decided to keep the concatenation design choice for SolvCAT while augmenting the data through random permutation of component orders during training. Potentially, the binary and ternary data sets can be merged together as one data set with a single model trained to predict either case easily if we use SolvGCN or SolvGNN, but requires setting the features of one of the components to zero for binary mixtures and keeping the ternary architecture if we use SolvCAT, which may result in biased selection of the component to be masked. Therefore, the integration of binary and ternary mixtures is beyond the scope of the current project, and we would like to consider this as future work in the further development of the tool.
2.5 Counterfactual analysis
To interpret the trained model, we adapted the counterfactual framework proposed in42 to understand which chemical structures and functional groups lead to certain activity coefficient predictions. Here, we generated two types of counterfactuals for our dataset. Counterfactual Type I (eqn (7)) focused on searching for mixture samples with minimal input differences but maximal output deviations from a base mixture. Counterfactual Type II (eqn (8)) focused on the mixture samples with the maximal input differences and minimal output deviations. The similarity between mixtures similarity (mixture, mixture′) was obtained via the mean Tanimoto similarity55 of the pair, and the difference between predicted activity coefficient predictions was computed with the absolute differences (MAE) between the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi values using the trained SolvGNN denoted as
γi values using the trained SolvGNN denoted as ![[f with combining circumflex]](https://www.rsc.org/images/entities/char_0066_0302.gif) . The parameter λ is a trade-off parameter that controls the relative importance of mixture (input) similarity and prediction (outcome) difference. The parameter λ was set to 0.9 to generate Type I counterfactuals with a similarity value of at least 0.6. The search space was limited to the 700 solvents in our data set to keep the computational cost tractable, especially for Type II counterfactuals.
. The parameter λ is a trade-off parameter that controls the relative importance of mixture (input) similarity and prediction (outcome) difference. The parameter λ was set to 0.9 to generate Type I counterfactuals with a similarity value of at least 0.6. The search space was limited to the 700 solvents in our data set to keep the computational cost tractable, especially for Type II counterfactuals.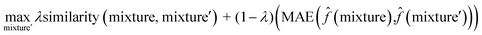 | (7) |
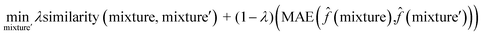 | (8) |
2.6 Phase behavior calculations
For an illustration of real-world applications, we set up a computational framework that can intake the chemical structures from diverse binary or ternary mixtures and make activity coefficient predictions with uncertainties by averaging the predicted values from individually trained SolvGNNs in each CV fold. For binary mixtures, P–x–y phase diagrams were then generated from the predicted activity coefficients γi using modified Raoult's Law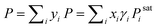 . When using modified Raoult's Law, we assume that the vapor phase is an ideal solution and that the liquid phase is incompressible with a pressure close to its saturation pressure. We also assume that the fugacity coefficients of the pure components in the vapor phase are approximately the same as the fugacity coefficients of the pure component at the saturation pressure. Such calculations make no assumptions about the ideality of the liquid phase.
. When using modified Raoult's Law, we assume that the vapor phase is an ideal solution and that the liquid phase is incompressible with a pressure close to its saturation pressure. We also assume that the fugacity coefficients of the pure components in the vapor phase are approximately the same as the fugacity coefficients of the pure component at the saturation pressure. Such calculations make no assumptions about the ideality of the liquid phase.
In this study, the saturation pressure Psati for each component was obtained using the Antoine Equation 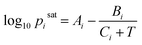 with coefficients collected from the National Institute of Standards and Technology (NIST) via web scraping.56 We sampled the liquid-phase compositions xi and calculated the equilibrium pressures P with the specified compositions at 298 K. For ternary systems, we computed phase behavior following the same method for the binary systems by sampling the mixture compositions followed by equilibrium pressure calculations.
with coefficients collected from the National Institute of Standards and Technology (NIST) via web scraping.56 We sampled the liquid-phase compositions xi and calculated the equilibrium pressures P with the specified compositions at 298 K. For ternary systems, we computed phase behavior following the same method for the binary systems by sampling the mixture compositions followed by equilibrium pressure calculations.
3 Results and discussion
3.1 Model performance on binary mixtures
We compared the three GNN architectures (SolvCAT, SolvGCN, and SolvGNN) introduced in the previous section in terms of their ability to predict the composition-dependent activity coefficients. SolvCAT takes the concatenation of mole fraction and embedded features after local graph convolutions on individual components; SolvGCN constructs a complete interaction network after local convolution without any assumptions on the edge weights for another layer of graph convolution at the global level. SolvGNN takes this SolvGCN one step further by introducing H-bond information as an example prior knowledge on intermolecular interactions for further message passing.The performance of the three GNN architectures was evaluated on the binary mixture data set by the cumulative frequency plot, as shown in Fig. 3a. The infinite dilution activity coefficients for these systems were included as extreme concentrations. More specifically, we assigned a mole fraction of 0 to the infinitely dilute component and a mole fraction of 1 to the other component (values were also reversed for each pair as well to capture both infinite dilution activity coefficients). In the cumulative frequency plot, the absolute errors of the natural logarithms of the activity coefficients, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ1 and ln
γ1 and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ2, (between true and predicted values from CV) for each data point were first averaged, and the cumulative frequencies for the averaged error values were then plotted in the ascending order. Among the three GNN architectures, SolvGNN exhibits the best performance; specifically, it shows that almost 97% of the data points are predicted with an error of less than 0.1. SolvCAT performs slightly worse, with 91% of the data points falling within the 0.1 error range. SolvGCN shows the worst performance, with only around 45% of the data points predicted with an error less than 0.1. These observations are also supported by the mean absolute errors (MAEs), which are 0.03, 0.05, and 0.31 for SolvGNN, SolvCAT, and SolvGCN (respectively). We also performed the same experiments on the binary mixture data set without infinite dilution activity coefficients, and the results are comparable (R2 = 0.98, MAE = 0.03, RMSE = 0.08; see Fig. S1†). Additionally, we developed a baseline model using XGBoost (R2 = 0.64, MAE = 0.21, RMSE = 0.50; see Fig. S2†), which was substantially less accurate than SolvGNN. These results are detailed in the ESI.†
γ2, (between true and predicted values from CV) for each data point were first averaged, and the cumulative frequencies for the averaged error values were then plotted in the ascending order. Among the three GNN architectures, SolvGNN exhibits the best performance; specifically, it shows that almost 97% of the data points are predicted with an error of less than 0.1. SolvCAT performs slightly worse, with 91% of the data points falling within the 0.1 error range. SolvGCN shows the worst performance, with only around 45% of the data points predicted with an error less than 0.1. These observations are also supported by the mean absolute errors (MAEs), which are 0.03, 0.05, and 0.31 for SolvGNN, SolvCAT, and SolvGCN (respectively). We also performed the same experiments on the binary mixture data set without infinite dilution activity coefficients, and the results are comparable (R2 = 0.98, MAE = 0.03, RMSE = 0.08; see Fig. S1†). Additionally, we developed a baseline model using XGBoost (R2 = 0.64, MAE = 0.21, RMSE = 0.50; see Fig. S2†), which was substantially less accurate than SolvGNN. These results are detailed in the ESI.†
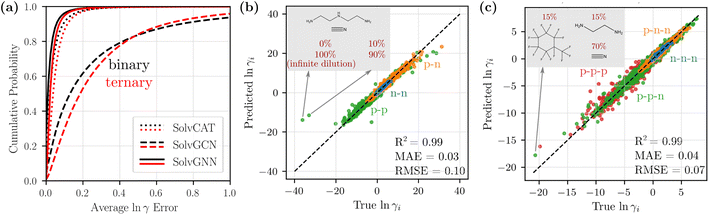 | ||
Fig. 3 Model comparison and parity plots for binary and ternary mixtures. (a) Cumulative frequency plots for the average ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi errors for binary (black) and ternary (red) mixtures to compare SolvCAT, SolvGCN, and SolvGNN. Additionally, the parity plots for individual ln γi errors for binary (black) and ternary (red) mixtures to compare SolvCAT, SolvGCN, and SolvGNN. Additionally, the parity plots for individual ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi's between the true (COSMO-RS) and predicted (SolvGNN) values from CV are displayed for binary (b) and ternary (c) mixtures. The points are colored by the type of mixtures defined in Table 1 based on polarity. γi's between the true (COSMO-RS) and predicted (SolvGNN) values from CV are displayed for binary (b) and ternary (c) mixtures. The points are colored by the type of mixtures defined in Table 1 based on polarity. | ||
The above results indicate that the inclusion of the global interaction network with H-bond information in SolvGNN provides an effective method for improving the prediction accuracy for activity coefficients. When H-bond information is excluded, the pure global graph convolution worsens the model performance, possibly due to the unbiased “averaging” without any physics-informed resemblance to intermolecular interactions. Additionally, when setting all the edge features to one in SolvGNN, the CV MAE was increased by 9% and the CV MSE was increased by 15%, suggesting the significance of the physics-informed edge features in the interaction network (more details in ESI†). The added model complexity of SolvGNN is also a decisive factor for the performance difference, since message passing enables and propagates edge features through an edge neural network. On the other hand, SolvCAT, despite the lack of explicit global graph convolution that depicts intermolecular interactions, still exhibits satisfactory predictive power. This is consistent with an earlier study,19 which has found that aggregation over latent features provides an effective approach to handle information of mixture composition. However, SolvCAT is not strictly permutation invariant to the order of the input components, even though the data were augmented by random order switching during training.
Fig. 3b shows the parity plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi's from SolvGNN for binary mixtures. All the predictions shown are from the validation process yet still exhibit high accuracy, with average ln
γi's from SolvGNN for binary mixtures. All the predictions shown are from the validation process yet still exhibit high accuracy, with average ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi MAE being 0.03 and average ln
γi MAE being 0.03 and average ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi RMSE being 0.10. The data points are colored by the mixture type defined earlier. In general, the values of ln
γi RMSE being 0.10. The data points are colored by the mixture type defined earlier. In general, the values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ for nonpolar–nonpolar interactions are close to 0 (ideal behavior) and have smaller MAE, while the values of ln
γ for nonpolar–nonpolar interactions are close to 0 (ideal behavior) and have smaller MAE, while the values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ for mixtures with polar components spread across the entire data range and have slightly larger MAE. With respect to composition, mixtures that are rich in one of the components (10%/90%) exhibit a slightly higher MAE (∼0.032), whereas the mixtures with equimolar components exhibit a relatively lower MAE (∼0.025). We also identified a couple of outliers in the plots; these mixtures contain amines with hydrogen-bonding solutes or solvents. The extreme ln
γ for mixtures with polar components spread across the entire data range and have slightly larger MAE. With respect to composition, mixtures that are rich in one of the components (10%/90%) exhibit a slightly higher MAE (∼0.032), whereas the mixtures with equimolar components exhibit a relatively lower MAE (∼0.025). We also identified a couple of outliers in the plots; these mixtures contain amines with hydrogen-bonding solutes or solvents. The extreme ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ values of these mixtures can be the result of limitations of COSMO-RS, which has been specifically noted to incorrectly simulate the interactions of secondary and tertiary amines when hydrogen-bond donors or acceptors are present in the system.57
γ values of these mixtures can be the result of limitations of COSMO-RS, which has been specifically noted to incorrectly simulate the interactions of secondary and tertiary amines when hydrogen-bond donors or acceptors are present in the system.57
Besides the regular CV using stratified sampling that relies on the type of mixture, we also tested the generalizability of the SolvGNN using an alternative CV method. Here, for each CV fold, we trained the model on only two of the three mixture types (polar–polar, polar–nonpolar, or nonpolar–nonpolar; see Table 1) and validated the rest. Results have shown that, although the model could achieve similar training losses to the regular CV, the validation accuracy was reduced accordingly. For the case where we trained the model with polar–polar and polar-nonpolar mixtures (94% of the data set) while validating on nonpolar–nonpolar mixtures, the model demonstrated suitable transferability by comparable validation losses (MAE = 0.04). However, when we trained the model on only polar–polar and nonpolar–nonpolar samples (64%) while validating on polar-nonpolar samples, the validation MAE increased by 0.16, which indicates the distinct nature of polar–nonpolar interactions and suggests that it is non-trivial and therefore cannot be omitted during model training. Additionally, we examined the condition when the model was trained on only polar–nonpolar and nonpolar–nonpolar mixtures (42%) and validated on polar–polar mixtures. The convergence plot (Fig. S3†) indicates over-training with high validation losses; such behavior was expected because the training size is less than half of the data set, and the majority of the training samples lack H-bond acceptors or donors, which are present in most of the validation set. This result again suggests that polar–polar and polar–nonpolar mixtures, despite possessing strong intermolecular interactions such as H-bonding in both cases, are intrinsically different and therefore are both required in the training process. These results are in general agreement with chemical intuition.
To further demonstrate the generalizability of the proposed SolvGNN, we conducted two additional data splitting methods that enforce all validation data to be unseen systems or components. sFor both experiments, SolvGNN still outperforms other architectures and still exhibits strong predictive performance based on the parity plots (detailed in the ESI†).
3.2 Scale up to ternary mixtures
We next scaled up the proposed SolvGNN architecture to ternary mixtures. As shown in Fig. 3a (red), the cumulative frequency of the average ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ errors demonstrates similar trends as in binary mixtures. SolvGNN provides the best model performance, followed by SolvCAT and SolvGCN. Here, we observed that the gaps between the curves appear wider, suggesting a more significant advantage of SolvGNN over SolvCAT and SolvGCN. For SolvGNN, more than 94% of the data points were predicted with an error less than 0.1. SolvCAT was the second-most accurate model, with around 86% of the data points falling within the 0.1 error range, showing a more notable performance drop (8%) than the results for binary mixtures (6%). SolvGCN continues to exhibit the worst performance, and only around 30% of the data points are predicted with an error less than 0.1. These observations are supported by MAE values, which are 0.04, 0.06, and 0.30 for SolvGNN, SolvCAT, and SolvGCN.
γ errors demonstrates similar trends as in binary mixtures. SolvGNN provides the best model performance, followed by SolvCAT and SolvGCN. Here, we observed that the gaps between the curves appear wider, suggesting a more significant advantage of SolvGNN over SolvCAT and SolvGCN. For SolvGNN, more than 94% of the data points were predicted with an error less than 0.1. SolvCAT was the second-most accurate model, with around 86% of the data points falling within the 0.1 error range, showing a more notable performance drop (8%) than the results for binary mixtures (6%). SolvGCN continues to exhibit the worst performance, and only around 30% of the data points are predicted with an error less than 0.1. These observations are supported by MAE values, which are 0.04, 0.06, and 0.30 for SolvGNN, SolvCAT, and SolvGCN.
For SolvGNN, comparable model accuracy was obtained even though the number of training/validation samples was reduced for the ternary mixture data set compared to the binary mixture data set, as shown in Fig. 3c. The CV R2, MAE, and RMSE are similar to the results from binary systems, with corresponding values around 0.99, 0.03, and 0.10. When breaking down the predicted values based on the mixture type, we found that samples containing only nonpolar components tend to have smaller errors and systems containing only polar components have larger errors. Mixtures with both polar and non–polar components have MAEs and RMSEs lying somewhere in between the extremes. When grouping by composition, mixtures that are rich in one of the components tend to have slightly higher prediction errors than equimolar mixtures. This observation is consistent with model performance on binary mixtures without infinite dilution data and could be caused by the fact that the majority of the training data are not equimolar systems.
Overall, SolvGNN exhibited satisfactory performance in making predictions for activity coefficients of binary and ternary systems, given the advantage of explicitly including H-bond information (as a representative and primary intermolecule force) via global message passing on the molecular interaction network. To the best of our knowledge, this is the first time that such a graph-based architecture (permutation invariant to the component order) is used to make predictions for composition-dependent activity coefficients (compared to models that predict infinite-dilution activity coefficients only) and for ternary systems (compared to binary systems).
3.3 Comparison to previous GNN for infinite-dilution activity coefficients
To compare SolvGNN with a recently developed GNN for infinite dilution activity coefficient (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞) prediction by Medina et al.,29 we conducted a benchmark of our model on the same experimental data set used in their study, which contains 2,810 binary mixtures (with specific solute/solvent assignment) and values of ln
γ∞) prediction by Medina et al.,29 we conducted a benchmark of our model on the same experimental data set used in their study, which contains 2,810 binary mixtures (with specific solute/solvent assignment) and values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞ for the solute. To conduct a fair comparison, we applied the same training/validation/testing method described in their research29 through ensemble learning (bagging), which splits the training/validation data randomly 30 times and averages the predictions. We also used the same batch size (32) and epoch number (200). Although the logarithmic values were used to train and validate the models, Medina et al.29 calculated the evaluation metrics on the unscaled γ∞ values. The error score functions are detailed in ESI.† For an easy comparison, we applied the same conversion to our data and summarized the results in Table 2 for a comparison of the test data. We observed that the performance of SolvGNN is better than the previous GNN model29 for ln
γ∞ for the solute. To conduct a fair comparison, we applied the same training/validation/testing method described in their research29 through ensemble learning (bagging), which splits the training/validation data randomly 30 times and averages the predictions. We also used the same batch size (32) and epoch number (200). Although the logarithmic values were used to train and validate the models, Medina et al.29 calculated the evaluation metrics on the unscaled γ∞ values. The error score functions are detailed in ESI.† For an easy comparison, we applied the same conversion to our data and summarized the results in Table 2 for a comparison of the test data. We observed that the performance of SolvGNN is better than the previous GNN model29 for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞ prediction. The proposed SolvGNN shows improvements in all metrics used to evaluate the model in the original paper, including a significant decrease in the mean absolute percent error (MAPE) by 50%.
γ∞ prediction. The proposed SolvGNN shows improvements in all metrics used to evaluate the model in the original paper, including a significant decrease in the mean absolute percent error (MAPE) by 50%.
| Model | MAE | SDEP | MSE | RMSE | MAPE | R 2 |
|---|---|---|---|---|---|---|
| Previous GNN29 | 3.91 | 26.73 | 729.69 | 27.01 | 22.66 | 0.82 |
| SolvGNN | 3.25 | 19.52 | 391.45 | 19.79 | 11.40 | 0.89 |
| % Difference | −17% | −27% | −46% | −27% | −50% | +9% |
In general, our results provide evidence that SolvGNN can be used to predict infinite-dilution activity coefficients in a satisfactory manner, thus illustrating that the architecture is versatile. Comparison of the evaluation metrics indicates that there is a benefit in including intermolecular interactions in the GNN architecture. These results also provide evidence that the SolvGNN architecture can be used to learn not only from simulation data (e.g., COSMO-RS) but also from experimental data.
3.4 Counterfactual analysis
We derived counterfactuals42 as a way to provide some interpretability to SolvGNN predictions. Here, we investigated two types of counterfactuals: mixtures with the highest similarity yet the most different predictions (Type I), and mixtures with the lowest similarity yet the most similar predictions (Type II). As illustrated in Fig. 4, we started with a base mixture (50% benzene and 50% toluene) that exhibits nearly ideal behavior (γi = 1 for both components). Since input chemical ratios are also a contributing factor to activity coefficients, we first identified the composition with the same two molecular species that leads to the farthest deviation in activity coefficients, as illustrated by counterfactual 1. We found that increasing the composition in benzene to the extreme has the most significant impact on activity coefficients, although the deviation from ideal behavior is still small. Next, we fixed one of the components and varied the other to find the mixture with the highest structural resemblance yet the most dissimilar activity coefficients, illustrated by counterfactual 2 and counterfactual 3. When fixing benzene, counterfactual 2 shows that replacing the methyl group with a hydroxyl group, coupled with a change in composition, largely influences activity coefficients. This can be explained by the fact that removing the methyl group converts one of the components from nonpolar to polar, thus resulting in strong deviations from ideal behavior. Counterfactual 3 shows a similar tendency. When fixing toluene, the other component in the counterfactual tends to converge to a more polar chemical, such as pyridine which converts one of the carbons on the benzene ring to nitrogen.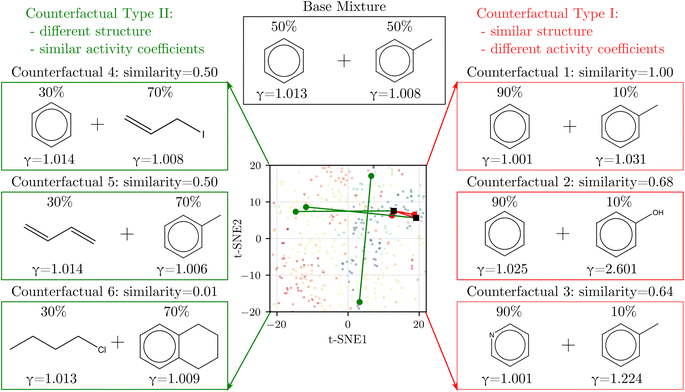 | ||
| Fig. 4 Counterfactual analysis. Type I (red) shows mixtures with the most similar structures but the most different activity coefficients from the base mixture whereas Type II (green) shows the opposite. The corresponding solvents are labeled on the 2D t-SNE map introduced in Fig. 1 to help illustrate similarity. | ||
On the other hand, Type II counterfactuals also reveal interesting trends to identify mixtures with dissimilar chemical structures but similar γi's. When fixing one of the components, counterfactuals 4 and 5 both acquire an alternative component that is nonpolar. In both cases, one of the aromatic components is replaced by a non-aromatic structure as the result of the effort to minimize similarity, but since the replacement is also nonpolar, the mixtures exhibit near-ideal behavior as reflected by the activity coefficients. Lastly, when we relaxed the constraint and allowed both components to vary, counterfactual 6 picks out the mixture from the data set that shows two nonpolar yet unlike chemical structures with near-ideal behavior.
In general, the counterfactual analysis has shown coherent physical insights regarding how compositions and structural features may lead to variations in activity coefficient, and these findings in turn agree with our chemical understanding of mixture behavior. Such interpretation, especially Type II counterfactuals, can be used to apply SolvGNN to procedures such as the selection of a candidate good solvent for a desired solute. For example, counterfactuals could be used to identify an antisolvent given a known good solvent for a specific polymer for polymer recycling applications.58,59 The antisolvent is expected to be miscible with the solvent while immiscible with the polymer, and therefore counterfactual Type I may be identified as the candidate antisolvent.
3.5 From activity coefficients to phase behavior
We next sought to utilize the activity coefficients obtained from SolvGNN to predict relevant phase behavior (e.g., azeotrope compositions). Therefore, we further developed a framework to generate phase diagrams directly from chemical structures using the trained SolvGNN. These results aim to show the potential use of SolvGNN in industrially-relevant applications or experimental studies (e.g., miscibility or separation of target components). The framework uniformly samples the compositions of the input mixtures and predicts the corresponding activity coefficients using SolvGNN, which are then used for calculating equilibrium bubble and dew pressures via modified Raoult's Law. Fig. 5 showcases several P–x–y phase diagrams generated from the framework for binary mixtures. We would like to point out that most of the shown mixtures (all except for water–methanol) are not in our training or validation data, so they can be viewed as additional test instances, in spite of the fact that they are commonly used as mixture examples with contrasting equilibrium behavior.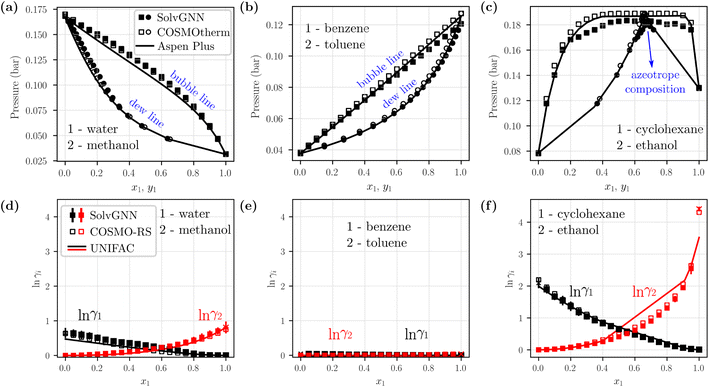 | ||
Fig. 5 Example phase diagrams generated from SolvGNN. (a–c) P–x–y diagrams of three binary mixtures, each representing a different type of mixture (polar–polar, nonpolar–nonpolar, and polar–nonpolar). The equilibrium pressure is computed with modified Raoult's Law using the predicted activity coefficients from SolvGNN. The phase diagrams are compared with those generated from two other state-of-the-art tools, including COSMOtherm that implements COSMO-RS57 and Aspen Plus that implements UNIFAC60 (as well as other activity models61–65). The vapor compositions (yi) are represented as circles and liquid compositions (xi) are represented as squares. (d–f) Predicted activity coefficients for individual components at different compositions from SolvGNN, COSMOtherm, and Aspen. “x” denotes activity coefficients at infinite dilution. In all phase diagram calculations, the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi's are obtained by averaging the predictions of SolvGNN trained from each CV fold, and the standard deviations are visualized as the error bars. γi's are obtained by averaging the predictions of SolvGNN trained from each CV fold, and the standard deviations are visualized as the error bars. | ||
Fig. 5a–c includes representative example phase diagrams of polar–polar, nonpolar–nonpolar, and polar–nonpolar binary mixtures. At 298 K, a water–methanol mixture deviates positively from ideal solution behavior and shows higher equilibrium bubble pressure as a result of unfavorable unlike-molecule interactions. By contrast, a benzene–toluene mixture exhibits near-ideal behavior, as indicated by a bubble line that is almost linear, which suggests a homogeneous solution where molecular interactions between like and unlike components are viewed the same. Additionally, we showcase a cyclohexane-ethanol mixture that forms an azeotrope, which was successfully identified by SolvGNN, and the predicted azeotrope composition (xcyclohexane ∼0.65) is consistent with the estimates from COSMOtherm (COSMO-RS) and Aspen Plus (UNIFAC). In all three cases, the predicted phase diagrams obtained by SolvGNN are consistent with the phase diagrams generated using COSMOtherm (COSMO-RS) or Aspen Plus (UNIFAC), and the MAE values in the equilibrium pressure range from 0.001 to 0.004 bar. We also observed that, compared to Aspen Plus (UNIFAC), SolvGNN tends to underestimate equilibrium pressure values, whereas COSMOtherm tends to overestimate these values. Upon inspecting the activity coefficients for the sample mixtures (Fig. 5d–f), we found that, although the activity coefficients were trained only on four compositions plus infinite dilution, SolvGNN was able to make relatively accurate predictions for compositions in a continuous space. We also compared experimental equilibrium data66 for cyclohexane-ethanol at similar temperatures for which data are available (293 K and 303 K) and found similar behavior and a similar azeotrope composition; these data as well as a few additional phase diagram examples along with their activity coefficient predictions are shown in ESI.†
Next, we computed vapor-liquid equilibrium (VLE) data for a ternary mixture of water–acetone–methyl isobutyl ketone (MIBK). Similar to the phase diagram calculations for binary systems, we sampled different liquid compositions and calculated the equilibrium pressures using modified Raoult's Law. For simplicity, we picked two pressures and computed corresponding liquid and vapor compositions; numerical comparisons between SolvGNN and COSMOtherm (COSMO-RS) are summarized in Table S4.† For the selected pressures, the predicted vapor-phase compositions (yi) have an MAE around 0.02 when comparing SolvGNN predictions to COSMOtherm data.
In summary, we were able to create binary phase diagrams (at 298 K) with a full range of compositions using SolvGNN that was only trained on a few sampled input ratios. The provided framework has shown great potential for high-throughput screening of mixtures for use cases including azeotrope identification and non-ideal behavior investigation for liquid mixtures. Incorporating SolvGNN into such phase equilibrium calculations bypasses the need to identify functional groups with human expertise and obtain interaction parameters (as needed in UNIFAC) or to conduct DFT calculations (as needed in COSMO-RS), especially when the chemicals in a mixture are relatively uncommon. Moreover, this framework could be used in conjunction with open-source process models (e.g., BioSteam67) as an addition to the existing computational models (e.g., UNIFAC) for generating thermodynamic data.
4 Conclusions and future outlook
We developed a GNN architecture (SolvGNN) that incorporates both local (intramolecular) and global (intermolecular) convolutions on graph representations and used this for predicting activity coefficients of solvent mixtures. SolvGNN explicitly integrates intermolecular interactions through the construction of the molecular interaction network that encodes H-bonding information. We found that with such feature embedding, SolvGNN can successfully estimate the activity coefficients that vary with chemical compositions for binary as well as ternary mixtures, which has not been explored much under the hood of ML, especially in the context of activity coefficients.Compared to the current state-of-the-art approach for general activity coefficient estimations (e.g., UNIFAC and COSMO-RS), SolvGNN achieves comparable model performance and is easy to use without any additional calculations for missing parameters or DFT. We also benchmarked SolvGNN on the same experimental dataset that was used in an earlier study for developing a GNN that predicts only the infinite-dilution activity coefficients of binary mixtures;29 SolvGNN outperforms the previously developed GNN in almost all evaluation metrics, proving the importance to use prior knowledge (in this case explicit topological prior pertinent to intermolecular interactions) when designing GNN architectures. These findings demonstrate the ability of SolvGNN to learn from simulation (e.g., COSMO-RS) and experimental data.
Moreover, we provided an open-source computational tool for creating phase diagrams (P–x–y) using SolvGNN as an example to show its potential for real-world applications. The generated phase diagrams were consistent with those obtained from COSMOtherm and Aspen Plus (with the selection of UNIFAC as the thermodynamic method), which further illustrated the generalization ability of SolvGNN that was only trained on a minimal subset of composition cases. Besides phase diagrams, we provided algorithms to obtain counterfactuals to aid model interpretation, which may help extract physical insights that are less known and help design solvent mixtures.
The architecture and study can be expanded in a number of ways. For example, so far we have only obtained activity coefficients at room temperature, and thus SolvGNN does not have temperature dependence. However, obtaining temperature-dependent activity coefficients from COSMO-RS and re-training SolvGNN with an additional temperature variable would be a relatively trivial, given that the computational framework is in place. Another limitation for phase equilibrium predictions is related to the availability of Antoine coefficients; in circumstances where Antoine coefficients are missing e.g., no measurements for the substance or outside of the temperature range, we cannot compute the corresponding phase diagrams. A potential solution could be to develop another GNN architecture for Antoine coefficient predictions or expand the output dimension of our current SolvGNN to make these predictions. Additionally, since the model weights that are related to concentrations are not constrained, unphysical activity coefficient trend may be present from the current SolvGNN predictions. This issue may be addressed in future studies through conditioning constraints on the model weights or theory-infused network architecture. Furthermore, the presented counterfactual analysis only searches the chemical space within the data set, and therefore to obtain more meaningful results, we will adapt some of the more established chemical search algorithms42,68 that have been designed for single chemicals to the case of mixtures. Future studies will also explore the use of SolvGNN for other mixture properties and investigate different possible representations of intermolecular interactions (e.g., Lennard-Jones potentials as additional edge features or replacing edge features by molecular-level node features). We are also interested in using these types of architectures to design solvents that can selectively solubilize target molecules in combination with generative models.69–71
Data availability
All data and scripts are available as open-source code at https://github.com/zavalab/ML/tree/SolvGNN.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based on work supported by the U.S. Department of Energy (DOE), Office of Science, Office of Advanced Scientific Computing Research, under Contract DE-AC02-06CH11357.References
- J. Huuskonen, M. Salo and J. Taskinen, Aqueous solubility prediction of drugs based on molecular topology and neural network modeling, J. Chem. Inf. Model., 1998, 38(3), 450–456 CrossRef CAS PubMed.
- A. Lusci, G. Pollastri and P. Baldi, Deep architectures and deep learning in chemoinformatics: the prediction of aqueous solubility for drug-like molecules, J. Chem. Inf. Model., 2013, 53(7), 1563–1575 CrossRef CAS PubMed.
- S. Boobier, D. R. Hose, A. J. Blacker and B. N. Nguyen, Machine learning with physicochemical relationships: solubility prediction in organic solvents and water, Nat. Commun., 2020, 11(1), 1–10 CrossRef PubMed.
- A. Mayr, G. Klambauer, T. Unterthiner and S. Hochreiter, DeepTox: toxicity prediction using deep learning, Front. Environ. Sci., 2016, 3, 80 Search PubMed.
- P. Banerjee, A. O. Eckert, A. K. Schrey and R. Preissner, ProTox-II: a webserver for the prediction of toxicity of chemicals, Nucleic Acids Res., 2018, 46(W1), W257–W263 CrossRef CAS PubMed.
- J. Jiang, R. Wang and G. W. Wei, GGL-Tox: Geometric Graph Learning for Toxicity Prediction, J. Chem. Inf. Model., 2021, 61(4), 1691–1700 CrossRef CAS PubMed.
- T. Schroeter, A. Schwaighofer, S. Mika, A. Ter Laak, D. Suelzle and U. Ganzer, et al., Machine learning models for lipophilicity and their domain of applicability, Mol. Pharmaceutics, 2007, 4(4), 524–538 CrossRef CAS PubMed.
- B. Tang, S. T. Kramer, M. Fang, Y. Qiu, Z. Wu and D. Xu, A self-attention based message passing neural network for predicting molecular lipophilicity and aqueous solubility, J. Cheminf., 2020, 12(1), 1–9 Search PubMed.
- H. L. Morgan, The generation of a unique machine description for chemical structures-a technique developed at chemical abstracts service, J. Chem. Doc., 1965, 5(2), 107–113 CrossRef CAS.
- D. Rogers and M. Hahn, Extended-connectivity fingerprints, J. Chem. Inf. Model., 2010, 50(5), 742–754 CrossRef CAS PubMed.
- M. Karelson, V. S. Lobanov and A. R. Katritzky, Quantum-chemical descriptors in QSAR/QSPR studies, Chem. Rev., 1996, 96(3), 1027–1044 CrossRef CAS PubMed.
- H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, Mordred: a molecular descriptor calculator, J. Cheminf., 2018, 10(1), 1–14 Search PubMed.
- Y. C. Lo, S. E. Rensi, W. Torng and R. B. Altman, Machine learning in chemoinformatics and drug discovery, Drug discovery today, 2018, 23(8), 1538–1546 CrossRef CAS PubMed.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, Neural networks for the prediction of organic chemistry reactions, ACS Cent. Sci., 2016, 2(10), 725–732 CrossRef CAS PubMed.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola and W. H. Green, et al., A graph-convolutional neural network model for the prediction of chemical reactivity, Chem. Sci., 2019, 10(2), 370–377 RSC.
- A. R. Natarajan and A. Van der Ven, Machine-learning the configurational energy of multicomponent crystalline solids, npj Comput. Mater., 2018, 4(1), 1–7 CrossRef.
- X. Liu, X. Li, Q. He, D. Liang, Z. Zhou and J. Ma, et al., Machine learning-based glass formation prediction in multicomponent alloys, Acta Mater., 2020, 201, 182–190 CrossRef CAS.
- L. Wilbraham, R. S. Sprick, K. E. Jelfs and M. A. Zwijnenburg, Mapping binary copolymer property space with neural networks, Chem. Sci., 2019, 10(19), 4973–4984 RSC.
- K. Hanaoka, Deep Neural Networks for Multicomponent Molecular Systems, ACS Omega, 2020, 5(33), 21042–21053 CrossRef CAS PubMed.
- I. Nakamura, Phase diagrams of polymer-containing liquid mixtures with a theory-embedded neural network, New J. Phys., 2020, 22(1), 015001 CrossRef.
- Y. Pan, X. Ji, L. Ding and J. Jiang, Prediction of lower flammability limits for binary hydrocarbon gases by quantitative structure—property relationship approach, Molecules, 2019, 24(4), 748 CrossRef CAS PubMed.
- S. Ajmani, S. C. Rogers, M. H. Barley and D. J. Livingstone, Application of QSPR to mixtures, J. Chem. Inf. Model., 2006, 46(5), 2043–2055 CrossRef CAS PubMed.
- A. R. Katritzky, I. B. Stoyanova-Slavova, K. Tämm, T. Tamm and M. Karelson, Application of the QSPR Approach to the Boiling Points of Azeotropes, J. Phys. Chem. A, 2011, 115(15), 3475–3479 CrossRef CAS PubMed.
- A. A. Oliferenko, P. V. Oliferenko, J. S. Torrecilla and A. R. Katritzky, Boiling points of ternary azeotropic mixtures modeled with the use of the universal solvation equation and neural networks, Ind. Eng. Chem. Res., 2012, 51(26), 9123–9128 CrossRef CAS.
- T. Wang, L. Tang, F. Luan and M. Cordeiro, Prediction of the toxicity of binary mixtures by QSAR approach using the hypothetical descriptors, Int. J. Mol. Sci., 2018, 19(11), 3423 CrossRef PubMed.
- G. Fayet and P. Rotureau, New QSPR Models to predict the flammability of binary liquid mixtures, Mol. Inf., 2019, 38(8–9), 1800122 CrossRef CAS PubMed.
- S. Chinta and R. Rengaswamy, Machine learning derived quantitative structure property relationship (QSPR) to predict drug solubility in binary solvent systems, Ind. Eng. Chem. Res., 2019, 58(8), 3082–3092 CrossRef CAS.
- F. Jirasek, R. A. Alves, J. Damay, R. A. Vandermeulen, R. Bamler and M. Bortz, et al., Machine learning in thermodynamics: Prediction of activity coefficients by matrix completion, J. Phys. Chem. Lett., 2020, 11(3), 981–985 CrossRef CAS PubMed.
- E. I. S. Medina, S. Linke, M. Stoll and K. Sundmacher, Graph Neural Networks for the prediction of infinite dilution activity coefficients, Digital Discovery, 2022 Search PubMed.
- B. Winter, C. Winter, J. Schilling, and A. Bardow. A smile is all you need: Predicting limiting activity coefficients from SMILES with natural language processing, 2022, preprint arXiv:220607048 Search PubMed.
- J. G. Rittig, K. B. Hicham, A. M. Schweidtmann, M. Dahmen, and A. Mitsos. Graph Neural Networks for Temperature-Dependent Activity Coefficient Prediction of Solutes in Ionic Liquids, 2022, preprint arXiv:220611776 Search PubMed.
- B. Winter, C. Winter, T. Esper, J. Schilling, A. Bardow. SPT-NRTL: A physics-guided machine learning model to predict thermodynamically consistent activity coefficients, 2022, arXiv, https://arxiv.org/abs/2209.04135 Search PubMed.
- F. Jirasek, R. Bamler, S. Fellenz, M. Bortz, M. Kloft and S. Mandt, et al., Making thermodynamic models of mixtures predictive by machine learning: matrix completion of pair interactions, Chem. Sci., 2022, 13(17), 4854–4862 RSC.
- D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel and A. Aspuru-Guzik, et al., Convolutional networks on graphs for learning molecular fingerprints, Adv. Neural Inf. Process Syst., 2015, 28 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl. Neural message passing for quantum chemistry, In, International Conference on Machine Learning, PMLR, 2017, pp. 1263–1272 Search PubMed.
- J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang and Z. Liu, et al., Graph neural networks: a review of methods and applications, AI Open, 2020, 1, 57–81 CrossRef.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse and A. S. Pappu, et al., MoleculeNet: a benchmark for molecular machine learning, Chem. Sci., 2018, 9(2), 513–530 RSC.
- S. Qin, T. Jin, R. C. Van Lehn and V. M. Zavala, Predicting Critical Micelle Concentrations for Surfactants using Graph Convolutional Neural Networks, J. Phys. Chem. B, 2021, 125(37), 10610–10620 CrossRef CAS PubMed.
- H. C. Carlson and A. P. Colburn, Vapor-liquid equilibria of nonideal solutions, Ind. Eng. Chem., 1942, 34(5), 581–589 CrossRef CAS.
- J. Damay, F. Jirasek, M. Kloft, M. Bortz and H. Hasse, Predicting Activity Coefficients at Infinite Dilution for Varying Temperatures by Matrix Completion, Ind. Eng. Chem. Res., 2021, 60(40), 14564–14578 CrossRef CAS.
- H. Benimam, C. Si-Moussa, M. Laidi and S. Hanini, Modeling the activity coefficient at infinite dilution of water in ionic liquids using artificial neural networks and support vector machines, Neural. Comput. Appl., 2020, 32(12), 8635–8653 CrossRef.
- G. P. Wellawatte, A. Seshadri and A. D. White, Model agnostic generation of counterfactual explanations for molecules, Chem. Sci., 2022 Search PubMed.
- C. M. Hansen, Hansen solubility parameters: a user's handbook, CRC press, 2007 Search PubMed.
- L. Van der Maaten and G. Hinton, Visualizing data using t-SNE, J. Mach. Learn. Res., 2008, 9(11) Search PubMed.
- G. Landrum, Rdkit documentation. Release., 2013, 1(1–79), 4 Search PubMed.
- A. Klamt, Conductor-like screening model for real solvents: a new approach to the quantitative calculation of solvation phenomena, J. Phys. Chem., 1995, 99(7), 2224–2235 CrossRef CAS.
- COSMOtherm R. 19, COSMOlogic GmbH & Co. KG, 2019.
- NCI/Cadd Chemical identifier resolver, U.S. Department of Health and Human Services, https://cactus.nci.nih.gov/chemical/structure.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank and Y. J. Franzke, et al., TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations, J. Chem. Phys., 2020, 152(18), 184107 CrossRef CAS PubMed.
- M. Li, J. Zhou, J. Hu, W. Fan, Y. Zhang and Y. Gu, et al., Dgl-lifesci: An open-source toolkit for deep learning on graphs in life science, ACS Omega, 2021, 6(41), 27233–27238 CrossRef CAS PubMed.
- T. N. Kipf, M. Welling. Semi-supervised classification with graph convolutional networks, arXiv, 2016, preprint arXiv:160902907 Search PubMed.
- K. Cho, B. Van Merriënboer, D. Bahdanau, Y. Bengio. On the properties of neural machine translation: Encoder-decoder approaches, 2014, preprint arXiv:14091259 Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury and G. Chanan, et al., Pytorch: an imperative style, high-performance deep learning library, Adv. Neural Inf. Process Syst., 2019, 32 Search PubMed.
- M. Wang, D. Zheng, Z. Ye, Q. Gan, M. Li, and X. Song, et al.Deep graph library: A graph-centric, highly-performant package for graph neural networks, 2019, preprint arXiv:190901315 Search PubMed.
- D. Bajusz, A. Rácz and K. Héberger, Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations?, J. Cheminf., 2015, 7(1), 1–13 CAS.
- O. Contreras, NIST-web-book-scraping, GitHub, 2019, https://github.com/oscarcontrerasnavas/NIST-web-book-scraping Search PubMed.
- A. Klamt, F. Eckert and W. Arlt, COSMO-RS: an alternative to simulation for calculating thermodynamic properties of liquid mixtures, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 101–122 CrossRef CAS PubMed.
- T. W. Walker, N. Frelka, Z. Shen, A. K. Chew, J. Banick and S. Grey, et al., Recycling of multilayer plastic packaging materials by solvent-targeted recovery and precipitation, Sci. Adv., 2020, 6(47), eaba7599 CrossRef PubMed.
- P. Zhou, K. L. Sánchez-Rivera, G. W. Huber and R. C. Van Lehn, Computational Approach for Rapidly Predicting Temperature-Dependent Polymer Solubilities Using Molecular-Scale Models, ChemSusChem, 2021, 14(19), 4307–4316 CrossRef CAS PubMed.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE J., 1975, 21(6), 1086–1099 CrossRef CAS.
- M. Margules, On the composition of saturated vapors of mixtures, Akad. Wiss. Wien, Math.-Naturwiss. Kl., 1895, 104, 1234–1239 Search PubMed.
- J. Van Laar, Über dampfspannungen von binären gemischen, Z. Phys. Chem., 1910, 72(1), 723–751 CrossRef CAS.
- G. M. Wilson, Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing, J. Am. Chem. Soc., 1964, 86(2), 127–130 CrossRef CAS.
- H. Renon and J. Prausnitz, Estimation of parameters for the NRTL equation for excess Gibbs energies of strongly nonideal liquid mixtures, Ind. Eng. Chem. Process Des. Dev., 1969, 8(3), 413–419 CrossRef CAS.
- D. S. Abrams and J. M. Prausnitz, Statistical thermodynamics of liquid mixtures: a new expression for the excess Gibbs energy of partly or completely miscible systems, AIChE J., 1975, 21(1), 116–128 CrossRef CAS.
- Dortmund Data Bank, Dortmund Data Bank, 2022, https://www.ddbst.com.
- Y. Cortes-Peña, D. Kumar, V. Singh and J. S. Guest, BioSTEAM: a fast and flexible platform for the design, simulation, and techno-economic analysis of biorefineries under uncertainty, ACS Sustainable Chem. Eng., 2020, 8(8), 3302–3310 CrossRef.
- A. Nigam, R. Pollice, M. Krenn, G. dos Passos Gomes and A. Aspuru-Guzik, Beyond generative models: superfast traversal, optimization, novelty, exploration and discovery (STONED) algorithm for molecules using SELFIES, Chem. Sci., 2021, 12(20), 7079–7090 RSC.
- T. Shen. Semi-Supervised Junction Tree Variational Autoencoder for Molecular Property Prediction, 2022, preprint, arXiv:220805119 Search PubMed.
- E. Bengio, M. Jain, M. Korablyov, D. Precup and Y. Bengio, Flow network based generative models for non-iterative diverse candidate generation, Adv. Neural Inf. Process Syst, 2021, 34, 27381–27394 Search PubMed.
- W. Jin, R. Barzilay, and T. Jaakkola. Junction tree variational autoencoder for molecular graph generation, In, International conference on machine learning. PMLR, 2018, pp. 2323–2332 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00045h |
| This journal is © The Royal Society of Chemistry 2023 |