Open Access Article
Open Access ArticlePredictive stochastic analysis of massive filter-based electrochemical reaction networks†
Daniel
Barter‡
a,
Evan Walter
Clark Spotte-Smith‡
 bc,
Nikita S.
Redkar
cd,
Aniruddh
Khanwale
bce,
Shyam
Dwaraknath
bc,
Nikita S.
Redkar
cd,
Aniruddh
Khanwale
bce,
Shyam
Dwaraknath
 f,
Kristin A.
Persson
f,
Kristin A.
Persson
 bg and
Samuel M.
Blau
bg and
Samuel M.
Blau
 *a
*a
aEnergy Technologies Area, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: smblau@lbl.gov
bDepartment of Materials Science and Engineering, University of California, Berkeley, CA 94720, USA
cMaterials Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
dDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, CA 94720, USA
eDepartment of Electrical Engineering and Computer Science, University of California, Berkeley, CA 94720, USA
fLuxembourg Institute of Science and Technology, Luxembourg
gMolecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 30th November 2022
Abstract
Chemical reaction networks (CRNs) are powerful tools for obtaining insight into complex reactive processes. However, they are difficult to employ in domains such as electrochemistry where reaction mechanisms and outcomes are not well understood. To overcome these limitations, we report new methods to assist in CRN construction and analysis. Beginning with a known set of potentially relevant species, we enumerate and then filter all stoichiometrically valid reactions, constructing CRNs without reaction templates. By applying efficient stochastic algorithms, we can then interrogate CRNs to predict network products and reveal reaction pathways to species of interest. We apply this methodology to study solid-electrolyte interphase (SEI) formation in Li-ion batteries, automatically recovering products from the literature and predicting previously unknown species. We validate these results by combining CRN-predicted pathways with first-principles mechanistic analysis, discovering novel mechanisms which could realistically contribute to SEI formation. This methodology enables the exploration of vast chemical spaces, with the potential for applications throughout electrochemistry.
Introduction
Electrochemistry has the power to unlock extremely useful reactions that are otherwise inaccessible. To design next-generation electrochemical technologies – ranging from batteries and fuel cells to electrosynthesis of value-added products – it is imperative to understand and eventually control reactions on the molecular level. Traditionally, studies of (electro)chemical reactivity have been conducted by hand using either trial-and-error experiments or low-throughput molecular simulations. Recent years have seen the development of a range of computational methods to automatically explore chemical reaction networks (CRNs),1,2 which are defined by a set of reactions R between species S. CRNs can facilitate the rapid discovery of key species and reactions in complex systems with minimal manual intervention. However, standard CRN approaches have thus far not been capable of describing electrochemical systems.CRNs are often generated3 by applying quantum chemical methods to explore a potential energy surface (PES).4 PES exploration techniques – including ab initio molecular dynamics,5 artificial force-induced reactions,6 and stochastic surface walking,7 among others – are useful for exploring a chemical space. PES exploration requires minimal initial information (e.g. a set of initial species) and allows for the identification of intermediates, reactive products, and elementary reaction steps (including energy barriers). Unfortunately, PES exploration techniques typically suffer from prohibitively high cost, limiting their application to simple systems involving only small molecules or exploring reactivity over very short (∼10 ps) time scales. While applications of semi-empirical methods8,9 and machine learning10,11 could soon alleviate this limitation in some domains, the ongoing challenges in simulating electrochemical dynamics even for simple systems (e.g. the hydrogen evolution reaction)12 suggest that PES exploration remains unsuitable for studies of complex electrochemistry.
When PES exploration is not used, CRNs are most commonly constructed based on human chemical intuition. By applying reaction templates to include only commonly observed mechanisms13–17 or pruning by the “chemical distance” between species (the number of bonds that must change for a reaction to occur, or the number of reactions required to transform reactants to products) to focus only on starting species and known products of interest,18 it is possible to create networks capable of elucidating reaction pathways. However, chemical intuition is limited and unreliable when describing new reactive spaces.19 In electrochemistry, studies of reaction mechanisms20,21 and characterization of reaction products22 are very challenging. Additionally, the linear scaling relations (i.e. Bell–Evans–Polanyi23,24) that are widely used to predict the rates of families of similar reactions in thermochemistry have not been well established in electrochemistry. As a result, CRN methods that rely on templates or the chemical distance to known products cannot yet be used to study electrochemical reactivity.
Aiming to bypass both the cost of PES exploration and the intuition required for template-based CRN generation, we recently developed the first method to construct and analyze electrochemical CRNs, which we used to study the formation of the solid electrolyte interphase (SEI) in lithium-ion batteries. After generating graph-based CRNs containing thousands of species and millions of reactions, we used shortest-path algorithms to identify optimal pathways to two key SEI products, lithium ethylene dicarbonate (LEDC)25 and lithium ethylene monocarbonate (LEMC).26 With this approach, we recovered known and proposed reaction mechanisms and predicted pathways that had not been previously reported.
In our prior work, the networks that we studied were limited by the computational cost of network analysis, in particular due to the poor scaling of shortest-path graph algorithms. These costs constrained the number of species as well as the number and types of reactions contained in the networks. Even more critically, our prior graph-based analysis approach was limited in its predictive capacity; in order to apply shortest-path algorithms, products of interest had to be known a priori. Here we confront the more challenging problem of exploring a reactive space without significant knowledge of end products. Specifically, we seek to search for many feasible pathways under various starting conditions to a range of products, byproducts, and intermediates, including species that might not be known to be important at the time of network construction.
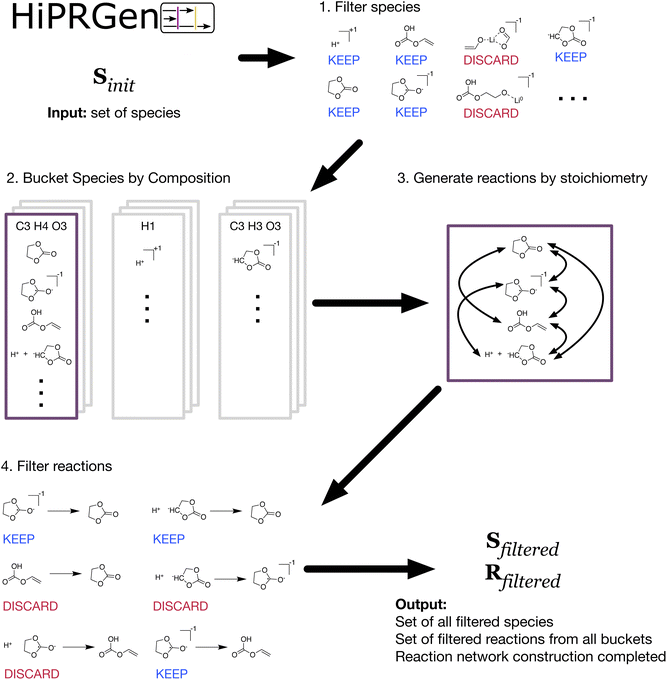
We present a new approach to construct and explore CRNs in electrochemistry that is capable of extracting unique insights and generating hypotheses to guide further in-depth analysis. First, we describe our method of High-Performance Reaction Generation (HiPRGen). Beginning with a set of possible species that could contribute to the chemistry of interest (Sinit), HiPRGen enumerates all stoichiometrically valid reactions and employs user-defined filters to eliminate reactions based on physical or practical criteria while aiming to retain a diverse and chemically reasonable set R. To overcome the scaling limitations of graph-based pathfinding, we explore CRNs with a stochastic approach, sampling the reactive space based without knowledge of reaction kinetics. We can then extract paths to any molecule formed in the trajectories and heuristically identify the products of the network as a function of initial conditions. The combination of HiPRGen with stochastic network analysis allows for the investigation of electrochemical reactivity without prior knowledge of reaction mechanisms or end products for the first time. We demonstrate and validate this approach with an application to SEI formation. We first identify 36 products of a HiPRGen-constructed network of roughly 5200 molecules and 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions by analyzing the average of many stochastic simulations. The identified network products include many species reported in the SEI literature as well as a range of unreported species. To demonstrate the plausibility of these network products and their associated formation pathways, we use first-principles calculations to refine the shortest thermodynamic paths to two previously unreported products, discovering chemically plausible elementary mechanisms. Further bespoke calculations indicate that several previously-unreported network products (or related intermediates) could reasonably emerge during SEI formation and could contribute to the production of other, experimentally-identified SEI products. The methods described here serve as a starting point for predictive studies of reactivity in electrochemistry where existing knowledge is limited.
000 reactions by analyzing the average of many stochastic simulations. The identified network products include many species reported in the SEI literature as well as a range of unreported species. To demonstrate the plausibility of these network products and their associated formation pathways, we use first-principles calculations to refine the shortest thermodynamic paths to two previously unreported products, discovering chemically plausible elementary mechanisms. Further bespoke calculations indicate that several previously-unreported network products (or related intermediates) could reasonably emerge during SEI formation and could contribute to the production of other, experimentally-identified SEI products. The methods described here serve as a starting point for predictive studies of reactivity in electrochemistry where existing knowledge is limited.
Template-free reaction network generation
Inspired by the previous work of Kim18 and Xie26 where the chemical distance between species was used to selectively include reactions in a CRN without employing templates, we have devised HiPRGen to construct CRNs by applying filters to initial collections of species and reactions.HiPRGen begins with some large dataset of species, the properties of which are known from e.g. quantum chemical calculations. We note that this work does not consider species dataset construction and assumes that an appropriate species dataset is already available (the dataset used in this work is described in Results and discussion; aims to construct electrochemical CRNs without an initial set of species are discussed in Future work). We then apply a series of filters, where each filter can remove species that are chemically unreasonable or otherwise undesirable under the conditions studied (Fig. 1-1). A list of species filters that we have designed and employed is described in Methods and is discussed in more detail in the ESI.† HiPRGen has been designed such that users can easily include additional filters, which might be necessary to apply HiPRGen to diverse chemistries.
The filtered set of species Sfiltered is then used to populate buckets that are each defined by a unique composition (Fig. 1-2). Buckets are populated by members containing either one or two species where the total composition of each member matches the composition of the bucket. This means that any pair of members in a given bucket define the reactants and products of a stoichiometrically balanced chemical reaction containing one or two reactants and one or two products. In order to reduce the number of possible reactions, we do not presently allow ternary reactions. While some elementary reactions with three products are possible, we expect them to be rare, and we do not generally believe that elementary reactions with three reactants are meaningful in electrochemistry. For each bucket, all combinations of two unique members yield unique reactions (Fig. 1-3). Note that, because we allow for electrochemical reactions, charge is not necessarily balanced in these reactions. For a system of several thousand species, there can easily be hundreds of billions or even trillions of stoichiometrically valid reactions. Reaction filters are therefore employed to remove reactions that, despite being stoichiometrically valid, are chemically implausible or otherwise undesirable (Fig. 1-4). All reaction filters employed in this work are described in Methods and are discussed in more detail in the ESI.† Finally, the reactions from each bucket that pass all filters are aggregated. The result of HiPRGen is a set of filtered species Sfiltered and filtered reactions Rfiltered, which constitute a CRN.
HiPRGen can enumerate and filter all possible reactions between up to approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 species, overcoming the scaling limitations of our previous approach.26 Further, to the best of our knowledge, HiPRGen is the first method that combines an exhaustive enumeration of stoichiometrically valid reactions with a range of chemically-motivated filters that leverage pre-computed molecular properties. In addition to improving the thoroughness and efficiency of reaction generation compared to previous methods (see ESI†), HiPRGen has the benefit that the filtering infrastructure was designed to be easily modified and extended by future users, making it facile to apply HiPRGen to new chemical domains.
000 species, overcoming the scaling limitations of our previous approach.26 Further, to the best of our knowledge, HiPRGen is the first method that combines an exhaustive enumeration of stoichiometrically valid reactions with a range of chemically-motivated filters that leverage pre-computed molecular properties. In addition to improving the thoroughness and efficiency of reaction generation compared to previous methods (see ESI†), HiPRGen has the benefit that the filtering infrastructure was designed to be easily modified and extended by future users, making it facile to apply HiPRGen to new chemical domains.
It is worth briefly comparing HiPRGen to template-based methods of reaction enumeration. HiPRGen is inherently inefficient compared to template-based CRN generation. Many of the reactions generated by HiPRGen may not occur in a single step, may not be kinetically accessible (due to excessively high energy barriers), or may not ever occur in the chemical system of interest because they require a reactant that will never form. While we are continuing to improve HiPRGen's filters in order to better avoid non-elementary or inaccessible reactions, in the absence of a general method to robustly identify plausible species and reactions in electrochemistry, this inefficiency cannot presently be avoided. Templates can also produce unreasonable reactions, and it can be difficult even for experts to identify such exceptions to chemical rules.27 Nonetheless, this problem is likely more severe for filter-based than template-based reactions. Where HiPRGen excels is in the inclusion of exceptional reactions that do not follow normal trends or patterns. Moreover, HiPRGen's method of bucketing ensures that no duplicate reactions will ever be added to a CRN (a particular reactant–product pair is only considered once), while in a naive template-based approach, duplicate reactions could easily be produced if multiple templates convert a set of reactants to the same products.
From the CRN generated by HiPRGen, it becomes possible to search for diverse products and reaction pathways to those products. However, even after filtering the set of stoichiometrically valid reactions, the number of remaining reactions can be so vast that a highly scalable method of network analysis is required.
Stochastic network analysis
While it might be desirable to use shortest-path algorithms to identify reaction pathways in graph-based CRNs, as we did previously,25,26 such algorithms become computationally intractable as network size increases. We therefore turn to the kinetic Monte Carlo (kMC) algorithm of Gillespie,28 which, with appropriate modifications,29 can scale sublinearly with number of reactions. In a kMC simulation, a system evolves from some user-defined initial state in a manner that is non-deterministic but consistent with the rate coefficients provided to the model.When templates are viable and accurately describe the reactivity in a system, they can be used to approximate reaction kinetics with minimal cost.13,17 In a template-free network of potentially millions of reactions, it is completely impossible to include accurate rate coefficients for all reactions. For the purposes of stochastic network exploration and analysis, we therefore assign rate coefficients by fiat. All unimolecular reactions are given the same rate coefficient k0; to ensure appropriate units, all bimolecular reactions have the rate coefficient k0/V, where V is a spatial term related to the (in this case fictitious) system volume.28,30
A critical note: most commonly, the Gillespie algorithm and kMC are used to study the time evolution of a reacting system. In such a case, the use of fiat rate coefficients would be inappropriate, as it likely would not lead to even qualitatively accurate dynamics. However, in this work we are not interested in reactive time evolution. Rather, as we discuss below, we use the Gillespie method in a somewhat unorthodox manner to obtain non-dynamic insights into reactivity, focusing mainly on which reactions proceed (without concern for how quickly they proceed or when they proceed in time) and which species form (without concern for quantitatively accurate ratios of products, which would require a notion of relative rates). Given sufficient sampling, all reactions included in the network that would occur given accurate kinetics will be observed in kMC simulations with fixed rate coefficients. In sum, because our aims do not include accurate time evolution or quantitative competition between possible products, we can employ kMC with arbitrary rate coefficients. We further note that the analysis of CRNs without kinetic information is not without precedent; for instance, Stocker et al.31 have previously used reaction thermodynamics and arbitrary energy barriers to explore a CRN describing combustion.
In addition to providing arbitrary and fixed rate coefficients, we consider only reactions with ΔG < 0 eV. This latter simplification is necessary to eliminate cycles or loops from the network. In reality, depending on temperature, reactions with ΔG above zero can occur. Furthermore, the inherent uncertainty in calculated reaction thermodynamics likely means that some number of reactions that we calculate to have ΔG slightly above zero (endergonic) in reality have ΔG slightly below zero instead (exergonic). However, the elimination of loops is practically necessary to enable CRN analysis. If all reactions have the same rate coefficient, then the presence of loops effectively ensures that any kMC simulation will be dominated by unimportant back-and-forth processes. This dramatically increases the noise in the simulations, making identification of important species and reactions difficult (see below). Beyond such practical and technical considerations, the elimination of endergonic reactions is reasonable on a physical basis within our domain of interest, electrochemistry. Electrochemical reaction cascades are often dominated by ion- and radical-driven reactions.32,33 Such cascades should, in general, be comprised entirely or almost entirely by (often rapid) exergonic steps, meaning that the elimination of endergonic steps should not significantly affect the predictions of our simulations.
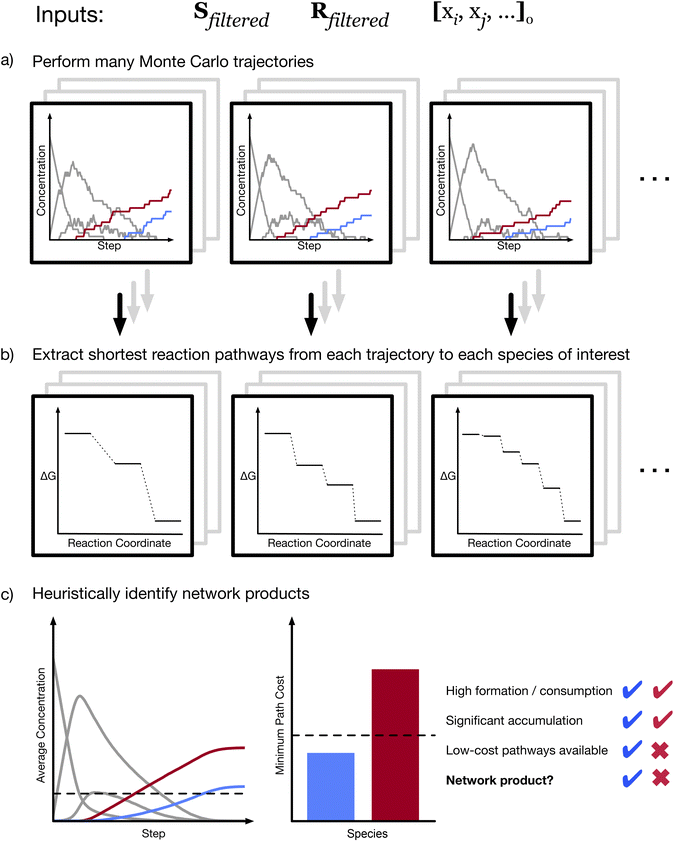
To analyze a CRN, we perform a large number of kMC simulations in parallel (Fig. 2a). The result of each simulation is a series of reactions defining a trajectory of the system state. If a molecule of interest is known, we can use these trajectories to identify potential formation pathways to that molecule. We trace each trajectory; if the molecule of interest is formed at any point, we then identify the shortest sequence of reactions leading to its first formation (Fig. 2b). Performing this method of stochastic pathfinding over many trajectories, we identify a range of possible pathways to the molecule of interest. We then rank the identified paths in order to identify the “best” paths among those observed, as defined by some cost function (see Methods). The thermodynamic pathways obtained from network analysis can then be subjected to further analysis to identify complete mechanisms, including transition-states (TS) and energy barriers.
However, pathfinding is useful only if one already knows what molecule to search for. Stochastic sampling with kMC, unlike graph-based pathfinding, enables the exploration of a reactive space without a specific target. This is because, while kMC trajectories can be used to search for a specific species, they are neither produced with any species in mind, nor are they biased towards any species. As a result, a unique capability of our approach is the ability to identify products of a CRN with minimal prior knowledge. To do this, we apply a set of heuristic criteria to the collection of trajectories (Fig. 2c). In line with the common-sense notion of a reaction product, we define a network product as any species that (i) is on average formed significantly more than it is consumed; (ii) accumulates significantly in the final state of an average trajectory; and (iii) can be reached by low-cost reaction pathways (see Methods). We note that the specific products that are identified depend on threshold values for these heuristics, which are arbitrarily selected. We further emphasize that the heuristics just described essentially require the elimination of endergonic reactions and reactive loops, as described above. If a species is involved in one or many loops, then the back-and-forth reactions would make exact counts of formation and consumption reactions meaningless. In addition, with loops present, a kMC simulation can in principle proceed indefinitely, which makes definition of accumulation in a “final” state problematic.
Using this heuristic method, we are able to analyze the structure of the CRN itself. The average trajectory (Fig. 2c) satisfies a rate equation of the system.34,35 We observe (see ESI†) that the average trajectory is smooth, indicating convergence to the exact expected dynamics. Because the rates used in our simulations are arbitrary, the dynamics themselves are not meaningful, but the trajectory smoothing ensures that we have sufficiently sampled reactive trajectories. Therefore, the identified products are well defined and invariant to changes in e.g. random seeds. The products of the network are not necessarily the metastable or stable products that would be observed experimentally, nor are they necessarily exhaustive (as they depend on which species are included in the CRN). Nonetheless, the network products provide useful hypotheses regarding what might form in an actual reactive system. We can then interrogate these hypotheses and validate them by either theoretical or experimental means. We note that in addition to the choice of heuristic thresholds, the choice of initial state can affect the network products identified via this method.
Results and discussion
Automatic identification of battery SEI network products
Using HiPRGen, we constructed a reaction network that seeks to describe SEI formation in lithium-ion batteries. An initial set of species taken from the lithium-ion battery electrolyte (LIBE) dataset,36 which was designed for studies of reactivity in battery electrolytes. LIBE contains the properties of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 species of various charges (−1, 0, 1) and spin multiplicities (1, 2, 3) calculated using density functional theory (DFT) at the ωB97X-V/def2-TZVPPD/SMD level of theory.37–39 These species were generated by quasi-exhaustively enumerating the sub-fragments of a set of initial electrolyte and interphase species and then selectively recombining a subset of those fragments based on valence rules and machine learning.26,40 Importantly, no knowledge of SEI formation mechanisms was used to generate LIBE. For this work, network construction began with a subset of LIBE containing all species comprised of only carbon, hydrogen, oxygen, and/or lithium. This subset, which we call LIBE-CHOLi, contains 8904 species.
190 species of various charges (−1, 0, 1) and spin multiplicities (1, 2, 3) calculated using density functional theory (DFT) at the ωB97X-V/def2-TZVPPD/SMD level of theory.37–39 These species were generated by quasi-exhaustively enumerating the sub-fragments of a set of initial electrolyte and interphase species and then selectively recombining a subset of those fragments based on valence rules and machine learning.26,40 Importantly, no knowledge of SEI formation mechanisms was used to generate LIBE. For this work, network construction began with a subset of LIBE containing all species comprised of only carbon, hydrogen, oxygen, and/or lithium. This subset, which we call LIBE-CHOLi, contains 8904 species.
Network construction resulted in a CRN containing 5193 filtered species and 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001
001![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275 filtered reactions. With this network, we conducted 100
275 filtered reactions. With this network, we conducted 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 stochastic trajectories under four conditions, with combinations of two different applied potentials (+0.0 V vs. Li/Li+ and +0.5 V vs. Li/Li+) and two different initial states (one consisting only of Li+ and ethylene carbonate (EC) and the other consisting of Li+, EC, and CO2). Average trajectories for each condition are shown in the ESI.† We emphasize that our goal is not to compute and observe the dynamics of SEI formation, but rather to identify key species and reaction pathways. We further note that we do not consider the effect of the electrode surface in our simulations. However, since the SEI can grow to a thickness of ∼10–100 nm, the effect of the electrode on the SEI chemistry should be small after the first reactions occur. Moreover, the products of the SEI are in general insensitive to the identity of the anode.41
000 stochastic trajectories under four conditions, with combinations of two different applied potentials (+0.0 V vs. Li/Li+ and +0.5 V vs. Li/Li+) and two different initial states (one consisting only of Li+ and ethylene carbonate (EC) and the other consisting of Li+, EC, and CO2). Average trajectories for each condition are shown in the ESI.† We emphasize that our goal is not to compute and observe the dynamics of SEI formation, but rather to identify key species and reaction pathways. We further note that we do not consider the effect of the electrode surface in our simulations. However, since the SEI can grow to a thickness of ∼10–100 nm, the effect of the electrode on the SEI chemistry should be small after the first reactions occur. Moreover, the products of the SEI are in general insensitive to the identity of the anode.41
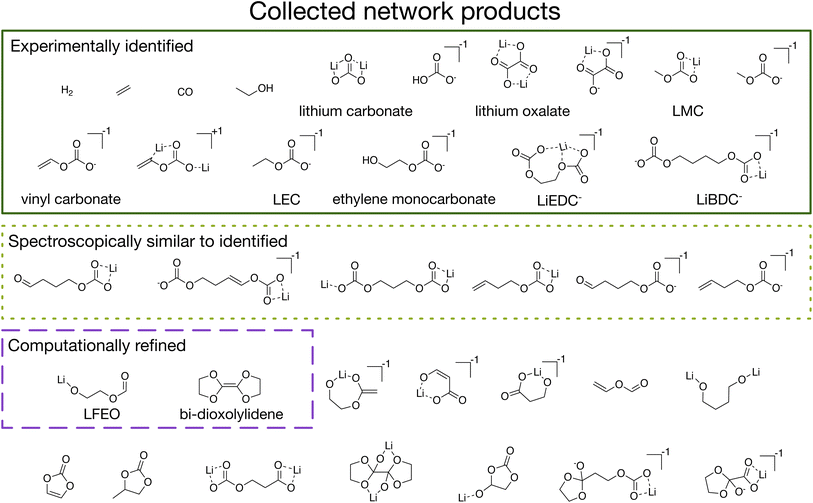
The utility of our approach is demonstrated through analysis of the 36 network products collected from the set of four conditions previously described (Fig. 3). We first note that our automated procedure recovers 16 species that include a majority of the experimentally observed products of SEI formation (Fig. 3 solid dark green). These include gases (H2, C2H4, CO),42 inorganic species (lithium carbonate (Li2CO3) and lithium oxalate (Li2C2O4)),43,44 and alkyl carbonates (including species closely related to LEDC43–45 and LEMC,22,44 as well as lithium methyl carbonate or LMC, lithium butylene dicarbonate or LBDC,44 and lithium vinyl carbonate).46 We emphasize that these species are recovered even though reaction kinetics are entirely ignored in network exploration.
In addition to these well-known species, there are also a number of novel products that have not previously been proposed to participate in SEI formation. Among these are six additional alkyl carbonates (Fig. 3 dotted light green) which are each very similar to known products in molecular size, composition, bonding, and contained functional groups. Due to the extreme difficulty of experimentally characterizing the SEI and the resulting limited ability to resolve small signal to noise,47 the likely spectroscopic similarity48 of these species to the known products means that they may be present in the SEI in small quantities but that they could not easily be positively identified.
Other network products include species with ester, carboxylate, and oxide functional groups, such as lithium 2-(formyloxy)ethan-1-olate, which we abbreviate as LFEO, as well as a number of cyclic species, such as 4,4′,5,5′-tetrahydro-2,2′-bi(1,3-dioxolylidene), which we abbreviate as bi-dioxolylidene. LFEO and bi-dioxolylidene (Fig. 3 dashed purple) were particularly unexpected given how distinct they are from other predicted SEI products and, in particular, the experimentally identified products. Evaluating whether or not these products will actually form in the SEI necessitates considering energy barriers, kinetics, and reactive competition. Using the shortest paths from stochastic network analysis to guide automated transition-state calculations, we identified elementary formation mechanisms to both LFEO and bi-dioxolylidene to evaluate their potential to participate in SEI formation (see CRN-derived elementary mechanisms to form unexpected network products).
On the other hand, there are some network products which do not reflect the corresponding chemical system in a real battery. Specifically, both vinylene carbonate (VC) and propylene carbonate (PC) are known to rapidly decompose when included in battery electrolytes.49,50 This contradiction indicates that there are reactions or species that are necessary to facilitate the decomposition of VC and PC must be missing from the network. The identification of this gap through the use of CRN analysis and network product prediction provides a tractable path forward to expand the CRN via selective addition of missing molecules that enable redox, decomposition, or recombination of network products with other abundant intermediate or product species.
CRN-derived elementary mechanisms to form unexpected network products
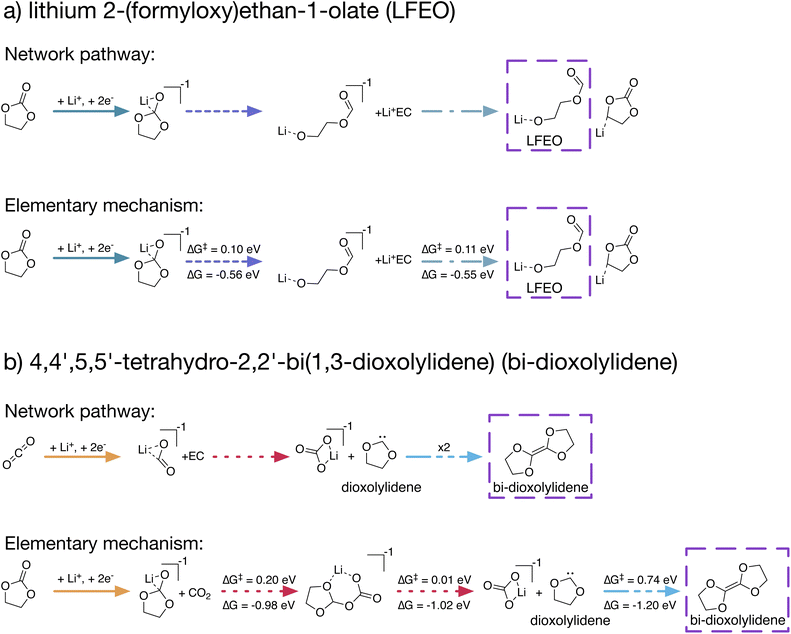
The reaction pathways produced by our stochastic approach involve no knowledge of reaction kinetics. In actuality, the dominant reaction pathways are heavily dependent on reaction energy barriers ΔG‡ and rate coefficients. In order for our approach of using kMC with arbitrary rate coefficients to provide useful chemical insights, it is critical that the predicted reaction pathways can be reasonably translated into elementary reaction mechanisms including TS and energy barriers.Using our stochastic approach, we can identify the N lowest-cost reaction pathways to the network products, ranked by a cost function that we have employed previously25 (see Methods). We selected two unexpected network products – LFEO and bi-dioxolylidene – and subjected their shortest pathways in order of cost to an automated procedure to identify the TS for each step along each pathway, allowing for the construction of complete reaction mechanisms. Fig. 4 highlights two formation paths obtained using this procedure, emphasizing the utility of network-generated reaction pathways to construct elementary mechanisms.
The network pathway shown in Fig. 4a has the 12th lowest cost with only Li+ and EC as starting species (no CO2) at +0.0 V vs. Li/Li+. In this pathway, Li+ coordinates with EC, and the Li+EC reduces twice. The doubly reduced Li+EC2− then ring-opens at the shoulder bond, after which this shoulder-ring-opened species can abstract a proton from an additional Li+EC, forming LFEO with a Li+EC–H− as a byproduct. The identified elementary mechanism follows this path exactly, with two TS – one for the ring-opening of Li+EC2− with a barrier ΔG‡ = 0.10 eV and one for proton abstraction from EC to form LFEO with ΔG‡ = 0.11 eV.
A path to form bi-dioxolylidene is shown in Fig. 4b. This network pathway has the 3rd lowest cost for simulations with CO2 was present as a starting species at 0.0 V vs. Li/Li+. In the pathway, CO2 reduces twice and coordinates with Li+, forming Li+CO22−. This Li+CO22− species reacts with EC to form Li+CO32− and the 1,3-dioxolylidene carbene, which we abbreviate as dioxolylidene. Two of these carbenes can then combine to form the dimer bi-dioxolylidene. The identified elementary mechanism follows the same general steps as the network pathway – coordinate and reduce, form dioxolylidene, and then dimerize two carbenes – but differs in two main ways. First, it is more favorable to reduce EC than CO2, which changes the initial steps of the mechanism. Second, we found that the carbene formation actually occurs via an addition–elimination mechanism with two elementary steps. The addition, which results in an EC–CO2 adduct, has a barrier ΔG‡ = 0.20 eV, and the elimination to produce Li+CO32− and dioxolylidene has a barrier ΔG‡ = 0.01 eV.
The identified elementary mechanisms to LFEO and bi-dioxolylidene involve steps that are predicted to be competitive with other known SEI formation processes. Both mechanisms rely on Li+EC2−, which can form easily at low potentials.41,51 After breaking the shoulder bond, the ring-opened Li+EC2− is known to decompose unimolecularly to Li+OCH2CH2O2− and CO with a predicted energy barrier between 0.09 eV (ref. 41) and 0.22 eV (ref. 51) depending on the level of theory used. Considering that the necessary precursor to LFEO formation, Li+EC, should be present in abundance during early SEI formation, this implies that LFEO could actually be a significant product during early SEI formation at low potentials.
The formation of bi-dioxolylidene is predicted to be less kinetically favorable than that of LFEO. The dimerization reaction has an energy barrier that is considerably higher than many major SEI formation pathways,41,51–54 implying that bi-dioxolylidene should not be a significant product. The formation of the carbene monomer, on the other hand, is plausible. Using the Eyring equation,55 the addition of CO2 to Li+EC2− with a 0.20 eV barrier has a predicted rate coefficient roughly 70 times lower than that of the shoulder ring-opening of Li+EC2− with a 0.09 eV barrier. However, dioxolylidene formation could be significant if CO2 is abundant, a plausible scenario considering that CO2 can form at either the anode56 or the cathode57 in Li-ion batteries. On this basis, we predict that while LFEO, Li+OCH2CH2O2−, and CO will be favored, dioxolylidene should at least form as a short-lived minority intermediate (considering the general reactivity of carbenes).58
CRN pathways and products guide investigation of expanded mechanisms
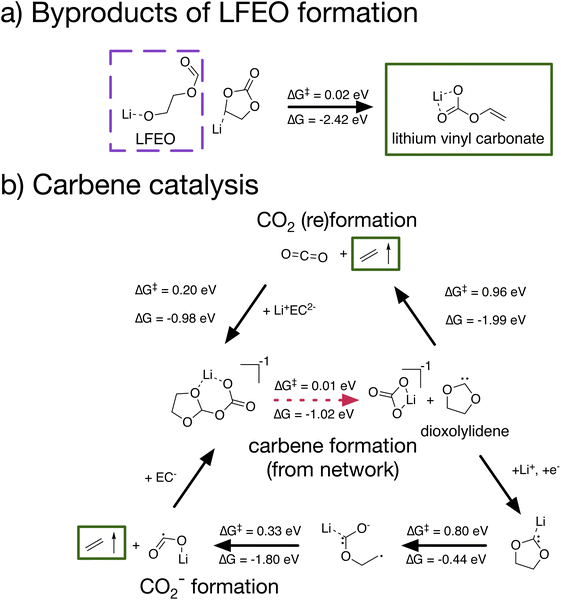
Leveraging CRN analysis, we have predicted network products and reaction paths that could be important to a complex electrochemical system but which have not been seriously studied in the literature before. We can now expand on these paths, using the calculated elementary formation mechanisms of LFEO and bi-dioxolylidene as starting points for studying how species along these paths may further react. In doing so, we demonstrate the utility of CRN-generated pathways as a tool for hypothesis generation to guide follow-up investigation (see Fig. 5).In the mechanism for LFEO formation identified in Fig. 4a, a byproduct is the deprotonated EC species Li+EC–H−. We suspected that this byproduct would be highly reactive and would likely decompose. Indeed, we found (Fig. 5a) that Li+EC–H− can open at the waist bond with an extremely low barrier (ΔG‡ = 0.02 eV), forming lithium vinyl carbonate. We note that lithium vinyl carbonate has previously been identified as an SEI product,46 though its formation mechanism has not been thoroughly studied. Therefore, not only is the formation of LFEO plausible on the basis of the low reaction barriers identified, but LFEO formation can potentially help to explain the formation of another SEI product.
We also considered the reactivity of the dioxolylidene carbene (Fig. 5b). In addition to the dimerization shown in Fig. 4b, we found that dioxolylidene could react in two other ways, either decomposing in a single step to form CO2 and C2H4 or decomposing to Li+CO2− and C2H4via a two-step process after coordination with Li+ and reduction. All reactions identified – dimerization and both decomposition mechanisms – involve relatively high energy barriers. Our understanding of the role of dioxolylidene in SEI formation remains incomplete, and further work must be done to elucidate its decomposition routes. However, if the barriers to dioxolylidene decomposition were lowered by e.g. a solvent effect59 or a reactive surface,60 the possibility exists for a catalytic loop in which dioxolylidene is repeatedly reformed via the reaction of CO2 with Li+EC2− or Li+CO2− with EC−.
Future work
The combination of CRN generation via HiPRGen and stochastic CRN analysis can lead to predictive and unique insights, as we have shown through our case study of SEI formation. Although the SEI has been intensely studied for roughly 30 years, our approach is able to predict new product and intermediate species that are likely to form in a real battery based on reaction kinetics and could perhaps even compete with known reaction mechanisms. Nonetheless, there remain both methodological and chemical challenges that limit the widespread applicability of our methodology.When PES exploration can be used to generate CRNs, new intermediate and product species can be identified automatically via reactions starting from known species. Likewise, when templates can be used, new species are generated by repeatedly applying reaction motifs to provided or previously generated reactants. As we have explained, neither PES exploration nor templates can presently be applied to electrochemistry. Instead, HiPRGen currently requires an input set of species containing all molecules to be included in the CRN and their calculated properties. For applications to Li-ion SEI formation, where the LIBE dataset of molecular thermochemistry already exists,36 this is not a significant limitation. More generally, the reliance on a pre-computed dataset of species is problematic, as it potentially creates a high computational barrier to entry for the user and limits predictive discovery of novel species and pathways they participate in. We are actively working to overcome this requirement, developing a framework to automatically generate CRNs from only a set of known starting molecules by leveraging calculated network products to strategically guide iterative network expansion and machine learning (ML) to reduce the number of required high-throughput DFT calculations.
An additional improvement could be made by incorporating reaction kinetics into CRN generation and stochastic analysis, as is common in the study of CRNs. We have shown that reaction thermodynamics alone can be sufficient to predict reasonable reaction pathways as well as network products, yet a network based on only thermodynamics certainly contains many reactions that are kinetically limited and therefore not important in practice. Although there are not currently any methods capable of predicting energy barriers or rate coefficients for solution-phase electrochemical reactions without relying on expensive electronic structure methods (which cannot be applied to millions of reactions), we believe that ML could eventually provide sufficiently accurate estimates to realistically constrain network construction at minimal cost given sufficient training data.61
Conclusions
In this article, we have described our approach to explore electrochemical reactivity using CRNs. The HiPRGen method allows for the enumeration of reactions for CRN construction in domains where reaction templates cannot be applied and where reaction mechanisms are poorly understood. The resulting networks can then be analyzed using stochastic simulations, allowing for the identification of network products and reaction pathways which can be further refined to discover elementary mechanisms. We applied this methodology to study SEI formation in Li-ion batteries, generating a network consisting of over 5000 species and over 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions. Network product prediction yielded many known SEI components as well as several species that had not previously been proposed. We identified elementary mechanisms for the formation of multiple novel network products (LFEO and bi-dioxolylidene) based on pathways obtained from CRN analysis and refined using automated DFT. CRN-derived pathways further guided the expansion of automatically obtained mechanisms, yielding additional insight. The mechanisms that we discovered validate our methods of product prediction and pathway identification and moreover indicate that LFEO could be a component of the early SEI. Our findings indicate that thermodynamic reaction pathways obtained via analysis of appropriately filtered CRNs can be used to efficiently search for transition-states of chemically meaningful reaction mechanisms, facilitating the construction of microkinetic models (an example of which we report in a separate publication).41 With the approach presented here, it will be possible to provide insights into a range of domains where fundamental understanding of reactivity is limited.
000 reactions. Network product prediction yielded many known SEI components as well as several species that had not previously been proposed. We identified elementary mechanisms for the formation of multiple novel network products (LFEO and bi-dioxolylidene) based on pathways obtained from CRN analysis and refined using automated DFT. CRN-derived pathways further guided the expansion of automatically obtained mechanisms, yielding additional insight. The mechanisms that we discovered validate our methods of product prediction and pathway identification and moreover indicate that LFEO could be a component of the early SEI. Our findings indicate that thermodynamic reaction pathways obtained via analysis of appropriately filtered CRNs can be used to efficiently search for transition-states of chemically meaningful reaction mechanisms, facilitating the construction of microkinetic models (an example of which we report in a separate publication).41 With the approach presented here, it will be possible to provide insights into a range of domains where fundamental understanding of reactivity is limited.
Computational methods
Modifying species thermodynamics
All calculations on the species present in LIBE were conducted in an implicit solvation environment. While implicit solvation is generally accurate enough for the calculation of properties such as the solvation energy62 and redox potentials of organic molecules,63 we have found that even highly accurate implicit solvation methods severely underestimate the stabilization of small ions, especially metal ions, by solvent. This means that species in LIBE containing Li+ ions with many coordination bonds are in many cases vastly more stable according to DFT than those with fewer coordination bonds, even if the corresponding species without lithium present are significantly less stable (an example is provided in the ESI†). This insufficient stabilization led to inaccurate thermodynamics for reactions where the overall charge of the system was constant but the number of coordinate bonds changed (non-redox reactions).To correct for insufficient metal ion stabilization, we optimized Li+ECn clusters at the ωB97X-D/def2-SVPD/PCM//ωB97X-V/def2-TZVPPD/SMD level of theory, with n ∈ 0, 1, 2, 3, 4 to estimate the stabilizing effect of each solvent molecule on Li+. The lower level of theory (ωB97X-D/def2-SVPD/PCM, ε = 18.5) was used for optimization due to the considerable computational cost of optimizing large clusters. We found (see ESI†) that each EC stabilized Li+ by ∼0.7 eV.
During reaction network construction, we consider two free energies for each species: one uncorrected, and one solvent-corrected. The uncorrected free energy is taken directly from LIBE. For the solvent-corrected free energy, we count the total number of coordinate bonds to all Li+ ions (see the ESI† for a description of the method for deducing metal coordination) and compare this to the maximum expected number of coordinate bonds (assuming that each Li+ would prefer to be coordinated by four neighbors).64 If any Li+ are undercoordinated, then the free energy is lowered by 0.68 eV for each “missing” coordinate bond. When calculating redox free energies, the uncorrected free energy is used; otherwise, the corrected free energy is used (see the ESI†).
Species filtering
In the HiPRGen package (see Code availability), we implement a number of filters that remove undesirable species. These filters take as input an object containing information about a molecule, including its species, coordinates, charge, spin multiplicity, partial charges, connectivity, and thermodynamics. Each filter, based on this information, can discard the molecule or pass it onto the next filter. For terminal filters, if the molecule passes, then it is included in the final filtered set Sfiltered. For this work, the following molecules were filtered out:• Molecules composed of two or more disconnected fragments.
• Metal-centric complexes, where two or more non-metal fragments are connected only by coordinate bonds to Li+.
• Molecules containing neutral or negative metal ions, where the charges are calculating by applying the natural bonding orbital (NBO) program version 5.0 (ref. 65 and 66) to a single-point energy calculation at the ωB97X-V/def2-TZVPPD/SMD level of theory in Q-Chem.
• Molecules with charge less than −1 or greater than 1.
In addition to these filters, which define types of molecules to be excluded from the final network, we further reduce the molecules in the network by removing redundant species. In LIBE, all molecules are unique based on the combination of their charge, spin multiplicity, and molecular connectivity. This means that there could be several molecules that differ only by spin multiplicity, or that differ only by the coordination environment of Li+ ions (what we call “coordimers”). When this occurs (when there are multiple molecules with the same covalent connectivity and charge but potentially with different coordination environments or spin multiplicities), we include only that species with the lowest solvation-corrected free energy in the final filtered set of species Sfiltered.
These filters are explained further in the ESI.† We emphasize that these filters are particular to the chemistry being studied in this work, but that HiPRGen has been engineered to enable straightforward addition, removal, or modification of filters in order to be easily applied across diverse chemical applications.
Reaction filtering
Reaction filters take as input a reaction, defined by a collection of reactants and a collection of products, and either discard the reaction or pass it onto the next filter until a terminal filter is reached. The following types of reactions were filtered out in this work:• Endergonic reactions with ΔG > 0 eV. The reaction free energies for non-redox reactions were taken as 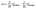 , where GC is the solvation-corrected free energy, m is the length of the product collection, and n is the length of the reactant collection. For redox reactions, ΔG = G0product − G0reactant + Δq(Ge), where G0 is the uncorrected free energy, Δq is the change in charge of the reaction, and Ge is the free energy of the electron (for +0.0 V vs. Li/Li+, Ge = −1.4 eV; for +0.5 V vs. Li/Li+, Ge = −1.9 eV).
, where GC is the solvation-corrected free energy, m is the length of the product collection, and n is the length of the reactant collection. For redox reactions, ΔG = G0product − G0reactant + Δq(Ge), where G0 is the uncorrected free energy, Δq is the change in charge of the reaction, and Ge is the free energy of the electron (for +0.0 V vs. Li/Li+, Ge = −1.4 eV; for +0.5 V vs. Li/Li+, Ge = −1.9 eV).
• Reactions involving a charge change |Δq| > 1.
• Redox reactions involving more than one reactant or more than one product.
• Unimolecular dissociative redox reactions in which |Δq| > 0 and covalent bonds form or break.
• Reactions involving more than two reactants or products (this is actually enforced by the species bucketing procedure of HiPRGen and is not a separate filter).
• Reactions involving spectators (species that do not change as a result of the reaction) e.g. A + B to A + C.
• Reactions involving more than two bond changes.
• Reactions in which two bonds form simultaneously or two bonds break simultaneously.
• Reactions in which covalent bonds change and metal ions coordinate/decoordinate (note that reactions in which metal ions remain coordinated but change their coordinate bonds are allowed).
Motivations for each of these filters, along with examples, are provided in the ESI.† Like species filters, the reaction filters can be easily modified and extended by end users to suit a broad range of chemical applications. Of course, removing filters will yield a larger final collection of reactions. We note that for the size of the species collection presented in this work, some filters are necessary to obtain a tractable number of reactions in the final collection. For thousands of species, it is further necessary to filter reactions in parallel and for each filter to be computationally efficient in order to allow filtering to complete in a reasonable amount of time (hours to days).
Monte Carlo methods
We developed a high-performance implementation of Gillespie's direct method,28 with dependency graph and logarithmically scaling sampler optimizations,29 which we call Reaction Network Monte Carlo (RNMC). RNMC is heavily based on the Stochastic Parallel Particle Kinetic Simulator (SPPARKS) package67,68 but with modifications to allow simulating networks with hundreds of millions of reactions and thousands of species. RNMC shares the reaction network and dependency graph between all running simulators and uses a lockless data structure for the dependency graph that allows it to be computed dynamically by all of the simulators in parallel.Using RNMC, we performed 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulations under each of the four chosen conditions (+0.0 V without CO2, +0.0 V with CO2, +0.5 V without CO2, and +0.5 V with CO2). For simulations without CO2, the initial state consisted of 30 Li+ and 30 EC; for those with CO2, the initial state also included 30 CO2. Because all reactions were exergonic and no energy barriers were considered, all rate coefficients were constant and equal (discussed in Stochastic network analysis). Each simulation was conducted to “completion” – that is, until there were no further reactions available for further simulation. Due to the relatively small number of initial species, most simulations took between roughly 200 and 500 steps. We reiterate that simulating to completion – especially with so few simulation steps – is only possible because the system contains only exergonic reactions and therefore contains no loops. The elimination of loops is critical to adequately sample the reactive space in a tractable number of simulations (see discussion in Stochastic network analysis).
000 simulations under each of the four chosen conditions (+0.0 V without CO2, +0.0 V with CO2, +0.5 V without CO2, and +0.5 V with CO2). For simulations without CO2, the initial state consisted of 30 Li+ and 30 EC; for those with CO2, the initial state also included 30 CO2. Because all reactions were exergonic and no energy barriers were considered, all rate coefficients were constant and equal (discussed in Stochastic network analysis). Each simulation was conducted to “completion” – that is, until there were no further reactions available for further simulation. Due to the relatively small number of initial species, most simulations took between roughly 200 and 500 steps. We reiterate that simulating to completion – especially with so few simulation steps – is only possible because the system contains only exergonic reactions and therefore contains no loops. The elimination of loops is critical to adequately sample the reactive space in a tractable number of simulations (see discussion in Stochastic network analysis).
Identification of thermodynamic reaction pathways
To identify a single reaction pathway to a species of interest, we look through an individual kMC trajectory. If the species of interest is formed in that trajectory, then we trace back the series of reactions leading to the first formation of that species (see ESI† for an illustration of this process). For instance, if we are searching for pathways to species X, we might find that it is first formed by the reaction V + W → X. We then look for the first reaction(s) forming V and W, and then for the first reaction(s) forming the reactants of those formation reactions, until all reactions can occur from only starting species of the simulation. The series of reactions obtained in this way define a reaction pathway to X.In general, we are not interested in a single reaction pathway but rather the myriad pathways to the species of interest. Therefore, for each species of interest, we repeat the pathway identification procedure above for each trajectory, collecting all unique pathways. We then rank these pathways by some cost function. Here, the cost Φ of a given reaction is defined as Φ = exp(ΔG/kBT) + 1, where ΔG is the reaction free energy (uncorrected for a redox reaction, and solvation-corrected otherwise).25 The total cost of a reaction pathway is the sum of the costs of the individual reactions. We note that, because all reactions included in our network are exergonic, the constant term tends to dominate, though this cost function retains a preference for highly exergonic reactions over those that are only slightly exergonic.
Identification of network products
After all simulations have completed, the resulting trajectories are analyzed to determine product species. Products are defined by three criteria: the ratio of formation and consumption, relative accumulation, and availability of low-cost pathways.To determine the ratio of formation and consumption, each trajectory was interrogated to find all reactions involving each species. If a given species is a reactant of an identified reaction, then that means it was consumed; if it is a product of the reaction, then that means it was formed. If the ratio of the total number of instances of formation across all trajectories to the total number of instances of consumption across all trajectories is greater than some threshold (here chosen as 1.5, meaning that three of the species are produced for every two consumed), then it could be a network product.
For relative accumulation, we take the average of all trajectories. The expected value of a species is the average of the final state – how many of the molecule will persist once the average simulation has completed. If this expected value is greater than some threshold (here 0.1, meaning that one of this species is produced and is present in the final state for every ten simulations), then that species could be a product.
Finally, for those species with formation/consumption ratios and expected values that pass the chosen thresholds, we perform pathfinding analysis. If the pathway with the lowest cost has a cost less than some threshold (here 10.0), then we consider the species to be a product of the network.
The species reported in Fig. 3 are network products in at least one – but not necessarily all – of the four conditions considered (see ESI† for details). We note that we add one additional constraint to the products reported here: spin multiplicity. While open-shell species can be products of the network, they are highly unlikely to be stable or meta-stable (long-lived radicals are generally rare). In the hopes of extracting useful chemical insights from network products, we therefore only consider network products that are singlets.
Kinetic refinement of reaction mechanisms
The thermodynamic reaction pathways obtained via stochastic analysis were interrogated to determine the actual elementary steps. For the network products considered here (LFEO and bi-dioxolylidene), several low-cost thermodynamic reaction pathways were selected. For each elementary step along these pathways – excluding coordination reactions and redox reactions – we attempted to locate the TS using the AutoTS workflow,69 an end-to-end workflow to identify TS and reaction pathways that is built on top of the Jaguar electronic structure code (version 11.2).70 All AutoTS calculations were conducted at a ωB97X-D/def2-SVPD(-f)/PCM level of theory,38,71,72 with water as the solvent. In some cases, for reactions involving two bonds changing, AutoTS identified two TS (for instance, one to form a bond and one to break a bond); these were optimized separately.In cases where AutoTS was unable to find a TS for a given reaction, we searched using the single-ended growing string method (SE-GSM), as implemented in the pyGSM code.73 SE-GSM calculations were conducted with a Q-Chem backend (version 5.3.2) at the ωB97X-D/def2-SVPD/PCM level of theory.74 To be as consistent as possible, TS found using SE-GSM in Q-Chem were re-optimized in Jaguar at the ωB97X-D/def2-SVPD(-f)/PCM level of theory.
For each TS, we confirmed that the optimized structure possessed one imaginary frequency and confirmed that it connected the expected endpoints. For cases where the endpoints consist of two molecules that are not covalently bound (typically bound only by coordination to Li+), we allow small imaginary frequencies (less than 75i cm−1). These small imaginary modes can prove extremely difficult to remove using conventional geometry optimization methods, especially when they involve the motion of Li+ ions, and typically do not significantly affect the free energy. We note that in some cases, the barriers that we report are based on the difference between the TS and the reactants or products at infinite separation, rather than the entrance or exit complex. The electronic energies of all optimized structures (TS and endpoints) were corrected using a single-point calculation at a higher level of theory (ωB97X-V/def2-TZVPPD/SMD) in Q-Chem. The SMD parameters used were the same used for the construction of the LIBE dataset.36 We note that we used Q-Chem for these calculations, rather than Jaguar, because the SMD implicit solvent model is not implemented in Jaguar at the time of this writing.
All AutoTS and pyGSM calculations were automated using workflows that we have implemented in the MPcat code (see Code availability). These workflows are designed for high-throughput transition-state searches and reaction pathway analysis. Note that we use a fork of the original pyGSM code for SE-GSM (see Code availability).
Data availability
Molecular data used for network construction are the CHOLi subset of the lithium ion battery electrolyte (LIBE) dataset. LIBE is provided in Javascript Object Notation (JSON) format at https://doi.org/10.6084/m9.figshare.14226464.v2. All data used to construct mechanisms (molecular structures, thermodynamics, vibrational frequencies, and frequency modes) are also provided in JSON format in the ESI “reaction_pathways.json”.†Code availability
All codes discussed here (HiPRGen, RNMC, MPcat, and pyGSM) are released open source on Github. A Python implementation of the HiPRGen method can be found at https://github.com/BlauGroup/HiPRGen. Please refer to the v0.1 release. RNMC, a performant kinetic Monte Carlo code in C++ and based on SPPARKS, can be found at https://github.com/BlauGroup/RNMC. Please refer to the v0.1 release. AutoTS and SE-GSM calculations were performed using the automated workflows defined in MPcat, which can be found at https://github.com/espottesmith/MPcat. Please refer to the v0.0.1 release. SE-GSM calculations specifically used a fork of the original pyGSM code, which can be found at https://github.com/espottesmith/pyGSM/tree/c8cd99fcac451b1584f3f75e676f9d325e7ad6d4.Author contributions
D. B. and E. W. C. S.-S. both have the right to list their names first when presenting this research or listing it in their CVs. D. B., E. W. C. S.-S., and S. M. B. conceived of the study and approach; D. B. implemented HiPRGen, RNMC, and stochastic analysis methods with feedback from S. M. B.; D. B., E. W. C. S.-S., S. D., and S. M. B. designed species and reaction filters; D. B., S. D., and S. M. B. designed the methods for network product identification; E. W. C. S.-S., N. S. R., and A. K. performed quantum chemical calculations; E. W. C. S.-S., A. K., and S. M. B. analyzed data; K. A. P. and S. M. B. secured funding; D. B., E. W. C. S.-S., and S. M. B. wrote the original manuscript; all authors edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Laboratory Directed Research and Development Program of Lawrence Berkeley National Laboratory under U.S. Department of Energy Contract No. DE-AC02-05CH11231, the Joint Center for Energy Storage Research, an Energy Innovation Hub funded by the US Department of Energy, Office of Science, Basic Energy Sciences, and the Silicon Consortium Project directed by Brian Cunningham under the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of Vehicle Technologies of the U.S. Department of Energy, Contract No. DE-AC02-05CH11231. Computational resources were provided by the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility under Contract No. DE-AC02-05CH11231, and by the Department of Energy's Office of Energy Efficiency and Renewable Energy's Eagle supercomputer located at the National Renewable Energy Laboratory. This research also used the Lawrencium computational cluster resource provided by the IT Division at the Lawrence Berkeley National Laboratory (supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231). Schrödinger, Inc. provided access to Jaguar and AutoTS software, as well as technical advice regarding their use.Notes and references
- J. P. Unsleber and M. Reiher, Annu. Rev. Phys. Chem., 2020, 71, 121–142 CrossRef CAS PubMed.
- I. Ismail, R. Chantreau Majerus and S. Habershon, J. Phys. Chem. A, 2022, 126, 7051–7069 CrossRef CAS PubMed.
- S. Maeda and K. Morokuma, J. Chem. Theory Comput., 2012, 8, 380–385 CrossRef CAS PubMed.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- J. S. Tse, Annu. Rev. Phys. Chem., 2002, 53, 249–290 CrossRef CAS PubMed.
- S. Maeda, Y. Harabuchi, M. Takagi, T. Taketsugu and K. Morokuma, Chem. Rec., 2016, 16, 2232–2248 CrossRef CAS PubMed.
- C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- Q. Zhao and B. M. Savoie, Nature Computational Science, 2021, 1, 479–490 CrossRef.
- P.-L. Kang, C. Shang and Z.-P. Liu, Acc. Chem. Res., 2020, 53, 2119–2129 CrossRef CAS PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 1–11 Search PubMed.
- N. Holmberg and K. Laasonen, J. Phys. Chem. C, 2015, 119, 16166–16178 CrossRef CAS.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- C. F. Goldsmith and R. H. West, J. Phys. Chem. C, 2017, 121, 9970–9981 CrossRef CAS.
- D. Rappoport and A. Aspuru-Guzik, J. Chem. Theory Comput., 2019, 15, 4099–4112 CrossRef CAS PubMed.
- A. Wołos, R. Roszak, A. Żądło Dobrowolska, W. Beker, B. Mikulak-Klucznik, G. Spólnik, M. Dygas, S. Szymkuć and B. A. Grzybowski, Science, 2020, 369, 1–12 CrossRef PubMed.
- M. Liu, A. Grinberg Dana, M. S. Johnson, M. J. Goldman, A. Jocher, A. M. Payne, C. A. Grambow, K. Han, N. W. Yee, E. J. Mazeau, K. Blondal, R. H. West, C. F. Goldsmith and W. H. Green, J. Chem. Inf. Model., 2021, 61, 2686–2696 CrossRef CAS PubMed.
- Y. Kim, J. W. Kim, Z. Kim and W. Y. Kim, Chem. Sci., 2018, 9, 825–835 RSC.
- X. Jia, A. Lynch, Y. Huang, M. Danielson, I. Lang'at, A. Milder, A. E. Ruby, H. Wang, S. A. Friedler, A. J. Norquist and J. Schrier, Nature, 2019, 573, 251–255 CrossRef CAS PubMed.
- F. Calle-Vallejo and M. T. M. Koper, Electrochim. Acta, 2012, 84, 3–11 CrossRef CAS.
- Y. Y. Birdja, E. Pérez-Gallent, M. C. Figueiredo, A. J. Göttle, F. Calle-Vallejo and M. T. M. Koper, Nat. Energy, 2019, 4, 732–745 CrossRef CAS.
- L. Wang, A. Menakath, F. Han, Y. Wang, P. Y. Zavalij, K. J. Gaskell, O. Borodin, D. Iuga, S. P. Brown, C. Wang, K. Xu and B. W. Eichhorn, Nat. Chem., 2019, 11, 789–796 CrossRef CAS PubMed.
- R. P. Bell and C. N. Hinshelwood, Proc. R. Soc. London, Ser. A, 1936, 154, 414–429 Search PubMed.
- M. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333–1360 RSC.
- S. M. Blau, H. D. Patel, E. W. Clark Spotte-Smith, X. Xie, S. Dwaraknath and K. A. Persson, Chem. Sci., 2021, 12, 4931–4939 RSC.
- X. Xie, E. W. Clark Spotte-Smith, M. Wen, H. D. Patel, S. M. Blau and K. A. Persson, J. Am. Chem. Soc., 2021, 143, 13245–13258 CrossRef CAS PubMed.
- M. H. Segler, M. Preuss and M. P. Waller, Nature, 2018, 555, 604–610 CrossRef CAS PubMed.
- D. T. Gillespie, J. Comput. Phys., 1976, 22, 403–434 CrossRef CAS.
- M. A. Gibson and J. Bruck, J. Phys. Chem. A, 2000, 104, 1876–1889 CrossRef CAS.
- D. T. Gillespie, et al. , Annu. Rev. Phys. Chem., 2007, 58, 35–55 CrossRef CAS PubMed.
- S. Stocker, G. Csányi, K. Reuter and J. T. Margraf, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
- M. P. Plesniak, H.-M. Huang and D. J. Procter, Nat. Rev. Chem., 2017, 1, 1–16 CrossRef.
- Y. Yuan, Y. Chen, S. Tang, Z. Huang and A. Lei, Sci. Adv., 2018, 4, eaat5312 CrossRef CAS PubMed.
- J. C. Baez, Adv. Math. Phys., 2018, 2018, e7676309 Search PubMed.
- J. C. Baez and J. Biamonte, arXiv:1209.3632 [math-ph, physics:quant-ph], 2019.
- E. W. C. Spotte-Smith, S. M. Blau, X. Xie, H. D. Patel, M. Wen, B. Wood, S. Dwaraknath and K. A. Persson, Sci. Data, 2021, 8, 203 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- M. Wen, S. M. Blau, E. W. C. Spotte-Smith, S. Dwaraknath and K. A. Persson, Chem. Sci., 2021, 12, 1858–1868 RSC.
- E. W. C. Spotte-Smith, R. L. Kam, D. Barter, X. Xie, T. Hou, S. Dwaraknath, S. M. Blau and K. A. Persson, ACS Energy Lett., 2022, 7, 1446–1453 CrossRef CAS.
- B. Rowden and N. Garcia-Araez, Energy Reports, 2020, 6, 10–18 CrossRef.
- P. Verma, P. Maire and P. Novák, Electrochim. Acta, 2010, 55, 6332–6341 CrossRef CAS.
- B. L. D. Rinkel, D. S. Hall, I. Temprano and C. P. Grey, J. Am. Chem. Soc., 2020, 22 Search PubMed.
- S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood, Carbon, 2016, 105, 52–76 CrossRef CAS.
- R. Mogi, M. Inaba, Y. Iriyama, T. Abe and Z. Ogumi, J. Power Sources, 2003, 119–121, 597–603 CrossRef CAS.
- J. Nanda, G. Yang, T. Hou, D. N. Voylov, X. Li, R. E. Ruther, M. Naguib, K. Persson, G. M. Veith and A. P. Sokolov, Joule, 2019, 3, 2001–2019 CrossRef CAS.
- S. Tsubouchi, Y. Domi, T. Doi, M. Ochida, H. Nakagawa, T. Yamanaka, T. Abe and Z. Ogumi, J. Electrochem. Soc., 2012, 159, A1786–A1790 CrossRef CAS.
- M. Nie, D. P. Abraham, D. M. Seo, Y. Chen, A. Bose and B. L. Lucht, J. Phys. Chem. C, 2013, 117, 25381–25389 CrossRef CAS.
- M. Nie, J. Demeaux, B. T. Young, D. R. Heskett, Y. Chen, A. Bose, J. C. Woicik and B. L. Lucht, J. Electrochem. Soc., 2015, 162, A7008 CrossRef CAS.
- K. Leung, Chem. Phys. Lett., 2013, 568, 1–8 CrossRef.
- Y. Wang, S. Nakamura, M. Ue and P. B. Balbuena, J. Am. Chem. Soc., 2001, 123, 11708–11718 CrossRef CAS PubMed.
- L. D. Gibson and J. Pfaendtner, Phys. Chem. Chem. Phys., 2020, 22, 21494–21503 RSC.
- D. Kuai and P. B. Balbuena, ACS Appl. Mater. Interfaces, 2022, 14, 2817–2824 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- M. Onuki, S. Kinoshita, Y. Sakata, M. Yanagidate, Y. Otake, M. Ue and M. Deguchi, J. Electrochem. Soc., 2008, 155, A794 CrossRef CAS.
- B. L. D. Rinkel, D. S. Hall, I. Temprano and C. P. Grey, J. Am. Chem. Soc., 2020, 142, 15058–15074 CrossRef CAS PubMed.
- R. A. Moss and M. P. Doyle, Contemporary carbene chemistry, John Wiley & Sons, 2013 Search PubMed.
- M. J. Boyer and G. S. Hwang, J. Phys. Chem. C, 2019, 123, 17695–17702 CrossRef CAS.
- J. Young, P. M. Kulick, T. R. Juran and M. Smeu, ACS Appl. Energy Mater., 2019, 2, 1676–1684 CrossRef CAS.
- C. A. Grambow, L. Pattanaik and W. H. Green, J. Phys. Chem. Lett., 2020, 11, 2992–2997 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543 CrossRef CAS PubMed.
- J. J. Guerard and J. S. Arey, J. Chem. Theory Comput., 2013, 9, 5046–5058 CrossRef CAS PubMed.
- M. I. Chaudhari, J. R. Nair, L. R. Pratt, F. A. Soto, P. B. Balbuena and S. B. Rempe, J. Chem. Theory Comput., 2016, 12, 5709–5718 CrossRef CAS PubMed.
- E. Glendening, J. Badenhoop, A. Reed, J. Carpenter, J. Bohmann, C. Morales and F. Weinhold, NBO 5.0 program, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, USA, 2001 Search PubMed.
- F. Weinhold, C. Landis and E. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440 Search PubMed.
- S. Plimpton, A. Thompson and A. Slepoy, Stochastic Parallel PARticle Kinetic Simulator, Technical Report SPPARKS, Sandia National Lab (SNL-NM), Albuquerque, NM, USA, 2008 Search PubMed.
- S. Plimpton, C. Battaile, M. Ch, L. Holm, A. Thompson, V. Tikare, G. Wagner, X. Zhou, C. G. Cardona and A. Slepoy, Crossing the Mesoscale No-Man's Land via Parallel Kinetic Monte Carlo, 2009 Search PubMed.
- L. D. Jacobson, A. D. Bochevarov, M. A. Watson, T. F. Hughes, D. Rinaldo, S. Ehrlich, T. B. Steinbrecher, S. Vaitheeswaran, D. M. Philipp, M. D. Halls and R. A. Friesner, J. Chem. Theory Comput., 2017, 13, 5780–5797 CrossRef CAS PubMed.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- B. Mennucci, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404 CAS.
- C. Aldaz, J. A. Kammeraad and P. M. Zimmerman, Phys. Chem. Chem. Phys., 2018, 20, 27394–27405 RSC.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, A. Jasz, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjanszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, A. Rak, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00117a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |