Open Access Article
Open Access ArticleDeep learning models for the estimation of free energy of permeation of small molecules across lipid membranes†
Prantar
Dutta
,
Deepak
Jain
,
Rakesh
Gupta
 * and
Beena
Rai
* and
Beena
Rai
Physical Sciences Research Area, Tata Research Development and Design Centre, TCS Research, 54-B, Hadapsar Industrial Estate, Pune 411013, India. E-mail: gupta.rakesh2@tcs.com; Tel: + 91-20-66086422
First published on 21st December 2022
Abstract
Calculating the free energy of drug permeation across membranes carries great importance in pharmaceutical and related applications. Traditional methods, including experiments and molecular simulations, are expensive and time-consuming, and existing statistical methods suffer from low accuracy. In this work, we propose a hybrid approach that combines molecular dynamics simulations and deep learning techniques to predict the free energy of permeation of small drug-like molecules across lipid membranes with high accuracy and at a fraction of the computational cost of advanced sampling methods like umbrella sampling. We have performed several molecular dynamics simulations of molecules in water and lipid bilayers to obtain multidimensional time-series data of features. Deep learning architectures based on Long Short-Term Memory networks, attention mechanisms, and dense layers are built to estimate free energy from the time series data. The prediction errors for the test set and an external validation set are much lower than that of existing data-driven approaches, with R2 of the best model around 0.99 and 0.82 for the two cases. Our approach estimates free energy with satisfactory accuracy using deep learning models within an order-of-magnitude less computational time than required by extensive simulations. This work presents an attractive option for high-throughput virtual screening of molecules based on their membrane permeabilities, demonstrates the applicability of language processing techniques in biochemical problems, and suggests a novel way of integrating physics with statistical learning to great success.
1 Introduction
The permeability of drugs across biological membranes is one of the key factors determining their overall fate in drug delivery applications. Irrespective of the administration route, drug molecules must cross a few lipid bilayers to reach the target cells. For example, transdermal delivery involves penetrating through multiple lipid layers of the epidermis (the outermost layer of the skin),1,2 while oral drug delivery requires crossing the single-layered intestinal epithelium (the outer lining of the large and small intestine of the gastrointestinal tract).3,4 These layers control the molecular transport and protect various organs from undesirable foreign entities like microbes, chemicals, toxins, and allergens by offering a barrier to permeation. But drugs are required to breach these barriers to reach their targets, and hence drug design inevitably considers the permeability of lead candidates across lipid bilayers.Drug transport across membranes occurs mainly in three ways – passive, carrier-facilitated, and active. Passive diffusion is the simple movement of molecules from a higher concentration region to a lower concentration region without any energy expenditure, driven by the concentration gradient. Carrier-facilitated transport relies on membrane proteins that bind to the drug molecules at one side of the membrane, undergo a conformational change, and release the drug on the other side. This mechanism follows the concentration gradient and does not require cellular energy but is useful for polar molecules with a low affinity towards the hydrophobic membrane core. Active transport refers to the protein-mediated movement of molecules from a lower concentration region to a higher concentration region that exploits energy from adenosine triphosphate (ATP) hydrolysis. As passive diffusion predominantly governs the permeation of most available drugs, its study is crucial for gaining mechanistic insights into a fundamental biological phenomenon and designing novel formulations in the pharmaceutical industry. Passive permeability depends on physicochemical properties like size and hydrophobicity for small organic molecules. It can be measured by both experiments5,6 and molecular simulations.7,8
According to the inhomogeneous solubility-diffusion model, the permeability is expressed as:
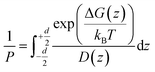 | (1) |
While experimental methods are available for permeability calculations, they are not conducive to high throughput screening of potential drug candidates due to the enormous time and cost of sampling the vast small-molecule chemical space of more than 1060 compounds.13 Molecular dynamics (MD) simulations offer an alternative, in silico approach for calculating PMF and diffusivity. MD-based enhanced sampling algorithms like umbrella sampling (US)14,15 and metadynamics16 have been widely used for obtaining free energy profiles of drug-membrane permeations as a function of intermolecular and intramolecular coordinates.7,17–21 However, the computational expense of MD limits the applicability of these algorithms to studying only hundreds and thousands of molecules within a realistic time frame, even with coarse-grained (CG) modeling techniques.22 Recent developments in Machine Learning (ML) methods and tools permit high throughput computation of physicochemical and pharmaceutical properties.23 The pipeline for this process includes obtaining fingerprints and/or descriptors from cheminformatics packages to represent molecules, building predictive models using suitable statistical learning techniques, and evaluating the models on different datasets. Chen et al. followed this procedure to investigate the permeability of drug-like molecules across lipid membranes.24 Although the computational cost of ML algorithms is minuscule compared to MD simulations, they suffer from several drawbacks like moderate accuracy, low interpretability, sparse training data, and lack of transferability. Combining MD simulations and ML within an integrated computational framework can leverage the best of both worlds and minimize their individual limitations. Physical insights from MD inform ML models to make better predictions, leading to improved accuracy and interpretability, while handling thousands of molecules. Additionally, simulations generate training data when experiments are not available.
Riniker proposed molecular dynamics fingerprints (MDFPs) to featurize small molecules.25 To encode enthalpic and entropic information, the mean, standard deviation, and median of properties like potential-energy components, solvent-accessible surface area, and radius of gyration were extracted from short MD simulations of the molecules in water and vacuum. Combined with simple 2D counts, these fingerprints were used to train ML models to estimate solvation free energies and partition coefficients in various solvents. This approach increased prediction accuracy without being computationally expensive like MD-based methods and attracted a flurry of interest. MDFPs in diverse forms have been employed for identifying P-glycoprotein substrates,26 studying the impact of mutations on protein–ligand binding affinity,27 virtual screening of caspase-8 inhibitors against Alzheimer's disease,28 predicting water–octanol partition coefficients of small molecules,29 computing self-solvation free energies and limiting activity coefficients of chemicals,30 screening ligands for ERK2 Kinase inhibition31 and other applications. Bennett et al. predicted transfer free energies of small molecules from water to cyclohexane using convolutional neural networks, with both voxel-based and graph-based featurization from MD simulations.32 Although their models were trained on a large dataset, the accuracy was moderate, and the implementation was quite complex.
All the studies discussed above flatten the MD trajectories to obtain statistical quantities and hence do not utilize the enormous data generated by simulations. While this makes the data handling easier, a lot of the entropic contribution to free energy is ignored, leading to low model accuracies. Additionally, the features are calculated only from the simulations of the small molecules, and thus the models of free energy prediction of drug permeation fail to capture the differences in lipids.
Two modifications to existing approaches are necessary to capture the physics of permeation effectively: (i) inclusion of the interactions of drugs with both the lipid bilayer and the surrounding aqueous phase in the feature space, and (ii) accounting for the entropic information more rigorously. We accomplished both these refinements by considering MD trajectories as multidimensional time series, with each snapshot described by a vector of features based on drug-lipid and drug-water interactions. This treatment of trajectories allowed us to apply state-of-the-art sequence modeling techniques from natural language processing (NLP) and signal processing to simulation data. In view of this, Deep Learning (DL) algorithms developed for tasks such as machine translation, document classification, sentiment analysis, speech-to-text and text-to-speech conversions, and image captioning can be adapted for predicting properties from short MD runs. Berishvili et al. utilized this strategy for protein–ligand binding affinity prediction and observed better results for time series-based models than average feature-based models.33 Despite model overfitting, their work demonstrated the capability of DL in solving biochemical problems and aiding researchers in the high-throughput virtual screening of molecules. Tsai et al. contributed important theoretical insights and discussion on applying language models on MD trajectories to study the dynamics of complex systems.34
In this work, we developed regression models for predicting the free energy of permeation of small drug-like molecules from the aqueous phase to different lipid bilayers using DL. Free energy data of CG solutes in six phospholipid membranes were obtained from the database reported by Hoffmann and co-workers.35 We performed several short MD simulations of the molecules in water and within the bilayer to calculate time series features. Long short-term memory (LSTM)36 network, a specialized technique for sequence modeling, was used to build the DL architectures. LSTMs are said to resolve the vanishing gradient problem of traditional recurrent neural networks by using a gating mechanism. They learn long-term dependencies in sequences and can be particularly useful in analysing MD trajectories as the volume of data generated by MD simulations is enormous. We further investigate the applicability of the attention mechanism,37,38 the ubiquitous component of modern language models, for the first time in the context of property prediction from simulation data. This study generates highly accurate models of drug permeability and instantiates the potential of physics-informed statistical learning in biochemical sciences.
2 Methods
The methodology of this work involves extracting CG molecules and their corresponding free energies of permeation from the database, performing MD simulations, generating features from the trajectories, and building deep learning models. Each of these tasks is described in the following subsections. Fig. 1 illustrates the overview of our entire workflow – from simulation to model evaluation.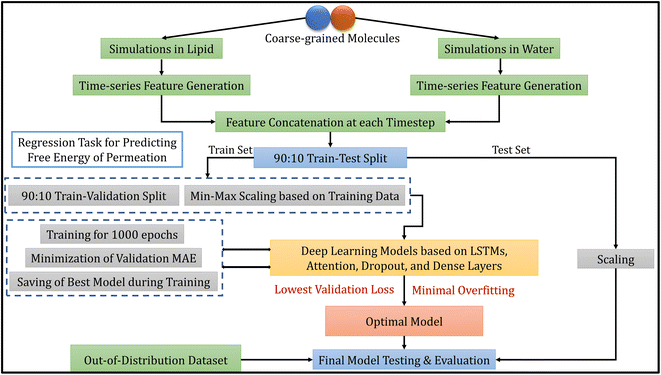 | ||
| Fig. 1 Overall model development workflow, including molecular dynamics simulations, data processing, model selection and evaluation. | ||
2.1 Dataset
The chosen database contains detailed US trajectories of a diverse set of small molecules and lipids, along with the computed PMF profiles.35 The CG Martini model, suitable for reproducing experimental partitioning data, described all the compounds in the system.39 Martini constructs molecules based on 18 bead types, including 14 neutral and 4 charged. The authors considered all possible dimers of neutral beads, amounting to a total of 105 compounds. Due to the modularity and transferability of the Martini model, this small set of solutes represents more than 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 small molecules. US simulations were performed for the 105 dimers in 6 single-component phospholipid membranes – 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC), 1,2-diarachidonoyl-sn-glycero-3-phosphocholine (DAPC), and 1,2-dilinoleoyl-sn-glycero-3-phosphocholine (DIPC), leading to a total of 630 drug-membrane systems. All the PMFs were calculated along the z-axis (bilayer normal) using 24 US simulations for each system, followed by reconstruction with the weighted histogram analysis method.40,41 The detailed simulation and analysis protocols can be found in the original paper of this database. The available 15
000 small molecules. US simulations were performed for the 105 dimers in 6 single-component phospholipid membranes – 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC), 1,2-diarachidonoyl-sn-glycero-3-phosphocholine (DAPC), and 1,2-dilinoleoyl-sn-glycero-3-phosphocholine (DIPC), leading to a total of 630 drug-membrane systems. All the PMFs were calculated along the z-axis (bilayer normal) using 24 US simulations for each system, followed by reconstruction with the weighted histogram analysis method.40,41 The detailed simulation and analysis protocols can be found in the original paper of this database. The available 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 trajectories (630 systems × 24 simulations) have biased potentials due to harmonic restraints applied on the solute and are not suitable for feature generation. Consequently, we only take starting structures from the trajectories. The output labels for our dataset are the free energies of drug permeation in membranes. We obtain these values from the PMF profiles as the difference between the free energies at the lipid bilayer midplane (z = 0.0 nm) and in water away from the interface (z = 4.1 nm). Fig. 2 summarizes the information present in the database.
120 trajectories (630 systems × 24 simulations) have biased potentials due to harmonic restraints applied on the solute and are not suitable for feature generation. Consequently, we only take starting structures from the trajectories. The output labels for our dataset are the free energies of drug permeation in membranes. We obtain these values from the PMF profiles as the difference between the free energies at the lipid bilayer midplane (z = 0.0 nm) and in water away from the interface (z = 4.1 nm). Fig. 2 summarizes the information present in the database.
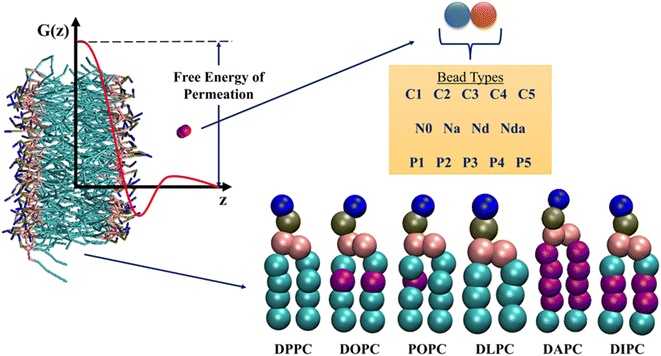 | ||
| Fig. 2 Overview of the information present in the database by Hoffmann and co-workers.35 Potential of Mean Force (PMF) profiles of 105 neutral Martini dimers in six phospholipids are reported. Purple beads in the lipid tails indicate unsaturation. The free energies of permeation are extracted from the PMF profiles, as shown. See ESI† for details on the bead types. | ||
We further tested and evaluated our models on an out-of-distribution dataset. In another study, Hoffmann et al. published the free energies of permeation of many linear trimers and tetramers of Martini beads from aqueous phase to DOPC bilayer.42 We selected 50 linear trimers for testing from the reported 694 in the dataset. The subset was chosen so that its distribution was similar to that of the entire set. This validation was performed to ensure the generalizability of our deep learning models to molecules of relatively bigger sizes, thus ensuring that a greater portion of the small-molecule chemical space is covered.
2.2 Molecular dynamics simulations
We performed unrestrained MD simulations of the 105 CG solutes in the six lipid membranes and in water (aqueous system). The initial configurations for the drug-lipid simulations were obtained from the US trajectories at z = 0.0 nm. The membranes comprised of 64 lipids in each leaflet, with the drug placed at the bilayer midplane. Martini water particles, including 90% non-polarizable and 10% anti-freeze beads, were used to solvate the systems. For the additional test set of linear trimers, the molecules were manually inserted at the centre of a solvated DOPC bilayer. Unlike previous efforts in which free energy and permeability data calculated from CG MD was combined with atomistic feature generation,24,43 we implemented our entire method in the CG space to ensure the scalability of the models for high throughput virtual screening. The non-bonded interactions were cut off beyond a radial distance of 1.2 nm. The Lennard–Jones (LJ) forces decayed smoothly to zero between 0.9 nm and 1.2 nm, and the reaction-field method44 accounted for the long-range electrostatics. All initial structures were energy minimized using the steepest descent method, followed by 2 ns NVT and 5 ns NPT equilibrations. The actual production runs were performed for 21 ns, and we stored the output after every 2000 steps. The temperature was coupled at 300 K by the Parrinello–Bussi velocity rescale thermostat45 with 1 ps time constant. The Berendsen barostat46 with 6 ps time constant and the Parrinello–Rahman barostat47 with 12 ps time constant were used for semi-isotropic pressure coupling at 1 bar during equilibration and production, respectively. The leapfrog integrator solved the equations of motion with a timestep of 20 fs during equilibrations and 30 fs during production. Periodic boundary conditions were implemented in all three directions. We maintained consistency in simulation settings with the database paper. For the drug-water simulations, we placed single solute molecules at the centre of 3 nm × 3 nm × 3 nm cubic boxes and solvated the systems with water beads. A protocol similar to drug-lipid simulations was followed, involving energy minimization, 2 ns NVT equilibration, 5 ns NPT equilibration, and 21 ns production. Except for the pressure coupling being isotropic, other settings were kept the same. All simulations were performed using the GROMACS 2018.4 software.48–502.3 Featurization and data pre-processing
Selecting appropriate descriptors is a challenging task that requires deep domain knowledge and often multiple iterations. Traditional cheminformatics tools generate hundreds to thousands of descriptors, most of which are not tailored for specific applications, and lack of expert feature engineering can lead to poor model quality. For the sequential models, we included 8 time-series features for describing the data – 4 from the drug-lipid simulations and 4 from the drug-water simulations.Three out of eight features (lj-mol-wat, lj-mol-lip, sasa) were normalized by the number of CG beads making up the drug (two in the case of dimers) to make our model scalable and generalizable. In total, 350 snapshots were saved from each MD trajectory, and a vector of features described each snapshot. The vectors from drug-lipid and drug-water simulations were concatenated at every timestep. Inspired by Berishvili et al.,33 we represent the input data for one sample as a 2D array with 350 rows (timesteps) and 8 columns (features). Table 1 lists the features used along with their brief descriptions. While choosing them, we took hints from existing literature on ML models involving biomolecules, as well as the theoretical conception of statistical mechanics and molecular simulations. A feature was selected considering two conditions – it should be easily calculable using GROMACS without any additional functionality, and it should at least have a qualitative physical or thermodynamic relation with the free energy. Our procedure encodes the simulation data in terms of collective variables. It thus captures the physics of the systems without storing and handling entire trajectories consisting of particle positions and velocities at all time steps.
| Feature | Description |
|---|---|
| Bondener | Bond energy of a molecule in water |
| lj-mol-wat | Lennard–Jones interaction energy between molecule and water; normalized by the number of beads making up the molecule |
| Molwat-enthalpy | Enthalpy of the molecule-in-water system |
| Sasa | Solvent accessible surface area of molecule in water; normalized by the number of beads making up the molecule |
| lj-mol-lip | Lennard–Jones interaction energy between molecule and lipid; normalized by the number of beads making up the molecule |
| Apl | Area per lipid of bilayer |
| rmsd-lip | Root mean square deviation of lipid |
| rmsd-mollip | Root mean square deviation of molecule + lipid |
The dataset was randomly split into training and test sets with a train-test ratio of 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. Furthermore, 10% of the data from the training set was taken to be the validation set, and the rest was used for model building. Hence, there were 510 training examples, 57 validation examples, and 63 test examples. Multiple training, validation, test sets were created with different random splits to verify the model reliability (please see ESI† for details). We applied min–max normalization to the time-series features such that the rescaled features were between 0 and 1. The data pre-processing was performed with the Scikit-learn library.51
10. Furthermore, 10% of the data from the training set was taken to be the validation set, and the rest was used for model building. Hence, there were 510 training examples, 57 validation examples, and 63 test examples. Multiple training, validation, test sets were created with different random splits to verify the model reliability (please see ESI† for details). We applied min–max normalization to the time-series features such that the rescaled features were between 0 and 1. The data pre-processing was performed with the Scikit-learn library.51
2.4 Model development
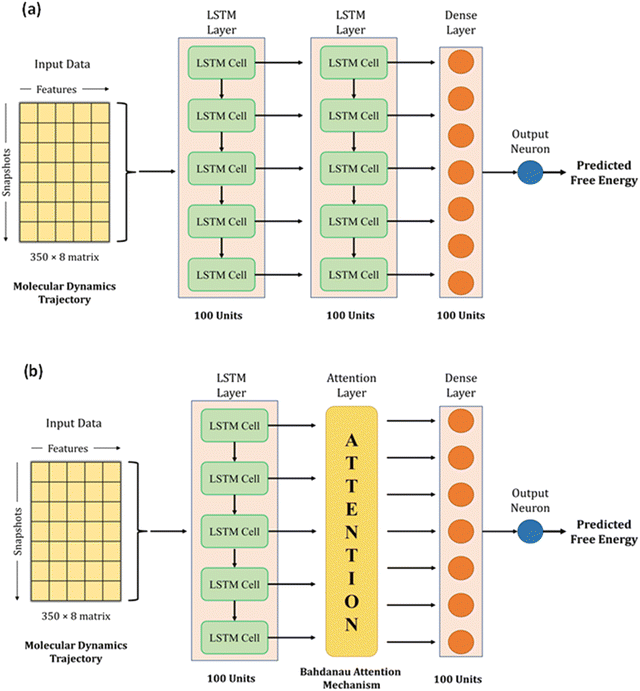
We used LSTM, attention, and dense layers to build our deep learning models. Our first model consisted of two consecutive LSTM layers, a dense layer, and the final output neuron, as shown in Fig. 3a. Each LSTM layer consisted of 100 hidden units with hyperbolic tangent activation function, and the dropout technique was employed with 0.5 probability to reduce overfitting. The dense layer was made up of 100 neurons with a rectified linear unit (ReLU) activation function. The input data of 2D arrays were fed to the network in batches of 32. The Adam optimizer with a learning rate of 0.0003 and mean absolute error (MAE) loss function were used to train the model. During the training process of 1000 epochs, the model with the lowest validation loss was saved as the best model. We experimented with different model architectures, loss functions, and learning rates; the selected choices optimized the loss, the extent of overfitting, and training time per epoch. We calculated MAE, root mean square error (RMSE), and R2 for training, validation, and test sets to monitor model performance.With the conjecture that DL techniques developed for NLP work well with time series, we leveraged the attention mechanism to learn from our trajectory data. Earlier, neural network-based machine translation relied on encoder-decoder architectures where the encoder transforms the input sentences into fixed-length vectors from which the decoder produces the translated output. Bahdanau et al. hypothesized that the fixed length encoding vector is a bottleneck because the decoder has restricted knowledge of the input information.37 They proposed the attention mechanism to overcome this bottleneck, which identifies parts of the input sentence pertinent to an output word.
We adopted the Bahdanau attention mechanism to sequentially compute the alignment score, weights, and context vector. In translation tasks, the context vector is fed to the decoder at each time step. However, our network has no decoder; we simply replace the second LSTM layer in our first model with the attention mechanism. Therefore, the output of the first LSTM layer is fed to the attention layer, which generates the context vector that acts as an input to the dense layer. Fig. 3b shows the architecture of this hybrid model. The training protocol and settings were kept the same as the first model. Henceforth, the first model with two LSTM layers and a dense layer will be referred to as Model-L, and the second model with an attention mechanism in place of an LSTM layer will be referred to as Model-LA. A magnified view of the architecture, along with technical details about LSTM and attention mechanism, is presented in Section S4 (ESI†).
We also built a baseline deep neural network (DNN) model, also known as multilayer perceptron, to compare the results with those of Model-L and Model-LA. The eight features were averaged over the entire 21 ns trajectory, and an input vector, instead of an input matrix, was obtained corresponding to each free energy value. The data splitting and training protocols of the DNN model were kept similar to those of Model-L and Model-LA. The optimal model consisted of the input layer, two hidden layers with 128 neurons each, and the output neuron. The rectified linear unit (ReLU) activation function was used for both the hidden layers, along with the dropout technique with a probability of 0.3. All the models were implemented using the Keras API of TensorFlow 2.52
3 Results and discussion
3.1 Exploratory data analysis
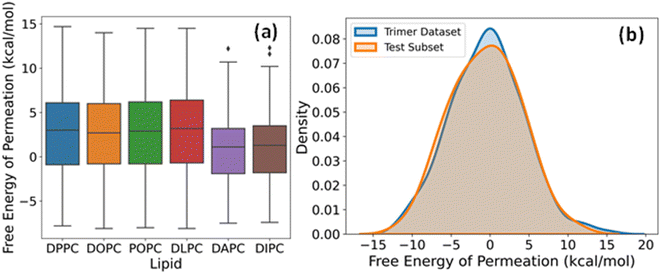
The label for our regression problem is the free energy of permeation of small molecules from the aqueous phase to the lipid bilayer. This quantity is positive for hydrophilic molecules that prefer to stay in the water and negative for hydrophobic molecules that show more affinity towards the bilayer core. The free energy values indicate relative permeabilities of molecules across lipid membranes at a constant temperature and pressure. Hence, for large scale virtual screening of candidates for pharmaceutical and other biological applications, fast estimation of accurate free energy is imperative. Fig. 4a shows the distribution of free energies of the drug-lipid systems in our database. The median, range, and distribution of free energies for small molecules with DPPC, DOPC, POPC, and DLPC are alike. For DAPC and DIPC, both median and variability are slightly lower. Lipids are often assumed to be identical and approximated by simpler organic solvents like octanol for free energy calculations. However, there are subtle differences due to chain length and degree of unsaturation of lipids, which affect their phase behaviour and consequently the free energy.53–56 The boxplots show that our dataset includes sufficiently diverse species in the small molecule chemical space despite having two-bead molecules only.The dataset of free energies of permeation of linear trimers of CG beads from the aqueous phase to the DOPC bilayer consists of 694 entries. We chose a subset of 50 representatives among them in a quasi-random way for additional testing and validation of our DL models. A series of subsets were generated using different random states and subjected to the two-sample Kolmogorov–Smirnov (KS) test for goodness of fit with the complete set, and the one with the lowest value of KS statistic was selected. The kernel density estimation plots of the entire trimer dataset and the final test set of 50 overlap almost entirely, as evident from Fig. 4b. This sampling method maximizes the likelihood that the performance metrics on this test data, hereafter referred to as trimer-test set, represent our model's general relevance to linear trimers. If the prediction errors are within an acceptable range, the applicability of the model increases to a few hundred thousand more small molecules.
3.2 Model performance
The predictions of the DL networks are compared with the actual free energy values computed using US to evaluate model performances. For the models to be reliable for high-throughput free energy estimation, the statistical error must be within tolerable limits. Due to the natural thermal fluctuations in MD simulation-based methods, an error around 1–2 kBT (∼0.6–1.2 kcal mol−1 at 300 K) can be considered sufficiently accurate. The major decrease in training and validation losses occurred within the first 100 epochs during the training phase. We continued to train for another 900 epochs to reduce the losses further and find the best model. After around 500 to 600 epochs, both architectures, with and without attention, started overfitting the training data. The loss history plots of the two models are shown in Fig. S3 (ESI†).
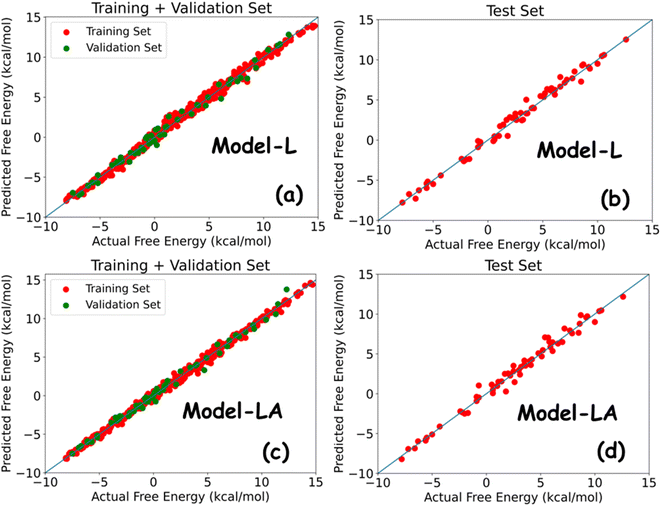
Table 2 summarizes the performance metrics of Model-L and Model-LA on the training, validation, and test sets. The results show that both models are powerful in predicting the free energy of permeation from the multidimensional time series generated using MD simulations. The MAEs and RMSEs on all datasets are lower than standard errors in US, with R2 being around 0.99. The comparable results in all three cases indicate the generalizability of our models. Model-LA performed marginally better than Model-L on the training and validation data, while the accuracy was similar for test data for both the models. To the best of our knowledge, this work presents the most accurate statistical approach for predicting permeation free energies of small molecules in membranes to date. More model refinements are not meaningful since our test errors are already less than the magnitude of energy fluctuations. We also compared the performances of Model-L and Model-LA with a baseline case of the DNN model trained on trajectory-averaged features. The MAEs for the training, validation, and test sets are 0.87 kcal mol−1, 0.91 kcal mol−1, and 0.95 kcal mol−1, respectively, which are more than twice of the other two models. Fig. 5 plots the predicted free energies of the two sequential models with the actual free energies from the dataset. No significant outliers can be visually detected in either case. The maximum deviations of the test predictions from the actual values were 1.52 kcal mol−1 (∼2.5 kBT) and 1.68 kcal mol−1 (∼2.8 kBT) for Model-L and Model-LA, respectively. Hence, these models can estimate the free energy of permeation of the ∼400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 small molecules that maps to two Martini beads in various phospholipid membranes, using a combination of CG MD and DL, at a of the computational expense of US, with high accuracy.
000 small molecules that maps to two Martini beads in various phospholipid membranes, using a combination of CG MD and DL, at a of the computational expense of US, with high accuracy.
| Model | Performance metrics | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Training set | Validation set | Test set | |||||||
| MAE | RMSE | R 2 | MAE | RMSE | R 2 | MAE | RMSE | R 2 | |
| Model-L | 0.30 | 0.39 | 0.993 | 0.44 | 0.54 | 0.988 | 0.45 | 0.56 | 0.987 |
| Model-LA | 0.24 | 0.32 | 0.996 | 0.34 | 0.46 | 0.992 | 0.46 | 0.61 | 0.984 |
Neural network architectures like LSTMs are regularly applied for diverse time series problems in science and engineering with reasonable success. Hence, their superior performance with MD simulation data comes as no surprise. However, in this case, the key challenge is the representation of complex trajectories in terms of a few variables. Unlike other problems where the raw time series is modeled, feature selection and engineering play a critical role in determining model performance. We studied the inclusion of several additional features like the radius of gyration of the small molecule, LJ interaction between the lipid molecules, and LJ interaction between the lipid and water molecules, but they did not improve the models. The features are further discussed in Section 3.4 in terms of model generalizability. Continuing with the assumption that sentences in natural languages and time series are both sequences and hence analogous, the attention mechanism becomes an obvious choice for building a network to model the latter. We implemented a simple block in Model-LA, similar to the encoder section of Bahdanau attention, for computing the context vector from the output of our first LSTM layer. The results show that Model-LA achieves comparable or better performance than Model-L, thus justifying the analogy. Moreover, the training time per epoch for Model-LA is half of that for Model-L, making it cheaper to train.
3.3 Effect of trajectory length
The simulation time and the number of snapshots used for generating the time series features can play a crucial role in determining the model performances. 350 snapshots from a 21 ns simulation serve as the input to our models. Although CG MD simulations of systems described in this work are fast, reducing the required trajectory lengths will be beneficial for accelerating the process. But a shorter trajectory can affect the prediction accuracy as MD simulations often rely on extended simulations to compute properties reliably. We trained DL models with the same architecture and hyperparameters as Model-L and Model-LA but with three different sizes of the trajectory as input: (i) 300 snapshots from an 18 ns simulation, (ii) 200 snapshots from a 12 ns simulation, and (iii) 100 snapshots from a 6 ns simulation. Table 3 presents the model performance for all these computational experiments. As evident, the performance metrics of the shorter and longer trajectories are comparable. In the case of Model-L, the shortest trajectory of 6 ns simulation with 100 snapshots shows the lowest error for all three sets. Mixed results for different datasets are observed for Model-LA, but the 6 ns trajectory can be considered an optimal choice based on the test error and R2. Hence, we can fine-tune our models and predict the free energy of permeation using a lesser amount of data. However, it should be noted that the slight improvements in model performances are not too significant since our errors are lower than kBT. The main advantage is from the speed-up perspective – the simulation time required for featurization becomes less than 30% of the original. It is also of use to consider how the smaller input size influences the predictions for out-of-distribution data. The effect of trajectory length on the model performance for the external test set is elaborated in the next section.| Model | Simulation Time | Performance metrics | |||||
|---|---|---|---|---|---|---|---|
| Training set | Validation set | Test set | |||||
| MAE | R 2 | MAE | R 2 | MAE | R 2 | ||
| Model-L | 6 ns | 0.30 | 0.994 | 0.33 | 0.993 | 0.42 | 0.988 |
| 12 ns | 0.40 | 0.988 | 0.47 | 0.986 | 0.50 | 0.983 | |
| 18 ns | 0.35 | 0.992 | 0.39 | 0.990 | 0.49 | 0.983 | |
| Model-LA | 6 ns | 0.27 | 0.994 | 0.34 | 0.990 | 0.40 | 0.989 |
| 12 ns | 0.23 | 0.995 | 0.31 | 0.993 | 0.47 | 0.984 | |
| 18 ns | 0.22 | 0.996 | 0.36 | 0.992 | 0.39 | 0.986 | |
This lesser data requirement can be attributed to the simpler physics of CG systems whose interactions are reliably represented with short trajectories. We don't need to capture any biophysical phenomena with slow kinetics and long relaxation times. Furthermore, the energy minimization and equilibration of the systems before the production runs ensure high-quality data right from the start of the simulations. Simulations longer than what is used in our work may have a detrimental effect on the model quality, in addition to being computationally expensive. Molecules with extreme degrees of hydrophobicity or hydrophilicity may spontaneously diffuse from the lipid phase to the aqueous phase or vice versa during the simulation, leading to undesirable data points in the time series. However, an exact interpretation of neural network performances based on the physics of the system is still elusive. Although further optimization may be possible, we consider both 21 ns and 6 ns CG MD of small drug-water and drug-lipid systems to be extremely viable tasks for high-throughput free energy calculations, especially using modern computing resources with hardware accelerators and massive parallelization.
3.4 Validation with external data
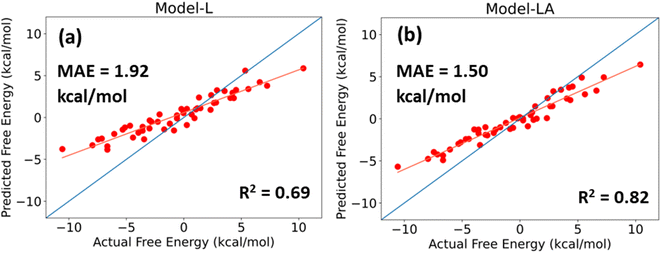
For a DL model to be effective, it must be tested and evaluated on a dataset whose characteristics differ from the data on which it is trained. We use the trimer-test set of 50 samples for this task. Fig. 6 shows the predicted values of Model-L and Model-LA with the actual values reported in the database and performance metrics for inputs with 350 data points in the time series from 21 ns simulations. The prediction accuracies for the trimer-test set are lower than those for the original test set discussed earlier. As the training dataset included two-bead molecules only, a slight drop in prediction accuracy for the external validation set is expected due to the differences in size and chemistry of two- and three-bead molecules. Nonetheless, the performances are still comparable to or superior to that of existing data-driven models in literature. The attention-based network proves to be more scalable due to its lower error and better R2. The MAE of Model-LA drops to 1.37 kcal mol−1 if the two outliers at the extreme ends are removed. In these validation experiments with trimers, it was observed that Model-LA when trained with longer trajectories performs better in comparison to training with shorter ones. For Model-LA trained with 100 data points from 6 ns simulations, the MAE and R2 are 1.68 kcal mol−1 and 0.76, respectively.It is often more vital in virtual screening applications to correctly rank molecules based on their relative free energy of permeation even if the absolute predictions are not too accurate. Generally, a few top candidates are chosen from hundreds or thousands after screening and subjected to explicit simulations or in vitro experiments. The Pearson correlation coefficient and Spearman's rank correlation coefficient for Model-LA with the trimer-test set were calculated to be 0.969 and 0.967, respectively. Fig. 6 also reveals the linear, monotonous relationship between the actual and predicted free energy values. Hence, this model can be reliably deployed to screen small drug-like molecules represented by three beads, even though the training data only involved two-bead molecules.
The normalization of the three properties – LJ interaction between molecule and water, solvent accessible surface area, and LJ interaction between molecule and lipids, by the number of beads constituting the molecules, enables the models' scale-up. The model predictions are especially sensitive to the two LJ interaction features. We studied models without this normalization and observed errors over 5 kcal mol−1 and negative R2 for the trimer-test set. If we compare a dimer and a trimer made of a single bead type, the permeation free energies should ideally be similar because of their comparable hydrophobicity or hydrophilicity. But the average LJ interaction values for the trimer are about one and a half times that of the dimer due to their bead counts. As the models are trained on dimers only, they do not generalize to trimers without the normalization. The radius of gyration, a popular choice as a feature for studying small molecules, caused no significant change in the model performance for dimers but considerably worsened the trimer predictions and was omitted.
3.5 Time advantage
The primary objective of our work is to devise a solution to estimate the free energy of permeation of small molecules across membranes with similar accuracy as MD simulation-based methods but at a much faster rate. As most virtual screening tasks involve hundreds or thousands of molecules, the computational paradigm must be well equipped to handle them within a realistic time frame. Our simulations and training processes were benchmarked on a single AMD Ryzen 5 3500U processor with 4 GB RAM. No parallelization of the GROMACS code was involved. The drug-water simulation of each system, including equilibration, took around 6.5 minutes for 21 ns runs, whereas 105 minutes were required for drug-lipid simulations. If we consider 6 ns production for featurization, approximately 55 minutes is necessary for completing both simulations of each drug-lipid combination. For US simulations of drug permeation in membranes, 25 to 30 simulation windows are usually deployed. Restraining harmonic potentials are applied for each window, and equilibration and about 20 ns production runs are performed. Thus, the approximate time required for each system on the same computer is 45 to 55 hours. US also needs extensive setup and postprocessing routines. Comparing the two approaches, we observe that a speed-up of 25× (using 21 ns trajectories) to 50× (using 6 ns trajectories) can be achieved by following our hybrid method of combining MD with DL. Similar speed-ups are expected for other system architectures like GPUs and clusters.Our approach can be best utilized in combination with the Auto-martini tool,57 which constructs Martini structure and topology file for simulation in GROMACS from simplified molecular-input line-entry system (SMILES) notation of small organic molecules. More than 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules fall within the scope of our DL models and hence can be easily converted to CG representations. Using our method, high-performance computing systems can potentially screen hundreds to thousands of molecules per day, depending on their configuration. End-users with limited computational resources too can compute free energies of hundreds of molecules within a realistic time frame using standard personal computers.
000 molecules fall within the scope of our DL models and hence can be easily converted to CG representations. Using our method, high-performance computing systems can potentially screen hundreds to thousands of molecules per day, depending on their configuration. End-users with limited computational resources too can compute free energies of hundreds of molecules within a realistic time frame using standard personal computers.
The training times per epoch using the same processor were 6 seconds and 3 seconds for Model-L and Model-LA, respectively, with 350 data points from the entire 21 ns trajectory as input. They were reduced to 2 seconds and 1 second, respectively, when only 6 ns simulation data was used. Therefore, replacing the second LSTM layer in Model-L with an attention mechanism halves the training duration. This decrease can be particularly advantageous when the amount of training data is enormous. The errors can also be minimized below desired levels by only training for 200 to 300 epochs. Hence, our architectures, especially Model-LA, can be easily retrained with more data to cover an even larger section of the small molecule chemical space.
3.6 Comparison and contextualization
Although we cannot directly compare our findings with existing literature due to differences in size and nature of the datasets, we closely look at related works on permeability. Chen et al. obtained maximum R2 value around 0.7 using deep neural networks and fingerprint featurization in their work on permeability of small molecules across lipid membranes.24 Bennett et al. calculated the water-cyclohexane transfer free energies of small molecules using convolutional neural networks trained on graph-based, voxel-based, and MD-derived features, with R2 of the best model around 0.8.32 Dutta et al. developed data driven equations of drug-membrane permeability which are highly interpretable, and the maximum obtained R2 being around 0.85.43 Our method outperforms all these models with much lesser data and considering different kinds of lipid membranes, although the complexity of our dataset is lower due to coarse graining of the molecules. Using an approach like ours, albeit for a different problem of protein–ligand binding affinity, Berishvili et al. obtained maximum validation R2 lower than 0.5.33 In Riniker's work on MDFPs, RMSEs calculated for a wide range of free energy estimation problems were found to be around 1 kcal mol−1 or higher.25The primary motive behind integrating MD simulations and ML is enormous data being generated in form of trajectory, while the power of ML models increase as more data is fed into it. Hence, combining the two techniques can help in generating deeper insights and making better predictions at low computational costs, along with acceleration and automation of molecule and material design pipelines. In this work, we use data from entire trajectories instead of compressing them into average quantities to leverage the power of advanced sequence modeling techniques like LSTM and attention mechanism. Calculation of free energy from simulations is challenging since the entropy contribution to free energy cannot be estimated simply by averaging over the snapshots of a trajectory, unlike other thermodynamic quantities like temperature, pressure, density, and enthalpy. For accurate computation, MD-based methods like free energy perturbation, Bennett acceptance ratio, umbrella sampling, and metadynamics rely on extensive sampling of the system to capture various relevant configurations at different states of interest. By representing the trajectories as multidimensional series of features, we similarly incorporate information regarding multiple microstates during the temporal evolution of the system along a low dimensional space of eight parameters. Properties like LJ interactions, bond energy, and solvent-accessible surface area are not functions of time themselves, but their fluctuating values over a trajectory help us in constructing time series to encode vital entropic information. Moreover, free energy is a thermodynamic quantity whose calculation using simulations relies on extensive sampling of a molecular system and our approach incorporates multiple relevant microstates in the model. As a result, the two models developed in this paper performs better than traditional neural networks trained on static or average data. Our approach also captures the exact physics required to study permeation–the interaction of the small molecule with water and with the lipid bilayer, unlike the existing works discussed previously where bulk simulation of the molecule or molecule in water simulation is performed.
Application of ML in MD simulations is a growing field of inquiry, especially with the rise in deep learning and high-performance computing. Researchers have applied data-driven techniques, including advanced neural networks, for a wide range of fundamental and applied tasks like force field development, coarse graining of molecules, prediction of thermodynamic and physicochemical properties, improvement of sampling efficiency, and acceleration of the simulations. An excellent review of the state-of-the-art can be found in the article by Frank Noé and co-workers.58 Simultaneously, development of open-source software tools like TorchMD59 is critical for easier and faster implementation and benchmarking of new ideas. The simulation design, trajectory handling, and modeling approaches proposed in our work can generalize to other applications as well, if aided by relevant domain expertise in problem formulation and feature selection.
4 Conclusions
In this paper, we developed a hybrid modeling approach by combining physics-based and data-driven methods to estimate the free energy of permeation of small drug-like molecules across phospholipid membranes. Time series features calculated from MD simulation trajectories were used to build DL models comprised of LSTMs, attention mechanism, and dense layers. Our models were trained on molecules made up of two CG beads and tested on both two-bead and three-bead molecules. The predictions were highly accurate, with errors lower than the intrinsic thermal fluctuations for two-bead molecules and existing data-driven methods for three-bead molecules. Additionally, free energy estimations can be sped up by 25 to 50 times compared to traditional MD-based methods. The main novelties of this work include featurization from drug-lipid and drug-water simulations and the use of attention mechanism to learn from simulation data. Comparing errors, rank correlations, and time scales, we conclude that our modeling framework can serve in pharmaceutical and related applications as an attractive option for high-throughput virtual screening of small molecules based on their membrane permeabilities.Although our models are powerful, their scope and robustness can be enhanced by training with datasets of trimers, tetramers, or even larger molecules. The initial simulations to generate data may be computationally expensive because the number of possible combinations of beads blows up as the bead count increases. Still, eventually, it can replace US as the go-to alternative when only the free energy value is needed and not the PMF profile and mechanistic details. Recently, Kadupitiya et al. showed that the statistical errors associated with MD trajectories can be leveraged to improve neural network predictions—a noteworthy contribution that can influence the development of more generalizable DL models based on simulation data in the future.60 This work does not cover free energy barriers at the lipid–water interface for permeation, which may play a crucial role in some instances. Building models which learn from simulation of molecules at interfaces and can simultaneously predict the free energy of permeation and interface barrier can be a topic of future study. Developing an automated framework that integrates coarse-graining tools, MD simulations using GROMACS, and DL models will be hugely beneficial for practical purposes. Such a framework would require the SMILES string and the lipid type as an input from the user and furnish the predicted free energy as the output after carrying out the intermediate operations. This work also demonstrates the relevance of adopting recent progress in NLP to problems in biochemistry and provides insights that can be useful for studying other biomolecular systems and processes.
Data availability
The free energy data used for building and evaluating the models in this paper are obtained from the databases reported by Hoffmann and co-workers,35,42 and are available publicly. All technical details relating to software tools, data processing, simulation design, feature extraction, model building, and model evaluation are provided in the manuscript text for easy reproduction of the results. However, the authors are unable to share the full codes due to organizational policies and intellectual property rights of their employer.Author contributions
D. J. and R. G. conceived the project idea. P. D. and R. G. designed the MD simulations and featurization. P. D. and D. J. developed the deep learning models. All authors contributed to the interpretation and discussion of the results and preparation of this manuscript.Conflicts of interest
A part of this work is filed as an Indian patent, with application number 202221016248, on March 23, 2022, with the title “Method And System For Determining Free Energy Of Permeation For Molecules”.Acknowledgements
The authors would like to thank Mr K Ananth Krishnan, CTO, Tata Consultancy Services and Dr Gautam Shroff, Head of Research, Tata Consultancy Services, for their constant encouragement and support during this project.References
- M. R. Prausnitz, S. Mitragotri and R. Langer, Current status and future potential of transdermal drug delivery, Nat. Rev. Drug Discovery, 2004, 3(2), 115–124 CrossRef CAS PubMed.
- Y. Badhe, R. Gupta and B. Rai, Structural and barrier properties of the skin ceramide lipid bilayer: a molecular dynamics simulation study, J. Mol. Model., 2019, 25(5), 140 CrossRef PubMed.
- A. Banerjee, K. Ibsen, T. Brown, R. Chen, C. Agatemor and S. Mitragotri, Ionic liquids for oral insulin delivery, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(28), 7296–7301 CrossRef CAS PubMed.
- R. Gupta, Y. Badhe, S. Mitragotri and B. Rai, Permeation of nanoparticles across the intestinal lipid membrane: dependence on shape and surface chemistry studied through molecular simulations, Nanoscale, 2020, 12(11), 6318–6333 RSC.
- M. Kansy, F. Senner and K. Gubernator, Physicochemical High Throughput Screening: Parallel Artificial Membrane Permeation Assay in the Description of Passive Absorption Processes, J. Med. Chem., 1998, 41(7), 1007–1010 CrossRef CAS PubMed.
- G. E. Flaten, A. B. Dhanikula, K. Luthman and M. Brandl, Drug permeability across a phospholipid vesicle based barrier: A novel approach for studying passive diffusion, Eur. J. Pharm. Sci., 2006, 27(1), 80–90 CrossRef CAS PubMed.
- R. M. Venable, A. Krämer and R. W. Pastor, Molecular Dynamics Simulations of Membrane Permeability, Chem. Rev., 2019, 119(9), 5954–5997 CrossRef CAS PubMed.
- S. Carpenter Timothy, A. Kirshner Daniel, Y. Lau Edmond, E. Wong Sergio, P. Nilmeier Jerome and C. Lightstone Felice, A Method to Predict Blood–Brain Barrier Permeability of Drug-Like Compounds Using Molecular Dynamics Simulations, Biophys. J., 2014, 107(3), 630–641 CrossRef CAS PubMed.
- J. M. Diamond and Y. Katz, Interpretation of nonelectrolyte partition coefficients between dimyristoyl lecithin and water, J. Membr. Biol., 1974, 17(1), 121–154 CrossRef CAS PubMed.
- S.-J. Marrink and H. J. C. Berendsen, Simulation of water transport through a lipid membrane, J. Phys. Chem., 1994, 98(15), 4155–4168 CrossRef CAS.
- R. Menichetti, K. H. Kanekal and T. Bereau, Drug–Membrane Permeability across Chemical Space, ACS Cent. Sci., 2019, 5(2), 290–298 CrossRef CAS PubMed.
- C. A. Ellison, K. O. Tankersley, C. M. Obringer, G. J. Carr, J. Manwaring and H. Rothe, et al., Partition coefficient and diffusion coefficient determinations of 50 compounds in human intact skin, isolated skin layers and isolated stratum corneum lipids, Toxicol. in Vitro, 2020, 69, 104990 CrossRef CAS PubMed.
- C. M. Dobson, Chemical space and biology, Nature, 2004, 432, 824–828 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid, Chem. Phys. Lett., 1974, 28(4), 578–581 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling, J. Comput. Phys., 1977, 23(2), 187–199 CrossRef.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(20), 12562–12566 CrossRef CAS PubMed.
- E. Awoonor-Williams and C. N. Rowley, Molecular simulation of nonfacilitated membrane permeation, Biochim. Biophys. Acta, Biomembr., 2016, 1858(7), 1672–1687 CrossRef CAS PubMed.
- R. Sun, Y. Han, J. M. J. Swanson, J. S. Tan, J. P. Rose and G. A. Voth, Molecular transport through membranes: Accurate permeability coefficients from multidimensional potentials of mean force and local diffusion constants, J. Chem. Phys., 2018, 149(7), 072310 CrossRef PubMed.
- R. Gupta, D. B. Sridhar and B. Rai, Molecular Dynamics Simulation Study of Permeation of Molecules through Skin Lipid Bilayer, J. Phys. Chem. B, 2016, 120(34), 8987–8996 CrossRef CAS PubMed.
- D. Bochicchio, E. Panizon, R. Ferrando, L. Monticelli and G. Rossi, Calculating the free energy of transfer of small solutes into a model lipid membrane: Comparison between metadynamics and umbrella sampling, J. Chem. Phys., 2015, 143(14), 144108 CrossRef PubMed.
- R. Sun, J. F. Dama, J. S. Tan, J. P. Rose and G. A. Voth, Transition-Tempered Metadynamics Is a Promising Tool for Studying the Permeation of Drug-like Molecules through Membranes, J. Chem. Theory Comput., 2016, 12(10), 5157–5169 CrossRef CAS PubMed.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino and F. Grünewald, et al., Martini 3: a general purpose force field for coarse-grained molecular dynamics, Nat. Methods, 2021, 18(4), 382–388 CrossRef CAS PubMed.
- Z. Wu, B. Ramsundar, N. E. Feinberg, J. Gomes, C. Geniesse and S. A. Pappu, et al., MoleculeNet: a benchmark for molecular machine learning, Chem. Sci., 2018, 9(2), 513–530 RSC.
- G. Chen, Z. Shen and Y. Li, A machine-learning-assisted study of the permeability of small drug-like molecules across lipid membranes, Phys. Chem. Chem. Phys., 2020, 22(35), 19687–19696 RSC.
- S. Riniker, Molecular Dynamics Fingerprints (MDFP): Machine Learning from MD Data To Predict Free-Energy Differences, J. Chem. Inf. Model., 2017, 57(4), 726–741 CrossRef CAS PubMed.
- C. Esposito, S. Wang, U. E. W. Lange, F. Oellien and S. Riniker, Combining Machine Learning and Molecular Dynamics to Predict P-Glycoprotein Substrates, J. Chem. Inf. Model., 2020, 60(10), 4730–4749 CrossRef CAS PubMed.
- D. D. Wang, L. Ou-Yang, H. Xie, M. Zhu and H. Yan, Predicting the impacts of mutations on protein–ligand binding affinity based on molecular dynamics simulations and machine learning methods, Comput. Struct. Biotechnol. J., 2020, 18, 439–454 CrossRef CAS PubMed.
- S. Jamal, A. Grover and S. Grover, Machine Learning From Molecular Dynamics Trajectories to Predict Caspase-8 Inhibitors Against Alzheimer’s Disease, Front. Pharmacol., 2019, 10, 780 CrossRef CAS PubMed.
- S. Wang and S. Riniker, Use of molecular dynamics fingerprints (MDFPs) in SAMPL6 octanol–water log P blind challenge, J. Comput.-Aided Mol. Des., 2019, 34(4), 393–403 CrossRef PubMed.
- J. Gebhardt, M. Kiesel, S. Riniker and N. Hansen, Combining Molecular Dynamics and Machine Learning to Predict Self-Solvation Free Energies and Limiting Activity Coefficients, J. Chem. Inf. Model., 2020, 60(11), 5319–5330 CrossRef CAS PubMed.
- J. Ash and D. Fourches, Characterizing the Chemical Space of ERK2 Kinase Inhibitors Using Descriptors Computed from Molecular Dynamics Trajectories, J. Chem. Inf. Model., 2017, 57(6), 1286–1299 CrossRef CAS PubMed.
- W. F. D. Bennett, S. He, C. L. Bilodeau, D. Jones, D. Sun and H. Kim, et al., Predicting Small Molecule Transfer Free Energies by Combining Molecular Dynamics Simulations and Deep Learning, J. Chem. Inf. Model., 2020, 60(11), 5375–5381 CrossRef CAS PubMed.
- V. P. Berishvili, V. O. Perkin, A. E. Voronkov, E. V. Radchenko, R. Syed and C. Venkata Ramana Reddy, et al., Time-Domain Analysis of Molecular Dynamics Trajectories Using Deep Neural Networks: Application to Activity Ranking of Tankyrase Inhibitors, J. Chem. Inf. Model., 2019, 59(8), 3519–3532 CrossRef CAS PubMed.
- S.-T. Tsai, E.-J. Kuo and P. Tiwary, Learning molecular dynamics with simple language model built upon long short-term memory neural network, Nat. Commun., 2020, 11(1), 5115 CrossRef CAS PubMed.
- C. Hoffmann, A. Centi, R. Menichetti and T. Bereau, Molecular dynamics trajectories for 630 coarse-grained drug-membrane permeations, Sci. Data, 2020, 7(1), 51 CrossRef CAS PubMed.
- S. Hochreiter and J. Schmidhuber, Long Short-Term Memory, Neural Comput., 1997, 9(8), 1735–1780 CrossRef CAS PubMed.
- D. Bahdanau, K. Cho and Y. Bengio, Neural Machine Translation by Jointly Learning to Align and Translate, in ICLR 2015: International Conference on Learning Representations, 2015, https://arxiv.org/abs/1409.0473 Search PubMed.
- M.-T. Luong, H. Pham and C. D. Manning, Effective Approaches to Attention-based Neural Machine Translation, in Conference on Empirical Methods in Natural Language Processing, 2015, https://arxiv.org/abs/1508.04025 Search PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations, J. Phys. Chem. B, 2007, 111(27), 7812–7824 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13(8), 1011–1021 CrossRef CAS.
- M. Souaille and B. Roux, Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations, Comput. Phys. Commun., 2001, 135(1), 40–57 CrossRef CAS.
- C. Hoffmann, R. Menichetti, K. H. Kanekal and T. Bereau, Controlled exploration of chemical space by machine learning of coarse-grained representations, Phys. Rev. E, 2019, 100(3), 033302 CrossRef CAS PubMed.
- A. Dutta, J. Vreeken, L. M. Ghiringhelli and T. Bereau, Data-driven equation for drug–membrane permeability across drugs and membranes, J. Chem. Phys., 2021, 154(24), 244114 CrossRef CAS PubMed.
- J. A. Barker and R. O. Watts, Monte Carlo studies of the dielectric properties of water-like models, Mol. Phys., 1973, 26(3), 789–792 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81(8), 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52(12), 7182–7190 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith and B. Hess, et al., GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26(16), 1701–1718 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4(3), 435–447 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12(85), 2825–2830 Search PubMed.
- F. Chollet, et al., Keras, GitHub, 2015, https://github.com/fchollet/keras Search PubMed.
- M. N. Triba, P. F. Devaux and D. E. Warschawski, Effects of Lipid Chain Length and Unsaturation on Bicelles Stability. A Phosphorus NMR Study, Biophys. J., 2006, 91(4), 1357–1367 CrossRef CAS PubMed.
- I. Ermilova and A. P. Lyubartsev, Cholesterol in phospholipid bilayers: positions and orientations inside membranes with different unsaturation degrees, Soft Matter, 2018, 15(1), 78–93 RSC.
- R. Gupta, B. S. Dwadasi and B. Rai, Molecular Dynamics Simulation of Skin Lipids: Effect of Ceramide Chain Lengths on Bilayer Properties, J. Phys. Chem. B, 2016, 120(49), 12536–12546 CrossRef CAS PubMed.
- R. Gupta and B. Rai, Molecular Dynamics Simulation Study of Skin Lipids: Effects of the Molar Ratio of Individual Components over a Wide Temperature Range, J. Phys. Chem. B, 2015, 119(35), 11643–11655 CrossRef CAS PubMed.
- T. Bereau and K. Kremer, Automated Parametrization of the Coarse-Grained Martini Force Field for Small Organic Molecules, J. Chem. Theory Comput., 2015, 11(6), 2783–2791 CrossRef CAS PubMed.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Machine Learning for Molecular Simulation, Annu. Rev. Phys. Chem., 2020, 71(1), 361–390 CrossRef PubMed.
- S. Doerr, M. Majewski, A. Pérez, A. Krämer, C. Clementi and F. Noe, et al., TorchMD: A Deep Learning Framework for Molecular Simulations, J. Chem. Theory Comput., 2021, 17(4), 2355–2363 CrossRef CAS PubMed.
- J. C. S. Kadupitiya, N. Anousheh and V. Jadhao, Designing Machine Learning Surrogates using Outputs of Molecular Dynamics Simulations as Soft Labels, arXiv, 2021, Preprint, https://arxiv.org/abs/2110.14714.
Footnote |
| † Electronic supplementary information (ESI) available: Martini bead types; alternate training-validation-test data splits; molecules in trimer-test set; Unravelling LSTM and Attention mechanism; Loss history plots. See DOI: https://doi.org/10.1039/d2dd00119e |
| This journal is © The Royal Society of Chemistry 2023 |