Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurately predicting solvation free energy in aqueous and organic solvents beyond 298 K by combining deep learning and the 1D reference interaction site model†
Daniel J.
Fowles
,
Rose G.
McHardy
,
Abdullah
Ahmad
and
David S.
Palmer
 *
*
Department of Pure and Applied Chemistry, University of Strathclyde, Thomas Graham Building, 295 Cathedral Street, Glasgow G1 1XL, Scotland, UK. E-mail: david.palmer@strath.ac.uk
First published on 14th December 2022
Abstract
We report a method to predict the absolute solvation free energy (SFE) of small organic and druglike molecules in water, carbon tetrachloride and chloroform solvents beyond 298 K by combining the 1 Dimensional Reference Interaction Site Model (1D-RISM) and deep learning. RISM is a statistical mechanics based method for modelling molecular solutions that is computationally inexpensive but is too inaccurate for routine SFE calculations in its common form. By replacing the 1D-RISM SFE functional with a 1D convolutional neural network (CNN) trained on RISM correlation functions, we show that predictions approaching chemical accuracy can be obtained for aqueous and non-aqueous solvents at a wide-range of temperatures. This method builds upon the previously reported RISM-MOL-INF procedure which applied RISM to accurately characterise solvation and desolvation processes through solute–solvent correlation functions [Palmer et al., Mol. Pharm., 2015, 12, 3420–3432]. Unlike RISM-MOL-INF however, the newly developed pyRISM-CNN model applied here is capable of rapidly modelling these processes in several different solvents and at a wide-range of temperatures. The pyRISM-CNN functional reduces the predictive error by up to 40-fold as compared to the standard 1D-RISM theory. Prediction errors below 1 kcal mol−1 are obtained for organic solutes in carbon tetrachloride or chloroform solvent systems at 298 K and water solvent systems at 273–373 K. pyRISM-CNN has been implemented in our in-house 1D-RISM solver (pyRISM), which is made freely available as open-source software.
1 Introduction
Solvation thermodynamic parameters are important in modelling many industrial processes, from the behaviour of candidate drugs in the body, to the distribution of potential pollutants in the environment. State-of-the-art computational methodologies are capable of making accurate predictions of solvation thermodynamics for aqueous systems, and have commonly done so in the calculation of pKa,1–3 protein–ligand binding affinities4 and aqueous solubility.5,6 However, there has been a lack of development for organic solvents or non-ambient temperatures.Methods of estimating SFE can generally be separated into two categories, implicit and explicit solvent models. The most common implicit models treat bulk solvent as a uniform polarisable medium defined by a dielectric constant, and have found extensive use through models such as the solvation model based on solute electron density (SMD)7 and the polarisable continuum model (PCM).8,9 However, implicit models fail to capture important short-ranged solute–solvent interactions and only include molecular level details intrinsic to the dielectric constant, which limits their applicability as an approach to determining solvation free energy for complex systems. Explicit solvent models, such as molecular dynamics (MD), offer a viable alternative to implicit continuum based approaches10 but at far greater computational cost.
The reference interaction site model (RISM) is a third approach, capable of calculating solvation dependent thermodynamic parameters at a lower computational cost than explicit models, whilst modelling specific solute–solvent interactions. The RISM theory uses a simplified form of the high-dimensional molecular Ornstein–Zernike (MOZ) equations to model solvent density distribution around a solute molecule through a set of correlation functions, from which two distinct methods have been developed. The most commonly used of these is 3D-RISM, which approximates the MOZ equations by a set of three-dimensional integral equations. With the recent development of several semi-empirical11,12 and theoretical free energy functionals,13,14 3D RISM has found frequent use as a method to predict SFE.15–19 By contrast, the 1D-RISM theory, in which the MOZ equations are approximated as a set of one-dimensional integral equations, is rarely used for quantitative calculations of solvation thermodynamics because it is considered to be too inaccurate in its common form.
Within the RISM framework, solvation free energy predictions are made analytically using one of several available free energy functionals. In 1D-RISM many of these functionals fail to accurately predict the energetic parameters of the chemical system under investigation. These functionals, such as the Hyper-Netted Chain (1D-RISM/HNC) model,20 are too inaccurate for routine use and typically achieve absolute prediction errors above 20 kcal mol−1. Much effort has been put into improving the predictive capabilities of 1D-RISM based functionals for SFE calculations. Some of these improved models, such as the Gaussian Fluctuations (1D-RISM/GF) and Partial Wave models (1D-RISM/PW), can more accurately predict SFE than previous methods.21,22 Although reasonable qualitative agreement with experimental data has been reported, large predictive errors are still commonly observed for many chemical systems.
A novel method for improving the accuracy of 1D-RISM calculated solvation free energies was introduced by Ratkova et al.23 This method combines RISM and cheminformatics into a hybrid approach by making empirical corrections to 1D-RISM calculated SFE. By including correction parameters determined from chemical descriptors, this structural descriptors correction (SDC) model was able to lower the prediction error of small organic molecules in aqueous solvent at 298 K to 1.2 kcal mol−1. However, the inclusion of dataset specific descriptors limits the wider applicability of this approach, with the potential need for reparameterisation when new molecules are introduced. SFE calculations are limited to 298 K and aqueous solvent by the standard SDC model.
In previous work, Palmer et al. reported a new method of accurately predicting physico-chemical properties of drug-like molecules from 1D-RISM characterised solvation and desolvation processes.24 This method, RISM-MOL-INF, trained partial least squares (PLS) models on 1D-RISM correlation functions generated from a dataset of small organic molecules. By replacing the inaccurate 1D-RISM free energy functionals, it was shown that RISM-MOL-INF could make accurate predictions of hydration free energy and caco-2 cell permeability. However, RISM-MOL-INF is untested beyond a limited subset of small organic molecules in aqueous solvent at 298 K. As partial least squares was the only reported model, it is unknown whether a non-linear statistical method may be more suited for this approach. Further, the RISM-MOl-INF method used the RISM-MOL solver, which includes hard-coded solvent and temperature limitations, preventing simulations beyond aqueous solvent and 298 K.
Here, we present an overhaul of the RISM-MOL-INF process with our in-house 1D-RISM solver.25 This solver, pyRISM, provides a more adaptable solver for the solute–solvent 1D RISM equations. Unlike its predecessors, which were limited to aqueous solutions at 298 K, pyRISM is capable of rapidly modelling solvation thermodynamics in both water and most common organic solvents, and at a wide-range of temperatures. By replacing existing machine learning models with a deep learning approach, pyRISM-CNN can make significantly more accurate SFE predictions and has been tested on a considerably larger dataset of organic molecules. These predictions, just as with the pyRISM 1D-RISM implementation, can be expanded to organic solvents and temperatures beyond 298 K. Moving from 1D-RISM calculation to pyRISM-CNN prediction requires minimal additional computational expense as descriptors can be generated as part of the typical 1D-RISM workflow.
2 Theory
2.1 1D-RISM
The details of the general RISM theory have been discussed in depth elsewhere,26 and so only the 1D-RISM theory will be explained here. 1D-RISM uses an approximated one-dimensional form of the molecular Ornstein–Zernike equation with spherically symmetric site–site correlation functions for the modelling of molecular solutions. Both solute and solvent molecules are treated as spherically symmetric sites that solely depend on the distance between these sites, with an individual atom being the simplest representation. There are three types of site–site correlation functions that are considered in RISM: intramolecular correlation functions, total correlation functions and direct correlation functions. The intramolecular correlation functions describe the structure of a given molecule. For two sites within a molecule, s and s′, the intramolecular correlation function is written as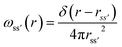 | (1) |
Intermolecular solute–solvent correlations are defined for each pair of solute and solvent sites by the total correlation functions hsα(r) and direct correlation functions csα(r). Here, s refers to a solute site and α to a solvent site. The total correlation functions are closely related to the radial distribution function (RDF) as
| hsα(r) = gsα(r) − 1 | (2) |
The total and direct correlation functions are related via a set of RISM equations
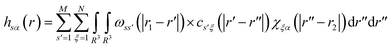 | (3) |
| χξα(r) = ωsolvξα(r) + ρhsolvξα(r) | (4) |
The solvent–solvent site hsolvξα(r) and ωsolvξα(r) are obtained from preliminary solvent–solvent 1D-RISM calculations and molecular structure. To complete the set of RISM equations, closure relations must be introduced
| hsα(r) = exp(−βusα(r) + γsα(r) + Bsα(r)) − 1 | (5) |
The exact bridge functions are typically unknown and so an approximation is needed to solve for the total correlation functions and direct correlation functions. A commonly used closure is the Kovalenko and Hirata (KH) closure27
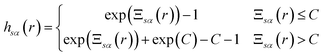 | (6) |
There are multiple expressions available within RISM for determining solvation free energy once the total and direct correlation functions have been solved. The functional is usually selected to be consistent with the closure used within the 1D-RISM calculations. The Gaussian fluctuations approximation (GF),28 KH29 and hypernetted chain (HNC)20 expressions are shown below.
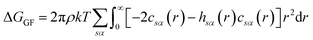 | (7) |
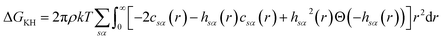 | (8) |
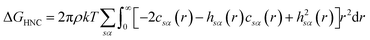 | (9) |
2.2 pyRISM
The pyRISM program25 includes a general method of obtaining variables which contain solvation and desolvation relevant descriptors from the standard 1D-RISM free energy functionals. Previously this method was applied within the RISM-MOL framework and has been described in detail elsewhere,24,30 so only a short summary of the process will be described here. Each of the free energy functionals described in eqn (7)–(9) can be condensed into a generalised form: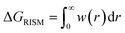 | (10) |
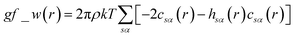 | (11) |
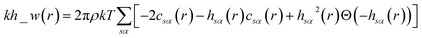 | (12) |
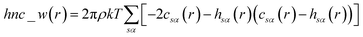 | (13) |
When the 1D-RISM equations are solved, the total and direct correlation functions are represented on a fine grid. The values of the SFED functions at selected grid points provide variables that are denoted as m_w_n, where m is the 1D-RISM free energy functional from which the variable is based and n is the grid point at which the variable is evaluated. Machine learning algorithms are then trained on these variables and the subsequent model can be used for solvation free energy prediction.
3 Methods
3.1 Dataset preparation
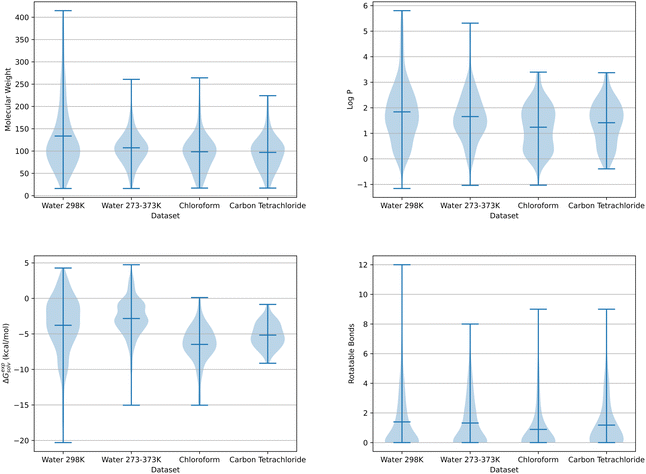
Two sources with known experimental solvation free energies for small organic molecules were used to generate the datasets applied within this work: the Minnesota Solvation Database (MSD)31 and those developed by Chamberlin et al.32,33 The MSD contains experimental solvation free energies in water and several organic solvents at 298 K. Experimental data obtained from Chamberlin et al. includes hydration free energies in a 273–373 K temperature range.As hydration free energies were available over a range of temperatures, two aqueous solvent datasets were compiled. The first dataset contained 521 solute molecules with known experimental hydration free energies at 298 K, 133 of which were obtained from Chamberlin et al.32,33 and 388 from the Minnesota Solvation Database. The second dataset was exclusively taken from Chamberlin et al. and included free energy data in a 273–373 K temperature range for 272 solute molecules. By using free energies over a range of temperatures, a total of 3053 datapoints were available for this multiple temperature dataset. As experimental solvation free energies were only available from the MSD at 298 K, a single dataset was compiled each for chloroform and carbon tetrachloride with 109 and 79 solute molecules respectively. Three additional datasets were compiled, containing SFED descriptors from each solvent. These multi-solvent datasets were separated by temperature into a single 298 K and two 273–373 K datasets. The 298 K dataset was made up of aqueous and organic solvent data taken from the MSD. The first of the multi-temperature datasets combined Chamberlin et al. 273–373 K water data and MSD water and organic solvent data, while the other dataset excluded the additional MSD 298 K water data. Fig. 1 shows the distribution of solute molecules across four chemical descriptors for the chloroform, carbon tetrachloride, water and multi-temperature water datasets discussed here. These molecular properties include molecular weight, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, experimental solvation free energy and the number of rotatable bonds per solute.
P, experimental solvation free energy and the number of rotatable bonds per solute.
The InChi34 function within Open Babel35 was used to generate a unique InChi descriptor for each solute within the MSD and Chamberlin et al. datasets. Any duplicate molecules were then removed using the “unique” parameter within Open Babel.
A conformational search was performed on each solute molecule using MacroModel36 with the OPLS-2005 forcefield37 to obtain the lowest energy conformer for each solute. Each dataset then underwent 1D-RISM calculations as part of the pyRISM package to obtain free energy descriptors.
3.2 1D-RISM calculations
1D-RISM calculations were carried out with pyRISM using the KH closure within a system of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 grid points over 20.48 Å from the solute. Aqueous solvent calculations used the dielectrically consistent reference interaction site model (DRISM),38,39 while organic solvent calculations applied the extended reference interaction site model (XRISM).40 Organic solvent calculations were found to converge more consistently with XRISM than with DRISM. Solvation free energy calculations with the KH, HNC and GF free energy functionals were performed for both aqueous and organic solvent systems. For all calculations it was assumed that solute molecules were embedded within an infinitely dilute aqueous solution. A convergence tolerance of 10−12 was set for all calculations, with a minimum tolerance of 10−5 if the initial calculation failed to converge. The impact from lowering the minimum convergence tolerance to 10−5, as well as the choice of model for 1D-RISM calculations (DRISM or XRISM) on the quality of SFED generated was found to be negligible. A comparison of tolerance threshold and model choice for 1D-RISM calculations is available from Fig. 1 and 2 in the ESI.†
384 grid points over 20.48 Å from the solute. Aqueous solvent calculations used the dielectrically consistent reference interaction site model (DRISM),38,39 while organic solvent calculations applied the extended reference interaction site model (XRISM).40 Organic solvent calculations were found to converge more consistently with XRISM than with DRISM. Solvation free energy calculations with the KH, HNC and GF free energy functionals were performed for both aqueous and organic solvent systems. For all calculations it was assumed that solute molecules were embedded within an infinitely dilute aqueous solution. A convergence tolerance of 10−12 was set for all calculations, with a minimum tolerance of 10−5 if the initial calculation failed to converge. The impact from lowering the minimum convergence tolerance to 10−5, as well as the choice of model for 1D-RISM calculations (DRISM or XRISM) on the quality of SFED generated was found to be negligible. A comparison of tolerance threshold and model choice for 1D-RISM calculations is available from Fig. 1 and 2 in the ESI.†
 .
.
3.3 Obtaining RISM solvation free energy descriptors
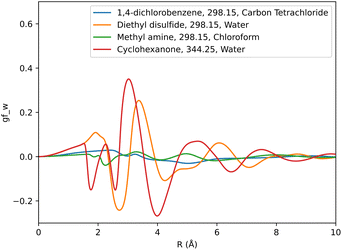
Solute specific SFE descriptors were obtained as a 1D-RISM calculation output using the pyRISM program. A descriptor set was generated for each free energy functional, totaling three sets per set of solute forcefield parameters. As the grid used to represent the 1D-RISM total and direct correlation functions was very fine, leading to multiple correlated variables, a coarser grid-spacing was used to obtain SFE descriptors. To minimise the inclusion of redundant data and to exclude data at long solute–solvent separations in the region where SFEDs approach zero, only every 40th grid point from r = 0 Å to r = 8 Å was considered. This approach produced 160 descriptors per SFE functional for each solute 1D-RISM calculation.These descriptors were then used as an input to machine learning models to predict experimental solvation free energy. For each solvent a total of six separate SFED datasets were compiled. Each of these SFED datasets contain solute specific descriptors generated from pyRISM calculations involving combinations of the KH, HNC and GF free energy functionals and OPLS, GAFF based solute parameters. For example, a typical breakdown of the 298 K chloroform dataset would look like: chloroform-298-KH-GAFF, chloroform-298-HNC-GAFF, chloroform-298-GF-GAFF, chloroform-298-KH-OPLS, chloroform-298-HNC-OPLS, chloroform-298-GF-OPLS. Multi-solvent datasets were also compiled for all the relevant free energy functional and forcefield combinations, which included SFED from each solvent. Multi-temperature datasets were tested in two separate formats, with one including an additional descriptor representing the temperature at which each solute's respective experimental SFE was recorded. Table 1 provides a breakdown of each dataset and its contents. Fig. 2 shows descriptors produced from the GF functional for GAFF parameterised solute molecules in carbon tetrachloride, chloroform and water solvent.
| Solvent | Temperature range | Temp. descr. | SFE functional | Solute parameters | Datapoints |
|---|---|---|---|---|---|
| a Each of these six datasets can be separated according to the free energy functional and forcefield used to parameterise solute molecules, while the multi-temperature datasets can also be separated by the inclusion of temperature descriptors. The multi-solvent/multi-temperature datasets can be further separated by the inclusion of additional MSD 298 K water data, which the dataset with 3629 datapoints includes. | |||||
| Carbon tetrachloride | 298 K | No | KH/HNC/GF | GAFF/OPLS | 79 |
| Chloroform | 298 K | No | KH/HNC/GF | GAFF/OPLS | 109 |
| 298 K | No | KH/HNC/GF | GAFF/OPLS | 521 | |
| Water | 273–373 K | No | KH/HNC/GF | GAFF/OPLS | 3053 |
| 273–373 K | Yes | KH/HNC/GF | GAFF/OPLS | 3053 | |
| 298 K | No | KH/HNC/GF | GAFF/OPLS | 709 | |
| 273–373 K | No | KH/HNC/GF | GAFF/OPLS | 3241 | |
| Multi-solvent | 273–373 K | Yes | KH/HNC/GF | GAFF/OPLS | 3241 |
| 273–373 K | No | KH/HNC/GF | GAFF/OPLS | 3629 | |
| 273–373 K | Yes | KH/HNC/GF | GAFF/OPLS | 3629 | |
3.4 Machine learning models
Machine learning models were trained on all six SFED variations for each of the solvent datasets, as well as a combined solvent dataset. Models were validated by nested cross-validation (CV), with hyper parameters tuned by an inner 5-fold CV loop. Final tuned model performance was evaluated by an outer 50-fold Monte Carlo cross-validation loop with a 70% train/30% test split. A stratified sampling approach was taken for multi-temperature and multi-solvent datasets to ensure datapoints were separated by molecule before splitting into training, validation and test sets. More details on hyper parameter selection for our convolutional neural network (CNN), partial least squares (PLS) and random forest (RF) models can be found in Sections 3.4.1, 3.4.2 and 3.4.3 respectively. Each variable was centered by subtracting its mean value in the training data, and scaled by dividing by the standard deviation of its values in the training data. A repository of SFED datasets and scripts to train CNN, PLS and RF models can be found at: https://doi.org/10.5281/zenodo.7108371.The final architecture included three blocks of Conv1D-MaxPooling1D-BatchNormalisation with a subsequent Flatten layer and Dense output layer. Convolutional layers were created using the ‘Conv1D’ layer package in Keras with 32 output filters, a kernal size of 3 and stride length of 2. No padding was included and the rectified linear activation function (ReLu)51 was used. Each of the subsequent layers were also taken from Keras, with the max pool size within MaxPooling1D layers set to 2. Default parameters were used for BatchNormalisation and Flatten layers. The loss function and metric was set to ‘mse’ (mean squared error), with the ‘Adam’ optimiser.52 Each model could run for a maximum of 60 epochs with a patience of 20 epochs included through the Keras ‘EarlyStopping’ callback.
3.5 Statistical analysis
Solvation free energy predictions were evaluated against experimental values of SFE using the coefficient of determination (R2) and root mean squared deviation (RMSD).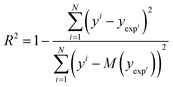 | (14) |
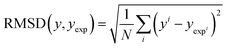 | (15) |
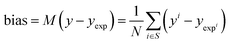 | (16) |
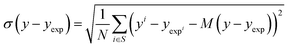 | (17) |
The bias provides the systematic error, while the standard deviation gives the random error that is not explained by the model. The bias and standard deviation are connected to the RMSD by:
| RMSD(y,yexp)2 = M(y − yexp)2 + σ(y − yexp)2 | (18) |
A model which reports an RMSD greater than the standard deviation of the experimental data provides less accurate predictions than the null model provided by the mean of the experimental data.
Statistical analyses were performed in a Python environment using the ‘sklearn.metrics' module available in scikit-learn.53
4 Results and discussion
4.1 pyRISM solvation free energy predictions
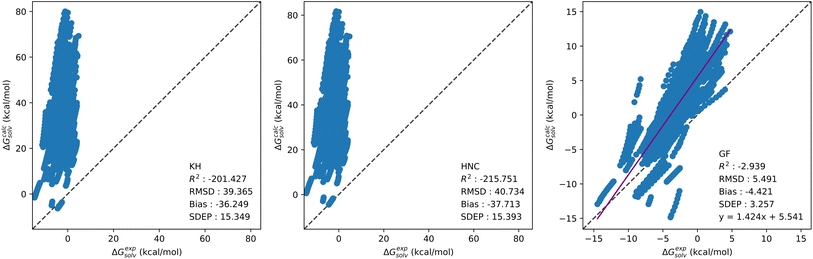
Solvation free energy calculations were performed using our in-house 1D-RISM solver, with the KH, HNC and GF free energy functionals. Table 2 provides a breakdown of SFEs calculated by the standard 1D-RISM theory (i.e.eqn (7)–(9)) separated by solvent, temperature and solute parameters. In-line with previous studies, 1D-RISM free energy functionals are generally unable to accurately predict solvation free energy. The KH and HNC functionals are particularly inaccurate, with a root mean squared deviation (RMSD) exceeding 40 kcal mol−1 for hydration free energies. As noted in the Theory section, the functional is usually selected to be consistent with the closure used within the 1D-RISM calculation. Therefore, using the HNC functional with the KH closure is not standard practice, but the results are provided here as a direct comparison for the CNN model trained on the related SFEDs; using the HNC functional with the HNC closure also results in large errors.24 Conversely, the GF functional provides the most accurate predictions, with an average RMSD between OPLS and GAFF of 1.67, 2.31 and 6.86 kcal mol−1 for carbon tetrachloride, chloroform and water respectively. A similar trend is seen from a comparison of R2, which shows that only the GF functional is able to provide reasonable correlation between experimental and predicted SFE. Large negative R2 values suggest most of these models fit the data worse than the mean of experimental SFE data (more information on the statistical analysis used in this study can be found in Section 3.5). The choice of solute forcefield parameters also impacts prediction accuracy. This is clearest for aqueous solvent calculations performed at 298 K, with OPLS giving a higher RMSD than GAFF by 5.08, 4.95 and 3.01 kcal mol−1 for KH, HNC and GF respectively. To a lesser extent the same trend is observed for multi-temperature aqueous solvent calculations, with an average decrease in RMSD of 1.63 kcal mol−1 from OPLS to GAFF over all functionals. Organic solvent models were the least affected by the choice of solute forcefield parameters, leading to an average change in RMSD for chloroform and carbon tetrachloride of 0.47 kcal mol−1 over all functionals. The noticeable divergence in prediction accuracy between aqueous and organic solvents may be due to differences in dataset size and composition, rather than a particular failure of RISM to model organic solvents. The 298 K water dataset, with roughly five times more solutes present than in the chloroform or carbon tetrachloride datasets, is considerably larger. Combining this with the greater range of values present within each of the four chemical descriptors shown in Fig. 1, may explain the poor aqueous solvent predictions. Further, although the increase in dataset size for the multi-temperature dataset is not as significant, a drop in 1D-RISM performance may be occurring for calculations outwith 298 K. Fig. 3 shows the correlation plots of calculated solvation free energy against experimental values for the multi-temperature water dataset with the GF functional and GAFF solute parameters.| Solvent | Temperature | R 2 | RMSD | Bias | SDEP | R 2 | RMSD | Bias | SDEP |
|---|---|---|---|---|---|---|---|---|---|
| a Predictions are separated by solute parameters, temperature and solvent. Units are in kcal mol−1. Organic solvents were modelled with GAFF parameters, and water solvent was modelled with MSPC/E. | |||||||||
| KH | GAFF | OPLS | |||||||
| Water | 298 K | −109.24 | 44.13 | −39.50 | 19.69 | −135.63 | 49.21 | −44.04 | 21.95 |
| Water | 273–373 K | −201.43 | 39.37 | −36.25 | 15.35 | −219.61 | 41.10 | −38.22 | 15.11 |
| Chloroform | 298 K | −35.72 | 16.12 | −15.04 | 5.80 | −42.16 | 17.48 | −16.45 | 5.91 |
| Carbon tetrachloride | 298 K | −100.96 | 17.46 | −16.55 | 5.59 | −104.14 | 17.73 | −16.82 | 5.61 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| HNC | GAFF | OPLS | |||||||
| Water | 298 K | −117.20 | 45.70 | −41.09 | 20.00 | −143.78 | 50.65 | −45.51 | 22.23 |
| Water | 273–373 K | −215.75 | 40.73 | −37.71 | 15.39 | −233.86 | 42.40 | −39.60 | 15.16 |
| Chloroform | 298 K | −40.86 | 17.21 | −16.16 | 5.93 | −47.15 | 18.46 | −17.44 | 6.04 |
| Carbon tetrachloride | 298 K | −121.71 | 19.16 | −18.25 | 5.83 | −125.50 | 19.45 | −18.55 | 5.86 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| GF | GAFF | OPLS | |||||||
| Water | 298 K | −1.03 | 5.98 | −3.53 | 4.83 | −3.56 | 8.99 | −7.50 | 4.96 |
| Water | 273–373 K | −2.94 | 5.49 | −4.42 | 3.26 | −5.36 | 6.98 | −6.45 | 2.66 |
| Chloroform | 298 K | 0.10 | 2.52 | 1.59 | 1.95 | 0.39 | 2.09 | 0.43 | 2.04 |
| Carbon tetrachloride | 298 K | −0.04 | 1.76 | 0.67 | 1.63 | 0.16 | 1.59 | 0.55 | 1.49 |
4.2 Convolutional neural network predictions
| Solvent | Temp. | Temp. descr. | Datapoints | R 2 | RMSD | Bias | SDEP | R 2 | RMSD | Bias | SDEP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Predictions are separated by temperature, inclusion of a temperature descriptor, solute forcefield parameters and number of datapoints. Results for each model are taken from test set predictions. Units are in kcal mol−1. Water solvent was modelled with MSPC/E. The standard deviation of each statistic per model is available in the ESI. | |||||||||||
| KH | GAFF | OPLS | |||||||||
| 298 K | No | 521 | 0.95 | 0.91 | 0.04 | 0.89 | 0.95 | 0.89 | 0.01 | 0.85 | |
| Water | 273–373 K | No | 3053 | 0.93 | 0.66 | −0.01 | 0.65 | 0.91 | 0.75 | 0.02 | 0.74 |
| 273–373 K | Yes | 3053 | 0.95 | 0.55 | 0.01 | 0.54 | 0.93 | 0.65 | 0.01 | 0.64 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| HNC | GAFF | OPLS | |||||||||
| 298 K | No | 521 | 0.94 | 0.94 | −0.14 | 0.91 | 0.95 | 0.88 | −0.01 | 0.85 | |
| Water | 273–373 K | No | 3053 | 0.94 | 0.64 | −0.01 | 0.63 | 0.90 | 0.75 | 0.03 | 0.74 |
| 273–373 K | Yes | 3053 | 0.94 | 0.57 | 0.02 | 0.56 | 0.91 | 0.71 | 0.03 | 0.70 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| GF | GAFF | OPLS | |||||||||
| 298 K | No | 521 | 0.94 | 0.96 | −0.06 | 0.91 | 0.95 | 0.88 | 0.02 | 0.86 | |
| Water | 273–373 K | No | 3053 | 0.93 | 0.65 | 0.02 | 0.64 | 0.92 | 0.68 | 0.03 | 0.67 |
| 273–373 K | Yes | 3053 | 0.94 | 0.62 | 0.01 | 0.61 | 0.94 | 0.59 | 0.01 | 0.58 | |
The CNN models give significantly more accurate predictions of SFE than the standard 1D-RISM theory. From a direct comparison of SFEs computed by the standard 1D-RISM theory and by the CNN models, taken from Tables 2 and 3 respectively, a significant improvement across all measurements can be seen. In stark contrast to the standard 1D-RISM theory, from which predictions using all SFE functionals give RMSDs greater than 5 kcal mol−1, all 18 CNN models achieve an RMSD below 1 kcal mol−1. A remarkable consistency can be seen between CNN trained on kh_w, hnc_w and gf_w calculated descriptors. This consistency across functionals suggests important and solute specific physical data is present within 1D-RISM free energy functionals that cannot be applied during their routine use, regardless of their accuracy. Indeed the only change in RMSD above 0.1 kcal mol−1 between functionals occurs for the multi-temperature OPLS water dataset with temperature descriptors, which notes an increase from 0.59 kcal mol−1 for gf_w to 0.71 kcal mol−1 for hnc_w.
The choice of forcefield for solute parameters has a marginal impact on prediction accuracy. Between GAFF and OPLS datasets, an average change in RMSD of 0.07, 0.10 and 0.05 kcal mol−1 is observed for KH, HNC and GF functionals respectively. Fig. 4 shows how the choice of forcefield affects the shape and magnitude of a set of descriptors, where the GF functional has been used to generate these descriptors. From this example it can be noted that both forcefields affect SFED magnitude, while maintaining a similar shape across the 1D-RISM grid, which may suggest that the shape of a given SFED is more important to a CNN for accurate SFE predictions.
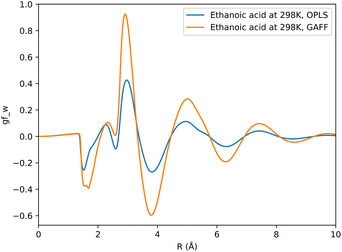 | ||
| Fig. 4 Comparison of descriptors generated using the GF functional for ethanoic acid in aqueous solvent, where the solute has been parameterised using either GAFF or OPLS forcefield parameters. | ||
Including temperature descriptors in a CNN model appears to have a limited impact on performance across all functionals and forcefields. On average, over all multi-temperature dataset variations, RMSD decreases by 0.07 kcal mol−1 when temperature descriptors are included.
| Solvent | Temp. | Temp. descr. | Datapoints | R 2 | RMSD | Bias | SDEP | R 2 | RMSD | Bias | SDEP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Predictions are separated by temperature, inclusion of a temperature descriptor, solute forcefield parameters and number of datapoints. Results for each model are taken from test set predictions. Units are in kcal mol−1. Organic solvents were modelled with GAFF parameters. Carbon tet. refers to Carbon tetrachloride. The standard deviation of each statistic per model is available in the ESI. | |||||||||||
| KH | GAFF | OPLS | |||||||||
| Carbon tet. | 298 K | No | 79 | 0.93 | 0.44 | 0.06 | 0.42 | 0.91 | 0.45 | 0.03 | 0.40 |
| Chloroform | 298 K | No | 109 | 0.92 | 0.74 | 0.00 | 0.72 | 0.90 | 0.76 | −0.01 | 0.75 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| HNC | GAFF | OPLS | |||||||||
| Carbon tet. | 298 K | No | 79 | 0.93 | 0.45 | 0.03 | 0.43 | 0.91 | 0.47 | −0.01 | 0.44 |
| Chloroform | 298 K | No | 109 | 0.89 | 0.78 | −0.00 | 0.76 | 0.90 | 0.74 | 0.03 | 0.72 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| GF | GAFF | OPLS | |||||||||
| Carbon tet. | 298 K | No | 79 | 0.91 | 0.47 | 0.05 | 0.44 | 0.90 | 0.51 | −0.01 | 0.47 |
| Chloroform | 298 K | No | 109 | 0.89 | 0.80 | 0.01 | 0.77 | 0.91 | 0.73 | 0.00 | 0.72 |
Similarly to CNN models trained on aqueous solvent datasets, those trained on organic solvents consistently outperformed the standard 1D-RISM theory. The best performing CNN models achieved an RMSD of 0.44 and 0.73 kcal mol−1 for carbon tetrachloride and chloroform respectively, whereas the RMSD of the most accurate 1D-RISM predictions were three times higher.
From Table 4, the impact of both OPLS and GAFF solute parameters to the overall accuracy of CNN models can be seen, with an average change in RMSD from OPLS to GAFF parameterised solutes of 0.01, 0.03 and 0.05 kcal mol−1 for kh_w, hnc_w and gf_w respectively. Further, with consistent performance across all functionals the viewpoint that solvation descriptors can be generated from any 1D-RISM free energy functional, regardless of its performance during 1D-RISM calculations, is reinforced. These points again suggest chemically relevant solvation data is present within these 1D-RISM generated descriptors.
The number of solute molecules per solvent dataset appears to have a negligible impact on SFE prediction accuracy. Chloroform and carbon tetrachloride have considerably fewer solutes than water at 298 K: 79 and 109 solutes, compared to 521 for water. However, organic solvent models make SFE predictions to a similar accuracy as their aqueous counterparts.
| Solvent | Temp. | Temp. descr. | Datapoints | R 2 | RMSD | Bias | SDEP | R 2 | RMSD | Bias | SDEP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Predictions are separated by temperature, inclusion of a temperature descriptor, solute forcefield parameters and number of datapoints. Results for each model are taken from test set predictions. Units are in kcal mol−1. Organic solvents were modelled with GAFF parameters, and water solvent was modelled with MSPC/E. The standard deviation of each statistic per model is available in the ESI. | |||||||||||
| KH | GAFF | OPLS | |||||||||
| 298 K | No | 709 | 0.95 | 0.83 | −0.01 | 0.82 | 0.95 | 0.82 | −0.02 | 0.80 | |
| 273–373 K | No | 3241 | 0.88 | 0.94 | 0.08 | 0.92 | 0.89 | 0.91 | 0.03 | 0.88 | |
| Multi-solvent | 273–373 K | Yes | 3241 | 0.88 | 0.97 | 0.06 | 0.95 | 0.87 | 1.01 | 0.03 | 0.98 |
| 273–373 K | No | 3629 | 0.93 | 1.01 | 0.10 | 1.00 | 0.91 | 1.12 | 0.00 | 1.10 | |
| 273–373 K | Yes | 3629 | 0.93 | 1.03 | 0.21 | 1.00 | 0.92 | 1.06 | −0.02 | 1.05 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| HNC | GAFF | OPLS | |||||||||
| 298 K | No | 709 | 0.95 | 0.84 | 0.06 | 0.83 | 0.95 | 0.80 | 0.02 | 0.79 | |
| 273–373 K | No | 3241 | 0.89 | 0.93 | 0.08 | 0.90 | 0.77 | 1.15 | 0.05 | 1.11 | |
| Multi-solvent | 273–373 K | Yes | 3241 | 0.88 | 0.98 | 0.11 | 0.95 | 0.86 | 1.04 | 0.07 | 1.01 |
| 273–373 K | No | 3629 | 0.93 | 1.00 | 0.09 | 0.98 | 0.93 | 0.98 | 0.00 | 0.97 | |
| 273–373 K | Yes | 3629 | 0.93 | 0.97 | 0.12 | 0.95 | 0.92 | 1.08 | 0.03 | 1.07 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| GF | GAFF | OPLS | |||||||||
| 298K | No | 709 | 0.95 | 0.87 | 0.05 | 0.85 | 0.95 | 0.77 | 0.01 | 0.76 | |
| 273–373K | No | 3241 | 0.90 | 0.91 | 0.03 | 0.89 | 0.36 | 1.27 | 0.07 | 1.24 | |
| Multi-solvent | 273–373K | Yes | 3241 | 0.88 | 0.97 | 0.10 | 0.93 | 0.74 | 1.10 | −0.02 | 1.07 |
| 273–373K | No | 3629 | 0.94 | 0.97 | 0.04 | 0.96 | 0.94 | 0.93 | 0.05 | 0.91 | |
| 273–373K | Yes | 3629 | 0.94 | 0.95 | 0.04 | 0.95 | 0.93 | 1.04 | 0.03 | 1.03 | |
From Table 5, a drop in accuracy is observed for OPLS based multi-temperature datasets when compared to their GAFF counterparts. This drop in model performance is clearest for multi-temperature datasets that do not include the additional 298 K water data from the MSD (3241 datapoint models). For these models, on average between like-for-like multi-temperature datasets, the use of OPLS results in a 0.13 kcal mol−1 increase in prediction error. Significant variations in correlation between experimental and predicted SFE are also only observed for these OPLS datasets. When CNN are trained on datasets which include the additional 298 K water data, prediction errors only increase by 0.05 kcal mol−1 on average against their GAFF counterparts. This drop in accuracy is not observed for single solvents, nor is it present in multi-solvent GAFF models, suggesting the use of SFE descriptors generated from OPLS parameterised solutes in multi-solvent models will interfere in prediction quality. As with the single-solvent aqueous and organic models, negligible changes in model performance are seen across the multi-solvent kh_w, hnc_w and gf_w datasets. As GAFF based models are consistent across KH, HNC and GF, the drop in performance of OPLS based models is likely only caused by the use of OPLS parameters. Including a temperature descriptor for multi-temperature models also has a negligible impact on prediction accuracy. CNN trained on multi-solvent and multi-temperature GAFF datasets predict SFE to below 1 kcal mol−1 of experiment without any need for reparameterisation. Fig. 5 provides the correlation plot for the 3629 datapoint multi-solvent and multi-temperature dataset generated using GAFF and GF without any temperature descriptors.
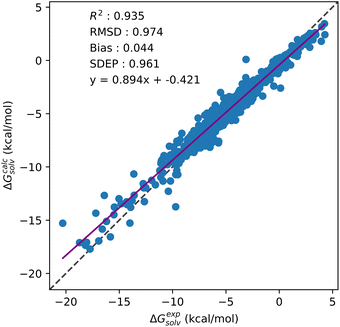 | ||
| Fig. 5 Correlation plot showing test set solvation free energy predictions against experimental values for the GF and GAFF based multi-solvent and multi-temperature dataset. | ||
A breakdown of solvation free energy predictions for individual solvents within multi-solvent datasets generated using the GF functional is shown in Table 6. Training CNN on multi-solvent SFED datasets results in an average increase in prediction error for chloroform and carbon tetrachloride solvents of 0.26 and 0.32 kcal mol−1 respectively against their corresponding single solvent models. A drop in accuracy is not observed for water however, and may be due to there being significantly more experimental data available for water (as compared to the organic solvents). Despite the fact each multi-solvent dataset includes disproportionately more aqueous solvent datapoints than organics solvent, SFE prediction errors for chloroform and carbon tetrachloride only peak at 1.14 and 0.81 kcal mol−1 respectively. The greatest prediction error for each solvent is below the standard deviation of experimental SFE values at 4.21, 2.85, 2.67 and 1.74 kcal mol−1 for water 298 K, water 273–373 K, chloroform and carbon tetrachloride respectively.
| GF | GAFF | OPLS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solvent | Temp. | Temp. descr. | Datapoints | R 2 | RMSD | Bias | SDEP | R 2 | RMSD | Bias | SDEP |
| a SFE predictions are separated by temperature, inclusion of a temperature descriptor, solute forcefield parameters and number of datapoints. Results for each model are taken from test set predictions. Units are in kcal mol−1. Organic solvents were modelled with GAFF parameters, and water solvent was modelled with MSPC/E. Carbon tet. refers to Carbon tetrachloride. | |||||||||||
| Water | 0.96 | 0.83 | −0.02 | 0.81 | 0.96 | 0.79 | −0.00 | 0.78 | |||
| Chloroform | 298 K | No | 709 | 0.83 | 1.03 | 0.25 | 0.93 | 0.89 | 0.78 | 0.06 | 0.73 |
| Carbon tet. | 0.74 | 0.81 | 0.25 | 0.68 | 0.86 | 0.61 | 0.03 | 0.54 | |||
| Water | 0.95 | 0.95 | 0.01 | 0.94 | 0.95 | 0.92 | 0.01 | 0.91 | |||
| Chloroform | 273–373 K | No | 3629 | 0.80 | 1.14 | 0.13 | 1.08 | 0.82 | 1.05 | 0.11 | 0.98 |
| Carbon tet. | 0.80 | 0.76 | 0.12 | 0.68 | 0.82 | 0.71 | 0.13 | 0.61 | |||
| Water | 0.95 | 0.96 | −0.02 | 0.95 | 0.94 | 1.07 | 0.04 | 1.06 | |||
| Chloroform | 273–373 K | Yes | 3629 | 0.85 | 1.01 | 0.10 | 0.97 | 0.81 | 1.13 | 0.04 | 1.03 |
| Carbon tet. | 0.77 | 0.80 | 0.20 | 0.74 | 0.81 | 0.72 | 0.00 | 0.62 | |||
pyRISM-CNN is capable of predicting the solvation free energies of small organic molecules with comparable accuracy to state-of-the-art methods. MD based free energy perturbation (FEP) calculations have been reported for a dataset of 239 small molecules in water, achieving an average unsigned error (AUE) of 1.10 kcal mol−1.56 The semi empirical universal correction (UC) free energy functional paired with 3D-RISM has been shown to accurately predict hydration free energies for a set of 504 organic molecules, with an RMSD of 1.18 kcal mol−1.11 The most comprehensive comparisons can be made against the SMD, which has been tested extensively against both aqueous and non-aqueous solvents at 298 K.7 By solvent, AUE of 0.52, 0.84 and 0.59 kcal mol−1 were reported for carbon tetrachloride, chloroform and water respectively with the SMD. Although not directly comparable, RMSD values of 0.76, 1.14 and 0.95 kcal mol−1 were determined with the GF based multi-solvent pyRISM-CNN model. These errors drop to 0.47, 0.8 and 0.65 kcal mol−1 for carbon tetrachloride, chloroform and water respectively with the GF based single solvent output pyRISM-CNN models.
5 Conclusions
Here we have applied pyRISM, a new 1D-RISM solver capable of applying the standard 1D-RISM theory beyond 298 K, to water and a wide range of common organic solvents. Further, by combining pyRISM with a deep learning model, accurate SFE predictions can be made far beyond the capabilities of the standard 1D-RISM theory. Replacing the standard 1D-RISM SFE functionals with a CNN delivers a 40-fold improvement compared to the standard 1D-RISM theory, with consistent prediction errors below 1 kcal mol−1 as compared to experiment for organic solvents at 298 K and aqueous solvent at 273–373 K. This move from 1D-RISM calculations to pyRISM-CNN predictions requires minimal additional computational expenditure as descriptors can be generated as part of the typical 1D-RISM workflow. Efforts are ongoing to assess the generalisability of pyRISM-CNN and gather experimental SFE data in other organic solvents against which to test and further develop the model.Data availability
The pyRISM v0.1.1 code for solving 1D RISM equations and computing solvation free energy density functions can be found as freely available and open-source software at https://zenodo.org/record/7107645. Future versions of this software will be released at https://github.com/2AUK/pyRISM. Software and datasets used to develop the pyRISM-CNN models are freely available as open-source software at https://doi.org/10.5281/zenodo.7108371. The molecular structures and experimental solvation free energy data contained within this repository were initially obtained from: A. V. Marenich, C. P. Kelly, J. D. Thompson, G. D. Hawkins, C. C. Chambers, D. J. Giesen, P. Winget, C. J. Cramer and D. G. Truhlar, Minnesota Solvation Database – version 2012, University of Minnesota, Minneapolis, 2012. A. C. Chamberlin, C. J. Cramer and D. G. Truhlar, J. Chem. Phys. B, 2006, 110, 5665–5675. A. C. Chamberlin, C. J. Cramer and D. G. Truhlar, J. Chem. Phys. B, 2008, 112, 3024–3039.Author contributions
Conceptualization: DSP; methodology: DJF, RGMcH, AA; software: DJF, RGMcH, AA; validation/verification: DJF, RGMcH, AA, DSP; formal analysis: DJF, RGMcH; investigation: DJF, RGMcH, AA; resources: DSP, AA; data curation: DJF, RGMcH; writing – original draft: DJF; writing – review editing: DJF, RGMcH, AA, DSP; visualization: DJF, DSP; supervision: DSP; project administration: DSP, DJF; funding acquisition: DSP.Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. J. F and D. S. P thank the EPSRC for funding via Prosperity Partnership EP/S035990/1. A. A thanks EPSRC for funding. R. G. McH thanks the University of Strathclyde for funding. The authors thank the ARCHIE-WeSt High-Performance Computing Centre (https://www.archie-west.ac.uk/) for computational resources.Notes and references
- L. Xu and M. L. Coote, J. Phys. Chem. A, 2019, 123, 7430–7438 CrossRef CAS PubMed.
- M. S. Bodnarchuk, D. M. Heyes, D. Dini, S. Chahine and S. Edwards, J. Chem. Theory Comput., 2014, 10, 2537–2545 CrossRef CAS PubMed.
- F. R. Dutra, C. de Souza Silva and R. Custodio, J. Phys. Chem. A, 2021, 125, 65–73 CrossRef CAS PubMed.
- S. Genheden, T. Luchko, S. Gusarov, A. Kovalenko and U. Ryde, J. Phys. Chem. B, 2010, 114, 8505–8516 CrossRef CAS PubMed.
- D. S. Palmer, J. L. McDonagh, J. B. O. Mitchell, T. van Mourik and M. V. Fedorov, J. Chem. Theory Comput., 2012, 8, 3322–3337 CrossRef CAS PubMed.
- D. J. Fowles, D. S. Palmer, R. Guo, S. L. Price and J. B. O. Mitchell, J. Chem. Theory Comput., 2021, 17, 3700–3709 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cances, J. Mol. Struct., 1999, 464, 211–226 CrossRef CAS.
- S.-T. Lin and C.-M. Hsieh, J. Chem. Phys., 2005, 125, 124103 CrossRef PubMed.
- D. L. Mobley, C. I. Bayly, M. D. Cooper, M. R. Shirts and K. A. Dill, J. Chem. Theory Comput., 2009, 5, 350–358 CrossRef CAS PubMed.
- J.-F. Truchon, B. M. Pettitt and P. Labute, J. Chem. Theory Comput., 2014, 10, 934–941 CrossRef CAS PubMed.
- D. S. Palmer, A. I. Frolov, E. L. Ratkova and M. V. Fedorov, J. Phys.: Condens. Matter, 2010, 22, 492101 CrossRef PubMed.
- V. Sergiievskyi, G. Jeanmairet, M. Levesque and D. Borgis, J. Chem. Phys., 2015, 143, 184116 CrossRef PubMed.
- M. Misin, M. V. Fedorov and D. S. Palmer, J. Chem. Phys., 2015, 142, 091105 CrossRef PubMed.
- S. Tanimoto, N. Yoshida, T. Yamaguchi, S. L. Ten-no and H. Nakano, J. Chem. Inf. Model., 2019, 59, 3770–3781 CrossRef CAS PubMed.
- D. Roy and A. Kovalenko, J. Phys. Chem. A, 2019, 123, 4087–4093 CrossRef CAS PubMed.
- M. Misin, D. S. Palmer and M. V. Fedorov, J. Phys. Chem. B, 2016, 120, 5724–5731 CrossRef CAS PubMed.
- M. Misin, P. A. Vainikka, M. V. Fedorov and D. S. Palmer, J. Chem. Phys., 2016, 145, 194501 CrossRef.
- M. Misin, M. V. Fedorov and D. S. Palmer, J. Phys. Chem. B, 2016, 120, 975–983 CrossRef CAS PubMed.
- S. J. Singer and D. Chandler, Mol. Phys., 1985, 55, 621–625 CrossRef CAS.
- K. Sato, H. Chuman and S. Ten-no, J. Phys. Chem. B, 2005, 109, 17290–17295 CrossRef CAS PubMed.
- S. Ten-no, J. Jung, H. Chuman and Y. Kawashima, Mol. Phys., 2010, 108, 327–336 CrossRef CAS.
- E. L. Ratkova, G. N. Chuev, V. P. Sergiievskyi and M. V. Fedorov, J. Phys. Chem. B, 2010, 114, 12068–12079 CrossRef CAS PubMed.
- D. S. Palmer, M. Misin, M. V. Fedorov and A. Llinas, Mol. Pharmaceutics, 2015, 12, 3420–3432 CrossRef CAS PubMed.
- A. Ahmad, 2AUK/pyRISM: v0.1.1, 2022, DOI:10.5281/zenodo.7107645.
- E. L. Ratkova, D. S. Palmer and M. V. Fedorov, Chem. Rev., 2015, 115, 6312–6356 CrossRef CAS PubMed.
- A. Kovalenko and F. Hirata, J. Phys. Chem. B, 1999, 103, 7942–7957 CrossRef CAS.
- S. Ten-no, J. Chem. Phys., 2001, 115, 3724–3731 CrossRef CAS.
- F. Hirata, Molecular Theory of Solvation, Kluwer Academic Publishers, Dordrecht, The Netherlands, 1st edn, 2003 Search PubMed.
- V. P. Sergiievskyi, W. Hackbusch and M. V. Fedorov, J. Comput. Chem., 2011, 32, 1982–1992 CrossRef CAS PubMed.
- A. V. Marenich, C. P. Kelly, J. D. Thompson, G. D. Hawkins, C. C. Chambers, D. J. Giesen, P. Winget, C. J. Cramer and D. G. Truhlar, Minnesota Solvation Database – version 2012, University of Minnesota, Minneapolis, 2012 Search PubMed.
- A. C. Chamberlin, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 5665–5675 CrossRef CAS PubMed.
- A. C. Chamberlin, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2008, 112, 3024–3039 CrossRef CAS PubMed.
- S. R. Heller, A. McNaught, I. Pletnev, S. Stein and D. Tchekhovskoi, J. Cheminf., 2015, 7, 23 Search PubMed.
- N. M. O’Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33 Search PubMed.
- Schrödinger Suite 2008, Maestro Version 8.5, MacroModel Version 9.6, Schrödinger LLC, New York, NY, 2008 Search PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. Perkyns and B. M. Pettitt, J. Chem. Phys., 1992, 97, 7656–7666 CrossRef CAS.
- J. Perkyns and B. M. Pettitt, Chem. Phys. Lett., 1992, 190, 626–630 CrossRef CAS.
- P. H. Lee and G. Maggiora, J. Phys. Chem., 1993, 97, 10175–10185 CrossRef CAS.
- L. Lue and D. Blankschtein, J. Phys. Chem., 1992, 96, 8582–8594 CrossRef CAS.
- F. Hirata, P. J. Rossky and B. M. Pettitt, J. Chem. Phys., 1982, 78, 4133 CrossRef.
- G. N. Chuev, M. V. Fedorov and J. Crain, Chem. Phys. Lett., 2007, 448, 198–202 CrossRef CAS.
- H. A. D. A. Case, K. Belfon, I. Ben-Shalom, J. Berryman, S. Brozell, D. Cerutti, T. Cheatham, G. C. III, V. Cruzeiro, T. Darden, R. Duke, G. Giambasu, M. Gilson, H. Gohlke, A. Goetz, R. Harris, S. Izadi, S. Izmailov, K. Kasavajhala, M. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. O'Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. Simmerling, N. Skrynnikov, J. Smith, J. Swails, R. Walker, J. Wang, J. Wang, H. Wei, R. Wolf, X. Wu, Y. Xiong, Y. Xue, D. York, S. Zhao, and P. Kollman, Amber 2018, 2018 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. L. Banks, H. S. Beard, Y. Cao, A. E. Cho, W. Damm, R. Farid, A. K. Felts, T. A. Halgren, D. T. Mainz, J. R. Maple, R. Murphy, D. M. Philipp, M. P. Repasky, L. Y. Zhang, B. J. Berne, R. A. Friesner, E. Gallicchio and R. M. Levy, J. Comput. Chem., 2005, 26, 1752–1780 CrossRef CAS PubMed.
- Schrödinger Release 2022–3: Maestro, Schrödinger, LLC, New York, N Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/ Search PubMed.
- F. Chollet, et al., Keras, 2015, https://github.com/fchollet/keras Search PubMed.
- A. F. Agarap, arXiv:1803.08375, preprint, 2018.
- D. Kingma and J. Ba, International Conference on Learning Representations, 2014 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- M. Eklund, U. Norinder, S. Boyer and L. Carlsson, J. Chem. Inf. Model., 2014, 54, 837–843 CrossRef CAS PubMed.
- D. S. Palmer and J. B. O. Mitchell, Mol. Pharmaceutics, 2014, 11, 2962–2972 CrossRef CAS PubMed.
- D. Shivakumar, J. Williams, Y. Wu, W. Damm, J. Shelley and W. Sherman, J. Chem. Theory Comput., 2010, 6, 1509–1519 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00103a |
| This journal is © The Royal Society of Chemistry 2023 |