Open Access Article
Open Access ArticleA SAR and QSAR study on cyclin dependent kinase 4 inhibitors using machine learning methods†
Xiaoyang
Pang
a,
Yunyang
Zhao
a,
Guo
Li
a,
Jianrong
Liu
*b and
Aixia
Yan
 *a
*a
aState Key Laboratory of Chemical Resource Engineering, Department of Pharmaceutical Engineering, Beijing University of Chemical Technology, Beijing, P. R. China. E-mail: yanax@mail.buct.edu.cn
bBUCT-Paris Curie Engineer School, Beijing University of Chemical Technology, Beijing 100029, P. R. China. E-mail: liujianrong2017@126.com
First published on 31st May 2023
Abstract
Cyclin dependent kinase 4 (CDK4) is a promising target for cancer treatment, and developing new effective CDK4 inhibitors is of great significance in anticancer therapy. In this study, we conducted a structure activity relationship (SAR) study on 3018 CDK4 inhibitors. We applied four machine learning methods, which were Multiple Linear Regression (MLR), Random Forest (RF), Support Vector Machine (SVM) and Deep Neural Network (DNN), to develop 18 classification models based on 3018 inhibitors (dataset 1), 18 classification models based on dataset 1 and decoys, and 24 quantitative structure–activity relationship (QSAR) models based on 1427 inhibitors (dataset 2). We obtained some optimal models. Based on dataset 1, Model A2, built by SVM and MACCS fingerprints, has a prediction accuracy (Q) of 92.68% and a Matthews correlation coefficient (MCC) of 0.874 for the test set. Based on dataset 1 and decoys, Model C2, built by SVM and MACCS fingerprints, has a Q of 98.5% and a MCC of 0.937 for the test set. Based on dataset 2, Model F7, built by SVM and MOE descriptors, has a coefficient of determination (R2) of 0.824 and a root mean squared error (RMSE) of 0.534 for the test set. For classification models, it was found that the more samples used for modelling, the more robust the models, and the better the performance of the models. Moreover, we clustered 3018 inhibitors into 12 subsets, and analysed their scaffolds and fragment features. It was found that 2-aminopyrimidine, pyridine, piperazine and cyclopentane were common scaffolds and fragments in highly active inhibitors. This study can provide guidance for the discovery and optimization of CDK4 inhibitor lead compounds.
Introduction
Cyclin dependent kinase 4 (CDK4) (EC 2.7.11.22), a member of the cyclin dependent kinases family, which belongs to serine/threonine protein kinases,1 plays an essential role in cell cycle regulation. CDK4 is important in the cell cycle transition from the G1 phase to S phase,2 binding to cyclin D, after which it phosphorylates and inhibits retinoblastoma (RB) family proteins, and hyper-phosphorylated RB releases E2F, activating a transcriptional program that initiates the S phase.3 In many cancers, CDK4 is hyper-activated, thereby driving uncontrolled cell proliferation.4 Hyper-activation of CDK4 is reported in breast cancer, non-small cell lung cancer, melanoma, and endometrial cancer.5 Therefore, CDK4 is an important antitumor target.There are five drugs that have been launched so far that target CDK4, namely palbociclib,6 ribociclib,7 abemaciclib,8 trilaciclib9 and dalpiciclib.10 Their structures and activities are shown in Table 1, and they are used to treat breast cancer11–15 and extensive-stage small cell lung cancer.16 But nowadays there are breast cancer patients resistant to CDK4 inhibitors and endocrine therapy in the clinic.17–20 Therefore, it is necessary to develop new CDK4 inhibitors.
Computer-aided drug design (CADD) as a convenient and low-cost approach21 is used to discover CDK4 inhibitor lead compounds. As a method of CADD, a classification model22–26 is used for structure–activity relationship research and virtual screening of inhibitors, and a QSAR model27–39 is used to predict the inhibitory activity of a compound. Wu et al.22 built classification models and QSAR models to study the structure–activity relationship of tyrosinase inhibitors. Huo et al.26 built classification models and QSAR models of EGFR inhibitors, and used them for virtual screening. 18 novel EGFR inhibitors were predicted to be highly active, and nine of the 18 novel EGFR inhibitors have been proved to be effective by experiments. As for the study of CDK4 inhibitors, Omar Husham Ahmed et al.39 designed 52 pyrido[2,3-d]pyrimidin-7-one-based CDK4 inhibitors, and then developed 2D- (R2 = 0.6974, RMSE = 0.7193) and 3D-quantitative structure–activity relationship (QSAR) models (R2 = 0.7649, RMSE = 0.5809). Virtual screening of the ChEMBL database was carried out using the validated QSAR model and the molecular docking procedure. A total of six compounds were identified as potentially novel CDK4 inhibitor lead compounds. Le et al.40 built 3D-QSAR models with comparative molecular field analysis (CoMFA) (CDK4: Q2 = 0.543, R2 = 0.967; CDK6: Q2 = 0.624, R2 = 0.984) and comparative molecular similarity indices analysis (CoMSIA) (CDK4: Q2 = 0.518, R2 = 0.937; CDK6: Q2 = 0.584, R2 = 0.975) based on 52 dual CDK4/6 inhibitors, and then designed 10 novel compounds with expected activity and ADME/T properties. Sarhan et al.38 synthesized novel 6-bromo-coumarin-ethylidene-hydrazonyl-thiazolyl and 6-bromo-coumarin-thiazolyl based derivatives, and built a QSAR model (R2 = 0.92, RMSE = 0.44) based on 16 previously reported thiazolyl-hydrazono-coumarin compounds. Five compounds predicted by the QSAR model were verified to have potential anticancer activities, and one of them was considered as a selective radiotherapy agent for solid tumours with promising anticancer activity based on the results of experiments in vitro. Therefore, the classification model and QSAR model are helpful for the discovery and optimization of CDK4 inhibitors.
The previous studies on CDK4 inhibitors were carried out based on a certain scaffold, so it is not easy to find novel scaffolds of inhibitors. To address this issue, in this work, 3018 CDK4 inhibitors were collected to research the structure–activity relationship in this study. We calculated MACCS fingerprints, ECFP4 fingerprints and Corina descriptors, using Random Forest, Support Vector Machine and Deep Neural Network methods to build classification models, to distinguish highly/weakly active inhibitors. Then we calculated Corina, MOE and RDKit descriptors, using Multiple Linear Regression, Random Forest, Support Vector Machine and Deep Neural Network methods to build QSAR models, to predict the CDK4 inhibitory activity of the compound. In addition, we clustered 3018 CDK4 inhibitors to 12 subsets and analysed the features of the scaffolds and fragments. This work aims to study the relationship between the structures and activities of CDK4 inhibitors, and investigate the scaffolds and fragment features of highly active CDK4 inhibitors.
Materials and methods
Dataset
For classification models, a total of 3018 CDK4 inhibitors and their IC50 were collected from 250 pieces of literature (access date: 2022.8) as dataset 1, with IC50 ranging from 0.13 nM to 1000 μM.We selected 200 nM as a threshold to distinguish highly and weakly active inhibitors. If the IC50 of one compound is less than 200 nM, it is defined as a highly active inhibitor with a label of 1; in contrast, if the IC50 of one compound is more than 200 nM, it is defined as a weakly active inhibitor with a label of 0. As a result, 1642 compounds were distinguished as highly active inhibitors, and 1376 compounds were distinguished as weakly active inhibitors. We divided dataset 1 into training set 1 (2266 inhibitors) and test set 1 (752 inhibitors) by a Self-Organizing Map (SOM)41 and divided dataset 1 into training set 2 (2263 inhibitors) and test set 2 (755 inhibitors) by a random method. SOM is performed by SONNIA software42 and MACCS fingerprints of compounds, and it enables the chemical space of the training set to cover that of the entire dataset as much as possible. The training set divided by SOM can have rich chemical structure diversity.
In addition, because it is well known that decoys are necessary to evaluate virtual screening methods,43 we also added decoys into dataset 1 to build classification models. To avoid decoy bias, we used two different decoy generation methods for the training set and test set, respectively.44
We used Deepcoy45 to generate decoys based on the training set. Training set 1 contains 2266 inhibitors, 1204 of which are highly active, and based on these highly active inhibitors, we generated 5951 decoys, training set 1 and these decoys form training set 3, which includes 8217 molecules. Training set 2 contains 2263 inhibitors, 1231 of which are highly active, and based on these highly active inhibitors, we generated 6085 decoys, training set 2 and these decoys form training set 4, which includes 8348 molecules. We used MUBD-DecoyMaker2.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 to generate decoys based on the test set. Test set 1 contains 752 inhibitors, 438 of which are highly active, and based on these highly active inhibitors, we generated 2377 decoys, test set 1 and these decoys form test set 3, which includes 3129 molecules. Test set 2 contains 755 inhibitors, 411 of which are highly active, and based on these highly active inhibitors, we generated 2379 decoys, test set 2 and these decoys form test set 4, which includes 3134 molecules.
46 to generate decoys based on the test set. Test set 1 contains 752 inhibitors, 438 of which are highly active, and based on these highly active inhibitors, we generated 2377 decoys, test set 1 and these decoys form test set 3, which includes 3129 molecules. Test set 2 contains 755 inhibitors, 411 of which are highly active, and based on these highly active inhibitors, we generated 2379 decoys, test set 2 and these decoys form test set 4, which includes 3134 molecules.
For QSAR models, based on dataset 1, 1427 compounds whose IC50 was detected by a radiolabeling method were selected as dataset 2, with IC50 ranging from 0.13 nM to 1000 μM. Before modelling, we need to convert IC50 into pIC50 (pIC50 = log(IC50), in the unit of mol L−1), to eliminate the influence of magnitudes. pIC50 ranges from 3 to 9.89. We divided dataset 2 into training set 5 and test set 5 by SOM, and divided dataset 2 into training set 6 and test set 6 by a random method.
Generated decoys evaluation
The optimal embedding score (DOE score) and doppelganger score were used to evaluate generated decoys.45 The DOE score measures the quality of the embedding of actives and decoys in chemical space. An optimal embedding of actives and decoys achieves a DOE score of zero, while complete separation in physicochemical space results in a DOE score of 0.5. The average doppelganger score is a measure of the structural similarity between actives and decoys, when the value is less than 0.4, indicating that the generated decoys have an allowable false negative bias.Calculation and extraction of descriptors
For classification models, we calculated three types of descriptors for modelling, MACCS fingerprints,47 ECFP4 fingerprints48 and Corina descriptors.49 MACCS fingerprints have 166 bits, and ECFP4 fingerprints have 1024 bits, and both of them are calculated by the RDkit v2020.09.1 package.50 The Corina descriptors consist of 108 descriptors calculated by CORINA Symphony software.49The extraction of descriptors is based on the training set. As for MACCS and ECFP4 fingerprints, we calculated the variance of each bit, and extracted the bits whose variance is larger than the mean variance. As for Corina descriptors, we calculated the Pearson coefficient51 between descriptors and activity, and then extracted the descriptors whose coefficient with activity is larger than 0.1, then when the coefficient between the two descriptors is larger than 0.9, we extracted the descriptor whose coefficient with activity is larger than another. As a result, we got a set of Corina descriptors for modelling. Before modelling, the selected Corina descriptors' values were scaled to [0.1, 0.9] using eqn (1):
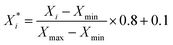 | (1) |
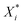 is the scaled value, Xi is the original value, and Xmin and Xmax represent the minimum and maximum values in the training set, respectively.
is the scaled value, Xi is the original value, and Xmin and Xmax represent the minimum and maximum values in the training set, respectively.
For classification models based on dataset 1 and decoys, we also calculated MACCS fingerprints, ECFP4 fingerprints and Corina descriptors. Based on the training set, as for MACCS and ECFP4 fingerprints, we calculated the variance of each bit to extract descriptors, and as for Corina descriptors, we calculated the Pearson coefficient between descriptors and activity to extract descriptors. Before modelling, the extracted Corina descriptors' values were scaled to [0.1, 0.9] using eqn (1).
For QSAR models, we calculated three types of descriptors for modelling, Corina descriptors, MOE descriptors52 and RDkit descriptors.50 The MOE descriptors consist of 206 descriptors calculated by MOE software.52 The RDkit descriptors consist of 208 descriptors calculated by the RDkit v2020.09.1 package.50 Based on the training set, we calculated the Pearson coefficient51 between descriptors and activity to extract descriptors, and then scaled the extracted descriptors using eqn (1) to build QSAR models.
Modelling methods
For classification models, we used Random Forest (RF),53 Support Vector Machine (SVM)54 and Deep Neural Network (DNN)55 methods to build models. Random Forest53 is an ensemble algorithm that scores based on the results of multiple decision trees. Support Vector Machine54 distinguishes samples by mapping them to a higher dimensional space. The Scikit-learn v1.0.2 package56 was used to build RF models and SVM models, and Grid Search57 which is based on the 5-fold cross-validation accuracy58 and repeated training59 was used to find the optimal parameters. In this study, DNN models have three hidden layers, and a batch normalization layer60 was added after each layer to prevent model overfitting. The optimization algorithm used was Adam.61 We took the 5-fold cross-validation and repeated training strategy59 to train the DNN models, and adopted early-stopping function62 to stop training, when the binary cross entropy on the validation set is not improved in 30 consecutive epochs. The Pytorch v1.10.0 package63 was used to build DNN models.For QSAR models, we used Multiple Linear Regression (MLR),64 Random Forest (RF),53 Support Vector Machine (SVM)54 and Deep Neural Network (DNN)55 methods to build models. Multiple Linear Regression64 belongs to linear regression and has poor fitting for nonlinear problems. Both Random Forest53 and Support Vector Machine54 can be used to solve classification and regression problems. As for the early-stopping function of DNN models, the evaluation parameter is mean squared error (MSE).65 The training strategy of QSAR models is the same as that of the classification models. The Scikit-learn v1.0.2 package56 was used to build MLR, RF and SVM models, while the Pytorch v1.10.0 package63 was used to build DNN models.
Model evaluation
For classification models, the accuracy (Q), sensitivity (SE),66 specificity (SP)66 and Matthews correlation coefficient (MCC)67 of the training and testing sets were used to evaluate performance. The cross-validation of 5-fold (5-CV)58 on the training set was used to evaluate the robustness of the model.For QSAR models, the coefficient of determination (R2),68 mean absolute error (MAE)65 and root mean squared error (RMSE)65 were used to evaluate performance.
Applicability domain
For classification models, dSTD-PRO,69 the predictive reliability of compounds was used to define the application domain of the model. DSTD-PRO can be calculated based on the prediction probability of all models, and compound J's dSTD-PRO can be calculated using eqn (2).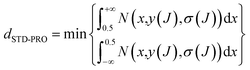 | (2) |
For QSAR models, the Williams plot70 is used to visualize the application domain of the model. In the Williams plot, the standardized residuals (σ) and leverage (h) values of the compounds are calculated to determine whether they are in the application domain of the model. The σ value is the difference between the true value and predicted value. The h value of a compound can be calculated using eqn (3). When the leverage value of a compound is less than the leverage warning value (h*), it is in the application domain. The h* value can be calculated using eqn (4).
| hi = xTi(XTX)−1xi | (3) |
| h* = 3(p + 1)/n | (4) |
Clustering methods
We used two clustering methods to cluster inhibitors, which are K-means71 and hierarchical clustering (HC).72 In addition, we used two dimension-reduction methods to reduce the high dimensions data to two-dimensions, which are t-Distributed Stochastic Neighbour Embedding (TSNE)73 and Uniform Manifold Approximation and Projection (UMAP).72K-Means71 belongs to unsupervised machine learning. It achieves the effect of clustering by constantly taking the samples closest to the mean of seed points to aggregate data. HC72 consists in building a binary merge tree, starting from the molecules stored at the leaves and merging them until reaching the root of the tree that contains all the molecules of the dataset. TSNE73 is an embedding model that can map data from a high-dimensional space to a low-dimensional space and retain the local characteristics of the data. UMAP72 is a non-linear dimensionality reduction algorithm that seeks to learn the manifold structure of the data and find a low-dimensional embedding while preserving the essential topological structure of that manifold. K-Means, HC, TSNE and UMAP are implemented by the Scikit-learn v1.0.2 package.56Clustering evaluation
To measure the quality of clustering, we considered three unsupervised metrics to evaluate the clustering quality results, the silhouette coefficient, the Calinski–Harabasz (CH) score, and the Davies–Bouldin (DB) score.72 As for the silhouette coefficient, the best value is 1, and the worst value is −1; negative values generally indicate that a molecule has been assigned to the wrong cluster as a different cluster is more similar. As for the CH score, a higher value relates to a model with better-defined clusters. As for the DB score, the minimum score is zero, with lower values indicating better clustering. These metrics are implemented by the Scikit-learn v1.0.2 package.Statistical methods for analysing fragments
We used the BRICS function in the RDkit v2020.09.1 package50 to split molecular structures into a set of fragments, and then counted the frequencies of each fragment in highly and weakly active inhibitors respectively to analyse fragment features. When the proportion of highly/weakly active inhibitors in the subset was less than 10%, these compounds were considered not statistically significant and were not counted.Results and discussion
Classification models (based on dataset 1)
For training set 1 (divided by SOM), we calculated and extracted three types of descriptors (76 MACCS fingerprints, 294 ECFP4 fingerprints, and 24 Corina descriptors), using three machine learning methods (RF, SVM and DNN) to build Models A1–A9. For training set 2 (divided by a random method), we calculated and extracted three types of descriptors (76 MACCS fingerprints, 293 ECFP4 fingerprints, and 24 Corina descriptors), using three machine learning methods (RF, SVM and DNN) to build Models B1–B9. The performances of the 18 classification models are shown in Table 2. The optimal hyper-parameters of each model are given in the ESI.†| Model | Training set/test set | Input descriptors | Methods | Training set | Test set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | n | Q (%) | 5-CVc (%) | MCCd | Q (%) | SEe (%) | SPf(%) | MCC | |||
| a n, number of descriptors. b Q, accuracy. c 5-CV, 5-fold cross-validation. d MCC, Matthews correlation coefficient. e SE, sensitivity. f SP, specificity. | |||||||||||
| Model A1 | 2266/752 | MACCS | 76 | RF | 85.79 | 82.44 | 0.715 | 90.03 | 90.41 | 89.49 | 0.796 |
| Model A2 | 2266/752 | MACCS | 76 | SVM | 89.36 | 83.85 | 0.787 | 93.88 | 94.75 | 92.68 | 0.874 |
| Model A3 | 2266/752 | MACCS | 76 | DNN | 87.03 | 85.99 | 0.739 | 90.43 | 89.04 | 92.36 | 0.807 |
| Model A4 | 2266/752 | ECFP4 | 294 | RF | 87.29 | 84.91 | 0.745 | 91.49 | 89.95 | 93.63 | 0.829 |
| Model A5 | 2266/752 | ECFP4 | 294 | SVM | 91.92 | 86.23 | 0.838 | 93.62 | 93.38 | 93.95 | 0.870 |
| Model A6 | 2266/752 | ECFP4 | 294 | DNN | 87.95 | 86.96 | 0.759 | 90.56 | 88.58 | 93.31 | 0.811 |
| Model A7 | 2266/752 | Corina | 24 | RF | 89.23 | 83.62 | 0.784 | 91.20 | 89.93 | 92.97 | 0.822 |
| Model A8 | 2266/752 | Corina | 24 | SVM | 89.32 | 84.64 | 0.785 | 92.27 | 91.30 | 93.61 | 0.843 |
| Model A9 | 2266/752 | Corina | 24 | DNN | 86.14 | 85.12 | 0.722 | 90.13 | 89.24 | 91.37 | 0.800 |
| Model B1 | 2263/755 | MACCS | 76 | RF | 86.92 | 84.58 | 0.736 | 87.15 | 87.83 | 86.34 | 0.741 |
| Model B2 | 2263/755 | MACCS | 76 | SVM | 91.21 | 86.30 | 0.823 | 88.48 | 90.27 | 86.34 | 0.768 |
| Model B3 | 2263/755 | MACCS | 76 | DNN | 89.35 | 88.30 | 0.786 | 86.89 | 89.78 | 83.43 | 0.735 |
| Model B4 | 2263/755 | ECFP4 | 293 | RF | 88.73 | 86.39 | 0.773 | 88.61 | 87.59 | 89.83 | 0.772 |
| Model B5 | 2263/755 | ECFP4 | 293 | SVM | 93.28 | 87.58 | 0.865 | 89.93 | 90.02 | 89.83 | 0.798 |
| Model B6 | 2263/755 | ECFP4 | 293 | DNN | 90.01 | 89.49 | 0.800 | 86.62 | 89.78 | 82.85 | 0.730 |
| Model B7 | 2263/755 | Corina | 24 | RF | 90.53 | 86.02 | 0.809 | 85.70 | 85.89 | 85.47 | 0.712 |
| Model B8 | 2263/755 | Corina | 24 | SVM | 93.01 | 87.08 | 0.859 | 86.49 | 86.62 | 86.34 | 0.728 |
| Model B9 | 2263/755 | Corina | 24 | DNN | 86.95 | 86.68 | 0.738 | 87.02 | 89.78 | 83.72 | 0.738 |
According to Table 2, it was found that the differences between SE and SP of all models are very small, indicating that all models can balance different types of inhibitors very well. The 5-CV accuracies of all models are greater than 82%, indicating that all models are robust. The MCC values on the test set of all models are greater than 0.77, indicating that all models have good performance. The prediction accuracies on the training set and test set of all models are more than 85%, indicating that all models have good performance of fitting and prediction respectively.
Comparing the performances of models built by different methods, it was found that the models built by SVM have the best performance on the test set, and the models built by DNN have the best robustness. Comparing the performances of models based on different descriptors, it was found that the models based on ECFP4 fingerprints have the best performance on the test set. The models based on Corina descriptors have good performance with a small number of descriptors, indicating that the extracted Corina descriptors are very important for inhibitory activity.
Comparing the performances of models based on the two different training sets, the optimal models were selected according to the prediction MCC on the test set. It was found that among Models A1–A9 based on training set 1 (divided by SOM), Model A2 is the optimal model, which is built by MACCS fingerprints and SVM, and the prediction accuracy on the test set is 93.88%, and MCC is 0.874. Among Models B1–B9 based on training set 2 (divided by a random method), Model B5 is the optimal model, which is built by ECFP4 fingerprints and SVM, and the prediction accuracy on the test set is 89.93%, and MCC is 0.798. The two optimal models are both SVM models, indicating that SVM is a suitable method for this study.
Application domain of classification models
Based on the 18 classification models, we calculated the dSTD-PRO69 of each compound. As for the training set, the prediction probabilities of the models were replaced by the 5-CV probabilities. When the 5-CV accuracy of the model is 90%, the model is considered reliable. Therefore, we selected the threshold to make the 5-CV accuracy exactly 90% (Threshold0.90). Table 3 shows the threshold, and the coverage and performances on the training set and test set within application domain.| Model | Threshold0.90a | Training set | Test set | ||||
|---|---|---|---|---|---|---|---|
| Coverageb(%) | 5-CVc (%) | MCCd | Coverage (%) | Q (%) | MCC | ||
| a Threshold0.90, the threshold of the model when the accumulative accuracy of 5-fold cross-validation is close to 90%. b Coverage, the proportion of compounds corresponding to Threshold0.90. c 5-CV, 5-fold cross-validation. d MCC, Matthews correlation coefficient. e Q, accuracy | |||||||
| Model A1 | 0.107 | 81.95 | 90.03 | 0.799 | 87.20 | 94.95 | 0.897 |
| Model A2 | 0.114 | 82.66 | 90.01 | 0.798 | 87.60 | 96.35 | 0.925 |
| Model A3 | 0.108 | 82.08 | 90.05 | 0.799 | 87.33 | 96.03 | 0.919 |
| Model A4 | 0.131 | 83.98 | 90.01 | 0.799 | 88.40 | 95.93 | 0.917 |
| Model A5 | 0.096 | 80.76 | 90.05 | 0.799 | 86.40 | 95.83 | 0.915 |
| Model A6 | 0.107 | 81.95 | 90.03 | 0.799 | 87.20 | 96.33 | 0.925 |
| Model A7 | 0.086 | 79.79 | 90.04 | 0.799 | 86.00 | 95.50 | 0.909 |
| Model A8 | 0.089 | 80.23 | 90.04 | 0.799 | 86.27 | 94.28 | 0.884 |
| Model A9 | 0.083 | 79.35 | 90.04 | 0.799 | 85.73 | 95.96 | 0.917 |
| Model B1 | 0.176 | 87.04 | 90.04 | 0.798 | 90.07 | 91.03 | 0.819 |
| Model B2 | 0.231 | 90.40 | 90.01 | 0.798 | 92.19 | 90.66 | 0.812 |
| Model B3 | 0.222 | 89.87 | 90.00 | 0.798 | 92.05 | 90.94 | 0.817 |
| Model B4 | 0.223 | 90.05 | 90.02 | 0.798 | 92.05 | 91.80 | 0.835 |
| Model B5 | 0.186 | 87.48 | 90.04 | 0.798 | 90.46 | 90.34 | 0.806 |
| Model B6 | 0.176 | 86.91 | 90.02 | 0.798 | 89.93 | 89.69 | 0.793 |
| Model B7 | 0.154 | 85.71 | 90.04 | 0.798 | 88.87 | 90.46 | 0.807 |
| Model B8 | 0.198 | 88.41 | 90.04 | 0.798 | 91.13 | 89.83 | 0.794 |
| Model B9 | 0.191 | 87.75 | 90.02 | 0.799 | 90.73 | 90.95 | 0.817 |
According to Table 3, we found that within application domain, the prediction accuracy and MCC on the test set are improved. The threshold of Models A1–A9 ranges from 0.08 to 0.13, and the coverage of the training set and test set ranges from 80% to 87%, respectively. The threshold of Models B1–B9 ranges from 0.15 to 0.23, and the coverage of the training set and test set ranges from 87% to 90%, respectively. According to the MCC on the test set, Model A2 was the optimal model. Model A2 is the model built by MACCS fingerprints and SVM, with the threshold of 0.114. The coverage of the training set and test set is 82.66% and 87.6%, respectively, and the prediction accuracy on the test set is 96.35% and MCC is 0.925.
Classification models (based on dataset 1 and decoys)
Firstly, we measured the quality of generated decoys. The evaluation of generated decoys is shown in Table S1 in the ESI.† According to Table S1,† it was found that the DOE score between the training set/test set and generated decoys is less than 0.1, indicating that the quality of the embedding of actives and decoys in chemical space is good, and the average doppelganger score between training set/test set and generated decoys is less than 0.25, indicating that the structural similarity between actives and decoys is low, and the generated decoys have a good false negative bias, and the quality of generated decoys is good.For training set 3, we calculated and extracted three types of descriptors (81 MACCS fingerprints, 299 ECFP4 fingerprints, and 13 Corina descriptors), using three machine learning methods (RF, SVM and DNN) to build Models C1–C9. For training set 4, we calculated and extracted three types of descriptors (81 MACCS fingerprints, 298 ECFP4 fingerprints, and 16 Corina descriptors), using three machine learning methods (RF, SVM and DNN) to build Models D1–D9. The performances of the 18 classification models are shown in Table 4. The optimal hyper-parameters of each model are given in the ESI.†
| Model | Training set/test set | Input descriptors | Methods | Training set | Test set | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | n | Q (%) | 5-CV (%) | MCC | Q (%) | SE (%) | SP (%) | MCC | |||
| Model C1 | 8217/3129 | MACCS | 81 | RF | 98.93 | 93.90 | 0.957 | 98.40 | 92.91 | 99.29 | 0.933 |
| Model C2 | 8217/3129 | MACCS | 81 | SVM | 98.54 | 93.89 | 0.942 | 98.50 | 92.22 | 99.52 | 0.937 |
| Model C3 | 8217/3129 | MACCS | 81 | DNN | 98.78 | 95.64 | 0.951 | 96.52 | 88.79 | 97.77 | 0.857 |
| Model C4 | 8217/3129 | ECFP4 | 299 | RF | 99.99 | 95.85 | 1.000 | 97.67 | 92.22 | 98.55 | 0.903 |
| Model C5 | 8217/3129 | ECFP4 | 299 | SVM | 99.94 | 95.61 | 0.998 | 98.34 | 93.14 | 99.18 | 0.930 |
| Model C6 | 8217/3129 | ECFP4 | 299 | DNN | 98.47 | 90.96 | 0.938 | 96.74 | 85.81 | 98.51 | 0.862 |
| Model C7 | 8217/3129 | Corina | 13 | RF | 99.60 | 93.55 | 0.984 | 97.12 | 82.61 | 99.48 | 0.876 |
| Model C8 | 8217/3129 | Corina | 13 | SVM | 96.73 | 94.39 | 0.868 | 96.71 | 86.27 | 98.40 | 0.861 |
| Model C9 | 8217/3129 | Corina | 13 | DNN | 94.01 | 93.24 | 0.750 | 94.95 | 76.20 | 97.99 | 0.781 |
| Model D1 | 8348/3134 | MACCS | 81 | RF | 99.09 | 95.29 | 0.964 | 96.49 | 82.97 | 98.53 | 0.842 |
| Model D2 | 8348/3134 | MACCS | 81 | SVM | 96.61 | 95.27 | 0.863 | 96.49 | 82.48 | 98.60 | 0.841 |
| Model D3 | 8348/3134 | MACCS | 81 | DNN | 98.97 | 97.22 | 0.959 | 93.94 | 79.81 | 96.07 | 0.741 |
| Model D4 | 8348/3134 | ECFP4 | 298 | RF | 99.99 | 96.31 | 1.000 | 97.19 | 86.37 | 98.82 | 0.874 |
| Model D5 | 8348/3134 | ECFP4 | 298 | SVM | 97.07 | 96.24 | 0.884 | 97.32 | 88.81 | 98.60 | 0.881 |
| Model D6 | 8348/3134 | ECFP4 | 298 | DNN | 98.51 | 91.81 | 0.940 | 96.20 | 80.78 | 98.53 | 0.828 |
| Model D7 | 8348/3134 | Corina | 16 | RF | 99.69 | 94.85 | 0.988 | 95.88 | 75.67 | 98.93 | 0.810 |
| Model D8 | 8348/3134 | Corina | 16 | SVM | 96.62 | 95.40 | 0.863 | 95.98 | 82.73 | 97.98 | 0.821 |
| Model D9 | 8348/3134 | Corina | 16 | DNN | 94.69 | 93.33 | 0.782 | 94.54 | 73.72 | 97.69 | 0.751 |
According to Table 4, we found that the differences between SE and SP of most models are within the permissible limits, especially the models based on training set 3, indicating that the models can balance different types of inhibitors very well. The 5-CV accuracies of all models are greater than 90%, indicating that all models are robust. The MCC values on the test set of all models are greater than 0.74, indicating that all models have good performance. The prediction accuracies on the training set and test set of all models are more than 93%, indicating that all models have good performance of fitting and prediction respectively.
Compared to the models without decoys (Models A1–A9 and B1–B9 in Table 2), the 5-CV accuracies, average MCC and prediction accuracies for the training set and test set get better, indicating that the more samples used for modelling, the more robust the models, and the better the performance of the models.
While the differences between SE and SP increased to some extent, the reason for which is that the number of weakly active inhibitors has increased significantly, the different types of inhibitors used for modelling are unevenly distributed.
Comparing the performances of models built by different methods, it was found that the models built by SVM and RF have better performance on the test set than other models. Comparing the performances of models based on different descriptors, it was found that the models based on ECFP4 fingerprints have the best performance on the test set.
Comparing the performances of models based on the two different training sets, the optimal models were selected according to the prediction MCC on the test set. It was found that among Models C1–C9 based on training set 3, Model C2 is the optimal model, which is built by MACCS fingerprints and SVM, and the prediction accuracy on the test set is 98.5%, while MCC is 0.937. Among Models D1–D9 based on training set 4, Model D5 is the optimal model, which is built by ECFP4 fingerprints and SVM, and the prediction accuracy on test set 4 is 87.32%, while MCC is 0.881.
QSAR models
For training set 5 (divided by SOM), we calculated and extracted three types of descriptors (24 Corina descriptors, 33 MOE descriptors, and 31 RDkit descriptors), using four machine learning methods (MLR, RF, SVM and DNN) to build Models E1–E12. For training set 6 (divided by a random method), we calculated and extracted three types of descriptors (27 Corina descriptors, 43 MOE descriptors, and 45 RDkit descriptors), using four machine learning methods (MLR, RF, SVM and DNN) to build Models F1–F12. The performances of the 24 QSAR models are shown in Table 5. The optimal hyper-parameters of each model are given in the ESI.†| Model | Training set/test set | Input descriptors | Methods | Training set | Test set | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type | n | R 2 | MAEc | RMSEd | R 2 | MAE | RMSE | |||
| a n, number of descriptors. b R 2, coefficient of determination. c MAE, mean absolute error. d RMSE, root mean squared error. | ||||||||||
| Model E1 | 1061/366 | Corina | 24 | MLR | 0.621 | 0.605 | 0.764 | 0.588 | 0.647 | 0.816 |
| Model E2 | 1061/366 | Corina | 24 | RF | 0.901 | 0.311 | 0.390 | 0.774 | 0.453 | 0.605 |
| Model E3 | 1061/366 | Corina | 24 | SVM | 0.920 | 0.279 | 0.351 | 0.805 | 0.421 | 0.561 |
| Model E4 | 1061/366 | Corina | 24 | DNN | 0.886 | 0.330 | 0.418 | 0.778 | 0.460 | 0.598 |
| Model E5 | 1061/366 | MOE | 33 | MLR | 0.689 | 0.547 | 0.692 | 0.650 | 0.595 | 0.752 |
| Model E6 | 1061/366 | MOE | 33 | RF | 0.905 | 0.304 | 0.383 | 0.764 | 0.462 | 0.617 |
| Model E7 | 1061/366 | MOE | 33 | SVM | 0.927 | 0.214 | 0.336 | 0.793 | 0.437 | 0.579 |
| Model E8 | 1061/366 | MOE | 33 | DNN | 0.932 | 0.250 | 0.323 | 0.789 | 0.440 | 0.583 |
| Model E9 | 1061/366 | RDkit | 31 | MLR | 0.671 | 0.564 | 0.712 | 0.660 | 0.581 | 0.743 |
| Model E10 | 1061/366 | RDkit | 31 | RF | 0.904 | 0.306 | 0.385 | 0.796 | 0.432 | 0.574 |
| Model E11 | 1061/366 | RDkit | 31 | SVM | 0.936 | 0.217 | 0.313 | 0.805 | 0.410 | 0.562 |
| Model E12 | 1061/366 | RDkit | 31 | DNN | 0.932 | 0.250 | 0.323 | 0.770 | 0.460 | 0.610 |
| Model F1 | 1050/357 | Corina | 27 | MLR | 0.655 | 0.548 | 0.729 | 0.567 | 0.639 | 0.838 |
| Model F2 | 1050/357 | Corina | 27 | RF | 0.901 | 0.311 | 0.391 | 0.744 | 0.462 | 0.644 |
| Model F3 | 1050/357 | Corina | 27 | SVM | 0.918 | 0.279 | 0.356 | 0.807 | 0.427 | 0.559 |
| Model F4 | 1050/357 | Corina | 27 | DNN | 0.916 | 0.280 | 0.359 | 0.791 | 0.441 | 0.582 |
| Model F5 | 1050/357 | MOE | 43 | MLR | 0.721 | 0.512 | 0.655 | 0.657 | 0.578 | 0.745 |
| Model F6 | 1050/357 | MOE | 43 | RF | 0.908 | 0.298 | 0.376 | 0.763 | 0.444 | 0.619 |
| Model F7 | 1050/357 | MOE | 43 | SVM | 0.969 | 0.160 | 0.218 | 0.824 | 0.404 | 0.534 |
| Model F8 | 1050/357 | MOE | 43 | DNN | 0.943 | 0.225 | 0.296 | 0.807 | 0.427 | 0.559 |
| Model F9 | 1050/357 | RDkit | 45 | MLR | 0.713 | 0.518 | 0.665 | 0.665 | 0.564 | 0.737 |
| Model F10 | 1050/357 | RDkit | 45 | RF | 0.910 | 0.297 | 0.373 | 0.784 | 0.435 | 0.592 |
| Model F11 | 1050/357 | RDkit | 45 | SVM | 0.939 | 0.216 | 0.306 | 0.790 | 0.440 | 0.583 |
| Model F12 | 1050/357 | RDkit | 45 | DNN | 0.939 | 0.235 | 0.306 | 0.774 | 0.457 | 0.605 |
We selected R2 as the most important evaluation standard, and found that except for the multiple linear regression models, the prediction R2 of the other 18 models on the test set was greater than 0.74, indicating that the 18 QSAR models have good performances. The range of RMSE on the test set is 0.534–0.644, and the range of MAE is 0.404–0.579, that means the prediction error is within the acceptable range.
Comparing the performances of models built by different methods, it was found that the models built by SVM have the best performance on the test set, indicating that SVM is the best method for building QSAR models. Comparing the performances of models based on different descriptors, it was found that the models built by MOE descriptors have the best performance on the test set, indicating that the extracted MOE descriptors are very important for inhibitory activity.
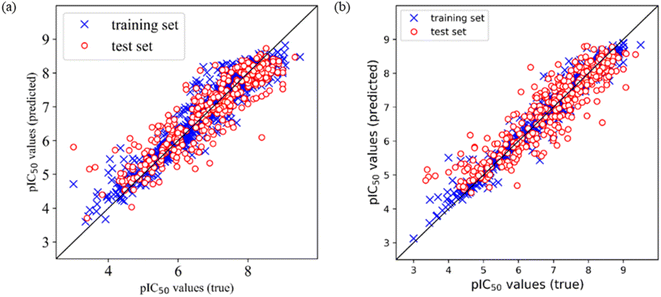
Comparing the performances of models based on the two different training sets, the optimal models were selected according to the prediction R2 on the test set. It was found that among Models E1–E12 based on training set 5 (divided by SOM), Model E3 is the optimal model, which is built by Corina descriptors and SVM, and the prediction R2 on the test set is 0.805, and RMSE is 0.561. Among Models F1–F12 based on training set 6 (divided by a random method), Model F7 is the optimal model, which is built by MOE descriptors and SVM, and the prediction R2 on the test set is 0.824, and RMSE is 0.534. Furthermore, we draw the prediction results of Model E3 and Model F7, as shown in Fig. 1.
Application domain of QSAR models
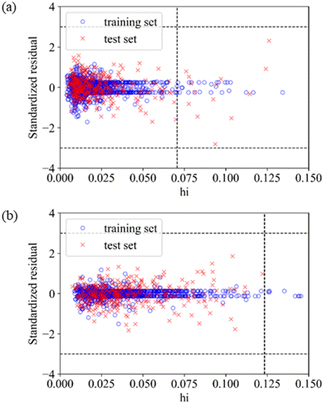
The application domain of QSAR models is visualized by the Williams plot,70 and the Williams plots of Model E3 and Model F7 are shown in Fig. 2. The points in the left region surrounded by three dashed lines are all inhibitors in the application domain of the model. According to statistics, the coverages of the training set and test set are 97.64% and 95.63% for Model E3, respectively, and they are 98.50% and 99.94% for Model F7, respectively.Table 6 shows the performances of the two optimal models in the application domain. It was found that the RMSE of the two models on the test set shows an improvement, indicating that the application domain can screen out some outliers with large prediction deviation, and the prediction of compounds in the application domain is considered to be reliable.
| Model | Training set | Test set | ||||
|---|---|---|---|---|---|---|
| R 2 | MAE | RMSE | R 2 | MAE | RMSE | |
| Model E3 | 0.920 | 0.279 | 0.351 | 0.805 | 0.421 | 0.561 |
| Model E3 (AD) | 0.918 | 0.280 | 0.354 | 0.828 | 0.403 | 0.519 |
| Model F7 | 0.969 | 0.160 | 0.218 | 0.824 | 0.404 | 0.534 |
| Model F7 (AD) | 0.968 | 0.161 | 0.219 | 0.827 | 0.400 | 0.528 |
Clustering results and analysis
In order to study the structure activity relationship of CDK4 inhibitors, we performed clustering, as well as scaffolds and fragment features analysis.On the basis of dataset 1, we clustered inhibitors based on their ECFP4 fingerprints. The clustering methods are K-means and hierarchical clustering, while the dimension-reduction methods are TSNE and UMAP, so we tried two clustering methods and four combinations (TSNE + K-means, TSNE + HC, UMAP + K-means, and UMAP + HC) which are dimension reduction followed by clustering, so there are 6 different methods. We set the number of categories to 11, and carried out 6 methods to clustering, and then evaluated the results, as shown in Table 7.
| Method | Silhouette | CH score | DB score |
|---|---|---|---|
| K-Means | 0.13 | 144.82 | 2.39 |
| HC | 0.13 | 145.40 | 2.71 |
| TSNE + K-means | 0.53 | 4882.42 | 0.64 |
| TSNE + HC | 0.50 | 4414.13 | 0.66 |
| UMAP + K-means | 0.67 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780.75 780.75 |
0.45 |
| UMAP + HC | 0.64 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900.34 900.34 |
0.49 |
According to Table 7, it was found that UMAP + K-means has the best performance in the 6 different methods, with the lowest values of silhouette coefficient and DB score, and the highest value of CH score. So, we used this method to explore the appropriate number of categories. We set the number from 9 to 15, and evaluated the clustering results, as shown in Table 8.
According to Table 8, it was found that when the number is 12, the clustering result has the best silhouette coefficient, good DB score and best CH score. Therefore, we chose 12 as the number of categories.
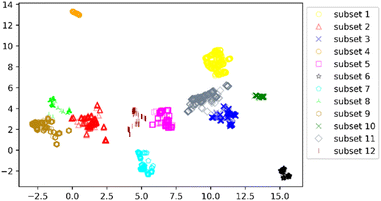
We clustered 3018 CDK4 inhibitors into 12 subsets by UMAP and K-means, and visualized them by the UMAP two-dimensional vector. Fig. 3 shows the clustering result.
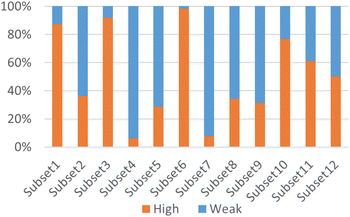
According to Fig. 3, it was found that the distribution of each subset is relatively concentrated, and there is a clear boundary between them and other subsets. The percentages of highly and weakly active inhibitors in the 12 subsets are shown in Fig. 4. And it was found that subsets 1, 3 and 6 have a large proportion of highly active inhibitors, while subsets 4 and 7 have a large proportion of weakly active inhibitors.
Since dimension reduction will lead to the loss of molecular structure information of compounds, the use of UMAP two-dimensional vectors for clustering will cause the compounds in the same subset to maybe have different molecular scaffolds. We analysed the main scaffolds with a high number of compounds in each subset, and analysed fragment features of inhibitors containing these scaffolds by using statistical methods. Table 9 shows the scaffolds and fragment features on each subset.
| Subset (high/weak) | Main scaffolds (high/weak) | Fragment | |||
|---|---|---|---|---|---|
| Structure | p_Higha | p_Weaka | Diffb | ||
| a p_High and p_Weak are the frequency of the fragment in highly and weakly active inhibitors, respectively. b Diff, difference between p_High and p_Weak. | |||||
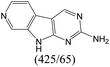
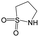
| Subset 1 (469/68) |
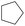
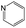
|
|
0.66 | 0.34 | 0.32 |
|
0.41 | 0.65 | −0.24 | ||
|
0.20 | 0.40 | −0.20 | ||
| Subset 2 (121/214) |
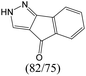
|
|
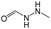
0.44 | 0.05 | 0.39 |

|
0.84 | 0.47 | 0.37 | ||
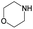
|
0.35 | 0.03 | 0.33 | ||

|
0.38 | 0.11 | 0.27 | ||
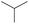
|
0.07 | 0.23 | 0.15 | ||
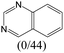
|
|
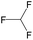
— | 0.73 | — | |
|
— | 0.73 | — | ||
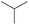
|
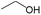
|
0.60 | 0.12 | 0.48 | |
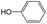
|
0.60 | 0.16 | 0.44 | ||
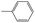
|
0.40 | 0.04 | 0.36 | ||
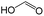
|
0.00 | 0.84 | −0.84 | ||
|
0.00 | 0.84 | −0.84 | ||

|
0.00 | 0.84 | −0.84 | ||
| Subset 3 (311/28) |
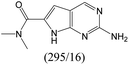
|
|
0.82 | — | — |
|
0.77 | — | — | ||
|
0.47 | — | — | ||
| Subset 4 (6/93) |
|
|
— | 0.95 | — |
|
— | 0.78 | — | ||
| Subset 5 (64/160) |
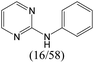
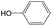
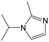
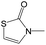
|

|
0.75 | 0.47 | 0.28 |
|
0.56 | 0.36 | 0.20 | ||
|
0.25 | 0.10 | 0.15 | ||
|
0.00 | 0.12 | −0.12 | ||
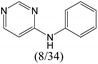
|
|
0.63 | 0.06 | 0.57 | |

|
0.38 | 0.03 | 0.35 | ||
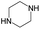
|
0.25 | 0.09 | 0.16 | ||
|
0.00 | 0.32 | −0.32 | ||
|
0.38 | 0.62 | −0.24 | ||
|
|
0.86 | 0.63 | 0.22 | |
|
0.21 | 0.03 | 0.18 | ||

|
0.25 | 0.53 | −0.28 | ||
|
0.11 | 0.33 | −0.23 | ||
|
0.11 | 0.30 | −0.19 | ||
| Subset 6 (153/3) |
|
|
0.89 | — | — |
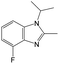
|
0.87 | — | — | ||
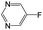
|
0.82 | — | — | ||
| Subset 7 (21/249) |
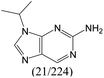
|

|
— | 0.95 | — |
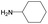
|
— | 0.71 | — | ||
| Subset 8 (52/101) |
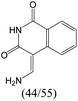
|
|
0.55 | 0.22 | 0.33 |
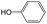
|
0.34 | 0.07 | 0.27 | ||
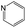
|
0.32 | 0.13 | 0.19 | ||
|
0.14 | 0.40 | −0.26 | ||
|
0.16 | 0.35 | −0.19 | ||
|
|
1.00 | 0.48 | 0.52 | |
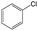
|
1.00 | 0.48 | 0.52 | ||
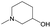
|
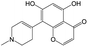
0.60 | 0.28 | 0.32 | ||
|
0.00 | 0.40 | −0.40 | ||
| Subset 9 (112/247) |
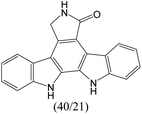
|

|
0.35 | 0.14 | 0.21 |
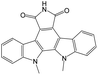
|
0.00 | 0.19 | −0.19 | ||
|
|
0.27 | 0.00 | 0.27 | |
|
0.00 | 0.25 | −0.25 | ||
|
0.02 | 0.25 | −0.23 | ||
|
|
— | 0.63 | — | |
| Subset 10 (86/26) |
|
|
0.88 | — | — |
|
0.80 | — | — | ||
|
0.63 | — | — | ||
| Subset 11 (168/108) |
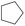
|
|
0.82 | 0.31 | 0.51 |
|
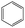
0.64 | 0.21 | 0.42 | ||
|
0.58 | 0.69 | −0.11 | ||
| Subset 12 (79/79) |
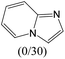
|
|
— | 0.57 | — |
|
— | 0.57 | — | ||
|
— | 0.5 | — | ||
|

|
0.98 | — | — | |
|
0.34 | — | — | ||
|

|
0.57 | 0.09 | 0.48 | |
|
1.00 | 0.70 | 0.30 | ||

|
1.00 | 0.78 | 0.22 | ||

|
0.29 | 0.96 | −0.67 | ||
|
0.29 | 0.78 | −0.50 | ||
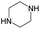
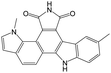
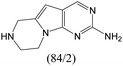
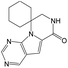
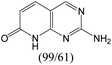
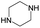
According to Table 9, it was found that the compounds in subsets 1, 3, 7, 10, and 11 are 2-aminopyrimidine derivatives. The main scaffold of subset 1 is 9H-pyrido[4′,3′:4,5]pyrrolo[2,3-d]pyrimidin-2-amine, there were 425 highly active inhibitors and 65 weakly active inhibitors, and it was found that cyclopentane was more likely to appear in highly active inhibitors, while the hydroxyl group was more likely to appear in weakly active inhibitors. The main scaffold of subset 3 is 2-amino-N,N-dimethyl-7H-pyrrolo[2,3-d]pyrimidine-6-carboxamide, ribociclib7 has this scaffold, there were 295 highly active inhibitors and 16 weakly active inhibitors, and it was found that cyclopentane, pyridine and piperazine were the most frequent fragments in the highly active inhibitors. The main scaffold of subset 7 is 9-(prop-2-yl)purin-2-amine, there were 21 highly active inhibitors and 224 weakly active inhibitors, and it was found that butane and cyclohexanamine were the most frequent fragments in the weakly active inhibitors. The main scaffold of subset 10 is 6,7,8,9-tetrahydropyrazino[2′,1′:5,1]pyrrolo[2,3-d]pyrimidin-2-amine, trilaciclib9 has this scaffold, there were 84 highly active inhibitors and 2 weakly active inhibitors, and it was found that pyridine, piperazine and 7′,8′-dihydro-6′H-spiro[cyclohexane-1,9′-pyrazino[2′,1′:5,1]pyrrolo[2,3-d]pyrimidine]-6′-one were the most frequent fragments in the highly active inhibitors. The main scaffold of subset 11 is 2-amino-7,8-dihydropyrido[2,3-d]pyrimidin-7-one, palbociclib6 has this scaffold, there were 99 highly active inhibitors and 61 weakly active inhibitors, and it was found that cyclopentane and piperazine were more likely to appear in highly active inhibitors, while benzene was more likely to appear in weakly active inhibitors.
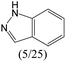
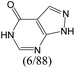
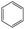
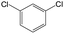
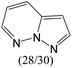
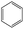
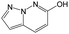
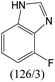
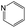
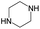
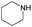
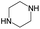
The compounds in subsets 2, 4, and 6 are pyrazol derivatives. The compounds in subset 2 contain three main scaffolds, the first one is 2,4-dihydroindeno[1,2-c]pyrazol-4-one, there were 82 highly active inhibitors and 75 weakly active inhibitors, and it was found that 2-methyldiazane-1-carbaldehyde, the hydroxyl group, 1,4-oxazinane and thiophene were more likely to appear in highly active inhibitors, while isobutane was more likely to appear in weakly active inhibitors; the second one is quinazoline, there were 44 weakly active inhibitors, and it was found that fluoroform and isobutane were the most frequent fragments in the weakly active inhibitors; the third one is 1H-indazole, there were 5 highly active inhibitors and 25 weakly active inhibitors, and it was found that ethanol, phenol and methylbenzene were more likely to appear in highly active inhibitors, while formic acid, 1λ6-1,2-thiazolidine-1,1-dione and methanethiol were more likely to appear in weakly active inhibitors. The main scaffold of subset 4 is 4,5-dihydro-1H-pyrazolo[3,4-d]pyrimidin-4-one, there were 6 highly active inhibitors and 88 weakly active inhibitors, and it was found that 1,3-dichlorobenzene and benzene were the most frequent fragments in the weakly active inhibitors. The main scaffold of subset 6 is 4-fluoro-1H-benzo[d]imidazole, abemaciclib8 has this scaffold, there were 126 highly active inhibitors and 3 weakly active inhibitors, and it was found that pyridine, 5-fluoropyrimidine and 4-fluoro-2-methyl-1-(prop-2-yl)benzo[d]imidazole were the most frequent fragments in the highly active inhibitors.
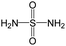
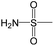
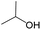
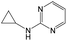
The compounds in subset 5 contain three main scaffolds, the first one is 2-(phenylamino)pyrimidine, there were 16 highly active inhibitors and 58 weakly active inhibitors, and it was found that propane, phenol and 2-methyl-1-(prop-2-yl)imidazole were more likely to appear in highly active inhibitors, while 3-methyl-3H,2H-1,3-thiazol-2-one was more likely to appear in weakly active inhibitors; the second one is 4-(phenylamino)pyrimidine, there were 8 highly active inhibitors and 34 weakly active inhibitors, and it was found that azanesulfonamide, acetonitrile and piperazine were more likely to appear in highly active inhibitors, while methanesulfonamide and propan-2-ol were more likely to appear in weakly active inhibitors; the third one is pyrazolo[5,1-f][1,2]diazine, there were 28 highly active inhibitors and 30 weakly active inhibitors, and it was found that benzene and piperazine were more likely to appear in highly active inhibitors, while propane, 2-(cyclopropylamino)pyrimidine and pyrazolo[5,1-f][1,2]diazin-6-ol were more likely to appear in weakly active inhibitors.
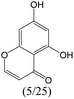
The compounds in subset 8 contain two main scaffolds, the first one is 4-[(Z)-aminomethylidene]-1,2,3,4-tetrahydroisoquinoline-1,3-dione, there were 44 highly active inhibitors and 55 weakly active inhibitors, and it was found that phenol, pyridine and benzene-1,2-diol were more likely to appear in highly active inhibitors, while piperazine and hexahydropyridine were more likely to appear in weakly active inhibitors; the second one is 5,7-dihydroxy-4H-chromen-4-one, there were 5 highly active inhibitors and 25 weakly active inhibitors, and it was found that isobutane, chlorobenzene and 1-methylhexahydropyridin-3-ol were more likely to appear in highly active inhibitors, while 5,7-dihydroxy-8-(1-methyl-1,2,3,6-tetrahydropyridin-4-yl)-4H-chromen-4-one was more likely to appear in weakly active inhibitors.
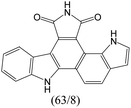
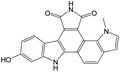
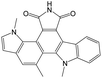
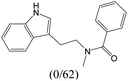
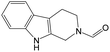
The compounds in subset 9 contain three main scaffolds, the first one is 6,7,12,13-tetrahydro-5H-pyrrolo[4,3-c]indolo[2,3-a]carbazol-5-one, there were 40 highly active inhibitors and 21 weakly active inhibitors, and it was found that propan-1-ol was more likely to appear in highly active inhibitors, while 12,13-dimethyl-6H-pyrrolo[4,3-c]indolo[2,3-a]carbazole-5,7-dione was more likely to appear in weakly active inhibitors; the second one is 5,11-dihydro-3H-pyrrolo[4,3-c]indolo[6,7-a]carbazole-4,6-dione, there were 63 highly active inhibitors and 8 weakly active inhibitors, and it was found that 9-hydroxy-3-methyl-5,11-dihydropyrrolo[4,3-c]indolo[6,7-a]carbazole-4,6-dione was more likely to appear in highly active inhibitors, while 3,8-dimethyl-5,11-dihydropyrrolo[4,3-c]indolo[6,7-a]carbazole-4,6-dione was more likely to appear in weakly active inhibitors; the third one is N-[2-(1H-indol-3-yl)ethyl]-N-methylbenzamide, there were 62 weakly active inhibitors, and it was found that 2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-2-carbaldehyde was the most frequent fragment in the weakly active inhibitors.
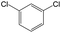
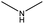
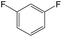
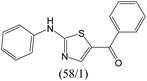
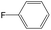
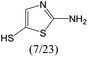
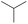
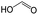
The compounds in subset 12 contain three main scaffolds, the first one is imidazo[1,2-a]pyridine, there were 30 weakly active inhibitors, and it was found that 1,3-dichlorobenzene, dimethylamine and 1,3-difluorobenzene were the most frequent fragments in the weakly active inhibitors; the second one is phenyl[2-(phenylamino)-1,3-thiazol-5-yl]methanone, there were 58 highly active inhibitors and 1 weakly active inhibitor, and it was found that methanol and fluorobenzene were the most frequent fragments in the highly active inhibitors; the third one is 2-amino-1,3-thiazole-5-thiol, there were 7 highly active inhibitors and 23 weakly active inhibitors, and it was found that pyridine and isobutane were more likely to appear in highly active inhibitors, while formaldehyde and formic acid were more likely to appear in weakly active inhibitors.
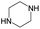
In summary, it was found that piperazine, cyclopentane, pyridine and 2-aminopyrimidine were common fragments in highly active inhibitors.
Conclusion
In this study, we collected 3018 CDK4 inhibitors and their IC50 values. Two training sets and test sets were divided by SOM and random method. MACCS fingerprints, ECFP4 fingerprints and Corina descriptors were calculated and extracted. 18 classification models were built by inputting three types of descriptors and using Random Forest, Support Vector Machine and Deep Neural Network methods. Model A2 and Model B5 are the optimal models based on the two different training sets. The prediction accuracy of Model A2 on the test set is 93.88% and MCC is 0.874. The prediction accuracy of Model B5 on the test set is 89.93% and MCC is 0.798. The application domain of the 18 classification models was calculated, and the performances of the models in the application domain were recalculated, and it was found that the performances had improved in the application domain.We considered adding decoys to train models and evaluate their performance, because decoys are necessary to evaluate virtual screening methods. Therefore, we used two different decoy generation methods in training and test sets, respectively. Then, MACCS fingerprints, ECFP4 fingerprints and Corina descriptors were calculated and extracted. The 18 classification models were built by inputting three types of descriptors and using Random Forest, Support Vector Machine and Deep Neural Network methods. Model C2 and Model D5 are the optimal models based on the two different training sets. The prediction accuracy of Model C2 on the test set is 98.5% and MCC is 0.937. The prediction accuracy of Model D5 on the test set is 87.32% and MCC is 0.881. Compared to the other 18 classification models (Models A1–A9 and B1–B9 in Table 2), it was found that the more samples used for modelling, the more robust the models, and the better the performance of the models.
On the basis of 3018 CDK4 inhibitors, we selected 1427 CDK4 inhibitors whose IC50 was detected by a radiolabeling method to build QSAR models. Two training sets and test sets were divided by SOM and random method. Corina, MOE and RDkit descriptors of the compounds were calculated and extracted, and 24 QSAR models were built by inputting three types of descriptors and using Multiple Linear Regression, Random Forest, Support Vector Machine and Deep Neural Network methods. Model E3 and Model F7 are the optimal models based on the two different training sets. The prediction R2 of Model E3 on the test set is 0.805 and RMSE is 0.561. The prediction R2 of Model F7 on the test set is 0.824 and RMSE is 0.534. The application domain of Model E3 and Model F7 was calculated, and the performances of the models in the application domain were recalculated, and it was found that the RMSE predicted on the test set had improved in the application domain, indicating that some outliers with large prediction deviation could be deleted in the application domain, and the compound prediction in the application domain was considered to be reliable.
In addition, we used UMAP and K-means to cluster 3018 inhibitors into 12 subsets and analysed the scaffolds and fragment features of CDK4 inhibitors. It was found that piperazine, cyclopentane, 2-aminopyrimidine and pyridine were important structures in the highly active inhibitors.
Data availability
All the data (dataset) used for modelling and all of the code of this study are provided at https://github.com/pangxiaoyang/qsar/tree/master.Author contributions
Xiaoyang Pang built the models and analysed the structural features. Yunyang Zhao and Guo Li performed the analysis of the results of the models. Jianrong Liu and Aixia Yan provided the main idea of this work. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Molecular Networks GmbH, Nuremberg, Germany, for providing the programs CORINA Symphony and SONNIA for our scientific work.References
- T. Adon, D. Shanmugarajan and H. Y. Kumar, RSC Adv., 2021, 11, 29227–29246 RSC.
- R. Wang, K. Xu, F. Gao, J. Huang and X. Guan, Biochim. Biophys. Acta, Rev. Cancer, 2021, 1876, 188590 CrossRef CAS PubMed.
- V. Wagner and J. Gil, Oncogene, 2020, 39, 5165–5176 CrossRef CAS PubMed.
- A. Fassl, Y. Geng and P. Sicinski, Science, 2022, 375, eabc1495 CrossRef CAS PubMed.
- C. L. Braal, E. M. Jongbloed, S. M. Wilting, R. H. J. Mathijssen, S. L. W. Koolen and A. Jager, Drugs, 2021, 81, 317–331 CrossRef CAS PubMed.
- P. L. Toogood, P. J. Harvey, J. T. Repine, D. J. Sheehan, S. N. VanderWel, H. Zhou, P. R. Keller, D. J. McNamara, D. Sherry, T. Zhu, J. Brodfuehrer, C. Choi, M. R. Barvian and D. W. Fry, J. Med. Chem., 2005, 48, 2388–2406 CrossRef CAS PubMed.
- U. Asghar, A. K. Witkiewicz, N. C. Turner and E. S. Knudsen, Nat. Rev. Drug Discovery, 2015, 14, 130–146 CrossRef CAS PubMed.
- C. Zha, W. Deng, Y. Fu, S. Tang, X. Lan, Y. Ye, Y. Su, L. Jiang, Y. Chen, Y. Huang, J. Ding, M. Geng, M. Huang and H. Wan, Eur. J. Med. Chem., 2018, 148, 140–153 CrossRef CAS PubMed.
- C. Sánchez-Martínez, M. J. Lallena, S. G. Sanfeliciano and A. de Dios, Bioorg. Med. Chem. Lett., 2019, 29, 126637 CrossRef PubMed.
- X. Li, P. Sun, J. Lan, J. Peng, Y. Chen, B. Wang and Q. Dong, WO Patent, WO2014183520A1, 2014.
- F. R. Wilson, A. Varu, D. Mitra, C. Cameron and S. Iyer, Breast Cancer Res. Treat., 2017, 166, 167–177 CrossRef CAS PubMed.
- G. N. Hortobagyi, S. M. Stemmer, H. A. Burris, Y. S. Yap, G. S. Sonke, S. Paluch-Shimon, M. Campone, K. L. Blackwell, F. Andre, E. P. Winer, W. Janni, S. Verma, P. Conte, C. L. Arteaga, D. A. Cameron, K. Petrakova, L. L. Hart, C. Villanueva, A. Chan, E. Jakobsen, A. Nusch, O. Burdaeva, E. M. Grischke, E. Alba, E. Wist, N. Marschner, A. M. Favret, D. Yardley, T. Bachelot, L. M. Tseng, S. Blau, F. Xuan, F. Souami, M. Miller, C. Germa, S. Hirawat and J. O'Shaughnessy, N. Engl. J. Med., 2016, 375, 1738–1748 CrossRef CAS PubMed.
- M. N. Dickler, S. M. Tolaney, H. S. Rugo, J. Cortes, V. Dieras, D. Patt, H. Wildiers, C. A. Hudis, J. O'Shaughnessy, E. Zamora, D. A. Yardley, M. Frenzel, A. Koustenis and J. Baselga, Clin. Cancer Res., 2017, 23, 5218–5224 CrossRef CAS PubMed.
- M. P. Goetz, M. Toi, M. Campone, J. Sohn, S. Paluch-Shimon, J. Huober, I. H. Park, O. Trédan, S. C. Chen, L. Manso, O. C. Freedman, G. Garnica Jaliffe, T. Forrester, M. Frenzel, S. Barriga, I. C. Smith, N. Bourayou and A. Di Leo, J. Clin. Oncol., 2017, 35, 3638–3646 CrossRef CAS PubMed.
- G. W. Sledge Jr, M. Toi, P. Neven, J. Sohn, K. Inoue, X. Pivot, O. Burdaeva, M. Okera, N. Masuda, P. A. Kaufman, H. Koh, E. M. Grischke, M. Frenzel, Y. Lin, S. Barriga, I. C. Smith, N. Bourayou and A. Llombart-Cussac, J. Clin. Oncol., 2017, 35, 2875–2884 CrossRef PubMed.
- A. Y. Lai, J. A. Sorrentino, K. H. Dragnev, J. M. Weiss, T. K. Owonikoko, J. A. Rytlewski, J. Hood, Z. Yang, R. K. Malik, J. C. Strum and P. J. Roberts, Immunother. Cancer, 2020, 8, e000847 CrossRef PubMed.
- N. Portman, S. Alexandrou, E. Carson, S. Wang, E. Lim and C. E. Caldon, Endocr.-Relat. Cancer, 2019, 26, R15–R30 CAS.
- J. L. F. Teh and A. E. Aplin, Clin. Cancer Res., 2019, 25, 921–927 CrossRef CAS PubMed.
- K. Pandey, H. J. An, S. K. Kim, S. A. Lee, S. Kim, S. M. Lim, G. M. Kim, J. Sohn and Y. W. Moon, Int. J. Cancer, 2019, 145, 1179–1188 CrossRef CAS PubMed.
- M. Álvarez-Fernández and M. Malumbres, Cancer Cell, 2020, 37, 514–529 CrossRef PubMed.
- V. T. Sabe, T. Ntombela, L. A. Jhamba, G. E. M. Maguire, T. Govender, T. Naicker and H. G. Kruger, Eur. J. Med. Chem., 2021, 224, 113705 CrossRef CAS PubMed.
- Y. Wu, D. Huo, G. Chen and A. Yan, SAR QSAR Environ. Res., 2021, 32, 85–110 CrossRef CAS PubMed.
- Z. Zhang, Y. Tian and A. Yan, CCF Trans. High Perform. Comput., 2021, 3, 353–364 CrossRef.
- R. Qin, H. Wang and A. Yan, SAR QSAR Environ. Res., 2021, 32, 411–431 CrossRef CAS PubMed.
- D. Qu, A. Yan and J. S. Zhang, SAR QSAR Environ. Res., 2017, 28, 111–132 CrossRef CAS.
- D. Huo, S. Wang, Y. Kong, Z. Qin and A. Yan, J. Chem. Inf. Model., 2021, 5149–5164, DOI:10.1021/acs.jcim.1c00884.
- M. N. Gomes, R. C. Braga, E. M. Grzelak, B. J. Neves, E. Muratov, R. Ma, L. L. Klein, S. Cho, G. R. Oliveira, S. G. Franzblau and C. H. Andrade, Eur. J. Med. Chem., 2017, 137, 126–138 CrossRef CAS PubMed.
- B.-q. Cai, H.-x. Jin, X.-j. Yan, P. Zhu and G.-x. Hu, Acta Pharmacol. Sin., 2014, 35, 151–160 CrossRef CAS PubMed.
- N. Dessalew and P. V. Bharatam, Eur. J. Med. Chem., 2007, 42, 1014–1027 CrossRef CAS PubMed.
- V. Divya, V. L. Pushpa and K. B. Manoj, J. Mol. Struct., 2019, 1183, 263–273 CrossRef CAS.
- M. Gupta and A. K. Madan, J. Chem. Sci., 2013, 125, 483–493 CrossRef CAS.
- X.-Y. Lu, Y.-D. Chen, N.-y. Sun, Y.-J. Jiang and Q.-D. You, J. Mol. Model., 2010, 16, 163–173 CrossRef CAS PubMed.
- H. Lv, Y. Du, X. Sheng, Z. Gao and J. Shen, Future Med. Chem., 2021, 13, 1317–1339 CrossRef CAS PubMed.
- M. Muzaffar-ur-Rehman, S. K. Gunda, L. Corrie and B. P. Kumar, Indo Am. J. Pharm. Sci., 2017, 4, 2981–2993 CAS.
- A. Pandrangi, J. Pharm. Innov., 2014, 3, 164–169 CrossRef.
- R. Rondla, L. S. Padma Rao, V. Ramatenki, R. Vadija, T. Mukkera, S. R. Potlapally and U. Vuruputuri, J. Mol. Struct., 2017, 1134, 482–491 CrossRef CAS.
- A. Sharma and N. Agarwal, Pharm. Chem. J., 2021, 13, 26–43 CAS.
- M. O. Sarhan, S. S. Abd El-Karim, M. M. Anwar, R. H. Gouda, W. A. Zaghary and M. A. Khedr, Molecules, 2021, 26, 2273 CrossRef CAS PubMed.
- A.-A. Omar Husham Ahmed and M. Mohd Nizam, J. Appl. Pharm. Sci., 2022, 165–175, DOI:10.7324/japs.2021.120116.
- F. Le, L.-N. Zhao, H.-M. Guo, Y. Na, W.-X. Quan, C. Yi, S. Mao, W. Rui and Z.-H. Lin, Chin. J. Struct. Chem., 2022, 41, 2203108–2203124 CAS.
- S. Misra, H. Li and J. He, in Machine Learning for Subsurface Characterization, ed. S. Misra, H. Li and J. He, Gulf Professional Publishing, 2020, pp. 129–155, DOI:10.1016/B978-0-12-817736-5.00005-3.
- SONNIA, Version 4.2; MolecularNetworksGmbH: Erlangen, Germany.[EB/OL], 2020.03.12, http://www.molecular-networks.com Search PubMed.
- Y. O. Adeshina, E. J. Deeds and J. Karanicolas, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 18477–18488 CrossRef CAS PubMed.
- P. J. Ballester, Drug Discovery Today: Technol., 2019, 32–33, 81–87 CrossRef PubMed.
- F. Imrie, A. R. Bradley and C. M. Deane, Bioinformatics, 2021, 37, 2134–2141 CrossRef CAS PubMed.
- J. Xia, S. Li, Y. Ding, S. Wu and X. S. Wang, Mol. Inf., 2020, 39, e1900151 CrossRef PubMed.
- P. Carracedo-Reboredo, J. Liñares-Blanco, N. Rodríguez-Fernández, F. Cedrón, F. J. Novoa, A. Carballal, V. Maojo, A. Pazos and C. Fernandez-Lozano, Comput. Struct. Biotechnol. J., 2021, 19, 4538–4558 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- DrugBank Release Version 5.1.3 – DrugBank[EB/OL], 2020.03.12, http://www.molecularnetworks.com Search PubMed.
- G. Landrum, Rdkit: Open-source cheminformatics software[EB/OL]. 2020.09.1, http://www.rdkit.org/ Search PubMed.
- D. Nettleton, in Commercial Data Mining, ed. D. Nettleton, Morgan Kaufmann, Boston, 2014, pp. 79–104, DOI: DOI:10.1016/B978-0-12-416602-8.00006-6.
- Chemical Computing Group Inc., Molecular Operating Environment (MOE), Montreal, QC, Canada, 2016 Search PubMed.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297 Search PubMed.
- Y. Xu, J. Ma, A. Liaw, R. P. Sheridan and V. Svetnik, J. Chem. Inf. Model., 2017, 57, 2490–2504 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- M. Mete, U. Sakoglu, J. S. Spence, M. D. Devous, T. S. Harris and B. Adinoff, BMC Bioinf., 2016, 17, 357 CrossRef PubMed.
- Y. Jung and J. Hu, J. Nonparametric Stat., 2015, 27, 167–179 CrossRef PubMed.
- D. Krstajic, L. J. Buturovic, D. E. Leahy and S. Thomas, J. Cheminf., 2014, 6, 10 Search PubMed.
- S. Ioffe, C. Szegedy, International Conference on Machine Learning, 2015, vol. 37, pp. 448–456 Search PubMed.
- D. P. Kingma and J. Ba, Computer Science, 2014, 1–15 Search PubMed.
- L. Prechelt, Neural Networks, 1998, 11, 761–767 CrossRef PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang and S. Chintala, PyTorch: An Imperative Style, High-Performance Deep Learning Library, 2019 Search PubMed.
- D. J. Livingstone and D. W. Salt, J. Med. Chem., 2005, 48, 661–663 CrossRef CAS PubMed.
- M. Baltruschat and P. Czodrowski, F1000Research, 2020, 9, 1–16 Search PubMed.
- R. Parikh, A. Mathai, S. Parikh, G. Chandra Sekhar and R. Thomas, Indian J. Ophthalmol., 2008, 56, 45–50 CrossRef PubMed.
- D. Chicco, N. Tötsch and G. Jurman, BioData Min., 2021, 14, 13 CrossRef PubMed.
- S. Vad, A. Eskinazi, T. Corbett, T. McGloughlin and J. P. Vande Geest, J. Biomech. Eng., 2010, 132, 121007 CrossRef PubMed.
- I. Sushko, S. Novotarskyi, R. Körner, A. K. Pandey, A. Cherkasov, J. Li, P. Gramatica, K. Hansen, T. Schroeter, K.-R. Müller, L. Xi, H. Liu, X. Yao, T. Öberg, F. Hormozdiari, P. Dao, C. Sahinalp, R. Todeschini, P. Polishchuk, A. Artemenko, V. Kuz'min, T. M. Martin, D. M. Young, D. Fourches, E. Muratov, A. Tropsha, I. Baskin, D. Horvath, G. Marcou, C. Muller, A. Varnek, V. V. Prokopenko and I. V. Tetko, J. Chem. Inf. Model., 2010, 50, 2094–2111 CrossRef CAS PubMed.
- P. Gramatica, QSAR Comb. Sci., 2007, 26, 694–701 CrossRef CAS.
- F. Camastra and A. Verri, IEEE Trans. Pattern Anal. Mach. Intell., 2005, 27, 801–805 Search PubMed.
- S. Hernández-Hernández and P. J. Ballester, Biomolecules, 2023, 13, 1–19 Search PubMed.
- V. D. M. Laurens and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00143h |
| This journal is © The Royal Society of Chemistry 2023 |