Open Access Article
Open Access ArticleCalibration and generalizability of probabilistic models on low-data chemical datasets with DIONYSUS†
Gary
Tom
 abc,
Riley J.
Hickman
abc,
Riley J.
Hickman
 abc,
Aniket
Zinzuwadia
d,
Afshan
Mohajeri
abc,
Aniket
Zinzuwadia
d,
Afshan
Mohajeri
 e,
Benjamin
Sanchez-Lengeling
e,
Benjamin
Sanchez-Lengeling
 f and
Alán
Aspuru-Guzik
*abcghi
f and
Alán
Aspuru-Guzik
*abcghi
aChemical Physics Theory Group, Department of Chemistry, University of Toronto, Toronto, ON, Canada. E-mail: alan@aspuru.com
bDepartment of Computer Science, University of Toronto, Toronto, ON, Canada
cVector Institute for Artificial Intelligence, Toronto, ON, Canada
dHarvard Medical School, Harvard University, Boston, MA, USA
eDepartment of Chemistry, Shiraz University, Shiraz, Iran
fGoogle Research, Brain Team, USA
gDepartment of Chemical Engineering & Applied Chemistry, University of Toronto, Toronto, ON, Canada
hDepartment of Materials Science & Engineering, University of Toronto, Toronto, ON, Canada
iLebovic Fellow, Canadian Institute for Advanced Research, Toronto, ON, Canada
First published on 2nd May 2023
Abstract
Deep learning models that leverage large datasets are often the state of the art for modelling molecular properties. When the datasets are smaller (<2000 molecules), it is not clear that deep learning approaches are the right modelling tool. In this work we perform an extensive study of the calibration and generalizability of probabilistic machine learning models on small chemical datasets. Using different molecular representations and models, we analyse the quality of their predictions and uncertainties in a variety of tasks (regression or binary classification) and datasets. We also introduce two simulated experiments that evaluate their performance: (1) Bayesian optimization guided molecular design, (2) inference on out-of-distribution data via ablated cluster splits. We offer practical insights into model and feature choice for modelling small chemical datasets, a common scenario in new chemical experiments. We have packaged our analysis into the DIONYSUS repository, which is open sourced to aid in reproducibility and extension to new datasets.
1. Introduction
The design and discovery of molecular materials routinely enables technologies which have crucial societal consequences. Given a library of compounds, prediction of molecular functionality from its structure enables ranking and selection of promising candidates prior to experimental validation or other screening filters. Therefore, building accurate quantitative structure–activity relationship models (QSAR) is key to accelerated chemical design and efficient experimental decision-making.1 Models that leverage statistical patterns in data are now often the state of the art on such tasks. Specifically, data science and machine learning (ML) have played critical roles in modern science in general,2 enabling the utilization of data at unprecedented scales. Deep learning (DL) models are able to extract statistical patterns in dataset features and give accurate QSAR predictions and classifications.3 When compared to traditional ab initio techniques, such as density functional theory (DFT), ML models are less computationally demanding, and can learn statistical patterns directly from experimental data. However, the quality of such models is determined by the quality of the original datasets they are trained on, and thus the models are still affected by the cost of accurate data generation.To date, many studies consider molecular property prediction tasks where training data is plentiful.4,5 In real-world molecular design campaigns, particularly in the initial stages, only small molecular datasets (<2000 data points) are available due to the expense (monetary, resource, or labour) associated with the design, synthesis, and characterization of chemicals. In addition to the datasets examined in this work, examples of applications in the low-data regime include design of optoelectronic materials (i.e. organic photovoltaics,6 or photoswitching molecules7), prediction of biochemical properties (i.e. olfactory response,8,9 or mosquito repellency10), and drug discovery.11,12 Despite the practical importance of this regime, molecular property prediction using ML with limited data instances has been relatively under-explored, and remains a challenging task, especially for deep learning models which often require large amounts of training instances due to large number of model parameters.
In the low-data setting, understanding a ML model's performance is important since predictions inform decisions about further research directions, or, in a sequential learning setting, promote molecules to be subject to property measurement. In particular, we place emphasis on (1) the generalizability, the ability of a model to predict accurately on new chemical data, and (2) uncertainty calibration, the ability of a model to estimate the confidence of its predictions (Fig. 1).
Adequate generalizability, the ability for a model to make accurate predictions on out-of-distribution (OOD) data, is paramount for many learning tasks, such as in the hit-to-lead and early lead optimization phases of drug discovery.12,13 After identification of a biological target (usually a protein or nucleic acid), initial molecular hits are optimized in an expensive and time-consuming make-design-test cycle. Using ML to predict molecular properties has indeed been shown to reduce the number of syntheses and measurements required.14–16 Commonly, drug discovery project permit the synthesis and measurement of hundreds of candidate molecules due to constraints in expense, and typically involve functionalizations of a common molecular core or scaffold. Model generalization is therefore critical for the reuse of QSAR models for unstudied molecular scaffolds.17,18
Uncertainty calibration is the ability of a probabilistic model to produce accurate estimates of its confidence, and is also a crucial aspect of the molecular design process and high-risk decision making.19 Here, the goal is to learn a ML model that is not only accurate, but also furnishes its predictions with a notion of uncertainty. For instance, in a safety critical molecular property prediction scenario, e.g. the prediction of the severity of drug-induced liver injury,20,21 predictive uncertainty estimates can be an effective way of quantifying and communicating risk that can preserve time, resources, and human well-being. Additionally, strategies for sequential learning, such as Bayesian optimization22–24 or active learning25 commonly use uncertainties to construct utility functions, which determine how to promote molecules for property measurement based on their expected performance or informativeness. Previous studies have demonstrated that many state-of-the-art DL models are, although accurate, poorly calibrated.26 Poorly calibrated predictions may have an adverse effect on decision-making.27
We maintain that the topics of molecular property prediction in the low-data regime on one hand, and uncertainty quantification and model generalizability on the other, are intimately related, as they are all commonly encountered in realistic molecular design and discovery campaigns. In the spirit of providing the community with a “handbook” on best practices thereof, we contribute DIONYSUS: a Python software package for facile evaluation of uncertainty quantification and generalizability of molecular property prediction models, accompanied by the current study, in which we showcase DIONYSUS by evaluating and analyzing these topics on several QSAR datasets.
The contributions of this work are as follows:
• We present a comprehensive study of the relationship between features and models in the low data regime across multiple axes: predictive performance, calibration of uncertainty, generalization and quality of uncertainty in optimization campaigns.
• We perform two experiments with associated metrics that can be conducted on generic regression and classification tasks: iterative molecule selection with Bayesian optimization and generalization on out-of-distribution (OOD) molecules.
• We introduce a novel type of split to better benchmark predictive models on clusters of molecules.
• This contribution describes our software which enables the extension of all analyses shown in this work to arbitrary molecular datasets. Most of the analysis is agnostic of ML model library and featurization strategy.
Code and experiments are packaged as DIONYSUS https://github.com/aspuru-guzik-group/dionysus.
• We provide a “handbook” of practical recommendations for building and comparing models in the low-data regime.
2. Related work
2.1 Probabilistic models
A variety of supervised learning models are available for representing predictive uncertainty. They can be broadly classified into two categories: those approaches derived from frequentist statistics and those based on Bayesian inference.Frequentist methods lack construction of a prior, and are instead concerned with the frequency of results over multiple trials. Ensemble methods are widely used examples of frequentist probabilistic machine learning.28 Ensemble-based methods generate uncertainty estimates based on the variance in the prediction of an ensemble of models that are trained on random subsets of data, as is the case of random forests (RF),29,30 or trained with randomly initialized parameters, as is often the case with weights of neural networks.31 For DL models, uncertainties can be estimated using Monte Carlo-dropout, in which the ensemble is created by randomly dropping out weights in a trained model at inference time.32,33 This approach is less computationally expensive, as it does not require training multiple neural networks with different weights.
Methods based on Bayesian inference seek to update a prior distribution, which summarizes pre-existing belief, in light of new observations. Commonly used Bayesian strategies for molecular property prediction in the low-data regime include Gaussian processes (GPs),34–36 and Bayesian neural networks (BNNs).37–39 GPs have more recently been combined with deep neural networks to produce more expressive models that naturally output uncertainties.40,41 Several studies have highlighted the accuracy and calibration of such models on larger datasets.5,42,43
2.2 Calibration and quantification of model uncertainties
Despite the fact that many approaches exist to produce predictive uncertainties, they are not guaranteed to be calibrated. In fact, it is well known that many modern DL strategies are poorly calibrated, despite their accuracy.26,46 For classification tasks, confidence calibration seeks to adjust probability estimates such that they reproduce the true correctness likelihood. Several calibration methods, such as isotonic regression,47 Platt scaling,48 and temperature scaling49 can be applied as a learned post-processing step to any predictive model. Similar approaches can be extended confidence calibration to a regression task setting.Techniques have also been developed for ensuring ML models produce calibrated uncertainties through the use of regularization during training.50–52 In one particular case, Soleimany et al.51 leverage evidential deep learning53,54 for molecular property prediction. While effective, such methods require careful choice of hyperparameters, as model confidence is sensitive to regularization strength. Multiple models must often be trained for each predictive task and molecular representation to determine the optimal evidential uncertainty hyperparameter(s).
Uncertainty quantification has since been studied for chemical prediction and classification tasks by numerous works.38,55 Hirschfield et al. studied and compared the performance of several neural network based uncertainty estimating techniques for regression on molecular properties.56 Similarly, Hwang et al. employed graph neural networks (GNNs) for binary classification tasks on molecules.52 Similar issues with confidence calibration were observed, and corrections were applied through loss regularization.
2.3 Downstream applications of probabilistic models
Probabilistic ML models are the central component in real-world decision making. In the molecular design and discovery setting, they are commonly used in sequential learning frameworks, such as in high-throughput virtual screening, Bayesian optimization,22–24 and active learning.25 Common to these frameworks are a machine-learned surrogate model which approximates the true underlying structure–property relation, and a utility function which determines which molecules to subject to measurement based on their expected informativeness. Typically, utility functions balance exploitative and explorative sampling behavior by considering both the surrogate model's predictive mean and variance.Although such frameworks have been demonstrated in the context of molecular design and discovery, many applications have focused on tasks with large pools of available candidates. For example, Graff et al. report accelerated structure-based virtual screening large computational docking libraries (>108 compounds) using scalable models trained using mean-variance estimation.13,57 Ryu et al. used Bayesian deep learning to screen the ChEMBL dataset58 for active inhibitor molecules.39 It was found that the Bayesian model returned active inhibitors at a significantly greater “hit rate” than did baseline strategies, suggesting that ML models with reliable uncertainty estimates execute more efficient screening campaigns. Studies considering smaller molecular datasets (≤1000) also exist. For instance, Zhang et al. used Bayesian semi-supervised graph convolutional neural networks to learn structure–bioactivity relationships with statistically principled uncertainty estimates.38 The authors showed estimations of uncertainty in the low-data regime can drive an active learning cycle, obtaining low model error with limited queries for training set data. Despite the strong work reported in previous studies, the relationship between performance of an active learner and the calibration and generalizability of the surrogate model has been relatively underexplored, particularly in the low-data molecular setting.
3. Methods
3.1 Molecular features
Molecules must be represented in machine-readable format to enable computational property prediction. Several featurization methods are explored in DIONYSUS (Fig. 2). All information is derived from the molecular graph, parsed from a SMILES string. The features used are categorized into 2 types: vector-valued and graph-valued. A d-dimensional vector-valued feature x ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d comprise bit-vectors or physicochemical descriptors of a molecule, while graph-valued features are represented as a tuple G = (U,V,E). When referring abstractly to a molecular feature type, we use X to represent either x or G from herein.
d comprise bit-vectors or physicochemical descriptors of a molecule, while graph-valued features are represented as a tuple G = (U,V,E). When referring abstractly to a molecular feature type, we use X to represent either x or G from herein.
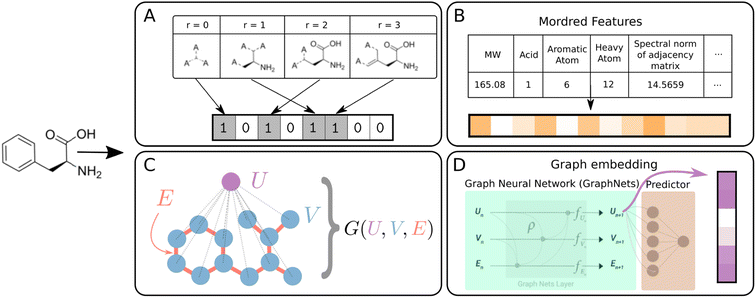 | ||
| Fig. 2 Schematic summary of molecular featurization methods. All methods are available in DIONYSUS. (A) Morgan fingerprints (MFP) are bit-vectors representing circular fragments of certain radii around heavy atoms.44 (B) Mordred descriptors are physicochemical descriptors generated from the molecular graph. (C) Graph representations consist of the vertices (atoms) and edges (bonds) of a chemical graph, and the global node that is connected to all the atoms. (D) Graph embeddings are extracted from the global node of a GraphNets GNN predictor pretrained on the molecules and targets of the dataset.45 Molecules in the test set are not accessible during pretraining to ensure no data leakage. | ||
Morgan fingerprints (MFPs) are generated by iterating over atomic centres and assigning bits according to neighboring structures up to a certain radius away.59 A hashing algorithm is then used to generate a high dimensional bit-vector unique to the molecule. For our experiments, we use d = 2048 dimensional MFPs with radius 3, generated using the open-source cheminformatics package RDKit.60 A radius of 3 was chosen in order to capture important molecular motifs such as the aromatic six-member ring structure, present in many organic molecules in our datasets.61
In addition to fingerprints, physicochemical molecular descriptors are often used for prediction of properties of molecules in cheminformatics techniques such as quantitative structure–activity/property relationship (QSAR/QSPR) models. We use the Mordred package to generate up to 1613 chemical descriptors from 2D molecular structures.62
The molecular graph can also be directly encoded in graph representation, written as G = (U,V,E).45,63 The du-dimensional global attributes describe global properties of the molecule. V is the set of node (atom) attributes {vi}i=1Nv for a molecule with Nv atoms, where vi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dv. The set of edge (bond) features E = {(ek,rk,sk)}k=1Ne comprise information about each of the Ne bonds in the molecule. Here, ek ∈
dv. The set of edge (bond) features E = {(ek,rk,sk)}k=1Ne comprise information about each of the Ne bonds in the molecule. Here, ek ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) de stores properties of the kth bond, while the indices rk and sk ∈ {1, …, Nv} indicate the two vertices that the bond joins together. The atom and bond features used are listed in Table S5,† while the global feature vector is zero-initialized.
de stores properties of the kth bond, while the indices rk and sk ∈ {1, …, Nv} indicate the two vertices that the bond joins together. The atom and bond features used are listed in Table S5,† while the global feature vector is zero-initialized.
The graphs can be directly used as inputs for graph neural networks (GNN) predictor/classifier. From this representation, we also generate learned vector-based features, in which the graph-to-feature transformation is learned from the dataset. The graphs are passed through 3 GraphNet blocks and the resulting global vectors enter a prediction layer (Fig. 2D). The global vectors from the trained network are the graph embeddings which are saved as vector-valued features for the various models.9
3.2 Datasets and preprocessing
To evaluate model performance and calibration, we selected several datasets which contain experimentally determined properties for small organic molecules. The prediction task type, number of molecules, heavy atom types, and the chemical property measured are summarized in Table 1. A dataset of N molecules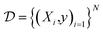 are comprised of pairs of molecular features X and target properties y ∈
are comprised of pairs of molecular features X and target properties y ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) for regression tasks and y ∈ {0, 1} for binary classification tasks.
for regression tasks and y ∈ {0, 1} for binary classification tasks.
| Dataset name | Task type | Number of molecules | Heavy atom types | Experimental value |
|---|---|---|---|---|
| BioHL64 | Regression | 150 | C, S | Biodegradability half-life |
| Freesolv65 | Regression | 637 | C, N, O, F, P, S, Cl, Br, I | Free energy of solvation |
| Delaney66 | Regression | 1116 | C, N, O, F, P, S, Cl, Br, I | Log aqueous solubility |
| BACE67 | Binary classification | 1513 | C, N, O, F, S, Cl, Br, I | Binds to human BACE-1 protein |
| RBioDeg64 | Binary classification | 1608 | C, N, O, F, Na, Si, P, S, Cl, Br, I | Readily biodegradable |
| BBBP68 | Binary classification | 1870 | B, C, N, O, F, P, S, Cl, Br, I | Blood–brain barrier permeability |
For all datasets, the SMILES were canonicalized using RDKit, while duplicated or invalid SMILES, and entries with fragments or salts are removed. Additionally, all features that have zero variance across the molecules were removed to reduce the size of feature space along redundant dimensions, and improve speed of the models.
3.3 Models implemented
For each dataset and each featurization, we train and test five different models and evaluate the performance and uncertainty calibration of each: (1) NGBoost,69 (2) Gaussian process (GP),34 (3) spectral-normalized GP (SNGP),42 (4) graph neural network GP (GNNGP),43 and (5) Bayesian neural networks (BNNs).37NGBoost is a random forest method that makes use of natural gradient boosting, similar to XGBoost,70 to estimate the parameters of the conditional probability distribution of a certain observation given the input feature. An ensemble of up to 2000 decision trees with at most 3 layers comprise the ensemble, which will predict the parameters for a probability distribution; a Gaussian distribution for regression, and a Bernoulli distribution for binary classification. The ensemble is then fitted with the natural gradient to maximize the likelihood of the distribution for the given data.
BNNs are probabilistic deep learning models that replace deterministic weight values of a neural network with weight distributions.37 This allows the model to capture the epistemic uncertainty of the predictions due to limited training data. In our experiments, we use the local reparameterization estimator71 to approximate the Gaussian prior distributions of 100 nodes of a single hidden layer. The output is passed through a rectified linear unit (ReLU) activation function and a final linear layer is used to generate a prediction.
GP is a distance-aware Bayesian model in which predictions are made via transformed relative distances between data points, dictated by a kernel function. Unlike Bayesian deep learning, which require approximate inference of the posterior distribution such as through variational methods,37,72 GPs allow for exact inference of the posterior predictive distribution directly from the input, using relatively few parameters and making it more robust to overfitting. Additionally, exact inference becomes computationally expensive in larger datasets, making GPs an ideal choice for low-data probabilistic predictions, as demonstrated in many previous works.7,36,73,74 We use the GPFlow package to implement the GP.75,76 For the MFP features, we use a kernel based on the Tanimoto distance measure commonly used for high-dimensional binary vectors, which has been implemented in Moss et al.55 The standard radial basis function (RBF) kernel was used for all other vector-valued features.
A SNGP is a deep kernel GP method, in which the kernel function is learned by training the model end-to-end. The kernel is a multi-layer perceptron (MLP) with a spectral normalization procedure on the weights of each layer to inject distance awareness in the intermediate latent representations of the network.42 The features are then passed through a random features GP, which approximates a RBF kernel GP using a two-layer neural network.77
A GNNGP is a graph-based model, trained end-to-end with the random features GP to combine the expressive power of graph representations with the probabilistic estimates of GPs. Like the GNN used to generate the graph embeddings, this model takes in graphs and has the same architecture as described above. The final predictive layer is replaced with the random features GP layers to produce predictive uncertainties.
3.4 Evaluation metrics
DIONYSUS is designed in a modular way such that all predictions and uncertainties are saved, and metrics for the performance and calibration are calculated separately. Predictions and uncertainties from other models and datasets can be easily processed.Binary classification tasks are evaluated by the area under the receiver-operating curve (AUROC), which compares the true positive and true negative rates at different discrimination thresholds. An AUROC of 1.0 indicates a perfect binary classifier, while a score of 0.5 indicates random classifications.
While there are many metrics that have been used, here we will use statistics generated from the reliability diagram, also known as the calibration diagram.26 For regression tasks, the reliability diagram is given by the C(q) score plotted as a function of quantile q, in which the Z-score statistic is used to compare the prediction and uncertainty with the ground truth.55 For a set of predictions ŷ(X) with variances ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) 2(X)
2(X)
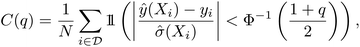 | (1) |
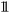 is the indicator function.
is the indicator function.
For the qth quantile, a well-calibrated model would have q fraction of predictions Z-scores within the quantile, i.e. C(q) = q. When C(q) < q, the model is overconfident, and when C(q) > q, the model is underconfident. The calibration metric obtained from the diagram is the absolute miscalibration area
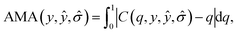 | (2) |
For binary classification, the uncertainty of the model is given by the probability p = ŷ(X), or the mean of the Bernoulli distribution. The reliability diagram is given by the plot of the classification accuracy as a function of confidence p.26 The predicted probabilities p are binned into M = 10 uniform intervals Bm, where m ∈ {1⋯M}, and averaged for the confidence
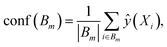 | (3) |
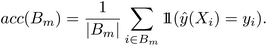 | (4) |
Similar to the case of regression, we expect the accuracy to be equal to the given confidence, for example, at p = 0.5, we would expect only half the predictions in the bin to be accurately classified.
The metric derived from the binary classification reliability diagram is known as the expected calibration error (ECE),79
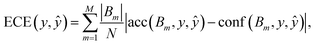 | (5) |
3.5 Cluster splits
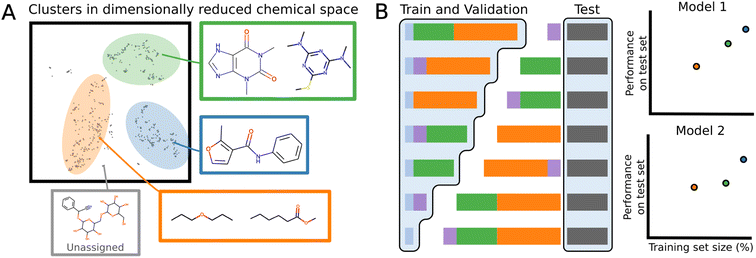
Datasets have often several structural motifs and we can identify them via a clustering algorithm. A cluster split separates a dataset into train and test via a cluster label. The test set will contain the structural motif and the training set will not. Performance on such splits can give an idea as to how well a model generalizes to new chemical classes. A cluster split can be viewed as a more general version of scaffold splitting which tends to involved a specific molecular core.78To build cluster splits, molecules are first assigned clusters based on the MFPs, which are decomposed into lower dimensional bit-vectors representing structural motifs using latent Dirichlet allocation.80 The vectors are then appended to a bit representation of the dataset labels: for regression tasks, the values are binned into 10 discrete one-hot categories, and for binary classification, the classification label is used. This ensures that the individual clusters will not have extremely imbalanced labels. The joint labels are then further decomposed onto a 5-dimensional manifold using UMAP,81 and the resulting vectors are clustered with the HDBScan algorithm.82 The number of molecules in each cluster varies, and similar structures are indeed found within the same cluster (Fig. 3A).
To evaluate the generalizability, a test set is separately generated by iterative stratified splitting 20% of the dataset appended to the cluster labels, creating an unbiased test set across all the clusters.83 The remaining molecules form various clusters which are partitioned into combinations of differently sized training sets (Fig. 3B). Validation set is a 15% iterative stratified split of the training set.
4. Experiments and results
4.1 Predictive performance and uncertainty calibration
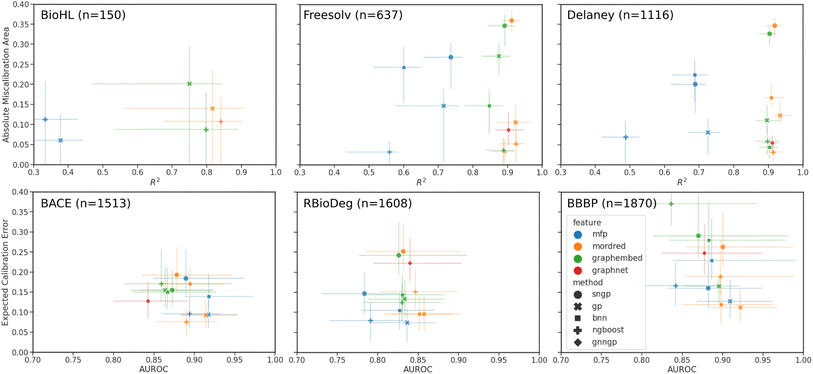
In preparation for supervised learning experiments, regression datasets were randomly split into 70/10/20 percent training/validation/testing sets, while binary classification datasets were split using stratified splitting to ensure a similar proportion of classes in all three sets. Each model is trained with the described featurizations until an early stopping criteria is reached on the validation set to prevent overfitting to the training set. Finally, the predictions and uncertainties are made and saved for the testing set, and the models are evaluated by the aforementioned performance and calibration metrics. The 95% confidence intervals were generated by bootstrapping from the test set results.Plots comparing the calibration and performance metrics are shown in Fig. 4 for each of the datasets. The models and features with the best performance are found in the lower right of each plot, where the calibration error is minimized and the performance metric is maximized. The results are also tabulated in Table S6† for regression, and in Table S7† for classification.
In the regression data, we can observe much wider ranges in the performance metrics, particularly in the lower data regime of the BioHL and Freesolv datasets, with R2 < 0.3 being truncated from the plot. The MFP feature has markedly lower R2 scores and comparable AMA, with the Tanimoto kernel GPs performing the best. In the case of the BioHL dataset, all deep learning models (SNGP, BNN, GNNGP) struggled to compete with GPs and the NGBoost models trained on Mordred descriptors and, surprisingly, graph embeddings, despite the small amount of data available. GNNGPs and BNNs on Mordred and graph embeddings achieve competitive results in Freesolv and Delaney, likely due to the larger amount available training data. In all three regression datasets, the SNGP models achieve poor calibration, with high R2 scores in Freesolv and Delaney.
We note that the Mordred features contain 21 descriptors that are related to the Crippen partition coefficient and molar refractivity, which are parameterized to experimental solubility measurements.84 To ensure that there is no advantage provided to the solvation datasets (Freesolv and Delaney), the Crippen-related descriptors are masked, and the predictions are repeated for the datasets (Fig. S1†). Indeed we see no statistically significant difference between predictions on the original Mordred features, and those that have the Crippen-related descriptors removed, indicating that the impact of the Crippen values in the Mordred features on the performance of the model on the solvation datasets is low.
In the binary classification data, the AUROC of all models and features are similar, likely due to the larger size of the datasets, and more data points representing the two binary classes in the discrete target than the continuous target, relative to the regression datasets. The error bars in the ECE score are much larger than those of the AMA in regression, since, in the low-data regime, there may be sparsely populated bins in the reliability diagram, and hence greater variability when bootstrapping. The best results are observed in GPs and NGBoost models trained on Mordred and MFPs, possibly due to the importance of certain fragments represented by the MFP in the classification tasks represented here. Within the MFP results, we observe the best performance in the Tanimoto kernel GPs. Graph embeddings for all models gave higher calibration error. Among the deep learning models, SNGP and GNNGPs achieved good AUROC scores, but poorer calibration, while BNNs, when provided Mordred descriptors, performed comparably to GPs and NGBoost models. We also observe an overall increase in classification miscalibration as the dataset size increases.
4.2 Bayesian optimization
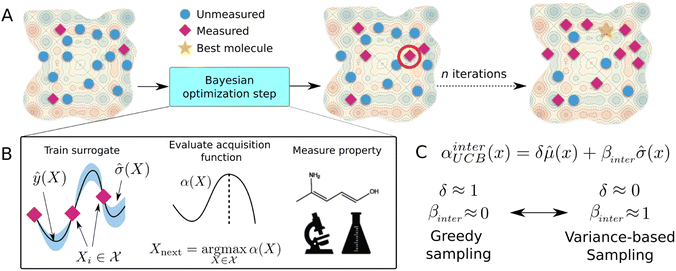
Bayesian optimization (BO) is a global, model-based optimization strategy which consists of two main steps: (1) the inference of a probabilistic surrogate model to the unknown objective function based on all current measurements, and (2) the selection of new candidates for subsequent measurements using an acquisition function which balances the expected performance of each candidate and uncertainty of the surrogate model. BO has been employed as a promising optimization framework across multiple disciplines,85 including automatic machine learning,86–88 robotics,89,90 and experimental design.91,92 More recently, BO has been employed to efficiently search through libraries of candidate molecules for those candidates which exhibit optimal properties.13,93,94 Formally, for the minimization of a molecular property over candidate space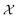 , the optimization problem is
, the optimization problem is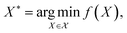 | (6) |
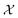 which consists of a finite set of N molecular candidates defined a priori to experimentation, i.e.
which consists of a finite set of N molecular candidates defined a priori to experimentation, i.e.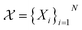 (Fig. 5). At each iteration, newly evaluated molecules are appended to a dataset of K input–output pairs,
(Fig. 5). At each iteration, newly evaluated molecules are appended to a dataset of K input–output pairs, 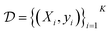 , which is used to train the surrogate model.
, which is used to train the surrogate model.
The mean (prediction) and variance (uncertainty) of the model output are used to calculate the acquisition function. A plethora of acquisition functions have been proposed for BO. We consider the commonly used upper confidence bound (UCB)
αUCB(X) = ŷ(X) + β![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (X), (X), | (7) |
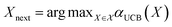 .
.
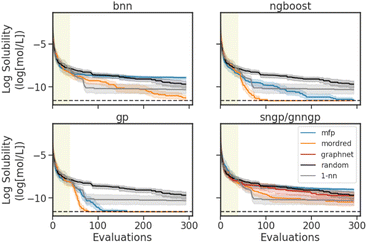
Representative results of simulated BO experiments using the Delaney dataset are shown in Fig. 6. Optimization traces for experiments on the remaining datasets are shown in Fig. S1D.† The algorithm aims to minimize the log aqueous solubility, finding the molecule within the Delaney dataset that has the lowest water solubility. The BO traces represent the cumulative best log aqueous solubility value identified by each surrogate and feature, averaged over 30 independently seeded runs. For regression, the initial design dataset comprises 5% of the dataset size and is randomly sampled based on the seed of the run, with a minimum of 25 molecules. For binary classification, we start with 10%, with a maximum of 100 molecules, to avoid only sampling molecules of the same class. In the case of the Delaney dataset, which comprises 1116 molecules, we use 56 for the initial design. For all datasets except for BioHL, the allotted budget is 250 measurements, excluding the randomly sampled initial design. The budget for the BioHL dataset is reduced to 75 measurements due to the small size of the dataset.
Although several studies73,95 have shown that a smaller initial design set (as low as 5 data points) can result in increased BO performance on materials science design tasks, we elect not to vary the number of initial design points, as we are focused on the effects of the surrogates and the molecular features on the optimization. The aforementioned studies both employ only GP or tree-based surrogate models, which have been observed to perform sufficiently well with limited training data, while in this study, we also consider neural network surrogate models, which typically have trouble training in such data regimes. Additionally, the studies employ expert-crafted low-dimensional features tailored to their respective datasets, which have been shown to improve BO performance,93 while we use general purpose higher-dimensional features across multiple datasets and tasks. Thus, we select relatively larger initial design sets of 5% and 10% of the datasets for regression and binary classification, respectively, in order to account for the inclusion of deep surrogate models, and the effects of higher-dimensional but multi-purpose molecular features.
As baseline search strategies, we use a random search (random) and a 1-nearest-neighbour strategy (1-nn), the latter of which queries the molecule which has the highest MFP Tanimoto similarity to the current best for measurement. Note that graph embeddings were not used, as the GraphNets GNN embedder requires training on the targets. While the embeddings may be effective when trained on the entire dataset, the GNN embedder would have seen the data prior to measurement in the setting of a BO experiment. Instead, the embeddings would have to be trained from the data available to the BO algorithm (∼25−100), and would not be informative, provided the performance of the GraphNets architecture in the GNNGP on BioHL (Fig. 4).
In Fig. 6, we see the best optimization performances with the Mordred descriptors, and the GP and NGBoost models. Similar to the results observed in the performance/calibration experiments (Section 4.1), the MFP performs best with the Tanimoto kernel GP model. The deep learning models struggle with the sparse data. BNN and SNGP perform best with the Mordred descriptors, with the BNN performing better than the 1-nn baseline model in the later stages of the optimization. SNGP on the other hand performs better random search, but fails to surpass the 1-nn search method. The GNNGP is unable to achieve better optimization with the graph inputs. Interestingly, in the early stages of BO, the 1-nn search is quite effective, especially when compared to random search. But the method quickly plateaus, and is stuck in a local minimum due to the exploitative nature of the search.
To succinctly summarize all experiments, the number of hit molecules are recorded for the optimization trace over the separate runs, not including those found by serendipity in the initial random search. The number of hits is normalized by the total number of possible hits accessible throughout the optimization to give a fraction of hits achieved, mimicking a real-life molecular design scenario of finding as many materials that extremize a certain property as possible. The results for the datasets of interest are shown in Tables 2 and 3. In a regression task, a molecule is considered a hit if it is within the top 10% of the dataset. In a classification task, as we are using a greedy strategy, a hit is a positive binary label. Looking at the fraction of hits for the Delaney BO experiment, we see that the best feature and surrogate models agree with the results in the optimization traces, with GPs and NGBoost using Mordred features achieving the highest scores.
| MFP | Mordred | Graph | |
|---|---|---|---|
| BioHL | |||
| Random | 0.610 ± 0.044 | ||
| 1-nn | 0.635 ± 0.035 | ||
| SNGP | 0.721 ± 0.042 | 0.585 ± 0.041 | |
| GP | 0.779 ± 0.083 | 0.796 ± 0.030 | |
| BNN | 0.729 ± 0.034 | 0.538 ± 0.040 | |
| NGBoost | 0.769 ± 0.040 | 0.802 ± 0.042 | |
| GNNGP | 0.738 ± 0.043 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Freesolv | |||
| Random | 0.520 ± 0.020 | ||
| 1-nn | 0.638 ± 0.073 | ||
| SNGP | 0.750 ± 0.024 | 0.690 ± 0.036 | |
| GP | 0.946 ± 0.011 | 0.954 ± 0.010 | |
| BNN | 0.792 ± 0.031 | 0.786 ± 0.048 | |
| NGBoost | 0.907 ± 0.013 | 0.953 ± 0.011 | |
| GNNGP | 0.482 ± 0.026 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Delaney | |||
| Random | 0.276 ± 0.016 | ||
| 1-nn | 0.439 ± 0.043 | ||
| SNGP | 0.371 ± 0.018 | 0.343 ± 0.023 | |
| GP | 0.838 ± 0.012 | 0.953 ± 0.021 | |
| BNN | 0.393 ± 0.018 | 0.417 ± 0.022 | |
| NGBoost | 0.786 ± 0.013 | 0.959 ± 0.007 | |
| GNNGP | 0.189 ± 0.015 | ||
| BACE | MFP | Mordred | Graph |
|---|---|---|---|
| Random | 0.212 ± 0.005 | ||
| 1-nn | 0.253 ± 0.008 | ||
| SNGP | 0.259 ± 0.005 | 0.236 ± 0.006 | |
| GP | 0.362 ± 0.004 | 0.372 ± 0.004 | |
| BNN | 0.265 ± 0.005 | 0.229 ± 0.005 | |
| NGBoost | 0.352 ± 0.003 | 0.347 ± 0.004 | |
| GNNGP | 0.221 ± 0.004 |
| MFP | Mordred | Graph-based | |
|---|---|---|---|
| RBioDeg | |||
| Random | 0.193 ± 0.004 | ||
| 1-nn | 0.310 ± 0.014 | ||
| SNGP | 0.206 ± 0.004 | 0.200 ± 0.006 | |
| GP | 0.396 ± 0.006 | 0.388 ± 0.003 | |
| BNN | 0.202 ± 0.004 | 0.209 ± 0.007 | |
| NGBoost | 0.360 ± 0.004 | 0.360 ± 0.004 | |
| GNNGP | 0.228 ± 0.005 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| BBBP | |||
| Random | 0.167 ± 0.002 | ||
| 1-nn | 0.171 ± 0.011 | ||
| SNGP | 0.156 ± 0.002 | 0.161 ± 0.003 | |
| GP | 0.212 ± 0.001 | 0.210 ± 0.001 | |
| BNN | 0.155 ± 0.002 | 0.165 ± 0.003 | |
| NGBoost | 0.198 ± 0.002 | 0.190 ± 0.003 | |
| GNNGP | 0.171 ± 0.002 | ||
In BioHL, due to the small data size, all search methods, including random search and 1-nn, are able to find the optimal molecule within the allotted budget (Fig. S2A†). In the fraction of hits achieved, on average, GPs/NGBoost with Mordred features achieved the highest scores, overlapping with results using MFP with GP, NGBoost and BNN. We note that the confidence intervals are relatively large due to the small size of BioHL; there are not many molecules in the top 10%. In the Freesolv dataset, we again observe that GP and NGBoost with Mordred attain the highest fraction of hit molecules and the fastest optimization (Fig. S2B†). As observed in the previous experiments, the Tanimoto kernel GP with MFP is better than the other surrogates with MFP, which is seen in both the BO traces, and the fraction of hits achieved. Among the deep surrogate models, the BNN manages to find the most number of hits, and find the optimal molecules within the budget. We generally see poor optimization performance with MFPs, with the exception of the GP surrogate, with search efficiency similar to random and 1-nn search.
In the binary classification datasets, the highest fraction of hits are found by GP and NGBoost surrogate models trained on MFP and Mordred descriptors, with GPs performing slightly better, particularly in the RBioDeg and BBBP datasets. Again, the GPs perform better with MFP through the Tanimoto kernel. In general, the deep models perform similar to random search, and worse than 1-nn method, indicating ineffective surrogate models. Interestingly, in the optimization traces (Fig. S3†), at around ∼300 evaluations, the traces for the deep learning models start climbing at a steeper slope, indicating more efficient optimization and better suggestions from the surrogate at this threshold.
To study the effects of the acquisition function on the surrogate model performance and calibration over the course of optimization, we use a modified UCB acquisition function,
αinterUCB(X) = δŷ(X) + βinter![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (X) (X) | (8) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) across the entire molecular candidate pool such that their values can be considered on equal footing. As βinter approaches 0, greater weight is placed on the predictive mean, and the sampling behaviour should resemble that of a “greedy” strategy (exploitation). As βinter approaches 1, greater emphasis is placed on the predictive uncertainty (exploration) (Fig. 5C).
across the entire molecular candidate pool such that their values can be considered on equal footing. As βinter approaches 0, greater weight is placed on the predictive mean, and the sampling behaviour should resemble that of a “greedy” strategy (exploitation). As βinter approaches 1, greater emphasis is placed on the predictive uncertainty (exploration) (Fig. 5C).
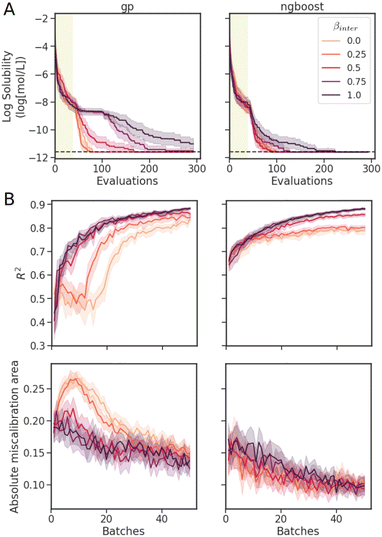
The results of the optimization with varying βinter on the Delaney dataset are shown in Fig. 7. The scans were performed only on GP and NGBoost models with Mordred descriptors, which were among the most promising model–feature combinations observed in the BO traces of Fig. 6. In the BO traces (Fig. 7A), the best mean trace values correspond to βinter = 0.25 for GPs, and βinter = 0.5 for NGBoost, although there is overlap in the confidence intervals with lower βinter traces. This corresponds to β = 0.33 and 1, respectively, in the typical UCB acquisition function (eqn (7)). At higher values of βinter, optimization performance quickly degrades in the GP model, while NGBoost remains performant, identifying the optimal molecule within the budget. In general, NGBoost performs better than GP at data regimes of ∼100 molecules.
The performance and calibration metrics on a separate test set of the model at every batch of 5 evaluations are shown in Fig. 7B. Despite poorer optimization, the fully variance-based sampling strategy achieves better R2 and AMA scores than the greedy strategy. The variance-based exploration strategy suggests more diverse candidates at each iteration, allowing the models to train on a more diverse set of molecules, hence improving the prediction and calibration metrics on the test set. Models with better predictions and calibration do not necessarily give faster Bayesian optimization. A good balance of optimization search efficiency and surrogate model performance is achieved at βinter = 0.25 for GPs, and 0.5 for NGBoost. At these values, we observe improved predictions and uncertainty calibration, especially at early stages of the optimization, with similar search efficiencies to those of more exploitative (lower βinter) strategies.
For both models, we observe the general trend of better predictions and uncertainties with more data. Overall, NGBoost achieves higher R2 and lower AMA. We also observe a severe drop in early optimization performance at around batch 10 for the GPs at βinter = 0 and 0.25. As the exploitation strategy becomes exhaustive, molecules further in feature space are included in the dataset. Due to sensitivity of GPs to distances in the feature space, the model prediction and uncertainty metrics drop until enough data is provided to improve the performance of the GPs again. This drop in performance is not observed in the NGBoost model, as random forest models can arbitrarily divide the feature space, rather than relying on the kernel function for feature distances. Interestingly, despite this pronounced drop in performance, BO at βinter = 0 and 0.25 with GPs achieved optimization trace results comparable to NGBoost.
4.3 Generalizability
Generalizability of predictive models is important in order to make accurate and reliable predictions on new chemical structures, especially in the low-data regime, where there is access to only a small slice of the chemical space. While models can predict and classify on molecules similar to the training set, we are often concerned with the performance and calibration when extrapolating to molecules that are OOD. Measuring the predictive performance of a model on the test set of a single random split only provides a partial view to its generalization capabilities—the biases in a single split can give an overconfident or underconfident estimate of performance.To simulate prediction of OOD molecules, the models and featurizations are trained and tested on cluster splits of the datasets, as shown in Fig. 3. The clusters of molecules represent “distributions” of similarly structured molecules and are aggregated in different combinations to create a series of training sets with difference sizes.
Visualizations of model prediction and uncertainty quality as a function of amount of accessible training data for the regression datasets are shown in Fig. 8 and 9. As a metric of generalizability, the median performance over the cluster splits are shown in Table 4. Here, only the Mordred descriptors and the graph representation (for GNNGP) are studied.
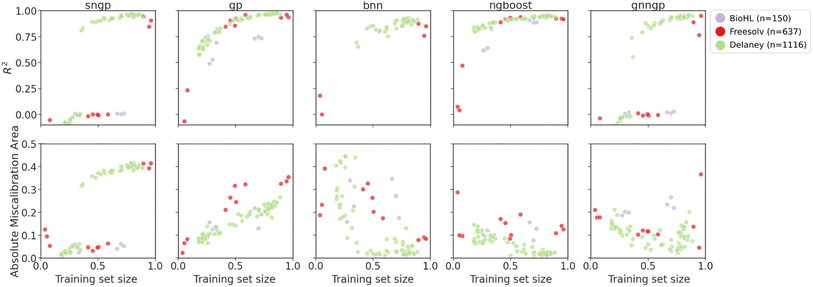 | ||
| Fig. 8 Plots of metrics of regression models on ablated cluster splits. Graph representations are used for GNNGP, while the remaining models used Mordred descriptors. | ||
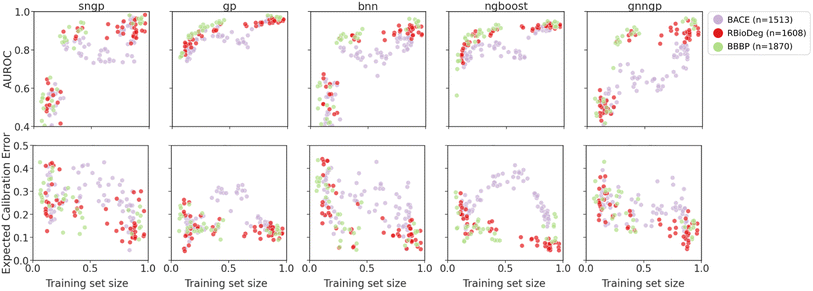 | ||
| Fig. 9 Plots of metrics of binary classification models on ablated cluster splits. Graph representations are used for GNNGP, while the remaining models used Mordred descriptors. | ||
| BNN | GP | NGBoost | SNGP | GNNGP | |
|---|---|---|---|---|---|
| BioHL | −2.511 | 0.710 | 0.853 | 0.007 | 0.016 |
| Freesolv | −0.207 | 0.916 | 0.905 | −0.001 | −0.006 |
| Delaney | 0.828 | 0.929 | 0.920 | 0.923 | 0.880 |
| BACE | 0.779 | 0.874 | 0.817 | 0.780 | 0.648 |
| RBioDeg | 0.876 | 0.933 | 0.909 | 0.875 | 0.873 |
| BBBP | 0.858 | 0.921 | 0.892 | 0.856 | 0.868 |
For the regression datasets, we observe an increase in the R2 score with increasing training data. For the smallest BioHL dataset, there are not enough clusters to form ablated sets that span the gamut of training set sizes. Deep learning models like SNGP, BNN and GNNGP are unable to achieve R2 > 0 for BioHL, as previously observed in the supervised learning studies (Section 4.1). There is a clear jump in performance for deep models at around 40% and 60% of training set for Delaney and Freesolv, respectively. This indicates that the deep learning models require at least ∼300 molecules to achieve sufficient performance.
We observe better performance on Freesolv and BioHL using GPs and NGBoost, with NGBoost achieving higher R2 and lower calibration errors, particularly when only given access to small number of clusters in the chemical space, indicating better performance at lower data regimes. However, as observed in the Delaney dataset performance, GPs are able to achieve higher R2 scores once enough data is provided, indicating better generalization. In the calibration metric of the cluster splits, we observe a general decrease in the error for BNN, and NGBoost. However, for SNGP, GNNGP, and GP, we observe an increase in AMA, particularly for the smaller datasets. A possible explanation for this: as the GP models gain more access to chemical space with more clusters, the covariance matrix determined by the kernel function gives larger uncertainties, due to low similarity of new inputs from different clusters, giving underconfident predictions.
The generalizability results for binary classification datasets are seen in Fig. 9. Again, we observe that the deep learning models are only able to get decent performance at around 25–30% of the training data, corresponding to ∼300 data points. The GPs and NGBoost models both achieved similar AUROC scores in this data regime, but the GPs are able to reach higher performance metrics, indicating better generalizability. In the calibration metrics, all models exhibit decrease in ECE with more training data, with NGBoost achieving the lowest score. For all models, there is a dip in performance at training set size of about 50% for BACE due to the distribution of molecules in the chemical space of the dataset. The cluster splits feature space is shown in Fig. S5.† The BACE molecule clusters predominantly fall into two larger superclusters. Initially, we observe an increase in AUROC and decrease in ECE due to inclusion of more training data. However, at around 50% of the training set size, the training set becomes more concentrated around one of the superclusters, and hence is less representative of the test set (Fig. S6†). This is particularly pronounced in the calibration metrics, in which there is a rise in ECE at around 50% of the BACE dataset. This not only explains the characteristic shape of the model performance metrics for BACE ablated cluster splits, but also demonstrates the ability of the cluster splits to simulate OOD molecules within molecular datasets.
5. Conclusion
In this work, we have performed a comprehensive study of the performance and application of probabilistic models on small molecular datasets, for both regression and binary classification tasks. Several models were trained and tested on the datasets with a variety of molecular input features. We evaluate the models based on their prediction accuracy and uncertainty calibration, and their effects on a simulated experimental optimization campaign and the generalizability OOD clusters.Based on the results, we compile a “handbook” of recommendations for predictive tasks with ML models on small molecular datasets:
• Mordred features are quite robust, independent of model choice.
• GPs with Mordred features are a solid modelling choice for small datasets. This combination fared well in all tasks and experiments. Model setup and optimization is relatively straightforward.
• Out of the models tested, GPs seem to perform best on OOD molecules.
• NGBoost performs best for much smaller datasets (<100 molecules).
• If using MFP features, GPs with the Tanimoto kernel provide best results.
• Deep learning techniques suffer from bad performance for very low data regimes (<300 molecules). Their performance starts to become comparable to GPs after dataset sizes of 500 molecules. Nonetheless, these techniques require more careful setup to properly train and regularize, such as selecting training hyperparameters, and model architecture.
• When provided enough molecules, BNN with Mordred descriptors and GNNGP with graph inputs both give robust predictions and calibrated uncertainties.
• Learned graph embeddings are expressive and viable features, even at low data regimes of ∼150 molecules, provided that the features are used with GPs or NGBoost.
• When performing Bayesian optimization, even though purely predictive models (UCB with β = 0) find hits faster, their model performance is worse than a model with some exploratory component (β > 0). We found that for the UCB acquisition function on the Delaney dataset using Mordred features, GP with β = 0.33, and NGBoost with β = 1.0 tends to give best model performance while achieving fast optimization.
• Good prediction and calibration of a surrogate model on a test set does not necessarily correspond to better Bayesian optimization.
There are some caveats to our analysis that may be addressed in future work. While we only look at particular metrics for the performance and calibration, there are a number of other metrics, particularly for calibration such as negative log-likelihood or ranking coefficients between the error and the uncertainties, which may provide different perspectives for the observed results. Additionally, we do not perform any optimization of the hyperparameters or architectures, which would typically be done for each model, dataset, and molecule representation. For other future work, besides the addition of more models and features, the study can be extended to multi-classification molecular tasks. Regardless of these potential future extensions, we believe that the work here presented here provides important insights to the development and application of probabilistic models on low data chemical datasets.
Data availability
The data and code used to produce the experiments in this work are available on the following GitHub repository https://github.com/aspuru-guzik-group/dionysus under an MIT license.Author contributions
CRediT contributions are created with latex-credits. Conceptualization: G. T., R. J. H., A. Z., A. M., B. S.-L., A. A.-G.; Data curation: G. T., R. J. H., B. S.-L.; Formal analysis: G. T., R. J. H., B. S.-L.; Funding acquisition: A. A.-G.; Investigation: G. T., R. J. H., B. S.-L.; Methodology: G. T., R. J. H., A. Z., A. M., B. S.-L., A. A.-G.; Project administration: G. T., B. S.-L. A. A.-G.; Resources: A. A.-G.; Software: G. T., R. J. H., A. Z., A. M, B. S.-L.; Supervision: G. T., B. S.-L. A. A.-G.; Validation: G. T., R. J. H., B. S.-L.; Visualization: G. T., R. J. H., B. S.-L.; Writing – original draft: G. T., R. J. H., B. S.-L.; Writing – review & editing: G. T., R. J. H., A. Z., A. M, B. S.-L., A. A.-G.Conflicts of interest
The authors declare no competing interests.Acknowledgements
G. T. acknowledges the support of Natural Sciences and Engineering Research Council of Canada (NSERC) through the Postgraduate Scholarships-Doctoral Program (PSGD3-559078-2021). R. J. H. gratefully acknowledges NSERC for provision of the Postgraduate Scholarships-Doctoral Program (PGSD3-534584-2019), as well as support from the Vector Institute. A. A.-G. acknowledges support from the Canada 150 Research Chairs program and CIFAR, as well as the generous support of Anders G. Frøseth. Computations reported in this work were performed on the computing clusters of the Vector Institute and on the Niagara supercomputer, managed by the Digital Research Alliance of Canada and the SciNet HPC Consortium.96,97 Resources used in preparing this research were provided, in part, by the Province of Ontario, the Government of Canada through CIFAR, and companies sponsoring the Vector Institute. SciNet is funded by the Canada Foundation for Innovation, the Government of Ontario, Ontario Research Fund – Research Excellence, and by the University of Toronto.References
- E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov and V. Poroikov, et al., QSAR without borders, Chem. Soc. Rev., 2020, 49(11), 3525–3564 RSC.
- A. J. Hey, S. Tansley, K. M. Tolle, et al., The fourth paradigm: data-intensive scientific discovery, vol. 1, 2009 Search PubMed.
- W. P. Walters and R. Barzilay, Applications of Deep Learning in Molecule Generation and Molecular Property Prediction, Acc. Chem. Res., 2021, 54(2), 263–270 CrossRef CAS PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural message passing for quantum chemistry, in International conference on machine learning, PMLR, 2017, p. 1263–1272 Search PubMed.
- J. Busk, P. B. Jørgensen, A. Bhowmik, M. N. Schmidt, O. Winther and T. Vegge, Calibrated uncertainty for molecular property prediction using ensembles of message passing neural networks, Mach. Learn.: Sci. Technol., 2021, 3(1), 015012 Search PubMed.
- Y. Miyake and A. Saeki, Machine learning-assisted development of organic solar cell materials: issues, analyses, and outlooks, J. Phys. Chem. Lett., 2021, 12(51), 12391–12401 CrossRef CAS PubMed.
- R. R. Griffiths, J. L. Greenfield, A. R. Thawani, A. R. Jamasb, H. B. Moss and A. Bourached, et al., Data-driven discovery of molecular photoswitches with multioutput Gaussian processes, Chem. Sci., 2022, 13(45), 13541–13551 RSC.
- A. Keller and L. B. Vosshall, Olfactory perception of chemically diverse molecules, BMC Neurosci., 2016, 17, 1–17 CrossRef PubMed.
- B. Sanchez-Lengeling, J. N. Wei, B. K. Lee, R. C. Gerkin, A. Aspuru-Guzik and A. B. Wiltschko, Machine learning for scent: learning generalizable perceptual representations of small molecules, arXiv, 2019, preprint, arXiv:191010685 DOI:10.48550/arXiv.1910.10685.
- J. N. Wei, M. Vlot, B. Sanchez-Lengeling, B. K. Lee, L. Berning, M. W. Vos, et al., A deep learning and digital archaeology approach for mosquito repellent discovery, bioRxiv, 2022, preprint, DOI:10.1101/2022.09.01.504601.
- K. M. Gayvert, N. S. Madhukar and O. Elemento, A data-driven approach to predicting successes and failures of clinical trials, Cell Chem. Biol., 2016, 23(10), 1294–1301 CrossRef CAS PubMed.
- A. Nigam, R. Pollice, M. F. Hurley, R. J. Hickman, M. Aldeghi and N. Yoshikawa, et al., Assigning confidence to molecular property prediction, Expet Opin. Drug Discov., 2021, 16(9), 1009–1023 CrossRef PubMed.
- D. E. Graff, E. I. Shakhnovich and C. W. Coley, Accelerating high-throughput virtual screening through molecular pool-based active learning, Chem. Sci., 2021, 12, 7866–7881 RSC.
- P. Schneider, W. P. Walters, A. T. Plowright, N. Sieroka, J. Listgarten and R. A. Goodnow, et al., Rethinking drug design in the artificial intelligence era, Nat. Rev. Drug Discovery, 2020, 19(5), 353–364 CrossRef CAS PubMed.
- D. Sydow, L. Burggraaff, A. Szengel, H. W. T. van Vlijmen, A. P. IJzerman and G. J. P. van Westen, et al., Advances and Challenges in Computational Target Prediction, J. Chem. Inf. Model., 2019, 59(5), 1728–1742 CrossRef CAS PubMed.
- A. Varnek and I. Baskin, Machine Learning Methods for Property Prediction in Chemoinformatics: Quo Vadis?, J. Chem. Inf. Model., 2012, 52(6), 1413–1437 CrossRef CAS PubMed.
- H. Altae-Tran, B. Ramsundar, A. S. Pappu and V. Pande, Low Data Drug Discovery with One-Shot Learning, ACS Cent. Sci., 2017, 3(4), 283–293 CrossRef CAS PubMed.
- M. Stanley, J. F. Bronskill, K. Maziarz, H. Misztela, J. Lanini, M. Segler, et al., FS-Mol: A Few-Shot Learning Dataset of Molecules, in Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), 2021 Search PubMed.
- Y. Ovadia, E. Fertig, J. Ren, Z. Nado, D. Sculley and S. Nowozin, et al., Can you trust your model’s uncertainty? evaluating predictive uncertainty under dataset shift, Adv. Neural Inf. Process. Syst., 2019, 32 DOI:10.48550/arXiv.1906.02530.
- D. P. Williams, S. E. Lazic, A. J. Foster, E. Semenova and P. Morgan, Predicting Drug-Induced Liver Injury with Bayesian Machine Learning, Chem. Res. Toxicol., 2020, 33(1), 239–248 Search PubMed.
- E. Semenova, D. P. Williams, A. M. Afzal and S. E. Lazic, A Bayesian neural network for toxicity prediction, Comput. Toxicol., 2020, 16, 100133 Search PubMed.
- J. Močkus, On Bayesian methods for seeking the extremum, in Optimization techniques IFIP technical conference, Springer, 1975, pp. 400–404 Search PubMed.
- J. Mockus, V. Tiesis and A. Zilinskas, The application of Bayesian methods for seeking the extremum, Towards global optimization, 1978, vol. 2, ch. 117–129, p. 2 Search PubMed.
- J. Mockus, Bayesian approach to global optimization: theory and applications, vol. 37, 2012 Search PubMed.
- B. Settles, Active learning literature survey, 2009 Search PubMed.
- C. Guo, G. Pleiss, Y. Sun and K. Q. Weinberger, On calibration of modern neural networks, in International conference on machine learning, PMLR, 2017, pp. 1321–1330 Search PubMed.
- N. Silver, The signal and the noise: why so many predictions fail–but some don't, 2012 Search PubMed.
- T. G. Dietterich, Ensemble methods in machine learning, in International workshop on multiple classifier systems, Springer, 2000, pp. 1–15 Search PubMed.
- R. P. Sheridan, Three useful dimensions for domain applicability in QSAR models using random forest, J. Chem. Inf. Model., 2012, 52(3), 814–823 CrossRef CAS PubMed.
- M. Toplak, R. Mocnik, M. Polajnar, Z. Bosnić, L. Carlsson and C. Hasselgren, et al., Assessment of machine learning reliability methods for quantifying the applicability domain of QSAR regression models, J. Chem. Inf. Model., 2014, 54(2), 431–441 CrossRef CAS PubMed.
- B. Lakshminarayanan, A. Pritzel and C. Blundell, Simple and scalable predictive uncertainty estimation using deep ensembles, Adv. Neural Inf. Process. Syst., 2017, 30 DOI:10.48550/arXiv.1612.01474.
- Y. Gal and Z. Ghahramani, Dropout as a bayesian approximation: Representing model uncertainty in deep learning, in International conference on machine learning, PMLR, 2016, pp. 1050–1059 Search PubMed.
- I. Cortes-Ciriano and A. Bender, Reliable prediction errors for deep neural networks using test-time dropout, J. Chem. Inf. Model., 2019, 59(7), 3330–3339 CrossRef CAS PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning. Adaptive computation and machine learning, Mass, Cambridge, 2006 Search PubMed.
- B. Hie, B. D. Bryson and B. Berger, Leveraging uncertainty in machine learning accelerates biological discovery and design, Cell Syst., 2020, 11(5), 461–477 CrossRef CAS PubMed.
- B. Sanchez-Lengeling, L. M. Roch, J. D. Perea, S. Langner, C. J. Brabec and A. Aspuru-Guzik, A Bayesian approach to predict solubility parameters, Adv. Theory Simul., 2019, 2(1), 1800069 CrossRef.
- C. Blundell, J. Cornebise, K. Kavukcuoglu and D. Wierstra, Weight Uncertainty in Neural Networks, 2015 Search PubMed.
- Y. Zhang and A. A. Lee, Bayesian semi-supervised learning for uncertainty-calibrated prediction of molecular properties and active learning, Chem. Sci., 2019, 10(35), 8154–8163 RSC.
- S. Ryu, Y. Kwon and W. Y. Kim, A Bayesian graph convolutional network for reliable prediction of molecular properties with uncertainty quantification, Chem. Sci., 2019, 10(36), 8438–8446 RSC.
- A. G. Wilson, Z. Hu, R. Salakhutdinov and E. P. Xing, Deep kernel learning, in Artificial intelligence and statistics, PMLR, 2016, pp. 370–378 Search PubMed.
- W. Huang, D. Zhao, F. Sun, H. Liu and E. Chang, Scalable Gaussian process regression using deep neural networks, in Twenty-fourth international joint conference on artificial intelligence, 2015 Search PubMed.
- J. Liu, Z. Lin, S. Padhy, D. Tran, T. Bedrax Weiss, B. Lakshminarayanan. Simple and Principled Uncertainty Estimation with Deterministic Deep Learning via Distance Awareness, in Advances in Neural Information Processing Systems, ed. H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan and H. Lin, 2020, vol. 33, pp. 7498–7512 Search PubMed.
- K. Han, B. Lakshminarayanan and J. Liu, Reliable graph neural networks for drug discovery under distributional shift, arXiv, 2021, preprint, arXiv:211112951 DOI:10.48550/arXiv.2111.12951.
- D. Bajusz, A. Rácz and K. Héberger, Chemical Data Formats, Fingerprints, and Other Molecular Descriptions for Database Analysis and Searching, Compr. Med. Chem. III., 2017, 3, 8 Search PubMed.
- B. Sanchez-Lengeling, E. Reif, A. Pearce and A. B. Wiltschko, A gentle introduction to graph neural networks, Distill, 2021, 6(9), e33 Search PubMed.
- Z. Nado, N. Band, M. Collier, J. Djolonga, M. W. Dusenberry, S. Farquhar, et al., Uncertainty Baselines: Benchmarks for uncertainty & robustness in deep learning, arXiv, 2021, preprint, arXiv:210604015 DOI:10.48550/arXiv.2106.04015.
- B. Zadrozny and C. Elkan, Transforming classifier scores into accurate multiclass probability estimates, in Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining, 2002, p. 694–699 Search PubMed.
- J. Platt, et al., Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods, Advances in large margin classifiers, 1999, ch. 3, vol. 10, pp. 61–74 Search PubMed.
- A. Niculescu-Mizil and R. Caruana, Predicting good probabilities with supervised learning, in Proceedings of the 22nd international conference on Machine learning, 2005, pp. 625–632 Search PubMed.
- P. Cui, W. Hu and J. Zhu, Calibrated Reliable Regression using Maximum Mean Discrepancy, Adv. Neural Inf. Process. Syst., 2020, 33, 17164–17175 Search PubMed.
- A. P. Soleimany, A. Amini, S. Goldman, D. Rus, S. N. Bhatia and C. W. Coley, Evidential Deep Learning for Guided Molecular Property Prediction and Discovery, ACS Cent. Sci., 2021, 7(8), 1356–1367 CrossRef CAS PubMed.
- D. Hwang, S. Yang, Y. Kwon, K. H. Lee, G. Lee and H. Jo, et al., Comprehensive study on molecular supervised learning with graph neural networks, J. Chem. Inf. Model., 2020, 60(12), 5936–5945 CrossRef CAS PubMed.
- M. Sensoy, L. Kaplan and M. Kandemir, Evidential Deep Learning to Quantify Classification Uncertainty, in Advances in Neural Information Processing Systems, ed. S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi and R. Garnett, 2018, vol. 31 Search PubMed.
- A. Amini, W. Schwarting, A. Soleimany and D. Rus, Deep Evidential Regression, in Advances in Neural Information Processing Systems, ed. H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan and H. Lin, 2020, vol. 33, pp. 14927–14937 Search PubMed.
- H. B. Moss and R. R. Griffiths, Gaussian process molecule property prediction with flowmo, arXiv, 2020, preprint, arXiv:201001118 DOI:10.48550/arXiv.2010.01118.
- L. Hirschfeld, K. Swanson, K. Yang, R. Barzilay and C. W. Coley, Uncertainty Quantification Using Neural Networks for Molecular Property Prediction, J. Chem. Inf. Model., 2020, 60(8), 3770–3780 CrossRef CAS PubMed.
- D. E. Graff, M. Aldeghi, J. A. Morrone, K. E. Jordan, E. O. Pyzer-Knapp and C. W. Coley, Self-focusing virtual screening with active design space pruning, J. Chem. Inf. Model., 2022, 62(16), 3854–3862 CrossRef CAS PubMed.
- A. Gaulton, A. Hersey, M. Nowotka, A. P. Bento, J. Chambers and D. Mendez, et al., The ChEMBL database in 2017, Nucleic Acids Res., 2017, 45(D1), D945–D954 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, Extended-Connectivity Fingerprints, J. Chem. Inf. Model., 2010, 50(5), 742–754 CrossRef CAS PubMed.
- G. Landrum, et al., RDKit: Open-Source Cheminformatics Software, 2022, available from: https://github.com/rdkit/rdkit/releases/tag/Release_2022_03_4 Search PubMed.
- K. Jorner, T. Brinck, P. O. Norrby and D. Buttar, Machine learning meets mechanistic modelling for accurate prediction of experimental activation energies, Chem. Sci., 2021, 12(3), 1163–1175 RSC.
- H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, Mordred: a molecular descriptor calculator, J. Cheminf., 2018, 10(1), 4, DOI:10.1186/s13321-018-0258-y.
- P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, et al., Relational inductive biases, deep learning, and graph networks, arXiv, 2018, preprint, arXiv:180601261 DOI:10.48550/arXiv.1806.01261.
- K. Mansouri, C. M. Grulke, R. S. Judson and A. J. Williams, OPERA models for predicting physicochemical properties and environmental fate endpoints, J. Cheminf., 2018, 10(1), 1–19 Search PubMed.
- D. L. Mobley and J. P. Guthrie, FreeSolv: a database of experimental and calculated hydration free energies, with input files, J. Comput.-Aided Mol. Des., 2014, 28(7), 711–720 CrossRef CAS PubMed.
- J. S. Delaney, ESOL: Estimating Aqueous Solubility Directly from Molecular Structure, J. Chem. Inf. Comput. Sci., 2004, 44(3), 1000–1005 CrossRef CAS PubMed.
- G. Subramanian, B. Ramsundar, V. Pande and R. A. Denny, Computational Modeling of B-Secretase 1 (BACE-1) Inhibitors Using Ligand Based Approaches, J. Chem. Inf. Model., 2016, 56(10), 1936–1949 CrossRef CAS PubMed.
- I. F. Martins, A. L. Teixeira, L. Pinheiro and A. O. Falcao, A Bayesian Approach to in Silico Blood–Brain Barrier Penetration Modeling, J. Chem. Inf. Model., 2012, 52(6), 1686–1697 CrossRef CAS PubMed.
- T. Duan, A. Anand, D. Y. Ding, K. K. Thai, S. Basu, A. Ng, et al., Ngboost: natural gradient boosting for probabilistic prediction, in International Conference on Machine Learning, PMLR, 2020, pp. 2690–2700 Search PubMed.
- T. Chen and C. Guestrin, Xgboost: a scalable tree boosting system, in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794 Search PubMed.
- D. P. Kingma, T. Salimans and M. Welling, Variational dropout and the local reparameterization trick, Adv. Neural Inf. Process. Syst., 2015, 28 Search PubMed.
- D. J. MacKay, Bayesian interpolation, Neural Comput., 1992, 4(3), 415–447 CrossRef.
- A. M. Deshwal, C. Simon and J. Rao Doppa, Bayesian optimization of nanoporous materials, Mol. Syst. Des. Eng., 2021, 6(12), 1066–1086 RSC.
- G. Agarwal, H. A. Doan, L. A. Robertson, L. Zhang and R. S. Assary, Discovery of Energy Storage Molecular Materials Using Quantum Chemistry-Guided Multiobjective Bayesian Optimization, Chem. Mater., 2021, 33(20), 8133–8144 CrossRef CAS.
- A. GdG. Matthews, M. van der Wilk, T. Nickson, K. Fujii, A. Boukouvalas and P. León-Villagrá, et al., GPflow: A Gaussian process library using TensorFlow, J. Mach. Learn. Res., 2017 apr, 18(40), 1–6 Search PubMed.
- M. van der Wilk, V. Dutordoir, S. John, A. Artemev, V. Adam and J. Hensman, A Framework for Interdomain and Multioutput Gaussian Processes, arXiv, 2020, preprint, arXiv:200301115 DOI:10.48550/arXiv.2003.01115.
- A. Rahimi and B. Recht, Random Features for Large-Scale Kernel Machines, in Advances in Neural Information Processing Systems, ed. J. Platt, D. Koller, Y. Singer and S. Roweis, vol. 20, 2007 Search PubMed.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse and A. S. Pappu, et al., MoleculeNet: a benchmark for molecular machine learning, Chem. Sci., 2018, 9(2), 513–530 RSC.
- M. P. Naeini, G. Cooper and M. Hauskrecht, Obtaining well calibrated probabilities using bayesian binning, in Twenty-Ninth AAAI Conference on Artificial Intelligence, 2015 Search PubMed.
- M. Hoffman, F. Bach and D. Blei, Online learning for latent dirichlet allocation, Adv. Neural Inf. Process. Syst., 2010, 23, 856–864 Search PubMed.
- L. McInnes, J. Healy and J. Melville, Umap: Uniform manifold approximation and projection for dimension reduction, arXiv, 2018, preprint, arXiv:180203426 DOI:10.48550/arXiv.1802.03426.
- R. J. G. B. Campello, D. Moulavi and J. Sander, Density-based clustering based on hierarchical density estimates, in Pacific-Asia conference on knowledge discovery and data mining, Springer, 2013, pp. 160–172 Search PubMed.
- P. Szymański and T. Kajdanowicz, A network perspective on stratification of multi-label data, in First International Workshop on Learning with Imbalanced Domains: Theory and Applications, PMLR, 2017, pp. 22–35 Search PubMed.
- S. A. Wildman and G. M. Crippen, Prediction of physicochemical parameters by atomic contributions, J. Chem. Inf. Comput. Sci., 1999, 39(5), 868–873 CrossRef CAS.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Taking the Human Out of the Loop: A Review of Bayesian Optimization, Proc. IEEE, 2016, 104(1), 148–175 Search PubMed.
- C. Thornton, F. Hutter, H. H. Hoos and K. Leyton-Brown, Auto-WEKA: Combined Selection and Hyperparameter Optimization of Classification Algorithms, in Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD'13, New York, NY, USA, 2013, pp. 847–855 Search PubMed.
- M. Feurer, A. Klein, K. Eggensperger, J. T. Springenberg, M. Blum and F. Hutter, in Auto-sklearn: Efficient and Robust Automated Machine Learning, ed. F. Hutter, L. Kotthoff and J. Vanschoren, Cham, 2019, pp. 113–134 Search PubMed.
- Automated Machine Learning - Methods, Systems, Challenges, ed. F. Hutter, L. Kotthoff and J. Vanschoren, 2019 Search PubMed.
- R. Calandra, A. Seyfarth, J. Peters and M. P. Deisenroth, Bayesian optimization for learning gaits under uncertainty, Ann. Math. Artif. Intell., 2016 Feb, 76(1), 5–23 Search PubMed.
- F. Berkenkamp, A. Krause and A. P. Schoellig, Bayesian optimization with safety constraints: safe and automatic parameter tuning in robotics, Machine Learning, 2021 Search PubMed.
- J. Vanlier, C. A. Tiemann, P. A. J. Hilbers and N. A. W. van Riel, A Bayesian approach to targeted experiment design, Bioinformatics, 2012, 28(8), 1136–1142 CrossRef CAS PubMed.
- A. Foster, M. Jankowiak, E. Bingham, P. Horsfall, Y. W. Teh, T. Rainforth, et al., Variational Bayesian Optimal Experimental Design, in Advances in Neural Information Processing Systems, ed. H. Wallach, H. Larochelle, A. Beygelzimer, F. d' Alché-Buc, E. Fox and R. Garnett, vol. 32, 2019 Search PubMed.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch and A. Aspuru-Guzik, Gryffin: An algorithm for Bayesian optimization of categorical variables informed by expert knowledge, Appl. Phys. Rev., 2021 Sep, 8(3), 031406 Search PubMed.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani and J. I. M. Alvarado, et al., Bayesian reaction optimization as a tool for chemical synthesis, Nature, 2021 Feb, 590(7844), 89–96 Search PubMed.
- J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor and T. Löffler, et al., Bayesian Optimization of High-Entropy Alloy Compositions for Electrocatalytic Oxygen Reduction, Angew. Chem., Int. Ed., 2021, 60(45), 24144–24152 CrossRef CAS PubMed.
- M. Ponce, R. van Zon, S. Northrup, D. Gruner, J. Chen, F. Ertinaz, et al., Deploying a top-100 supercomputer for large parallel workloads: the niagara supercomputer, in Proceedings of the Practice and Experience in Advanced Research Computing on Rise of the Machines (learning), 2019, pp. 1–8 Search PubMed.
- C. Loken, D. Gruner, L. Groer, R. Peltier, N. Bunn and M. Craig, et al., SciNet: lessons learned from building a power-efficient top-20 system and data centre, J. Phys. Conf., 2010, 256, 012026 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00146b |
| This journal is © The Royal Society of Chemistry 2023 |