Group SELFIES: a robust fragment-based molecular string representation

Abstract

We introduce Group SELFIES, a molecular string representation that leverages group tokens to represent functional groups or entire substructures while maintaining chemical robustness guarantees. Molecular string representations, such as SMILES and SELFIES, serve as the basis for molecular generation and optimization in chemical language models, deep generative models, and evolutionary methods. While SMILES and SELFIES leverage atomic representations, Group SELFIES builds on top of the chemical robustness guarantees of SELFIES by enabling group tokens, thereby creating additional flexibility to the representation. Moreover, the group tokens in Group SELFIES can take advantage of inductive biases of molecular fragments that capture meaningful chemical motifs. The advantages of capturing chemical motifs and flexibility are demonstrated in our experiments, which show that Group SELFIES improves distribution learning of common molecular datasets. Further experiments also show that random sampling of Group SELFIES strings improves the quality of generated molecules compared to regular SELFIES strings. Our open-source implementation of Group SELFIES is available at https://github.com/aspuru-guzik-group/group-selfies, which we hope will aid future research in molecular generation and optimization.

---

1 Introduction

The discovery of functional molecules for drugs and energy materials is crucial to tackling global challenges in public health and climate change. Different types of generative models can suggest potential molecules to synthesize and test, but the performance of the models and molecules heavily relies on the underlying molecular representation. Several models generate molecules represented as SMILES strings,^1–5 but their generated output can be invalid due to syntax errors or incorrect valency. SELFIES^6,7 is a molecular string representation that overcomes chemical invalidity challenges by ensuring that any string of SELFIES characters can be decoded to a molecule with valid valency. This not only makes it a natural representation for chemical language models that output molecular strings, but also for genetic algorithms such as GA+D, STONED, and JANUS^8–10 for molecular optimization.

SELFIES improves string-based molecular generation by encoding prior knowledge of valency constraints into the representation independently of the optimization method. The representation has been shown to improve distribution learning by language models,¹¹ as well as image2string and string2string translation^12,13 and molecular generation in data-sparse regimes.¹⁴ Additionally, simple add/replace/delete edits to SELFIES strings can generate new but similar molecules, enabling genetic algorithms that directly manipulate strings to generate molecules.⁸ Alternatively, guiding these simple string edits with Tanimoto similarity can interpolate between molecules as performed in STONED by Nigam et al.,⁹ which can then be applied as crossover operations in genetic algorithms such as JANUS.¹⁰ Molecular interpolation has also been used to find counterfactual decision boundaries that explain a molecular classifier's decisions.¹⁵

While SMILES and SELFIES represent molecules at the individual atom and bond level, human chemists typically think about molecules in terms of the substructures that they contain. Human chemists can distinguish molecular substructures based solely on the image of a molecule and induce the molecular properties those substructures usually imply. Many fragment-based generative models take advantage of this inductive bias^16–25 by constructing custom representations amenable to fragment-based molecular design. However, these approaches are not string-based, thereby losing desirable properties of string representations: easy manipulation, and direct input into established language models.

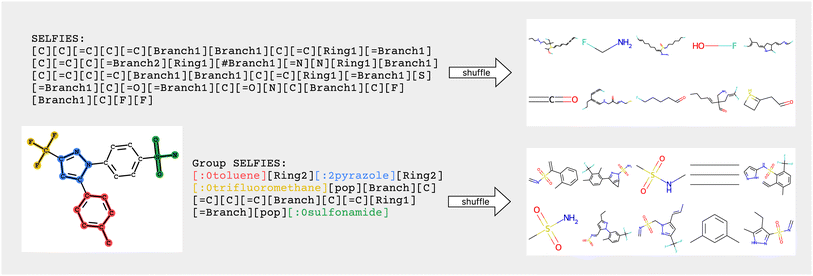
Similar to how SELFIES incorporates prior knowledge of valency constraints, we can also incorporate prior knowledge in the form of functional groups and molecular substructures into the representation. In this work, we combine the flexibility of string representations with the chemical robustness of SELFIES and the interpretability and inductive bias of fragment-based approaches into a novel string representation: Group SELFIES, a robust string representation that extends SELFIES to include tokens which represent functional groups or entire substructures (Fig. 1).

Fig. 1 Visual overview of SELFIES and Group SELFIES. SELFIES is robust, so shuffling tokens around will yield new molecules with correct valency. Group SELFIES maintains robustness while adding group tokens, highlighted in color. When Group SELFIES tokens are shuffled, structures like benzene rings are more often preserved, while shuffled SELFIES strings rarely ever preserve structures. Incidentally, Group SELFIES also improves the readability of molecular string representations since chemists can see what substructures are present.

In Section 2, we discuss how Group SELFIES fits into related research and then formally introduce the representation in Section 3. Specifically, we outline how molecules are encoded into and decoded from Group SELFIES, and we show that arbitrary Group SELFIES strings can be decoded to molecules with valid valency. The representation enables users to easily specify their own groups or extract fragments from a dataset, leveraging the wide area of cheminformatics research available there. In Section 4, we find that Group SELFIES is more compact than SMILES or SELFIES and improves distribution learning. Additionally, we compare molecules generated via randomly sampling SELFIES and Group SELFIES strings and find that Group SELFIES improves the quality of generated molecules. Molecular generation via random sampling provides greater emphasis on the representation itself by abstracting away the complexities of the type of generative method used, which we leave to future work as described in Section 5.

Overall, Group SELFIES provides the flexibility of group representation, the ability to represent extended chirality via chiral group tokens and chemical robustness as summarized in Table 1.

Table 1 Comparison of the capabilities of SMILES, SELFIES, and Group SELFIES. Group SELFIES provides group representation, representation of extended chirality, and chemical robustness. Additionally as shown in Section 4, Group SELFIES improves distribution learning compared to other representations

Representation	Robustness	Substructure control	Extended chirality	Distribution learning
SMILES	No	No	No	∼
SELFIES	Yes	No	No	∼
Group SELFIES	Yes	Yes	Yes	Improved

---

2 Related work

2.1 Fragment-based string representations

Group SELFIES is not the first fragment-based string representation that has been proposed. Historical string representations, such as Wiswesser Line Notation (WLN),^26–28 Hayward Notation,²⁹ and Skolnik Notation,³⁰ all predate SMILES and represent molecules non-atomically. They use tokens that represent functional groups, such as carboxyls or phenyls, as well as ring systems. WLN strings are usually shorter and sometimes easier for trained humans to understand than SMILES, as it is easier to recognize functional groups encoded as single characters than functional groups encoded atomically. SYBYL Line Notation (SLN)³¹ allows for “macro atoms” which specify multiple atoms in a substructure. The Hierarchical Editing Language for Macromolecules (HELM)³² represents complex biomolecules by declaring monomers and then connecting them in a polymer line notation. Human-Readable SMILES³³ applies common abbreviations for chemical substituents to process and compress SMILES strings into a more human-readable format. SMILES Pair Encoding³⁴ breaks down SMILES strings by tokenizing them in a data-driven way that recognizes common substructures.

2.2 Genetic programming

A string representation of molecules such as SELFIES can be thought of as a programming language where programs specify how to construct molecules. Genetic programming³⁵ uses genetic algorithms to design programs that fulfill desired constraints. In particular for linear genetic programming,³⁶ programs are represented as linear sequences of atomic instructions, rather than as a tree of expressions. Linear sequences of atomic instructions are easily mutated by changing any instruction in the sequence, since any sequence of atomic instructions will still be a runnable program. In this way, SELFIES and Group SELFIES can be thought of as domain-specific languages for linear genetic programming.

2.3 Learned grammars

Data-Efficient Graph Grammar Learning (DEG)²³ is a recent approach for extracting useful formal graph grammars from small datasets of molecules. In this context, a “useful grammar” means that molecules generated by applying random applicable production rules usually have high scores. The learned production rules of the graph grammar can be thought of as similar to functional groups applied in Group SELFIES. Group SELFIES allows for flexibility and fine control of substructures, which can extracted from any procedure including DEG.

3 Representation

3.1 SELFIES framework

Before introducing in Group SELFIES in greater detail, we summarize the primary features of SELFIES and the reasons underlying its chemical robustness. SELFIES is equipped with an encoder and a decoder. The encoder takes in a molecule and converts it to a SELFIES string, and the decoder takes in a SELFIES string and converts it to a molecule. To encode a molecule in SELFIES, one traverses its molecular graph and outputs the processed traversal as a string of SELFIES tokens. To decode a SELFIES string, one reads through the string token-by-token, building the molecular graph along the way until arriving at the finished graph. Since the encoding and decoding process alone does not guarantee chemical robustness, the SELFIES decoder further includes two important features:

(1) Each token in SELFIES is overloaded to ensure that it can be interpreted sensibly in all contexts. For instance, all tokens in SELFIES can also be interpreted as numbers, which is useful when expressing branch and ring lengths.

(2) SELFIES keeps track of the available valency at each step in the decoding process; if a bond would be formed that would exceed this valency, it changes the bond order or ignores the bond. For instance, when decoding [C][O][=C], adding [=C] would exceed the valency of [O], so SELFIES changes the bond order and adds [C] instead.

By preserving these properties in the Group SELFIES decoder, we ensure chemical robustness is preserved.

3.2 Basic tokens in group SELFIES

Group SELFIES strings consist of the following fundamental tokens:

• [X] adds an atom with the atomic symbol X.

• [Branch] creates a new branch off the current atom and saves the current atom as a branchpoint to return to later, and is analogous to an opening parenthesis ( in SMILES. [pop] exits the current branch, returning to the most recent branchpoint, and is analogous to a closing parenthesis ) in SMILES. Unlike in SMILES, however, [Branch] and [pop] tokens need not come in pairs, which helps maintain robustness. A [Branch] that is never followed by a [pop] means that the created branch continues until the string ends. Any [pop] on the starting main branch is ignored. If [pop] happens to return to an atom with full valency, then decoding immediately ends. [Branch] is also different from the [BranchX] tokens in SELFIES. Experiments in ESI Section A.5† indicate this change does not substantially affect the performance of Group SELFIES.

• [RingX] indicates that a ring bond will be formed from the current atom. The next X tokens immediately following [RingX] will be interpreted as a number N, and we will count backwards N atoms in placement order to determine the target of the ring bond. For example, [Ring2] indicates that the next 2 tokens will be interpreted as a 2-digit base-16 number N. Ring bonds are stored until after all tokens have been read by the decoder; only then are ring bonds placed, and only if it would not violate valency. Due to the addition of groups, it is sometimes necessary to form ring bonds to atoms that are added after the current atom (e.g. ring bonds within groups). To indicate this, we use the [->] token before the number token to specify that we will count forwards instead of backwards.

All tokens except [pop] can be modified by adding =, #, \ or / to change the bond order or stereochemistry of their parent bond (e.g. [#Branch] or [/C]). The parent bond is the bond to the previous atom.

3.3 Groups

The primary difference between SELFIES and Group SELFIES is the addition of groups. Each group is defined as a set of atoms and bonds representing the molecular group with its attachment points, indicating how the group can participate in bonding. Each attachment point has a specified maximum valency, which allows us to continue tracking available valency while decoding. These attachment points are labeled by attachment indices, and the encoder and decoder will navigate around these attachment indices as described in Section 3.4.

Users must specify the groups they want to use using a dictionary that maps group names to groups. This tells the encoder what groups to recognize, and tells the decoder how to map group tokens to groups. We call this dictionary a “group set”, and every group set defines its own distinct instance of Group SELFIES. In particular, the decoder will not recognize a Group SELFIES string that contains group tokens not present in the current group set.

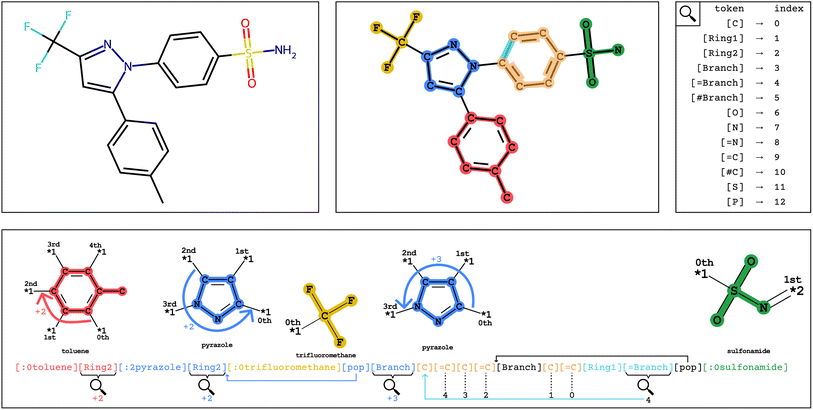
To distinguish group tokens from other tokens, we include a : character at the front of the token (e.g. [:1parabenzene]). All group tokens are of the form [:S<group-name>], where S is the starting attachment index of the group, and <group-name> is any alphanumeric string that does not contain dashes or start with a number.

Optionally, a priority value can be specified for each group, indicating the priority with which the group should be recognized when encoding into Group SELFIES. Priority affects the Group SELFIES encoder as described in Section 3.4. For each group, one can also specify its index overload value, which is the value the group token takes when the decoder must interpret the token as a number.

3.4 Encoding and decoding

3.4.1 Encoding. To encode a molecule in Group SELFIES, the encoder first recognizes and replaces substructure matches of groups from the molecule. By default, the encoder iterates through the group set and recognizes the largest groups first, but users can override this by specifying a priority for each group. Setting a high priority value for a group indicates that it will be recognized first when encoding into Group SELFIES, ensuring that other group replacements will not overlap with this group. This encoding strategy implies that increasing the size of the group set will increase the running time of the encoder linearly. We then traverse the graph similar to the encoding process for SMILES and SELFIES, while also placing the correct tokens for tracking the attachment indices of where the encoder entered and exited a group.

3.4.2 Decoding. When decoding Group SELFIES, the process is essentially the same as regular SELFIES except when reading group tokens. When a group token is read by the decoder, the group set dictionary determines the corresponding group. Subsequently, all atoms of the group are placed and the main chain is connected to the starting attachment point. The decoder selects the next attachment point to branch off from by reading in the next token as a relative index. By adding the current attachment index to a relative index modulo the total number of attachment points in the group, the decoder selects the next attachment point. From the specified attachment point, the decoder implicitly branches off of the group and continues traversing until a [pop] token is read. Once the branch is “popped”, the decoder returns to the group and can navigate to the next attachment point using another relative index. If the selected attachment point is occupied, then the next available attachment point is used. If all attachment points have been used up, then the group itself is immediately “popped”, returning to the most recent branchpoint before the group was placed.

In Fig. 2, encoding into Group SELFIES begins by placing a toluene group in red, and its starting attachment point index is 0. The next token is interpreted as a relative index, which indicates that the main chain should continue from the (0 + 2 = 2nd) attachment point of toluene. The next token places a pyrazole group in blue, and its starting attachment point index is 2. The token after that is interpreted as a relative index equal to 2, and then trifluoromethane is placed at the (2 + 2 mod 4 = 0th) attachment point of pyrazole. A subsequent [pop] token returns to the pyrazole group at the 0th attachment point. The next token is interpreted as a relative index equal to 3, indicating that the main chain should continue off of the (0 + 3 = 3rd) attachment point of pyrazole. The final series of tokens places individual carbons, creates a branch, and creates a ring, before returning to the last branchpoint and placing the sulfonamide group before terminating. We provide a detailed example of encoding/decoding the molecule celecoxib in ESI Section A.1.†

Fig. 2 Visual explanation of Group SELFIES encoding/decoding of celecoxib. Top-left: molecular structure of celecoxib. Top-middle: the structure of celecoxib colored by its groups and atoms. Top-right: index overload table in Group SELFIES, indicating how tokens are interpreted as numbers. Bottom: celecoxib represented in Group SELFIES. Tokens are colored by the groups and atoms they refer to. Index overloads are shown where interpreted. Colored arrows indicate how the decoder navigates around the attachment points of the groups.

We verified the robustness of Group SELFIES by encoding and decoding 25 M molecules from the eMolecules database.³⁷

Group SELFIES manages chirality differently than SMILES and SELFIES. Rather than use @-notation to specify tetrahedral chirality, all chiral centers must be specified as groups. We provide an “essential set” of 23 groups which encode all relevant chiral centers in the eMolecules database. Equipped with this essential set, every molecule can be encoded-decoded while maintaining chirality. It is also an option to not use the essential set, or only use a subset of it, depending on what chiral centers are relevant to the problem at hand. If a molecule has a chiral center not specified in the group set, then encode-decode will not preserve chirality.

3.5 Determining fragments

Group SELFIES has a built-in flexibility for assigning the set of fragments that make up a group set. Hence, the construction of a useful group set often remains an open design choice. Users can specify groups using a SMILES-like syntax (Fig. 3), which could be useful if one knows what groups are synthetically available or are expected to be useful for their particular design task. Fragments can also be obtained from several fragment libraries found in the literature.^38–40 Generally, a useful set of groups will appear in many molecules in the dataset and replace many atoms, with similar fragments merged together to reduce redundancy.

Fig. 3 Left: representation of a possible “parabenzene” group and its use in a corresponding group token. The *N notation represents an attachment point with valency N. Each attachment point is labeled with its attachment index 0th, 1st… The starting attachment point represented in the token is also highlighted. Right: Python code for defining a “parabenzene” group.

In our experiments, we also tested various fragmentation algorithms that extract fragments from a dataset, including a naïve technique that cleaves side chains from rings and a method based on matched molecular pair analysis.⁴¹ Several other fragmentation algorithms from cheminformatics can be readily applied^23,42–46 because any fragment specified as a SMILES string can be used as a group in Group SELFIES. However, we leave exploration of different group sets and fragmentation strategies to future work.

4 Experiments

The experiments in the subsequent sections outline some of the advantages of Group SELFIES compared to SMILES and regular SELFIES representations. Concretely, we show that: (1) Group SELFIES is shorter and more compressible than SMILES and SELFIES; (2) Group SELFIES preserves useful properties during generation; (3) Group SELFIES improves distribution learning.

4.1 Compactness

Group SELFIES strings are typically shorter than their SMILES and SELFIES equivalents when using a generic set of groups. In Fig. 4, this generic set was generated by taking a random selection of 10 000 molecules from ZINC-250k⁴⁷ and fragmenting them into 30 useful groups using various algorithms (see Determining fragments). We then combined these 30 groups with the 23 groups of the essential set. Fig. 4 shows histograms of the lengths of SMILES/SELFIES/Group SELFIES strings of the entire ZINC-250k dataset. Length is the number of characters in SMILES strings, and the number of tokens in (Group) SELFIES strings. Group SELFIES strings are usually shorter than their SELFIES and SMILES counterparts because group tokens can represent multiple atoms in a molecule.

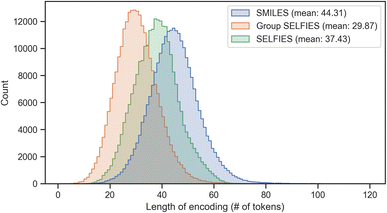Fig. 4 Histogram of lengths of SMILES, SELFIES, and Group SELFIES strings of the ZINC-250k dataset. Here, Group SELFIES uses a group set of 53 groups.

Since Group SELFIES has a larger alphabet than SMILES or SELFIES, we estimate the complexity of each representation with the compressed filesize of ZINC-250k. We find that out of all representations, Group SELFIES can be compressed the most (see ESI Section A.2†).

4.2 Molecular generation

To specifically compare the suitability of the SELFIES and Group SELFIES representations for molecular generation, we use a primitive generative model which samples random strings. First, we convert a subset of N = 100 000 molecules from ZINC-250k into (Group) SELFIES strings. Then, we tokenize all strings and combine them into a single bag of tokens. To generate a new string, we first pick a random (Group) SELFIES string from our chosen subset and take its length l. We then randomly sample l tokens from the bag, and concatenate into a generated string. We generate N random strings for each representation. For Group SELFIES, we use the same 53 groups used for the length histogram in Section 4.1.

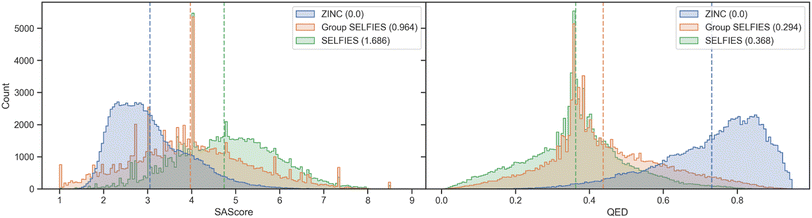
We show histograms of the SAScore⁴⁸ and QED⁴⁹ of molecules generated from ZINC in Fig. 5. The distributions of generated Group SELFIES more closely overlap with the original ZINC dataset than the generated SELFIES, showing that even with an extremely simplistic generative model, Group SELFIES can preserve important structural information. We perform a similar analysis for a dataset of nonfullerene acceptors (NFA)⁵⁰ in ESI Section A.3† and find that Group SELFIES preserves many aromatic rings in contrast to SELFIES, which rarely ever preserves aromatic rings.

Fig. 5 Molecules generated by our primitive generative model are binned by SAScore and QED. For both properties, generated Group SELFIES have greater overlap with the original ZINC distribution. Bracketed values indicate the Wasserstein distance (a measure of overlap) to the ZINC distribution. Dashed lines indicate the means.

4.3 Distribution learning

To further quantify the effectiveness of Group SELFIES in generative models, we use the MOSES benchmarking framework⁵¹ to evaluate variational autoencoders (VAEs) trained with both Group SELFIES and SELFIES strings. MOSES provides metrics for distribution learning on the ZINC Clean Leads dataset⁴⁷ of 2 M molecules, which is separated into train, test, and scaffold-test splits. The scaffold-test split (TestSF) contains scaffolds not found in the train or test split. Models were trained for 125 epochs. The group set for the Group SELFIES VAE was created by fragmenting the training set provided by MOSES and selecting the 300 most diverse groups. A set of 100 000 molecules was then generated from each model and evaluated on the metrics provided by MOSES (Table 2).

Table 2 Group SELFIES VAE and SELFIES VAE evaluated on MOSES metrics. The Group SELFIES VAE mostly matches or outperforms the SELFIES VAE

Model	Valid (↑)	Unique@1k (↑)	Unique@10k (↑)	FCD (↓)		SNN (↑)
				Test	TestSF	Test	TestSF
Train	1.0	1.0	1.0	0.008	0.4755	0.6419	0.5859
Group-VAE-125	1.0(0)	1.0(0)	0.9985(4)	0.1787(29)	0.734(109)	0.6051(4)	0.5599(3)
SELFIES-VAE-125	1.0(0)	0.9996(5)	0.9986(4)	0.6351(43)	1.3136(128)	0.6014(3)	0.5566(2)

---

Model	Frag (↑)		Scaf (↑)		IntDiv (↑)	IntDiv2 (↑)	Filters (↑)	Novelty (↑)
	Test	TestSF	Test	TestSF
Train	1.0	0.9986	0.9907	0.0	0.8567	0.8508	1.0	1.0
Group-VAE-125	0.9995(0)	0.9977(1)	0.9649(21)	0.0608(65)	0.8587(1)	0.8528(1)	0.9623(7)	0.7187(11)
SELFIES-VAE-125	0.9989(0)	0.9965(1)	0.9588(15)	0.0675(37)	0.8579(1)	0.8519(1)	0.96(4)	0.7345(16)

---

For most metrics, Group SELFIES performs approximately the same as SELFIES. Validity is the percentage of generated molecules that are accepted by RDKit's parser. Uniqueness is the percentage of generated molecules that are not identical to any other generated molecule. Similarity to nearest neighbor (SNN) is the average Tanimoto similarity between generated molecules and the nearest neighbor in the reference set. Fragment similarity (Frag) is a cosine similarity based on the distribution of BRICS fragments⁴⁶ of generated and reference molecules. Scaffold similarity (Scaf) is a cosine similarity based on the distribution of Bemis–Murcko scaffolds⁵² of generated and reference molecules. Internal diversity (IntDiv) measures the chemical diversity of the generated molecules using Tanimoto similarity. Filters is the fraction of generated molecules that pass filters for unwanted fragments. Novelty is the fraction of generated molecules not in the training set.

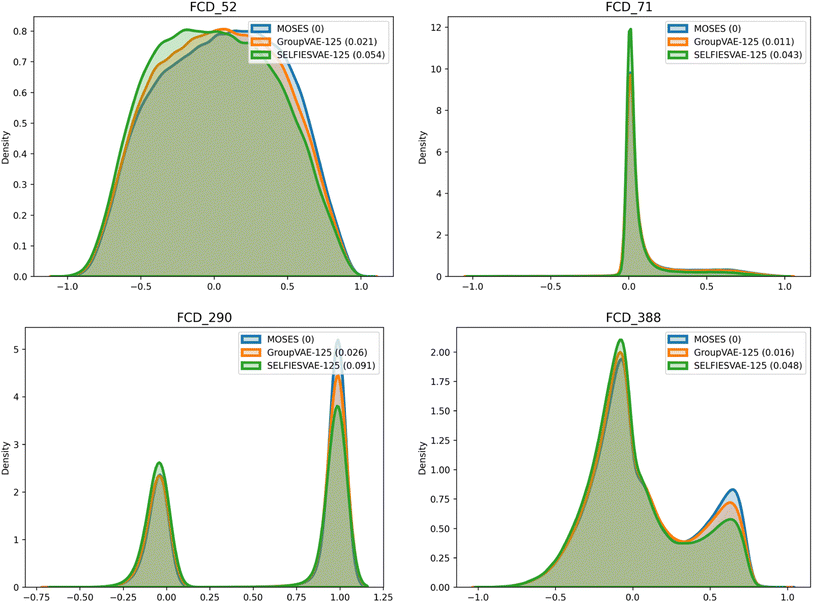
The Group SELFIES model performs especially well on the Fréchet ChemNet Distance (FCD) metric⁵³ when compared to SELFIES. FCD measures the difference between the activations of the penultimate layer of ChemNet (a model trained to predict the bioactivity of molecules) in the validation set and in the generated set. Due to how ChemNet was trained, the activations are likely to encode a mixture of biological and chemical properties important to drug likelihood. This makes comparing these activations more informative than comparing standard properties like logP or molecular weight, where the correlation to bioactivity is weaker and less deliberate. To visualize FCD, some indices of the penultimate activations of ChemNet are graphed in Fig. 6. Generated Group SELFIES match these distributions more closely than generated SELFIES. Additional plots comparing distributions of molecular weight, QED, SAScore, and logP are shown in ESI Section A.6.†

Fig. 6 Distribution of some values from the second-to-last layer of ChemNet for molecules generated by Group SELFIES and SELFIES compared to the validation set. The difference in distributions is used to calculate FCD. Bracketed values in the legend represent the Wasserstein distance to the original MOSES distribution.

5 Discussion

Our experiments show that Group SELFIES has noticeable advantages compared to SMILES and SELFIES representations, including greater readability provided by the group tokens. With regards to SMILES, the primary advantage is chemical robustness. The comparison with SELFIES is more nuanced, as discussed in the section below.

5.1 Group SELFIES vs. SELFIES

5.1.1 Substructure control. Group SELFIES provides more fine-grained control of substructures, which creates the following advantages: (1) an important scaffold can be preserved during optimization; (2) chiral and charged groups can be preserved during optimization, ensuring that charged tokens do not proliferate and create radicals; (3) synthetically accessible building blocks can be chosen as groups to improve synthesizability.

5.1.2 Substructure control with SELFIES. Various techniques applied to SELFIES can mitigate the challenges of preserving structure. One such example is to simply combine substrings of SELFIES strings together. Indeed, further experiments in ESI Section A.4† show that simply replacing all group tokens by their SELFIES substrings shows similar performance to Group SELFIES. Within the SELFIES framework, however, an inserted substring will not necessarily have that exact substructure when decoded because the first token of the inserted substring may need to be interpreted as a number, which can have cascading effects for the rest of the substring. It is also likely that upon further insertions, that substructure will not be preserved. Additionally, it is also not clear how an insertion based approach can create groups with 3 or more branches, since creating a third branch requires insertion in the middle of the group substring.

5.1.3 Computational speed. One tradeoff of Group SELFIES is that encoding and decoding is usually slower than with SELFIES, likely due to overhead of RDKit operations. The encoder is particularly slow as it relies on performing a substructure match for every group in the group set. The decoder is faster than the encoder, though still slower than the SELFIES decoder. See ESI Section A.7† for timing. To improve computational performance in future work, one could exploit substructure control of Group SELFIES to reduce the number of encode/decode calls needed to obtain high performers. Additionally, the speed of encoding and decoding operations can be improved with distributed computing, since Group SELFIES is trivially parallelizable for a fixed group set.

5.2 Future work

5.2.1 Extended chirality. Group SELFIES is theoretically capable of representing molecules with extended chirality which are traditionally not able to be represented with SMILES and SELFIES. These representations can only handle local chirality – that is, chirality with a single atom as the chiral center. This is in contrast to global chirality, where there may be an axis or plane of chirality. Group SELFIES can handle global chirality by taking an entire complex or chiral substructure and abstracting it into a group, leaving attachment points on the outside for varying functionalization. Fig. 7 shows examples of groups with local and global chirality that Group SELFIES can handle. We leave the proper implementation of generating molecules with global chirality to future work.

Fig. 7 Examples of chiral groups that can be represented in Group SELFIES. Tetrahedral carbon, hexoses, and octahedral metal centers have local chirality, whereas allenes, metallocenes, helicenes, and substituted biphenyls have global chirality.

Since extended chirality cannot be represented in SMILES or RDKit, storing these chiral groups would require specification of a new representation. One way this might be done is to specify each chiral group in 3D coordinates, with special atoms indicating attachment points, while maintaining nonchiral components in a “2D” representation as in SMILES/SELFIES.

5.2.2 Fragment analysis. It would be interesting to study how the set of groups used by Group SELFIES affects its performance in a generative model. Many fragmentation algorithms are available^23,42–46 to generate different sets of groups. In particular, it would be interesting to determine how large and diverse of a group set is needed to generate molecules with good performance. Group sets can be compared to the size and diversity of the original dataset, referencing fragment analysis studies of common datasets such as Enamine REAL,⁵⁴ ChEMBL,^55,56 and ZINC.⁵⁷

One promising extension of Group SELFIES is to incorporate more flexibility into the representation. In such a case, a group token can represent an entire scaffold, except without the atom identities. Other tokens can then identify the atom types on the scaffolds. This would allow optimization of the atom types while maintaining the topological structure of the scaffold. Another current limitation of Group SELFIES is that groups cannot overlap; more work is needed to develop a representation that acknowledges how groups might overlap, particularly for generating polycyclic compounds. A sequence-based representation of cellular complexes⁵⁸ or hypergraphs might suggest a promising direction.

Finally, given this paper's focus on the molecular representation, we only applied rather simple generative modeling methods. We hope that future work can leverage Group SELFIES to perform molecular generation with more advanced generative methods, including chemical language models, deep generative models, and evolutionary methods.

Data availability

The code for Group SELFIES and experiments reported in this work can be found at https://github.com/aspuru-guzik-group/group-selfies.

Conflicts of interest

A. A.-G is the Chief Visionary Officer and founding member of Kebotix, Inc.

Acknowledgements

We thank Luca Thiede, Akshat Nigam, Robert Pollice, Kjell Jorner, Gary Tom, Nathanael Kusanda, Edwin Yu, Naruki Yoshikawa, and Felix Strieth-Kalthoff for useful discussions. Calculations testing the robustness of Group SELFIES were performed on the Niagara supercomputer at the SciNet HPC Consortium. SciNet is funded by: the Canada Foundation for Innovation; the Government of Ontario; Ontario Research Fund – Research Excellence; and the University of Toronto. This research was partially supported by funds from Intel Corporation. A. A.-G. thanks Anders G. Frøseth for his generous support. A. A.-G. also acknowledges the generous support of Natural Resources Canada and the Canada 150 Research Chairs program.

References

1. S. Chithrananda, G. Grand and B. Ramsundar, ChemBERTa: large-scale self-supervised pretraining for molecular property prediction, arXiv preprint arXiv:201009885, 2020.
2. R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling and D. Sheberla, et al., Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4(2), 268–276.
3. T. Blaschke, J. Arús-Pous, H. Chen, C. Margreitter, C. Tyrchan and O. Engkvist, et al., REINVENT 2.0: an AI tool for de novo drug design, J. Chem. Inf. Model., 2020, 60(12), 5918–5922.
4. H. Moss, D. Leslie, D. Beck, J. Gonzalez and P. Rayson, BOSS: Bayesian optimization over string spaces, Advances in Neural Information Processing Systems, 2020, 33, 15476–15486.
5. B. Sanchez-Lengeling, C. Outeiral, G. L. Guimaraes and A. Aspuru-Guzik, Optimizing distributions over molecular space. An objective-reinforced generative adversarial network for inverse-design chemistry (ORGANIC), ChemRxiv preprint, 2017, available from: https://chemrxiv.org/engage/chemrxiv/article-details/60c73d91702a9beea7189bc2.
6. M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Self-referencing embedded strings (SELFIES): a 100% robust molecular string representation, Machine Learning: Science and Technology, 2020, 1(4), 045024.
7. M. Krenn, Q. Ai, S. Barthel, N. Carson, A. Frei and N. C. Frey, et al., SELFIES and the future of molecular string representations, Patterns, 2022, 3(10), 100588.
8. A. Nigam, P. Friederich, M. Krenn and A. Aspuru-Guzik, Augmenting Genetic Algorithms with Deep Neural Networks for Exploring the Chemical Space, in 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26–30, 2020, OpenReview.net, available from: https://openreview.net/forum?id=H1lmyRNFvr.
9. A. Nigam, R. Pollice, M. Krenn, G. dos Passos Gomes and A. Aspuru-Guzik, Beyond generative models: superfast traversal, optimization, novelty, exploration and discovery (STONED) algorithm for molecules using SELFIES, Chem. Sci., 2021, 12(20), 7079–7090.
10. A. Nigam, R. Pollice and A. Aspuru-Guzik, Parallel tempered genetic algorithm guided by deep neural networks for inverse molecular design, Digital Discovery, 2022, 1(4), 390–404.
11. D. Flam-Shepherd, K. Zhu and A. Aspuru-Guzik, Language models can learn complex molecular distributions, Nat. Commun., 2022, 13(1), 1–10.
12. K. Rajan, A. Zielesny and C. Steinbeck, DECIMER: towards deep learning for chemical image recognition, J. Cheminf., 2020, 12(1), 1–9.
13. K. Rajan, A. Zielesny and C. Steinbeck, STOUT: SMILES to IUPAC names using neural machine translation, J. Cheminf., 2021, 13(1), 1–14.
14. N. C. Frey, V. Gadepally and B. Ramsundar, FastFlows: flow-based models for molecular graph generation, arXiv preprint arXiv:220112419, 2022.
15. G. P. Wellawatte, A. Seshadri and A. D. White, Model agnostic generation of counterfactual explanations for molecules, Chem. Sci., 2022, 13(13), 3697–3705.
16. J. H. Jensen, A graph-based genetic algorithm and generative model/Monte Carlo tree search for the exploration of chemical space, Chem. Sci., 2019, 10(12), 3567–3572.
17. W. Jin, R. Barzilay and T. Jaakkola, Junction tree variational autoencoder for molecular graph generation, in International Conference on Machine Learning, PMLR, 2018, pp. 2323–2332.
18. Y. Xie, C. Shi, H. Zhou, Y. Yang, W. Zhang, Y. Yu, et al., MARS: Markov Molecular Sampling for Multi-objective Drug Discovery, in International Conference on Learning Representations, 2021, available from: https://openreview.net/forum?id=kHSu4ebxFXY.
19. E. Bengio, M. Jain, M. Korablyov, D. Precup and Y. Bengio, Flow network based generative models for non-iterative diverse candidate generation, Advances in Neural Information Processing Systems, 2021, 34, 27381–27394.
20. W. Jin, R. Barzilay and T. Jaakkola, Multi-objective molecule generation using interpretable substructures, in International Conference on Machine Learning, PMLR, 2020, pp. 4849–4859.
21. S. Yang, D. Hwang, S. Lee, S. Ryu and S. J. Hwang, Hit and lead discovery with explorative RL and fragment-based molecule generation, Advances in Neural Information Processing Systems, 2021, 34, 7924–7936.
22. D. Flam-Shepherd, A. Zhigalin and A. Aspuru-Guzik, Scalable Fragment-Based 3D Molecular Design with Reinforcement Learning, arXiv preprint arXiv:220200658, 2022.
23. M. Guo, V. Thost, B. Li, P. Das, J. Chen and W. Matusik, Data-Efficient Graph Grammar Learning for Molecular Generation, in International Conference on Learning Representations, 2022, available from: https://openreview.net/forum?id=l4IHywGq6a.
24. Q. Liu, M. Allamanis, M. Brockschmidt and A. Gaunt, Constrained graph variational autoencoders for molecule design, Advances in Neural Information Processing Systems, 2018, 31, 7806–7815.
25. P. Polishchuk, CReM: chemically reasonable mutations framework for structure generation, J. Cheminf., 2020, 12(1), 1–18.
26. W. Wiswesser, Simplified chemical coding for automatic sorting and printing machinery, Willson Products Inc., Reading, PA, 1951.
27. W. J. Wiswesser, 107 years of line-formula notations (1861-1968), J. Chem. Doc., 1968, 8(3), 146–150.
28. J. J. Vollmer, Wiswesser line notation: an introduction, J. Chem. Educ., 1983, 60(3), 192.
29. H. W. Hayward, A new sequential enumeration and line formula notation system for organic compounds, Office of Research and Development, Patent Office, 1961, p. 21.
30. H. Skolnik and A. Clow, A Notation System for Indexing Pesticides, J. Chem. Doc., 1964, 4(4), 221–227.
31. R. W. Homer, J. Swanson, R. J. Jilek, T. Hurst and R. D. Clark, SYBYL line notation (SLN): a single notation to represent chemical structures, queries, reactions, and virtual libraries, J. Chem. Inf. Model., 2008, 48(12), 2294–2307.
32. T. Zhang, H. Li, H. Xi, R. V. Stanton and S. H. Rotstein, HELM: A Hierarchical Notation Language for Complex Biomolecule Structure Representation, ACS Publications, 2012,  DOI:10.1021/ci3001925.
33. D. Garay-Ruiz, C. Bo and D. G. Ruiz, Human-Readable SMILES: Translating Cheminformatics to Chemistry, ChemRxiv preprint, 2021,  DOI:10.26434/chemrxiv.14230034.v1.
34. X. Li and D. Fourches, SMILES pair encoding: a data-driven substructure tokenization algorithm for deep learning, J. Chem. Inf. Model., 2021, 61(4), 1560–1569.
35. J. R. Koza and R. Poli, Genetic programming, in Search methodologies, Springer, 2005, pp. 127–164.
36. M. Brameier, W. Banzhaf and W. Banzhaf, Linear genetic programming, Springer, 2007, vol. 1.
37. Products: Structure Data Downloads – eMolecules, available from: https://search.emolecules.com/info/products-data-downloads.html.
38. B. Zdrazil and R. Guha, The rise and fall of a scaffold: a trend analysis of scaffolds in the medicinal chemistry literature, J. Med. Chem., 2017, 61(11), 4688–4703.
39. P. Ertl and T. Schuhmann, A systematic cheminformatics analysis of functional groups occurring in natural products, J. Nat. Prod., 2019, 82(5), 1258–1263.
40. S. Sharif, R. Liu, A. A. Orr, D. Khavrutskii, S. Jo, B. Lier, et al., Global-Chem: a Chemical Knowledge Graph of common small molecules and their IUPAC/SMILES/SMARTS for selection of compounds relevant to diverse chemical communities, 2022.
41. J. Hussain and C. Rea, Computationally efficient algorithm to identify matched molecular pairs (MMPs) in large data sets, J. Chem. Inf. Model., 2010, 50(3), 339–348.
42. C. Sheng and W. Zhang, Fragment informatics and computational fragment-based drug design: an overview and update, Med. Res. Rev., 2013, 33(3), 554–598.
43. T. Liu, M. Naderi, C. Alvin, S. Mukhopadhyay and M. Brylinski, Break down in order to build up: decomposing small molecules for fragment-based drug design with eMolfrag, J. Chem. Inf. Model., 2017, 57(4), 627–631.
44. P. S. Kutchukian, S. S. So, C. Fischer and C. L. Waller, Fragment library design: using cheminformatics and expert chemists to fill gaps in existing fragment libraries, in Fragment-Based Methods in Drug Discovery, Springer, 2015, pp. 43–53.
45. S. Müller, Flexible heuristic algorithm for automatic molecule fragmentation: application to the UNIFAC group contribution model, J. Cheminf., 2019, 11(1), 1–12.
46. J. Degen, C. Wegscheid-Gerlach, A. Zaliani and M. Rarey, On the Art of Compiling and Using ‘Drug-Like’ Chemical Fragment Spaces, ChemMedChem, 2008, 3(10), 1503–1507.
47. J. J. Irwin, K. G. Tang, J. Young, C. Dandarchuluun, B. R. Wong and M. Khurelbaatar, et al., ZINC20—a free ultralarge-scale chemical database for ligand discovery, J. Chem. Inf. Model., 2020, 60(12), 6065–6073.
48. P. Ertl and A. Schuffenhauer, Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions, J. Cheminf., 2009, 1(1), 1–11.
49. G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Quantifying the chemical beauty of drugs, Nat. Chem., 2012, 4(2), 90–98.
50. S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Design principles and top non-fullerene acceptor candidates for organic photovoltaics, Joule, 2017, 1(4), 857–870.
51. D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov and S. Belyaev, et al., Molecular Sets (MOSES): A Benchmarking Platform for Molecular Generation Models, Front. Pharmacol., 2020, 11, 565644.
52. M. A. Murcko and G. W. Bemis, The Properties of Known Drugs. 1. Molecular Frameworks, J. Med. Chem., 1996, 39, 2887–2893.
53. K. Preuer, P. Renz, T. Unterthiner, S. Hochreiter and G. Klambauer, Fréchet ChemNet Distance: A Metric for Generative Models for Molecules in Drug Discovery, J. Chem. Inf. Model., 2018, 58(9), 1736–1741,  DOI:10.1021/acs.jcim.8b00234.
54. O. O. Grygorenko, D. S. Radchenko, I. Dziuba, A. Chuprina, K. E. Gubina and Y. S. Moroz, Generating multibillion chemical space of readily accessible screening compounds, iScience, 2020, 23(11), 101681.
55. A. S. Gaur, L. John, N. Kumar, M. R. Vivek, S. Nagamani and H. J. Mahanta, et al., Towards systematic exploration of chemical space: building the fragment library module in molecular property diagnostic suite, Mol. Diversity, 2022, 1–10.
56. V. Khanna and S. Ranganathan, Structural diversity of biologically interesting datasets: a scaffold analysis approach, J. Cheminf., 2011, 3(1), 1–14.
57. Y. Shi and M. von Itzstein, How size matters: diversity for fragment library design, Molecules, 2019, 24(15), 2838.
58. M. Hajij, K. Istvan and G. Zamzmi, Cell complex neural networks, arXiv preprint arXiv:201000743, 2020.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00012e

‡ Equal contribution.

---