An interpretable machine learning framework for modelling macromolecular interaction mechanisms with nuclear magnetic resonance

Abstract

Macromolecular interactions, such as polymer–protein binding, determine the biological fate of biomaterials. However, in most macromolecular binding systems, underlying interaction mechanisms are unclear, limiting capabilities for in vitro prediction. In particular, the atomic-level structure–activity relationships that drive protein–polymer binding are confounding. To overcome this gap, we developed a machine learning framework that applies interaction data from direct saturation compensated nuclear magnetic resonance (DISCO NMR) to classify polymer proton descriptors to their interactive behaviors with mucin proteins. The framework constructs structure-interaction trends from cross-polymer atomic-level behavior patterns, and identifies “undervalued” inert polymer groups with potential to be engineered towards interaction. Trends are constructed from materials-agnostic interaction descriptors that combine chemical shift fingerprints, molecular weight, and cumulative DISCO effect from saturation transfer buildup, mapping proton chemical, physical, and conformational attributes together. In this work we constructed a fully-trained decision tree classifier to model structure–activity after applying principal component analysis (accuracy = 0.92, F₁ = 0.87) and interpreted its decision rules to improve scientific understanding of mucin binding. Several undervalued inert protons identified by the model include: HPC 80 kDa (4.58 ppm), HPMC 120 kDa (4.48 ppm), PVA 105 kDa (1.58 ppm), DEX 150 kDa (5.20 ppm), PVP 55 kDa (3.89 ppm), CMC 90 kDa (4.58 ppm), and PEOZ 50 kDa (3.42 ppm). The model additionally suggested a structure–activity relationship is shared by HPC, CMC, DEX, and HPMC protons in the 80–150 kDa range. More broadly, the framework and its descriptors can be applied for data-driven discovery of new polymer formulations using previously obscure cross-polymer sub-group trends, and is similarly applicable to any receptor-ligand system compatible with DISCO-NMR screening.

---

Introduction

A central challenge in biomaterial design remains a limited understanding of the mechanisms that underlie biomacromolecular interactions, leading several investigators to call for more research in this field.^1–3 The intractability of manually interrogating the biomaterial interaction problem space necessitates a paradigm shift in research from traditional Edisonian design frameworks, to machine-learning informed approaches for objective guidance in materials design.^2,4–10 Consequently, successful predictive frameworks for macromolecular biomaterial design have been demonstrated in several applications, such as: immune-instructive polymers, protein resistant surface coatings, protein-absorbent self-assembled monolayers, and medical nanoparticles.^3,11–14

Extending these modelling frameworks to interaction screening for inter-macromolecular systems has proven to be challenging. Primarily, there are countless variables that can influence when and where interactions will result, even within the scope of in vitro prediction.^2,4,15–20 Moreover, these interactions are highly sensitive to variations in ligand chemical composition, physical properties, and ligand-receptor spatial conformation, which requires the use of modelling descriptors that draw from each in concert.^9,15,20–23 Additionally, mechanistic influences exerted by non-bonded groups on related bonding groups remain understudied.^17,18 We set out to meet these challenges in the present work.

We focused on curating and modelling a high quality experimentally derived dataset of macromolecular ligand-receptor interaction mechanisms. Specifically, contrasting how polymer ligand examples of a wide variety of chemical and physical properties interact with a target protein. This represents a common reflection of the breadth of factors biomaterials researchers must consider in designing polymer delivery vehicles. Further, additional strategies are needed to navigate small, sparse, yet high quality datasets in materials science, as small datasets are expected to remain prevalent until automated experimentation is more widely adopted.²⁴ Thus, we direct our focus in this work to creating a useful workflow and tool for researchers to descriptively navigate such problem spaces with limited information, that is additionally capable of facilitating predictive modelling when scaled data collection processes, such as automation, become available.

Towards this aim, we investigated two objectives. First, we set out to develop a reproducible framework including data collection, preparation, feature engineering, hyperparameter tuning, and modelling steps from which a machine learning model can be trained to model inter-macromolecular structure activity. To provide actionable insights, we identified the best model of the full dataset using 5-fold stratified grid-search cross validation, and interpreted it descriptively to report structure-interaction trends we observed in the data collected for this work. These descriptive insights can be directly applied by researchers to inform design decisions across widely varying polymer chemical and physical species, in particular by shining a light on the normally unknown behaviors of non-bonded groups. The second investigation assessed the predictive performance metrics of the overall framework, using nested leave-one-out cross validation, to establish a benchmark in machine learning performance for this task.

Given the exploratory nature of this work, we focus on preserving end-to-end interpretability in modelling, while removing human bias, to both redirect intuition in this field towards data-driven insights and build trust.²⁵

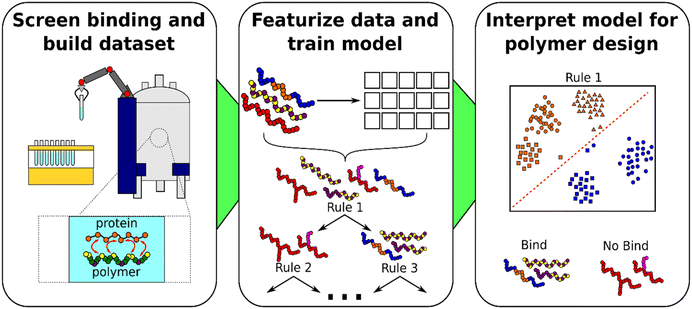
To screen macromolecular interactions for side-by-side comparison, while capturing a combination of chemical, physical, and spatial ligand-receptor data, we previously developed an experimental method using saturation transfer-based NMR (DISCO NMR).²⁶ This transfer-based NMR relies on the transfer of magnetic excitation through the nuclear Overhauser effect (NOE) from a receptor macromolecule to a ligand. The intensity of this transfer signal is proportional to the steady-state proximity between ligand and receptor protons. Through interaction screening with DISCO NMR, we obtain descriptors and labels pursuant to the attributes of each macromolecular ligand proton within a 5 Å radius of the receptor's binding site. These are, for each proton: δ¹H chemical shift (700 MHz, D₂O), a saturation transfer buildup curve, and a measure of proton interactive fate with the receptor. Downstream feature engineering, linear principal component analysis (PCA), and interpretable supervised learning result in a set of design insights derived from underlying cross–polymer interaction mechanisms. In total, this data collection and interpretation pipeline is applicable to any solution-state binding system that is freely soluble in deuterated water. The NMR pulse sequences used in these experiments are based upon typical saturation transfer difference with excitation sculpting (STD-ES) experiments, which are easily accessible in most NMR spectrometers. In addition, this pipeline has the advantage of being minimally laborious as much of the handling and data preprocessing is easily automated. In this work all stages of experimentation were automated apart from the selection of candidate materials and preparation of samples for NMR.

As a proof of concept, we scoped the present work to examine the mechanism of adhesive interactions resulting between popular biomedical polymer ligands and a mucin protein receptor (mucoadhesive interactions). Previously, limitations with measurement reproducibility prevented the collection of sufficient screening data to facilitate side-by-side comparisons of polymer mucoadhesive interactions,^27–29 and they remain largely unexplored in this regard.^1,30 In addition, the mucoadhesion process of polymeric biomaterials is complex, leading to several competing mechanistic theories and some prominent examples of contradictory adhesive behavior between identical materials.^1,31,32 More generally, understanding the link between polymeric biomaterials performance and the underlying chemistry and structures of those polymers has been deemed a “formidable challenge”.^33,34 Data-driven approaches relying on ML have been suggested to address this challenge, specifically in aiding to untangle their complexity.^33,34 To the best of the authors knowledge, the present work is the first machine-learning directed exploration conducted to date of mucoadhesive interaction mechanisms from atomic-level data.

As a whole, we expect this framework to lay a foundation for data-driven experimentation in macromolecular design. In particular, this framework will benefit researchers focused on designing polymeric or other macromolecular ligands, to target receptor interactions in vitro, by providing unbiased and experimentally actionable mechanistic insights using descriptive analysis, and establish a new machine learning performance benchmark in the runway towards predictive design of biomaterials for targeted interactions.

Experimental

Dataset materials

To create a dataset that mapped clear polymer structure-interaction information at molecular resolution, we experimentally characterized 18 chemically and structurally distinct biomedical polymers (i.e. varying chemistry and molecular weight) for their interactions with bovine submaxillary mucin in solution with DISCO NMR, using previously reported methodology.²⁶ We selected a variety of popular biomedical polymers previously studied for their mucoadhesive, mucus-inert, or confounding (previously reported as adhesive, and inert) properties with mucin. The total list of subject polymers, their molecular weights, and associated protons are outlined in Table 1 (representative chemical structures are provided in ESI Table 1†). All chemicals used in these experiments were purchased from Millipore Sigma and used without additional purification, unless otherwise noted. 131 kDa CMC was purchased from Fisher Scientific, bovine submaxillary mucin was purchased from Cedarlane (Burlington, ON). Proton chemical shifts are given as δ¹H chemical shift (700 MHz, D₂O). NMR integral regions for each polymer are referenced to the literature values for the residual HDO peak.³⁵ We note that while the total number of proton samples in the dataset (99) is small in the scheme of machine learning research, other works conducted at the intersection of experimental biomaterial interaction screening and supervised learning have similarly analyzed datasets on the order of 100 data points.^7,9,36–43 The end-to-end analysis workflow comprising this computational framework for interaction screening is depicted in Fig. 1.

Table 1 Summary of dataset polymers, their target concentrations, and δ¹H chemical shift (700 MHz, D₂O)

Polymer name	Abbreviation	Avg. MW (kDa)	C (μM)	δ ^1H chemical shift (700 MHz, D2O)
Hydroxypropyl methyl cellulose	HPMC	86, 120	20	4.48, 4.05, 3.71, 3.38, 3.08, 1.16
Hydroxypropyl cellulose	HPC	80, 370	20	4.58, 4.07, 3.77, 3.46, 3.14, 1.13
Carboxymethyl cellulose	CMC	90, 131	20	4.58, 4.36, 4.25, 4.09, 3.93, 3.76, 3.58, 3.35, 3.14
Dextran from Leuconostoc mesenteroides	DEX	150	20	5.30, 5.20, 4.22, 4.02, 3.88, 3.72, 3.48
Poloxamer 407	P407	12.6	50	3.76, 3.60, 3.54, 3.47, 1.19
Poly(2-ethyl-2-oxazoline)	PEOZ	50	40	3.62, 3.42, 2.41, 2.32, 2.22, 1.01
Poly(vinylpyrrolidone)	PVP	55, 1300	20, 20	3.89, 3.60, 3.22, 2.51, 2.27, 2.03, 1.78, 1.54
Poly((2-dimethylamino)ethyl methacrylate)	PDMAEMA	10	200	4.40, 3.46, 2.89, 2.05, 1.42, 1.30, 1.13, 0.92
Poly-(N-(2-hydroxypropyl)methacrylamide)	PHPMA	40	20	3.92, 3.19, 3.04, 1.82, 1.16, 0.94
Poly(acrylic) acid	PAA	450	20	2.03, 1.54, 1.28
Polyethylene glycol	PEG	2, 10, 20	20	3.70
Poly(vinyl) alcohol 86–89%	PVA	105	20	4.08, 2.12, 1.58

---

Fig. 1 Workflow diagram describing the computational framework for polymer–protein interaction screening and insight generation. (Left) Polymer–protein interaction data is screened experimentally using DISCO NMR. Experimental results yield a labeled dataset describing the attributes of polymer protons within 5 Å of the protein binding site and their interaction behavior. (Center) Proton modelling features are engineered, principal component analysis transforms the feature set, and the highest importance features are applied to interpretably relate protons to their interaction outcome by a supervised decision tree classifier. (Right) Final model decision rule junctions are interpreted using principal component biplots to summarize cross-polymer trends and inspire scientific hypotheses.

Model task formulation

The problem was formulated as a binary proton interaction classification task, where the positive class label (1) signified a proton as interactive, and the negative class (0) signified it as inert. Of the subject polymers, 6 possessed protons that showed significant mucoadhesive interactions, while all protons in the remaining 12 polymers were inert. This translated to 15 interactive protons, and 84 inert, as labeled by testing whether their DISCO Effect (t) saturation time dependent buildup curves were statistically distinguishable from zero effect (Students' t test, p < 0.05, n ≥ 3) using previously reported methodology.²⁶ Capturing the attributes of the negative class accurately for modelling was a primary focus in this work, as we hypothesized that inert protons would be a robust source of information for deconvoluting positive class interaction behaviors.¹⁶

Feature engineering

In supervised machine learning, the design of input descriptors for modelling (referred to as “feature engineering”) is an essential foundation for generating high quality machine-learned insights.⁸ Feature engineering polymer descriptors for biomaterial interaction screening with machine learning remains an active area of study,^7,44,45 however, successful exploratory works of this nature have been conducted previously using experimentally derived feature sets from analytical screening.^12,38 Along these lines, here we developed a machine learning feature set using only data obtained from DISCO NMR, and polymer molecular weight, with the joint aims of maximizing interpretability of macromolecular ligand design attributes, and accurately modelling proton-interaction relationships. We elected to derive new modelling features from raw analytical DISCO NMR results to avoid pooling the variance from DISCO NMR with external variance introduced by a feature representation framework. From DISCO NMR results, we obtain high precision, atomic-level descriptors of polymer chemical monomers in the form of proton δ¹H chemical shift, and polymer conformation information, as measured by saturation transfer buildup curves.²³ Polymer molecular weight, as an indicator of polymer size, was used as reported by the manufacturer. To pool this variance with an additional feature framework or third-party dataset introduces the risk of diluting the precise signals we observed from these analytical measurements during modelling. DISCO NMR results provide chemical, physical, and conformational information at the atomic level, and thus merit modelling by a standalone objective function without pooled variance.⁴⁶

The meaning underlying each modelling feature, and the workflow to vectorize them from experimental data, is outlined below. An exemplary feature vector is shown in Table 2 for HPC 4.07 ppm proton. Specifically, the feature set includes: sample proton δ¹H chemical shift, proton cumulative DISCO effect, polymer molecular weight, and a contextual polymer-level chemical shift fingerprint. The feature vector input to the model training in this work had 35 columns. Each of the features is described in more detail below.

Table 2 Example feature vector, HPC 370 kDa 4.07 ppm proton sample

Sample proton attributes			Cohort proton fingerprint vector
ppm	mW	CDE	(1.0, 1.1]	(1.1, 1.2]	…	(3.1, 3.2]	(3.2, 3.3]	(3.3, 3.4]	(3.4, 3.5]	…	(3.7, 3.8]	…	(4.0, 4.1]	…	(4.5, 4.6]	…
4.07	370	−0.61	0	1	0	1	0	0	1	0	1	0	0	0	1	0

---

δ ¹H chemical shift

The chemical shift of each proton was obtained using DISCO NMR. Beyond being a chemical identifier for each proton, the chemical shift provides meaningful insight into the extent of electron shielding or de-shielding and electronegativity of neighboring groups, present at a given polymer site. In NMR, “upfield” chemical shifts refer to lower magnitude, electron dense, shielded shifts, which can correlate to lower electronegativity of neighboring functional groups. Alternatively, “downfield” shifts are those of higher magnitude, lower electron density, and increased neighboring functional group electronegativity. The level of electron shielding experienced at groups neighboring a proton during protein binding offers essential directly measured mechanistic insight.

Polymer molecular weight

The impact of polymer molecular weight on mucoadhesion is an ongoing area of research, given confounding reports of increasing molecular weight being in some cases an enhancer of mucoadhesion, yet in others reducing it.^32,47 The influence that polymer molecular weight exerts on resulting interactions is unclear,¹⁵ therefore it is unlikely to be a standalone predictor, though it provides a proxy measure for physical macromolecular structural influences on proton level interaction.

δ ¹H chemical shift fingerprint vector

Given there are cooperative forces occurring among polymer sub-groups that influence global polymer interaction outcomes^16,23,26 we used an additional vector to one-hot-encode chemical identities of the full proton set detected in a given polymer, in terms of their binned interval of the NMR spectrum. Herein, the term “cohort” refers to the set of chemical identities (δ¹H chemical shift) of all protons detected at a given polymer's binding site using DISCO NMR, excluding that of the sample proton being represented (n_cohort = n_polymer − 1). The hashing workflow applied to encode the cohort vector, and some guidance for post hoc interpretation of cohort shifts is described in the ESI.†

To convey the idea of a “cohort proton” versus a “sample proton”, consider the feature vector representation (Table 2), where the 4.07 ppm chemical shift in HPC 370 kDa is a sample proton. In the vector, two columns map to the unique attributes of the sample proton: chemical shift (ppm), and cumulative DISCO effect (CDE). Molecular weight is encoded from the parent polymer of the sample proton. The cohort vector is then appended to coarsely represent chemical context relevant to the sample proton. In HPC, there are 6 total protons detected at the binding site, meaning its data representation always has one dedicated sample proton, and the other five encoded as cohort chemical shifts. Hence, the cohort vector changes within a polymer to exclude the interval of the sample proton. Every proton measured in the dataset is represented once as a sample proton, with the corresponding cohort.

Cumulative DISCO effect

To incorporate cross-polymer positional differences measured with respect to the receptor, we created the Cumulative DISCO Effect (CDE) descriptor. CDE is computed from a weighted cumulative sum of the standardized DISCO Effect (t) saturation transfer buildup curve of each proton. The DISCO Effect (t) buildup curve is a time-series that relays the relative spatial positioning of ligand protons with respect to the receptor at each time point, regardless of the interaction outcome of the ligand. The effect curve is computed at each NMR saturation time point (0.25 s, 0.50 s, 0.75 s, 1.0 s, 1.25 s, 1.50 s, and 1.75 s) and averaged across technical replicates. In addition to CDE, we benchmarked alternative pipelines using various DISCO Effect (t) derived modelling features and compared pipeline holdout performance metrics with nested cross validation. Detailed description of the benchmarking workflow and results are provided in ESI Tables 2 and 3.† CDE is computed specifically by linear PCA of the time-series DISCO Effect (t) buildup curve for each proton. Only the first principal component is retained, reducing the signal from seven dimensions (t = 0.25 s, 0.50 s, 0.75 s, 1.0 s, 1.25 s, 1.50 s, 1.75 s) to one. CDE, the retained principal component, is thus interpretable as a weighted cumulative sum of the DISCO Effect (t) for a given ligand proton, over the entirety of the receptor-ligand saturation time series. 68.8% of proton buildup curve variance in the final model was explained by CDE. Further discussion of the computation and interpretation of CDE is provided in the ESI.†

Feature transformation by principal component analysis

For each analysis, all data preprocessing steps prior to cross validation were conducted through a single pipeline (sklearn.pipeline). A pipeline is a method for assembling steps to be cross validated together, such that defined steps are trained on only training data folds, and applied to transform validation data folds. The first step in the pipeline computed the CDE feature as previously described. Next, the CDE feature alongside the chemical property and physical property features (i.e. sample proton δ¹H chemical shift, molecular weight, cohort fingerprint, and CDE, totalling 35 features) were passed into a principal component analysis workflow. We added this principal component analysis workflow to the pipeline as a means of removing intercorrelations in the modelling features while keeping underlying information intact.^18,48

A challenge characteristic of polymer machine learning is that polymer attributes are often inherently intercorrelated,⁴⁴ which impedes the ability of a model to learn independent relationships.⁴⁹ The retained number of principal components for modelling,³¹ was selected by Minka's MLE.⁵⁰ The scree plot and factor loadings for the retained principal components are provided in ESI Fig. 2 and 3.† Principal component factor loadings are generally interpreted as linear combinations of the input variables, and represent the criteria used to score protons on each component. The magnitudes of the loadings correspond to the magnitude of the underlying proton attribute importance to the associated component. The sign of the loadings corresponds to the direction of the correlation between the attribute and the principal component score.

Modeling structure-interaction with decision tree learners

The first objective of this framework was to improve our scientific understanding of macromolecular interaction mechanisms, and construct descriptive polymer interaction design guidelines without human-bias. Hence, we focused on interpretable modelling approaches. Decision trees are best known for their “glass box” interpretability among supervised classifiers, providing traceable explanations for each prediction made.^19,51 Accordingly, decision trees have been popular for similar biological modelling tasks dependent on interpretability, such as deconvoluting toxicological interaction mechanisms pursuant to medical nanoparticle design.^18,52–54 On these merits, we selected a decision tree classifier to interpretably relate proton attributes to their interactive fate. Decision trees were trained using the DecisionTreeClassifier estimator from the scikit-learn Python package (scikit-learn package version 0.23.2, Python version 3.8.8 used throughout) which is provided as an optimized implementation of the Classification and Regression Tree (CART) algorithm.⁵⁵

A decision tree classifier constructs a set of interpretable rules that split the dataset into subsets, as a function of maximizing class purity. To this effect, the decision tree automatically selects training features in the dataset (j) that are optimal for splitting at fixed threshold values (s). Consequently, each node of the tree can be considered a characteristic region of the dataset (R), whose proton samples share similar structure-interaction behaviors. For example, two characteristic regions R₁ and R₂ would be created by splitting the proton dataset X at feature j and threshold s as follows:⁵¹

R_1(j,s) = {X|X_j ≤ s} and R_2(j,s) = {X|X_j > s}

Such that feature j and threshold s are learned by the algorithm. Where a region is terminal (a leaf node), the hyperparameters of the tree constrain further splitting, and classification labels are assigned based on a predefined decision threshold, such as a percentage of a given class present in the leaf.

Here, the algorithm optimized tree leaf nodes to maximize proton-level interaction classification purity (i.e. interactive protons cluster together, inert together). However, given the polymer–proton hierarchy in the data, the tree also naturally captures interpretable polymer-level interaction trends in intermediate nodes.

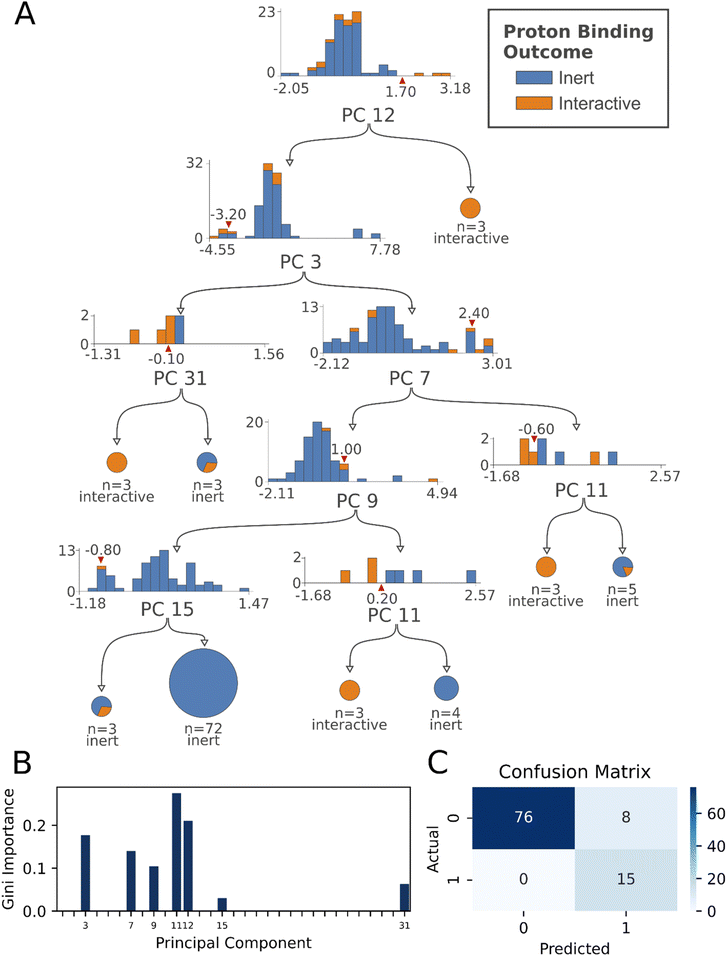
To select hyperparameters for the descriptive model's decision tree, we employed 5-fold stratified grid search cross validation, using the hyperparameter grid in ESI Table 3.† The process returned a tree with a cross-validated AUC of 0.635, having a maximum depth of 5, minimum samples per leaf of 3, and no constraint on minimum samples per split. Choosing descriptive model hyperparameters based on a cross validated grid search served to mitigate overfitting.

Finally, we fully trained a decision tree having the architecture returned from grid search cross validation to create a descriptive tree to interpret for insights. The principal component biplots shown in this work correspond in entirety to the set of decisions made in the descriptive tree.

Decision tree descriptive model performance assessment

The descriptive fully trained tree is depicted in Fig. 2A, alongside its feature importance plot (Fig. 2B), and confusion matrix (Fig. 2C). Leaf nodes were predicted as interactive by the model where a 20% or greater fraction of its protons were interactive in computing the metrics.

Fig. 2 Incorporating DISCO Effect as a modelling feature significantly improved modelling pipeline performance in terms of Holdout F₁ scores from nested cross validation (n = 3 random seeds, p ≪ 0.05, independent two sample t-test). The error bars depict standard error of the mean. The feature set without CDE comprised only the chemical shift, cohort fingerprint, and molecular weight descriptors. Models trained without CDE performed worse on average than the null model baseline F₁ = 0.46, indicating DISCO Effect is essential to mapping an objective function for the dataset.

There are no pre-existing benchmarks for model performance in this task, as atomic-level mucoadhesive interactions have not previously been modelled with machine learning. Thus, for a performance baseline we use a null model, a majority “dummy classifier,” where all samples are reported as the majority class (all protons classified inert). Class-specific F₁ scores, precision, and recall for the descriptive model are provided in Table 3 (F₁ = 0.87). The model's 0.87 F₁ score represents an 89% improvement over the null model F₁ = 0.46 (Table 4).

Table 3 Fully-trained decision tree classification metrics

	Precision	Recall	F 1 score	Accuracy
Inert protons	1.0	0.9	0.95	—
Interactive protons	0.65	1.0	0.79	—
Macro average	0.83	0.95	0.87	0.92
Weighted average	0.95	0.92	0.93	—

---

Table 4 Null model metrics. All examples predicted as majority class

	Precision	Recall	F 1 score	Accuracy
Inert protons	0.85	1.0	0.92	—
Interactive protons	0.0	0.0	0.0	—
Macro average	0.42	0.50	0.46	0.85
Weighted average	0.72	0.85	0.78	—

---

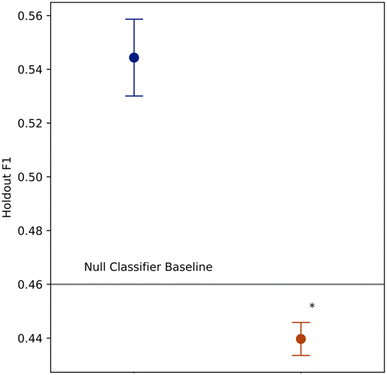
Predictive assessment of modelling pipeline

Towards the second objective of establishing a predictive benchmark for this task, we report estimates of pipeline out of sample performance using nested grid-search cross validation. The inner loop comprised a 5-fold stratified grid search cross validation, and the outer loop leave-one-out cross validation, to provide a test set assessment of the modelling pipeline and compute holdout F₁ score. We benchmarked the holdout F₁ score of the modelling pipeline with a cumulative DISCO effect feature against the null model baseline, and a version of the modelling pipeline with the same feature set only excluding a feature from DISCO Effect (Fig. 2). Two pipelines with alternative DISCO Effect feature representations were also benchmarked, which are described in further detail in ESI Table 2 and Fig. 1.† Each benchmark was conducted at three random seeds.

Holdout F₁ for the cumulative DISCO effect feature set, i.e. the pipeline used to create the descriptive model, demonstrated a 20% improvement over the null model (Average Holdout F₁ = 0.547, n = 3), indicating that the modelling pipeline performed well in the classification task. In contrast, the assessment for the feature set using only the chemical shift, cohort fingerprint and molecular weight features failed to beat the null model baseline (Average Holdout F₁ = 0.440, n = 3).

Thus, we learned that information at the intersection of proton chemical shift, polymer molecular weight, and physical conformation (DISCO Effect) was necessary to map an objective function of cross-polymer trends in interaction surpassing the null model. With these positive results, we next sought to interpret the descriptive model's representation of the data for insights in polymer interaction design at the intersection of chemical, physical, and conformational behavior.

Results and discussion

We interpreted the model's eight decision tree classification rules to study mucoadhesive interaction mechanisms across polymers in the dataset. In this work, the set of decision rules constructed by the model directly corresponds to areas in the dataset to investigate for interaction behaviour insights. To assess the similarities or differences between classified data points, we used principal component biplots, a popular methodology to ease interpretability of classification.⁵⁶ Each biplot illustrates a two-dimensional representation of essential variations in the data the model used to distinguish inert and interactive proton classes by constructing a rule. We can study the boundary between inert and interactive classes by visually examining which inert-labelled protons are proximal to interactive protons in the biplots.

The modelling exercise provided a path to data interpretation in several ways within this complex problem space: first by identifying which principal components enabled interaction classification, second by segregating subsets of data to leaf nodes that should be considered together, and finally constructing decision rule boundaries themselves. We follow an approach to data analysis as such, by examining the principal components and datapoints segregated to each decision node holistically.

In addition to constructing principal component biplots for each decision tree rule, we further examined the principal component factor loadings underlying the decision rules to ascertain the polymer attributes that correlated to each interaction classification, in the form of heuristics. Detailed description of each decision tree heuristic, including principal components, and factor loadings are provided in ESI Table 5.† To simplify the loadings for interpretation of the heuristics, only loadings greater than or equal to 0.1 are examined in the discussion.

Herein, from a bird's eye view, we draw attention to several key insights from the interpretation of principal component biplots that teach us about the behavior of mucoadhesive materials. The principal components used in the biplots are, in all cases, the pairings that create the decision rule in the tree being plotted, in the sequence shown in Fig. 3.

Fig. 3 Fully trained decision tree, resulting feature importance, and confusion matrix. (A) The best performing decision tree identified from 5-fold stratified grid search cross validation is shown (F₁ = 0.87, random seed = 148). Decision rules are indicated by red wedges, separating underlying proton descriptor distributions, where blue data indicates inert protons, and orange data indicates interactive protons, circles indicate final classification with simple majority membership and class indicated by the text below each. (B) Feature importance plot showing the most informative principal components. (C) Model confusion matrix. For all metrics, the optimized probability threshold for classification was used (0.2).

Identifying inert proton candidates for tuning towards designed polymer interactions

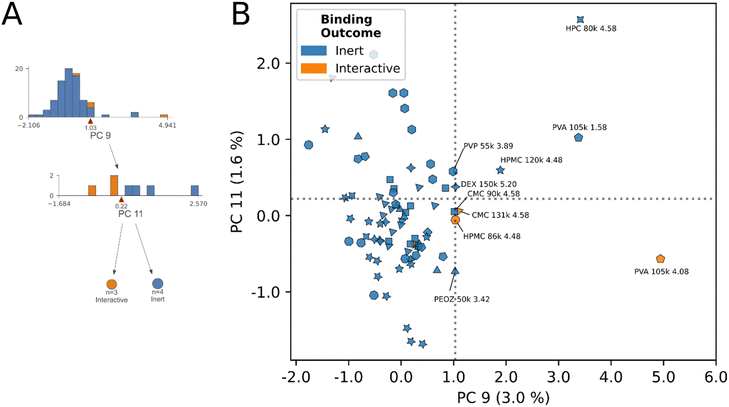
Each principal component biplot distilled high dimensional information from problem space interrogation into simple 2D planes. By visual examination of the boundary between inert and interactive classes in decision regions of the model, we identify which inert protons exhibited similar principal component scores to interactive protons. Herein, we discuss the identities of protons present at each decision rule, with particular interest in inert labelled protons having scores close to the interactive class.

In general, polymer interaction mechanisms having three or more strongly contributing protons (PAA, PDMAEMA, HPC), had sufficient interactive subset size to yield individual classification branches in the tree (Fig. 4). Where polymer interactions were specific to one or two proton sites, or where the dataset contained multiple examples of the same polymer with altered physical properties and interaction outcomes (CMC, HPMC, PVA, HPC) the model was forced to draw more nuanced cross-polymer comparisons to achieve its optimization objective (Fig. 5 and 6). It is in these nuanced cross-polymer comparisons we can elucidate the shared characteristics of interactive protons across polymer species, and the identities of the inert-labelled protons that closely border interactive decision regions. In other words, we can identify and enumerate “undervalued” inert protons that are worthy targets for engineering towards interaction.

Fig. 4 Principal component biplots summarizing decision rules 1, 2, and 5. (A) Decision tree subsection indicates the nodes describing rules 1 and 2. (B) Principal component biplot showing the data underlying rules 1 and 2, which classify PAA and PDMAEMA respectively as interactive. ¹H chemical shifts of protons are annotated. Marker shapes correspond to polymer species. (C) Decision tree subsection indicates the node describing rule 5. (D) Principal component biplot showing the data underlying rule 5, which classifies a subset of protons from HPC 370 kDa as interactive from the inert subset possessed by HPC 80 kDa. ¹H chemical shifts are annotated. Interactive protons from HPC 370 kDa (1.13, 3.46, 3.77, 4.07), inert protons from HPC 370 kDa (3.14) HPC 80 kDa (1.13, 3.77, 4.07). Marker shapes correspond to polymer species, identities for relevant species are annotated.

Fig. 5 Principal component biplots summarizing decision rules 6 and 7. (A) Decision tree subsection indicates the nodes describing decision rules 6 and 7. (B) Principal component biplot showing decision rules 6 and 7 and the underlying data. Abbreviated polymer names, MW, and ¹H chemical shifts of classified protons, as well as protons immediately bordering the decision boundary, are annotated. Decision rule 6 (PC9 = 1.03) groups protons from PVA, HPC, HPMC, DEX, CMC with the following average properties: chemical shift ppm_9>1.03 = 4.14 ppm, avg. CDE_9>1.03 = 3.63, avg. MW_9>1.03 = 111 kDa. Decision rule 7 (PC11 = 0.22) identifies the three true proton interactions within the proton subset across polymer species and MW. Marker shapes correspond to polymer species, identities for relevant species are annotated.

Fig. 6 Principal component biplot summarizing decision rule 8. (A) Decision tree subsection indicates the node describing rule 8. (B) Principal component biplot showing the data underlying rule 8. Abbreviated polymer names, MW, and ¹H chemical shifts of classified protons are annotated. Protons across species are bimodally distributed on chemical composition as indicated by PC15 factor loadings. The cluster scoring lowest on PC15 contains a true interactive proton, whereas the cluster scoring higher in PC15 contains purely inert protons. Marker shapes correspond to polymer species, identities are annotated.

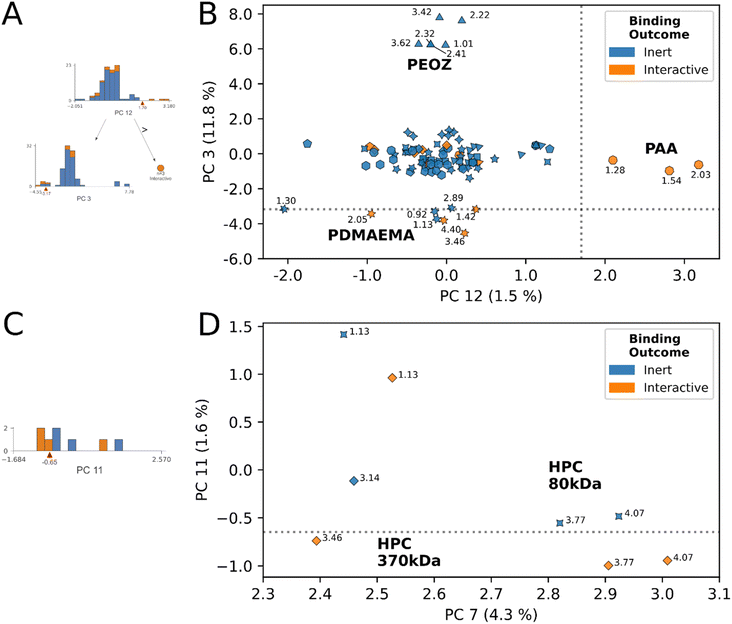
An example of this phenomenon is demonstrated by the HPC proton decision boundary (Fig. 4D). In HPC, the model learned that tuning molecular weight, without additional chemical functionalization, enabled interaction. HPC 370 kDa achieved stable mucoadhesive interactions at 4.07, 3.77, 3.46, and 1.13 ppm, and remained inert at 3.14 ppm. No interactions resulted at any HPC 80 kDa molecular weight protons. In addition to changes in molecular weight, we observed the average CDE of HPC protons below the decision boundary was lower than those above it, and ppm were shifted more downfield (avg. CDE_PC11≤0.65 = −0.74, avg. CDE_PC11>0.65 = −0.62), (avg. ppm_PC11≤0.65 = 3.77 ppm, avg. ppm_PC11>0.65 = 2.64 ppm). While in this example, CDE, ppm and molecular weight data exhibit clear directional trends across the decision rule, across different polymer species the nature of these relationships is increasingly complex. However, despite this complexity, by simple visual examination of the decision rule plots for inert-labelled protons from materials that border the interaction boundary, we can identify undervalued, inert labelled protons. In this instance, these are the three inert protons from HPC 80 kDa that appeared in this decision region (4.07, 3.77, 1.13).

The ability to create such an objective function from datapoints that vary across diverse polymer species in a small dataset is granted by the CDE descriptor (Fig. 2), which provides orthogonal continuous numeric data contextualizing the coarser changes in chemical shift, molecular weight, and cohort fingerprint. The hierarchy of descriptors, combining atomic-level data with polymer-level property data accounts for variance sources at multiple length scales.

The model's decision rules as an engine for identifying “undervalued” inert-labeled protons is best demonstrated in Fig. 5B. Chemically identical proton sites from CMC (4.58 ppm), and HPMC (4.48 ppm) at two molecular weights respectively, have opposite interaction outcomes in this region. At 131 kDa molecular weight the 4.58 ppm site in CMC interacts, however this interaction is lost at 90 kDa. In HPMC the direction of the trend is opposite, interaction occurred at 86 kDa molecular weight, yet was lost at 120 kDa. In spite of the conflicting directionality of the trend, the model correctly identified the true interactive protons across these species, and scored their chemically identical inert counterparts on the exterior of the decision boundaries in Fig. 5B. Here, we posit that other inert-labeled protons scoring within or near the decision boundaries of rules 6 & 7 are similarly “undervalued”, and correspond to candidates for within-species physical property tuning to unlock dominant interactions. These protons are: HPC 80 kDa (4.58 ppm), PVA (1.58 ppm), DEX150 (5.20 ppm), PVP 55 kDa (3.89 ppm), PEOZ 50 kDa (3.42 ppm), CMC 90 kDa (4.58 ppm), and HPMC 120 kDa (4.48 ppm), annotated in Fig. 5B. As described previously, the latter two inert protons are experimentally verified to unlock interaction through within-species tuning of molecular weight.²³

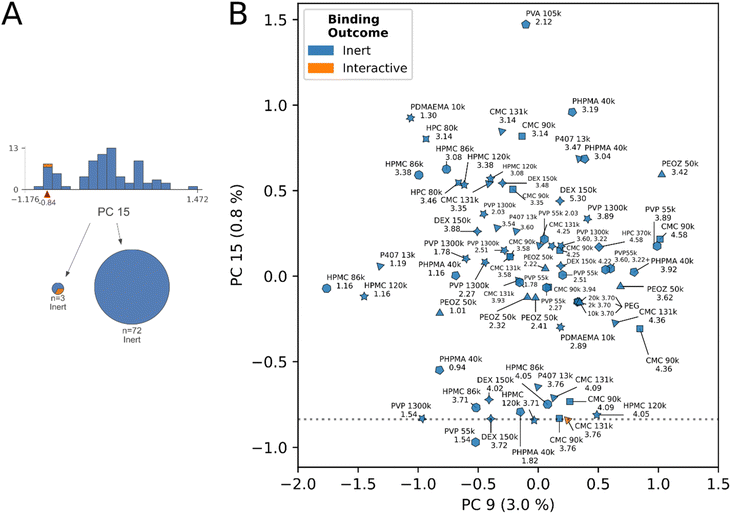
Fig. 6 shows the remaining unclassified protons in the dataset. The final decision rule in PC 15 intersects a cluster subset of the datapoints, a largely inert group containing a single interactive proton. The interactive proton is a secondary interaction from CMC 131 kDa at 3.76 ppm. We identify and enumerate the neighboring undervalued protons clustering this decision rule, which may correlate to secondary interactions in their respective species. These are: CMC 131 kDa (4.09 ppm), CMC 90 kDa (4.58 ppm, 4.09 ppm), DEX 150 kDa (3.72 ppm, 4.02 ppm), HPMC 120 kDa (3.71 ppm, 4.05 ppm), HPMC 86 kDa (3.71 ppm, 4.05 ppm), PHPMA 40 kDa (0.94 ppm, 1.82 ppm), PVP 55 kDa (1.54 ppm, 3.89 ppm), PVP 1300 kDa (1.54 ppm), P407 13 kDa (3.76 ppm), PEOZ 50 kDa (3.42 ppm).

For the protons of the larger second cluster, which does not contain a decision rule, we make no additional distinctions.

Identifying cross-polymer structure–activity trends

The data suggests a structure–activity relationship may exist at select proton sites across materials, in the molecular weight range of 80–150 kDa. The relevant proton sites were identified by detailed examination of decision rules 7 and 8 in the ESI,† alongside review of Fig. 5 and 6.

DEX, CMC, HPC, and HPMC in molecular weight range 80–150 kDa shared a cohort chemical shift interval of (4.0, 4.1] where downfield dominant interactions were either correctly identified, or were “undervalued” by the model in Fig. 5B. Specifically, we observed the (4.0, 4.1] cohort shift was present with: DEX 150 kDa (5.20 ppm, undervalued), CMC 131 kDa (4.58 ppm, interactive), HPMC 86 kDa (4.48 ppm, interactive), HPC 80 kDa (4.58 ppm, undervalued).

This trend is expanded to secondary interactions, with the observation that the (4.0, 4.1] and (3.7, 3.8] chemical shift intervals repeatedly appear together in the secondary interaction cluster apparent in Fig. 6B and the analysis of decision rule 8. These observations were: CMC 131 kDa (4.09 ppm, 3.76 ppm (interactive)), CMC 90 kDa (4.09 ppm, 3.76 ppm), DEX 150 kDa (4.02 ppm, 3.72 ppm), HPMC 86 kDa (4.05 ppm, 3.71 ppm), and HPMC 120 kDa (4.05 ppm, 3.71 ppm). P407 at 3.76 ppm additionally clustered, without a (4.0, 4.1] shift.

Hypothesis generation and interpretation from undervalued proton candidates

There are many approaches to investigate the hypotheses generated in this work, such that physical property adjustments without additional functionalization may enable inert to interactive polymer transitions. Approaches that constrain polymer mobility merit further investigation as a means of inducing changes to polymer orientation, and subsequently interactions such as mucoadhesion. For example, given neither molecular weight PVP (55 kDa, 1300 kDa) incurred any mucoadhesive interactions, we expect physical property tuning approaches other than molecular weight may be beneficial for adjusting the interaction conformation of PVP protons towards mucoadhesion, particularly at 3.89 ppm and 1.54 ppm sites.

In general, the dynamic, multivariate, and counterintuitive nature of the cross-species interaction mechanisms modelled in this work emphasizes that researchers will achieve the best designed polymer interaction outcomes by applying data-driven frameworks such as this, that outsource the interrogation of problem spaces to a computational model informed by chemical, physical, and conformational data, while clearly informing human researchers of the most efficient path to proceed.

Conclusions

In this work we developed a knowledge framework for extracting and interpreting structure-interaction trends in macromolecular systems and applied it to extract descriptive insights. We additionally established a benchmark for the framework's predictive capability. The framework uses ligand proton interaction data obtained from saturation transfer-based NMR (DISCO NMR) experiments, principal component analysis, and supervised decision tree classification to interpretably relate proton descriptors to their binarized interactive fate. To build structure–activity models, we developed a set of materials-agnostic macromolecular proton descriptors that apply a combination of ligand chemical shift fingerprinting, ligand molecular weight, and cumulative DISCO effect data captured from proton saturation transfer buildup curves. The descriptors encapsulated proton chemical, physical, and conformational attributes together. The predictive assessment of modelling pipelines demonstrated that incorporating a DISCO effect feature alongside chemical shift and molecular weight was essential to beat a null model performance benchmark and convey trends. For proof of concept, we applied the framework to descriptively highlight differences in the mucoadhesive interaction mechanisms underlying a variety of popular biomedical polymer ligands with mucin protein. We interpreted the decision rules of a fully trained descriptive model created using 5-fold stratified grid search cross validation (F₁ = 0.87), yielding several key insights in polymer design. Firstly, undervalued protons chemically suitable for interaction, yet in need of physical property tuning to unlock stable interaction, were identified by complex hierarchical patterns in proton cumulative DISCO effect. Some undervalued candidates belonging to this class were: HPC 80 kDa (4.58 ppm), HPMC 120 kDa (4.48 ppm), PVA (1.58 ppm), DEX 150 kDa (5.2 ppm), PVP 55 kDa (3.89 ppm), CMC 90 kDa (4.58 ppm), and PEOZ 50 kDa (3.42 ppm). The model additionally revealed a potential structure-interaction relationship shared by HPC, CMC, DEX, and HPMC pursuant to influences of their (4.0, 4.1] and (3.7, 3.8] chemical shifts on various downfield interactive sites, within the 80–150 kDa molecular weight range. Globally, the mechanistic understanding obtained from this framework reinforces the multivariate nature of inter-macromolecular interactions and underscores the need to shift the design paradigm to data-driven discovery for targeted biomaterial interactions. Along these lines, our results provide an actionable foundation for data-driven research in mucoadhesive polymer design. Looking ahead, we expect this framework to be readily applied for screening and interpreting the interaction mechanisms underlying other polymer–protein systems with DISCO NMR and accelerate progress towards predictive macromolecule designs for targeted interactions, or lack thereof.

Data availability

The experimental data and python code used to conduct this study are available in a public GitHub repository at: https://github.com/Frank-Gu-Lab/infrno.

Author contributions

S. S. contributed the majority of the methodology, formal analysis, software, visualization, and writing (original draft). S. S. and J. W. contributed equally to the conceptualization, data curation, investigation, writing (review & editing), and validation. F. X. G. contributed to the project administration, supervision, and funding acquisition. All authors contributed to the revision and editing of this manuscript and have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was undertaken thanks in part to funding provided to the University of Toronto's Acceleration Consortium from the Canada First Research Excellence Fund. This work was also supported by NSERC Discovery Grant #06441 and the NSERC Senior Industrial Research Chair program. The authors would like to acknowledge J. Tram-Su and M. Oliveira for refactoring and unit testing the data processing python code. S. Stuart is supported by the NSERC Alexander Graham Bell Canada Graduate Scholarship and the Canadian Federation of University Women 1989 École Polytechnique Commemorative Award. J. Watchorn is supported by the Queen Elizabeth II/Dupont Canada Scholarship in Science and Technology and the Mclean Foundation Graduate Scholarship in Science and Technology.

Notes and references

1. A. R. Mackie, F. M. Goycoolea, B. Menchicchi, C. M. Caramella, F. Saporito, S. Lee, K. Stephansen, I. S. Chronakis, M. Hiorth, M. Adamczak, M. Waldner, H. M. Nielsen and L. Marcelloni, Macromol. Biosci., 2017, 17, 1600534.
2. D. K. Brubaker and D. A. Lauffenburger, Science, 2020, 367, 742–743.
3. J. Lazarovits, S. Sindhwani, A. J. Tavares, Y. Zhang, F. Song, J. Audet, J. R. Krieger, A. M. Syed, B. Stordy and W. C. W. Chan, ACS Nano, 2019, 13, 8023–8034.
4. D. K. Brubaker, J. A. Paulo, S. Sheth, E. J. Poulin, O. Popow, B. A. Joughin, S. D. Strasser, A. Starchenko, S. P. Gygi, D. A. Lauffenburger and K. M. Haigis, Cell Syst., 2019, 9, 258–270.e6.
5. J. J. Richardson and F. Caruso, Nano Lett., 2020, 20, 1481–1482.
6. P. McGillivray, D. Clarke, W. Meyerson, J. Zhang, D. Lee, M. Gu, S. Kumar, H. Zhou and M. Gerstein, Annu. Rev. Biomed. Data Sci., 2018, 1, 153–180.
7. A. Suwardi, F. K. Wang, K. Xue, M. Y. Han, P. Teo, P. Wang, S. Wang, Y. Liu, E. Ye, Z. Li and X. J. Loh, Adv. Mater., 2022, 34(1), 2102703.
8. R. J. Kwaria, E. A. Q. Mondarte, H. Tahara, R. Chang and T. Hayashi, ACS Biomater. Sci. Eng., 2020, 6, 4949–4956.
9. Z. Ban, P. Yuan, F. Yu, T. Peng, Q. Zhou and X. Hu, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 10492–10499.
10. B. Fadeel and C. Alexiou, Biochem. Biophys. Res. Commun., 2020, 533, 36–49.
11. R. Marchetti, S. Perez, A. Arda, A. Imberty, J. Jimenez-Barbero, A. Silipo and A. Molinaro, ChemistryOpen, 2016, 5, 274–296.
12. H. M. Rostam, L. E. Fisher, A. L. Hook, L. Burroughs, J. C. Luckett, G. P. Figueredo, C. Mbadugha, A. C. K. Teo, A. Latif, L. Kämmerling, M. Day, K. Lawler, D. Barrett, S. Elsheikh, M. Ilyas, D. A. Winkler, M. R. Alexander and A. M. Ghaemmaghami, Matter, 2020, 2, 1564–1581.
13. M. Germain, F. Caputo, S. Metcalfe, G. Tosi, K. Spring, A. K. O. Åslund, A. Pottier, R. Schiffelers, A. Ceccaldi and R. Schmid, J. Controlled Release, 2020, 326, 164–171.
14. Y. Zhu, W. Xu, J. Zhang, Y. Du, J. Zhang, Q. Liu, C. Yang and S. Wu, 2022, preprint, arXiv:2103.03036,  DOI:10.48550/arxiv.2103.03036.
15. R. Kumar, ACS Appl. Bio Mater., 2022, 5, 2507–2535.
16. J. Watchorn, A. J. Clasky, G. Prakash, I. A. E. Johnston, P. Z. Chen and F. X. Gu, ACS Biomater. Sci. Eng., 2022, 8, 1396–1426.
17. H. S. Leong, K. S. Butler, C. J. Brinker, M. Azzawi, S. Conlan, C. Dufés, A. Owen, S. Rannard, C. Scott, C. Chen, M. A. Dobrovolskaia, S. V. Kozlov, A. Prina-Mello, R. Schmid, P. Wick, F. Caputo, P. Boisseau, R. M. Crist, S. E. McNeil, B. Fadeel, L. Tran, S. F. Hansen, N. B. Hartmann, L. P. W. Clausen, L. M. Skjolding, A. Baun, M. Ågerstrand, Z. Gu, D. A. Lamprou, C. Hoskins, L. Huang, W. Song, H. Cao, X. Liu, K. D. Jandt, W. Jiang, B. Y. S. Kim, K. E. Wheeler, A. J. Chetwynd, I. Lynch, S. M. Moghimi, A. Nel, T. Xia, P. S. Weiss, B. Sarmento, J. das Neves, H. A. Santos, L. Santos, S. Mitragotri, S. Little, D. Peer, M. M. Amiji, M. J. Alonso, A. Petri-Fink, S. Balog, A. Lee, B. Drasler, B. Rothen-Rutishauser, S. Wilhelm, H. Acar, R. G. Harrison, C. Mao, P. Mukherjee, R. Ramesh, L. R. McNally, S. Busatto, J. Wolfram, P. Bergese, M. Ferrari, R. H. Fang, L. Zhang, J. Zheng, C. Peng, B. Du, M. Yu, D. M. Charron, G. Zheng and C. Pastore, Nat. Nanotechnol., 2019, 14, 629–635.
18. A. V. Singh, D. Rosenkranz, M. H. D. Ansari, R. Singh, A. Kanase, S. P. Singh, B. Johnston, J. Tentschert, P. Laux and A. Luch, Adv. Intell. Syst., 2020, 2, 2000084.
19. P. Bannigan, M. Aldeghi, Z. Bao, F. Häse, A. Aspuru-Guzik and C. Allen, Adv. Drug Delivery Rev., 2021, 175, 113806.
20. M. M. Cencer, J. S. Moore and R. S. Assary, Polym. Int., 2022, 71, 537–542.
21. R. Upadhya, S. Kosuri, M. Tamasi, T. A. Meyer, S. Atta, M. A. Webb and A. J. Gormley, Adv. Drug Delivery Rev., 2021, 171, 1–28.
22. F. Cravero, S. A. Schustik, M. J. Martínez, G. E. Vázquez, M. F. Díaz and I. Ponzoni, J. Chem. Inf. Model., 2020, 60, 592–603.
23. J. Watchorn, S. Stuart, D. C. Burns and F. X. Gu, ACS Appl. Polym. Mater., 2022, 4, 7537–7546.
24. P. Xu, X. Ji, M. Li and W. Lu, npj Comput. Mater., 2023, 9, 42.
25. C. Rudin, Nat. Mach. Intell., 2019, 1, 206–215.
26. J. Watchorn, D. Burns, S. Stuart and F. X. Gu, Biomacromolecules, 2022, 23, 67–76.
27. E. Jabbari, N. Wisniewski and N. A. Peppas, J. Controlled Release, 1993, 26, 99–108.
28. G. Uccello-Barretta, S. Nazzi, F. Balzano and M. Sansó, Int. J. Pharm., 2011, 406, 78–83.
29. M. P. Brown and C. Royer, Curr. Opin. Biotechnol., 1997, 8, 45–49.
30. L. Wu, W. Shan, Z. Zhang and Y. Huang, Adv. Drug Delivery Rev., 2018, 124, 150–163.
31. A. Popov, E. Enlow, J. Bourassa and H. Chen, Nanomedicine, 2016, 12, 1863–1871.
32. Y. Y. Wang, S. K. Lai, J. S. Suk, A. Pace, R. Cone and J. Hanes, Angew. Chem., Int. Ed., 2008, 47, 9726–9729.
33. A. Suwardi, F. Wang, K. Xue, M. Han, P. Teo, P. Wang, S. Wang, Y. Liu, E. Ye, Z. Li and X. J. Loh, Adv. Mater., 2022, 34, 2102703.
34. S. Stuart, J. Watchorn and F. X. Gu, npj Comput. Mater., 2023, 9, 102.
35. H. E. Gottlieb, V. Kotlyar and A. Nudelman, J. Org. Chem., 1997, 62, 7512–7515.
36. T. C. Le, M. Penna, D. A. Winkler and I. Yarovsky, Sci. Rep., 2019, 9, 265.
37. C. Yan, X. Feng, C. Wick, A. Peters and G. Li, Polymer, 2021, 214, 123351.
38. R. Kumar, N. Le, Z. Tan, M. E. Brown, S. Jiang and T. M. Reineke, ACS Nano, 2020, 14, 17626–17639.
39. R. A. Patel and M. A. Webb, ACS Appl. Bio Mater., 2023 DOI:10.1021/acsabm.2c00962.
40. S. Kosuri, C. H. Borca, H. Mugnier, M. Tamasi, R. A. Patel, I. Perez, S. Kumar, Z. Finkel, R. Schloss, L. Cai, M. L. Yarmush, M. A. Webb and A. J. Gormley, Adv. Healthcare Mater., 2022, 11(10), 2102101.
41. S. Kosuri, C. H. Borca, H. Mugnier, M. Tamasi, R. A. Patel, I. Perez, S. Kumar, Z. Finkel, R. Schloss, L. Cai, M. L. Yarmush, M. A. Webb and A. J. Gormley, Adv. Healthcare Mater., 2022, 11, 2102101.
42. B. Panganiban, B. Qiao, T. Jiang, C. DelRe, M. M. Obadia, T. D. Nguyen, A. A. A. Smith, A. Hall, I. Sit, M. G. Crosby, P. B. Dennis, E. Drockenmuller, M. Olvera de la Cruz and T. Xu, Science, 2018, 359, 1239–1243.
43. M. J. Tamasi, R. A. Patel, C. H. Borca, S. Kosuri, H. Mugnier, R. Upadhya, N. S. Murthy, M. A. Webb and A. J. Gormley, Adv. Mater., 2022, 34, 2201809.
44. C. Kuenneth, A. C. Rajan, H. Tran, L. Chen, C. Kim and R. Ramprasad, Patterns, 2021, 2, 100238.
45. E. R. Antoniuk, P. Li, B. Kailkhura and A. M. Hiszpanski, J. Chem. Inf. Model., 2022, 62, 5435–5445.
46. T. A. Meyer, C. Ramirez, M. J. Tamasi and A. J. Gormley, ACS Polym. Au, 2023, 3, 141–157.
47. S. K. Lai, Y. Y. Wang and J. Hanes, Adv. Drug Delivery Rev., 2009, 61, 158–171.
48. R. Fino, R. Byrne, C. A. Softley, M. Sattler, G. Schneider and G. M. Popowicz, Comput. Struct. Biotechnol. J., 2020, 18, 603–611.
49. T. Sirimongkolkasem and R. Drikvandi, Ann. Data Sci., 2019, 6, 737–763.
50. T. Minka, in Advances in Neural Information Processing Systems, ed. T. Leen, T. Dietterich and V. Tresp, MIT Press, 2000, vol. 13.
51. T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Springer New York, New York, NY, 2nd edn, 2009.
52. D. E. Jones, H. Ghandehari and J. C. Facelli, Beilstein J. Nanotechnol., 2015, 6, 1886.
53. A. Gajewicz, T. Puzyn, K. Odziomek, P. Urbaszek, A. Haase, C. Riebeling, A. Luch, M. A. Irfan, R. Landsiedel, M. van der Zande and H. Bouwmeester, Nanotoxicology, 2018, 12, 1–17.
54. G. Chen, W. J. G. M. Peijnenburg, V. Kovalishyn and M. G. Vijver, RSC Adv., 2016, 6, 52227–52235.
55. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg and others, J. Mach. Learn. Res., 2011, 12, 2825–2830.
56. R. Bro and A. K. Smilde, Anal. Methods, 2014, 6, 2812–2831.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00009e

‡ Both authors contributed equally to this work.

---