Open Access Article
Open Access ArticleAtomic fragment approximation from a tensor network†
Haoxiang
Lin
 and
Xi
Zhu
and
Xi
Zhu
 *
*
School of Science and Engineering, The Chinese University of Hong Kong, Shenzhen, Guangdong, China. E-mail: zhuxi@cuhk.edu.cn
First published on 13th October 2023
Abstract
We propose atomic-fragment approximation (AFA), which uses the tensor network (TN) as a platform to estimate the molecular properties through “adding up” fragment properties. The AFA framework employs graph neural networks to predict the matrix product states (MPSs) for atoms and matrix product operators (MPOs) for bonds, which are then contracted to obtain the full TN for the full molecule. Subsequent neural network layers then predict molecular properties based on the TN contraction outcome. AFA addresses the limitation of density functional approximation (DFA) by reusing previously calculated results and maintaining constant complexity in fragment contraction regardless of the fragment size. We further show that AFA can overcome error accumulation by optimizing the intermediate fragments. AFA demonstrates the ability to predict the reaction intermediates by calculating and comparing the bond-breaking energies. The experiment also showcases excellent accuracy in reaction intermediate prediction and reaction energy prediction.
Introduction
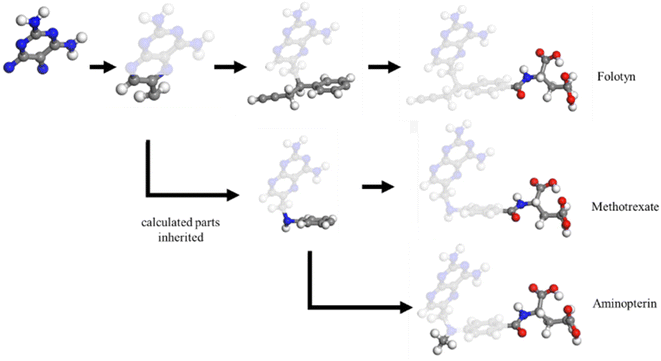
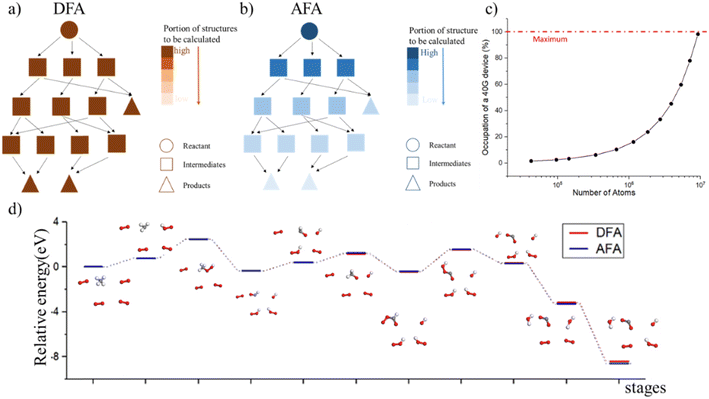
Determining the structure–property relationship is essential for discovering drugs,1 proteins,2 and catalysts.3 The most commonly used method is the parameter-free first principles approach, including solving Schrodinger's equation, the density functional approximation (DFA),4 or density functional theory (DFT). However, DFA lacks transferability from fragments to the whole system, thus similar structures require a duplicate calculation in an “ab initio” way, as shown in Fig. 1. Chemical reaction discovery is the key to the design of new reactions, typically necessitating DFA calculations and specialized expertise.5 Notably, the calculation complexity of DFA scales approximately cubically with molecule size,6,7 making non-reaction regions computationally expensive compared to the reaction region, which is usually much smaller.Many machine learning/deep learning approaches have been developed to address the size and charge problems in DFA.8 Generally, machine learning/deep learning approaches predict by learning patterns in training data, adjusting internal parameters during training, and then applying these learned patterns to make predictions on new, unseen data. One class of these approaches, known as DFA-NNs,9–11 employ deep learning models that utilize the electron-density-related properties as intermediates, primarily for fitting purposes. However, a significant drawback of DFA-NNs is the unavoidable increase in error with system size, typically exhibiting linear growth.7,9,11 This problem is also known as error accumulation. As shown in ESI S1,† even state-of-the-art models like torchANI7 and torchANI-2x12 still encounter this problem of error accumulation. This accumulation makes distinguishing between energy differences caused by different chemical groups and those resulting from calculation errors difficult. To address this issue, one possible solution is to reuse and modify the calculated results for shared fragments. The fragment molecular orbital method (FMO)13 implements this approach by using molecular orbital fragments. However, the intermediate step of FMO includes self-consistent approaches, which we expect to bypass via machine learning.
The tensor network (TN) framework is a geometry of low-order contracted tensors,14,15 whose calculation process is fragment-by-fragment, close to the “adding” of properties. Traditional TN methods are mainly first-principles-based, meaning they rely on fundamental physical laws and principles to derive their results, with few relying on the experiment data. In ref. 16, the authors use TN methods to solve the Hubbard model starting from its Hamiltonian. These ab initio density matrix renormalization group (DMRG) methods are also included in benchmark systems like π-electron systems, main-group and transition metal dimers, and Mn-oxo-salen and Fe-porphine organometallic compounds.17 Meanwhile, the TN is a powerful tool in the area whose correlation or entanglement entropy satisfies the area law,18,19 besides quantum physics,20–22 thus, the TN is expected to be the solution for simulating the “adding” of properties. These traditional tensor network methods greatly inspired us.
In this work, we propose the atomic-fragment approximation (AFA) to provide the structure–property relationship by “adding up” fragments. We first demonstrate the algorithm of AFA. The AFA framework employs a graph neural network to predict the matrix product states (MPSs) for atoms and matrix product operators (MPOs) for bonds, which are then used in a contraction scheme to obtain the TN for the full molecule. A neural network layer is then used to predict the molecular properties based on the TN contraction results. Thanks to the step-by-step contraction scheme of the TN, AFA can realize the “adding up” of fragment properties. AFA is designed to capture the correlation between radicals, which is also applicable to large molecules. This ability makes AFA overcome the limitation of density functional approximation (DFA) by reusing previously calculated results, and we also show that the AFA algorithm can be used for chemical reaction prediction. Through experiments, we show that AFA can reduce the error accumulation in both momenta and real space by optimizing the internal TN states. Error accumulation is a problem that current DFA-simulating NN can never overcome, due to the contaminated correlation of electron density between radicals. We also demonstrate that the AFA algorithm can predict the intermediate with high accuracy and accurately predict the energy barrier for transforming reactants into transient intermediates and then forming the product.
Theoretical background
The tensor network as a platform for estimating molecular properties
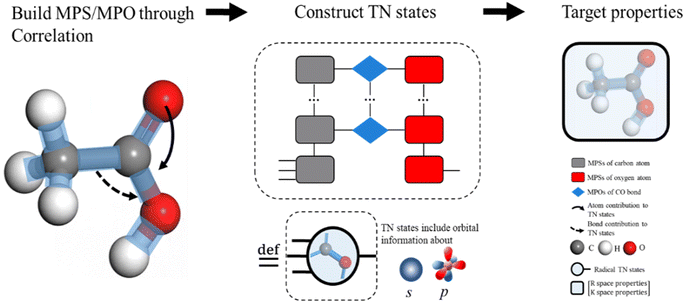
AFA predicts the structure–property relationship through an “adding” process for each fragment, which has three steps. First, we transform the input molecule into a geometry-enhanced representation (GER),23 which focuses on the correlation between bonds and the correlation between atoms. After that, we map the wavefunction ansatz of these fragments into their corresponding TN states, including matrix product states24 (MPSs) for atoms and matrix product operators (MPOs) for bonds. Here atoms and bonds are entirely separated. Finally, these TN states build the tensor network, whose contraction results go through a decoding layer for the target properties. Thanks to the algorithm, AFA can calculate the target properties fragment-by-fragment, which enables the reuse of calculated information.We first transformed the input molecule structure into the geometry-enhanced representation (GER),23 which specifically focuses on two parts, the atom-bond graph G, representing the correlation between atoms, and the bond-angle graph D representing the correlation between bonds. In this process, we utilize the atom-bond graph for the atom's MPS, while the bond-angle graph is employed for the bond's MPO. Detailed information about the GER is given in ESI S2.†
We begin the second step, mapping into TN states, by defining the high-dimensional space of wave function. Here we work in the Born–Oppenheimer approximation; the wavefunction of the entire molecule depends on the atom positions (r1, r2,…, rn), where n is the total number of atoms. The wavefunction ansatz Ψ(molecule) is represented by local map multiplications of MPSs A = {A1, A2,…,An}:
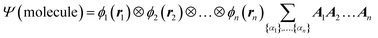 | (1) |
The MPS of atoms A1, A2,…,An (like the grey rounded rectangles for a carbon atom and the red rounded rectangles for an oxygen atom, as shown in Fig. 2, step from correlation to TN states) is estimated through a GNN.
| Ai = fGNN(ri, bG(ri)) | (2) |
The MPOs of bond Oi,j = {O(0)i,j, O(1)i,j,…,O(K)i,j} for atom i and j are estimated through a GNN, whose input is this bond's nearest bond obtained from the bond-angle graph D of the GER:
| O(k)i,j = fGNN,(k)(ri,bD(i,j)) | (3) |
The target property is calculated from the decoding of the obtained TN states. We assume that pairs of atoms have no impact for the target properties unless a bond exists between them. As shown in Fig. 2, step from TN states to target properties, the final prediction P for the desired property comes from the TN contraction results 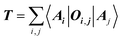 :
:
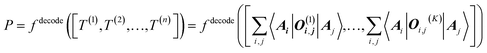 | (4) |
“Add” the fragments
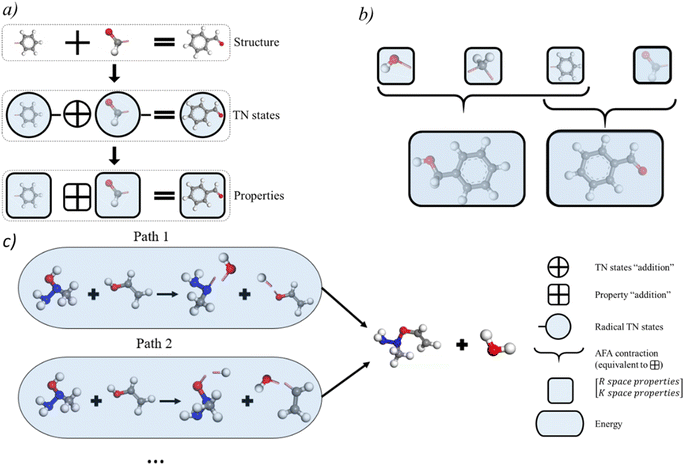
Thanks to the tensor contraction in eqn (4), AFA can “add” the fragment properties to obtain the properties of their combination. These steps evaluate the correlation between various fragment radicals. We use radicals instead of closed-shell molecules because many large molecules are formulated from radicals, and the TN states of radicals encompass vital information for forming bonds with other radicals. As shown in Fig. 2, the contraction of MPSs (grey blocks for the carbon atom and red blocks for the oxygen atom) and MPOs (the blue blocks) gives a radical TN state with three dangling edges. These edges refer to the bonds to be connected. This radical TN state can be used for all molecules that share such fragments. Polarization and charge transfer commonly exist between functional parts of large molecules. When dealing with unknown molecules, we leverage information from molecules with similar radicals to account for these effects. During the fragment “adding” process, the 3D structure can be modified by changing the bond angle and bond length in bG(ri). Therefore, as shown in Fig. 3a, AFA first maps the structure summation into the TN state summation. Mathematically, AFA is trying to add the interaction terms between multiple dependent features: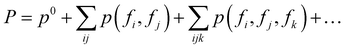 | (5) |
Our methodology draws inspiration from the fragment molecular orbital (FMO) methods, where interactions between multiple fragments are primarily captured by higher-order terms in the FMO expansion.26 The tensor network framework we employ has the capability to account for these fragment interactions, effectively describing the higher-order terms in FMO.
One advantage of AFA is the constant complexity for the contraction of pairs of radical TN states. The computation complexity of AFA must not exceed a constant once all essential molecule component information is provided. The total time complexity of one radical contraction must not exceed the constant Ctotal:
| Ctotal = n × CM+ CNN+ Cb | (6) |
The basic premise for chemical reaction prediction is the prediction of the intermediate and the energy requirement for transforming reactants into transient intermediates and then forming the product. Here we show that AFA has the potential for reaction pathway prediction using one-step reactions. The one-step reactions are shown to achieve a balance of computational cost and reaction coverage in exploring reaction networks. We developed a refined method for chemical reaction prediction using AFA, as illustrated in Fig. 3c, drawing inspiration from YARP's two-step process.27 This process involves identifying the reaction centre by analyzing the structural changes in reactants and subsequently predicting the reaction outcome by considering the identified centre, reactants, and reagents to generate the most probable products.27 Initially, we computed the energies of reactants and products, retaining intermediate fragment results. Subsequently, we identified all bonds within reactants and products, calculating bond-breaking energies while excluding those involved in ring breaking or formation, for which we re-calculated the energy. We proceeded to determine all viable combinations of bond-breaking, approximating bond-breaking energy for each combination and selecting alternatives. The selection criteria encompass the exclusion of high-energy alternatives and the preference for intermediates present in both the lists of reactant and product intermediates. Once we established the resulting molecules for both reactants and products, we compared alternative intermediate lists, opting for intermediates present in both reactant and product lists. Lastly, we assessed the energy of all chosen intermediate molecules, including those with ring breaking or formation, selecting the intermediate with the lowest transition energy as the predicted intermediate. A detailed description of the algorithm is given in ESI S8.†
Methods
To test the accuracy of molecular property prediction, we created the million molecule dataset obtained from QM9,28 bindingDB,29 Chembl,30 and BDE.31 We combine the molecular topology of all these datasets as input molecules. We removed some unstable structures and the number of samples is exactly one million. Properties are calculated through Gaussian 09 (ref. 32) at the PBE level of theory with basis 6-31G, including momentum (K) space properties and real (R) space properties. The unit is converted from Hartree to eV. The properties contain SMILES, the atomic position, the element type, the energy and the orbital energies. Here the orbital energies range from the fifth highest occupied molecular orbital-5 (HOMO-5) to the fifth lowest occupied molecular orbital (LUMO+5). Details on the dataset and unit conversion are given in ESI S9.†The reaction graph depth (RGD1) dataset33 is implemented to test the performance of chemical reaction prediction. It contains 176![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 organic reactions with validated transition states, activation energy, heat of reaction, reactant and product geometries, frequencies, and atom mapping. The reactions cover C, H, O, and N-containing molecules with up to 10 heavy atoms. The data are supplied at the GFN2-xTB and B3LYP-D3/TZVP levels of theory. We randomly selected 20% of the datasets for training and used the remaining 80% for testing. This is because the dataset implements different basis and our model requires fine-tuning.
992 organic reactions with validated transition states, activation energy, heat of reaction, reactant and product geometries, frequencies, and atom mapping. The reactions cover C, H, O, and N-containing molecules with up to 10 heavy atoms. The data are supplied at the GFN2-xTB and B3LYP-D3/TZVP levels of theory. We randomly selected 20% of the datasets for training and used the remaining 80% for testing. This is because the dataset implements different basis and our model requires fine-tuning.
Results
The reduction of error accumulation
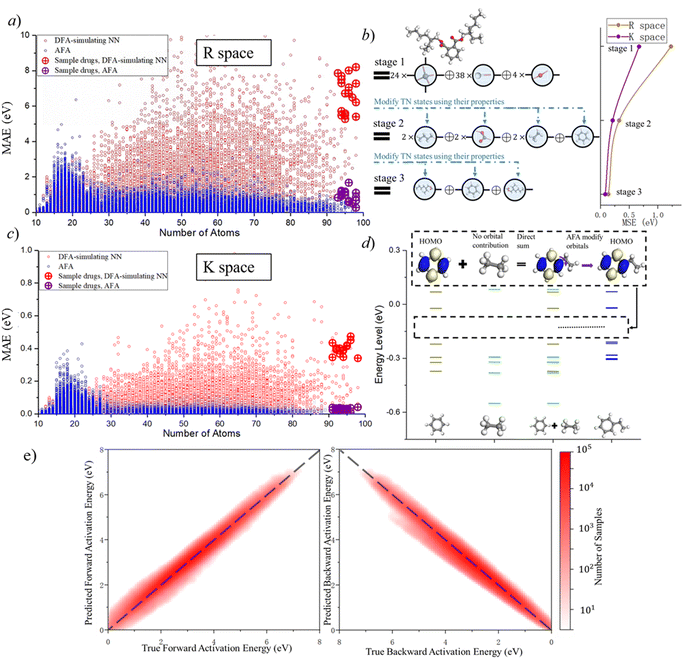
AFA has two major advantages, the reduction of error accumulation and the avoidance of redundant calculation. We will first discuss the advantage of accuracy, while the advantage of calculation will be discussed later. Fig. 4a–d show the R and K space errors for AFA and DFA-simulating NN. In this case, the atomization energy serves as an example of the R space property, while the orbital energy represents the K space property. We select quantum deep field (QDF)9 as an example of DFA-simulating NN due to its transferability and its underlying physics. QDF exhibits excellent transferability from small to large molecules, indicating its ability to reduce error accumulation. Meanwhile, QDF directly uses the electron density as the intermediate. In contrast, most other DFA-NNs typically use properties related to electron density, such as orbitals. Other state-of-the-art models like torchANI7 and ANI-2x12 also exhibit a similar tendency of error accumulation as shown in ESI.† Here the R space error corresponds to the mean absolute error (MAE) for the total energy,| R space error = |Epredict − EDFA| | (7) |
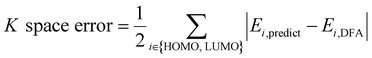 | (8) |
AFA and DFT-NNs exhibit notably different tendencies: with enlarged molecule size, the error for DFA-NNs increases, while the error for AFA stays relatively flat. Here we use the DFT calculation results as the benchmark. Theoretically, DFT-NNs show a similar tendency to DFT since they share the same computation processes. The circle with a plus symbol inside shows the results for selected drugs, whose names are given in ESI S10.† One may notice a peak around the number of atoms 10–20 due to the first appearance of ring molecules. This peak information on this structure cannot be obtained through AFA method. The calculation details for QDF in Fig. 4 are given in ESI S11.† More detailed experiment results and the experiment parameters for AFA are given in ESI S12.†
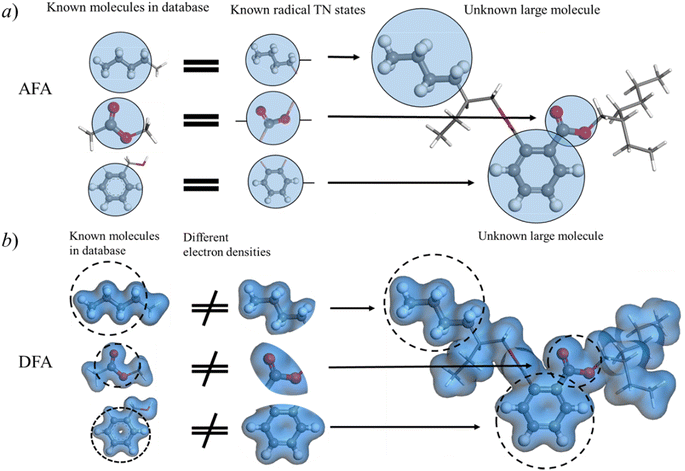
Fig. 4 shows the reduction of error accumulation in R space. This difference in tendency between AFA and DFT-NNs is due to the transferability difference, poor transferability accumulates error, especially with molecular size. DFA focuses on the pseudo-potential of atoms, but AFA focuses on the correlation. The error accumulation is addressed through the modification of intermediate TN states in AFA, as shown in Fig. 4b. For an unknown large molecule like the di(2-ethylhexyl)phthalate (DEHP) molecule, AFA first decomposes this molecule into atomic TN states (the blue circle with edges), like atomic TN states of carbon with four unconnected bonds. Then their combination gives the radical TN states, which refer to stage 2 as mentioned in Fig. 4b. Then AFA further modifies them using their properties. The given TN states go through the neural network layer for the target properties, while the intermediate TN states can also be optimized through backpropagation. Then the intermediate TN states are modified using their properties iteratively until these intermediate radicals cannot merge into a known radical. The merging of radicals refers to the stage in Fig. 4b. This modification process greatly reduces error accumulation.
The reduction of error accumulation also holds in K space. The K space property mainly focuses on the orbital energies. Here we use ethyl benzene as an example, which is made by the contraction of a radical phenyl and the ethyl group. From the training set, AFA obtained the necessary information about these radicals from benzene and ethane. AFA first directly adds the energy level of these two radicals together and then modifies their orbitals. The yellow, blue, and green lines represent the energy levels of benzene, ethyl, and benzene ethyl, respectively. For the HOMO calculation of ethyl benzene, AFA first directly merges the HOMO of benzene with ethyl. Here ethyl contributes no orbital. By modifying the merged orbitals, AFA can predict the HOMO of ethylbenzene. Fig. 4d shows the example of the HOMO. Such a calculation of orbital energy is similar to that of R space property calculation. Therefore, it is not surprising that the reduction of error accumulation still holds in momentum space.
AFA can be used for suggesting potential reaction pathways, which include two aspects: the prediction of intermediates and the energy requirement for transforming reactants into transient intermediates before forming the product. The intermediate prediction accuracy of AFA is 94.34%, while a recent model has an accuracy of 93.8%.34 Here the accuracy is measured as top-2 accuracy, where AFA provides the top two most likely intermediate candidates; if the correct intermediate has the same structure as one of them, we consider the prediction to be accurate. Generally speaking, small effects may affect the possible reaction pathways, so further validation and refinement are required to clearly identify the reaction pathway. Fig. 4e shows the accuracy of forward activation energy and backward activation energy, with the colour bar representing the number of samples. AFA demonstrates strong performance in the chemical reaction prediction for both intermediate candidate prediction and the energy difference calculation.
The avoidance of redundant calculation
AFA's advantage of avoidance of redundant calculation makes it useful in chemical reaction prediction as shown in Fig. 5. Such an advantage also reduces the memory requirement for property prediction as shown in ESI S13.† During the molecular dynamics process, each step is similar to the previous step, with simply one bond breaking or formation. However, if each step is fully calculated, the computation device will be quickly fulfilled, as shown in Fig. 5c. Therefore, the adaption of previously calculated results greatly avoids redundant calculations. However, DFA can hardly re-use the calculated results. Fig. 6d shows the prediction result for methane combustion, AFA has an excellent agreement with DFA results, with an MAE less than 0.01 eV.Discussion
Correlation contamination
AFA captures essential information about radicals from known molecules and transfers this knowledge to unknown large molecules. Here we made a comparison between AFA and DFA to show that current DFA-NN models face challenges when incorporating fragments due to their intermediate, density and related properties. This radical information includes both the radical itself and the correlation between this radical and other radicals. As depicted in Fig. 6a, although di(2-ethylhexyl)phthalate (DEHP) is an unknown large molecule, all its fragments appear in known molecules. We adopted the idea of tight binding, where the nearest radicals contribute most to the target properties. In the training set, besides the radical itself, AFA is trained with the correlation between pairs of radicals. For example, in benzyl alcohol, AFA is trained with radicals like o-phenylene and the correlation between radicals, like the correlation between o-phenylene and the carbinol group as shown in Fig. 6a.However, correlation contamination occurs in the electron density calculations. DFA-NN (like QDF,9 OrbNet,11 and others35) utilizes the electron densities or their related properties for the intermediate step, which impedes the reuse of calculated information. For example, as illustrated in Fig. 6, in the connection area of phenyl and carbinol groups of benzene alcohol, it is challenging to tell which radical contributes the electron density. The iteration of the Kohn–Sham equation simply gives the electron density functional, but it has nothing to say about the correlation between radicals.
Conclusion
In this work, we developed atomic-fragment approximation (AFA), a novel approach for estimating the molecular structure–property relationship by mapping each fragment into its tensor network (TN) states and then contracting them. We show that AFA possesses two key advantages: avoiding redundant calculation and reducing error accumulation. The calculated result for radicals can be re-used for all molecules. The complexity of obtaining a molecule's properties is always constant, independent of the fragment’s size, due to sufficient information on the fragments' TN state. Additionally, we have demonstrated that AFA can overcome error accumulation by optimizing intermediate radical TN states. AFA greatly avoids redundant calculation, and exhibits excellent accuracy in chemical reaction prediction. The MPS-based tensor network can be estimated through quantum computing,20 indicating that a quantum computer can greatly enhance AFA. The AFA framework, combined with artificial intelligence techniques, holds great potential for advancing the field of physics.Data availability
The AFA model related code can be found at https://github.com/hxlin97/AFA.Author contributions
The manuscript was written with contributions from all authors. All authors approved the final version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Funding from the Shenzhen Fundamental Research Foundation (JCYJ20210324142213036) and China's National Natural Science Foundation (grant no. 22075240) is greatly appreciated.References
- J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah and M. Spitzer, Nat. Rev. Drug Discovery, 2019, 18, 463–477 CrossRef CAS PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek and A. Potapenko, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- P. Schlexer Lamoureux, K. T. Winther, J. A. Garrido Torres, V. Streibel, M. Zhao, M. Bajdich, F. Abild-Pedersen and T. Bligaard, ChemCatChem, 2019, 11, 3581–3601 CrossRef CAS.
- A. M. Teale, T. Helgaker, A. Savin, C. Adamo, B. Aradi, A. V. Arbuznikov, P. W. Ayers, E. J. Baerends, V. Barone and P. Calaminici, Phys. Chem. Chem. Phys., 2022, 24, 28700–28781 RSC.
- J. Burés and I. Larrosa, Nature, 2023, 613, 689–695 CrossRef PubMed.
- F. Brockherde, L. Vogt, L. Li, M. E. Tuckerman, K. Burke and K.-R. Müller, Nat. Commun., 2017, 8, 1–10 CrossRef CAS PubMed.
- X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, J. Chem. Inf. Model., 2020, 60, 3408–3415 CrossRef CAS PubMed.
- J. Kirkpatrick, B. McMorrow, D. H. P. Turban, A. L. Gaunt, J. S. Spencer, A. G. D. G. Matthews, A. Obika, L. Thiry, M. Fortunato, D. Pfau, L. R. Castellanos, S. Petersen, A. W. R. Nelson, P. Kohli, P. Mori-Sánchez, D. Hassabis and A. J. Cohen, Science, 2021, 374, 1385–1389 CrossRef CAS PubMed.
- M. Tsubaki and T. Mizoguchi, Phys. Rev. Lett., 2020, 125, 206401 CrossRef CAS PubMed.
- H. Lin, S. Ye and X. Zhu, Carbon, 2022, 186, 313–319 CrossRef CAS.
- Z. Qiao, M. Welborn, A. Anandkumar, F. R. Manby and T. F. Miller III, J. Chem. Phys., 2020, 153, 124111 CrossRef CAS PubMed.
- C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202 CrossRef CAS PubMed.
- D. G. Fedorov, T. Nagata and K. Kitaura, Phys. Chem. Chem. Phys., 2012, 14, 7562–7577 RSC.
- R. Orús, Ann. Phys., 2014, 349, 117–158 Search PubMed.
- R. Orús, Nat. Rev. Phys., 2019, 1, 538–550 CrossRef.
- J. P. LeBlanc, A. E. Antipov, F. Becca, I. W. Bulik, G. K.-L. Chan, C.-M. Chung, Y. Deng, M. Ferrero, T. M. Henderson and C. A. Jiménez-Hoyos, Phys. Rev. X., 2015, 5, 041041 Search PubMed.
- R. Olivares-Amaya, W. Hu, N. Nakatani, S. Sharma, J. Yang and G. K.-L. Chan, J. Chem. Phys., 2015, 142, 034102 CrossRef PubMed.
- M. M. Wolf, F. Verstraete, M. B. Hastings and J. I. Cirac, Phys. Rev. Lett., 2008, 100, 070502 CrossRef PubMed.
- J. Eisert, M. Cramer and M. B. Plenio, Rev. Mod. Phys., 2010, 82, 277 CrossRef.
- G. Vidal, Phys. Rev. Lett., 2007, 99, 220405 CrossRef CAS PubMed.
- W. Huggins, P. Patil, B. Mitchell, K. B. Whaley and E. M. Stoudenmire, Quantum Sci. Technol., 2019, 4, 024001 CrossRef.
- I. Convy, W. Huggins, H. Liao and K. B. Whaley, Mach. Learn.: Sci. Technol., 2022, 3, 015017 Search PubMed.
- X. Fang, L. Liu, J. Lei, D. He, S. Zhang, J. Zhou, F. Wang, H. Wu and H. Wang, Nat. Mach. Intell., 2022, 1–8 Search PubMed.
- U. Schollwöck, Ann. Phys., 2011, 326, 96–192 Search PubMed.
- R. Nesbet, Phys. Rev., 1958, 109, 1632 CrossRef CAS.
- S. Tanaka, Fragment Molecular Orbital Method as Cluster Expansion, Recent Advances of the Fragment Molecular Orbital Method: Enhanced Performance and Applicability, 2021, pp. 3–14 Search PubMed.
- Q. Zhao and B. M. Savoie, Nat. Comput. Sci., 2021, 1, 479–490 CrossRef.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Sci. Data, 2014, 1, 1–7 Search PubMed.
- T. Liu, Y. Lin, X. Wen, R. N. Jorissen and M. K. Gilson, Nucleic Acids Res., 2007, 35, D198–D201 CrossRef CAS PubMed.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich and B. Al-Lazikani, Nucleic Acids Res., 2012, 40, D1100–D1107 CrossRef CAS PubMed.
- P. C. St John, Y. Guan, Y. Kim, B. D. Etz, S. Kim and R. S. Paton, Quantum chemical calculations for over 200,000 organic radical species and 40,000 associated closed-shell molecules, Sci. Data, 2020, 7, 1–6 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Q. Zhao, S. M. Vaddadi, M. Woulfe, L. A. Ogunfowora, S. S. Garimella, O. Isayev and B. M. Savoie, Sci. Data, 2023, 10, 145 CrossRef CAS PubMed.
- S. Choi, Nat. Commun., 2023, 14, 1168 CrossRef CAS PubMed.
- More references for DFA-NN are written in Ref_of_DFA_simulating_NN.txt.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00130j |
| This journal is © The Royal Society of Chemistry 2023 |