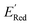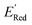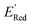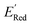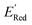Open Access Article
Open Access ArticleIn silico discovery of a new class of anolyte redoxmers for non-aqueous redox flow batteries†
Akash
Jain
 ab,
Ilya A.
Shkrob
ab,
Ilya A.
Shkrob
 ac,
Hieu A.
Doan
ac,
Hieu A.
Doan
 ab,
Lily A.
Robertson
ab,
Lily A.
Robertson
 ac,
Lu
Zhang
ac,
Lu
Zhang
 ac and
Rajeev S.
Assary
ac and
Rajeev S.
Assary
 *ab
*ab
aJoint Center for Energy Storage Research (JCESR), Argonne National Laboratory, Lemont, IL 60439, USA. E-mail: assary@anl.gov; Tel: +1-630-252-3536
bMaterials Science Division, Argonne National Laboratory, Lemont, IL 60439, USA
cChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL 60439, USA
First published on 20th July 2023
Abstract
Organic non-aqueous redox flow batteries (O-NRFBs) are emerging devices for storing intermittent renewable energy in the electric grid. For this application, redox-active organic molecules (redoxmers) are required that have suitable redox potentials, excellent solubility in electrolytes, and adequate stability in all states of charge. Due to the large available design space of redoxmers, machine learning is useful to identify optimal molecules that combine these properties. In this contribution, we propose a probabilistic algorithm that simultaneously expands structural diversity in a molecular library of redoxmer derivatives and limits it to synthetically accessible structures. A Bayesian optimization-based active learning algorithm is then used to discover promising molecules with a minimal number of computationally expensive quantum chemistry calculations. To demonstrate the power of this approach, we investigated derivatives of a redox active molecule, 2,1,3-benzothiadiazole. A library of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 molecules was explored, and a new class of tricyclic derivatives with unusually low reduction potentials was discovered. We analyze and report the correlation between low reduction potentials, cyclic moieties, and positional specificity of functional groups. In addition, we report the electrochemical stability of selected molecules that display low reduction potentials and suggested molecules for the experimental validation of their promising electrochemical properties.
500 molecules was explored, and a new class of tricyclic derivatives with unusually low reduction potentials was discovered. We analyze and report the correlation between low reduction potentials, cyclic moieties, and positional specificity of functional groups. In addition, we report the electrochemical stability of selected molecules that display low reduction potentials and suggested molecules for the experimental validation of their promising electrochemical properties.
1 Introduction
Organic non-aqueous redox flow batteries (O-NRFBs) are promising energy storage devices for integrating intermittent renewable energy sources into the electric grid. The attractive features of these devices include their relatively low materials cost, scalability, wider electrochemical stability windows compared to aqueous electrolyte solutions, and large design space of organic redox-active molecules (redoxmers).1,2 However, their adoption on a commercial scale is hindered by low energy density and short battery cycle life.2–5 That, in turn, can be traced to the difficulty of finding redoxmers that satisfy numerous requirements imposed on the materials that include, but are not limited to, the synthetic ease, high solubility in electrolytes, exceptional stability in all states of charge, and the extreme redox potentials that take advantage of the wide electrochemical windows. Such requirements can be difficult to harmonize and require exhaustive screening of large chemical spaces.The volumetric energy density of the O-NRFB is determined by the cell voltage and the molar concentration of redoxmers.6 The open circuit voltage is given by the difference in the redox potentials of the catholyte (positive charge storage) and anolyte (negative charge storage) molecules.2,3 Thus, one way to achieve a higher energy density is to lower the reduction potential of the anolyte and increase the oxidation potential of the catholyte. Generally, these extreme redox potentials decrease the stability of charged molecules.7 Radical ions of organic molecules react with each other, parent molecules, and other species in solution,8 and these side reactions decrease the cycle life of a battery. Further loss of capacity involves the crossover of redoxmer molecules through the membranes that separate cell compartments.9 For these reasons,1,8,10,11 finding redoxmers that have extreme redox potentials and stable charged states is a major challenge for O-NRFB development.
In the literature, the redox potential, solubility, and stability of various all or partially organic-derived redoxmers such as metallocene,12–14 dialkoxy benzene,8,15,16 nitroxide radicals,17–21 and other molecules22 have been modified through derivatization of core molecules, which are typically aromatic rings with pi-systems that can accommodate extra charges. Polar substituents improve the solubility of these molecules in electrolytes while electron-donating or electron-withdrawing substituents tune the redox potential. Thus, for each core molecule there exists a large space of derivatives to explore. One promising discovery strategy is high-throughput screening using computational methods such as density functional theory (DFT) calculations to compute the properties of interest.23–25 However, such calculations can be expensive and time-consuming. To further accelerate materials screening, machine learning (ML) models have been employed for extremely fast property evaluation. Several recent studies have developed ML models to predict material properties such as adsorption energies26,27 and melting temperature.28,29 However, the accuracy of such methods depends on the diversity, quantity, and quality of the data used for model training, so massive experimental data and/or computations are still required to train the ML models for reliable predictions.30–32
Among various ML methods, active learning (AL) algorithms are particularly promising for problems in which data sampling is limited.33–42 The AL algorithm uses a surrogate model and a global optimization routine to explore a search space with the minimal number of evaluations.42–44 Several studies have applied the AL to the discovery of new materials with optimal properties. For example, Kim et al.36 and Jablonka et al.35 discovered polymers with optimal physical properties, Bassman et al.34 have identified layered materials with optimal band gaps, Xue et al.37 suggested shape-memory alloys with low thermal hysteresis, and Janet et al.45 identified transition metal complexes for aqueous redox flow batteries. Recently, Doan and co-workers,38,39 used the AL algorithms to discover high-potential redoxmers and optimize multiple properties such as reduction potential, solvation free-energies, and absorption wavelength of redox active materials. Despite these pertinent demonstrations of the AL methods for molecules (and materials) design, we find the lack of constraints on structural complexity and synthesizability in the AL algorithm often leads to discovered species of limited practical interest because of the complex structure and complex synthesis route.38,39
One approach to overcome this problem is to use AL algorithm with a constraint such as synthesizability scores (retrosynthetic accessibility score (RAScore)46 or synthetic Bayesian accessibility (SYBA) score47) to discover molecules that are more likely synthesizable as shown by Hickman et al.42 Other approach is to apply the AL algorithm to a search space that contains synthetically accessible molecules. Generative algorithms are shown to be promising methods to generate novel molecules and can be used to create a molecular search space besides molecular enumeration. However, generative methods often generate molecules that are not synthesizable.48–51
Our approach to finding synthesizable molecules with AL algorithm is to engineer a search space that mostly contains structurally diverse yet simple molecules. The approach resembles planning like a synthetic chemist in which larger structures are built sequentially by the addition of chemical blocks or synthons, and the growth of a molecule is interrupted by cyclization of the growing chains. Thus, we propose a synthesis-aware rule-based molecule generation algorithm (SRMGA) that probabilistically generates a large library of preoptimized derivatives. We use this library to identify promising redoxmer candidates in a minimal number of DFT calculations with AL.
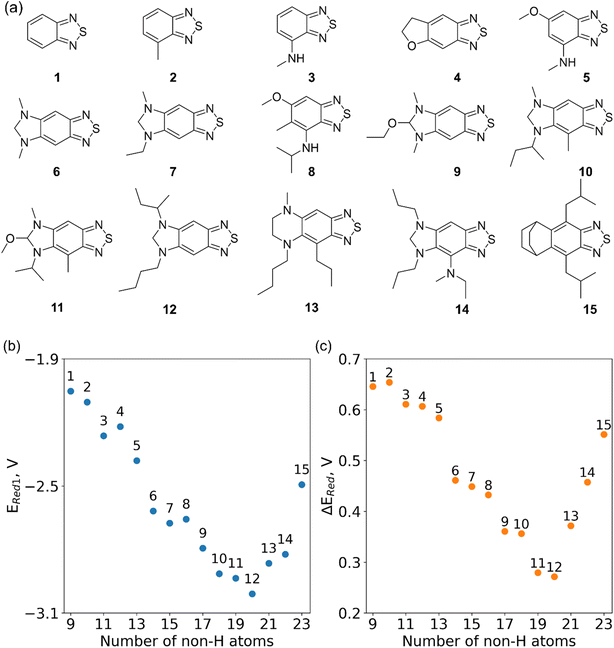
To demonstrate the effectiveness of this approach, we chose 2,1,3-benzothiadiazole (BTZ), a promising anolyte that has been extensively studied because of its low reduction potential, low molecular weight, high solubility, and outstanding electrochemical cycling stability.7,52,53 In this study, we aimed to find synthetically accessible BTZ derivatives with the lowest one-electron reduction potentials. Here we report how the combined use of SRMGA and AL methods led us to the discovery of a new class of tricyclic BTZ molecules with anomalously low reduction potentials. We also show that low reduction potential molecules are associated with extra cyclic moieties and a specific placement of functional groups at benzene ring of BTZ molecule. In addition, we evaluate the electrochemical stability of 15 selected molecules using the first and second reduction potentials, and proton affinities of radical anions, and show the tradeoff between the low reduction potential and electrochemical stability of molecules.
The remainder of this paper is organized as follows. In Section 2, we provide details of DFT calculations, SRMGA, and the AL workflow. In Section 3, we discuss BTZ molecular library generation with SRMGA, exploration of a molecular library with AL algorithm, the correlation between reduction potential and chemical structure of low reduction potential molecules, electrochemical stability of 15 selected anolyte candidates, and provide retrosynthetic analysis of a promising scaffold molecule. Finally, in Section 4, we provide a summary of our work and concluding remarks.
2 Methods
2.1. Density functional theory (DFT) computations
The calculations were performed using the Gaussian 16 software package54 at the B3LYP/6-31+G(d,p) level of theory.55,56 The acetonitrile solvent was simulated using the conductor-like polarizable continuum model (CPCM).57,58 Geometry optimization and vibration frequency calculations of neutral and charged molecules were performed in the solvent dielectric to calculate the electronic energies at T = 0 K and Gibbs free energies at T = 298 K. The first reduction potential of a molecule with or without the vibration frequency corrections (designated ERed1 and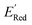 , respectively), and the second reduction potential (ERed2) were calculated using eqn (1)–(3),
, respectively), and the second reduction potential (ERed2) were calculated using eqn (1)–(3),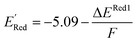 | (1) |
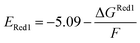 | (2) |
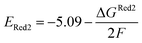 | (3) |
| ΔGH+ = GAH − GA− − GH+, | (4) |
2.2. The molecular library generation
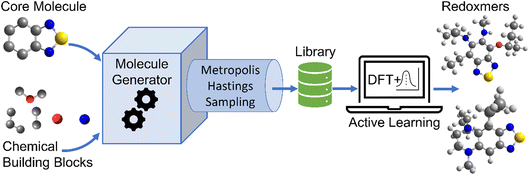
The schematic of molecular generation from a core structure, development of a database and molecular discovery with AL is shown in Scheme 1. Specifically, it shows how a core molecule (or a molecular scaffold) and building blocks are combined by a generator complemented with a Metropolis type sampler that biases the process to simpler molecules. After the molecular generation, AL is used to identify the promising molecules with the minimum number of DFT calculations.To populate the molecular library, we devised the SRMGA illustrated in Fig. 1, in which the functional groups and chemical building blocks are added randomly to a molecular scaffold (or core molecule), with a bias to smaller building blocks. The SRMGA starts with a molecular scaffold (BTZ molecule shown in Fig. 1), functional groups, and chemical building blocks provided in Tables 1 and 2. The parent BTZ molecule has four possible derivatization sites at carbons 4 to 7 in the benzene ring. As we seek to further reduce the redox potential of this molecule, the substituents (provided in Tables 1 and 2) are chosen as electron donating or neutral groups, such as the alkyl, amino, alkoxy, amide, and carboxylate, that are known to decrease the reduction potential of molecules. The structural casts of these groups are given in Table 1. All casts and chemical building blocks are presented in the symbolic Simplified Molecular-Input Line-Entry System (SMILES) format so that the molecule building operations involve symbolic manipulation of SMILES strings using a Python program based on the standard RDKit routines.60 For example, the cast for an amino group would be –NXY, where synthetic blocks X and Y are growth points shown by orange circles in Fig. 1 and chosen from Table 2. This set includes the H atom, straight and branched alkyl groups, and functional groups such as polyethylene oxide (CCOX) or amines (CCNXY) that are added to make a molecule more soluble in acetonitrile. These blocks contain new growth points (orange circles in Fig. 1), so the chains can elongate and branch out (Fig. 1). The probability of randomly drawing chemical building blocks (Pd) from Table 2 is provided for each chemical building block. The SRMGA uses the Pd values to bias the selection of simple chemical building blocks for structure growth. The chemical building blocks with the higher Pd get selected more frequently than the chemical building blocks with smaller Pd values. Therefore, smaller (and simple) chemical building blocks (like H, C, and CC) were given higher Pd than larger (and complex) chemical building blocks (like CCN(Y)(Y) and CCOY). By recursively adding (“daisy chaining”) the synthetic blocks, the growth points are terminated or substituted further until no such points remains (Fig. 1). Provisions are made so that the chains can “recombine” with one of the initial growth sites making cycles (Fig. 1). We want to highlight that additional cycles generated by the SRMGA are saturated and not aromatic, therefore in this work the molecular search space does not include BTZ molecules with an additional aromatic or unsaturated cycle. Although additional aromatic or unsaturated cycles may modify the BTZ properties, we do not study them here and it will be discussed elsewhere. The blocks and chains are added either non-symmetrically or symmetrically (as the non-symmetric molecules could be more difficult to synthesize). The functional groups and synthetic blocks are chosen at random from Tables 1 and 2, i.e., therefore the generator is probabilistic. For that reason, duplicates can occur and need to be removed by comparing the canonical SMILES. As the generation is fast, this duplication is a minor computational expense compared to DFT calculations.
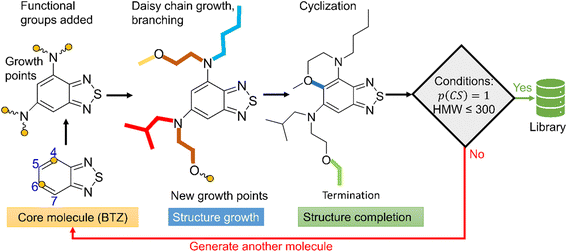 | ||
| Fig. 1 Workflow of SRMGA. In the example shown above, a core molecule (BTZ) has two sites tagged for substitution (orange circles). Groups listed in Table 1 (in this case, the amine groups, –NXY) are added to these points at random. Each cast adds two more growth points (blocks X and Y). Subsequent growth with chemical building blocks (Table 2) elongates the groups through recursive daisy chain growth, branching or cyclization. This growth stops when all growth points are terminated with blocks containing no growth points. A molecule satisfying all user-defined rules is added to the library, otherwise the process is repeated. In the diagram, HMW is the molecular weight (g mol−1) of non-hydrogen atoms in a molecule, and p(CS) is defined in eqn (5). | ||
| Cast | Comment |
|---|---|
| H | Hydrogen atom |
| X | Growth point (any chemical block in Table 2) |
| Y | Growth point (any chemical block in Table 2 except H atom) |
| N(X)(Y) | Amine cast with growth points |
| OY | Alkoxy cast with growth points |
\[N+](X)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C([O–])/Y C([O–])/Y |
Amide cast (zwitterionic form) with growth points |
OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)Y O)Y |
Carboxylate cast with growth points |
| SMILES | P d |
|---|---|
| H | 0.47 |
| C | 0.24 |
| CC | 0.12 |
| CCC | 0.04 |
| C(C)C | 0.04 |
| CCCC | 0.02 |
| C(C)CC | 0.02 |
| CC(C)C | 0.02 |
| CCOY | 0.02 |
| CCN(Y)(Y) | 0.01 |
The SRMGA keeps track of all additions to a molecular scaffold with the complexity score (CS). The core molecule has a CS score of zero (CS = 0). The CS value is incremented by one each time a non-hydrogen (non-H) substituent (for example –CH3, or –OCH3) is added to the molecule. In this fashion, the CS provides a crude estimate for the synthetic complexity of a molecule. It is important to note that the value of CS is determined by the order in which substituents are added to a core molecule. Additionally, it is possible to derive a molecule from the core molecule through multiple routes as the selection of chemical blocks and functional groups is random. As a result, a given derivative molecule may have different CS values in different independent runs of SRMGA, even if using the same core molecule.
As mentioned earlier, the goal of the SRMGA is to bias molecular search towards less complex molecules. While providing explicit bias towards smaller building blocks in Table 2 helps to reduce complexity, there is still overabundance of synthetically inaccessible structures with high CS. While we need complex structures in the library, they can overrun the search space with these molecules. Taking inspiration from the Metropolis–Hastings sampling61 mentioned in Fig. 1, we define a condition, p(CS), to accept (p(CS) = 1) or reject (p(CS) = 0) a molecule in the library based on its complexity score,
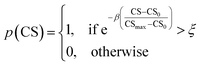 | (5) |
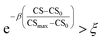 . In eqn (5), β is the penalizing factor that is analogous to the Boltzmann factor 1/kT in thermodynamics. The higher is the “temperature” (the smaller is β > 0), the weaker is the penalization of molecular complexity.
. In eqn (5), β is the penalizing factor that is analogous to the Boltzmann factor 1/kT in thermodynamics. The higher is the “temperature” (the smaller is β > 0), the weaker is the penalization of molecular complexity.
Besides the p(CS), the SRMGA can also check if a new molecule satisfies other user-defined rules (see Section 3.1). For example, we can limit the number of atoms and/or molecular weight of a molecule. The latter is important as larger molecules (due to their excessive molar volume) cannot satisfy volumetric energy density requirements in O-NRFBs.15,16 If a new molecule satisfies all user-defined rules, the SRMGA checks for duplicates and adds it to the library, otherwise, it starts the process over again until we get desired number of molecules in the library (Fig. 1).
2.3. The active learning (AL) methodology
The next step is using machine learning to navigate the large library generated by SRMGA. To this end, we used the Bayesian optimization-based active learning algorithm illustrated in Fig. 2. In this algorithm, each molecule is first represented by a vector of 49 descriptors (consistent with ref. 37 and 38) which was generated from its canonical SMILES using the RDKit software (see Table S1†).60 To train a surrogate model faster with a reasonable accuracy we reduced the number of descriptors using the principal component analysis. Specifically, we used 16 principal components as features (Fig. S3†), Xij, that explain at least 99% variance in the data, where Xij is the ith principal component of molecule j. To start the algorithm, we select at random n molecules (e.g., n = 10) from the SRMGA library and use DFT to compute their properties of interest here reduction potential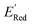 . From eqn (1) and (2), we note that
. From eqn (1) and (2), we note that 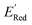 and ERed1 differ only by the vibrational frequency and entropy corrections, and our calculations show the value of these corrections
and ERed1 differ only by the vibrational frequency and entropy corrections, and our calculations show the value of these corrections 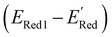 has an average value of 0.1 eV with a small variance (Fig. S20†). Thus, we omitted vibrational frequency calculation and used
has an average value of 0.1 eV with a small variance (Fig. S20†). Thus, we omitted vibrational frequency calculation and used 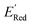 instead of ERed1 for computational efficiency and faster screening of molecules.
instead of ERed1 for computational efficiency and faster screening of molecules.
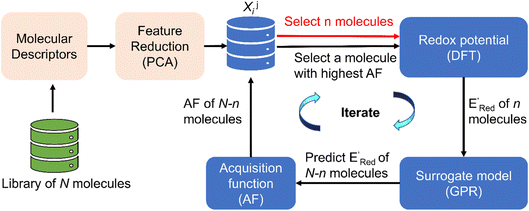 | ||
| Fig. 2 The AL algorithm to discover promising redoxmers with optimal redox potential in a library of N molecules. AF is the acquisition function (eqn (6)), DFT is the density functional theory calculations, PCA is the principal component analysis, and GPR is the Gaussian process regression. Xij are the reduced features (principal components with the index i) associated with a molecule with the index j. | ||
Using 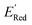 values as labels (the dependent variable) and 16 principal components of 49 molecular features (as independent variables) of these n molecules, we train a surrogate model (a Gaussian process regression model, or GPR) to predict the mean (µ) and standard deviation (σ) of the
values as labels (the dependent variable) and 16 principal components of 49 molecular features (as independent variables) of these n molecules, we train a surrogate model (a Gaussian process regression model, or GPR) to predict the mean (µ) and standard deviation (σ) of the 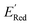 values for the remaining molecules in the library. Further, we use an acquisition function (eqn (6)) to select, based on GPR predicted µ and σ values, the next molecule(s) to be evaluated for
values for the remaining molecules in the library. Further, we use an acquisition function (eqn (6)) to select, based on GPR predicted µ and σ values, the next molecule(s) to be evaluated for 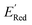 calculation and to optimize the objective function (minimize
calculation and to optimize the objective function (minimize 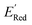 ) in the labeled data set (molecules with DFT calculated
) in the labeled data set (molecules with DFT calculated 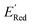 ). Among several acquisition functions, we selected the expected improvement (EI), which has been successfully used for redoxmer discovery.38,39 We calculate the EI of each molecule in the library and select the molecule with the highest EI for the next DFT calculation. After this DFT calculation, we add the selected molecule to the labeled dataset to complete one iteration of the AL algorithm.
). Among several acquisition functions, we selected the expected improvement (EI), which has been successfully used for redoxmer discovery.38,39 We calculate the EI of each molecule in the library and select the molecule with the highest EI for the next DFT calculation. After this DFT calculation, we add the selected molecule to the labeled dataset to complete one iteration of the AL algorithm.
In subsequent iterations, we use the updated labeled dataset to retrain the GPR model and predict the EI of all molecules to select another unlabeled molecule. With more iterations of the AL algorithm, we add new data points in the labeled data set that typically improve the accuracy of GPR model predictions so that the AL algorithm finds more optimal molecules for labeling (next DFT calculations). We stop the AL algorithm iterations when we either obtain several molecules with the 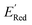 in the desired low range or use up our computational resources. For a more detailed description of this AL algorithm, we refer readers to Agarwal and Doan et al.38,39
in the desired low range or use up our computational resources. For a more detailed description of this AL algorithm, we refer readers to Agarwal and Doan et al.38,39
Here, we used GPR models62 with the Matérn kernel with the smoothness parameter (ν) equal to 1.5 (Fig. S4†) by utilizing GPyTorch package.63 The EI acquisition function is given by,34
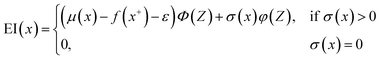 | (6) |
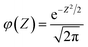 | (7) |
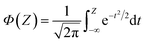 | (8) |
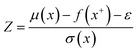 | (9) |
3 Results and discussion
3.1. Molecular library generation
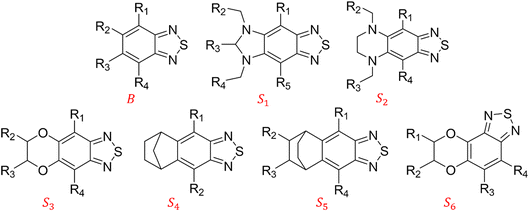
We constructed a diverse library of BTZ based molecules using SRMGA. The parent molecule (B in Fig. 3) is decorated with cyclic and acyclic functional groups. Additionally, in Fig. 3, we show additional scaffolds S1 to S6, (SMILES in Table S2†) that were originally identified among the cyclic structures originating from the parent molecule (B in Fig. 3) and were selected to generate new molecules for closer scrutiny to understand the effect of adding extra cyclic moieties on the reduction potential. In our molecular library, the BTZ derivatives were accepted if they satisfied the following conditions:(1) p(CS) = 1, where CS0 = 3, CSmax = 8, and β = 5 in eqn (5).
(2) Molecular weight of non-hydrogen atoms ≤ 300 g mol−1.
(3) No hydroxylamine, hydroxyl, and carboxyl groups.
Regarding rules 3, we excluded the molecules that can protonate BTZ radical anions.10,53,64
In Fig. 4, the “bird's-eye” view of a diverse library of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 molecules is shown. In this library, 78% molecules are generated using the original BTZ core, B (Fig. 4a), while 22% of the molecules are generated from other scaffolds. In the library, fractions of S1 to S6 molecules are smaller than B, because SRMGA is biased towards simpler molecules that satisfy all three rules mentioned in the preceding paragraph, hence many S1 to S6 derivative molecules were rejected by SRMGA. The heavy atom molecular weight varies between 132 and 298 g mol−1. Complexity wise, 33% molecules have CS > 6, while 3% molecules have CS ≤ 3 (Fig. 4b). The number of heteroatoms (nHt) ranges from three (as in the parent molecule) to nine; 97% molecules have four to seven heteroatoms (Fig. 4c). While most of these molecules (56%) are bicyclic (Fig. 4d), 34% molecules are tricyclic and 10% are polycyclic.
500 molecules is shown. In this library, 78% molecules are generated using the original BTZ core, B (Fig. 4a), while 22% of the molecules are generated from other scaffolds. In the library, fractions of S1 to S6 molecules are smaller than B, because SRMGA is biased towards simpler molecules that satisfy all three rules mentioned in the preceding paragraph, hence many S1 to S6 derivative molecules were rejected by SRMGA. The heavy atom molecular weight varies between 132 and 298 g mol−1. Complexity wise, 33% molecules have CS > 6, while 3% molecules have CS ≤ 3 (Fig. 4b). The number of heteroatoms (nHt) ranges from three (as in the parent molecule) to nine; 97% molecules have four to seven heteroatoms (Fig. 4c). While most of these molecules (56%) are bicyclic (Fig. 4d), 34% molecules are tricyclic and 10% are polycyclic.
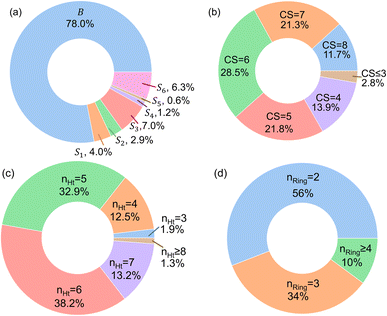 | ||
Fig. 4 The bird's-eye view of our molecular library (35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 compounds). The fractions of (a) each scaffold that are shown in Fig. 3, (b) the complexity score (CS) of the molecules, (c) the number of hetero atoms (nHt), and (d) the total number of aliphatic and aromatic rings (nRing). 500 compounds). The fractions of (a) each scaffold that are shown in Fig. 3, (b) the complexity score (CS) of the molecules, (c) the number of hetero atoms (nHt), and (d) the total number of aliphatic and aromatic rings (nRing). | ||
3.2. Application of the active learning (AL) method to a library of computed molecules
We first applied the AL algorithm to a subset of 1500 randomly selected molecules from our library of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 to demonstrate that the AL algorithm can find the global minimum in
500 to demonstrate that the AL algorithm can find the global minimum in 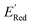 in a small number of iterations and exclusively select molecules with low
in a small number of iterations and exclusively select molecules with low 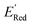 . To this end, using DFT, we calculated the
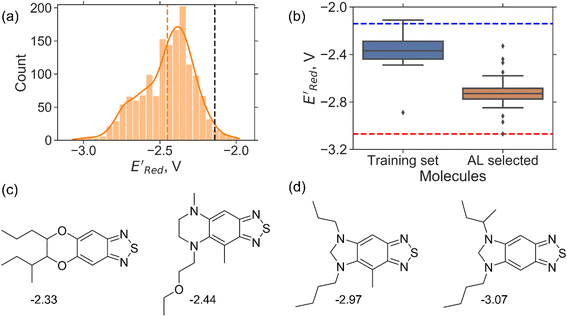
. To this end, using DFT, we calculated the 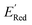 for all 1500 molecules. A summary of the DFT calculations including distribution of computed reduction potentials and selected BTZ molecules is shown in Fig. 5. We note that the SMILES and
for all 1500 molecules. A summary of the DFT calculations including distribution of computed reduction potentials and selected BTZ molecules is shown in Fig. 5. We note that the SMILES and 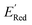 for these 1500 molecules are provided in the ESI,† and additional analyses of properties were shown in Fig. S1 and S2.† The computed
for these 1500 molecules are provided in the ESI,† and additional analyses of properties were shown in Fig. S1 and S2.† The computed 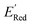 of the parent BTZ molecule is −2.14 V; the computed
of the parent BTZ molecule is −2.14 V; the computed 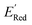 (redox potentials) span −3.07 V to −1.98 V (see the histogram in Fig. 5a and the map plot in Fig. S2(c)).† From Fig. 5a, the molecules with the lowest 10% of the
(redox potentials) span −3.07 V to −1.98 V (see the histogram in Fig. 5a and the map plot in Fig. S2(c)).† From Fig. 5a, the molecules with the lowest 10% of the 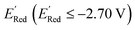 almost exclusively had the S1 scaffolds, precisely ∼87% (142 out of 164). Using the RDKit package,60 we generated molecular descriptors for each molecule (Table S1†) and then selected 16 principal components (PCs) that accounted for 99.3% of the cumulative variance in the DFT data (Fig. S3†). These PCs were used as features in the AL search as described in Section 2.3.
almost exclusively had the S1 scaffolds, precisely ∼87% (142 out of 164). Using the RDKit package,60 we generated molecular descriptors for each molecule (Table S1†) and then selected 16 principal components (PCs) that accounted for 99.3% of the cumulative variance in the DFT data (Fig. S3†). These PCs were used as features in the AL search as described in Section 2.3.
We started the AL algorithm by randomly sampling 10 molecules from the dataset of 1500 molecules and performed 75 iterations to sample new molecules from the remaining set of 1490 molecules. Note that since all 1500 molecules have been evaluated for 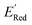 , each iteration does not invoke a DFT calculation but instead executes a look-up function. To test the method convergence within 75 iterations, the AL algorithm was repeated 20 times using different initial training sets (Fig. S5†). In 9 out of 20 runs, the AL algorithm found the global minimum in less than 75 iterations; in the remaining 11 trials, the AL algorithm finished within 0.1 V from the global minimum. Hence, we found 75 iterations are sufficient for the AL algorithm to reach close to the global minima in this data. Fig. 5b shows one of the AL runs. In the initial training set, the
, each iteration does not invoke a DFT calculation but instead executes a look-up function. To test the method convergence within 75 iterations, the AL algorithm was repeated 20 times using different initial training sets (Fig. S5†). In 9 out of 20 runs, the AL algorithm found the global minimum in less than 75 iterations; in the remaining 11 trials, the AL algorithm finished within 0.1 V from the global minimum. Hence, we found 75 iterations are sufficient for the AL algorithm to reach close to the global minima in this data. Fig. 5b shows one of the AL runs. In the initial training set, the 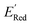 varied between −2.89 and −2.11 V. In the AL-selected dataset of 75 molecules, the
varied between −2.89 and −2.11 V. In the AL-selected dataset of 75 molecules, the 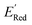 varied between −3.07 and −2.33 V, with a median
varied between −3.07 and −2.33 V, with a median 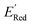 of −2.70 V which shows that AL algorithm mostly selected molecules with low
of −2.70 V which shows that AL algorithm mostly selected molecules with low 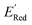 from a narrow window of −3.07 V ≤
from a narrow window of −3.07 V ≤ 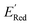 ≤ −2.70 V (lowest 10% of
≤ −2.70 V (lowest 10% of 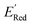 , Fig. 5a). The AL algorithm also found the global minimum of −3.07 V in just 14 iterations (Fig. S5(a)†). Structural formulae for the found molecules with the highest and lowest
, Fig. 5a). The AL algorithm also found the global minimum of −3.07 V in just 14 iterations (Fig. S5(a)†). Structural formulae for the found molecules with the highest and lowest 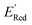 are shown in Fig. 5c and d, respectively.
are shown in Fig. 5c and d, respectively.
3.3. Searching a larger molecular space
Encouraged by these results, we used the AL approach for searching low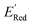 molecules from remaining library (34
molecules from remaining library (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 unevaluated compounds) in smaller number of iterations. Again, we randomly selected 10 molecules from this library as the initial set and subsequently completed 75 iterations. In this run, each iteration requires the DFT evaluation of the suggested molecule. The mean and minimum values for
000 unevaluated compounds) in smaller number of iterations. Again, we randomly selected 10 molecules from this library as the initial set and subsequently completed 75 iterations. In this run, each iteration requires the DFT evaluation of the suggested molecule. The mean and minimum values for 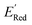 of the AL-selected molecules are ∼0.5 V smaller than in the initial set (Fig. 6a). The structures of the molecules with the smallest redox potentials are shown in Fig. 6, panel (b)–(g). Among the 75 molecules selected by the AL algorithm, 43 (∼57% of 75) species have S1 scaffolds that display 0.45 to 0.76 V (or 21.03% to 35.51%) smaller
of the AL-selected molecules are ∼0.5 V smaller than in the initial set (Fig. 6a). The structures of the molecules with the smallest redox potentials are shown in Fig. 6, panel (b)–(g). Among the 75 molecules selected by the AL algorithm, 43 (∼57% of 75) species have S1 scaffolds that display 0.45 to 0.76 V (or 21.03% to 35.51%) smaller 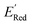 values compared to the BTZ molecule. Remaining molecules show a modest decrease of 0 to 21% in
values compared to the BTZ molecule. Remaining molecules show a modest decrease of 0 to 21% in 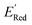 values relative to the BTZ molecule. Overall, AL algorithm mostly selected molecules with low
values relative to the BTZ molecule. Overall, AL algorithm mostly selected molecules with low 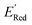 values like Fig. 5b. Low
values like Fig. 5b. Low 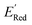 values of S1 scaffold-based molecules among 75 AL-selected molecules and the observation from Fig. 5a that the molecules with the lowest 10% of the
values of S1 scaffold-based molecules among 75 AL-selected molecules and the observation from Fig. 5a that the molecules with the lowest 10% of the 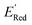 in 1500 dataset almost exclusively had the S1 scaffolds indicates that the S1 scaffold-based molecules are more promising molecules in the library.
in 1500 dataset almost exclusively had the S1 scaffolds indicates that the S1 scaffold-based molecules are more promising molecules in the library.
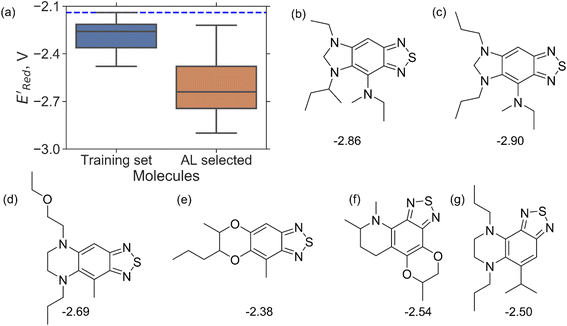 | ||
Fig. 6 (a) The boxplot shows the spread of  of 10 molecules in the initial training set (blue) and 75 molecules selected by the AL algorithm (orange) from a library of 34 of 10 molecules in the initial training set (blue) and 75 molecules selected by the AL algorithm (orange) from a library of 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. The blue dashed horizontal line corresponds to the 000 molecules. The blue dashed horizontal line corresponds to the  of the parent BTZ molecule, and the boxplots are as in Fig. 5b. (b and c) Two S1 molecules with the lowest redox potentials. (d–g) Four other low-potential molecules with their of the parent BTZ molecule, and the boxplots are as in Fig. 5b. (b and c) Two S1 molecules with the lowest redox potentials. (d–g) Four other low-potential molecules with their  shown in plot. shown in plot. | ||
To further explore the S1 class molecules, we calculated the redox potentials for all remaining S1 molecules in our library to give the total of 1400 S1 molecules (Fig. 7). These molecules were then compared with 1362 non-S1 molecules in our original library of computed molecules (complemented with the molecules generated during AL searches) that included 198 S2, 141 S3, 81 S4, 93 S5, 58 S6, and 791 generic BTZ molecules (Fig. 7).
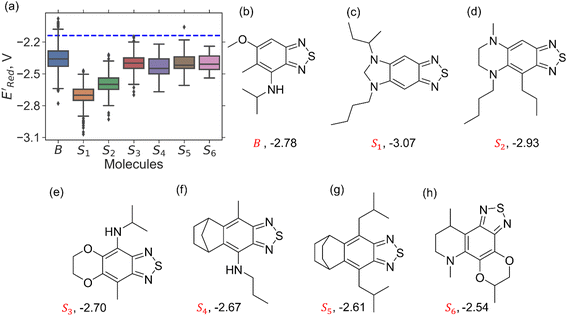 | ||
Fig. 7 (a) The boxplot shows the spread of 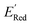 of 1400 S1 (orange), 198 S2 (green), 141 S3 (red), 81 S4 (violet), 93 S5 (brown), 58 S6 (pink), and 791 generic BTZ molecules (blue). The blue dashed horizontal line corresponds to the of 1400 S1 (orange), 198 S2 (green), 141 S3 (red), 81 S4 (violet), 93 S5 (brown), 58 S6 (pink), and 791 generic BTZ molecules (blue). The blue dashed horizontal line corresponds to the 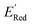 of the parent BTZ molecule. The solid horizontal lines correspond to the quartile positions. Panels (b)–(h) show the molecules with the lowest redox potentials in each class. Notes: the schematic structures of B, S1 to S6 are shown in Fig. 3. of the parent BTZ molecule. The solid horizontal lines correspond to the quartile positions. Panels (b)–(h) show the molecules with the lowest redox potentials in each class. Notes: the schematic structures of B, S1 to S6 are shown in Fig. 3. | ||
Fig. 7a shows the spread of redox potentials for each scaffold class shown in Fig. 3, and Fig. 7b–h show the molecules with the lowest redox potentials in these classes (more examples are given in Fig. S6–S12†). It is clear from this examination that 5,6-diamino derivatives with S1 and S2 scaffolds have the lowest redox potentials, both in the absolute sense (yielding the molecules with the lowest 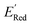 values) and on the average (as a class).
values) and on the average (as a class).
We also note that in a set of 1400 S1 molecules, 14 molecules have 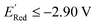 , with −3.07 V as the global minimum. However, 12 out of these 14 S1 molecules are part of the 1500 molecules that are randomly selected to test the AL algorithm (Fig. 5a) while the remaining 2 molecules with
, with −3.07 V as the global minimum. However, 12 out of these 14 S1 molecules are part of the 1500 molecules that are randomly selected to test the AL algorithm (Fig. 5a) while the remaining 2 molecules with 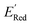 equal to −2.96 V and −2.90 V are part of the larger library of 34
equal to −2.96 V and −2.90 V are part of the larger library of 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules, therefore the global minimum in the library of 34
000 molecules, therefore the global minimum in the library of 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules is −2.96 V. With the AL algorithm, we discovered a molecule with
000 molecules is −2.96 V. With the AL algorithm, we discovered a molecule with 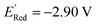 and finished within 0.06 V from the global minimum of −2.96 V in only 75 iterations or by sampling under 0.25% of the 34
and finished within 0.06 V from the global minimum of −2.96 V in only 75 iterations or by sampling under 0.25% of the 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. This demonstrates the effectiveness of the AL algorithm in finding optimal data points in a minimal number of evaluations from a large search space.
000 molecules. This demonstrates the effectiveness of the AL algorithm in finding optimal data points in a minimal number of evaluations from a large search space.
3.4. Identification of optimal molecular scaffolds
Given that amino groups have strong electron donating properties, it is not surprising that BTZ molecules in these two classes (S1 and S2) have lower redox potentials. The surprising feature is the positional specificity and the strong effect of cyclization.To better understand the positional specificity, we investigated first atoms bonded to carbons 4 to 7 in the benzene ring of BTZ molecule (Fig. 1) and found 130 unique configurations of atoms (X1X2X3X4) in calculated molecules, where X1, X2, X3, and X4 are the symbols for first atoms bonded to carbons 4 to 7 in the benzene ring of BTZ, with the symmetry taken into account, so that X1X2X3X4 and X4X3X2X1 configurations are counted as one. Further, we used one-hot-encoding method to create feature vectors of 130 binary descriptors (i.e., 130 unique X1X2X3X4 patterns in the library). The descriptor is 1 if the configuration occurs in a BTZ molecule and 0 otherwise. We also introduced a categorical descriptor xNNx to classify all BTZ molecules that have two nitrogen atoms in the 5,6-positions and any atoms in the 4,7-positions. To study the dependence of 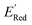 on these descriptors, a multivariate linear regression model was trained on these custom descriptors along with the standard 1-dimensional descriptors (such as atom type and ring counts) from the Mordred package.65 A genetic algorithm described in Section S4 of the ref. 66 was used to select 15 descriptors that minimized the root square deviation of the predicted data. To include more examples of acyclic 5,6-diamino substituted molecules, 300 such molecules from the library were examined and their DFT computed
on these descriptors, a multivariate linear regression model was trained on these custom descriptors along with the standard 1-dimensional descriptors (such as atom type and ring counts) from the Mordred package.65 A genetic algorithm described in Section S4 of the ref. 66 was used to select 15 descriptors that minimized the root square deviation of the predicted data. To include more examples of acyclic 5,6-diamino substituted molecules, 300 such molecules from the library were examined and their DFT computed 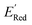 added to the library of computed molecules. Among the various positional descriptors that we introduced, the xNNx descriptor has the largest impact, suggesting a very strong effect of 5,6-diamino substitution on the redox potential (Fig. S13†). This effect is seen both in the cyclic and acyclic structures, but it becomes amplified in the cyclic structures. To show this amplified effect of substitutions in cyclic structures, we examined the cyclic (S1 and S2) and acyclic 5,6-diamino molecules. We identified that the S1 molecules had lower redox potentials followed by the S2 molecules followed by acyclic 5,6-diamino molecules like Fig. 7a (Fig. S14†). Based on our analysis, the increase in the redox potentials is correlated with the mean angle θ between the nitrogen lone pair orbital in the amino groups and the benzene ring (Fig. S14†). When this custom descriptor was added to the standard 1- and 2- dimensional descriptors from the Mordred package, it was consistently selected as one of the main predictors for the redox potential (Fig. S15†).
added to the library of computed molecules. Among the various positional descriptors that we introduced, the xNNx descriptor has the largest impact, suggesting a very strong effect of 5,6-diamino substitution on the redox potential (Fig. S13†). This effect is seen both in the cyclic and acyclic structures, but it becomes amplified in the cyclic structures. To show this amplified effect of substitutions in cyclic structures, we examined the cyclic (S1 and S2) and acyclic 5,6-diamino molecules. We identified that the S1 molecules had lower redox potentials followed by the S2 molecules followed by acyclic 5,6-diamino molecules like Fig. 7a (Fig. S14†). Based on our analysis, the increase in the redox potentials is correlated with the mean angle θ between the nitrogen lone pair orbital in the amino groups and the benzene ring (Fig. S14†). When this custom descriptor was added to the standard 1- and 2- dimensional descriptors from the Mordred package, it was consistently selected as one of the main predictors for the redox potential (Fig. S15†).
Thus, the scaffolds S1 and S2 are chosen by our AL algorithm for two reasons. One is that amino groups have strong electron donating properties, and second the placement of two amino groups into the 5,6-positions decreases the redox potential of a BTZ molecule more efficiently than practically any other placement of electron donating groups. This trend becomes amplified when there is a cyclization that forces the pi-system of the benzene ring to extend to these two nitrogen atoms. This can be demonstrated explicitly by using symmetry preserving rotation of 5,6-amino groups in acyclic molecules (Fig. S16†). The more the N 2p orbitals are rotated out of the plane of the benzene ring, the greater is the reduction in the redox potential (Fig. S16†). It is this trend that we observed statistically in Fig. S14 and S15.† Thus, using our methods, we have inadvertently discovered BTZ scaffolds that minimize the redox potential through the interplay of cyclization-induced strain and orbital structure. While we were able to rationalize this AL discovery a posteriori, we failed to anticipate it with our own intelligence.
3.5. The stability of low-potential radical anions
In Fig. 8, we focus on the BTZ molecules that have the lowest redox potentials among all molecules with the given number of heavy atoms (Fig. S17†). As there are relatively few such molecules, we can compute properties that would be too expensive to compute for all molecules in the data set. The first quantities of interest are the redox potentials (with vibrational correction unlike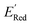 ) shown in Fig. 8b. The highest 1e− redox potential ERed of −2.05 V is for the parent BTZ molecule 1 while the lowest (−3.01 V) is for molecule 12 in Fig. 8b. As the 1e− redox potential decreases, the potential gap ΔERed between the singly and doubly reduced anolyte molecules decreases from 0.65 V to 0.27 V (Fig. 8c). From electrochemical studies,7,10 it is known that BTZ dianions are very unstable, decaying on the time scale of cyclic voltammetry (<1 s). The proximity of such unstable dianion states to the radical anion states in energy is problematic in two ways. First, it requires tight control of the cell potential or voltage during electrochemical reduction, which could be impossible due to overpotentials arising from kinetic limitations. Second, ΔERed corresponds to the free energy of disproportionation of two radical anions. Even though this reaction is endergonic (ΔERed > 0), the equilibrium is shifted by the decomposition of dianion, and it leads to slow decomposition of the radical anion in the equilibrium with the unstable form. The narrower the ΔERed gap, the more efficient is the shifting of this equilibrium, causing faster decay of the radical anion at higher concentrations.
) shown in Fig. 8b. The highest 1e− redox potential ERed of −2.05 V is for the parent BTZ molecule 1 while the lowest (−3.01 V) is for molecule 12 in Fig. 8b. As the 1e− redox potential decreases, the potential gap ΔERed between the singly and doubly reduced anolyte molecules decreases from 0.65 V to 0.27 V (Fig. 8c). From electrochemical studies,7,10 it is known that BTZ dianions are very unstable, decaying on the time scale of cyclic voltammetry (<1 s). The proximity of such unstable dianion states to the radical anion states in energy is problematic in two ways. First, it requires tight control of the cell potential or voltage during electrochemical reduction, which could be impossible due to overpotentials arising from kinetic limitations. Second, ΔERed corresponds to the free energy of disproportionation of two radical anions. Even though this reaction is endergonic (ΔERed > 0), the equilibrium is shifted by the decomposition of dianion, and it leads to slow decomposition of the radical anion in the equilibrium with the unstable form. The narrower the ΔERed gap, the more efficient is the shifting of this equilibrium, causing faster decay of the radical anion at higher concentrations.
It is precisely such side reactions that cause the general trend for reduced chemical stability of low-potential anolyte molecules noted in the introduction. Such intrinsic limitations are in full display in our data (Fig. 8c). While in silico molecular engineering can lower the redox potential significantly, we found it impossible to decrease this potential without narrowing the energy gap between the two reduced states, which means likely lower stability of the radical anion. Such tradeoffs are inherent in the redoxmer optimization, therefore, the molecules such as 6, 7 and 14 (Fig. 8a) that straddle the middle ground can be preferable to molecules 11 and 12 despite their higher redox potential.
While the disproportionation reaction requires two species, the stability of a radical anion in dilute solution is mainly determined by the facility for protonation that correlates with the proton affinity of the radical anion. We have identified the likely protonation sites (Fig. S18†), and computed proton affinities (Fig. S19†) for molecules shown in Fig. 8.8,67,68 Unsurprisingly, as the redox potential decreases, the proton affinities increase by 0.5–1.1 V. This is another indication that decreasing the redox potential is likely to lower electrochemical stability, both in dilute and concentrated solutions, and a compromise needs to be struck between this tendency and the desire to lower the redox potential. The AL algorithm implemented in this study can be used to negotiate such compromises by minimizing the redox potential while maximizing the energy gap and/or minimizing the proton affinity, but these more complex optimizations are beyond the scope of this study.
3.6. Chemical synthesis of tricyclic BTZ derivatives
As observed above, one of the most interesting outcomes of this study is the discovery of a new class of low-potential BTZ derivatives. In SRMGA, the complexity score does not fully reflect the synthetic effort going into molecular synthesis that can only be determined by an experienced organic chemist. In Fig. S21,† we present a retrosynthetic analysis of the S1 molecular scaffold. The final benzoimidazolidine is first decyclized to an N-alkylated ortho-substituted BTZ, which is further deconstructed to 1,2,4,5-tetraaminobenzene. The parent BTZ derivatives are primarily synthesized by reaction of o-diaminobenzene with thionyl chloride.69 In our design, the two ortho amino groups fused to the 2,1,3-thiadiazole ring would be alkylated followed by an aldehyde condensation reaction to complete the imidazolidine ring.70 While this synthetic route is more complex compared to the simpler BTZ derivatives, it is not much more complex than other redoxmer syntheses in the literature. In this sense, low CS scores for S1 molecules did reflect their synthetic accessibility.4 Conclusion
A priori identification of improved redoxmers based on simulations and machine learning can enable cost efficient development of redox flow batteries. For redoxmers, structural complexity is doubly penalized: complex molecules are prohibitively expensive to synthesize in bulk quantities (which are implicit in grid size storage) and large molecules cannot reach volumetric energy density required for RFB competitiveness. Here we show how to populate search spaces with structurally simple yet diverse molecules, negotiating the compromise between the molecule complexity and the desired redox potential. In this contribution, we proposed a Metropolis-like algorithm with built-in penalization of structural complexity. The resulting search space has robust (for the smallest structures, exhaustive) representation of smaller structures while keeping the “typical” larger molecules. Further, we used this pre-optimized set to apply a Bayesian optimization-based active learning (AL) algorithm to discover promising anolyte molecules. By searching through 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 structures, we needed to compute < 10% of these structures, with most of the DFT computations used either to initiate the algorithm (1500 structures) or to rationalize our search results; the AL search itself included DFT computations of <100 (0.3% of 35
500 structures, we needed to compute < 10% of these structures, with most of the DFT computations used either to initiate the algorithm (1500 structures) or to rationalize our search results; the AL search itself included DFT computations of <100 (0.3% of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) structures. The method surpassed our expectations by identifying two heretofore unknown classes of tricyclic BTZ molecules with unusually low redox potentials, which is exciting for electrochemical experiments.
000) structures. The method surpassed our expectations by identifying two heretofore unknown classes of tricyclic BTZ molecules with unusually low redox potentials, which is exciting for electrochemical experiments.
While this success is gratifying, our study highlights the fundamental difficulty of finding redoxmers that satisfy all requirements posed by the application. For BTZ derivatives, lowering of the redox potentials has narrowed the gap between the 1e− and 2e− reduction states (that facilitates disproportionation of radical anions in solution) and increased proton affinity of radical anions. It follows from our computational results that in this anolyte family it may be impossible to simultaneously achieve the lowest redox potentials and the exceptional stability of radical anions no matter how the BTZ molecule is derivatized. Fortunately, the AL methods not only provide a means of identifying the necessity of compromise but also a means of reaching this compromise through multiple property optimization. As new redox-active core molecules are identified, the space of their derivatives can be rapidly examined with such expert systems to identify the strengths and limitations of these new scaffolds. Given the generality of our approach, we hope that our methods will become the standard tool in the materials development in the battery sciences and molecular discovery.
Data availability
We provide the SRMGA code (for a molecular library generation) and data of different molecular libraries (SMILES, complexity score and redox potentials in CSV files) on GitHub at https://github.com/akashjn/MolGenerator. We provide the active learning code on GitHub at https://github.com/akashjn/Machine_Learning_Chemistry/blob/main/BTZ_1500_mols/Active_Learning_for_1500_BTZmols.ipynb. Additionally, we provide the ESI† which includes (i) a pdf file containing the additional tables, figures and references, and (ii) zipped CSV files containing SMILES, complexity scores, and redox potentials for different libraries.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. IAS is grateful to Jacob A. Shkrob and Anna Pluzhnikov for discussions of statistical approaches that lead to the molecule generation algorithms implemented in this study. We gratefully acknowledge the computing resources provided on “Bebop”, a 1024-node computing cluster operated by the Laboratory Computing Resource Center at Argonne National Laboratory. The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne, a U.S. Department of Energy Office of Science laboratory, is operated under Contract No. DE-AC02-06CH11357. The U.S. Government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the Government.References
- J. A. Kowalski, L. Su, J. D. Milshtein and F. R. Brushett, Curr. Opin. Chem. Eng., 2016, 13, 45–52 CrossRef
.
- M. Li, Z. Rhodes, J. R. Cabrera-Pardo and S. D. Minteer, Sustainable Energy Fuels, 2020, 4, 4370–4389 RSC
.
- M. Skyllas-Kazacos, M. Chakrabarti, S. Hajimolana, F. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158, R55 CrossRef CAS
.
- S.-K. Park, J. Shim, J. Yang, K.-H. Shin, C.-S. Jin, B. S. Lee, Y.-S. Lee and J.-D. Jeon, Electrochem. Commun., 2015, 59, 68–71 CrossRef CAS
.
- W. Duan, R. S. Vemuri, J. D. Milshtein, S. Laramie, R. D. Dmello, J. Huang, L. Zhang, D. Hu, M. Vijayakumar and W. Wang, and others, J. Mater. Chem. A, 2016, 4, 5448–5456 RSC
.
- Y. Yao, J. Lei, Y. Shi, F. Ai and Y.-C. Lu, Nat. Energy, 2021, 6, 582–588 CrossRef
.
- J. Zhang, J. Huang, L. A. Robertson, I. A. Shkrob and L. Zhang, J. Power Sources, 2018, 397, 214–222 CrossRef CAS
.
- X. Wei, W. Xu, J. Huang, L. Zhang, E. Walter, C. Lawrence, M. Vijayakumar, W. A. Henderson, T. Liu and L. Cosimbescu, Angew. Chem., Int. Ed., 2015, 54, 8684–8687 CrossRef CAS PubMed
.
- M. L. Perry, J. D. Saraidaridis and R. M. Darling, Curr. Opin. Electrochem., 2020, 21, 311–318 CrossRef CAS
.
- J. Zhang, J. Huang, L. A. Robertson, R. S. Assary, I. A. Shkrob and L. Zhang, J. Phys. Chem. C, 2018, 122, 8116–8127 CrossRef CAS
.
- A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164 CrossRef CAS
.
- E. S. Beh, D. De Porcellinis, R. L. Gracia, K. T. Xia, R. G. Gordon and M. J. Aziz, ACS Energy Lett., 2017, 2, 639–644 CrossRef CAS
.
- X. Wei, L. Cosimbescu, W. Xu, J. Z. Hu, M. Vijayakumar, J. Feng, M. Y. Hu, X. Deng, J. Xiao and J. Liu, Adv. Energy Mater., 2015, 5, 1400678 CrossRef
.
- Y. Zhao, Y. Ding, J. Song, G. Li, G. Dong, J. B. Goodenough and G. Yu, Angew. Chem., 2014, 126, 11216–11220 CrossRef
.
- J. Huang, L. Su, J. A. Kowalski, J. L. Barton, M. Ferrandon, A. K. Burrell, F. R. Brushett and L. Zhang, J. Mater. Chem. A, 2015, 3, 14971–14976 RSC
.
- J. Huang, B. Pan, W. Duan, X. Wei, R. S. Assary, L. Su, F. R. Brushett, L. Cheng, C. Liao and M. S. Ferrandon, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed
.
- T. Liu, X. Wei, Z. Nie, V. Sprenkle and W. Wang, Adv. Energy Mater., 2016, 6, 1501449 CrossRef
.
- J. D. Milshtein, J. L. Barton, R. M. Darling and F. R. Brushett, J. Power Sources, 2016, 327, 151–159 CrossRef CAS
.
- X. Wei, W. Xu, M. Vijayakumar, L. Cosimbescu, T. Liu, V. Sprenkle and W. Wang, Adv. Mater., 2014, 26, 7649–7653 CrossRef CAS PubMed
.
- K. Takechi, Y. Kato and Y. Hase, Adv. Mater., 2015, 27, 2501–2506 CrossRef CAS PubMed
.
- J. Winsberg, C. Stolze, S. Muench, F. Liedl, M. D. Hager and U. S. Schubert, ACS Energy Lett., 2016, 1, 976–980 CrossRef CAS
.
- Y. Ding, C. Zhang, L. Zhang, Y. Zhou and G. Yu, Chem. Soc. Rev., 2018, 47, 69–103 RSC
.
- J. E. Bachman, L. A. Curtiss and R. S. Assary, J. Phys. Chem. A, 2014, 118, 8852–8860 CrossRef CAS PubMed
.
- C. de la Cruz, A. Molina, N. Patil, E. Ventosa, R. Marcilla and A. Mavrandonakis, Sustainable Energy Fuels, 2020, 4, 5513–5521 RSC
.
- L. Cheng, R. S. Assary, X. Qu, A. Jain, S. P. Ong, N. N. Rajput, K. Persson and L. A. Curtiss, J. Phys. Chem. Lett., 2015, 6, 283–291 CrossRef CAS PubMed
.
- A. J. Chowdhury, W. Yang, E. Walker, O. Mamun, A. Heyden and G. A. Terejanu, J. Phys. Chem. C, 2018, 122, 28142–28150 CrossRef CAS
.
- M. Pardakhti, E. Moharreri, D. Wanik, S. L. Suib and R. Srivastava, ACS Comb. Sci., 2017, 19, 640–645 CrossRef CAS PubMed
.
- T. Gu, W. Lu, X. Bao and N. Chen, Solid State Sci., 2006, 8, 129–136 CrossRef CAS
.
- J. Qin, Z. Liu, M. Ma and Y. Li, ACS Sustainable Chem. Eng., 2022, 10, 1554–1564 CrossRef CAS
.
- C. Sutton, M. Boley, L. M. Ghiringhelli, M. Rupp, J. Vreeken and M. Scheffler, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed
.
- G. Pilania, Comput. Mater. Sci., 2021, 193, 110360 CrossRef CAS
.
- H. A. Doan, C. Li, L. Ward, M. Zhou, L. A. Curtiss and R. S. Assary, Digit. Discov., 2023, 2, 59–68 RSC
.
- A. M. Gopakumar, P. V. Balachandran, D. Xue, J. E. Gubernatis and T. Lookman, Sci. Rep., 2018, 8, 1–12 CAS
.
- L. Bassman, P. Rajak, R. K. Kalia, A. Nakano, F. Sha, J. Sun, D. J. Singh, M. Aykol, P. Huck and K. Persson, npj Comput. Mater., 2018, 4, 1–9 CrossRef
.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed
.
- C. Kim, A. Chandrasekaran, A. Jha and R. Ramprasad, MRS Commun., 2019, 9, 860–866 CrossRef CAS
.
- D. Xue, P. V. Balachandran, J. Hogden, J. Theiler, D. Xue and T. Lookman, Nat. Commun., 2016, 7, 1–9 Search PubMed
.
- H. A. Doan, G. Agarwal, H. Qian, M. J. Counihan, J. Rodríguez-López, J. S. Moore and R. S. Assary, Chem. Mater., 2020, 32, 6338–6346 CrossRef CAS
.
- G. Agarwal, H. A. Doan, L. A. Robertson, L. Zhang and R. S. Assary, Chem. Mater., 2021, 33, 8133–8144 CrossRef CAS
.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, npj Comput. Mater., 2019, 5, 1–17 CrossRef
.
- A. Mannodi-Kanakkithodi, G. Pilania, T. D. Huan, T. Lookman and R. Ramprasad, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed
.
- R. J. Hickman, M. Aldeghi, F. Häse and A. Aspuru-Guzik, Digit. Discov., 2022, 1, 732–744 RSC
.
- J. Mockus, V. Tiesis and A. Zilinskas, J. Glob. Optim., 1978, 2, 2 Search PubMed
.
-
M. Pelikan, in Hierarchical Bayesian optimization algorithm, Springer, 2005, pp. 31–48 Search PubMed
.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, ACS Cent. Sci., 2020, 6, 513–524 CrossRef CAS PubMed
.
- A. Thakkar, V. Chadimová, E. J. Bjerrum, O. Engkvist and J.-L. Reymond, Chem. Sci., 2021, 12, 3339–3349 RSC
.
- M. Voršilák, M. Kolář, I. Čmelo and D. Svozil, J. Cheminf., 2020, 12, 1–13 Search PubMed
.
-
J. Noh, D.-W. Jeong, K. Kim, S. Han, M. Lee, H. Lee and Y. Jung, in International Conference on Machine Learning, PMLR, 2022, pp. 16952–16968 Search PubMed
.
- W. Gao and C. W. Coley, J. Chem. Inf. Model., 2020, 60, 5714–5723 CrossRef CAS PubMed
.
- A. Nigam, R. Pollice and A. Aspuru-Guzik, Digit. Discov., 2022, 1, 390–404 RSC
.
- W. Gao, R. Mercado and C. W. Coley, arXiv, preprint, arXiv:2110.06389, DOI:10.48550/arXiv.2110.06389.
- J. Huang, W. Duan, J. Zhang, I. A. Shkrob, R. S. Assary, B. Pan, C. Liao, Z. Zhang, X. Wei and L. Zhang, J. Mater. Chem. A, 2018, 6, 6251–6254 RSC
.
- W. Duan, J. Huang, J. A. Kowalski, I. A. Shkrob, M. Vijayakumar, E. Walter, B. Pan, Z. Yang, J. D. Milshtein and B. Li, ACS Energy Lett., 2017, 2, 1156–1161 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984 CrossRef CAS
.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS
.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed
.
- In CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, 93rd edn, p. 80 Search PubMed.
- G. Landrum, RDKit, Q2, 2010, https://www.rdkit.org/ Search PubMed.
- S. Chib and E. Greenberg, Am. Stat., 1995, 49, 327–335 Search PubMed
.
-
C. E. Rasmussen, in Summer school on machine learning, Springer, 2003, pp. 63–71 Search PubMed
.
- J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger and A. G. Wilson, arXiv, preprint, arXiv:1809.11165, DOI:10.48550/arXiv.1809.11165.
- C. G. Armstrong and K. E. Toghill, Electrochem. Commun., 2018, 91, 19–24 CrossRef CAS
.
- H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminf., 2018, 10, 1–14 Search PubMed
.
- J. Zhang, R. Corman, J. K. Schuh, R. H. Ewoldt, I. A. Shkrob and L. Zhang, J. Phys. Chem. C, 2018, 122, 8159–8172 CrossRef CAS
.
- P. S. Engel, W. K. Lee, G. E. Marschke and H. J. Shine, J. Org. Chem., 1987, 52, 2813–2817 CrossRef CAS
.
- V. S. Bryantsev, V. Giordani, W. Walker, M. Blanco, S. Zecevic, K. Sasaki, J. Uddin, D. Addison and G. V. Chase, J. Phys. Chem. A, 2011, 115, 12399–12409 CrossRef CAS PubMed
.
- B. A. Neto, A. A. Lapis, E. N. da Silva Júnior and J. Dupont, Eur. J. Org. Chem., 2013, 2013, 228–255 CrossRef CAS
.
- R. Ferm and J. Riebsomer, Chem. Rev., 1954, 54, 593–613 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00050h |
| This journal is © The Royal Society of Chemistry 2023 |