Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Neural networks trained on synthetically generated crystals can extract structural information from ICSD powder X-ray diffractograms†
Henrik
Schopmans
 ab,
Patrick
Reiser
ab,
Patrick
Reiser
 ab and
Pascal
Friederich
ab and
Pascal
Friederich
 *ab
*ab
aInstitute of Theoretical Informatics, Karlsruhe Institute of Technology, Engler-Bunte-Ring 8, 76131 Karlsruhe, Germany. E-mail: pascal.friederich@kit.edu
bInstitute of Nanotechnology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
First published on 16th August 2023
Abstract
Machine learning techniques have successfully been used to extract structural information such as the crystal space group from powder X-ray diffractograms. However, training directly on simulated diffractograms from databases such as the ICSD is challenging due to its limited size, class-inhomogeneity, and bias toward certain structure types. We propose an alternative approach of generating synthetic crystals with random coordinates by using the symmetry operations of each space group. Based on this approach, we demonstrate online training of deep ResNet-like models on up to a few million unique on-the-fly generated synthetic diffractograms per hour. For our chosen task of space group classification, we achieved a test accuracy of 79.9% on unseen ICSD structure types from most space groups. This surpasses the 56.1% accuracy of the current state-of-the-art approach of training on ICSD crystals directly. Our results demonstrate that synthetically generated crystals can be used to extract structural information from ICSD powder diffractograms, which makes it possible to apply very large state-of-the-art machine learning models in the area of powder X-ray diffraction. We further show first steps toward applying our methodology to experimental data, where automated XRD data analysis is crucial, especially in high-throughput settings. While we focused on the prediction of the space group, our approach has the potential to be extended to related tasks in the future.
1 Introduction
Machine learning techniques have emerged as a powerful tool in the toolkit of materials scientists. While they are often used to make predictions on the properties of materials or find new materials with certain properties, an increasingly interesting domain is the automated analysis of raw experimental measurements guided by machine learning.1With the advent of high-throughput experiments, the amount of gathered data is vast and the analysis often becomes a bottleneck in the processing pipeline.2 Powder X-ray diffraction (XRD) is an important measurement technique used to obtain structural information from polycrystalline samples.3 The diffractograms are an information-dense fingerprint of the structure of the material. However, analyzing these diffractograms is not an easy task.4 Full structure solutions and Rietveld refinement take time and require expert knowledge, both about the analysis technique and the materials class at hand. This is not feasible in high-throughput experiments on a larger scale. Therefore, the question arises whether it is possible to automatically analyze powder diffractograms with machine learning models trained on large amounts of data, making it possible to run inference almost instantaneously.
During the last few years, there have been several studies tackling this objective by applying machine learning models to various tasks concerning the analysis of powder diffractograms such as phase classification,5–9 phase fraction determination,10 space group classification,11–16 machine-learning-guided Rietveld refinement,17,18 extraction of lattice parameters16,19–21 and crystallite sizes,16,19 and also novelty detection based on unsupervised techniques.22 Since an abundant source of experimental diffractograms is hard to come by, most applications train their models on simulated diffractograms from the Inorganic Crystal Structure Database (ICSD),23 which contains a total of 272![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 structures (October 2022).
260 structures (October 2022).
Lee et al. used a deep convolutional neural network (CNN) trained on a large dataset of multiphase compositions from the quaternary Sr–Li–Al–O pool to classify present phases in the diffractogram.5 In a follow-up study, they further showed good results for phase fraction inference in the quaternary Li–La–Zr–O pool.10 Schuetzke et al. performed phase classification on iron ores and cement compounds and used data augmentation with respect to lattice parameters, crystallite sizes, and preferred orientation.7 They showed that especially the lattice parameter variations enhance the classification accuracy significantly.
Instead of the analysis of phase composition, Dong et al. performed regression of scale factors, lattice parameters, and crystallite sizes in a five-phase catalytic materials system.19 In contrast to supervised tasks, Banko et al. used a variational autoencoder to visualize variations in space group, preferred orientation, crystallite size, and peak shifts.22 Park et al. used a deep CNN to classify space groups of single-phase diffractograms, reaching a test accuracy of 81.14% on simulated diffractograms.11 However, as we will show later in this paper, this accuracy is highly overestimated and drops to 56.1% when test splits are designed in a way to reduce data leakage in non-IID datasets such as the ICSD. Vecsei et al. developed a similar approach and applied their classifier to experimental diffractograms from the RRUFF mineral database,14,24 reaching an experimental test accuracy of 54%.
While the ICSD contains a large number of structures spanning many different classes of materials, it still falls short in size, distribution, and generality compared to the datasets used to train very large state-of-the-art models of other fields such as computer vision. Furthermore, the ICSD database is highly imbalanced with respect to space groups, as can be seen in the histogram in Fig. 1. This makes the classification of space groups more difficult, as shown and discussed by Zaloga et al.13 The ICSD also contains a limited number of different structure types that may not adequately represent the crystal structures analyzed in future experiments.
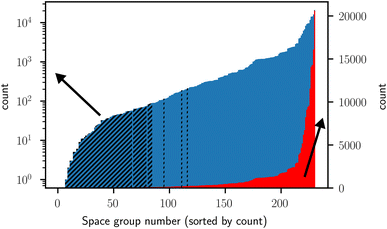 | ||
| Fig. 1 Distribution (logarithmic scale in blue, linear scale in red) of space groups in the ICSD. Space groups are sorted by count (see Fig. S13 in the ESI† for the distribution without sorting by count). The population of the space groups varies by multiple orders of magnitude, showing that the ICSD is a highly imbalanced dataset regarding space groups. The space groups excluded due to insufficient statistics are visualized with black stripes. The histogram displays the distribution of the full ICSD, while the exclusion of space groups that do not contain enough samples is based on the statistics dataset (which does not include the test dataset, see Section 2.4) that we used to guide the random crystal generation. Therefore, the excluded space groups are not exactly the first 85 counted from the left. | ||
To overcome these shortcomings, we propose to train machine learning models on diffractograms simulated from synthetic crystal structures randomly generated based on the symmetry operations of the space groups. This makes it possible to train on structures with new structure types not present in the ICSD. We used the crystals from the ICSD only to determine vague statistics guiding the random generation and for calculating the test accuracy. Our approach goes one step further than classical data augmentation by fully detaching itself from the individual entries in the ICSD database. The generated synthetic crystals form a training dataset that includes stable ICSD crystal structures, unstable crystal structures, but also stable structures that are not yet present in the ICSD. By training a model on the full dataset, we can also expect improvements on the unknown stable crystal structures. Furthermore, we propose viewing the problem as a mathematical task of getting back some of the real-space information leading to given powder X-ray diffractograms. Therefore, even the unstable structures included in our generated dataset will help to learn to classify the stable structures.
Here, we applied this approach to the classification of the crystal symmetry, namely the space group. The space group is usually one of the first structural pieces of information needed after synthesizing a new material. This task is well-suited to showcase the strengths of using a synthetic dataset and to benchmark it. We further show the results of using our methodology to infer space group labels of an experimental dataset.
We embedded our synthetic generation algorithm in a framework with distributed computing capabilities to generate and simulate diffractograms on multiple nodes in parallel using the Python library Ray.25 In contrast to the traditional approach of generating a simulated dataset before training, we used this distributed computing architecture to build an infinite stream of synthetically generated and simulated diffractograms to perform batch-wise online learning. This increases the generalization performance, eliminates the problem of overfitting, and allows very large models to be trained.
2 Methods
2.1 Generating synthetic crystals
To generate synthetic crystals, we randomly place atoms on the Wyckoff positions of a given space group following the Wyckoff occupation probabilities extracted from the ICSD and then apply the respective symmetry operations. The algorithm is explained in the following (see also Fig. 2a for a flow diagram of the algorithm). We only explain the most important steps, details can be found in Section S1 of the ESI.†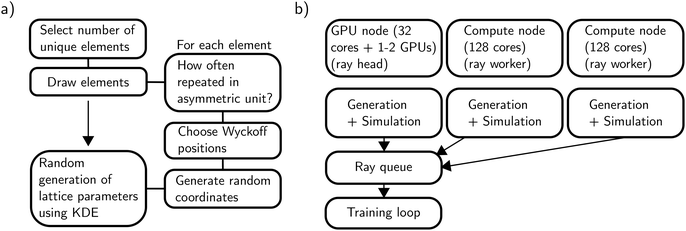 | ||
| Fig. 2 (a) Flowchart of how the generation algorithm produces synthetic crystals. Atoms are independently placed on the Wyckoff positions and random coordinates are drawn. (b) Overview of the distributed computing system implemented using the Python library Ray.25 Two compute nodes (that generate and simulate diffractograms) are connected to the Ray head node using a Ray queue object. | ||
1. Sampling of a space group from the space group distribution of the ICSD.
2. Sample unique elements of the crystal and their number of repetitions in the asymmetric unit.
3. Place atoms onto the Wyckoff positions and draw uniform coordinates for each.
4. Draw lattice parameters from a kernel density estimate based on the ICSD.
5. Apply space group symmetry operations.
Parts of this algorithm were inspired by the generation algorithm of the Python library PyXtal.26 We only keep generated crystals for training if the conventional unit cell volume is below 7000 Å3 and if there are less than 100 atoms in the asymmetric unit. We did not employ any form of distance checks on the coordinates, as we found this to have no meaningful impact on space group classification accuracy. We only prevented the algorithm from placing more than one atom onto a Wyckoff position that does not have a degree of freedom. We also did not use partial occupancies. We chose this algorithm for its simplicity and its capability to reproduce many important characteristics of ICSD crystals adequately (see Section 3.1).
For some space groups, there are not enough crystals in the ICSD to form a representative kernel density estimate for the volume or to calculate suitable occupation probabilities for individual Wyckoff positions. Therefore, we chose to only perform the classification on space groups with 50 or more crystals available in the statistics dataset we used to extract the probabilities (see Section 2.4), resulting in the exclusion of 85 space groups (see Fig. 1). A classifier trained directly on ICSD data of all space groups will likely not be able to properly identify these space groups containing very few samples.
If a similar performance for all space groups is desired, a uniform distribution of space groups in the training dataset is needed. This is trivially possible with our synthetic approach, in contrast to training directly on the ICSD, where weighting, over-, or undersampling methods are needed.27 To allow a direct and fair comparison between our approach and the original approach of training directly on ICSD entries, we still followed the same distribution of space groups of the ICSD in our synthetic training dataset. This eliminates the problem that the effective number of total space groups is smaller when training on a highly imbalanced dataset, making it easier to reach high accuracies.
Our choice of not sampling the space groups uniformly and using general statistics extracted from the ICSD to guide the crystal generation algorithm further builds upon the hypothesis that future crystals will roughly follow the more general statistics already present in the ICSD. With the chosen crystal generation algorithm we tried to find a middle ground between being much more general than using the ICSD crystals directly and not being too general such that it is very hard to extract structural information at all.
2.2 Simulating diffractograms
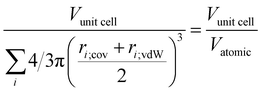
To simulate powder X-ray diffractograms based on the generated crystals, we used the implementation found in the Python library Pymatgen.28 We optimized the simulation code using the LLVM just-in-time compiler Numba.29 This increases the performance of the main loop over the reciprocal lattice vectors of the crystal significantly and makes the continuous simulation while training (discussed in the next section) possible.We used the wavelength 1.5406 Å (Cu Kα1 line) to simulate all diffractograms. The obtained peaks were further broadened with a Gaussian peak profile to form the full diffractogram. To obtain the peak widths, we used the Scherrer equation30
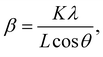 | (1) |
Diffractograms were generated in the range 2θ ∈ [5, 90]° with step size 0.01°. After generating each diffractogram, it was rescaled to fit in the intensity range [0, 1]. In Fig. S9 of the ESI† we show an exemplary diffractogram simulated from the ICSD, Fig. S10† shows an exemplary diffractogram simulated from a synthetic crystal.
2.3 Continuous generation of training data
Typically, machine learning models are trained with a fixed dataset predefined at the beginning of training. Sometimes, data augmentation is applied to further increase the effective size of this dataset. In contrast to that, we generated our dataset on-the-fly, parallel to model training. The main advantage of using this approach compared to a fixed-size dataset is the eliminated possibility to overfit to individual diffractograms since every diffractogram is only used once. Furthermore, not having to pre-simulate a dataset before training makes this approach more flexible when changing simulation parameters.We used a distributed architecture on multiple nodes using the Python framework Ray,25 which enabled the training on 1–2 GPUs and simultaneous generation of training data on more than 200 CPU cores (see Fig. 2b and ESI Section S2.2†). Depending on the model size and corresponding training speed, this setup allows training with up to millions of unique diffractograms per hour.
2.4 Dataset split
The ICSD database contains many structures that are very similar with slightly different lattice parameters and coordinates. For example, there are 25 entries for NaCl (October 2022). Furthermore, there are 3898 entries that have the same structure type as NaCl and thus also similar powder diffractograms. If some of them appear in the training dataset and some in the test dataset, the classification will be simplified to recognizing the structure type or structure. In that case, the test set accuracy will not represent the true generalization performance of the neural network. To quantify the true generalization performance, we split the dataset in such a way that the same structure type appears either only in the training or in the test dataset. We used the structure type definitions provided by the ICSD. The obtained accuracy on the test dataset reflects the accuracy of our network when being used on a novel sample with a structure type not yet present in the ICSD database.We want to emphasize that the used test split is very important for the task of space group classification and not a trivial choice. The ICSD contains many subtypes of structure types (for example, subtypes of perovskites), which we regarded as separate structure types in our split. Considering the subtypes as the same structure type may also be a viable option when performing the split. A combination of a split based on structure type and sum formula or similar approaches are also possible.
Depending on the experimental setting, it further might make more sense in some cases to not do a structure type-based split. If the likelihood of finding structures similar to already-discovered structure types in the planned experiment is high, training should definitely include those structure types to evaluate the performance of the model. However, in a pure discovery setting, new structure types can appear. To evaluate the expected model performance in this scenario and thus quantify the true generalization error to unseen data, we chose the most strict structure type-based split.
We divided the ICSD (database version 2021, June 15) in a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 split. For our synthetic crystal approach, the 70% part (which we call statistics or training dataset) was only used to create the kernel density estimates and to calculate the Wyckoff occupation probabilities needed for the generation algorithm. Since we can judge the performance of the synthetic generation algorithm by comparing the training accuracy (on synthetic crystals) with the accuracy tested on diffractograms simulated directly from the statistics dataset, an additional validation dataset was not needed. For comparison with the original approach of directly training on ICSD crystals,11 we simulated crystals directly from the statistics dataset and trained on them.
30 split. For our synthetic crystal approach, the 70% part (which we call statistics or training dataset) was only used to create the kernel density estimates and to calculate the Wyckoff occupation probabilities needed for the generation algorithm. Since we can judge the performance of the synthetic generation algorithm by comparing the training accuracy (on synthetic crystals) with the accuracy tested on diffractograms simulated directly from the statistics dataset, an additional validation dataset was not needed. For comparison with the original approach of directly training on ICSD crystals,11 we simulated crystals directly from the statistics dataset and trained on them.
Analogous to the synthetic generation, we only used crystals with a conventional unit cell volume below 7000 Å3 and with less than 100 atoms in the asymmetric unit for the statistics and test dataset. This covers ≈94% of the ICSD crystals.
2.5 Models and computational experiments
As a baseline, we first used the CNN models introduced by Park et al.11 They used three models, one for the classification of crystal systems (“parkCNN small”), one for extinction groups (“parkCNN medium”), and one for space groups (“parkCNN big”). All models have three convolution layers with two hidden fully connected layers and one output layer. The three models differ in the number of neurons in the hidden fully connected layers, increasing the number of model parameters with the number of target labels. Here, we only used the models “parkCNN medium” and “parkCNN big” and applied both to the classification of space groups. When using ICSD crystals to train the “parkCNN” models, dropout was used, while the training of the “parkCNN” models on synthetic crystals did not use dropout.
Since the approach of using an infinite stream of generated training data eliminates the problem of overfitting, we further used deeper models with a higher number of model parameters. For this, we used the deep convolutional neural networks ResNet-10, ResNet-50, and ResNet-101, which were introduced by He et al.31 in 2015.
Details of the machine learning setup can be found in the ESI Section 2.2.† Overall, our setup allowed us the training of models over up to 2000 epochs with more than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 unique, newly generated crystals and corresponding diffractograms in each epoch (see the upper x-axis of Fig. 5).
000 unique, newly generated crystals and corresponding diffractograms in each epoch (see the upper x-axis of Fig. 5).
In particular, we first performed an experiment with the “parkCNN medium” model trained directly on the diffractograms simulated from the ICSD statistics dataset with a fully random train–test split (similar to ref. 11), instead of splitting by the structure type of the crystals. This experiment makes a comparison of the two different methods of train–test split possible. We then trained the “parkCNN big” model using the structure type-based split, again directly on ICSD diffractograms. We further repeated the same experiment using the smaller model “parkCNN medium” to resolve potential overfitting to the ICSD diffractograms.
For the experiments performed on our continuously generated dataset based on synthetic crystals, we used the structure type-based split. As discussed in Section 2.4, the training/statistics dataset was only used to extract more general statistics, such as the element distribution. First, we trained the “parkCNN big” model. For each batch, we generated 435 random crystals and simulated two diffractograms with different crystallite sizes for each of them. This resulted in the batch size of 870. Since our synthetic crystal generation algorithm yields an infinite stream of unique diffractograms to train on, using much larger models than for the fixed ICSD dataset is possible without overfitting. We performed experiments for the ResNet-10, ResNet-50, and ResNet-101 models. Instead of generating two diffractograms with different uniformly sampled crystallite sizes for each generated crystal (as we did for the “parkCNN big” model), we now created only one diffractogram for each of the 145 crystals generated for one batch. This is due to the slower training of the ResNet models, which means that reusing the same diffractogram with different crystallite sizes is not necessary to generate training data fast enough.
To obtain the highest-possible ICSD test accuracy, we further applied the square root function as a preprocessing step to the input diffractograms of the network when using the ResNet models. This was suggested by Zaloga et al.13 and in their case improved classification accuracy by approximately 2 percentage points. Some initial tests suggested that this approach also yields a higher accuracy in our case, so we used this preprocessing step to train the ResNet models.
While we focused mainly on the methodology of using synthetic crystals to extract structural information from powder diffractograms, we also show some initial steps toward applying our methods to experimental data. We used the publicly available RRUFF mineral database24 which provides experimental measurements, including powder diffractograms (see Fig. S11 in the ESI† for an exemplary diffractogram from the RRUFF). In order to imitate experimental diffractograms, we added Gaussian additive and multiplicative noise (similar to ref. 8 and 14) and a background function based on samples from a Gaussian process to our simulated diffractograms. Furthermore, we added a small amount of an impurity phase to each diffractogram. Details about the experimental data generation protocol can be found in the ESI Section S4, Fig. S12† shows an exemplary synthetic diffractogram with noise, background and an impurity phase. Using the ResNet-50 model, we performed two experiments for experimental data, one with the mentioned impurity phase, and one without.
3 Results and discussion
3.1 Synthetic distribution
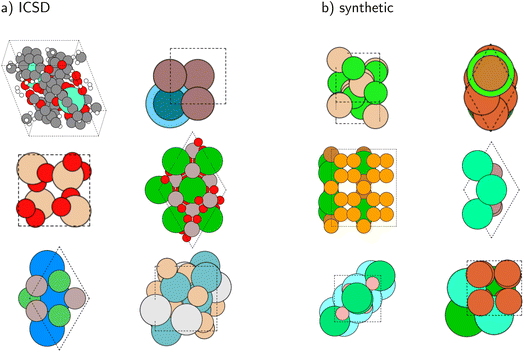
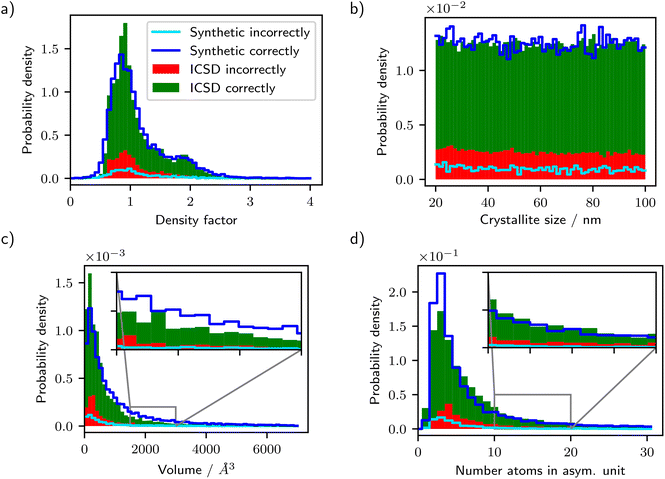
We first present an analysis of the generated synthetic crystals. Fig. 3 shows some randomly chosen and thus representative examples of ICSD and synthetic crystal structures side-by-side. Visually, the crystals appear very similar. However, no physical or chemical considerations regarding stability, clashing atoms, and element combinations are taken into account in the generation of synthetic crystals. As discussed earlier, our goal is to demonstrate that this is not problematic when using these crystals for the extraction of structural information from powder diffractograms. In contrast, we expect the synthetic crystals to be a better basis for generalization to fundamentally new crystal structures than existing finite databases.To compare the distribution of ICSD crystals with the synthetic distribution, we evaluated structural descriptors, i.e. density factors, crystallite sizes, unit cell volumes, and numbers of atoms in the asymmetric unit, and compare their histograms in Fig. 4. One can see that the overall distributions of the synthetic and ICSD crystals are very similar for all four descriptors. This shows that our chosen generation algorithm reproduces crystals that are similar to ICSD crystals in terms of these more general descriptors.
3.2 Classification results
The main results of our experiments (see Section 2.5) to classify the space group of powder diffractograms can be found in Table 1. In ESI Table S2,† we further provide the training time and total number of unique diffractograms for each computational experiment. The goal of our experiments is to systematically analyse and quantify the changes in classification accuracy introduced by our two main contributions: A more challenging dataset split, and training on continuously generated synthetic data.| Split | Training dataset | Testing dataset | Model | Number of parameters | Training acc./% | Test acc./% |
|---|---|---|---|---|---|---|
| a Here, the split type refers to the statistics and the test dataset, rather than the training and the test dataset. | ||||||
| Random | ICSD | ICSD | parkCNN medium | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
88.4 | 83.2 |
| Structure type | ICSD | ICSD | parkCNN big | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 959 959![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 585 585 |
87.2 | 56.1 |
| parkCNN medium | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
90.9 | 55.9 | |||
| Structure typea | Synthetic | ICSD | parkCNN big | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 959 959![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 585 585 |
74.2 | 57.7 |
| ResNet-10 | 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395 395![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 025 025 |
87.2 | 73.4 | |||
| ResNet-50 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362 362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 385 |
91.8 | 79.3 | |||
| ResNet-101 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 354 354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
92.2 | 79.9 | |||
We started by repeating previously reported experiments11 trained directly using ICSD crystals with a random train–test split instead of the split based on structure types. This model achieved a very high test accuracy of 83.2%. We note that the previous publication that we compare our results to ref. 11 removed data from the training dataset, “[…] heavily duplicated data […]”,11 but did not specify the exact criterions used. In contrast, we did not exclude any duplicates in this experiment based on a random train–test split. Furthermore, as discussed in Section 2.1, we excluded crystals with a very high unit cell volume and a very high number of atoms in the asymmetric unit. This is likely the reason for the slightly higher classification accuracy that we observed, compared to the originally reported 81.1%.
When splitting randomly, the model merely needs to recognize structures or structure types and assign the correct space group. This task is much easier than actually extracting the space group using more general patterns. When going from random splits to structure type-based splits (see Section 2.4), it becomes obvious that both the “parkCNN big” as well as the “parkCNN medium” models overfit the training data and do not generalize well to unseen structure types in the test set (see Table 1). The “parkCNN medium” model, which achieved 83.2% on a random split, now only yields 55.9% with the structure type-based split.
Training the models by Park et al., in particular the “parkCNN big” model, on synthetic crystals leads to a 1.6 percentage points higher test accuracy than the “parkCNN big” model trained on ICSD diffractograms. At the same time, the training accuracy drops from the 87.2% when we trained the model directly on the ICSD to 74.2% on the synthetic distribution indicating that the model is now limited more by missing capacity rather than by overfitting, which is why we explored larger models, which will be discussed later. The gap between training and test accuracy is 31.1 percentage points when training on ICSD data, while for training using synthetic crystals, the gap is only 16.5 percentage points. We note that this gap between training using synthetic crystals and testing using ICSD crystals cannot stem from overfitting, since no diffractograms are repeated for the synthetic training. The difference rather stems from the differences between the synthetic distribution and the ICSD distribution of crystals.
While the “parkCNN big” model trained on synthetic crystals outperforms the approach of training directly on ICSD crystals by only 1.6 percentage points, the advantage of training on an infinite stream of synthetic data increases when using models with more parameters and thus higher capacity. In contrast to training directly on a finite set of ICSD crystals, it is possible to train very large models using the infinite synthetic data stream without the potential of overfitting. As found in the last lines of Table 1, ResNet-10, ResNet-50, and ResNet-101 based models achieve ICSD test accuracies of 73.4%, 79.3%, and 79.9%. This is a significant increase from the 57.7% achieved by the “parkCNN big” model. Fig. S4 in the ESI† further shows the top-k accuracy over k for the ResNet-101 model. With increasing k the accuracy exceeds 95% at k = 5. This means that our model can not only determine the correct space group with a high probability but can also generate an almost complete list of possible space group candidates.
Fig. 5 shows the ICSD test accuracy, the training accuracy (on synthetic data), and the ICSD top-5 test accuracy for all three ResNet variants as a function of epochs trained. For all three metrics, the difference between ResNet-50 and ResNet-101 is comparably small, while the step from ResNet-10 to ResNet-50 is substantial (5.9 percentage points in ICSD test accuracy, see Table 1). This shows that going beyond the model size of the ResNet-101 will likely not yield a big improvement in accuracy. In contrast to the 79.9% accuracy reached in the top-1 ICSD test accuracy, the top-5 ICSD test accuracy of the ResNet-101 model reaches 96%. However, for all three ResNet variants, a gap between training using synthetic crystals and testing using the ICSD remains (12.3 percentage points for ResNet-101). As also shown in Fig. S5 in the ESI,† the accuracy convergence can be approximately described by a power law, indicating that exponentially more training time will substantially reduce classification errors and thus potentially lead to top-1 accuracies of 90% and above, at the cost of a 100-fold increase in training times. Considering the current training times provided in Table S2 of the ESI,† this is currently infeasible or only possible with tremendous hardware resources.
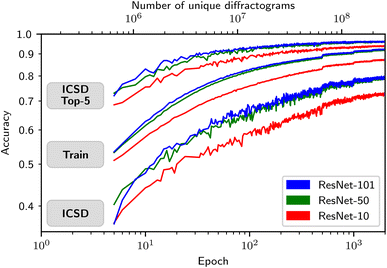 | ||
| Fig. 5 Test accuracy (ICSD), training accuracy (synthetic crystals), and test top-5 accuracy (ICSD) as a function of epochs (bottom axis). Since each additional epoch contains newly generated unique diffractograms, we further show the accuracies as a function of the total number of unique synthetic diffractograms (top axis). We show all three metrics for the models ResNet-101, ResNet-50, and ResNet-10. To better show the scaling behavior, both axes use logarithmic scaling. Fig. S6† shows the same plot but without logarithmic scaling. To better see the exponential behaviour, see Fig. S5 in the ESI.† | ||
The histograms in Fig. 4 show, next to the overall distribution, also the fraction of diffractograms classified wrongly for testing on the ICSD (red bar) and on the synthetic data (below the light blue line) for the ResNet-101 model. First, one can see that throughout almost all regions of the distributions, the accuracy on the synthetic data is slightly higher than that on the ICSD. This is related to the aforementioned gap of 12.3 percentage points between train and test accuracy and can be attributed to differences between the synthetic and ICSD distribution of crystals. This will be discussed in detail in the next section. It is surprising to see that the dependence on crystallite sizes is rather weak, as smaller crystallite sizes result in broader peaks (see Scherrer equation, eqn (1)), potentially making the classification harder due to more peak overlaps.
In summary, the maximum ICSD test accuracy of 79.9% that we achieved using the ResNet-101 model almost reaches the previously reported11 81.14% for the space group classification. However, our accuracy is based on a train–test split based on structure types, in contrast to a random split. This creates a much harder but also realistic task to solve since the model needs to generalize to other structure types without merely recognizing diffractograms or structure types that it has already seen during training. This becomes especially apparent from our experiment directly trained on diffractograms from ICSD crystals with the split based on structure types, which reached only 56.1% instead of the previously reported11 81.14%.
Vecsei et al. performed similar experiments of space group classification on the same database. Using an ensemble of 10 fully connected neural networks, they reached a classification accuracy of 54%.14 While our obtained accuracy is significantly lower, our approach is much more general: In contrast to our approach, the training dataset was based on simulated diffractograms of structures of the ICSD,14 which contains almost all RRUFF structures, leading to high similarities of training and test data. Therefore, the model needed to simply recognize the minerals, instead of directly inferring the space group using the symmetry elements - as our method needs to do.
We want to emphasize that our efforts to apply the methodology to experimental data are only preliminary. We expect improved results with an improved data generation protocol since the procedure contains many parameters to be tuned. Ideally, one would use a generative machine learning approach to add the experimental effects (noise, background, impurities) to the pure diffractograms. We also want to point out that the noise level and quality of data in the RRUFF dataset are limited. Application of the presented methodology to other experimental datasets is desirable. As discussed above, for the classification of pure diffractograms we observed the ResNet-50 to have the best cost–benefit ratio, since the ResNet-101 yielded only slight improvements. For the more complicated problem of classifying diffractograms with experimental imperfections, bigger models and longer training times might be necessary.
Next to improving the modeling of experimental imperfections and therefore the overall accuracy on experimental data, the practical application of deep neural networks for analyzing powder diffractograms yields further challenges that we want to discuss. Since experimental setups differ, e.g., concerning the used wavelength, a different 2θ step size, or a different 2θ range, a new neural network would need to be trained for each situation. Since our largest model requires a significant computational investment, this might not be feasible in all situations. Arguably, though, for large high-throughput experiments, the 11 day training of a ResNet-50 should not be unreasonable, especially if it can speed up the data analysis significantly and allow in-loop adaptive experimentation. For smaller setups, where this is not feasible, other solutions must be found. First, one can use a form of transfer learning from a pre-trained model to fine-tune to the desired experimental setup. This, however, would only work for a change in wavelength, since a change in step size or 2θ range would change the input dimensions of the network. However, to handle a change in the 2θ range, it might be possible to include a form of zero-masking in the synthetic training data, such that different input ranges (with zeros where no measurement was made) can be used, which would lead to a more flexible model, not requiring new training data when applied to a new 2θ range. For a change in the step size, a cubic spline interpolation might be helpful. We plan to address these challenges in future work.
Furthermore, analysis of the loss value or gradient norm associated with particular samples, i.e. crystal structures, during training on synthesis crystals or during transfer learning from synthetic to experimental data can help to better understand the relevance and informativeness of given samples for the model. This can help in generating more relevant synthetic data based on experimental crystal structures that are underrepresented in the synthetic data distribution.
3.3 Differences between synthetic crystals and ICSD crystals
We showed that training directly on crystals from the ICSD yields a gap between the training and test accuracy due to overfitting. The training on the synthetic dataset also shows a gap between the training and test accuracy (see Table 1), but it is smaller than when training directly on ICSD crystals. Furthermore, this gap is not due to overfitting, since overfitting to singular diffractograms is not possible when the model is trained using an infinite stream of generated synthetic crystals. The gap rather stems from systematic differences between the synthetic and ICSD distribution of crystals.To analyze those differences, we created three modifications of the ICSD test dataset (see ESI Section S3† for details). In the first modification, the fractional coordinates of the atoms in the asymmetric unit of the crystals of the ICSD test dataset were randomly uniformly resampled (as in the synthetic crystal generation algorithm). In the second modification, the lattice parameters were randomized following the kernel density estimate used in the synthetic generation algorithm. The third modification combines both previous modifications, i.e. both the coordinates and the lattice parameters were resampled. These three modified test datasets bring the ICSD test dataset closer to the distribution used for training and let us quantify which factors contribute to the gap between training on synthetic crystals and testing on the ICSD.
We evaluated the test accuracies on the randomized datasets for the experiment using the ResNet-101 model trained using synthetic crystals. We found that randomizing the coordinates yields an increase in test accuracy of 4.89 percentage points. Randomizing the lattice parameters results in an increase of 0.79 percentage points. Randomizing both the coordinates and the lattice parameters leads to an increase of 5.70 percentage points, explaining almost half of the gap of 12.3 percentage points between synthetic training and ICSD test accuracy.
So far, we have randomized the lattice parameters and coordinates of the test dataset, such that they follow a distribution that is based on the statistics extracted from the statistics dataset. However, this does not take into account the different Wyckoff position occupation probabilities between the test and statistics datasets. For this, we repeated a similar analysis, for which we applied the randomizations to the statistics dataset rather than the test dataset. Without any modifications, testing on the statistics dataset instead of the test dataset yielded 3.89 percentage points higher accuracy. This can be explained by slight differences in the overall statistics between the test and statistics datasets. Randomizing the coordinates yields a further increase of 4.72 percentage points, randomizing the lattice 1.16 percentage points, and randomizing both the coordinates and the lattice parameters 6.68 percentage points. In total, testing on the statistics dataset with randomized coordinates and lattice parameters yields a 10.57 percentage points higher accuracy than on the unmodified test dataset. This almost completely explains the gap of 12.3 percentage points between the training accuracy on synthetic crystals and the test accuracy on the ICSD. The remaining part is likely due to our algorithm that places atoms on Wyckoff positions not reproducing the ICSD distribution exactly. However, the remaining difference is remarkably small.
In Fig. 6 we show the test classification error in each bin for the unit cell volume and the number of atoms in the asymmetric unit using the ResNet-101 model trained on diffractograms of synthetic crystals. The classification error is shown both for testing on diffractograms from synthetic crystals and on ICSD diffractograms. One can see that for small volumes and a small number of atoms in the asymmetric unit, the difference between classifying ICSD diffractograms and diffractograms from synthetic crystals is relatively small. As the volume and number of atoms in the asymmetric unit increase, the gap between the two errors increases, too. We already identified the uniformly sampled atom coordinates in the synthetic distribution as the main contributor to the gap in accuracy between the synthetic crystals and ICSD crystals. Therefore, it seems that the uniform sampling of atom coordinates works well for small number of atoms in the asymmetric unit and small volumes, while the error due to this sampling strategy increases slightly for higher volumes and higher number of atoms in the asymmetric unit.
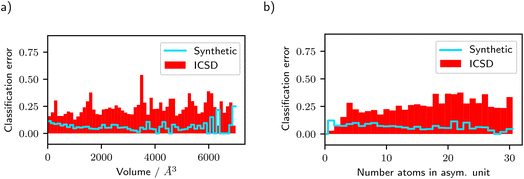 | ||
| Fig. 6 Classification error for each bin of (a) the unit cell volume (conventional cell settings) and (b) the number of atoms in the asymmetric unit. The reported classification performance is based on the ResNet-101 model trained on diffractograms from synthetic crystals. This visualization clearly shows the error rate within each bin, in contrast to Fig. 4, which additionally includes the relative proportion of the crystals of the respective bin to the total amount of crystals. | ||
When looking at the distribution of crystals in the ICSD, the number of atoms in the asymmetric unit tends to be larger for lower-symmetry space groups (for example, in the triclinic crystal system) than for higher-symmetry space groups such as those from the cubic crystal system. Therefore, the increasing test error on diffractograms from ICSD crystals with a higher number of atoms in the asymmetric unit is especially relevant for these lower-symmetry space groups. It might be possible that a different scheme of generating atom positions in the unit cell (compared to the independent uniform sampling that we used) works better for a high number of atoms in the asymmetric unit.
Overall, it is important to note that the distribution of ICSD crystals is (apart from a few Wyckoff position occupation probabilities which are exactly zero in the statistics dataset‡) almost completely encompassed by the much larger distribution of synthetic crystals that we used for training. However, due to finite training times and model capacity, a performance gap remains. This gap can be improved by using (substantially) more computing power or by narrowing the very general synthetic distribution, e.g., by using a different algorithm to generate atom positions. This indicates an inherent challenge in XRD classification but more generally in materials property prediction: Machine learning models are ultimately trained to be employed in real-world tasks, which are typically related to novel, i.e. yet unseen materials and structures. At the same time, the machine learning models are tested based on an IID assumption, i.e. the assumption that the distribution of training and testing data is the same. While not being a contradiction in the limit of infinite training data and model capacity, this becomes an (unsolvable) challenge in reality, when facing finite datasets and models. In our case, our model trained on a large distribution of synthetic crystal structures will likely generalize better to completely new crystal structures different from any crystal structure contained in the ICSD database. At the same time, it suffers from smaller ICSD test set errors, even though the ICSD distribution is contained in the synthetic data generation distribution.
4 Conclusion
We developed an algorithm based on the symmetry operations of the space groups to generate synthetic crystals that follow the distribution found in the ICSD database in terms of general descriptors like volume, density, or types of elements. The generated crystals have randomly sampled coordinates and span a wide range of structure types, many of which do not appear in the ICSD. We showed that, compared to using ICSD crystals directly, simulating the training data based on the synthetic crystals can improve the performance of tasks that extract structural information from powder diffractograms, in this case, the space group. The more general dataset that also contains unstable structures helps to classify unseen stable crystal structures.We trained on an infinite on-the-fly generated stream of synthetic crystals and simulated batches of diffractograms using a distributed framework based on the Python library Ray.25 This allows the training of very large networks without overfitting. The best-performing model (ResNet-101) reached a space group classification accuracy of 79.9% vs. 56.1% when training on ICSD structures directly. By performing the train–test split using the structure type, we forced our models to not just recognize structure types or individual structures, but to actually learn rules to distinguish different space groups by their symmetry elements. This shows the true generalization capabilities to new structure types and novel classes of materials. We also demonstrated first steps toward applying the presented methodology to an experimental dataset. We expect further improvements in this area using improved models of experimental imperfections, as well as larger ML models and longer training times.
Even though models trained on the synthetic distribution transfer well when tested on ICSD crystals, we found a gap of 12.3 percentage points (ResNet-101) between the training accuracy on synthetic crystals and test accuracy on the ICSD. We showed that the main contribution to this gap stems from the independently uniformly sampled atom coordinates. An improved approach may be needed to artificially generate more ordered structures, which contain more ordered diffraction planes than a cloud of uniformly sampled points. This might be especially important for crystals with a high number of atoms in the asymmetric unit.
Lastly, the developed algorithm to synthetically generate crystals can be used for other XRD-related tasks in the future, such as the extraction of crystallite sizes, lattice parameters, information about the occupation of Wyckoff positions, etc. Furthermore, instead of generating synthetic crystals of all space groups, one can also generate crystals of given structure types to solve more specialized tasks. This would allow the use of very large models for tasks that are typically strongly limited by the dataset size when using only the entries of the ICSD. Also, tasks concerning multi-phase diffractograms or augmentations such as strain in given crystal structures can benefit from our batch-wise online learning approach.
Data availability
The source code of all machine learning models, of the generation of synthetic crystals, of the optimized simulation of diffractograms, and of the distributed computing architecture can be found on https://github.com/aimat-lab/ML4pXRDs (v1.0). The used machine learning models are further discussed in detail in the ESI.† The ICSD data used to evaluate the models (database version 2021, June 15) belongs to FIZ Karlsruhe, from which academic and non-academic licenses are available. The RRUFF mineral database (access date: 2022, Jan 12) for the evaluation on experimental data can be obtained from https://rruff.info/.Author contributions
All authors contributed to the idea and the preparation of the manuscript. H. S. implemented the methods and conducted the computational experiments.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
P. F. acknowledges support by the Federal Ministry of Education and Research (BMBF) under Grant No. 01DM21001B (German-Canadian Materials Acceleration Center). H. S. acknowledges financial support by the German Research Foundation (DFG) through the Research Training Group 2450 “Tailored Scale-Bridging Approaches to Computational Nanoscience”. The authors acknowledge support by the state of Baden-Württemberg through bwHPC. Parts of this work were performed on the HoreKa supercomputer funded by the Ministry of Science, Research and the Arts Baden-Württemberg and by the Federal Ministry of Education and Research.References
- A. Radovic, M. Williams, D. Rousseau, M. Kagan, D. Bonacorsi, A. Himmel, A. Aurisano, K. Terao and T. Wongjirad, Nature, 2018, 560, 41–48 CrossRef CAS PubMed.
- F. Rahmanian, J. Flowers, D. Guevarra, M. Richter, M. Fichtner, P. Donnely, J. M. Gregoire and H. S. Stein, Adv. Mater. Interfaces, 2022, 9, 2101987 CrossRef.
- K. D. M. Harris, M. Tremayne and B. M. Kariuki, Angew. Chem., Int. Ed., 2001, 40, 1626–1651 CrossRef CAS PubMed.
- C. F. Holder and R. E. Schaak, ACS Nano, 2019, 13, 7359–7365 CrossRef CAS PubMed.
- J.-W. Lee, W. B. Park, J. H. Lee, S. P. Singh and K.-S. Sohn, Nat. Commun., 2020, 11, 86 CrossRef CAS PubMed.
- P. M. Maffettone, L. Banko, P. Cui, Y. Lysogorskiy, M. A. Little, D. Olds, A. Ludwig and A. I. Cooper, Nat. Comput. Sci., 2021, 1, 290–297 CrossRef.
- J. Schuetzke, A. Benedix, R. Mikut and M. Reischl, IUCrJ, 2021, 8, 408–420 CrossRef CAS PubMed.
- N. J. Szymanski, C. J. Bartel, Y. Zeng, Q. Tu and G. Ceder, Chem. Mater., 2021, 33, 4204–4215 CrossRef CAS.
- H. Wang, Y. Xie, D. Li, H. Deng, Y. Zhao, M. Xin and J. Lin, J. Chem. Inf. Model., 2020, 60, 2004–2011 CrossRef CAS PubMed.
- J.-W. Lee, W. Bae Park, M. Kim, S. P. Singh, M. Pyo and K.-S. Sohn, Inorg. Chem. Front., 2021, 8, 2492–2504 RSC.
- W. B. Park, J. Chung, J. Jung, K. Sohn, S. P. Singh, M. Pyo, N. Shin and K.-S. Sohn, IUCrJ, 2017, 4, 486–494 CrossRef CAS PubMed.
- F. Oviedo, Z. Ren, S. Sun, C. Settens, Z. Liu, N. T. P. Hartono, S. Ramasamy, B. L. DeCost, S. I. P. Tian, G. Romano, A. Gilad Kusne and T. Buonassisi, npj Comput. Mater., 2019, 5, 1–9 CrossRef CAS.
- A. N. Zaloga, V. V. Stanovov, O. E. Bezrukova, P. S. Dubinin and I. S. Yakimov, Mater. Today Commun., 2020, 25, 101662 CrossRef CAS.
- P. M. Vecsei, K. Choo, J. Chang and T. Neupert, Phys. Rev. B, 2019, 99, 245120 CrossRef CAS.
- Y. Suzuki, H. Hino, T. Hawai, K. Saito, M. Kotsugi and K. Ono, Sci. Rep., 2020, 10, 21790 CrossRef CAS PubMed.
- A. Chakraborty and R. Sharma, Vis. Comput., 2022, 38, 1275–1282 CrossRef.
- Y. Ozaki, Y. Suzuki, T. Hawai, K. Saito, M. Onishi and K. Ono, npj Comput. Mater., 2020, 6, 1–7 CrossRef.
- Z. Feng, Q. Hou, Y. Zheng, W. Ren, J.-Y. Ge, T. Li, C. Cheng, W. Lu, S. Cao, J. Zhang and T. Zhang, Comput. Mater. Sci., 2019, 156, 310–314 CrossRef.
- H. Dong, K. T. Butler, D. Matras, S. W. T. Price, Y. Odarchenko, R. Khatry, A. Thompson, V. Middelkoop, S. D. M. Jacques, A. M. Beale and A. Vamvakeros, npj Comput. Mater., 2021, 7, 1–9 CrossRef.
- S. R. Chitturi, D. Ratner, R. C. Walroth, V. Thampy, E. J. Reed, M. Dunne, C. J. Tassone and K. H. Stone, J. Appl. Crystallogr., 2021, 54, 1799–1810 CrossRef CAS PubMed.
- S. Habershon, E. Y. Cheung, K. D. M. Harris and R. L. Johnston, J. Phys. Chem. A, 2004, 108, 711–716 CrossRef CAS.
- L. Banko, P. M. Maffettone, D. Naujoks, D. Olds and A. Ludwig, npj Comput. Mater., 2021, 7, 1–6 CrossRef.
- G. Bergerhoff and I. Brown, Crystallographic Databases, 1987 Search PubMed.
- B. Lafuente, R. T. Downs, H. Yang and N. Stone, The Power of Databases: The RRUFF Project in Highlights in Mineralogical Crystallography, De Gruyter (O), 2015 Search PubMed.
- P. Moritz, R. Nishihara, S. Wang, A. Tumanov, R. Liaw, E. Liang, M. Elibol, Z. Yang, W. Paul, M. I. Jordan and I. Stoica, 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18), 2018, pp. 561–577 Search PubMed.
- S. Fredericks, K. Parrish, D. Sayre and Q. Zhu, Comput. Phys. Commun., 2021, 261, 107810 CrossRef CAS.
- Y. Sun, A. K. C. Wong and M. S. Kamel, Int. J. Pattern Recogn. Artif. Intell., 2009, 23, 687–719 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- S. K. Lam, A. Pitrou and S. Seibert, Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, New York, NY, USA, 2015, pp. 1–6 Search PubMed.
- International Tables for Crystallography Volume H: Powder Diffraction, ed. C. J. Gilmore, J. A. Kaduk and H. Schenk, Wiley, 1st edn, 2019 Search PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 770–778 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00071k |
| ‡ Setting them to small non-zero values typically leads to the generation of rather large unit cells, as the general Wyckoff positions have high multiplicities. |
| This journal is © The Royal Society of Chemistry 2023 |