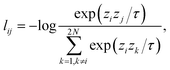Incorporation of density scaling constraint in density functional design via contrastive representation learning

Abstract

In a data-driven paradigm, machine learning (ML) is the central component for developing accurate and universal exchange–correlation (XC) functionals in density functional theory (DFT). It is well known that XC functionals must satisfy several exact conditions and physical constraints, such as density scaling, spin scaling, and derivative discontinuity. However, these physical constraints are generally not incorporated implicitly into machine learning through model design or pre-processing on large material datasets. In this work, we demonstrate that contrastive learning is a computationally efficient and flexible method to incorporate a physical constraint, especially when the constraint is defined by an equality, in ML-based density functional design. We propose a schematic approach to incorporate the uniform density scaling property of electron density for exchange energies by adopting contrastive representation learning during the pretraining task. The pretrained hidden representation is transferred to the downstream task to predict the exchange energies calculated by DFT. Based on the computed electron density and exchange energies of around 10 000 molecules in the QM9 database, the augmented molecular density dataset is generated using the density scaling property of exchange energy functionals based on the chosen scaling factors. The electron density encoder transferred from the pretraining task based on contrastive learning predicts exchange energies that satisfy the scaling property, while the model trained without using contrastive learning gives poor predictions for the scaling-transformed electron density systems. Furthermore, the model with pretrained encoder gives satisfactory performance with only small fractions of the whole augmented dataset labeled, comparable to the model trained from scratch using the whole dataset. The results demonstrate that incorporating exact constraints through contrastive learning can enhance the understanding of density-energy mapping using neural network (NN) models with less data labeling, which will be beneficial to generalize the application of NN-based XC functionals in a wide range of scenarios which are not always available experimentally but are theoretically available and justified. This work represents a viable pathway toward the machine learning design of a universal density functional via representation learning.

---

1 Introduction

Density functional theory (DFT) is an indispensable tool in computational chemistry and materials science due to its combination of efficiency and accuracy.^1,2 As the standard computational method that is widely applied in physics, chemistry, and materials research, DFT has achieved high prediction accuracy enabled by the continued development of approximations of the exchange–correlation (XC) energy as a functional of electron density.^3–7 An appropriately approximated density functional enables more accurate first-principles calculations for molecules and material systems on a larger scale. In different forms of approximations, the XC functionals must satisfy several exact conditions and constraints,⁸ such as uniform scaling property,⁹ spin scaling property¹⁰ and derivative discontinuity.¹¹ So far, all popular approximations suffer from systematic errors that arise from the violation of mathematical properties of the exact functional. It is expected that the performance and generality of density functionals can be improved by satisfying these constraints. For instance, the recently developed strongly constrained and appropriately normed (SCAN) functional⁷ that satisfied 17 exact constraints achieved great performance for both molecules and solids. Despite the development made so far, there is no systematic way to discover or satisfy more exact constraints and appropriate norms. Alternatively, in a data-driven paradigm, machine learning (ML) provides a possible route to make the density functionals both more predictive and more interpolative,⁸ by imposing the exact constraints during the training process. There has been a growing interest in applying ML in physics, chemistry, and materials science, with the aim of achieving the same or even higher prediction accuracy for molecules and materials with much less computational cost compared to first principles simulations. Recently, ML has been applied to parametrize XC functionals without domain knowledge of humans by using various methods such as kernel ridge regression (KRR),¹² fully connected neural networks (NN)^13–15 and convolutional neural networks (CNN).¹⁶ Being trained in a supervised manner, these ML models are highly accurate across a small set of molecule systems similar to those on which the models are trained, while in many cases they show a worse performance on larger molecular datasets than they do on small ones. Neither of them demonstrates the same level of universality compared to conventional XC functionals.

Plenty of effort has been devoted to leveraging physical constraints in ML of XC functionals. In a previous work by Lei et al.,¹⁶ by using CNN as encoders, rotationally invariant descriptors were extracted and projected on a basis using spherical harmonic kernels. In another work by Hollingsworth et al.,¹⁷ it was found that the scaling property, which is one of the exact conditions that the exchange energy must satisfy, can be utilized to improve the machine learning of XC functionals. The study is limited to one-dimensional systems and lacks the generalizability to two- and three-dimensional systems. Machine-learning can however follow human-devised strategies to satisfy exact constraints faithfully, even in three dimensions. This is especially true for semilocal functional forms, such as GGAs and meta-GGAs. In this way, the SCAN meta-GGA,⁷ which satisfies 17 exact constraints, has been combined with machine-learning in the works of Dick and Fernandez-Serra¹⁴ and of Nagai, Akashi, and Sugino.¹⁸ In these works, the uniform density scaling constraint on the exchange energy functional is satisfied exactly by employing an exchange enhancement factor that is a machine-learned function of semilocal descriptors d(r) that scale to d(γr) when the electron density n(r) scales to γ³n(γr). Ref. 18 preserved many of the exact constraints satisfied by SCAN in a machine-learned functional fitted to data for small molecules. These works suggest that SCAN is close to the limit of what a meta-GGA can achieve, but that meta-GGA accuracy for molecules can still be boosted by machine learning. The approach that we will present here satisfies the uniform density scaling constraint only approximately, but is not limited to human-devised functional forms. More recently, another exact condition – derivative discontinuity – was incorporated into the NN-based XC functional design,¹⁹ while the study is again limited to one-dimensional systems. A more recent work has demonstrated that the fundamental limitation can be overcome by training a neural network on molecular data and on fictitious systems with fractional charge and spin,²⁰ and the resulting NN-based functional DeepMind-21 demonstrated the universality and greatly improved predictive power for molecule energetics and dynamics. At the same time this work was written, schemes incorporating the Lieb–Oxford bound²¹ and spin scaling property¹⁰ into the machine learning density functional design were proposed.²²

Many of the previous works use data augmentation to improve model performance by directly increasing the amount of labeled data following a given physical constraint. However, increasing the amount of data is not always possible due to the computational cost. Going beyond data augmentation, self-supervised learning has gained popularity because of its ability to avoid the cost of annotating large-scale datasets. It adopts self-defined pseudo labels as supervision and uses the learned representations for downstream tasks. Self-supervised learning has been widely used in image representation learning²³ and natural language processing,²⁴ and has been applied in molecular machine learning.^25,26 Specifically, contrastive learning (CL) has recently become a dominant branch in self-supervised learning methods for computer vision, natural language processing, and other domains.²⁷ It aims at embedding augmented versions of the same sample close to each other while trying to push away embeddings from different samples in the representation space. The goal of contrastive learning is to learn such an embedding space in which similar sample pairs stay close to each other while dissimilar ones are far apart, and the CL process can be applied in both unsupervised and supervised settings.²⁸ In molecular systems, the application of contrastive learning, in conjunction with molecular graph representation,^29–31 has emerged as an effective strategy. This method has shown promise in enhancing predictive accuracy and training efficiency, particularly in scenarios where data availability is limited. In this work, we will explore the incorporation of physical constraints in density functional learning through contrastive learning.

One of the most important and fundamental constraints for the exchange energy of an electron system is derived from the principle of uniform scaling.⁹ Consider an electron density distribution n(r) and a uniformly scaled density

n_γ(r) = γ³n(γr)

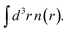where γ is a positive factor that scales the density around an arbitrary origin for r without changing the electron number Uniform scaling preserves the shape of the density, apart from an overall change of length scale. (Unless the origin of r is at the center of electronic charge, scaling also translates that center relative to the origin, from 〈r〉 to 〈r〉/γ.) Several important exact constraints on density functionals can be written using the scaled density. In this work, we focus on the exchange energy E_x[n], and its scaling property:⁹

E_x[n_γ] = γE_x[n]

This important constraint is satisfied exactly in almost all human-designed density functionals, whether non-empirical or semi-empirical. As a chemical example, atomic one-electron ions of nuclear charge Z are scaled versions of the hydrogen atom with scale factor γ = Z. The exchange energy, −5Ze²/(16a₀), in this case cancels the Hartree electrostatic interaction of the density with itself. Using this constraint as an important and illustrative example, we propose a schematic approach to incorporate any physical constraints (represented by equalities) via contrastive learning into the NN-based model design.

Specifically, we found that traditional supervised learning without data augmentation was not able to incorporate the scaling constraint into the ML functional when training the electron density encoder solely on a dataset of unscaled electron densities, as the model demonstrated a lack of extrapolability on scaled densities. To incorporate the scaling constraint, we chose to pre-train an electron density encoder by maximizing the similarity between molecular electron density and its scaled version with a randomly chosen scaling factor, within the framework of SimCLR,³² which is a widely used framework for contrastive learning of image pretraining. To obtain an encoder that gives similar representations (while different by a scaling factor) for scaled and unscaled electron densities, we added a scaling factor predictor component to the framework. The pre-trained encoder was then transferred to the downstream task to predict the exchange energies of scaled electron densities of molecule systems. We compared the model performance using this method with that of supervised learning with data augmentation. It is found that the model pretrained using contrastive learning is able to make predictions that are more consistent with the scaling relation and outperforms the supervised learning model in terms of predicting exchange energies. We will show that contrastively learned encoders are capable of encoding molecular electron density with less labeling cost based on the fact that they give comparable predictions by fine-tuning using only a small percentage of labeled data, compared to the model trained on the whole labeled dataset by supervised learning. This shows that contrastive learning using constraints can enhance the understanding of DFT theory for neural network models with a small amount of labeled data while generalizing the application of NN XC functionals in a wide range of scenarios which are not always available experimentally but are theoretically available and justified.

2 Results

2.1 Grid-based electron density

In this work, self-consistent energy density matrices were calculated for ∼10 000 molecular systems following the procedures described in the Methods section. These matrices were then projected onto a grid of size (129, 129, 129) within a cube of edge length 40 angstroms to create the unscaled density n(r), with the center of mass located at the center of the cube. To generate the scaled density n_γ(r), the uniform density scaling constraint of n_γ(r) = γ³n(γr) was applied by taking the value of n(r) at γr and multiplying it by γ³. Inherent to this model choice for representing electron densities, using a larger number of grids generally leads to improved model performance. However, it is necessary to achieve a balance between model performance and computational cost, as the storage requirement for the volumetric data and the training time for the model will increase exponentially with the size of the grid. To partially mitigate this issue, we implemented a down-sampling technique. The input data on the (129, 129, 129) grid is passed to a fully connected linear layer with a rectified linear unit (ReLU) activation to create data on a (65, 65, 65) grid. The down-sampled data have more information than those data obtained by projecting the density matrix directly on a (65, 65, 65) grid. A comparison of model performance with and without down-sampling is provided in the ESI.†

2.2 Electron density encoder

In the language of machine learning, an encoder usually refers to a model that transforms the raw input data into a desired representation, typically with a smaller size. In this work, to efficiently handle a large amount of three-dimensional grid-based electron density data, the 3D convolutional neural network with a Residual Network (ResNet) architecture was used as the electron density encoder. A brief introduction of ResNet is given in the ESI.†

2.3 Contrastive learning of uniform density scaling property

Contrastive learning (CL) is a self-supervised learning (SSL) strategy that learns useful representations using unlabeled data by manually designing pre-training tasks with automatically generated labels or label relations. Typically, when applied in image recognition, data augmentations such as random shifting, random cropping and random rotation are applied to generate different views of images. The raw and augmented images are then passed to an image encoder to generate hidden representations that are passed to a projection head projecting representations onto a high dimensional unit sphere. The projected representations are used to calculate contrastive loss that maximizes the similarity between projected representations of the same input image, while minimizing the similarity between those of different images. By minimizing contrastive loss and updating the model parameters through backpropagation, the image encoder is aware that the different views are from the same raw image, which introduces invariance to the model for imperfect inputs. Intuitively, an encoder trained by contrastive learning groups different views of the same image into the same cluster while pushing clusters from different images far away from each other.

In this work, we intend to design a pre-training task such that the electron density encoder is aware of the uniform density scaling property. In order to do so, unscaled and scaled electron densities on a fixed-size spatial grid are generated using the PySCF code³³ with low computation cost, represented as three-dimensional arrays x_i, x̃_iγ ∈ [Doublestruck R]^d×d×d, where the scaling factor γ is chosen from five different scales: 1/3, 1/2, 1, 2, and 3. The scaled density is then translated randomly in the three-dimensional space to incorporate the translational symmetry. We included translational symmetry because our uniform density scaling translates the center of electronic charge, but this additional constraint was not found to be numerically important (Table 1). Electron density arrays are encoded as hidden representations h_i = f(x_i), h̃_iγ = f(x̃_iγ) ∈ [Doublestruck R]^m through the density encoder that is a mapping f: [Doublestruck R]^d×d×d → [Doublestruck R]^m to be learned. The hidden representations are then projected as a set of points z_i = g(h_i) ∈ [Doublestruck R]ⁿ on a high dimensional unit sphere by a mapping g: [Doublestruck R]^m → [Doublestruck R]ⁿ (n < m) that is a multilayer perceptron (MLP). For a batch of N molecules, the output Z ∈ [Doublestruck R]^2N×m contains projected representations of unscaled and scaled densities. Then we calculate the normalized temperature-scaled cross entropy (NT-Xent) loss³² that is defined as:

where the temperature factor τ is a small positive real number, and the exponential term when k = i is excluded in the summation in the denominator to ensure that the loss is zero if dissimilar projected representations are antiparallel and similar ones are parallel. Details on the NT-Xent loss are provided in the ESI.†

Table 1 The MAE of ResNet (in eV) for predicting exchange energies of molecule systems in the QM9 database. A down-sampling is applied to the input data to down-sample the data on grid (129, 129, 129) to a grid (65, 65, 65). Performance is tested for a model trained from scratch in a supervised manner and models trained in a contrastive learning (with and without random translations) plus transfer learning scheme with train/validate split. MAE on unscaled (1000 data with scale equals to 1) and scaled (5000 data with 5 different scales) test sets is used to represent the model performance

Train/validate split	MAE on test set (eV)
	Unscaled (size = 1000) (γ = 1)	Scaled (size = 5000) (γ = 1/3, 1/2, 1, 2, 3)
Supervised learning with data augmentation
40 000/5000	0.481	0.757
Contrastive + transfer learning
40 000/5000	0.461	0.739
32 000/5000	0.505	0.874
24 000/5000	0.561	0.932
16 000/5000	0.738	1.070
8000/5000	0.973	1.289

---

In the original SimCLR framework,³² augmented and unaugmented views of the same input form positive pairs, while those of different inputs form negative pairs. We would emphasize that, without any modules added to distinguish positive pairs, the encoder trained would be too “lazy” to learn different representations for the two “views” of the same input, since the simplest mapping f that minimizes the loss learns the same hidden representation for the augmented and unaugmented input from the same image, which satisfies h̃_iγ = f(x̃_iγ) = f(x_i) = h_i. Therefore, a module predicting the scaling factor from two hidden representations of the same molecule is added to distinguish the scaled density data from unscaled data. The final loss of the contrastive pretraining task is the summation of these two losses. The workflow of the pretraining task is shown in Fig. 1(a).

Fig. 1 (a) The workflow of the proposed contrastive learning framework. For a given molecule, an unscaled and a scaled and translated electron density are fed into the density encoder to obtain hidden representations. The subsequent modules are divided into two parts: a projection head that produces the projected representations, from which the contrastive similarity loss is calculated; a scale predictor that predicts the scaling factor from the hidden representation pairs, from which the mean squared error loss is calculated. (b) The two electron densities from the same molecule form positive pairs, while those from different molecules form negative pairs. (c) The visualization of general contrastive learning. Multiple “views” of the same input molecule are generated by data augmentation. After encoding and projection, representations from the same molecule attract each other, while those from different molecules repel each other. (d) The architecture of the density encoder, the projection module, and the ResNet building block.

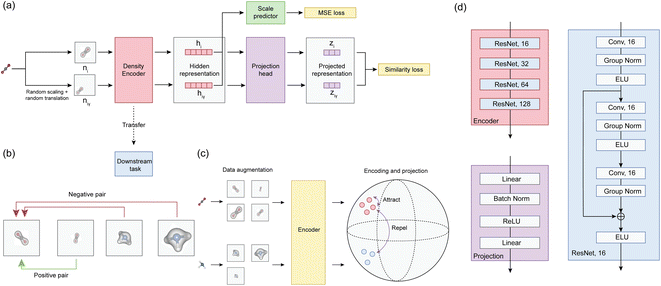
The cosine similarity of learned projected representations z and z̃ for a batch of 32 molecules is shown in Fig. 2(a). As expected, the cosine similarity shows maximum values for positive pairs – unscaled and scaled densities of the same molecules, while the value is close to zero for negative pairs – densities of different molecules. As shown in Fig. 2(b), we further verify that projected representations of different molecules are well separated from each other by computing the t-distributed neighbor embedding (t-SNE). In Fig. 2(c), two examples of molecules, learned projected representations and predictions on scaling factors are shown. The best model achieves 0.01976 contrastive loss and 2 × 10⁻⁴ mean square error for scaling factor prediction.

Fig. 2 (a) The cosine similarity between the learned projected representations of unscaled and scaled densities for a batch of 32 molecules. Each element in the matrix is computed as cos(z_i, z̃_j): = z_iz̃_j. The brighter it is, the closer the value is to 1. (b) The t-distributed stochastic neighbor embedding (t-SNE) of 32 learned projected representations. (c) Two molecule examples, the corresponding learned projected representations, and the predictions on scaling factors.

2.4 Supervised learning using unscaled electron densities

Supervised learning of neural networks is one of the most widely used machine learning strategies in materials science. In machine learned-XC functionals, by training with a large amount of electron densities with the corresponding exchange energies, the model can give predictions with a small discrepancy with the energy values. However, one of the limitations of supervised learning is the fact that an outstanding performance on a given dataset does not guarantee equally good performance on other datasets. In this section, we will show that the model trained by supervised learning on unscaled density data achieves a very high prediction accuracy for predicting exchange energies from unscaled molecular electron densities, but at the same time demonstrates a large prediction error for scaled densities. This observation clearly shows that the model trained on unscaled density dataset with supervised learning does not understand the uniform scaling property that exchange energy functionals must satisfy.

Within the data-driven paradigm, the mapping of molecular electron density to the exchange energy is directly learned in a supervised manner by feeding electron densities to an electron density encoder, with the corresponding exchange energies calculated from first-principles calculations as the learning targets. Electron density in three-dimensional space is represented by a three-dimensional array, with the dimension along each axis equal to the grid dimension along the same axis. Encoding and decoding of volumetric data in three-dimensional space has been previously studied in 3D-UNet,³⁴ with a DoubleConv layer consisting of two subsequent 3D convolutional layers as the building block. In the same 3D-UNet framework, instead of DoubleConv, residual networks can be used as the building block to extract useful information from raw three-dimensional volumetric data.³⁵ In this work, the mapping of electron density to the exchange energy will be learned, so only the encoder part will be adopted from 3D-UNet. The encoder consists of several connected building block layers, being either DoubleConv or ResNet (see Methods). Due to the fact that ResNet outperforms DoubleConv for our learning tasks, as shown in the ESI,† we chose ResNet as the building block of the encoder.

The architecture of the encoder is shown in Fig. 1(b). A hidden representation that captures density-energy correlation is learned and fed to a subsequent fully connected prediction layer to give a single value prediction on the exchange energy. The original electron densities of molecules (with a scaling factor equal to one) are included in the dataset. For reliable evaluation of the models, the dataset is split into 80%, 10%, and 10% as training, validation, and testing datasets, containing 8000, 1000, and 1000 unscaled data, respectively. The training set is employed to train the model for 500 epochs by minimizing the mean squared error (MSE) loss, and the model is then applied to validate the performance on the testing set using the mean absolute error (MAE) as the measure.

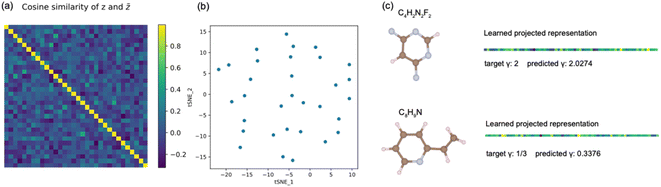
To investigate whether the model trained with only unscaled densities understands the uniform density scaling property, we test its performance on both unscaled and scaled density datasets. As shown in Fig. 3(a), the difference in energy between predictions and targets on the unscaled dataset is close to 0.45 eV on average. Instead of minimizing this prediction error for unscaled electron density by improving existing learning frameworks, the focus in this work is to demonstrate the role of contrastive learning in the process of incorporating physical constraints in density functional design. A clear observation is that the model does not provide reasonable predictions for the exchange energies of the scaled density dataset. This indicates that the models trained in a supervised manner using only unscaled density in general do not satisfy the uniform density scaling property and thus give unreliable predictions for scaled densities, although they may achieve very high accuracy on the unscaled density dataset. This motivates us to apply contrastive learning in a pretraining task to give our model the ability to understand the density scaling property. As shown in Fig. 3(b), the model trained by our approach provides reasonable predictions even for scaled electron density. This shows the capability of the model trained by our approach to obey the uniform density scaling property.

Fig. 3 Performance comparison of supervised learning model and contrastive learning model on datasets with different scaling factors. (a) Supervised learning model (without data augmentation) shows large prediction errors on scaled datasets. (b) Model trained by contrastive learning give much more reliable predictions on all datasets (both scaled and unscaled).

2.5 Contrastive learning model performance with different amounts of training data

Now we investigate the model for predicting exchange energies from electron densities. The density encoder part of the model is transferred from the contrastive pretraining task. In a comparative test, the model is trained from scratch and its performance is compared to the transferred model. When fine-tuning the transferred model, we adopt five different training/validation/testing data splits: 40 000/5000/5000, 32 000/5000/5000, 24 000/5000/5000, 16 000/5000/5000 and 8000/5000/5000. As shown in Table 1, using the same dataset, our approach outperforms supervised learning with data augmentation in terms of exchange energy prediction accuracy, as demonstrated by smaller mean absolute errors (MAE) after fine-tuning with the same amount of training data (40 000). Based on this set of results, we can estimate that the two learning approaches may achieve the same prediction accuracy on a training dataset with size between 32 000 and 40 000. It demonstrates that our contrastive learning model can reduce the need for a large amount of data while achieving comparable performance.

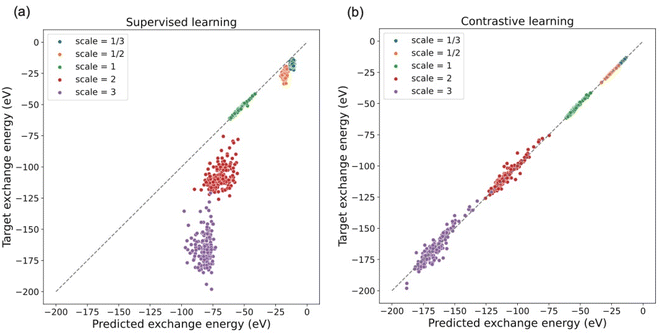
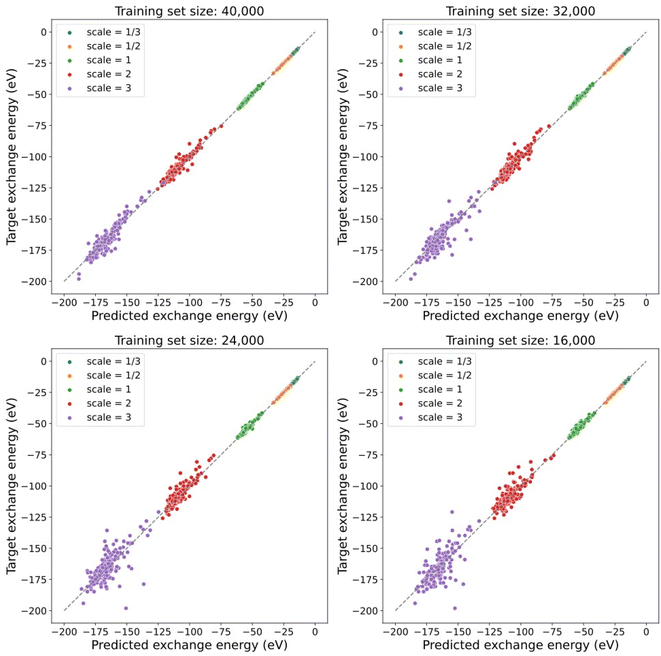
Furthermore, the model trained with the contrastive learning method gives a prediction of exchange energies that satisfy the uniform density scaling property. As shown in Fig. 4, predicted and target exchange energies demonstrate a strong linear correlation even when the number of training data is decreased. Note that for the case of using 8000 training data, the model uses the same number of training data as that of the supervised learning task in a previous section. The dramatic difference of performance between models shown in Fig. 3 shows the understandability of uniform scaling property which is enabled by our proposed models. Because of the choice of using the same uniform grids for both scaled and unscaled densities, when the electron densities are “squeezed”, the number of effective grid points with finite density values is decreased. As a result, the prediction accuracy for the scaled electron densities with γ > 1 is in general worse. Note that the model prediction accuracy can be further improved by using nonuniform density grids or representing the electron densities by a set of local orbitals.¹⁴ Alternatively, this can be addressed in future studies by learning the exchange energy directly from density matrices instead of a projected uniform grid with limited resolution.

Fig. 4 Performance of contrastively pre-trained models fine-tuned with four different training set sizes. The model keeps the capability to give predictions of exchange energies with relatively small error even when the number of training data decreases.

Note that our contrastive learning model demonstrates the interpolatability to provide predictions of exchange energies satisfying the uniform scaling property for electron densities with random scaling factors that are not present in the training data. This demonstrates the capability of our contrastive learning approach when generalizing to those scaling factors not seen during training. The details of the interpolatability test are provided in the ESI.†

3 Discussion

In this work, contrastive learning is adapted to a pretrained electron density encoder to incorporate the uniform density scaling property for exchange energy predictions. Generated from first-principles calculations, the scaled and unscaled electron densities of molecules from the QM9 dataset are used to contrastively train the electron density encoder. Scaled and unscaled densities of the same molecule are treated as similar pairs, while those from different molecules as dissimilar ones. The pretrained model achieves a 0.01976 contrastive loss. It also predicts the scaling factors from hidden representations of scaled and unscaled densities, with a 2 × 10⁻⁴ MSE accuracy. The encoder is then transferred to a downstream task to predict the computed exchange energies from electron densities with different scaling factors. Using contrastive learning as the pretraining method, our model performs well for the prediction of exchange energies of both scaled and unscaled electron densities that satisfy the uniform scaling property, while the model trained using only unscaled densities in a supervised manner demonstrates unreliable performance for the prediction of exchange energies of scaled densities. This clearly demonstrates that contrastive learning is an effective approach in a data-driven paradigm to enable the neural network to learn physical principles in the process of mapping electron densities to energies.

We expect that the MAE can be further reduced by increasing the training steps or using a larger dataset. Our model currently includes only 10 000 molecules from the QM9 dataset. Adding more molecules will improve the prediction accuracy. The dataset we used, which is based on a large cubic grid of dimensions (129 × 129 × 129), is approaching the limits of our computation power. According to the DM21 study,²⁰ using a different type of grid such as the Treutler grid³⁶ might improve our model's efficiency and accuracy.

In the current study, our methods yield non-self-consistent predictions, which means we obtain energy values directly from the electron densities without adjusting or repeating the predictions until they converge based on a required accuracy. A method for incorporating ML in self-consistent predictions is suggested in a recent work,³⁷ which incorporates a machine learning module that predicts exchange–correlation energy from electron densities and works in combination with other modules that solve the Kohn–Sham equations and extract kinetic energies. In this framework, the exchange–correlation potential can be obtained by taking the functional derivative of the predicted exchange–correlation energy functional through automatic differentiation. The self-consistent energy can therefore be obtained by following the workflow from ref. 37. From this point of view, the development of accurate and efficient machine learning models for predicting the energies of electron densities can greatly accelerate the self-consistent Kohn–Sham calculations.

The method proposed in this study is most effective for incorporating constraints formulated as equalities. This presents an opportunity for incorporating more equality-based constraints among the 17 exact constraints. For instance, the spin scaling property,¹⁰ size-extensivity property, and the second-order gradient expansion³⁸ are likely candidates for applying our proposed contrastive learning method to push forward the development of universal and accurate machine learning density functionals.

4 Conclusions

In conclusion, we show that contrastive learning can be used as an adaptive and effective method to incorporate the uniform scaling property of DFT theory into the machine learning model design. Moreover, the contrastive learning method proposed in this work has the potential to be generalized to other exact physical constraints, such as rotational symmetry, spin scaling property, and so on. Incorporating physical constraints into machine learning model design through contrastive learning can lead to a significant reduction of the need of training data while providing insights into the machine learning XC density functionals and beyond.

A similar effect occurs with human-designed density functionals: those that are constructed to satisfy more exact constraints require fewer fit parameters that can be determined from smaller sets of molecular data, and a nonempirical meta-GGA functional⁷ satisfying 17 exact constraints can perform rather well without any fitting to molecular data. The improvement of generalized gradient approximations (GGAs) or meta-GGAs by their global hybridization³⁹ with exact exchange is a good example, since the exact constraints on the underlying GGA or meta-GGA are preserved for any value of the fraction of exact exchange that is mixed with a complementary fraction of GGA or meta-GGA exchange.

Appendix

A Methods

A.1 Molecular electron density dataset. We chose 10 000 molecules from the QM9 dataset^40,41 by imposing the following criteria: (i) each molecule contains less than 20 atoms; (ii) each molecule does not contain atoms with an atomic number larger than 36 (element Kr); (iii) the size of each molecule is less than 12 angstroms; and (iv) the DFT calculated exchange energy of the molecule should be greater than −200 eV. Molecular density matrices are calculated by DFT with the PBE functional³ as implemented in the PySCF package.³³ To prepare the grid-like input data with fixed dimensions, we project the density matrices onto real space grid points with a shape (65, 65, 65) on a fixed size cube centered at the origin with a length of 40 angstroms. The number of grid points is set to odd integers to include the origin. A larger grid with shape (129, 129, 129) is also used to construct more detailed density data. Due to the limit of storage for the whole dataset, an average pooling down-sampling pre-process is applied to reduce the grid dimensions from 129 to 65. A comparison of the results using these two grids is given in the ESI.† The projection of density matrices on grids in three-dimensional space is performed by using the PySCF code.³³ The exchange energies are calculated from the density matrices as they would be in Hartree–Fock or exact exchange theories using the NWChem code.⁴²

A.2 Training and evaluation of supervised learning task. To demonstrate that the model trained with supervised learning without data augmentation does not understand the uniform scaling property, supervised learning was performed on unscaled dataset. The dataset contains the unscaled electron density in real space of 10 000 molecules from QM9 dataset. To find out the best model that encodes the electron density, two different types of building block layers: ResNet and DoubleConv, were tested to build the density encoder. The model was built and trained using the PyTorch-Lightning package⁴³ which is a framework based on the PyTorch package.⁴⁴ The whole dataset is split into 80%, 10% and 10% for training, validation and testing, containing 8000, 1000 and 1000 data samples, respectively. Training loss is backpropagated to update the model parameters by an Adam optimizer⁴⁵ with a learning rate of 0.001. The best model was chosen to be that with the smallest MAE after 500 epochs.

A.3 Training and evaluation of contrastive learning task. The dataset consists of electron densities of 10 000 molecules chosen from QM9 dataset. Each raw electron density is augmented by a scaled one with the scaling factor chosen from 1/3, 1/2, 1, 2, and 3, leading to a dataset with 50 000 data. The scaled density is then translated randomly in the three-dimensional space. As a result of hyperparameter searching, ResNet with feature maps (16, 32, 64, 128) and DoubleConv with feature maps (32, 64, 128) are chosen for the comparison of performance on the downstream task. The whole dataset is split into 80%, 10% and 10% for training, validation and testing, containing 40 000, 5000 and 5000 data, respectively. (See Fig. 3 and 4, and Table 1.) The total training loss is the summation of contrastive loss and scaling factor prediction loss, which is then backpropagated to update the model parameters by an Adam optimizer with a learning rate of 0.001. The best model was chosen to be that with smallest total loss after 1000 epochs.

A.4 Training and evaluation of downstream task using transfer learning and supervised learning. The dataset consists of original unscaled and four augmented electron densities that are scaled by four scaling factors (1/3, 1/2, 2, and 3) for 10 000 molecules chosen from the QM9 dataset, resulting in a dataset containing 50 000 electron densities. The whole dataset is split into 80%, 10% and 10% for training, validation and testing, with a total of 40 000 training data, 5000 validation data and 5000 testing data. The model consists of an encoder that transferred from the contrastive learning task and a simple linear layer. For a given scaled density data n_γ, the model predicts the scaling factor γ and the unscaled exchange energy E_γ=1 from which the predicted scaled energy can easily been calculated by E_γ = γE_γ=1. The total loss is calculated by the mean squared error between the real and predicted γ and E_γ=1. To ensure a fair comparison, we also train a model from scratch without using the transferred encoder, which represents the simple method of supervised learning with data augmentation. The comparison results are shown in Table 1.

Data availability

Data used for training and validation in this work is available through the Digital Repository Service of Northeastern University at https://hdl.handle.net/2047/D20517730. Also, this study was carried out using publicly available data from the QM9 dataset at https://figshare.com/collections/Quantum_chemistry_structures_and_properties_of_134_kilo_molecules/978904. The code for this work can be found at https://github.com/qmatyanlab/DFCL.

Author contributions

Q. Y. conceived the research. W. G. conducted the first-principle calculations and designed the contrastive learning framework. W. G. and Q. Y. wrote the manuscript. T. S., H. B., S. T. U. R. C., P. C., A. A. and J. Y. were involved in the discussion and manuscript revisions. H. L., J. P. P. and Q. Y. supervised the project.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

W. Gong and Q. Yan acknowledge support from the U.S. Department of Energy, Office of Science, under award number DE-SC0023664. S. T. U. R. Chowdhury and J. P. Perdew acknowledge support from the U.S. National Science Foundation under Grant No. DMR-1939528. This work benefitted from the supercomputing resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. H. Ling acknowledge the support from SBU-BNL Seed Grant.

References

1. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871.
2. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138.
3. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
4. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401.
5. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Workhorse Semilocal Density Functional for Condensed Matter Physics and Quantum Chemistry, Phys. Rev. Lett., 2009, 103(2), 026403.
6. J. Sun, B. Xiao and A. Ruzsinszky, Communication: Effect of the orbital-overlap dependence in the meta generalized gradient approximation, J. Chem. Phys., 2012, 137(5), 051101.
7. J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115(3), 036402.
8. A. D. Kaplan, M. Levy and J. P. Perdew, Predictive Power of the Exact Constraints and Appropriate Norms in Density Functional Theory, Annu. Rev. Phys. Chem., 2023, 74(1), 193–218.
9. M. Levy and J. P. Perdew, Hellmann-Feynman, virial, and scaling requisites for the exact universal density functionals. Shape of the correlation potential and diamagnetic susceptibility for atoms, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32(4), 2010–2021.
10. G. L. Oliver and J. P. Perdew, Spin-density gradient expansion for the kinetic energy, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20(2), 397–403.
11. J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy, Phys. Rev. Lett., 1982, 49(23), 1691–1694.
12. F. Brockherde, et al., Bypassing the Kohn-Sham equations with machine learning, Nat. Commun., 2017, 8(1), 872.
13. S. Dick and M. Fernandez-Serra, Learning from the density to correct total energy and forces in first principle simulations, J. Chem. Phys., 2019, 151(14), 144102.
14. S. Dick and M. Fernandez-Serra, Machine learning accurate exchange and correlation functionals of the electronic density, Nat. Commun., 2020, 11(1), 3509.
15. A. Ryabov, I. Akhatov and P. Zhilyaev, Neural network interpolation of exchange-correlation functional, Sci. Rep., 2020, 10(1), 8000.
16. X. Lei and A. J. Medford, Design and analysis of machine learning exchange-correlation functionals via rotationally invariant convolutional descriptors, Phys. Rev. Mater., 2019, 3(6), 063801.
17. J. Hollingsworth, L. Li, T. E. Baker and K. Burke, Can exact conditions improve machine-learned density functionals?, J. Chem. Phys., 2018, 148(24), 241743.
18. R. Nagai, R. Akashi and O. Sugino, Machine-learning-based exchange correlation functional with physical asymptotic constraints, Phys. Rev. Res., 2022, 4(1), 013106.
19. J. Gedeon, et al., Machine learning the derivative discontinuity of density-functional theory, Mach. Learn.: Sci. Technol., 2022, 3(1), 015011.
20. J. Kirkpatrick, et al., Pushing the frontiers of density functionals by solving the fractional electron problem, Science, 2021, 374(6573), 1385–1389.
21. E. H. Lieb and S. Oxford, Improved lower bound on the indirect Coulomb energy, Int. J. Quantum Chem., 1981, 19(3), 427–439.
22. K. Pokharel, Exact constraints and appropriate norms in machine learned exchange-correlation functionals, J. Chem. Phys., 2022, 157, 174106.
23. A. Kolesnikov, X. Zhai and L. Beyer, Revisiting self-supervised visual representation learning, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Long Beach, CA, USA, 2019, pp. 1920–1929.
24. J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding, in Proceedings of NAACL-HLT, Minneapolis, MN, USA, 2019, pp. 4171–4186.
25. S. Chithrananda, G. Grand and B. Ramsundar, ChemBERTa: Large-Scale Self-Supervised Pretraining for Molecular Property Prediction, arXiv, 2020, preprint, arXiv:2010.09885,  DOI:10.48550/arXiv.2010.09885.
26. Y. Rong, et al., Self-Supervised Graph Transformer on Large-Scale Molecular Data, Advances in Neural Information Processing Systems 33 (NeurIPS 2020), 2020.
27. A. Jaiswal, A. R. Babu, M. Zaki Zadeh, D. Banerjee and F. Makedon, A Survey on Contrastive Self-supervised Learning, 2022 2nd International Conference on Artificial Intelligence (ICAI), 2022.
28. P. Khosla, et al., Supervised Contrastive Learning, Advances in Neural Information Processing Systems 33 (NeurIPS 2020), 2020, pp. 18661–18673.
29. Y. Wang, J. Wang, Z. Cao and A. Barati Farimani, Molecular contrastive learning of representations via graph neural networks, Nat. Mach. Intell., 2022, 4(3), 279–287.
30. Y. Fang, et al., Knowledge graph-enhanced molecular contrastive learning with functional prompt, Nat. Mach. Intell., 2023, 5(5), 542–553.
31. G. A. Pinheiro, J. L. F. Da Silva and M. G. Quiles, SMICLR: Contrastive Learning on Multiple Molecular Representations for Semisupervised and Unsupervised Representation Learning, J. Chem. Inf. Model., 2022, 62(17), 3948–3960.
32. T. Chen, S. Kornblith, M. Norouzi and G. Hinton, A simple framework for contrastive learning of visual representations, in International conference on machine learning, Vienna, Austria, 2020, pp. 1597–1607.
33. Q. Sun, et al., PySCF: the Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1340.
34. Ö. Çiçek, A. Abdulkadir, S. S. Lienkamp, T. Brox and O. Ronneberger, 3D U-Net: learning dense volumetric segmentation from sparse annotation, in International conference on medical image computing and computer-assisted intervention, Athens, Greece, 2016, pp. 424–432.
35. K. Lee, J. Zung, P. Li, V. Jain and H. S. Seung, Superhuman accuracy on the SNEMI3D connectomics challenge, in Conference on Neural Information Processing Systems (NIPS 2017),Long Beach, CA, USA, 2017.
36. O. Treutler and R. Ahlrichs, Efficient molecular numerical integration schemes, J. Chem. Phys., 1995, 102(1), 346–354.
37. L. Li, et al., Kohn-Sham Equations as Regularizer: Building Prior Knowledge into Machine-Learned Physics, Phys. Rev. Lett., 2021, 126(3), 036401.
38. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244–13249.
39. J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105(22), 9982–9985.
40. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1(1), 1–7.
41. L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17, J. Chem. Inf. Model., 2012, 52(11), 2864–2875.
42. E. Aprà, et al., NWChem: Past, present, and future, J. Chem. Phys., 2020, 152(18), 184102.
43. W. Falcon, Pytorch lightning, GitHub, Note: https://github.com/PyTorchLightning/pytorch-lightning, 2019.
44. A. Paszke, et al., PyTorch: an imperative style, high-performance deep learning library, in Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 2019, pp. 8024–8035.
45. D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, in International Conference on Learning Representations (ICLR), San Diego, CA, USA, 2015.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00114h

‡ Present address: Department of Physics and Engineering Physics, Tulane University, New Orleans, LA 70118, USA. E-mail: E-mail: perdew@tulane.edu

---