Open Access Article
Open Access ArticleUnderstanding and improving zeroth-order optimization methods on AI-driven molecule optimization†
Elvin
Lo
 a and
Pin-Yu
Chen
a and
Pin-Yu
Chen
 *b
*b
aHorace Greeley High School, Chappaqua, NY 10514, USA. E-mail: elvinlo922@gmail.com
bIBM Research, Yorktown Heights, NY 10598, USA. E-mail: pin-yu.chen@ibm.com
First published on 10th August 2023
Abstract
Molecule optimization is an important problem in chemical discovery and has been approached using many techniques, including generative modeling, reinforcement learning, genetic algorithms, and much more. Recent work has also applied zeroth-order (ZO) optimization, a subset of gradient-free optimization that solves problems similarly to gradient-based methods, for optimizing latent vector representations from an autoencoder. In this paper, we study the effectiveness of various ZO optimization methods for optimizing molecular objectives, which are characterized by variable smoothness, infrequent optima, and other challenges. We provide insights into the robustness of various ZO optimizers in this setting, show the underperformance of the ZO gradient descent (ZO-GD) and advantages of the ZO sign-based gradient descent (ZO-signGD), discuss how ZO optimization can be used practically in realistic discovery tasks, and demonstrate the potential effectiveness of ZO optimization methods on widely used benchmark tasks from the Guacamol suite. The code is available at: https://github.com/IBM/QMO-bench.
1. Introduction
The goal of molecule optimization is to efficiently find molecules possessing desirable chemical properties. As the ability to effectively solve difficult molecule optimization tasks would greatly accelerate the discovery of promising drug candidates and decrease the immense resources necessary for drug development, significant efforts have been dedicated to designing molecule optimization algorithms leveraging a variety of techniques, including deep reinforcement learning,1 genetic algorithms,2 Bayesian optimization,3 variational autoencoders,4,5 and more. Several molecule optimization benchmark tasks have also been proposed, including similarity-based oracles6 and docking scores.7In this paper, we extend the work of Hoffman et al.,8 who proposed the use of zeroth-order (ZO) optimization in their query-based molecule optimization (QMO) framework, an end-to-end framework which decouples molecule representation learning and property prediction. ZO optimization is a class of methods used for solving black-box problems by estimating gradients using only zeroth-order function evaluations and performing iterative updates as in first-order methods like gradient descent (GD).9 Many types of ZO optimization algorithms have been developed, including the ZO gradient descent (ZO-GD),10 ZO sign-based gradient descent (ZO-signGD),11 ZO adaptive momentum method (ZO-AdaMM, or ZO-Adam specifically for the Adam variant),12 and more.13,14 The optimality of ZO optimization methods has also been studied under given problem assumptions.15 ZO optimization methods have achieved impressive feats in adversarial machine learning, where they have been used for adversarial example generation in black-box settings and demonstrated comparable success to first-order white-box attacks.16,17 They have also been shown to be able to generate contrastive explanations for black-box models.18 Finally, Hoffman et al.8 showed how ZO optimization methods can also be applied to molecule optimization with their QMO framework.
QMO iteratively optimizes a starting molecule, making it well suited for lead optimization tasks, but it can also start from random points and traverse large distances to find optimal molecules. In comparison with the work of Hoffman et al.8 which experiments with only one optimizer, we experiment with variations of QMO using different ZO optimizers. Furthermore, we add more benchmark tasks from Guacamol6 (whose use has been encouraged by the molecule optimization community3,19 and used by Gao et al.20 to benchmark many design algorithms in a standardized setting) and provide insights into the challenges of ZO optimization on molecular objectives.
Specifically, we evaluate several ZO optimization methods for the problem of molecule optimization in terms of convergence speed, convergence accuracy, and robustness to the unusual function landscapes (described further in Section 2.4) of molecular objectives. Our experiments on molecule optimization tasks from Guacamol show that ZO-GD underperforms other ZO methods, while ZO-signGD11 performs comparably and in several cases better than ZO-Adam despite being known to have worse convergence accuracy than ZO-Adam for other problems like adversarial attacks.11 Our results indicate that the sign operation may potentially increase robustness to the function landscapes of molecular objectives. Furthermore, we provide insights into practical application of ZO optimization in drug discovery scenarios for both lead optimization tasks and the discovery of novel molecules, as well as propose the use of a hybrid approach combining others models with QMO.
2. Methods
2.1. Background on the QMO framework
Following the QMO framework by Hoffman et al.,8 we use an autoencoder to encode molecules with encoder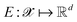 and decode latent vectors with decoder
and decode latent vectors with decoder 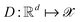 , where
, where 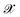 denotes the discrete chemical space of all drug candidates. We denote with
denotes the discrete chemical space of all drug candidates. We denote with 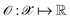 a black-box oracle returning a scalar corresponding to a molecular property of interest (which may also be modified by adding losses related to other properties), and for ease of notation with the QMO framework, we define our optimization objective loss function as
a black-box oracle returning a scalar corresponding to a molecular property of interest (which may also be modified by adding losses related to other properties), and for ease of notation with the QMO framework, we define our optimization objective loss function as 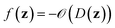 for latent representations
for latent representations  . As each function query f(z) queries the oracle
. As each function query f(z) queries the oracle 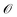 with the decoded molecule corresponding to z, one function query is equivalent to one oracle query.
with the decoded molecule corresponding to z, one function query is equivalent to one oracle query.
In QMO, we use ZO optimization methods to navigate the latent space to solve minzf(z). Specifically, given a starting molecule and its latent representation z0, we iteratively update the current latent representation following some optimizer, as in first-order gradient-based methods like gradient descent. But as we do not have any first-order oracle, we instead use gradients estimated using only evaluations of f following some gradient estimator. The QMO framework, which closely follows a generic ZO optimization procedure, is summarized in Algorithm 1.
Algorithm 1 Generic QMO framework for molecule optimization
In principle, QMO is a generic framework which can guide searches over any continuous learned representation based on any discrete space and use any ZO optimization method. Hoffman et al.8 used the pre-trained SMILES-based21 autoencoder (CDDD model) from Winter et al.22 with embedding dimension d = 512 and ZO-Adam. Here, we use the same autoencoder but consider several variations of QMO using different gradient estimators and optimizers to provide a comprehensive study on the effect of ZO optimization methods.
Of note, QMO may be applied to molecule optimization with design constraints by modifying the objective accordingly. For example, a possible formulation is to consider a set of property scores 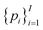 to be optimized with positive coefficients (weights)
to be optimized with positive coefficients (weights) 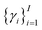 and a set of property constraints
and a set of property constraints 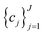 with thresholds
with thresholds 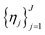 , and then to define the oracle as
, and then to define the oracle as
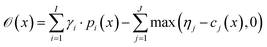 | (1) |
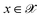 . The vectors
. The vectors 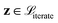 not satisfying cj(D(z)) ≥ ηj for all j ∈ {1, 2, …, J} can then be removed from
not satisfying cj(D(z)) ≥ ηj for all j ∈ {1, 2, …, J} can then be removed from  . While we do not formulate the objective functions in our experiments in this way, the experiments of Hoffman et al.8 are examples of this formulation and are described in further detail in Section 2.5.
. While we do not formulate the objective functions in our experiments in this way, the experiments of Hoffman et al.8 are examples of this formulation and are described in further detail in Section 2.5.
2.2. ZO gradient estimators
We consider two main ZO gradient estimators. Both average finite differences over Q independently sampled random perturbations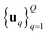 include a smoothing parameter β, and follow the form:
include a smoothing parameter β, and follow the form: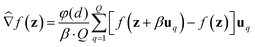 | (2) |
The two gradient estimators differ mainly in the sampling method for each random direction uq, and also in the dimension-dependent factor φ(d). They are:
1. Gaussian smoothing (GS):10,23 when we sample each direction from the uniform distribution (HTML translation failed) on the unit sphere. For GS, φ(d) = d.
2. Bernoulli smoothing-shrinkage (BeS-shrink):24 when we craft each random direction by independently sampling each of its d entries from (B0.5 − 0.5)/m, where B0.5 follows the Bernoulli distribution with a probability of 0.5 and 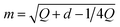 is an optimal shrinking factor. For BeS-shrink, φ(d) = 1.
is an optimal shrinking factor. For BeS-shrink, φ(d) = 1.
The gradient estimators average over Q random directions to decrease the estimation error, but increasing Q increases oracle complexity in sampling. The gradient estimation operation requires querying Q + 1 different points (which are each decoded into a molecule and used to query oracle  ). We therefore require Q + 1 oracle evaluations for each optimization iteration.
). We therefore require Q + 1 oracle evaluations for each optimization iteration.
Additionally, because the above gradient estimators use a (forward) finite difference of 2 points to estimate the gradient for each random perturbation, we refer to it as a 2-point gradient estimator. An alternative to the 2-point GS and BeS-shrink gradient estimators is their 1-point alternative, which instead have the form:
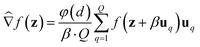 | (3) |
Similar to 2-point gradient estimators, 1-point estimators require Q + 1 oracle queries at each iteration (the estimation operation itself requires only Q queries, but this does not account for querying the updated molecule after each iteration). However, 1-point estimators are not commonly used in practice due to higher variance.
2.3. ZO optimizers
We consider three main optimizers, each having its own updating operation that consists of computing a descent direction mt and then updating the current point. Each optimizer can be paired with any ZO gradient estimator. The three are as follows:1. ZO gradient descent (ZO-GD):10 analogous to stochastic gradient descent (SGD) in the first-order stochastic setting. ZO-GD uses the current gradient estimate as the descent direction 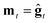 and updates the current point via the rule zt+1 = zt − αmt.
and updates the current point via the rule zt+1 = zt − αmt.
2. ZO sign-based gradient descent (ZO-signGD):11 analogous to sign-based SGD (signSGD)25 in the first-order stochastic setting. ZO-signGD uses the same point updating rule as ZO-GD but instead uses the sign of the current estimate as the descent direction 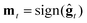 , where sign(·) denotes the element-wise sign operation.
, where sign(·) denotes the element-wise sign operation.
3. ZO-Adam:12 analogous to Adam26 in the first-order stochastic setting. ZO-Adam adopts a momentum-type descent direction and an adaptive learning rate.
The ZO optimization methods compared in this paper are summarized in Table 1.
| ZO optimization method | Gradient estimator | Optimizer |
|---|---|---|
| Adam-2p-BeS-shrink | 2-point BeS-shrink | Adam |
| Adam-2p-GS | 2-point GS | Adam |
| GD-2p-BeS-shrink | 2-point BeS-shrink | GD |
| GD-2p-GS | 2-point GS | GD |
| signGD-2p-BeS-shrink | 2-point BeS-shrink | signGD |
| signGD-2p-GS | 2-point GS | signGD |
2.4. Motivating the comparison of ZO optimization methods for molecule optimization
We motivate our comparison of optimizers not only in terms of convergence speed and convergence accuracy, but also in terms of robustness to the unfriendly function landscapes of molecular objectives. Indeed, molecule optimization is made difficult by variable function smoothness due to “activity cliffs” in the molecular space where small structural changes cause large changes in oracle values.19 As optima are infrequent, there are also large and extremely “flat” unfavorable regions in space, where the oracle values change minimally and may be very small. Furthermore, because our objective function f obtains values by querying the oracle using discrete molecular representations obtained from decoding the latent vectors, the function landscape is made discrete and thus further non-smooth (i.e., the function value may have a discrete “jump” at the borders between adjacent regions of latent vectors which decode to different molecules, see Fig. 2). Thus, being able to effectively navigate the latent chemical space and not get stuck in unfavorable regions is an important and non-trivial attribute to pursue in optimization methods.
using discrete molecular representations obtained from decoding the latent vectors, the function landscape is made discrete and thus further non-smooth (i.e., the function value may have a discrete “jump” at the borders between adjacent regions of latent vectors which decode to different molecules, see Fig. 2). Thus, being able to effectively navigate the latent chemical space and not get stuck in unfavorable regions is an important and non-trivial attribute to pursue in optimization methods.
Sign-based gradient descent is known to be effective in achieving fast convergence speed in stochastic settings: in the stochastic first-order oracle setting, Bernstein et al.25 showed that signSGD could have faster empirical convergence speed than SGD, and in the zeroth-order stochastic setting, Liu et al.11 similarly showed that ZO-signSGD has faster convergence speed than many ZO optimization methods at the cost of worse accuracy (i.e., converging only to the neighborhood of an optima). The fast convergence of sign-based methods is motivated by the idea that the sign operation is more robust to stochastic noise, and though our formulation of molecule optimization is non-stochastic, the sign operation is potentially more robust to the difficult landscapes of molecular objective functions. Adaptive momentum methods like Adam also make use of the sign of stochastic gradients for determining the descent direction in addition to variance adaption,27 and thus ZO-Adam may also show improved robustness to the function landscapes.
2.5. Practical usage of QMO for drug discovery
We imagine that QMO can be applied for two main cases: (1) identifying novel lead molecules (i.e., finding molecules significantly different from known leads), and (2) lead optimization (i.e., finding slightly modified versions of known leads).For the former application case, it may be counterproductive to use known leads as the starting molecule in QMO, as these leads may be in the close neighborhood of a local optima (or a local optima themselves) in the function landscape, in which the optimizer would likely get stuck (preventing the exploration of different areas of the latent chemical space). Instead, it may be more promising to start at a random point in chemical space. QMO also has the advantage that it guides search without the use of a training set, which aids in finding candidates vastly different from known molecules. However, finding a highly diverse set of novel leads may be unlikely within a single run of QMO as the optimization methods converge to some neighborhood, meaning that multiple random restarts would likely be necessary to discover a diverse set of lead molecules.
For the latter application case, it is much more sensible to use known leads as the starting molecule input to QMO. Additionally, rather than using an oracle 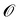 evaluating only the main desired drug property (i.e., activity against a biological target), it may be advantageous to use a modified oracle. For example, Hoffman et al.8 applied QMO for lead optimization of known SARS-CoV-2 main protease inhibitors and antimicrobial peptides (AMPs) following the constrained molecule optimization setting of eqn (1), with pre-trained property predictors for each task. They set similarity to the original lead molecule as the property score psim to be optimized, and set constraints on properties of interest (binding affinity caff for the SARS-CoV-2 task, or toxicity prediction value ctox and AMP prediction value cAMP for the AMP task). In these formulations, the main optimization objective is actually molecular similarity rather than the main properties of interest.
evaluating only the main desired drug property (i.e., activity against a biological target), it may be advantageous to use a modified oracle. For example, Hoffman et al.8 applied QMO for lead optimization of known SARS-CoV-2 main protease inhibitors and antimicrobial peptides (AMPs) following the constrained molecule optimization setting of eqn (1), with pre-trained property predictors for each task. They set similarity to the original lead molecule as the property score psim to be optimized, and set constraints on properties of interest (binding affinity caff for the SARS-CoV-2 task, or toxicity prediction value ctox and AMP prediction value cAMP for the AMP task). In these formulations, the main optimization objective is actually molecular similarity rather than the main properties of interest.
3. Results
To benchmark QMO, we select three tasks (oracles) from the Therapeutic Data Commons (TDC)28 (https://tdcommons.ai) implementation of Guacamol6 (https://github.com/BenevolentAI/guacamol), a popular benchmarking suite. While a high-quality ubiquitous benchmark for molecule optimization algorithms is yet to be determined, Guacamol has emerged as a standard benchmark with reasonable computational cost.3,19 Guacamol tasks are also the core of the open-source Practical Molecular Optimization (PMO) benchmark20 (https://github.com/wenhao-gao/mol_opt).We select one task from each of the three main categories of Guacamol oracles: similarity-based multi-property objectives, isomer-based objectives, and SMARTS-based objectives. First, the perindopril_mpo function outputs the geometric mean of Tanimoto similarity with perindopril, calculated with ECFC4 fingerprints, and a Gaussian modifier function that targets 2 aromatic rings, giving high scores when the number of aromatic rings is close to 2 (while perindopril has no aromatic rings). Second, the zaleplon_mpo function outputs the geometric mean of Tanimoto similarity with zaleplon, calculated with ECFC4 fingerprints, and an isomer scoring function targeting the molecular formula C19H17N3O2 (while the molecular formula of zaleplon is C17H15N5O). It is also worth noting that the zaleplon_mpo task is known to be particularly difficult among Guacamol objectives.19 Third, the deco_hop function outputs the arithmetic mean of Tanimoto similarity with a particular SMILES string and three SMARTS scoring functions each returning 0 or 1 depending on whether a particular substructure is present or absent. See Fig. 1 for the relevant similarity targets and SMARTS patterns.
 | ||
| Fig. 2 Function landscapes for various optimized molecules found by QMO. Each point on the 2D plots corresponds to a latent vector from the higher-dimensional vector space (of embedding dimension d = 512) in which the chemical space is embedded. The color of each point on the plot represents the Guacamol function score of that corresponding molecule. Specifically, the origin of each plot corresponds to the latent vector encoding some QMO-optimized molecule, and each other point on the plot corresponds to the latent vector obtained by perturbing the QMO-optimized latent vector by a linear combination of two random unit vectors vx and vy (also of dimension d) that are uniformly sampled from the unit sphere. The SMILES strings s1, …, s9 of the optimized molecules are listed in ESI Section B.2.† | ||
While the similarity-based nature of the selected Guacamol objectives lends itself to using the similarity target molecules (e.g., perindopril for the perindopril_mpo task) as the starting molecule for QMO, essentially formulating a lead optimization problem from Section 2.5, we find that doing so makes finding high-scoring molecules trivial within only around 50 iterations. Thus, to benchmark QMO and show that QMO can find solutions even when starting far from any high scoring molecules (which we would need to do when searching for novel lead molecules), we choose the starting molecules for QMO to be the lowest-scoring molecules on the Guacamol oracles from the ZINC 250K dataset.29 Our setup thus mimics the novel lead molecule discovery task from Section 2.5.
We also select two baselines, a graph-based genetic algorithm (Graph-GA)2 and Gaussian process Bayesian optimization (GPBO),3,30 both of which are known to be high-performing molecule optimization algorithms.20 For each of the selected Guacamol tasks, we then run experiments using QMO only, baselines only, and hybrid approaches.
Note that for our experiments, we consider only the score of the top scoring molecule found so far for a given run. Additionally, we run QMO only with 2-point gradient estimators, though we also compare 1-point estimators for QED31 optimization in ESI Section B.1† where we verify the advantage of 2-point estimators.
3.1. Function landscapes of selected Guacamol objectives
Fig. 2 shows the function landscapes of the selected Guacamol objectives. To visualize the high-dimensional function landscapes, we use the common approach of projecting to two random vectors.33 The origin corresponds to an optimized latent vector found by QMO, and the vector is perturbed along two random directions vx and vy sampled from the uniform distribution on the unit sphere. Fig. 3 shows the QMO-optimized molecules themselves.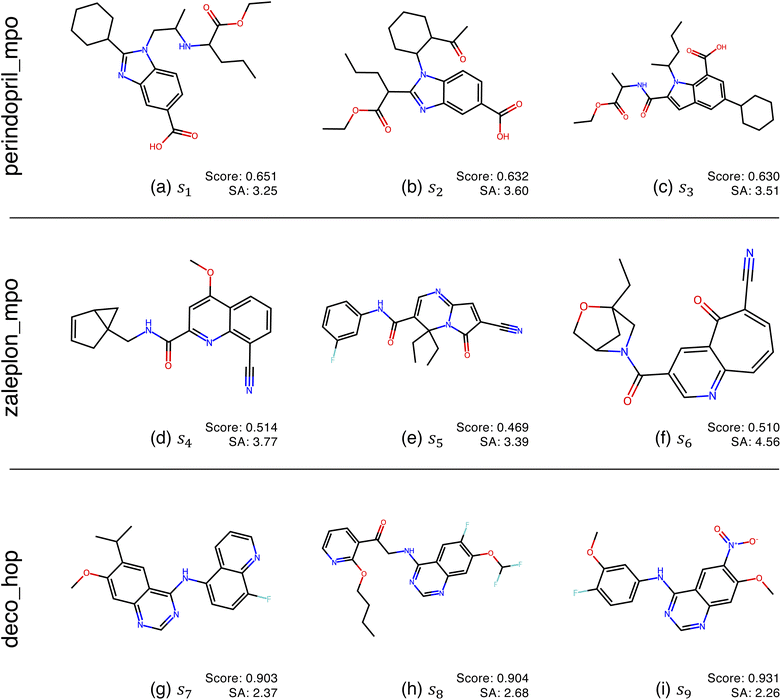 | ||
| Fig. 3 QMO-optimized molecules for the selected Guacamol objectives, with objective function scores and synthetic accessibility (SA)32 scores. SA is a heuristic calculated as the combination of fragment contributions and complexity penalties. The molecules correspond to the SMILES strings s1, …, s9 used in Fig. 2, which are fully listed in ESI Section B.2.† | ||
As shown, the zaleplon_mpo task has the smallest central area consisting of high scoring molecules and a relatively flat landscape elsewhere, meaning that the QMO optimizer needs to traverse a very flat unfavorable region to enter a very small optimal neighborhood. This matches the observation that zaleplon_mpo is a highly difficult task. The deco_hop task, while not nearly as difficult of a task, still exhibits a very discrete jump in values around the central region, which makes it more difficult for the QMO optimizer to find the true optimal neighborhood. Finally, perindopril_mpo appears to be the most smooth function. The optimal central area is larger than that for zaleplon_mpo, and the discrete jumps in function values are not as large as in the other tasks.
3.2. Convergence of ZO optimization methods
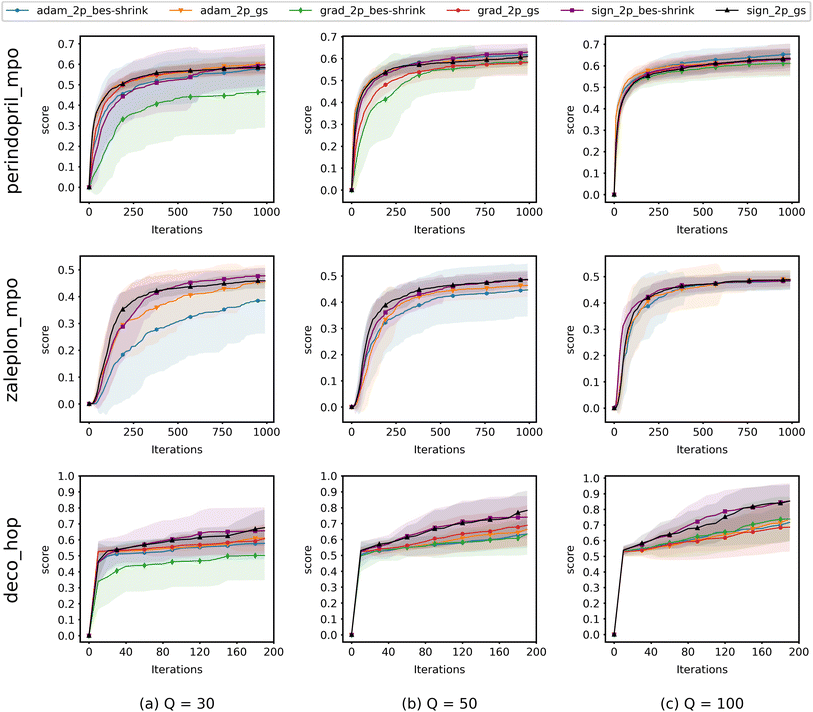
When running experiments using QMO only, we run experiments with several different ZO optimization methods and try Q = {30, 50, 100} for each, where Q is the number of random directions over which the gradient estimator averages at each iteration to decrease the estimation error and Q + 1 is the number of oracle evaluations at each iteration. We set T = 1000 iterations for perindopril_mpo and zaleplon_mpo or T = 200 for deco_hop, and average runs from 20 distinct starting molecules with 2 random restarts each (40 runs total).For each task, we choose to use the 20 lowest-scoring molecules on the oracle from the ZINC 250K dataset29 as the starting molecules. As aforementioned, we do this in order to show that QMO can find solutions even when starting far from any high scoring molecules, which we would likely need to do when searching for novel lead molecules.
Fig. 4 shows the results from experiments run using QMO only and compares the convergence of ZO optimization methods with different Q. Here, adam_2p_bes-shrink refers to QMO using the ZO-Adam optimizer with the 2-point BeS-shrink gradient estimator (QMO-Adam-2p-BeS-shrink), and similarly to the other ZO optimization methods. Diversity scores of the optimized molecules found by QMO are also reported in ESI Section B.3.†
Most importantly, the results indicate that ZO-GD tends to underperform with respect to the other ZO methods. Under the Q = 100 setting, the performance of ZO-GD is similar to that of other methods on the perindopril_mpo task and similar to that of ZO-Adam on the deco_hop task. However, the convergence of ZO-GD using the 2-point BeS-shrink gradient estimator is often noticeably slower or less accurate than that of the other methods under the settings of Q = 30 and Q = 50. Thus, the performance of ZO-GD on the perindopril_mpo and deco_hop tasks does not present any advantages in convergence speed or accuracy over that of ZO-Adam or ZO-signGD. However, the most notable indication that ZO-GD may be less useful than ZO-Adam or ZO-signGD for molecule optimization is that ZO-GD is completely unsuccessful for the zaleplon_mpo task: even when searching a wide range of hyperparameters and testing several molecules, ZO-GD is unable to find any molecules with zaleplon_mpo scores above 0.2 within the first 100 iterations, and often cannot even get above 0.01. Inspection revealed that the gradient vectors were too small for ZO-GD to make meaningful point updates, and so full zaleplon_mpo experiments were not run using ZO-GD.
The performance of ZO-Adam and ZO-signGD is very similar for the perindopril_mpo task, but ZO-signGD noticeably outperforms ZO-Adam on the deco_hop task. On the zaleplon_mpo task, ZO-signGD noticeably outperforms ZO-Adam for lower settings of Q, suggesting that ZO-signGD could be more query-efficient, but the convergence speed of ZO-Adam approaches that of ZO-signGD for Q = 100 and their accuracies become very similar. While the performances of both algorithms are comparable overall, the difference in their performances on less smooth functions like zaleplon_mpo and deco_hop (see Section 3.1) also suggests that ZO-signGD is the most robust to difficult function landscapes of molecular objectives. The comparison of convergence accuracies between ZO-signGD and ZO-Adam on the selected Guacamol objectives is particularly interesting because ZO-Adam converges with much greater accuracy in other problems like adversarial example generation,12 demonstrating the challenges presented by molecular objectives and reinforcing the evidence that ZO-signGD may have improved robustness to their function landscapes.
Finally, the results of GS and BeS-shrink gradient estimators do not differ greatly, though GS seems to converge faster for lower Q.
3.3. Query efficiency of QMO versus other approaches
Fig. 5 shows the optimization curves when limiting optimization to a 10K query budget, including experiments run using QMO only (specifically, only QMO-sign-2p-GS is shown), baseline models only, and hybrid approaches. Precise numbers and area under curve (AUC) scores are also reported in ESI Section B.4.†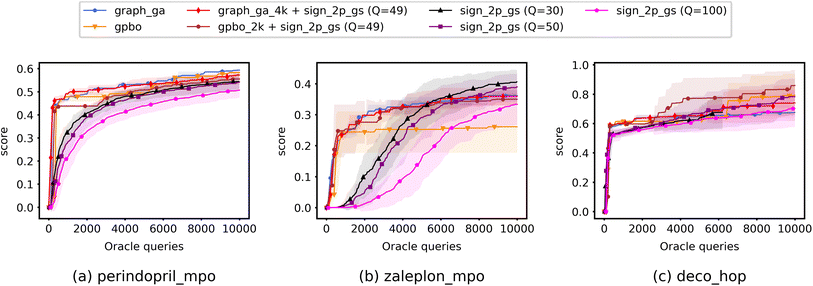 | ||
| Fig. 5 Optimization curves of QMO, baseline models, and hybrid methods on selected Guacamol objectives. The results are averaged over multiple trials and shaded regions correspond to the standard deviation over the trials. Descriptions of the Guacamol objectives and experimental details are provided in Section 3. Precise numbers and area under curve (AUC) scores are also reported in ESI Section B.4.† | ||
When running baseline models alone, we average runs with two random seeds and limit the number of oracle queries to 10K. When running hybrid approaches, for each baseline model we use a portion of the 10K query budget to run the model (4K queries for Graph-GA and 2K for GPBO) and use the remaining query budget to optimize only the top generated molecule using QMO with the ZO-signGD optimizer and 2-point GS gradient estimator (QMO-sign-2p-GS) with Q = 49. For hybrid approaches, we again run the baseline models with two random seeds and use QMO to further optimize the top generated molecule from each run with 5 random restarts, ultimately averaging a total of 10 trials.
The baseline models (Graph-GA and GPBO) and hybrid methods demonstrate faster convergence speed than QMO alone, while the convergence accuracies of all methods differ slightly for each task but are comparable overall. It is worth noting that the hybrid approaches combining baseline models with QMO (e.g., Graph GA + sign_2p_gs) produce curves similar to those of their baseline model counterparts even for zaleplon_mpo and deco_hop, where QMO has higher convergence accuracy than the baseline models, so further investigation may be necessary to optimally integrate QMO into hybrid approaches. However, these preliminary results serve as a proof of concept for the potential of hybrid approaches: experiments on Guacamol show that hybrid approaches successfully improve the convergence speed of QMO, and the capacity of QMO for local search in chemical space makes it a promising option for refining a molecule in more complex design scenarios to satisfy the numerous property constraints of pharmaceutical drugs.
4. Conclusions
In this paper, we study the application of ZO optimization methods to molecule optimization. Experimentation on tasks from the Guacamol suite reveals that ZO-GD underperforms other ZO methods, while ZO-signGD11 performs comparably and in several cases better than ZO-Adam, especially for more difficult function landscapes with small regions of optima, flat regions, and discrete jumps. Accordingly, we observe that the sign operation may increase robustness to the difficult function landscapes of molecular objectives, while also achieving higher query efficiency compared to other optimizer updating methods. We also discuss how the generic QMO framework can be applied practically in realistic drug discovery scenarios, which includes a hybrid approach with other models that can improve the convergence speed of QMO. We hope that better characterizing the performance of ZO methods for molecule optimization and providing preliminary experiments with hybrid approaches as a proof of concept may inform future applications of QMO for drug discovery.To conclude, we would like to mention a few limitations of this study. First, synthesizability of molecules is not accounted for, though one possible approach is to modify the objective function with a synthesizability loss. For example, we might add a loss penalizing higher synthetic accessibility (SA)32 scores, though SA is often a lacking metric. A more expensive approach for quantifying synthesizability could be to plan synthetic pathways with synthesis planning programs.34 Second, our results may be biased towards similarity-based oracles. Third, the effect of autoencoder choice and latent dimension is not thoroughly investigated for the selected benchmark tasks, though Hoffman et al.8 provided analysis for their antimicrobial peptide task. Finally, while Hoffman et al.8 also showed that training an oracle prediction model (to predict property scores from latent representations) has significant disadvantages in optimization accuracy compared to always using the oracle itself, we do not thoroughly investigate the impact it would have on the objective function landscapes in latent space.
Data availability
The code for QMO and all test sets of starting molecules are available in the following GitHub repository: https://github.com/IBM/QMO-bench. All test sets of molecules were originally extracted from the ZINC database29 which is free for use by anyone. The pre-trained autoencoder (CDDD model) by Winter et al.22 is available at https://github.com/jrwnter/cddd. For the Graph-GA and GPBO baseline models, we adopt the implementation of Gao et al.20 which is available at https://github.com/wenhao-gao/mol_opt. For the Guacamol6 benchmark tasks, we use the implementation the Therapeutic Data Commons (TDC)28 (https://tdcommons.ai).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Vijil Chenthamarakshan and Payel Das from IBM Research in acknowledgment of their valuable feedback.Notes and references
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminf., 2017, 9, 48 Search PubMed.
- J. H. Jensen, Chem. Sci., 2019, 10, 3567–3572 RSC.
- A. Tripp, G. N. C. Simm and J. M. Hernández-Lobato, NeurIPS 2021 AI for Science Workshop, 2021 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- W. Jin, R. Barzilay and T. Jaakkola, Proceedings of the 35th International Conference on Machine Learning, 2018, pp. 2323–2332 Search PubMed.
- N. Brown, M. Fiscato, M. H. Segler and A. C. Vaucher, J. Chem. Inf. Model., 2019, 59, 1096–1108 CrossRef CAS PubMed.
- M. García-Ortegón, G. N. C. Simm, A. J. Tripp, J. M. Hernández-Lobato, A. Bender and S. Bacallado, J. Chem. Inf. Model., 2022, 62, 3486–3502 CrossRef PubMed.
- S. C. Hoffman, V. Chenthamarakshan, K. Wadhawan, P.-Y. Chen and P. Das, Nat. Mach. Intell., 2022, 4, 21–31 CrossRef.
- S. Liu, P.-Y. Chen, B. Kailkhura, G. Zhang, A. O. Hero III and P. K. Varshney, IEEE Signal Process. Mag., 2020, 37, 43–54 Search PubMed.
- Y. Nesterov and V. Spokoiny, Found. Comput. Math., 2017, 17, 527–566 CrossRef.
- S. Liu, P.-Y. Chen, X. Chen and M. Hong, International Conference on Learning Representations, 2019 Search PubMed.
- X. Chen, S. Liu, K. Xu, X. Li, X. Lin, M. Hong and D. Cox, Advances in Neural Information Processing Systems, 2019 Search PubMed.
- X. Lian, H. Zhang, C.-J. Hsieh, Y. Huang and J. Liu, Advances in Neural Information Processing Systems, 2016 Search PubMed.
- Z. Li, P.-Y. Chen, S. Liu, S. Lu and Y. Xu, Proc. Innov. Appl. Artif. Intell. Conf., 2022, 36, 7453–7461 Search PubMed.
- G. Kornowski and O. Shamir, Adv. Neural Inf. Process., 2021, 324–334 Search PubMed.
- P.-Y. Chen, H. Zhang, Y. Sharma, J. Yi and C.-J. Hsieh, Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas Texas USA, 2017, pp. 15–26 Search PubMed.
- C.-C. Tu, P. Ting, P.-Y. Chen, S. Liu, H. Zhang, J. Yi, C.-J. Hsieh and S.-M. Cheng, Proc. Innov. Appl. Artif. Intell. Conf., 2019, 33, 742–749 Search PubMed.
- A. Dhurandhar, T. Pedapati, A. Balakrishnan, P.-Y. Chen, K. Shanmugam and R. Puri, Model Agnostic Contrastive Explanations for Structured Data, 2019 Search PubMed.
- A. Tripp, W. Chen and J. M. Hernández-Lobato, ICLR2022 Machine Learning for Drug Discovery, 2022 Search PubMed.
- W. Gao, T. Fu, J. Sun and C. W. Coley, Thirty-Sixth Conference on Neural Information Processing Systems Datasets and Benchmarks Track, 2022 Search PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- R. Winter, F. Montanari, F. Noé and D.-A. Clevert, Chem. Sci., 2019, 10, 1692–1701 RSC.
- A. D. Flaxman, A. T. Kalai and H. B. McMahan, Proceedings of the Sixteenth Annual ACM-SIAM Symposium on Discrete Algorithms, USA, 2005, pp. 385–394 Search PubMed.
- K. Gao and O. Sener, Proceedings of the 39th International Conference on Machine Learning, 2022, pp. 7077–7101 Search PubMed.
- J. Bernstein, Y.-X. Wang, K. Azizzadenesheli and A. Anandkumar, Proceedings of the 35th International Conference on Machine Learning, 2018, pp. 560–569 Search PubMed.
- D. P. Kingma and J. Ba, International Conference on Learning Representations, 2015 Search PubMed.
- L. Balles and P. Hennig, Proceedings of the 35th International Conference on Machine Learning, 2018, pp. 404–413 Search PubMed.
- K. Huang, T. Fu, W. Gao, Y. Zhao, Y. H. Roohani, J. Leskovec, C. W. Coley, C. Xiao, J. Sun and M. Zitnik, Thirty-Fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 1), 2021 Search PubMed.
- T. Sterling and J. J. Irwin, J. Chem. Inf. Model., 2015, 55, 2324–2337 CrossRef CAS PubMed.
- N. Srinivas, A. Krause, S. Kakade and M. Seeger, Proceedings of the 27th International Conference on International Conference on Machine Learning, 2010, pp. 1015–1022 Search PubMed.
- G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Nat. Chem., 2012, 4, 90–98 CrossRef CAS PubMed.
- P. Ertl and A. Schuffenhauer, J. Cheminf., 2009, 1, 8 Search PubMed.
- H. Li, Z. Xu, G. Taylor, C. Studer and T. Goldstein, Advances in Neural Information Processing Systems, 2018 Search PubMed.
- W. Gao and C. W. Coley, J. Chem. Inf. Model., 2020, 60, 5714–5723 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00076a |
| This journal is © The Royal Society of Chemistry 2023 |


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)(
O)(