Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density functional theory and machine learning for electrochemical square-scheme prediction: an application to quinone-type molecules relevant to redox flow batteries†
Arsalan
Hashemi
 *a,
Reza
Khakpour
a,
Amir
Mahdian
a,
Michael
Busch
b,
Pekka
Peljo
*a,
Reza
Khakpour
a,
Amir
Mahdian
a,
Michael
Busch
b,
Pekka
Peljo
 c and
Kari
Laasonen
c and
Kari
Laasonen
 a
a
aDepartment of Chemistry and Material Science, School of Chemical Engineering, Aalto University, 02150 Espoo, Finland. E-mail: arsalan.hashemi@aalto.fi
bInstitute of Theoretical Chemistry, Ulm University, Albert-Einstein Allee 11, 89069 Ulm, Germany
cResearch Group of Battery Materials and Technologies, Department of Mechanical and Materials Engineering, Faculty of Technology, University of Turku, 20014 Turun Yliopisto, Finland
First published on 12th September 2023
Abstract
Proton–electron transfer (PET) reactions are rather common in chemistry and crucial in energy storage applications. How electrons and protons are involved or which mechanism dominates is strongly molecule and pH dependent. Quantum chemical methods can be used to assess redox potential (Ered.) and acidity constant (pKa) values but the computations are rather time consuming. In this work, supervised machine learning (ML) models are used to predict PET reactions and analyze molecular space. The data for ML have been created by density functional theory (DFT) calculations. Random forest regression models are trained and tested on a dataset that we created. The dataset contains more than 8200 quinone-type organic molecules that each underwent two proton and two electron transfer reactions. Both structural and chemical descriptors are used. The HOMO of the reactant and LUMO of the product participating in the oxidation reaction appeared to be strongly associated with Ered.. Trained models using a SMILES-based structural descriptor can efficiently predict the pKa and Ered. with a mean absolute error of less than 1 and 66 mV, respectively. Good prediction accuracy of R2 > 0.76 and >0.90 was also obtained on the external test set for Ered. and pKa, respectively. This hybrid DFT-ML study can be applied to speed up the screening of quinone-type molecules for energy storage and other applications.
Introduction
Proton–electron transfer (PET) is a fundamental reaction in electrochemistry,1–3 biochemistry,4,5 material science,6,7 and in some other fields.8,9 To give one example, we can consider the charging and discharging processes in aqueous redox flow batteries,10–14 in which the two elementary steps, i.e., electron transfer (ET) and proton transfer (PT), are taken either competitively or jointly to interconvert electricity and chemical energy. Therefore, understanding the pathways from reactants to products through PET reactions is crucial to understand flow battery performance.In the recent development of redox flow batteries (RFB), water-soluble organic molecules are at the forefront of attention due to their affordability, safety, and structural diversity.15,16 In water, pH will impact the protonated/deprotonated form of the reduced or oxidized molecules participating in the redox reaction.17–20 When the proton concentration is lowered, i.e., the pH is raised, even strong bases may not be protonated. Hence, pH-potential diagrams of the electrolyte species, known as Pourbaix diagrams,21 should be assessed early in the battery design process. The Pourbaix diagram can be constructed using the redox potential (Ered.) and pKa of the involved species.
Rational designing and testing of materials in order to find better candidates is the focus of molecular engineering. Organic molecules can be modified either by their functional groups or their backbones. Numerous experimental studies have been performed to improve solubility, electrochemical redox properties, and cycling stability by modifying functional groups.19,20,22–26 For instance, Wedege et al.20 and Wiberg et al.22 in separate studies observed that solubility and redox potential is influenced by the position, type, and number of functional groups. Moreover, another study showed that heterocycles, where one carbon is substituted by oxygen, sulfur, and nitrogen, can change charge states and improve reactivity.27 Nevertheless, the experimental verification of the RFB active molecules is slow, especially if new molecules need to be synthesised, the computational pre-screening is very useful.
In the past few years, there have been several computational high-throughput studies that combined quantum mechanical density functional theory (DFT) and machine learning (ML) to find potential candidates for flow batteries.28–43 Mostly, for sets of limited isomeric backbones, these studies primarily focused on solubility and redox potential of the hydrogen atom transfer reaction at pH = 0 when functional groups were decorated. ChemAxon software44 has also developed powerful models for predicting pKa and solubility. However, its accuracy always depends on both the quality and the size of the dataset. To the best of our knowledge, the PET reaction mechanism has not yet been studied in a systematic high-throughput manner.
This contribution attempts to carefully map the chemical and structural characteristics of a library of quinone-type compounds45,46 to their square-scheme representations of the potential for ET and PT. In this report, we provide (i) a deeper understanding of molecule design for energy storage applications from a screening of large chemical space and (ii) a trained ML model to predict so far unknown redox-active molecules.
Theoretical framework
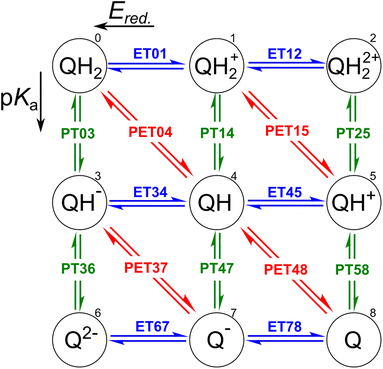
The redox properties of a molecule can be described in two ways: as a proton–electron transfer (PET; red arrows in Fig. 1), or as a decoupled sequence of electron transfer (ET; blue arrows in Fig. 1) and proton transfer (PT; green arrows in Fig. 1). In this study, a molecule QH2 (Q) is oxidized (reduced) to Q (QH2) by releasing (accepting) two electrons and two protons as follows:| QH2 ⇌ Q + 2H+ + 2e−, | (1) |
In order to assess the redox reaction (eqn (1)), it is necessary to calculate Gibbs free energy change ΔG at each ET/PT step: ΔG leads to the measurable reduction potential Ered. and acidity constant pKa for the ET and PT reactions, respectively. One can also predict the number of transferred electrons and protons at the given solution pH and electrode potential using these quantities.
Clearly, the most delicate part of ΔG calculation is to determine the energetics of the involved proton and electron transfers without explicit solvent and physical electrode in our model system. We use a three-step protocol to determine ΔG of PET, PT, and ET reactions in order:
(i) Following earlier works, the energetics of the PET step can be computed using the computational standard hydrogen electrode (SHE).47,48 According to this method, the energetic of a PET step, e.g. for QH → Q + H+ + e−, under standard condition, i.e. pH = 0, is given by
 | (2) |
(ii) The ΔG of a PT step, e.g. for QH+ → Q + H+, is computed using the isodesmic method, as follows:
| ΔGPT = G(Q, aq) + G(H+, aq) − G(QH+, aq). | (3) |
It leads us to calculate the measurable pKa value as follows:
 | (4) |
| HCOOH ⇒ HCOO− + H+. | (5) |
Using eqn (4) and, subsequently, eqn (3), the values of ΔGPT and GH+ are calculated. Having the latter quantity enables us to compute the pKa value of any PT reaction.
The obtained pKa values then need to be scaled to overcome shortcomings of the implicit solvation model52 used in the present study53–56 as follows:
| pKscaleda = 0.49pKa + 3.2, | (6) |
(iii) The potential associated with the ET step is finally computed as the difference between the energetics of the PET and the PT step as57,58
| ΔGET = ΔGPET − ΔGscaledPT. | (7) |
In addition to ΔGPET, ΔGET values are also referenced to the computational standard hydrogen electrode (SHE).
Generally, the accuracy of the calculated data in comparison to experiments depends essentially on the adopted approximations and the electronic structure calculations to compute Gibbs free energy values. In other words, a negligible systematic error can be expected at this level of calculations.
It is worth noting that, in accordance with the IUPAC convention,59 we state every electrochemical potential as a reduction reaction potential. Hereafter, E0 = ΔGPET/e and Ered. = ΔGET/e are indicators for H atom and e− affinity of molecule Q participating oxidation reaction (i.e. eqn (1)), respectively. The theoretical framework employed in this study has previously been established and extensively used for the pKa, Ered., and E0 estimations.43,53,60–62 When compared to the experiments, the predictability of the DFT-calculated Ered. and E0 is very good.43
CompBatPET database
Our CompBatPET database consists of 8213 organic compounds undergoing two-proton two-electron reactions. The data are stored in the comma-separated values (CSV) file format and XYZ file. One data set was made for each ET, PT, and PET reaction, containing the molecular weights, cavity volumes, highest occupied orbital energies (HOMOs), lowest unoccupied orbital energies (LUMOs), and simplified molecular input line entry system (SMILES) string representations of only the reactants involved in the oxidation and deprotonation reactions. Open Babel63 software was used to record the SMILES. Since SMILES contains information about H-bond changes but not net electron charges, we also add the sample's net charge to the data sets. Note that the molecular weights, cavity volumes, and molecular orbital energies are reported in atomic units, Å3, and Hartree, respectively.Each reactant of the oxidation reaction, namely QH2, QH2+, QH−, QH, Q2−, and Q−, is accompanied by its target variable Ered.. While, pKa is featured by the protonated samples found in the QH2, QH2+, QH22+, QH−, QH, and QH+ forms. Deprotonation converts alcohol (C–OH) fragments into ketone (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). In addition, QH2, QH2+, QH−, and QH are considered as reactants for PET reactions when E0 is the target variable. All the numerical values are imported up to three digits after the decimal point.
O). In addition, QH2, QH2+, QH−, and QH are considered as reactants for PET reactions when E0 is the target variable. All the numerical values are imported up to three digits after the decimal point.
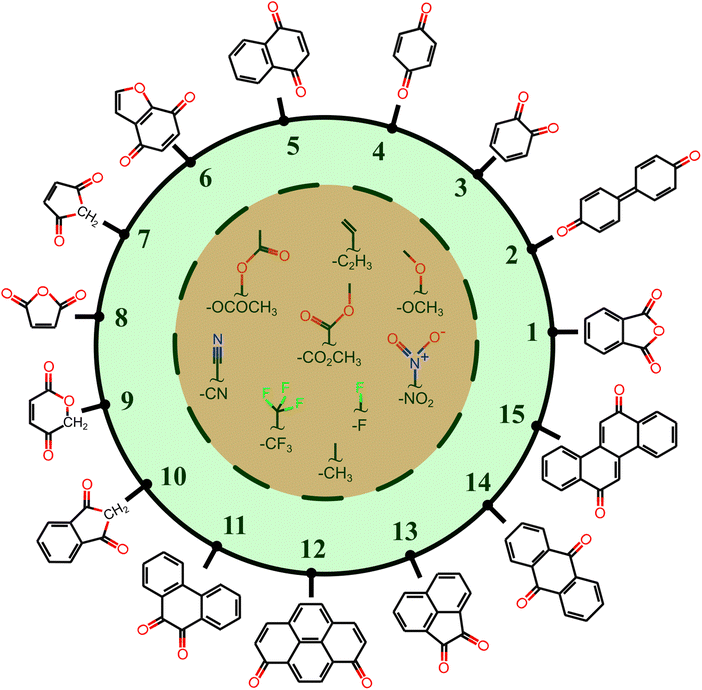
All the molecules in the database are built upon a group of 15 core structures, as schematized in Fig. 2, decorated by –CH3, –CF3, –OCH3, –C2H3, –F, –CN, –NO2, –OCOCH3, and –CO2CH3 functional groups. These functional groups do not participate in the PT reaction, but they have either electron-donating or electron-withdrawing characteristics. The IUPAC names of the core structures can be found in Fig. S1 of ESI.†
Each core is manually designed by one or two functional groups. The task of functional group enumeration is performed using the Maestro modeling interface of Schrödinger Material Science Suite (SMSS).64 The combinatorial search of molecular structures results in 8213 molecules with a diversity of (1:254, 2:605, 3:267, 4:139, 5:644, 6:523, 7:55, 8:55, 9:100, 10:271, 11:1187, 12:970, 13:649, 14:604, and 15:1890). We provide open access to full source code and data sets at https://doi.org/10.5281/zenodo.7952777.
Computational details
All DFT calculations were performed using Gaussian 16 revision C.01 (ref. 65) software. First, the semi-empirical PM7 (ref. 66) method was used to optimize the geometry of molecular structures solvated in PCM67,68 implicit water model. Note that for each molecule the initial atomic coordinates were prepared by Maestro, as mentioned before, and visually inspected by the authors. At this stage, the energetics of two different structures were compared in order to determine the most stable tautomers of the individual QH−, QH, and QH+ forms. After the structure optimization, harmonic vibrational frequencies were assessed for free energy stability evaluation. The structure of a molecule with an imaginary frequency less than −200 cm−1 was modulated and reoptimized until the stable structure was obtained. Then, the total energy was computed for each optimized structure using M06-2X69 together with a Def2-TZVP basis set70 and the more accurate SMD solvation model. This exchange–correlation functional was found to provide the best accuracy for predicting redox potentials of organic molecules.60 To compute the Gibbs free energy, thermal correction to Gibbs free energy and total energy were obtained from the computationally cheaper PM7 (the first step) and high accuracy M06-2X calculations (the second step), respectively. The thermal correction includes the zero-point vibrational energy as well as vibrational enthalpy and entropic contribution to the free energy. This procedure leads to moderate computational cost and has been validated previously.36For high-throughput screening, we used Random Forest Regressor (RFR) as implemented in Scikit-learn package71 of Python. The optimal set of hyperparameters was computed using a cross-validation score over a grid of predefined space. More specifically, the training data was split into ten groups, or folds, where nine were used to train the model and one is used to evaluate its performance. Mean squared error (MSE) was used as an evaluation metric for hyperparameter optimization. To train our RFR model, the data set was initially randomized, then 80% of the data were used for training the model, while 20% for validation. Subsequently, the trained models were used to predict the electrochemical square-schemes, i.e. Ered., pKa, and E0 values. Note, for each target variable listed above a separate model is trained.
The isomeric SMILES representation of the molecules is transformed into a bit-vector using extended-connectivity fingerprints (ECFPs) algorithm.72,73 We used RDKit package74 to rapidly calculate ECFPs. In general, they work by circularly analyzing the environment of each atom and, then, hashing the information to create the fingerprints (FPs). A radius of 3 nearest neighbors was used. Chirality was also considered for the FP assessment. It is critical for backbone 2. The bit vector contains 0 and 1 with a length of 1024 for each molecule.
It is often difficult to interpret the output of ML models because the methods provide very little information on the descriptors' contribution to the output. We employed Shapley additive explanation75 (SHAP) to test whether our chemical intuition agrees with the results of the ML model. Feature importance analysis is also performed. Additionally, Matplotlib,76 Seaborn,77 and Pandas78 as the main Python visualization and data manipulation libraries were used. The ESI† provides more details on the package dependencies as well as a suitable environment for ML calculations.
Results and discussion
Data analysis
In order to inspect the data, we examine the distribution of Ered., pKa, and E0 as shown in Fig. 3. Detailed statistical data was presented in Table S1.† In chemistry, Ered. is defined as the tendency of a molecule to accept an electron: a more positive Ered. indicates a stronger electron-accepting ability of the reactant participating in the reduction reactions. The distribution of Ered. potential is shown in Fig. 3(a): (i) as a result of different ET reactions, there are six distinct peaks, (ii) each ET case shows a multimodal distribution with a dominant peak in the center, (iii) when the number of protons is constant, the second electron donation reaction occurs at a lower Ered. value, (iv) protonation makes reduction reaction thermodynamically more favorable, and (v) Ered. ranges from −1.629 to 2.426 VSHE.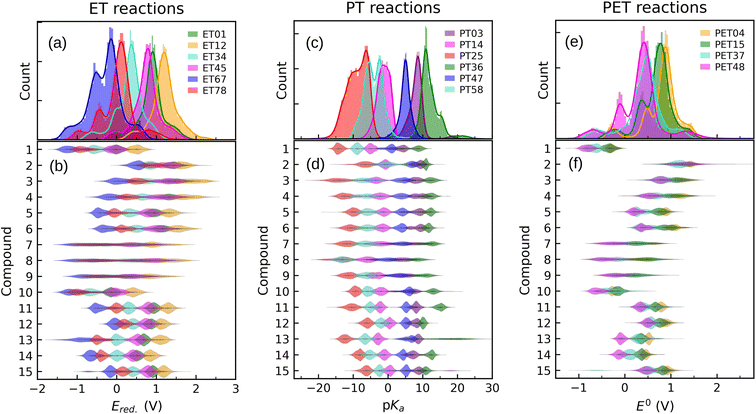 | ||
| Fig. 3 Data distribution accompanied by violin plots showing the contributions of each compound (i = 1, …, 15) for ((a) and (b)) ET, ((c) and (d)) PT, and ((e) and (f)) PET. The reactions in the plots are shown in Fig. 1. The ease of ET, PT, and PET reactions is indicated by the target values Ered., pKa, and E0, respectively. Ered. and E0 were referenced to the SHE. | ||
The impact of the core architecture and functionalization on the Ered. is demonstrated in Fig. 3(b). A violin plot depicts the shape of the data distribution: the broader section of a violin represents a higher variation of Ered.. A narrow bit thick in the middle of the plot indicates that data is highly concentrated around the median. One can also say that a fairly uniform violin plot with long tails indicates (cores 7 to 9) that functional type and/or position have a significant impact on that type of core. When compared to other counterparts, cores 1 and 10 have the highest electron-donating characteristic. ET reduction reactions are thermodynamically less favorable for molecules in these two families. We found that small single-ring compounds 3, 4, 7, 8, and 9 are sensitive to functional group addition. This is not very surprising since inductive/mesomeric effects will pump in or remove the electron density for carbons.79
Fig. 3(c) depicts the pKa distribution: each of the PT03, PT14, and PT47 deprotonation reactions is determined by a unimodal peak, while the others are bimodal. The conversion to a ketone through oxidation increases the acidity of the molecules while deprotonation decreases it. This is in line with common trends in acid–base chemistry which clearly indicate that ketones are very strong acids.79 Additional negatively charged or the removal of positively charged functional groups reduce the acid strength (i.e. increase the pKa).61 Therefore, compounds in QH22+ and QH− states represent the strongest and weakest acids, respectively. Those with negative pKa are unstable in normal solutions and they release proton into the solution even at pH = 0. As a general rule, deprotonation occurs whenever the pH of the solution is greater than the pKa of the solvated molecule. Note that not all the studied QH2 terminate to Q at pH = 0. It is seen from the partially positive pKa of QH+ (i.e. PT58 reaction). In other words, some molecules are deprotonated in a less acidic media.
For each backbone, the pKa values are shown in Fig. 3(d). The acidity strength of the reactants participating in reactions PT25, PT58, PT14, PT47, PT03, and PT36 decreases systematically, with the exception of backbones 2 and 8 where PT58 data overlaps with PT14 and PT25, respectively. The pKa of compound 13 involved in reaction PT36 is widely distributed. With all data taken into account, pKa ranges from −22 to 30.
The data distribution relative to the PET reactions is multimodal, as shown in Fig. 3(e). Each reaction showed a dominant peak centered at a positive value. There is a resemblance between the energy spectrum of PET15 and PET37 with that of PET04, respectively, and PET48. Similarities in the proton states of the reactants may explain it. E0 ranges from −1.222 to 2.722 VSHE.
By removing hydrogen atoms, molecules in the form of QH2 are converted into partially and fully oxidized forms of QH and Q, respectively. Another possibility is that QH2 initially undergoes an ET or PT reaction, then a PET, such as PET15 and PET37. Whenever these reactions take place, the redox potential in water at pH = 0 equals E0. According to our results, the PET reactions mostly take place within the water electrochemical potential window of ca. −1.5 to +1.5 VSHE.80Fig. 3(f) illustrates the backbone effects and demonstrates that compounds 1 and 10 are highly driven to lose hydrogen atoms. Compounds 7, 8, and 9 partially and to a lesser extent exhibit the same behavior. Otherwise, the PET reactions are endothermic. We see no outliers in the data, and it is well-prepared for further analysis.
Machine learning
Property- and structure-based descriptors are two alternative features that are used to train ML models. DFT calculations are used to determine chemical characteristics such as molecular orbitals. Whereas, the structure-based descriptor is produced directly from SMILES, which includes information about the topology, connectivity, and subfragment of the molecules. The latter enables high-throughput screening of candidates at a significantly lower computational cost, i.e. without DFT calculations.The RFR models are trained with 200 trees. Cross-validation shows that the default values can be used for the remaining hyperparameters. Model performance was evaluated using a coefficient-of-determination (R2), root-mean-squared-error (RMSE), and mean-absolute-error (MAE). These performance metrics were defined in the ESI.† The performance assessment is performed five times: every time the data set is split, the model is trained and tested, and the worst performance result is reported.
For Ered. and pKa, the data set of chemical properties contains 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 278 samples, while the structure-based one contains 49
278 samples, while the structure-based one contains 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 samples altogether. There are seven fewer samples in the second data set because of the molecules' rotational symmetry. The SMILES duplicate check found them, and they were removed. Additionally, the relevant information of QH2, QH2+, QH−, and QH compounds was stored for predicting E0. There are 32
271 samples altogether. There are seven fewer samples in the second data set because of the molecules' rotational symmetry. The SMILES duplicate check found them, and they were removed. Additionally, the relevant information of QH2, QH2+, QH−, and QH compounds was stored for predicting E0. There are 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 865 samples in this dataset.
865 samples in this dataset.
Property-based descriptor
In addition to HOMO, HOMO−1, LUMO, and LUMO+1 energies for spin-up and spin-down channels, the chemical parameters include net charge, number of atoms, chemical weight, and volume. Here the volume means the cavity volume used in the solvation model for each molecule. This group is called Descriptor I. All numbers were collected from SMD/M06-2X calculations.It is clear that net charge plays a significant role in the feature space. It affects electron density, resulting in a change in the orbital energies. In order to gain insight into orbital impacts on the target values, we considered only orbital energies (e.g., HOMO, HOMO−1, LUMO, LUMO+1) as Descriptor II. We also made Descriptor III which includes only HOMO. This was used for Ered. and E0 predictions.
To analyze the results of ML models trained on different descriptors, the performance metrics were obtained in Table 1. The closer R2 to 1 or the lower the RMSE and MAE values are, the more accurate the model is. When considering the prediction accuracy of various models trained on the data in Descriptor I, Ered., pKa, and E0 are predicted by MAE ≤ 0.062 V, ≤0.759 pKa unit, and ≤0.106 V, respectively, which are extremely good. For the ET steps an error of roughly 0.1 V is obtained with CCSD(T) while the error bars for pKa values are also of the same order of magnitude.56,60 A well-trained model and excellent correlation between features and target parameters are also shown by the RMSE and R2 values. Moving to Descriptor II feature space causes the performance of the models to somewhat deteriorate but is still comparable to chemical accuracy, e.g. the MAEs are of the order of 0.05 V. It means that a limited number of molecular orbitals carry sufficient information for ML model training.
| Model | Descriptor | Target | RMSE | MAE | R trn 2 | R tst 2 | R oob 2 |
|---|---|---|---|---|---|---|---|
| 1 | I | E red. | 0.093 | 0.062 | 1.00 | 0.98 | 0.98 |
| 2 | II | E red. | 0.102 | 0.068 | 0.99 | 0.97 | 0.97 |
| 3 | III | E red. | 0.229 | 0.177 | 0.92 | 0.87 | 0.87 |
| 4 | I | pKa | 1.203 | 0.759 | 0.99 | 0.97 | 0.97 |
| 5 | II | pKa | 1.477 | 0.929 | 0.99 | 0.96 | 0.96 |
| 6 | I | E 0 | 0.106 | 0.073 | 0.99 | 0.94 | 0.94 |
| 7 | II | E 0 | 0.127 | 0.084 | 0.98 | 0.92 | 0.92 |
| 8 | III | E 0 | 0.397 | 0.305 | 0.53 | 0.22 | 0.22 |
| 9 | IV | E red. | 0.132 | 0.081 | 0.99 | 0.96 | 0.96 |
| 10 | IV | pKa | 1.406 | 0.909 | 0.99 | 0.97 | 0.97 |
| 11 | IV | E 0 | 0.157 | 0.106 | 0.94 | 0.88 | 0.90 |
| 12 | FP | E red. | 0.099 | 0.066 | 0.99 | 0.99 | 0.96 |
| 13 | FP | pKa | 1.003 | 0.628 | 0.99 | 0.98 | 0.97 |
| 14 | FP | E 0 | 0.102 | 0.065 | 0.96 | 0.95 | 0.96 |
Note that by comparing the energy of the orbitals of the spin-up and spin-down channels, as shown in Fig. S2(a) and (b),† it can be seen that the HOMO spin-up channel has a higher energy level than the spin-down channel for the reactants participated in the ET and PET reactions through the oxidation reactions. Therefore, when we discuss HOMO, we are referring to the spin-up channel orbitals. Through SHAP, we carried out feature importance analysis that determines the attribution of feature variables of each sample on the model prediction.81 HOMO state is the most important feature in model training to predict Ered. and E0, as shown in Fig. S3.† The absence of this feature in some samples can deteriorate Ered. prediction beyond ±1.5 V. This value for E0 is around ±1 V. For the pKa prediction, those orbitals positioned at the edge of the HOMO–LUMO gap are the most important.
The HOMO alone, Descriptor III, can predict Ered. reasonably good even with RMSE = 0.229 and MAE = 0.177 V. Whereas, the E0 forecasting is unsatisfactory and the contribution of the other states is necessary. Plotting target value versus HOMO reveals more sparsity for E0 values in comparison to Ered. (see Fig. S4(a) and (b)†).
We carried out comparative analyses to determine the influence of product attributes on the target values. Descriptor IV is introduced as an equivalent to Descriptor II, but it contains the product species information. In general, models 9–11 have predictability comparable to those trained on reactants' feature space.
We found that the key to successfully predicting the Ered. and E0 values is the LUMO of products participating in the oxidation reactions (see Fig. S5†). Prediction of pKa is strongly dependent on HOMOs. Overall, as shown in Fig. S4,† the reactant's HOMO and the product's LUMO participating in the oxidation reactions are inversely correlated to Ered. and E0. Based on Koopmans' theorem, the ionization energy of molecules inversely correlates with their negative HOMO energies.82 There have been reports of a similar trend in recent years.83,84
Structure-based descriptor
To create structure-based feature space (Descriptor FP), we (i) generate FPs from SMILES, and (ii) concatenate bit-strings from step (i) with the net charge of each sample. Before feeding the ML model, it is also critical to double-check for duplicates. In order to determine whether the bit-vector is long enough, we gather only the SMILES of the state QH2 and then check for duplicates versus bit length. A vector length of 1024 is needed to generate a distinct vector for each sample. Adding the electron charge states (0, ±1, ±2) will give us a feature space of 1025 dimensions for each sample.
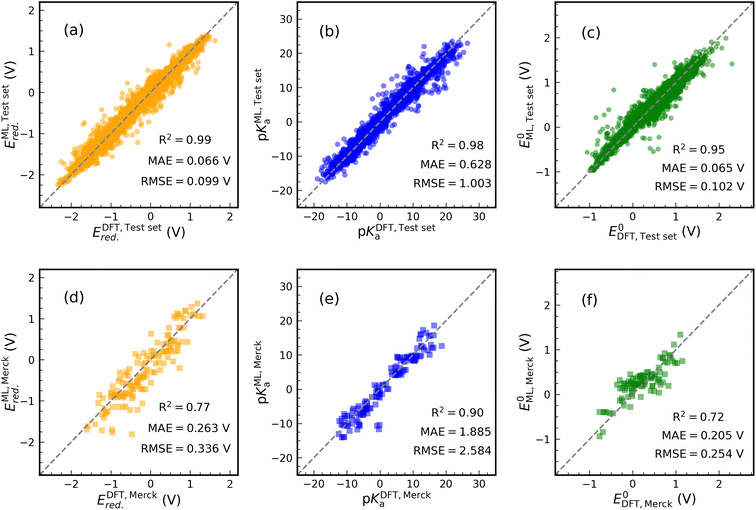
Fig. 4 shows the results of our predictive models when compared against the actual data. Each graph contains the performance metrics values (they are also in Table 1 with FP Descriptor). We use two data sets to validate the ML models: (i) an internal test set (20% of data set in each case) resulting from the splitting of the data set and (ii) an external data set containing 24 synthesized molecule structures purchasable from the Merck company website. The molecules of the external data set were sketched in Fig. S6.† DFT calculations are used to determine the thermodynamics of 144 samples (24 × 6 reactions) undergoing ET and PT reactions for the external data set. For PET, 96 samples (24 × 4 reactions) are evaluated. Only C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O subfragments of these molecules undergo protonation reactions.
O subfragments of these molecules undergo protonation reactions.
The prediction of Ered. achieved a R2 value of 0.99 on the internal test set (see Fig. 4(a)). Furthermore, MAE and RMSE reached values of 0.066 and 0.099 V, respectively, which are close to the performance of model 1 in Table 1. Training an ML model on ECFPs feature space produces a slightly better prediction for pKa than model 4 (see Fig. 4(b)). There are values of 1.003, 0.628, and 0.98 for RMSE, MAE, and R2. Similar to other models, the structural model used to predict E0 delivers low RMSE and MAE values of 0.102 and 0.065 eV, respectively, accompanied by R2 = 0.95 (see Fig. 4(c)).
The performance of the structural models appeared to be good on the external test set (see Fig. 4(d)–(f)). In this case, for Ered., R2, MAE, and RMSE are equivalent to 0.77, 0.263 V, and 0.336 V. For pKa and E0 prediction, models result in R2 = 0.90, MAE = 1.885 V, RMSE = 2.584 V and R2 = 0.72, MAE = 0.205 V, RMSE = 0.254 V, respectively. The addition of some Merck compounds to our CompBatPET database would improve the model's predictability, although it requires extensive additional DFT calculations.
However, there are a few points to keep in mind regarding the prediction of the external test set: (i) the property-based feature space needs DFT-level computations to provide each attribute, but the structure-based descriptor only requires the SMILES of the molecule. Besides the significant difference in the computational cost, i.e. the former takes hours of CPU time while the latter requires only minutes, the SMILES are easily accessible in several chemistry software but DFT computations require more expertise. (ii) The simple backbones used to generate the database for training ML models can be thought of as the building blocks for more complicated ones, such as the Merck data set. (iii) The ML model prediction is still reliable enough to broadly screen the thermodynamics of PET reactions.
Applicability of square-scheme and ML models
As the second test, we compute the Pourbaix diagram for 2,2-propionate ether anthraquinone (abbreviated 2,2PEAQ), which is recently experimentally investigated by Amini et al.85 Our database contains the core structure, but not the functional group in ref. 85. We only look at two-proton two-electron transfer reactions. Fig. S7† shows its molecular structure as well as the square-scheme representation of reactions. In addition to DFT, structural models using FPs were used to calculate the related quantities.We consider 2,2PEAQ at the pH range of 0 to 14. In this range, direct protonation of 2,2PEAQ does not occur (path PT58 is closed). In the presence of the electrode, the first ET appears at a potential of −0.464 VSHE. Depending on the pH of the solution, ET or PT may occur in the following step. If pH ≤ 5, the reduction reaction is followed by a PT reaction for an applied potential between −0.464 and −0.762 VSHE. In contrast, a PET reaction (2,2PEAQ to 2,2PEAQ-H) is even more likely to occur under strongly acidic conditions, as indicated by the E0 value of −0.159 VSHE. According to the Nernst equation,86 which will be covered in more detail in the text that follows, this value drops by −0.059 VSHE per pH at room temperature which makes a step-wise reaction (ET/PT) more likely around pH = 5. It is, then, thermodynamically favorable to convert 2,2PEAQ-H to 2,2PEAQ-H2 through a PET reaction. When 2,2PEAQ-H2 is in a reverse reaction towards 2,2PEAQ, two PET reactions are more likely to occur around pH = 5: despite the second PET always being favorable, the first PET (e.g. occurring at −0.352 VSHE at pH = 0) becomes more favorable with an increment of +0.059 V per pH.
At 5 < pH < 8, the reduction reaction still takes place by incorporating 2 electrons and 2 protons along the ET-PET-PT path. The maximum applied potential required for the PET reduction reaction is −0.52 VSHE occurring at pH of 8 (i.e., the reduction potential at pH = 0, −0.048 V, lowers by −0.059/pH). To oxidize 2,2PEAQ-H2 to 2,2PEAQ, the same 2PET reaction is anticipated to occur in the reversible pathway.
There are two electrons and one proton engaged through the ET-PET route for the reduction reaction at a pH range of 8 to 13. Eventually, there are only two electron steps in the very basic medium (pH > 13) and when applied potential is less than −0.763 VSHE.
The reduction potential E0 under nonstandard conditions depends on the activity of the reduced and oxidized species, which may differ from unity. The Nernst equation describes this deviation from the standard one as pH dependence
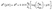 | (8) |
| E0 = E0PET04 + E0PET48. | (9) |
Fig. 5 shows the Pourbaix diagram of the 2,2PEAQ compound. When compared to the experimental data, both DFT and ML have excellent predictability. Small discrepancy relates to pKa differences between different schemes. Despite calculations showing that two-proton two-electron dominates up to a pKa of 8, the experiment suggests a similar reaction up to a pKa of 10. A variation of this magnitude coincides with computational and predictive accuracy.
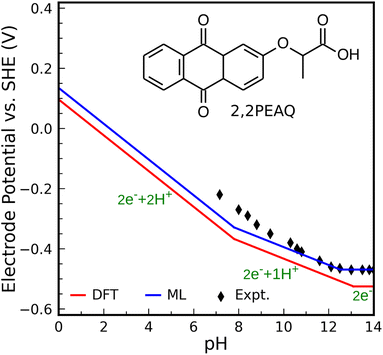 | ||
| Fig. 5 Predicted Pourbaix diagram of 2,2-propionate ether anthraquinone (2,2PEAQ) by DFT (red solid line) and ML models (blue solid line) versus experimental data.85 | ||
Conclusion
To predict ET and PT processes a combined DFT-ML technique was used. We looked at a wide range of quinone type compounds at different charge and protonation states. For all these systems the redox potential and acidity constant were computed. We presented a dataset consisting of about 8200 compounds made up of 15 backbones decorated with 1–2 functional groups taken from a list of 9 groups. The data were extensively examined from a chemical and statistical perspective. As a result, we were able to train random forest models according to the structures and attributes. The molecular space can be described by chemical properties and/or structural characteristics. The most crucial features for the predictions of the acidity constant and redox potential, respectively, are the HOMO and LUMO energy levels. Strong predictability is demonstrated on the external test sets by models created using SMILES strings. While on the internal test sets, great accuracy was reached by all trained models. Although we tested the method on quinone derivatives, it applies to other types of redox compounds as well.Data availability
The Zenodo database contains the data for this paper, which can be downloaded at https://doi.org/10.5281/zenodo.7952777.Author contributions
Arsalan Hashemi: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, writing – original draft. Reza Khakpour: methodology, software, review & editing. Amir Mahdian: writing – review & editing. Michael Busch: methodology, review & editing. Pekka Peljo: writing – review & editing. Kari Laasonen: conceptualization, resources, funding acquisition, project administration, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Digipower project, supported by Teknologiateollisuuden 100v säätiö and Jane ja Aatos Erkon säätiö, and the Horizon 2020 Framework Programme CompBat with Project No. 875565, for financing this study. M. B. acknowledges financial support through the Dr Barbara Mez-Starck Foundation. This work has also partially emanated from the research of P. P. supported by the European Research Council (Starting Grant, agreement no. 950038). P. P. also gratefully acknowledges the Academy Research Fellow funding by the Academy of Finland (Grant No. 315739). We also thank CSC-IT Center for Science Ltd for generous grants of computer time.References
- P. R. D. Murray, J. H. Cox, N. D. Chiappini, C. B. Roos, E. A. McLoughlin, B. G. Hejna, S. T. Nguyen, H. H. Ripberger, J. M. Ganley, E. Tsui, N. Y. Shin, B. Koronkiewicz, G. Qiu and R. R. Knowles, Photochemical and Electrochemical Applications of Proton-Coupled Electron Transfer in Organic Synthesis, Chem. Rev., 2022, 122, 2017–2291 CrossRef CAS PubMed.
- T. Kikuchi, K. Yamada, T. Yasui and Y. Yamamoto, Synthesis of Benzo-Fused Cyclic Ketones via Metal-Free Ring Expansion of Cyclopropanols Enabled by Proton-Coupled Electron Transfer, Org. Lett., 2021, 23, 4710–4714 CrossRef CAS PubMed.
- D. C. Miller, K. T. Tarantino and R. R. Knowles, Proton-Coupled Electron Transfer in Organic Synthesis: Fundamentals, Applications, and Opportunities, Top. Curr. Chem., 2016, 374, 30 CrossRef PubMed.
- S. Y. Reece and D. G. Nocera, Proton-coupled electron transfer in biology: results from synergistic studies in natural and model systems, Annu. Rev. Biochem., 2009, 78, 673–699 CrossRef CAS PubMed.
- J. Pann, W. Viertl, H. Roithmeyer, R. Pehn, T. S. Hofer and P. Brüggeller, Insights into Proton Coupled Electron Transfer in the Field of Artificial Photosynthesis, Isr. J. Chem., 2022, 62, e202100035 CrossRef CAS.
- R. G. Agarwal, S. C. Coste, B. D. Groff, A. M. Heuer, H. Noh, G. A. Parada, C. F. Wise, E. M. Nichols, J. J. Warren and J. M. Mayer, Free Energies of Proton-Coupled Electron Transfer Reagents and Their Applications, Chem. Rev., 2022, 122, 1–49 CrossRef CAS PubMed.
- D. G. Nocera, Proton-Coupled Electron Transfer: The Engine of Energy Conversion and Storage, J. Am. Chem. Soc., 2022, 144, 1069–1081 CrossRef CAS PubMed.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Proton-Coupled Electron Transfer, Chem. Rev., 2012, 112, 4016–4093 CrossRef CAS PubMed.
- R. Tyburski, T. Liu, S. D. Glover and L. Hammarström, Proton-Coupled Electron Transfer Guidelines, Fair and Square, J. Am. Chem. Soc., 2021, 143, 560–576 CrossRef CAS PubMed.
- R. Feng, X. Zhang, V. Murugesan, A. Hollas, Y. Chen, Y. Shao, E. Walter, N. P. N. Wellala, L. Yan, K. M. Rosso and W. Wang, Reversible ketone hydrogenation and dehydrogenation for aqueous organic redox flow batteries, Science, 2021, 372, 836–840 CrossRef CAS PubMed.
- E. Martínez-González, C. Amador-Bedolla and V. M. Ugalde-Saldivar, Reversible Redox Chemistry in a Phenoxazine-Based Organic Compound: A Two-Electron Storage Negolyte for Alkaline Flow Batteries, ACS Appl. Energy Mater., 2022, 5, 14748–14759 CrossRef.
- M. E. Tessensohn and R. D. Webster, Voltammetric applications of hydrogen bonding and proton-coupled electron transfer reactions of organic molecules, Curr. Opin. Electrochem., 2019, 15, 27–33 CrossRef CAS.
- R. Chen, Toward High-Voltage, Energy-Dense, and Durable Aqueous Organic Redox Flow Batteries: Role of the Supporting Electrolytes, ChemElectroChem, 2019, 6, 603–612 CrossRef CAS.
- X. Wang, R. K. Gautam and J. J. Jiang, Strategies for Improving Solubility of Redox-Active Organic Species in Aqueous Redox Flow Batteries: A Review, Batteries Supercaps, 2022, 5, e202200298 CrossRef CAS.
- A. Ramar, F.-M. Wang, R. Foeng and R. Hsing, Organic redox flow battery: Are organic redox materials suited to aqueous solvents or organic solvents?, J. Power Sources, 2023, 558, 232611 CrossRef CAS.
- C. O. Wilhelmsen, J. Muff and J. L. Sørensen, Are biologically synthesized electrolytes the future in green energy storage?, Energy Storage, 2023, e450 CrossRef.
- C. Wang, B. Yu, Y. Liu, H. Wang, Z. Zhang, C. Xie, X. Li, H. Zhang and Z. Jin, N-alkyl-carboxylate-functionalized anthraquinone for long-cycling aqueous redox flow batteries, Energy Storage Mater., 2021, 36, 417–426 CrossRef.
- Y. Y. Lai, X. Li, K. Liu, W.-Y. Tung, C.-F. Cheng and Y. Zhu, Stable Low-Cost Organic Dye Anolyte for Aqueous Organic Redox Flow Battery, ACS Appl. Energy Mater., 2020, 3, 2290–2295 CrossRef CAS.
- C. Wang, X. Li, B. Yu, Y. Wang, Z. Yang, H. Wang, H. Lin, J. Ma, G. Li and Z. Jin, Molecular Design of Fused-Ring Phenazine Derivatives for Long-Cycling Alkaline Redox Flow Batteries, ACS Energy Lett., 2020, 5, 411–417 CrossRef CAS.
- K. Wedege, E. Dražević, D. Konya and A. Bentien, Organic Redox Species in Aqueous Flow Batteries: Redox Potentials, Chemical Stability and Solubility, Sci. Rep., 2016, 6, 39101 CrossRef CAS PubMed.
- M. Pourbaix, Atlas of electrochemical equilibria in aqueous solutions, National Association of Corrosion Engineers, Houston, Tex, 2nd edn, 1974 Search PubMed.
- C. Wiberg, M. Busch, L. Evenäs and E. Ahlberg, The electrochemical response of core-functionalized naphthalene Diimides (NDI) – a combined computational and experimental investigation, Electrochim. Acta, 2021, 367, 137480 CrossRef CAS.
- K. Lin, R. Gómez-Bombarelli, E. S. Beh, L. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, A redox-flow battery with an alloxazine-based organic electrolyte, Nat. Energy, 2016, 1, 16102 CrossRef CAS.
- C. Zhang, Z. Niu, Y. Ding, L. Zhang, Y. Zhou, X. Guo, X. Zhang, Y. Zhao and G. Yu, Highly Concentrated Phthalimide-Based Anolytes for Organic Redox Flow Batteries with Enhanced Reversibility, Chem, 2018, 4, 2814–2825 CAS.
- J. Rodriguez, C. Niemet and L. D. Pozzo, Fluorenone Based Anolyte for an Aqueous Organic Redox-Flow Battery, ECS Trans., 2019, 89, 49 CrossRef CAS.
- S. Pang, X. Wang, P. Wang and Y. Ji, Biomimetic Amino Acid Functionalized Phenazine Flow Batteries with Long Lifetime at Near-Neutral pH, Angew. Chem., Int. Ed., 2021, 60, 5289–5298 CrossRef CAS PubMed.
- Y. Yan, R. Walser-Kuntz and M. S. Sanford, Targeted Optimization of Phenoxazine Redox Center for Nonaqueous Redox Flow Batteries, ACS Mater. Lett., 2022, 4, 733–739 CrossRef CAS.
- S. Er, C. Suh, M. P. Marshak and A. Aspuru-Guzik, Computational design of molecules for an all-quinone redox flow battery, Chem. Sci., 2015, 6, 885–893 RSC.
- A. Jinich, B. Sanchez-Lengeling, H. Ren, R. Harman and A. Aspuru-Guzik, A Mixed Quantum Chemistry/Machine Learning Approach for the Fast and Accurate Prediction of Biochemical Redox Potentials and Its Large-Scale Application to 315 000 Redox Reactions, ACS Cent. Sci., 2019, 5, 1199–1210 CrossRef CAS PubMed.
- J. Barker, L.-S. Berg, J. Hamaekers and A. Maass, Rapid Prescreening of Organic Compounds for Redox Flow Batteries: A Graph Convolutional Network for Predicting Reaction Enthalpies from SMILES, Batteries Supercaps, 2021, 4, 1482–1490 CrossRef CAS.
- Q. Zhang, A. Khetan, E. Sorkun, F. Niu, A. Loss, I. Pucher and S. Er, Data-driven discovery of small electroactive molecules for energy storage in aqueous redox flow batteries, Energy Storage Mater., 2022, 47, 167–177 CrossRef.
- C.-H. Li and D. P. Tabor, Discovery of lead low-potential radical candidates for organic radical polymer batteries with machine-learning-assisted virtual screening, J. Mater. Chem. A, 2022, 10, 8273–8282 RSC.
- E. Sorkun, Q. Zhang, A. Khetan, M. C. Sorkun and S. Er, RedDB, a Computational Database of Electroactive Molecules for Aqueous Redox Flow Batteries, Sci. Data, 2022, 9, 718 CrossRef CAS PubMed.
- R. P. Fornari, M. Mesta, J. Hjelm, T. Vegge and P. de Silva, Molecular Engineering Strategies for Symmetric Aqueous Organic Redox Flow Batteries, ACS Mater. Lett., 2020, 2, 239–246 CrossRef CAS.
- R. P. Fornari and P. de Silva, Molecular modeling of organic redox-active battery materials, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1495 CAS.
- R. P. Fornari and P. de Silva, A Computational Protocol Combining DFT and Cheminformatics for Prediction of pH-Dependent Redox Potentials, Molecules, 2021, 26, 3978 CrossRef CAS PubMed.
- J. Li, H. Xu, J. Wang, Y. Wang, D. Lu, J. Liu and J. Wu, Theoretical insights on the hydration of quinones as catholytes in aqueous redox flow batteries, Chin. J. Chem. Eng., 2021, 37, 72–78 CrossRef CAS.
- Q. Zhang, A. Khetan, E. Sorkun and S. Er, Discovery of aza-aromatic anolytes for aqueous redox flow batteries via high-throughput screening, J. Mater. Chem. A, 2022, 10, 22214–22227 RSC.
- C. de la Cruz, A. Molina, N. Patil, E. Ventosa, R. Marcilla and A. Mavrandonakis, New insights into phenazine-based organic redox flow batteries by using high-throughput DFT modelling, Sustainable Energy Fuels, 2020, 4, 5513–5521 RSC.
- Y. Ding, C. Zhang, L. Zhang, Y. Zhou and G. Yu, Molecular engineering of organic electroactive materials for redox flow batteries, Chem. Soc. Rev., 2018, 47, 69–103 RSC.
- K. M. Pelzer, L. Cheng and L. A. Curtiss, Effects of Functional Groups in Redox-Active Organic Molecules: A High-Throughput Screening Approach, J. Phys. Chem. C, 2017, 121, 237–245 CrossRef CAS.
- J. Asenjo-Pascual, I. Salmeron-Sanchez, P. Mauleón, M. Agirre, A. C. Lopes, O. Zugazua, E. Sánchez-Díez, J. R. Avilés-Moreno and P. Ocón, DFT calculation, a practical tool to predict the electrochemical behaviour of organic electrolytes in aqueous redox flow batteries, J. Power Sources, 2023, 564, 232817 CrossRef CAS.
- A. Hamza, F. Németh, Á. Madarász, A. Nechaev, P. Pihko, P. Peljo and I. Pápai, N-alkylated pyridoxal derivatives as negative electrolyte materials for aqueous organic flow batteries: computational screening, Chem.–Eur. J., 2023, 29, e202300996 CrossRef CAS PubMed.
- ChemAxon, Calculator (Version 19.26.0), Developed by ChemAxon, 2019 Search PubMed.
- P. Symons, Quinones for redox flow batteries, Curr. Opin. Electrochem., 2021, 29, 100759 CrossRef CAS.
- E. J. Son, J. H. Kim, K. Kim and C. B. Park, Quinone and its derivatives for energy harvesting and storage materials, J. Mater. Chem. A, 2016, 4, 11179–11202 RSC.
- J. Rossmeisl, A. Logadottir and J. Nørskov, Electrolysis of water on (oxidized) metal surfaces, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. Nørskov, Electrolysis of water on oxide surfaces, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- J. Ho and M. L. Coote, A universal approach for continuum solvent pKa calculations: are we there yet?, Theor. Chem. Acc., 2009, 125, 3 Search PubMed.
- J. Ho, Predicting pKa in Implicit Solvents: Current Status and Future Directions<a class=”reftools”, Aust. J. Chem., 2014, 67, 1441–1460 CrossRef CAS.
- J. Ho and M. L. Coote, A universal approach for continuum solvent pKa calculations: are we there yet?, Theor. Chem. Acc., 2009, 125, 3 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- A. Klamt, F. Eckert, M. Diedenhofen and M. E. Beck, First Principles Calculations of Aqueous pKa Values for Organic and Inorganic Acids Using COSMO–RS Reveal an Inconsistency in the Slope of the pKa Scale, J. Phys. Chem. A, 2003, 107, 9380–9386 CrossRef CAS PubMed.
- T. N. Brown and N. Mora-Diez, Computational Determination of Aqueous pKa Values of Protonated Benzimidazoles (Part 1), J. Phys. Chem. B, 2006, 110, 9270–9279 CrossRef CAS PubMed.
- A. D. Bochevarov, M. A. Watson, J. R. Greenwood and D. M. Philipp, Multiconformation, Density Functional Theory-Based pKa Prediction in Application to Large, Flexible Organic Molecules with Diverse Functional Groups, J. Chem. Theory Comput., 2016, 12, 6001–6019 CrossRef CAS PubMed.
- M. Busch, E. Ahlberg, E. Ahlberg and K. Laasonen, How to Predict the pKa of Any Compound in Any Solvent, ACS Omega, 2022, 7, 17369–17383 CrossRef CAS PubMed.
- R. Khakpour, D. Lindberg, K. Laasonen and M. Busch, CO2 or Carbonates–What is the Active Species in Electrochemical CO2 Reduction over Fe-Porphyrin?, ChemCatChem, 2023, 15, e202201671 CrossRef CAS.
- R. Khakpour, K. Laasonen and M. Busch, Selectivity of CO2, carbonic acid and bicarbonate electroreduction over Iron-porphyrin catalyst: a DFT study, Electrochim. Acta, 2023, 141784 CrossRef CAS.
- International Union of Pure and Applied Chemistry, IUPAC Compendium of Chemical Terminology – The Gold Book, 2009, https://goldbook.iupac.org/ Search PubMed.
- M. Busch, K. Laasonen and E. Ahlberg, Method for the accurate prediction of electron transfer potentials using an effective absolute potential, Phys. Chem. Chem. Phys., 2020, 22, 25833–25840 RSC.
- M. Busch, E. Ahlberg and K. Laasonen, Universal Trends between Acid Dissociation Constants in Protic and Aprotic Solvents, Chem.–Eur. J., 2022, 28, e202201667 CrossRef CAS PubMed.
- T. Gaudin and J.-M. Aubry, Prediction of Pourbaix diagrams of quinones for redox flow battery by COSMO-RS, J. Energy Storage, 2022, 49, 104152 CrossRef.
- Open Babel development team, Open Babel, https://openbabel.org/wiki/Main_Page Search PubMed.
- L. Schrödinger, Maestro Modeling Interface, Schrödinger Materials Science Suite, 2021, https://www.schrodinger.com/materials-science Search PubMed.
- M. J. Frisch, et al., Gaussian 16 Revision C.01, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- J. J. P. Stewart, Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- G. Scalmani and M. J. Frisch, Continuous surface charge polarizable continuum models of solvation. I. General formalism, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- B. Mennucci, R. Cammi and J. Tomasi, Excited states and solvatochromic shifts within a nonequilibrium solvation approach: A new formulation of the integral equation formalism method at the self-consistent field, configuration interaction, and multiconfiguration self-consistent field level, J. Chem. Phys., 1998, 109, 2798–2807 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- D. Rogers and M. Hahn, Extended-Connectivity Fingerprints, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- A. Cereto-Massagué, M. J. Ojeda, C. Valls, M. Mulero, S. Garcia-Vallvé and G. Pujadas, Molecular fingerprint similarity search in virtual screening, Methods, 2015, 71, 58–63 CrossRef PubMed.
- G. Landrum, RDKit: Open-Source Cheminformatics Software, 2016 Search PubMed.
- S. M. Lundberg and S.-I. Lee, in Advances in Neural Information Processing Systems 30, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017, pp. 4765–4774 Search PubMed.
- J. D. Hunter, Matplotlib: A 2D graphics environment, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- M. Waskom, et al., mwaskom/seaborn: v0.8.1, 2017, https://doi.org/10.5281/zenodo.883859 Search PubMed.
- W. McKinney, Data structures for statistical computing in python, Proceedings of the 9th Python in Science Conference, 2010, pp. 51–56 Search PubMed.
- R. Morrison and R. Boyd, Organic Chemistry, Prentice Hall PTR, 1998 Search PubMed.
- D. Pavlov, Lead-Acid Batteries: Science and Technology, Elsevier Science, 2011 Search PubMed.
- R. Kronberg, H. Lappalainen and K. Laasonen, Hydrogen Adsorption on Defective Nitrogen-Doped Carbon Nanotubes Explained via Machine Learning Augmented DFT Calculations and Game-Theoretic Feature Attributions, J. Phys. Chem. C, 2021, 125, 15918–15933 CrossRef CAS.
- T. Koopmans, Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms, Physica, 1934, 1, 104–113 CrossRef.
- Y. Lv, Y. Liu, T. Feng, J. Zhang, S. Lu, H. Wang and Y. Xiang, Structure reorganization-controlled electron transfer of bipyridine derivatives as organic redox couples, J. Mater. Chem. A, 2019, 7, 27016–27022 RSC.
- Y. Liu, Y. Li, P. Zuo, Q. Chen, G. Tang, P. Sun, Z. Yang and T. Xu, Screening Viologen Derivatives for Neutral Aqueous Organic Redox Flow Batteries, ChemSusChem, 2020, 13, 2245–2249 CrossRef CAS PubMed.
- K. Amini, E. F. Kerr, T. Y. George, A. M. Alfaraidi, Y. Jing, T. Tsukamoto, R. G. Gordon and M. J. Aziz, An Extremely Stable, Highly Soluble Monosubstituted Anthraquinone for Aqueous Redox Flow Batteries, Adv. Funct. Mater., 2023, 33, 2211338 CrossRef CAS.
- M. M. Walczak, D. A. Dryer, D. D. Jacobson, M. G. Foss and N. T. Flynn, pH Dependent Redox Couple: An Illustration of the Nernst Equation, J. Chem. Educ., 1997, 74, 1195 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00091e |
| This journal is © The Royal Society of Chemistry 2023 |