Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combined data-driven and mechanism-based approaches for human-intestinal-absorption prediction in the early drug-discovery stage†
Koichi
Handa
 *a,
Sakae
Sugiyama
b,
Michiharu
Kageyama
a and
Takeshi
Iijima
a
*a,
Sakae
Sugiyama
b,
Michiharu
Kageyama
a and
Takeshi
Iijima
a
aToxicology & DMPK Research Department, Teijin Institute for Bio-medical Research, Teijin Pharma Limited, 4-3-2 Asahigaoka, Hino-shi, Tokyo 191-8512, Japan. E-mail: ko.handa@teijin.co.jp; koichi.handa.0722@gmail.com
bMedicinal Chemistry Research Laboratories, Teijin Institute for Bio-medical Research, Teijin Pharma Limited, 4-3-2 Asahigaoka, Hino-shi, Tokyo 191-8512, Japan
First published on 22nd September 2023
Abstract
It is important to precisely predict the intestinal absorption ratio (Fa) at an early stage in the discovery of orally available drugs because it directly influences drug efficacy. Gastrointestinal unified theoretical framework (GUTFW) and machine learning (ML) are commonly used to predict the percentage of Fa. In GUTFW, the Fa of a drug is estimated using an equation based on the mechanism of human intestinal absorption, dose, solubility, membrane permeability, and dissolution of the drug. The experimental values of these in vitro parameters are required to accurately predict Fa. However, most of these values are unavailable at early stages of development. ML uses a limited dataset of the observed Fa values of drugs in humans. In this study we combined GUTFW and ML to compensate for each defect. We collected published data on the chemical structures of 460 drugs, including Fa and dose amounts. The key parameters of the GUTFW (Do, dose number; Dn, dissolution number; Pn, permeation number), solubility, membrane permeability, and structural descriptors were calculated and used as explanatory variables for ML. ML algorithms, namely, the random forest (RF) and message-passing neural network (MPNN; Chemprop), were investigated. The GUTFW model was compared to the conventional ML method, which uses only structural descriptors, and combined ML method, which uses both structural descriptors and GUTFW parameters. In addition, using the Chemprop framework, we investigated important substructures of Fa. Our result suggested that combinational ML produced higher predictivity than the GUTFW model and conventional ML model in the test dataset (20% of the dataset) [R2 value and RMSE in the combinational ML method: 0.611 and 19.7 (RF), 0.520 and 21.6 (Chemprop); in conventional ML: 0.339 and 25.4 (RF), 0.497 and 22.1 (Chemprop); in GUTFW: 0.353 and 31.9]. Additionally, most of the substructures indicated by the Chemprop framework were consistent with the common knowledge of medicinal chemistry. We developed an accurate prediction method for human Fa using a combination of data-driven ML and mechanism-based GUTFW, where the parameters could be calculated without experimental data, enabling the model to efficiently promote early drug discovery.
Introduction
The oral absorption of a drug is indispensable for a patient's quality of life and economic viability.1 Pharmaceutical companies are trying to develop orally available drugs. However, the difficulty in drug development increases every year.2 The success or failure of clinical trials causes sponsor companies to thrive or endanger themselves.3 The human absorption rate (Fa) of a drug is closely related to its bioavailability and is an important parameter that is directly related to drug efficacy. Thus, the estimation of the human Fa of a candidate drug before clinical trials is an important issue because it greatly affects the success rate of subsequent clinical trials.Regarding in vitro systems, JP2 solubility,4 PAMPA,5 and Caco-2 (ref. 6) are well-known methods for predicting drug absorption in humans at the non-clinical stage. However, the mechanism of absorption is too complex and is related to the diffusion of the compound for solubility,7,8 membrane permeability,9,10 and active efflux transport by transporters, such as P-gp.11 Therefore, it is difficult to predict the human Fa with high accuracy, even if any of these in vitro experiments are combined. In ex vivo experiments, in situ perfusion through isolated intestinal segments in rats is well known; however, it is not a perfect predictor of absorption.12 In in vivo experiments, specifically animal PK experiments, only research on soluble compounds has been performed, and the Fa values of rats and monkeys could be extrapolated to humans.13–15 However, there is a lack of sufficient data regarding solubility and dissolution.16
Human Fa data have been obtained for several hundred compounds from various clinical trials. Based on these data, the structural descriptor of the compound has been used as an explanatory variable to build data-driven machine learning models; however, most of them are 2-class classifiers,17–23 which might reflect the complex mechanism of absorption, as PK prediction of per os (p.o.) is more difficult than that of intravenous (i.v.).24 Recently, two studies were conducted to predict Fa. In the first study in 2019, the authors aimed to use multiple-class classifiers using Caco-2 permeability and DMSO solubility as explanatory variables, and finally they built a 3-class classifier with high predictability with accuracy and kappa values of 0.836 and 0.560, respectively.25 In the second study, conducted in 2023, the authors focused on specific compounds with serotonergic activity and built a 2-class classifier (AUC 0.72 using the test set) and a regression model (R2 = 0.047 using the test set).26 Hence, to advance the prediction of human Fa, we aimed to build a quantitative regression structure–activity relationship (QSAR) model without dataset selection. The merit of a regression model is that it can show the exact number as a percentage of Fa, which can be easily understood by users. Disregarding dataset selection ensures the applicability domain of the predictive model.
From another viewpoint, the published machine learning models completely ignored the dose amount; namely, there were no dose-related items as explanatory variables.17–23,25,26 However, for solubility-limited drugs, human Fa may vary according to dosage,27 necessitating the investigation of the effect of the dosage. A mechanism-based Fa prediction method that converts drug solubility, diffusion, and membrane permeability into a mathematical model, known as the gastrointestinal unified theoretical framework (GUTFW) model, has been published.28 In this model, parameters such as solubility, diffusion, and membrane permeability were obtained experimentally, and Fa was calculated using these parameters considering the dose. Therefore, when these parameters are accurately expressed as experimental values, they are expected to exhibit good prediction accuracy for various compounds. However, if various parameters are predicted using only the compound structure, the calculated Fa could have an estimation error for the necessary predicted parameters, which inevitably reduces the prediction accuracy.29
Therefore, in this study, regarding the missing parts of the existing machine learning model, namely lack of dose information and insufficient predictability (solubility, diffusion, and membrane permeability using only chemical structures) in GUTFW, we propose a novel Fa prediction model that compensates for both aspects. Although this model does not require experimental data, it is expected to be accurate and extrapolative because it incorporates the mechanism of drug absorption as a concept. To assess and validate its performance, a 10-fold cross-validation (CV) procedure and test datasets were used.
In addition, research on model interpretation in deep learning models has progressed in recent years.30,31 Based on this, we aim to contribute to the early drug discovery stage by predicting Fa as well as estimating and calculating the substructures that are considered important for Fa absorption.
Materials and methods
Method overview
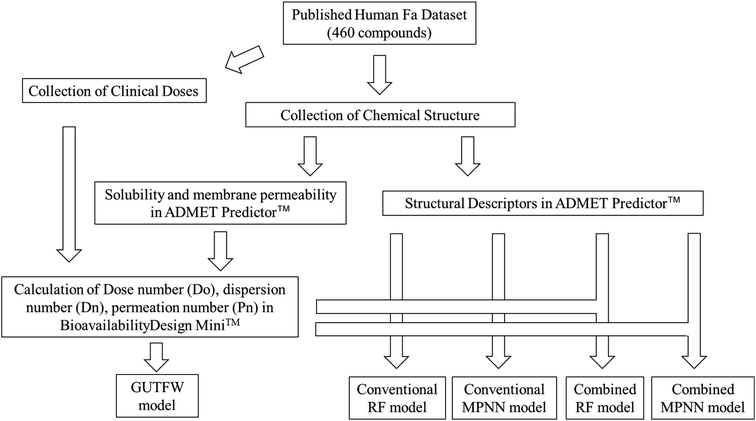
We developed a novel method that combines the key parameters of GUTFW with structure descriptors calculated by ADMET Predictor™ 9.0 (AP)32 to predict human Fa. For comparison, we predicted human Fa using the GUTFW and conventional machine learning (ML) methods. These methods are outlined in Fig. 1.Data collection and standardization of compound representations
All 460 compounds used in this study had Fa values observed in humans.29 Each clinical dose was collected using published information from articles and clinical websites, as presented in Table S1.† The structured data (SD) files of all compounds were obtained from PubChem.33Analysis of the chemical space of the complete dataset
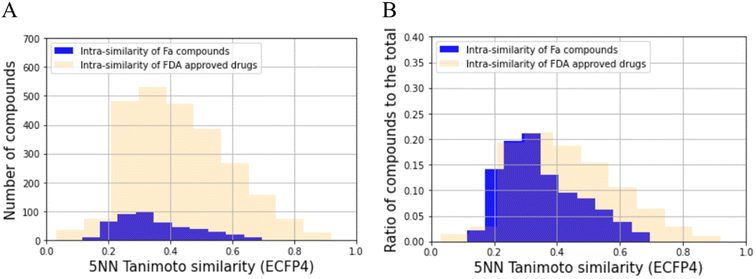
The distribution of the Tanimoto similarity of the five-nearest neighborhood (5NN) was calculated with ECFP4 using the RDKit (version 2020.09.01) Chem functions.34 This was then compared with the Food and Drug Administration (FDA)-approved drugs, consisting of 2503 compounds obtained from DrugBank (version 5.1.8), using canonical SMILES obtained through the same process for prepared compounds mentioned above as the input structure.35 The distributions were then assessed for significant differences using the Kolmogorov–Smirnov test. To achieve this, we utilized the stats.ks_2samp function from the Scipy (version 1.7.0) library with the alternative option set to ‘two-sided.’ For each compound, 5NN similarity was calculated using the Balk–Tanimoto similarity function in RDkit (version 2020.09.01) by averaging the similarity scores of the top five most similar compounds.34Analysis of the chemical space of training and test dataset
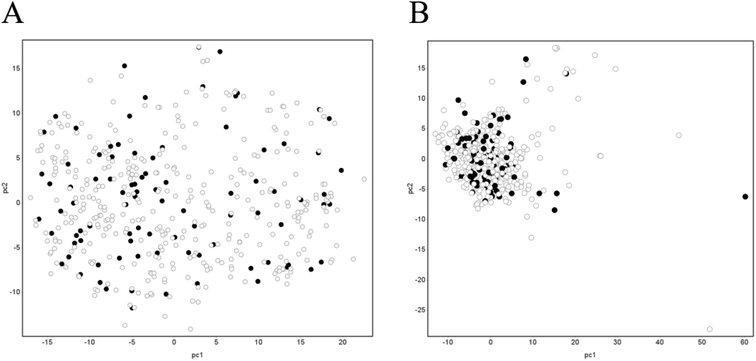
Principal component analysis (PCA) was performed using DataWarrior (version 5.2.1).36 Specifically, canonical SMILES of the dataset were used to calculate FragFp37 fingerprints. FragFP fingerprints were used to calculate the normalized PCA scores for the two components. Furthermore, we performed the same process using all of 278 descriptors calculated in AP.Generation of chemical descriptors
The SD files of the chemical structures considered in this study were used as inputs for AP. The pH value when calculating the structure descriptors was 7.4 according to the physiological conditions, and these were used to specify the ionization state of each compound. We obtained 38 descriptors out of 278 using the correlation filter (<0.7). In this process, we retained the first listed descriptor in the original column output from AP, and removed other correlated descriptors. Additionally, the predicted solubility and membrane permeability were calculated. According to the manuscript of AP,32 the root mean square error (RMSE) and R2 value in the test dataset for solubility were 0.605 and 0.908 with 955 test compounds and 2641 training compounds (S+Sw model). Those values in the test dataset for membrane permeability were 0.482 and 0.718 with 57 test compounds and 286 training compounds (S+MDCK model).Generation of key parameters in the gastrointestinal unified theoretical framework
Do, dose number; Dn, dissolution number; and Pn, permeation number were calculated using Bioavailability Design Mini™ 1.2; the theoretical background is shown in the following eqn (1) to (3); where Dose, S, VGI, kdiss, Tsi, and kperm are the amount of dose, solubility, volume of gastrointestinal tract, dissolution rate coefficient, intestinal transit time, and permeation rate coefficient, respectively.38 The solubility calculated with AP was used as S. The membrane permeability calculated with AP was used to calculate kperm in Bioavailability Design Mini™ 1.2. See the original article in detail.29,39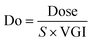 | (1) |
| Dn = kdiss × Tsi | (2) |
| Pn = kperm × Tsi | (3) |
Fa can be obtained using eqn (4).
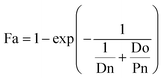 | (4) |
Machine learning models
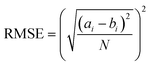 | (5) |
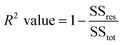 | (6) |
Descriptor importance evaluation
We used the mean decrease in the Gini coefficient as the Gini index included in the RF algorithm to rank the descriptors associated with the predictions of Fa in the combined RF model. This method quantifies the factors contributing to the regression accuracy.45Important substructure search
We also estimated the important substructures of Fa using a conventional MPNN model with Monte Carlo tree search.31 For this calculation, we used two models to investigate the positive and negative substructures of Fa. To achieve this, an additional MPNN model with an objective variable of 100 Fa (%) was constructed based on the building process in the conventional MPNN model. For the Monte Carlo tree search, “Chemprop.interpret.py” was used in Python (ver. 3.7.10) from the Chemprop library (version 1.3.1), and the parameters were set to default.41,44 The positive substructures were clustered into 30 groups using FragFp in Data Warrior (version 5.2.1).36 The centroid structure was selected as representative of each cluster. The compounds that included these substructures and whose Fa were >95% were scrutinized. All negative substructures were scrutinized with compounds whose Fa were below 5%. To understand the substructural properties, we calculated cLogP and PSA using ChemDraw (version 15.1.0.144) and BIOVIA Insight for Excel 2021 (Dassault Systèmes SE), respectively.Results and discussion
Analysis of the chemical space of compounds used compared with FDA-approved drugs
Before building the QSAR model for Fa, we analyzed the chemical space of the prepared dataset to check its bias using the 5NN of the Tanimoto similarity. The results of this analysis are shown in Fig. 2A. The average 5NN Tanimoto similarity in the dataset collected in this study was 0.352, which was lower than that of FDA-approved drugs (0.429). The p-value of the average of 5NN Tanimoto similarity between the compounds collected and FDA-approved drugs was 2.11 × 10−15. In absolute terms, a similarity above approximately 0.3 in the ECFP4/Tanimoto space often indicates similar bioactivity.46 Furthermore, we checked the ratio of the compounds to the total number of compounds (Fig. 2B), and the diversity of the compounds also seemed to be more than that of FDA approved drugs. Hence, the compounds prepared in this study have moderate diversity. Specifically, the QSAR model built in this study can be expected to be applied to a wide range of compounds.Training dataset and test dataset
Next, to check whether the separation of the dataset into training and test datasets did not include any bias and whether the test dataset could be covered by the training dataset, we performed PCA analysis using FragFP. The results are shown in Fig. 3A. The cumulative explained variance percentages of PC1 and PC2 were 28.2%. The training and test datasets were evenly distributed in chemical space. Furthermore, we checked it using AP descriptors; although the distribution was more condensed than that using FragFP, the result was the same with FragFP that training and test datasets were evenly distributed in chemical space (Fig. 3B). The cumulative explained variance percentages of PC1 and PC2 were 28.8%. Therefore, the chemical space of the test dataset was covered by that of the training dataset.Predictivity of the mechanism-based model—gastrointestinal unified theoretical framework model
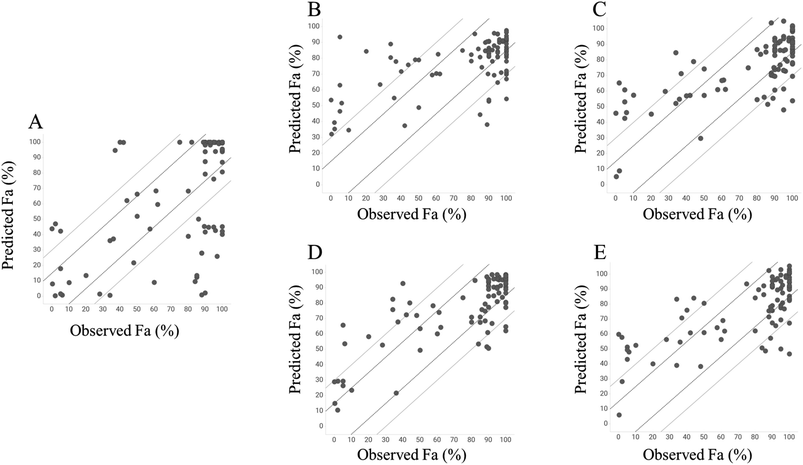
To investigate the predictive ability of the model, we calculated the Fa values using the GUTFW method. Because GUTFW is not a data-driven method, the separation of datasets into training and test datasets is not required to evaluate this model. However, in this study, the models were easily compared by dividing the dataset for the GUTFW model, same as that for other models. The results are presented in Table 1 and a plot of the observed and predicted Fa values in the test dataset is shown in Fig. 4A. The RMSE values of the GUTFW model were 37.6% and 31.9% for training and testing, respectively; therefore, its predictivity may pose a potential risk of over 30% error in human intestinal absorption at the clinical stage (Table 1). Next, we counted the number of compounds that were underestimated by less than −15% and −30% (this means worse predictivity than 15%) and overestimated by more than 15% and 30% (this means worse predictivity than 15%). The plot in GUTFW indicates the tendency of this predictivity to be oriented toward underprediction. The number of compounds that were underestimated by less than −15% and −30% was 20 and 24, respectively, and the number of compounds that were overestimated by more than 15% and 30% was 10 and 6, respectively (Fig. 4A). The difficulty of predicting Fa using only chemical structures was highlighted by Sugano et al.29 In particular, using the GUTFW model without experimental data led to predictive errors associated with the in silico values, which were the solubility and membrane permeability values predicted by AP in this study. This indicates that the predictive ability of the GUTFW model can be improved by introducing a more accurate calculator for these parameters.| Method | GUTFW | RF with AP descriptors | Chemprop | RF with AP descriptors and Do, Dn, and Pn | Chemprop with Do, Dn, and Pn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Evaluation | Training data | Test | 10-fold CV | Test | 10-fold CV | Test | 10-fold CV | Test | 10-fold CV | Test |
| N | 368 | 92 | 368 | 92 | 368 | 92 | 368 | 92 | 368 | 92 |
| R 2 | 0.181 | 0.353 | 0.233 | 0.339 | 0.396 | 0.497 | 0.449 | 0.611 | 0.415 | 0.520 |
| RMSE (%) | 37.6 | 31.9 | 27.9 | 25.4 | 23.5 | 22.1 | 23.7 | 19.7 | 23.1 | 21.6 |
Predictivity of the conventional machine learning model using only the chemical structure as an explanatory variable
Next, we investigated the conventional ML model to predict Fa and compared its predictivity with that of the GUTFW model. The R2 value and RMSE in the 10-fold CV and test datasets are shown in Table 1, and the plot between observed and predicted values is shown in Fig. 4B and C. First, in the case of the RF model using AP descriptors as explanatory variables, the R2 values (0.233) in the 10-fold CV were higher than those in the GUTFW model (0.181), and the RMSE (27.9%) in the 10-fold CV was lower than that in the GUTFW model (37.6%). In the test dataset, the R2 value (0.339) was lower than that of the GUTFW model (0.353), whereas the RMSE (25.4%) in 10-fold CV was lower than that of the GUTFW model (31.9%). There was no clear tendency of predictivity. In particular, the number of compounds underestimated by less than −15% and −30% was 20 and 8, respectively, whereas the number of compounds overestimated by more than 15% and 30% was 20 and 16, respectively (Fig. 4B). Hence, we can conclude that the predictive ability of the RF model is better than that of the GUTFW model. Second, in the case of the Chemprop model, in the 10-fold CV and test datasets, the R2 values, which were 0.396 and 0.497, respectively, were higher than those in the GUTFW model. Furthermore, the RMSE values for 10-fold CV and test datasets, which were 23.5% and 22.1%, respectively, were lower than those of the GUTFW model. Therefore, the predictivity of the Chemprop model for Fa surpasses not only that of the GUTFW model but also that of the RF model. The number of compounds with less than −15% and −30% underestimation was 27 and 6, respectively, whereas the number of compounds with more than 15% and 30% overestimation was 18 and 11, respectively (Fig. 4C). Therefore, from the results, this model may tend toward underprediction. Nevertheless, we conclude that this model has a better predictability than the GUTFW model. When comparing the RF and Chemprop models, the Chemprop model was superior to the RF model, which might be derived from the difference in the representation of chemical structures. Although the superiority of graph representation over chemistry descriptors is controversial,47 in the case of the QSAR model for human Fa using only the chemical structure, the graph is preferable.Predictivity of the combined machine learning model using both GUTFW key parameters and chemistry structure descriptors
To develop a more accurate method for predicting Fa, we introduced key GUTFW parameters (Do, Dn, and Pn) into the ML models. The statistical results are shown in Table 1, and plots of the observed versus predicted Fa values are shown in Fig. 4D and E. First, Do, Dn, and Pn were used as descriptors in the same manner as the AP descriptors in the RF model. In both 10-fold CV, R2 value and RMSE were much higher (0.449) and lower (23.7%) than the GUTFW model (0.181 and 37.6%) and the conventional RF model (0.233 and 27.9%), respectively. Furthermore, we confirmed a higher R2 value (0.611) and lower RMSE (19.7%) for the test dataset compared with the GUTFW model (0.353 and 31.9%) and the conventional RF models (0.339 and 25.4%). When comparing the plot of the observed and predicted Fa using the combined RF model and the conventional RF model, there was a noticeable improvement; namely, the number of compounds underestimated by less than −15% and −30% was 12 and 5, respectively, whereas the number of compounds overestimated by more than 15% and 30% was 16 and 9, respectively [the numbers in the conventional RF model were 20, 8 (underestimated), and 20, 16 (overestimated), respectively] (Fig. 4D). Therefore, the introduction of Do, Dn, and Pn into the conventional RF model improved the predictivity. Recently, there has been much research into ML models that use many types of parameters as explanatory variables and are known as multimodal models. The improvement in the predictive accuracy of the RF model in this study was consistent with the results of previous studies.48–51 Second, Do, Dn, and Pn were used as external features to represent the graph in Chemprop. In both 10-fold CVs, the R2 value and RMSE were much higher (0.415) and lower (23.1%) than those of the GUTFW model (0.181 and 37.6%) and the conventional Chemprop model (0.396 and 23.5%). Furthermore, we confirmed a higher R2 value (0.520) and lower RMSE (21.6%) in the test dataset compared with the GUTFW model (0.353 and 31.9%) and the conventional Chemprop model (0.497 and 22.1%), respectively. When comparing the plot of the observed and predicted Fa values using the combined Chemprop model with the conventional Chemprop model, an improvement was noted for overestimation. In particular, the number of compounds underestimated less than −15% and −30% were 18 and 6, respectively, while the number of compounds overestimated more than 15% and 30% were 18 and 12, respectively [the numbers in the conventional Chemprop model were 27, 6 (underestimated), and 18, 11 (overestimated), respectively]. Therefore, although this was relatively limited compared to the RF model, Do, Dn, and Pn improved the predictive accuracy. When we reconsidered the combined effect of descriptors in the graph-based method, a report on in vivo clearance indicated that graph representation may not always outperform chemical structure descriptors.48,51Furthermore, we investigated the outliers from another viewpoint. We focused on the 30% outliers of the test dataset in GUTFW model; there were 26 outliers. When we checked those 26 predictivity in the other predictive models, we could find that 17 compounds were recovered by the conventional RF model. We found that the 9 compounds which were not recovered by this conventional RF model had mostly low Fa; 6 compounds out of 9 had less than 50% of Fa. When comparing GUTFW with the conventional Chemprop model in the same manner, 20 compounds were recovered, and 4 out of 6 unrecovered compounds had less than 50% of Fa. When comparing GUTFW with the combined RF model, 19 compounds were recovered, and 4 out of 7 unrecovered compounds had less than 50% of Fa. When comparing GUTFW with the combined Chemprop model, 18 compounds were recovered, and 5 out of 8 unrecovered compounds had less than 50% of Fa. In the test dataset of 92 compounds, the number of compounds with Fa less than 50% was only 19. Hence we conclude that further studies are required since most of the compounds which seem hard to be predicted have low Fa by any models built in this study.
Importance of Do, Dn, and Pn
According to the results of the combined study of the chemical structure and key GUTFW parameters in ML, the parameters are highly important in the prediction of Fa. Therefore, to quantify their importance, we calculated the Gini index, and the results are shown in Fig. 5. Pn was the most important parameter with a Gini index of 17.9. Dn ranked third with a Gini index of 7.5. Do ranked 14th among all 38 descriptors, with a Gini index of 2.0. Based on these results, all three key GUTFW parameters are important for Fa prediction in the combined RF model. However, Do exhibited the lowest importance among the three key GUTFW parameters, in contrast to our initial prediction. This may be due to the lack of accurate dosage information when Fa was observed. This is because the dosage we collected was not always the same as that used in human clinical studies to investigate Fa. In a few cases, we made a few assumptions; for example, the p.o. dose is the same as the i.v. dose, or the dose of the pro-drug is the same as the dose of the active form (see Table S1† for details).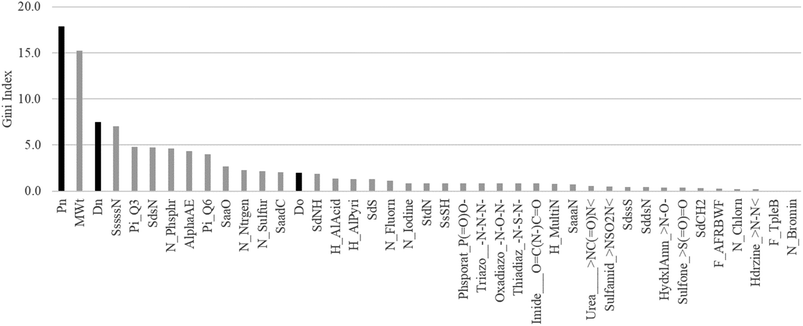 | ||
| Fig. 5 Plot of Gini index of 38 AP descriptors and Do, Dn, and Pn used in the random forest (RF) model. Each bar represents a Gini index. The three black bars represent the key parameters of the GUTFW: Pn, Dn, and Do. The description of these 38 AP descriptors is shown in Fig. S2.† | ||
When we investigated other descriptors of AP, the molecular weight was the second most important, with a Gini index of 15.2. This is consistent with the concept of “the rule of five,” which states that smaller compounds (specifically, less than 500 g mol−1) are more likely to be absorbed in the body, and vice versa.52 We can speculate on the interpretation of other descriptors; however, in this study, we simply selected descriptors based on multicollinearity. Therefore, to avoid misinterpretation, substructure analysis was performed using the Chemprop model, as described in the following section.
Estimation of important substructures
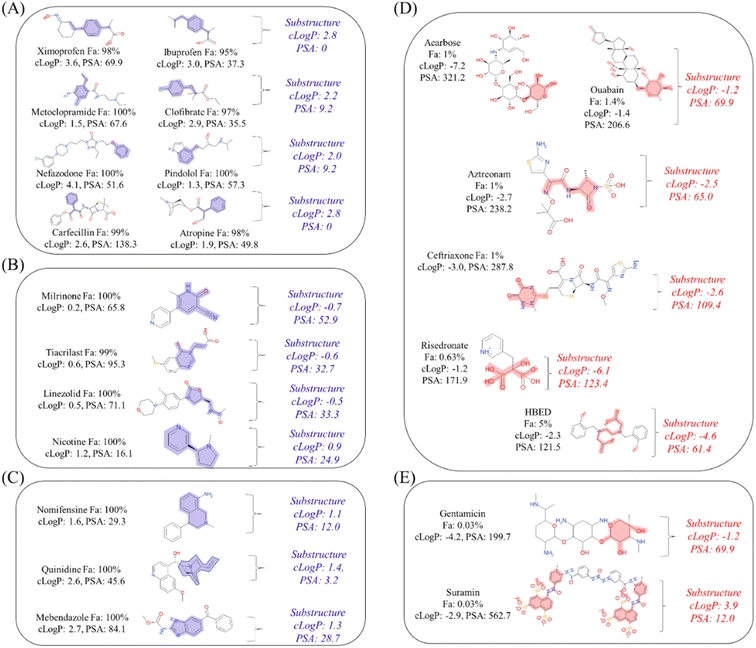
Next, to determine the important substructures of Fa, we performed a numerical analysis using the Chemprop framework. The analysis was performed using two Chemprop models. For the positive Fa substructures, the model we have already built in the previous section (Predictivity of conventional machine learning model using only chemical structures as explanatory variables) was used, and its predictivities were Rtest2: 0.497 and RMSEtest: 22.1% (Table 1). For the negative Fa substructures, we built a new model, and its predictivities were Rtest2: 0.516 and RMSEtest: 21.7%. Based on this predictivity, we can conclude that both models are acceptable for analyzing substructures. The results of the representative 30 substructures for positive Fa selected by clustering and 23 substructures for negative Fa are shown in Fig. S1 and S2,† respectively.To interpret the estimated substructures, we selected drugs whose suggested important substructures either agreed or disagreed with the knowledge of medicinal chemistry. We categorized the Fa-positive substructures into three cases: A to C. The substructures of case A are shown in Fig. 6A. The feature of category A is that the compounds have high Fa (>95%) and the estimated substructures contribute to the increasement of lipophilicity against the entire structure. For example, cLogP and PSA of the suggested substructure 1-ethyl-4-methylbenzene were 2.8 and 0, respectively. The values of the whole compound structures were 3.6 and 69.6 (ximoprofen) and 3.0 and 37.3 (ibuprofen), respectively. The other examples in case A are the same. Hence, we can conclude that each substructure contributes to an increase in lipophilicity compared to the entire structure, which can lead to improved membrane permeability. The substructures of case B are shown in Fig. 6B. The feature of category B is that the compounds have high Fa (>95%) and the estimated substructures contribute to the decrease of lipophilicity against the entire structure. For example, cLogP and PSA of the suggested substructure 2-oxo-1,2-dihydropyridine-3-carbonitrile were −0.7 and 52.9, respectively. The values of the whole compound structure (milrinone) were 0.2 and 65.8, respectively. The other examples in case B are the same. Thus, we can conclude that each substructure contributes to a decrease in lipophilicity compared to the entire structure, which can lead to improved solubility. The substructures of case C are shown in Fig. 6C. The feature of category C is that the compounds have high Fa (>95%) and the estimated substructures contribute to the maintenance of lipophilicity balance against the entire structure. For example, the cLogP and PSA values of the suggested 1,2,3,4-tetrahydroisoquinoline substructure were 1.1 and 12.0, respectively. The values of the whole compound structure (nomifensine) were 1.6 and 29.3, respectively. Other examples in case C were the same. Therefore, each substructure contributes to maintaining balanced lipophilicity against the entire structure, which can lead to improved membrane permeability and solubility. Additionally, a substructure, (1S,3R,4S)-3-methylquinuclidine (cLogP: 1.4, PSA: 3.2), suggested with quinidine (cLogP: 2.6, PSA: 45.6) in case C, contributed to not only maintaining balanced lipophilicity but also disrupting the planarity of the whole molecule, which can lead to better solubility. Although not all substructures for positive Fa could be interpreted, we could not find any substructures that completely disagreed with the common knowledge and sense of medicinal chemists.
Next, we categorized the Fa-negative substructures into two cases: D and E. The substructures of case D are shown in Fig. 6D. The feature of category D is that the compounds have low Fa (<5%) and the estimated substructures contribute to the decrease of lipophilicity against the entire structure. For example, the cLogP and PSA values of the suggested substructure (2R,3R,5S, or R)-tetrahydro-2H-pyran-2,3,5-triol were −1.2 and 69.9, respectively. The values of the whole compound structures were −7.2 and 321.2 (acarbose): −1.4 and 206.6 (ouabain), respectively. Hence, we conclude that each substructure contributes substantially to the decrease in lipophilicity compared to its entire structure, which can worsen membrane permeability. The substructures for case E are shown in Fig. 6E. The feature of category E is that the compounds have low Fa (<5%) and the estimated effect of each substructure on the whole structure is not consistent with the results published in previous reports. For example, tetrahydro-2H-pyran-2,3,5-triol (cLogP: −1.2 and PSA: 69.9) was suggested as an important substructure in gentamicin (cLogP: −4.2 and PSA: 199.7). A low permeability of gentamicin has also been reported.53 Although we can barely interpret that several hydroxyl groups (H-bond donors) of this substructure contributed to the decrease in lipophilicity and could lead to the worsening of membrane permeability, several amine groups, which were not included in the suggested substructure, were considered to contribute to the decrease in lipophilicity rather than the hydroxyl group. Another example is N-benzylnaphthalen-1-amine (cLogP: −2.9 and PSA: 562.7), which was suggested as an important substructure in suramin (cLogP: 3.9 and PSA: 12.0). Although it cannot be inferred that the high planarity and lipophilicity of naphthalene rings contribute to the increase in lipophilicity and can lead to the worsening of its solubility, several sulfone groups, which were not included in the suggested substructure, were considered to contribute to the decrease in lipophilicity and could lead to the worsening of membrane permeability. This was supported by the high solubility of suramin (>50 mg mL−1).54 Based on these results, the important substructures estimated using the Chemprop framework partially agreed with the results of previous reports.
Regarding the cLogP and PSA used in this section for discussion, in the AP descriptors originally calculated, similar descriptors were included as Moriguchi descriptors which constitute MLogP, a well-known LogP calculated value55 and T_PSA (topological polar surface area). Therefore, through the success of the RF model with AP descriptors, we have also examined the effect of cLogP and PSA indirectly.
Conclusion
In this study, we collected published data on 460 drugs with moderate diversity in chemical structures, Fa, and dose amounts in humans. To determine the most accurate Fa prediction method, we combined mechanism-based and data-driven methods. The novel ML method, which incorporated both structural descriptors and GUTFW parameters, demonstrated a higher predictivity than GUTFW and conventional ML models for the 10-fold CV and test datasets. Hence, we developed a more accurate prediction method for human Fa using a combination of data-driven ML and a mechanism-based GUTFW that does not require any experimental data using the RF algorithm. This model is expected to have applications in the early drug discovery stage because it does not require experimental data, whereas the GUTFW prediction appears to be suitable for the late drug development stage because it requires accurate experimental data. Furthermore, the important substructures calculated in the Chemprop framework partially agree with the knowledge and experience of medicinal chemists. Considering these limitations, further computational studies are required to assess and improve the efficiencies of candidate drugs.Data availability
The compounds used in this study are available in Table S1.† The programmes used in this study below are freely available. Random forest: https://cran.rproject.org/web/packages/randomForest/index.html. Chemprop: https://chemprop.readthedocs.io/en/latest/#.Author contributions
The manuscript was written with contributions from all authors. All authors approved the final version of the manuscript.Conflicts of interest
The authors declare no conflicts of interest associated with this manuscript.Abbreviations
| Fa | Intestinal absorption ratio |
| GUTFW | Gastrointestinal unified theoretical framework |
| ML | Machine learning |
| Do | Dose number |
| Dn | Dissolution number |
| Pn | Permeation number |
| RF | Random forest |
| MPNN | Message-passing neural network |
| QSAR | Quantitative structure–activity relationship |
| CV | Cross-validation |
| AP | ADMET Predictor™ 9.0 |
| SD | Structured data |
| 5NN | Five-nearest neighborhood |
| FDA | Food and Drug Administration |
| PCA | Principal component analysis |
| RMSE | Root mean square error |
Acknowledgements
Seishiro Sakamoto and Shin Umeda from TEIJIN Pharma Ltd made valuable contributions to the discussions.References
- M. S. Alqahtani, M. Kazi, M. A. Alsenaidy and M. Z. Ahmad, Advances in Oral Drug Delivery, Front. Pharmacol, 2021, 12, 618411, DOI:10.3389/fphar.2021.618411.
- A. D. Hingorani, V. Kuan, C. Finan, F. A. Kruger, A. Gaulton, S. Chopade, R. Sofat, R. J. MacAllister, J. P. Overington, H. Hemingway, S. Denaxas, D. Prieto and J. P. Casas, Improving the Odds of Drug Development Success through Human Genomics: Modelling Study, Sci. Rep., 2019, 9, 18911, DOI:10.1038/s41598-019-54849-w.
- O. Dyer, Firm Involved in Drug Trial Fiasco Files for Bankruptcy, BMJ, 2006, 333, 114, DOI:10.1136/bmj.333.7559.114-a.
- T. Nakauchi, E. Takeuchi, T. Okamoto, K. Teramoto, A. Nozaki, F. Seko, K. Yuminoki, J. Katakawa and N. Hashimoto, Equivalence Studies of Pravastatin Original and Generic Drugs by Dissolution Test, J. Pharm. Soc. Jpn., 2012, 132, 939–944, DOI:10.1248/yakushi.132.939.
- G. Ottaviani, S. Martel and P.-A. Carrupt, Parallel Artificial Membrane Permeability Assay: A New Membrane for the Fast Prediction of Passive Human Skin Permeability, J. Med. Chem., 2006, 49, 3948–3954, DOI:10.1021/jm060230+.
- R. B. van Breemen and Y. Li, Caco-2 Cell Permeability Assays to Measure Drug Absorption, Expert Opin. Drug Metab. Toxicol., 2005, 1, 175–185, DOI:10.1517/17425255.1.2.175.
- Y. Fujioka, K. Kadono, Y. Fujie, Y. Metsugi, K. Ogawara, K. Higaki and T. Kimura, Prediction of Oral Absorption of Griseofulvin, a BCS Class II Drug, Based on GITA Model: Utilization of a More Suitable Medium for In-Vitro Dissolution Study, J. Controlled Release, 2007, 119, 222–228, DOI:10.1016/j.jconrel.2007.03.002.
- R. Takano, K. Sugano, A. Higashida, Y. Hayashi, M. Machida, Y. Aso and S. Yamashita, Oral Absorption of Poorly Water-Soluble Drugs: Computer Simulation of Fraction Absorbed in Humans from a Miniscale Dissolution Test, Pharm. Res., 2006, 23, 1144–1156, DOI:10.1007/s11095-006-0162-4.
- G. E. Amidon, W. I. Higuchi and N. F. Ho, Theoretical and Experimental Studies of Transport of Micelle-Solubilized Solutes, J. Pharm. Sci., 1982, 71, 77–84, DOI:10.1002/jps.2600710120.
- K. Sugano, Estimation of Effective Intestinal Membrane Permeability Considering Bile Micelle Solubilisation, Int. J. Pharm., 2009, 368, 116–122, DOI:10.1016/j.ijpharm.2008.10.001.
- R. Lu, Y. Zhou, J. Ma, Y. Wang and X. Miao, Strategies and Mechanism in Reversing Intestinal Drug Efflux in Oral Drug Delivery, Pharmaceutics, 2022, 14, 113, DOI:10.3390/pharmaceutics14061131.
- K. Sano, J. Homma, H. Sekine, E. Kobayashi and T. Shimizu, Intermittent Application of External Positive Pressure Helps to Preserve Organ Viability during Ex Vivo Perfusion and Culture, J. Artif. Organs, 2020, 23, 36–45, DOI:10.1007/s10047-019-01141-3.
- W. L. Chiou, H. Y. Jeong, S. M. Chung and T. C. Wu, Evaluation of Using Dog as an Animal Model to Study the Fraction of Oral Dose Absorbed of 43 Drugs in Humans, Pharm. Res., 2000, 17, 135–140, DOI:10.1023/a:1007552927404.
- W. L. Chiou and P. W. Buehler, Comparison of Oral Absorption and Bioavailablity of Drugs between Monkey and Human, Pharm. Res., 2002, 19, 868–874, DOI:10.1023/a:1016169202830.
- W. L. Chiou and A. Barve, Linear Correlation of the Fraction of Oral Dose Absorbed of 64 Drugs between Humans and Rats, Pharm. Res., 1998, 15, 1792–1795, DOI:10.1023/a:1011981317451.
- K. Sugano, Species Difference, in Biopharmaceutics Modeling and Simulations: Theory, Practice, Methods, and Applications, Wiley, 2012, pp. 412–429 Search PubMed.
- T. Niwa, Using General Regression and Probabilistic Neural Networks to Predict Human Intestinal Absorption with Topological Descriptors Derived from Two-Dimensional Chemical Structures, J. Chem. Inf. Comput. Sci., 2003, 43, 113–119 CrossRef CAS PubMed.
- T. Hou, J. Wang, W. Zhang and X. Xu, ADME Evaluation in Drug Discovery. 7. Prediction of Oral Absorption by Correlation and Classification, J. Chem. Inf. Model., 2007, 47, 208–218 CrossRef CAS PubMed.
- N. Basant, S. Gupta and K. P. Singh, Predicting Human Intestinal Absorption of Diverse Chemicals Using Ensemble Learning Based QSAR Modeling Approaches, Comput. Biol. Chem., 2016, 61, 178–196 CrossRef CAS PubMed.
- O. Obrezanova and M. D. Segall, Gaussian Processes for Classification: QSAR Modeling of ADMET and Target Activity, J. Chem. Inf. Model., 2010, 50, 1053–1061 CrossRef CAS PubMed.
- J. Shen, F. Cheng, Y. Xu, W. Li and Y. Tang, Estimation of ADME Properties with Substructure Pattern Recognition, J. Chem. Inf. Model., 2010, 50, 1034–1041 CrossRef CAS PubMed.
- D. Newby, A. A. Freitas and T. Ghafourian, Decision Trees to Characterise the Roles of Permeability and Solubility on the Prediction of Oral Absorption, Eur. J. Med. Chem., 2015, 90, 751–765 CrossRef CAS PubMed.
- N.-N. Wang, C. Huang, J. Dong, Z. Yao, M. Zhu, Z. Deng, B. Lv, A. Lu, A. F. Chen and D. Cao, Predicting Human Intestinal Absorption with Modified Random Forest Approach: A Comprehensive Evaluation of Molecular Representation, Unbalanced Data, and Applicability Domain Issues, RSC Adv., 2017, 7, 19007–19018 RSC.
- K. Handa, P. Wright, S. Yoshimura, M. Kageyama, T. Iijima and A. Bender, Prediction of Compound Plasma Concentration-Time Profiles in Mice Using Random Forest, Mol. Pharm., 2023, 20, 3060–3072, DOI:10.1021/acs.molpharmaceut.3c00071.
- T. Esaki, R. Ohashi, R. Watanabe, Y. Natsume-Kitatani, H. Kawashima, C. Nagao, H. Komura and K. Mizuguchi, Constructing an In Silico Three-Class Predictor of Human Intestinal Absorption with Caco-2 Permeability and Dried-DMSO Solubility, J. Pharm. Sci., 2019, 108, 3630–3639, DOI:10.1016/j.xphs.2019.07.014.
- N. Czub, J. Szlęk, A. Pacławski, K. Klimończyk, M. Puccetti and A. Mendyk, Artificial Intelligence-Based Quantitative Structure-Property Relationship Model for Predicting Human Intestinal Absorption of Compounds with Serotonergic Activity, Mol. Pharm., 2023, 20, 2545–2555, DOI:10.1021/acs.molpharmaceut.2c01117.
- K. Yano, Physicochemical Profiling and Drug Absorption at the Drug Discovery Stage, Folia Pharmacol. Jpn., 2009, 133, 270–273 CrossRef CAS PubMed.
- K. Sugano, Fraction of a Dose Absorbed Estimation for Structurally Diverse Low Solubility Compounds, Int. J. Pharm., 2011, 405, 79–89, DOI:10.1016/j.ijpharm.2010.11.049.
- K. Sugano, Validation of Mechanistic Models, in Biopharmaceutics Modeling and Simulations: Theory, Practice, Methods, and Applications, Wiley, 2012, pp. 266–321 Search PubMed.
- J. Jiménez-Luna, F. Grisoni and G. Schneider, Drug Discovery with Explainable Artificial Intelligence, Nature Machine Intelligence, 2020, 2, 573–584, DOI:10.1038/s42256-020-00236-4.
- W. Jin, R. Barzilay and T. Jaakkola, Multi-objective Molecule Generation Using Interpretable Substructures, in Proceedings of the 37th International Conference on Machine Learning, arXiv:2002.03244v3, July 12, 2020 Search PubMed.
- ADMET Predictor™ 9.0, https://www.simulations-plus.com/software/admetpredictor/, accessed date, June 30, 2023.
- PubChem, https://pubchem.ncbi.nlm.nih.gov/, accessed date, June 30, 2023.
- RD-Kit, https://www.rdkit.org/docs/index.html#, accessed date, June 30, 2023.
- D. S. Wishart, Y. D. Feunang, A. C. Guo, E. J. Lo, A. Marcu, J. R. Grant, T. Sajed, D. Johnson, C. Li, Z. Sayeeda, N. Assempour, I. Iynkkaran, Y. Liu, A. Maciejewski, N. Gale, A. Wilson, L. Chin, R. Cummings, D. Le, A. Pon, C. Knox and M. Wilson, DrugBank 5.0: A Major Update to the DrugBank Database for 2018, Nucleic Acids Res., 2018, 46, D1074–D1082, DOI:10.1093/nar/gkx1037.
- T. Sander, J. Freyss, M. von Korff and C. Rufener, DataWarrior: An Open-Source Program for Chemistry Aware Data Visualization and Analysis, J. Chem. Inf. Model., 2015, 55, 460–473, DOI:10.1021/ci500588j.
- P. Ertl, L. Patiny, T. Sander, C. Rufener and M. Zasso, Wikipedia Chemical Structure Explorer: Substructure and Similarity Searching of Molecules from Wikipedia, J. Cheminf., 2015, 7, 10, DOI:10.1186/s13321-015-0061-y.
- BioavailabilityDesign Mini™ 1.2, http://bioavailabilitydesign.com/, accessed date, June 30, 2023.
- K. Sugano, Introduction to Computational Oral Absorption Simulation, Expert Opin. Drug Metab. Toxicol., 2009, 5, 259–293, DOI:10.1517/17425250902835506.
- L. Breiman, Random Forests, Mach. Learn., 2001, 45, 5–32, DOI:10.1023/A:1010933404324.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, Analyzing Learned Molecular Representations for Property Prediction, J. Chem. Inf. Model., 2019, 59, 3370–3388, DOI:10.1021/acs.jcim.9b00237.
- Caret Package Information, https://cran.r-project.org/web/checks/check_results_caret.html, accessed date, Jun 30, 2023.
- Random Forest Package Information, https://cran.rproject.org/web/packages/randomForest/index.html, accessed date, June 30, 2023.
- https://chemprop.readthedocs.io/en/latest/#, accessed date, Jun 30, 2023.
- P. P. Graczyk, Gini Coefficient: A New Way to Express Selectivity of Kinase Inhibitors against a Family of Kinases, J. Med. Chem., 2007, 50, 5773–5779 CrossRef CAS PubMed.
- J. Hert, P. Willett, D. J. Wilton, P. Acklin, K. Azzaoui, E. Jacoby and A. Schuffenhauer, Comparison of Topological Descriptors for Similarity-Based Virtual Screening Using Multiple Bioactive Reference Structures, Org. Biomol. Chem., 2004, 2, 3256–3266, 10.1039/B409865J.
- M. Lee and K. Min, A Comparative Study of the Performance for Predicting Biodegradability Classification: The Quantitative Structure-Activity Relationship Model vs. the Graph Convolutional Network, ACS Omega, 2022, 7, 3649–3655, DOI:10.1021/acsomega.1c06274.
- H. Iwata, T. Matsuo, H. Mamada, T. Motomura, M. Matsushita, T. Fujiwara, M. Kazuya and K. Handa, Prediction of Total Drug Clearance in Humans Using Animal Data: Proposal of a Multimodal Learning Method Based on Deep Learning, J. Pharm. Sci., 2021, 110, 1834–1841, DOI:10.1016/j.xphs.2021.01.020.
- Y. Kosugi and N. Hosea, Prediction of Oral Pharmacokinetics Using a Combination of In Silico Descriptors and In Vitro ADME Properties, Mol. Pharm., 2021, 18, 1071–1079, DOI:10.1021/acs.molpharmaceut.0c01009.
- O. Obrezanova, A. Martinsson, T. Whitehead, S. Mahmoud, A. Bender, F. Miljković, P. Grabowski, B. Irwin, I. Oprisiu, G. Conduit, M. Segall, G. F. Smith, B. Williamson, S. Winiwarter and N. Greene, Prediction of In Vivo Pharmacokinetic Parameters and Time-Exposure Curves in Rats Using Machine Learning from the Chemical Structure, Mol. Pharm., 2022, 19, 1488–1504, DOI:10.1021/acs.molpharmaceut.2c00027.
- H. Iwata, T. Matsuo, H. Mamada, T. Motomura, M. Matsushita, T. Fujiwara, K. Maeda and K. Handa, Predicting Total Drug Clearance and Volumes of Distribution Using the Machine Learning-Mediated Multimodal Method through the Imputation of Various Nonclinical Data, J. Chem. Inf. Model., 2022, 62, 4057–4065, DOI:10.1021/acs.jcim.2c00318.
- M. P. Pollastri, Overview on the Rule of Five, Curr. Protoc. Pharmacol., 2010 DOI:10.1002/0471141755.ph0912s49 , Chapter 9, Unit 9.12..
- J. Qiu, Y. Nie, Y. Zhao, Y. Zhang, L. Li, R. Wang, M. Wang, S. Chen, J. Wang, Y. Q. Li and J. Xia, Safeguarding Intestine Cells against Enteropathogenic Escherichia coli by Intracellular Protein Reaction, a Preventive Antibacterial Mechanism, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 5260–5268 CrossRef CAS PubMed.
- https://www.sigmaaldrich.com/deepweb/assets/sigmaaldrich/product/documents/427/584/s2671pis.pdf, accessed date, June 7, 2023.
- I. Moriguchi, S. Hirono, Q. Liu, I. Nakagome and Y. Matsushita, Simple method of calculating octanol/water partition coefficient, Chem. Pharm. Bull., 1992, 40, 127–130 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00144j |
| This journal is © The Royal Society of Chemistry 2023 |