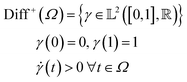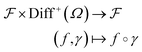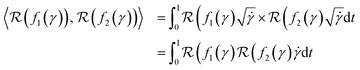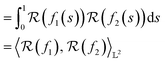Open Access Article
Open Access ArticleMetric geometry tools for automatic structure phase map generation†
Kiran
Vaddi
 *a,
Karen
Li
*a,
Karen
Li
 b and
Lilo D.
Pozzo
b and
Lilo D.
Pozzo
 c
c
aDepartment of Chemical Engineering, eScience Institute, University of Washington, Seattle, WA 98195, USA. E-mail: kiranvad@uw.edu
bDepartment of Chemical Engineering, University of Washington, Seattle, WA 98195, USA. E-mail: kli625@uw.edu
cDepartment of Materials Science and Engineering, eScience Institute, University of Washington, Seattle, WA 98195, USA. E-mail: dpozzo@uw.edu
First published on 29th August 2023
Abstract
Extracting a phase map that provides a hierarchical summary of high-throughput experiments is a long-standing bottleneck for the modern goal of achieving automation and acceleration in material discovery. A phase map that underpins the inherent properties of materials is typically denoted using a composition-structure map but can be extended to other relevant parameters such as synthesis. This paper describes a computational statistical tool to efficiently obtain a phase map from multi-scale experimental measurement profiles obtained from high-throughput measurements. We motivate the construction of a phase map as the problem of learning the underlying metric geometry defined by a set of templates in infinite-dimensional function spaces. We provide a statistical analysis tool to obtain a phase map as an asymptotic of the diffusion of resulting distance functions on the composition. Using examples from small-angle X-ray scattering experiments of polymer blend systems, we show that learned metric geometry can efficiently differentiate ordered phase regions with shifted, missing, and broad Bragg peaks along with features related to non-Bragg behavior of soft-matter systems. The metric geometry allows us to define a shape distance between scattering profiles invariant to phase-independent transformations thus valuable for obtaining a phase map. We also apply the methodology to benchmark experimental diffraction data to showcase potential utility and broad applicability.
1. Introduction
Geometry always played a significant role in the study of phase rules such as the number of phases possible by a system and their co-existence. It was the driving force for many of the earlier formulations as described by J. W. Gibbs in his 1873 paper titled, “A method of geometrical representation of the thermodynamic properties of substances by the means of surfaces”.1 The Gibbs rule of phase co-existence is often posed as a set of conditions on the second derivative of a free energy function for continuous systems and its discrete geometric alternative in a convex envelope.2–4 Both approaches can be unified by defining a metric under an appropriate basis as described in a series of papers by F. Weinhold.5–7 In all of the above cases, the phase map is essentially a projection of a geometric surface to its domain under the right metric that tessellates the domain in a meaningful way. The geometric surface is typically generated by considering a scalar response variable (such as the free energy). However, the introduction of robotics and high-throughput equipment (HTE) to experiments posed a different challenge where the response under which the system needs to be ‘phase mapped’ is a multi-scale measurement such as X-ray diffraction (XRD), small-angle X-ray scattering (SAXS), or UV-Vis spectroscopic profiles. One of the main roles of ‘phase mapping’ in HTE is as a down selection tool to perform analysis that requires manual expert intervention, mapping the structural subgroups to a performance measure of interest, or fitting known mathematical models for estimating structural information. Earlier works for structure-based phase mapping explored the application of statistical methods to multi-scale measurement data by considering them as signals represented in a matrix form (rows as different samples and columns as discrete evaluations of the corresponding measurement domains). One such example is non-negative matrix factorization (NMF) to learn parts-based basis representations8 to encode each signal as a weighted linear combination of a ‘basis’. The statistical similarity of the weights from NMF is used to group together signals into a phase map.9–12 Another approach involves directly learning the groups using clustering13,14 or segmentation15 techniques which can be viewed as defining the ‘base’ phases as belonging to the dataset itself and using similarity between each spectrum and the learned ‘base’ spectra to obtain the phase map. A common aspect of all the existing methods for phase mapping is that they consider measured profiles as signals from a stochastic measurement and are limited in expressing invariant features important for the analysis of material structure such as shifted, missing, and broad peaks.The mathematical basis of this paper is the notion of ‘shape’ popularized by mathematician David Kendall in the 1980s16 who used triangles as an example to showcase that ‘shape’ is what remains after discounting invariant transformations. Kendall also showed that after discounting for the triangle's position, scale and orientation, the remaining structure defines an equivalence class of triangles into isosceles, equilateral, scalene, etc., that result in a spherical manifold for the space of triangles. In this work, we extend the statistical shape theory ideas to experimentally measured one-dimensional profiles by considering them as points in an infinite-dimensional function space. In particular, we use the amplitude-phase distance defined in (ref. 17) to construct a ‘shape’ distance between profiles by only considering the aligned amplitude distance that effectively quotients the distance contribution from shape independent features. The amplitude distance defined can be used as an alternative to the Euclidean distance to learn shape-based representations and thus identify a shape-invariant metric structure of the data. A perennial issue of the existing signal-based statistical methods in the construction of phase maps is the lack of continuity in the composition domain. Several approaches were proposed to overcome this such as imposing continuity constraints18 when learning representative ‘basis’, and using smooth kernels in clustering and segmentation.19 In this work, we consider continuity as the result of the local geometry where the correlation between structures of compositionally varying materials is characterized by a continuous function. We then model the continuity using a stochastic model where variations in the local statistical similarities are represented by the diffusion of the corresponding distance function. A phase map is then obtained by considering the asymptotic properties of the distance function thus attaining a local smoothness or continuity.
The goal of this paper is not to provide an algorithm that outperforms other methods used for the automatic generation of structure phase maps but rather to provide a principled approach to realize phase maps purely from analyzing them as functionals (i.e. functions of functions) and exploring the results from an empirical behavior point of view. We argue that the presented approach performs much better at alleviating problems in defining distance that is aligned with the physical intuition of analysis applied (primarily) to diffraction or scattering and demonstrate this with a few example case studies. We focus mainly on the application to SAXS data as they are much more challenging to phase map with the information pertaining to the structure encoded in higher-order features of the profile such as the curvature. The rest of the paper is arranged as follows: we first describe the overall workflow of the autophasemap algorithm in Section 3 and introduce concepts of metric geometry (in Section 4) and diffusion (in Section 5) as relevant to the computational tools presented in this study. We then apply it to an experimental SAXS data set of self-assembled block-copolymer blend materials synthesized and characterized using SAXS by us and ternary alloys dataset from (ref. 20) characterized using XRD. We analyze the results in Sections 6–8 and provide insights into the generation of a phase map and list our conclusion and contributions in Section 9.
2. Small angle X-ray scattering (SAXS)
In its most popular form, Small Angle X-ray Scattering or SAXS consists of a highly collimated X-ray beam directed at a sample and a detector measuring the intensity of the interfered secondary waves scattering out from the structure as a function of the scattering angle θ. SAXS allows indirect measurement of nanostructures in their natural environment and is a rapid high-throughput alternative to other direct time-consuming microscopy methods. The physical principles behind SAXS are very similar to diffraction measurements and it subsumes the popularly known Bragg's law for periodic or crystalline structures. Scattering profiles (or curves) are analyzed by plotting the scattered radiation with respect to the scattering vector,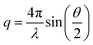 , which is related to the scattering angle θ but is independent of the incident X-ray wavelength λ. All electrons in the sample are potential sources of secondary waves with spatially dependent phases. Thus an isolated nanostructure within the sample will contribute to the intensity that is detected as the square of the amplitude of the scattered secondary waves – referred to as the form factor. The form factor is a function of q as the interference pattern changes with the length scale and the resulting phase of the secondary waves. Real experimental samples consist of ensembles of nanostructures distributed across space. Particles and molecules interact via colloidal and molecular forces that, under concentrated conditions or strong interaction limits, result in the emergence of spatial correlations. The contributions to the scattering from these spatial correlations are generally referred to as the structure factor. The term ‘factor’ comes from the fact that for simple homogeneous systems, the average observed intensity can be expressed as a multiplication of the form factor and structure factor. The interplay between the form factor and structure factor makes the analysis of SAXS profiles complicated as they are difficult to resolve from experimental curves with little to no understanding of the nanoscale features of the sample. For example, in the case of an ordered three-dimensional nanostructure, some of the peaks may be missing because either the structure factor or the form factor has local minima in its q-dependent intensity. This phenomenon is not unique to periodic structures, as interactions and particle aggregation can significantly change the observed intensity profile. Similar to powder X-ray diffraction data (XRD), the finite size of the periodic structures and instrument limitations (e.g. smearing) can result in shifts and the broadening of peaks. In the case of soft-matter systems, such as the micelles studied in this work, the shifts and widening of peaks can occur at much larger ranges of the q values in comparison to inorganic crystals because of the wide range of lattice parameters that are possible. For a detailed explanation of the techniques and fundamentals of SAXS, readers are referred to ref. (21,22). Frequently, practical SAXS analysis relies on solutions to analytical form and structure factors, and general scaling relations (i.e. Guinier or Kratky plots) to compare and analyze SAXS curves, or uses heuristics such as expectations of power-law scalings between intensity and q values for certain nanostructures and shapes. In this work, we describe a mathematical framework that provides a robust pipeline for performing a comparative analysis of the shape of SAXS profiles to automatically generate phase maps, the foundations of which are detailed next. Such phase-maps can then be used as a starting point for the automated application of detailed analyses to samples for which these are applicable, and also avoid the incorrect application of model fits data when they would be inappropriate to use.
, which is related to the scattering angle θ but is independent of the incident X-ray wavelength λ. All electrons in the sample are potential sources of secondary waves with spatially dependent phases. Thus an isolated nanostructure within the sample will contribute to the intensity that is detected as the square of the amplitude of the scattered secondary waves – referred to as the form factor. The form factor is a function of q as the interference pattern changes with the length scale and the resulting phase of the secondary waves. Real experimental samples consist of ensembles of nanostructures distributed across space. Particles and molecules interact via colloidal and molecular forces that, under concentrated conditions or strong interaction limits, result in the emergence of spatial correlations. The contributions to the scattering from these spatial correlations are generally referred to as the structure factor. The term ‘factor’ comes from the fact that for simple homogeneous systems, the average observed intensity can be expressed as a multiplication of the form factor and structure factor. The interplay between the form factor and structure factor makes the analysis of SAXS profiles complicated as they are difficult to resolve from experimental curves with little to no understanding of the nanoscale features of the sample. For example, in the case of an ordered three-dimensional nanostructure, some of the peaks may be missing because either the structure factor or the form factor has local minima in its q-dependent intensity. This phenomenon is not unique to periodic structures, as interactions and particle aggregation can significantly change the observed intensity profile. Similar to powder X-ray diffraction data (XRD), the finite size of the periodic structures and instrument limitations (e.g. smearing) can result in shifts and the broadening of peaks. In the case of soft-matter systems, such as the micelles studied in this work, the shifts and widening of peaks can occur at much larger ranges of the q values in comparison to inorganic crystals because of the wide range of lattice parameters that are possible. For a detailed explanation of the techniques and fundamentals of SAXS, readers are referred to ref. (21,22). Frequently, practical SAXS analysis relies on solutions to analytical form and structure factors, and general scaling relations (i.e. Guinier or Kratky plots) to compare and analyze SAXS curves, or uses heuristics such as expectations of power-law scalings between intensity and q values for certain nanostructures and shapes. In this work, we describe a mathematical framework that provides a robust pipeline for performing a comparative analysis of the shape of SAXS profiles to automatically generate phase maps, the foundations of which are detailed next. Such phase-maps can then be used as a starting point for the automated application of detailed analyses to samples for which these are applicable, and also avoid the incorrect application of model fits data when they would be inappropriate to use.
3. Autophasemap: an algorithm for determining (structure) phase map
A pictorial representation of the proposed algorithm (referred to as autophasemap) is depicted in Fig. 1. The proposed algorithm for phase map determination involves two steps: (a) identification: identifying a set of template functions that best represents the observed ‘shapes’ of the spectra. This is performed by measuring the similarity (using a distance function as described next in Section 4) between sampled profiles and a template. This provides us with a ‘global’ view of the data i.e. the distance functions defined using each template are true in an average sense but not necessarily for each one of the observed spectra; (b) assignment: assigning a label to each point in the design space such that ‘locally’ the distance function is smooth to model the expected smooth phase transitions. This is achieved using geometric diffusion on the graph of composition as described next in Section 5. This is equivalent to computing the asymptotic diffusion of the similarity functions identified in step (a) and assigning a label based on the posterior of diffused functions. The template functions are learned iteratively from the data by first aligning each profile to the current templates and grouping them based on the shape distance described in eqn (4) next. In each iteration, the templates are updated to be the average of the aligned data in each group. In this work, we combine the identification and assignment steps and learn the phase map iteratively along with the template functions. This would ensure that the phase maps are compositionally continuous up to an arbitrary diffusion length scale. The identification step follows the elastic k-means algorithm from (ref. 23) to compute the template functions. The template functions are then used to compute the distance functions over the composition and are approximated via their (truncated) asymptotic diffusion operator. Each approximated operator for the diffusion estimates a posterior probability of a profile belonging to the group characterized by the template via shape distance in eqn (4). By iterating through the identification and assignment steps, we obtain a phase map with convergence defined by absolute improvement between the template functions in their natural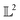 space.
space.
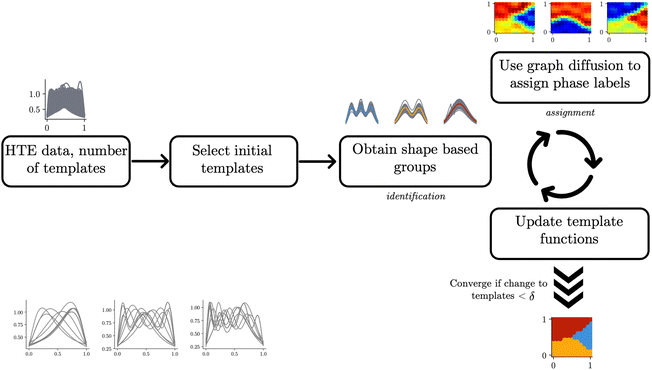 | ||
| Fig. 1 A pictorial representation of the autophasemap algorithm with the iteration between the identification and assignment steps depicted as curved arrows. Some of the steps are annotated with plots corresponding to a synthetic data set of Gaussian peak shapes generated using the procedure from (ref. 23) (Section 4). The plots are for the final converged results. The input data (a random sample for clarity) is shown in the lower left corner which depicts three groups based on the number of peaks but arbitrarily shifted over the design space. | ||
4. Metric geometry of function spaces
The starting point of our analysis is the consideration of measurement profiles as points in an infinite-dimensional function space. Some of our recent work has used this approach to analyze UV-Vis spectroscopic curves of nanostructures in problems related to explorative study for design rules24 and material retrosynthesis.17 A function space is a vector space analog for functions as points equipped with an appropriate inner product that can be used to measure lengths and angles. The inner product can be used to define a distance measure to perform comparisons and statistical analysis of functional data such as the scattering curves we are interested in this work. A commonly used inner-product structure is an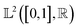 space of one-dimensional functions with the domain mapped to a unit interval [0,1]. The inner product for two functions
space of one-dimensional functions with the domain mapped to a unit interval [0,1]. The inner product for two functions 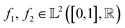 is given by eqn (1):
is given by eqn (1):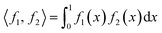 | (1) |
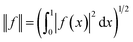 | (2) |
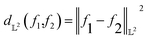 | (3) |
The norm of a function in the 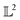 space can be used to normalize the data, for example, to have a unit norm giving rise to interesting manifold structures to the data.
space can be used to normalize the data, for example, to have a unit norm giving rise to interesting manifold structures to the data.
One of the most fundamental notions required to perform statistical analysis on data belonging to a manifold is to compute distances between points. Since we are interested in measuring the ‘shape’ distance between two profiles represented as functions, we need a distance that is invariant to various warping actions. Warping functions are the translation and rotation equivalents of functions to define a shape following the original definition by Kendall.16 Warping actions are defined as a right composition of a function with a warping function that maps the domain to itself. The warping functions belong to a class of mathematical objects called diffeomorphisms which are smooth functions with an inverse. Consider a space of functions 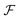 with their domain mapped to a unit interval Ω = [0,1] and the set of boundary-preserving diffeomorphism as the set:
with their domain mapped to a unit interval Ω = [0,1] and the set of boundary-preserving diffeomorphism as the set:
For any given function 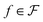 , we can formalize action of a warping function γ using the function composition as follows:
, we can formalize action of a warping function γ using the function composition as follows:
A shape space for the functions can now be defined as the space of function 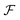 that is left behind after quotienting out the set Diff+(Ω). Once again, going back to the original ideas of Kendall and applying the notion of a shape to a collection of triangles, the rotations play the role of diffeomorphisms that quotient out the orientation before comparing a pair of triangular shapes. Using the shape-preserving diffeomorphisms, we can define a ‘shape space’ to be
that is left behind after quotienting out the set Diff+(Ω). Once again, going back to the original ideas of Kendall and applying the notion of a shape to a collection of triangles, the rotations play the role of diffeomorphisms that quotient out the orientation before comparing a pair of triangular shapes. Using the shape-preserving diffeomorphisms, we can define a ‘shape space’ to be 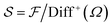 and obtain the following definition for a shape distance:
and obtain the following definition for a shape distance:
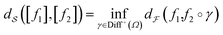 | (4) |
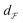 that is defined using functions and the warping function. One way to define a warping invariant
that is defined using functions and the warping function. One way to define a warping invariant 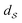 is to exploit certain transformations between two spaces that allow a metric to be pulled back from one of the spaces for which there exists a known metric. One such transformation is the Square Root Slope Framework (SRSF) in eqn (5) introduced in (ref. 25) that results in a warping invariant metric via pullback from
is to exploit certain transformations between two spaces that allow a metric to be pulled back from one of the spaces for which there exists a known metric. One such transformation is the Square Root Slope Framework (SRSF) in eqn (5) introduced in (ref. 25) that results in a warping invariant metric via pullback from 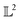 .
.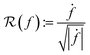 | (5) |
The invariance of the resulting pullback metric can be observed by considering the case where two functions are warped by the same γ function:
We can now use a change of variables to obtain:
Defining 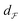 using the SRSF and the pullback metric, we obtain a distance whose infimum over Diff+(Ω) is the distance that is invariant to warping function. This is because fixing f1 and solving for a γ to warp f2 is equivalent to finding the distance after quotienting out any distance contributions from domain warping alone. In practice, we solve for
using the SRSF and the pullback metric, we obtain a distance whose infimum over Diff+(Ω) is the distance that is invariant to warping function. This is because fixing f1 and solving for a γ to warp f2 is equivalent to finding the distance after quotienting out any distance contributions from domain warping alone. In practice, we solve for 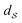 by minimizing E(γ) given in eqn (6) using techniques such as Dynamic Programming25 or Riemannian gradient descent.26
by minimizing E(γ) given in eqn (6) using techniques such as Dynamic Programming25 or Riemannian gradient descent.26
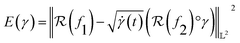 | (6) |
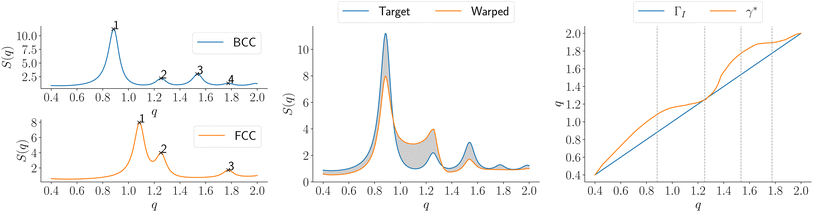
The shape distance in eqn (4) is invariant to various domain warpings denoted by γ. For scattering (or diffraction) profiles, the γ function can be used to quotient out the distance contribution from non-phase-specific changes (such as peak shifts and missing peaks) and also instrument-limited features (such as peak widths). We illustrate the computation using a simulated scattering profile of a face-centered cubic (FCC) and body-centered cubic (BCC) phase (using the simulator from (ref. 27)) in Fig. 2. The two simulated SAXS profiles shown in the left-most panel of Fig. 2 are for the BCC phase (top panel, with peak ratios 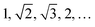 ) and for an FCC phase (bottom panel with peak ratios
) and for an FCC phase (bottom panel with peak ratios 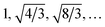 ). Fig. 2 depicts the scenario when we are trying to compute a distance to quantify, how dissimilar the FCC phase curve is from a BCC phase based on the shape. As mentioned above, the first task in computing the distance is to (peak-)align the two functions which are shown in the middle panel of Fig. 2. The amplitude distance – defined as the
). Fig. 2 depicts the scenario when we are trying to compute a distance to quantify, how dissimilar the FCC phase curve is from a BCC phase based on the shape. As mentioned above, the first task in computing the distance is to (peak-)align the two functions which are shown in the middle panel of Fig. 2. The amplitude distance – defined as the 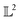 distance between the (peak-)aligned functions – (roughly) measures the area between the functions. The key component of this computation, the optimal warping function, is shown in the rightmost panel of Fig. 2 as a map from the domain (the q – values) to itself. The action of the warping function can be understood by observing where it deviates from its identity (solid blue line). We observe that there are two regions where the orange curve deviates from the blue curve each corresponding to the alignment of peaks numbered 1 and 3 in the leftmost panel of Fig. 2. Furthermore, the alignment distorted the second peak of the FCC phase because the peak separation between 1 and 2 is not the same as the reference BCC phase. The distortion contributes the most to the amplitude distance, as seen from the shaded region between the curves in the middle panel of Fig. 2. Similarly, we can show that the warping function assigns almost no distortion when the peaks are perfectly aligned but shifted uniformly resulting in a minimal distance (see ESI†).
distance between the (peak-)aligned functions – (roughly) measures the area between the functions. The key component of this computation, the optimal warping function, is shown in the rightmost panel of Fig. 2 as a map from the domain (the q – values) to itself. The action of the warping function can be understood by observing where it deviates from its identity (solid blue line). We observe that there are two regions where the orange curve deviates from the blue curve each corresponding to the alignment of peaks numbered 1 and 3 in the leftmost panel of Fig. 2. Furthermore, the alignment distorted the second peak of the FCC phase because the peak separation between 1 and 2 is not the same as the reference BCC phase. The distortion contributes the most to the amplitude distance, as seen from the shaded region between the curves in the middle panel of Fig. 2. Similarly, we can show that the warping function assigns almost no distortion when the peaks are perfectly aligned but shifted uniformly resulting in a minimal distance (see ESI†).
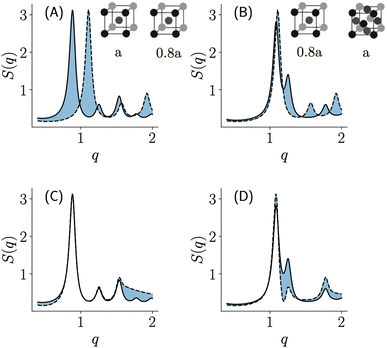
In Fig. 3, we depict an example of using a distance measure to make phase assignments using scattering curves given a template as a reference. The top row (panels A, B) in Fig. 3 depicts a case where we are using the standard vector-based distances (such as Euclidean) to compute the similarity to a given reference profile (dotted line corresponding to a BCC phase with the lattice parameter being 8 nm). The solid lines in panels A, and B correspond to a BCC, and FCC phase respectively both with the lattice parameter 20% greater than the reference in the dotted line. Visually, we can observe that any distance measure that simply measures the overlap (i.e. the shaded region) would consider that a shifted BCC is more similar to an FCC phase than it is to the BCC phase. We can observe that this is primarily because the distance emphasizes the high-intensity peak disproportionately and fails to account for the mismatched pattern of peaks that encode the periodicity of the structure represented in scattering. The bottom row (panels C, D) of Fig. 3 depicts a similar exercise using the shape distance. Unlike traditional distance measures, an assignment based on the overlaps (as shown using the blue-shaded regions) would assign the pair of BCC phases to be more similar to each other. This example clearly illustrates that using shape distance results in template-based phase assignments that are more aligned with an expert understanding of scattering curves.
In this work, we clearly distinguish between a metric and a distance function. Although both are defined as maps that take two points and produce a scalar output, a metric is only defined infinitesimally between tangent vectors and often changes from point to point. A distance function, however, is defined between any two points in the space and thus can be far less restricted in its structure such as not following the triangle inequality. Because we are interested in building phase maps, we need a distance function that measures the distance to any scattering curve from a template that serves as the representative curve for a particular phase. This distance function identifies each curve with a distance closer to zero with the same phase as the template. Changes to the distance function over the design space (such as the composition) are constrained by continuity such that phase transitions occur gradually within a transition width. For polymer materials that are of interest to this work, the transition width is finite thus we also need to encode the continuity into our definition of distance. One way to ensure this is to obtain the distance as a solution to a diffusion equation defined on the design space. In this work, we use the idea of diffusion maps to obtain one such solution as described next.
5. Diffusion maps and its asymptotics
Diffusion maps28 – originally introduced in the context of dimensionality reduction – work with the idea that the geometry of a set S can be studied through the analysis of the space of functions defined on them and linear operators over those spaces. In this work, however, we will use the idea of a diffusion map primarily to solve for an asymptotic of the diffusion operator that can be used to approximate a continuous distance function. The motivation to use diffusion maps as a solution method comes from the observation that we only have access to distance function values based on the scattering curves we have obtained by discretely sampling the design space. Given a set S (i.e. discretely sampled design space) equipped with a kernel k(., .) (encoding the diffusion length or phase transition width), diffusion maps consider quadratic forms of the form shown in eqn (7) with an objective to minimize some form of Dirichlet energy such as the one defined in eqn (8).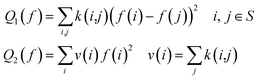 | (7) |
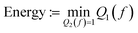 | (8) |
The minimization problem boils down to finding generalized eigenvalues of the form Af = λf, A = Q2−1Q1 which defines an infinitesimal generator of the diffusion defined by e−At. Following the terminology of diffusion maps in (ref. 28), we consider the number of hops between graph nodes as the time steps of diffusion. Thus, the diffusion of information on the set S can now be expressed in a lower-dimensional form using the eigenvalues of the infinitesimal generator A effectively filtering out the higher modes of the function f making it smooth over the domain. In the special case of a weighted graph of the set S, Q1 is the graph Laplacian, and Q2 is the normalization factor giving rise to the normalized graph Laplacian as the generator of the diffusion process on the graph. The resulting generator has a discrete sequence of Eigenvalues upper bound by one. By truncating higher eigenvalues of the generator, we obtain an asymptotic solution to the diffusion problem resulting in a lower-dimensional approximation of the diffusion operator Â. In this work, we use the asymptotic diffusion operator  and apply it to various distance functions to obtain an asymptotic distance defined using the shape distance (eqn (4)) from a set of template functions learned from the data. We can interpret the asymptotic distance as a (continuous) posterior probability of a measured profile being closest to the corresponding template function.28
We evaluate the proposed phase mapping algorithm qualitatively on two different data modalities (SAXS and XRD) to showcase its versatility and generalizability. For the first case study, we synthesized and collected SAXS data of a self-assembling block copolymer that has a previously reported phasemap.29 We then applied the same methodology (with no additional data processing or customization) to generate a phase map from XRD data of ternary metal alloy systems to showcase the versatility and generalizability of the presented approach. Finally, we showcase the utility of the proposed approach in generating and analyzing phase maps of a novel system using SAXS data of self-assembling polymer blends.
6. Phase mapping temperature-dependent micellization of pluronic based on SAXS
In this case study, we apply the autophasemap algorithm to reconstruct the underlying phase diagram of temperature-dependent self-assembly and thermo-gelling behavior of Pluronic P123 (a symmetric triblock copolymer comprising of polyethylene oxide (PEO) and polypropylene oxide (PPO) in an alternating linear fashion, PEO–PPO–PEO). The design space for our high-throughput experiment consisted of the weight fraction of Pluronic P123, and the temperature uniformly spaced at increments of 5 and 10 units respectively. Details on experimental methodology, sample preparation, processing, and characterization are provided in the ESI.† It has been shown before that below a critical micelle temperature and concentration, individual block copolymers are in solution as unimers form micelles as the concentration/temperature is increased.30,31 The micellar systems further assemble into semi- or crystalline-mesophases beyond an order–disorder transition point defined in terms of temperature and concentration. Examples of mesophases include a cubic arrangement (Face-Centered Cubic (FCC), Body-Centered Cubic (BCC)), hexagonal arrays of micelles (cylindrical micelles in a hexagonal lattice (HEX), hexagonally packed spherical micelles (HCP)), lamellar arrays of 2D sheets (LAM), and/or composite phases that may include more than one of these. As mentioned in Section 2, these materials show a strong signal (both Bragg and non-Bragg-like) when measured using SAXS. Our goal is to determine the phase transitions as boundaries of the resulting phase map from autophasemap using the SAXS characterization of samples.Self-assembly of the P123 pluronic system has been previously studied using computational and one-at-a-time experimental approaches29 thus we had access to a set of expected phases to recreate a manual annotation of the phase diagram. We used this knowledge to create a phase diagram shown in Fig. 4.
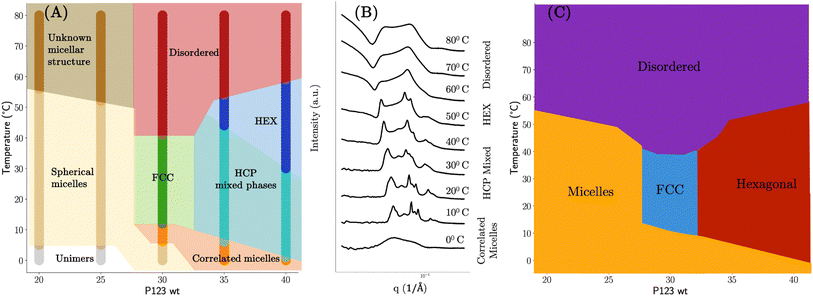 | ||
| Fig. 4 Manually annotated phase diagrams based on the SAXS patterns of P123 pluronic with varying temperature. (A) Expert labeled phase diagram: disordered phase – no self-assembly as evidenced by a lack of sharp peaks in their SAXS curve; spherical micelles – broad peaks that oscillate towards higher q values; ordered structures (FCC, HCP, HEX) are adjudged by matching peak spacing ratios obtained from the literature. (B) Observed phase transitions with an increase of temperature: SAXS patterns of pluronic P123 in a 35% weight fraction of water resembled that of correlated micelles at lower temperatures which self-assembled into a mixed phase of cubic and hexagonal lattices. Upon further increase of the temperature beyond 40 °C only the features corresponding to the hexagonal phase were observed that turned into a single broad peak at temperatures beyond 50 °C signifying a disordered phase of hexagonally self-assembled structures. (C) Phase diagram with only four reference sets similar to the one proposed in ref. 29. | ||
Lower concentrations of P123 (≤25 wt%) at low temperatures exist as unimers (simple polymer strands) with no peaks in the SAXS spectra. SAXS of dilute P123 with increasing temperatures shows spherical micelles. At high temperatures, an unknown micellar structure appears with insufficient information at the measured range of q to identify the structure. As P123 concentration increases, diffraction peaks appear, indicating the micelles have self-assembled into crystalline mesophases. The structures formed by P123 micelles were identified by matching the diffraction peaks to a sequence of peak position ratios. The scattering vector of the primary peak, q1, was chosen such that the scattering vector of subsequent peaks matches those calculated with the position ratios. Based on this, we identified that the P123 forms FCC 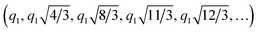 , HCP (q1, q11.06, q11.13, q11.46, q11.73, q11.87, q12.03, …), and HEX
, HCP (q1, q11.06, q11.13, q11.46, q11.73, q11.87, q12.03, …), and HEX 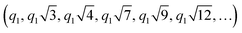 phases. The diffraction peaks of some of the SAXS profiles could not be matched to a distinct phase and thus were fitted to multiple phases, to account for all possible phases. P123 spectra that show peaks at low temperatures indicate the micelles are assembling but have not fully organized to FCC, HCP, or HEX and thus were characterized as being ‘correlated micelles’ with strong interactions. Concentrated P123 at high temperatures exhibits peaks but no definitive organized structure.
phases. The diffraction peaks of some of the SAXS profiles could not be matched to a distinct phase and thus were fitted to multiple phases, to account for all possible phases. P123 spectra that show peaks at low temperatures indicate the micelles are assembling but have not fully organized to FCC, HCP, or HEX and thus were characterized as being ‘correlated micelles’ with strong interactions. Concentrated P123 at high temperatures exhibits peaks but no definitive organized structure.
A set of reference phases may not be available for novel systems thus we should treat this as a variable in our algorithm. For example, if we had access to only four reference phases – micellar solutions, self-assembled mesoscopic order of a cubic and hexagonal lattice, and disordered particles of different lattices – we would have ended up with the phase diagram shown in Fig. 4C. In fact, this phase diagram resembles one of the earlier demonstrations of experimental phase mapping of P123 pluronic systems shown in (ref. 29).
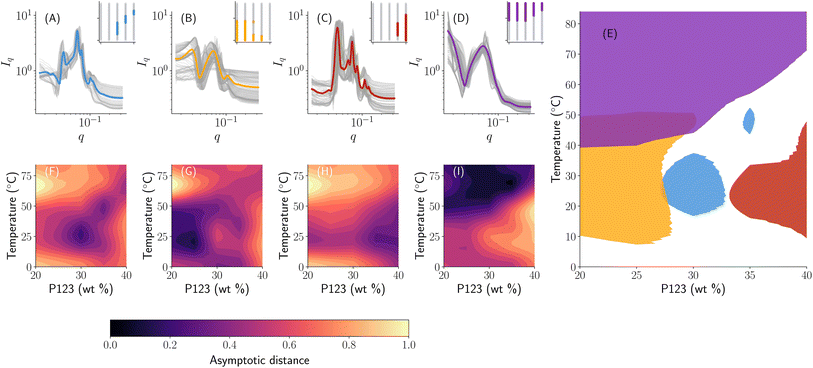
One strategy then would be to start with a phase map that ‘broadly’ classifies the samples such as Fig. 4C and then further refine each observed region into specific subclasses to obtain a phase map that looks like Fig. 4A. This is akin to having a hierarchy in the phase map that is controlled by a number of reference sets available based on prior knowledge. In our autophasemap algorithm, this hierarchy is controlled by the number of template functions. As shown in Fig. 5 and 6, we indeed obtain this hierarchy where the phase map shown in panel (E) of Fig. 5 roughly corresponding to the phase diagram with four reference phases (Fig. 4C), while that in panel (H) of Fig. 6 roughly corresponds to Fig. 4A. This can be verified by observing that the shaded region of each learned template corresponds to a particular phase in the phase diagram obtained using the same number of reference sets thus the hierarchy observed in manual annotation was recovered by increasing the number of template functions. In Fig. 6, we show the set of templates (in a solid color) and the assigned experimental SAXS curves (overlayed in grey color) along with their location in the design space. The partition of design space into phase regions is highlighted in the inset plot in each panel with the concentration of P123 on the x-axis (ranging from 0–40 weight percentage) and temperature on the y-axis (ranging from 0–85 degree Celsius). Once again, observing for peak spacing ratios, we obtain that the template functions in (A) to be a mixture of HCP and HEX; (B) HEX; (C, D) to be disorganized correlated micelles; and (G) to be FCC. The above analysis also suggests that the phase map can be used to assign phase labels by performing complex and laborious phase labeling techniques only on a small number of template functions, thus potentially accelerating the learning while performing the high-throughout measurements.
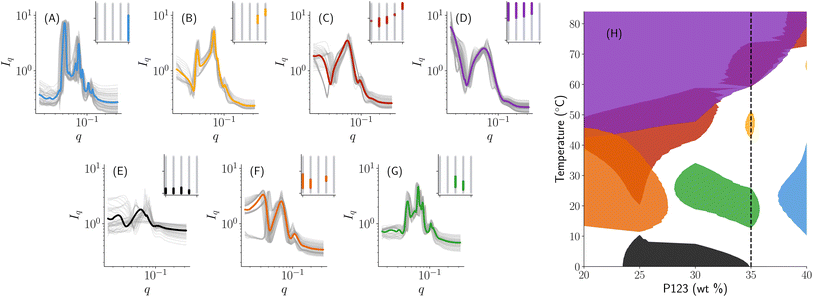 | ||
| Fig. 6 Phase map learned with 7 template functions shows a hierarchical partition of Fig. 5: (A–G) SAXS curves (in the grey color) assigned to each learned template (in a solid color) with the corresponding region in the composition space identified in the inset; (H) a phase map obtained by considering regions of distance from the template up to a threshold of 0.35 units. The color of the templates in (A–G) matches the corresponding phase region in (H). | ||
Although we represented the phase diagram in Fig. 4 using sharp boundaries representing a phase region, this is purely for visualization. In fact, as shown in the middle panel of Fig. 4, there is a smooth transition between different phases with an increase in temperature. Once again, we observe that the continuous nature of distance functions as shown in Fig. 7 allows us to extract this phase transition behavior along with the labels obtained from phase ‘templates’ shown in Fig. 6. For example, we observe that the 35% weight fraction of P123 (highlighted using a solid white line in Fig. 6) passes through zero distance along panels B, C, D, E, and G each corresponding to different template function. SAXS curves at lower temperatures are the closest to the template of panel (E) corresponding to unimers and they slowly diverge from it with an increase in temperature and become closer in shape to the template of panel (G) (as evidenced by the color gradient of the distance) that correspond to an FCC structure. Upon further increase beyond 25 °C, the SAXS curves slowly converge towards the shape of the template in (B) (i.e. a hexagonal self-assembly of cylindrical micelles) as measured by distance approaching zero. An increase in temperature beyond 50 °C results in a smooth divergence from the shape of the template in panel (B) towards that of panel (D) – a disordered phase – signifying a smooth phase transition. This showcases the advantages of using the autophasemap algorithm for high-throughput experimental systems to extract phase mapping and transition information purely based on SAXS patterns.
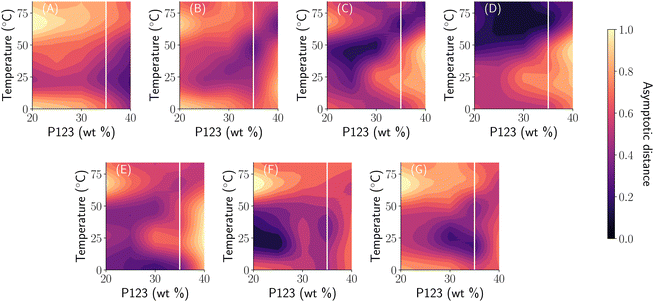 | ||
| Fig. 7 Learned distance functions of the phase map in Fig. 6 with 7 templates. Panels are arranged in the same sequence as that of Fig. 6. | ||
7. Application to benchmark X-ray diffraction data
The algorithm presented in this paper broadly applies to classes of characterization data that can be represented as functions. Much of the initial development of an algorithm for phase mapping focused on using XRD9–13,15 with a few exceptions.14,19 While there have been several attempts to overcome two key issues related to the continuity and invariance of the desired phase maps, none of the methods propose a unifying framework to solve them. The currently available solutions require extensive prior information such as the extent of expected peak shifts.13,32 In this case study, we show that the metric geometry tools presented so far provide a reasonable solution without the need for expert intervention. We apply our methodology to a widely used high-throughout combinatorial XRD data from (ref. 20) and depict the resulting phase map similar to the SAXS case study in Fig. 8 with 5 templates. We analyze the phase map in Fig. 8 with a focus on the continuity of the phase map, and the region of a phase with a significant peak shift (region E). In (ref. 33), the authors have deduced that region (E) in Fig. 8 is a BCC phase of iron with peak shift using manual expert labeling (see Fig. 4b in (ref. 33)) that was difficult to correctly identify using the existing methods for phase mapping.13,15,19 We can see from Fig. 8 that along with the continuous nature of similar phase regions, the proposed algorithm was able to correctly identify the phase with a shift. However, as mentioned before, the goal of this paper is not to present another method to solve the peak shifting issue for automatically classifying high-throughput XRD data but rather to provide that it is possible to account for physics in analysis by carefully considering the mathematical representations of the data under consideration. As shown using this case study, a generic mathematically grounded data representation can alleviate the need for expert intervention in using a data-driven model.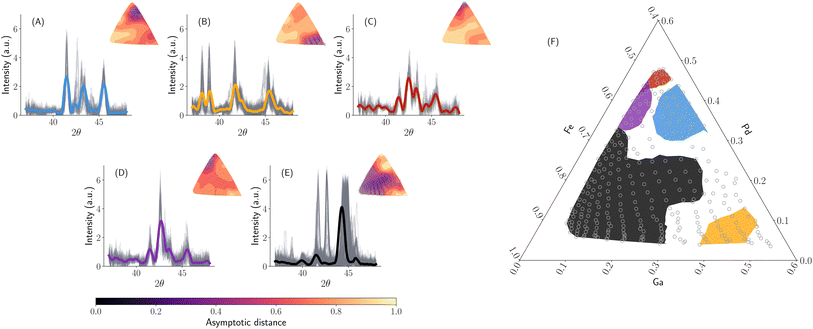 | ||
| Fig. 8 Fe–Ga–Pd phase map learned with 5 templates to compare with expert labeled phase diagrams from (ref. 33). (A–E) Shows learned template functions in solid color with smoothened XRD spectrum (Savitsky–Golay filtering with a 1.0) radians of window length and a third-order polynomial as implemented in (ref. 34). The inset plot shows the distance distribution from the template to all the XRD curves along with points identified to be closer to the template in clustering. (F) A phase map is obtained by selecting a distance threshold of 0.5 units. All the ternary plots represent the weight fraction of elements on the axis. | ||
8. Phase mapping novel polymer blends for OMIECs
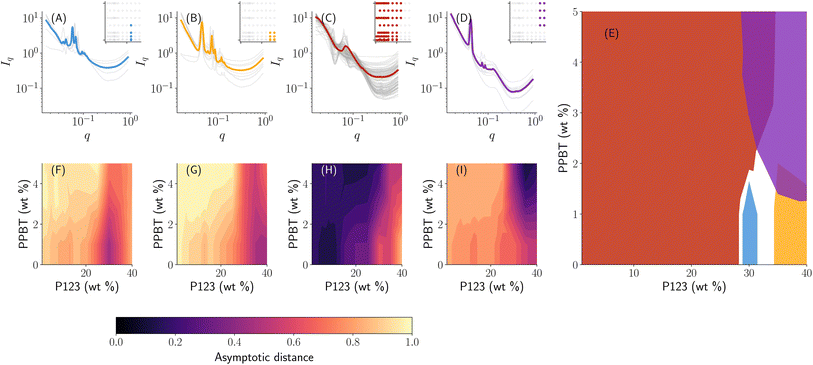
A novel material system of interest for this work is the structured self-assembly of organic mixed ionic–electronic conductors (OMIECs) based on blends of block-copolymer and conjugated homopolymers. Specifically, the sampled design space consists of materials where an electronic conjugated polymer is blended with an ion-conducting block copolymer in a common solvent at a particular temperature. The interactions between the block-copolymer and the conjugated polymer can also form composite micellar systems into semi- or crystalline-mesophases. Our goal in this work is to generate a phase map when we have synthesized the materials in a high-throughput manner. Specifically, we have collected a total of 93 SAXS measurements from a combinatorial sampling of Pluronic 123 and poly(3-[potassium-4-butanoate]thiophene) (PPBT) co-dissolved in aqueous solutions. The resulting phase map from autophasemap algorithm is shown in Fig. 9 with 4 template functions that roughly correspond to a (A) FCC-like structure with peak spacing ratios 1.0, 1.145, 1.581, 1.854, 2.545, 2.818…; (B) HEX-like structure with some HCP influence with peak spacing ratios 1.0, 1.328, 1.611, 1.865, 2.582…; (C) micelles in solution; and (D) disorganized hexagonal cylinders with peak spacing ratios 1.0, 1.746, 2.015….The phase diagram in Fig. 9 can be used for further planning targeted synthesis and measurements in an iterative fashion. For example, to achieve long-range order that facilitates electron transport, we can use the phase map in Fig. 9 as a starting point and down select regions of design space that form crystalline phases (i.e. regions (A), (B), and (D)).
9. Conclusions
In this paper, we have introduced an automatic structure phase mapping algorithm for characterization data representable using the mathematical structure of function spaces. Specifically, we have shown the applicability of infinite-dimensional function space representations and shape distances to scattering and diffraction data. Furthermore, we have demonstrated the application of graph-based diffusion to deduce the phase map as a solution to a stochastic model to analyze local dynamics of the phase transitions in the design space. The function space data representations are combined with diffusion map tools to derive an iterative algorithm for phase map generation.In the case of scattering data from small-angle X-ray scattering of pluronic systems, we constructed a phase diagram from high-throughput data for two systems (one with temperature variance and the other with polymer blends). We have shown that the resulting phase diagram is (topologically) continuous with each phase corresponding to a set of scattering profiles similar in shape. For regions of the phase map with potentially ordered crystal phases, the phase map is also invariant to peak shifts and experimentally limited features to phase assignment. Furthermore, the phase map is shown to be a hierarchical partition function of the design space that shows higher-order hierarchical relations with an increase in the number of template functions used in the algorithm. Finally, the broad applicability of the algorithm is shown using a known benchmark data set of X-ray diffraction studies. We have also shown the ability of the current approach in augmenting the traditional techniques to rapidly map out interesting phase regions and down-select a small set of template curves. Using the case studies we have shown the utility of learned templates in performing time-consuming traditional labeling approaches on only select curves rather than the entire dataset.
As a part of future work, the present phase mapping framework can be extended to run in a closed-loop manner for example using active learning. The diffusion of similarity functions can be used to determine an acquisition function that encourages sampling near the boundaries of the phase map (for example, by maximizing the gradient of the diffused similarity function). The learned template functions also serve as the low-throughput summary of the phases formed in a synthesis study thus allowing users to obtain a rapid analysis of the experiments. Furthermore, learned phase maps (either via online or offline mode) can be further used in property optimization (measured by various performance measures of interest) for rapid development and understanding of its relations to the underlying structure.
Data availability
All the data and code to reproduce the case studies presented in this paper are available at https://github.com/pozzo-research-group/papers/tree/main/autophasemap. Warping functions are computed by reproducing the part of the code from fdasrsf.35 Parallel computations are performed using ray36 and computation of label functions using.37 All the code is implemented in Python with reliance on numpy,38 scipy34 for numerical computing, and matplotlib39 for plotting routines.Author contributions
All the authors contributed equally to conceptualization, problem formulation, manuscript writing, and reviews. K. V developed the theoretical and algorithmic framework for automatic phase mapping and performed the case studies. K. L performed the experimental synthesis, data collection, and analysis.Conflicts of interest
The authors declare no competing interests.Acknowledgements
Funding for this work was primarily by the US Department of Energy (DOE), Office of Science, and Office of Basic Energy Sciences (BES) under award number DE-SC0019911. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The authors thank Dr Aaron Gilad Kusne (NIST) for valuable suggestions regarding the method and for providing data and insights for the XRD case study. We are also thankful for the help of Dr Soenke Seifert and the beamline staff of APS 12-ID-C. K. V. would like to thank Dr Nina Miolane (UCSB) for valuable initial discussions on using shape-based measures for functions, building statistical models, and suggesting the elastic k-means paper23 for template learning. This work was also facilitated through the use of advanced computational, storage, and networking infrastructure provided by the Hyak supercomputer system and the Department of Chemical Engineering at the University of Washington.References
- J. W. Gibbs. A method of geometrical representation of the thermodynamic properties of substances by means of surfaces collected works, ed., J. W. Gibbs, 1928 Search PubMed.
- O. Ryll, S. Blagov and H. Hasse, Convex envelope method for the determination of fluid phase diagrams, Fluid Phase Equilib., 2012, 324, 108–116 CrossRef CAS.
- K. Vaddi, H. Liu, B. Sesha, S. Pokuri, B. Ganapathysubramanian and O. Wodo, Construction and high throughput exploration of phase diagrams of multi-component organic blends, Comput. Mater. Sci., 2023, 216, 111829 CrossRef CAS.
- S. Mao, D. Kuldinow, M. P. Haataja and A. Košmrlj, Phase behavior and morphology of multicomponent liquid mixtures, Soft Matter, 2019, 15(6), 1297–1311 RSC.
- W. Frank, Metric geometry of equilibrium thermodynamics, J. Chem. Phys., 1975, 63(6), 2479–2483 CrossRef.
- F. Weinhold, Metric geometry of equilibrium thermodynamics. iii. elementary formal structure of a vector-algebraic representation of equilibrium thermodynamics, J. Chem. Phys., 1975, 63(6), 2488–2495 CrossRef CAS.
- F. Weinhold, Metric geometry of equilibrium thermodynamics. v. aspects of heterogeneous equilibrium, J. Chem. Phys., 1976, 65(2), 559–564 CrossRef CAS.
- D. D. Lee and H. S. Seung, Learning the parts of objects by non-negative matrix factorization, Nature, 1999, 401(6755), 788–791 CrossRef CAS PubMed.
- C. J. Long, D. Bunker, X. Li, V. L. Karen and I. Takeuchi, Rapid identification of structural phases in combinatorial thin-film libraries using x-ray diffraction and non-negative matrix factorization, Rev. Sci. Instrum., 2009, 80(10), 103902 CrossRef CAS PubMed.
- P. M. Maffettone, A. C. Daly and D. Olds, Constrained non-negative matrix factorization enabling real-time insights of in situ and high-throughput experiments, Appl. Phys. Rev., 2021, 8(4), 041410 CAS.
- V. Stanev, V. V. Vesselinov, A. G. Kusne, A. Graham, I. Takeuchi and S. A. Boian, Unsupervised phase mapping of x-ray diffraction data by nonnegative matrix factorization integrated with custom clustering, npj Comput. Mater., 2018, 4(1), 1–10 CrossRef.
- J. Bai, S. Ament, G. Perez, J. Gregoire, and C. Gomes. An efficient relaxed projection method for constrained non-negative matrix factorization with application to the phase-mapping problem in materials science, In, International Conference on the Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Springer, 2018, pp. 52–62 Search PubMed.
- A. G. Kusne, D. Keller, A. Anderson, A. Zaban and I. Takeuchi, High-throughput determination of structural phase diagram and constituent phases using Grendel, Nanotechnology, 2015, 26(44), 444002 CrossRef CAS PubMed.
- V. Lutz-Bueno, C. Arboleda, L. Leu, M. J. Blunt, A. Busch, A. Georgiadis, P. Bertier, J. Schmatz, Z. Varga and P. Villanueva-Perez, et al., Model-free classification of x-ray scattering signals applied to image segmentation, J. Appl. Crystallogr., 2018, 51(5), 1378–1386 CrossRef CAS PubMed.
- X. Zheng, Y. He, J. R. Hattrick-Simpers and J. Hu, Automated phase segmentation for large-scale x-ray diffraction data using a graph-based phase segmentation (gphase) algorithm, ACS Comb. Sci., 2017, 19(3), 137–144 CrossRef PubMed.
- D. G. Kendall, A survey of the statistical theory of shape, Stat. Sci., 1989, 4(2), 87–99 Search PubMed.
- K. Vaddi, H. T. Chiang and L. D. Pozzo, Autonomous retrosynthesis of gold nanoparticles via spectral shape matching, Digit. Discov., 2022, 1(4), 502–510 RSC.
- S. K. Suram, J. A. Haber, J. Jin and J. M. Gregoire, Generating information-rich high-throughput experimental materials genomes using functional clustering via multitree genetic programming and information theory, ACS Comb. Sci., 2015, 17(4), 224–233 CrossRef CAS PubMed.
- K. Vaddi and O. Wodo, Metric learning for high-throughput combinatorial data sets, ACS Comb. Sci., 2019, 21(11), 726–735 CrossRef CAS PubMed.
- C. J. Long, J. Hattrick-Simpers, M. Murakami, R. C. Srivastava, I. Takeuchi, V. L. Karen and X. Li, Rapid structural mapping of ternary metallic alloy systems using the combinatorial approach and cluster analysis, Rev. Sci. Instrum., 2007, 78(7), 072217 CrossRef CAS PubMed.
- C. J. Gommes, S. Jaksch and H. Frielinghaus, Small-angle scattering for beginners, J. Appl. Crystallogr., 2021, 54(6), 1832–1843 CrossRef CAS PubMed.
- P. Lindner and T. Zemb, Neutron, X-Ray and Light Scattering: Introduction to an Investigative Tool for Colloidal and Polymeric Systems, 1991 Search PubMed.
- X. Zang, S. Kurtek, O. Chkrebtii, and J. D. Tucker, Elastic k-means clustering of functional data for posterior exploration, with an application to inference on acute respiratory infection dynamics, arXiv preprint arXiv:2011.12397, 2020.
- K. J. Lachowski, K. Vaddi, N. Y. Naser, F. Baneyx and L. D. Pozzo, Multivariate analysis of peptide-driven nucleation and growth of au nanoparticles, Digit. Discov., 2022, 1(4), 427–439 RSC.
- A. Srivastava and E. P. Klassen, Functional and Shape Data Analysis, Springer, 2016, vol. 1 Search PubMed.
- W. Huang, K. A. Gallivan, A. Srivastava, P.-A. Absil, et al., Riemannian optimization for elastic shape analysis, Mathematical theory of Networks and Systems, 2014 Search PubMed.
- J. L. K. G. Yager and Y. Zhang, Scattersim, https://github.com/CFN-softbio/ScatterSim, 2022 Search PubMed.
- R. R. Coifman, S. Lafon, A. B. Lee, M. Maggioni, B. Nadler, F. Warner and S. W. Zucker, Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(21), 7426–7431 CrossRef CAS PubMed.
- G. Wanka, H. Hoffmann and W. Ulbricht, Phase diagrams and aggregation behavior of poly(oxyethylene)–poly(oxypropylene)–poly(oxyethylene) triblock copolymers in aqueous solutions, Macromolecules, 1994, 27(15), 4145–4159 CrossRef CAS.
- G. Wanka, H. Hoffmann and W. Ulbricht, Phase diagrams and aggregation behavior of poly (oxyethylene)-poly (oxypropylene)-poly (oxyethylene) triblock copolymers in aqueous solutions, Macromolecules, 1994, 27(15), 4145–4159 CrossRef CAS.
- U. Ashraf, O. Ahmad Chat, M. Maswal, S. Jabeen and A. Ahmad Dar, An investigation of pluronic p123–sodium cholate mixed system: micellization, gelation and encapsulation behavior, RSC Adv., 2015, 5(102), 83608–83618 RSC.
- Y. Iwasaki, A. G. Kusne and I. Takeuchi, Comparison of dissimilarity measures for cluster analysis of X-ray diffraction data from combinatorial libraries, npj Comput. Mater., 2017, 3(1), 1–9 CrossRef CAS.
- J. Kenneth Bunn, J. Hu and J. R. Hattrick-Simpers, Semi-supervised approach to phase identification from combinatorial sample diffraction patterns, JOM, 2016, 68(8), 2116–2125 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Warren and J. Bright, et al., Scipy 1.0: fundamental algorithms for scientific computing in python, Nat. Methods, 2020, 17(3), 261–272 CrossRef CAS PubMed.
- J. D. Tucker, W. Wu and A. Srivastava, Generative models for functional data using phase and amplitude separation, Comput. Stat. Data Anal., 2013, 61, 50–66 CrossRef.
- P. Moritz, R. Nishihara, S. Wang, A. Tumanov, R. Liaw, E. Liang, M. Elibol, Z. Yang, W. Paul, M. I. Jordan, et al., Ray: A distributed framework for emerging {AI} applications, In 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18), 2018, pp. 561–577 Search PubMed.
- J. Levy-Kramer, k-Means-Constrained, https://github.com/joshlk/k-means-constrained, 2022 Search PubMed.
- C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg and N. J. Smith, et al., Array programming with numpy, Nature, 2020, 585(7825), 357–362 CrossRef CAS PubMed.
- J. D. Hunter, Matplotlib: A 2d graphics environment, Comput. Sci. Eng., 2007, 9(3), 90–95 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00105a |
| This journal is © The Royal Society of Chemistry 2023 |