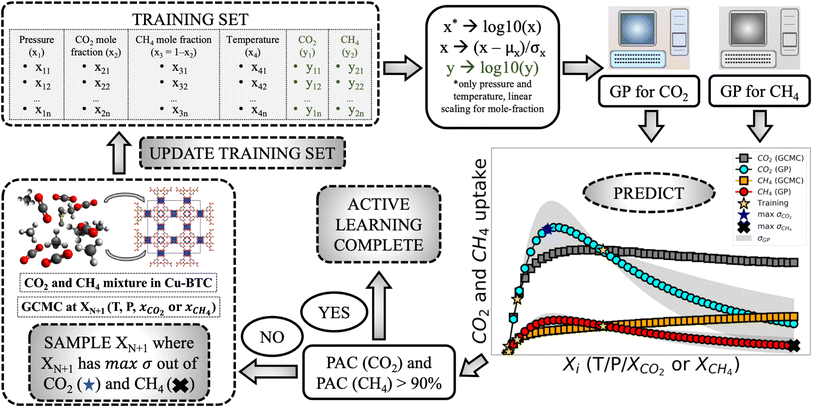
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Active learning for efficient navigation of multi-component gas adsorption landscapes in a MOF†
Krishnendu
Mukherjee
 ,
Etinosa
Osaro
,
Etinosa
Osaro
 and
Yamil J.
Colón
and
Yamil J.
Colón
 *
*
University of Notre Dame, Notre Dame, IN, USA. E-mail: ycolon@nd.edu
First published on 24th August 2023
Abstract
In recent decades, metal–organic frameworks (MOFs) have gained recognition for their potential in multicomponent gas separations. Though molecular simulations have revealed structure–property relationships of MOF–adsorbate systems, they can be computationally expensive and there is a need for surrogate models that can predict the adsorption data faster. In this work, an active learning (AL) protocol is introduced that can predict multicomponent gas adsorption in a MOF for a range of thermodynamic conditions. This methodology is applied to build a model for the adsorption of three different gas mixtures (CO2–CH4, Xe–Kr, and H2S–CO2) in the MOF Cu-BTC. A Gaussian process regression (GPR) model is used to fit the data as well to leverage its predicted uncertainty to drive the learning. The training data is generated using grand-canonical Monte Carlo (GCMC) simulations as points are iteratively added to the model to minimize the predicted uncertainty. Also, a criteria which captures the perceived performance of the GPs is introduced to terminate the AL process when the perceived accuracy threshold is met. The three systems are tested for a pressure–mole fraction (P–X), and a pressure–mole fraction–temperature (P–X–T) feature space. It is demonstrated that AL one only needs a fraction of the data from simulations to build a reliable surrogate model for predicting mixture adsorption. Further, the final GP fit from AL outperforms ideal adsorbed solution theory predictions.
1 Introduction
Metal–organic frameworks (MOFs), a class of crystalline nanoporous materials, are known for their high surface area and pore volume.1 These materials are self-assembled from two components – organic linker molecules and inorganic metal nodes or metal clusters – a property that provides infinite choices of structures that can be synthesized in a laboratory. MOFs have demonstrated applicability for energy storage, gas separations, and sensing.2–7 Despite the potential of these materials and their increasing numbers reported in experiments, there is a challenge to determine which are the best MOFs and what are the conditions (e.g., temperature, pressure) that maximize their performance. For these decisions, the adsorption isotherms are very useful. This data helps to select structures that might be a good fit depending on either selectivity, or adsorption (say at condition of pressure and temperature of P and T, respectively) or just total gas uptake at a T but for different pressures.8 Molecular simulations have played an important role in the design and discovery of MOFs for a variety of applications.9 However, the number of MOFs in existence has kept increasing and new procedures have been introduced to enhance computational capabilities.10–13 The use of large-scale, high-throughput computational screening techniques on databases of MOF structures (experimental or computationally generated) has revealed structure–property relationships and identified top performing materials for many applications.14–19In this work, we focus on multi-component adsorption in MOFs. Gas mixtures are ubiquitous in nature and studying their interactions with materials is essential for a number of purposes. For example, MOFs can be used for separating impurities in hydrogen gas which then can be fed to hydro-cracker and hydro-processing units, to capture carbon dioxide for tackling climate change, or for separating hydrogen sulphide from refinery waste streams to eventually extract solid sulphur as well as enhance gasoline quality.20–22 In many of these applications, nanoporous materials can be utilized for adsorption and separation of different species in gas mixtures. Since multicomponent gas adsorption can take place at a variety of conditions, it is important to understand how they affect MOF adsorption for the relevant set of adsorbates in the mixture. Conventionally, grand-canonical Monte Carlo (GCMC) simulations are employed for generating adsorption isotherm for these mixtures in MOFs, and depending on the system size they can take considerable time to finish.23,24 Further, each GCMC simulation is done at specific operating conditions and to get an isotherm one has to conduct many such simulations. This can rapidly increase the total computational cost of a project. Further, in many computing environments, the resources might be very limited. For example, to calculate the uptake for a n pressure × n temperature points, one has to conduct n2 number of simulations. Adding more features can very well prohibit the study and one has to either look for theoretical models or drastically reduce the design space. Thus, there is a need for a surrogate model which can provide us these properties with only a fraction of these conventional simulations/experiments from the input space.
1.1 Machine learning combined with molecular simulations for gas adsorption in MOFs
The emergence of big data has also allowed researchers to employ machine learning (ML) algorithms for a variety of chemistry applications.25,26 Many of these ML models have been applied for gas adsorption and separation problems.27–35 These models have provided important physical insight through the development of new descriptors capable of capturing important factors for applications of interest.36–40 Further, alternate training methods such as transfer learning have also shown promise in terms of saving training cost while building these models.41,42 However, therein lies a challenge and bottleneck for workflows that rely on ML for predictions—large dataset are needed for the proper training and deployment of many ML algorithms. In cases where obtaining high-fidelity data is difficult or prohibitive, the potential of ML algorithms and workflows is limited. Another concern with the way ML models are built, is the static nature of the training dataset. Conventionally, building the ML model using molecular simulation data is a passive learning strategy, in which all the training points are sampled at once by the user.9,26,43 Hence, not all data contribute to the performance of the model equally. However, one can potentially get the same performance with far less number of training points if an intelligent and efficient way of choosing them is adopted. This would result in savings of computational power and efficient generation of training data. In the latter case, each new point added in the training set will contribute to a performance or betterment of the model. As pointed out earlier for adsorption problems, each simulation can be very expensive and particularly for multi-feature design space, it can quickly become very difficult to generate the desired training set. Hence, there is a need for surrogate model for multi-feature adsorption problems that are data efficient and that can generate the desired adsorption data with good performance.1.2 Active learning as an alternate strategy for surrogate models
To tackle the challenges highlighted in building a ML-based model for mixture adsorption, an alternative strategy known as an active learning (AL) can be adopted.44 In AL, the algorithm learns the desired target distribution in a ‘Bayesian’ style process, i.e. algorithm-directed new points are added to the training set and fitting is done iteratively until a certain criteria for learning is satisfied.43,45 An AL methodology can balance the performance of the predictive models while minimizing the number of data points one is needed to acquire. This can be particularly attractive in situations where the feature space is “small” (such as composition of multicomponent adsorption while varying temperature and pressure conditions) and/or time-consuming or resource-intensive experiments/simulations are needed. In this regard, GPRs (Gaussian process regression) stand out among other ML models. GPRs are flexible non-parametric models than can emulate any distribution with fewer data points. Further they provide an estimate of the standard deviation along with output, which is very useful to perform AL. Currently, there are two approaches in general adopted to model mixture adsorption. The first, which is also done in experiments, is to gather the pure component isotherms (many pressures, one temperature) and use them as inputs to ideal adsorbed solution theory (IAST) to make the predictions of the mixture adsorption at the chosen temperature.46 This has many drawbacks, including the inaccuracies of IAST in many regions of the adsorption space and the necessity of the pure component isotherms.47 The second, which is only for simulations as experiments of mixture adsorption are very rare, is to directly simulate the mixture adsorption with GCMC. This can be extremely data intensive as this is typically done by exhaustively simulating temperature, pressure, and compositions of the mixture. Given the intelligent selection of the simulations with the proposed AL approach, we can generate accurate surrogate models for the mixture with significant data savings. Further, for predicting isotherms, ML models have been used but very rarely have been employed in an active learning-oriented approach.48–50 Furthermore, GPs have shown better performance for small sized datasets compared with models like Bayesian neural networks (BNNs) or neural network ensembles, which can also provide uncertainty estimates.51,52 This makes GPs well suited for predictions for adsorption like problems where generating large dataset is expensive. These approaches are already gaining popularity in the molecular simulation space. For example, they have been used to calculate inter-molecular potential energy surfaces, force fields, and to connect different length and time scales.53–55 Most of these works have used AL where the next simulation points were chosen based on predicted model uncertainty through a query-by-committee approach. In our previous work, we showed that AL can be used to predict adsorption isotherms for pure components in a MOF up to two features: temperature and pressure.56 Recently, Osaro et al. also predicted pure-component isotherms of four different molecules using an AL approach and extended to multiple MOFs.57 A branches and team also showed that phase diagram of deep-eutectics and ternary mixtures can be constructed efficiently using a thermodynamics-informed AL approach.58 All these works have shown surrogate models built through AL require an order of magnitude less number of simulations. In this work, we apply the AL protocol to model adsorption of three binary gas mixtures (CO2–CH4, Xe–Kr, and H2S–CO2) in a MOF. These mixtures are selected due to the diverse characteristics of the individual components. CH4 is non-polar with no charge while CO2 is also non-polar but is charged. Xe and Kr are both noble gases, while H2S is charged as well as polar. The selection of these mixtures allows to explore a wide range of target adsorption distribution. For modeling the mixture adsorption, a dual-GPR (Gaussian process regression) model is applied for the mixtures using the predicted uncertainty to select the next point.59 A dual-GPR model here describes the application of two GPs, where each GP is a surrogate model tasked with learning the adsorption of only one species in the mixture. Therefore, the input features to both the GPs are same except for the mole-fraction (which is Xi to the first GP and 1 − Xi to other GP), however both the GPs are trained to predict the uptake of their respective species in the mixture. Further, we introduce a new GP's perceived performance based convergence criteria called perceived accuracy to terminate the learning. We also test this protocol up to 3 features (pressure, mole fraction, and temperature). Finally, we demonstrate how the method can emulate adsorption isotherm for mixtures with only simulating a fraction of data points with reliable performance across different performance indicators. We compare the final GP results with ideal adsorbed solution theory (IAST)-predicted isotherms based on the Langmuir model.46,60 Through this comparison we show that AL-generated adsorption isotherm outperforms IAST and are very close to the GCMC results for all three gas mixtures.2 Methods
2.1 Ground truth generation
The Monte Carlo modeling suite, RASPA, was used to generate the ground truth.61 Grand canonical Monte Carlo (GCMC) simulations were performed, which has resulted in accurate predictions when compared to experimental adsorption isotherms.23,24 5000 and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles were used for initialization and production respectively for generating the ground truth for the mixtures in the P–X and P–X–T feature spaces. The ground truth data was used for two purposes. First, a part of the ground truth was used for providing the initial training set to the GP as well as to provide the next samples to the GP. Second, it was used as a benchmark to compare with the final GP fit (the state when AL ends), calculate the mean relative error (MRE), and correlation coefficient (R2) of the GP predicted adsorption with the GCMC simulations. The universal forcefield (UFF) was used for modeling the non-bonded interactions for Cu-BTC MOF and the Transferable Potentials for Phase Equilibria (TraPPE) for adsorbate molecules.62,63 Charges for Cu-BTC were taken from Castillo et al., where the Cu-BTC partial charges were obtained via fitting different set of charges to reproduce water adsorption data.64,65 Furthermore, the combination of GCMC simulated isotherm based on UFF forcefield and TraPPE for mixture adsorbates have been previously utilized for mixtures simulation. Zhong and team performed GCMC simulations for equimolar binary mixtures of CO2, CH4, and H2 in Cu-BTC MOF and found very close agreement with experiments.66 Wang and coworkers also studied many hydrocarbon mixtures with carbon dioxide using TraPPE models in Cu-BTC and found excellent matching with experimental data.67 Also, the IAST adsorption data was produced from fitting pure-component isotherm of the relevant gases in the mixtures using py-IAST developed by Simon and coauthors.46,68 The Langmuir model with model isotherm() function of py-IAST was used to generate the IAST prediction from the pure component isotherms of the respective species. The pure component isotherm were based on the same pressure and temperature conditions for which IAST prediction for the mixture condition were generated.
000 cycles were used for initialization and production respectively for generating the ground truth for the mixtures in the P–X and P–X–T feature spaces. The ground truth data was used for two purposes. First, a part of the ground truth was used for providing the initial training set to the GP as well as to provide the next samples to the GP. Second, it was used as a benchmark to compare with the final GP fit (the state when AL ends), calculate the mean relative error (MRE), and correlation coefficient (R2) of the GP predicted adsorption with the GCMC simulations. The universal forcefield (UFF) was used for modeling the non-bonded interactions for Cu-BTC MOF and the Transferable Potentials for Phase Equilibria (TraPPE) for adsorbate molecules.62,63 Charges for Cu-BTC were taken from Castillo et al., where the Cu-BTC partial charges were obtained via fitting different set of charges to reproduce water adsorption data.64,65 Furthermore, the combination of GCMC simulated isotherm based on UFF forcefield and TraPPE for mixture adsorbates have been previously utilized for mixtures simulation. Zhong and team performed GCMC simulations for equimolar binary mixtures of CO2, CH4, and H2 in Cu-BTC MOF and found very close agreement with experiments.66 Wang and coworkers also studied many hydrocarbon mixtures with carbon dioxide using TraPPE models in Cu-BTC and found excellent matching with experimental data.67 Also, the IAST adsorption data was produced from fitting pure-component isotherm of the relevant gases in the mixtures using py-IAST developed by Simon and coauthors.46,68 The Langmuir model with model isotherm() function of py-IAST was used to generate the IAST prediction from the pure component isotherms of the respective species. The pure component isotherm were based on the same pressure and temperature conditions for which IAST prediction for the mixture condition were generated.
2.2 Initial training set selection criteria
The initial training set selection for this work was based on ‘boundary-informed’ scheme, as first detailed in our previous work.56 This scheme is based on adding the pressure grid points in a geometric progression with a factor of 10. Thus, it covers both the low- and high-pressure points within the boundaries of the test dataset. The rest of the features in the scheme are linearly distributed within the defined limits. The points for the pressure feature were set at the boundaries of range (such as 10−6, 10−5, 10−4, and so on for pressure), but was linearly spaced for mole fraction and temperature features.56 Also, for all the 3 mixtures tested, the initial training set input points (for all the features) had the same set of values for a fair comparison. The initial training set for the P–X is given in the Table 1 as an example. As AL progressed more data points were added to the training set. During the AL, the GPs are fit using the complete training set. The test set distribution was not known and was only used for prediction purposes. The test set limits for mole-fraction, and temperature were: [0.02, 0.98] and [200 K, 400 K], respectively. For pressure, the lower limit was 10−6 bar for all cases but the upper limit was different for different mixtures. For CO2–CH4 it was 300 bar, for Xe–Kr it was 200 bar, and for H2S–CO2 it was 100 bar. Also a linear distribution of the features was adopted for the test set.| Pressure (in bar) | Mole fraction | Temperature (in K) |
|---|---|---|
| 10−6 | 0.02 | 300 |
| 10−5 | 0.20 | |
| 10−4 | 0.40 | |
| 10−3 | 0.60 | |
| 10−2 | 0.80 | |
| 10−1 | 0.98 | |
| 100 | ||
| 101 | ||
| 102 |
2.3 Active learning workflow
The AL workflow that was applied can be divided in these steps:• Data pre-processing—First the log base 10 transformation of the pressure and temperature (both in P–X and P–X–T) features is performed in the dataset. Then, they are standardized against their mean and standard deviation of the test set. Only the mole fraction feature is linearly scaled to −1 and 1. The standardized version of mole fraction was tested but the linear scaling model worked better, and hence it is adopted. Also the target variable (adsorption y) is log (base 10) transformed.
• Model training—The engine of the AL workflow is the GP regression model. A dual GP model was chosen with two independent GPs, one for each species in the binary gas mixtures. Both GPs were independently trained with the same input in pressure and temperature (for P–X–T), and corresponding mole fraction of the species. Thus, each GP was provided three features for P–X–T and two for P–X. GPs are multivariate normal distribution models where each data entry adds a new dimension to the model:59
| f(x) ∼ N(μ(x),k(xi,xj)), | (1) |
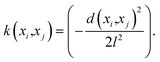 | (2) |
Also, an α regularization term was added to the covariance matrix with a value of 10−4 for CO2–CH4 and H2S–CO2, while 10−5 for Xe–Kr. This is a constant which is added to the diagonal of the covariance matrix to provide an uncertainty threshold so that the data is not overfitted. Please refer to Fig. S3 in the ESI† for further details.
• Model prediction and convergence criteria—After the training is complete, the test set is passed through the trained GP models for prediction. For the binary mixtures, we obtain two GP outputs (y1 and y2), which are scaled back to adsorption by taking the inverse-log of these outputs. Also, the GP gives us the uncertainty distribution in the prediction for each test point, σn which is obtained from the covariance matrix. The σn is then used to find the most uncertain region in the test set, which shows which areas to actively sample in the next iteration and add to the training set. However, before sampling, we calculate a perceived accuracy (PAC) term which is the stopping criterion for the AL protocol. We define the PAC for adsorption for species i in a mixture as:
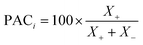 | (3) |
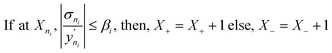 | (4) |
This PAC value is the fraction of points in the test set whose GP relative errors are above a desired relative error threshold. Thus, PAC is a measure of the performance ‘perceived’ by the GP model, which it calculates by counting the number of predictions which fall under a desired relative error limit. In eqn (3) and (4), σni and 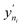 are the GP-predicted uncertainty and adsorption value (log) associated with the test point Xni. Therefore, the concept of PAC is first introduced in this work and has potential to be used for any AL based tasks. This parameter was inspired from the use of the term accuracy in regular classification tasks.70 Accuracy in a classification task is defined as the ratio of correctly classified test cases to total number of test cases. In classification tasks, the accuracy is determined with respect to ground-truth data. Here a similar concept is used but it is applied to a regression problem (adsorption uptake prediction) while using the βi threshold as a cut-off for determining PAC. This is a different use of the accuracy measure which comes from GP models during the prediction phase and is not produced from comparing the model prediction with the ground-truth (as is done for a regular classification task). The threshold value βi is user-defined and can be set on the basis of the desired performance the user needs. Also, the β values were kept same for the all the species in mixture. We had β set to 2% for the P–X feature space, while it was set to 5% for AL in the P–X–T space. This was done since the test set in the P–X–T was much sparser than that of P–X one (21 × 11 × 11 points in the P–X–T feature space, compared to 51 × 49 points for P–X). The test size reduction in the P–X–T was done to avoid a high computational cost. Including an extra feature while keeping the same test size necessitates the increase in the sparseness of the test set. In scenarios of sparse data, the GP model tends to have large uncertainty while the true performance does not deteriorate or scales down in proportion to the size reduction of the test set. As observed, the final model performance for the same gas mixture for the two cases (P–X and P–X–T) were comparable even though they had different β values (refer Tables 2 and 4). We observed either the individual MREs for the P–X–T case remained the same as P–X or they were twice as high in the worst case. Lastly, the PAC was compared to the threshold of convergence, which is set to 90% for all the mixtures for the both the feature-space studies. If 90% of the test set predictions for both the species are less than or equal to β, then the learning is finished and no new point is further sampled. If the PAC policy is not satisfied then the next step is followed.
are the GP-predicted uncertainty and adsorption value (log) associated with the test point Xni. Therefore, the concept of PAC is first introduced in this work and has potential to be used for any AL based tasks. This parameter was inspired from the use of the term accuracy in regular classification tasks.70 Accuracy in a classification task is defined as the ratio of correctly classified test cases to total number of test cases. In classification tasks, the accuracy is determined with respect to ground-truth data. Here a similar concept is used but it is applied to a regression problem (adsorption uptake prediction) while using the βi threshold as a cut-off for determining PAC. This is a different use of the accuracy measure which comes from GP models during the prediction phase and is not produced from comparing the model prediction with the ground-truth (as is done for a regular classification task). The threshold value βi is user-defined and can be set on the basis of the desired performance the user needs. Also, the β values were kept same for the all the species in mixture. We had β set to 2% for the P–X feature space, while it was set to 5% for AL in the P–X–T space. This was done since the test set in the P–X–T was much sparser than that of P–X one (21 × 11 × 11 points in the P–X–T feature space, compared to 51 × 49 points for P–X). The test size reduction in the P–X–T was done to avoid a high computational cost. Including an extra feature while keeping the same test size necessitates the increase in the sparseness of the test set. In scenarios of sparse data, the GP model tends to have large uncertainty while the true performance does not deteriorate or scales down in proportion to the size reduction of the test set. As observed, the final model performance for the same gas mixture for the two cases (P–X and P–X–T) were comparable even though they had different β values (refer Tables 2 and 4). We observed either the individual MREs for the P–X–T case remained the same as P–X or they were twice as high in the worst case. Lastly, the PAC was compared to the threshold of convergence, which is set to 90% for all the mixtures for the both the feature-space studies. If 90% of the test set predictions for both the species are less than or equal to β, then the learning is finished and no new point is further sampled. If the PAC policy is not satisfied then the next step is followed.
| Mixture | Kernel | Iterations | Data requirement (in %) | MRE(species 1) (in %) | MRE(species 2) (in %) | R (species 1) 2 | R (species 2) 2 |
|---|---|---|---|---|---|---|---|
| CO2–CH4 | RBF | 21 | 3.001 | 5.263 | 5.417 | 0.986 | 0.999 |
| Xe–Kr | RQ | 11 | 2.601 | 6.526 | 6.394 | 0.985 | 0.998 |
| H2S–CO2 | RQ | 10 | 2.561 | 7.149 | 7.154 | 0.982 | 0.995 |
• Training set update—In case any of the two PAC criteria are not satisfied then this protocol is followed. The highest uncertain point in the test set is chosen from both the species (based on σni value) and then the point with maximum σni of the two species is sampled through GCMC. After sampling this point, it is added to the training data set and then the AL restarts. The protocol continues until the PAC condition is satisfied for both the species. Fig. 1 depicts the full AL workflow.
• Hyperparameters—Before building the adsorption model, we had to decide on different hyperparameters for a GPR including kernels and regularization parameters. Three different kernel options and their combinations were tested: rational quadratic (RQ), Matérn, and radial basis function (RBF). We note that the parameters inside all the kernels, such as length-scale l or α in RQ are optimized in the GP fitting process to get to the maximum log-likelihood. The only parameter that is not optimized is the ν parameter in Matérn, which was set to 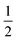 since this value gave the best fit as well as consistency in subsequent iterations. Further, the bounds of l and α chosen were 10−13 to 1013. The equation for RQ and Matérn kernels are:
since this value gave the best fit as well as consistency in subsequent iterations. Further, the bounds of l and α chosen were 10−13 to 1013. The equation for RQ and Matérn kernels are:
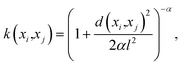 | (5) |
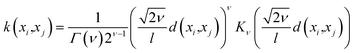 | (6) |
The RQ kernel (eqn (5)) has an extra parameter α when compared to RBF in eqn (2). In eqn (6), Kν(·) is the modified Bessel function, and Γ(·) is the gamma function. Different values of ν correspond to different functions. ν, as a parameter is used to control the smoothness of the Matérn function. Kernel optimization results for all the different combinations are provided in the ESI.†
• Performance metrics—After selecting the best kernel combination AL fit performance is assessed by various metrics. The GP predicted uncertainties (which are used to find the next point for sampling) are given here for each point.
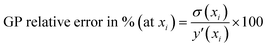 | (7) |
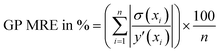 | (8) |
The next metric is the mean relative error (MRE) where the GP-predicted adsorption (YGP-predict, scaled back from y′) is compared with GCMC data (YGCMC) for all points in the test set and their average is calculated.
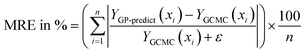 | (9) |
The ε (=10−3) is added to the denominator to avoid numerical issues since adsorption in some feature spaces can reach 0. The same equation is used to find MRE with respect to IAST predictions in Table 5. Only YGCMC is replaced by uptake predictions by the IAST-Langmuir model in the mixture space.
AL was performed for both the P–X and P–X–T feature spaces. The major differences for these two cases and the three binary gas mixtures are listed here:
• The points included in the initial training dataset for P–X are 9P × 6X (=54 points) and 5P × 6X × 3T (=90 points) for P–X–T. Details are shared in Tables 1 and 3. A detailed discussion for this difference is provided in the P–X–T results section.
• n_restart_optimizer: This was set to 100 for P–X and 1000 for P–X–T. This parameter is number of restarts of the L-BGFS-B algorithm while training a GP. The higher the number of restarts, it increases the chances for the GP of finding the kernel parameters which maximizes the log-maximum likelihood function.
• α (the regularization parameter) = 10−4 for CO2–CH4 and H2S–CO2, and 10−5 for Xe–Kr (same for both P–X and P–X–T). The parameter was selected from testing on initial training data. More information is shared in the ESI.†
• Kernel combination tested for P–X feature-space were single (k1) and double additive kernels (k1 + k2). For P–X–T, all the permutations of single, double, and triple additive kernels (k1 + k2 + k3) were tested. This made a total of 9 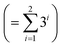 combinations for P–X and 39
combinations for P–X and 39 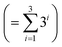 for P–X–T. The details of kernel evaluation and results are provided in the ESI.†
for P–X–T. The details of kernel evaluation and results are provided in the ESI.†
• The β value, the relative error constraint which classifies the confident and under-confident regions of the GP for PAC calculation, is 5% for P–X–T while kept 2% for P–X.
3 Results and discussion
3.1 P–X feature space
In the P–X feature space, the best kernel for CO2–CH4 mixture was a single RBF. The model based on RBF kernel was chosen as the final surrogate for CO2–CH4. In Fig. 2, the GP-predicted adsorption isotherms for three XCO2 values are compared with GCMC data. The training points (shown in the star marker) indicate points GPs were trained on, and here in Fig. 2a we observe that the GP predictions are far from the GCMC and very high uncertainty (σCO2(GP)). In Fig. 2b, the AL adds a new training point to the training set (based on the highest uncertainty between CO2 and CH4 uptake) and we find a significant improvement in the adsorption isotherms. This first point added to the training set is at the feature of [p = 300 bar, XCO2 = 0.86]. Thus the uncertainties and predictions of the isotherms at the mole-fraction of 0.80 and 0.50 values show high improvement compared to that of 0.20. Further, the region of high uncertainty also shifts to that of low mole-fraction isotherms. Subsequent additions of data points to training set continues this improvement, as shown by plots (c) and (d) with reduced uncertainty σCO2(GP) and closer agreement of yCO2(GP) with GCMC. Also, out of 49 isotherms (one each XCO2), only 3 representative isotherms are shown here. We find that out of the 10 points that are added, only a single point belonging to this sub-region was added to the training set (refer plot (d)) training point marked at 300 bar and XCO2 = 0.20). However, since training points added to adjacent regions improves performance, we find a consistent improvement in performance in the regions shown here. Lastly Fig. S2 of the ESI† compares the error heat maps of GP-predicted relative error and absolute relative error for these stages of AL. There we also observe that adding a new point to the training set improves the error maps and the GP-predicted error map starts to converge to the true relative error. For the CO2–CH4 mixture case, only up to 10 plus the initial training points are shown here. The AL continues further, adding 21 more points to the training set to reach an accuracy of 90% for both the GPs (see Table 2). | ||
| Fig. 2 Comparison of GP predicted CO2 uptake in Cu-BTC with GCMC in the CO2–CH4 mixture for the CO2 mole-fractions of 0.80, 0.50, and 0.20 at P–X phase at 300 K. The progression are shown for (a) initial training data only (= 54 point training set), (b) 1-point + initial training data (=55 point training set), (c) 5-points + initial training (=59 point training set), and (d) 10 points + initial training (=64 point training set). These plots illustrate this: as the AL algorithm continues to add new training points, the gap between GP predictions and ground truth significantly reduces. Further, the uncertainty of the GPs (shown as shaded regions above) also improves. The corresponding GP-predicted relative error maps and the relative error maps are shown in Fig. S2 of ESI.† | ||
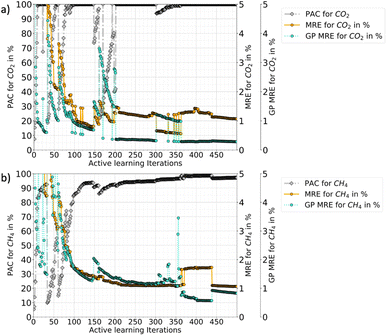
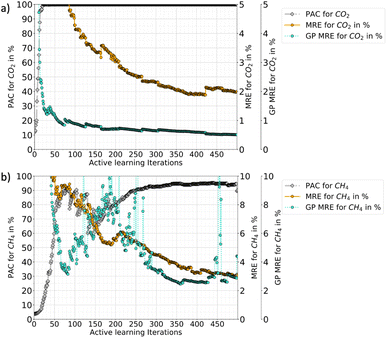
In Fig. 3, the progression of the AL protocol (up to 500 iterations) for CO2–CH4 with the RBF kernel is shown. The GPs meet the desired PAC limit quickly with only 21 additional iterations (≈3% of the ground truth data). However, the PAC in subsequent iterations fluctuates. This is because new samples added to the training data often leads to increase in GP uncertainty. This happens because with addition of new data the GP algorithm updates its predictions and learns about regions where its earlier predictions were wrong. The algorithm thus updates the uncertainties and that is why with more iterations the gap between MRE and GP-MRE starts to reduce. Only when few more samples are added, an improvement as well as stability in the PAC trend is observed. Also, the fluctuations in the MRE parameter is about 1–2%, which indicates these variations are not as pronounced for MRE as it is for the PAC. This also shows that the newly introduced PAC parameter is quite sensitive to the GP-predicted uncertainty distribution. However, a high PAC does result in low MREs and for all the cases tested (three mixtures as well as the two different feature-spaces), a high PAC provided very good fits. Thus, a high-enough PAC ensures a low MRE, which allows to employ PAC as a policy to stop the learning when the criteria is met for both species (refer to Tables 2 and 4 for other gas mixtures and for P–X–T feature space). Also, PAC carries additional advantages compared to maximum relative error threshold criteria, which was used for pure components in our earlier work.56 Some of the reasons of using PAC are listed below:
• PAC is a fractional quantity (reported in %) of the GP's perceived prediction performance. Therefore, it does not depend on the absolute value of the GP relative error (σn/y) or on the absolute standard deviations σn. Depending on the system one is investigating, the distribution of σn could be skewed for some regions and hence taking a maximum relative error or even a mean of relative errors or a mean of σn itself could pose a problem in determining the cut-off values. Since PAC is a fraction and works on aggregate performance, the same cut-off could work for many diverse systems.
• Due to the fractional nature of the PAC, it can be applied to multiple species (or multiple GPs) with the same cut-off limit. Therefore, it could help to scale the algorithm to multi-output problems.
• For mixture adsorption systems (three different mixtures in Cu-BTC, up to 3 features), it was empirically observed that an PAC cut-off of 90% ensures MREs finish within 11% and a R2 close to one. However, one may need to tune the β parameter.
Fig. 3 also shows that the GP for CO2 takes more iterations to stabilize than CH4 (CO2 PAC stabilizes around 200 iterations while CH4 at around 100). This happens because the CO2 adsorption in the mixture has an increasing and then decreasing trend at low-concentration of CO2 and eventually follows a type-I adsorption trend at medium to high-CO2 concentrations (refer Fig. 5). This behaviour was also reported by Tan and coauthors, where they studied mixture adsorption of polar and non-polar gases in carbonaceous nanopores.71 This feature space where CO2 adsorption is high at low pressure, corresponds to the synergistic zone where electrostatic interaction of CO2 with the MOF is stronger. The adsorbates with stronger inter-molecular interactions accumulate near the adsorbent surface and continue to adsorb, out-competing the other gas with weaker adsorbate–adsorbate interaction. However, as pressure is increased CH4 begins to replace CO2. Thus, these two effects results in very different isotherms for different feature space regions. Hence in the CO2–CH4 mixture, the CO2 uptake is a difficult target variable to learn (compared to CH4), requiring more iterations for stabilization.
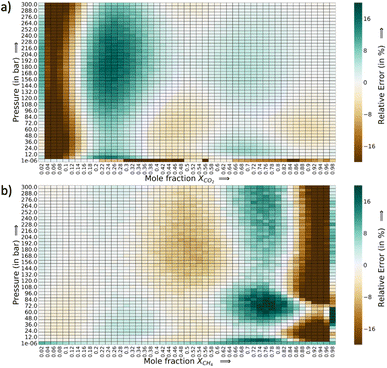
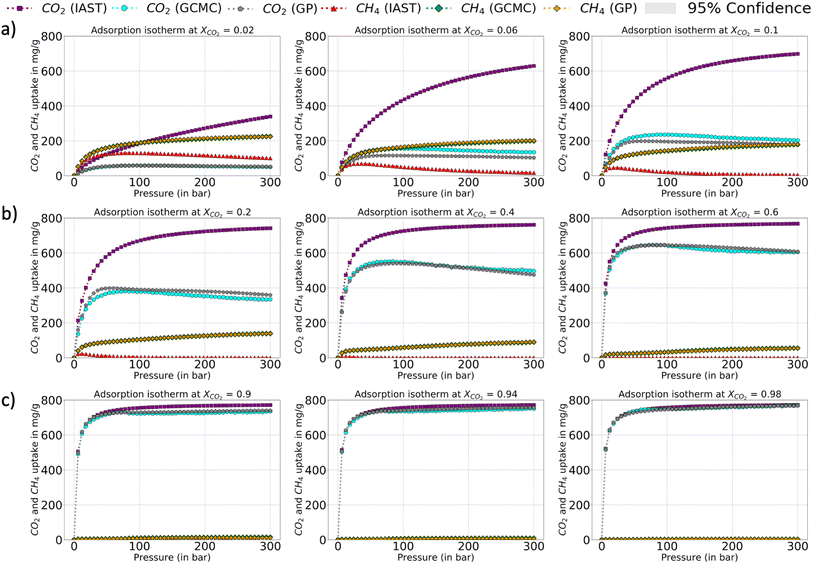
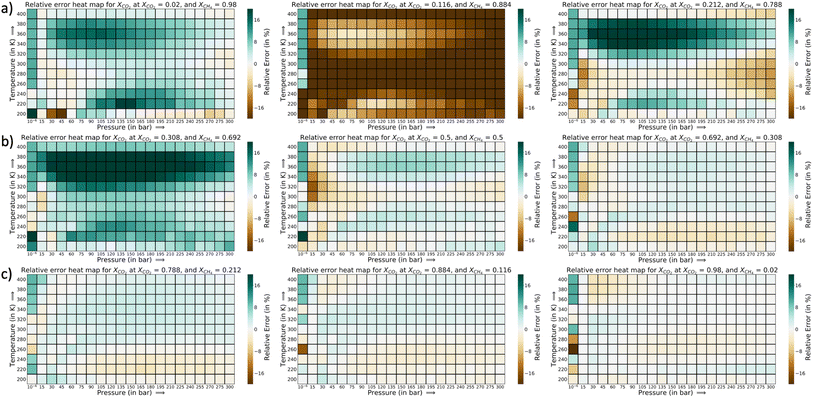
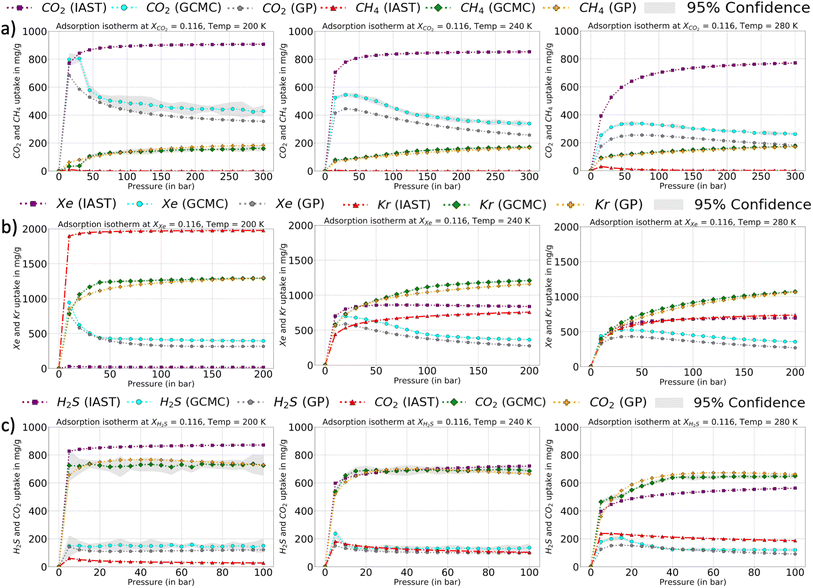
The relative error heat maps when the PAC conditions are met are reported in Fig. 4, which shows relative error (with respect to GCMC) for each point of the P–X grid for both species. In this figure, the errors are higher when CO2 is at a lower concentration (or CH4 concentration is high). This corresponds to the range of XCO2 = 0.02 to 0.20. Following this, the adsorption plots in Fig. 5 are also shown, which compares GP-predicted adsorption with GCMC (ground truth) and IAST predictions, for three-different features of the CO2–CH4 mixture (at the state when PAC constraints are met). First, in Fig. 5a, we find that GP-predicted CO2 uptake is under-predicted compared to the GCMC data. For compositions beyond XCO2 = 0.10, the GP starts to over-predict uptake. Then after the value of XCO2 = 0.20, the GP fit for CO2 has good agreement with the GCMC data. Comparing the GP predictions with IAST, we see it fails to capture the trend completely at low to mid concentrations of CO2. While comparing the performance of GP-predicted uptake for both the species, it performs far better than IAST predictions. Only at high values of XCO2 (>0.80), does IAST perform well and closely follows the GCMC data. Also, at the low concentration of XCO2 (0.02–0.20), IAST has high absolute deviation from GCMC and fails to capture the increasing trend of the CO2 adsorption. In this range, IAST predicts a type-I isotherm for CO2, while an increase and then decreasing trend for CH4, both of which are far from the ground truth. In contrast, the GP predicted isotherms are consistent with the GCMC data, despite some absolute deviations, there is good agreement with the adsorption trends from GCMC.
The error maps and adsorption plots (compared with GCMC and IAST predictions at the PAC of 90% state) for H2S–CO2 and Xe–Kr are provided in the ESI† and they show very similar behavior to that of CO2–CH4 at the PAC cut-off of 90% (Fig. S5–S8†). Though there are slight differences observed, the final GP fits of Xe–Kr at lower Xe concentration are relatively better than CO2, while in the case of H2S–CO2, the GP-GCMC errors are more distributed throughout the feature space. Also, the IAST predictions for Xe–Kr as well for H2S–CO2 show large deviations with respect to the GCMC data except at high Xe and H2S compositions. Thus, like the CO2–CH4 mixture, GP predictions outperform IAST and show similar trends to the GCMC data even when there is a high relative error. IAST fails to capture the trends and has high errors for the majority of the feature space. From the adsorption plots for all the three mixtures, it can be concluded that the species which is more attracted to the Cu-BTC MOF shows high error at low concentration. Since these species (CO2, Xe, and H2S) are more attracted to the Cu-BTC structure they can replace the other one quickly as the concentration is increased. This makes it harder for the GP to capture this rapid change when it moves along the small mole-fraction of the more dominant species. This is one of the pitfalls of the PAC protocol that it may not ensure a perfect fit with GCMC at the 90% cut-off. Hence, one has to balance out the need for a model which is accurate with respect to GCMC at all features ranges but might have errors at certain sections/ranges of the test set or one can let the AL continue to 95% or 99%, so that the model is confident at all feature spaces.
In Table 2, different performance indicators for the GP models are summarized when AL is terminated for the P–X feature space. Since the initial training set (54 points) was kept the same for all gas mixtures, the number of initial training datapoints is also added to calculate the data requirement parameter, which is given below.
 | (10) |
Thus, the data requirement is the fraction of total data provided to the GPs to reach the cut-off of 90% PAC for both the species. The other parameters are the MREs and correlation coefficient for both the species. In Table 2, the data requirement is found to be small (within 3% of ground truth) for the 3 mixtures. The MREs for all the species are also good, around 5–7% for the three mixtures. The last quantity, R2, is close to one (∼0.98–0.99) for all the species, showing that the GP captures the adsorption trend quite well. Thus, in this section it is shown how AL can be used to build reliable surrogate models which work for different gas mixtures and can give a satisfactory performance. With these results it is demonstrated that the cut-off of 90% PAC gives low relative errors and provides good agreement with the ground truth data. This AL termination protocol can thus balance the number of iterations or simulations one needs to conduct versus the performance of the model.
3.2 P–X–T feature space
This section deals with AL in the P–X–T feature space. As stated before, the initial training set size in this P–X–T study is increased to 90 points. This is done because with three features the initial training dataset has to include a new feature: temperature. The distribution for initial training set P–X–T is 5P × 6X × 3T (as shown in Table 3). This particular distribution is arranged so that the most sensitive features gets a high share of points in the initial dataset, hence only 3 points are for temperature while 6 points are given for the mole fraction. Also, the magnitude of initial training input points are kept equal for all three gas mixtures for a fair comparison between mixtures (just like the P–X case). The kernel selection plots for P–X–T case is provided in the ESI.† For CO2–CH4 mixture, the triple-RBF kernel was selected for the AL (see Fig. S9† for details). The desired PAC was met after 64 iterations of active learning, which amounts to a data expenditure of 6.61% (Table 3). The MREs for both species had a slight difference: CH4 has an MRE of 9.25% whereas CO2 has 5.46%. These are good results considering only 6.61% of data is used for training from the ground truth.| Pressure (in bar) | Mole fraction | Temperature (in K) |
|---|---|---|
| 10−6 | 0.02 | 200 |
| 10−4 | 0.20 | 300 |
| 10−2 | 0.40 | 400 |
| 100 | 0.60 | |
| 10+2 | 0.80 | |
| 0.98 |
Fig. 6 shows the progression of AL for triple RBF kernel for CO2–CH4 mixture in the P–X–T feature space (up to 500 iterations). Here, the fluctuations in the PAC value is less compared to the P–X counterpart. Also, there are sharp drops in PAC for CH4 which reflects that with new data the GP model's uncertainty is increased in the prediction, until its gets additional data points to reduce the uncertainties. Like P–X, the PAC cut-off was set to 90% and the model reaches this threshold relatively slowly compared to P–X. Fig. 6 also shows if the learning had continued beyond the cut-off of 90%, around 400 total iterations are needed to meet the 95% PAC threshold. This means that around 20% of the ground truth has to be included in the training set and this would have resulted in an MRE of 2% and 3% for CO2 and CH4, respectively. This finding shows the cost-performance ratio of the learning process and demonstrates that adding more data leads to a slow improvement in the model. Hence, an early cut-off of 90% can provide a ‘good-enough’ model, instead of spending 20% of ground-truth (400 more iterations) to get only a 5% gain in the PAC or 2–4% drop in MREs.
The error heat maps for each mole fraction of CO2 and CH4 (at the AL state when PAC criteria is met) are provided in Fig. 7 and 8. For CO2, the highest error region corresponds to XCO2 = 0.116, followed by XCO2 = 0.308. The rest of the region has very low relative errors, irrespective of the pressure or temperature values. Also, the errors are marginally high in the low temperature range. At the highest temperature of 400 K, the errors are very small. In Fig. 8, a similar trend in the error distribution of CH4 is observed. However the errors are distributed more than CO2 from the feature value of XCH4 = 0.02 to XCH4 = 0.50. In this range of CH4 mole-fraction, the CH4 uptake is small which can explain the rise in the relative error. As the adsorption plots shows, the GP-predictions strongly correlates with the GCMC data. Further in this plot, the errors are slightly high as temperature is increased. This is in the opposite direction of CO2 relative error trend. As temperature increases, CH4 adsorption falls and the relative error spikes because of the smaller y1 in the denominator. However with CO2, with rise in temperature the synergistic effect weakens at low CO2 mole-fraction and the increase and decrease trend of the CO2 isotherm shifts to higher concentration of CO2. Thus, the GP is able to capture that trend well at high temperatures for CO2. Fig. S18 and S19† show the adsorption data for these highest relative error region for CO2 and CH4. Thus, through this analysis it becomes clear that errors for each species are very sensitive to the mole fraction and temperature in the P–X–T phase space.
The corresponding adsorption plots for the region of XCO2 = 0.116 is provided in Fig. 9a, and through them it is observed that the GP model, in many places, fails to capture the true adsorption values for CO2. However, it succeeds in capturing the overall trend of the GCMC, compared with IAST. The IAST trends for both CO2 and CH4 across the temperature fails very similarly to the P–X space. IAST deviates from the GCMC data completely in this region while GP shows moderate relative errors. In Fig. 8, the error heat map for CH4 is shown. Here the errors are more distributed with mole-fraction compared to CO2. Also, the errors are high only in the region when CH4 is less than 0.50 mole-fraction. The adsorption plots for these high error region had been added in Fig. S18 of ESI,† where the adsorption isotherm at these high error region of XCH4 = 0.884 (XCO2 = 0.116) are shown. The CH4 GP fit follows the GCMC data very closely however has a moderate deviation in absolute value. Also, the CH4 uptake is very small in these regions which disproportionately increases the MRE values (y2 being the denominator in MRE calculation). The overall MRE of 9.25% can be thus attributed to region where CH4 uptake is small. Further in Table 4, the R2 for CH4 very close to 1, which shows a very strong correlation of final GP fit with GCMC data. In Fig. S27,† we have also added a comparison plot for the GP-predicted CO2 and CH4 uptakes with the experimental data from Hamon et al. (obtained from the BISON dataset).72,73 There also we find a very close agreement of the GP predicted uptakes with experiments for the three different ratios of CO2 and CH4 at 303 K.
| Mixture | Kernel | Iterations | Data requirement (in %) | MRE(species 1) (in %) | MRE(species 2) (in %) | R (species 1) 2 | R (species 2) 2 |
|---|---|---|---|---|---|---|---|
| CO2–CH4 | Triple-RBF | 78 | 6.611 | 5.461 | 9.256 | 0.988 | 0.990 |
| Xe–Kr | Triple-RBF | 79 | 6.650 | 4.850 | 7.025 | 0.990 | 0.990 |
| H2S–CO2 | RQ | 51 | 5.549 | 8.276 | 11.682 | 0.976 | 0.986 |
In Fig. 9b and c, a comparison of the GP fits with highest relative errors is shown along with IAST predictions for the other two mixtures. The figures for these mixtures are included with the same set of input features (Xspecies 1 = 0.116, and T = 200, 240, and 280 K) which had shown highest relative errors in the error heat maps previously. The highest deviation (compared to GCMC) of IAST predictions comes from the species which has more affinity towards Cu-BTC. Comparing them with the GP predictions, the GPs also have high errors but it does follow the trend of GCMC isotherms (same as P–X space). Thus, IAST predictions fail again in the mixture states for P–X–T feature space for the three mixtures. However since GPs have been trained on a fraction of the ground truth, it has the necessary information to generate the adsorption profiles close to GCMC.
In Table 4, the AL performance for all three mixtures for P–X–T feature space is shown. All the MREs are in acceptable range of 4–11%, and R2's are close to 1. The data requirement is close to 5–6% with the triple-RBF kernel providing best fit for CO2–CH4 and Xe–Kr, and a RQ for H2S–CO2. From these results, it is apparent that the GP model does a good job in emulating the adsorption isotherm at different conditions. The only section with moderate errors is the range with small concentration of species with high affinity towards the MOF structure (CO2, Xe, and H2S). Comparing this to IAST performance for the feature-spaces and mixtures (shown in Table 5), we find the errors are very high (varying from 30% to 91.09%). Therefore, the aggregate performance of AL-based isotherms are much better than IAST-based predictions.
| Mixture | Features | MRE(species 1) (in %) | MRE(species 2) (in %) |
|---|---|---|---|
| CO2–CH4 | P–X | 53.97 | 91.09 |
| Xe–Kr | P–X | 27.90 | 50.20 |
| H2S–CO2 | P–X | 25.04 | 28.69 |
| CO2–CH4 | P–X–T | 48.26 | 98.06 |
| Xe–Kr | P–X–T | 35.76 | 46.15 |
| H2S–CO2 | P–X–T | 27.93 | 63.96 |
The error maps and adsorption plots (for region with highest relative errors) for Xe–Kr and H2S–CO2 are provided in Fig. S14 to S23 in the ESI.† A similar trend in error and adsorption isotherms (like CO2–CH4) was observed for Xe–Kr. In that mixture, most of the error are in the low concentration of the species with strong affinity to Cu-BTC (Xe for Xe–Kr). For H2S–CO2 the scenario is different as the errors are more distributed in the mole fraction feature space. This is due to the nature of target adsorption distribution in the H2S–CO2 mixture where both the species have a high affinity towards the MOF. Therefore the changes in adsorption isotherm are more distributed and the errors in GP fit too gets extended or flattened out with respect to mole-fraction. This is an interesting aspect of the protocol which demonstrates that the GP can learn diverse target adsorption isotherms with very good performance. In this direction, we have also added correlation plots for all the three mixtures in the ESI, Fig. S23–S25.† These plots show the location of points sampled by the algorithm beyond the initial training set. These plots illustrate that pressure points are more frequently sampled along the boundaries of the test set range. For mole-fraction points we see a similar profile as pressure but there are more points in the middle range than pressure. We see the most uniform sampling along the temperature feature for all the three mixtures.
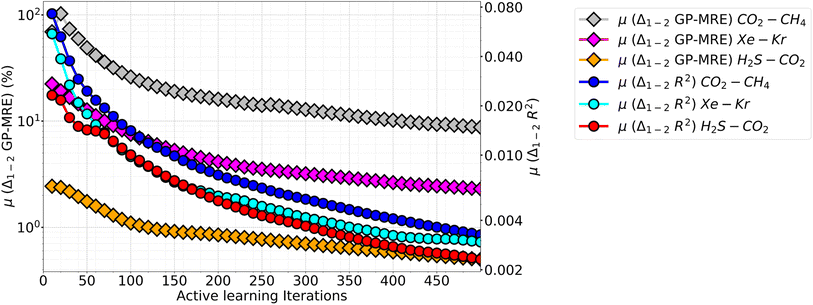
We also note an interesting observation when looking at the difference in individual species GP performance are compared for all mixtures. In Fig. 10 the mean difference between the species GP-MRE and R2 are plotted against iterations (calculated cumulatively at interval of ten points). This plot both covers the difference in GP's perceived performance (GP-MRE) and the actual performance (shown by R2) among the species. In this plot, a hierarchy in the GP-MRE and R2 difference is observed among the three mixtures. CO2–CH4 have the highest mean difference in GP-MRE and R2, followed by Xe–Kr, and then H2S–CO2. In Fig. 10, the differences in GP-MRE and R2 among the mixtures shows that CO2–CH4 has high difference in the model performance between the two species. This affects both the final performance at the AL termination as well as the total number of iterations required to meet the cut-off PAC. The difference in the individual species perceived performance creates the demand for more ground-truth data to be provided to the model. In Table 4, we observe that CO2–CH4 has higher values of MRE compared with Xe–Kr, while both mixtures take almost the same number of iterations to reach 90% PAC (78 iterations against 79). Again in Table 4, when CO2–CH4 is compared with H2S–CO2, it has slightly lower MRE, but the latter mixture took significantly less number of iterations to fulfil the PAC criteria. Going back to Fig. 10, we emphasize that CO2–CH4 inter-species model differences is followed by Xe–Kr and H2S–CO2. Therefore, Xe–Kr and H2S–CO2 are more closer in absolute values for the inter-species model difference than Xe–Kr is to CO2–CH4. Because the y-axis is shown in the log10 scale, the relative difference among mixtures looks equal for the three mixtures. Further, when AL results of the P–X feature space is taken into account (Table 2), CO2–CH4 again takes twice the number of iterations to reach 90% PAC compared to other two mixtures, while there is only 1–2% reduction is observed in the MRE values, while R2 values are in the same range as other mixtures.
All gases taken together, our results suggest AL performance is affected by the similarities in the intermolecular interactions of species in a given gas mixture. This difference in inter-species model behaviour of the GPs can also be examined via the nature of adsorbate species. Out of the five molecules in three mixture base, one is polar (H2S) while other four are non-polar (CO2, CH4, Xe, and Kr). Also, the models of CO2 and H2S have charges in their respective atoms while the models for CH4, Xe, and Kr do not carry charges.63 Therefore in CO2–CH4 mixture, both the species exhibit very different adsorbate–adsorbate interactions as well as have differences in their affinity towards the MOF. CO2 has much stronger adsorbate–adsorbate interaction as well as strong electrostatic interaction with the Cu-BTC (along with Lennard-Jones interaction). This can be demonstrated by comparing the pure component adsorption of these species. For the pure component adsorption, at 300 bar and 300 K, CO2 uptake is 777.084 mg g−1, while at those conditions the CH4 uptake in Cu-BTC is 240.84 mg g−1. This difference in adsorbate–adsorbate as well as adsorbate–MOF interaction translates itself into very different individual adsorption isotherms among these species. Therefore, the AL for individual species progresses very differently in CO2–CH4. This is reflected as a disparity in the GP-MRE of individual species and thus affects the choice of the next point to be sampled. In essence, CO2–CH4 needs more AL iterations to reach the same cut-off PAC. In case of Xe–Kr, their pure component uptakes at 200 bar and 300 K are 1494.33 and 1254.80 mg g−1, respectively. Lastly, in case of H2S–CO2, CO2 and H2S at 100 bar and 300 K have an uptake of 751.93 and 631.22 mg g−1. In the case of Xe–Kr, Xe has a higher uptake (1494.33 mg g−1) than Kr (1254.80 mg g−1) as pure components. Since both species are non-polar and noble gases, the difference can be mostly attributed to adsorbate–adsorbate interactions. Therefore, Xe demonstrates a stronger adsorbate–MOF interaction than Kr, and thus there is some disparity in the isotherms, which translates to the difference in model performance, though not in the same order as CO2–CH4. Finally, in case of H2S–CO2, the difference in both type of interaction are similar for both adsorbates and hence their respective GP models performance are very close to one another (also refer to Fig. S13†). Thus both these two mixtures have less difference in their inter-species GPs performance as they have similar inter-adsorbate and MOF–adsorbate interaction. Extending this analysis, one can envisage that a mixture of CH4 and H2S would have similar problems like that of CO2–CH4. This shows that gas mixtures based on components with similar inter-adsorbate and adsorbate–MOF interaction would have better AL results (in terms of iterations to model performance) than mixtures which have diverse adsorbate–adsorbate and adsorbate–MOF interactions.
4 Conclusions
From the analysis of gas mixture adsorption in Cu-BTC, we found that the GCMC isotherms are highly sensitive to mole fraction followed by the changes in pressure and temperature. Depending on the input feature spaces the isotherm can change from a type-I to a very different trend (first rise and then sharp decline). Thus, non-parametric surrogate models which are flexible and can emulate any target distribution are well suited to capture such trends. As shown in this work by the proposed AL protocol, a model based on GPs can be built to predict mixture adsorption in MOFs. Further, each GCMC simulation point for a gas mixture can take from a few hours to more than a day (based on RASPA calculations). On the other side, GPs only takes a few minutes to train and do the prediction, thus the method could save huge in terms of computational costs. Also, AL-based adsorption predictions are better than IAST predictions, which currently are used for multi-component adsorption prediction. The proposed algorithm has been shown to work for two different feature spaces with three different binary gas mixtures which had varying degree of adsorbate–adsorbate as well as adsorbate–adsorbent interactions. Further, AL doesn't need many training points and only with a fraction of ground truth (3–6%), it provides a very good approximation of the target adsorption. The savings in data, however can vary depending on the mixture system, and also on type and number of features. Though on most occasions, more than 90% savings in data sampling requirement were observed. While in this work only up to three features were tested, it would be interesting to find how the model will perform with more features. From the increase in the data requirement from P–X to P–X–T (almost double in % term for each mixture), one can hypothesize that addition of adsorption sensitive features to the test set may increase the requirement of training data if the desired perceived accuracy threshold performance is kept the same as that of low feature space.In this work, an perceived accuracy parameter was also introduced as a condition for the AL convergence. The parameter was inspired from the accuracy metric used for the classification tasks but here it was slightly modified to capture GP's perceived performance. It was observed that the gain in performance does not necessarily increase proportionally as more data was provided to the model. Therefore it is important to have a condition for convergence which can act as a proxy for the desired performance. One disadvantage of this approach could be that the PAC criteria only ensures an aggregate performance, i.e. majority of predictions will be in acceptable range while a small fraction, depending on the PAC limit, may underperform. While in this work singularly large deviations were not observed, given the large option of feature spaces there can be cases where deviations could become significantly large. Further, depending on the application, even moderate deviations cannot be accepted. In this direction, more research is needed to ensure a high performance expectation throughout each domains in the test set, and not just as an aggregate.
A further look could be given on the algorithm recommended sampling process too. In this work, sequential sampling of a single data point was used (only one point per iteration), but there could be methods to sample multiple points in a single iteration. Only concern is to find the policy of batching or the criteria of selecting the collection of points in the next batch. If one considers only the collection of points with highest uncertainty then many of them may fall under the same sub-space of the design space, and addition of multiple points may not bring the desired benefit one might expect. A recent work by Zavala and team successfully showed two parallel sampling schemes for Bayesian optimization, which shows promising results.74 One was based on informed partitioning of the input space using the target function. Another was the level-set partition criteria, which used a low-fidelity reference model for approximating the target function and perform the partitioning. Though AL is not an optimization problem, one might test and design novel strategies that could be transferred from these works to an adsorption problem. In another direction, calculating the next set of simulations for multiple pressure points (with other features constant) can also be explored since many MC engines or sometime even laboratory experiments could be more efficient in generating adsorption at a fixed temperature rather sampling at different temperatures. Ultimately, there can be more efficient ways to add training points and build a model with high reliability and performance. Further, the methods can be tuned based on the constraints and leverages of the ground truth evaluation procedure. In essence, there are many frontiers of the AL paradigm that could be explored to reduce computational cost and further better the performance of the surrogate models. Adsorption is an unique physical process and as more MOFs and target applications continue to emerge, it would become difficult to perform experiments to identify a MOF for a certain application. The efficiency and scale-ability of computational methods can prove valuable for these situations.
Data availability
The code written during this work is available at Github: https://github.com/mukherjee07/Active-Learning-for-multicomponent-adsorption-in-a-MOF.Conflicts of interest
There are no conflicts to declare.Acknowledgements
KM would like to thank the ND Energy's Eilers Family Graduate fellowship. EO would like to thank the Lucy Family Institute for Data and Society. All Authors gratefully acknowledge NSF CAREER Award CBET-2143346. The authors would like to acknowledge the Colón group members, specifically João Dinis Oliveira Abranches and Sanoj, for their helpful feedback on this project. We also thank the Center for Research Computing at the University of Notre Dame for computational resources.Notes and references
- M. Kondo, T. Yoshitomi, H. Matsuzaka, S. Kitagawa and K. Seki, Angew. Chem., Int. Ed. Engl., 1997, 36, 1725–1727 CrossRef CAS.
- O. K. Farha, I. Eryazici, N. C. Jeong, B. G. Hauser, C. E. Wilmer, A. A. Sarjeant, R. Q. Snurr, S. T. Nguyen, A. z. Yazaydin and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 15016–15021 CrossRef CAS PubMed.
- H. W. Langmi, J. Ren, B. North, M. Mathe and D. Bessarabov, Electrochim. Acta, 2014, 128, 368–392 CrossRef CAS.
- Z. Hu, Y. Wang, B. B. Shah and D. Zhao, Adv. Sustainable Syst., 2019, 3, 1800080 CrossRef.
- P. Boyd, A. Chidambaram, E. García-Díez, C. Ireland, T. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. Moosavi, M. Maroto-Valer, J. Reimer, J. Navarro, T. Woo, S. Garcia, K. Stylianou and B. Smit, Nature, 2019, 576, 253–256 CrossRef CAS PubMed.
- R.-B. Lin, S. Xiang, H. Xing, W. Zhou and B. Chen, Coord. Chem. Rev., 2019, 87–103 CrossRef CAS.
- J. Gonzalez, K. Mukherjee and Y. J. Colón, J. Chem. Eng. Data, 2023, 68, 291–302 CrossRef CAS.
- S. Sircar, Ind. Eng. Chem. Res., 2002, 41, 1389–1392 CrossRef CAS.
- A. Sturluson, M. T. Huynh, A. R. Kaija, C. Laird, S. Yoon, F. Hou, Z. Feng, C. E. Wilmer, Y. J. Colón, Y. G. Chung, D. W. Siderius and C. M. Simon, Mol. Simul., 2019, 45, 1082–1121 CrossRef CAS PubMed.
- P. Z. Moghadam, A. Li, X.-W. Liu, R. Bueno-Perez, S.-D. Wang, S. B. Wiggin, P. A. Wood and D. Fairen-Jimenez, Chem. Sci., 2020, 11, 8373–8387 RSC.
- N. Rampal, A. Ajenifuja, A. Tao, C. Balzer, M. S. Cummings, A. Evans, R. Bueno-Perez, D. J. Law, L. W. Bolton, C. Petit, F. Siperstein, M. P. Attfield, M. Jobson, P. Z. Moghadam and D. Fairen-Jimenez, Chem. Sci., 2021, 12, 12068–12081 RSC.
- R. B. Getman, Y.-S. Bae, C. E. Wilmer and R. Q. Snurr, Chem. Rev., 2012, 112, 703–723 CrossRef CAS PubMed.
- Q. Yang and C. Zhong, J. Phys. Chem. B, 2006, 110, 17776–17783 CrossRef CAS PubMed.
- P. Li, N. A. Vermeulen, C. D. Malliakas, D. A. Gómez-Gualdrón, A. J. Howarth, B. L. Mehdi, A. Dohnalkova, N. D. Browning, M. O'Keeffe and O. K. Farha, Science, 2017, 356, 624–627 CrossRef CAS PubMed.
- F.-X. Coudert and A. H. Fuchs, Coord. Chem. Rev., 2016, 307, 211–236 CrossRef CAS.
- Y. G. Chung, J. Camp, M. Haranczyk, B. J. Sikora, W. Bury, V. Krungleviciute, T. Yildirim, O. K. Farha, D. S. Sholl and R. Q. Snurr, Chem. Mater., 2014, 26, 6185–6192 CrossRef CAS.
- C. Wilmer, M. Leaf, C. Lee, O. Farha, B. Hauser, J. Hupp and R. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- P. Wollmann, M. Leistner, U. Stoeck, R. Grünker, K. Gedrich, N. Klein, O. Throl, W. Grählert, I. Senkovska, F. Dreisbach and S. Kaskel, Chem. Commun., 2011, 47, 5151–5153 RSC.
- S. Li, Y. G. Chung and R. Q. Snurr, Langmuir, 2016, 32, 10368–10376 CrossRef CAS PubMed.
- M. H. Hiller, J. J. Lacatena and G. Q. Miller, Hydrogen for hydroprocessing operations, National Petroleum Refiners Association, Washington, DC, 1987 Search PubMed.
- G. Sneddon, A. Greenaway and H. H. P. Yiu, Adv. Energy Mater., 2014, 4, 1301873 CrossRef.
- H. D. Frazier and A. L. Kohl, Ind. Eng. Chem., 1950, 42, 2288–2292 CrossRef CAS.
- G. Maurin, P. L. Llewellyn and R. G. Bell, J. Phys. Chem. B, 2005, 109, 16084–16091 CrossRef CAS PubMed.
- R. Q. Snurr, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1993, 97, 13742–13752 CrossRef CAS.
- G. B. Goh, N. O. Hodas and A. Vishnu, J. Comput. Chem., 2017, 38, 1291–1307 CrossRef CAS PubMed.
- K. Mukherjee and Y. J. Colón, Mol. Simul., 2021, 47, 857–877 CrossRef CAS.
- Z. Shi, W. Yang, X. Deng, C. Cai, Y. Yan, H. Liang, Z. Liu and Z. Qiao, Mol. Syst. Des. Eng., 2020, 5, 725–742 RSC.
- A. Erfani and M. Asghari, J. Chem. Technol. Biotechnol., 2020, 95, 2951–2963 CrossRef CAS.
- M. Z. Aghaji, M. Fernandez, P. G. Boyd, T. D. Daff and T. K. Woo, Eur. J. Inorg. Chem., 2016, 2016, 4505–4511 CrossRef CAS.
- Y. G. Chung, D. A. Gómez-Gualdrón, P. Li, K. T. Leperi, P. Deria, H. Zhang, N. A. Vermeulen, J. F. Stoddart, F. You, J. T. Hupp, O. K. Farha and R. Q. Snurr, Sci. Adv., 2016, 2, e1600909 CrossRef PubMed.
- A. W. Thornton, C. M. Simon, J. Kim, O. Kwon, K. S. Deeg, K. Konstas, S. J. Pas, M. R. Hill, D. A. Winkler, M. Haranczyk and B. Smit, Chem. Mater., 2017, 29, 2844–2854 CrossRef CAS PubMed.
- N. S. Bobbitt and R. Q. Snurr, Mol. Simul., 2019, 45, 1069–1081 CrossRef CAS.
- M. Pardakhti, E. Moharreri, D. Wanik, S. L. Suib and R. Srivastava, ACS Comb. Sci., 2017, 19, 640–645 CrossRef CAS PubMed.
- G. S. Fanourgakis, K. Gkagkas, E. Tylianakis, E. Klontzas and G. Froudakis, J. Phys. Chem. A, 2019, 123, 6080–6087 CrossRef CAS PubMed.
- C. M. Simon, R. Mercado, S. K. Schnell, B. Smit and M. Haranczyk, Chem. Mater., 2015, 27, 4459–4475 CrossRef CAS.
- M. Fernandez and A. S. Barnard, ACS Comb. Sci., 2016, 18, 243–252 CrossRef CAS PubMed.
- M. Fernandez, P. G. Boyd, T. D. Daff, M. Z. Aghaji and T. K. Woo, J. Phys. Chem. Lett., 2014, 5, 3056–3060 CrossRef CAS PubMed.
- B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Mol. Syst. Des. Eng., 2019, 4, 162–174 RSC.
- A. Sturluson, M. T. Huynh, A. H. P. York and C. M. Simon, ACS Cent. Sci., 2018, 4, 1663–1676 CrossRef CAS PubMed.
- B. J. Befort, R. S. DeFever, G. M. Tow, A. W. Dowling and E. J. Maginn, Machine Learning Directed Optimization of Classical Molecular Modeling Force Fields, 2021 Search PubMed.
- R. Ma, Y. J. Colón and T. Luo, ACS Appl. Mater. Interfaces, 2020, 12, 34041–34048 CrossRef CAS PubMed.
- G. M. Cooper and Y. J. Colón, Mol. Syst. Des. Eng., 2023, 8(8), 1049–1059 RSC.
- F. Ricci, L. Rokach and B. Shapira, in Recommender Systems Handbook, 2010, vol. 1–35, pp. 1–35 Search PubMed.
- D. Cohn, Z. Ghahramani and M. Jordan, Advances in Neural Information Processing Systems, 1994 Search PubMed.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175 Search PubMed.
- K. S. Walton and D. S. Sholl, AIChE J., 2015, 61, 2757–2762 CrossRef CAS.
- R. Krishna and J. M. van Baten, ACS Omega, 2021, 6, 15499–15513 CrossRef CAS PubMed.
- G. Sivaraman, N. E. Jackson, B. Sanchez-Lengeling, Á. Vázquez-Mayagoitia, A. Aspuru-Guzik, V. Vishwanath and J. J. de Pablo, Mach. Learn.: Sci. Technol., 2020, 1, 025015 Search PubMed.
- V. Vovk, in Kernel Ridge Regression, ed. B. Schölkopf, Z. Luo and V. Vovk, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 105–116 Search PubMed.
- S. Suthaharan, in Support Vector Machine, Springer US, Boston, MA, 2016, pp. 207–235 Search PubMed.
- S. Myren and E. Lawrence, Stat. Anal. Data Min., 2021, 14, 606–623 CrossRef.
- A. Kamath, R. A. Vargas-Hernández, R. V. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148(24), 241702 CrossRef PubMed.
- E. Uteva, R. S. Graham, R. D. Wilkinson and R. J. Wheatley, J. Chem. Phys., 2018, 149, 174114 CrossRef PubMed.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, On-the-Fly Active Learning of Interpretable Bayesian Force Fields for Atomistic Rare Events, 2019 Search PubMed.
- J. E. Santos, M. Mehana, H. Wu, M. Prodanović, Q. Kang, N. Lubbers, H. Viswanathan and M. J. Pyrcz, J. Phys. Chem. C, 2020, 124, 22200–22211 CrossRef CAS.
- K. Mukherjee, A. W. Dowling and Y. J. Colón, Mol. Syst. Des. Eng., 2022, 7, 248–259 RSC.
- E. Osaro, K. Mukherjee and Y. J. Colón, Ind. Eng. Chem. Res., 2023, 62(33), 13009–13024 CrossRef CAS.
- D. O. Abranches, E. J. Maginn and Y. J. Colón, AIChE J., 2023, 69(8), e18141 CrossRef CAS.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006 Search PubMed.
- A. L. Myers and J. M. Prausnitz, AIChE J., 1965, 11, 121–127 CrossRef CAS.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- B. Eggimann, A. Sunnarborg, H. Stern, A. Bliss and J. Siepmann, Mol. Simul., 2014, 40, 101–105 CrossRef CAS.
- S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- J. M. Castillo, T. J. H. Vlugt and S. Calero, J. Phys. Chem. C, 2008, 112, 15934–15939 CrossRef CAS.
- Q. Yang and C. Zhong, J. Phys. Chem. B, 2006, 110, 17776–17783 CrossRef CAS PubMed.
- S. Wang, Q. Yang and C. Zhong, Sep. Purif. Technol., 2008, 60, 30–35 CrossRef CAS.
- C. M. Simon, B. Smit and M. Haranczyk, Comput. Phys. Commun., 2016, 200, 364–380 CrossRef CAS.
- D. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- J. D. Novaković, A. Veljović, S. S. Ilić, Ž. Papić and M. Tomović, Theory Appl. Math. Comput. Sci., 2017, 7, 39 Search PubMed.
- S. J. Tan, L. Liu and J. W. Chew, Langmuir, 2021, 37, 6754–6764 CrossRef CAS PubMed.
- L. Hamon, E. Jolimaître and G. D. Pirngruber, Ind. Eng. Chem. Res., 2010, 49, 7497–7503 CrossRef CAS.
- X. Cai, F. Gharagheizi, L. W. Bingel, D. Shade, K. S. Walton and D. S. Sholl, Ind. Eng. Chem. Res., 2021, 60, 639–651 CrossRef CAS.
- L. D. González and V. M. Zavala, Comput. Chem. Eng., 2023, 170, 108110 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00106g |
| This journal is © The Royal Society of Chemistry 2023 |