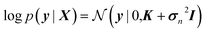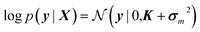Open Access Article
Open Access ArticleSpeeding up high-throughput characterization of materials libraries by active learning: autonomous electrical resistance measurements†
Felix
Thelen
 ,
Lars
Banko
,
Lars
Banko
 ,
Rico
Zehl
,
Rico
Zehl
 ,
Sabrina
Baha
,
Sabrina
Baha
 and
Alfred
Ludwig
and
Alfred
Ludwig
 *
*
Chair for Materials Discovery and Interfaces, Institute for Materials, Ruhr University Bochum, Universitätsstraße 150, 44780 Bochum, Germany. E-mail: alfred.ludwig@rub.de
First published on 19th September 2023
Abstract
High-throughput experimentation enables efficient search space exploration for the discovery and optimization of new materials. However, large search spaces, e.g. of compositionally complex materials, require decreasing characterization times significantly. Here, an autonomous measurement algorithm was developed, which leverages active learning with a Gaussian process model capable of iteratively scanning a materials library based on the highest uncertainty. The algorithm is applied to a four-point probe electrical resistance measurement device, frequently used to obtain indications for regions of interest in materials libraries. Ten libraries with different complexities of composition and property trends are analyzed to validate the model. By stopping the process before the entire library is characterized and predicting the remaining areas, the measurement efficiency can be improved drastically. As robustness is essential for autonomous measurements, intrinsic outlier handling is built into the model and a dynamic stopping criterion based on the mean predicted covariance is proposed. A measurement time reduction of about 70–90% was observed while still ensuring an accuracy above 90%.
Introduction
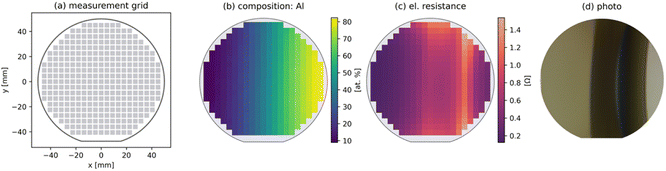
The emerging of complex materials such as high entropy alloys (HEA) or compositionally complex solid solutions (CCSS) results in an immense multidimensional search space, making the use of efficient research methods and strategies mandatory.1 One approach of dealing with this complexity are combinatorial materials science and high-throughput experimentation, which involve synthesizing a large number of materials in parallel and performing rapid automated characterization of a variety of materials properties.2High-throughput experiments usually consist of three main stages, starting with the combinatorial fabrication of hundreds of well-defined chemical compositions in the form of thin-film materials libraries.3 These can either have a continuous compositional gradient, e.g., generated by co-deposition magnetron sputtering,4 or can be ordered discretely, i.e., by inkjet printing techniques.5,6 An example of a co-sputtered materials library is shown in Fig. 1. After fabrication, the libraries are characterized by multiple techniques ideally in parallel or by automated serial methods. These include, first, identification of the chemical compositions and their crystallographic structure, e.g., by energy dispersive X-ray analysis (EDX) and X-ray diffraction (XRD) respectively. Second, functional properties are investigated based on the use cases of the fabricated materials, which include for example electrical resistance or band gap measurements.1 Thereby, most high-throughput characterization instruments consist of an automated positioning system which moves a sensor system over the materials library. After characterization, the large amounts of data generated along these steps are then used to plan follow-up experiments. Many characterization techniques remain, however, rather time-consuming compared to the synthesis process, e.g., performing XRD measurements for hundreds of measurement areas on a single library can take 12–14 hours.7
Especially for the last stage, the application of machine learning and data mining under the paradigm of materials informatics8,9 has contributed significantly to navigate, explore, and exploit the high-dimensional materials search space more efficiently. In order to decrease the necessary time for high-throughput characterization, active learning together with Gaussian process regression can be leveraged to autonomously determine materials properties across libraries. Instead of measuring all, typically hundreds of measurement areas of a library consecutively with fixed coordinates, the algorithm decides the measurement sequence by building and updating a Gaussian process model during the procedure. Once the model's prediction is accurate enough, the process can be terminated, decreasing the total measurement time drastically: related work10,11 indicates a 10-fold time reduction. An essential factor for autonomous characterization is the robustness of a model as it needs to be applicable to a wide variety of materials and measurement procedures can be affected by systematic measurement errors.
To investigate the possibilities and limitations of this approach, the algorithm is tested on a custom-built high-throughput test-stand12 measuring the electrical resistance of materials libraries using the four-point probe method. The electrical resistivity in alloys is dependent on the crystal structure and is further influenced by all defects in the materials as electrons are scattered at lattice defects like voids, impurities, dislocations, and grain boundaries.7 Therefore, a mapping of the electrical resistance of a library can indicate different phase zones/regions and their boundaries1,12 and is thus a useful descriptor for finding areas of interest.
Ten libraries comprising a variety of metallic materials systems fabricated with different methods such as co- and multilayer-sputtering, were measured and analyzed to validate the performance of the developed algorithm.
Methods
Four-point probe measurement
Thin film resistance is frequently measured by the four-point probe method.13,14 The probe consists of four spring contact pins (Feinmetall F238, d < 0.3 mm) with an equidistant spacing of about 0.5 mm. Due to the attachment to a computer-controlled stage movable in x, y, and z-direction (UHL F9S-3-M), the vertical as well as the horizontal positioning of the pins with respect to the sample can be adjusted on the micrometer level. By using a source meter (Keithley 2400), a direct current I0 is induced in the two outer contact pins while the voltage V is measured at the two inner pins. In order to accommodate for varying pin orientations resulting from the touchdown of the probe, each measurement area on the library is measured three times and during each touch down, ten measurements are conducted to decrease measurement noise. The components are controlled via a custom application implemented in Python running on an Intel® Core™ i7 8 GB RAM Windows PC.12Active learning in materials discovery
In the majority of machine learning approaches, a learner is treated as a passive recipient of the data by providing the whole training datasets at once.15 In contrast, active learning differs from that approach by allowing an algorithm to choose the data from which it learns, resulting in a higher performance with less training effort.16 In an active learning process, a so called surrogate model is iteratively choosing from a pool of unknown training data via a query algorithm. The selected instances are then passed to an oracle (e.g., a human annotator or a measurement system), which assigns the instances with a label. After labelling, the model is updated with the query result.17 Depending on the intended purpose of the algorithm, a variety of learning models are available, e.g., support vector machines, naïve Bayes, decision trees or neural networks.15 In the regression setting, a Gaussian process is used most often due to its flexibility and ability of uncertainty quantification independently from the actual observations.18,19 A Gaussian process is a generalization of the multivariate Gaussian probability distribution, which describes the relation of n-random variables depending on a mean vector μ and a covariance matrix Σ. In stochastic processes like the Gaussian process, every point of a function (xi|f(xi)) is treated as a single random variable. These points can then be approximated by adjusting the mean vector and covariance matrix of the Gaussian process, described in this setting as the mean function m(x) and covariance function k(x, x′).20 In terms of the mean function, m(x) = 0 is most often assumed, as the data can be standardized, and the Gaussian process is generally flexible enough to model the mean sufficiently well.21 The covariance function consists of a kernel function, which returns the similarity of two random variables and therefore controls the function's shape. There are a number of different kernels, each with its own set of hyperparameters, the most common being the squared exponential (SE) kernel. Other kernels with a higher number of parameters are the Matérn kernels and the rational quadratic kernel, which generally provide a more flexible fit. The kernel needs to be selected depending on the use case.19,22,23After optimization of the hyperparameters, the predictions of a Gaussian process, given by the posterior mean and covariance, can be used to determine which additional training data instance can result in the highest model improvement. As the covariance is a measure of uncertainty of the Gaussian process model, selecting the instance with the highest covariance reduces the overall uncertainty efficiently.24
This learning approach is especially useful in scenarios in which labels are expensive or time-consuming to generate. Therefore, active learning fits the conditions of materials discovery with its mostly elaborate measurement techniques.25 Examples of applications of active learning for materials discovery can be found in ref. 26–28.
Closely related to active learning is Bayesian optimization, which is in comparison more frequently applied in the field of materials discovery. In contrast to active learning, instead of learning an underlying function as efficiently as possible, Bayesian optimization aims to maximize a function globally.19 As materials discovery most often has the aim to identify materials with optimized properties while reducing the number of experiments, Bayesian optimization is applied frequently in literature.10,25,29–34
Active learning for autonomous measurement processes
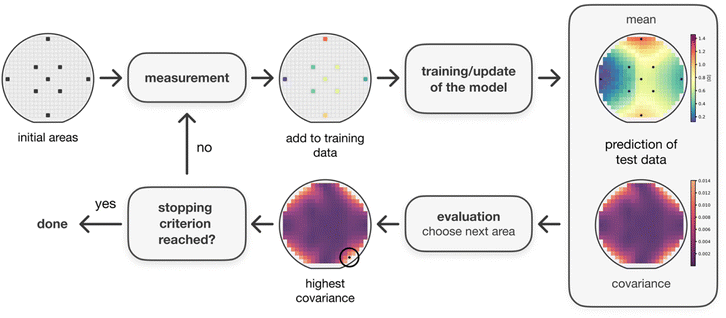
The measurement algorithm was implemented in Python and bases on a Gaussian process TensorFlow implementation called GPflow.35Fig. 2 shows the structure of the algorithm. Before incorporating any training data, the Gaussian process predicts the same mean and covariance for the entire library. Therefore, the procedure is initialized with nine predefined measurement areas evenly distributed across the library. A too small number of initialization areas can result in divergence of the process, a too large number reduces the achieved efficiency improvement by the algorithm. More information about the initialization areas can be found in the ESI.† Automatic relevance determination was used to increase the flexibility of the model. The initialization measurement areas are labelled by the oracle afterwards, which means the resistance is measured by the described setup. Therefore, the measured resistances are used as labels for the model. The Gaussian process is then trained on the acquired data by adjusting the model's hyperparameters using marginal likelihood optimization. The optimization is handled by a L-BFGS-B optimizer inside GPflow. The resulting model is subsequently used to predict the unmeasured areas afterwards, and the next area is selected based on the predicted covariance. This process continues until a stopping criterion is met.Results and discussion
To assess the ability of the algorithm to perform well on a variety of libraries, the ground truth for ten test libraries with different materials systems was fully measured in advance, so that the accuracy of the prediction at each iteration can be determined via the coefficient of determination R2. The tests were performed on a simulated version of the described device, but the developed algorithm was implemented into the physical device as well. Table 1 shows an overview of the measured libraries, details can be found in the ESI.† The test libraries were selected in order to cover different fabrication methods, number of constituents and materials systems.| Material system | Sputter method | Substrate | T deposit | T anneal |
|---|---|---|---|---|
| Co–Fe–Mo–Ni–V | Co-sputtering | Si + SiO2 | 25 °C | — |
| Co–Fe–Mo–Ni–W–Cu | Co-sputtering | Si + SiO2 | 25 °C | — |
| Co–Cr–Fe–Mo–Ni | Co-sputtering | Si + SiO2 | 25 °C | — |
| Cr–Fe–Mn–Mo–Ni | Co-sputtering | Si + SiO2 | 25 °C | — |
| Co–Cr–Fe–Mn–Mo | Co-sputtering | Si + SiO2 | 25 °C | — |
| Ni–Al | Co-sputtering | Si + SiO2 | 25 °C | — |
| Co–Cr–W 1 | Multilayer | Al2O3 | 150 °C | 900 °C |
| Co–Cr–W 2 | Multilayer | Al2O3 | 150 °C | 750 °C |
| Co–Cr–W 3 | Multilayer | Al2O3 | 25 °C | 600 °C |
| Co–Cr–Mo | Multilayer | Al2O3 | 25 °C | 900 °C |
To increase the robustness of the algorithm, modifications to the standard Gaussian process were tested, ranging from the incorporation of the substrate information into the training data to including the measurement variance into the model. Furthermore, a kernel test was done by comparing the performance of the Gaussian process with various kernel functions.
Choice of input parameters
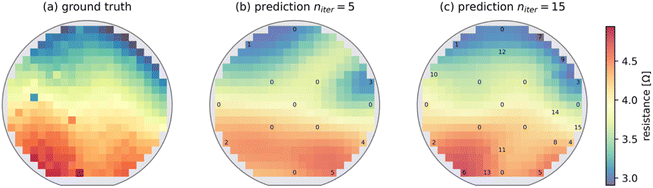
In order to give the active learning algorithm additional information of the library to be measured, the chemical composition determined by EDX (Oxford X-act, accuracy 1 at%) was used as an input for the algorithm. Since EDX is normally done directly after deposition of the library, the composition data is available prior to the resistance measurements.Fig. 3 shows two iterations of the autonomous measurement on the example of the Co–Cr–Fe–Mn–Mo library. After measuring nine areas for initialization, the algorithm first selects areas at the edge of the library, before concentrating on the inner parts. While parts of the library are still incorrectly predicted after five iterations, the ground truth and the prediction are almost visually identical after 15 iterations.
Depending on acceleration voltage and materials, the electron beam reaches different depths up to several micrometers. Therefore, not only the deposited elements, but also the substrate material can be included in the analysis. This can support the autonomous resistance measurements, as substrate information can generally be correlated with film thickness, which in turn influences the electrical resistance.
The performance of a standard Gaussian process with SE kernel was observed to test the influence of the selection of constituents. One model was trained only on the compositional information of the deposited elements, and another on the composition data including the substrate contents. The (normalized) x- and y-coordinates were added to the training data as well, to help the Gaussian process to model the thickness as a hidden dimension, which is an x–y-dependent property. Input and output standardization were used to improve numerical stability. The mean function of the Gaussian process was set to zero, as the model needs to be applicable to a variety of material systems and there is no physical equation of the resistance distribution. The results of the first 250 training iterations are shown in Fig. 4. For more iterations, the Gaussian process tends to memorize the added training data, generally referred to as overfitting. Therefore, following iterations are neglected.
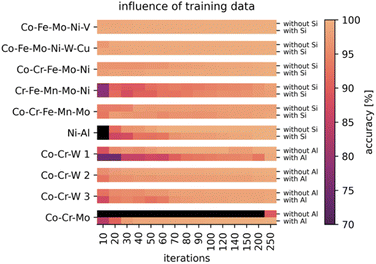
For most tested libraries, an accuracy higher than 90% after 50 iterations was observed using the standard implementation of the Gaussian process. The highest performance was achieved for the measurement of libraries which generally show unidirectional resistance gradients (the first five in Table 1).
Including the substrate information in the training data was mostly found to either not affect the performance or slightly improve the accuracy and robustness of the prediction. This is because the electrical resistance depends both on composition and thickness. Only in one case (Co–Cr–Mo) of the tested 10 different libraries the inclusion of substrate information showed a substantially improved result. Therefore, in case of this material, the resistance is mainly dependent on the thickness instead of the composition.
For the libraries Co–Cr–W 1 as well as Ni–Al, the Gaussian process shows a decrease in performance when trained on the substrate information, indicating that the resistance mainly depends on the composition. However, automatic relevance determination enables the Gaussian process to assign less weight to the importance of the substrate information, therefore still enabling a sufficient fit. Additional noise brought into the training data by the substrate information is not visibly affecting the performance. Consequently, because including thickness information via the substrate content was shown to enable a more robust prediction, as much information as available should be added to the training data.
Incorporation of the measurement standard deviation into the model
There are generally two types of measurement errors which can occur during a four-point probe measurement. Due to the spring mechanism of the sensor pins, the contact to the sample can be slightly different between touchdowns, resulting in resistance deviations of 0.1–2%. Up to 1–3 times during an entire library mapping, the contact pins can touch each other, resulting in a short circuit which lets the source meter output values in the positive or negative MΩ-range. To account for these errors, every area is measured three times, and during each contact ten resistance values are recorded. A standard Gaussian process is unable to work with ambiguous data in which multiple output data points are assigned to the same input data, which is why the mean of the conducted measurements is normally calculated prior to training. However, with this approach, available information about the reliability of the measurement results is lost. The solution is to modify the marginal likelihood of the Gaussian process. In a standard Gaussian process, the hyperparameters are estimated by maximizing the marginal likelihood given bywhere X and y are the input and output training data, K denotes the covariance matrix and σn2 the noise variance. A mean of μ = 0 is normally assumed.20 Instead of determining the noise variance via hyperparameter optimization, the variances σm2 of the output training data points obtained by the 30 individual measurements can be used to compute the marginal likelihood of the model.35
This enables the Gaussian process to automatically weigh the measurement results based on their reliability without modifying its architecture significantly. With this modification, the model is capable of dealing with homoscedastic as well as heteroscedastic aleatoric uncertainty, which originate in the respective measurement setup as a result of dirty or rough surfaces and the touching of the contact pins respectively.
Fig. 5(a) compares the standard Gaussian process to the one trained with the measurement variance over the first 250 iterations. A full visualization can be found in the ESI.† Without outliers, both implementations show almost identical results, the mean deviation of accuracy across all tested libraries is 0.2%. This small improvement originates from the ability of the algorithm to detect minor measurement errors caused by variations of the pin's orientation during each individual measurement. In order to investigate the performance with higher measurement noise, the accidental short-circuit of the pins was simulated by adding randomly generated noise in the range of 0.8–1.2 MΩ to three measurement areas across all libraries. The resulting resistance distributions can be found in the ESI.† In this simulation, it is assumed that one out of three touchdowns feature ten resistance measurement results with a large variance. The resulting performance of the vanilla Gaussian process and the one based on the measurement variance is shown in Fig. 5(b).
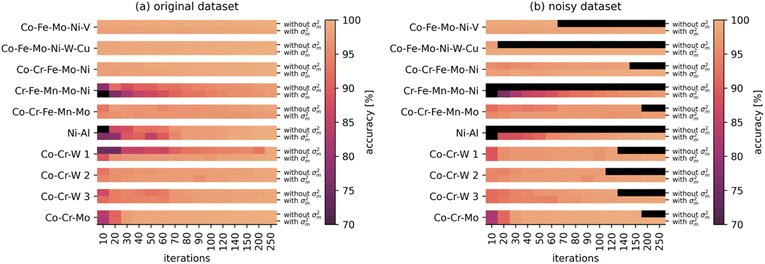 | ||
| Fig. 5 Performance of the standard Gaussian process and the one with information about the measurement variance σm2. Both algorithms show comparable performances when trained on data with low noise levels (a), but when three artificially added random outliers are added (b), the prediction of the standard Gaussian process fails as soon as an area with an outlier is reached.‡ | ||
While the standard Gaussian process fails predicting the distribution as soon as an outlier is measured, the active learning algorithm with integrated measurement variance continues the optimization once an outlier is reached, as it is capable of automatically weighting the output training data relative to its reliability.
Kernel test
As the kernel of a Gaussian process controls the shape of the regression function, choosing an appropriate kernel is important for ensuring a robust operation of the autonomous measurement. Here, four kernels are compared, the SE kernel, rational quadratic (RQ) kernel, and two kernels of the Matérn class (with ν = 3/2, M32 and ν = 5/2, M52).Since the algorithm needs to be suitable for a large variety of different materials and libraries, sufficient adaptability and stability are the most important factors for choosing the kernel. Each library was autonomously measured with each kernel and ranked by their performance. The results are summarized in Table 2.
| Material system | Rated kernel performance | n iters until stopped | ||||
|---|---|---|---|---|---|---|
| SE | RQ | M32 | M52 | Optimal | Criterion | |
| Co–Fe–Mo–Ni–V | 3 | 0 | 3 | 4 | 20 | 41 |
| Co–Fe–Mo–Ni–W–Cu | 3 | 2 | 1 | 4 | 10 | 41 |
| Co–Cr–Fe–Mo–Ni | 2 | 0 | 3 | 4 | 16 | 46 |
| Cr–Fe–Mn–Mo–Ni | 2 | 0 | 3 | 4 | 35 | 47 |
| Co–Cr–Fe–Mn–Mo | 2 | 1 | 4 | 3 | 30 | 41 |
| Ni–Al | 3 | 3 | 4 | 2 | 80 | 88 |
| Co–Cr–W 1 | 3 | 4 | 2 | 2 | 40 | 41 |
| Co–Cr–W 2 | 3 | 3 | 4 | 4 | 50 | 52 |
| Co–Cr–W 3 | 3 | 2 | 2 | 4 | 80 | 100 |
| Co–Cr–Mo | 3 | 3 | 2 | 4 | 35 | 49 |
| Mean | 2.7 | 1.8 | 2.8 | 3.5 | ||
The accuracy improvement over the iterations can be found in the ESI.† Except for the RQ kernel, the performances of the different kernels across all materials libraries were found being very similar. While there was no kernel performing best for each of the ten libraries tested, the Matérn kernels were found to have slightly better prediction accuracy. Reasons for this are their larger set of hyperparameters and the resulting greater flexibility. The rational quadratic kernel on the other hand was the only kernel unable to approximate all libraries and failed in four occasions entirely. For future uses of the algorithm, the Matérn52 kernel was chosen.
Stopping criteria
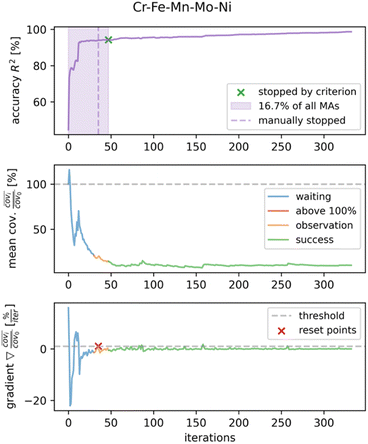
By formulating a suitable stopping criterion, the measurement process can be terminated before all areas are measured, thus improving the efficiency of the measurement process. A robust implementation is the most important factor when choosing a stopping criterion, as it needs to be applicable for a wide variety of libraries and directly influences the final accuracy of the measurement. Outside the test environment, the accuracy of the algorithm (e.g., quantified by the coefficient of determination) cannot be used as a stopping criterion, since the ground truth is unknown prior to the actual measurement. Therefore, independent stopping criteria need to be considered. A static approach is to stop the autonomous measurement after a specific number of iterations determined by testing of a variety of different libraries. However, given the large variety of materials to characterize with the resistance measurement, it is unlikely to find a quantity of iterations suitable for all experiments. Another approach which is easy to implement is a human-in-the-loop,10 who can stop the measurement process by interacting with a graphical user interface. This supervisor can then judge the quality of the optimization based on the current state, which requires the supervisor's attention and availability at all times.In order to overcome this, a dynamic stopping criterion based on the predicted uncertainty of the Gaussian process is proposed. However, simply defining an uncertainty threshold under which the process is terminated is not applicable either, as each measured library will have a different range of uncertainties depending on the noise level of the measurement and potential outliers. Therefore, the uncertainty over the training iterations needs to be observed relative to the initial uncertainty. The stopping logic is shown in Fig. 6 on the example of the Co–Cr–Fe–Mo–Ni library. The (unknown) accuracy of the optimization process, the normalized mean covariance predicted by the Gaussian process as well as the numerically determined gradient of the normalized mean covariance are plotted over the training iterations.
After initialization of the Gaussian process, 30 areas are measured independent of the performance ensuring a basic approximation of the dataset. Afterwards, the normalized predicted covariance of each iteration is observed. If the covariance of the current iteration is smaller than the initial covariance, the numeric derivative of the normalized mean covariance is calculated, and its progression is observed over the next ten iterations. This criterion is driven by the notion, that in order to terminate the process, the model at least needs to have an uncertainty lower than the one of the initial iteration. If the model continues to improve its fit over the next ten iterations (indicated by a steady decrease in the mean covariance), the measurement process is stopped. This is determined by observing the gradient of the mean covariance, specifically by ensuring that it stays below the empirically found threshold of 1% per iteration. Otherwise, if the gradient is positive, the observation is reset and at least ten additional measurements are taken until the next termination is possible.
Visualizations of the stopping criterion applied to the other libraries can be found in the ESI.†Table 2 compares the number of iterations determined via the shown stopping criterion and the optimal stopping decision based on observing the accuracy of the algorithm until it hits 90% accuracy as well as a visual representation of the prediction. In most cases, the developed stopping criterion is overestimating the number of measurements to perform by a factor of 1.5–4. Although this can be finetuned by changing the fixed number of initial iterations or the number of iterations in which the mean covariance is supposed to decrease, this behavior is beneficial for this early implementation of the algorithm. In order to apply autonomous measurements to real-world every-day scientific workflow, enough trust in this technology needs to be established, that is why higher safety margins are useful during early adoption. However, for most tested libraries, the autonomous measurement could ideally be stopped after 6–16% of the normally measured areas of a library without a significant loss in quality. This applies especially to the tested co-sputtered HEA libraries, which feature uniform resistance gradients with less resistance variations. Less good predictions were obtained on the libraries Ni–Al and Co–Cr–W 3. Reasons for this could be missing information, e.g., on surface oxidation or phase formation, in the training data. For further studies, the incorporation of visual or crystal structure information could help improving the prediction in those cases. An analysis of the visual information of a library could also improve the selection of initial measurement areas.
Conclusions
The presented active learning approach for autonomous measurements shows great potential in increasing the efficiency of combinatorial experiments. Depending on the measured materials library, a measurement time reduction of about 70–90% was observed when considering the optimal iteration for stopping the process. As there is no criterion resulting in the optimal stopping for every experiment, the number of measurements to perform are increased by a factor of 1.4–4 when using the developed dynamic stopping criterion. The autonomous measurement procedure was implemented into the existing measurement device enabling faster characterization for newly developed materials.In order to gain additional insight and trust into the autonomous measurement procedure, the performance of the method can be evaluated in a longtime study while still measuring the entire library and therefore not taking the risk of less accurate or even wrong experiment results. Despite the achieved high efficiency improvement, the autonomous measurement only decreases the absolute measurement duration by about 30–40 minutes due to the already fast four-point probe measurement procedure. This is still important when a multitude of libraries needs to be measured as fast as possible, and the implementation is part of a (semi)autonomous experimentation campaign. However, the application into materials characterization devices demanding much more time can result in even higher absolute efficiency improvements. An example are temperature-dependent resistance measurements, where temperature cycling is inherently slow with 20–50 hours36 depending on the number of temperature steps and the temperature interval. In addition, the widely used EDX or XRD measurement techniques can profit from active learning optimization as well. Further progress in these areas depends on manufacturers, who need to provide application programming interfaces (APIs) for their highly specialized devices, which would enable intervening into the measurement processes via custom made software.
Data availability
Electronic Supplementary Information (ESI), the source code, the composition and resistance data of this study as well as animations of the optimization processes are publicly available at https://pub.mdi.ruhr-uni-bochum.de/rubric/active-learning-resistance or at https://10.5281/zenodo.8349729.Author contributions
F. Thelen: conceptualization, data curation, formal analysis, investigation, ML fabrication, software, validation, visualization, writing – original draft. L. Banko: conceptualization, validation, supervision, writing – review & editing. R. Zehl: materials library fabrication, investigation, writing – review and editing. S. Baha: materials library fabrication, writing – review and editing. A. Ludwig: conceptualization, resources, writing – review and editing, supervision, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported from different projects. A. Ludwig and F. Thelen acknowledge funding from Mercator Foundation, Mercur Project DIMENSION (Ex-2021-0034) and from the Zentrales Innovationsprogramm Mittelstand (ZIM) KK5380601ZG1. Funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project 190389738 are acknowledged by R. Zehl and DFG Project LU1175/31-1 by S. Baha. For their support in synthesizing the material libraries, the authors would like to thank the student research assistants Katherine Guzey, Cedric Benedict Kaiser and Annika Gatzki. ZGH at Ruhr-University Bochum is acknowledged for the use of the scanning electron microscope.Notes and references
- A. Ludwig, npj Comput. Mater., 2019, 5, 70 CrossRef.
- H. Koinuma and I. Takeuchi, Nat. Mater., 2004, 3, 429–438 CrossRef CAS PubMed.
- P. J. McGinn, ACS Comb. Sci., 2019, 21, 501–515 CrossRef CAS PubMed.
- J. T. Gudmundsson and D. Lundin, in High Power Impulse Magnetron Sputtering, ed. D. Lundin, T. Minea and J. T. Gudmundsson, Elsevier, 2020, pp. 1–48 Search PubMed.
- X. Liu, Y. Shen, R. Yang, S. Zou, X. Ji, L. Shi, Y. Zhang, D. Liu, L. Xiao, X. Zheng, S. Li, J. Fan and G. D. Stucky, Nano Lett., 2012, 12, 5733–5739 CrossRef CAS.
- J. M. Gregoire, L. Zhou and J. A. Haber, Nat. Synth., 2023, 2(6), 493–504 CrossRef.
- S. Thienhaus, D. Naujoks, J. Pfetzing-Micklich, D. König and A. Ludwig, ACS Comb. Sci., 2014, 16, 686–694 CrossRef CAS.
- K. Rajan, Mater. Today, 2005, 8, 38–45 CrossRef CAS.
- S. Ramakrishna, T.-Y. Zhang, W.-C. Lu, Q. Qian, J. S. C. Low, J. H. R. Yune, D. Z. L. Tan, S. Bressan, S. Sanvito and S. R. Kalidindi, J. Intell. Manuf., 2019, 30, 2307–2326 CrossRef.
- A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. DeCost, S. Sarker, C. Oses, C. Toher, S. Curtarolo, A. V. Davydov, R. Agarwal, L. A. Bendersky, M. Li, A. Mehta and I. Takeuchi, Nat. Commun., 2020, 11, 5966 CrossRef CAS.
- M. Stricker, L. Banko, N. Sarazin, N. Siemer, J. Neugebauer and A. Ludwig, arXiv, preprint, arXiv:2212.04804, 2022, 10.48550/arXiv.2212.04804 Search PubMed.
- S. Thienhaus, S. Hamann and A. Ludwig, Sci. Technol. Adv. Mater., 2011, 12, 054206 CrossRef.
- F. M. Smits, Bell Syst. Tech. J., 1958, 37, 711–718 CrossRef.
- D. Dew-Hughes, A. H. Jones and G. E. Brock, Rev. Sci. Instrum., 2004, 30, 920–922 CrossRef.
- A. Krishnakumar, Technical Reports, University of California Search PubMed.
- S. Tong, Dissertation, Stanford University, 2001.
- B. Settles, Computer Sciences Technical Report Search PubMed.
- X. Yue, Y. Wen, J. H. Hunt and J. Shi, IEEE Trans. Autom. Sci. Eng., 2021, 18, 36–46 Search PubMed.
- E. Brochu, V. M. Cora and N. De Freitas, arXiv, preprint, arXiv:1012.2599, 2010, DOI:10.48550/arXiv.1012.2599.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, Massachusetts, 2006 Search PubMed.
- K. P. Murphy, Machine Learning: A Probabilistic Perspective, The MIT Press, Cambridge, London, 2012 Search PubMed.
- D. Duvenaud, The Kernel Cookbook: Advice on Covariance functions, https://www.cs.toronto.edu/%7Eduvenaud/cookbook/, accessed 01.06 2023 Search PubMed.
- B. Matérn, Spatial Variation, Springer Verlag Berlin-Heidelberg GmbH, Enebyberg, 2nd edn, 2013, vol. 36 Search PubMed.
- L. Sun and X. Wang, in 2010 International Conference on Machine Learning and Cybernetics, 2010, vol. 1, pp. 161–166 Search PubMed.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, npj Comput. Mater., 2019, 5, 21 CrossRef.
- M. M. Noack, K. G. Yager, M. Fukuto, G. S. Doerk, R. Li and J. A. Sethian, Sci. Rep., 2019, 9, 11809 CrossRef PubMed.
- Y. Tian, T. Lookman and D. Xue, Chin. Phys. B, 2021, 30, 050705 CrossRef.
- H. S. Stein, A. Sanin, F. Rahmanian, B. Zhang, M. Vogler, J. K. Flowers, L. Fischer, S. Fuchs, N. Choudhary and L. Schroeder, Curr. Opin. Electrochem., 2022, 35, 101053 CrossRef CAS.
- B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber, M. Aykol, S. K. Suram and J. M. Gregoire, Chem. Sci., 2020, 11, 2696–2706 RSC.
- J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor, T. Löffler, V. A. Mints, L. Banko, M. Arenz, A. Savan, W. Schuhmann, A. Ludwig and J. Rossmeisl, Angew. Chem., 2021, 133, 24346–24354 CrossRef.
- A. McDannald, M. Frontzek, A. T. Savici, M. Doucet, E. E. Rodriguez, K. Meuse, J. Opsahl-Ong, D. Samarov, I. Takeuchi, W. Ratcliff and A. G. Kusne, Appl. Phys. Rev., 2022, 9, 021408 CAS.
- Z. del Rosario, M. Rupp, Y. Kim, E. Antono and J. Ling, J. Chem. Phys., 2020, 153, 024112 CrossRef PubMed.
- B. P. MacLeod, F. G. L. Parlane, T. D. Morrissey, F. Häse, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. E. Yunker, M. B. Rooney, J. R. Deeth, V. Lai, G. J. Ng, H. Situ, R. H. Zhang, M. S. Elliott, T. H. Haley, D. J. Dvorak, A. Aspuru-Guzik, J. E. Hein and C. P. Berlinguette, Sci. Adv., 2020, 6(20), eaaz8867 CrossRef CAS.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- A. G. d. G. Matthews, M. van der Wilk, T. Nickson, K. Fujii, A. Boukouvalas, P. Leon-Villagra, Z. Ghahramani and J. Hensman, J. Mach. Learn. Res., 2017, 18, 1–6 Search PubMed.
- S. Thienhaus, C. Zamponi, H. Rumpf, J. Hattrick-Simpers, I. Takeuchi and A. Ludwig, MRS Online Proc. Libr., 2005, 894, LL06-06 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00125c |
| ‡ A detailed version of the training accuracy and the noiseless and noisy training data can be found in the ESI. |
| This journal is © The Royal Society of Chemistry 2023 |