Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Using GPT-4 in parameter selection of polymer informatics: improving predictive accuracy amidst data scarcity and ‘Ugly Duckling’ dilemma†
Kan
Hatakeyama-Sato
 *a,
Seigo
Watanabe
*a,
Seigo
Watanabe
 b,
Naoki
Yamane
c,
Yasuhiko
Igarashi
c and
Kenichi
Oyaizu
b,
Naoki
Yamane
c,
Yasuhiko
Igarashi
c and
Kenichi
Oyaizu
 *b
*b
aMaterials Science and Engineering, School of Materials and Chemical Technology, Tokyo Institute of Technology, Tokyo 152-8552, Japan. E-mail: hatakeyama.k.ac@m.titech.ac.jp
bDepartment of Applied Chemistry, Waseda University, Tokyo 169-8555, Japan. E-mail: oyaizu@waseda.jp
cFaculty of Engineering, Information and Systems, University of Tsukuba, Ibaraki 305-8573, Japan
First published on 12th September 2023
Abstract
Materials informatics and cheminformatics struggle with data scarcity, hindering the extraction of significant relationships between structures and properties. The “Ugly Duckling” theorem, suggesting the difficulty of data processing without assumptions or prior knowledge, exacerbates this problem. Current methodologies don't entirely bypass this theorem and may lead to decreased accuracy with unfamiliar data. We propose using OpenAI generative pretrained transformer 4 (GPT-4) language model for explanatory variable selection, leveraging its extensive knowledge and logical reasoning capabilities to embed domain knowledge in tasks predicting structure–property correlations, such as the refractive index of polymers. This can partially alleviate challenges posed by the “Ugly Duckling” theorem and limited data availability.
Introduction
Materials informatics and cheminformatics are scientific disciplines aiming to process and derive meaningful chemical and physical insights from correlations between the structures and properties of compounds and materials.1–5 One key feature of these approaches is their capacity to rapidly extract statistically significant relationships from constructed databases using data science techniques.6 These methodologies have achieved success in fields such as drug discovery and inorganic material exploration.4,5,7 They enable the efficient extraction of molecules with significant pharmacological activity from a vast pool of candidate substances.2,5,6 Moreover, in materials science, analyses of large databases have led to the discovery of new luminescent molecules,8 ion conductors,9,10 heat conductors,11 and novel alloys.12However, the application of materials informatics in experimental projects faces an apparent problem of data insufficiency. Unlike in the field of biology, where large, standardized databases are available (e.g., Protein Data Bank),13,14 such databases are not necessarily present in materials science.15 For inorganic materials, theoretical computation databases such as the materials project and open catalyst project are available.16,17 Similarly, in the realm of polymers, theoretical computation projects like RadonPy are underway.18,19 However, the accuracy of theoretical calculations can be challenging for organic materials and polymers due to the significant influence of molecular, meso, and bulk scale continuity on material properties.15 In such cases, experimental databases become necessary.15
Although experimental datasets like PolyInfo are available in polymer field,20 these primarily contain general material properties like mechanical strength and often lack uniformity in sample preparation methods or measurement conditions. When we narrow down to a specific application or functionality, the size of experimental datasets typically remains limited to a few tens to hundreds of instances.15,21–25
A well-known theorem in statistics further illustrates the predicament, the “Ugly Duckling” theorem, which suggests that informatics with small-scale data is exceptionally challenging.26,27 This theorem posits that tasks like pattern recognition, classification, and regression are impossible without certain assumptions or prior knowledge. For instance, in the tale of the “Ugly Duckling,” the judgment that the black duckling is ugly arises from prior exposure to a large dataset – namely, the common knowledge that typical ducklings are yellow. A person, or an AI, who has only seen two or three ducklings would not be able to judge that the black duckling is ugly.
The “Ugly Duckling” theorem potentially poses a critical problem in materials informatics and cheminformatics.15 Identifying significant relationships between material structures and properties can become extremely challenging without a large and diverse dataset for these fields. Therefore, the development of standardized, comprehensive databases for materials science is a pressing issue that requires collective action and coordinated effort from the global scientific community.15
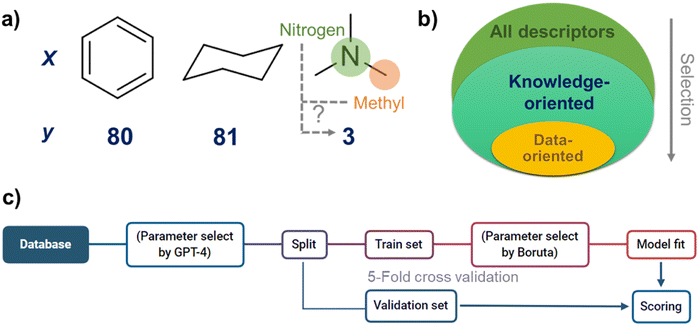
In cheminformatics, the discussion often revolves around the correlation between molecular structure and property. For example, consider the three organic molecules illustrated in Fig. 1a: toluene, cyclohexane, and trimethylamine. It is experimentally known that the boiling point of trimethylamine is lower than that of the other two molecules. Readers with a background in chemistry may intuitively conclude that the lower boiling point of trimethylamine is due to its smaller molecular weight.
However, for readers without a background in chemistry or AI algorithms, identifying the factors that determine boiling points from merely three data points would be challenging. One could posit that the methyl groups in trimethylamine contribute to its lower boiling point, or perhaps that the presence of the nitrogen atom is responsible. This predicament shares the same logical structure as the dilemma introduced by the “Ugly Duckling” theorem.
Discussing the issue more quantitatively, the dilemma arises from an imbalance between the dimensions of the explanatory variables and the number of data points available for learning. Over years of cheminformatics research, numerous methods have been proposed to describe the characteristics of molecular structures numerically.28,29 Typical molecular descriptors have dimensions in the hundreds, and fingerprints can possess bits in the thousands.28,29 Recent advancements in deep learning for molecular recognition often involve latent vectors of several hundred dimensions.7,30,31 Consequently, a vector of several hundred dimensions is generally required to characterize a molecular structure.
While there is no general rule determining the minimum ratio between the dimensions of explanatory variables and the number of learning data points, one benchmark suggests that a ratio of over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is a good starting point.32 Therefore, having at least a few thousand data points is desirable as a general guideline for progressing molecular informatics. Unfortunately, most experimental informatics projects fail to meet this requirement, illustrating a critical challenge in the field.15
1 is a good starting point.32 Therefore, having at least a few thousand data points is desirable as a general guideline for progressing molecular informatics. Unfortunately, most experimental informatics projects fail to meet this requirement, illustrating a critical challenge in the field.15
Several data science methodologies, such as sparse modeling techniques like Lasso and Ridge,33 feature engineering techniques like Boruta,34 and information criterion (e.g., Akaike criterion),35 have been reported to fit well with databases. These methodologies remove parameters with low relevance to the target variable based on certain statistical rules. Such data science tools are compatible with experimental informatics that struggle with small-scale data, producing notable results.10,21,25 However, these techniques do not essentially transcend the “Ugly Duckling” theorem, often resulting in decreased accuracy with untrained data.15
These problems arise from data-oriented feature selection methods, overfitting to the training data, or mismatches between the mathematical algorithms used for dimensionality reduction and the behavior of the target material system. According to the “Ugly Duckling” theorem, the only way to successfully apply machine learning to small-scale data sets is to provide some assumptions or prior knowledge of the regression system. This corresponds to the task of pre-extracting parameters correlated with the predicted properties, based on the domain knowledge of the user of the prediction model — in this case, knowledge of chemistry or materials science.15
Alternatively, recent deep learning approaches have gained attention, such as multimodal and transfer learning methods that deploy deep learning models trained on specific structure–property correlations to other material systems.9,11,36 Deep learning models require a substantial number of learnable parameters and vast amounts of data for model construction. This corresponds to the demands of the Ugly Duckling theorem. However, under the proper system design, the knowledge obtained by deep learning models can be transferred to other domain areas. The specific deep learning model to be transferred in this context is an encoder that automatically transforms molecular structures into numerical spaces. Thus, specifying a particular trained model for transfer is essentially the same as humans choosing explanatory variables generated by cheminformatics techniques.
These knowledge-oriented variable selection approaches are at the heart of data science (Fig. 1b). However, there has been no effective methodology because variable selection requires a deep understanding of both experimental and data science.15 This task has been performed by personnel based on their unique intuition and know-how15 However, these individuals may not have perfect experimental and data science knowledge, and objectively verifying this process in the scientific community has been difficult.
To address these problems, we propose using the large language model GPT-4,37 to choose explanatory variables. GPT-4 is a model that possesses vast knowledge, including science, and is capable of logical reasoning. As of the writing of this paper, only two months have passed since its public release, and revolutionary results are being reported one after another by GPT-4 and a large language model (LLM). Examples include the selection of machine learning algorithms,38 predicting structure–property correlations,39 in-context learning,40 and controlling robotic arms.41 Our approach utilizes the scientific knowledge that GPT-4 possesses for the purpose of embedding domain knowledge in tasks predicting structure–property correlations.
Experimental section
The code related to this study is made available on GitHub (https://github.com/KanHatakeyama/RefractiveIndexGPT).Dataset preparation
We chose the refractive index as the target parameter for machine learning based on several considerations. Applications such as high-refractive-index lenses have been garnering attention recently.42–44 Moreover, there's a well-established theoretical formula known as the Lorentz–Lorenz equation (Fig. 2), which suggests that the refractive index is determined by the molecule's volume and its polarizability.43,45 However, simulating the two parameters with flawless accuracy is challenging due to the intricate interactions of polymer chains.43,45–47 Thus, in this study, we put forth a machine learning-based correction method. Fortunately, there exists a highly verifiable open dataset polymer pertaining to the refractive index that has been made available to the public: CROW (https://polymerdatabase.com/). | ||
| Fig. 2 Conversation between the author and GPT-4 to select molecular descriptors. See ESI† for the full text. | ||
We collected data of all 44 conventional homopolymers whose chemical structures were specified in the original database. Although there are other larger databases like PolyInfo that record the experimental properties of polymers,20 they do not permit comprehensive data collection or redistribution. In contrast, CROW's data is widely available on the web, making it highly shareable. This is why we opted for CROW in our study. The molecular structures of these polymers are shown in Fig. S1.† The number 44 represents a value frequently observed in experimental informatics with a small amount of data. In this study, the unit structure of the polymers was recognized in SMILES format, from which the task of predicting the refractive index was set. The molecular weight and higher-order structures of the polymers were not considered.
Descriptor calculation
Several molecular descriptors were calculated as explanatory variables that can determine the refractive index (Table S1†). In all methods, we calculated not the polymer itself but its individual unit structure. The structure corresponding to the repeating unit was capped with a proton atom. For methods (1)–(3), we calculated the properties of a single molecule, while in (4), we calculated the packing of multiple molecules.(1) Basic molecular descriptors (rdkit_**): we calculated descriptors outputted by the RDKit module (ver. 2022.9.5).
(2) Values calculated by PM7 (PM7_**): first, we roughly optimized the molecular structures using the ‘localopt’ function from the Pybel module after optimizing the structure using the semi-empirical PM7 level method in Gaussian16,48 we calculated electronic energy, dipole moment in each axis direction (dipole_), total dipole moment (dipole_Tot), HOMO, LUMO, and molecular polarization at 656 nm with the same method. These parameters were selected due to their low computational cost, clear physical meaning, and frequent use as explanatory variables in data science.21,49 Calculations were conducted in vacuo.
(3) Property values predicted by the group contribution method50–52 (JR_**): we calculated predicted values such as boiling point using a reported package (JRgui: a Python Program of Joback and Reid Method).53 Although the accuracy can depend on the types of parameters, the group contribution method can show a predictive performance with a coefficient of determination of 0.9 or more for general organic compounds.50–52
(4) Molecular volume estimated by the approximate DFT-MD method (DFTMD_vol): the most significant parameters presented in the Lorentz–Lorenz equation are molecular polarization and molecular volume. Given their importance in this context, we deemed it appropriate to compute and include the molecular volume as part of our calculations. Using a module of the AI molecular simulator Matlantis (v. 3.0.0),54 we estimated the volume occupied by a single molecule. This method packs 20 low molecules into a cell and estimates molecular volume by optimizing the structure (Fig. S2†). Although systematic errors accompanied by low molecular approximation were present, the correlation coefficient with the actual measured volume was 0.993, making it a useful value as an explanatory variable.
Regression scheme
A regression task was set with the above parameters as explanatory variables and the actual measured refractive index as the target variable (Fig. 1c). The database was evaluated with 5-fold cross-validation, and mean absolute error (MAE) and root mean squared error (RMSE) were calculated against the validation dataset. As regression models, we selected general algorithms such as Ridge, Lasso, support vector machines (SVM), Gaussian process regression (GPR, RBF + white kernel), random forest regression (RFR), and gradient boosting regression (GBR). All were driven on the scikit-learn (1.2.2) module.55 Ridge and Lasso used the RidgeCV and LassoCV classes to optimize the regularization term automatically. Other models, less influenced by hyperparameters, were operated with default settings. During regression, all parameters were standardized using the StandardScaler class of scikit-learn.Parameter selection as a baseline
The variables used for regression were pre-selected by the following methods as baselines.All: this is the case where all variables are used (235 parameters, Table S1†).
Random-10: this is the case where 10 randomly selected variables are used (Table S2†).
Random-20: this is the case where 20 randomly selected variables are used (Table S2†).
Boruta: statistically significant parameters between the explanatory variables and target parameters in each training dataset were selected by the Boruta algorithm with default hyperparameters (v0.3). A random forest was chosen as the regressor. In Fig. 3, the descriptor set of Boruta is given as the selected parameters for the train data during first cross-validation step. In the case of Lasso, an entire dataset was introduced to discuss typical descriptors. In order to assess statistical results, we performed the random selection process a total of four times (Table S3 and Fig. S3†). In addition to Random-X, the notations Random-X-1, Random-X-2, and Random-X-3 represent independent random trials (X = 10, 20).
Parameter selection by GPT-4
We selected explanatory variables by asking ChatGPT Plus (May 12 Version, GPT-4) for preferred parameters (Fig. 2, see ESI† for the full chat log).56 The question task consists of three parts:(1) Instruct GPT-4 to consider the theoretical formula that determines the refractive index of the molecule. This was to induce reasoning based on physical chemistry.
(2) Ask what explanatory variables should be used for polymers. In doing so, we wrote out all the explanatory variables and supplemented the meanings of prefixes such as ‘PM7_’ and ‘rdkit_’.
(3) Command GPT-4 to output the list of selected descriptors.
The ChatGPT answers could change each time the question was asked slightly, mainly due to the inclusion of a temperature parameter related to randomness as an internal variable of the LLM (Fig. S4†). The randomness can be controlled only by using the API. In this study, we adopted the first answer that came up in the interface on ChatGPT.
While our research predominantly centers on structure–property correlations utilizing the CROW database, especially in predicting refractive indices, it's pivotal to recognize the potential broader applications of our findings. For instance, the explanatory variables determined by GPT-4 maintain their respective physical meanings accurately within this specific context. Yet, we acknowledge that the efficacy of GPT-4 in correctly interpreting explanatory variables not mentioned, or parameters not employed in this study, remains to be fully validated. This warrants future in-depth exploration and underscores the potential for extending our methodology to other domains beyond solely polymer dataset modeling.
Results and discussion
Explanatory parameter extraction by GPT-4
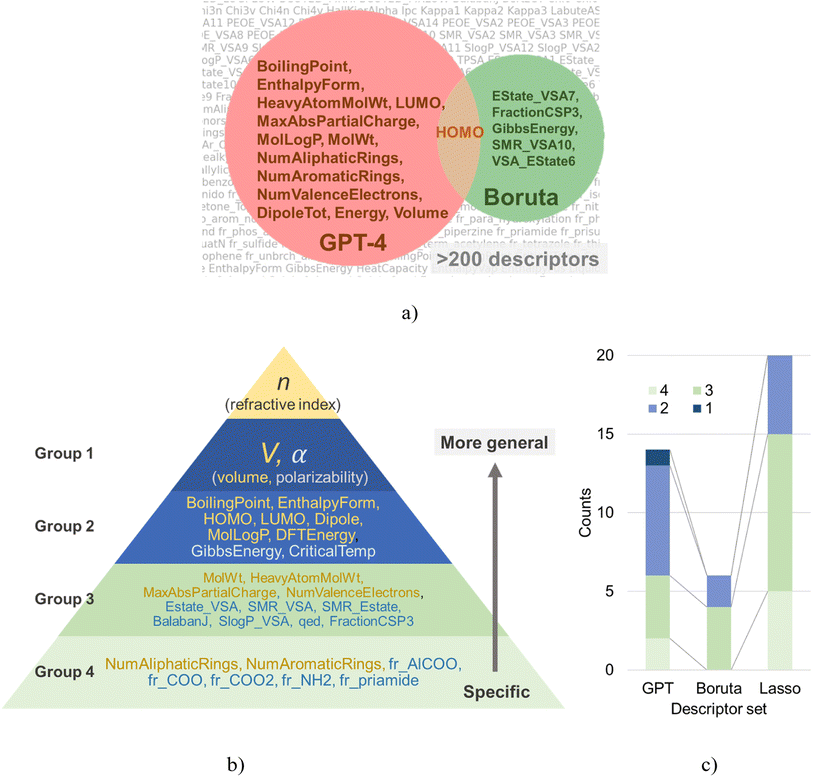
In this study, we employed ChatGPT, the May 12 version, an LLM with knowledge spanning various technical disciplines, including chemistry and programming, as a new approach to molecular descriptor selection. In response to the initial question regarding the theoretical formula to determine the refractive index, GPT-4 accurately identified the Lorentz–Lorenz equation as a key determinant (Fig. 2). As this equation is one of the most common formulas used for predicting the molecular refractive index,42–45,50 this verified GPT-4's capability to provide pertinent insights.Subsequently, we asked GPT-4 to highlight factors essential for predicting the refractive index of polymers based on the theoretical formula. This yielded 14 molecular descriptors, including boiling point, enthalpy of formation, and heavy atom count, as shown in Fig. 3a.
Three significant points should be inferred from these responses. First, despite our omission in explaining explanatory parameters, GPT-4 demonstrated the ability to interpret them correctly. For instance, we did not explicitly define the abbreviation “DipoleTot,” but GPT-4 replied, “Total dipole moment, directly related to polarizability.” This shows that GPT-4 correctly deciphered the meaning of the abbreviation and made an accurate inference on the substantial influence of the dipole moment on polarizability, a critical factor in the Lorentz–Lorenz equation.
The second advantage of this approach lies in the physical–chemical relevance of the chosen parameters (see the Discussion in the ESI† for a physical and chemical examination of each selected parameter).5,15,28,49,53,57–59
According to the Lorentz–Lorenz equation, molecular density (volume) and polarizability are vital in determining the refractive index. These parameters correspond to PM7_alpha656 nm and DFTMD_vol in our descriptors list. Although PM7_alpha656 nm was not selected by GPT-4, the DipoleTot, which can serve as a substitute, was chosen. Furthermore, as we expected, DFTMD_vol was set. In addition to these two parameters, GPT-4 also selected descriptors like boiling point and enthalpy of formation, which could be seen as corrective factors. These parameters strongly correlate with the refractive index,42–45,50 and their selection demonstrates the chemically sound judgment made by GPT-4.
The third point of significance lies in the interpretability of the chosen parameters. All the selected variables possessed straightforward physical–chemical meanings and were accompanied by concise explanatory notes from GPT-4. The series of inferential processes carried out by GPT-4 seemed to agree with the decision-making of an experienced researcher well-versed in chemistry and informatics.42–45,50 This suggests that embedding domain knowledge could be delegated to an LLM. Furthermore, the fact that this process of descriptor selection was accomplished in significantly less time than a human (in a matter of seconds) is intriguing. A human researcher, requiring ample time for reading and interpreting the descriptors, would need tens of minutes or more. This finding hints at the potential for significant efficiency gains by integrating LLMs in similar scientific workflows.
Data-oriented explanatory parameter extraction by Boruta and Lasso
Boruta algorithm extracts statistically significant explanatory variables through repetitive testing procedures. For a given dataset, Boruta identified the following six explanatory variables: EState_VSA7, FractionCSP3, GibbsEnergy, HOMO, SMR_VSA10, VSA_EState6 (Fig. 3a). The noticeable differences between the variable selection results of GPT-4 and Boruta lay in (a) the number of selected variables, and (b) the nature of the variables themselves.GPT-4 proposed 14 parameters as candidate explanatory variables, whereas Boruta only suggested six. Given a dataset size of 44, this outcome could be deemed reasonable. However, parameters statistically significant in the training dataset do not necessarily remain effective in unfamiliar datasets. This assumption holds only when the dataset size is sufficiently large and the quality of training and validation (or testing) datasets is comparable. For small-scale data, as in our case, the applicability of such a hypothesis is dubious. Another issue with Boruta is the interpretability of the proposed explanatory variables. Although the suggested parameters, such as EState_VSA7, SMR_VSA10, and VSA_EState6, might help predict the refractive index, they are highly specialized parameters that no one outside of cheminformatics experts may fully interpret.
Lasso regression, a widespread technique in statistical modeling, has also been utilized to extract a series of parameters (Fig. S5†). The list of extracted parameters includes the following: BalabanJ, CriticalTemp, dipoleX, dipoleY, EState_VSA7, EState_VSA8, fr_Al_COO, fr_COO, fr_COO2, fr_NH2, fr_priamide, FractionCSP3, GibbsEnergy, LUMO, qed, SlogP_VSA12, SlogP_VSA8, SMR_VSA4, SMR_VSA7, and VSA_EState3. These parameters cover a broad spectrum, ranging from conventional descriptors like critical temperature (CriticalTemp) to more specific ones such as the functional group counts (e.g., fr_NH2, fr_priamide). Approximately half of these parameters might not be immediately familiar to experimental chemists.
Comparison of parameter selection trends
In order to enhance our understanding of the trends in the parameters extracted by each algorithm, we classified each parameter into one of four groups (Fig. 3b). Group 1 encompasses parameters that determine refractive index based on the Lorentz–Lorenz equation, specifically, polarizability (α) and volume (V). Group 2 consists of physical properties that are relatively familiar to chemists, such as boiling points, HOMO, and LUMO energies. Group 3 refers to typical molecular descriptors, such as molecular weight and MaxAbsPartialCharge. Group 4 contains geometric descriptors, like counts of specific functional groups.Each group can be understood as forming a hierarchical structure. Lower-numbered groups (i.e., groups 1 and 2) are seen as dependent variables of higher-numbered groups. Although there are no golden rules for selecting parameters for regression, as a rule of thumb, smaller group number parameters are more likely to generalize well. For instance, a descriptor counting the number of –NH2 bonds in a molecule (group 4) does not generalize well to bonds with similar properties like >NH. If one wants to discuss molecular polarity, one should use higher-order parameters such as dipole (group 2), which are determined as dependent variables of the various functional groups. Therefore, an effective variable selection strategy for small datasets is to choose parameters likely to generalize well (i.e., those from smaller group numbers) as the basis, then add lower-order variables as correction terms.
Interestingly, about 60% of the explanatory variables selected by GPT-4 belonged to groups 1 and 2, indicating a justifiable parameter selection from a physical chemistry perspective (Fig. 3c). Conversely, the proportions for Boruta and Lasso were approximately 30% and 25%, respectively. In other words, from a physical chemistry perspective, these data-oriented methods chose parameters that are not necessarily easy to generalize in over 70% of cases, which may have contributed to a decline in the aftermentioned performance in cross-validation. Such data-oriented approaches can only deal with raw numerical data, without considering the meaning of the given explanatory variables. They fail to consider the hierarchical nature of the parameters, an issue directly connected to the “Ugly Duckling” theorem. If data-oriented approaches want to account for hierarchical relationships between parameters, they must prepare a suitable scale database. However, this is often impractical in experimental informatics due to the high data acquisition cost, thus leaving the dilemma unresolved.
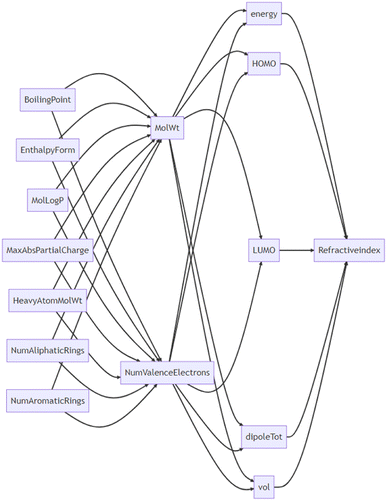
On the other hand, GPT-4, having been trained on a vast amount of scientific data, can make feature selections that consider the context of physical chemistry and the hierarchy of the parameters. We can call this a LLM-oriented feature selection. We performed prompts to infer their causal relationships to confirm whether GPT-4 truly understands the hierarchical relationships between variables (Fig. 4, see ESI† for the actual conversation). The model postulated that the refractive index is a function of a molecule's energy, HOMO, LUMO, dipole moment, and volume. It also suggested that these parameters are functions of lower-order variables such as the number of valence electrons and molecular weight. There were some instances where the model made incorrect physical–chemical interpretations, such as boiling point being an independent variable for the number of valence electrons. The cause seems to be either that GPT-4's inferential ability is still insufficient, that it lacks sufficient chemical knowledge, or possibly both. Regardless, the relationships between variables were generally captured correctly. Combining this with data-oriented methods is expected to achieve higher regression performance.
Regression results
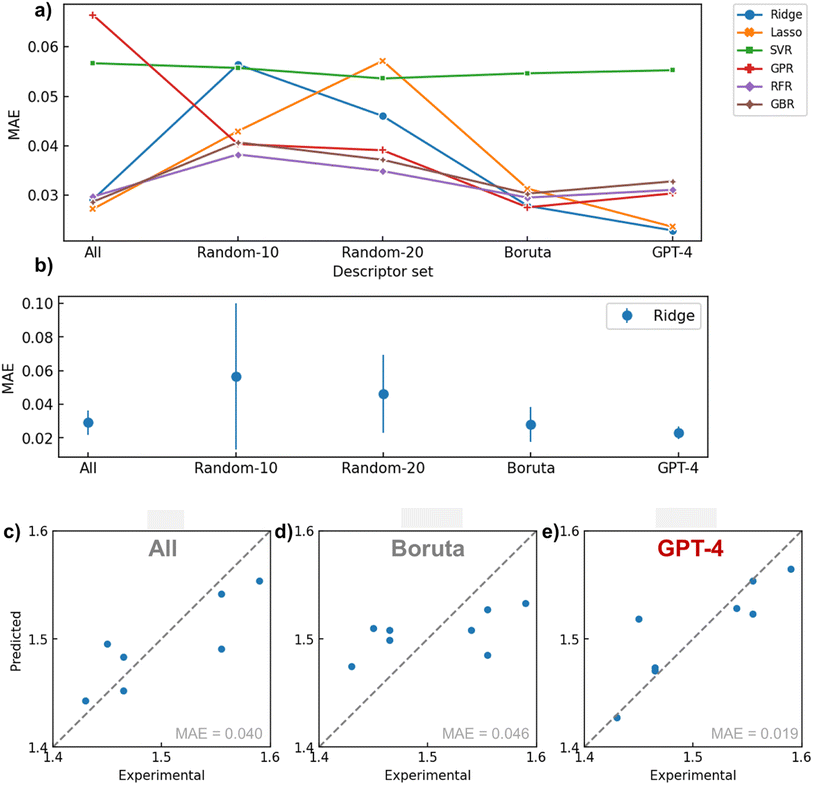
Fig. 5a illustrates the performance provided by each descriptor set (All, Random-10, 20, Boruta, GPT-4) generated by the respective algorithms during a 5-fold cross-validation task (see Tables 1 and S3† for actual values). Overall, the combination of GPT-4 and Ridge (MAE = 0.0229) offered the best regression performance, followed by Lasso (0.0236). RMSE followed a similar trend with MAE, indicating that outliers did not affect results significantly. When calculating the standard deviation of the MAE in cross validation for the Ridge regression model, GPT-4 showed the smallest error bar, indicating that it provided the most reliable results (Fig. 5b). The next best performance was achieved under the condition of using all variables with Lasso (0.0272). In GPT-4's descriptor set, only one parameter (MaxAbsPartialCharge) had a coefficient reduced to zero by Lasso regression, indicating that GPT-4 selected instrumental variables for defining the refractive index from both physical chemistry and statistical perspectives (Fig. S5b†). These results imply that if a crucial variable selection is conducted in advance by applying physical chemistry knowledge, the performance of the regression model can be improved.| Descriptor | Model | MAE | RMSE |
|---|---|---|---|
| GPT-4 | Ridge | 0.0229 | 0.0310 |
| GPT-4 | Lasso | 0.0236 | 0.0320 |
| All | Lasso | 0.0272 | 0.0334 |
| Boruta | GPR | 0.0276 | 0.0339 |
| Boruta | Ridge | 0.0279 | 0.0345 |
| All | GBR | 0.0287 | 0.0374 |
| All | Ridge | 0.0291 | 0.0373 |
| Boruta | RFR | 0.0295 | 0.0391 |
| All | RFR | 0.0297 | 0.0394 |
| Boruta | GBR | 0.0304 | 0.0384 |
In other words, it is demonstrated that tasks traditionally considered unique to human expertise, such as embedding domain knowledge, can be delegated to LLMs. To our knowledge, there are scarcely any reported material research examples of assigning such high-level abstract intellectual work in data science to AI.
Another implication of these findings is that even algorithms that automatically perform variable selection, like sparse modeling, cannot ideally determine parameters solely based on the given dataset. This result entirely agrees with the “Ugly Duckling” theorem. Boruta, another critical baseline, provided a relatively good predictive performance on average (MAE = ca. 0.03) but failed to reach the maximum performance of GPT-4. This reveals the limitations of variable selection procedures that solely rely on the given dataset, much like sparse modeling.
The worst predictive performance occurred when descriptors were randomly selected, likely due to the omission of crucial variables affecting the refractive index. Furthermore, this method exhibited significant variability in predictive error from trial to trial, demonstrating poor reproducibility (Fig. 5b and S3†). The performance of GPR improved with the use of Boruta and GPT-4. Since GPR lacks an internal system for variable selection, the model probably failed with the ‘All’ option due to an excess of explanatory variables. SVR generally delivered poor predictive performance, possibly due to an overabundance of model degrees of freedom relative to the available data for learning. RFR and GBR models, which typically have high predictive performance, failed to match the conditions of GPT-4 combined with linear models, even when combined with Boruta, for the limited data set in this study. Given the nature of these decision tree-based algorithms, it is plausible that they struggled to regress flexibly on small datasets.
To observe actual prediction plots, examples of regression results performed during cross-validation using the Ridge model with several descriptor sets are presented in Fig. 5c–e. When all descriptors were used, there was a variance in the overall correlation with the actual values. In the case of using Boruta, the predictions were biased toward the average value. This could be due to Boruta selecting explanatory variables using a nonlinear mechanism, which may not have been appropriate for ridge regression. Conversely, GPT-4 reduced variance and bias compared to the previous two methods, supporting the efficacy of variable selection based on domain knowledge.
Conclusions
In this study, we demonstrated that the preselection of explanatory variables, a task historically performed by human scientists through the application of domain knowledge, can be delegated to large language models like GPT-4. Large language models can quickly and objectively verify and delegate such tasks. For example, we set a task to predict the refractive index from molecular structure using a small dataset of approximately 40 polymer records. Instead of providing an actual dataset, we asked GPT-4, which ‘knows’ physical chemistry, to select variables that could influence the refractive index. This approach revealed that superior predictive performance could be achieved compared to algorithms like Boruta and sparse modeling that perform variable selection based on given only numerical datasets. This success indicates the importance of utilizing domain knowledge, especially for small datasets, aligning with the “Ugly Duckling Theorem.”Future work needs to incorporate chemical and material information for more specialized targets. Since GPT-4 only has general physical chemistry knowledge, mechanisms for learning through retrieving recent literature or fine-tuning are necessary. Even in cases where no theoretical equation exists, we expect that the language model will have some knowledge about many general parameters. Therefore, while the accuracy might decrease, we anticipate that it should still be feasible to apply the methodology. This poses an important question that future studies need to explore. Building more advanced large language models could also automate machine learning tasks by suggesting descriptors to calculate from scratch or designing regression models.
Alternatively, combining with models like symbolic regression that align well with theoretical research could provide interpretability and superior predictive performance. The linguistic selection process must also be revealed objectively by scientific approaches. By continuing to investigate these specific cases, we aim to uncover the extent to which large language models can serve as a potent tool in various chemical and material sciences.
Data availability
Data and processing scripts for this paper, including databases and regression programs, are available at GitHub (https://github.com/KanHatakeyama/RefractiveIndexGPT).Author contributions
K. H. wrote the code, designed the experiments, and wrote the manuscript. Other authors participated in the discussion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by Grants-in-Aid for Scientific Research (No. 21H04695, 21H02017, 22KJ2927, and 22H04623) from the Ministry of Education, Culture, Sports, Science and Technology, Japan, by the JST FOREST Program (Grant Number JPMJFR213V). The manuscript was drafted using GPT-4.References
- L. M. Antunes, R. Grau-Crespo and K. T. Butler, NPJ Comput. Mater., 2022, 8, 44 CrossRef.
- W. Chaikittisilp, Y. Yamauchi and K. Ariga, Adv. Mater., 2022, 34, e2107212 CrossRef PubMed.
- J. Hu, S. Stefanov, Y. Song, S. S. Omee, S.-Y. Louis, E. M. D. Siriwardane, Y. Zhao and L. Wei, NPJ Comput. Mater., 2022, 8, 65 CrossRef.
- L. Shen, J. Zhou, T. Yang, M. Yang and Y. P. Feng, Acc. Mater. Res., 2022, 3, 572–583 CrossRef CAS.
- Y. Chen and J. Kirchmair, Mol. Inform., 2020, 39, e2000171 CrossRef PubMed.
- E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek, A. Roitberg, O. Isayev, S. Curtarolo, D. Fourches, Y. Cohen, A. Aspuru-Guzik, D. A. Winkler, D. Agrafiotis, A. Cherkasov and A. Tropsha, Chem. Soc. Rev., 2020, 49, 3525–3564 RSC.
- D. Jiang, Z. Wu, C. Y. Hsieh, G. Chen, B. Liao, Z. Wang, C. Shen, D. Cao, J. Wu and T. Hou, J. Cheminform., 2021, 13, 12 CrossRef CAS PubMed.
- T. C. Wu, A. Aguilar-Granda, K. Hotta, S. A. Yazdani, R. Pollice, J. Vestfrid, H. Hao, C. Lavigne, M. Seifrid, N. Angello, F. Bencheikh, J. E. Hein, M. Burke, C. Adachi and A. Aspuru-Guzik, Adv. Mater., 2023, 35, e2207070 CrossRef PubMed.
- K. Hatakeyama-Sato, T. Tezuka, M. Umeki and K. Oyaizu, J. Am. Chem. Soc., 2020, 142, 3301–3305 CrossRef CAS PubMed.
- K. Hatakeyama-Sato, M. Umeki, H. Adachi, N. Kuwata, G. Hasegawa and K. Oyaizu, NPJ Comput. Mater., 2022, 8, 170 CrossRef.
- S. Wu, Y. Kondo, M.-a. Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. Xu, J. Shiomi, C. Schick, J. Morikawa and R. Yoshida, NPJ Comput. Mater., 2019, 5, 66 CrossRef.
- J. M. Rickman, H. M. Chan, M. P. Harmer, J. A. Smeltzer, C. J. Marvel, A. Roy and G. Balasubramanian, Nat. Commun., 2019, 10, 2618 CrossRef CAS PubMed.
- L. Y. Geer, A. Marchler-Bauer, R. C. Geer, L. Han, J. He, S. He, C. Liu, W. Shi and S. H. Bryant, Nucleic Acids Res., 2010, 38, D492–D496 CrossRef CAS PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Zidek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- K. Hatakeyama-Sato, Polym. J., 2022, 55, 117–131 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS.
- Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, NPJ Comput. Mater., 2022, 8, 222 CrossRef CAS.
- C. Kim, A. Chandrasekaran, T. D. Huan, D. Das and R. Ramprasad, J. Phys. Chem. C, 2018, 122, 17575–17585 CrossRef CAS.
- S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu and M. Yamazaki, 2011 International Conference on Emerging Intelligent Data and Web Technologies, 2011, pp. 22–29, DOI:10.1109/eidwt.2011.13.
- T. Komura, K. Sakano, Y. Igarashi, H. Numazawa, H. Imai and Y. Oaki, ACS Appl. Energy Mater., 2022, 5, 8990–8998 CrossRef CAS.
- Y. Zhang and C. Ling, NPJ Comput. Mater., 2018, 4, 25 CrossRef.
- S. Pruksawan, G. Lambard, S. Samitsu, K. Sodeyama and M. Naito, Sci. Technol. Adv. Mater., 2019, 20, 1010–1021 CrossRef CAS PubMed.
- G. Lambard and E. Gracheva, Mach. Learn. Sci. Technol., 2020, 1, 025004 CrossRef.
- R. Mizuguchi, Y. Igarashi, H. Imai and Y. Oaki, Nanoscale, 2021, 13, 3853–3859 RSC.
- S. Watanabe, Knowing and Guessing; A Quantitative Study of Inference and Information, New York, Wiley, 1969 Search PubMed.
- Z. Wang, S. Chen, J. Liu and D. Zhang, IEEE Trans. Neural Netw. Learn. Syst., 2008, 19, 758–769 Search PubMed.
- H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, J. Cheminform., 2018, 10, 4 CrossRef PubMed.
- A. Capecchi, D. Probst and J. L. Reymond, J. Cheminform., 2020, 12, 43 CrossRef CAS PubMed.
- J. Park, Y. Shim, F. Lee, A. Rammohan, S. Goyal, M. Shim, C. Jeong and D. S. Kim, ACS Polym. Au, 2022, 2, 213–222 CrossRef CAS.
- O. Wieder, S. Kohlbacher, M. Kuenemann, A. Garon, P. Ducrot, T. Seidel and T. Langer, Drug Discovery Today Technol., 2020, 37, 1–12 CrossRef PubMed.
- P. Peduzzi, J. Concato, A. R. Feinstein and T. R. Holford, J. Clin. Epidemiol., 1995, 48, 1503–1510 CrossRef CAS PubMed.
- J. Mairal, F. Bach and J. Ponce, arXiv, 2014, preprint, arXiv:1411.3230.
- M. Kursa and W. Rudnicki, J. Stat. Softw., 2010, 36, 1–13 Search PubMed.
- P. Stoica and Y. Selen, IEEE Signal Process. Mag., 2004, 21, 36–47 CrossRef.
- O. Queen, G. A. McCarver, S. Thatigotla, B. P. Abolins, C. L. Brown, V. Maroulas and K. D. Vogiatzis, NPJ Comput. Mater., 2023, 9, 90 CrossRef.
- OpenAI, GPT-4 Technical Report, 2023, https://cdn.openai.com/papers/gpt-4.pdf Search PubMed.
- S. Zhang, C. Gong, L. Wu, X. Liu and M. Zhou, arXiv, 2023, preprint, arXiv:2305.02499.
- A. M. Bran, S. Cox, A. D. White and P. Schwaller, arXiv, 2023, preprint, arXiv:2304.05376.
- M. C. Ramos, S. S. Michtavy, M. D. Porosoff and A. D. White, arXiv, 2023, preprint, arXiv:2304.05341.
- M. Skreta, N. Yoshikawa, S. Arellano-Rubach, Z. Ji, L. B. Kristensen, K. Darvish, A. Aspuru-Guzik, F. Shkurti and A. Garg, arXiv, 2023, preprint, arXiv:2303.14100.
- V. Venkatraman and B. K. Alsberg, Polymers, 2018, 10, 103 CrossRef PubMed.
- J. P. Lightstone, L. Chen, C. Kim, R. Batra and R. Ramprasad, J. Appl. Phys., 2020, 127, 215105 CrossRef.
- S. A. Schustik, F. Cravero, I. Ponzoni and M. F. Díaz, Comput. Mater. Sci., 2021, 194, 110460 CrossRef CAS.
- P. R. Duchowicz, S. E. Fioressi, D. E. Bacelo, L. M. Saavedra, A. P. Toropova and A. A. Toropov, Chemom. Intell. Lab. Syst., 2015, 140, 86–91 CrossRef CAS.
- T. Okada, R. Ishige and S. Ando, Polymer, 2018, 146, 386–395 CrossRef CAS.
- M. A. F. Afzal, C. Cheng and J. Hachmann, J. Chem. Phys., 2018, 148, 241712 CrossRef PubMed.
- J. J. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- Y. Oaki and Y. Igarashi, Bull. Chem. Soc. Jpn., 2021, 94, 2410–2422 CrossRef CAS.
- F. Gharagheizi, P. Ilani-Kashkouli, A. Kamari, A. H. Mohammadi and D. Ramjugernath, J. Chem. Eng. Data, 2014, 59, 1930–1943 CrossRef CAS.
- E. Stefanis, L. Constantinou and C. Panayiotou, Ind. Eng. Chem. Res., 2004, 43, 6253–6261 CrossRef CAS.
- Q. Wang, P. Ma, C. Wang and S. Xia, Chin. J. Chem. Eng., 2009, 17, 254–258 CrossRef CAS.
- C. Shi and T. B. Borchardt, ACS Omega, 2017, 2, 8682–8688 CrossRef CAS PubMed.
- S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, T. Watanabe, Y. Yayama, H. Iriguchi, Y. Asano, T. Onodera, T. Ishii, T. Kudo, H. Ono, R. Sawada, R. Ishitani, M. Ong, T. Yamaguchi, T. Kataoka, A. Hayashi, N. Charoenphakdee and T. Ibuka, Nat. Commun., 2022, 13, 2991 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- https://chat.openai.com/ .
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, NPJ Comput. Mater., 2017, 3, 54 CrossRef.
- N. Huo and W. E. Tenhaeff, Macromolecules, 2023, 56, 2113–2122 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00138e |
| This journal is © The Royal Society of Chemistry 2023 |