Expansion of bond dissociation prediction with machine learning to medicinally and environmentally relevant chemical space

Abstract

Bond dissociation energetics underpin the thermodynamics of chemical transformations where bonds are broken or formed and can also be used to predict reaction rates and selectivities. Current machine learning (ML) models to predict bond dissociation energy (BDE) are largely limited in their elemental coverage to hydrogen and the second-row elements. This has restricted the applicability of ML-derived BDE predictions, particularly for molecules of medicinal relevance, since the heteroatoms S, Cl, F, P, Br, and I are commonly found in approved pharmaceuticals. Atmospherically and environmentally relevant molecules containing multiple halogen atoms have been similarly inaccessible. In this study, we considerably expand the size, elemental composition, and bond types of an extensive BDE database and train a new ML BDE model that includes C, H, N, O, S, Cl, F, P, Br, and I. We curate a new quantum chemical dataset of 531 244 unique zero-point energy inclusive homolytic dissociations of organic compounds. We investigate accuracy for out-of-sample molecules and implement iterative training and testing cycles during model development to improve the model accuracy. Improvements in predictive accuracy were achieved for datasets of pharmaceutically relevant molecules containing multiple C(sp²)–halogen bonds from 5.7 to 0.8 kcal mol⁻¹ and polyhaloalkyl compounds with multiple C(sp³)–halogen bonds from 2.7 to 1.2 kcal mol⁻¹ through the targeted augmentation of training data by as little as eight additional molecules. Our updated and expanded model (ALFABET) achieves a mean absolute error of 0.6 kcal mol⁻¹ for both enthalpies and free energies compared to the quantum chemical ground truth. The graph-based representations utilized here outperform traditional cheminformatics features such as radial fingerprints, and there is no discernible improvement in accuracy by including more expensive QM-derived parameters, such as optimized bond lengths. Finally, we illustrate high accuracy in external prediction tasks for large halogenated natural products, pharmaceutically relevant halogenated molecules, atmospherically important halocarbons, and polyfluoroalkyl substances related to environmental toxicity.

---

Introduction

The homolytic bond dissociation enthalpy (BDE) quantifies the thermodynamic stabilities of product radical fragments formed by the homolysis of a covalent bond in a reactant molecule. The quantitative evaluation of BDE values provides detailed insight into the thermodynamics of bond-breaking and forming reactions, and can also be related to kinetics and selectivity by using linear free-energy relationships or empirical scaling relations. This fundamental importance has led to the use of BDE (and its free energy counterpart) values across multiple domains in chemistry, ranging from the determination of possible reaction mechanisms to computational mass spectroscopy.¹ For example, BDE values have been used to assess the difference in bond strengths of primary, secondary, and tertiary C–H bonds,² to quantify the geometric deformation necessary to reach the transition structures for Pd-catalyzed carbon-halogen insertion,³ for the prediction of likely molecular fragments observed in the mass spectra of short peptides,⁴ breakdown of large biomass such as lignin,⁵ comparing the stability of organic radicals⁶ and design of de novo radicals for organic redox flow batteries.⁷ Due to the broad utility and applicability of BDE values, significant effort has been invested in obtaining quantitative measurements. Experimental techniques such as pyrolysis,⁸ radical kinetics photoionization mass spectrometry, acidity/electron affinity cycles,² and electrochemistry have been used to obtain BDE measurements.⁹

Besides experimental measurements, quantum-mechanical (QM) calculations have become pivotal in assessing and predicting BDE values. Emerging computational methods for the automated enumeration and exploration of reaction mechanisms use estimated BDE values to identify energetically favorable paths among the numerous possibilities.¹⁰ High levels of accuracy are attainable with composite ab initio computations of BDEs at 0 K (D₀). For example, the CBS-QB3 method yields mean absolute errors (MAEs) of 0.58 kcal mol^−l relative to experimental values for small molecules such as diatomics, hydrocarbons, and hydrides of N, S, Be, Li, and Si.^11,12 However, density functional theory (DFT) calculations are often more practical for larger, conformationally flexible compounds and have been increasingly used to compute BDEs:¹³ the M06-2X hybrid meta-GGA functional gives an MAE of 2.1 kcal mol⁻¹ relative to experimental hydrocarbon BDE measurements.^14,15 Compared to experimental measurements, which typically give information about the weakest bond(s) in a molecule, computations can be used to study all possible homolytic dissociations. However, due to the exponential scaling of electronic structure calculations with the number of basis functions (and hence molecular size), performing quantum chemical predictions for larger molecules or sizable datasets is challenging, if not intractable. Additionally, a detailed analysis of conformational space may be necessary to identify the most important stationary points on the potential energy surface of both the parent molecule and the two radicals formed upon homolysis. These practical limitations have led to the development of alternative approaches for BDE estimation, such as quantitative structure–property relationship (QSPR) and machine learning (ML) models.^16–18 A machine learning derived, fast, accurate bond dissociation enthalpy tool (ALFABET), which uses a 2D graph representation of the molecules where atom and bonds are encoded as nodes and edges respectively, achieved an MAE of 0.58 kcal mol^−l (vs. an M06-2X/def2-TZVPP oracle) for BDEs of unseen molecules containing C, H, N, O atoms using a message-passing graph-convolutional neural network (GNN), and has found utility in multiple applications.^14,19 Rapid and accurate predictions of BDEs have enabled the application of ML to various domains of chemistry including biological metabolism and combustion chemistry. However, these models have been predominantly limited in element scope to second-row elements. This has restricted the application of BDE predictions in medicinal, atmospheric, and environmental domains, where molecules containing multiple larger heteroatoms or halogen atoms are frequently encountered.

Herein, we present an expanded and updated GNN model for BDE prediction. We also consider BDFE (bond dissociation free energy) values, the standard free energy change associated with the dissociation. The inclusion of S, Cl, F, P, Br, and I was motivated by the frequency of these elements alongside C, H, N, and O in approved drugs and enables ML-based BDE predictions to be applied routinely to medicinally and pharmaceutically relevant molecules. We describe the development of a large dataset (BDE-db2) containing over 530 000 unique M06-2X/def2-TZVP computed BDE and BDFE values, which underpins this effort. We explore the performance of the model on focused datasets of C(sp²) and C(sp³) halogenated molecules relevant to medicinal (polyhalogenated building blocks), atmospheric (halocarbons), and environmental chemistry (per- and polyfluoroalkyl substances, PFAS). Improvements in predictive performance are obtained by analyzing the latent space covered by these datasets and by the addition of a small number of new training samples. The expanded model retains the same levels of accuracy for C, H, N, and O as in previous work while significantly expanding the applicability to new bond types, which are predicted with similarly high levels of accuracy.

Results and discussion

Computational BDE dataset curation

Efforts to construct generalizable models for BDE prediction of multiple bond types have been greatly enabled by the development of large computational datasets. Aires-de-sousa and coworkers developed a dataset¹⁷ of computed BDE values for 1000 neutral molecules from the fragment-like subset of the ZINC database.^20,21 Reference bond dissociation energies exclusive of zero-point vibrational energy (ZPE) were generated for 12 834 unique bonds (single and double) between C, H, N, O, and S at the B3LYP/6-311++G(d,p) level of theory. All geometries were optimized with the semi-empirical DFTB3 Hamiltonian. Subsequently, St. John and coworkers developed the BDE-db dataset,²² taking 42 557 neutral C_xH_yO_zN_m molecules from the PubChem compound database. This study used an automated fragmentation, conformer generation, and DFT computation workflow to obtain 290 664 unique ZPE-inclusive bond dissociation enthalpies at the M06-2X/def2-TZVP level of theory,²³ which gave the best empirical performance when compared with values from the experimental iBond database.^14,24 Motivated by energy storage and electrolyte applications, Persson and coworkers constructed the BDNCM dataset of 64 312 homolytic and heterolytic bond dissociations for 8518 neutral and charged molecules containing C, H, O, F, and Li. BDFE values were obtained at the SMD-ωB97X-V/def2-TZVPPD level of theory. Additionally, DiLabio and coworkers have curated a high-quality benchmark dataset including 4502 datapoints of bond separation energies including H, B, C, N, O, F, Si, P, S, and Cl atoms at (RO)CBS-QB3 level of theory.²⁵

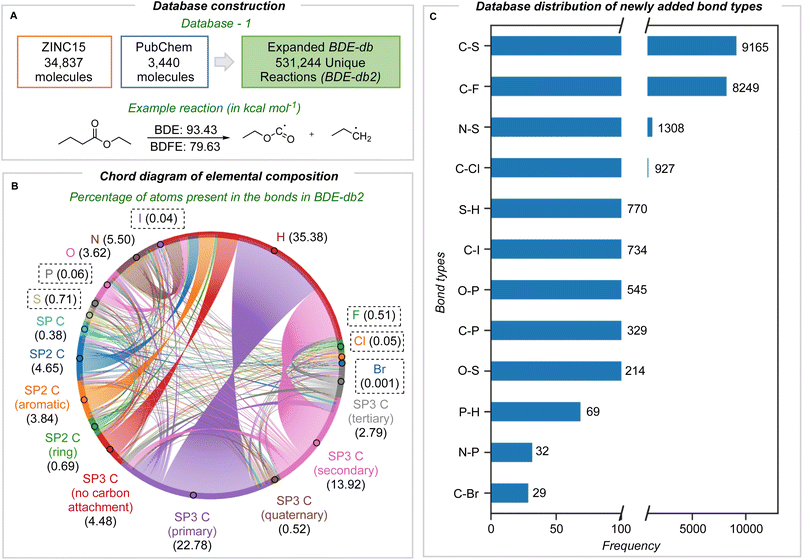
In this work, we describe one of the most comprehensive quantum chemical bond dissociation datasets, BDE-db2, containing 531 244 unique homolytic BDE and BDFE values at the M06-2X/def2-TZVP level of theory (Fig. 1A). 332 035 unique dissociations absent from other datasets have been newly added. We included the ten most common elements in approved pharmaceuticals: C, H, O, N, S, Cl, F, P, Br, and I atoms (in order of their abundance).²⁶ In addition to compounds originally sourced from PubChem present in BDE-db, we sourced 38 277 additional small molecules (10 heavy atoms or fewer) containing the above heteroatoms from the ZINC15 and PubChem compound libraries. M06-2X/def2-TZVP enthalpies (including the unscaled ZPE) and RRHO Gibbs energies (1 atm, 298 K) were computed: the accuracy of this level of theory for halogenated molecules has been benchmarked, showing that hybrid functionals with a high proportion of exact exchange or long-range corrections are more accurate.^27–30 An automated workflow generated the structures of parent and radical fragments from SMILES inputs by enumerating all possible exocyclic single-bond dissociations. Following conformational analysis with RDKit, the most stable conformers were optimized with DFT (further details in Section 1 ESI†). Structures with imaginary frequencies or having undergone structural rearrangements or fragmentations were removed. Further, recent studies highlighting unphysical and anomalous harmonic vibrations computed for open-shell species (with double-hybrid density functionals)³¹ led us to implement an additional filter for dissociations with abnormally large contributions from ΔZPE: 373 further dissociations with statistically significant deviations were removed in this way (Section 1 ESI†).

Fig. 1 (A) Composition of the BDE-db2 database. (B) Chord diagram representing the bond types present in the database. Link thickness between different segments of the circle reflects the number of bonds between those two atom types. Elemental composition (%) is shown in black. (C) The distribution of newly added bond types (where n > 25) in the BDE-db2 database.

The elemental and bond composition of the BDE-db2 dataset is shown in Fig. 1B, which contains 806 433 bond-breaking reactions. After sampling chemical compounds in PubChem and ZINC15 randomly, the elements S, F, P, Cl, I, and Br are present in around 1.4% (22 385) of all bond dissociations alongside C, H, N, and O. The majority (54%) of bonds broken involve at least one carbon atom, with bonds to H the next most populous (35%). Bonds to carbon in all formal hybridization states and degree of substitution are well sampled (Fig. 1B). The frequency density of newly added bond types is shown in Fig. 1C, with the highest number corresponding to C–S bonds (9165). Following this is C–F bonds with 8249. C–Cl, C–Br, and C–P bonds are around an order of magnitude less frequent than C–F bonds, while C–Br bonds are the most scarce, with 29. The counts of all bond types in the BDE-db2 are present in the ESI (Section 2†).

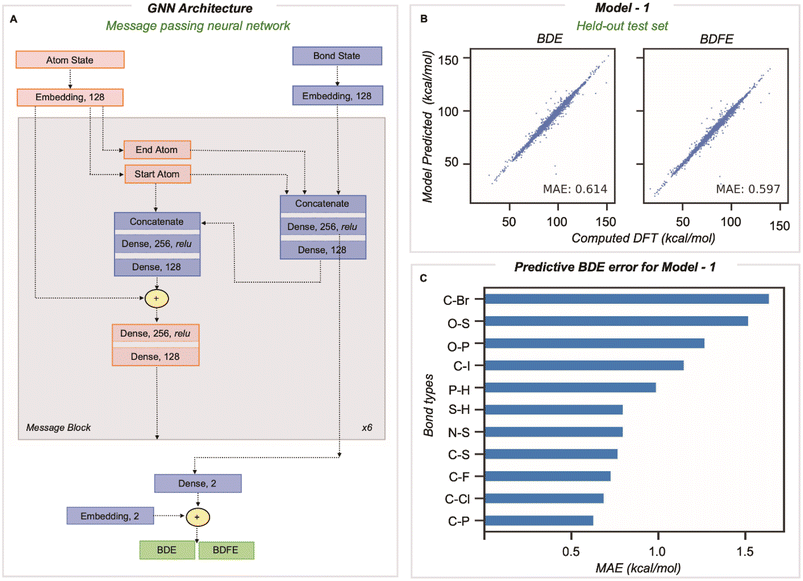
A message passing GNN was then trained to predict the M06-2X/def2-TZVP values of homolytic BDE and BDFE directly from SMILES line notation (Fig. 2A).³² In this approach, molecules input as SMILES are embedded as 2D-molecular graphs using rdkit.³³ Nodes (atoms) and edges (bonds) are then assigned to independent classes depending on several features easily obtained from rdkit: for atoms, the element, atomic number, formal charge, chiral tag, aromatic state, ring state, degree, and the number of attached H atoms, while for bonds, the pair of bonded elements, formal bond order, and ring state. We encode no 3D information in atom and bond representations used by the model. The embedded vector representations (of length 128) used for atoms and bonds are updated in every message-passing layer of the GNN, utilizing the representations of neighboring bonds and atoms. Benchmarking the number of message-passing layers reveals no gain in accuracy beyond six.¹⁴ During message passing, bond states are updated based on adjacent atoms first, after which atom states are updated systematically (grey box in Fig. 2A). Having performed this process six times, atom and bond representations have been encoded with structural information from up to 5/6 bonds away.¹⁴ Bond states from the final message passing layer are reduced to BDE and BDFE predictions by passing them through a linear output layer. Model learning performance was enhanced by utilizing the AdamW optimizer with an inverse time decay schedule for both learning rate (10⁻³) and weight decay (10⁻⁵), and model performance was assessed by measuring the mean absolute error during training for 500 epochs for a batch size of 128 molecules.

Fig. 2 (A) The GNN architecture utilized for the prediction of BDE and BDFE. (B) Predictions for held-out test set (test set – 1). (C) BDE prediction error for a held-out test set based on bond types.

Our training and validation set was randomly sampled and consisted of 514 942 and 8128 unique BDEs, and the performance of the final model was tested on a held-out test set of 1000 molecules comprising 8084 unique dissociations. The inputs for BDE predictions correspond to the 2D molecular graph, including minimal RDKit features as outlined above. The MAE on this test set (vs. DFT) is 0.61 and 0.60 kcal mol⁻¹ for BDE and BDFE, respectively (Fig. 2B). This significantly outperforms chemical descriptor-based approaches, such as that based on an associative neural network (ASNN), giving an MAE of 3.35 kcal mol⁻¹ for 887 BDE values involving C, H, O, N, or S. The predictive accuracy is comparable with previous GNN models, ALFABET and BonDNet, with MAE values of 0.58 and 0.50 kcal mol⁻¹, respectively, while encompassing many more bond types. Analysis of the 20 most populous bond types in the held-out test set (Section 3 ESI†) shows that C–C and C–H bonds, which are the most frequently encountered, are well predicted (with MAEs of 0.77 kcal mol⁻¹ and 0.74 kcal mol⁻¹). Encouragingly, newly added bond types that are less frequently encountered are predicted with only slightly (0.5–0.7 kcal mol⁻¹) higher MAE values and all errors fall under 1.7 kcal mol⁻¹. This includes bond types rarely sampled, such as C–Br, P–H, and O–S, where there are tens to hundreds of values in the dataset, in contrast to hundreds of thousands of C–C and C–H bonds. Comparable predictive accuracy is obtained for BDE and BDFE values, which is perhaps unsurprising since these ground truth values are highly correlated.

Application to aryl halide building block compounds

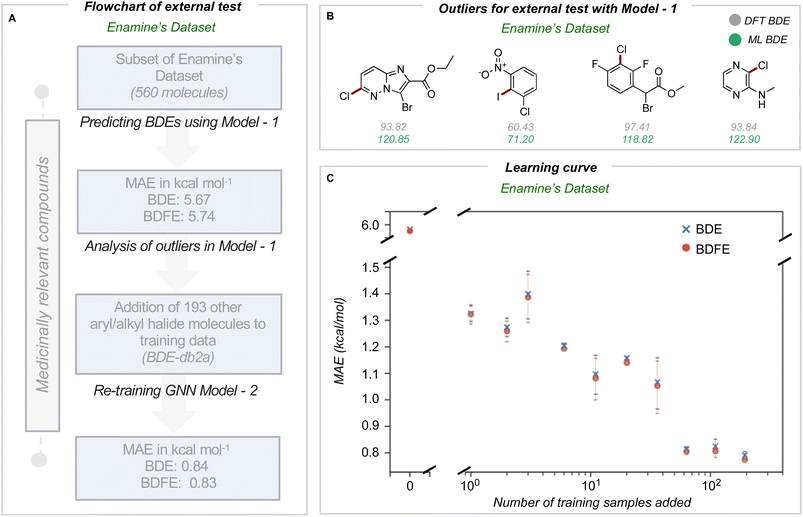
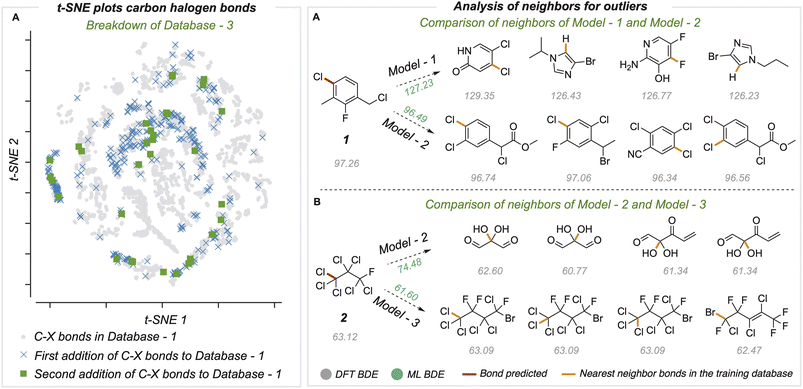
In medicinal chemistry, the modular synthesis of novel drug candidates can be carried out using building blocks, functionalized chemical reagents typically selected for their drug-like properties.^34–37 Aromatic and heteroaromatic fragments are typically functionalized by one or multiple halogen atoms, enabling an array of cross-coupling reactions to be performed. Computed carbon–halogen BDE values have been used to predict the relative rates of oxidative addition by a Pd-catalyst, enabling site-selectivities in the Suzuki cross-couplings of polyhalogenated aromatics to be predicted.³ The general ability to accurately predict C–X BDE values for singly- and multiply-halogenated (hetero)aromatics with ML is thus desirable from the perspective of synthesis planning and reaction prediction. We thus focused on commercially available building block libraries for medicinal chemistry developed by Enamine.³⁸ We tested our newly developed model (herein model 1) on halogenated compounds from the Enamine database:^39,40 a randomly sampled subset of 624 aryl and alkyl halogenated compounds, each with at least one C–F, C–Cl, C–Br or C–I bond, were selected 64 molecules were common to the original training set and were removed, leaving 560 molecules. These halogenated molecules were fragmented and optimized to generate DFT values for all exocyclic bond dissociations. A total of 6295 BDEs (with 4078 unique BDEs) were collected (test set 2) containing 792 C–X bonds (with 696 unique C–X bonds), with a breakdown of 213 C–F, 265 C–Cl, 276 C–Br, and 38 C–I bonds (Fig. 3A).

Fig. 3 (A) Workflow for model optimization for C(sp²)–halogen BDE prediction. (B) Outliers when using model 1 for BDE prediction of Enamine's dataset. (C) GNN learning curve showing systematic improvements in the MAE upon the addition of halogenated molecules to BDE-db2 to obtain BDE-db2a. The error bar corresponds to three different runs.

BDE and BDFE predictions for these halogenated molecules initially gave MAEs of 5.67 and 5.74 kcal mol⁻¹ relative to the DFT oracle. These errors significantly exceed those obtained for the original test set (Fig. 2C), primarily due to poor performance for C–Cl and C–I bonds with MAEs of 12 and 8 kcal mol⁻¹ (Section 4 ESI†). To understand the origin of prediction outliers, we compared the composition of test set 2 with the training database. Comparing test set 2 against molecules in the training database reveals differences in the total number of atoms and the number of halogen and nitrogen atoms. The most pronounced outlier molecules (Fig. 3B) contain structural motifs absent from the original training set, such as multiple halogen atoms, and can have errors >20 kcal mol⁻¹ (Section 5 ESI†). To improve model performance, molecules containing multiple halogens were randomly sampled and added to the training dataset (BDE-db2a). These additional molecules correspond to a distinct subset from the total enamine database: we used 193 molecules with 1634 unique BDEs, 413 of which correspond to C–X bonds (139 C–F, 141 C–Cl, 119 C–Br and 14 C–I). This corresponds to an increase in training set size by a modest 0.3%. This expanded dataset was used to train a new GNN (model 2) whose architecture is the same as Fig. 2A. Upon testing on the Enamine dataset, model performance is considerably improved, giving MAEs of 0.84 and 0.83 kcal mol⁻¹ for BDE and BDFE values, respectively without degraded performance on the original test set 1 (0.64 and 0.62 kcal mol⁻¹, Section 6 ESI†). To determine how adding new structures to the training data enhances model performance, we experimented by adding different numbers of randomly sampled halogenated structures (Fig. 3C). These runs were performed in triplicate. Surprisingly, the addition of fewer than ten additional structures reduces MAE values to around ∼ 1 kcal mol⁻¹, while continuous improvement is observed as more structures are added to reach a limiting accuracy at around 100 additional structures. This behavior suggests that model performance for fairly broad areas of chemical space, such as poly-halogenated heterocycles, can be improved by adding a relatively small but targeted number of compounds to the training process.

Application to environmentally relevant compounds

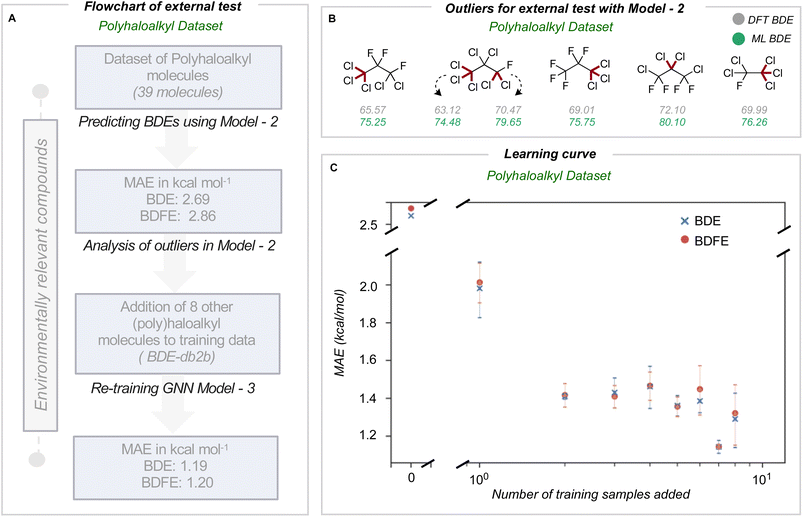
We next assessed the model's predictive accuracy for polyhaloalkyl compounds, such as environmentally relevant chlorofluorocarbons containing several C(sp³)–X bonds. A dataset of 40 molecules (test set 3) containing 274 bond dissociations (155 unique bond dissociations) was curated from PubChem, following which systematic fragmentation and DFT optimizations were performed. One molecule was common to the original training set and was removed. The total number of C–X bonds is 212 (104 unique C–X bonds), with a breakdown of 123 C–F, 85 C–Cl, and 4 C–Br bonds (Section 7 ESI†). Applying the improved model 2 on this dataset led to MAEs of 2.69 and 2.86 kcal mol⁻¹ for BDE and BDFE values (parity plots are shown in Section 8 ESI†).

For this dataset, we found relatively large errors for the weakest bonds (BDE values under 80 kcal mol⁻¹). These outliers correspond to dissociation at multiply halogenated carbons, which yield resonance-stabilized radicals and hence smaller BDE values (Fig. 4B). Looking to see if similar molecules existed in our training database from BDE-db2a, we found that only 3.4% of molecules (2102 of 61 630 molecules) have multiple halogens on the same atom. In comparison, 0.2% (1407 of 516 570 unique bonds) of the bond-breaking reactions had at least one fragment with >1 halogen atom on the radical atom. Based on our earlier observations, we hypothesized that adding a relatively small number of compounds bearing multiply-halogenated carbon atoms to training data could considerably improve predictive accuracy for this dataset. Eight molecules were constructed and added to the training dataset to build BDE-db2b (Section 9 ESI†) and develop a new GNN model 3. This new model showed a notable reduction in MAE values to 1.19 and 1.20 kcal mol⁻¹ (Table 1). Additionally, the learning curve depicts how the mean MAE values over three different types of additions vary when each molecule is added (Fig. 4C). Prediction accuracies with this model are maintained for prior test sets (Section 10 ESI†). The results of the successive improvements made to the BDE prediction model are summarized in Table 1. Based on the improvements from adding more data to cover a broader range of chemical space, the newly developed model (model 3) can be applied to neutral molecules containing C, H, N, O, S, Cl, F, P, Br and I, including multiply-halogenated aromatic and aliphatic compounds. To extend into further regions of chemical space, we suggest sampling around ∼100 s of representative molecules and to systematically incorporate around 10 additional training molecules per training iteration. A learning curve can then be produced to establish model performance as the training set size increases and to determine the number of additional molecules required to obtain 1 kcal mol⁻¹ accuracy for a new region of chemical space. Overall, we have shown that small, representative datasets can be used to improve existing machine learning models.

Fig. 4 (A) Workflow for model optimization for C(sp³)–halogen BDE prediction. (B) Outliers when using model 2 for BDE prediction of polyhaloalkyl compounds. (C) GNN learning curve showing systematic improvements in the MAE upon the addition of halogenated molecules to BDE-db2a to obtain BDE-db2b. The error bar corresponds to three different runs.

Table 1 BDE and BDFE prediction accuracy (MAE in kcal mol⁻¹) obtained from GNN following test–train cycles

	Model 1		Model 2		Model 3
	BDE	BDFE	BDE	BDFE	BDE	BDFE
General test set (n = 1000)	0.61	0.60	0.64	0.62	0.64	0.61
Haloheterocycle set (n = 560)	5.67	5.74	0.84	0.83	0.74	0.70
Polyhaloalkyl set (n = 39)	2.78	2.74	2.69	2.86	1.19	1.20

---

Chemical space and neighbor analysis

To understand the relationship between prediction accuracy and training set composition, we visualized the representations of bonds learned by the final model (Fig. 5A). Since the bond states have a dimension of 128, we performed dimensionality reduction with the t-SNE method to project 8924 different C–X bonds in two dimensions. The newly added C–X bonds used to build BDE-db2a and BDE-db2b are spread in chemical space and cover regions not present in the original dataset. Further, we studied specific examples of outlier predictions that were improved by successive generations of our model (Fig. 5B). For these bonds, we found the ten nearest neighbors (in the model's 128-dimensional latent space) from the training dataset and computed the mean distance of these nearest neighbors. In each case, we found that poor predictions result where the closest training bonds are highly chemically dissimilar to the query bond. Previous work has also shown that determining the distance in latent space enables the identification of high and low confidence points.⁴¹ Overall, the systematic improvement in performance can be attributed to the incorporation of new regions of chemical space in the training set containing more diverse structural features.

Fig. 5 (A) t-SNE plot showing a reduced dimensionality projection of embeddings representing the final bond states used for BDE prediction for C–F, C–Cl, C–Br, and C–I bonds. (B) Analysis of neighbors of one outlier in Enamine's dataset and polyhaloalkyl datasets.

Comparison of current GNN models with traditional cheminformatics features and QM features

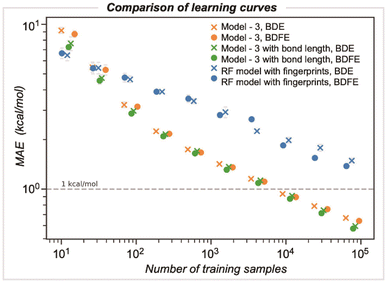
We compared the performance of end-to-end learned representations, as in our GNN model, against cheminformatics-based features such as circular atomic fingerprints. We also evaluated whether our GNN could be improved by including additional features, such as DFT-optimized bond lengths (Fig. 6).⁴² We studied these models' learning by systematically increasing the number of training samples: while the number of samples was randomly selected for three different runs, they were kept consistent across the different models. For GNN model 3, the MAE decreases with training dataset size, achieving kcal mol⁻¹ accuracy at around ∼5000 samples. In contrast, a random forest (RF) based model using Morgan fingerprints generated for the bonded pair of atoms (radius of 3 encoded as 512 bits) demonstrates slower learning, with a BDE error of 2.2 kcal mol⁻¹ for the same training set size. Ultimately, achieving chemical accuracy with this model would require training on a dataset more than an order of magnitude larger than that used to train the GNN. Including optimized bond lengths as part of the initial embedding before GNN model training led to an improvement in performance only for very small dataset sizes (<100), while in the limit of larger datasets, there was a negligible reduction in MAE values. This result suggests that representation learning occurs efficiently for this problem, with datasets on the scale of BDE-db2 containing tens of thousands of training examples.

Fig. 6 Model learning behavior, comparing the original GNN model (orange), a GNN model with features augmented by DFT-optimized bond lengths (green), and a random forest regression using Morgan fingerprints (blue).

Validation against computed and experimental BDE values for diverse halogenated compounds

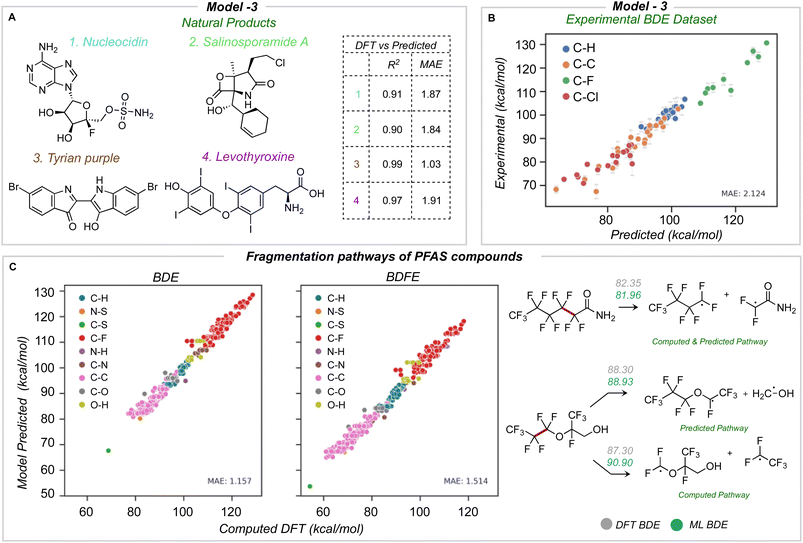
The newly developed model was validated using three external datasets: halogenated natural products and environmentally relevant polyfluoroalkyl substances (PFAS), for which we computed reference BDE values at the M06-2X/def2-TZVP level of theory,⁴³ and an experimental dataset of BDE values for aliphatic chlorofluorocarbons.

Four natural products containing F, Cl, Br, and I were identified (Fig. 7A): nucleocidin,⁴⁴ salinosporamide A,⁴⁵ tyrian purple,⁴⁶ and levothyroxine.⁴⁷ All of these natural products were fragmented and optimized with a similar method as the training database. The average number of heavy atoms is 23, more than twice the size of those in the training database. Across all four molecules, an MAE of 1.76 and 1.75 kcal mol⁻¹ is obtained for BDE and BDFE for 65 unique bonds. Using model 3 for predictions is orders of magnitude faster (∼seconds) than the quantum chemical reference values (∼2 days per molecule of CPU time). The predicted BDE values for each molecule have an R² equal to or high er than 0.9 and a mean absolute error under 2 kcal mol⁻¹ (Fig. 7A).

Fig. 7 (A) BDE prediction of halogenated natural products: R² and MAE relative to DFT ground truth for each molecule shown. (B) Comparison of predicted and experimental BDE values for chlorofluorocarbons (CFCs) and hydrochlorofluorocarbons (HFCs). (C) Predicted BDE and BDFE values for PFAS relative to DFT ground truth. Homolysis of the weakest bond as a potential mechanism of PFAS thermal decomposition. All values in kcal mol⁻¹.

The second validation set comprises experimentally reported bond dissociation enthalpies of 40 fluorinated and chlorinated alkanes, including chlorofluorocarbons (CFCs) and hydrochlorofluorocarbons (HFCs), atmospheric trace gases that influence stratospheric ozone, climate, and air quality.^43,48 Primary mechanisms of atmospheric degradation, such as photolysis, are influenced by the C–halogen bond strength, while the reactions of HFCs with hydroxyl radicals are influenced by C–H bond strengths, and so their prediction is of practical importance. We removed 7 molecules from this dataset present in our original training database to avoid data leakage. ML-predicted bond dissociation enthalpies for the remaining compounds compare well with experimental values, with a correlation coefficient of 0.96 and an MAE of 2.12 kcal mol⁻¹ for 69 unique bonds (23 C–C, 20 C–H, 10 C–F, and 16 C–Cl bonds) (Fig. 7B). This is encouraging since no experimental data was used to train the model, and the largest error obtained for this test set is ∼3 kcal mol⁻¹.

Finally, we test the model's predictive power in determining the weakest homolytic bond dissociation in per- and polyfluoroalkyl substances (PFAS) containing ether, alcohol, amide, and sulfonamide functional groups. Thermodynamic BDE values have been related to breakdown pathways during combustion,¹⁴ while the mechanisms of PFAS degradation have been linked to BDE values.^49,50 We studied 57 molecules, with 557 C–F bonds and a total of 697 unique bonds overall. On comparing different bond types, C–S and C–C bonds have lower BDE values: we would expect these bonds to undergo homolysis first during pyrolytic decomposition (Fig. 7C). The accuracy of prediction against DFT is 1.15 and 1.51 kcal mol⁻¹ for BDE and BDFE respectively. Previous data-driven models have focused on the prediction of C–F BDE values in PFAS molecules;⁴⁹ however, with the ability to predict across the breadth of bond types present in these compounds, we observe that C–S and C–C bonds (rather than C–F) are thermodynamically much more likely candidates for the primary site of homolysis. For 60% of the PFAS considered, the ML-predicted weakest bond matches DFT, while for the remaining 40% of cases, the weakest bond (from DFT) lies within 4 kcal mol⁻¹ from the ML-minimum energy. This suggests one possible use of ML could be to quickly survey and rank possible homolytic cleavages, returning a focused set of candidate bonds to be investigated in greater depth with QM calculations.

Conclusion

Bond dissociation enthalpies and free energies are fundamental quantities used to assess reaction thermodynamics. BDE values also influence reaction kinetics and are often used as essential ingredients to understand mechanism and selectivity. We have developed a broadly applicable BDE prediction tool based on a graph neural network that yields quantitative predictions close to DFT values across a range of organic molecules containing heteroatoms. This tool enables a broader range of chemical space to be studied by this approach than was previously possible, which now includes aromatic and aliphatic compounds with multiple halogen atoms relevant to medicinal and atmospheric applications. For multiply halogenated chlorofluorocarbons, this approach yields results within 2 kcal mol⁻¹ of experimental BDE values. For training dataset sizes on the order of thousands or tens of thousands of compounds, we observe that the learned embeddings of the GNN are not improved by the addition of additional QM descriptors and that the model learning performance (in terms of the number of training samples required to obtain a predictive accuracy of 1 kcal mol⁻¹) surpasses a more traditional cheminformatics approach using fixed circular fingerprints by more than an order of magnitude. While the requirement for training datasets containing thousands of compounds qualifies as a data-hungry approach, we observed that successive expansion of the model's domain of applicability to encompass new bond types was possible through the addition of relatively small (i.e., fewer than hundreds) targeted compound libraries to the training data. We suggest that this may indicate some level of model generalization according to molecular substitution patterns around the site of dissociation, such that only a few examples of new bond types are required. This suggests that relatively small, focused datasets can be used to continually expand the scope of this, and other GNN-based models for property predictions.

Data availability

The BDE-db2, dataset is hosted on FigShare at https://doi.org/10.6084/m9.figshare.19367051.v1. Other training and test data can be found in the GitHub repository (https://github.com/patonlab/bde-db2).

Conflicts of interest

The authors have no conflicts of interest to disclose.

Acknowledgements

This work was supported by the National Science Foundation under the NSF Center for Computer-Assisted Synthesis (C-CAS), grant number CHE–2202693. RSP and SVSS acknowledge the Alpine high performance computing resource at the University of Colorado Boulder, jointly funded by the University of Colorado Boulder, the University of Colorado Anschutz, Colorado State University, and the National Science Foundation (award 2201538), and the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) through allocation TG-CHE180056. This work was authored in part by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the US Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. The US Government retains and the publisher, by accepting the article for publication, acknowledges that the US Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work or allow others to do so, for US Government purposes.

References

1. A. W. Hill and R. J. Mortishire-Smith, Automated assignment of high-resolution collisionally activated dissociation mass spectra using a systematic bond disconnection approach, Rapid Commun. Mass Spectrom., 2005, 19, 3111–3118.
2. S. J. Blanksby and G. B. Ellison, Bond dissociation energies of organic molecules, Acc. Chem. Res., 2003, 36, 255–263.
3. Y. Garcia, F. Schoenebeck, C. Y. Legault, C. A. Merlic and K. N. Houk, Theoretical bond dissociation energies of halo-heterocycles: trends and relationships to regioselectivity in palladium-catalyzed cross-coupling reactions, J. Am. Chem. Soc., 2009, 131, 6632–6639.
4. O. I. Obolensky, W. W. Wu, R.-F. Shen and Y.-K. Yu, Using dissociation energies to predict observability of b- and y-peaks in mass spectra of short peptides, Rapid Commun. Mass Spectrom., 2012, 26, 915–920.
5. S. Kim, S. C. Chmely, M. R. Nimlos, Y. J. Bomble, T. D. Foust, R. S. Paton and G. T. Beckham, Computational Study of bond dissociation enthalpies for a large range of native and modified lignins, J. Phys. Chem. Lett., 2011, 2, 2846–2852.
6. S. V. Shree Sowndarya, P. C. St. John and R. S. Paton, A quantitative metric for organic radical stability and persistence using thermodynamic and kinetic features, Chem. Sci., 2021, 12, 13158–13166.
7. S. V. Shree Sowndarya, J. N. Law, C. E. Tripp, D. Duplyakin, E. Skordilis, D. Biagioni, R. S. Paton and P. C. St. John, Multi-objective goal-directed optimization of de novo stable organic radicals for aqueous redox flow batteries, Nat. Mach. Intell., 2022, 4, 720–730.
8. M. Szwarc, The Determination of bond dissociation energies by pyrolytic methods, Chem. Rev., 1950, 47, 75–173.
9. Y. Fu, L. Liu, Y.-M. Wang, J.-N. Li, T.-Q. Yu and Q.-X. Guo, Quantum-chemical predictions of redox potentials of organic anions in dimethyl sulfoxide and reevaluation of bond dissociation enthalpies measured by the electrochemical methods, J. Phys. Chem. A, 2006, 110, 5874–5886.
10. M. Koerstz, M. H. Rasmussen and J. H. Jensen, Fast and automated identification of reactions with low barriers: the decomposition of 3-hydroperoxypropanal, SciPost Chem, 2021, 1, 003.
11. Y. Zhao and D. G. Truhlar, How well can new-generation density functionals describe the energetics of bond-dissociation reactions producing radicals?, J. Phys. Chem. A, 2008, 112, 1095–1099.
12. J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, A complete basis set model chemistry. VI. Use of density functional geometries and frequencies, J. Chem. Phys., 1999, 110, 2822–2827.
13. N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115, 2315–2372.
14. P. C. St. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Prediction of organic homolytic bond dissociation enthalpies at near chemical accuracy with sub-second computational cost, Nat. Commun., 2020, 11, 2328.
15. N. Q. Trung, A. Mechler, N. T. Hoa and Q. V. Vo, Calculating bond dissociation energies of X−H (X=C, N, O, S) bonds of aromatic systems via density functional theory: a detailed comparison of methods, R. Soc. Open Sci., 2022, 9, 220177.
16. H. Yu, Y. Wang, X. Wang, J. Zhang, S. Ye, Y. Huang, Y. Luo, E. Sharman, S. Chen and J. Jiang, Using machine learning to predict the dissociation energy of organic carbonyls, J. Phys. Chem. A, 2020, 124, 3844–3850.
17. X. Qu, D. A. Latino and J. Aires-De-Sousa, A big data approach to the ultra-fast prediction of DFT-calculated bond energies, J. Cheminform., 2013, 5, 34.
18. C. X. Xue, R. S. Zhang, H. X. Liu, X. J. Yao, M. C. Liu, Z. D. Hu and B. T. Fan, An accurate QSPR study of O–H bond dissociation energy in substituted phenols based on support vector machines, J. Chem. Inf. Comput. Sci., 2004, 44, 669–677.
19. B. Zulueta, S. V. Tulyani, P. R. Westmoreland, M. J. Frisch, E. J. Petersson, G. A. Petersson and J. A. Keith, A bond-energy/bond-order and populations relationship, J. Chem. Theory Comput., 2022, 18, 4774–4794.
20. J. J. Irwin, T. Sterling, M. M. Mysinger, E. S. Bolstad and R. G. Coleman, ZINC: a free tool to discover chemistry for biology, J. Chem. Inf. Model., 2012, 52, 1757–1768.
21. R. A. E. Carr, M. Congreve, C. W. Murray and D. C. Rees, Fragment-based lead discovery: leads by design, Drug Discov. Today, 2005, 10, 987–992.
22. P. St. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, BDE-db: A collection of 290,664 Homolytic Bond Dissociation Enthalpies for Small Organic Molecules, FigShare, 2019,  DOI:10.6084/m9.figshare.10248932.v1.
23. P. C. St. John, Y. Guan, Y. Kim, B. D. Etz, S. Kim and R. S. Paton, Quantum chemical calculations for over 200,000 organic radical species and 40,000 associated closed-shell molecules, Sci. Data, 2020, 7, 244.
24. Internet Bond-energy Databank (pKa and BDE)—iBonD Home Page, 2022, https://ibond.nankai.edu.cn/.
25. V. K. Prasad, M. H. Khalilian, A. Otero-de-la-Roza and G. A. DiLabio, BSE49, a diverse, high-quality benchmark dataset of separation energies of chemical bonds, Sci. Data, 2021, 8, 300.
26. B. R. Smith, C. M. Eastman and J. T. Njardarson, Beyond C, H, O, and N! analysis of the elemental composition of U.S. FDA approved drug architectures, J. Med. Chem., 2014, 57, 9764–9773.
27. S. Kozuch and J. M. L. Martin, Halogen bonds: benchmarks and theoretical analysis, J. Chem. Theory Comput., 2013, 9, 1918–1931.
28. A. Forni, S. Pieraccini, S. Rendine and M. Sironi, Halogen bonds with benzene: an assessment of DFT functionals, J. Comput. Chem., 2014, 35, 386–394.
29. A. Siiskonen and A. Priimagi, Benchmarking DFT methods with small basis sets for the calculation of halogen-bond strengths, J. Mol. Model., 2017, 23, 50.
30. S. Xu, Q.-D. Wang, M.-M. Sun, G. Yin and J. Liang, Benchmark calculations for bond dissociation energies and enthalpy of formation of chlorinated and brominated polycyclic aromatic hydrocarbons, RSC Adv., 2021, 11, 29690–29701.
31. J. M. Simmie and K. P. Somers, Snakes on the rungs of Jacob's Ladder: anomalous vibrational spectra from double-hybrid DFT methods, J. Phys. Chem. A, 2020, 124, 6899–6902.
32. P. C. St. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Prediction of organic homolytic bond dissociation enthalpies at near chemical accuracy with sub-second computational cost, Nat. Commun., 2020, 11(1), 1–12.
33. S. Riniker and G. A. Landrum, Better informed distance geometry: using what we know to improve conformation generation, J. Chem. Inf. Model., 2015, 55, 2562–2574.
34. Y. Zabolotna, D. M. Volochnyuk, S. V. Ryabukhin, D. Horvath, K. S. Gavrilenko, G. Marcou, Y. S. Moroz, O. Oksiuta and A. Varnek, A close-up look at the chemical space of commercially available building blocks for medicinal chemistry, J. Chem. Inf. Model., 2022, 62, 2171–2185.
35. O. O. Grygorenko, D. M. Volochnyuk and B. V. Vashchenko, Emerging building blocks for medicinal chemistry: recent synthetic advances, Eur. J. Org Chem., 2021, 2021, 6478–6510.
36. T. Kalliokoski, Price-focused analysis of commercially available building blocks for combinatorial library synthesis, ACS Comb. Sci., 2015, 17, 600–607.
37. C. J. Helal, M. Bundesmann, S. Hammond, M. Holmstrom, J. Klug-McLeod, B. A. Lefker, D. McLeod, C. Subramanyam, O. Zakaryants and S. Sakata, Quick building blocks (QBB): an innovative and efficient business model to speed medicinal chemistry analog synthesis, ACS Med. Chem. Lett., 2019, 10, 1104–1109.
38. Y. Zabolotna, D. M. Volochnyuk, S. V. Ryabukhin, D. Horvath, K. S. Gavrilenko, G. Marcou, Y. S. Moroz, O. Oksiuta and A. Varnek, A close-up look at the chemical space of commercially available building blocks for medicinal chemistry, J. Chem. Inf. Model., 2021, 2171–2185.
39. Enamine Functional Classes: Alkyl Halides, 2020, https://enamine.net/building-blocks/functional-classes/alkyl-halides.
40. Enamine Functional Classes: Aryl Halides, 2020, https://enamine.net/building-blocks/functional-classes/aryl-halides.
41. J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A quantitative uncertainty metric controls error in neural network-driven chemical discovery, Chem. Sci., 2019, 10, 7913–7922.
42. (a) L. C. Gallegos, G. Luchini, P. C. St. John, S. Kim and R. S. Paton, Importance of engineered and learned molecular representations in predicting organic reactivity, selectivity, and chemical properties, Acc. Chem. Res., 2021, 54, 827–836; (b) This would of course not be a practical approach for rapid BDE prediction; rather, we performed this analysis to see whether the learned embeddings were optimal or could be further improved through the addition of expensive DFT-level features..
43. J. Shi, J. He and H.-J. Wang, A computational study of C–X (X = H, C, F, Cl) bond dissociation enthalpies (BDEs) in polyhalogenated methanes and ethanes, J. Phys. Org. Chem., 2011, 24, 65–73.
44. M. F. Carvalho and R. S. Oliveira, Natural production of fluorinated compounds and biotechnological prospects of the fluorinase enzyme, Crit. Rev. Biotechnol., 2017, 37, 880–897.
45. J. Zeng and J. Zhan, Chlorinated natural products and related halogenases, Isr. J. Chem., 2019, 59, 387–402.
46. C. Cooksey, Tyrian purple: 6,6′-dibromoindigo and related compounds, Molecules, 2001, 6, 736–769.
47. A. C. Bianco, D. Salvatore, B. Z. Gereben, M. J. Berry and P. R. Larsen, Biochemistry, cellular and molecular biology, and physiological roles of the iodothyronine selenodeiodinases, Endocr. Rev., 2002, 23, 38–89.
48. Y. R. Luo, Bond disassociation energies, in CRC handbook of Chemistry and Physics, CRC press, Boca Raton, 2002.
49. A. Raza, S. Bardhan, L. Xu, S. S. R. K. C. Yamijala, C. Lian, H. Kwon and B. M. Wong, A machine learning approach for predicting defluorination of per- and polyfluoroalkyl substances (PFAS) for their efficient treatment and removal, Environ. Sci. Technol. Lett., 2019, 6, 624–629.
50. D. Kurniawan, H. Arai, S. Morita and K. Kitagawa, Chemical degradation of Nafion ionomer at a catalyst interface of polymer electrolyte fuel cell by hydrogen and oxygen feeding in the anode, Microchem. J., 2013, 106, 384–388.

---

Footnote

† Electronic supplementary information (ESI) available: All datasets containing computed and experimental BDE and BDFE values and the final GNN model for ALFABET can be found in the open-access GitHub repository (https://github.com/patonlab/bde-db2). See DOI: https://doi.org/10.1039/d3dd00169e

---